Open Access Article
Open Access ArticleMeta-stability through intermolecular interactions protecting the identity of atomic metal clusters: ab initio evidences in (Cu5–Cu5)n (n < 3) cases†
Berta
Fernández
 *a and
María Pilar
de Lara-Castells
*a and
María Pilar
de Lara-Castells
 *b
*b
aDepartment of Physical Chemistry, University of Santiago de Compostela, E-15782 Santiago de Compostela, Spain. E-mail: berta.fernandez@usc.es
bInstitute of Fundamental Physics (AbinitSim Unit), Consejo Superior de Investigaciones Científicas (CSIC), E-28006 Madrid, Spain. E-mail: Pilar.deLara.Castells@csic.es
First published on 21st October 2022
Abstract
Recent developments in new synthesis techniques have allowed the production of precise monodisperse metal clusters composed of a few atoms. These atomic metal clusters (AMCs) often feature a molecule-like electronic structure, which makes their physical and chemical properties particularly interesting in nanotechnology. Regarding potential applications, there is a major concern about the sintering of AMCs in nanoparticles due to the loss of their special properties. In this work, multireference ab initio theory is applied to demonstrate the formation of coupled AMC–AMC clusters in which the AMC partners maintain their ‘identity’ to a large extent in terms of their initial structures and atomic Mulliken charges, and their further oligomerization.
1 Introduction
Recent developments of highly selective experimental techniques enabling the synthesis of subnanometer metal clusters are pushing the understanding of these, more “molecular” than “metallic”, systems far beyond the present knowledge in materials science. In this way, when the atomic metal cluster (AMC) size is reduced to a small (less than 10) number of atoms, high stability and novel properties are achieved, that allow the AMC integration into materials. Additionally, interaction with the environment has the potential to boost the performance in applications particularly interesting in nanotechnology, including luminescence, sensing, bioimaging, theranostics, energy conversion, catalysis, and photocatalysis (see, e.g., ref. 1 and 2 for recent reviews). From a more fundamental point of view, it has also been shown how modification of popular materials such as TiO2 with AMCs can convert them into “reporters” of fundamental surface polaron properties.3–5 From the microscopic point of view, the above behaviour is explained in terms of the d-band of the metal splitting into a subnanometric network of discrete molecule-like d orbitals, with fluxional inter-connections having the length of a chemical bond (1–2 Å). The spatial structures of these molecular orbitals make all the metal atoms cooperatively active and accessible and confer molecular characteristics to the complexes, that are responsible of their stability and properties.Among the different AMCs, copper clusters have attracted much attention as catalysts6 since they have shown important catalytic properties e.g. for the oxidation of CO,7,8 the selective hydrogenation of olefin and carbonyl groups,9,10 and in C–X (being X = C, N, S, P) bond forming reactions.11 The oxidative dehydrogenation of cyclohexene on atomically precise subnanometer bimetallic Cu–Pd (tetramer) clusters is also worth mentioning.12 Moreover, the work in ref. 13 showed an outstanding chemical and thermodynamical stability of atomic copper clusters in solution over the whole pH range. First-principles modelling, including methods beyond the state-of-the-art and an interplay with cutting-edge experiments, is helping to understand the special properties of AMCs at the most fundamental molecular level. Thus, the use of first-principles methods has disclosed the fundamental reasons why Cu5 clusters experience a reversible oxidation,14 and are capable of increasing and extending into the visible region the solar absorption of TiO2,15 also considering the decomposition and photo-activation of CO2 as a prototypical (photo-)catalytic reaction.16
In spite of their potential applications, there is a major concern about the sintering of AMCs in metallic nanoparticles with the consequent loss of their special properties. In order to analyze the possible existence of metastable states in which Cu5 preserves its identity, multireference Rayleigh Schrödinger (second-order) perturbation theory17 (RS2C) is applied here, allowing evidence of the formation and further oligomerization of coupled Cu5–Cu5 clusters at a high level of ab initio theory. It should be stressed that in our work preservation of identity at a molecular level encompasses a concept considerably broader than just aggregation by weak (dispersion-dominated) van der Waals (vdW) forces. It also includes the formation of covalent bonds between molecular sub-units, yet conserving their initial structures and, to a large extent, their atomic charge distributions.
2 Results and discussion
We optimized the Cu5 cluster geometries in vacuum, their two main geometrical arrangements are shown in Fig. 1 (top panel): a planar trapezoidal two-dimensional (2D) structure with a spin quantum number equal to 1/2 and a trigonal bipyramidal tri-dimensional (3D) arrangement with spin equal to 3/2. In agreement with previous studies (see, e.g., ref. 11 and 18), the 2D structure is the most stable configuration by 0.6–0.7 eV (see Table 1). It can also be observed in Table 1 that the relative energies calculated at coupled-cluster and multireference perturbation levels of theory, using the largest active space, differ by less than 0.1 eV, thus indicating the accuracy of the latter.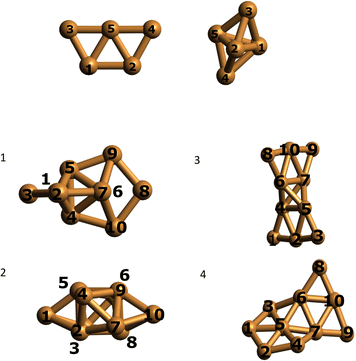 | ||
| Fig. 1 Optimized structures of individual Cu5 clusters (at the CCSD/Def2-TZVP level above) and coupled Cu5–Cu5 clusters (at the CAS(10,10)/cc-pVTZ-PP level below) in vacuum. Atom numbering included. | ||
| Cu5 | 2S + 1 | CCSD | RS2C(5,5) | RS2C(7,7) |
|---|---|---|---|---|
| Planar (Min) | 2 | 0 | 0 | 0 |
| Planar (TS) | 4 | 2.0 | 2.0 | 2.0 |
| Bipyramidal (TS) | 2 | 0.3 | 0.2 | 0.3 |
| Bipyramidal (Min) | 4 | 0.7 | 0.5 | 0.6 |
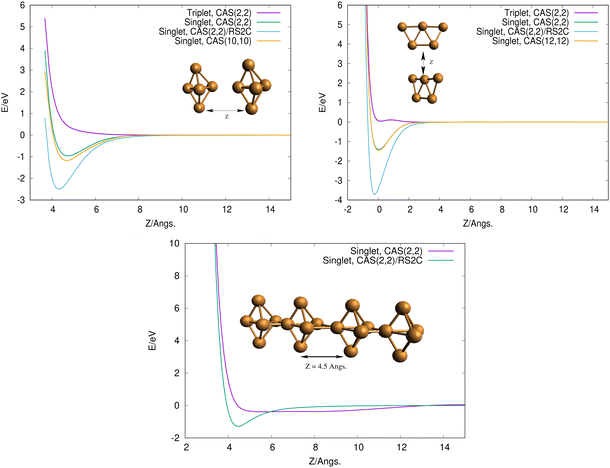
To get some insights on how 3D and 2D Cu5 clusters interact as a function of their relative distances, we evaluated interaction energies keeping the intramolecular geometries fixed at the optimized values (see Fig. 2, top panels). Interestingly, for both structures, the interaction is repulsive in the triplet spin state but it becomes strongly attractive (by a few eV) in the singlet spin state. This outcome can be explained by considering that unpaired electrons occupying s-type orbitals on the two Cu5 clusters feature repulsion/attraction to each other in parallel/anti-parallel spin configurations, producing repulsive/attractive inter-molecular interactions, as is the case for the interaction between two hydrogen atoms. It can also be observed that the attractive interaction is significantly enhanced when dynamical correlation is accounted for using the RS2C method (see the Appendix for the computational details). Interestingly, the interaction energies are hardly modified when the CASSCF space is enlarged from a minimal (2,2) space (2 electrons in 2 orbitals) to larger spaces (see Fig. 2, top panels).
Using the computational strategy described in the Appendix, the structures of coupled Cu5–Cu5 clusters shown in the middle and bottom panels of Fig. 1 have been obtained. The corresponding interaction energies are indicated in Table 2 at both multiconfigurational (referred to as DF-CASSCF) and multireference Rayleigh Schrödinger (second-order), internally contracted, perturbation levels of theory (denoted RS2C). With the exception of the structure labeled as ‘4’,19 note that the increase of the active space from that considering 10 electrons in 10 active orbitals [denoted as (10,10)] to that including 12 electrons in 12 active orbitals [referred to as (12,12)] modifies the energies up to 0.2 eV when dynamical correlation is not accounted for, while the consideration of the latter makes the interaction energies almost identical for both active spaces. It should be mentioned that the inclusion of the dynamical correlation with RS2C is crucial, accounting for ca. 70% of the attractive Cu5–Cu5 interaction in cluster 1 (−5.2 eV, see Table 2). This value agrees well with that obtained using the natural orbital coupled-cluster approach DLPNO-CCSD(T)20 (−4.9 eV from ref. 21). The good agreement with the interaction energy and structure of the lowest-energy isomer obtained with the DFT-D4 ansatz (−5.4 eV from ref. 21) is also worth-mentioning. A similar coupled Cu5–Cu5 structure is also predicted to be more stable at the DFT-D4 level. Moreover (see Table S2 of the ESI†), the average values of the Cu–Cu bond lengths for the Cu5 partners (2.5 Å) are in between those obtained through the DF-CASSCF and the RS2C optimizations (2.7 and 2.4 Å, respectively). It should also be considered that we are dealing with fluxional clusters bearing wide amplitude Cu–Cu motions (see below). For instance, an ab initio molecular dynamics simulation21 has shown that the values of Cu–Cu distances in circumpyrene-supported Cu5–(O2)4 at 473 K experience large fluctuations (within 0.5 Å).
| Cu5–Cu5 | DF-CAS(10,10)/RS2C | DF-CAS(12,12)/RS2C |
|---|---|---|
| 1 (Min) | −1.5/−5.2 | −1.6/−5.2 |
| 2 (Min) | −1.5/−5.0 | −1.7/−5.0 |
| 3 (Min) | −1.8/−2.3 | −1.7/−2.3 |
| 4 (Min) | −1.4/−3.3 | −2.3/−2.8 |
| 5 (TS) | −1.3/−4.7 | −1.5/−4.7 |
In contrast to the case of isolated Cu5 clusters, for which the 2D structures are energetically favored, it can be observed in Table 2 that the most stable (by ca. 2 eV) arrangements of coupled Cu5–Cu5 clusters correspond to coupled 3D structures. This structure (of D2d symmetry) is similar to that reported in ref. 18 for Cu10. The inclusion of dynamical correlation is clearly responsible for such behaviour. In fact, without considering it, the interaction energies are up to 0.7 eV more attractive upon the coupling of planar 2D structures than in the case of coupled 3D geometries.
We performed a Mulliken charge analysis of natural orbitals for both isolated Cu5 and coupled Cu5–Cu5 clusters using the geometries optimized at the DF-CASSCF level (see Table 3). Note that Mulliken charges are larger in the 3D Cu5 structure than in the 2D Cu5 structure. As a result, the electrostatic contribution to the Cu5–Cu5 intermolecular interaction is favored when 3D Cu5 clusters become coupled to each other. Most importantly, the values of Mulliken charges on all Cu atoms are (within numerical accuracy) the same for the two Cu5 clusters within Cu5–Cu5 in clusters 1 and 3, leading to a symmetric structure of the complex with respect to the two Cu5 units. It is remarkable that, in spite of being strongly bound (interaction Cu5–Cu5 energies of −5.2 eV using the RS2C method on geometries optimized at the DF-CASSCF level), the two Cu5 clusters maintain their spatial arrangements in a symmetric way. Moreover, although the charge distributions in the coupled structures are not identical to those in isolated clusters, their modification is relatively modest on DF-CASSCF-based optimized structures. For the 3D structure of isolated Cu5, atomic Mulliken charges vary in between −0.07 and 0.10 a.u., while in the lowest-energy Cu5–Cu5 structure found in this study, they range from −0.11 to 0.16 a.u. These modifications can be understood on the basis of polarization effects causing a higher electron localization on the peripheral, lower coordinated Cu atoms. The preservation of 3D and 2D Cu5 structures in some of the coupled Cu5–Cu5 clusters is also clear in Fig. 1, being more evident in the case of the 2D geometries (see also Fig. S1 in the ESI†). Altogether, these outcomes indicate the protection of the identity of the Cu5 partners, yet in a way differing significantly from that characterizing weakly bound van der Waals aggregates. Thus, recently, it has been shown that, upon heating, the Cu5 sub-units of coupled Cu5–Cu5ne structures experience a decoupling through fluxional rotational motion but none spatial separation,21 in contrast to the case of vdW aggregates. Additionally, upon exposition to environmental O2 molecules, a high oxygen gas pressure is necessary to achieve the individualization of Cu5 sub-units.21
| Individual Cu5 clusters | ||
|---|---|---|
| Label | 2D (Min) | 3D (Min) |
| 1 | –0.02 | –0.07 (–0.06) |
| 2 | –0.03 | –0.07 (–0.06) |
| 3 | 0.01 | 0.10 (0.10) |
| 4 | 0.01 | 0.10 (0.10) |
| 5 | 0.03 | –0.07 (–0.06) |
| Coupled Cu5–Cu5 clusters | ||||
|---|---|---|---|---|
| Label | 1 (Min) | 2 (Min) | 3 (Min) | 4 (Min) |
| 1 | −0.11 | −0.14 | 0.15 | −0.04 |
| 2 | −0.11 | 0.10 | −0.21 | −0.06 |
| 3 | −0.10 | 0.04 | 0.15 | −0.01 |
| 4 | 0.16 | −0.28 | −0.05 | 0.01 |
| 5 | 0.16 | 0.28 | −0.04 | 0.09 |
| 6 | 0.16 | −0.27 | −0.04 | 0.02 |
| 7 | 0.16 | 0.03 | −0.05 | 0.01 |
| 8 | −0.10 | 0.09 | 0.15 | 0.02 |
| 9 | −0.11 | 0.29 | 0.15 | 0.01 |
| 10 | −0.11 | −0.14 | −0.21 | −0.06 |
It is interesting to note that the energy difference between structures 1 and 2 in Fig. 1 is just 0.2 eV (see Table 2). Hence, the interconversion between them can be expected to be reversible. Although the potential energy landscape of Cu5–Cu5 clusters has been carefully explored (see Appendix), many local minima with similar energies could co-exist with those found in this work. The existence of many meta-stable states bearing very close energies is a typical feature characterizing atomic metal clusters due to their fluxional nature and associated wide amplitude inter-atomic motions. The concept of structural fluxionality has recently been advocated to explain the catalytic activity of AMCs (see, e.g., ref. 1, 16, 22 and 23). The occurrence of fluxional dynamics has also been suggested from recent spectroscopic observations.24 Recent ab initio molecular dynamics simulations have also shown the fluxional rotational motion between the two Cu5 units of the coupled Cu5–Cu5 clusters upon heating.21
Finally, to get some insight into the interaction between two coupled Cu5–Cu5 clusters, we evaluated the interaction energy as a function of their relative distance (see the bottom panel in Fig. 2). As expected from the closed-shell nature of the coupled clusters, the attractive interaction is extremely weak when the dynamical correlation is not accounted for. In contrast, the two coupled clusters become strongly bound (by ca. 2 eV) when the latter is included through the multireference RS2C perturbation method. Thus, the formation of covalent bonds between the clusters is clearly apparent in the minimum (see inset in the bottom panel of Fig. 2). The electrostatic contribution is expected to be responsible for the strong interaction between Cu5 clusters, ultimately giving rise to their oligomerization. It can be expected that more stable structures might exist, even implying the sintering in a Cu20 structure in which the Cu5 clusters have lost their identity. However, it should be stressed that the existence of many metastable states of fluxional, but strongly bound, oligomers might quench such structural re-arrangements at experimentally relevant ranges of temperature. In this sense, it is worth pointing out that the individualization of Cu5 clusters at certain conditions of oxygen pressure and temperature has been recently suggested, particularly in an O2-rich environment.21
3 Conclusions
In the quest for a fundamental level understanding of the outstanding stability experimentally probed for AMCs such as Cu5,13 we have explored the possibility that AMCs couple to each other in such a way that their initial structures are preserved and, although their initial charge distributions experience modifications due to polarization effects, initial charge patterns can yet be recognized in the combined clusters. This concept of ‘identity’ thus goes beyond the classical concept of preservation of identity through the formation of vdW aggregates. In this work, we have found clear ab initio evidences on the favored coupled cluster formation and oligomerization of Cu5 clusters in such a way that the Cu5 units to a large extent keep their identity in terms of their structures. This outcome is reflected in the geometrical arrangements and in the Mulliken charge analyses of the resulting electronic structures. Additionally, the existence of metastable states of coupled Cu5 clusters bearing very close energies has been found and can be interpreted as a consequence of the cluster fluxional nature. Our results could be valuable in the interpretation of experimental spectroscopic measurements of the (photo-)catalytic activities of atomic metal clusters, calling for high-resolution scanning electron microscopic probes on the formation of coupled clusters and their further oligomerization. From a theoretical perspective, additional work is necessary to analyze the concept of oligomerization of AMCs, including, e.g., molecular dynamics simulations on surface-supported AMCs as a function of temperature and even stronger tests using different methods at high level ab initio theory, including some that allow an analysis of interaction energy contributions.Author contributions
Both co-authors have contributed equally to the manuscript in all the required steps (investigation, writing and editing). All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Appendix
Computational methods and additional details
Density fitting single-state multi-configurational self-consistent-field (DF-CASSCF) calculations have been carried out, as implemented in the last version of the MOLPRO code.25 We used the polarized correlation-consistent triple-ζ cc-pVTZ-PP basis set for copper atoms,26 including a small (10-valence-electron) relativistic pseudopotential. The DF-CASSCF approach is employed to account for the most important non-dynamical correlation effects. Then, the internally contracted multireference Rayleigh Schrödinguer (second-order) perturbation theory RS2C method17 has been applied to cover dynamical correlation effects. The RS2C method is basically a modified version of CASPT2 (complete active space with second-order perturbation theory) developed by Celani and Werner,17 using CASSCF wave functions as a reference in the RS2C calculations. For complex 1 of the coupled Cu5–Cu5 clusters, the CASSCF wave functions comprise up to 226![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 configuration state functions (CFSs). The subsequent RS2C wave function consists of 700 × 106 contracted CSFs. The RS2C method thus allows the use of reference wave functions with large active spaces and internally contracted configurations are used as a basis. For density fitting, the associated MP2FIT and JKFIT bases have been used in DF-CASSCF calculations. The diagonalization of the first-order reduced density matrix obtained from the wave function in DF-CASSCF calculations allowed us to obtain natural orbitals. An analysis of the Mulliken charges27 was accomplished for both Cu5 and Cu5–Cu5 clusters. Additionally, for the sake of comparison, Coupled Cluster Singles and Doubles (CCSD) calculations have been carried out as implemented in the GAUSSIAN 09 code.28
512 configuration state functions (CFSs). The subsequent RS2C wave function consists of 700 × 106 contracted CSFs. The RS2C method thus allows the use of reference wave functions with large active spaces and internally contracted configurations are used as a basis. For density fitting, the associated MP2FIT and JKFIT bases have been used in DF-CASSCF calculations. The diagonalization of the first-order reduced density matrix obtained from the wave function in DF-CASSCF calculations allowed us to obtain natural orbitals. An analysis of the Mulliken charges27 was accomplished for both Cu5 and Cu5–Cu5 clusters. Additionally, for the sake of comparison, Coupled Cluster Singles and Doubles (CCSD) calculations have been carried out as implemented in the GAUSSIAN 09 code.28
Initial optimizations of the coupled Cu5–Cu5 cluster geometries were performed at PBE and B3LYP levels,29,30 using D4 Grimme's parameterization31 to account for the dispersion correction. An excellent performance has been achieved with the predecessor PBE-D3(BJ) ansatz32 in describing both supported and unsupported subnanometer silver3,33 and copper16,34 clusters. We used the atom-centered Def2-SVP35 basis set for copper atoms. All dispersion-corrected DFT-based calculations have been performed with the ORCA suite of programs (version 5.0.1).36–38
We started our coupled Cu5–Cu5 cluster calculations with a bipyramidal arrangement for the Cu5 sub-unit. In this way, we placed together two trigonal bypiramidal arrangements with the center of mass of one of them located in the origin of the coordinate system and the corresponding main symmetry axis along the Z axis. The position of the second Cu5 molecule with respect to the first one was modified in a range of distances and orientations. For this, we varied the distance between the two centers of mass along each of the axes, making it equal to 4.0, 5.0 and 6.0 Å for X, 6.0 and 7.0 Å for Y, and 7.0 and 8.0 Å for displacements along the Z-axis. Regarding the angles we considered three rotations for each of the geometries, i.e. the first one around the X-axis and with values of 0, 60, and 90 degrees; the second one around the Z axis, taking angles of 0, 45, and 90 degrees; and the last one around the X axis and with values of 0, 60, 120, 180, 240, 300, 360 degrees. The resulting geometries were fully optimized at the dispersion-corrected DFT levels, and those corresponding to the lowest energies were selected for further optimizations through DF-CASSCF calculations. The active spaces in DF-CASSCF calculations [m electrons in m orbitals, referred as (m,m) active space] varied until convergence was achieved in the follow-up RS2C calculations of coupled Cu5–Cu5 cluster energies. In all cases we considered the singlet ground state of the clusters and no symmetry restrictions were imposed in the calculations. The results of the preliminary DFT calculations can be obtained from the authors upon request. Results on previous theoretical evaluations of copper cluster geometries are available in the literature, see for instance ref. 39 and 40, but as far as we are aware, the authors of these investigations applied DFT level and not multireference ab initio approaches, with the resulting geometries differing from those obtained in this work. All interaction energies (Einter) were calculated as follows:
| Einter = {ECu5–Cu5}Min − {ECu5–Cu5}Asymp |
Acknowledgements
We thank Lyudmila Moskaleva, Alexander O. Mitrushchenkov, and Alexander Zanchet for very useful discussions. This work has been partly supported by the Spanish Agencia Estatal de Investigación (AEI) under Grant No. PID2020-117605GB-I00. This publication is also based upon work of COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology). We are also greatly thankful for the support of the EU Doctoral Network PHYMOL 101073474 (project call reference HORIZON-MSCA-2021-DN-01. One of the authors (B. F.) acknowledges Xunta de Galicia (grant number ED431C 2021/40) for further financial support. The CESGA supercomputer center (Spain) is acknowledged for having provided the computational resources. We also acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).Notes and references
- M. P. de Lara-Castells, J. Colloid Interface Sci., 2022, 612, 737–759 CrossRef CAS.
- J. Juraj, A. Fortunelli and S. Vajda, Phys. Chem. Chem. Phys., 2022, 24, 12083–12115 RSC.
- P. López-Caballero, J. M. Ramallo-López, L. J. Giovanetti, D. Buceta, S. Miret-Artés, M. A. López-Quintela, F. G. Requejo and M. P. de Lara-Castells, J. Mater. Chem. A, 2020, 8, 6842–6853 RSC.
- P. López-Caballero, S. Miret-Artés, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Chem. Phys., 2020, 153, 164702 CrossRef.
- M. P. de Lara-Castells and S. Miret-Artés, Europhys. News, 2022, 53, 7–9 CrossRef.
- P. Concepción, M. Boronat, S. García-García, E. Fernández and A. Corma, ACS Catal., 2017, 7, 3560–3568 CrossRef.
- A. Halder, L. A. Curtiss, A. Fortunelli and S. Vajda, J. Chem. Phys., 2018, 148, 110901 CrossRef.
- S. Hirabayashi and M. Ichihashi, Phys. Chem. Chem. Phys., 2014, 16, 26500–26505 RSC.
- B. Yang, C. Liu, A. Halder, E. C. Tyo, A. B. F. Martinson, S. Seifert, P. Zapol, L. A. Curtiss and S. Vajda, J. Phys. Chem. C, 2017, 121, 10406–10412 CrossRef CAS.
- P. Maity, S. Yamazoe and T. Tsukuda, ACS Catal., 2013, 3, 182–185 CrossRef CAS.
- J. Oliver-Messeguer, L. Liu, S. García-García, C. Canós-Giménez, I. Domínguez, R. Gavara, A. Doménech-Carbó, P. Concepción, A. Leyva-Pérez and A. Corma, J. Am. Chem. Soc., 2015, 137, 3894–3900 CrossRef PubMed.
- J. Jašik, S. Valtera, M. Vaidulych, M. Bunian, Y. Lei, A. Halder, H. Tarábková, M. Jindra, L. Kavan, O. Frank, S. Bartling and S. Vajda, Faraday Discuss., 2022 10.1039/D2FD00108J.
- S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908 CrossRef CAS.
- D. Buceta, S. Huseyinova, M. Cuerva, H. Lozano, L. J. Giovanetti, J. M. Ramallo-López, P. Lóopez-Caballero, A. Zanchet, A. O. Mitrushchenkov, A. W. Hauser, G. Barone, C. Huck-Iriart, C. Escudero, J. C. Hernández-Garrido, J. Calvino, M. Lopez-Haro, M. P. de Lara-Castells, F. G. Requejo and M. A. López-Quintela, ChemRxiv, 2021, preprint DOI:10.26434/chemrxiv.13661081.v1.
- M. P. de Lara-Castells, A. W. Hauser, J. M. Ramallo-López, D. Buceta, L. J. Giovanetti, M. A. López-Quintela and F. G. Requejo, J. Mater. Chem. A, 2019, 7, 7489–7500 RSC.
- P. López-Caballero, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 23064–23074 CrossRef PubMed.
- P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557 CrossRef CAS.
- A. S. Chaves, G. G. Rondina, M. J. Piotrowski, P. Tereshchuk and J. L. F. Da Silva, J. Phys. Chem. A, 2014, 118, 10813–10821 CrossRef CAS PubMed.
- Dynamical correlation contributions associated to state ‘4’ are found to be rather dependent on the geometry. In this way, when the geometry optimized with the (12,12) space at DF-CASSCF level is used in the RS2C calculation with the (10,10) space, the resulting energy (−2.9 eV) differs by just 0.1 eV from that obtained considering the (12,12) space at RS2C level (−2.8 eV, see Table 2 of the main manuscript).
- A. Kubas, D. Berger, H. Oberhofer, D. Maganas, K. Reuter and F. Neese, J. Phys. Chem. Lett., 2016, 7, 4207–4212 CrossRef CAS PubMed.
- J. Garrido-Aldea and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2022, 24, 24810–24822 RSC.
- H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911 CrossRef CAS.
- Q.-Y. Fan, Y. Wang and J. Cheng, J. Phys. Chem. Lett., 2021, 12, 3891–3897 CrossRef CAS PubMed.
- O. V. Lushchikova, H. Tahmasbi, S. Reijmer, R. Platte, J. Meyer and J. M. Bakker, J. Phys. Chem. A, 2021, 125, 2836–2848 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS.
- D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1962, 36, 3428–3439 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.1, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem. Lett., 1994, 98, 11623–11627 CAS.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. P. de Lara-Castells, C. Cabrillo, D. A. Micha, A. O. Mitrushchenkov and T. Vazhappilly, Phys. Chem. Chem. Phys., 2018, 20, 19110–19119 RSC.
- S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- U. J. Rangel-Peña, R. L. Camacho-Mendoza, S. González-Montiel, L. Feria and J. Cruz-Borbolla, J. Cluster Sci., 2021, 32, 1155–1173 CrossRef.
- P. Jaque and A. Toro-Labbé, J. Chem. Phys., 2002, 117, 3208–3218 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of optimized structures appearing in Fig. 1, complex 1 structure and charges, Cu–Cu distance Table. See DOI: https://doi.org/10.1039/d2cp03537e |
| This journal is © the Owner Societies 2022 |