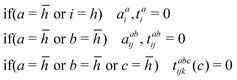Accurate core excitation and ionization energies from a state-specific coupled-cluster singles and doubles approach†
Juan E.
Arias-Martinez
 *ab,
Leonardo A.
Cunha
*ab,
Leonardo A.
Cunha
 ab,
Katherine J.
Oosterbaan
a,
Joonho
Lee
ab,
Katherine J.
Oosterbaan
a,
Joonho
Lee
 c and
Martin
Head-Gordon
c and
Martin
Head-Gordon
 *ab
*ab
aKenneth S. Pitzer Center for Theoretical Chemistry, Department of Chemistry, University of California, Berkeley, California 94720, USA. E-mail: juanes@berkeley.edu; mhg@cchem.berkeley.edu
bChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
cDepartment of Chemistry, Columbia University, New York 10027, USA
First published on 17th August 2022
Abstract
We investigate the use of orbital-optimized references in conjunction with single-reference coupled-cluster theory with single and double substitutions (CCSD) for the study of core excitations and ionizations of 18 small organic molecules, without the use of response theory or equation-of-motion (EOM) formalisms. Three schemes are employed to successfully address the convergence difficulties associated with the coupled-cluster equations, and the spin contamination resulting from the use of a spin symmetry-broken reference, in the case of excitations. In order to gauge the inherent potential of the methods studied, an effort is made to provide reasonable basis set limit estimates for the transition energies. Overall, we find that the two best-performing schemes studied here for ΔCCSD are capable of predicting excitation and ionization energies with errors comparable to experimental accuracies. The proposed ΔCCSD schemes reduces statistical errors against experimental excitation energies by more than a factor of two when compared to the frozen-core core–valence separated (FC-CVS) EOM-CCSD approach – a successful variant of EOM-CCSD tailored towards core excitations.
Introduction
Recent decades have seen improvements in the handling of high-energy ultra-violet (XUV) and X-ray light in terms of coherence,1,2 intensity,2 and time control.2–4 As a result, scientists have been able to observe phenomena in chemistry,5–7 material sciences,8,9 and physics10,11 that were previously inaccessible. Furthermore, the increasing availability of table-top equipment12–15 capable of generating the light required for core spectroscopies has extended the use of said techniques for a variety of new studies.16 Efficiently and accurately modeling core excited states presents challenges that a useful methodology should address, chief among them the large charge rearrangement associated with the creation of the core hole. Within the independent particle model, this charge rearrangement results in a strong contraction of the orbitals due to the decreased nuclear screening – this is referred to as orbital relaxation in the literature. The most widely used method for calculating valence excited states, time-dependent density functional theory (TD-DFT), struggles to describe core excited states (and charge transfer states in general) because the linear-response (LR) formalism fails to account for the charge rearrangement when standard exchange–correlation functionals are used.17–20 This failure of TD-DFT has been associated with the self-interaction error and/or the difficulty of describing orbital relaxation, and it manifests through errors on the order of tens of eV for the K-edge of main group with larger errors being observed for heavier elements.21–23 When used to assess experimental results, the TD-DFT spectra is often shifted to either match the first or the brightest feature, or else to have it match the experimental results as much as possible.15 Progress in the use of LR-based DFT for core spectroscopies has been made through the design of functionals specialized to core excitations.17To circumvent the uncertainty associated with the choice of functionals, established wave function theories that are well-regarded for their accuracy in describing valence excitations, such as EOM-CC theory and algebraic diagrammatic construction (ADC), have been extended to core excitations by implementing techniques that target the high-energy roots of their effective Hamiltonians.24–31 A challenge that some techniques implemented in the last decade faced27,28 is the fact that core excited states are resonances embedded in an Auger continuum. The earlier idea of the core–valence separation (CVS),24,25 where the continuum is explicitly decoupled from the core excited states in some way, emerged as a successful solution to the problem, and therefore as the preferred protocol to target core excitations.26,29,31 It is worth noting, however, that the details of the CVS implementation may lead to differences on the order of eVs.31
An alternative approach followed by state-specific methods such as ΔSCF32,33 and its correlated relatives,34–41 the closely-related Transition Potential (TP)-SCF approaches,32,42–44 a number of multi-reference (MR) wave function models,45–48 excited state mean field theory,49 and Monte-Carlo-based approaches,50 is to account for relaxation in some way by optimizing for a target state. The ΔSCF approach, for example, converges a set of orbitals in a configuration that resembles the one-electron picture of the core excitation in question. These are non-Aufbau solutions to the self-consistent field (SCF) equations and are often saddle points in orbital space. Similarly, TP-SCF employs configurations optimized for a fractional core occupancy in the hopes of providing a reference of similar quality for both the ground and the core excited states. A difficulty of orbital-optimized excited state approaches is the possibility of landing on an undesired SCF solution of lower energy. In the context of mean-field approaches, such as Hartree–Fock (HF) and density functional theory (DFT), this issue has been addressed by algorithms specialized for excited state optimization, such as the maximum overlap method (MOM),51 and, more recently, the initial MOM (IMOM),52 square-gradient minimization (SGM)33 and state-targeted energy projection (STEP)53 methods.
ΔSCF has been used for decades to calculate core ionizations with success.32,34,37 In the cases where there are symmetry-equivalent atoms present in the system, an orbital localization procedure (such as that of Boys54) must be carried out on the core orbitals prior to SCF re-optimization to allow for proper orbital relaxation.38,55,56 The spatial symmetry breaking technically renders these situations multi-reference (MR) since multiple configurations must be re-combined via non-orthogonal configuration interaction (NOCI) to yield states of the proper spatial symmetry. In practice, the splitting between the symmetry-adapted configurations is small,57,58 so that the MR character associated with the core hole localization can be disregarded without serious error. The ΔSCF ionization energies, as calculated with the spatially symmetry-broken configurations are often good estimates of what would be observed in an experiment.
Studies on core excitations with ΔSCF have been more sparse until recently.34 In some measure this is due to the fact that MR character now factors in because of the need for two configurations for a spin-pure description of the excited state. The approximate spin-projection scheme (AP) established a way to estimate the excitation energy of the pure singlet, provided that the energies of a spin-contaminated singlet and the pure triplet are known.59,60 An attractive alternative to AP for ΔSCF calculations is the use of restricted open-shell Kohn–Sham orbitals (ROKS), which optimizes the spin-pure singlet energy as computed via the AP scheme for a mixed and a triplet (Ms = 1) configuration sharing the same set of restricted open-shell (RO) orbitals.61–64 Recently, this technique (and a generalized version for radicals65) has been used to study core excited states with the best-performing functional (SCAN) achieving an impressive 0.2 eV root-mean-squared-deviation (RMSD) from experimental results for a representative set of small organic molecules.22 With an appropriate treatment of scalar relativistic effects, ROKS has also been employed to tackle the K-edge of third-group elements.23
Excited SCF solutions are often a better reference than the ground state for finding alternative solutions to the CC equations, which in turn are reasonable approximations to the true excited states.66 Explicit SCF re-optimization takes care of the strong orbital relaxation and allows single-reference (SR) post-HF methods such as second order Møller–Plesset perturbation theory (MP2) and CC to focus on addressing the remaining dynamic correlation of a system. Core ionized states of closed-shell systems are perfect cases to be treated by these models and they have been studied via ΔMP232,34–37 and, more recently, ΔCCSD(T).38–40 The last decade has seen an effort to also employed explicitly-relaxed orbitals on a (wave-function-based) correlated calculation for singlet excited states.34,40,41,45–48,67 Among these, the wave function theories employing explicit MR construction often constrain them to study few molecules in small basis sets, which means they can only be compared to other computational methods in the same small basis sets.45–48 Simons and Matthews have recently proposed a theory, TP CC, that employs a TP SCF reference for an EOM-CC calculation of the core excited states.68 This model inherits some of the advantages of both state-specific methods – orbital relaxation – while retaining the advantages of EOM-CC: inherent spin-adaptation of the excited states, a full spectrum with a single calculation, and straightforward transition properties. The cost to pay comes from relying on a deteriorated description of the ground state relative to standard CC, controlled by tuning the fractional occupation number of the core orbital. Even though this renders the model arbitrary, to some extent, Simons and Matthews have carried out a study to find an optimal core occupancy parameter transferable across edges of the same element, making this a promising method for reliable and affordable high-accuracy wave function X-ray calculations.69
Owing to the simple nature of the MR character of singly core excited states of closed shell systems (namely, a two-determinant CSF) the objective of this paper is to assess the use of SR CC formalism (limited to the level of singles and doubles – CCSD) with orbital-optimized references for the prediction of core excited state energies. We believe the schemes proposed and analyzed in the present work could be useful for providing theoretical benchmark numbers for core excited and ionized states. As observed in this study, the best ΔCCSD models significantly outperforms FC-CVS-EOM-CCSD while retaining its ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N6) scaling, with N being the size of the one-electron basis set employed. Furthermore, unlike FC-CVS-EOM-CC, it does not rely on cancellation of errors.31 Per previous studies, the formally-correct CVS-EOM-CC implementation27 is likely to require full triples, i.e.
(N6) scaling, with N being the size of the one-electron basis set employed. Furthermore, unlike FC-CVS-EOM-CC, it does not rely on cancellation of errors.31 Per previous studies, the formally-correct CVS-EOM-CC implementation27 is likely to require full triples, i.e. ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N8) – scaling CVS-EOM-CCSDT, to reach similar accuracy.57,67 In contrast, the protocols presented here are well-defined in that only the molecule and the transition of interest needs to be specified – the proper ground state CC wave function and energies are used as is, unlike in the FC-CVS approach or the TP CC method, and no compromise in the excited state wave function is made either.
(N8) – scaling CVS-EOM-CCSDT, to reach similar accuracy.57,67 In contrast, the protocols presented here are well-defined in that only the molecule and the transition of interest needs to be specified – the proper ground state CC wave function and energies are used as is, unlike in the FC-CVS approach or the TP CC method, and no compromise in the excited state wave function is made either.
In early work along the lines of ΔCCSD, where Nooijen and Bartlett employed a relaxed core-ionized reference for a subsequent electron-attachment (EA) EOM-CCSD for the calculation of core excited states, they recognized two major challenges related to these sort of calculations.55 The first is how to treat the electron correlation effects that couple core orbitals with either other core levels or valence levels. De-excitation into the core hole can lead either to numerical instabilities or variational collapse towards the ground state. Therefore a suitable adaptation of SR CCSD for state-specific optimization of core excited states must treat core correlation, as well as removing potentially ill-behaved amplitudes. The second is the issue of ensuring proper spin symmetry in the final CC wave function.
This paper is organized as follows. After a review of the appropriate theory, we describe three candidate approaches that we deem potentially promising. Two of them employ Yamaguchi's AP approach,59 while the third one instead enforces correct spin symmetry at the ROHF level by constraining the amplitude of the double substitution that flips the spins of the two half-occupied orbitals to +1 for singlet and −1 for triplet states. A comparison of these approaches is then made against successful core excited state theories, ROKS(SCF) and FC-CVS-EOM-CC, with the ultimate judge being the experimental results. The energetic differences between the singlet and triplet core excited states, presumed to be accurate enough to make a statement about them, are presented. An effort is made to reach basis set convergence for all methods in order to exclude this factor from the discussion as much as possible and focus on their inherent performance. Despite the computational demands of approaching the basis set limit (BSL) for CC methods constraining us to molecules with at most two heavy atoms, the data set is diverse in terms of the elements targeted (Be, C, N, O, F, Ne) and in terms of the excited state character (σ*, π*, Rydberg). In total, a set of 21 excitations and 18 ionizations on 18 small closed-shell organic molecules is used.
We emphasize that our focus is on reporting excitation energies obtained through different proposed schemes within the ΔCC framework. At present, our work does not extend the discussion of ΔCC to compute transition properties. Obtaining such properties would be cumbersome and expensive due to, in part, the use of different sets of amplitudes for the bra and ket CC states. As pointed out in ref. 40, a potentially useful strategy to circumvent this exponential cost would be to use linearized wave functions obtained from the CC amplitudes from either the ground or core excited states, but we did not explore this further in our study.
Background
Following convention, we will reserve the indexes i, j, k,… for any occupied orbital, a, b, c,… for any virtual orbital, and p, q, r,… for an arbitrary orbital. For the CCSD amplitudes, we will use the symbols tai and tabij, collected in T1 and T2.For a set of orbitals that are not necessarily canonical, the CCSD amplitude equations take the following form:
| Daitai = Fia + wai(T1, T2) | (1) |
| Dabijtabij = 〈ij||ab〉 + wabij(T1, T2) | (2) |
| Dai = εi − εa | (3) |
| Dabij = εi + εj − εa − εb | (4) |
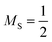 doublet references for the calculation of core ionized states. In the case of the spin-pure triplet and pure doublet references, standard ROHF is used in conjunction with MOM. The use of unrestricted orbitals for the symmetry-broken reference was found to be detrimental to some of our ΔCC schemes, so ROKS(HF) orbitals, followed by a Fock-build for the broken-symmetry singlet state and further pseudocanonicalization, were employed instead.
doublet references for the calculation of core ionized states. In the case of the spin-pure triplet and pure doublet references, standard ROHF is used in conjunction with MOM. The use of unrestricted orbitals for the symmetry-broken reference was found to be detrimental to some of our ΔCC schemes, so ROKS(HF) orbitals, followed by a Fock-build for the broken-symmetry singlet state and further pseudocanonicalization, were employed instead.
With these choices of reference, and specific to the case of core excitations, the presence of a virtual orbital with a large negative energy representing the core hole (we reserve the indexes h and ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) for the occupied alpha core orbital and the virtual beta core orbital) allows for denominators Dai and Dabij to be positive when a =
for the occupied alpha core orbital and the virtual beta core orbital) allows for denominators Dai and Dabij to be positive when a = ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) . In the case of single excitations, a†
. In the case of single excitations, a†![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) ai, this occurs when the occupied orbital has a higher orbital energy than the core virtual
ai, this occurs when the occupied orbital has a higher orbital energy than the core virtual
εi > ε![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) | (5) |
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) aia†baj, D
aia†baj, D![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) bij will be positive when
bij will be positive whenεi + εj − εb > ε![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) | (6) |
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) ai involves a valence occupied orbital and the excitation a†baj involves only valence orbitals.55 The denominator D
ai involves a valence occupied orbital and the excitation a†baj involves only valence orbitals.55 The denominator D![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) bij can still be negative if the other virtual has an orbital energy εb positive and large enough to break eqn (6). Furthermore, the orbital energies can conspire to make εi + εj − εb ≈ ε
bij can still be negative if the other virtual has an orbital energy εb positive and large enough to break eqn (6). Furthermore, the orbital energies can conspire to make εi + εj − εb ≈ ε![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) , rendering Dabij ≈ 0. Depending on the ability of the basis set to describe the high-lying virtual orbitals associated with the continuum, the denominator associated with double excitations can get arbitrarily close to zero, leading to numerical difficulties in solving for the T amplitudes (and of course divergence of perturbation theory methods, such as MP2).
, rendering Dabij ≈ 0. Depending on the ability of the basis set to describe the high-lying virtual orbitals associated with the continuum, the denominator associated with double excitations can get arbitrarily close to zero, leading to numerical difficulties in solving for the T amplitudes (and of course divergence of perturbation theory methods, such as MP2).
Close-to-zero denominators also yield numerical instabilities in the context of EOM-CC. In their study of EOM-CC-IP for K-edge ionization energies, Liu et al. found that spurious high-lying valence excited states that are quasi-degenerate with the core excited state result in erratically-converging correlation energies with respect to basis set.57 The CVS scheme is a proposed solution to this numerical problem; in this approach, core excitations are excluded from the ground state amplitudes, and all-valence excitations are excluded from the EOM amplitudes.31 The spurious couplings with the high-lying continuum excited states are then removed by design.
In a spirit similar to the CVS scheme, Zheng et al. proposed to exclude the virtual core orbital from the correlation treatment to address the divergence problem in the ΔCC calculations of core ionizations.38,39 Some of us adopted a similar strategy where we freeze up the doubly-vacant core orbital all together when studying double-core excitations.40 Zheng et al. found the missing correlation to be relevant for accurate core ionizations and uses estimates from fully-correlated CC calculations with decreasing denominator thresholds to account for it.
Computational details
A development version of Q-Chem 5.471 was used for all calculations. Experimental geometries available on the NIST computational database72 were used throughout this work. An atomic relativistic correction calculated via the Douglas–Kroll–Hell method, found to be nearly independent of basis-set and molecule for the main group elements, is added to all calculations (0.012, 0.09, 0.18, 0.34, 0.57, and 0.91 eV for Be, C, N, O, F, and Ne).73 For two of the three schemes of ΔCC we employ, the calculated singlet excited states are spin contaminated; the AP method is used to estimate the spin-pure excitation energies. Aside from the amplitudes excluded in the different schemes, the CC calculations of both the ground and excited states are all-electron.Our best attempt was made at comparing the excitation or ionization energies near their BSL values. To that end, different procedures involving specialized basis sets were employed for obtaining an approximate BSL for the different methods. The aug-pcX-3 (heavy)/aug-pcseg-2 (hydrogen) basis was used to approximate the BSL for the ROKS(SCF) calculations.74 A (99, 590) Euler–Maclaurin–Lebedev grid was used for the computation of the exchange–correlation integrals for the ROKS(SCAN) calculations. The aug-ccX-nZ (heavy)/aug-cc-pVTZ (hydrogen) bases,75 extrapolated using the two-point X−3 scheme76,77 with n = T, Q, were used to approximate the BSL for the EOM-CC calculations. As noted in a recent study, such an extrapolation scheme is appropriate for core excitations via EOM-CC.78 All ROKS(SCF) and EOM-CC calculations were also run with the standard Dunning aug-cc-pCVXZ (X = D, T, Q) family of bases79,80 and a slower convergence towards a similar BSL value was observed (ESI†).
Of the basis sets available, none were designed with both explicit orbital relaxation via SCF and correlation with wave function methods in mind. We used the TQ-extrapolated aug-cc-pCVXZ (heavy)/aug-cc-pVDZ (hydrogen) numbers as the best BSL estimate of the correlated Δ calculations.
The only exception to these choices of basis set was for the calculated Rydberg excitations in Ne. As expected for a full-fledged Rydberg excitation, significant differences between the aug-cc-pCVXZ and its doubly-augmented counterparts were observed in this case. The BSL core excited states for this atom are given by the d-aug-cc-pCV5Z for ROKS(SCF), Q5-extrapolated d-aug-cc-pCVXZ for EOM-CC, and TQ-extrapolated d-aug-cc-pCVXZ for the correlated Δ methods. No severe difference of a similar sort was found in any other molecule studied in this data set, including the rest of the isoelectronic ten electron series (ESI†).
Approaches to inclusion of core–valence correlation
Scheme 0: using the full set of amplitudes
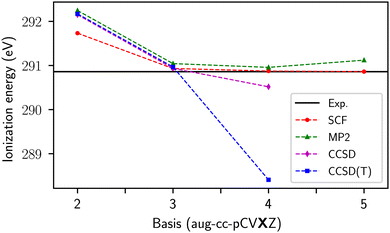
To motivate the need for the schemes presented in the following sections, we begin by exploring the behavior of the correlated methods with no modifications. The Fock matrix and MO coefficients of the optimized excited reference are passed to the correlated calculation and all amplitudes (e.g. all singles and doubles in CCSD) are included; we refer to this as Scheme 0 (S0). Scheme S0 would not be of use for real applications because of the possibility of variational collapse, and limitations of today's standard iterative CC solvers. Nevertheless, it provides useful insight in the few cases where the coupled cluster equations do converge. Such systems are few-atom molecules in a small basis, where there are no orbitals of the right energy to make the denominators small enough.Fig. 1 shows the basis set convergence of the CH4 core ionization energies, as calculated with the Δ-based methods, with respect to increasing cardinality of the aug-cc-pCVXZ basis set. The ΔSCF values converge quickly, with the 5Z result decreasing the calculated ionization energy by only 0.014 eV from the QZ numbers. The results for all the correlated Δ methods are within 0.1 eV of each other up until the QZ level, where they begin to diverge. At the 5Z level, the CCSD equations fail to converge and the ΔMP2 results break monotonicity. An analysis of the denominators associated with excitations into the core virtual (Fig. 2) reveals that, for all basis sets, there are positive denominators and, furthermore, that a close-to-zero denominator appears at the QZ level. Once the complexity of the molecule increases, the virtual space will begin to populate the problematic orbital energy range associated with near-zero denominators even when using small basis sets. Yet the CCSD(S0) results, at the very least, suggest that accurate results via Δ-based methods could be obtained if the irregularities caused by small denominators were addressed.
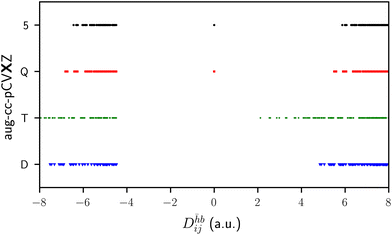 | ||
| Fig. 2 Some values for the denominators associated with excitation into the core virtual for the CH4 core-ionized reference. | ||
Scheme 1: deleting all amplitudes involving the core virtual
We make use of three additional schemes to address the numerical instabilities discussed previously. The first, which we refer as Scheme 1 (S1), is that proposed Zheng et al.38 and employed by Lee and Head-Gordon.40 This scheme simply excludes any amplitude involving the core virtual. Additionally, we chose to exclude singles amplitudes that excite the occupied core electron.Under these conditions, the ill-behaved amplitudes are removed by design. However, by excluding amplitudes that involve the core virtual, we are also excluding part of the correlation between the remaining core electron and valence electrons, as will become more clear below. The de-excitation amplitudes in the Lambda equations, solved to obtain CC properties like 〈S2〉, are treated in a completely analogous way. Under these constraints, the Lambda equations converged to yield to similar 〈S2〉 values than without them, but at a much accelerated pace.
Scheme 2: half-occupied core with zero spin-complement amplitude
To incorporate some of the correlation missing in S1, Scheme 2 (S2) allows for the double substitutions involving the core virtual,![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) , that also promote the occupied electron in the same core orbital, h – these were found to be the leading amplitudes for some of the larger well-behaved S0 calculations. This treatment of the correlation involving the virtual core orbital is closely related to that55 employed by Matthews in their study of core excitations67via the state-specific two-determinant Hilbert-space MR-CC,82,83 and by Zhang et al. for ΔCCSD(T) core ionizations.107 S2 is pleasing in that, even though core substitutions are involved, they are all associated with configurations that retain a core occupancy of 1.
, that also promote the occupied electron in the same core orbital, h – these were found to be the leading amplitudes for some of the larger well-behaved S0 calculations. This treatment of the correlation involving the virtual core orbital is closely related to that55 employed by Matthews in their study of core excitations67via the state-specific two-determinant Hilbert-space MR-CC,82,83 and by Zhang et al. for ΔCCSD(T) core ionizations.107 S2 is pleasing in that, even though core substitutions are involved, they are all associated with configurations that retain a core occupancy of 1.As for S1, the CC de-excitation amplitudes are treated in a completely analogous way. We found that, in the case of the mixed singlets, allowing for the double substitution that generates the spin complement of the reference, a†
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) a
a![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) a†tah with t being the target orbital, leads the CC iterations to converge towards the (lower energy) triplet excited state, resulting 〈S2〉 values that deviate significantly from 1. Therefore, an additional constraint was placed on calculations for the mixed singlet: the amplitude associated with said excitation is also set to zero. This helped ensure that the 〈S2〉 value of the CCSD wave function remained close to 1, signifying that it is a mixed spin configuration. Therefore, as with S1, the spin contamination is removed by evaluating the singlet energy via Yamaguchi's AP expression.
a†tah with t being the target orbital, leads the CC iterations to converge towards the (lower energy) triplet excited state, resulting 〈S2〉 values that deviate significantly from 1. Therefore, an additional constraint was placed on calculations for the mixed singlet: the amplitude associated with said excitation is also set to zero. This helped ensure that the 〈S2〉 value of the CCSD wave function remained close to 1, signifying that it is a mixed spin configuration. Therefore, as with S1, the spin contamination is removed by evaluating the singlet energy via Yamaguchi's AP expression.
Scheme 3: half-occupied core with unit spin-complement amplitude
As a final scheme, and exclusively for the calculations on the mixed singlet state, we propose to incorporate all of the conditions of S2 but, instead of neglecting the double substitution amplitude, a†![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) a
a![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) a†tah, associated with the spin complement of the reference, we set it to 1.0; we refer to this as Scheme 3 (S3). These conditions force the CC iterations to look for the pure singlet starting from the mixed reference. As previously, the exact same S3 conditions are imposed on the de-excitation amplitudes for the left eigenvectors of the similarity transformed Hamiltonian. We found that the lambda equations were able to converge even when the de-excitation amplitude associated with the spin complement is not forced to be 1.0. Enforcing said condition accelerated the convergence to result in the same value for 〈S2〉 An attractive feature of S3, as will be elaborated on in the Results section, is that it bypasses the need for AP altogether because the resulting states have 〈S2〉 values relatively close to 0. S3 is, in fact, similar in spirit to the bi-configurational MR-CC model proposed by Oliphant and Adamowicz in 1991.81 However S3 is dramatically simpler because additional triple and quadruple excitations that are necessary in MR-CC (in order to account for the single and double excitations on top of the “secondary reference”) are omitted here.
a†tah, associated with the spin complement of the reference, we set it to 1.0; we refer to this as Scheme 3 (S3). These conditions force the CC iterations to look for the pure singlet starting from the mixed reference. As previously, the exact same S3 conditions are imposed on the de-excitation amplitudes for the left eigenvectors of the similarity transformed Hamiltonian. We found that the lambda equations were able to converge even when the de-excitation amplitude associated with the spin complement is not forced to be 1.0. Enforcing said condition accelerated the convergence to result in the same value for 〈S2〉 An attractive feature of S3, as will be elaborated on in the Results section, is that it bypasses the need for AP altogether because the resulting states have 〈S2〉 values relatively close to 0. S3 is, in fact, similar in spirit to the bi-configurational MR-CC model proposed by Oliphant and Adamowicz in 1991.81 However S3 is dramatically simpler because additional triple and quadruple excitations that are necessary in MR-CC (in order to account for the single and double excitations on top of the “secondary reference”) are omitted here.
The amplitude of the spin complement can also be set to −1.0 to access the Ms = 0 triplet. This allows us to asses the reliability of S3 by comparing its calculated triplet, Ms = 0 numbers against the Ms = ±1 triplet numbers obtained via S2. In the absence of spin–orbit coupling or external magnetic fields, the Ms = 1 and Ms = 0 triplet states should be degenerate, so any differences reflect the failures of S3 with respect to S2. Naturally, one source of error will be the fact that, in S3, the correlation methods treat each individual configuration of the CSF unequally.
Results and discussion
Before discussing the correlated methods, it is worth revisiting the spin-pure open shell singlet HF results (labeled as ROKS(HF), as this can be viewed as a special case of OO-DFT64). For the excitations considered, ROKS(HF) achieves a mean absolute error (MAE) and RMSE of 0.43 and 0.52 eV. All of the excitations involving carbon and nitrogen, and the O 1s–σ*/Rydberg transitions are overestimated. All of the fluorine and neon excitations, and the O 1s–π* transitions are underestimated. This element-dependent error distribution with respect to experiment leads to a relatively small mean signed error (MSE) of 0.18 eV. Using ROKS with the standard SCAN functional,84 the best-performing functional according to a recent study, reduces the MAE to 0.16 eV, the RMSE to an impressive 0.19 eV,22 and the MSE to −0.08 eV. How well can CC methods limited to double or perturbative triple substitutions compete with these results?We begin the analysis by noting that the FC-CVS-EOM-CCSD approach cannot match ROKS(SCAN), and in fact it scarcely outperforms the simple ROKS(HF): FC-CVS-EOM-CCSD achieves an MAE and RMSE of 0.34 and 0.41 eV. FC-CVS-EOM-CCSD tends to underestimate the excitations out of carbon, with an overestimation of 0.34 eV for the CH3OH 1s → 3s transition being the only serious exception. All other excitations are overestimated by FC-CVS-EOM-CCSD, except for the N2 1s → π* and Be 1s → 2p excitations, which are underestimated by 0.25 and 0.68 eV, respectively. The latter might be a failure of the FC-CVS model.
In regards to the correlated Δ methods, addressing the offending denominators, either by eliminating all excitations into the core virtual (S1) or including only those that retain a core occupancy of 1 (S2 and S3) resulted in well-behaved, monotonically convergent CC calculations in all cases. Furthermore, for Schemes S1 and S2, the MP2, CCSD, and CCSD(T) correlation energies of the excited states, and the calculated excitation energies seem to converge monotonically towards a well defined BSL.
As observed in Fig. 3 and the ESI,† correlated calculations via Scheme S1 always overestimate the excitation energy. ΔMP2(S1), ΔCCSD(S1), and ΔCCSD(T)(S1) achieve MAEs of 0.82, 0.58, 0.63 eV, and RMSEs of 0.88, 0.60, 0.65 eV. ΔCCSD(S1) attenuates the most severe failures of ΔMP2(S1) – where it overestimates experiment by more than 1 eV: H2CO 1s → π*, HCN 1s → π*, HCN 1s → π*, N2 1s → π*, and F2 1s → σ*. These are all cases where ΔMP2(S1) changes the ROKS(HF) results the most – in all cases for worse – with F2 having the largest change in magnitude, at 2.3 eV. ΔCCSD(T)(S1), more often than not, seems to very slightly increase the error against experiment when compared to ΔCCSD(S1). Including correlation employing S1, either via MP2, CCSD, or CCSD(T) only decreases the calculated values relative to ΔHF in roughly half the cases. The MSEs for all the correlated methods under S1 are identical to their MAEs, which is consistent with a systematic overestimation of the excitation energies or, conversely, an under-correlation of the excited states. Since the results are expected to be well near the BSL, and the perturbative triples correction changes the CCSD results by a small amount, we attribute this to the configurations excluded from the correlation treatment for the sake of proper convergence.
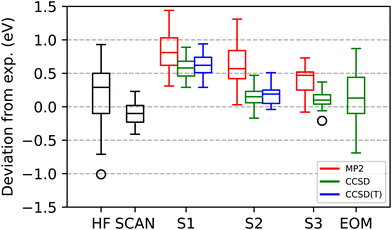 | ||
| Fig. 3 Statistical summary of the accuracy of calculated K-shell core excitations relative to experimental values for the 21 transitions shown in Table 1, as evaluated by ROKS(HF), ROKS(SCAN), the correlated Δ methods (Schemes S1, S2 and S3), and FC-CVS-EOM-CCSD-EE. For the S1 and S2 approaches, in addition to CCSD itself, the corresponding MP2 and CCSD(T) values are also shown. The specific values corresponding to these statistics are given in Table 1 and the ESI.† | ||
As proposed in the previous section, not all configurations involving excitations into the core virtual need to be excluded for a safe convergence of the iterative CC procedure. Fig. 3 and ESI† show that including some of the missing configurations with S2 indeed reduces the error relative to S1. ΔMP2(S2), ΔCCSD(S2), and ΔCCSD(T)(S2) achieves MAEs of 0.62, 0.18, and 0.20 eV, and RMSEs of 0.69, 0.22 and 0.25 eV. A small systematic overestimation remains, as suggested by MSEs of 0.61, 0.16, and 0.20 eV. Two relevant statistical observations are that ΔMP2(S2) still fails to offer an improvement over ROKS(HF), and that the (T) correction slightly worsens the ΔCCSD results. We note how the well-behaved excitations involving the core account for roughly 0.4 eV of the calculated excitation energy, as measured by the statistical differences between ΔCCSD(S1) and ΔCCSD(S2). This is in agreement with the findings of Zheng et al.38 and emphasizes that, if quantitative agreement is desired, a CVS scheme like S1 is inadequate.
Before discussing the performance of S3 in predicting excitation energies, we make some other relevant remarks on the scheme. The de-excitation amplitudes were usually converged without any modifications to yield a CCSD 〈S2〉 close to 0 (or 2, if the triplet state was being targeted). Naturally, it often takes many iterations for these amplitudes to respond to the large excitation amplitude in T2. Imposing the condition analogous to S3 for the de-excitation amplitudes accelerated the convergence, never taking more than 35 iterations without DIIS for the cases that we studied. As is noted in the ESI,† a residual deviation from an 〈S2〉 value of 0 remained for all calculations. The largest of these deviations was for the C2H2 1s → π* state, with an 〈S2〉 of 0.069, the average being 0.033. We suspect that this might be due to the missing excitations described in the discussion of S3.
The spin-forbidden excitations into the triplet Ms = 0 manifold were calculated with ΔCCSD(S3) by forcing the amplitude of the spin complement of the reference to be −1.0; they are listed in ESI.† We compared these against the triplet Ms = 1 excitation energies as calculated by ΔCCSD(S2). The largest deviation was of 0.09 eV for the H2CO 1s → π* state, the average being 0.04 eV. The Ms = 0 triplet excitations were higher than the Ms = 1 results for all but one case, Be 1s → 2p, where the difference is −0.01 eV. This is also consistent with the idea that for the Ms = 0 triplets, as for the singlets, we are undercorrelating the excited state due to missing excitations. An undercorrelation is not present for the Ms = 1 triplet because, aside from any spatial symmetry breaking, this is purely a SR situation that S2 should be able to address. The triplet numbers, as calculated by ΔCCSD(S2), match fairly well with the two experimental numbers that we found for these spin-forbidden transitions: 114.3 eV for Be 1s → 2p and 400.12 eV for N2 1s → π*.85,86 ΔCCSD(S2) predicts them to be 114.37 eV and 400.24 eV, respectively. The average energy difference between the singlet and triplet excited states for the set of molecules studied here, as calculated by ΔCCSD(S3), is 0.44 eV. Some cases worthy of notice are Be 1s → 2p, where the splitting is 1.16 eV, and CO 1s → π*, with the largest splitting of all: 1.42 eV. Interestingly, the splitting for CO 1s → π* is only 0.34 eV. Another case of relevance are the two Rydberg excitations Ne 1s → 3s and Ne 1s → 3p, which have the smallest splittings: 0.06 eV and 0.05 eV, respectively.
In Table 1, we present the calculated excitation energies of the singlet excited states for the most successful scheme, ΔCCSD(S3), against ROKS(HF), ROKS(SCAN), and FC-CVS-EOM-CCSD-EE.31 All the statistics provided are compared against their most recent and/or accurate experimental values. The per-molecule results for the remaining schemes are listed in the ESI.† Overall, ΔCCSD(S3) achieves an MAE and RMSE of 0.14 and 0.18 eV. The most challenging excitation for this method is H2CO 1s → π*, with an overestimation of 0.37 eV from the experimental value of 287.98 eV by Remmers et al.87 A small systematic overestimation remains, as suggested by a MSE of 0.12 eV. The only excitation that ΔCCSD(S3) significantly underestimates is CO 1s → π*, which is below Sodhi and Brion's result of 534.21 ± 0.09 eV by 0.21 eV.88
| Transition | ROKS(HF) | ROKS(SCAN) | ΔCCSD(S3) | EOM-CCSD | Experiment |
|---|---|---|---|---|---|
| Be 1s–2p | 115.37 | 115.34 | 115.53 | 114.79 | 115.4785 |
| C2H4 1s–π* | 285.27 | 284.70 | 284.77 | 284.68 | 284.68 (0.1)89 |
| H2CO 1s–π* | 286.42 | 285.74 | 285.96 | 285.62 | 285.5987 |
| C2H2 1s–π* | 286.40 | 285.67 | 285.84 | 285.55 | 285.9 (0.1)89 |
| HCN 1s–π* | 286.98 | 286.35 | 286.51 | 286.07 | 286.3790 |
| CO 1s–π* | 288.05 | 286.99 | 287.46 | 286.71 | 287.40 (0.02)88 |
| CH3OH 1s–3s | 288.91 | 288.18 | 288.34 | 288.26 | 287.9891 |
| CH4 1s–3p(t2) | 288.38 | 287.96 | 288.02 | 287.9 | 288.00 (0.2)92 |
| HCN 1s–π* | 400.00 | 399.60 | 399.80 | 399.74 | 399.790 |
| NH3 1s–3s | 400.97 | 400.42 | 400.63 | 400.82 | 400.66 (0.2)92 |
| N2 1s–π* | 401.18 | 400.80 | 401.02 | 400.63 | 400.88 (0.02)88 |
| NH3 1s–3p(e) | 402.62 | 402.18 | 402.41 | 402.46 | 402.33 (0.2)92 |
| H2CO 1s–π* | 530.67 | 530.83 | 530.86 | 531.26 | 530.8287 |
| H2O 1s–3s | 534.15 | 533.84 | 534.14 | 534.44 | 534.0 (0.2)92 |
| CH3OH 1s–3s | 534.16 | 533.98 | 534.24 | 534.64 | 534.1291 |
| CO 1s–π* | 533.68 | 533.97 | 534.00 | 534.50 | 534.21 (0.09)88 |
| H2O 1s–3p (b2) | 536.03 | 535.65 | 536.08 | 536.21 | 535.9 (0.2)92 |
| F2 1s–σ* | 681.19 | 682.43 | 682.41 | 683.07 | 682.2 (0.1)93 |
| HF 1s–σ* | 687.31 | 687.44 | 687.76 | 688.05 | 687.4 (0.2)93 |
| Ne 1s–3s | 864.75 | 865.18 | 865.37 | 865.54 | 865.1 (0.1)93 |
| Ne 1s–3p | 866.58 | 866.96 | 867.30 | 867.40 | 867.2994 |
| MSE | 0.15 | −0.09 | 0.12 | 0.11 | |
| MAE | 0.43 | 0.15 | 0.14 | 0.34 | |
| RMSE | 0.52 | 0.19 | 0.18 | 0.41 | |
| MAX | 1.01 | 0.41 | 0.37 | 0.87 |
A recent study that is closely-related to our approach is the application of a direct two-determinant (TD) CCSD protocol82 to study core excited states.67 This procedure follows the ΔCC framework through orbital-optimizing a core excited configuration, constructing a CSF, and carrying out TD-CCSD on top of it. To address the dangerous denominators, an equivalent of our Scheme 2 is employed.55 It is shown that TD-CCSD results have a comparable accuracy to the ΔCCSD results reported here, with a MAE of 0.10 eV and RMSE of 0.11 eV against the Coriani implementation of CVS-EOM-EE-CCSDT for the three lowest lying core excitations of HCN, CO, NH3, and H2O. The ΔCC approaches presented in our work have the advantage of halving the number of amplitudes as compared to the bi-configurational TD-CCSD, by virtue of employing pure SR formalism. Furthermore, employing the Scheme of choice to accelerate the convergence of the Lambda equations enables calculations of excited state properties such as gradients and 〈S2〉.
It is worth emphasizing that, as noted by Vidal et al. in their report,31 the good performance of the FC-CVS relative to the earlier CVS scheme29 is due to a cancellation of errors. The ground state CC wave function is under-correlated by imposing the frozen core approximation, bringing down the excitation energy to better match the experimental value. The CVS scheme of Coriani et al.29 includes all excitations for the ground state and decouples the core excited states via projection from the valence states in the EOM component of the procedure. As such, it does not benefit from the error cancellation present in the FC-CVS scheme and despite being preferable on formal grounds, it performs worse when comparing to experiment.
Table 2 compares the ΔCCSD(S2) core ionizations, against those calculated by ΔSCF(HF), ΔSCF(SCAN) and FC-CVS-EOM-CCSD-IP. Fig. 4 shows box-whisker plots for both the S1 and S2 methods applied to MP2, CCSD, and CCSD(T) relative to the same existing methods. The experimental values used as a reference are the ones given by Jolly et al.95 unless a more recent study was found. ΔSCF(HF) has a MSE, MAE, and RMSE of −0.15, 0.45, and 0.58 eV, respectively. The two most challenging cases for ΔSCF in the ionization data set, CO and F2, are the only cases with an error greater than 1 eV. ΔSCF(SCAN) reduces the ΔSCF(HF) errors by more than a factor of two, with an MAE and RMSE of 0.21 and 0.25 eV. In contrast to excitations, all ionizations except two, F2 and Ne, are overestimated with ΔSCF(SCAN), resulting in an MSE similar to its MAE: 0.18 eV. The most challenging case for ΔSCF(SCAN) is Be, over estimated by 0.51 eV. Somewhat surprisingly ΔSCF(HF) predicts the experimental Be ionization perfectly.
| Transition | ΔSCF(HF) | ΔSCF(SCAN) | ΔCCSD(S2) | EOM-CCSD | Experiment |
|---|---|---|---|---|---|
| Be 1s–ion | 123.35 | 123.92 | 123.65 | 123.49 | 123.3585 |
| C2H4 1s–ion | 290.71 | 290.92 | 290.72 | 290.95 | 290.8895 |
| CH4 1s–ion | 290.86 | 290.92 | 290.69 | 290.68 | 290.8395 |
| C2H2 1s–ion | 291.39 | 291.47 | 291.21 | 291.26 | 291.1495 |
| CH3OH 1s–ion | 292.63 | 292.63 | 292.44 | 292.52 | 292.3 (0.2)96 |
| HCN 1s–ion | 293.76 | 293.68 | 293.43 | 293.34 | 293.5095 |
| H2CO 1s–ion | 294.91 | 294.75 | 294.50 | 294.70 | 294.3587 |
| CO 1s–ion | 297.23 | 296.58 | 296.47 | 296.43 | 296.2495 |
| NH3 1s–ion | 405.48 | 405.70 | 405.51 | 405.77 | 405.5295 |
| HCN 1s–ion | 406.74 | 406.96 | 406.78 | 407.10 | 406.895 |
| N2 1s–ion | 410.21 | 410.15 | 409.99 | 409.89 | 409.995 |
| CH3OH 1s–ion | 538.43 | 539.08 | 538.90 | 539.64 | 539.06 (0.2)96 |
| H2CO 1s–ion | 538.51 | 539.47 | 539.29 | 540.28 | 539.3087 |
| H2O 1s–ion | 539.49 | 539.96 | 539.82 | 540.29 | 539.9295 |
| CO 1s–ion | 541.79 | 542.65 | 542.43 | 543.10 | 542.5795 |
| HF 1s–ion | 693.62 | 694.30 | 694.25 | 694.80 | 694.095 |
| F2 1s–ion | 695.36 | 696.54 | 696.58 | 697.58 | 696.7195 |
| Ne 1s–ion | 869.54 | 870.21 | 870.31 | 870.49 | 870.3394 |
| MSE | −0.15 | 0.18 | 0.01 | 0.31 | |
| MAE | 0.45 | 0.21 | 0.12 | 0.35 | |
| RMSE | 0.58 | 0.25 | 0.15 | 0.45 | |
| MAX | 1.35 | 0.57 | 0.30 | 0.98 |
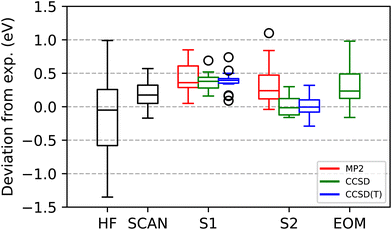 | ||
| Fig. 4 Statistical summary of the accuracy of calculated K-shell core ionizations relative to experimental values for the 18 ionizations shown in Table 2, as evaluated by ROHF(SCF), the correlated Δ methods (Schemes S1 and S2), and FC-CVS-EOM-CCSD-IP. For the S1 and S2 approaches, in addition to CCSD itself, the corresponding MP2 and CCSD(T) values are also shown. The specific values corresponding to these statistics are given in Table 2 and the ESI.† | ||
The performance of ΔSCF(HF) against the much more sophisticated FC-CVS-EOM-IP-CCSD is once again remarkable, with the MAE and RMSE of the latter being 0.35 and 0.45 eV. Elaborating on the previous discussion on the specific details of the CVS implementation, we note that these FC-CVS-EOM-IP-CCSD errors are roughly five times smaller than those reported by Liu et al. for the Coriani-style CVS-EOM-IP-CCSD.57 A similar situation takes place within the context of EOM-EE-CCSD for core excitations, as reported by Vidal et al.31
In contrast to excitations, the correlated Δ methods using the S1 model manage to slightly improve upon ΔHF for ionization. ΔMP2(S1) increases the HF ionization energy in almost all cases, and over 1 eV in several of them: H2CO, CH3OH, CO, HF, F2, and Ne. The only case where ΔMP2(S1) decreases the ionization predicted by ΔHF is CO, which is also the second most challenging case for ΔHF, right after F2. The problematic Be is overestimated by 0.81 eV by ΔMP2(S1). Once again, ΔCCSD(S1) alleviates the worst cases in ΔMP2(S1). CO is anomalous in that this is the only case where ΔCCSD(S1) significantly worsens the ΔMP2(S1) result, and also the only one where the (T) seems to significantly improve the result, correcting the ΔCCSD(S1) result by 0.17 eV. Overall, the S1 methods result in MAEs and RMSEs of 0.42, 0.37, 0.38 eV and 0.49, 0.39, 0.41 eV for MP2, CCSD, and CCSD(T). As Lubijic37 noted in their study, ΔMP2(S1) seldom warrants the additional cost over ΔSCF and neither extending to CCSD or CCSD(T) seems to improve the results to an extent that justifies their cost. As for excitations, a consistent overestimation of the core ionization energies, as evidenced by the MSEs being equal to the MAEs for all the S1 correlated methods, hints at the configurations neglected by the S1 scheme being important.
Indeed, the improvement in calculated core ionization energies provided by the correlated methods under model S2, relative to S1, is even more dramatic than it is for the excitations. In contrast with ΔMP2(S1), ΔMP2(S2) manages to somewhat improve the statistics from ΔHF, bringing down the MAE and RMSE to 0.33 and 0.44 eV. S2 improves the S1 results for MP2 in almost all cases, the only significant exception being Be, where ΔMP2(S2) performs the worst: an overestimation of 1.1 eV. As with S1, ΔCCSD(S2) alleviates the failures of ΔMP2(S2) (significantly for Be) and brings the MAE and RMSE down to 0.12 and 0.15 eV. ΔCCSD(T) slightly worsens the statistics by bringing the MAE and RMSE to 0.13 and 0.17 eV. The RMSE for ΔCCSD(S2) is more than 2.5 times smaller than for FC-CVS-EOM-IP-CCSD.
The results presented here are comparable to those in Table 5 of Zheng et al.38 The differences can be associated with the different basis sets used and the way we are treating the correlation associated with the core virtual. Whereas in their study, they make estimates to the correlation missing due to freezing the core orbital completely (S1) by carrying out unconstrained (S0) calculations with denominator thresholds, S2 recovers it by a well-defined protocol. In a subsequent study, the same team found the relevance of going beyond S1 (CVS0 in their work) and using an equivalent to our S2 (CVS-ΔCCSD(T) in their work), they found excellent agreement with experiment as well.107 The numbers they report on the third column of their Table 1, corresponding to their CVS-ΔCCSD(T) model with a TQ5-extrapolated cc-pCVXZ BSL, yield an MSE, MAE, and RMSE of 0.11, 0.13, and 0.17 eV for the subset of molecules common in both our data-sets (all of the ones presented here except Be and Ne,) using the experimental values we collected. Furthermore, they show that high-order relativistic effects (i.e., going beyond the exact two-component theory in its one-electron variant, or X2C-1e) are not relevant for second-row K-edge ionizations but they amount to −0.80 eV for Si, quickly increasing with the atomic number of the probed atom.
Conclusions
We have studied the use of core–hole orbital-optimized references in SR correlated methods to describe core excited and core ionized states of 18 small closed-shell organic molecules, and compared them against two of the most successful approaches so far: ROKS(SCAN) and FC-CVS-EOM-CC. The use of three different schemes (S1, S2, S3) to address the convergence problems of the CC equations, and the spin contamination of the excited states, were employed. S1 excludes all amplitudes involving the half-occupied core orbital associated with the excitation or ionization. S2 allows for the ones that retain a core occupancy of 1. S3, exclusively for CCSD core excitations, fixes the T2 amplitude associated with the spin compliment of a spin symmetry-broken core excited reference to ±1.0, thereby ensuring the proper reference CSF is present in the cluster expansion. As evidenced by the energetic difference between the singlet and the triplet core excited states, addressing the spin contamination associated with using a symmetry broken reference is essential for quantitative studies using the correlated Δ methods unless Rydberg states are being targeted.To compare with experimental core excitations and ionizations requires careful attention to basis set convergence, which we have addressed by using the aug-cc-pCVXZ basis set for heavy atoms (n = T, Q, with extrapolation), and aug-cc-pVDZ for hydrogen. With this protocol, ΔCCSD(S3) performs the best among the correlated Δ methods for core excitations, reaching an MAE and RMSE of 0.14 and 0.18 eV for CCSD. These statistics are on par with the most successful orbital-optimized DFT approach, ROKS(SCAN). ΔCCSD(S2) follows closely behind, with an MAE and RMSE of 0.18 and 0.22 eV. As such, ΔCCSD with either S2 or S3 roughly halves the errors of FC-CVS-EOM-CCSD-EE. A similar situation takes place for ionizations, where S2 in conjunction with CCSD performs the best, by achieving a MAE and RMSE of 0.13 and 0.17 eV, respectively. ΔCCSD(S2) reduces the FC-CVS-EOM-CCSD-IP error by more than a factor of 2.5, and outperforms ΔSCF(SCAN), which has an MAE and RMSE of 0.21 and 0.25 eV.
The use of a CVS scheme like S1 for the correlated Δ methods is discouraged, if quantitative agreement is sought after. Furthermore, as has previously been concluded by others,37 we cannot recommend the use of ΔMP2 for the prediction of core excitations or ionizations. In the future, it may be interesting to explore whether regularization or further orbital re-optimization40,97 can address the limitations of ΔMP2. Finally, we note that the use of the perturbative (T) triples correction with the best scheme that allows for it, S2, does not seem to offer a significant improvement over CCSD. Perhaps this is because the effect of triples is small (based on the excellent results obtained with ΔCCSD(S2) and ΔCCSD(S3)) or perhaps a full triples treatment is needed to obtain further significant improvement.
There are additional sources for the disagreement with regards to experimental values. Difficulties in measuring XAS spectra often result in slightly different experimental values from different sources (refer to ref. 94 for example) which are often on the order of the errors observed here. We have made our best effort to obtain the most recent and reliable information available at the moment. Additionally, physical effects lacking in our model may also contribute to a disagreement with the experiment. There are two such effects that we expect to be of relevance. The first is the fact that we are treating core excited states as formally bound, whereas in reality they are resonances coupling with the Auger continuum.98 Said effect is expected to shift the energy of the resonance. The second is that we are computing vertical excitation energies – a more complete model would incorporate vibronic effects.99–102
Despite its shortcomings, the main tool for routine calculation of XAS is TD-DFT. Furthermore, due to the recent advances in LR-DFT-based theory103,104 the efficient implementations of ΔSCF methods,105 and specialized basis sets,74 techniques based on mean field approaches will likely remain the workhorses for the calculation of core spectra. Nonetheless, considering an accuracy of less than 0.2 eV attained by the ΔCCSD schemes S2 and S3 for specific transitions, we expect these to be a promising method for providing benchmark theory-based core excitation/ionization numbers. Furthermore, the ΔCCSD methods presented here retain the formal ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N6) scaling of CCSD. Therefore, the hard limit due to computational resources on the size of the systems that can be tackled by ΔCCSD is equivalent to that of standard SR CCSD. The challenges to making ΔCCSD a practical method for the calculation of excitation energies, as can now be done with EOM-CCSD, is largely implementational. Specialized and efficient amplitude windowing algorithms to carry out the particular ΔCC scheme and a robust workflow that allows for the ΔCCSD calculation on a number of states of interest (which can be carried out in parallel)105 could eventually lead to routine ΔCCSD calculations for transition energies. Furthermore, the question of compact and efficient basis sets for these orbital-optimized, wave-function-based correlated calculations deserves future attention. New developments for the calculation of transition properties, such as oscillator strengths, within the ΔCCSD framework are still needed in order to make this approach an attractive alternative to conventional CC methods for excited states. As a final outlook, we point out to the possibility of employing these accurate core excited and core-ionized SR CC reference states as the starting point for EOM calculations to open up new avenues for investigating satellite peaks – formally higher excited states beyond the reach of the traditional EOM formalism – in core spectroscopies.106
(N6) scaling of CCSD. Therefore, the hard limit due to computational resources on the size of the systems that can be tackled by ΔCCSD is equivalent to that of standard SR CCSD. The challenges to making ΔCCSD a practical method for the calculation of excitation energies, as can now be done with EOM-CCSD, is largely implementational. Specialized and efficient amplitude windowing algorithms to carry out the particular ΔCC scheme and a robust workflow that allows for the ΔCCSD calculation on a number of states of interest (which can be carried out in parallel)105 could eventually lead to routine ΔCCSD calculations for transition energies. Furthermore, the question of compact and efficient basis sets for these orbital-optimized, wave-function-based correlated calculations deserves future attention. New developments for the calculation of transition properties, such as oscillator strengths, within the ΔCCSD framework are still needed in order to make this approach an attractive alternative to conventional CC methods for excited states. As a final outlook, we point out to the possibility of employing these accurate core excited and core-ionized SR CC reference states as the starting point for EOM calculations to open up new avenues for investigating satellite peaks – formally higher excited states beyond the reach of the traditional EOM formalism – in core spectroscopies.106
Conflicts of interest
M. H.-G. is a part-owner of Q-Chem, which is the software platform in which the developments described here were implemented.Acknowledgements
The authors thank Diptarka Hait for fruitful discussions. J. L. thanks David Reichman for support. This work was supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy, under Contract No. DE-AC02-05CH11231.References
- L. H. Yu and T. Shaftan, Towards coherent X-ray free-electron lasers, Nat. Photonics, 2019, 13, 513–515 CrossRef CAS.
- A. Halavanau, A. Benediktovitch, A. A. Lutman, D. DePonte, D. Cocco, N. Rohringer, U. Bergmann and C. Pellegrini, Population inversion X-ray laser oscillator, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 15511–15516 CrossRef CAS PubMed.
- P. Kumar Maroju, et al., Attosecond pulse shaping using a seeded free-electron laser, Nature, 2005, 386, 578 Search PubMed.
- J. Duris, et al., Tunable isolated attosecond X-ray pulses with gigawatt peak power from a free-electron laser, Nat. Photonics, 2019, 14, 30–36 CrossRef.
- K. F. Chang, M. Reduzzi, H. Wang, S. M. Poullain, Y. Kobayashi, L. Barreau, D. Prendergast, D. M. Neumark and S. R. Leone, Revealing electronic state-switching at conical intersections in alkyl iodides by ultrafast XUV transient absorption spectroscopy, Nat. Commun., 2020, 11, 1–7 CrossRef PubMed.
- Z. H. Loh, et al., Observation of the fastest chemical processes in the radiolysis of water, Science, 2020, 367, 179–182 CrossRef CAS PubMed.
- Y. C. Lin, A. P. Fidler, A. Sandhu, R. R. Lucchese, C. W. McCurdy, S. R. Leone and D. M. Neumark, Coupled nuclear–electronic decay dynamics of O2 inner valence excited states revealed by attosecond XUV wave-mixing spectroscopy, Faraday Discuss., 2021, 228, 537–554 RSC.
- F. Sette, M. H. Krisch, C. Masciovecchio, G. Ruocco and G. Monaco, Dynamics of glasses and glass-forming liquids studied by inelastic X- ray scattering, Science, 1998, 280, 1550–1555 CrossRef CAS.
- A. R. Attar, H.-T. Chang, A. Britz, X. Zhang, M.-F. Lin, A. Krishnamoorthy, T. Linker, D. Fritz, D. M. Neumark, R. K. Kalia, A. Nakano, P. Ajayan, P. Vashishta, U. Bergmann and S. R. Leone, Simultaneous Observation of Carrier- Specific Redistribution and Coherent Lattice Dynamics in 2H-MoTe 2 with Femtosecond Core-Level Spectroscopy, ACS Nano, 2020, 14, 15829–15840 CrossRef PubMed.
- T. Mazza, et al., Mapping Resonance Structures in Transient Core-Ionized Atoms, Phys. Rev. X, 2020, 10, 041056 CAS.
- D. C. Haynes, et al., Clocking Auger electrons, Nat. Phys., 2021, 17, 512–518 Search PubMed.
- T. Popmintchev, et al., Bright coherent ultrahigh harmonics in the kev X-ray regime from mid-infrared femtosecond lasers, Science, 2012, 336, 1287–1291 CrossRef CAS PubMed.
- P. Zimmermann, S. Peredkov, P. M. Abdala, S. DeBeer, M. Tromp, C. Muller and J. A. van Bokhoven, Modern X-ray spectroscopy: XAS and XES in the laboratory, Coord. Chem. Rev., 2020, 423, 213466 CrossRef CAS.
- L. Barreau, A. D. Ross, S. Garg, P. M. Kraus, D. M. Neumark and S. R. Leone, Efficient table-top dual-wavelength beamline for ultrafast transient absorption spectroscopy in the soft X-ray region, Sci. Rep., 2020, 10, 1–9 CrossRef PubMed.
- V. Scutelnic, S. Tsuru, M. Papai, Z. Yang, M. Epshtein, T. Xue, E. Haugen, Y. Kobayashi, A. I. Krylov, K. B. Møller, S. Coriani and S. R. Leone, X-ray transient absorption reveals the 1Au (nπ*) state of pyrazine in electronic relaxation, Nat. Commun., 2021, 12, 6–13 CrossRef PubMed.
- M. Epshtein, V. Scutelnic, Z. Yang, T. Xue, M. L. Vidal, A. I. Krylov, S. Coriani and S. R. Leone, Table-Top X-ray Spectroscopy of Benzene Radical Cation, J. Phys. Chem. A, 2020, 124, 9524–9531 CrossRef CAS PubMed.
- N. A. Besley and F. A. Asmuruf, Time-dependent density functional theory calculations of the spectroscopy of core electrons, Phys. Chem. Chem. Phys., 2010, 12, 12024–12039 RSC.
- K. Lyon, R. Preciado-Rivas and C. Zamora-Ledezma, Charge transfer in time-dependent density functional theory, J. Phys.: Condens. Matter, 2017, 29, 423001 CrossRef PubMed.
- N. T. Maitra, Charge transfer in time-dependent density functional theory, J. Phys. Condens. Matter, 2017, 29, 423001 CrossRef PubMed.
- N. T. Maitra, Double and Charge-Transfer Excitations in Time-Dependent Density Functional Theory, Annu. Rev. Phys. Chem., 2022, 73, 117–140 CrossRef PubMed.
- A. Dreuw and M. Head-Gordon, Failure of Time-Dependent Density Functional Theory for Long-Range Charge-Transfer Excited States: The Zincbacteriochlorin-Bacteriochlorin and Bacteriochlorophyll-Spheroidene Complexes, J. Am. Chem. Soc., 2004, 126, 4007–4016 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, Highly Accurate Prediction of Core Spectra of Molecules at Density Functional Theory Cost: Attaining Sub-electronvolt Error from a Restricted Open-Shell Kohn-Sham Approach, J. Phys. Chem. Lett., 2020, 11, 775–786 CrossRef CAS PubMed.
- L. A. Cunha, D. Hait, R. Kang, Y. Mao and M. Head-Gordon, Relativistic Orbital-Optimized Density Functional Theory for Accurate Core-Level Spectroscopy, J. Phys. Chem. Lett., 2022, 13, 3438–3449 CrossRef CAS PubMed.
- L. S. Cederbaum, W. Domcke and J. Schirmer, Many-body theory of core holes, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 206 CrossRef CAS.
- A. Barth and L. S. Cederbaum, Many-body theory of core–valence excitations, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 23, 1038 CrossRef CAS.
- A. Barth and J. Schirmer, Theoretical core-level excitation spectra of N2 and CO by a new polarisation propagator method, J. Phys. B: At. Mol. Phys., 1985, 18, 867–885 CrossRef CAS.
- S. Coriani, O. Christiansen, T. Fransson and P. Norman, Coupled-cluster response theory for near-edge X-ray-absorption fine structure of atoms and molecules, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 22507 CrossRef.
- J. Kauczor, P. Norman, O. Christiansen and S. Coriani, Communication: A reducedspace algorithm for the solution of the complex linear response equations used in coupled cluster damped response theory, J. Chem. Phys., 2013, 139, 211102 CrossRef PubMed.
- S. Coriani and H. Koch, Communication: X-ray absorption spectra and core-ionization potentials within a core–valence separated coupled cluster framework, J. Chem. Phys., 2015, 143, 181103 CrossRef PubMed.
- J. Wenzel, A. Holzer, M. Wormit and A. Dreuw, Analysis and comparison of CVS-ADC approaches up to third order for the calculation of core-excited states, J. Chem. Phys., 2015, 142, 214104 CrossRef PubMed.
- M. L. Vidal, X. Feng, E. Epifanovsky, A. I. Krylov and S. Coriani, New and Efficient Equation-of-Motion Coupled-Cluster Framework for Core-Excited and Core-Ionized States, J. Chem. Theory Comput., 2019, 15, 3117–3133 CrossRef CAS PubMed.
- L. Triguero, O. Plashkevych, L. G. Pettersson and H. Agren, Separate state vs. transition state Kohn-Sham calculations of X-ray photoelectron binding energies and chemical shifts, J. Electron Spectrosc. Relat. Phenom., 1999, 104, 195–207 CrossRef CAS.
- D. Hait and M. Head-Gordon, Excited State Orbital Optimization via Minimizing the Square of the Gradient: General Approach and Application to Singly and Doubly Excited States via Density Functional Theory, J. Chem. Theory Comput., 2020, 16, 1699–1710 CrossRef CAS PubMed.
- N. A. Besley, A. T. Gilbert and P. M. Gill, Self-consistent-field calculations of core excited states, J. Chem. Phys., 2009, 130, 124308 CrossRef PubMed.
- D. Duflot, J. P. Flament, J. Heinesch and M. J. Hubin-Franskin, The K-shell spectra of tetrahydrofuran studied by electron energy loss spectroscopy and ab initio calculations, Chem. Phys. Lett., 2010, 495, 27–32 CrossRef CAS.
- J. Shim, M. Klobukowski, M. Barysz and J. Leszczynski, Calibration and applications of the ΔmP2 method for calculating core electron binding energies, Phys. Chem. Chem. Phys., 2011, 13, 5703–5711 RSC.
- I. Ljubic, Reliability of density functional and perturbation theories for calculating core-ionization spectra of free radicals, J. Chem. Theory Comput., 2014, 10, 2333–2343 CrossRef CAS PubMed.
- X. Zheng and L. Cheng, Performance of Delta-Coupled-Cluster Methods for Calculations of Core-Ionization Energies of First-Row Elements, J. Chem. Theory Comput., 2019, 15, 4945–4955 CrossRef CAS PubMed.
- X. Zheng, J. Liu, G. Doumy, L. Young and L. Cheng, Hetero-site Double Core Ionization Energies with Sub-electronvolt Accuracy from Delta-Coupled-Cluster Calculations, J. Phys. Chem. A, 2020, 124, 4413–4426 CrossRef CAS PubMed.
- J. Lee, D. W. Small and M. Head-Gordon, Excited states via coupled cluster theory without equation-of-motion methods: Seeking higher roots with application to doubly excited states and double core hole states, J. Chem. Phys., 2019, 151, 214103 CrossRef PubMed.
- M. Huang, C. Li and F. A. Evangelista, Theoretical Calculation of Core-Excited States along Dissociative Pathways beyond Second-Order Perturbation Theory, J. Chem. Theory Comput., 2022, 18, 219–233 CrossRef CAS PubMed.
- C. H. Hu and D. P. Chong, Density functional computations for inner-shell excitation spectroscopy, Chem. Phys. Lett., 1996, 262, 729–732 CrossRef CAS.
- L. Triguero, L. Pettersson and H. Agren, Calculations of near-edge x-ray-absorption spectra of gas-phase and chemisorbed molecules by means of density-functional and transition-potential theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 8097–8110 CrossRef CAS.
- G. S. Michelitsch and K. Reuter, Efficient simulation of near-edge X-ray absorption fine structure (NEXAFS) in density-functional theory: Comparison of core-level constraining approaches, J. Chem. Phys., 2019, 150, 074104 CrossRef PubMed.
- J. Brabec, K. Bhaskaran-Nair, N. Govind, J. Pittner and K. Kowalski, Communication: Application of state-specific multireference coupled cluster methods to core-level excitations, J. Chem. Phys., 2012, 137, 1–5 CrossRef PubMed.
- S. Sen, A. Shee and D. Mukherjee, A study of the ionisation and excitation energies of core electrons using a unitary group adapted state universal approach, Mol. Phys., 2013, 111, 2625–2639 CrossRef CAS.
- A. K. Dutta, J. Gupta, N. Vaval and S. Pal, Intermediate Hamiltonian Fock space multireference coupled cluster approach to core excitation spectra, J. Chem. Theory Comput., 2014, 10, 3656–3668 CrossRef CAS PubMed.
- D. Maganas, J. K. Kowalska, M. Nooijen, S. Debeer and F. Neese, Comparison of multireference ab initio wavefunction methodologies for X-ray absorption edges: A case study on [Fe(II/III)Cl 4] 2-/1-molecules, J. Chem. Phys., 2019, 150 Search PubMed.
- S. M. Garner and E. Neuscamman, Core excitations with excited state mean field and perturbation theory, J. Chem. Phys., 2020, 153, 154102 CrossRef CAS PubMed.
- S. M. Garner and E. Neuscamman, A variational Monte Carlo approach for core excitations, J. Chem. Phys., 2020, 153, 144108 CrossRef CAS PubMed.
- A. T. Gilbert, N. A. Besley and P. M. Gill, Self-consistent field calculations of excited states using the maximum overlap method (MOM), J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed.
- G. M. Barca, A. T. Gilbert and P. M. Gill, Simple models for difficult electronic excitations, J. Chem. Theory Comput., 2018, 14, 1501–1509 CrossRef CAS PubMed.
- K. Carter-Fenk and J. M. Herbert, State-Targeted Energy Projection: A Simple and Robust Approach to Orbital Relaxation of Non-Aufbau Self-Consistent Field Solutions, J. Chem. Theory Comput., 2020, 16, 5067–5082 CrossRef CAS PubMed.
- S. F. Boys, Construction of some molecular orbitals to be approximately invariant for changes from one molecule to another, Rev. Mod. Phys., 1960, 32, 296–299 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, Description of core-excitation spectra by the openshell electron-attachment equation-of-motion coupled cluster method, J. Chem. Phys., 1995, 102, 6735–6756 CrossRef CAS.
- I. E. Brumboiu and T. Fransson, Core–hole delocalization for modeling x-ray spectroscopies: A cautionary tale, J. Chem. Phys., 2022, 156, 214109 CrossRef CAS PubMed.
- J. Liu, D. Matthews, S. Coriani and L. Cheng, Benchmark Calculations of K-Edge Ionization Energies for First-Row Elements Using Scalar-Relativistic Core-Valence- Separated Equation-of-Motion Coupled-Cluster Methods, J. Chem. Theory Comput., 2019, 15, 1642–1651 CrossRef CAS PubMed.
- K. J. Oosterbaan, A. F. White, D. Hait and M. Head-Gordon, Generalized single excitation configuration interaction: An investigation into the impact of the inclusion of non-orthogonality on the calculation of core-excited states, Phys. Chem. Chem. Phys., 2020, 22, 8182–8192 RSC.
- K. Yamaguchi, F. Jensen, A. Dorigo and K. Houk, A spin correction procedure for unrestricted Hartree-Fock and Moller-Plesset wavefunctions for singlet diradicals and polyradicals, Chem. Phys. Lett., 1988, 149, 537–542 CrossRef CAS.
- Y. Kitagawa, T. Saito, Y. Nakanishi, Y. Kataoka, T. Matsui, T. Kawakami, M. Okumura and K. Yamaguchi, Spin contamination error in optimized geometry of singlet carbene (1A1) by broken-symmetry method, J. Phys. Chem. A, 2009, 113, 15041–15046 CrossRef CAS PubMed.
- I. Frank, J. Hutter, D. Marx and M. Parrinello, Molecular dynamics in low-spin excited states, J. Chem. Phys., 1998, 108, 4060–4069 CrossRef CAS.
- M. Filatov and S. Shaik, A spin-restricted ensemble-referenced Kohn-Sham method and its application to diradicaloid situations, Chem. Phys. Lett., 1999, 304, 429–437 CrossRef CAS.
- T. Kowalczyk, T. Tsuchimochi, P.-T. Chen, L. Top and T. Van Voorhis, Excitation energies and Stokes shifts from a restricted open-shell Kohn-Sham approach, J. Chem. Phys., 2013, 138, 164101 CrossRef PubMed.
- D. Hait and M. Head-Gordon, Orbital optimized density functional theory for electronic excited states, J. Phys. Chem. Lett., 2021, 12, 4517–4529 CrossRef CAS PubMed.
- D. Hait, E. A. Haugen, Z. Yang, K. J. Oosterbaan, S. R. Leone and M. Head-Gordon, Accurate prediction of core-level spectra of radicals at density functional theory cost via square gradient minimization and recoupling of mixed configurations, J. Chem. Phys., 2020, 153, 134108 CrossRef CAS PubMed.
- L. M. Balkova and A. Bartlett, Multiple solutions of the single-reference coupledcluster method, Chem. Phys. Lett., 1993, 2, 12 Search PubMed.
- D. A. Matthews, EOM-CC methods with approximate triple excitations applied to core excitation and ionisation energies, Mol. Phys., 2020, 118, e1771448 CrossRef.
- M. Simons and D. A. Matthews, Transition-potential coupled cluster, J. Chem. Phys., 2021, 154, 014106 CrossRef CAS PubMed.
- M. Simons and D. A. Matthews, Transition-Potential Coupled Cluster II: Optimization of the Core Orbital Occupation Number, 2022.
- J. F. Stanton, J. Gauss, J. D. Watts and R. J. Bartlett, A direct product decomposition approach for symmetry exploitation in many-body methods. I. Energy calculations, J. Chem. Phys., 1991, 94, 4334–4345 CrossRef CAS.
- E. Epifanovsky, et al., Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- National Institute of Standards and Technology, Security Requirements for Cryptographic Modules, 2001.
- O. Takahashi, Relativistic corrections for single- and double-core excitation at the Kand L-edges from Li to Kr, Comput. Theor. Chem., 2017, 1102, 80–86 CrossRef CAS.
- M. A. Ambroise and F. Jensen, Probing Basis Set Requirements for Calculating Core Ionization and Core Excitation Spectroscopy by the δ Self-Consistent-Field Approach, J. Chem. Theory Comput., 2019, 15, 325–337 CrossRef CAS PubMed.
- M. A. Ambroise, A. Dreuw and F. Jensen, Probing Basis Set Requirements for Calculating Core Ionization and Core Excitation Spectra Using Correlated Wave Function Methods, J. Chem. Theory Comput., 2021, 17, 2832–2842 CrossRef CAS PubMed.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Basis-set convergence in correlated calculations on Ne, N2, and H2O, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- J. P. Carbone, L. Cheng, R. H. Myhre, D. Matthews, H. Koch and S. Coriani, Advances in Quantum Chemistry, Elsevier Inc., 1st edn, 2019, vol. 79, pp. 241–261 Search PubMed.
- D. E. Woon and T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- K. A. Peterson and T. H. Dunning Jr, Accurate correlation consistent basis sets for molecular core–valence correlation effects: The second row atoms Al–Ar, and the first row atoms B–Ne revisited, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- N. Oliphant and L. Adamowicz, Multireference coupled-cluster method using a singlereference formalism, J. Chem. Phys., 1991, 94, 1229 CrossRef CAS.
- S. A. Kucharski and R. J. Bartlett, Hilbert space multireference coupled-cluster methods. I. the single and double excitation model, J. Chem. Phys., 1991, 95, 8227–8238 CrossRef CAS.
- A. Balkova and R. J. Bartlett, Coupled-cluster method for open-shell singlet states, Chem. Phys. Lett., 1992, 193, 364–372 CrossRef CAS.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly constrained and appropriately normed semilocal density functional, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- A. Kramida and W. C. Martin, A Compilation of Energy Levels and Wavelengths for the Spectrum of Neutral Beryllium (Be I), J. Phys. Chem. Ref. Data, 2009, 26, 1185 CrossRef.
- D. A. Shaw, G. C. King, F. H. Read and D. Cvejanovic, The observation of electricdipole-forbidden inner-shell transitions in N2 and Ar by the electron energy-loss technique, J. Phys. B: At. Mol. Phys., 1982, 15, 1785–1793 CrossRef CAS.
- G. Remmers, M. Domke, A. Puschmann, T. Mandel, C. Xue, G. Kaindl, E. Hudson and D. A. Shirley, High-resolution K-shell photoabsorption in formaldehyde, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 3935–3944 CrossRef CAS PubMed.
- R. N. Sodhi and C. E. Brion, Reference energies for inner shell electron energy-loss spectroscopy, J. Electron Spectrosc. Relat. Phenom., 1984, 34, 363–372 CrossRef CAS.
- A. P. Hitchcock and C. E. Brion, Carbon K-shell excitation of C2H2, C2H4, C2H6 and C6H6 by 2.5 keV electron impact, J. Electron Spectrosc. Relat. Phenom., 1977, 10, 317–330 CrossRef CAS.
- A. P. Hitchcock and C. E. Brion, Inner shell electron energy loss studies of HCN and C2N2, Chem. Phys., 1979, 37, 319–331 CrossRef CAS.
- K. C. Prince, R. Richter, M. De Simone, M. Alagia and M. Coreno, Near edge X-ray absorption spectra of some small polyatomic molecules, J. Phys. Chem. A, 2003, 107, 1955–1963 CrossRef CAS.
- J. Schirmer, A. B. Trofimov, K. J. Randall, J. Feldhaus, A. M. Bradshaw, Y. Ma, C. T. Chen and F. Sette, K-shell excitation of the water, ammonia, and methane molecules using high-resolution photoabsorption spectroscopy, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 1136–1147 CrossRef CAS PubMed.
- A. P. Hitchcock and C. E. Brion, K-shell excitation of HF and F2 studied by electron energy-loss spectroscopy, J. Phys. B: At. Mol. Phys., 1981, 14, 4399–4413 CrossRef CAS.
- A. Muller, D. Bernhardt, A. Borovik, T. Buhr, J. Hellhund, K. Holste, A. L. D. Kilcoyne, S. Klumpp, M. Martins, S. Ricz, J. Seltmann, J. Viefhaus and S. Schippers, Photoionization of Ne Atoms and Ne + Ions Near the K Edge: PrecisionSpectroscopy and Absolute Cross-sections, Astrophys. J., 2017, 836, 166 CrossRef.
- W. L. Jolly, K. D. Bomben and C. J. Eyermann, Core-electron binding energies for gaseous atoms and molecules, At. Data Nucl. Data Tables, 1984, 31, 433–493 CrossRef CAS.
- A. Hempelmann, M. N. Piancastelli, F. Heiser, O. Gessner, A. Rudel and U. Becker, Resonant photofragmentation of methanol at the carbon and oxygen K-edge by highresolution ion-yield spectroscopy, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, 2677–2689 CrossRef CAS.
- J. Shee, M. Loipersberger, A. Rettig, J. Lee and M. Head-Gordon, Regularized secondorder Møller–Plesset theory: A more accurate alternative to conventional MP2 for noncovalent interactions and transition metal thermochemistry for the same computational cost, J. Phys. Chem. Lett., 2021, 12, 12084–12097 CrossRef CAS PubMed.
- V. Carravetta, H. Agren and A. Cesar, Is the core photoelectron band of neon asymmetric or not?, Chem. Phys. Lett., 1991, 180, 358–364 CrossRef CAS.
- M. Coreno, M. De Simone, K. C. Prince, R. Richter, M. Vondracek, L. Avaldi and R. Camilloni, Vibrationally resolved oxygen K → Π * spectra of O2 and CO, Chem. Phys. Lett., 1999, 306, 269–274 CrossRef CAS.
- K. C. Prince, L. Avaldi, M. Coreno, R. Camilloni and M. De Simone, Vibrational structure of core to Rydberg state excitations of carbon dioxide and dinitrogen oxide, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, 2551–2567 CrossRef CAS.
- M. De Simone, M. Coreno, M. Alagia, R. Richter and K. C. Prince, Inner shell excitation spectroscopy of the tetrahedral molecules CX4 (X = H, F, Cl), J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 61–75 CrossRef CAS.
- D. Duflot, J. P. Flament, A. Giuliani, J. Heinesch and M. J. Hubin-Franskin, Core shell excitation of furan at the O1s and C1s edges: An experimental and ab initio study, J. Chem. Phys., 2003, 119, 8946 CrossRef CAS.
- D. Hait, K. J. Oosterbaan, K. Carter-Fenk and M. Head-Gordon, Computing x-ray absorption spectra from linear-response particles atop optimized holes, J. Chem. Phys., 2022, 156, 201104 CrossRef CAS PubMed.
- W. Park, M. Alıas-Rodrıguez, D. Cho, S. Lee, M. Huix-Rotllant and C. H. Choi, Mixed-Reference Spin-Flip Time-Dependent Density Functional Theory for Accurate X-ray Absorption Spectroscopy, ChemRxiv, 2022 DOI:10.26434/chemrxiv-2022-mw4gp.
- C. Ehlert and T. Klamroth, PSIXAS: A Psi4 plugin for efficient simulations of X-ray absorption spectra based on the transition-potential and Δ-Kohn–Sham method, J. Comput. Chem., 2020, 41, 1781–1789 CrossRef CAS PubMed.
- R. C. Couto, L. Kjellsson, H. Agren, V. Carravetta, S. L. Sorensen, M. Kubin, C. Bulow, M. Timm, V. Zamudio-Bayer, B. Von Issendorff, J. T. Lau, J. Soderstrom, J. E. Rubensson and R. Lindblad, The carbon and oxygen K-edge NEXAFS spectra of CO+, Phys. Chem. Chem. Phys., 2020, 22, 16215–16223 RSC.
- X. Zheng, C. Zhang, Z. Jin, S. H. Southworth and L. Cheng, Benchmark relativistic delta-coupled-cluster calculations of K-edge core-ionization energies of third-row elements, Phys. Chem. Chem. Phys., 2022, 24, 13587–13596 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: For both excitations and ionizations via the three ΔCC schemes, the following data is provided: SCF energies, correlation energies, SCF and CCSD 〈S〉2 values. For the ROKS(SCAN) and FC-CVS-EOM-EE-CCSD and FC-CVS-EOM-IP-CCSD calculations, the excitation energies are provided. See DOI: https://doi.org/10.1039/d2cp01998a |
| This journal is © the Owner Societies 2022 |