The carbon chain growth during the onset of CVD graphene formation on γ-Al₂O₃ is promoted by unsaturated CH₂ ends

Abstract

Chemical vapor deposition of methane onto a template of alumina (Al₂O₃) nanoparticles is a prominent synthetic strategy of graphene meso-sponge, a new class of nano porous carbon materials consisting of single-layer graphene walls. However, the elementary steps controlling the early stages of graphene growth on Al₂O₃ surfaces are still not well understood. In this study, density functional theory calculations provide insights into the initial stages of graphene growth. We have modelled the mechanism of CH₄ dissociation on the (111), (110), (100), and (001) γ-Al₂O₃ surfaces. Subsequently, we have considered the reaction pathway leading to the formation of a C6 ring. The γ-Al₂O₃(110) and γ-Al₂O₃(100) are both active for CH₄ dissociation, but the (100) surface has higher catalytic activity towards the carbon growth reaction. The overall mechanism involves the formation of the reactive intermediate CH₂* that then can couple to form C_nH_2n* (n = 2–6) intermediates with unsaturated CH₂ ends. The formation of these species, which are not bound to the surface-active sites, promotes the sustained carbon growth in a nearly barrierless process. Also, the short distance between terminal carbon atoms leads to strong interactions, which might lead to the high activity between unsaturated CH₂* of the hydrocarbon chain. Analysis of the electron localization and geometries of the carbon chains reveals the formation of C–Al–σ bonds with the chain growing towards the vacuum rather than C–Al–π bonds covering the γ-Al₂O₃(100) surface. This growth behaviour prevents catalyst poisoning during the initial stage of graphene nucleation.

---

1. Introduction

Graphene, an atomic thick layer of carbon, has been called a ‘wonder material’ due to its superior properties such as its high charge carrier mobility, high optical transmissivity, high tensile strength, and excellent thermal conductivity.^1–4 Geim and Novoselov first produced graphene by using a mechanical exfoliation technique using Scotch® tape, which provides monolayer and defect-free graphene.¹ However, this method is only applicable to small-area production. A variety of methods have then been developed to produce large-area and high-quality graphene including chemical exfoliation,¹ electrochemical exfoliation,^5,6 chemical synthesis,^7,8 and chemical vapor deposition (CVD).^9,10 Among these techniques, CVD is one of the most promising synthesis methods because it can produce monolayer graphene over a large area.^7,8,11–14

Various hydrocarbon feedstocks have been successfully used as carbon sources, ranging from gases such as methane (CH₄)^3,15,16 and ethylene,¹⁷ liquids such as benzene,¹⁸ to solids such as polymethylmethacrylate (PMMA)¹⁹ and amorphous carbon thin films.^20,21 Since it can generate single-layered graphene (SLG), the most popular combination of carbon feedstock and substrates for graphene production is CH₄ on Cu.²² In addition to Cu, different metal substrates, including Ni,^14,23–26 Ru,^27–29 Ir,^30–32 Co,^33,34 Fe,³⁵ Au,³⁶ Rh,³⁷ Pt,^38,39 and their alloys,^40,41 have been used for CVD synthesis of graphene films. Also, graphene layers can directly grow on insulating substrates such as SiC,^41,42 sapphire,⁴³ SiO₂,^44,45 and h-BN.^46,47 Previously, Li et al.^48,49 provided an atomic picture of the step-by-step nucleation process of graphene growth on the metal Cu (111) surface. This work demonstrated that at the early stages of the CVD process, linear chains form on the Cu surface, followed by Y-type (furcate) carbon species when new carbon atoms absorb on the side of the linear chains. Finally, ring-containing carbon species and graphene islands form spontaneously stepwise.

Recently, oxides of earth abundant catalysts without noble metal supporting like MgO,⁵⁰ CaO,⁵¹ and Al₂O₃⁵² have been reported as substrates in the synthesis of novel graphene meso-sponge (GMS), a new class of mesoporous carbon materials consisting mainly of single-layer graphene walls with a unique set of properties compared to traditional graphene materials: higher surface area, more developed mesopores, higher oxidation resistance,^53,54 higher softness and elasticity, lower bulk modulus, and force-driven reversible liquid–gas phase transition.⁵⁵ But until now, there is a lack of an atomistic description of the steps controlling the early stages of graphene nucleation on metal oxides. Hence, a better understanding of the reaction mechanisms is required to modify the catalytic sites and make them more active in the processes involved. These processes include the activation of adsorbed methane (CH₄*), formation of carbon–hydrogen nuclei, and the subsequent edge growth of graphene islands. By combining experiments and density functional theory (DFT), we previously found that oxygen vacancies on the metal oxide surface of γ-Al₂O₃,^56,57 play an influential role in the CH₄* activation. Park et al. reported calculations of the graphene nucleation mechanism on γ-Al₂O₃.⁵⁷ In this work, the hypothesis was that growth occurs from adsorbed carbon (C*) atoms. Page et al.⁵⁸ also reported graphene nucleation on γ-Al₂O₃ using a simplified surface model that did not consider hydroxylated surfaces, which we recently demonstrated to be important in experimental conditions.⁵⁶

In this work, we focus on the mechanism of carbon chain growth during the initial stages of graphene formation on hydroxylated models of γ-Al₂O₃ using DFT calculations. CH₄* activation and the early stages of graphene nucleation occur preferentially on the γ-Al₂O₃ (100) surface. In the complete dehydrogenation process from CH₄* to C*, methylene (CH₂*) is the most stable species on the γ-Al₂O₃ surface whilst C* is highly unstable. The CH₂* radical is involved in the CH₄ conversion into various C_nH_2n* (n = 2–6) intermediates to form carbon chains on γ-Al₂O₃ (100) during the initial CVD of graphene.

2. Computational details

The “Vienna ab initio simulation package” (VASP.5.4.1) was used to conduct spin polarized DFT calculations. The Perdew–Burke–Ernzerhof (PBE) generalized-gradient approximation (GGA) was adopted to describe the exchange and correlation terms,⁵⁹ together with the Grimme's-D3 dispersion correction⁶⁰ to provide a more accurate description of the ionic induce dipole interaction than standard DFT–GGA methods.⁶¹ A plane-wave basis set was employed within the framework of the projector augmented wave method.⁶² The transition states (TSs) for the elementary reactions were located using the climbing image nudged elastic band (CI-NEB) method,⁶³ setting the convergence criteria at 0.05 eV Å⁻¹ during the TS searching.¹ A Monkhorst–Pack k-point grid of (3 × 3 × 1) and a plane-wave cut-off of 450 eV were used throughout calculations. All atoms were relaxed during the structural optimization of γ-Al₂O₃ and reaction intermediates.

Our previous IR experiments showed that isolated hydroxyl (OH) groups (around 3701 cm⁻¹) at the γ-Al₂O₃ surfaces are present even after annealing at 900 °C for 30 min.⁵⁶ Therefore, the surface of γ-Al₂O₃ was modelled using a supercell approach with periodic boundary conditions. The coordinates of γ-Al₂O₃ (the P2₁/m space group)⁶⁴ were used as the starting geometry to optimise the internal coordinates and cell parameters of the bulk structure of γ-Al₂O₃.⁶⁵ The values of the optimized lattice parameters of γ-Al₂O₃ were a = 5.538 Å, b = 8.347 Å, c = 8.024 Å, β = 90.60° and α = β = 90.00° (Fig. S1, ESI†). The partially hydroxylated slabs of γ-Al₂O₃ (100), γ-Al₂O₃ (110), γ-Al₂O₃ (001), and γ-Al₂O₃ (111) surface containing four atomic layers of the oxide and 15 Å vacuum were constructed starting from the optimised bulk structure. All atoms were relaxed during the optimization. The structures of the surfaces are provided in Section S2 of the ESI.† The mechanisms of CH₄ activation and the early stages of graphene nucleation were investigated using the OH-covered γ-Al₂O₃ (111), γ-Al₂O₃ (110) and γ-Al₂O₃ (001) surfaces. These models are shown in Fig. S2 (ESI†). The adsorption energies of CH₄ on the γ-Al₂O₃ surfaces were computed using the following expression:

E_ads = E(adsorbate⋯CH₄) − E(CH₄) − E(slab) (1)

where the first term is the energy of the optimized surface slab with CH₄ adsorbed, the second term is the energy of the isolated optimized adsorbed molecule, and the third term is the energy of the optimized bare surface slab. A negative value of E_ads corresponds to an exothermic adsorption process. The free energy differences of the elementary steps were computed according to the following expression:

ΔG = ΔE_DFT + ΔE_ZPE − TΔS (2)

where ΔE_DFT is the total energy difference from the DFT calculations, ΔE_ZPE is the zero-point energy (ZPE) correction from the frequency analysis, and TΔS is the entropy contribution in which the T was fixed at the experimental conditions of T = 1000 K.⁵⁶

3. Results and discussion

3.1 Methane activation on γ-Al₂O₃

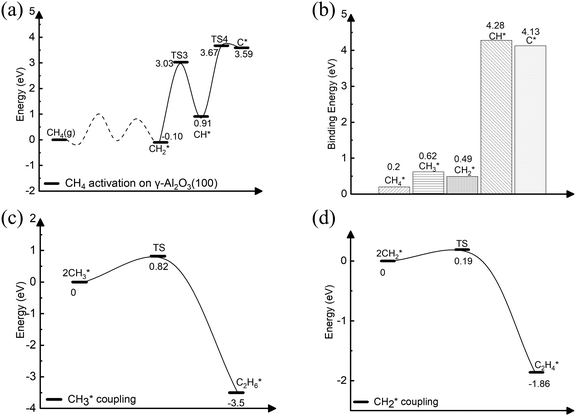
We report the calculations of the intermediates and transition states of the first two steps of the CH₄* dehydrogenation, CH₄* → CH₃* + H* and CH₃* → CH₂* + H*. The profiles in Fig. 1 show the ability to activate CH₄* depending on the surface of γ-Al₂O₃: (100), (110), (111), and (001). The structures of the intermediates and transitions states on the γ-Al₂O₃ (100) surface are reported in Fig. 2. For the other surfaces, these structures are shown in Fig. S3 of the ESI.†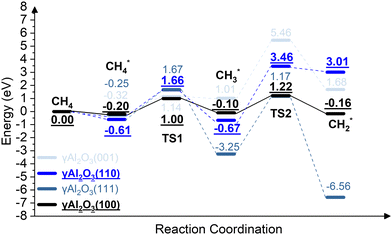

Fig. 1 The energy profiles of the first two steps of the CH₄* dehydrogenation, CH₄* → CH₃* + H* and CH₃* → CH₂* + H*, on the γ-Al₂O₃ (001), γ-Al₂O₃ (111), γ-Al₂O₃ (110), and γ-Al₂O₃ (100) surfaces.

Fig. 2 The structures of intermediates and transition states of the first two CH₄* dehydrogenation steps on the γ-Al₂O₃ (100) surface. (a) Al₂O₃(100); (b) CH₄*; (c) TS1; (d) CH₃*; (e) TS2; (f) CH₂*. (Red, blue, grey, and white spheres represent O, Al, C, and H, respectively).

On γ-Al₂O₃ (100), after the exothermic adsorption of CH₄* (E_ads = −0.20 eV), the breakage of the first C–H bond has a barrier of 1.20 eV and a reaction energy of 0.10 eV. The subsequent dehydrogenation of CH₃* has a barrier of 1.32 eV and reaction energy of −0.06 eV. The barriers for the dissociation step CH₄* → CH₃* + H* on the (111), (001), and (110)^57,66 are 1.92 eV, 1.46 eV, and 2.20 eV, respectively (Fig. 1). The subsequent step, CH₃* → CH₂* + H*, on these surfaces requires even higher barriers. Consequently, the first two CH₄* dehydrogenation steps are kinetically favorable on the γ-Al₂O₃ (100) surface. Martínez et al. reported that CH₂* leads to spontaneous C–C chain growth.⁶⁷ Hence, the ability to promote the CH₃* dehydrogenation step to generate a stable CH₂* species will also denote the catalytic activity towards carbon growth. However, CH₂* will be a trapped species on the (111) surface due to highly exothermic conversion energies depicted in Fig. 1. We have considered the γ-Al₂O₃ (100) surface to investigate the subsequent steps of CH₂* coupling that initiates the graphene growth due to its favorable CH₄ dissociation properties (Fig. 1). Note also that the (111) surface is more unstable than the (100) and (110) surfaces.⁶⁸ In addition, the C–H bond activation barrier on the three-coordinated Al site of the γ-Al₂O₃ (110) surface obtained in this work (1.9 eV) is slightly higher than the one reported by Wischert et al. (1.6 eV).⁶⁹ Such a difference might be mainly related to differences in the surface model and methods adopted, including the OH coverage, surface unit size, the distance between OH and active sites as well as exchange–correlation functional, pseudopotentials used in the calculations. However, the barriers of the CH₄* → CH₃* + H* and CH₃* → CH₂* + H* steps on the (100) surface are 1.0 eV and 1.2 eV, respectively. These barriers are still lower than the value of 1.6 eV reported by Wischert et al. for the (110) surface. In this work the conclusion that the first two CH₄* dehydrogenation steps are kinetically favourable on (100) is still significant.

Park et al.^57,66 and Cholewinski et al.^57,66 reported that γ-Al₂O₃ (110) can have different levels of hydroxyl coverages that in turn could affect the strength of CH₄* interaction with the surface. The work by Digne et al. on the stability of the γ-Al₂O₃ (110) surface as a function of temperature for different hydroxyl coverage⁶⁸ showed that at T = 1000 K, the approximate temperature necessary to grow porous nanographene on γ-alumina nanoparticles,^56,57 the low OH coverage model (2OH/θ = 2.4 nm⁻²) is the most stable surface. Moreover, in our previously reported experimental work of the CH₄-CVD, air and moisture were excluded by supplying Ar and CH₄ gases,⁵⁴ which decreases the concentration of hydroxyl groups as the reaction proceeds. These previous reports justify the use of a low OH coverage model for the γ-Al₂O₃(110) surface.

3.2 Contribution of the (100) and (110) surfaces to CH₂ generation

CH₂ generation on the γ-Al₂O₃ surface is a pseudo-first order reaction on the methane partial pressure.⁵⁶ If the entropy contribution is negligible, the activation rate constant k can be approximated with an Eyring-like equation as a function of reaction temperature T,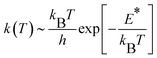where k_B and h are the Boltzmann and Planck constants, and E* represents the effective activation energy experimentally measurable via Arrhenius plots.⁷⁰ Here, we use the rate constant k to evaluate the contributions of the (100) and (110) surfaces on the CH₄ activation. For the (100) surface, the CH₄ is weakly physisorbed on the surface (E_ads (CH₄*) = −0.20 eV) and E* is calculated as the energy difference between E_ads (TS2) and E_ads (CH₄). For (110), the CH₄ adsorption energy (E_ads (CH₄*) is −0.61 eV) and E* is the difference between E_ads (TS2) and E_ads (CH₄*).⁶⁷Table 1 summarizes the effective activation energies and rate constants at T = 900 °C. The value of E* = 1.22 eV for (100) agrees with the experimental value (1.29 eV). The associated value of k (T = 900 °C) is 1.40 × 10⁸ s⁻¹. For (110), the value of E* = 3.46 eV is larger and, consequently, the rate is negligibly small (k (T = 900 °C) = 8.74 × 10² s⁻¹). The generation of CH₂ is, therefore, likely to occur on the (100) surface. The hydroxylated surface can generate CH₃, as shown in Fig. 1. However, subsequent dehydrogenation is kinetically unfavorable. Hereafter, we focus on the reactions on the (100) surface.

Table 1 Effective activation energies (E*) for the generation of CH₂ with the associated rate constants k(T) at T = 900 °C were obtained using eqn (2)

Surface	E* (eV)	k (s^−1)
a Rate constant estimated using the experimental barrier.^56
(100)	1.22	1.40 × 10^8
(110)	3.46	8.74 × 10^2
Experiment^a	1.29	7.01 × 10^7

---

3.3 Onset of graphene formation: methylene coupling and carbon chain growth

The complete dehydrogenation of CH₄ on γ-Al₂O₃ would lead to the formation of an adsorbed carbon atom (C*). We have computed the energy profile of CH₄ dehydrogenation on γ-Al₂O₃ (100) as a representative surface leading to C*. Fig. 3(a) shows that while the first two dehydrogenation steps CH₄* → CH₃* + H* and CH₃* + H* → CH₂* + 2H* are both favourable, the subsequent steps CH₂* + 2H* → CH* + 3H* and CH* + 3H* → C* + 4H* are endothermic with high activation barriers. But since the pyrolytic carbon deposition of CH₄ occurs at temperatures higher than 800 °C,⁵⁶ CH₄ could still dissociate into CH₃*, CH₂*, CH* and C* species on the catalyst surface. To verify the relative stability of these species, we have compared in Fig. 3(b) the binding energies (E_b) of CH_n (n = 0–4) on γ-Al₂O₃ (100). For CH₄*, CH₃*, and CH₂*, the values of E_b are 0.2, 0.6, and 0.5 eV, respectively, but for CH* and C* they are above 4 eV. According to the Sabatier principle, the strong binding of CH* and C* on γ-Al₂O₃ (100) may poison the active centres. Therefore, we propose that the initial CVD growth of graphene on alumina does not involve CH* and C* species. The next steps in the formation of C–C bonds on the γ-Al₂O₃ (100) surface are the coupling reactions 2CH₃* → C₂H₆* (Fig. 3(c)) and 2CH₂* → C₂H₄* (Fig. 3(d)). The pathway leading to C₂H₄* in Fig. 3(d) has a lower activation barrier (0.2 eV) compared to C₃H₆* (0.8 eV) in Fig. 3(c). Moreover, the subsequent coupling of CH₃* with the C₂H₆* intermediate is unlikely to occur as the CH₃ ends of the molecule are saturated (the C atom has reached the four coordination), inhibiting further growth as shown in Fig. S4 of the ESI.† We have also calculated the dehydrogenation of C₂H₆* into C₂H₄* but this process is both kinetically hindered (overall E_a = 4.01 eV) and thermodynamically unfavourable (overall ΔE = 2.05 eV) as shown in Fig. S5 (ESI†). Based on the above results, we conclude that CH₂* is the key intermediate for the subsequent carbon growth steps on the γ-Al₂O₃ (100) surface.

Fig. 3 Energy profiles of the CH₄* dissociation, CH_x* (x = 0–4) binding, and CH_y* (y = 2, 3) coupling reaction on the γ-Al₂O₃ (100) surface. (a) Complete CH₄* dehydrogenation; (b) binding energies of CH₄*, CH₃*, CH₂*, CH* and C; (c) CH₃* coupling; (d) CH₂* coupling. The asterisk (*) denotes a molecule adsorbed on the γ-Al₂O₃ (100) surface.

Starting from C₂H₄*, we have considered the methylene coupling processes to form linear C_nH_2n* (n = 3–6) species and the C₆H₁₂ ring unit, the minimal unit of graphene on γ-Al₂O₃ (100). The energy profile of the chain growth reactions and the corresponding snapshots are shown in Fig. 4 and 5, respectively. Like the CH₂* to C₂H₄* coupling reaction, Fig. 4 shows that the subsequent methylene coupling processes are thermodynamically favourable with each adsorption step, C_nH_2n + CH₂(g) → C_nH_2n + CH₂*, having negative reaction energies of approximately −2 eV. The formation of the linear species C₂H₄*, C₃H₆*, C₅H₁₀*, and C₆H₁₂* and of the C6 ring have low activation barriers, all well below 1 eV. The exception is the step CH₂* + C₃H₆* →C₄H₈* with an activation energy of 1.87 eV (see Section 3.4 for explanation).

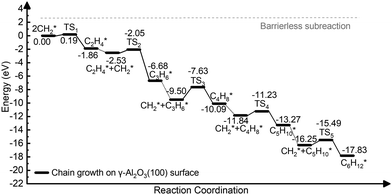Fig. 4 Energy profile of the formation of C_nH_2n* (n = 2–6) species via CH₂* coupling on the γ-Al₂O₃ (100) surface.

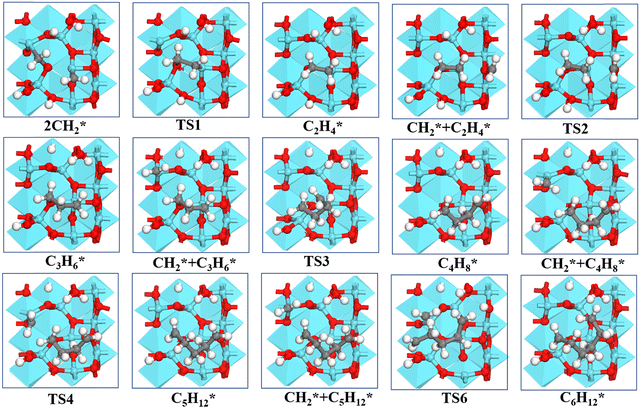Fig. 5 Structures of the formation of C_nH_2n* (n = 2–6) species via CH₂* coupling on the γ-Al₂O₃ (100) surface.

The formation of CH₂* from CH₄ is favourable in entropy but unfavourable in enthalpy on most facets. However, chain growth and cyclization are favourable in enthalpy and unfavourable in entropy. Both factors impact the reaction kinetics and, consequently, how fast the graphene layer grows. To address the role of entropy, we have performed frequency calculations of the reaction intermediates in Fig. 4 involved in C_nH_2n* (n = 2–6) species formation via CH₂* coupling on the γ-Al₂O₃ (100) surface. The Gibbs free energy diagram confirms that the chain growth is overall a thermodynamically favourable process as well. In the calculation of the reaction barriers, the ZPEs for some systems are non-negligible,^71,72 while in some surface catalytic reactions, adsorption removes many of the degrees of freedom associated with the reaction vacuum, and the ZPE contribution would be negligible relative to the calculated electronic energy.⁷³ Since our case is similar to the latter, we have neglected ZPE corrections in reaction barrier calculations. These results confirm that the role of unsaturated CH₂* ends for carbon chain growth during the graphene nucleation stage, which makes the initial growth process highly favourable.

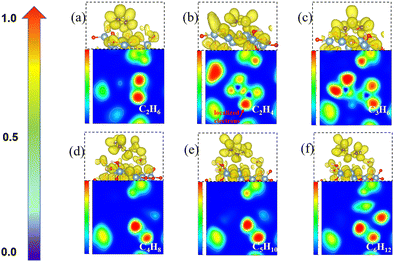
3.4 The role of unsaturated CH₂ end in promoting graphene growth

To understand the process of CH₂* coupling leading to the carbon chain growth on the γ-Al₂O₃ (100) surface, we have computed the electron localization function (ELF) of the linear C_nH_2n (n = 2–6) intermediates. The ELF maps in Fig. 6 represent the electron cloud localized and delocalized around atoms. Using this information, we can determine critical points, chemical bonds, and regions relevant for reactivity (red and orange).

Fig. 6 The electron localization function maps and corresponding side view structures with localized electrons of the C_nH_2n* (n = 2–6) species on the γ-Al₂O₃ (100) surface: (a) C₂H₆*; (b) C₂H₄*; (c) C₃H₆*; (d) C₄H₈*; (e) C₅H₁₀*; and (f) C₆H₁₂*. Ongoing from the blue to the red area, there is an increase in the electron density (red areas indicate electron localization).

The ELF map for the C₂H₄* structure in Fig. 6(b) shows a localized electron around one end of CH₂* (red area) and a lower electronic charge density distribution around the other end. This weakly saturated CH₂* end allows coupling with free CH₂* on the γ-Al₂O₃ (100) surface making the formation of C₂H₄* highly favorable (Fig. 4). When the longer carbon chains C₄H₈*, C₅H₁₀* and C₆H₁₂* are formed, the sole CH₂* in one position of C_nH_2n* is located on the γ-Al₂O₃ (100) surface as shown in Fig. 6(d)–(f). Consequently, the initial growth direction of carbon occurs in the vacuum, away from the surface, and the long carbon species form a C–Al–σ bond with the γ-Al₂O₃ (100) surface rather than grow along the catalytic surface to form a C–Al–π bond. This protects the CVD graphene nucleation reaction sites on γ-Al₂O₃ (100). Otherwise, the accumulation of C_nH_2n* species on the surface would poison the catalyst in the early stage by covering these heavy carbon species on the surface. This ‘loop’ away surface carbon growth mechanism was previously proposed by Zhu et al.⁷⁴ in the case of Ni clusters.

The ELF analysis can be used to rationalize the high activation energy (1.87 eV) of the CH₂* + C₃H₆* coupling step shown in Fig. 4. The ELF map of C₃H₆* (Fig. 6(c)) shows the high localization of the electron density on both ends of CH₂* ends in C₃H₆* on the catalyst surface. The high barrier is because the two ends of C₃H₆* are bound to the surface-active sites forming highly hindered carbon ends. This is not beneficial for the coupling with the next CH₂*. Therefore, we propose that the carbon chain growth mechanism mostly involves the free CH₂* ends. The work by Lidia Martínez et al.⁶⁷ also demonstrated that the presence of CH₂ leads to efficient C–C chain growth producing micron-length fibres under metal-catalyst-free gas-phase synthesis. This situation leads to a high barrier for the CH₂* + C₃H₆*→ C₄H₈* step (Fig. 4) as both the CH₂* ends have been bonded with surface hindering further reaction. Therefore, unsaturated CH₂* species play a crucial role in promoting the nucleation reaction on γ-Al₂O₃.

The detachment after the carbon chain growth on γ-Al₂O₃(100) can be rationalized because the length between the C_nH_2n ends and the active sites on the catalyst surface increases with the chain growth (Fig. S7, ESI†). This is beneficial for the release of the carbon chain as reported by Martínez et al.⁶⁷ In long carbon chains, the unsaturated CH₂* end would drive sustainable chain growth. There is also a termination pathway that involves the coupling of such open ends with CH₃* species (1.83 eV barrier and −1.79 exothermic reaction energy, as shown in Fig. S8, ESI† depicted). This path would suppress the chain growth as the saturated hydrocarbon will desorb, especially if it occurs at the early stage. Thus, not all reactions will lead to the formation of graphene as there are parallel reactions that form other heavier hydrocarbons which also compete for methane.⁵⁶

The length of the C–C bonds in the C_nH_2n species binding on γ-Al₂O₃(100) expands with the chain length (Fig. 7), which could support the carbon units growing away from the γ-Al₂O₃ (100) surface with the formation of C–Al–σ bonds rather than C–Al–π bonds covering the surface.⁶⁷ In addition, the C–C length between carbon atoms close to the solid surface is longer than the C–C length of the carbon atoms away from the surface. For instance, the structure of C₆H₁₂* in Fig. 7(g) shows that for the C atoms in the middle positions, C1, C2, C3 and C4, the distances are d(C1–C2) = 1.54 Å, d(C1–C3) = 1.54 Å, d(C2–C4) = 1.54 Å. In comparison, for the terminal C atoms, C5 and C6, d(C4–C6) = 1.49 Å and d(C3–C5) = 1.49 Å. A similar situation can be found in C₄H₈* and C₅H₁₀*. Short bond lengths between terminal carbons correspond to strong interatomic interaction, which might contribute to the high activity among the unsaturated CH₂* of the hydrocarbon chain.

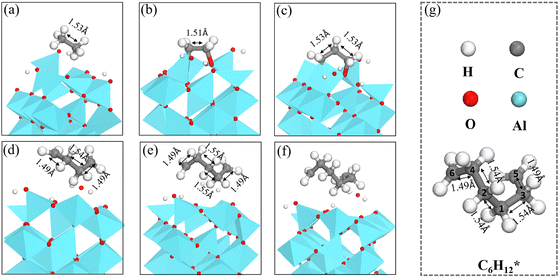Fig. 7 The structures of (a) C₂H₆*, (b) C₂H₄*, (c) C₃H₆*, (d) C₄H₈*, (e) C₅H₁₀*, (f) and C₆H₁₂* on γ-Al₂O₃(100). (g) Bond lengths in C₆H₁₂*.

3.5 Dehydrogenation of C_nH_2n species and ring condensation

Methylene coupling reaction on γ-Al₂O₃ leading to C_nH_2n species is favorable compared to the complete CH₄* dehydrogenation (Fig. 3(a) and 4). Consequently, according to our simulations the species involved in the early stage of graphene growth will contain hydrogen atoms. Previous experimental works showed that metal oxides such as alumina⁷⁵ and zirconia⁷⁶ can effectively catalyze the dehydrogenation of small alkanes such as propane at high temperatures.

Given the high temperature used in the CVD process, we have computed the dehydrogenation of the intermediates C₃H₆* and C₆H₁₂* with unsaturated CH₂ ends: C₃H₆* to C₃H₄* and C₆H₁₂* to C₆H₁₀*. In a related computational study, Dixit and co-workers investigated the propane dehydrogenation on γ-Al₂O₃ according to two possible surface mechanisms: the concerted and stepwise pathways.^77,78 In the former the olefin formation occurs in a single step, whereas the latter occurs sequential abstraction of hydrogen atoms from the reactant. For the propane molecule, Dixit and co-workers concluded that the concerted pathway was preferred over the stepwise mechanism. As the C_nH_2n* intermediates considered in this study (Fig. 5) are not alkanes, as in the work by Dixit and co-workers,⁷⁸ but hydrocarbon chains with unsaturated CH₂* ends they will behave differently.

The energy profiles of C₃H₆* and C₆H₁₂* dehydrogenation according to the concerted mechanism are reported in Fig. S9 of the ESI.† In the concerted pathway, the initial step (C–H activation) involves a six-membered transition state, and the dehydrogenation of C_nH_2n* generates two surface-bound hydrogens on the acid–base pair. In the second step (H₂ production), the two surface-bound hydrogen atoms recombine to form molecular hydrogen. For both C₃H₆* and C₆H₁₂* unsaturated intermediates, the dehydrogenation and H₂ formation steps have much higher reaction energies and activation barriers than those reported by Dixit et al. for propane on γ-Al₂O₃ (100).⁷⁸ The energy profiles of C₃H₆* and C₆H₁₂* dehydrogenation, computed according to the stepwise mechanism, are reported in Fig. S10 of the ESI.† In the stepwise pathway, the initial step (C–H activation) occurs by the abstraction of a proton by a surface oxygen atom followed by a H₂ formation through β-hydrogen elimination⁷⁸ elimination. Notwithstanding, the stepwise pathway (Fig. S10, ESI†) is favoured compared to the concerted one (Fig. S9, ESI†), and the stepwise dehydrogenation reactions have much higher activation barriers than the CH₂* coupling reaction in Fig. 4.

The carbon coupling reaction forming a C6 ring was also explored since it represents the early stage of graphene nucleation.⁷⁹ As shown in Fig. 8, the ring formation from C₆H₁₂* is energetically favourable (−3.09 eV) and has a low activation barrier (0.34 eV). The calculations suggest that even at the high temperatures at which CVD occurs, the dehydrogenation of the C₂H_2n intermediates during initial stage is unlikely because the process is kinetically and thermodynamically unfavourable compared to the ring formation. In addition, as depicted in Fig. S10 (ESI†), the activation barriers of the two elementary dehydrogenation steps of C₃H₆* (4.15 eV and 3.85 eV) are much higher than those of C₆H₁₂* (1.58 eV and 1.96 eV). This could indicate that the dehydrogenation of longer carbon chains could be easier than that of short ones. Thus, in the initial nucleation stage, small-size carbon species may not be stable without hydrogen until they grow to a specific size.

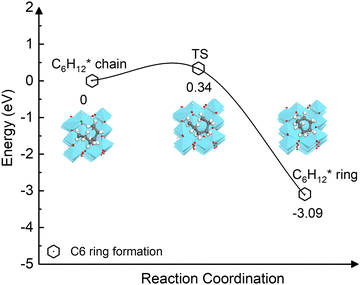Fig. 8 Energy profile of the ring formation from the carbon chain C₆H₁₂* species on the γ-Al₂O₃ (100) surface.

These results indicate that the initial steps of graphene growth involve carbon species that contain hydrogen atoms and confirm that the process does not occur through the formation of single carbon. These hydrogen atoms could also hinder the formation of a binding carbon island covering the catalyst surface. Based on these results, an interesting question is when hydrogen-free graphene flake would nucleate. A possible mechanism is that small carbon-containing species are not stable without hydrogen until they grow to a defined size. However, in the early nucleation stage, hydrogen transfer among carbon atoms is much easier than hydrogen desorption from carbon (Fig. S11, ESI†). In perspective, we look forward to answering this question with our future work and understanding the link between hydrogen-free graphene nucleation and hydrocarbon sub-intermediates.

4. Conclusions

This work has reported a systematic investigation of the mechanism of CH₄* dissociation and formation of C_nH_2n (n = 2–6) species on γ-Al₂O₃. We found γ-Al₂O₃ (100) to be the most active for the CH₄* dissociation compared with other low-index surfaces of γ-Al₂O₃. On the (100) surface, methylene coupled to C₂H₄* is kinetically and thermodynamically favoured over the complete CH₄* dehydrogenation to C. Starting from C₂H₄*, we have modelled the formation of linear C_nH_2n* (n = 3–6) species and the C₆H₁₂ ring unit, which is the fundamental graphene unit. We found that this early carbon chain formation stage before graphene nucleation is nearly barrierless. Electron localization function and structural analyses of carbon chains reveal that the early stages of nucleation involve the formation of C–Al–σ bonds with chains “looping” away from the catalyst surface and the unsaturated CH₂* end remaining active. This is favorable for the initial steps of graphene growth. Our calculations show that hydrogenated carbon species are involved in the early stages of graphene nucleation. These protective bonded hydrogen atoms could weaken the direct C–Al interaction and protect the active sites from carbon covering the γ-Al₂O₃ (100) surface. In summary, our calculations illustrate the first steps of graphene nucleation on γ-Al₂O₃ surfaces and provide insight into the role of active species during the catalytic process.

Author contributions

Qi Zhao, Rachel Crespo-Otero and Devis Di Tommaso conceived and designed the project, and summarized all the ideas provided by co-authors. Qi Zhao conducted the quantum chemistry calculations and wrote the original draft. Hirotomo Nishihara, Masanori Yamamoto, and Kaoru Yamazaki provided valuable comments and suggestions for the original draft. All authors contributed to review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Cooperative Research Program for CORE lab of “Five-star Alliance”, JST SICORP Grant no. JPMJSC2112, Ensemble Grant for Early Career Researchers at Tohoku University, and the UK's Royal Society International Exchanges Cost Share (IEC\R3\193106). Q. Z. thanks the China Scholarship Council for financial support. K. Y. is grateful for the financial support from the Building of Consortia for the Development of Human Resources in Science and Technology funded by MEXT and the Core Research for Evolutional Science and Technology of the Japan Science and Technology Agency (JST CREST, Grant No. JPMJCR16P3). D. D. T. acknowledges the ACT program (Accelerating CCS Technologies, Horizon2020 Project No. 294766), which funded the FUNMIN project. Financial contributions were made from Department for Business, Energy & Industrial Strategy (BEIS) together with extra funding from NERC and EPSRC research councils, United Kingdom, ADEME (FR), MINECO-AEI (ES). We are grateful to the UK Materials and Molecular Model-ling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service (https://www.archer.ac.uk). This research utilized Queen Mary's Apocrita HPC facility, supported by QMUL Research-IT. https://doi.org/10.5281/zenodo.438045.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
2. A. Balandin, Nat. Mater., 2011, 10, 569–581.
3. A. A. Balandin, Nat. Nanotechnol., 2010, 5, 574–578.
4. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388.
5. P. Yu, S. E. Lowe, G. P. Simon and Y. L. Zhong, Curr. Opin. Colloid Interface Sci., 2015, 20, 329–338.
6. J. Liu, Graphene-based composites for electrochemical energy storage, Springer, Singapore, 2017.
7. S. Eigler, M. Enzelberger-Heim, S. Grimm, P. Hofmann, W. Kroener, A. Geworski, C. Dotzer, M. Röckert, J. Xiao and C. Papp, Adv. Mater., 2013, 25, 3583–3587.
8. S. Stankovich, D. A. Dikin, R. D. Piner, K. A. Kohlhaas, A. Kleinhammes, Y. Jia, Y. Wu, S. T. Nguyen and R. S. Ruoff, Carbon, 2007, 45, 1558–1565.
9. A. Reina, S. Thiele, X. Jia, S. Bhaviripudi, M. S. Dresselhaus, J. A. Schaefer and J. Kong, Nano Res., 2009, 2, 509–516.
10. X. Li, W. Cai, L. Colombo and R. S. Ruoff, ACS Nano Lett., 2009, 9, 4268–4272.
11. K. Parvez, S. Yang, X. Feng and K. Müllen, Synth. Met., 2015, 210, 123–132.
12. Y. Zhang, L. Zhang and C. Zhou, Acc. Chem. Res., 2013, 46, 2329–2339.
13. M. A. Azam, N. N. Zulkapli, N. Dorah, R. N. A. R. Seman, M. H. Ani, M. S. Sirat, E. Ismail, F. B. Fauzi, M. A. Mohamed and B. Y. Majlis, ECS J. Solid State Sci. Technol., 2017, 6, M3035–M3048.
14. A. Reina, X. Jia, J. Ho, D. Nezich, H. Son, V. Bulovic, M. S. Dresselhaus and J. Kong, ACS Nano Lett., 2009, 9, 30–35.
15. X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung and E. Tutuc, Science, 2009, 324, 1312–1314.
16. J. K. Wassei, M. Mecklenburg, J. A. Torres, J. D. Fowler, B. Regan, R. B. Kaner and B. Weiller, Small, 2012, 8, 1415–1422.
17. L. Gao, J. R. Guest and N. P. Guisinger, ACS Nano Lett., 2010, 10, 3512–3516.
18. Z. Li, P. Wu, C. Wang, X. Fan, W. Zhang, X. Zhai, C. Zeng, Z. Li, J. Yang and J. Hou, ACS Nano, 2011, 5, 3385–3390.
19. Z. Sun, Z. Yan, J. Yao, E. Beitler, Y. Zhu and J. M. Tour, Nature, 2010, 468, 549–552.
20. T. Liang, Y. Kong, H. Chen and M. Xu, Chin. J. Chem., 2016, 34, 32–40.
21. H. Ji, Y. Hao, Y. Ren, M. Charlton, W. H. Lee, Q. Wu, H. Li, Y. Zhu, Y. Wu and R. Piner, ACS Nano, 2011, 5, 7656–7661.
22. P. Wu, W. Zhang, Z. Li and J. Yang, Small, 2014, 10, 2136–2150.
23. M. Xu, D. Fujita, K. Sagisaka, E. Watanabe and N. Hanagata, ACS Nano, 2011, 5, 1522–1528.
24. Q. Yu, J. Lian, S. Siriponglert, H. Li, Y. P. Chen and S. S. Pei, Appl. Phys. Lett., 2008, 93, 113103.
25. K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J. H. Ahn, P. Kim, J. Y. Choi and B. H. Hong, Nature, 2009, 457, 706–710.
26. J. Lahiri, T. Miller, L. Adamska, I. I. Oleynik and M. Batzill, ACS Nano Lett., 2011, 11, 518–522.
27. P. W. Sutter, J. I. Flege and E. A. Sutter, Nat. Mater., 2008, 7, 406–411.
28. E. Loginova, N. C. Bartelt, P. J. Feibelman and K. F. McCarty, New J. Phys., 2008, 10, 093026.
29. E. Loginova, N. Bartelt, P. Feibelman and K. McCarty, New J. Phys., 2009, 11, 063046.
30. E. Loginova, S. Nie, K. Thürmer, N. C. Bartelt and K. F. McCarty, Phys. Rev. B, 2009, 80, 085430.
31. J. Coraux, M. Engler, C. Busse, D. Wall, N. Buckanie, F. J. M. Zu Heringdorf, R. Van Gastel, B. Poelsema and T. Michely, New J. Phys., 2009, 11, 023006.
32. P. Lacovig, M. Pozzo, D. Alfe, P. Vilmercati, A. Baraldi and S. Lizzit, Phys. Rev. Lett., 2009, 103, 166101.
33. O. Rader, A. Varykhalov, J. Sánchez-Barriga, D. Marchenko, A. Rybkin and A. Shikin, Phys. Rev. Lett., 2009, 102, 057602.
34. D. Eom, D. Prezzi, K. T. Rim, H. Zhou, M. Lefenfeld, S. Xiao, C. Nuckolls, M. S. Hybertsen, T. F. Heinz and G. W. Flynn, Nano Lett., 2009, 9, 2844–2848.
35. N. A. Vinogradov, A. A. Zakharov, V. Kocevski, J. Rusz, K. A. Simonov, O. Eriksson, A. Mikkelsen, E. Lundgren, A. S. Vinogradov, N. Mårtensson and A. B. Preobrajenski, Phys. Rev. Lett., 2012, 109, 026101.
36. S. Nie, N. C. Bartelt, J. M. Wofford, O. D. Dubon, K. F. McCarty and K. Thürmer, Phys. Rev. B, 2012, 85, 205406.
37. E. N. Voloshina, Y. S. Dedkov, S. Torbrügge, A. Thissen and M. Fonin, Appl. Phys. Lett., 2012, 100, 241606.
38. P. Sutter, J. T. Sadowski and E. Sutter, Phys. Rev. B, 2009, 80, 245411.
39. X. Feng, J. Wu, A. T. Bell and M. Salmeron, J. Phys. Chem. C, 2015, 119, 7124–7129.
40. X. Liu, L. Fu, N. Liu, T. Gao, Y. Zhang, L. Liao and Z. Liu, J. Phys. Chem. C, 2011, 115, 11976–11982.
41. T. Wu, X. Zhang, Q. Yuan, J. Xue, G. Lu, Z. Liu, H. Wang, H. Wang, F. Ding, Q. Yu, X. Xie and M. Jiang, Nat. Mater., 2016, 15, 43–47.
42. C. Riedl, C. Coletti, T. Iwasaki, A. A. Zakharov and U. Starke, Phys. Rev. Lett., 2009, 103, 246804.
43. M. K. Jeonghyun Hwang, D. Campbell, H. A. Alsalman, J. Young Kwak, S. Shivaraman, A. R. Woll, A. K. Singh, R. G. Hennig, S. Gorantla, M. H. Rümmeli and M. G. Spencer, ACS Nano, 2013, 7, 385–395.
44. J. Chen, Y. Wen, Y. Guo, B. Wu, L. Huang, Y. Xue, D. Geng, D. Wang, G. Yu and Y. Liu, J. Am. Chem. Soc., 2011, 133, 17548–17551.
45. H. Bi, S. Sun, F. Huang, X. Xie and M. Jiang, J. Mater. Chem., 2012, 22, 411–416.
46. J. Xue, J. Sanchez Yamagishi, D. Bulmash, P. Jacquod, A. Deshpande, K. Watanabe, T. Taniguchi, P. Jarillo Herrero and B. J. LeRoy, Nat. Mater., 2011, 10, 282–285.
47. W. Yang, G. Chen, Z. Shi, C.-C. Liu, L. Zhang, G. Xie, M. Cheng, D. Wang, R. Yang, D. Shi, K. Watanabe, T. Taniguchi, Y. Yao, Y. Zhang and G. Zhang, Nat. Mater., 2013, 12, 792–797.
48. Y. Li, M. Li, T. Wang, F. Bai and Y. X. Yu, Phys. Chem. Chem. Phys., 2014, 16, 5213–5220.
49. Y. Li, M. Li, T. Gu, F. Bai, Y. Yu, M. Trevor and Y. Yu, Appl. Surf. Sci., 2013, 284, 207–213.
50. S. Sunahiro, K. Nomura, S. Goto, K. Kanamaru, R. Tang, M. Yamamoto, T. Yoshii, J. N. Kondo, Q. Zhao, A. Ghulam Nabi, R. Crespo-Otero, D. Di Tommaso, T. Kyotani and H. Nishihara, J. Mater. Chem. A, 2021, 9, 14296–14308.
51. C. Tang, B. Q. Li, Q. Zhang, L. Zhu, H. F. Wang, J. L. Shi and F. Wei, Adv. Funct. Mater., 2016, 26, 577–585.
52. H. Nishihara, T. Simura, S. Kobayashi, K. Nomura, R. Berenguer, M. Ito, M. Uchimura, H. Iden, K. Arihara, A. Ohma, Y. Hayasaka and T. Kyotani, Adv. Funct. Mater., 2016, 26, 6418–6427.
53. M. Yamamoto, S. Goto, R. Tang, K. Nomura, Y. Hayasaka, Y. Yoshioka, M. Ito, M. Morooka, H. Nishihara and T. Kyotani, ACS Appl. Mater. Interfaces, 2021, 13, 38613–38622.
54. K. Nomura, H. Nishihara, N. Kobayashi, T. Asada and T. Kyotani, Energy Environ. Sci., 2019, 12, 1542–1549.
55. K. Nomura, H. Nishihara, M. Yamamoto, A. Gabe, M. Ito, M. Uchimura, Y. Nishina, H. Tanaka, M. T. Miyahara and T. Kyotani, Nat. Commun., 2019, 10, 2559.
56. M. Yamamoto, Q. Zhao, S. Goto, Y. Gu, T. Toriyama, T. Yamamoto, H. Nishihara, A. Aziz, R. Crespo Otero and D. Di Tommaso, Chem. Sci., 2022, 13, 3140–3146.
57. J. Park, J. Lee, J. H. Choi, D. K. Hwang and Y. W. Song, Sci. Rep., 2015, 5, 11839.
58. A. J. Page, S. Saha, H. B. Li, S. Irle and K. Morokuma, J. Am. Chem. Soc., 2015, 137, 9281–9288.
59. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
60. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
61. P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979.
62. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775.
63. J. Paier, R. Hirschl, M. Marsman and G. Kresse, J. Chem. Phys., 2005, 122, 234102.
64. J. Gu, J. Wang and J. Leszczynski, ACS Omega, 2018, 3, 1881–1888.
65. G. Paglia, C. E. Buckley, A. L. Rohl, R. D. Hart, K. Winter, A. J. Studer, B. A. Hunter and J. V. Hanna, Chem. Mater., 2004, 16, 220–236.
66. M. C. Cholewinski, M. Dixit and G. Mpourmpakis, ACS Omega, 2018, 3, 18242–18250.
67. L. Martínez, P. Merino, G. Santoro, J. I. Martínez, S. Katsanoulis, J. Ault, Á. Mayoral, L. Vázquez, M. Accolla, A. Dazzi, J. Mathurin, F. Borondics, E. Blázquez Blázquez, N. Shauloff, R. Lebrón Aguilar, J. E. Quintanilla López, R. Jelinek, J. Cernicharo, H. A. Stone, V. A. de la Peña O’Shea, P. L. de Andres, G. Haller, G. J. Ellis and J. A. Martín Gago, Nat. Commun., 2021, 12, 5937.
68. M. Digne, J. Catal., 2004, 226, 54–68.
69. R. Wischert, P. Laurent, C. Copéret, F. Delbecq and P. Sautet, J. Am. Chem. Soc., 2012, 134, 14430–14449.
70. W. Grünert, Angew. Chem., 2012, 51, 5289.
71. Y. X. Yu, J. Phys. Chem. C, 2019, 123, 205–213.
72. R. Gholizadeh and Y. X. Yu, Appl. Surf. Sci., 2015, 357, 1187–1195.
73. M. D. Higham, M. G. Quesne and C. R. A. Catlow, Dalton Trans., 2020, 49, 8478–8497.
74. W. Zhu, A. Börjesson and K. Bolton, Carbon, 2010, 48, 470–478.
75. P. Wang, Z. Xu, T. Wang, Y. Yue, X. Bao and H. Zhu, Catal. Sci. Technol., 2020, 10, 3537–3541.
76. Y. Zhang, Y. Zhao, T. Otroshchenko, H. Lund, M.-M. Pohl, U. Rodemerck, D. Linke, H. Jiao, G. Jiang and E. V. Kondratenko, Nat. Commun., 2018, 9, 1–10.
77. J. Joubert, F. Delbecq and P. Sautet, J. Catal., 2007, 251, 507–513.
78. M. Dixit, P. Kostetskyy and G. Mpourmpakis, ACS Catal., 2018, 8, 11570–11578.
79. W. Zhang, P. Wu, Z. Li and J. Yang, J. Phys. Chem. C, 2011, 115, 17782–17787.

---

Footnotes

† Electronic supplementary information (ESI) available: See the supplementary material for the bulk cell of γ-Al₂O₃ (Fig. S1); structural models for CH₄ adsorption on γ-Al₂O₃(111), γ-Al₂O₃(110), γ-Al₂O₃(100), and γ-Al₂O₃(001) catalyst surfaces (Fig. S2); the energy diagram of the first two CH₄ dehydrogenation steps on γ-Al₂O₃ different main exposed surfaces (Fig. S3); energy diagram and intermediate structures for C₂H₆ interacting with surface flexible carbon species (Fig. S4); energy diagram and structures of the C₂H₆ dehydrogenation (Fig. S5); Gibbs energy profile of (a) complete CH₄* dehydrogenation and (b) the formation of C_nH_2n* (n = 2–6) species via CH₂* coupling on the γ-Al₂O₃ (100) surface at an experimental temperature of 1000 K (Fig. S6); structures and bond lengths between carbon end near surface and center sites of (a) C₂H₄*, (b) C₃H₆*, (c) C₄H₈*, (d) C₅H₁₀*, and (e) C₆H₁₂* on the γ-Al₂O₃(100) surface (Fig. S7); the energy profiles and structures for C₆H₁₂* chain ends with CH₃* on the γ-Al₂O₃(100) surface (Fig. S8); the energy profiles and structures for the concerted mechanism and stepwise mechanism dehydrogenation of C₃H₆* and C₆H₁₂* on γ-Al₂O₃ (100) (Fig. S9 and S10); energy diagram and structures for further H behaviour after carbon ring formation (Fig. S11). See DOI: https://doi.org/10.1039/d2cp01554d

‡ Present address: RIKEN Center for Advanced Photonics, RIKEN, 2-1 Hirosawa, Wako, Saitama 351-0198, Japan.

---