All-electron many-body approach to resonant inelastic X-ray scattering
Received
1st March 2022
, Accepted 11th May 2022
First published on 12th May 2022
Abstract
We present a formalism for the resonant inelastic X-ray scattering (RIXS) cross section. The resulting compact expression in terms of polarizability matrix elements, particularly lends itself to the implementation in an all-electron many-body perturbation theory (MBPT) framework, which is realized in the full-potential package exciting. With the carbon K edge RIXS of diamond and the oxygen K edge RIXS of β-Ga2O3, respectively, we demonstrate the importance of electron-hole correlation and atomic coherence in the RIXS spectra.
1 Introduction
Resonant inelastic X-ray scattering (RIXS) is a “photon-in-photon-out” scattering process, consisting of a coherent X-ray absorption and X-ray emission process.1,2 The energy difference between the absorbed and emitted X-ray photons is transferred to the system. Being bulk-sensitive, element- and orbital-specific and giving access to a large scattering phase space, RIXS has become a widely used experimental probe of elementary excitations in molecules3–5 and solids.1,2,6,7 Accurate ab initio simulations can provide insight into the complex RIXS process and predict the corresponding spectra. In this context, the electron-hole correlations of the X-ray absorption and emission processes as well as the quantum coherence between them is a challenge for ab initio approaches.
For the first-principles calculations of both valence and core excitations in solids, the Bethe–Salpeter equation (BSE) formalism8–13 has become the state of the art in recent decades. However, only few applications of the BSE formalism to RIXS14–20 have been presented so far. All of them relied on the pseudopotential approximation where only selected valence and conduction orbitals are explicitly included in the calculation, while more strongly-bound electrons are only treated implicitly through the pseudopotential. The wavefunctions required for the calculations of X-ray absorption and scattering in these BSE implementations14,18,21–23 rely on the pseudopotential approximations via the projector augmented-wave method.24–27
In this work, we go beyond by presenting an all-electron full-potential BSE approach to RIXS. We derive a compact analytical expression of the RIXS cross section within many-body perturbation theory (MBPT) that contains both the effects of electron-hole correlation and of the quantum coherence of the resonant scattering. We have implemented this novel expression in the all-electron many-body perturbation theory code exciting,28–30 where we make use of consistent BSE calculations of core and valence excitations, based on the explicit access to core, valence, and conduction orbitals and matrix elements between them. To demonstrate our approach, we have chosen two representative examples: In the carbon K edge of diamond, we particularly study the influence of electron-hole correlation, while in the oxygen K edge of β-Ga2O3, we show how the coherence between excitations at different atomic sites impacts the RIXS spectra.
2 Theory
The double-differential cross section (DDCS) d2σ/dΩ2dω2 for the scattering of a photon with energy ω1, polarization e1, and momentum K1 into a photon with energy ω2, polarization e2, and momentum K2 is given by the generalized Kramers–Heisenberg31 formula| | 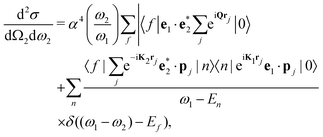 | (1) |
where |0〉 and |f〉 are the initial and final electronic state with energy E0 = 0 and Ef, respectively. Eqn (1) includes both the non-resonant scattering (NRIXS), in which the momentum transfer Q = K1 − K2 appears explicitly, and the resonant scattering (RIXS). If the photon energy ω1 is in resonance with the excitation energies En of the electronic system, the second, resonant term dominates and the non-resonant part can be neglected, leading to| | 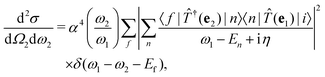 | (2) |
where we have introduced the transition operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (e) in the dipole approximation, i.e.,
(e) in the dipole approximation, i.e., 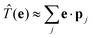 . Microscopically, the resonant scattering process is as follows: The absorption of the initial X-ray photon with energy ω1 excites a core electron into the conduction band, leaving a core hole behind. The intermediate system, after the excitation, is in an excited many-body state |n〉. The core hole can now be filled by a valence electron, which loses the energy ω2 by emitting an X-ray photon. This process is known as direct RIXS. Alternatively, the presence of the core-hole and excited electron can lead to the formation of a secondary electron-hole pair in the intermediate state. The initially excited can then fill the core hole. This process is known as indirect RIXS.2,32 Involving excited states beyond singlet excitations, its contribution is neglected in the following. We recall that indirect RIXS is mostly devoted to magnetic excitations, like magnon scattering.
. Microscopically, the resonant scattering process is as follows: The absorption of the initial X-ray photon with energy ω1 excites a core electron into the conduction band, leaving a core hole behind. The intermediate system, after the excitation, is in an excited many-body state |n〉. The core hole can now be filled by a valence electron, which loses the energy ω2 by emitting an X-ray photon. This process is known as direct RIXS. Alternatively, the presence of the core-hole and excited electron can lead to the formation of a secondary electron-hole pair in the intermediate state. The initially excited can then fill the core hole. This process is known as indirect RIXS.2,32 Involving excited states beyond singlet excitations, its contribution is neglected in the following. We recall that indirect RIXS is mostly devoted to magnetic excitations, like magnon scattering.
In the final many-body state |f〉, a hole is present in a valence state and an excited electron in a conduction state. While both the absorbed and emitted photon have energies in the X-ray region, the difference between them, the energy loss ω1 − ω2, is typically in the range of several eV. The final excited many-body state of the RIXS process corresponds to an excited state as typically created by optical absorption. The intricacy of the RIXS formalism, described in eqn (2), arises from the transitions between three many-body states, i.e., |0〉 → |n〉 and |n〉 → |f〉 and from the coherent summation over all possible intermediate and final many-body states. This inherent complexity of the microscopic RIXS process poses challenges for any theoretical description, as both the effects of electron-hole interaction, as well as the coherence of the RIXS process have to be included.
2.1 Independent-particle approximation to RIXS
It is instructive to discuss the RIXS process within the independent-particle approximation (IPA) before the scattering in the fully interactive system is considered. In the IPA, the many-body groundstate wavefunction is given by a single Slater determinant, and both the intermediate many-body state |n〉 and the final one |f〉 are singlet excitations of the groundstate without any relaxation of the system. We know a priori that the intermediate states contain a core hole μk and an excited electron in a conduction state ck, such that we can express them in second quantization as 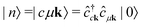 with energy En = εck − εμk. Furthermore, the final states contain an excited electron in a specific conduction state c′k′ and a valence hole in the state vk', such that
with energy En = εck − εμk. Furthermore, the final states contain an excited electron in a specific conduction state c′k′ and a valence hole in the state vk', such that 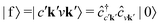 and
and 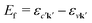 . Then, eqn (2) becomes
. Then, eqn (2) becomes| | 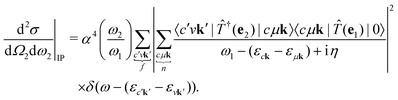 | (3) |
In second quantization, we express the transition operator as 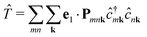 , where Pmnk = 〈 mk|p|nk〉 are the momentum matrix elements. Inserting these operators in eqn (3) yields
, where Pmnk = 〈 mk|p|nk〉 are the momentum matrix elements. Inserting these operators in eqn (3) yields| | 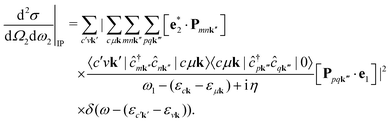 | (4) |
We note that the summations over p and q in eqn (4) are not restricted to either core, valence, or conduction states. Restrictions to these indices can be inferred from the matrix elements of the creation and annihilation operators. We find that| | 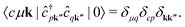 | (5) |
The term 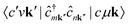 requires a more careful treatment. Applying Wick's theorem and restricting only to terms that correspond to the RIXS process, we obtain
requires a more careful treatment. Applying Wick's theorem and restricting only to terms that correspond to the RIXS process, we obtain
| | 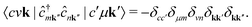 | (6) |
A more detailed derivation of
eqn (6) is provided in the Appendix. Inserting
eqn (5) and (6) into
eqn (4) yields
| | 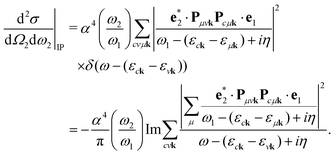 | (7) |
This equation has been widely applied to calculate the RIXS cross section in solids.
33–38
2.2 RIXS beyond the independent-particle approximation
The neglected electron-hole interaction is the reason for the poor performance of the IPA for optical and X-ray excitation spectra in crystalline semiconductors and insulators. A more accurate approach is provided by many-body perturbation theory based on solutions of the BSE.10,39,40 This approach is now the state of the art to determine optical9,11,39,41–43 and X-ray absorption spectra22,25,29,44–55 in solids. In the following, we derive an analytical expression for RIXS that takes the electron-hole interaction into account.
Following ref. 14 and 17, we define an intermediate many-body state as
| | 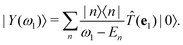 | (8) |
Similar intermediate states have been defined as
response vectors in the context of non-linear spectroscopy in molecular systems.
56,57 Inserting these intermediate states into
eqn (2), the RIXS cross section becomes
| | 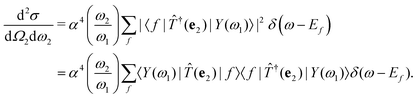 | (9) |
The intermediate states |
Y (
ω1)〉 contain the information about all possible excitation processes and can be understood as the excited many-body states produced by the absorption of a photon with energy
ω1. Inserting a finite broadening
η for the excited many-body states, the cross section becomes
| | 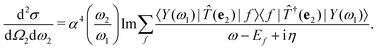 | (10) |
Within the Tamm–Dancoff approximation, we assume that both the intermediate and final states are linear combinations of singlet excitations of the groundstate. We can thus infer
| | 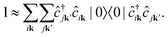 | (11) |
While this approximation has been found to yield good results for the excited states probed in both optical and X-ray absorption spectroscopy of solids,
29,30 it explicitly limits our approach to
direct RIXS, as the intermediate states in
indirect RIXS contain two electron-hole pairs and therefore can not be expressed as a linear combination of singlet excitations of the groundstate. Inserting
eqn (11) into
eqn (8) yields
| | 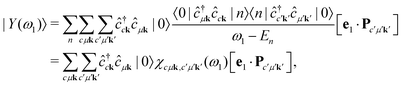 | (12) |
where we have made use of the Lehmann representation of the polarizability
χ(
ω). We can now evaluate the expectation value of the intermediate state
| | 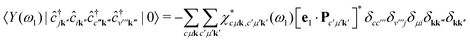 | (13) |
where we have used
eqn (6). This eventually yields the double-differential cross section as
| | 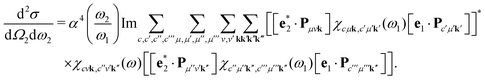 | (14) |
Eqn (14) represents a main result of this paper: The RIXS cross section is expressed solely in terms of the polarizability χ. The polarizability is evaluated twice, once at the X-ray excitation energy ω1, and once at the energy loss ω = ω1 − ω2. The cumbersome summations over all intermediate and final many-body states are thus included in the polarizability, and eqn (14) avoids any explicit summations over many-body states.
2.3 Many-body perturbation theory applied to RIXS
Within MBPT, the polarizability is given by| | 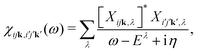 | (15) |
where Xijk,λ and Eλ are the eigenstates and -values of the BSE equationwhere the Hamiltonian is given by| | | HBSE = ΔEIP + 2V − W. | (17) |
Here, ΔEIP are the single-particle energy differences which are taken from DFT Kohn-Sham calculations and are corrected by a scissors operator. The corresponding values for conduction states and core states are chosen such to simulate the zero-order polarizability in the BSE calculations.59V are the matrix elements of the bare electron-hole exchange, and W those of the statically screened direct interaction.
Inserting eqn (15) into eqn (14) allows for a significant simplification of the RIXS cross section. We first consider the last bracket of eqn (14) and express it as
| | 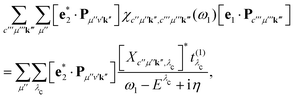 | (18) |
where
Xc′′μ′′k′′ and
Eλc are the eigenvectors and -values of the core-level BSE, respectively. We define the core-excitation oscillator strength
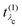
as
| | 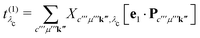 | (19) |
and the excitation pathway
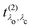
as
| | 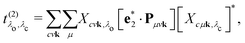 | (20) |
where
Xcvk,λo and
Eλo are the eigenvectors and -values of the BSE Hamiltonian of the valence-conduction transitions, respectively. Here, we discern the index of the valence-conduction excitations,
λo, from the index
λc of the core-conduction ones.
Inserting eqn (18) and (20) into eqn (14) yields
| | 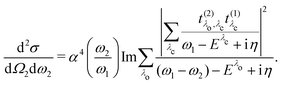 | (21) |
Finally, we define the RIXS oscillator strength
t(3)λ(
ω1) as
| | 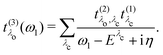 | (22) |
Using the definition of the oscillator strength
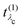
in
eqn (19) and the excitation pathway
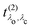
in
eqn (20), allows for the compact expression of the RIXS cross section as
| | 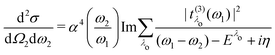 | (23) |
which closely resembles the BSE expression for optical and X-ray absorption spectra. The cross section depends explicitly on the energy loss
ω =
ω1 −
ω2, while its dependence on the excitation energy is contained in the oscillator strength
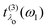
. It has poles in the energy loss at the optical excitation energies
Eλo of the system, independent of the excitation energy, while the oscillator strength of each of these excitations depends on it. The oscillator strength defined in
eqn (22), gives further insight into the many-body processes that occur in RIXS. The rate of the initial X-ray absorption event is given by
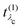
, combined with the energy conservation rule (the denominator
ω1 −
Eλc +
iη in
eqn (22)). The absorption leads to an intermediate core-excited state, characterized by the excitation index
λc. The final RIXS spectrum is then given by the rate of the absorption combined with the pathway
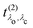
that describes the many-body transition |
λc〉 →|
λo〉. These pathways are far from obvious, as the mixing between
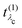
and
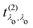
can develop in destructive or constructive interference, attesting the many-body character of such process.
With eqn (23), we have derived a compact analytical expression for the double-differential RIXS cross section with only two assumptions: First, we presume in eqn (11) that the intermediate and final states are singlet excitations. While this assumption limits our approach to direct RIXS, it is consistent with the Tamm–Dancoff approximation in the BSE formalism. Second, we assume that the latter yield accurate core and valence excited states. Therefore, these approximations are interconnected. For systems, such as diamond and Ga2O3 studied here, where BSE yields accurate absorption spectra, our approach yields accurate RIXS spectra as well. For highly correlated states, BSE results may strongly depend on the starting point, i.e., the underlying one-particle states. It might happen, for instance, that semilocal DFT leads to a poor representation of the system. In this case, even the BSE result will be poor. This is neither a problem of BSE nor of the RIXS formulation. Here, one-particle wave functions coming from hybrid functionals, or self-consistent COHSEX or GW will be required, as shown for copper and vanadium oxides.60,61 Such calculations are, however, not standard to date as they are numerically very involved. All in all, the RIXS formulation provided here, is very general and fully ab initio, and it applies to a large variety of systems.
3 Implementation
The implementation of eqn (23) requires explicit access to the BSE eigenvectors Xcvkλo both in terms of valence-conduction transitions Xcμkλc as well as core-conduction transitions, while cross terms of the form Xvμkλ are not needed. Thus, the calculation of the RIXS cross section can be separated into three independent calculations, one for the core-conduction, one for the valence-conduction excitations, and finally a convolution step to obtain the RIXS cross section. Overall, momentum matrix elements Pcμk between core and conduction states and Pμvk between valence and core states determine the excitation and de-excitation process, respectively. The coherence between core and valence excitations in the RIXS process is apparent in eqn (20) from the summation over k. (For this reason, core and valence excitations are calculated on the same {k}-grid.) Coherence occurs, since the absorption and emission processes conserve the crystal momentum k.1
For the specific implementation, we make use of the core-conduction and valence-conduction BSE eigenvectors and corresponding matrix elements obtained from the all-electron package exciting.28–30 The output of the two BSE calculations is evaluated by the BRIXS (BSE for RIXS) code.62,63 In this step, the oscillator strength t(1) of the core excitation and the excitation pathways t(2) are determined. From these intermediate quantities, the RIXS oscillator strength t(3)(ω1) is generated for a list of excitation energies ω1 defined by the user. Execution of BRIXS requires only a minimal number of input parameters: Besides {ω1}, the number of core-conduction (Nλc) and valence-conduction excitations (Nλo), the lifetime broadening (η), and the polarization vector of the X-ray beam (e1) are required. A detailed description of the implementation is provided in ref. 64.
4 Results
4.1 Electron-hole correlation in the RIXS of diamond
To demonstrate the importance of electron-hole correlation in RIXS, we study the carbon K edge in diamond. Both optical absorption12,58,66–68 and core excitations65,69,70 have been investigated intensively before. RIXS measurements33,65 and calculations14,17 are also available for this edge. As such, this material acts as a good example to demonstrate our approach and benchmark the resulting spectra.
In a first step, the optical and core spectra are calculated from the solution of the BSE, as shown in Fig. 1, both in excellent agreement with experiment. In addition, we show the results obtained within the independent-particle approximation (IPA). They are blue-shifted relative to experiment, as electron-hole attraction is not included. Also the spectral shape of the core spectra disagrees with the experimental one, as it misses the peak at the absorption onset and shows too much spectral weight at high energies.
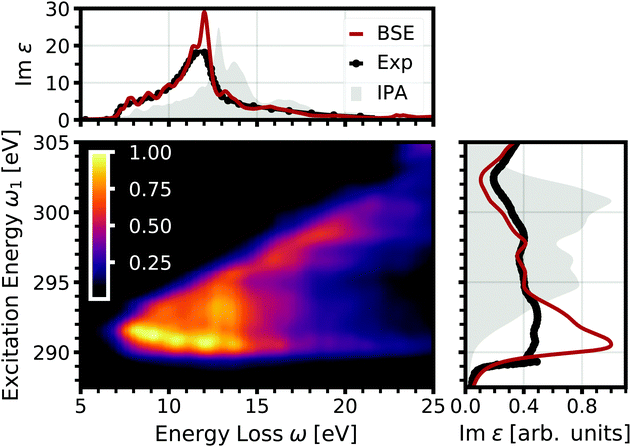 |
| | Fig. 1 Normalized double-differential RIXS cross section of the carbon K edge in diamond as a function of excitation energy and energy loss (center). On the top, the optical absorption spectrum obtained from BSE (red) and the IPA (gray) is shown, compared to the experimental spectrum (black) from ref. 58. On the right, the corresponding core excitation is depicted. | |
From the BSE spectra, we determine the RIXS specrtra shown in Fig. 1. Following eqn (21) and (22), it comes natural to display the RIXS double-differential cross section d2σ/dΩ2dω2 as a function of the excitation energy ω1 and the energy loss ω = ω1 − ω2. For excitation energies below the core absorption edge, i.e., at approximately 290 eV (see Fig. 2, right), the intensity is negligible, since the excitation energy is not in resonance with any carbon 1s excitation. Once the excitation energy reaches resonance with the absorption edge, the RIXS cross section increases considerably. The emission occurs over a wide range of the energy loss up to around 20 eV, but is strongest at low emission at the onset of optical absorption (compare Fig. 1, top). With increasing excitation energy, the emission reduces due to the reduced rate of absorption beyond the onset. Furthermore, the emission at low energy loss vanishes as the excitation energy increases. At a value of about 295 eV (300 eV), no emission with an energy loss below approximately 12 eV (20 eV) is observed. Due to this linear dispersion of the energy loss with the excitation energy, the emission energies stay more or less constant, as can be seen in Fig. 2, where the RIXS cross section is shown as a function of the emission energy for selected excitation energies.
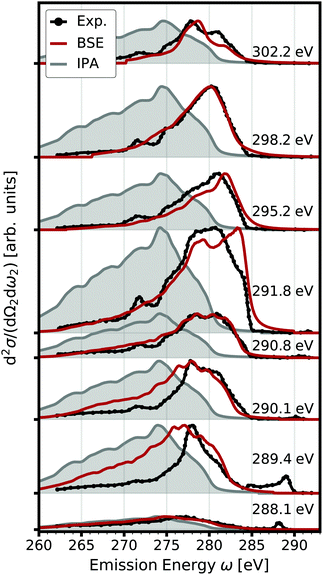 |
| | Fig. 2 Double differential RIXS cross section (red) accounting for electron-hole interaction. The spectra calculated for several excitation energies are offset for clarity. Experimental data from ref. 65 are shown in black, the IPA results in gray. | |
In Fig. 2, we also show the RIXS cross section obtained within the IPA, following eqn (7). Overall, the IPA spectra exhibit lower emission energies due to the overestimation of the excitation energies in the optical absorption (see Fig. 1). Especially for lower excitation energies, there are significant deviations. The intensity at higher emission energies is underestimated, and the spectra are too broad. Both features are due to the neglect of electron-hole interaction which increases the intensity at low energies, i.e., leads to a sharper absorption onsets. This effect is especially pronounced for the core excitations. At higher excitation energies, the discrepancy between IPA and BSE results decreases. While IPA reproduces the spectral shape correctly, the spectrum is still blue-shifted. Our BSE results are in excellent agreement with experiment for all excitations energies, both in relative position and spectral shape.
4.2 Atomic coherence in the RIXS of Ga2O3
Now, we like to showcase the importance of atomic coherence on RIXS spectra. Considering the coherent sum over atomic excitations in eqn (21), interference terms appear when the crystal contains inequivalent atomic positions, i.e.,| | 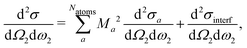 | (24) |
where d2σa/dΩ2dω2 is the RIXS cross section for the inequivalent atom a with multiplicity Ma and d2σinterf/dΩ2dω2 is the interference term. Mathematically, the interference term originates from the square modulus of t(3)λ(ω1) in eqn (21) that contains the sum of the core excitations on all atoms in the unit cell. The O K edge in the monoclinic β phase of Ga2O3 serves as an example. The unit cell contains three inequivalent oxygen sites denoted O1,O2, and O3, all of them with multiplicity 1. Fig. 3 shows that the RIXS spectrum shows pronounced fluorescence behavior,71,72i.e., significant features occur at basically constant emission energies. The contributions of all oxygen atoms are nearly identical for excitation energies below 532 eV. Above that, the contribution of O2 dominates the spectrum. For a quantitative analysis, we define relative atomic contributions by integrating the atomic RIXS spectra over the emission energies ω2 and normalizing with respect to the total spectrum. The result, shown in Fig. 4, demonstrates that the relative atomic contributions vary between 20 and 50%, depending on the excitation energy, and that none of the contributions can be neglected even if one of them – here O2 – dominates. The interference term contributes up to 15% of the total RIXS spectrum, yet decreasing quickly as the excitation energy increases beyond the absorption onset. At higher excitation energies, it only contributes 5–7%. The importance of interference at the absorption onset indicates that it originates from electronic correlation.
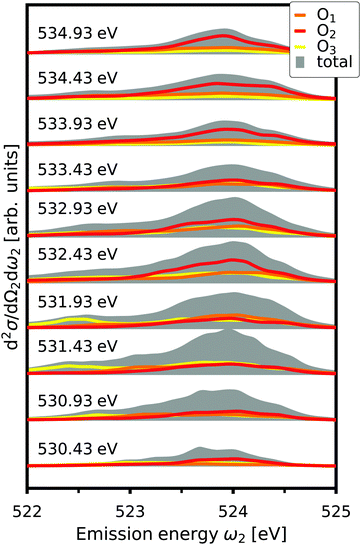 |
| | Fig. 3 Total O K edge RIXS in β-Ga2O3 as a function of emission energy, ω2, for selected excitation energies, together with the contributions from O1,O2, and O3. The spectra are offset for clarity. | |
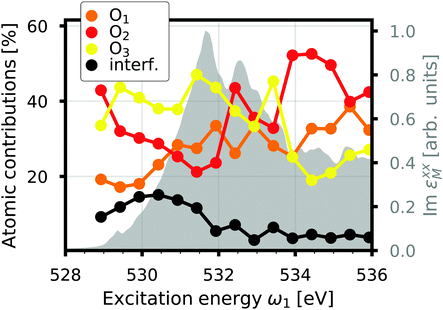 |
| | Fig. 4 Interference contribution to the O K edge RIXS of β-Ga2O3 as a function of excitation energy compared to the atomic contributions and the normalized total spectrum (gray). | |
5 Conclusions
We have derived a compact analytical expression for the RIXS cross section within many-body perturbation theory. This expression retains the intuitive interpretation of the RIXS process as a coherent absorption-emission process, while including the effects of electron-hole correlation, which are paramount for an accurate description of excitations in semiconductors and insulators. Our implementation in an all-electron BSE framework, i.e., the exciting package, making use of BSE eigenstates for core and valence excitations, introduces only small computational overhead compared to valence and core BSE calculations. For the example of the carbon K edge RIXS in diamond, we demonstrate that our approach yields spectra in excellent agreement with available experimental spectra. We furthermore show that electron-hole correlations not only shift spectral features in energy but also affect their shape, especially in excitations at the absorption edge. The influence of atomic coherence is exemplified with the oxygen K edge in β-Ga2O3, where it turns out non-negligible, especially close to the absorption onset.
Author contributions
All authors have devised the project. FS and CV derived the RIXS formalism, CV implemented it in the all-electron package exciting and carried out the calculations. All authors contributed to the writing of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Appendix. Derivation of matrix elements
In the following, we provide the derivation of eqn (6). We initially employ Wick's theorem73 to evaluate the expectation value of the product of three pairs of annihilation and creation operators, i.e.,| | 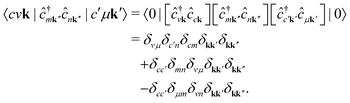 | (25) |
Each of the three contributions correspond to different processes in the DDCS. To analyze them, we insert eqn (25) into eqn (7). Ignoring cross-terms, this yields the following expressions:| |  | (26) |
An intuitive interpretation of the three terms is obtained by considering their poles: Term (a) has poles at the excitation energies ω1 = εck − εμk, where a core state μk is excited into a conduction state ck. Poles in the emission energy occur at 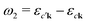 where the excited electron transitions to another conduction state
where the excited electron transitions to another conduction state  . Thus, the final state of this scattering process contains a core hole at μk and an excited electron in
. Thus, the final state of this scattering process contains a core hole at μk and an excited electron in 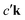 . As such, this scattering process does not correspond to the RIXS process.
. As such, this scattering process does not correspond to the RIXS process.
Term (b) does not describe a resonant scattering process, as the emission energy ω2 vanishes (corresponding to transitions mk → mk). However, for each state, the momentum matrix element Pmmk = 0. Thus, term (b) does not contribute to the DDCS.
Finally, term (c) corresponds to the RIXS process: Poles occur at excitation energies ω1 = εck − εμk and at emission energies ω2 = εvk − εμk. Thus, the scattering consists of an excitation μk → ck and a subsequent de-excitation vk → μk. The final state contains a valence hole vk and an excited electron ck.
Overall, as long we only consider RIXS, we can neglect terms (a) and (b), and we arrive at eqn (14). The analysis also justifies why the cross terms between the terms (a), (b), and (c) can be neglected. The different terms have poles in vastly different energy regions, thus making cross terms small.
Numerical parameters
Carbon K edge in diamond
The electronic structure is determined from DFT-PBE calculations within the exciting code. All calculations are performed for the experimental lattice parameter of 6.746![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0. The reciprocal space is sampled with a 9 × 9 × 9 k-grid, and we include basis functions up to a cut-off of RmaxMT·|G + q|max = 8. To correct the electronic structure, we apply a scissors operator Δω = 1.9 eV, such to reproduce the measured indirect band gap of 5.48 eV.74 Another scissors operator of 22 eV is employed to correct the position of the 1s level.
a0. The reciprocal space is sampled with a 9 × 9 × 9 k-grid, and we include basis functions up to a cut-off of RmaxMT·|G + q|max = 8. To correct the electronic structure, we apply a scissors operator Δω = 1.9 eV, such to reproduce the measured indirect band gap of 5.48 eV.74 Another scissors operator of 22 eV is employed to correct the position of the 1s level.
Optical BSE spectra are calculated on a 13 × 13 × 13 k-grid, and local-field effects are included up to a cut-off |G + q|max = 3.5 a0−1. The calculations include all 4 valence bands and 10 conduction bands. 100 conduction bands are included in the random-phase approximation (RPA) calculation to obtain the screened Coulomb potential. The carbon K edge BSE is performed on the same k-grid. The cut-off for local-field is chosen |G + q|max = 5.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0−1 such to provide a precise description of the more localized excitations. 40 unoccupied are included in the BSE calculation. For the BRIXS calculation, the 8.000 lowest-energy valence and 20
a0−1 such to provide a precise description of the more localized excitations. 40 unoccupied are included in the BSE calculation. For the BRIXS calculation, the 8.000 lowest-energy valence and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 carbon 1s excitations are taken into account.
000 carbon 1s excitations are taken into account.
Input and relevant output files of the electronic-structure and BSE calculations can be downloaded from the NOMAD Repository75,76 under the DOI provided in ref. 77.
O K edge in β-Ga2O3
Calculations for β-Ga2O3 are performed using the experimental lattice parameters a = 12.233![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å, b = 3.038
Å, b = 3.038![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å, c = 5.807
Å, c = 5.807![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å, and β = 103.82°.78 The electronic structure is determined on a 8 × 8 × 8 k-grid using basis functions up to a cut-off of RmaxMT·|G + q|max = 8. Our calculations with the PBEsol functional79 yield a Kohn-Sham gap of 2.89 eV. To match the experimental fundamental gap of of 5.72 eV,80 we apply a scissors operator of Δω = 2.6 eV. A scissors shift of Δω2 = 24.93 eV is applied to correct the position of the oxygen 1s state such to align the calculated O K edge XAS with the experimental one.81
Å, and β = 103.82°.78 The electronic structure is determined on a 8 × 8 × 8 k-grid using basis functions up to a cut-off of RmaxMT·|G + q|max = 8. Our calculations with the PBEsol functional79 yield a Kohn-Sham gap of 2.89 eV. To match the experimental fundamental gap of of 5.72 eV,80 we apply a scissors operator of Δω = 2.6 eV. A scissors shift of Δω2 = 24.93 eV is applied to correct the position of the oxygen 1s state such to align the calculated O K edge XAS with the experimental one.81
The optical BSE spectra are obtained from calculations on a 10 × 10 × 10 k-grid with a cut-off |G + q|max = 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0−1 for local-field effects. The 10 highest valence bands and 10 lowest conduction bands form the transition space. 30 conduction bands are used in the RPA calculation of the screened Coulomb potential.
a0−1 for local-field effects. The 10 highest valence bands and 10 lowest conduction bands form the transition space. 30 conduction bands are used in the RPA calculation of the screened Coulomb potential.
The BSE calculation of the oxygen K edge are performed on the same k-grid and using the identical screened Coulomb potential as for the optical spectra. 20 conduction bands are used to form the transition space.
Input and relevant output files of the electronic-structure and BSE calculations can be downloaded from the NOMAD Repository75,76 under the DOI provided in ref. 82.
Acknowledgements
This work was supported by the project GraFOx, a Leibniz ScienceCampus, partially funded by the Leibniz Association. FS thanks the French Agence Nationale de la Recherche (ANR) for financial support (grant No. ANR-19-CE30-0011).
Notes and references
- A. Kotani and S. Shin, Rev. Mod. Phys., 2001, 73, 203–246 CrossRef CAS.
- L. J.-P. Ament, M. van Veenendaal, T. P. Devereaux, J. P. Hill and J. van den Brink, Rev. Mod. Phys., 2011, 83, 705–767 CrossRef CAS.
- A. Cesar, F. Gelmukhanov, Y. Luo, H. Ågren, P. Skytt, P. Glans, J. Guo, K. Gunnelin and J. Nordgren, J. Chem. Phys., 1997, 106, 3439–3456 CrossRef CAS.
- F. Hennies, S. Polyutov, I. Minkov, A. Pietzsch, M. Nagasono, H. Ågren, L. Triguero, M.-N. Piancastelli, W. Wurth, F. Gelmukhanov and A. Föhlisch, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 032505 CrossRef.
- I. Josefsson, K. Kunnus, S. Schreck, A. Föhlisch, F. de Groot, P. Wernet and M. Odelius, J. Phys. Chem. Lett., 2012, 3, 3565–3570 CrossRef CAS PubMed.
- G. Ghiringhelli, M. Matsubara, C. Dallera, F. Fracassi, R. Gusmeroli, A. Piazzalunga, A. Tagliaferri, N. B. Brookes, A. Kotani and L. Braicovich, J. Phys.: Condens. Matter, 2005, 17, 5397–5412 CrossRef CAS.
- R.-P. Wang, B. Liu, R. J. Green, M. U. Delgado-Jaime, M. Ghiasi, T. Schmitt, M. M. van Schooneveld and F. M.-F. de Groot, J. Phys. Chem. C, 2017, 121, 24919–24928 CrossRef CAS PubMed.
- L. Hedin, Phys. Rev., 1965, 139, A796–A823 CrossRef.
- M. S. Hybertsen and S. G. Louie, Phys. Rev. Lett., 1985, 55, 1418–1421 CrossRef CAS PubMed.
- G. Strinati, Riv. Nuovo Cimento, 1988, 11, 1–86 CrossRef CAS.
- G. Onida, L. Reining, R. W. Godby, R. Del Sole and W. Andreoni, Phys. Rev. Lett., 1995, 75, 818–821 CrossRef CAS PubMed.
- L. X. Benedict, E. L. Shirley and R. B. Bohn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, R9385–R9387 CrossRef CAS.
- M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 80, 3320–3323 CrossRef CAS.
- E. L. Shirley, J. Phys. Chem. Solids, 2000, 61, 445–447 CrossRef CAS.
- E. L. Shirley, J. Electron Spectrosc. Relat. Phenom., 2000, 110-111, 305–321 CrossRef CAS.
- E. L. Shirley, J. A. Soininen, G. P. Zhang, J. A. Carlisle, T. A. Callcott, D. L. Ederer, L. J. Terminello and R. C.-C. Perera, J. Electron Spectrosc. Relat. Phenom., 2001, 114-116, 939–946 CrossRef CAS.
-
J. Vinson, PhD thesis, University of Washington, 2012.
- J. Vinson, T. Jach, M. Müller, R. Unterumsberger and B. Beckhoff, Phys. Rev. B, 2017, 96, 205116 CrossRef PubMed.
- J. Vinson, T. Jach, M. Müller, R. Unterumsberger and B. Beckhoff, Phys. Rev. B, 2019, 100, 085143 CrossRef CAS PubMed.
- A. Geondzhian and K. Gilmore, Phys. Rev. B, 2018, 98, 214305 CrossRef CAS.
- E. L. Shirley, Phys. Rev. Lett., 1998, 80, 794–797 CrossRef CAS.
- K. Gilmore, J. Vinson, E. L. Shirley, D. Prendergast, C. D. Pemmaraju, J. J. Kas, F. D. Vila and J. J. Rehr, Comput. Phys. Commun., 2015, 197, 109–117 CrossRef CAS.
- J. Vinson, T. Jach, M. Müller, R. Unterumsberger and B. Beckhoff, Phys. Rev. B, 2016, 94, 035163 CrossRef PubMed.
- J. A. Carlisle, E. L. Shirley, L. J. Terminello, J. J. Jia, T. A. Callcott, D. L. Ederer, R. C.-C. Perera and F. J. Himpsel, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7433–7445 CrossRef CAS.
- J. Vinson, J. J. Rehr, J. J. Kas and E. L. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115106 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- N. A.-W. Holzwarth, A. R. Tackett and G. E. Matthews, Comput. Phys. Commun., 2001, 135, 329–347 CrossRef CAS.
- A. Gulans, S. Kontur, C. Meisenbichler, D. Nabok, P. Pavone, S. Rigamonti, S. Sagmeister, U. Werner and C. Draxl, J. Phys.: Condens. Matter, 2014, 26, 363202 CrossRef PubMed.
- C. Vorwerk, C. Cocchi and C. Draxl, Phys. Rev. B, 2017, 95, 155121 CrossRef.
- C. Vorwerk, B. Aurich, C. Cocchi and C. Draxl, Electron. Struct., 2019, 1, 037001 CrossRef CAS.
- P. A.-M. Dirac and R. H. Fowler, Proc. R. Soc. London, Ser. A, 1927, 114, 710–728 Search PubMed.
- M. van Veenendaal, X. Liu, M. H. Carpenter and S. P. Cramer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 045101 CrossRef.
- Y. Ma, N. Wassdahl, P. Skytt, J. Guo, J. Nordgren, P. D. Johnson, J.-E. Rubensson, T. Boske, W. Eberhardt and S. D. Kevan, Phys. Rev. Lett., 1992, 69, 2598–2601 CrossRef CAS PubMed.
- P. D. Johnson and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5024–5027 CrossRef CAS PubMed.
- J. J. Jia, T. A. Callcott, E. L. Shirley, J. A. Carlisle, L. J. Terminello, A. Asfaw, D. L. Ederer, F. J. Himpsel and R. C.-C. Perera, Phys. Rev. Lett., 1996, 76, 4054–4057 CrossRef CAS PubMed.
- V. N. Strocov, T. Schmitt, J.-E. Rubensson, P. Blaha, T. Paskova and P. O. Nilsson, Phys. Status Solidi B, 2004, 241, R27–R29 CrossRef CAS.
- V. N. Strocov, T. Schmitt, J.-E. Rubensson, P. Blaha, T. Paskova and P. O. Nilsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085221 CrossRef.
- Y. Nisikawa, M. Ibuki and M. Usuda, Phys. B, 2010, 405, 1415–1422 CrossRef CAS.
- L. Hedin, Phys. Rev., 1965, 139, A796–A823 CrossRef.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- S. Albrecht, G. Onida and L. Reining, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10278–10281 CrossRef CAS.
- L. X. Benedict, E. L. Shirley and R. B. Bohn, Phys. Rev. Lett., 1998, 80, 4514–4517 CrossRef CAS.
- M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 81, 2312–2315 CrossRef CAS.
- J. Vinson and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195135 CrossRef.
- Y. Noguchi, M. Hiyama, H. Akiyama, Y. Harada and N. Koga, J. Chem. Theory Comput., 2015, 11, 1668–1673 CrossRef CAS PubMed.
- C. Cocchi, H. Zschiesche, D. Nabok, A. Mogilatenko, M. Albrecht, Z. Galazka, H. Kirmse, C. Draxl and C. T. Koch, Phys. Rev. B, 2016, 94, 075147 CrossRef.
- F. Fossard, G. Hug, K. Gilmore, J. J. Kas, J. J. Rehr, F. D. Vila and E. L. Shirley, Phys. Rev. B, 2017, 95, 115112 CrossRef PubMed.
- R. Laskowski and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205104 CrossRef.
-
C. Draxl and C. Cocchi, 2017, arXiv preprint arXiv:1709.02288.
- W. Olovsson, I. Tanaka, T. Mizoguchi, P. Puschnig and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 041102 CrossRef.
- W. Olovsson, I. Tanaka, P. Puschnig and C. Ambrosch-Draxl, J. Phys.: Condens. Matter, 2009, 21, 104205 CrossRef CAS PubMed.
- W. Olovsson, I. Tanaka, T. Mizoguchi, G. Radtke, P. Puschnig and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195206 CrossRef.
- W. Olovsson, L. Weinhardt, O. Fuchs, I. Tanaka, P. Puschnig, E. Umbach, C. Heske and C. Draxl, J. Phys.: Condens. Matter, 2013, 25, 315501 CrossRef CAS PubMed.
- C. Cocchi and C. Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 205105 CrossRef.
- C. Vorwerk, C. Hartmann, C. Cocchi, G. Sadoughi, S. N. Habisreutinger, R. Félix, R. G. Wilks, H. J. Snaith, M. Bär and C. Draxl, J. Phys. Chem. Lett., 2018, 9, 1852–1858 CrossRef CAS PubMed.
- K. D. Nanda and A. I. Krylov, J. Phys. Chem. Lett., 2017, 8, 3256–3265 CrossRef CAS PubMed.
- K. D. Nanda, M. L. Vidal, R. Faber, S. Coriani and A. I. Krylov, Phys. Chem. Chem. Phys., 2020, 22, 2629–2641 RSC.
- H. R. Phillip and E. A. Taft, Phys. Rev., 1964, 136, A1445–A1448 CrossRef.
-
R. M. Martin, L. Reining and D. M. Ceperley, Interacting Electrons: Theory and Computational Approaches, Cambridge University Press, Cambridge, 2016 Search PubMed.
- F. Bruneval, N. Vast, L. Reining, M. Izquierdo, F. Sirotti and N. Barrett, Phys. Rev. Lett., 2006, 97, 267601 CrossRef PubMed.
- M. Gatti, F. Sottile and L. Reining, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195137 CrossRef.
-
C. Vorwerk, F. Sottile and C. Draxl, BRIXS, 2021, https://github.com/exciting/BRIXS.
- C. Vorwerk, F. Sottile and C. Draxl, Phys. Rev. Res., 2020, 2, 042003 CrossRef CAS.
-
C. W. Vorwerk, PhD thesis, Humboldt-Universität zu Berlin, 2021.
- A. V. Sokolov, E. Z. Kurmaev, S. Leitch, A. Moewes, J. Kortus, L. D. Finkelstein, N. A. Skorikov, C. Xiao and A. Hirose, J. Phys.: Condens. Matter, 2003, 15, 2081–2089 CrossRef CAS.
- P. H. Hahn, K. Seino, W. G. Schmidt, J. Furthmüller and F. Bechstedt, Phys. Status Solidi B, 2005, 242, 2720–2728 CrossRef CAS.
- W. Hanke and L. J. Sham, Phys. Rev. Lett., 1974, 33, 582–585 CrossRef CAS.
- D. Rocca, Y. Ping, R. Gebauer and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045116 CrossRef.
- J. A. Soininen and E. L. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 165112 CrossRef.
- M. Taillefumier, D. Cabaret, A.-M. Flank and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 195107 CrossRef.
- F. Pfaff, H. Fujiwara, G. Berner, A. Yamasaki, H. Niwa, H. Kiuchi, A. Gloskovskii, W. Drube, J. Gabel, O. Kirilmaz, A. Sekiyama, J. Miyawaki, Y. Harada, S. Suga, M. Sing and R. Claessen, Phys. Rev. B, 2018, 97, 035110 CrossRef CAS.
- H. Y. Huang, C. J. Jia, Z. Y. Chen, K. Wohlfeld, B. Moritz, T. P. Devereaux, W. B. Wu, J. Okamoto, W. S. Lee, M. Hashimoto, Y. He, Z. X. Shen, Y. Yoshida, H. Eisaki, C. Y. Mou, C. T. Chen and D. J. Huang, Sci. Rep., 2016, 6, 1–7 CrossRef CAS PubMed.
-
A. L. Fetter and J. D. Walecka, Quantum Theory of Many-particle Systems, Dover Publications Inc., 2003 Search PubMed.
- C. D. Clark, P. J. Dean, P. V. Harris and W. C. Price, Proc. R. Soc. London, Ser. A, 1964, 277, 312–329 CAS.
- C. Draxl and M. Scheffler, MRS Bull., 2018, 43, 676–682 CrossRef.
- C. Draxl and M. Scheffler, J. Phys. Mater., 2019, 2, 036001 CrossRef CAS.
-
C. Vorwerk and C. Draxl, NOMAD Dataset of calculations for diamond, 2020, https://dx.doi.org/10.17172/NOMAD/2020 Search PubMed.
- K. E. Lipinska-Kalita, P. E. Kalita, O. A. Hemmers and T. Hartmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 094123 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- A. Segura, L. Artús, R. Cuscó, R. Goldhahn and M. Feneberg, Phys. Rev. Mater., 2017, 1, 024604 CrossRef.
-
J. E. N. Swallow, C. Vorwerk, P. Mazzolini, P. Vogt, O. Bierwagen, A. Karg, M. Eickhoff, J. Schörmann, M. R. Wagner, J. W. Roberts, P. R. Chalker, M. J. Smiles, P. A. E. Murgatroyd, S. A. Razek, Z. W. Lebens-Higgins, L. F. J. Piper, L. A. H. Jones, P. K. Thakur, T.-L. Lee, J. B. Varley, J. Furthmüller, C. Draxl, T. D. Veal and A. Regoutz, 2020, arXiv:2005.13395 [cond-mat].
-
C. Vorwerk and C. Draxl, NOMAD Dataset of calculations for β-Ga2O3, 2020, https://dx.doi.org/10.17172/NOMAD/2020.07.14-4.
Footnote |
| † Current address: Pritzker School of Molecular Engineering, University of Chicago, Chicago, IL 60637, USA. |
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Francesco
Sottile
a,
Francesco
Sottile
 b and
Claudia
Draxl
*a
b and
Claudia
Draxl
*a
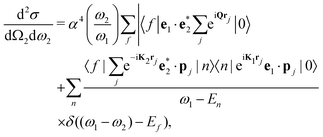
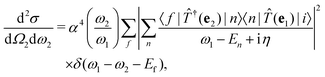
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (e) in the dipole approximation, i.e.,
(e) in the dipole approximation, i.e., 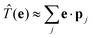 . Microscopically, the resonant scattering process is as follows: The absorption of the initial X-ray photon with energy ω1 excites a core electron into the conduction band, leaving a core hole behind. The intermediate system, after the excitation, is in an excited many-body state |n〉. The core hole can now be filled by a valence electron, which loses the energy ω2 by emitting an X-ray photon. This process is known as direct RIXS. Alternatively, the presence of the core-hole and excited electron can lead to the formation of a secondary electron-hole pair in the intermediate state. The initially excited can then fill the core hole. This process is known as indirect RIXS.2,32 Involving excited states beyond singlet excitations, its contribution is neglected in the following. We recall that indirect RIXS is mostly devoted to magnetic excitations, like magnon scattering.
. Microscopically, the resonant scattering process is as follows: The absorption of the initial X-ray photon with energy ω1 excites a core electron into the conduction band, leaving a core hole behind. The intermediate system, after the excitation, is in an excited many-body state |n〉. The core hole can now be filled by a valence electron, which loses the energy ω2 by emitting an X-ray photon. This process is known as direct RIXS. Alternatively, the presence of the core-hole and excited electron can lead to the formation of a secondary electron-hole pair in the intermediate state. The initially excited can then fill the core hole. This process is known as indirect RIXS.2,32 Involving excited states beyond singlet excitations, its contribution is neglected in the following. We recall that indirect RIXS is mostly devoted to magnetic excitations, like magnon scattering.
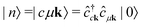 with energy En = εck − εμk. Furthermore, the final states contain an excited electron in a specific conduction state c′k′ and a valence hole in the state vk', such that
with energy En = εck − εμk. Furthermore, the final states contain an excited electron in a specific conduction state c′k′ and a valence hole in the state vk', such that 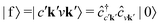 and
and 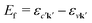 . Then, eqn (2) becomes
. Then, eqn (2) becomes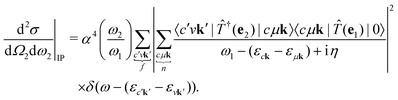
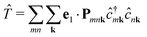 , where Pmnk = 〈 mk|p|nk〉 are the momentum matrix elements. Inserting these operators in eqn (3) yields
, where Pmnk = 〈 mk|p|nk〉 are the momentum matrix elements. Inserting these operators in eqn (3) yields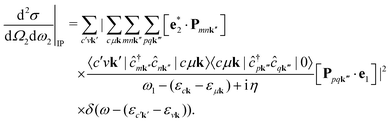
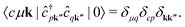
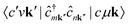 requires a more careful treatment. Applying Wick's theorem and restricting only to terms that correspond to the RIXS process, we obtain
requires a more careful treatment. Applying Wick's theorem and restricting only to terms that correspond to the RIXS process, we obtain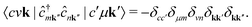
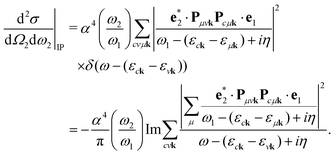
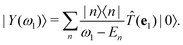
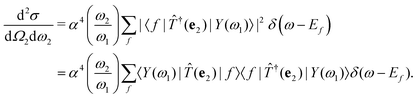
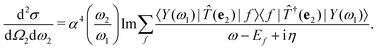
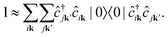
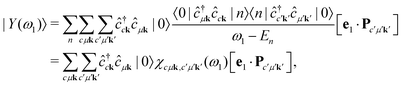
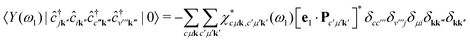
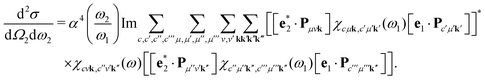
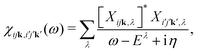
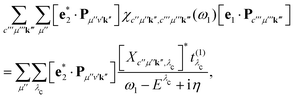
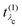 as
as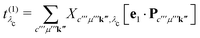
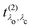 as
as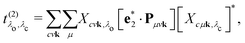
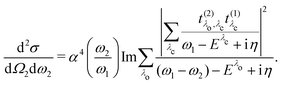
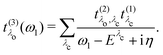
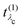 in eqn (19) and the excitation pathway
in eqn (19) and the excitation pathway 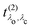 in eqn (20), allows for the compact expression of the RIXS cross section as
in eqn (20), allows for the compact expression of the RIXS cross section as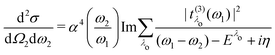
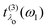 . It has poles in the energy loss at the optical excitation energies Eλo of the system, independent of the excitation energy, while the oscillator strength of each of these excitations depends on it. The oscillator strength defined in eqn (22), gives further insight into the many-body processes that occur in RIXS. The rate of the initial X-ray absorption event is given by
. It has poles in the energy loss at the optical excitation energies Eλo of the system, independent of the excitation energy, while the oscillator strength of each of these excitations depends on it. The oscillator strength defined in eqn (22), gives further insight into the many-body processes that occur in RIXS. The rate of the initial X-ray absorption event is given by 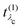 , combined with the energy conservation rule (the denominator ω1 − Eλc + iη in eqn (22)). The absorption leads to an intermediate core-excited state, characterized by the excitation index λc. The final RIXS spectrum is then given by the rate of the absorption combined with the pathway
, combined with the energy conservation rule (the denominator ω1 − Eλc + iη in eqn (22)). The absorption leads to an intermediate core-excited state, characterized by the excitation index λc. The final RIXS spectrum is then given by the rate of the absorption combined with the pathway 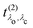 that describes the many-body transition |λc〉 →| λo〉. These pathways are far from obvious, as the mixing between
that describes the many-body transition |λc〉 →| λo〉. These pathways are far from obvious, as the mixing between 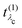 and
and 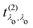 can develop in destructive or constructive interference, attesting the many-body character of such process.
can develop in destructive or constructive interference, attesting the many-body character of such process.


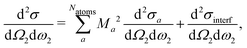


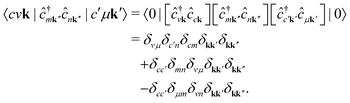

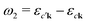 where the excited electron transitions to another conduction state
where the excited electron transitions to another conduction state 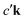 . Thus, the final state of this scattering process contains a core hole at μk and an excited electron in
. Thus, the final state of this scattering process contains a core hole at μk and an excited electron in 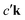 . As such, this scattering process does not correspond to the RIXS process.
. As such, this scattering process does not correspond to the RIXS process.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0. The reciprocal space is sampled with a 9 × 9 × 9 k-grid, and we include basis functions up to a cut-off of RmaxMT·|G + q|max = 8. To correct the electronic structure, we apply a scissors operator Δω = 1.9 eV, such to reproduce the measured indirect band gap of 5.48 eV.74 Another scissors operator of 22 eV is employed to correct the position of the 1s level.
a0. The reciprocal space is sampled with a 9 × 9 × 9 k-grid, and we include basis functions up to a cut-off of RmaxMT·|G + q|max = 8. To correct the electronic structure, we apply a scissors operator Δω = 1.9 eV, such to reproduce the measured indirect band gap of 5.48 eV.74 Another scissors operator of 22 eV is employed to correct the position of the 1s level.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0−1 such to provide a precise description of the more localized excitations. 40 unoccupied are included in the BSE calculation. For the BRIXS calculation, the 8.000 lowest-energy valence and 20
a0−1 such to provide a precise description of the more localized excitations. 40 unoccupied are included in the BSE calculation. For the BRIXS calculation, the 8.000 lowest-energy valence and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 carbon 1s excitations are taken into account.
000 carbon 1s excitations are taken into account.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å, b = 3.038
Å, b = 3.038![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å, c = 5.807
Å, c = 5.807![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å, and β = 103.82°.78 The electronic structure is determined on a 8 × 8 × 8 k-grid using basis functions up to a cut-off of RmaxMT·|G + q|max = 8. Our calculations with the PBEsol functional79 yield a Kohn-Sham gap of 2.89 eV. To match the experimental fundamental gap of of 5.72 eV,80 we apply a scissors operator of Δω = 2.6 eV. A scissors shift of Δω2 = 24.93 eV is applied to correct the position of the oxygen 1s state such to align the calculated O K edge XAS with the experimental one.81
Å, and β = 103.82°.78 The electronic structure is determined on a 8 × 8 × 8 k-grid using basis functions up to a cut-off of RmaxMT·|G + q|max = 8. Our calculations with the PBEsol functional79 yield a Kohn-Sham gap of 2.89 eV. To match the experimental fundamental gap of of 5.72 eV,80 we apply a scissors operator of Δω = 2.6 eV. A scissors shift of Δω2 = 24.93 eV is applied to correct the position of the oxygen 1s state such to align the calculated O K edge XAS with the experimental one.81
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0−1 for local-field effects. The 10 highest valence bands and 10 lowest conduction bands form the transition space. 30 conduction bands are used in the RPA calculation of the screened Coulomb potential.
a0−1 for local-field effects. The 10 highest valence bands and 10 lowest conduction bands form the transition space. 30 conduction bands are used in the RPA calculation of the screened Coulomb potential.