Open Access Article
Open Access ArticleInfluence of the emission site on the photoelectron circular dichroism in trifluoromethyloxirane†
Kilian
Fehre
a,
Florian
Trinter
 ab,
Nikolay M.
Novikovskiy
ab,
Nikolay M.
Novikovskiy
 cd,
Sven
Grundmann
cd,
Sven
Grundmann
 a,
Dimitrios
Tsitsonis
a,
Sebastian
Eckart
a,
Dimitrios
Tsitsonis
a,
Sebastian
Eckart
 a,
Leonie
Bauer
a,
Maria
Hilzinger
a,
Till
Jahnke
e,
Reinhard
Dörner
a,
Philipp V.
Demekhin
a,
Leonie
Bauer
a,
Maria
Hilzinger
a,
Till
Jahnke
e,
Reinhard
Dörner
a,
Philipp V.
Demekhin
 c and
Markus S.
Schöffler
c and
Markus S.
Schöffler
 *a
*a
aInstitut für Kernphysik, Goethe-Universität Frankfurt, Max-von-Laue-Straße 1, 60438 Frankfurt am Main, Germany. E-mail: fehre@atom.uni-frankfurt.de; schoeffler@atom.uni-frankfurt.de
bMolecular Physics, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany
cInstitut für Physik und CINSaT, Universität Kassel, Heinrich-Plett-Straße 40, 34132 Kassel, Germany. E-mail: demekhin@physik.uni-kassel.de
dInstitute of Physics, Southern Federal University, 344090 Rostov-on-Don, Russia
eEuropean XFEL GmbH, Holzkoppel 4, 22869 Schenefeld, Germany
First published on 27th May 2022
Abstract
We report a joint experimental and theoretical study of the differential photoelectron circular dichroism (PECD) in inner-shell photoionization of uniaxially oriented trifluoromethyloxirane. By adjusting the photon energy of the circularly polarized synchrotron radiation, we address 1s-photoionization of the oxygen, different carbon, and all fluorine atoms. The photon energies were chosen such that in all cases electrons with a similar kinetic energy of about 11 eV are emitted. Employing coincident detection of electrons and fragment ions, we concentrate on identical molecular fragmentation channels for all of the electron-emitter scenarios. Thereby, we systematically examine the influence of the emission site of the photoelectron wave on the differential PECD. We observe large differences in the PECD signals. The present experimental results are supported by corresponding relaxed-core Hartree–Fock calculations.
1 Introduction
Most large molecules, including most biomolecules and the building blocks of life, are chiral.1 Therefore, there is a great interest in the development of highly sensitive methods for chiral recognition in analytical chemistry and pharmacy. In the realm of gas-phase studies, several techniques have emerged so far, but, for example, the direct determination of the handedness of chiral molecules by Coulomb explosion imaging is currently restricted to small molecules.2,3 In the last two decades, exploiting photoelectron circular dichroism (PECD4) has become a new and promising tool for the recognition of chiral molecules in the gas phase.5–7 PECD signals are up to three orders of magnitude stronger as compared to those of the closely related conventional circular dichroism. While the latter one relies on a scalar observable, namely the helicity-dependent difference in the absorption probability of circularly polarized light by chiral molecules, a vectorial observable is investigated in the case of PECD (emerging from randomly oriented molecules), namely the helicity-dependent emission probability of the photoelectron as a function of its emission angle with respect to the light propagation direction. Due to the much larger signal strength, PECD is especially suitable for accurate examination of dilute gas-phase samples or samples with small enantiomeric excesses.8,9PECD is highly sensitive to the molecular structure,10 spatial orientation of the molecule,11–13 vibrational14–16 and conformational states,17–19 and to dimerization.20 The dynamics of chiral molecules was also investigated in time-resolved measurements.21–23 A further important advantage of PECD is its insensitivity to fluctuations in the target density or the photon flux. The effect of possible fluctuations is eliminated by normalization for differential signals.24 Besides on structural properties of the molecule, PECD also depends on many parameters, such as the photoelectron energy,25,26 possible intermediate states populated during the ionization process,27,28 or molecular resonances.29,30 In addition, the orbital from which the photoelectron is ionized influences the PECD signal.26,31,32
For randomly oriented molecules in the gas phase, PECD is typically on the order of a few percent. Its strength, however, can already be increased about ten times when fixing one molecular orientation axis in space.11,12 Moreover, for distinct molecular orientations, the normalized chiral asymmetry can exceed 50%,13 and such giant differential PECD of fully fixed-in-space chiral molecules provides higher sensitivity in the enantiomeric-excess determination. In our previous work, ref. 12, we reported on PECD as a function of a molecular fragmentation direction, i.e., on PECD of uniaxially oriented trifluoromethyloxirane (C3H3F3O, TFMOx). For O 1s-photoionization of TFMOx, we studied the energy dependence of the chiral asymmetry and its sensitivity to the molecular configuration, as compared to its close relative methyloxirane (C3H6O).
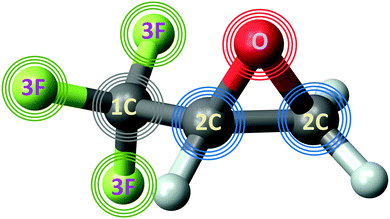
In the present work, we continue our investigation of such differential PECD in the inner-shell photoionization of uniaxially oriented TFMOx and study its emission-site sensitivity for a fixed photoelectron kinetic energy of 11 eV. To this end, we compare differential PECDs for O 1s-photoionization of TFMOx12 with that obtained for the 1s-photoionization of different carbon and all fluorine atoms in the molecule. The structure of TFMOx and the processes studied in the present work are schematically visualized in Fig. 1.
2 Experiment and theory
The experimental data for the O 1s-photoionization of TFMOx were recorded during the same experimental campaign as the data reported in ref. 12 at Synchrotron SOLEIL (Saint-Aubin, France) at beamline SEXTANTS. The respective experimental details can be found therein.12 The experiment providing the results for the F 1s-photoionization and the two cases of C 1s-photoionization was conducted at PETRA III, DESY (Hamburg, Germany) at beamline P04.33 To ensure equal experimental conditions for the two light helicities, we switched every two hours between circular left and circular right polarization. The R-TFMOx was brought into vacuum by supersonic expansion, expanding through a 60 μm nozzle. Subsequently, the gas jet was skimmed two times and crossed at right angle with the synchrotron light. About 95% of the non-used gas was recycled multiple times, using a closed-loop approach.34 The sample had an enantiomeric excess of 95% and a chemical purity of > 98%.12 In a coincident measurement, the photoelectron and the ionic fragments were recorded with 4π solid angle using the permanent COLTRIMS35–37 end-station at beamline P04 at DESY. The ion arm of the spectrometer consisted of a mesh-free homogeneous 17 cm long acceleration region guiding the ionic fragments onto a hexagonal delay-line detector with an active diameter of 75 mm. The electron arm was built in a time-focusing geometry,38 with 4.5 cm acceleration and 7.5 cm drift length, not being separated by a mesh. The electric field was set to 130 V cm−1 in order to separate the different fragmentation channels already in the photoion–photoion coincidence spectrum. With this voltage, electrons with kinetic energies up to 15 eV were captured with 4π solid angle without the need of applying a magnetic confinement field. Also, all ionic fragments considered in this manuscript were captured with full solid angle of 4π. From the particle's time-of-flight, its momentum along the direction of the electric field as well as the mass-to-charge ratio in case of ions can be deduced, based on the spectrometer geometry and field strength. From the impact position on the detector, the transverse momentum is derived. The electron-energy resolution in the detector plane was sufficient to resolve the energy difference between the C 1s-photoelectrons of the CF3-group and of the two carbon atoms in the oxirane ring; the energy resolution in the third dimension (typically referred to as the “time-of-flight” direction) was not sufficient for that purpose due to the high electric field in the spectrometer, required to separate the different ion masses (m/q), i.e., fragmentation channels. Therefore, only electron momenta restricted to the detector plane with |pz| < 0.35 a.u. were considered in the analysis. So-called funnel microchannel plates (MCPs) were used on the ion detector to increase the coincident detection efficiency39 by a factor of 2 for the two-body breakup. We first performed calibration measurements for both the electron and ion arms of the spectrometer using the known Ar 2p- and N2 1s-photoionizations. Thereafter, the photon energies were tuned such that photoelectrons of Ee = Eγ − Eb = 11 eV were emitted. Given the chemical shift of the different sites, this corresponded to photon energies of Eγ = 706 eV, 550 eV, 310 eV, and 305 eV for the F, O, C (trifluoromethyl group), and the C (oxirane ring) atoms.A typical approach to separate the real signal from false coincidences and background is to check whether the measured particles comply with momentum conservation. Since breakup channels with undetected (neutral) particles were used for the analysis in order to gather sufficient statistics, the background suppression via this approach was not as effective as for breakup channels where all fragments are detected. Instead, we used several, less strict gates to successfully suppress the background from desired fragmentation channels. The first gate selected the time-of-flight combinations in the photoion–photoion coincidence spectrum to have ions with the proper m/q ratio. In the second step, the momentum of each of the two measured ionic fragments was restricted to (85–145 a.u.)/(75–145 a.u.), (80–130 a.u.)/(105–155 a.u.), (85–145 a.u.)/(75–145 a.u.), and (75–165 a.u.)/(50–175 a.u.), respectively for the light/heavy charged fragment of the fragmentation channels CF3+(m/q = 69)–C2H2+(m/q = 26), CF3+(m/q = 69)–COH+(m/q = 29), CF2+(m/q = 50)–C2H2+(m/q = 26), and CF2+(m/q = 50)–COH+(m/q = 29). And third, the magnitude of the calculated sum momentum was selected to be smaller than 60 a.u. Assuming the validity of the axial-recoil approximation,40 the ionic fragments’ momenta are directly correlated with the orientation of a molecule in space at the instant of ionization. We used the momentum vector of the CF2,3+ fragment to define the angle β between the molecular breakup axis and the light propagation direction.
The calculations of the angle-resolved 1s-photoionization of all fluorine and carbon atoms in TFMOx were performed similarly to those reported in our previous study of the O 1s-photoionization of this molecule.12 Briefly, the calculations were performed at the equilibrium internuclear geometry of the electronic ground state of the neutral molecule in the relaxed-core Hartree–Fock approximation by the Single Center (SC) method.41,42 The SC expansions were restricted by the angular momenta and their projections ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m of 79 and 29, respectively, for the occupied and continuum orbitals. In the experiment, the asymptotic momenta of the detected ions are measured, and it is not straightforward to assign the emission directions of the fragments to the orientation of a particular molecular orientation axis at the instant of the photoionization. This is because for large fragments, whose centers of mass do not coincide with their centers of charge, rotations of the fragments with respect to each other take place during the complex fragmentation dynamics. Therefore, the molecular orientation axis at the instant of the photoionization process was used as a free parameter when comparing the measured data to the calculations.11,12 At first, the angle-resolved photoionization spectra were generated for different spatial orientations of the assumed fragmentation axis with respect to the light propagation direction, which are defined by the two Euler angles αo and βo. Since only one fragmentation direction is detected in the experiment, the computed spectra were then numerically integrated over the orientation angle αo to simulate a uniaxially oriented molecule. In addition, the spectra computed for individual fluorine atoms and, separately, for the two carbon atoms in the oxirane ring were averaged to simulate the experimentally unresolved PECD landscapes. Starting with an assumption based on the axial-recoil approximation,40 we searched for the optimal choice of the assumed molecular fragmentation axis, which provides the best visual correspondence11 between the computed and measured differential PECD.
m of 79 and 29, respectively, for the occupied and continuum orbitals. In the experiment, the asymptotic momenta of the detected ions are measured, and it is not straightforward to assign the emission directions of the fragments to the orientation of a particular molecular orientation axis at the instant of the photoionization. This is because for large fragments, whose centers of mass do not coincide with their centers of charge, rotations of the fragments with respect to each other take place during the complex fragmentation dynamics. Therefore, the molecular orientation axis at the instant of the photoionization process was used as a free parameter when comparing the measured data to the calculations.11,12 At first, the angle-resolved photoionization spectra were generated for different spatial orientations of the assumed fragmentation axis with respect to the light propagation direction, which are defined by the two Euler angles αo and βo. Since only one fragmentation direction is detected in the experiment, the computed spectra were then numerically integrated over the orientation angle αo to simulate a uniaxially oriented molecule. In addition, the spectra computed for individual fluorine atoms and, separately, for the two carbon atoms in the oxirane ring were averaged to simulate the experimentally unresolved PECD landscapes. Starting with an assumption based on the axial-recoil approximation,40 we searched for the optimal choice of the assumed molecular fragmentation axis, which provides the best visual correspondence11 between the computed and measured differential PECD.
3 Results and discussion
As discussed above, we studied the 1s-photoionization of all heavy atoms in R-TFMOx (indicated by coloured circles in Fig. 1). The K-shell ionization energies of different chemical elements (F, O, and C) differ by several hundreds of electron volts and, thus, can be addressed unambiguously. A very small difference between the 1s-binding energies of the three fluorine atoms (about 90 meV), Auger decay lifetime broadenings, very rich vibrational structures of the respective photoelectron lines, and the limited electron-energy resolution, all together, do not allow for resolving the respective photoelectrons in our experiment. We thus considered the unresolved photoelectron spectra of all three fluorine atoms (hereafter referred to as 3F). The 1s-binding energy of the carbon atom in the CF3-group is about 5 eV larger than that of the two carbon atoms in the oxirane ring, which allows to unambiguously resolve its 1s-photoelectrons (1C). On the contrary, the 1s-binding energies of the two carbon atoms in the oxirane ring differ only by a few 100 meV and, owing to the same reasons as for the fluorine atoms, could thus not be resolved in the present experiment (2C).At first, the angle-resolved spectra were analysed for each emitter case (O, 3F, 2C, and 1C) for randomly oriented molecules. We use the well-known parametrization4 of the photoelectron angular distributions induced by circularly polarized light with positive and negative helicities:
I±1(θ) = 1 ± β1P1(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) − ½β2P2(cos θ) − ½β2P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) θ) | (1) |
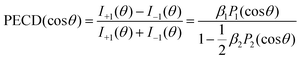 | (2) |
The result is demonstrated in the left-hand panels (a,d,g,j) of Fig. 2 for all emitters. There, the experimental data (red circles with error bars reflecting statistical uncertainties) are displayed together with black solid curves showing the fitting results for β2 and β1 using eqn (2). These values of β2 and β1 are compared with the computed parameters in Table 1, which illustrates a strong influence of the origin of the photoelectron wave on the PECD of randomly oriented molecules.
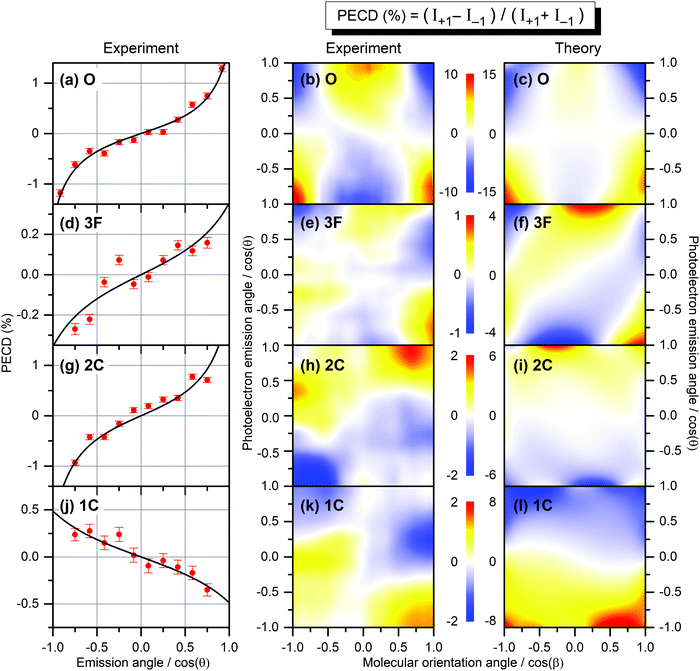 | ||
| Fig. 2 Experimental and theoretical PECD of R-TFMOx represented as the normalized difference of the electron emission probabilities, obtained for 1s-photoelectrons of the oxygen atom (a–c, O), all three fluorine atoms (d–f, 3F), the two carbon atoms from the oxirane ring (g–i, 2C), and the carbon atom in the trifluoromethyl group (j–l, 1C). Kinetic energy of all photoelectrons is equal to about 11 eV. The left-hand panels (a,d,g,j) illustrate the retrieval of the anisotropy β2 and dichroic β1 parameters by fitting (black curves) the PECD, measured for randomly oriented molecules (red circles), with eqn (2). The middle and the right-hand panels illustrate the experimental (b,e,h,k) and theoretical (c,f,i,l) differential PECD as a function of the photoelectron emission angle θ and molecular orientation angle β between the momentum vector of the CF2,3+ fragment and the light propagation direction. The statistical uncertainties, taken at the peak values of the experimental data, are: (b, O) ±0.45%; (e, 3F) ±0.17%; (h, 2C) ±0.25%; and (k, 1C) ±0.16%. | ||
While the computed and measured anisotropy parameters β2 agree well for all emitters, the agreement between the respective dichroic parameters β1 is rather poor. Possible reasons of such disagreement for the oxygen atom, where the computed and measured asymmetries have different signs, were discussed in ref. 12. For the three fluorine atoms (3F), both our theory and experiment yield the smallest chiral asymmetries among all emitter cases (yet, the theory predicts an asymmetry which is four times larger). The calculations show larger individual asymmetries for different fluorine atoms which compensate each other on average owing to different signs (see also ref. 26). For the two unresolved carbon atoms in the oxirane ring (2C), the computed and measured asymmetries have equal sign and are comparable in their magnitude (but still somewhat larger in the theory). For this kinetic energy of 11 eV, the computed dichroic parameter of the carbon atom in the chiral center is +3.6% and thus larger than that of the other carbon in the oxirane ring which is −0.6%. The latter even has an opposite sign, thereby reducing the average asymmetry to +1.7%. For the carbon atom in the CF3-group (1C), both the theory and experiment show equal sign of the asymmetry, which is opposite to that for the 2C-emitters. However, the computed asymmetry is about eight times stronger.
The influence of the origin of the photoelectron wave is even stronger if one considers the PECD of uniaxially oriented TFMOx being a two-dimensional function of the photoelectron emission angle θ and the molecular fragmentation angle β. To access this molecular fragmentation axis, the Coulomb explosion into two charged fragments was investigated, following the procedure developed in previous publications.11,12 For the oxygen atom, the combined fragmentation channels CF3+(m/q = 69)–C2H3O+(m/q = 43) and CF3+(m/q = 69)–C2H2O+(m/q = 42) were used in our previous work12 to access PECD(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos
θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β). However, for the 3F-emitters, these two fragmentation channels are strongly suppressed (about 75% weaker as compared to the O-case). Taking into account that the 3F-, 2C-, and 1C-emitters show smaller chiral asymmetry on average than the O-emitter (see Table 1), larger statistics or, in the other words, strongly contributing fragmentation channels need to be considered to investigate PECD of uniaxially oriented TFMOx for those emitters. As was already mentioned above, the molecular-frame orientation at the instant of the photoionization and the fragment frame detected by the directions of the fragments’ momentum vectors can be rather different.43 Thus, a priori, each breakup channel and ionization site have their own fragment frame and also molecular frame at the instant of the photoionization.
β). However, for the 3F-emitters, these two fragmentation channels are strongly suppressed (about 75% weaker as compared to the O-case). Taking into account that the 3F-, 2C-, and 1C-emitters show smaller chiral asymmetry on average than the O-emitter (see Table 1), larger statistics or, in the other words, strongly contributing fragmentation channels need to be considered to investigate PECD of uniaxially oriented TFMOx for those emitters. As was already mentioned above, the molecular-frame orientation at the instant of the photoionization and the fragment frame detected by the directions of the fragments’ momentum vectors can be rather different.43 Thus, a priori, each breakup channel and ionization site have their own fragment frame and also molecular frame at the instant of the photoionization.
In our analysis, we identified the following four incomplete fragmentation channels CF3+(m/q = 69)–C2H2+(m/q = 26), CF3+(m/q = 69)–COH+(m/q = 29), CF2+(m/q = 50)–C2H2+(m/q = 26), and CF2+(m/q = 50)–COH+(m/q = 29) as particularly suitable by matching the following four criteria: (i) they fulfill the axial-recoil approximation;40 (ii) the reconstructed molecular axis is rather similar for all four cases; (iii) the breakup channels yield a very similar PECD(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos
θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) pattern for the O-emitter as compared to that obtained in our previous work;12 (iv) at least one of the breakup channels contains sufficient statistics for the further analysis. With respect to (ii), dictated by momentum conservation for complete fragmentation channels, also the angle between the momentum vectors of the two detected ions for all analysed incomplete fragmentation channels is almost 180° (note that neutral fragments, which are not detected in the experiment, carry only a moderate momentum and have thus very limited influence on the fragmentation axis reconstructed via the measured momenta of the ions). The influence of the neutral undetected particles on the fragmentation axis was estimated to introduce an uncertainty of about 13–16°, which is in the range of the selected data binning. Combining those four incomplete fragmentation channels for the 3F-, 2C-, and 1C-emitters results in a total increase of the statistics by a factor of about 45, as compared to the two fragmentation channels used in our previous work12 for the O-emitter. In order to compare here PECD(cos
β) pattern for the O-emitter as compared to that obtained in our previous work;12 (iv) at least one of the breakup channels contains sufficient statistics for the further analysis. With respect to (ii), dictated by momentum conservation for complete fragmentation channels, also the angle between the momentum vectors of the two detected ions for all analysed incomplete fragmentation channels is almost 180° (note that neutral fragments, which are not detected in the experiment, carry only a moderate momentum and have thus very limited influence on the fragmentation axis reconstructed via the measured momenta of the ions). The influence of the neutral undetected particles on the fragmentation axis was estimated to introduce an uncertainty of about 13–16°, which is in the range of the selected data binning. Combining those four incomplete fragmentation channels for the 3F-, 2C-, and 1C-emitters results in a total increase of the statistics by a factor of about 45, as compared to the two fragmentation channels used in our previous work12 for the O-emitter. In order to compare here PECD(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos
θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) for different emitter sites, we reanalysed the experimental data of ref. 12 on the O-emitter, acquired for the photoelectron energy of 11 eV, using the aforementioned identified four incomplete fragmentation channels. However, employing different fragmentation channels with smaller statistics resulted in a somewhat weaker contrast of the PECD(cos
β) for different emitter sites, we reanalysed the experimental data of ref. 12 on the O-emitter, acquired for the photoelectron energy of 11 eV, using the aforementioned identified four incomplete fragmentation channels. However, employing different fragmentation channels with smaller statistics resulted in a somewhat weaker contrast of the PECD(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos
θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) for the O-emitter (±10% here as compared to ±18% in ref. 12), keeping the PECD landscape almost unchanged. Fig. S1 of the ESI† illustrates a satisfactorily robustness of the present analysis for all emitters with respect to the choice of only three out of the four identified channels.
β) for the O-emitter (±10% here as compared to ±18% in ref. 12), keeping the PECD landscape almost unchanged. Fig. S1 of the ESI† illustrates a satisfactorily robustness of the present analysis for all emitters with respect to the choice of only three out of the four identified channels.
The PECD(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos
θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) maps obtained in a similar way for all emitters as described above are depicted in the middle panels (b,e,h,k) of Fig. 2. As one can see, the scales of the measured differential PECDs differ by up to an order of magnitude for the emission from different sites. The O-emitter shows by far the strongest differential PECD. Similarly to the randomly oriented samples (Table 1), the differential asymmetry is smallest for the 3F-emitters (ten times smaller than for the O-emitter), being a result of compensations of individual contributions of different signs, as already discussed in the electron-energy-dependent study of the β1 parameter in ref. 26 (Fig. 2 there). For the O-emitter, the differential chiral asymmetry for uniaxially oriented TFMOx is about an order of magnitude larger than the average asymmetry for randomly oriented molecules (Table 1). For other emitters, however, the increase of the PECD for the uniaxially oriented molecules as compared to the randomly oriented samples is not as large, being between about 2 to 5 times. This strongly depends on the PECD landscape, i.e., on its dependence on the molecular orientation angle. In particular, for the O- and 3F-emitters, the PECDs change their signs if the fragmentation axis is oriented along or perpendicularly to the light propagation direction. As a consequence, an integration over the molecular orientation reduces the effect strongly. For the 2C- and 1C-emitters, the sign of differential PECDs is almost independent of the molecular orientation angle. This results in a smaller reduction of the asymmetry on average.
β) maps obtained in a similar way for all emitters as described above are depicted in the middle panels (b,e,h,k) of Fig. 2. As one can see, the scales of the measured differential PECDs differ by up to an order of magnitude for the emission from different sites. The O-emitter shows by far the strongest differential PECD. Similarly to the randomly oriented samples (Table 1), the differential asymmetry is smallest for the 3F-emitters (ten times smaller than for the O-emitter), being a result of compensations of individual contributions of different signs, as already discussed in the electron-energy-dependent study of the β1 parameter in ref. 26 (Fig. 2 there). For the O-emitter, the differential chiral asymmetry for uniaxially oriented TFMOx is about an order of magnitude larger than the average asymmetry for randomly oriented molecules (Table 1). For other emitters, however, the increase of the PECD for the uniaxially oriented molecules as compared to the randomly oriented samples is not as large, being between about 2 to 5 times. This strongly depends on the PECD landscape, i.e., on its dependence on the molecular orientation angle. In particular, for the O- and 3F-emitters, the PECDs change their signs if the fragmentation axis is oriented along or perpendicularly to the light propagation direction. As a consequence, an integration over the molecular orientation reduces the effect strongly. For the 2C- and 1C-emitters, the sign of differential PECDs is almost independent of the molecular orientation angle. This results in a smaller reduction of the asymmetry on average.
The results of our calculations of the differential PECD, obtained for optimal molecular fragmentation axes, are depicted in the right-hand panels (c,f,i,l) of Fig. 2. It turns out that, for the O- and 1C-emitters, the best description of the measured PECD(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos
θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) is provided by the fragmentation axis, which connects the CH2-group on the oxirane ring with the oxygen atom. For the 3F-emitters, the optimal axis connects the CH2-group and the carbon atom in the chiral center, and for the 2C-emitter the chiral center with the CF3-group. The fact that we found notably different optimal fragmentation axes for different emitters supports our statement on the intricate fragmentation dynamics triggered by the considered K-shell photoionization of TFMOx. As one can see from Fig. 2, our theory provides a semi-quantitative description of the measured differential PECD. While the calculations reproduce the overall landscapes seen in the measured PECDs including their signs, the magnitude of the theoretical asymmetry is about 1.5 to 4 times larger for the different emitters. This can be related to the fact of using incomplete fragmentation channels, where momentum conservation was used to derive the momentum of the neutral fragment and thus cannot be used to suppress false coincidences. Furthermore, the combination of data for several channels in the experiment leads to additional averaging of the measured asymmetry. As expected, the computed PECD landscapes obey the analytically derived asymmetry rule11 PECD(−cos
β) is provided by the fragmentation axis, which connects the CH2-group on the oxirane ring with the oxygen atom. For the 3F-emitters, the optimal axis connects the CH2-group and the carbon atom in the chiral center, and for the 2C-emitter the chiral center with the CF3-group. The fact that we found notably different optimal fragmentation axes for different emitters supports our statement on the intricate fragmentation dynamics triggered by the considered K-shell photoionization of TFMOx. As one can see from Fig. 2, our theory provides a semi-quantitative description of the measured differential PECD. While the calculations reproduce the overall landscapes seen in the measured PECDs including their signs, the magnitude of the theoretical asymmetry is about 1.5 to 4 times larger for the different emitters. This can be related to the fact of using incomplete fragmentation channels, where momentum conservation was used to derive the momentum of the neutral fragment and thus cannot be used to suppress false coincidences. Furthermore, the combination of data for several channels in the experiment leads to additional averaging of the measured asymmetry. As expected, the computed PECD landscapes obey the analytically derived asymmetry rule11 PECD(−cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,−cos
θ,−cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) = −PECD(cos
β) = −PECD(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,cos
θ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β), while there are noticeable deviations from this rule in the experiment indicating an insufficiency of the statistics in the acquired spectra.
β), while there are noticeable deviations from this rule in the experiment indicating an insufficiency of the statistics in the acquired spectra.
4 Conclusions
We demonstrate experimentally and theoretically that the starting point of the photoelectron wave has a decisive influence on the signal strength and sign of the PECD. For this purpose, we examined inner-shell photoionization of different atomic species of the R-TFMOx molecule at similar photoelectron kinetic energies. In particular, we compare the PECDs obtained for the oxygen atom, the three unresolved fluorine atoms, the two unresolved carbon atoms in the oxirane ring, and the carbon atom on the trifluoromethyl group being the electron emitters. We show that the differential PECD of uniaxially oriented molecules is increased as compared to that of randomly oriented molecules. However, the signal amplification is very different for different emitters, which is dictated by the dependence of the differential PECD on the molecular orientation angle. For a practical use of PECD measurements as a tool for chiral recognition in the gas phase, thus, not only a suitable photoelectron energy should be considered, but also the orbital from which the photoelectron is ionized needs to be carefully selected to maximize the sensitivity of the method.Author contributions
The project was supervised by R. D., P. V. D., and M. S. S. The experiment was prepared and carried out by K. F., F. T., S. G., D. T., S. E., L. B., M. H., T. J., and M. S. S. Data analysis was performed by K. F. and P. V. D. Theoretical calculations were carried out by N. M. N. and P. V. D. Initial draft was created by K. F., R. D., P. V. D., and M. S. S. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work at PETRA III was supported by BMBF (Bundesministerium für Bildung und Forschung). We thank the staff of PETRA III for running the facility and providing beamtime under project H-20010092 and beamline P04 for the excellent support. This research was supported in part through the Maxwell computational resources operated at DESY. This work was funded by the Deutsche Forschungsgemeinschaft (DFG) – Project No. 328961117 – SFB 1319 ELCH (Extreme light for sensing and driving molecular chirality). M. S. S. acknowledges financial support from the Adolf-Messer-foundation.References
- A. Zehnacker, Chiral Recognition in the Gas Phase, CRC Press, Hoboken, 2010 Search PubMed.
- M. Pitzer, M. Kunitski, A. S. Johnson, T. Jahnke, H. Sann, F. Sturm, L. P. H. Schmidt, H. Schmidt-Böcking, R. Dörner, J. Stohner, J. Kiedrowski, M. Reggelin, S. Marquardt, A. Schießer, R. Berger and M. S. Schöffler, Direct Determination of Absolute Molecular Stereochemistry in Gas Phase by Coulomb Explosion Imaging, Science, 2013, 341, 1096–1100 CrossRef CAS PubMed.
- M. Pitzer, et al., Absolute Configuration from Different Multifragmentation Pathways in Light-Induced Coulomb Explosion Imaging, ChemPhysChem, 2016, 17, 2465–2472 CrossRef CAS PubMed.
- L. Nahon, G. A. Garcia, C. J. Harding, E. Mikajlo and I. Powis, Determination of chiral asymmetries in the valence photoionization of camphor enantiomers by photoelectron imaging using tunable circularly polarized light, J. Chem. Phys., 2006, 125, 114309 CrossRef PubMed.
- J. Miles, D. Fernandes, A. Young, C. M. M. Bond, S. W. Crane, O. Ghafur, D. Townsend, J. Sá and J. B. Greenwood, A new technique for probing chirality via photoelectron circular dichroism, Anal. Chim. Acta, 2017, 984, 134–139 CrossRef CAS PubMed.
- M. M. R. Fanood, N. B. Ram, C. S. Lehmann, I. Powis and M. H. M. Janssen, Enantiomer-specific analysis of multi-component mixtures by correlated electron imaging–ion mass spectrometry, Nat. Commun., 2015, 6, 7511 CrossRef CAS PubMed.
- A. Comby, E. Bloch, C. M. M. Bond, D. Descamps, J. Miles, S. Petit, S. Rozen, J. B. Greenwood, V. Blanchet and Y. Mairesse, Real-time determination of enantiomeric and isomeric content using photoelectron elliptical dichroism, Nat. Commun., 2018, 9, 5212 CrossRef CAS PubMed.
- L. Nahon, L. Nag, G. A. Garcia, I. Myrgorodska, U. Meierhenrich, S. Beaulieu, V. Wanie, V. Blanchet, R. Géneaux and I. Powis, Determination of accurate electron chiral asymmetries in fenchone and camphor in the VUV range: sensitivity to isomerism and enantiomeric purity, Phys. Chem. Chem. Phys., 2016, 18, 12696–12706 RSC.
- A. Kastner, C. Lux, T. Ring, S. Züllighoven, C. Sarpe, A. Senftleben and T. Baumert, Enantiomeric Excess Sensitivity to Below One Percent by Using Femtosecond Photoelectron Circular Dichroism, ChemPhysChem, 2016, 17, 1119–1122 CrossRef CAS PubMed.
- G. A. Garcia, H. Dossmann, L. Nahon, S. Daly and I. Powis, Photoelectron circular dichroism and spectroscopy of trifluoromethyl- and methyl-oxirane: a comparative study, Phys. Chem. Chem. Phys., 2014, 16, 16214–16224 RSC.
- M. Tia, et al., Observation of Enhanced Chiral Asymmetries in the Inner-Shell Photoionization of Uniaxially Oriented Methyloxirane Enantiomers, J. Phys. Chem. Lett., 2017, 8, 2780–2786 CrossRef CAS PubMed.
- G. Nalin, et al., Photoelectron circular dichroism of O 1s-photoelectrons of uniaxially oriented trifluoromethyloxirane: energy dependence and sensitivity to molecular configuration, Phys. Chem. Chem. Phys., 2021, 23, 17248–17258 RSC.
- K. Fehre, et al., Fourfold Differential Photoelectron Circular Dichroism, Phys. Rev. Lett., 2021, 127, 103201 CrossRef CAS PubMed.
- G. A. Garcia, H. Dossmann, L. Nahon, S. Daly and I. Powis, Identifying and Understanding Strong Vibronic Interaction Effects Observed in the Asymmetry of Chiral Molecule Photoelectron Angular Distributions, ChemPhysChem, 2017, 18, 500–512 CrossRef CAS PubMed.
- G. A. Garcia, L. Nahon, S. Daly and I. Powis, Vibrationally induced inversion of photoelectron forward-backward asymmetry in chiral molecule photoionization by circularly polarized light, Nat. Commun., 2013, 4, 2132 CrossRef PubMed.
- H. Ganjitabar, R. Hadidi, G. A. Garcia, L. Nahon and I. Powis, Vibrationally-resolved photoelectron spectroscopy and photoelectron circular dichroism of bicyclic monoterpene enantiomers, J. Mol. Spectrosc., 2018, 353, 11–19 CrossRef CAS.
- D. Di Tommaso, M. Stener, G. Fronzoni and P. Decleva, Conformational Effects on Circular Dichroism in the Photoelectron Angular Distribution, ChemPhysChem, 2006, 7, 924–934 CrossRef CAS PubMed.
- S. Turchini, D. Catone, N. Zema, G. Contini, T. Prosperi, P. Decleva, M. Stener, F. Rondino, S. Piccirillo, K. C. Prince and M. Speranza, Conformational Sensitivity in Photoelectron Circular Dichroism of 3-Methylcyclopentanone, ChemPhysChem, 2013, 14, 1723–1732 CrossRef CAS PubMed.
- S. Turchini, Conformational effects in photoelectron circular dichroism, J. Phys.: Condens. Matter, 2017, 29, 503001 CrossRef CAS PubMed.
- L. Nahon, G. A. Garcia, H. Soldi-Lose, S. Daly and I. Powis, Effects of dimerization on the photoelectron angular distribution parameters from chiral camphor enantiomers obtained with circularly polarized vacuum-ultraviolet radiation, Phys. Rev. A, 2010, 82, 032514 CrossRef.
- S. Beaulieu, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, A. G. Harvey, F. Légaré, Z. Mašín, L. Nahon, A. F. Ordonez, S. Petit, B. Pons, Y. Mairesse, O. Smirnova and V. Blanchet, Photoexcitation circular dichroism in chiral molecules, Nat. Phys., 2018, 14, 484–489 Search PubMed.
- A. Comby, S. Beaulieu, M. Boggio-Pasqua, D. Descamps, F. Légaré, L. Nahon, S. Petit, B. Pons, B. Fabre, Y. Mairesse and V. Blanchet, Relaxation Dynamics in Photoexcited Chiral Molecules Studied by Time-Resolved Photoelectron Circular Dichroism: Toward Chiral Femtochemistry, J. Phys. Chem. Lett., 2016, 7, 4514–4519 Search PubMed.
- S. Beaulieu, A. Comby, B. Fabre, D. Descamps, A. Ferré, G. Garcia, R. Géneaux, F. Légaré, L. Nahon, S. Petit, T. Ruchon, B. Pons, V. Blanchet and Y. Mairesse, Probing ultrafast dynamics of chiral molecules using time-resolved photoelectron circular dichroism, Faraday Discuss., 2016, 194, 325–348 RSC.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, M. Hofmann, J. Rist, M. Weller, A. Hartung, L. P. H. Schmidt, T. Jahnke, H. Braun, T. Baumert, J. Stohner, P. V. Demekhin, M. S. Schöffler and R. Dörner, Strong Differential Photoion Circular Dichroism in Strong-Field Ionization of Chiral Molecules, Phys. Rev. Lett., 2021, 126, 083201 CrossRef CAS PubMed.
- M. Stener, G. Fronzoni, D. Di Tommaso and P. Decleva, Density functional study on the circular dichroism of photoelectron angular distribution from chiral derivatives of oxirane, J. Chem. Phys., 2004, 120, 3284 CrossRef CAS PubMed.
- M. Ilchen, G. Hartmann, P. Rupprecht, A. N. Artemyev, R. N. Coffee, Z. Li, H. Ohldag, H. Ogasawara, T. Osipov, D. Ray, P. Schmidt, T. J. A. Wolf, A. Ehresmann, S. Moeller, A. Knie and P. V. Demekhin, Emitter-site-selective photoelectron circular dichroism of trifluoromethyloxirane, Phys. Rev. A, 2017, 95, 053423 CrossRef.
- M. M. Rafiee Fanood, M. H. M. Janssen and I. Powis, Wavelength dependent photoelectron circular dichroism of limonene studied by femtosecond multiphoton laser ionization and electron-ion coincidence imaging, J. Chem. Phys., 2016, 145, 124320 CrossRef PubMed.
- A. Kastner, T. Ring, B. C. Krüger, G. B. Park, T. Schäfer, A. Senftleben and T. Baumert, Intermediate state dependence of the photoelectron circular dichroism of fenchone observed via femtosecond resonance-enhanced multi-photon ionization, J. Chem. Phys., 2017, 147, 013926 CrossRef PubMed.
- D. Catone, M. Stener, P. Decleva, G. Contini, N. Zema, T. Prosperi, V. Feyer, K. C. Prince and S. Turchini, Resonant Circular Dichroism of Chiral Metal-Organic Complex, Phys. Rev. Lett., 2012, 108, 083001 CrossRef CAS PubMed.
- G. Hartmann, M. Ilchen, P. Schmidt, C. Küstner-Wetekam, C. Ozga, F. Scholz, J. Buck, F. Trinter, J. Viefhaus, A. Ehresmann, M. S. Schöffler, A. Knie and P. V. Demekhin, Recovery of High-Energy Photoelectron Circular Dichroism through Fano Interference, Phys. Rev. Lett., 2019, 123, 043202 CrossRef CAS PubMed.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Asymmetry in Photoelectron Emission from Chiral Molecules Induced by Circularly Polarized Light, Phys. Rev. Lett., 2001, 86, 1187 CrossRef PubMed.
- I. Powis, C. J. Harding, S. Barth, S. Joshi, V. Ulrich and U. Hergenhahn, Chiral asymmetry in the angle-resolved O and C 1s−1 core photoemissions of the R enantiomer of glycidol, Phys. Rev. A, 2008, 78, 052501 CrossRef.
- J. Viefhaus, F. Scholz, S. Deinert, L. Glaser, M. Ilchen, J. Seltmann, P. Walter and F. Siewert, The Variable Polarization XUV Beamline P04 at PETRA III: Optics, mechanics and their performance, Nucl. Instrum. Methods Phys. Res., Sect. A, 2013, 710, 151–154 CrossRef CAS.
- K. Fehre, M. Pitzer, F. Trinter, R. Berger, A. Schießer, H. Schmidt-Böcking, R. Dörner and M. S. Schöffler, Closed-loop recycling of rare liquid samples for gas-phase experiments, Rev. Sci. Instrum., 2021, 92, 023205 CrossRef CAS PubMed.
- R. Dörner, V. Mergel, O. Jagutzki, L. Spielberger, J. Ullrich, R. Moshammer and H. Schmidt-Böcking, Cold Target Recoil Ion Momentum Spectroscopy: a ‘momentum microscope’ to view atomic collision dynamics, Phys. Rep., 2000, 330, 95–192 CrossRef.
- J. Ullrich, R. Moshammer, A. Dorn, R. Dörner, L. P. H. Schmidt and H. Schmidt-Böcking, Recoil-ion and electron momentum spectroscopy: reaction-microscopes, Rep. Prog. Phys., 2003, 66, 1463 CrossRef CAS.
- T. Jahnke, T. Weber, T. Osipov, A. L. Landers, O. Jagutzki, L. P. H. Schmidt, C. L. Cocke, M. H. Prior, H. Schmidt-Böcking and R. Dörner, Multicoincidence studies of photo and Auger electrons from fixed-in-space molecules using the COLTRIMS technique, J. Electron Spectrosc. Relat. Phenom., 2004, 141, 229–238 CrossRef CAS.
- W. C. Wiley and I. H. McLaren, Time-of-Flight Mass Spectrometer with Improved Resolution, Rev. Sci. Instrum., 1955, 26, 1150 CrossRef CAS.
- K. Fehre, D. Trojanowskaja, J. Gatzke, M. Kunitski, F. Trinter, S. Zeller, L. P. H. Schmidt, J. Stohner, R. Berger, A. Czasch, O. Jagutzki, T. Jahnke, R. Dörner and M. S. Schöffler, Absolute ion detection efficiencies of microchannel plates and funnel microchannel plates for multi-coincidence detection, Rev. Sci. Instrum., 2018, 89, 045112 CrossRef CAS PubMed.
- R. N. Zare, Photoejection dynamics, Mol. Photochem., 1972, 4, 1–37 CAS.
- P. V. Demekhin, A. Ehresmann and V. L. Sukhorukov, Single center method: A computational tool for ionization and electronic excitation studies of molecules, J. Chem. Phys., 2011, 134, 024113 CrossRef PubMed.
- S. A. Galitskiy, A. N. Artemyev, K. Jänkälä, B. M. Lagutin and P. V. Demekhin, Hartree-Fock calculation of the differential photoionization cross sections of small Li clusters, J. Chem. Phys., 2015, 142, 034306 CrossRef CAS PubMed.
- K. Fehre et al. , Enantiosensitive Structure Determination by Photoelectron Scattering on Single Molecules, arXiv:2101.03375 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00143h |
| This journal is © the Owner Societies 2022 |