 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Neutron reflection and the thermodynamics of the air–water interface
Jeffrey
Penfold
*ab and
Robert K.
Thomas
 b
b
aISIS Facility, Rutherford Appleton Laboratory, Harwell Campus, Didcot, Oxon, UK. E-mail: jeffrey.penfold@stfc.ac.uk
bPhysical and Theoretical Chemistry Laboratory, University of Oxford, South Parks Road, Oxford, UK
First published on 16th March 2022
Abstract
By means of isotopic substitution, measurements of the neutron reflectivity (NR) from a flat water surface generally give model independent measurements of the amount of a chosen solute at the surface irrespective of whether the layer is a mixture or whether there is any aggregation in the bulk solution. Previously, adsorption at air–water interfaces has been determined by applying the Gibbs equation to surface tension (ST) measurements, which requires assumptions about the composition of the surface and about the activity of the solute in the bulk, which, in turn, means that in practice the surface is assumed to consist of the pure solute or of a mixture of pure solutes, and that the activity of the solute in the bulk solution is known. The use of NR in combination with ST-Gibbs measurements makes it possible to (i) avoid these assumptions and hence understand several patterns of ST behaviour previously considered to be anomalous and (ii) to start to analyse quantitatively the behaviour of mixed surfactants both below and above the critical micelle concentration. These two developments in our understanding of the thermodynamics of the air–water interface are described with recent examples.
1 Introduction
A surface consists of a thin layer of matter, often an atomic or molecular monolayer, and it would be expected that such a layer would most effectively be probed by whatever particle or electromagnetic radiation is most sensitive to short range structure. Of the three main structural probes for exploring condensed matter at the molecular level, i.e. electrons, X-rays and neutrons, neutrons interact by far the most weakly, as is illustrated by the comparison of diffraction from a surface. Low energy electron diffraction can determine the structure of the surface of a single crystal with high accuracy whereas neutron diffraction requires a very high surface area of material, i.e. a powdered and therefore more disordered sample, to detect any diffraction from adsorbed material, and can therefore only be applied in a relatively approximate way to a small number of systems. However, the compensating advantage of the weak interaction of neutrons with matter is that neutron beams can access buried surfaces because they pass easily through a vapour phase (the air–water (A–W) interface is a buried interface for electrons) and reasonably easily through many solids and liquids. A feature of X-rays and neutrons that can be used to enhance the signal from such a buried interface is their strong and sometimes total reflection from a flat surface when close to grazing incidence. In the vicinity of total reflection the reflectivity is sensitive to the variation of composition along the direction normal to the surface. The reflection of light is also sensitive to refractive index but the relationship between refractive index and molecular structure is complicated. This can only be overcome partially by the use of ellipsometry, which exploits the difference in refractive index for two states of polarization. For neutrons and X-rays, the respective refractive indices depend only on the atomic composition, which is simple. X-ray beams are much more intense than neutron beams and this might suggest that low angle X-ray reflection would be more sensitive than low angle neutron reflection. However, nature has been extraordinarily kind to neutron scatterers in that the scattering of neutrons by H and D nuclei is opposite in phase and sufficiently strong that the contribution of O to the scattering from water is dominated by H or D so that total external reflection occurs at the air–D2O interface whereas total internal reflection occurs at the H2O–air interface. At a composition of about 8 mol% of D2O (null reflecting water or NRW) this phase difference cancels so that there is no reflection at all from an air–NRW interface. There is just a low level background from a mix of incoherent scattering (spin fllipped neutrons) and multiple scattering from the short range liquid structure. This background is 1–5 × 10−6 times total reflection whereas the signal from a typical perdeuterated surfactant layer in NRW would range up to 10−3 or higher depending on the composition and/or how low an angle the reflectivity measurement can reach.Neutron reflection (NR) has the complication that it requires a neutron beam from either a reactor or a spallation source, but at the level of the user both the experiment and the analysis of the data are relatively simple. For a horizontal liquid–air interface the solution is typically contained in a Teflon trough in a sealed and thermostatted container with quartz windows. The illuminated area of the surface of the liquid is typically about 10 × 5 cm2 and its volume 25–35 cm3. The beam is usually polychromatic, in which case the sample is stationary, and sometimes monochromatic, in which case the sample moves up and down and the beam is controlled by neutron mirrors. Following subtraction of the low level of background incoherent scattering mentioned above, the reflectivity is obtained as a function of the momentum transfer, κ, defined by
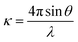 | (1) |
Before considering how NR data is analysed we examine some features of the surface of surfactant solutions that are relevant to the determination of the surface excess, which is our primary concern in this review. An adsorbed layer at the A–W interface may or may not be laterally uniform. If island formation occurs it will only affect the NR directly if the lateral dimension of the islands is larger than the in-plane coherence length of the neutrons, which in turn depends on the optics of the experimental set up, but is of the order of 104 Å. The layer would therefore have to be close to phase separation for anything other than an average lateral structure to be observed. If there is surface phase separation for a single amphiphile the reflectivity of an air–NRW surface half covered by a monolayer of deuterated surfactant would be approximately double that of the same amount of uniformly spread surfactant. Parallel considerations apply to mixtures of protonated and deuterated surfactants. The average thickness of an adsorbed layer depends on the length and orientation of the molecules and their thermal motion (capillary waves). A reasonable assumption is that the profile of the deuterium labelled part of the surfactant along the surface normal direction, which is what is essentially “seen” by NR, is Gaussian, i.e.
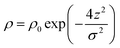 | (2) |
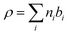 | (3) |
It is instructive to illustrate the quantitative analysis of the NR data by using an approximate model to analyse the reflectivity from a solution of perdeuterated surfactant in NRW. The kinematic approximation gives the reflectivity in terms of the Fourier transform of eqn (2) and leads to the following equation relating the surface excess and the reflectivity:2–4
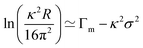 | (4) |
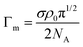 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 molar mixture of perdeuterated and hydrogenated surfactant.
50 molar mixture of perdeuterated and hydrogenated surfactant.
 | ||
| Fig. 1 Linear extrapolation of reflectivity data for C12E3 solutions to obtain the surface excess at various concentrations using eqn (4). Data redrawn from Lu et al.1 | ||
Fig. 1 and eqn (4) show that the surface excess of a perdeuterated surfactant at the A–NRW interface can be determined relatively directly using NR. Since most surfactants with a hydrocarbon tail give rise to only a small signal when adsorbed at the surface of NRW the same principle can be used to measure the surface excess of a deuterated surfactant in a mixture with one or more hydrogenated surfactants. Most commercial surfactant formulations rely on cooperative interactions of the surfactants in the mixture. Such cooperative (or anti-cooperative) effects are expected to lead to deviations of the composition from their ideal values but, until the advent of NR, they have been difficult to measure below the critical micelle concentration (CMC) and more or less impossible to measure above the CMC, which is the concentration at which they are often used. Provided that there is no sublayer structure, which is relatively easily identified by NR itself, measurement of the surface excess of a single deuterated surfactant in the presence of others is feasible down to an adsorbed fraction of about 5% of a monolayer. The signal can be improved and isotope effects can be assessed by using different combinations of hydrogenated and deuterated samples, e.g. single deuterated or pairs of deuterated surfactants can be used to study a ternary mixture and the final compositions determined by solving the resulting set of simultaneous equations to obtain the individual excesses.
The separation of the roughness from the surface excess and the definition of NR and ST surface excesses become more difficult for more soluble surface active species such as short chain alkanols and phenols. This results from a combination of the lower scattering length density of the adsorbed species and the non-zero scattering length density of the underlying solution. For example, there has recently been some discussion by Nguyen et al. on the significance of sublayer adsorption for the measured adsorption isotherm of hexanol in water.6–8 The authors attributed a low value of the measured surface excess for hexanol to their sum frequency generation (SFG) measurements not probing the inner part of the surface. A direct comparison can be made between NR and SFG for this case. Thus, Li et al.9 found excellent consistency between the NR excess and that determined from ST using the Gibbs equation up to the hexanol saturation limit of 60 mM. The SFG measurements gave a value of 6.5 μmol m−2 at a bulk concentration of 35 mM, where the interpolated value from NR (and ST) was only 5.5 ± 0.2 μmol m−2. In addition, Li et al. found a thickness of the hexanol layer of 18 ± 2 Å at maximum coverage, treated as a uniform slab. Although this is larger than the length of a hexanol molecule, it does not indicate the presence of a significant sublayer because the measured NR value necessarily includes all the thermal roughness. The SFG measurement in this case overestimates the coverage and there is no anomalous sublayer. However, for the shorter phenol molecule, Li et al.10 did find an unexpectedly large layer thickness of 19 ± 2 Å close to the solubility limit, a feature which has not yet been explained but which may indicate some deeper structure to the layer as a whole. In general, the depth of penetration of NR is such that in normal experimental conditions NR can respond to excess surfactant in the sublayer region, e.g. in the form of multilayers. The comparisons above have been made for nonionic species. There are two complications in making such comparisons for ionic species. First NR is not directly sensitive to small counterions, although it does respond to counterions with sufficiently high scattering lengths, e.g. tetramethyl ammonium11 or tosylate.12 and, secondly ST is sensitive to both any enhanced adsorption of a counterion and to the extra change in entropy from its adsorption. This is an area where the combination of the two techniques is effective and is therefore part of the following discussion.
There are three main contributions of NR to the understanding of the thermodynamics of adsorption at the A–W interface, (i) the broadening of the range of application of the Gibbs equation, (ii) the interpretation of the interfacial properties of multi-component mixtures, and (iii) the provision of structural information for statistical thermodynamic models of the interface. Although NR has also contributed to the general understanding of the structure of other types of interface involving liquids, i.e. solid–liquid and liquid–liquid, this has mostly been less specifically concerned with thermodynamic issues. This review concerns just the first two topics, i.e. the coupling of NR to the interpretation of the Gibbs equation at the A–W interface and the understanding of the mixing of surfactants at the same interface.
2 Neutron reflection and the Gibbs equation
For many years the two main applications of the Gibbs equation have been (i) that it has been more or less the only means of determining adsorption isotherms of solutes at the A–W interface, and (ii) that it converts models of adsorption into the surface tension (ST) behaviour of A–W and oil–water (O–W) interfaces, the second of which is obviously important for many practical applications, e.g. cleaning and coating surfaces. In the first of these applications, the equation is a typical thermodynamic equation in that it creates an opportunity for measurements of one easily accessed physical quantity (here the ST) to be used to derive the value of a different physical quantity that is hard to access (here the surface excess, Γ). Its simplest form is that for a nonionic solute at an A–W interface,−dσ =RTΓdln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a | (6) |
A further valuable feature of the NR measurement is that it is normally independent of the state of the underlying bulk solution and adsorption can therefore be studied in concentration ranges where the activities of the components of the solution are incompletely known and where there is then insufficient information for the Gibbs equation to be correctly applied. Examples are measurements above the CMC, measurements at low concentrations where depletion may occur, measurements on systems where there is unexpected association or ionization of the solute, or where there is polydispersity. Situations often arise in these systems where the independent determination of surface excess leads to a way of applying the Gibbs equation more correctly. The first part of this review examines situations where such a combination leads to a better understanding of the particular system and the second part examines adsorbed mixtures.
2.1 Ionic surfactants and nonionic impurities
Impurities are common in surfactant solutions. The most troublesome ones tend to be nonionic low solubility species that are very surface active. Apart from the need to eliminate them for a better understanding of the surfactant being studied, such species are also commonly used in surfactant formulations as, for example, perfumes, coatings, or disinfectants. This involves their solubilization into an aqueous formulation from which they end up being deposited as a coating on the target material after the detergent has been rinsed off. An understanding of the nature of the various processes involved would obviously be valuable. Part of this is understanding surface mixtures but another part is that the additive (or impurity) usually has an adsorption and micellization behaviour quite different from that of the surfactant itself. The presence of such a species requires a second term to be added to eqn (6) to give−dσ = RTΓsdln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) as + RTΓidln as + RTΓidln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ai ai | (7) |
The most widely studied example is the system sodium dodecylsulfate (SDS)-dodecanol where dodecanol is often formed by hydrolysis of the SDS. The effect of traces of dodecanol is qualitatively well understood.21 The ST of pure dodecanol in water falls to a constant and low value at its low solubility limit. Dodecanol is also solubilized into SDS micelles and, at concentrations well above the CMC of SDS, the solubilization lowers the dodecanol monomer concentration so that its effect on the ST becomes negligible. The intermediate behaviour depends on the pattern of co-micellization of dodecanol and SDS, which in turn depends on the specific details of the interaction of dodecanol and SDS, which are not known. NR has been used to measure the surface excesses of each component as a function of composition and concentration22 and Li et al.18 later used these and the integrated version of eqn (7) to make an approximate quantitative interpretation of the resulting ST. As expected from the discussion above the directly measured surface excess of dodecanol passes through a maximum just below the CMC of SDS and the amount of dodecanol slowly declines to a low value as it is incorporated into the SDS micelles. Corresponding to the strong maximum in the adsorption of dodecanol there is a sharp minimum in the ST, somewhat below the normal CMC.
A better defined example occurs for the surfactant dodecanoyl L-carnitine (C12CO2-LC), which behaves similarly to SDS/dodecanol in that the impurity is formed by hydrolysis. However, from the point of view of understanding the phenomenon, it has the advantage that the solubility of the impurity can be varied by changing the pH, which gives greater clarity to the processes described above for SDS-dodecanol. C-LC is a zwitterionic surfactant that hydrolyses to give dodecanoic acid and the amino-acid L-carnitine.23 Dodecanoic acid has a low solubility that is strongly affected by pH, as shown in Fig. 2(c). Its effect on the ST is largest at low pH, where its solubility is well below the CMC of C12CO2-LC, but negligible at pH 7 where its solubility limit is much higher. It therefore causes a sharp minimum in the ST at pH = 2 but the minimum more or less disappears at pH = 7 (Fig. 2(a)). The total surface excess of acid + C12CO2LC, as measured by NR, passes through a sharp maximum at pH = 2 before reaching a plateau, but proceeds directly to a plateau at pH = 7 (Fig. 2(b)). The level of the adsorption on the two plateaus in Fig. 2(b) is, however, quite different, being about 10% higher at pH = 2. At pH 2 the C12CO2LC is a cationic surfactant because the carboxylic group is a weak acid, but at pH 7 it is zwitterionic, i.e. overall neutral. The adsorbed layer would therefore be expected to be more closely packed at pH 7 than at pH 2, but this is the opposite of what is observed. This indicates that the higher adsorption observed at pH 2 must result from co-adsorption of the neutral acid with the C12CO2LC. The difference in the state of ionization of the C12CO2LC was further confirmed by neutron small angle scattering (SANS) from the micelles, which exhibits a charge interaction peak at pH 2 but not at pH 7. A large increase in ionic strength also raises the solubility of dodecanoic acid and hence the concentration at which it reaches a low ST. This also removes the minimum in the ST at pH 2, which illustrates why adding electrolyte is a useful means of reducing the effects of nonionic impurities in such measurements.24
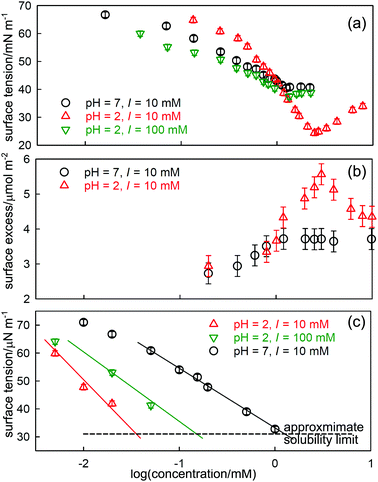 | ||
| Fig. 2 Effects of hydrolysis of dodecanoyl-L-carnitine on its ST behaviour, (a) ST at pH of 2 and 7 and different ionic strengths (I), (b) the total surface excess (dodecanoic acid and C12CO2LC), and (c) the ST of dodecanoic acid at different pH. Data redrawn from Liu et al.23 | ||
2.2 Counterion impurities in ionic surfactants
Any ionic material adsorbed at the A–W interface must form a neutral layer. For a surfactant MXzeqn (7) therefore becomes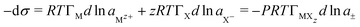 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte and 3 for a divalent counterion, which substantially changes the gradient of a Gibbs plot (σ against lnc). However, the main difference is usually that ions of higher charge decrease the CMC so that the Gibbs plot is displaced to lower concentrations. This change is large when a monovalent counterion is replaced by one of higher charge as in the adsorption of the ethylhexylsulfosuccinates of sodium and calcium (NaAOT and Ca(AOT)2).25,26 The surface activity of Ca(AOT)2 is much higher than NaOT, which means that low levels of contamination by Ca2+ significantly influence the behaviour of the ST at such low concentrations that it is extremely difficult to eliminate the effect of the ionic impurity. The effect can be identified by following the changes of ST with concentration of surfactant at constant electrolyte and of electrolyte at constant surfactant, as can be seen from eqn (8). Thus, for perfluorooctanoates, Shinoda and Nakayama27 examined the surface behaviour at constant surfactant and varying electrolyte concentration with various cations, H+, K+and Ba2+, and found that in all three cases the adsorption of the counterion was only about half that of the surfactant ion. Hall et al.28 later gave a more complete analysis of the theory of such a measurement, which included the calculated activity coefficients and a contribution from the co-ion, and also concluded that there was an apparent shortfall in the coverage of counterion. Fluorine atoms scatter neutrons strongly and it is relatively easy to determine the surface excess of the fluorooctanoate ion directly by NR. An et al.29 used NR to measure the surface excesses of the Na+, Cs+and H+forms of the perfluorooctanoate, without the complicating effect of added electrolyte, and showed that the ST + Gibbs determination underestimated the directly measured surface excess of surfactant by about 30%. This can only be explained as contamination with more strongly binding ions, i.e. ions of higher valence. That Ca2+ is the likely contaminant was shown by using EDTA to sequester any Ca2+ ions present, which removed the anomaly. More recently, Lunkenheimer et al. have refined the purification of the fluorooctanoates to a level where divalent ion impurities can be removed from this system.30
1 electrolyte and 3 for a divalent counterion, which substantially changes the gradient of a Gibbs plot (σ against lnc). However, the main difference is usually that ions of higher charge decrease the CMC so that the Gibbs plot is displaced to lower concentrations. This change is large when a monovalent counterion is replaced by one of higher charge as in the adsorption of the ethylhexylsulfosuccinates of sodium and calcium (NaAOT and Ca(AOT)2).25,26 The surface activity of Ca(AOT)2 is much higher than NaOT, which means that low levels of contamination by Ca2+ significantly influence the behaviour of the ST at such low concentrations that it is extremely difficult to eliminate the effect of the ionic impurity. The effect can be identified by following the changes of ST with concentration of surfactant at constant electrolyte and of electrolyte at constant surfactant, as can be seen from eqn (8). Thus, for perfluorooctanoates, Shinoda and Nakayama27 examined the surface behaviour at constant surfactant and varying electrolyte concentration with various cations, H+, K+and Ba2+, and found that in all three cases the adsorption of the counterion was only about half that of the surfactant ion. Hall et al.28 later gave a more complete analysis of the theory of such a measurement, which included the calculated activity coefficients and a contribution from the co-ion, and also concluded that there was an apparent shortfall in the coverage of counterion. Fluorine atoms scatter neutrons strongly and it is relatively easy to determine the surface excess of the fluorooctanoate ion directly by NR. An et al.29 used NR to measure the surface excesses of the Na+, Cs+and H+forms of the perfluorooctanoate, without the complicating effect of added electrolyte, and showed that the ST + Gibbs determination underestimated the directly measured surface excess of surfactant by about 30%. This can only be explained as contamination with more strongly binding ions, i.e. ions of higher valence. That Ca2+ is the likely contaminant was shown by using EDTA to sequester any Ca2+ ions present, which removed the anomaly. More recently, Lunkenheimer et al. have refined the purification of the fluorooctanoates to a level where divalent ion impurities can be removed from this system.30
2.3 Depletion in dilute solution
While depletion is not really the concern of thermodynamics, it sometimes leads to an apparent break in a Gibbs plot and there are several examples where a depletion break has been interpreted as micellization. Since the conditions of NR and ST measurements are different, the onset of depletion will also tend to occur at different concentrations. The incorporation of NR data into the integrated Gibbs equation and its comparison with the measured ST can be used to distinguish such breaks. Depletion can also affect the ST behaviour of polymers, but in a more complicated way. Since they are polydisperse, their STs are generally time dependent, e.g.,31 and measurements are often made at low molar concentrations where depletion is probable.A simple estimate of how much surfactant is required to cover the A–W surface of a container used for ST measurements suggests that it is typically equivalent to less than about 10−7 M in the bulk solution and such low concentrations are generally avoided. However, the direct comparison of NR and ST measurements shows that in many cases depletion of the solute occurs at significantly higher concentrations than 10−7 M. If depletion is only to the A–W interface NR can give the required correction to the bulk concentration directly using the measured excess and the geometry of the containment vessel. NR measurements generally use Teflon troughs and, since hydrocarbon surfactants do not normally adsorb on Teflon and the technique of NR requires no physical interaction with the surface other than the reflection of neutrons, a correction for depletion is relatively easy to make. On the other hand, many ST measurements use glass containers and often also a metal ring or metal plate to interact with the surface, on all of which adsorption of surfactants is expected to be strong so that the depletion is larger than just the loss to the A–W interface. This loss is therefore expected to be greater than in NR and can cause the ST-concentration relation to become uncertain at concentrations of 10−6 M or even higher, depending on the exact methodology of the measurement. The effect on the Gibbs plot will then be that it becomes concave up in the region where depletion starts, i.e. there is an apparent increase in coverage as the concentration is lowered. Such a change is not allowed thermodynamically unless bulk aggregation occurs in the higher concentration range.
Since depletion is unlikely to be the same in ST and NR experiments, the two techniques should give different results in any region of depletion. The effect is clear in NR and ST data for several different systems, of which two are shown in Fig. 3. In (a) and (c) the line represents the ST calculated from NR, with (a) being the results for a laboratory synthesized poloxamer (“Pluronic”), E23P52E23, and (c) the results for a monodisperse poly(vinylmethylether) (PVME) with a MW of 4k. In both cases, the ST calculated for region B uses the NR measurements and the appropriate prefactor of one in the Gibbs equation. The measured excesses from NR extend to concentrations below the low concentration break point, as shown by the calculated lines in the two figures and they do not agree with the ST measurements. Since there is also little indication of depletion in the NR results below the break point the problem must lie in the ST and only depletion can explain the shape of the ST curve. It is not essential to have parallel NR measurements to establish that a given ST curve is affected by depletion. Thus, the low concentration break in the ST behaviour of for hexadecyl–dodecyl–dimethyl bromide (C16C12DAB) in Fig. 3(b) has been attributed to a second CMC at 0.003 mM by Phan et al.33 and, assuming that the surfactant is fully dissociated in the most dilute region A, the surface excess in region A is 6.9 μmol m−2, which is anomalously high. The value of the CMC is much lower than the CMC of 0.04 ± 0.02mM determined by Tucker et al.35 for the related, but more hydrophobic compound diC16DAB using both ST and NR. Tucker et al. also used NR to determine a surface excess of 2.6 ± 0.1 μmol m−2 at the CMC of 0.04 mM. In addition they measured a surface excess of 1.3 μmol m−2 directly with NR at a concentration of 0.003 mM. This agrees exactly with that from Phan et al.'s slope in region B just below the A–B break in Fig. 3(b). Thus, the ST behaviour is only consistent with the intersection of regions A and B being the onset of depletion. The anomalous “CMC” for C16C12DAB in Fig. 3(b) is also at a substantially higher concentration than in (a) and (c). This difference may result from the number of moles removed by depletion being significantly larger for the smaller surfactant than for the two polymers. A comparable concentration depletion occurs in the surfactant Tween 60, for which the CMC was found to be 0.05 mM.36
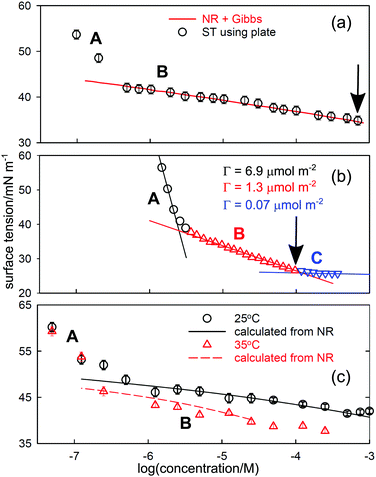 | ||
| Fig. 3 Surface tension behaviour of aqueous solutions of (a) the poloxamer E23P52E23, (b) the cationic double chained surfactant C16C12DAB, and (c) poly(vinylmethylether) of MW 4k. Region A is where surfactant is lost from the bulk solution by depletion to the various surfaces. In region B the calculated line uses NR and the integrated Gibbs equation in (a) and (c) but is the usual Gibbs plot in (b). The correct CMC in each case is marked by an arrow. The data are replotted from (a) Vieira et al.,32 (b) Phan et al.,33 and (c) An et al.34 | ||
Depletion is presented above as a type of false equilibrium, i.e. at long measurement times all the surfaces have equilibrium adsorbed amounts even if they are depleted, although there would necessarily be some variation from system to system. However, for polymer adsorption, since diffusion of polymers to the surface can be relatively slow, the equilibration times of the different MW species with the surface may also be “polydisperse”. This is potentially particularly troublesome in that short and long measurement times may be dominated by different MW fractions. The time dependence of polymer ST is well known and attempts have been made to demonstrate by direct measurement of the surface excess that polymer adsorption obeys the Gibbs equation. Thus, deFeijter and Benjamins37 found that the surface excesses from ST of a series of PVA (copolymers of vinyl alcohol and vinyl acetate), with MWs from 40k to 200k, were about 6× the value from ellipsometry, which they attributed to polydispersity. Comparison of NR and ST results from different MWs of PEO showed that the onset of depletion was at a concentration of about 3× lower for 20k than for 87k.16 This is a second example that suggests that the molar depletion can be reduced for species with a larger adsorbed area.
2.4 Adsorption above the critical Micelle concentration
The application of the Gibbs equation to the ST of surfactant solutions at concentrations above the CMC requires values of the activity, which is substantially different from the concentration and not easy to determine experimentally, although the abrupt onset of the change is an excellent method for determining the CMC. The most completely studied surfactant above its CMC is SDS, for which the ST, the surface excess and the mean activity have all been independently measured and the combined results analysed by Xu et al.17 Over a range of concentration from the CMC at about 8 mM up to about 6 × CMC (50 mM) the ST drops by about 3 mN m−1, or 7.5%38 and the surface excess correspondingly increases from a mean value of 3.9 to 4.6 μmol m−2 or 18%.17 Combination of these results in the Gibbs equation gives a change of about 17% in the mean activity of SDS over this concentration range. Two sets of direct measurements of the mean activity by Sasaki et al.39 and Cutler et al.40 give corresponding changes of 15% and 10% respectively. The agreement is sufficient to demonstrate that for SDS the Gibbs equation is obeyed above the CMC and that the gradient of a Gibbs plot above the CMC is not zero, as it would be above a true phase change, but it is much lower than below the CMC.An advantage of NR as a probe of the A–W interface is that it gives some structural information in addition to the surface excess, although at a lower level of accuracy. The resolution is sufficient to show that for SDS the increase in coverage measured by NR is all in the monolayer. However, for C14TAB NR measurements of the layer structure above the CMC indicate that extra adsorption above the CMC is in the form of a micellar or fragmented lamellar type of layer with an intervening layer of water separating it from the monolayer.41 The extra surface excess is about 10% at about 50 × CMC, similar to that for SDS, and there is a correspondingly similar drop of about 4 mN m−1 in the ST. However, the nature of the underlying adsorption must change from the mechanism below the CMC in that it must be driven by micelle-monolayer interaction rather than by simple amphiphilicity. Nevertheless, the underlying unit in the extra adsorbed sublayer must still have a stoichiometry that preserves surface neutrality. Unfortunately, there are no activity data to demonstrate the validity of the Gibbs equation for this case. The use of NR to examine surfaces above the CMC opens up an important area of research on mixtures of surfactants which is discussed further below.
2.5 Adsorption of multivalent ions and surfactants
We have already shown how trace quantities of ionic impurities seriously interfere with the application of the Gibbs equation to surfactants. More recently, the controlled addition of higher concentrations of multivalent ions to oppositely charged surfactant ions has identified several new patterns of A–W interfacial behaviour. The multivalency can be on a single atom, i.e. a metal ion, or distributed over a more extended structure, from an anion such as a sulphate ion through oligoions to a polyelectrolyte. The precipitating effect of ions such as Ca2 +and Mg2 +on anionic surfactant species is well known in connection with hard water. However, recent experiments with a wider range of cations, especially Al3+, have shown that such ions can induce an intermediate range of behaviour in many anionic surfactants, in which the surface behaviour is enhanced42 and layered structures form immediately below the surface,43–46 even in common surfactants such as AOT47 and SDS.48 Most of these involve Al3+ as the multivalent ion, but the effect can also be observed with Ca2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49,50 and trivalent ions other than Al3+.51 The effect is unexpected in that the multilayered surface structures often occur in concentration ranges where there seems to be no parallel aggregation in the bulk solution. An example is the surfactant sodium decyl diethylene glycol sulfate (SCSS).
49,50 and trivalent ions other than Al3+.51 The effect is unexpected in that the multilayered surface structures often occur in concentration ranges where there seems to be no parallel aggregation in the bulk solution. An example is the surfactant sodium decyl diethylene glycol sulfate (SCSS).
Fig. 4(a) shows the NR profiles from the A–W surface of mixtures of SC10E2S at a constant concentration of 5 mM SC10E2S (about CMC/2) following the addition of small amounts of AlCl3, which is completely hydrolysed to Al3+ ions at these low concentrations. At zero AlCl3the SC10E2S shows a reflectivity typical of a monolayer and this is enhanced by the addition of about 1 mol% of AlCl3 (0.05 mM). The featureless decay of the reflectivity of these two profiles is typical of the usual monolayer of surfactant, which we designate as S0. However, at slightly higher concentrations of AlCl3 the reflectivity shows a distinct single fringe, which becomes a double fringe at about 3 mol% AlCl3. The fringe is characteristic of a monolayer plus one complete bilayer (S1) and two fringes correspond to a monolayer plus two additional complete bilayers (S2). In some systems S3 structures and sometimes multilayer structures are observed. Fig. 4(c) shows the surface phase diagram for SC10E2S–AlCl3, in which the range of AlCl3 concentration over which the S1 and S2 structures are formed is large and extends to below the CMC of the pure surfactant. The behaviour of the ST is shown in Fig. 4(b). As expected the addition of small amounts of AlCl3 substantially decreases the ST because the (SC10E2S)3Al surfactant has a lower limiting ST and a lower CMC. As further SC10E2SNa is added the ST gradually returns to the higher value of SC10E2SNa on its own until it is close to the normal value for SC10E2SNa above its CMC. The region of positive slope in Fig. 4 corresponding to this change has been interpreted quantitatively by Alargova et al. as resulting from the removal of Al3 +ions from the bulk solution into micelles.42,52 Addition of extra AlCl3results in a greater fraction of the Al form of the surfactant at the base of the initial drop in the ST and hence the ST at this point decreases as [AlCl3] increases and the ST minimum deepens. Depending on the chain lengths of the alkyl and alkoxy groups in the surfactant, precipitation may occur between the initial drop in tension and its subsequent increase. Since precipitation is a proper phase transition the ST will become constant while there is precipitation and such a point is just about reached in Fig. 4(b) at the highest Al3+ concentration. Multilayers can form outside the range of precipitation, although the two processes are connected, as shown by the position of the phase boundary marked by a thick line in Fig. 4(c). The occurrence of multilayer structures at the A–W surface has been shown to be linked to the pattern of aggregation in the bulk solution of these systems,46 the effect of adding higher valency ions being to increase the packing fraction and to favour elongated or eventually lamellar structures.
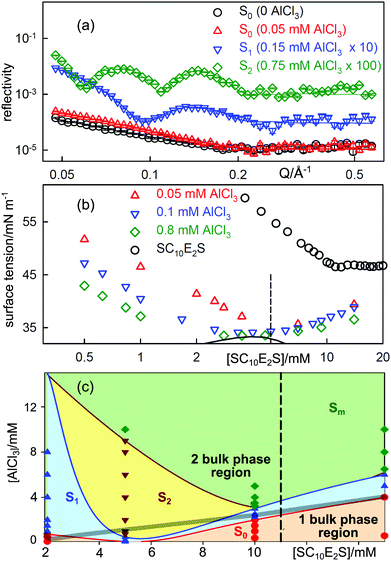 | ||
| Fig. 4 Stratification of solutions of the surfactant SC10E2S by AlCl3 at the A–W interface. (a) Evolution of fringes in the neutron reflectivity of a 5 mM solution of SC10E2S as AlCl3is added. (b) ST behaviour of SC10E2S/AlCl3 mixtures. The dashed line corresponds to the surfactant concentration in (a) and the solid line marks bulk phase separation. (c) Surface phase diagram of SC10E2S/AlCl3 mixtures with the bulk phase boundary between one and two phase regions marked by the thick grey line. S1, S2 and Sm denote surface structures consisting respectively of a normal monolayer plus one, two and several additonal bilayers (NR measurements of these structures are marked by coloured points). Data redrawn from Hui et al.44,46 | ||
The surface behaviour changes when the charge is spread from a single ion to an arrangement where the total charge is split into single charges on separate chemical groups, either relatively compact, such as the PO43− ion or more widely spaced, as in fully protonated oligoamines such as diethylene triamine53,54 and spermidine,55 where the conformation of the charges is flexible, or in melamine55 and trisodium naphthalene trisulfonate,56,57 in both of which the charges are fixed in a plane. All the cationics at low pH lower the CMC of SDS, increase the surface excess (NR), and decrease the ST at this lower CMC, similarly to the addition of Al3+ described above. Reducing the charge on the amine by increasing the pH usually approximately restores the ST behaviour to its pure value, although the binding of SDS may itself induce some ionization.58
The series of oligoanions of which the trisodium naphthalene trisulfonate (POS3, shown in Fig. 5(a)) is a smaller representative, are particularly interesting in that the behaviour of mixtures of the oligoions with the cationic C12TAB evolves until it is similar to the behaviour of anionic polymers with C12TAB, which we consider in the next section. The behaviour of the surface excess of C12TAB on its own and in mixtures with low fixed concentrations of 0.01 and 0.1 mM of the acid form of POS3, all measured using NR, is shown in Fig. 5(a). Fig. 5(b) compares the measured ST of the same solutions with that calculated from the integrated Gibbs equation using the measured surface excess from NR in (a). The Gibbs prefactor P (see eqn (8)) for C12TAB on its own is 2 but, for the solutions with added POS3 at a fixed concentration, it becomes 1 if the neutral adsorbed species is three C12TA+ and one POS3 ion (see also discussion in the following section). Thus, although the surface excess of C12TA+ is lower on its own, the magnitude of the slope of the Gibbs plot is greater, as observed. That the Gibbs equation accounts correctly for the ST of the three solutions in Fig. 5 up to the ST plateau shows that the onset of the plateau must be some sort of aggregation. Since no precipitation was observed by Jiang et al. for POS3, although precipitation was observed for the higher members of the series POS4and POS6,57 the only possible explanation of the plateau is that it is micellization, just as for Al3+ with SC10E2S in Fig. 4(b). The effect of the POS3 ion on the CMC and its associated effect on the surface excess and the ST at the CMC then approximately parallel that in Fig. 4(b). Just as in the SC10E2S–Al3 +system, the addition of further surfactant gradually solubilizes the POS3 ion into the bulk solution and its fraction at the surface decreases to zero. This will cause the ST eventually to change to a value closer to that for C12TAB on its own in solution, which is likely to be close to the initial plateau. Although the situation is more complicated than the usual surfactant adsorption, the successful application of the Gibbs equation to the initial drop in ST using NR shows that this must be the onset of aggregation. Menger and Shi15,56 and more recently Phan et al.33,59 have interpreted conductivity changes in the range above the CMC as a second CMC. However, this is a region where interpretation of the conductivity is complicated by exchange of the counterions POS33− and Br− between solution and micelles and, in any case, the break in conductivity is barely noticeable, as shown in Fig. 9 of Jiang et al.57
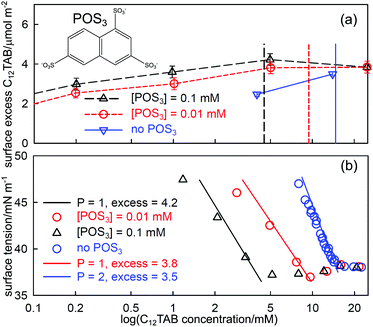 | ||
| Fig. 5 (a) Surface excesses of C12TA+measured by NR at the A–W interface of C12TAB on its own and with added amounts of 0.01 mM and 0.1 mM POS3 (trianion structure as shown in (a)), (b) the ST of the same set of solutions with fits of the integrated Gibbs equation using the prefactors and the surface excesses at the measured CMC given in the diagram, and the ST at the plateau. Data redrawn from Jiang et al.57 | ||
The approximate Gibbs equation for a polyelectrolyte can be written in terms of the counterion X as61,66
dσ = −ΓXRTdln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cXf± ≈ −ΓXRTdln cXf± ≈ −ΓXRTdln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cX cX | (9) |
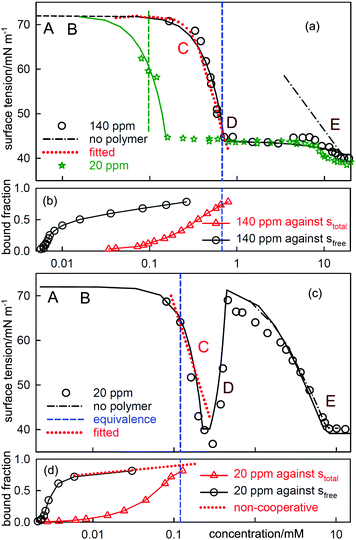 | ||
| Fig. 6 ST measurements for (a) C12TAB with NaPSS (MW = 18k) at concentrations of 140 ppm and 20 ppm and (c) SDS with 20 ppm PDDA (MW = 100k), and the corresponding independently determined binding isotherms in (b) and (d). The equivalence points are shown as vertical dashed lines. The horizontal axes in (b) and (d) refer to either total or free surfactant as indicated. The red dotted lines are calculated using the Gibbs equation with the observed surface excesses and free surfactant concentrations. The letters ABCDE are explained in the text. The continuous lines through the data are based on the application of a semi-empirical model of Bahramian et al.60 and are drawn primarily to guide the eye. The NR data are redrawn from ref. 61–63 and the binding isotherms redrawn and calculated in terms of total surfactant concentration using ref. 64 and 65. | ||
When electrolyte is present the whole appearance of the ST curve changes. In region A the presence of the background electrolyte prevents counterion condensation, i.e. f± is closer to unity. The ST behaviour is then determined approximately by the usual equation for a free surfactant with the same solution concentration as the total surfactant.71 This largely determines the gradient of the plot because the surface excess of surfactant ion is approximately constant. This effect of added electrolyte in region A is seen for both polymer–surfactant systems in Fig. 7. The same behaviour occurs without added electrolyte when the separation of charge in the polymer is too large for counterion condensation to occur, e.g. in SDS–polylysine mixtures.71 The initial and early decrease in ST therefore depends only on stotal. A further important difference is that the cooperative binding curve moves to higher concentration on addition of electrolyte, the opposite of the change in CMC of the surfactant.72 The stage of cooperative binding where sfree is almost constant (region B) again leads to a plateau in the ST, but this is now at a low value of the ST. At the end of cooperative binding the gradient of the decrease in the ST should again be much greater for the same reason as in the absence of electrolyte. This is observed for the PSS system, for which the decrease is towards the precipitation plateau. However, in the PDMA system there is an abrupt increase in the ST followed by a decrease that gradually becomes similar to that expected for the free surfactant.
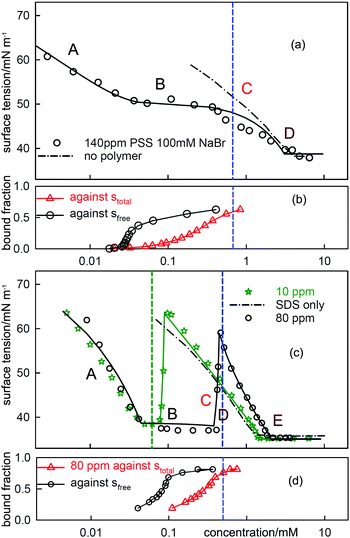 | ||
| Fig. 7 The equivalent measurements to those in Fig. 6 but with electrolyte, (a) C12TAB with NaPSS (MW = 18k) at a concentration of 140 ppm with 100 mM NaBr and (c) SDS with 10 ppm and 80 PDDA (MW = 100k) with 100 mM NaCl. The NR data are redrawn from ref. 69 and 70 and the binding isotherms redrawn from ref. 64 and 65. | ||
At the start of region D the ST should be dominated by the surface behaviour of the PE-S complex but by the end, when the polyelectrolyte has been fully solubilized, it should be dominated by surfactant. In systems such as PSS-C12TAB the start of region D is the onset of the ST plateau that signals phase separation,64 but in PDDA-SDS with electrolyte it starts with an ST peak. A peak sometimes also appears at some point along the plateau for PSS-CnTAB systems.73,74 As was shown by Staples et al. the ST peak in the PDDA-SDS system with electrolyte approximately coincides with precipitation.70 In the simple situation where both the precipitate and the adsorbed layer have the composition PS1.0 the Gibbs equation would require that there is no change in the ST. In that situation the positive ST gradient required for the onset of an ST peak could then only result from depletion, i.e. the limiting solubility is too low to sustain the adsorption at its correct equilibrium value. This is a known experimental difficulty when measuring the ST of substances of low solubility,75 but the true equilibrium ST should not change at the onset of precipitation.
NR gives a result that suggests the cause of this difference between the two systems, which is that the surface species for both PDDA-SDS and PSS-C12TAB are completely different for the two systems and each has a remarkably constant stoichiomety. For PDDA-SDS (in electrolyte) the adsorbed layer consists approximately of two polymer segments to one surfactant, i.e. P2S over regions B, C and D, whereas for PSS-CnTAB (no added electrolyte) it is PS2. The approximate constancy of the composition over a wide concentration range suggests that all alternative stoichiometries are not surface active. This is not surprising because at low stoichiometry the surfactants would be too far apart to screen high ST water from air, and at high stoichiometry they would tend to form either a hydrophobic rod or a three dimensional structure of surfactant aggregates, neither of which is likely to be surface active at the A–W interface. For a fixed surface stoichiometry, PSθ, adsorption will generally be optimized when the mean activity of PSθ in the solution is the same as in the complex, i.e. when the solution is also approximately PSθ. However, when precipitation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex occurs it has the effect of displacing the solution equilibria strongly towards the composition of the precipitate. Precipitation of a 1
1 complex occurs it has the effect of displacing the solution equilibria strongly towards the composition of the precipitate. Precipitation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 precipitate in the PDDA-SDS system should therefore cause a decrease in the mean solution activity of complex PS0.5. If this decrease occurs in region C, where sfree changes unusually sharply with stotal, it is possible that as well as an initial steep decrease in ST, precipitation may cause this to reverse and lead to corresponding sharp increase in ST. Indeed, the ST behaviour for PDDA-SDS without added electrolyte suggests just such a reversal between sharp negative gradient and sharp positive gradient. A decrease in the mean activity of the PS0.5 complex should also reduce its adsorption but this would not usually be a large effect. Some reduction in adsorption in the precipitation region was observed by Staples et al. That the corresponding effect does not occur for the PSS-C12TAB system is then simply that the activity of the surface complex, now PS2, is not affected at the onset of precipitation of the 1
1 precipitate in the PDDA-SDS system should therefore cause a decrease in the mean solution activity of complex PS0.5. If this decrease occurs in region C, where sfree changes unusually sharply with stotal, it is possible that as well as an initial steep decrease in ST, precipitation may cause this to reverse and lead to corresponding sharp increase in ST. Indeed, the ST behaviour for PDDA-SDS without added electrolyte suggests just such a reversal between sharp negative gradient and sharp positive gradient. A decrease in the mean activity of the PS0.5 complex should also reduce its adsorption but this would not usually be a large effect. Some reduction in adsorption in the precipitation region was observed by Staples et al. That the corresponding effect does not occur for the PSS-C12TAB system is then simply that the activity of the surface complex, now PS2, is not affected at the onset of precipitation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex.
1 complex.
When the surface active complex has a greater molar content of surfactant as in the PS2 complex of the PSS-C12TAB system its mean activity will not be reduced by precipitation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PS because PS can equilibrate with further S to maintain the bulk mean activity of any PSθ complex with θ > 1. Thus, no ST peak should occur for PSS-CnTAB provided that the precipitate remains the 1
1 PS because PS can equilibrate with further S to maintain the bulk mean activity of any PSθ complex with θ > 1. Thus, no ST peak should occur for PSS-CnTAB provided that the precipitate remains the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. The ternary phase diagram determined for NaPSS with C16TACl has been determined by Sitar et al.76 and by Nause et al.77 Although these studies were not done in the extremely dilute conditions of the surface experiments, it can be concluded that the precipitate develops along the plateau into a hexagonal phase incorporating up to about 15 molecules of extra surfactant76 close to the redissolution limit. The length of the plateau in the surface experiments also shows that the onset of region E, i.e. complete redissolution, is reached at a similar composition. Towards the end of the plateau, at a θ value >2 a relatively sharp peak is sometimes observed for C12TAB and C14TAB,73,74 and more definitely for C16TAB.73 One of the conditions that causes the peak in the PDDA-SDS system is that a precipitate of higher stoichiometry than PS2 reduces the solution activity of the PS2 complex, and that can apply to the PSS-CnTAB system at a correspondingly higher concentration. However, the extra sharpness arising from the cooperativity of the binding in PDDA-SDS is not present. This and the erratic appearance of the peak indicate that in the PSS-CnTAB system the peak is a result of either depletion or non-equilibrium.
1 complex. The ternary phase diagram determined for NaPSS with C16TACl has been determined by Sitar et al.76 and by Nause et al.77 Although these studies were not done in the extremely dilute conditions of the surface experiments, it can be concluded that the precipitate develops along the plateau into a hexagonal phase incorporating up to about 15 molecules of extra surfactant76 close to the redissolution limit. The length of the plateau in the surface experiments also shows that the onset of region E, i.e. complete redissolution, is reached at a similar composition. Towards the end of the plateau, at a θ value >2 a relatively sharp peak is sometimes observed for C12TAB and C14TAB,73,74 and more definitely for C16TAB.73 One of the conditions that causes the peak in the PDDA-SDS system is that a precipitate of higher stoichiometry than PS2 reduces the solution activity of the PS2 complex, and that can apply to the PSS-CnTAB system at a correspondingly higher concentration. However, the extra sharpness arising from the cooperativity of the binding in PDDA-SDS is not present. This and the erratic appearance of the peak indicate that in the PSS-CnTAB system the peak is a result of either depletion or non-equilibrium.
2.6 Association in solution
The main aggregation of surfactants in solution is usually micellization at the CMC. Micellization is not a true phase change and it is generally assumed to occur over a narrow but finite range of concentration,18,38i.e. micelles start to form just below the CMC and this is often referred to as premicellization. Such a process would be expected to be assisted by traces of impurity and it is then not surprising that it is difficult to establish unambigously whether it occurs in pure systems.78 However, surfactants with more complicated hydrophobic structures may dimerize or form limited small aggregates at concentrations well below the CMC, which we refer to here as dimerization or oligomerization, reserving the term “premicellization” for aggregation very close to the CMC. Gemini surfactants consist of two ionic surfactant groupings with their head groups attached by a link of varying length. The presence of two hydrocarbon chains is expected to favour dimerization and the presence of two head groups is expected to favour ion pairing in the bulk solution, as suggested by a model originally shown by Song and Rosen,79 and here shown in a more detailed form in Fig. 8. As well as being a possible conformation for a bulk dimer this model has relatively short distances between the charged groups, which would cause it to bind counterions.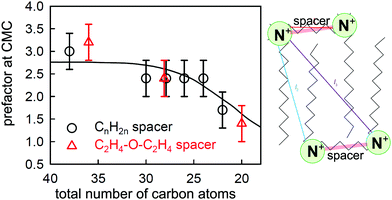 | ||
| Fig. 8 The experimentally determined prefactor P in the Gibbs equation at the CMC (points) of CnNMe2C6NMe2CnBr2 (black circles) and CnNMe2C2-O-C2NMe2CnBr2 (red triangles) and a calculated value (line) based on the structure shown alongside and a model described in the text. The two points at 28 carbons have been laterally displaced from each other for clarity. Key distances between charged groups are marked in the structure shown. Figure redrawn from Li et al.80 | ||
For a divalent gemini ion, the Gibbs equation can be written as
−dσ = −PΓRTdln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m±f± m±f± | (10) |
The series of geminis CnNMe2CmNMe2CnBr2, where Cn and Cm are hydrocarbon chains and the N are quaternary charged links, has been extensively investigated. ST and NR showed that for values of m of 3, 4, 6 and n = 12 the limiting value of P is close to 2 for all four compounds,81i.e. these gemini are mostly associated in solution in a way that makes P in eqn (10) equal to about 2 at the CMC instead of the expected value of 3. In earlier ST measurements on the same series Alami et al.82 had assumed that P was 3 and their studies on the same series of compounds using conductivity indicated no association.83–85 However, although conductivity is known to be sensitive to both ion pairing and to dimerization in geminis, these processes have opposite effects, which means that they tend to cancel, which further suggests that more than just an approximate cancellation may be required to explain the conductivity data, see e.g. ref. 86.
More recent NR measurements have been made on two sets of geminis using spacers of either C6H12 or C2H4OC2H4 as link, with a range of chain lengths of the two side chains.80 The value of P required to bring the limiting ST and NR measurements at the CMC into agreement is plotted against the total number of carbon atoms for these compounds in Fig. 8, and it varies from 3 for the longer chains to less than 2 for the shorter ones. This can only result from effects of dimerization and/or ion binding on either the prefactor P and/or the mean activity coefficient f± of the neutral GBr2 that adsorbs at the surface. Thus, the unambiguous result from the observed ratio from the two relatively simple measurements of NR and ST, without any detailed analysis, again shows that (i) there is some sort of association of the gemini ions in the bulk solution, (ii) this varies between different geminis, and (iii) it persists to concentrations significantly below the CMC. Li et al. devised a model to interpret this behaviour, which involved an empirical constant for dimerization, a known constant for ion binding in bolaform surfactants,87 and geometrical and statistical considerations based on the structure shown in Fig. 8 and the Gibbs equation, and were able to account for the general behaviour of the change in P at the CMC as shown in Fig. 8. However, the model did not account well for the variation of P with concentration for several of the geminis studied. Nevertheless, despite its limitations, it demonstrates covincingly that the association in the bulk solution of geminis involves both dimerization and ion pairing.
Examination of ST measurements on other series of geminis in the light of the NR/ST results described above indicates that the strength of dimerization and ion binding vary substantially according to head group and spacer structure. If the interactions are strong, some clear and interesting features appear in the ST curves on their own. The first of these concerns the CMC and the limiting ST at the CMC and was identified by Menger and Littau88 and analysed quantitatively by Rosen et al.79,89 The dimer drawn in Fig. 8 would obviously not be surface active and would not be a stable entity to exist in a micelle. Thus, if dimerization is significant the concentration of monomers is reduced with the effect that the overall concentration needed to attain micellization is reduced and the CMC shifts to a higher concentration, with a higher limiting ST, and this is indeed observed. Song and Rosen further concluded that geminis with a more flexible spacer were more likely to aggregate, in agreement with the observation of Li et al.81 that, in the series they studied, only the spacer containing the xylyl group was fully dissociated at the CMC. More recently, Cai et al. have explored a series of geminis with two bulky pyrrolidone head groups and an alkyl chain spacer.90 As the spacer is increased in length, the CMC and the limiting ST both increase, as analysed by Song and Rosen. However, what is more interesting is the behaviour of Cai et al.'s long spacer surfactants (LSS) at low concentrations. The greater carbon content of the LSS should make them unusually surface active at low concentrations so that they have an unusually long range of high surface activity, i.e. the surface excess should remain relatively constant over an unusually wide range of concentration. In the LSS of Cai et al. this long range makes it possible to observe a transition resulting from a change in P, i.e. the equilibrium Gibbs plot becomes steeper at low concentrations. Taking the simple model of Li et al.80 and assuming no change in the area per molecule between Cai et al.'s C12C16C12PB at its measured CMC in NaCl and that at the low concentration break in the absence of salt, the change in P should lead to apparent areas per molecule with a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, which is close to the observed values of 1.70
3, which is close to the observed values of 1.70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.78. This is consistent with the general features of the model of Li et al. However, that dimerization and ion binding should give rise to an apparently sharp break in the ST does not mean that this should be considered as a phase change analogous to the CMC. Chemical equilibria of this sort are normally plotted on a linear concentration scale. The use of log
3.78. This is consistent with the general features of the model of Li et al. However, that dimerization and ion binding should give rise to an apparently sharp break in the ST does not mean that this should be considered as a phase change analogous to the CMC. Chemical equilibria of this sort are normally plotted on a linear concentration scale. The use of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c and the significant error bars in a Gibbs plot may simply give an illusion of sharpness. Cai et al. also showed that the conductivity of these geminis followed the pattern expected for significant aggregation as the spacer length increased. This and the apparent sharpness of the break almost certainly results from the stronger aggregation and counterion binding in these pyrrolidone geminis compared with the simpler compounds studied by Li et al.
c and the significant error bars in a Gibbs plot may simply give an illusion of sharpness. Cai et al. also showed that the conductivity of these geminis followed the pattern expected for significant aggregation as the spacer length increased. This and the apparent sharpness of the break almost certainly results from the stronger aggregation and counterion binding in these pyrrolidone geminis compared with the simpler compounds studied by Li et al.
2.7 Dissociation in solution
Just as association in solution can have unexpected effects on the application of the Gibbs equation, as discussed above, so can unexpected dissociation. This is potentially a significant problem for polymers that are subject to either the incorporation of occasional charged groups via impurity monomer residues or via hydrolysis of a small fraction of residues. The presence of charged groups changes the P factor in the Gibbs equation, which can have a large effect on the ST of their solutions, even at a very low level. Polyacrylamide is an example of such a polymer and it is known to be susceptible to a low level of hydrolysis that leads to a fraction of carboxylic acid residues, and partial hydrolysis is often used deliberately to improve the solubility of commercial hydrophobically modified polyacrylamides.91Zhang et al. prepared a set of hydrophobically modified PAM with 0.5, 1 and 2% of the residues modified by the attachment of perdeuterated C12D25 hydrophobic groups.92 The structure and composition of layers adsorbed at the A–W interface was determined by NR on samples in null reflecting water and in D2O. This made it possible to determine directly the area per added hydrophobic unit by NR, and the corresponding values of the surface excess per hydrophobic segment are shown in Fig. 9(a) for three polymer samples with different fractions of hydrophobe. The adsorption is strongest for the sample of greatest hydrophobicity (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) and the surface excess of all three samples increases approximately linearly with logc. The ST results, shown in Fig. 9(b), also show a systematic pattern of behaviour that is qualitatively consistent with the NR measurements in that the ST has a negative slope that increases with concentration and hydrophobicity as would be expected. However, the magnitude of the slope is unexpectedly high for a neutral polymer.
50) and the surface excess of all three samples increases approximately linearly with logc. The ST results, shown in Fig. 9(b), also show a systematic pattern of behaviour that is qualitatively consistent with the NR measurements in that the ST has a negative slope that increases with concentration and hydrophobicity as would be expected. However, the magnitude of the slope is unexpectedly high for a neutral polymer.
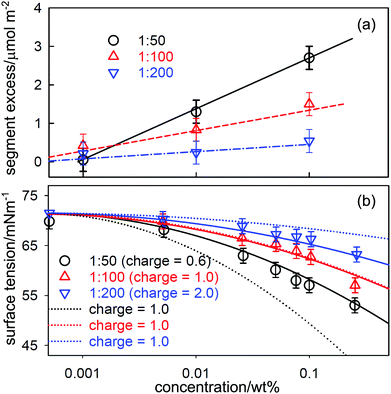 | ||
Fig. 9 (a) Surface excess, Γ, per hydrophobic segment for a hydrophobically modified PAM containing 1 hydrophobic group per 50, 100 and 200 residues as a function of concentration. The linear variation of Γ with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c shown in (a) was used in the Gibbs equation to calculate the surface tension behaviour in (b) using two assumptions. In the first (continuous lines) the charge on the PAM backbone was taken to be 1 per 100 backbone units making the charge per hydrophobic unit respectively 0.5, 1 or 2 for 2, 1 and 0.5 mol% HMPAM. In the second assumption (dotted lines) the charge along the backbone was taken to be one per hydrophobic unit. Reprinted by permission from Zhang et al.92 c shown in (a) was used in the Gibbs equation to calculate the surface tension behaviour in (b) using two assumptions. In the first (continuous lines) the charge on the PAM backbone was taken to be 1 per 100 backbone units making the charge per hydrophobic unit respectively 0.5, 1 or 2 for 2, 1 and 0.5 mol% HMPAM. In the second assumption (dotted lines) the charge along the backbone was taken to be one per hydrophobic unit. Reprinted by permission from Zhang et al.92 | ||
The steepness of the slopes in Fig. 9(b) can be explained if a low level of hydrolysis of acrylamide to acrylic acid groups occurs during the polymerization. This converts the polymer into a weak polyelectrolyte, for which the Gibbs equation can be written as61,66
dσ = −ΓXRTdln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cXf± ≈ −ΓXRTdln cXf± ≈ −ΓXRTdln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cX cX | (11) |
3 Mixing at the air–water surface and in micelles
We have already shown that NR can be used to study the surface composition of mixtures of surfactants above and below the critical micelle concentration (CMC.) The absence of sublayer structure in most micellar systems also shows that there is no interaction between the monolayer and the micelles in such systems and therefore the surface interactions that determine the optimum composition of the monolayer do not change at the CMC. Thus any changes in the surface composition above the CMC can result only from changes in the bulk monomer activities on micellization or, more simply, only from changes in the monomer concentrations above the CMC, which themselves are largely determined by the composition of the micelles. Thus, measurement of the variation of the surface composition offers a means of studying the interactions between surfactants not only in the monolayer but also in the micelles. Since the geometry of self-assembly in micelles and flat interfaces is different, differences in the interactions can also be expected between the two structures. This is an area that is uniquely accessible to NR and the results in this section are a survey of the progress that has so far been made. Although not strictly necessary for the analysis of some of the results presented, the independent technique of neutron small angle scattering (SANS) can also make use of isotopic substitution to measure the composition of mixed micelles. However, in that SANS is also affected by the shape and size of the micelle, it is not in principle as accurate a method as NR for the determination of composition.An expression for calculating the monomer and micellar composition of a ideal binary mixture of surfactants at concentrations above the CMC was first given by Clint.93 The calculation was extended to the micellization of non-ideally mixing surfactants by Rubingh, who used the regular solution model to account for the non-ideality.94 In this model the excess free energy of mixing in the micelle is
| ΔGE = BRTx1x2 | (12) |
The experimental limitations of the early work on surfactant mixtures were (i) that the only means of determining a fractional surface excess was to apply the Gibbs equation to one component at a time while maintaining the other(s) at a fixed concentration,19 (ii) that surface excesses could not be determined above the CMC, and (iii) there was no method for determining micellar composition. Nevertheless, it was shown that the CMC variation with composition could be explained in terms of the regular solution model and that the variation of the surface with the bulk composition could sometimes also be explained.98 The main difficulties from a theoretical point of view have been how to handle the dissociation of ionic surfactants in this framework, e.g. ref. 99 and 100, and that fitted values of the interaction parameter often vary with composition, indicating that the regular solution model is not being obeyed, e.g. ref. 101. This is not unexpected for the surface because the natural hexagonal packing in a plane does not favour the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 composition required by eqn (12) (see, e.g. ref. 102).
1 composition required by eqn (12) (see, e.g. ref. 102).
As already shown, NR can give direct access to the surface excess of a surfactant at the A–W interface, irrespective of either the presence of other surfactants at the surface or the state of aggregation in the underlying solution. For mixtures above the CMC the activities/concentrations of the monomers determine the surface composition via the adsorption isotherm and hence must also be determined. In addition, small angle neutron scattering (SANS) is able to determine the composition of mixed micelles using selective deuteration, similarly to NR, but usually reversed, i.e. the surfactant of interest is usually protonated with the remaining surfactants perdeuterated and D2O is used instead of null reflecting water.
The theoretical model used to describe mixing in either micelles or at the A–W interface derives from the Butler equation,103 which has recently been shown to conform with the Gibbs equation.104,105 The additional key approximation is then that the adsorbed layer consists only of surfactants, i.e. it contains no water and no empty space. For a binary mixture of uncharged surfactants at a fixed surface pressure, π,
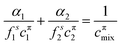 | (13) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fsi = Bsxj2 fsi = Bsxj2 | (14) |
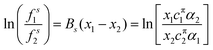 | (15) |
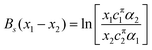 | (16) |
The restriction to the regular solution model is likely to be physically unrealistic for many adsorbed mixed layers. Ways of removing this restriction have tended to focus on dissociation or the electrostatic interaction when an ionic surfactant is part of the mixture, e.g. Ref. 99 However, the well established method for liquid mixtures is to expand the free energy of eqn (12) as the series
| Gexcess = RTx1x2[Bs + Cs (x1 − x2) + Ds (x1− x2)2 + …] | (17) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f1 = Bsx22 + x22 (3 − 4x2)Cs + x22 (5 − 16x2 + 12x22)Ds f1 = Bsx22 + x22 (3 − 4x2)Cs + x22 (5 − 16x2 + 12x22)Ds | (18) |
The calculation of the mixed CMC uses exactly the same equations as the surface layer at constant pressure except that the cπ are replaced throughout the above equations by cμ, the CMC, and Bs, Cs and Ds are replaced by the corresponding Bm, Cm and Dm. However, the more wide ranging set of measurements is of the surface coverage above the CMC and their calculation from the pseudophase model is more complicated. It requires two steps, one to calculate the monomer concentrations and the second to use the monomer concentrations to calculate the adsorption. The second of these steps is exactly the same as for below the CMC, i.e. as described above, but the first step is different.
The monomer concentration above the CMC for a binary mixture, cmi, is94
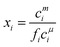 | (19) |
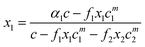 | (20) |
| F = Ax12 + (c − A) x1 − α1c | (21) |
| A = f2cm2 − f1cm1 | (22) |
The surface equations given so far apply at constant surface pressure π. In the case of measurements above the CMC, although the surface pressure is often constant with the bulk concentration, it can be quite different between the pure components and between the pure components and the mixture. However, Bs depends on the surface pressure because the values of cπi depend on π through
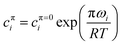 | (23) |
The extension of either the regular solution or the more general expansion of eqn (17) to more than two components is straightforward in principle. However, the expressions for the activity coefficients need to be evaluated following the procedure of Redlich and Kister106 and the iterations have to be followed particularly carefully when more than two components are used. Details of extensions to three and to five components have been given by Liley et al.112,113 A further difficulty is how to display the results. This was done by Liley et al. using triangular coordinates for the three component system, but the five component system had to be plotted as binary pairs. It might be thought that the analysis of such complicated mixtures is not worth the extra difficulty. However, many formulations contain more than five surfactants and such analyses are therefore of significant practical importance.
3.1 Binary mixtures close to ideal mixing
For binary mixtures of nonionic surfactants, or pairs of surfactants with similar structures, the mixing is expected to be close to ideal.19,98,115 On the basis of CMC data alone it is difficult to determine the small variations from ideality and their impact upon the evolution of the surface composition with solution concentration and composition. This is illustrated by a recent study of the adsorption and self-assembly in two alkyl α-sulfo-ester surfactants, which we abbreviate to CnMES in the case of the methyl ester. Xu et al.114 characterised the surface and micelle mixing in the eutectic mixture of C16MES and C18MES, in which the only difference is the alkyl chain length and therefore the mixing should be close to ideal. The variation in surface composition with solution concentration for the eutectic mixture at 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 mole ratio was measured by NR and is shown in Fig. 10. The impact of the onset of micellisation is clearly seen in the abrupt change in the surface composition with increasing surfactant concentration. Below the CMC the surface composition is constant and is dominated by the more surface active component, C18MES. Above the CMC the surface composition is close to the solution composition, but in the concentration range studied it has not yet evolved towards the solution composition of 65
35 mole ratio was measured by NR and is shown in Fig. 10. The impact of the onset of micellisation is clearly seen in the abrupt change in the surface composition with increasing surfactant concentration. Below the CMC the surface composition is constant and is dominated by the more surface active component, C18MES. Above the CMC the surface composition is close to the solution composition, but in the concentration range studied it has not yet evolved towards the solution composition of 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 mole ratio C16MES
35 mole ratio C16MES![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C18MES. The calculated lines in Fig. 10 are PPA calculations for a repulsive interaction both at the surface and in the micelle with Bs = 1.5 and Bm = 1.4 (units of RT), and the higher cubic or quartic contributions to the excess free energy of mixing are zero. Hence the regular solution approximation is adequate in this case. The derived interaction parameters are also consistent with the measured variation in the micelle composition by Xu et al.114 Overall, the data for the eutectic C16MES/C18MES mixture shows two distinct features. The surface composition above the CMC tends towards the solution composition, but below the CMC it is constant and rich in the more surface active component. Although the micelle composition must tend towards the solution compositions, as observed by Xu et al., in this case the surface has a different equilibrium composition because it is now in equilibrium with the free monomer composition in solution, which is different from the overall solution composition. Although the surface composition below the CMC may be constant, as it often is, this is not a constraint in that it will depend upon the relative surface activities of the different components of the mixture. A later example shows marked deviations from both of these trends for the surface of mixtures of the nonionic alkyl ethoxylates C12E3/C12E8.
C18MES. The calculated lines in Fig. 10 are PPA calculations for a repulsive interaction both at the surface and in the micelle with Bs = 1.5 and Bm = 1.4 (units of RT), and the higher cubic or quartic contributions to the excess free energy of mixing are zero. Hence the regular solution approximation is adequate in this case. The derived interaction parameters are also consistent with the measured variation in the micelle composition by Xu et al.114 Overall, the data for the eutectic C16MES/C18MES mixture shows two distinct features. The surface composition above the CMC tends towards the solution composition, but below the CMC it is constant and rich in the more surface active component. Although the micelle composition must tend towards the solution compositions, as observed by Xu et al., in this case the surface has a different equilibrium composition because it is now in equilibrium with the free monomer composition in solution, which is different from the overall solution composition. Although the surface composition below the CMC may be constant, as it often is, this is not a constraint in that it will depend upon the relative surface activities of the different components of the mixture. A later example shows marked deviations from both of these trends for the surface of mixtures of the nonionic alkyl ethoxylates C12E3/C12E8.
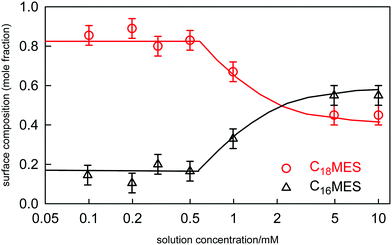 | ||
Fig. 10 Variation in surface composition with solution composition for the 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 mole ratio eutectic mixture of C16MES/C18MES. The lines are model calculations using the PPA with the parameters given in the text. Redrawn from Xu et al.114 35 mole ratio eutectic mixture of C16MES/C18MES. The lines are model calculations using the PPA with the parameters given in the text. Redrawn from Xu et al.114 | ||
In a related and complementary study Wang et al.116 explored the impact of changing the headgroup structure of CnMES by means of changes in the ester group on their mixing with other α-sulfo-ester surfactants. NR measurements for the methyl ester, C14MES, mixed with the ethyl ester, C14EES, and propyl ester, C14PES, surfactants showed that the surface adsorption was dominated increasingly by the more surface active component. Analysis of the mixing properties as a function of composition at a fixed concentration above the CMC showed that the surface mixing was close to ideal. However subtle variations and departures from ideal mixing still occur and were characterised using the PPA approach. The C14MES/C14EES mixture was weakly repulsive and close to a regular solution description, with Bs = 0.2, Cs = 0.0, and Ds = 0.0. The interaction between the two surfactants in the C14MES/C14PES mixture was stronger and weakly attractive (with Bs = −0.2, Cs = 0.4), and also unsymmetrical with respect to the surface composition. These small changes imply that changes in the packing associated with the two different mixtures may be quite subtle. They also suggest that the propyl ester group can pack more effectively with the methyl ester group so as to reduce the headgroup interaction and promote greater counterion binding.
Penfold et al.117,118 determined the surface mixing for the nonionic surfactant mixtures of C12E3/C12E8 by NR. Although the two surfactants have quite different packing requirements with saturation areas per molecule of 30 and 60 Å2 respectively, they have relatively close CMC values. Following the work of Rosen and Hua,98 who reported that the micelle and surface mixing was close to ideal, NR measurements were made from below the CMC to about 100 × CMC(mixed) for two different solution compositions with 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 and 30
50 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 mole ratios, as shown in Fig. 11. The variations in surface composition in Fig. 11 show three striking features, (i) there is an abrupt change in the variation in composition at the CMC due to the onset of micellisation, (ii) the surface composition at concentrations as high as 100 × CMC is significantly different to the solution composition, and (iii) below the CMC the surface composition varies strongly with concentration. Although the PPA analysis20 of the micelle data and the CMC variation, indicate a small synergistic interaction with Bm = −0.3, the surface interaction is different. The surface interaction is slightly repulsive and asymmetrical, with Bs = 0.8 and Cs = 1.2. This suggests that the repulsive interaction results from the frustration or steric hindrance in packing the different EO groups, E3 and E8, at the interface; whereas in the micelle the packing constraints are more relaxed. The frustration results in changes in the structure of the mixed layer compared with the pure components.118 The alkyl chain distributions of each surfactant were more extended in the mixture. The E3 group was less hydrated and the E8 group more hydrated and less extended on mixing. The marked variations below the CMC result from significantly different variations in the surface activity of the two components below the CMC. This occurs here because the two components have different limiting surface areas, STs, and different ST variations with concentration, resulting in a crossover in the surface activity at low concentrations. The NR results show a rich pattern of variation for a system so relatively close to ideal mixing and which was not previously evident. Furthermore the PPA analysis closely captures the main features and trends.
70 mole ratios, as shown in Fig. 11. The variations in surface composition in Fig. 11 show three striking features, (i) there is an abrupt change in the variation in composition at the CMC due to the onset of micellisation, (ii) the surface composition at concentrations as high as 100 × CMC is significantly different to the solution composition, and (iii) below the CMC the surface composition varies strongly with concentration. Although the PPA analysis20 of the micelle data and the CMC variation, indicate a small synergistic interaction with Bm = −0.3, the surface interaction is different. The surface interaction is slightly repulsive and asymmetrical, with Bs = 0.8 and Cs = 1.2. This suggests that the repulsive interaction results from the frustration or steric hindrance in packing the different EO groups, E3 and E8, at the interface; whereas in the micelle the packing constraints are more relaxed. The frustration results in changes in the structure of the mixed layer compared with the pure components.118 The alkyl chain distributions of each surfactant were more extended in the mixture. The E3 group was less hydrated and the E8 group more hydrated and less extended on mixing. The marked variations below the CMC result from significantly different variations in the surface activity of the two components below the CMC. This occurs here because the two components have different limiting surface areas, STs, and different ST variations with concentration, resulting in a crossover in the surface activity at low concentrations. The NR results show a rich pattern of variation for a system so relatively close to ideal mixing and which was not previously evident. Furthermore the PPA analysis closely captures the main features and trends.
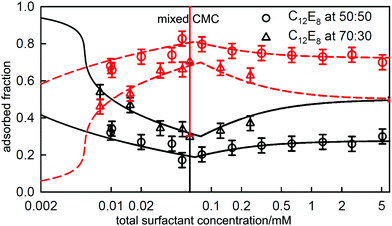 | ||
Fig. 11 Variation in surface composition with solution composition for C12E3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C12E8 at 50 C12E8 at 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 and 30 50 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 mole ratios. The lines are PPA calculations for Bm = −0.3, Bs = 0.8 and Cs = 1.2. Redrawn from ref. 20. 70 mole ratios. The lines are PPA calculations for Bm = −0.3, Bs = 0.8 and Cs = 1.2. Redrawn from ref. 20. | ||
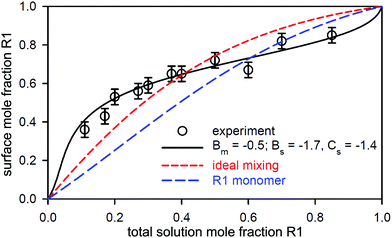 | ||
| Fig. 12 Variation in surface composition with solution composition for a 1 mM R1/R2 mixture. The black line is the best PPA description for the parameters shown (in units of RT), ideal surface mixing is shown as a short dashed red line, and the long dashed blue line is the associated monomer composition. Redrawn from Liley et al.113 | ||
In a study of the adsorption at the air–water interface of a quinary biosurfactant-surfactant mixture Liley et al.113 characterised the several associated binary pairs with NR, of which one was a mixture of the biosurfactants R1 (L-rhamnosyl-β-hydroxydecanoyl-β-hydroxydecanoyl) and R2 (L-rhamnosyl-L-rhamnosyl-β-hydroxydecanoyl-β-hydroxydecanoyl), which provides an interesting complement and contrast to the nonionic mixtures discussed above. The biosurfactants have the same alkyl chain structure, but R2 has a bulkier di-rhamnose headgroup. Recent studies indicate that they are only weakly ionic. The change in the headgroup structure from mono- to di-rhamnose results in an increased packing constraint at the interface, in which the saturation area/molecule increases from about 60 to about 90 Å2.119 NR measurements on the surface as a function of solution composition at a fixed concentration above the CMC show a marked departure from ideal mixing. Thus, although the micelle mixing parameters indicate only a slight departure from ideal mixing with Bm = −0.5, the parameters for the surface indicate a stronger asymmetric and synergistic interaction with Bs = −1.7 and Cs = −1.4. The latter gives rise to a minimum excess free energy of mixing, GE, which increases from −0.13RT for the micelle to −0.48RT for the surface. The minimum in GE for the R1/R2 mixing occurs at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 R1
1 R1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R2 stoichiometry, and the stronger synergy in the interaction indicates an improved packing at the interface on mixing compared with the C12E3/C12E8 mixture above. The implications for the quinary mixture involving R1 and R2 are discussed below.
R2 stoichiometry, and the stronger synergy in the interaction indicates an improved packing at the interface on mixing compared with the C12E3/C12E8 mixture above. The implications for the quinary mixture involving R1 and R2 are discussed below.
The important theme of the nature of the mixing of biosurfactants with conventional surfactants was continued in a recent study involving a rather different biosurfactant, the saponin, escin. Tucker et al.120 used NR to study the mixing of escin with the nonionic surfactants C12E5 and C12E8 at the air–water interface. Here the NR measurements are more challenging because only the conventional surfactants can be readily deuterium labelled, but it was still possible to determine the surface composition because the scattering length of escin is just sufficiently large enough without deuteration. Escin is only weakly ionic, so that mixing would be expected to be close to ideal. However saponins have a rather different molecular structure from conventional surfactants, with a triterpenoid hydrophobic region and a hydrophilic portion consisting of saccharide groups, and the nature of their mixing with more conventional surfactants was unknown. The CMC variations with C12E5 and C12E8 already indicate an important difference, and it is evident that there is a transition from a weakly to a strongly attractive interaction. The surface mixing was studied at a fixed concentration as a function of solution composition, and at a variable composition with increasing concentration, as shown for escin/C12E8 in Fig. 13.
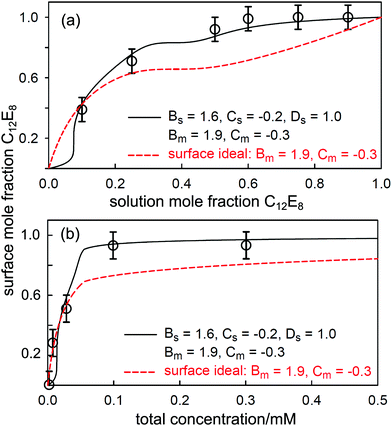 | ||
| Fig. 13 (a) Variation in surface composition with solution composition at a solution concentration of 0.3 mM for escin/C12E8, (b) variation in surface composition with total surfactant concentration for 0.09 mM escin in C12E8 solutions of varying concentration. The continuous lines are PPA calculations with non-ideal micellization and non-ideal surface mixing and the dashed lines are for non-ideal micellization and ideal surface mixing. Redrawn from Tucker et al.120 | ||
Fluorocarbon based surfactants offer different opportunities and advantages in some applications over their hydrocarbon equivalents and the mixing of fluorocarbon/hydrocarbon surfactants show some interesting differences because they are characterised predominantly by repulsive interactions. Jackson et al.107 used ST and NR to study the mixing of several partially fluorinated surfactants, e.g. C4F9C11H22TAB with C16TAB and C8F17C6H12TAB with C18TAB. The mixing was highly asymmetrical and required the quadratic, cubic and quartic terms in the PPA analysis. The mixing properties were quite different at low and high hydrocarbon mole fractions. At low hydrocarbon mole fractions the mixing was close to ideal and repulsive, with the minimum ΔGE ≈ 0.2 to 0.3RT at higher mole fractions. Complementary structural measurements, which provided access to the distribution of the different surfactant fragments at the surface, provided an important insight to those changes. At low volume fractions the ideal behaviour results from a balance between the energy gain associated with a reduced immersion of the fluorocarbon chain due to the presence of the hydrocarbon chain, and a loss from increased fluorocarbon/hydrocarbon repulsion. At the higher hydrocarbon volume fractions there is no space for further screening and the increasing fluorocarbon/hydrocarbon repulsion leads to the overall repulsive interaction.
Although in all of these examples in this section the departure from ideal mixing is relatively modest, the ability to characterise the evolution in the surface composition over a wide range of system parameters (mainly composition and concentration) provides the opportunity to probe in some detail the thermodynamics of mixing. It gives some detailed insights into the major factors affecting the mixing behaviour, and demonstrates the applicability of the PPA for such systems. It also illustrates the potential for correlating structural changes in the surface layer directly with the mixing properties.
3.2 Binary ionic/nonionic mixtures
SDS/nonionic surfactant mixtures are representative model systems for many of the mixed surfactant formulations used in home and personal care products and surfactant based formulations in other different product sectors. Penfold et al.121,122 used NR and SANS to investigate the mixing of SDS with a range of different nonionic surfactants, C12E3 and C12E6. The measurements were made in 0.1 M NaCl to reduce the impacts of electrostatic repulsion and the large differences in CMC values, as well as to correspond more closely to the conditions in many formulations. Penfold and Thomas20 more recently used the PPA to analyse the mixing properties of SDS/C12E3 and SDS/C12E6, along with some more recent measurements for SDS/C12E8.112,123 Analysis of the CMC variation and the surface composition, both as a function of surfactant concentration and solution composition, required the inclusion of quadratic and cubic terms in the expansion of the excess free energy of mixing, ΔGE. The variation of the free energy of mixing for the three systems is shown in Fig. 14, and the PPA parameters together with the minimum values of the excess free energy of mixing, ΔGE(min), and the compositions at the minimum, xSDS(min), for surface mixing are given in Table 1. All three mixtures have a relatively strong synergistic (attractive) interaction arising from the reduction of the electrostatic repulsion due to the inclusion of the nonionic component. This is further reduced by the presence of 0.1 M NaCl, and its specific impact is discussed later. The asymmetrical interaction with respect to the surface composition is clear in Fig. 14 and from the parameters in Table 1. The value of ΔGE(min) at the surface shifts from close to symmetrical for SDS/C12E3to distinctly asymmetrical for SDS with either C12E6or C12E8, and its value is increasingly reduced as the EO chain length increases. In an ordered 2-D mixture of charged and uncharged species in the absence of electrolyte the simplest arrangement for minimising the electrostatic repulsions is a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ionic
2 ionic![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nonionic ratio, as discussed elsewhere.99,102 However the asymmetry in the mixing will depend upon electrostatic interactions, differences in packing requirements and changes in hydration. In electrolyte, the electrostatic interactions will be less dominant and the results here indicate a significant contribution from packing requirements and changes in hydration. The decreasing synergy, as shown by ΔGE(min) implies an increasing packing constraint as the EO chain length increases. Furthermore the strength of the interaction is weaker for the micelles than the surface and this implies that the packing constraints are less severe in the micelle than at the surface. This was in part confirmed by Penfold et al.124 in a study of the impact of the nonionic headgroup size on the mixed SDS/nonionic surfactant micelle structure.
nonionic ratio, as discussed elsewhere.99,102 However the asymmetry in the mixing will depend upon electrostatic interactions, differences in packing requirements and changes in hydration. In electrolyte, the electrostatic interactions will be less dominant and the results here indicate a significant contribution from packing requirements and changes in hydration. The decreasing synergy, as shown by ΔGE(min) implies an increasing packing constraint as the EO chain length increases. Furthermore the strength of the interaction is weaker for the micelles than the surface and this implies that the packing constraints are less severe in the micelle than at the surface. This was in part confirmed by Penfold et al.124 in a study of the impact of the nonionic headgroup size on the mixed SDS/nonionic surfactant micelle structure.
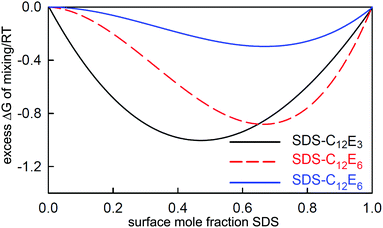 | ||
| Fig. 14 Excess free energy of mixing versus surface composition (mole fraction of SDS) for SDS/C12E3, SDS/C12E6 and SDS/C12E8 in 0.1 M NaCl. Redrawn from ref. 20. | ||
| mixture | Bm | Cm | Bs | Cs | x SDS (s)(min) | ΔGE (s)(min) |
|---|---|---|---|---|---|---|
| SDS/C12E3 | −1.4 | +1.4 | −4.0 | +0.5 | 0.47 | −1.0 |
| SDS/C12E6 | −2.0 | −2.0 | −3.0 | −2.9 | 0.67 | −0.9 |
| SDS/C12E8 | −1.0 | +1.0 | −1.0 | −1.0 | 0.67 | −0.3 |
As part of a wider study on ternary surfactant mixtures Liley et al.123 also explored the impact of electrolyte on the surface and micelle mixing of the SDS/C12E8 mixture. The key PPA parameters from the analysis of the NR and CMC data are summarised in Table 2 together with values of the ΔGE(min) for surface mixing, and the compositions at the minimum, xSDS(min). This direct comparison shows a clear effect of electrolyte on the mixing properties. In the absence of salt the optimal mixing ratio is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 nonionic
1 nonionic![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ionic, consistent with previous arguments, and consistent with the dominance of the electrostatic interaction. This is reinforced by the stronger interaction in the absence of electrolyte with ΔGE(min) ≈ −0.9RT. On the addition of electrolyte ΔGE(min) is significantly reduced and the optimal composition is also quite different, reflecting the suppression of the electrostatic interaction and the now greater significance of the packing constraints. In contrast, the addition of electrolyte has little impact upon the micelle mixing parameters.
ionic, consistent with previous arguments, and consistent with the dominance of the electrostatic interaction. This is reinforced by the stronger interaction in the absence of electrolyte with ΔGE(min) ≈ −0.9RT. On the addition of electrolyte ΔGE(min) is significantly reduced and the optimal composition is also quite different, reflecting the suppression of the electrostatic interaction and the now greater significance of the packing constraints. In contrast, the addition of electrolyte has little impact upon the micelle mixing parameters.
| Solution | Bm | Cm | Bs | Cs | x SDS (s)(min) | ΔGE (s)(min) |
|---|---|---|---|---|---|---|
| No salt | −1.0 | +1.0 | −3.0 | +2.9 | 0.33 | −0.9 |
| 0.1 M NaCl | −1.0 | +1.0 | −1.0 | −1.0 | 0.67 | −0.3 |
As a precursor to a study of the more complex ternary and quinary mixtures, the mixing of two different anionic surfactants, LAS and SLES, with C12E8 was studied by Liley et al.112,123 This also provided the opportunity to probe the impact of changing the molecular structure of the anionic surfactant on the mixing. SLES is similar to SDS but has a short E2 chain between the alkyl chain and sulfate headgroup. LAS has a dialkyl chain structure and a bulkier headgroup which includes a phenyl ring. Table 3 summarises the key PPA parameters obtained from the analysis of the NR and CMC data for C12E8 mixed with SDS, SLES, and LAS, in the absence and presence of 0.1 M NaCl. It is important to note that the sign of the cubic term changes according to which surfactant the coordinate x refers. In all three tables here x refers to the first named surfactant. Thus the sign is reversed between SDS-C12E8 and C12E8-SDS in Tables 2 and 3.
| (a) No salt | Bm | Cm | x m (min) | ΔGE(min) |
|---|---|---|---|---|
| SDS | −1.0 | −1.0 | 0.67 | −0.3 |
| SLES | −1.8 | −1.8 | 0.67 | −0.53 |
| LAS | −2.6 | −1.8 | 0.63 | −0.72 |
| Surface | Bs | Cs | x s (min) | ΔGE(min) |
|---|---|---|---|---|
| SDS | −3.0 | −3.0 | 0.67 | −0.89 |
| SLES | −2.0 | −2.0 | 0.67 | −0.59 |
| LAS | −4.4 | −0.8 | 0.54 | −1.1 |
| (b) 0.1 M NaCl | Bm | Cm | x m (min) | ΔGE(min) |
|---|---|---|---|---|
| SDS | −1.0 | −1.0 | 0.67 | −0.3 |
| SLES | 0 | 0 | — | — |
| LAS | −0.6 | −0.6 | 0.67 | −0.18 |
| Surface | Bs | Cs | x s (min) | ΔGE(min) |
|---|---|---|---|---|
| SDS | −1.0 | +1.0 | 0.33 | −0.3 |
| SLES | −0.3 | +0.3 | 0.33 | −0.09 |
| LAS | −2.2 | −1.0 | 0.6 | −0.58 |
Broadly similar trends are observed for all three anionic surfactants when mixed with the nonionic C12E8. The synergy in the surface mixing is stronger than for the micelle mixing, as previously discussed. The impact of electrolyte is to reduce the synergistic effect and change the value of xSDS (s)(min), consistent with the change from an interaction dominated by electrostatic repulsion to one dominated by steric or packing constraints. However the differences for the different anionic structures are significant. In the absence of salt the strength of the synergistic interaction at the surface is in the sequence LAS > SDS > SLES. This in part reflects the greater steric or packing contribution associated with the LAS dialkyl chain and the bulkier headgroup structures. SLES exhibits the lowest interaction strength, and this is in part associated with the weaker ionic nature of SLES compared with SDS or LAS, as reported by Xu et al.43,44 The addition of electrolyte to all three mixtures also has a significant impact, and implies larger steric or packing constraints for LAS.
In the discussion above of nonionic surfactant mixing it was observed that although the saponin, escin, behaves predominantly like a nonionic surfactant, its different molecular structure gives rise to non-ideal mixing. This was explored further by Tucker et al.,125 who investigated the mixing of escin with SDS, in the presence of electrolyte. The mixing was highly asymmetrical and synergistic, broadly consistent with the mixing of other nonionic/ionic mixtures. In this case the micelle mixing was more non-ideal than the surface and reflects the greater influence of the steric contribution due the rather different saponin structure compared to conventional surfactants.
The zwitterionic surfactants are an important class of surfactants, in that they have no overall charge but interact strongly with ionic surfactants. Their amphoteric nature results in a weaker interaction with biomaterials, and they are widely used in personal care formulations. Li et al.126 used NR and ST to investigate the surface properties of a series of mixtures, SDS and C12TAB, with two different zwitterionic surfactants dodecyldimethyl ammonium propane sulfonate, C12SB, and dodecyldimethyl ammonium acetate, C12CB. The interaction between SDS and C12SB was particularly strong and ΔGE highly asymmetric, as shown in Fig. 15. The asymmetry was characterised by the series expansion of ΔGE up to and including the quartic term. ΔGE(min) for the surface occurred at a SDS mole fraction of 0.35 and a depth of −2.8 RT. The micellar interaction was weaker and more asymmetric, with ΔGE(min) = −2.2RT at an SDS composition of 0.23. Li et al.126 observed that the strong synergistic interaction resulted in a strong peak in the total adsorption with composition, due to a significant increase in the packing in the mixed monolayer. The more efficient packing results from a structural rearrangement at the interface, which provides an effective reduction in the electrostatic repulsion, along the lines of the arrangement in Fig. 15. Significant differences in the packing constraints at the surface and in the micelles results in a marked difference in behaviour at the surface and in the micelles as also summarised in Fig. 15.
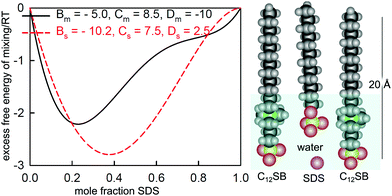 | ||
| Fig. 15 Dependence of the excess free energy of mixing for surface and micelles on the composition of SDS-C12SB mixtures, and a suggested molecular packing arrangement at the A–W interface. Redrawn from Li et al.126 | ||
3.3 Ternary mixtures
Liley et al.112 used NR to explore the surface mixing in the ternary surfactant mixture, SLES/LAS/C12E8; a surfactant mixture which represents the base formulation used in a wide range of home and personal care products. The micelle properties were evaluated on the basis of variations in the the mixed CMC, while the surface properties were investigated using NR measurements for concentrations above the CMC. A series of binary and ternary measurements were made as mapped out on the ternary diagram in Fig. 16. | ||
| Fig. 16 Ternary diagram for SLES/LAS/C12E8 mixture, indicating the compositions at which NR measurements were made. | ||
The PPA interaction parameters were determined from the binary pairs. The asymmetry in the interactions required both quadratic and cubic terms in the expansion of the excess free energy of mixing. The nature of the interactions for the anionic/nonionic pairs have been discussed earlier, and all three pairwise interactions are relatively weak. The interactions are dominated by the LAS/C12E8 interaction, for which ΔGE(min) ≈ −1.1RT, and the SLES/C12E8 and SLES/LAS interactions are weaker and comparable at ΔGE(min) ≈ −0.6RT. Although ΔGE(min) for the SLES/C12E8 and SLES/LAS interactions occurs close to a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 nonionic:anionic ratio, it is close to equimolar for LAS/C12E8. This indicates a significant contribution from steric constraints associated with the packing at the interface. The stronger LAS/C12E8 interaction results in the surface adsorption being dominated by the C12E8 and LAS, and there is little SLES at the interface. This is illustrated graphically in Fig. 17, where the PPA interaction parameters are used to reproduce the ternary behaviour at the interface at a fixed surfactant concentration of 2 mM. Importantly the binary interaction parameters provide, without further adjustment, a moderately accurate distribution of the experimental adsorbed fractions for the ternary mixture.
1 nonionic:anionic ratio, it is close to equimolar for LAS/C12E8. This indicates a significant contribution from steric constraints associated with the packing at the interface. The stronger LAS/C12E8 interaction results in the surface adsorption being dominated by the C12E8 and LAS, and there is little SLES at the interface. This is illustrated graphically in Fig. 17, where the PPA interaction parameters are used to reproduce the ternary behaviour at the interface at a fixed surfactant concentration of 2 mM. Importantly the binary interaction parameters provide, without further adjustment, a moderately accurate distribution of the experimental adsorbed fractions for the ternary mixture.
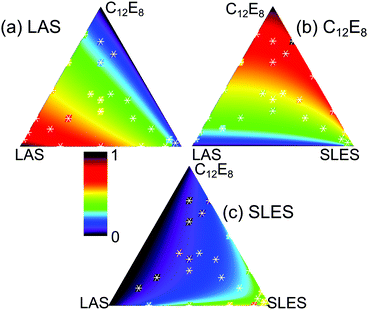 | ||
| Fig. 17 Composition of the adsorbed layer for the ternary SLES/LAS/C12E8 mixture at a solution concentration of 2 mM. Each triangular diagram, (a)–(c) represents the distribution of the adsorbed fraction of each component using the PPA parameters derived from the binary interactions. The data points are white asterisks on a coloured spot, which disappears when there is exact agreement between experiment and calculation. Redrawn from Liley et al.112 | ||
Liley et al.123 also explored the impact of electrolyte on the same ternary mixture. The addition of electrolyte, as discussed in the context of the binary mixtures earlier, weakens the synergistic interactions between SLES/C12E8 and LAS/C12E8. The SLES/LAS interaction, however, is hardly affected by the addition of electrolyte. These changes highlight the relative contributions of electrostatic and structural or packing factors. They also result in the surface of the ternary mixture being less strongly dominated by C12E8 and LAS adsorption, and consequently there is a greater adsorbed fraction of SLES at the interface. Importantly, these observations and comparisons show how manipulating the pairwise interactions through structural changes or the addition of electrolyte can impact directly upon the surface properties.
3.4 Quinary mixtures
The increasing interest in the use of biosurfactants in the development of more biosustainable and biodegradable surfactant based products has led to extensive studies of the R1–R2 rhamnolipid system from Pseudomonas aeruginosa bacteria and already examined in Fig. 12. Liley et al.113 have used NR to investigate the adsorption properties of a quinary mixture, in which 30 mole%, of the ternary mixture SLES/LAS/C12E8 mixture is replaced by the rhamnolipid mixture R1/R2. The quinary mixture has been shown to be a highly effective surfactant mixture in detergency related applications. It is characterised by strong surface interactions but weaker micelle interactions, in which R1 dominates the surface adsorption. The quinary behaviour is well characterised by the respective pairwise PPA interactions which require quadratic and cubic terms in the expansion of the excess free energy of mixing. A unique set of surface and micelle interaction parameters describe the binary, ternary and quinary mixtures, as illustrated in Fig. 18 for the quinary mixture at two different R1:R2 ratios.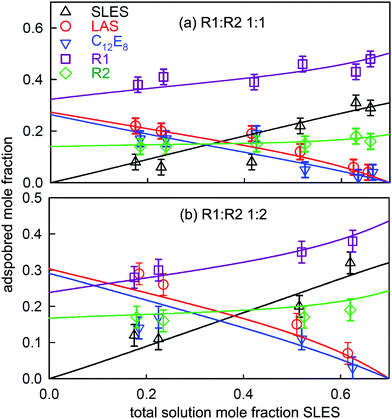 | ||
| Fig. 18 Variation in adsorbed mole fraction for each component in the quinary mixture, SLES/LAS/C12E8/R1/R2, containing fixed mole fractions of R1 and R2. Reproduced by permission from Liley et al.113 | ||
A significant proportion of the values of ΔGE(min) for the stronger interactions occur away from the regular solution value of x(min) = 0.5, as shown in Table 4, due to the combination of electrostatic and steric contributions to the pairwise interactions. The best fits to the data are dominated by the strong interactions. This results in the dominance of R1 at the interface and a greater adsorption of SLES at the interface compared with that observed in the SLES/LAS/C12E8 mixture. This study is important in that it demonstrates the extent to which NR can be used to investigate the adsorption of complex multi-component mixtures. It illustrates the applicability of the PPA, the role of pairwise interactions and the ability to replicate complex variations in the surface composition. The detailed characterisation of the surface composition and quantification of the strength of the interactions provides important insights into the effectiveness of such mixtures which result primarily from the dominance of R1 at the interface.
| Mixture | ΔGE(min) | x s (min) |
|---|---|---|
| LAS-R1 | −0.3 | 0.46 |
| C12E8-R1 | −0.38 | 0.55 |
| SLES-R1 | −0.81 | 0.55 |
| R1-R2 | −0.48 | 0.65 |
| LAS-R2 | −0.24 | 0.67 |
| C12E8-R2 | 0.0 | (0.5) |
| SLES-R2 | −0.24 | 0.33 |
| SLES-LAS | −0.59 | 0.61 |
| LAS-C12E8 | −1.11 | 0.46 |
| SLES-C12E8 | −0.59 | 0.33 |
3.5 Mixtures at the limit of the applicability of the PPA
Tucker et al.35,128–130 extensively studied the self-assembly and adsorption properties of the dialkyl chain cationic surfactant, dihexadecyl dimethyl ammonium bromide, DHDAB, mixed with a range of different nonionic surfactants. Such mixtures are important as they are representative of the surfactant ingredients in the formulations associated with hair and clothes care products and conditioners. The mixtures exhibited a rich pattern of structures in their bulk phase behaviour, and this impacts directly upon their adsorption properties. In solution DHDAB has a low or zero preferred spontaneous curvature and forms planar lamellar or vesicular structures. The nonionic cosurfactants explored, C12E3, C12E6 and C12E12, have an increasing spontaneous curvature, and their structures vary from planar to globular structures. For C12E6 and C12E12 their mixing with DHDAB results in a transition from planar structures, lamellae and vesicles, to globular micelles, via an extensive mixed phase region which depends upon solution concentration, and composition, and co-surfactant type. For the DHDAB/C12E3 mixture the preference for planar structures for both components results in planar structures with varying membrane rigidity across the entire composition range. The structural changes result in an extreme behaviour in the surface adsorption, as shown in Fig. 19(a). The surface mixing is highly non-ideal and for all three mixtures there is a solution composition threshold below which there is no measurable adsorption of the nonionic component at the interface. This threshold increases in the nonionic solution composition as the EO group of the nonionic component increases from 3 to 6 to 12. For C12E6 and C12E12 beyond the threshold, the nonionic mole fraction at the surface increases sharply, and is quite different to the general patterns of behaviour observed in many other mixtures. The pattern of behaviour for the DHDAB/C12E3 mixture is closer to that encountered in other surfactant mixtures. The general form of these adsorption patterns imply that below the composition threshold the nonionic monomer concentration is low and that the nonionic surfactant is mostly incorporated into the bulk aggregates.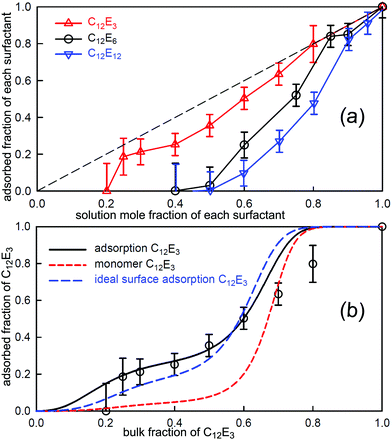 | ||
| Fig. 19 (a) Surface composition (mole fraction of nonionic) versus solution composition for 1.5 mM DHDAB/C12E3, C12E6 and C12E12. The lines are a guide to the eye only. (b) Variation in surface composition (mole fraction C12E3) with bulk solution composition for 1.5 mM DHDAB/C12E3. The lines are PPA calculations using the interaction parameters Bm = −6.5, Cm = −5.0, Dm = −5.0, Bs = −1.2, Cs = 0.3, and Ds = −0.3. The three surface parameters were set to zero for the ideal adsorption calculation. Redrawn from ref. 127. | ||
The sharp transition implies that the mixing parameters and interactions are highly asymmetrical. Penfold and Thomas127 explored the extent to which the PPA with the higher order terms, quadratic, cubic and quartic, in the series expansion of the excess free energy of mixing can replicate these features. The PPA broadly reproduces the main features of the adsorption of DHDAB/C12E3, as shown in Fig. 19(b) for the micelle and surface interaction parameters given in the figure caption. The extreme asymmetry required interaction parameters expanded to include the quartic term. The parameters imply that the surface mixing is close to ideal and that the surface composition is driven almost entirely by the bulk aggregation. Such large negative interaction parameters also imply that the system is close to phase separation. This could be within the same aggregated phase or as two separate phases; however, this is not evident from the observed bulk phase behaviour. It was not possible to obtain a meaningful description of the adsorption data for DHDAB mixed with C12E6 or C12E12. This suggests that the PPA and the expansion of the excess free energy of mixing in terms of a series is inadequate when the aggregated phases are more structured lamellar, hexagonal or cubic phases and where distinct changes between these different structures exist.
The solubilisation and co-adsorption at interfaces of small molecules, hydrotopes, such as perfumes, flavours, dyes, and drug molecules, are key aspects of the application of surfactants in detergency, cosmetics, foods, pesticides, and drug delivery. Bradbury et al.131 used NR to investigate the adsorption of perfume molecules by co-adsorption with the anionic surfactant LAS at the air–water interface. Their focus was on two model perfumes, phenyl ethanol, PE, and linalool, LL, with differing degrees of hydrophobicity and hydrophilicity, where PE is characteristic of a more hydrophilic perfume molecule and LL of a more hydrophobic one. This is reflected in their different log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values, 1.45 and 3.3. They also have quite different limiting solubilities, 150 and 10 mM respectively. What is particularly interesting and relevant to this review is the extent to which the non-ideal treatment of surfactant mixing applies. The variation in the LAS CMC with the addition of PE or LL was analysed assuming that the PPA model is valid when the effective CMC values are taken to be the limiting solubilities. Interaction parameters of B = +1.0 for LL and −4.0 for PE provide an adequate description of the CMC variation but the extensions to the calculation of the surface composition are less successful. The fuller PPA calculations imply that LAS/LL mixing is unfavourable and relatively close to ideal mixing, whereas LAS/PE mixing is less ideal and there is some synergy. The variation in the surface composition with solution composition for LAS/LL and LAS/PE (Fig. 20(b)) is well explained by the combination of the PPA and the use of the limiting solubility as the effective CMC. It also shows that the more hydrophobic LL competes more effectively for the surface than the relatively hydrophilic PE. Fig. 20(c) further shows that the optimum composition of the surface corresponds to a relatively low fraction of perfume, about 1/4 to 1/3, in the surface layer. This is consistent with the perfume requiring the hydrophobic environment of a relatively well packed surfactant layer in order to remain at the surface.
P values, 1.45 and 3.3. They also have quite different limiting solubilities, 150 and 10 mM respectively. What is particularly interesting and relevant to this review is the extent to which the non-ideal treatment of surfactant mixing applies. The variation in the LAS CMC with the addition of PE or LL was analysed assuming that the PPA model is valid when the effective CMC values are taken to be the limiting solubilities. Interaction parameters of B = +1.0 for LL and −4.0 for PE provide an adequate description of the CMC variation but the extensions to the calculation of the surface composition are less successful. The fuller PPA calculations imply that LAS/LL mixing is unfavourable and relatively close to ideal mixing, whereas LAS/PE mixing is less ideal and there is some synergy. The variation in the surface composition with solution composition for LAS/LL and LAS/PE (Fig. 20(b)) is well explained by the combination of the PPA and the use of the limiting solubility as the effective CMC. It also shows that the more hydrophobic LL competes more effectively for the surface than the relatively hydrophilic PE. Fig. 20(c) further shows that the optimum composition of the surface corresponds to a relatively low fraction of perfume, about 1/4 to 1/3, in the surface layer. This is consistent with the perfume requiring the hydrophobic environment of a relatively well packed surfactant layer in order to remain at the surface.
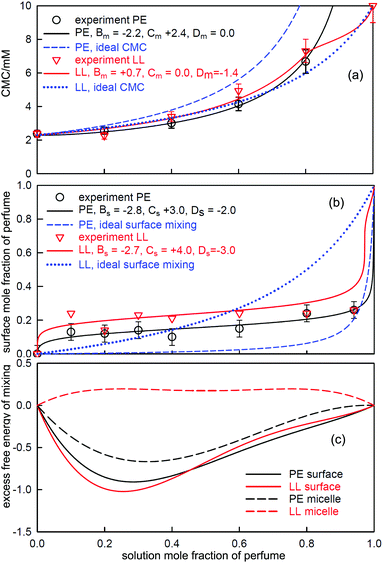 | ||
| Fig. 20 Variation in (a) CMC and (b) surface composition for LL/6LAS and PE/6LAS with solution mole fraction of perfume. The calculated lines are continuous for PPA calculations with the parameters given in the diagram and dashed for ideal micellar mixing. (c) Excess free energy of mixing for micellar solutions and at the surface. The data are from ref. 131. | ||
3.6 Summary and wider implications
For a long time the Gibbs equation has been used primarily to analyse ST behaviour to determine surface excesses at A–W and water–oil interfaces. However, its correct application requires a knowledge of the composition of the surface layer, which, because of the extremely low levels of impurity required to cover the surface, is often uncertain. NR is the first method to be able to determine directly the adsorbed amount of a given species at the A–W interface, either on its own or in a mixture. Not surprisingly the combination of NR and ST measurements both solves some previous observed anomalies and identifies some new ones. The anomalies are of several types. Contamination of the surface by nonionic impurities can be studied directly. Contamination by ionic impurities, which is a widely occurring phenomenon and which NR does not observe directly, can nevertheless be identified clearly by combining NR and ST. Comparison of NR and ST also clearly identifies the onset of depletion, which has previously been mistaken for the onset of aggregation in the bulk solution. Finally, unlike the Gibbs equation, NR measurements are not affected by situations where the activity and concentration are not the same, e.g. above the CMC. This leads to a further set of situations where comparison of NR and Gibbs gives important information about the state of the adsorbed species in the bulk solution.The most important feature of NR is its ability to determine the surface composition of mixtures above and below the CMC. Most formulations used in practice are carefully chosen mixtures and their optimum operation is often at concentrations above the CMC. The extensive range of data on surface and micelle mixing that can now be obtained from NR and the related small angle neutron scattering (SANS) has enabled a more detailed evaluation of the thermodynamics of surfactant mixing using the pseudophase approximation (PPA). The data is of a quality that makes it possible to include higher order terms in the series expansion of the excess free energy of mixing. As a result, it is now possible to use a global set of interaction parameters to describe all the data associated with a particular mixture and this provides a more accurate and relevant description of both surface and micellar mixing. This has been extensively demonstrated in a range of binary mixtures, which include nonionic mixtures and ionic nonionic mixtures, and has been extended to ternary and quinary mixtures. The analysis of the multicomponent mixtures here shows that pairwise interactions in both surface and micellar mixing are sufficient to describe mixtures with greater than two components. This is an important advance and allows the behaviour of more complex multicomponent mixtures to be predicted solely on the basis of the interactions between their different binary components. Limits to the range of application only start to appear when there is phase separation in either micelle or surface, as shown for DHDAB/nonionic and surfactant/perfume mixtures. The developments in the evaluation of surfactant mixing described in this review should provide both a framework in which a wider variety of multicomponent mixtures can be investigated and a basis for reaching a deeper theoretical understanding.
Author contributions
The authors contributed equally to all parts of this manuscript.Conflicts of interest
There are no conflicts to declare.Notes and references
- J. R. Lu, E. M. Lee, R. K. Thomas, J. Penfold and S. L. Flitsch, Langmuir, 1993, 9, 1352–1360 CrossRef CAS
.
- T. Crowley, E. Lee, E. Simister and R. Thomas, Phys. B, 1991, 173, 143–156 CrossRef
.
- J. R. Lu, R. K. Thomas and J. Penfold, Adv. Colloid Interface Sci., 2000, 84, 143–304 CrossRef CAS PubMed
.
- J. R. Lu, R. K. Thomas, B. P. Binks, D. Crichton, P. D. I. Fletcher, J. R. McNab and J. Penfold, J. Phys. Chem. B, 1998, 102, 5785–5793 CrossRef CAS
.
- J. R. Lu, T. J. Su, Z. X. Li, R. K. Thomas, E. J. Staples, I. Tucker and J. Penfold, J. Phys. Chem., 1997, 101, 10332–10339 CrossRef CAS
.
- A. Shahir, K. Nguyen and A. Nguyen, Phys. Chem. Chem. Phys., 2016, 18, 8794–8805 RSC
.
- A. Shahir, D. Arabadzhieva, H. Petkova, S. Karakashev, A. Nguyen and E. Mileva, J. Phys. Chem. C, 2017, 121, 11472–11487 CrossRef
.
- M. Peng, T. Duignan, C. Nguyen and A. Nguyen, Langmuir, 2021, 37, 2237–2255 CrossRef CAS PubMed
.
- Z. Li, R. Thomas, A. Rennie and J. Penfold, J. Chem. Soc., Faraday Trans., 1996, 92, 565–572 RSC
.
- Z. Li, R. Thomas, A. Rennie and J. Penfold, J. Phys. Chem. B, 1998, 102, 185–192 CrossRef CAS
.
- T. Su, R. Thomas and J. Penfold, Langmuir, 1997, 13, 2133–2142 CrossRef CAS
.
- Z. Li, C. Bain, R. Thomas, D. Duffy and J. Penfold, J. Phys. Chem. B, 1998, 102, 9473–9480 CrossRef CAS
.
- C. J. Radke, Adv. Colloid Interface Sci., 2015, 222, 600–614 CrossRef CAS PubMed
.
- S. Ikeda, Adv. Colloid Interface Sci., 1982, 18, 93–130 CrossRef CAS
.
- F. M. Menger, L. Shi and S. A. A. Rizvi, J. Am. Chem. Soc., 2009, 131, 10380–10831 CrossRef CAS PubMed
.
- P. Li, Z. Li, H. Shen, R. Thomas, J. Penfold and J. Lu, Langmuir, 2013, 29, 9324–9334 CrossRef CAS PubMed
.
- H. Xu, P. X. Li, K. Ma, R. K. Thomas, J. Penfold and J. R. Lu, Langmuir, 2013, 29, 9324–9334 CrossRef PubMed
.
- P. X. Li, R. K. Thomas and J. Penfold, Langmuir, 2014, 30, 6739–6747 CrossRef CAS PubMed
.
- E. Hutchinson, J. Colloid Sci., 1948, 3, 413–414 CrossRef CAS
.
- J. Penfold and R. Thomas, Mol. Phys., 2019, 117, 3376–3388 CrossRef CAS
.
-
R. Defay, I. Prigogine, A. Bellemans and D. H. Everett, Surface Tension and Adsorption, Longman, London, 1966 Search PubMed
.
- J. R. Lu, I. P. Purcell, E. M. Lee, E. A. Simister, R. K. Thomas, A. R. Rennie and J. Penfold, J. Colloid Interface Sci., 1995, 174, 441–455 CrossRef CAS
.
- H. Liu, X. Hua, Z. Li, K. Fa, H. Gong, K. Ma, M. Liao, P. Li, J. Webster, J. Petkov, R. Thomas and J. Lu, J. Colloid Interface Sci., 2021, 591, 106114 Search PubMed
.
- P. A. Kralchevsky, K. D. Danov, V. L. Kolev, G. Broze and A. Mehreteab, Langmuir, 2003, 19, 5004–5018 CrossRef CAS
.
- Z. Li, J. Lu and R. Thomas, Langmuir, 1997, 13, 3681–3685 CrossRef CAS
.
- Z. Li, E. Lee, R. Thomas and J. Penfold, J. Colloid Interface Sci., 1997, 187, 492–497 CrossRef CAS PubMed
.
- K. Shinoda and H. Nakayama, J. Colloid Interface Sci., 1963, 18, 705–712 CrossRef CAS
.
- D. G. Hall, B. A. Pethica and K. Shinoda, Bull. Chem. Soc. Jpn., 1975, 48, 324–326 CrossRef CAS
.
- S. W. An, J. R. Lu, R. K. Thomas and J. Penfold, Langmuir, 1996, 12, 2446–2453 CrossRef CAS
.
- K. Lunkenheimer, K. Geggel and D. Prescher, Langmuir, 2017, 33, 10216–10224 CrossRef CAS PubMed
.
- P. Linse and T. A. Hatton, Langmuir, 1997, 13, 4066–4078 CrossRef CAS
.
- J. B. Vieira, Z. X. Li and R. K. Thomas, J. Phys. Chem. B, 2002, 106, 5400–5407 CrossRef CAS
.
- C. Phan, S. Yusa, T. Honda, K. Sharker, A. Hyde and C. Nguyen, ACS Omega, 2018, 3, 10907–10911 CrossRef CAS
.
- S. An, R. Thomas, C. Forder, N. C. Billingham, S. P. Armes and J. Penfold, Langmuir, 2002, 18, 5064–5073 CrossRef CAS
.
- I. Tucker, J. Penfold, R. Thomas, I. Grillo, J. Barker and D. Mildner, Langmuir, 2008, 24, 6509–6520 CrossRef CAS PubMed
.
- J. Penfold, R. Thomas, P. Li, J. Petkov, I. Tucker, J. Webster and A. Terry, Langmuir, 2015, 31, 3003–3011 CrossRef CAS PubMed
.
- J. A. de Feijter and J. Benjamins, J. Colloid Interface Sci., 1981, 81, 91–107 CrossRef CAS
.
- P. H. Elworthy and K. J. Mysels, J. Colloid Interface Sci., 1966, 21, 331–347 CrossRef CAS
.
- T. Sasaki, M. Hattori, J. Sasaki and K. Nukina, Bull. Chem. Soc. Jpn., 1975, 48, 1397–1403 CrossRef CAS
.
- S. G. Cutler, P. Meares and D. G. Hall, J. Chem. Soc., Faraday Trans. I, 1978, 74, 1758–1767 RSC
.
- J. Lu, E. Simister, R. Thomas and J. Penfold, J. Phys. Chem., 1993, 97, 13907–13913 CrossRef CAS
.
- R. Alargova, J. Petkov, D. Petsev, I. B. Ivanov, G. Broze and A. Mehreteab, Langmuir, 1995, 11, 1530–1536 CrossRef CAS
.
- H. Xu, J. Penfold, R. K. Thomas, J. T. Petkov, I. Tucker and J. P. R. Webster, Langmuir, 2013, 29, 11656–11666 CrossRef CAS PubMed
.
- H. Xu, J. Penfold, R. K. Thomas, J. T. Petkov, I. Tucker and J. P. R. Webster, Langmuir, 2013, 29, 12744–12753 CrossRef CAS PubMed
.
- H. Xu, J. Penfold, R. K. Thomas, J. T. Petkov, I. Tucker, I. Grillo and A. Terry, Langmuir, 2013, 29, 13359–13366 CrossRef CAS PubMed
.
- P. Li, J. Penfold, R. Thomas and H. Xu, Adv. Colloid Interface Sci., 2019, 269, 43–86 CrossRef CAS PubMed
.
- Z. Wang, P. Li, K. Ma, Y. Chen, J. Webster, M. Campana, Z. Yan, J. Penfold and R. Thomas, J. Colloid Interface Sci., 2021, 597, 223–232 CrossRef CAS PubMed
.
- P. Li, Z. Wang, K. Ma, Y. Chen, Z. Yan, J. Penfold, R. Thomas, M. Campana, J. Webster and A. Washington, J. Colloid Interface Sci., 2020, 565, 567–581 CrossRef CAS PubMed
.
- I. Tucker, J. Penfold, R. Thomas, C. Dong, S. Golding, C. Gibson and I. Grillo, Langmuir, 2010, 26, 10614–10626 CrossRef CAS PubMed
.
- I. Tucker, J. Penfold, R. Thomas, C. Dong, S. Golding, C. Gibson and I. Grillo, Langmuir, 2011, 27, 6674–6682 CrossRef CAS PubMed
.
- H. Xu, J. Penfold, R. K. Thomas, J. T. Petkov, I. Tucker, J. P. R. Webster, I. Grillo and A. Terry, Langmuir, 2014, 30, 4694–4702 CrossRef CAS PubMed
.
- R. Alargova, K. Danov, J. Petkov, P. Kralchevsky, G. Broze and A. Mehreteab, Langmuir, 1997, 13, 5544–5551 CrossRef CAS
.
- J. Penfold, R. Thomas, X. Zhang and D. Taylor, Langmuir, 2009, 25, 3972–3980 CrossRef CAS PubMed
.
- S. Halacheva, J. Penfold, R. Thomas and J. Webster, Langmuir, 2013, 29, 5832–5840 CrossRef CAS PubMed
.
- J. Penfold, R. Thomas and P. Li, J. Colloid Interface Sci., 2016, 463, 199–206 CrossRef CAS PubMed
.
- F. M. Menger and L. Shi, J. Am. Chem. Soc., 2009, 131, 6672–6673 CrossRef CAS PubMed
.
- L. X. Jiang, J. B. Huang, A. Bahramian, P. X. Li, R. K. Thomas and J. Penfold, Langmuir, 2012, 28, 327–338 CrossRef CAS PubMed
.
- R. Meszaros, L. Thompson, M. Bos, I. Varga and T. Gilanyi, Langmuir, 2003, 19, 609–615 CrossRef CAS
.
- C. Phan, C. Nguyen, H. Nakahara, O. Shibata and T. Nguyen, Langmuir, 2016, 32, 12842–12847 CrossRef CAS PubMed
.
- A. Bahramian, R. K. Thomas and J. Penfold, J. Phys. Chem. B, 2014, 118, 2769–2783 CrossRef CAS PubMed
.
- J. Penfold and R. Thomas, J. Phys. Chem. B, 2020, 124, 6074–6094 CrossRef CAS PubMed
.
- D. J. F. Taylor, R. K. Thomas and J. Penfold, Langmuir, 2002, 18, 4748–4757 CrossRef CAS
.
- J. Penfold, I. Tucker, R. Thomas, D. Taylor, X. Zhang, C. Bell, C. Breward and P. Howell, Langmuir, 2007, 23, 3128–3136 CrossRef CAS PubMed
.
- P. Hansson and M. Almgren, Langmuir, 1994, 10, 2115–2124 CrossRef CAS
.
- K. Hayakawa and J. Kwak, J. Phys. Chem., 1982, 86, 3866–3870 CrossRef CAS
.
-
I. Prigogine, R. Defay, A. Bellemans and D. H. Everett, Surface tension and adsorption, Chapter XXI, Sections 8 and 9, Longman, London, 1966 Search PubMed
.
- G. Manning, Quart. Rev. Biophysics, 1978, 11, 179–246 CrossRef CAS PubMed
.
- N. Ise and T. Okubo, Macromolecules, 1978, 11, 439–447 CrossRef CAS
.
- D. J. F. Taylor, R. K. Thomas, P. X. Li and J. Penfold, Langmuir, 2003, 19, 3712–3719 CrossRef CAS
.
- E. Staples, I. Tucker, J. Penfold, N. Warren, R. K. Thomas and D. J. F. Taylor, Langmuir, 2002, 18, 5147–5153 CrossRef CAS
.
- J. H. Buckingham, J. Lucassen and F. Hollway, J. Colloid Interface Sci., 1978, 67, 423–431 CrossRef CAS
.
- A. J. Konop and R. H. Colby, Langmuir, 1999, 15, 58–65 CrossRef CAS
.
- D. J. F. Taylor, R. K. Thomas, P. X. Li and J. Penfold, Langmuir, 2003, 19, 3712–3719 CrossRef CAS
.
- I. Varga and R. A. Campbell, Langmuir, 2017, 33, 5915–5924 CrossRef CAS PubMed
.
- S. H. Myrick and E. I. Franses, Colloids Surf., A, 1998, 143, 503–515 CrossRef CAS
.
- S. Sitar, B. Goderis, P. Hansson and K. Kogej, J. Phys. Chem. B, 2012, 116, 4634–4645 CrossRef CAS PubMed
.
- R. G. Nause, D. A. Hoagland and H. H. Strey, Macromolecules, 2008, 41, 4012–4019 CrossRef CAS
.
- W. Al-Soufi, L. Pineiro and M. Novo, J. Colloid Interface Sci., 2012, 370, 102–110 CrossRef CAS PubMed
.
- L. Song and M. Rosen, Langmuir, 1996, 12, 1149–1153 CrossRef CAS
.
- P. X. Li, C. C. Dong, R. K. Thomas, J. Penfold and Y. L. Wang, Langmuir, 2011, 27, 2575–2586 CrossRef CAS PubMed
.
- Z. X. Li, C. C. Dong and R. K. Thomas, Langmuir, 1999, 15, 4392–4396 CrossRef CAS
.
- E. Alami, G. Beinert, P. Marie and R. Zana, Langmuir, 1993, 9, 1465–1467 CrossRef CAS
.
- R. Zana, M. Benrraou and R. Rueff, Langmuir, 1991, 7, 1072–1075 CrossRef CAS
.
- R. Zana, J. Colloid Interface Sci., 2002, 246, 182–190 CrossRef CAS PubMed
.
- R. Zana, J. Colloid Interface Sci., 2002, 248, 203–220 CrossRef CAS PubMed
.
- J. Wegrzyska, G. Para, J. Chlebicki, P. Warszyski and K. Wilk, Langmuir, 2008, 24, 3171–3180 CrossRef PubMed
.
- Y. Geng and L. S. Romsted, J. Phys. Chem. B, 2005, 109, 23629–23637 CrossRef CAS PubMed
.
- F. Menger and C. Littau, J. Am. Chem. Soc., 1993, 115, 10083–10090 CrossRef CAS
.
- M. J. Rosen, J. H. Mathias and L. Davenport, Langmuir, 1999, 15, 7340–7346 CrossRef CAS
.
- B. Cai, J. Dong, L. Cheng, Z. Jiang, Y. Yang and X. Li, Soft Matter, 2013, 9, 7637–7646 RSC
.
- F. François, D. Sarazin, T. Schwartz and G. Weill, Polymer, 1979, 20(969), 975 Search PubMed
.
- J. Zhang, R. Thomas and J. Penfold, Langmuir, 2020, 36, 11661–11675 CrossRef CAS PubMed
.
- J. H. Clint, J. Chem. Soc., Faraday Trans. I, 1975, 71, 1327–1334 RSC
.
-
D. N. Rubingh, Solution Chemistry of Surfactants, ed. K. L. Mittal, Plenum Press, New York, 1979, pp. 337–354 Search PubMed
.
- P. Holland and D. Rubingh, J. Phys. Chem., 1983, 87, 1984–1990 CrossRef CAS
.
- P. M. Holland, Adv. Colloid Interface Sci., 1986, 26, 111–129 CrossRef CAS
.
- B. Ingram, Colloid Polym. Sci., 1980, 258, 191–192 CrossRef CAS
.
- M. J. Rosen and X. Y. Hua, J. Colloid Surf. Sci., 1982, 86, 164–172 CrossRef CAS
.
- I. Reif and P. Somasundaran, Langmuir, 1999, 15, 3411–3417 CrossRef CAS
.
- H. Maeda, J. Phys. Chem. B, 2005, 109, 15933–15940 CrossRef CAS PubMed
.
- J. D. Hines, R. K. Thomas, P. R. Garrett, G. K. Rennie and J. Penfold, J. Phys. Chem. B, 1998, 102, 8834–8846 CrossRef CAS
.
- A. Patist, S. Devi and D. O. Shah, Langmuir, 1999, 15, 7403–7405 CrossRef CAS
.
- J. A. V. Butler, Proc. Royal Soc., 1932, A135, 348–375 Search PubMed
.
- E. H. Lucassen-Reynders, Progress Surface Membrane Science, 1976, 10, 253–360 CAS
.
- G. Kaptay, Langmuir, 2019, 35, 10987–10992 CrossRef CAS PubMed
.
- O. Redlich and A. T. Kister, Ind. Eng. Chem., 1948, 40, 345–348 CrossRef
.
- A. J. Jackson, P. X. Li, C. C. Dong, R. K. Thomas and J. Penfold, Langmuir, 2009, 25, 3957–3965 CrossRef CAS PubMed
.
-
J. D. Hoffman, Numerical Methods for Engineers and Scientists, Marcel Dekker Inc, New York, 2nd edn, 2001 Search PubMed
.
- P. Holland and D. N. Rubingh, ACS Symp. Ser., 1992, 501, 2–30 CrossRef CAS
.
- J. A. Barker, Australian J. Chem., 1953, 6, 207–210 CrossRef CAS
.
-
J. S. Rowlinson and F. L. Swinton, Liquids and Liquid Mixtures, Butterworth-Heinemann Ltd, London, 3rd edn, 1982 Search PubMed
.
- J. Liley, R. Thomas, J. Penfold, I. Tucker, J. Petkov, P. Stevenson and J. Webster, J. Phys. Chem. B, 2017, 121, 2825–2838 CrossRef CAS PubMed
.
- J. Liley, R. Thomas, J. Penfold, I. Tucker, J. Petkov, P. Stevenson, I. Banat, R. Marchant, M. Rudden and J. Webster, Langmuir, 2017, 33, 13027–13039 CrossRef CAS PubMed
.
- H. Xu, P. Li, K. Ma, R. Welbourn, J. Doutch, J. Penfold, R. Thomas, D. Roberts, J. Petkov, K. Choo and S. Khoo, J. Colloid Interface Sci., 2018, 516, 456–465 CrossRef CAS PubMed
.
- Y. Nikas, S. Pruuvada and D. Blankschtein, Langmuir, 1992, 8, 2680–2689 CrossRef CAS
.
- Z. Wang, P. Li, K. Ma, Y. Chen, Z. Yan, J. Penfold, R. Thomas, M. Campana, J. Webster, Z. Li, H. Neil, J. H. Xu, J. Petkov and D. Roberts, J. Colloid Interface Sci., 2021, 876–890 CrossRef PubMed
.
- J. Penfold, E. Staples, T. Crowley and I. Tucker, Colloids Surf., A, 1995, 102, 127–132 CrossRef CAS
.
- J. Penfold, E. Staples, I. Tucker, L. Thompson and R. Thomas, J. Colloid Interface Sci., 2002, 247, 404–411 CrossRef CAS PubMed
.
- M. Chen, J. Penfold, R. Thomas, T. Smyth, A. Perfumo, R. Marchant, I. Banat, P. Stevenson, A. Parry, I. Tucker and I. Grillo, Langmuir, 2010, 26, 18281–18292 CrossRef CAS PubMed
.
- I. Tucker, A. Burley, R. Petkova, S. Hosking, R. Thomas, J. Penfold, P. Li, K. Ma, J. Webster and R. Welbourn, J. Colloid Interface Sci., 2020, 574, 385–393 CrossRef CAS PubMed
.
- J. Penfold, E. Staples, L. Thompson, I. Tucker, J. Hines, R. Thomas and J. Lu, Langmuir, 1995, 11, 2496–2503 CrossRef CAS
.
- E. Staples, L. Thompson, I. Tucker, J. Penfold, R. Thomas and J. Lu, Langmuir, 1993, 9, 1651–1656 CrossRef CAS
.
- J. Liley, R. Thomas, J. Penfold, I. Tucker, J. Petkov, P. Stevenson and J. Webster, Langmuir, 2017, 33, 4301–4312 CrossRef CAS PubMed
.
- J. Penfold, I. Tucker, R. Thomas, E. Staples and R. Schuermann, J. Phys. Chem. B, 2005, 107, 10760–10770 CrossRef PubMed
.
- I. Tucker, A. Burley, R. Petkova, S. Hosking, J. Penfold, R. Thomas, P. Li, J. Webster and R. Welbourn, Langmuir, 2020, 36, 5997–6006 CrossRef CAS PubMed
.
- P. Li, K. Ma, R. Thomas and J. Penfold, J. Phys. Chem. B, 2016, 120, 3677–3691 CrossRef CAS PubMed
.
- J. Penfold and R. Thomas, Mol. Phys., 2019, 117, 3376–3388 CrossRef CAS
.
- I. Tucker, J. Penfold, R. Thomas, J. Barker and D. Mildner, Langmuir, 2008, 24, 7674–7687 CrossRef CAS PubMed
.
- I. Tucker, J. Penfold, R. Thomas, J. Barker and D. Mildner, Langmuir, 2008, 24, 10089–10098 CrossRef CAS PubMed
.
- J. Penfold, E. Staples, S. Ugazio, I. Tucker, L. Soubiran, J. Hubbard, M. Noro, B. O'Malley, A. Ferrante, G. Ford and H. Buron, J. Phys. Chem. B, 2005, 109, 18107–18116 CrossRef CAS PubMed
.
- R. Bradbury, J. Penfold, R. Thomas, I. Tucker, J. Petkov and C. Jones, Langmuir, 2013, 29, 3361–3369 CrossRef CAS PubMed
.
| This journal is © the Owner Societies 2022 |


