Resolving competing conical intersection pathways: time-resolved X-ray absorption spectroscopy of trans-1,3-butadiene†
Issaka
Seidu
 a,
Simon P.
Neville
a,
Ryan J.
MacDonell‡
a,
Simon P.
Neville
a,
Ryan J.
MacDonell‡
 b and
Michael S.
Schuurman
b and
Michael S.
Schuurman
 *ab
*ab
aNational Research Council Canada, 100 Sussex Drive, Ottawa, Ontario K1A 0R6, Canada. E-mail: Michael.Schuurman@uottawa.ca
bDepartment of Chemistry and Biomolecular Sciences, University of Ottawa, 10 Marie Curie, Ottawa, Ontario K1N 6N5, Canada
First published on 13th December 2021
Abstract
Time-resolved X-ray absorption spectroscopy is emerging as a uniquely powerful tool to probe coupled electronic-nuclear dynamics in photo-excited molecules. Theoretical studies to date have established that time-resolved X-ray absorption spectroscopy is an atom-specific probe of excited-state wave packet passage through a seam of conical intersections (CIs). However, in many molecular systems, there are competing dynamical pathways involving CIs of different electronic and nuclear character. Discerning these pathways remains an important challenge. Here, we demonstrate that time-resolved X-ray absorption spectroscopy (TRXAS) has the potential to resolve competing channels in excited-state non-adiabatic dynamics. Using the example of 1,3-butadiene, we show how TRXAS discerns the different electronic structures associated with passage through multiple conical intersections. trans-1,3-Butadiene exhibits a branching between polarized and radicaloid pathways associated with ethylenic “twisted-pyramidalized” and excited-state cis–trans isomerization dynamics, respectively. The differing electronic structures along these pathways give rise to different XAS signals, indicating the possibility of resolving them. Furthermore, this indicates that XAS, and other core-level spectroscopic techniques, offer the appealing prospect of directly probing the effects of selective chemical substitution and its ability to affect chemical control over excited-state molecular dynamics.
I. Introduction
Time-resolved spectroscopy has been extremely successful in the experimental interrogation of conical intersection (CI) mediated dynamics in molecular photo-physical processes.1–8 However, it is often the case that the time-evolution of specific spectroscopic observables display non-intuitive “mappings” to the time-evolution of the underlying coupled nuclear-electronic dynamics. The difficulty of uniquely assigning observable spectroscopic quantities to changes in the electronic and nuclear character of an excited-state wave packet has been previously addressed via the first-principles simulation of these time-resolved spectra.9–14 The rationale for this approach is that an accurate time-resolved spectral simulation will engender confidence in the underlying molecular dynamics calculations used to generate the computed spectrum. It is from these dynamics simulations that (detailed) mechanistic elements may be extracted.For systems that undergo CI-mediated non-adiabatic transitions, a key mechanistic detail that is often extracted from excited-state dynamics simulations is the identity of the CI seam(s) involved (i.e. the nuclear and electronic structure) in the electronic relaxation process. This detailed information can be difficult to discern from a spectroscopic signal alone. However, it has been recently demonstrated that core-level spectroscopy will offer a uniquely powerful means to track the change in electronic structure in the region of strong non-adiabatic coupling surrounding a CI seam,13–16 and may thus encode the approach of a wave packet to it. In many molecular systems, though, the electronic relaxation of an excited-state wave packet is not dominated by a single localized region of the CI seam. In fact, there may exist competition between multiple conical intersections and/or multiple seams, with a branching ratio determined by both nuclear (inertial) and electronic effects inherent in the prepared wave packet.5,11,17–20
The question posed in this work is this: to what extent is X-ray absorption spectroscopy sensitive to the different electronic structures associated with multiple, “competing”, conical intersection-mediated dynamical pathways? We will attempt to answer this question via simulation using as a paradigm example, the non-adiabatic dynamics of 1,3-butadiene (1,3-BD) following excitation to the bright ππ* state. In the ensuing multi-state dynamics, there exist (at least) two important nuclear configurations that are associated with internal conversion to the ground electronic states: the so-called twisted-pyramidalized (Tw-Py) and trans–cis isomerization (transoid) conical intersections.10,11,21 For reference, the Tw-Py and transoid minimum energy CI (MECI) geometries are shown in Fig. 2. The Tw-Py MECI is analogous to the twisted-pyramidalized intersection motif in ethylene,22,23 where the electronic structure of the S1 state is characterized by a separation of charge between the terminal and medial carbon atoms. There is an additional CI observed in simulation as a minor channel, in which the pyramidalization occurs at a medial (rather than terminal) C atom, which is denoted “mTw-Py” in Fig. 2(c). The transoid structure is realized via twisting about the C–C–C–C backbone (dihedral ∠Tw–B = 56.151°) in concert with a slight twisting of the terminal methylene groups.21 This twisting is accompanied by a mixing of the excited π*2 and ground (π*2–S0) electronic states. These transoid (and cisoid, together termed “kinked-diene”) structures have a tetraradical character and thus the lack of electronic polarization that is observed in the former pathway.11 Numerous previous works found that these pathways are both involved in the electronic de-excitation, and that the branching ratio between the two could be modified via chemical substitution,11 which affects both the relative “inertia” associated with the twisting as well as the relative energies of the different CI seam regions.11,19
Previous joint theoretical–experimental efforts using valence time-resolved photo-electron spectroscopy (TRPES)8,10,24 have provided incredible insight into: (i) the time-scale for electronic relaxation back to the ground state, (ii) how the initial nuclear motion involving the torsional coordinate can be encoded in the TRPES, and importantly for this work, (iii) how ab initio determinations of the TRPES based on non-adiabatic dynamics simulations are able to successfully capture many of the key features of the experimental spectra. What is more difficult to discern from these previous studies, however, are the spectral fingerprints of the CIs themselves. Any signal that simulation predict arises uniquely from the CI region is itself embedded in broad ionization features associated more generally with the excited electronic state(s). Rather, the nuclear and electronic character of these pathways are discerned indirectly via simulation alone, where the degree of fidelity between computed and measured (global) spectrum strongly informs how convincing such assignments may be. Clearly, a more “ideal” observable would be able to isolate those structures that simulation predicts are so central to the electronic decay process.
In the present work, we use a combination of ab initio multiple spawning (AIMS) dynamics simulations25,26 and X-ray absorption cross-section calculations, to simulate the time-resolved X-ray absorption spectrum (TRXAS) of trans-1,3-BD following excitation to the bright (ππ*) states. In the following, the ability of TRXAS to resolve both the nuclear and electronic characters of the seam regions accessed by the excited-state wave packet is interrogated via simulation.
II. Theoretical methods
A. Dynamics simulations
The excited-state dynamics of 1,3-BD was simulated using the AIMS method,25,26 which in this study involves invoking the independent first generation (IFG) approximation and employing a zeroth-order saddle-point approximation for the evaluation of the requisite Hamiltonian matrix elements over trajectory basis functions.27 Here, the total molecular wave function is given by: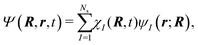 | (1) |
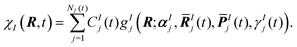 | (2) |
![[R with combining macron]](https://www.rsc.org/images/entities/b_i_char_0052_0304.gif) Ij(t) and
Ij(t) and ![[P with combining macron]](https://www.rsc.org/images/entities/b_i_char_0050_0304.gif) Ij(t), respectively, evolve according to classical equations of motion. The phases γIj(t) are propagated according to semi-classical equations, and the Gaussian widths αIj are time-independent. The expansion coefficients, CIj(t), are determined variationally by solving the time-dependent Schrödinger equation. During an AIMS calculation, the number of Gaussian basis functions, NI, is increased in regions of strong non-adiabatic coupling between electronic states in a process referred to as spawning, providing a description of internal conversion processes.28
Ij(t), respectively, evolve according to classical equations of motion. The phases γIj(t) are propagated according to semi-classical equations, and the Gaussian widths αIj are time-independent. The expansion coefficients, CIj(t), are determined variationally by solving the time-dependent Schrödinger equation. During an AIMS calculation, the number of Gaussian basis functions, NI, is increased in regions of strong non-adiabatic coupling between electronic states in a process referred to as spawning, providing a description of internal conversion processes.28
B. Simulation of time-resolved X-ray absorption spectra
The TRXAS was simulated as the incoherent sum of the X-ray absorption spectra computed at the centroid of each Gaussian basis function of the AIMS simulation, with a weighting factor given by the squared modulus of the corresponding expansion coefficient. That is, the TRXAS was approximated as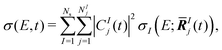 | (3) |
For the calculation of the excited-state X-ray absorption cross-sections, the core–valence separated combined density functional theory and multi-configurational configuration interaction (CVS-DFT/MRCI) method was used.29–36 This method has a key advantage of being able to correctly describe the types of multi-reference and doubly-excited core-excited states that often contribute to the X-ray absorption spectra of singly-valence-excited states.36 The ability to accurately handle states of these types is especially important in this application due to the complex nature of valence electronic states encountered. This is a key advantage of using DFT/MRCI compared to single-reference methods.35
The present simulations consider the isotropic axis distribution TRXAS (see Fig. 5) as well as the relative polarization of the pump and probe pulses, and we display the results for both the parallel and perpendicular pump/probe relative polarization in the Fig. S2 and S3 (ESI†). Specifically, these polarization-dependent spectra were simulated assuming that the pump pulse generates a cos(θ)2 distribution in the excited-state population, where θ is the angle between pump polarization and the transition dipole moment for the S0 → S1 transition. Practically, this done by weighting the oscillator strength of the core-transition by the cos(θ)2 axis distribution function, where θ is the angle between the pump and probe transition dipole moments. It was observed that this polarization resulted in the majority of the signal intensity in the perpendicular TRXAS.
C. Computational details
The electronic energies, gradients and non-adiabatic couplings required for the AIMS simulations were computed at the multi-reference configuration interaction with single excitations (MR-CIS) level of theory.37,38 An active space of 4 electrons in 4 orbital was used, comprising of HOMO and HOMO−1 π orbitals, and the LUMO and LUMO+1 π* orbitals. The 6-31G* basis set was used for the molecule. In the AIMS simulations, three electronic states were included, correlating with the S0, S1(π*2) and S2(ππ*) states at the S0 minimum geometry. A total of 39 initial conditions were initiated on the bright state, sampled from the ground-state Wigner distribution. For more information on the dynamics calculation, see ref. 11. The nuclear densities in internal coordinates were obtained via Monte-Carlo integration of Cartesian trajectory basis functions using an approach analogous to that described in ref. 39.In the CVS-DFT/MRCI calculations of the X-ray absorption cross-sections, the redesigned Hamiltonian of Heil et al. was used.33 The Turbomole set of programs40 and the Dalton software package41 were used for the calculation of the KS-DFT orbitals in these calculations. Here, the BH-LYP functional42–44 and aug-cc-pVDZ basis set were used exclusively.
We note that the level of electronic structure used in the dynamics and X-ray absorption cross-section calculations are different. As a consequence, the mapping between the sets of DFT/MRCI and MR-CIS valence-state adiabatic electronic wave functions had to be computed at each geometry ![[R with combining macron]](https://www.rsc.org/images/entities/b_i_char_0052_0304.gif) Ij arising from the AIMS simulations. This was achieved by calculating the overlap of the MR-CIS electronic state associated with each trajectory and a corresponding set of DFT/MRCI electronic wave functions. For >99.9% of all geometries and 100% of excited-state geometries, there was found to exist a DFT/MRCI state with an overlap >0.90 with each MR-CIS state of interest, enabling an unambiguous mapping between the different adiabatic states. The ability to generate a 1
Ij arising from the AIMS simulations. This was achieved by calculating the overlap of the MR-CIS electronic state associated with each trajectory and a corresponding set of DFT/MRCI electronic wave functions. For >99.9% of all geometries and 100% of excited-state geometries, there was found to exist a DFT/MRCI state with an overlap >0.90 with each MR-CIS state of interest, enabling an unambiguous mapping between the different adiabatic states. The ability to generate a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mapping between the MR-CIS states to DFT/MRCI states is fortuitous in this case, and not a general result. Specifically, the regions near CIs can lead to (near-)degeneracies at one level of theory that give rise to a mixing of the adiabatic electronic states that differs significantly from another level of theory, precluding the possibility of a simple and unique mapping. In those cases, the electronic states at one level of theory may need to be expanded in a basis of states at another in order to map the relevant absorption cross-sections to a different set of adiabats.
1 mapping between the MR-CIS states to DFT/MRCI states is fortuitous in this case, and not a general result. Specifically, the regions near CIs can lead to (near-)degeneracies at one level of theory that give rise to a mixing of the adiabatic electronic states that differs significantly from another level of theory, precluding the possibility of a simple and unique mapping. In those cases, the electronic states at one level of theory may need to be expanded in a basis of states at another in order to map the relevant absorption cross-sections to a different set of adiabats.
III. Results and discussion
A. Excited-state dynamics of 1,3-BD
We begin with an overview of the AIMS dynamics simulations of 1,3-BD. These simulations utilized the same level of electronic structure as in ref. 11 and the reader is directed to that work for a more detailed discussion of the excited-state dynamics. Here, we will only briefly summarize those results, while performing a number of new analyses to highlight those aspects of the dynamics that pertain directly to our discussion of the TRXAS.Fig. 1 shows the time-dependent adiabatic state populations, which are the same as those shown in Fig. 2(a) in ref. 11. Each trajectory basis function was initialized on the adiabatic surface corresponding to the optically bright ππ* state. At this level of ab initio theory (and sampling of the ground-state vibrational distribution), this is predominantly the S2 state, although ∼5% of trajectories were started on S1. As the figure shows, the total excited-state population decays with a time constant of roughly τ ≈ 210 fs.
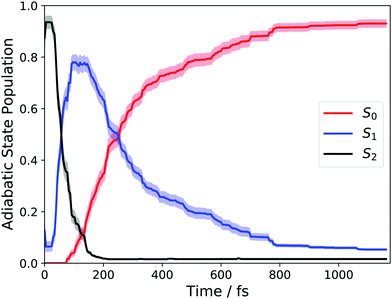 | ||
| Fig. 1 Adiabatic state populations calculated using AIMS following vertical excitation into S1 for 1,3-BD. | ||
Previous studies have interpreted the ultrafast relaxation to the ground electronic state primarily in terms of nuclear structural motifs. Specifically, ethylenic conical intersections involving large-amplitude torsion about a C–C bond (generally a terminal C–C bond), followed by pyramidalization (termed twisted-pyramidalized, Tw-Py), characteristic of the establishment of polarization across the C–C bond. Minor channels have previously been identified (and are observed here again) involving pyramidalization at a medial, rather than terminal carbon atom. The other primary motif, previously termed “transoid”,21 involves torsion about the medial C–C bond, heralding excited-state initiation of cis–trans isomerization. In contrast to the Tw-Py nuclear configurations, these structures do not display significant zwitterionic character, rather, multi-radical electronic structures are realized across the C–C–C–C backbone. The nuclear structures of the Tw-Py (both terminal and medial, the latter denoted mTw-Py) and transoid optimized MECIs are shown in Fig. 2. The cartesian coordinates of all reported nuclear structures are given as ESI† in Tables S3–S7.
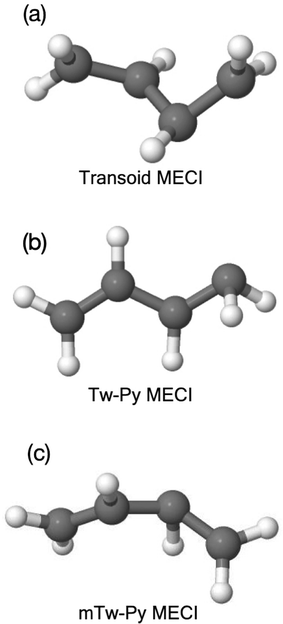 | ||
| Fig. 2 Minimum energy conical intersection (MECI) geometries, (a) transoid (b) Tw-Py and (c) medial Tw-Py (mTw-Py). | ||
The relative importance of these structures formed the basis of much analysis in previous studies,10,11,21,24 including the ability to affect the branching between the Tw-Py and transoid motifs using chemical substitution.24 However, as discussed in that previous work, characterizing nuclear structures as uniquely “Tw-Py” or “transoid” is often difficult, as the large-amplitude nuclear motion often involves displacements along both of these directions. Therefore, the present analysis will focus instead on the electronic structures associated with the CI-mediated electronic relaxation pathways.
Previous work has examined multiple techniques for evaluating atomic partial charges at nuclear configurations near conical intersections and employing the multi-reference electronic structures that characterize these regions of coordinate space.19 The iterative Hirshfeld approach was found to yield intuitive results that were also only weakly dependent on the level of theory employed.24 To quantify the degree of polarization between a terminal and medial carbon atom, these charges were computed for each sampled trajectory and at each time step, and the difference between these two sites were determined. The larger of the two charge differences (i.e. the largest magnitude difference of the quantity qmedial − qterminal, where the sign of the difference is maintained) will subsequently be denoted “Δq”. Structures evincing highly polarized characters gives rise to values of Δq ≈ 1, whereas those structures with negligible charge separation yield Δq ≈ 0. Fig. 3(a) plots these values for each trajectory basis function, at each time, weighted by the corresponding “population” (i.e. ‖CIj‖2 from eqn (2)). The bifurcation of the wave packet into ‘radicaloid’ and ‘polarized’ components is clearly shown by the Fig. 3(a), with (the predominant) branch centered about Δq = 0.3 corresponding to the former, and the branch centered about Δq = 1 corresponding to the latter. The spawn events are superimposed as circles on the charge plot in Fig. 3(a). Structures we denote as radicaloid or polarized spawns are colored red and blue, respectively. Interestingly, this plot also illustrates the presence of the third nuclear motif, involving pyramidalization at a medial (rather than terminal carbon atom). The corresponding negative charge at the medial carbon gives rise to a negative Δq and are identified with the black squares in Fig. 3(a).
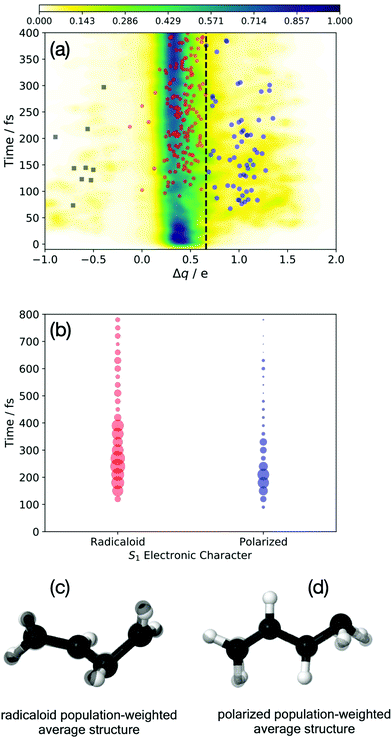 | ||
| Fig. 3 The evolution of the electronic character of the wave packet. The population-weighted polarization across the terminal C–C bond is shown in (a), Δq ≈ 0 (1) corresponds to radicaloid (polarized) structures. Spawn points are denoted by red (radicaloid) and blue circles (Tw-Py/polarized) and black squares (mTw-Py/polarized). The S1 → S0 spawn points are binned by electronic character in (b), where the circle radius is proportional to the population transferred. Population-weighted average nuclear structures (in black) are shown for the red (c) and blue points (d). These structures are superimposed on the transoid and Tw-Py MECI shown in Fig. 1. | ||
A further analysis of the S1 → S0 spawn geometries is shown in Fig. 3(b), in which the electronic characters at these points form the basis for distinguishing the relevant region of the CI seam. Specifically: the spawn events are “binned” according to the electronic character of the S1 state as well as in 25 fs time intervals, while the radius of the circles in Fig. 3(b) are proportional to the population spawned in each interval. We see that in the present dynamics simulation, electronic relaxation to the ground-state occurs primarily via radicaloid electronic structures, while the polarized structures are a minor channel. Analysis of the instantaneous energy gap between S1 and S0 at the spawn geometries is provided as ESI.† Fig. S4 (ESI†) shows that both the spawn events (irrespective of the popuation transferred), and the population transferred, shown in panels (a) and (c), respectively, is peaked about small energy gaps (ΔE < 0.2 eV for the radicaloid pathway). However, the corresponding analysis for the polarized pathway, shown in panels (b) and (d), evinces a much broader distribution in which the spawn events and population transfer are primarily associated with ΔE > 0.2. Indeed, the polarized CI structures show appreciable population transfer at spawn geometries where the S1/S0 energy gap is as large as 1 eV. This indicates that the that region of strong coupling that surrounds the polarized region of the CI seam is significantly extended in coordinate space.
While this analysis, which focuses on the electronic character of the wave packet, is highly illustrative (and relatively unambiguous), some consideration of the nuclear structures associated with the electronic decay is warranted. Fig. 3(c and d) plot the “average” spawn geometries for the radicaloid (c) and polarized (d) spawn geometries. These structures are the population-weighted average Cartesian spawn geometries for radicaloid and polarized “bins”, and which were determined only after the structures were placed into maximum coincidence.45 The small number of mTw-Py spawn events, as well as the more extended seam region sampled by these points, precluded this simple analysis for the spawn events denoted by the black squares in Fig. 3(a). The similarity of the structures in Fig. 3(c and d) (in all black) to the MECIs in Fig. 2(b and c), (which are superimposed with normal coloring), is striking. We see that the polarized structures correspond to the previously identified Tw-Py structures, while the radicaloid structures are characterized by large amplitude dihedral motion about the C–C–C–C backbone as observed for the transoid MECI.
B. Static X-ray absorption spectra
Before turning to the simulation of the time-resolved spectrum, we present first the static XAS at key nuclear configurations from the relevant electronic states. Fig. 4 shows the static XAS at the (a) Franck–Condon (FC) point, (b) Tw-Py S1–S0 MECI, and (c) transoid S1–S0 MECI.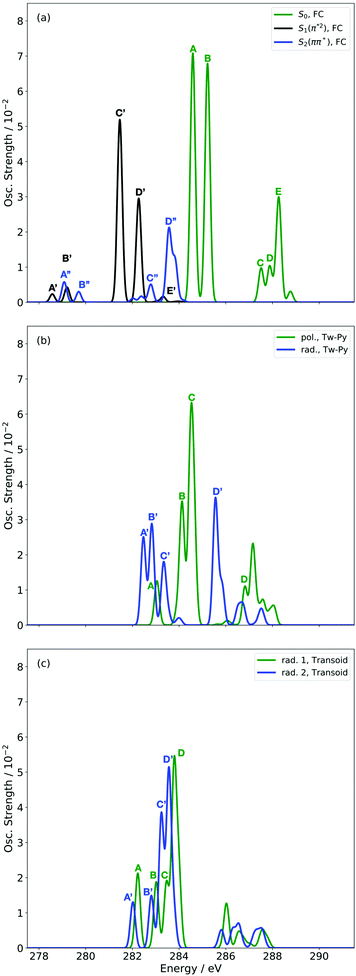 | ||
| Fig. 4 Simulated XAS at CVS-DFT/MRCI/aug-cc-pVDZ level of theory for S0, S1 and S2 states at the FC (a) and key MECI geometries (Tw-Py (b) and transoid (c)) of 1,3-BD. | ||
Fig. 4(a) presents three spectra, each computed at the ground-state minimum energy nuclear configuration: the XAS from the ground-state (S0), optically dark electronic state (denoted here as the S1 (π*2)), and bright ππ* (S2). For the S2 XAS at the S0 minimum, we observe four main peaks, and only one band near 283.5 eV about ∼1 eV to the red of the ground-state absorption, has appreciable intensity. The natural transition orbitals (NTOs), which diagonalize the transition density matrix and enable a hole-particle picture of electronic transitions, shown in Table 1, reveal that the first two peaks correspond (A′′ and B′′) to transitions into the unoccupied π-orbital, with a splitting of ∼0.4 eV between the pairs of 1s orbitals localised on the terminal and medial carbon atoms. The other two peaks (including the highest intensity peak D′′) are dominated by transitions into the Rydberg manifold. The S1 state has π*2 character and is optically dark. The two lowest intensity peaks (A′, B′) for this initial state are similar in character to the S2 NTOs for the same lowest energy transitions, but are the ++-combination of the 1s orbitals. The corresponding transitions of the +−-combination are found at higher energy and characterize peaks C′ and D′, with this pair forming the most intense transitions in the spectrum. The S0 XAS evinces five high intensity peaks, labeled A, B, C, D, and E. Peaks A and B, the two highest intensity transitions in the spectrum, correspond to excitation from different C1s orbitals into the LUMO π*, with the latter peak corresponding to a transition to a state that possesses mixed valence-Rydberg character. The remaining high intensity peaks involve transitions into orbitals of Rydberg character. In summary, the majority of the strongest intensity pre-edge transitions for all three states involve core-transitions into the π manifold; the empty π* for the ground-state, and into a hole in a π orbital for the electronically excited states. The highest intensity peak in the S2 XAS, however, corresponds to a transition between C1s and 3d Rydberg orbitals.
Anticipating their relevance in the assignment of the spectral features in the TRXAS, we also show simulated XAS for the S0 and S1 states at the Tw-Py and transoid S1–S0 MECIs in Fig. 4(b and c), respectively. Since the adiabatic labels S0 and S1 are arbitrary at a point of degeneracy, we instead denote the states as polarized (pol.) or radicaloid (rad.) in Fig. 4(b). Neither electronic state displays significant polarization at the transoid MECI, so the states are labeled “rad. 1” and “rad. 2”, where the former corresponds to the S1 electronic character upon approach to the MECI from the FC region. The NTOs for these spectra are presented as supplementary material. Fig. 4(b) shows a low intensity peak A, at 283.0 eV, significantly red-shifted from a higher intensity doublet centered (peaks B and C) around ∼284.5 eV. As Table S2 (ESI†) shows, peak A corresponds to a transition from the pyramidalized C 1s orbital to the hole in π-type orbital. The large partial negative charge localised around the pyramidalised C atom induces a large chemical shift in a manner analogous to that observed previously in a simulated TRXAS of ethylene.46 Peaks B and C arise from the transitions from the other C 1s orbitals on the backbone into π-type orbitals. The spectrum arising from the radicaloid electronic state displays little overlap with that of the polarized state, with peaks A–D again arising from transitions into π-type orbitals. Conversely, the spectra for the rad. 1 and rad. 2 states, computed at the transoid MECI and shown in Fig. 4(c), display a high degree of overlap. However, the main spectral features are red-shifted (∼283.5 eV vs. ∼284.5 eV) relative to the high intensity peaks B and C for the polarized electronic state at the Tw-Py, suggesting the two structural motifs are potentially resolvable via their distinct XAS.
C. Simulation of the time-resolved X-ray absorption spectrum
In the absence of experimental results, we have chosen to present the isotropic spectrum, the polarization dependent spectra are given as ESI† in Fig. S2 and S3. The perpendicular pump–probe relative polarization configuration is predicted to yield signal an order of magnitude higher than the parallel polarization and is nearly identical to the isotropic simulation. Fig. 5 shows the full time-resolved spectrum, which employs a global energy shift, for all initial states, of 3.5 eV. This value was chosen so as to align the main peaks in ground-state XAS, see Fig. S1 (ESI†).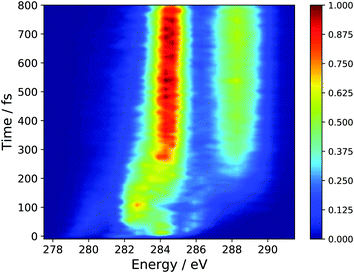 | ||
| Fig. 5 Simulated TRXAS spectrum employing the results of AIMS dynamics simulations and CVS-DFT/MRCI X-ray absorption cross-sections. An isotropic axis distribution was assumed. | ||
The spectral features present at time, t = 0, correspond to the peaks present in the static S2 XAS at the S0 minimum (Peaks A′′, B′′, C′′, D′′). In particular, the high intensity peak at ∼284.0 corresponds to the high intensity peak labeled D′′ in Fig. 4(a) for the S2 state. This transition is assigned to an excitation of the 1s orbitals on the terminal C-atoms into a 3d Rydberg orbital. This spectral feature sweeps to higher energy with a period of ∼50 fs and tracks the electronic relaxation from the S2 to the S1 state. Support for this assignment is evinced by the decomposition of the TRXAS into contributions from the adiabatic states shown in Fig. 6. The spectral features in the static S1 XAS shown in Fig. 4 map onto the shorter time features in Fig. 6(b), assigned to S1 adiabatic state contribution. This change in adiabatic state would appear to also correspond to a change of the wave packet to the “dark” π*2 electronic character. At short times, prior to large amplitude motion about the C–C–C–C backbone, Fig. 4(a) shows that the XAS transitions from the π*2 state are red-shifted to those of the initially prepared ππ* state by 1.5–2 eV (i.e. peaks C′ and D′). Furthermore, at longer times, the analysis of the dynamics results show that the transoid structures are the primary relaxation nuclear motif. Fig. 4(c) shows that the radicaloid electronic structures lead to XAS transitions at energies less than 283.5 eV, while the high intensity absorption lines in the XAS for polarized electronic structures occur at energies greater than 283.5 eV (i.e. peaks B and C in Fig. 4(b)).
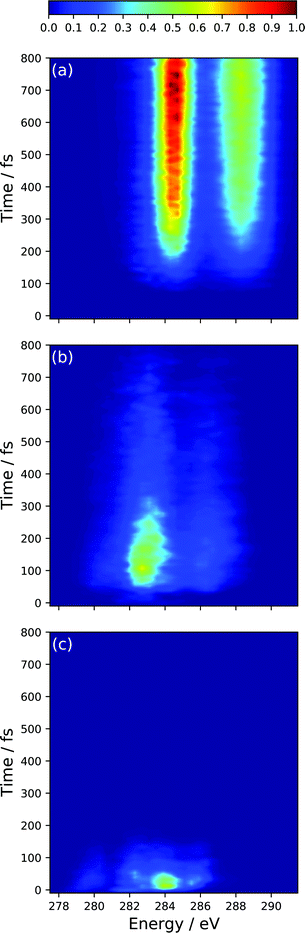 | ||
| Fig. 6 Simulated TRXAS at CVS-DFT/MRCI/aug-cc-pVDZ level of theory, decomposed into contributions from the (a) S0, (b) S1 and (c) S2 adiabatic states. | ||
The spectral features that characterize the TRXAS at longer times (>300 fs) correspond to the return of the wave packet to the vibrationally hot ground-state, as shown in Fig. 6(c). These spectral features, though dramatically broadened, align well with peaks A and B for the band around 284.5 eV and peaks C–E for the band above 287.5 eV.
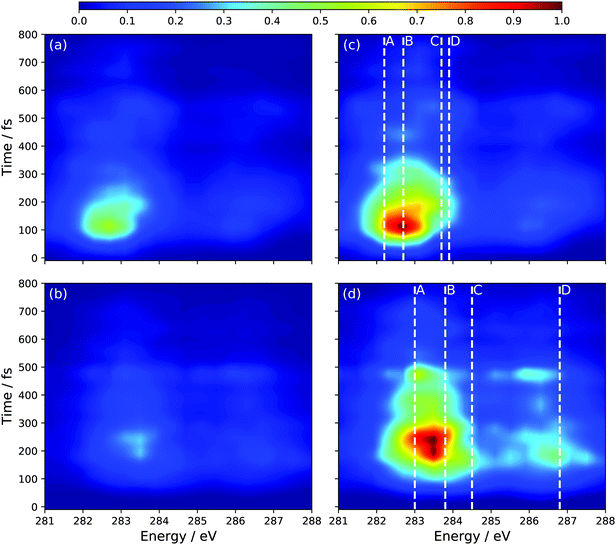
The remaining question is to what extent the S1 component to the TRXAS spectrum can be decomposed into contributions from the two electronic configurations associated with the polarized and radicaloid decay pathways. Using the bifurcation of the wave packet evinced by Fig. 3, we decompose the S1 adiabatic state contribution to the TRXAS (Fig. 6(b)) into contributions from those trajectory basis functions with Δq < 0.55 (radicaloid) and Δq > 0.55 (polarized). Fig. 7 shows the decomposed spectra. Panels (a) and (b) show the two contributions where the normalization of the intensity is chosen to be consistent with Fig. 6 so that the sum of the contributions yield that spectrum. Panels (c) and (d) re-normalize the intensity of each individual contribution to aid in the visualization of the predicted spectral signal from each electronic character.
Consistent with our analysis of the spawned geometries, as well as the bifurcation of the wave packet into components with radicaloid and polarized characters, a comparison of the relative intensities in Fig. 7(a and b) shows that the spectrum is dominated by the component of the wave packet with radicaloid character. Indeed, the (broad) bands around 283.5 eV and 286.5 eV in Fig. 7(a and c) correspond closely to the peaks in the static XAS in Fig. 4(c) computed at the transoid MECI. The excitation energies of the main peaks in the static XAS in Fig. 4(c) are shown as dashed lines (where the line labels correspond to the peak labels in Fig. 4) to facilitate the comparison.
While the signal assigned to polarized structures overlaps strongly with the radicaloid signal, the dominant main bands in the component spectra in 7(b) and (d) (284.5 eV and 287.5 eV) are both blue-shifted by ∼1 eV relative to the radicaloid peaks. Furthermore, these bands corresponds closely to the peaks in the static spectrum for the polarized electronic state at the Tw-Py structure in Fig. 4(b). The dominant structural feature in the polarized-component TRXAS lies between peaks A and B in the static spectrum, due to significant spectral broadening arising from the significant vibrational energy on the S1 surface. Peak D in the static spectrum, though, is clearly discernable in Fig. 7(d). That said, the main issue in resolving these pathways is that the polarized component of the TRXAS is of significantly lower intensity since the transoid CI relaxation channel is dominant in the present dynamics simulation. However, previous work11,19 has shown that the branching between these paths can be influenced via chemical substitution at specific sites on the C-backbone. This can be achieved either by methyl-group or functional group substitution. The former, when employed at the terminal C-atoms,24 has been shown to further reduce the prevalence of the polarized structures. Conversely, substitution of the π-donor nitrile group has been predicted, via simulation,11 to dramatically lower the energy of polarized structures when placed at specific points on the C–C–C–C backbone. Since the dynamics are largely gradient directed, changing of the ‘steepest descent’ direction can dramatically influence the branching between multiple energetically-accessible decay pathways.
IV. Conclusion
On the basis of high-level nuclear dynamics simulations and quantum chemical computations, we here demonstrate the ability of time-resolved X-ray absorption spectroscopy to resolve the electronic structures corresponding to the different conical intersections that are observed in the excited-state dynamics of trans-1,3-BD. When a wave packet is initialized on the lowest-energy bright electronic state in the FC region, the resulting non-adiabatic dynamics ultimately result in a return to the ground-state via two excited-state electronic structures: a tetraradical species associated with nuclear structures along the trans–cis isomerization coordinate, and a highly polarized transient structure analogous to the Tw-Py MECI of ethylene. Employing an ab initio multiple spawning dynamics simulation, and the component trajectory basis functions, we simulated the TRXAS using the recently developed CVS-DFT/MRCI method, which is capable of describing the electronic structures that result from core-excitation of highly multi-reference initial valence states. The TRXAS was then decomposed into contributions arising from not only each adiabatic state, but also from the radicaloid and polarized electronic components of the total excited-state wave packet. We found that while the initially prepared S2 is unambiguously of bright ππ* character, the wave packet on S1 was, unsurprisingly a mixture of nuclear and electronic structures. Decomposition of the TRXAS into contributions in terms of the radicaloid and polarized structures revealed that the key spectral features could be resolved and that the present simulation strongly favors the transoid structures for electronic relaxation to the ground-state.We close by noting that although the dynamics of 1,3-BD (simulated using the particular potential energy surfaces of the present study) strongly favors one of the two pathways, this result can be influenced via selective chemical substitution. Previous work has shown that selective stabilization (de-stabilization) of the polarized electronic structures associated with the Tw-Py can inhibit (promote) the cis–trans isomerization pathway. Tuning this branching between the different dynamical pathways, and simulating the associated time-resolved core spectroscopies to assess their utility in discerning the different electronic and nuclear structures, will serve as the basis for future work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank A. Stolow for helpful comments during the preparation of this manuscript. MSS acknowledges the financial support of Natural Sciences and Engineering Research Council of Canada (NSERC) through the Discovery Grant program.References
- V. Blanchet, M. Z. Zgierski, T. Seideman and A. Stolow, Nature, 1999, 401, 52–54 CrossRef CAS.
- A. Stolow, Annu. Rev. Phys. Chem., 2003, 54, 89–119 CrossRef CAS PubMed.
- A. Stolow, A. E. Bragg and D. M. Neumark, Chem. Rev., 2004, 104, 1719–1758 CrossRef CAS PubMed.
- A. Hofmann and R. de Vivie-Riedle, Chem. Phys. Lett., 2001, 346, 299–304 CrossRef CAS.
- M. S. Schuurman and A. Stolow, Annu. Rev. Phys. Chem., 2018, 69, 427–450 CrossRef CAS PubMed.
- J. Voll, T. Kerscher, D. Geppert and R. de Vivie-Riedle, J. Photochem. Photobiol., A, 2007, 190, 352–358 CrossRef CAS.
- R. Geneaux, H. J. B. Marroux, A. Guggenmos, D. M. Neumark and S. R. Leone, Philos. Trans. R. Soc. A, 2019, 377, 20170463 CrossRef CAS PubMed.
- A. E. Boguslavskiy, O. Schalk, N. Gador, W. J. Glover, T. Mori, T. Schultz, M. S. Schuurman, T. J. Martínez and A. Stolow, J. Chem. Phys., 2018, 148, 164302 CrossRef PubMed.
- H. R. Hudock, B. G. Levine, A. L. Thompson, H. Satzger, D. Townsend, N. Gador, S. Ullrich, A. Stolow and T. J. Martínez, J. Phys. Chem. A, 2007, 111, 8500–8508 CrossRef CAS PubMed.
- W. J. Glover, T. Mori, M. S. Schuurman, A. E. Boguslavskiy, O. Schalk, A. Stolow and T. J. Martínez, J. Chem. Phys., 2018, 148, 164303 CrossRef PubMed.
- R. J. MacDonell and M. S. Schuurman, J. Phys. Chem. A, 2019, 123, 4693–4701 CrossRef CAS PubMed.
- S. Tsuru, M. L. Vidal, M. Pápai, A. I. Krylov, K. B. Møller and S. Coriani, Struct. Dyn., 2021, 8, 024101 CrossRef CAS PubMed.
- N. V. Golubev, J. Vaníček and A. I. Kuleff, Phys. Rev. Lett., 2021, 127, 123001 CrossRef CAS PubMed.
- T. Northey, J. Norell, A. E. A. Fouda, N. A. Besley, M. Odelius and T. J. Penfold, Phys. Chem. Chem. Phys., 2020, 22, 2667–2676 RSC.
- S. P. Neville, M. Chergui, A. Stolow and M. S. Schuurman, Phys. Rev. Lett., 2018, 120, 243001 CrossRef PubMed.
- K. S. Zinchenko, F. Ardana-Lamas, I. Seidu, S. P. Neville, J. van der Veen, V. U. Lanfaloni, M. S. Schuurman and H. J. Wörner, Science, 2021, 371, 489–494 CrossRef CAS PubMed.
- G. Wu, A. E. Boguslavskiy, O. Schalk, M. S. Schuurman and A. Stolow, J. Chem. Phys., 2011, 135, 164309 CrossRef PubMed.
- R. J. MacDonell, O. Schalk, T. Geng, R. D. Thomas, R. Feifel, T. Hansson and M. S. Schuurman, J. Chem. Phys., 2016, 145, 114306 CrossRef.
- R. J. MacDonell and M. S. Schuurman, Chem. Phys., 2018, 515, 360–368 CrossRef CAS.
- K. R. Herperger, A. Röder, R. J. MacDonell, A. E. Boguslavskiy, A. B. Skov, A. Stolow and M. S. Schuurman, J. Chem. Phys., 2020, 153, 244307 CrossRef CAS PubMed.
- B. G. Levine and T. J. Martínez, J. Phys. Chem. A, 2009, 113, 12815–12824 CrossRef CAS PubMed.
- M. Ben-Nun and T. J. Martínez, Chem. Phys. Lett., 1998, 298, 57–65 CrossRef CAS.
- T. Mori, W. J. Glover, M. S. Schuurman and T. J. Martínez, J. Phys. Chem. A, 2012, 116, 2808–2818 CrossRef CAS PubMed.
- R. J. MacDonell, M. E. Corrales, A. E. Boguslavskiy, L. Bañares, A. Stolow and M. S. Schuurman, J. Chem. Phys., 2020, 152, 084308 CrossRef CAS PubMed.
- M. Ben-Nun, J. Quenneville and T. J. Martínez, J. Phys. Chem. A, 2000, 104, 5161–5175 CrossRef CAS.
- T. J. Martínez, Acc. Chem. Res., 2006, 39, 119–126 CrossRef PubMed.
- B. Mignolet and B. F. E. Curchod, J. Chem. Phys., 2018, 148, 134110 CrossRef PubMed.
- S. Yang, J. D. Coe, B. Kaduk and T. J. Martínez, J. Chem. Phys., 2009, 130, 134113 CrossRef PubMed.
- S. Grimme, Chem. Phys. Lett., 1996, 259, 128–137 CrossRef CAS.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655 CrossRef CAS.
- A. Heil, K. Gollnisch, M. Kleinschmidt and C. M. Marian, Mol. Phys., 2016, 114, 407–422 CAS.
- A. Heil and C. M. Marian, J. Chem. Phys., 2017, 147, 194104 CrossRef PubMed.
- I. Lyskov, M. Kleinschmidt and C. M. Marian, J. Chem. Phys., 2016, 144, 034104 CrossRef PubMed.
- M. Kleinschmidt, J. Tatchen and C. M. Marian, J. Comput. Chem., 2002, 23, 824–833 CrossRef CAS PubMed.
- C. M. Marian, A. Heil and M. Kleinschmidt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1394 Search PubMed.
- I. Seidu, S. P. Neville, M. Kleinschmidt, A. Heil, C. M. Marian and M. S. Schuurman, J. Chem. Phys., 2019, 151, 144104 CrossRef PubMed.
- H. Lischka, T. Müller, P. G. Szalay, I. Shavitt, R. M. Pitzer and R. Shepard, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 191–199 CAS.
- H. Lischka, R. Shepard, I. Shavitt, R. M. Pitzer, M. Dallos, T. Müller, P. G. Szalay, F. B. Brown, R. Ahlrichs, H. J. Böhm, A. Chang, D. C. Comeau, R. Gdanitz, H. Dachsel, C. Ehrhardt, M. Ernzerhof, P. Höchtl, S. Irle, G. Kedziora, T. Kovar, V. Parasuk, M. J. M. Pepper, P. Scharf, H. Schiffer, M. Schindler, M. Schüler, M. Seth, E. A. Stahlberg, J.-G. Zhao, S. Yabushita, Z. Zhang, M. Barbatti, S. Matsika, M. S. Schuurman, D. R. Yarkony, S. R. Brozell, E. V. Beck, J.-P. Blaudeau, M. Ruckenbauer, B. Sellner, F. Plasser and J. J. Szymczak, COLUMBUS, an ab initio electronic structure program, release 7.0, 2012 Search PubMed.
- J. D. Coe, B. G. Levine and T. J. Martínez, J. Phys. Chem. A, 2007, 111, 11302–11310 CrossRef CAS PubMed.
- TURBOMOLE V6.1 2009, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, TURBOMOLE GmbH, 2007, http://www.turbomole.com Search PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- W. Kabsch, Acta Crystallogr., 1976, 32, 922–923 CrossRef.
- S. P. Neville, M. Chergui, A. Stolow and M. S. Schuurman, Phys. Rev. Lett., 2018, 120, 243001 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp05085k |
| ‡ Present address: School of Chemistry, University of Sydney, NSW 2006, Australia. |
| This journal is © the Owner Societies 2022 |