NMR methods for the analysis of mixtures

Abstract

NMR spectroscopy is a powerful approach for the analysis of mixtures. Its usefulness arises in large part from the vast landscape of methods, and corresponding pulse sequences, that have been and are being designed to tackle the specific properties of mixtures of small molecules. This feature article describes a selection of methods that aim to address the complexity, the low concentrations, and the changing nature that mixtures can display. These notably include pure-shift and diffusion NMR methods, hyperpolarisation methods, and fast 2D NMR methods such as ultrafast 2D NMR and non-uniform sampling. Examples or applications are also described, in fields such as reaction monitoring and metabolomics, to illustrate the relevance and limitations of different methods.

---

Jean-Nicolas Dumez

Jean-Nicolas Dumez is a CNRS researcher (Centre National de la Recherche Scientifique) currently working at Nantes Université. He received his PhD in 2011 from Ecole Normale Supérieure de Lyon, and carried out post-doctoral research at the Weizmann Institute of Science and Southampton University, before moving in 2014 to Université Paris-Saclay as a CNRS researcher, then to Nantes in 2018. His research interests include the development of methods for the analysis of mixtures, NMR pulse sequences, and spin dynamics.

---

1. Introduction

Mixtures of molecules in solution are ubiquitous in chemical science. Samples of biological, environmental and agricultural origins are frequently found or handled in the form of mixtures. In chemical synthesis, samples usually involve a mixture of reactants, products, and side or by products. Analytical sciences strive to provide a characterisation of mixtures that is as complete as possible. Ideally, the identity and concentration of all the components in a mixture should be accessed. In the case of samples that are out of equilibrium, this information is sought after as a function of time.

Nuclear magnetic resonance (NMR) spectroscopy is a powerful approach for the analysis of mixtures.^1,2 The most common NMR experiment has several essential features that are highly favourable for mixture analysis. It relies on a “pulse-acquire” pulse sequence, carried out at thermal spin equilibrium, to yield 1D spectra, most commonly for ¹H spins. This experiment is simple to implement, it can be fast, and it already yields a wealth of structural information, which is useful to identify components. It is also non-invasive and non-destructive, meaning that the sample can be retrieved after analysis for storage or other analyses, and also, in the case of monitoring applications, that experiments can be repeated multiple times on the same sample as a function of time. 1D ¹H NMR also provides straightforward access to quantitative information on concentrations.

The power of NMR spectroscopy also results from the vast space of possible experiments that can be carried out, with a given instrument and a given sample, through the use of different pulse sequences. This makes it possible, through the controlled manipulations of nuclear spins, to access chemical information that would otherwise remain invisible or inaccessible. The process of developing NMR pulse sequences has sometimes been referred to as “spin choreography” or “spin alchemy”.³

In the case of mixture analysis, classic 1D experiments carried out at thermal spin equilibrium may turn out to be insufficient for a variety of reasons. One of them is the complexity of the sample, and of the resulting spectroscopic data. The superimposed information available in 1D spectra may be difficult to disentangle. As a result, signals that are detected cannot always be analysed. Another possible reason is the concentration of the components, in light of the modest sensitivity of NMR spectroscopy. NMR is sometimes referred to as a “universal” detector, since there are virtually no criteria other than concentration for a small molecule to be detectable by NMR. However, the limits of detection for NMR experiments are very unfavourable compared to other analytical methods, and this, together with issues of dynamic range, sets a limit on the range of samples that may be analysed. A third limitation concerns the analysis of samples that change over time. While classic 1D experiments are relatively fast, the methods available to address the complexity of mixtures usually require more time, thus limiting the throughput of the analysis and making them incompatible with real-time analyses on short time scales. These three types of obstacles are met in many uses of NMR spectroscopy, such as the high-throughput analysis of mixtures for metabolomics applications, or the real-time monitoring of reactions in chemical synthesis. This provides a motivation for “spin alchemists” to design NMR methods that address the challenges of mixture analysis, and make them available to the broad chemical science community.

This feature article describes a selection of NMR methods that are designed and used for the analysis of mixtures. It is organised in three main sections, corresponding to methods to address the complexity, concentrations, and changing nature of mixtures, as illustrated in Fig. 1. An additional section briefly describes opportunities to access broader operating conditions through the use of flow NMR. For each of the methods, the type of information that can be accessed is highlighted. The underlying NMR concepts are also sketched, with minimal technical details. In practice, NMR solutions are rarely universal, and they usually come with a trade-off such as, for example, resolution or speed at the expense of sensitivity. This is also why there is a large variety of them. This article also aims at helping the interested reader to navigate the landscape of NMR methods for the analysis of mixtures. Note that this necessarily limited overview only covers homogeneous solutions, and focuses on small molecules.

Fig. 1 The challenges of mixture analysis and NMR methods to address them.

2. Complexity

The most commonly used NMR experiment for mixture analysis is the 1D ¹H pulse-acquire experiment. Protons have a spin I = 1/2, over 99% natural abundance, and the largest gyromagnetic ratio among stable nuclei, resulting in favourable sensitivity from an NMR point of view. However, the chemical-shift dispersion in ¹H spectra is limited to 10–15 ppm. In addition, the large abundance of ¹H nuclei result in the ubiquitous presence of ¹H–¹H couplings, that yield diverse multiplet structures and broaden NMR signals. Overall, the spectra of all but the simplest mixtures are usually complex.

The complexity of the NMR spectra for mixtures has several origins. First, similar compounds have similar spectra and as a result the spectrum of a mixture may be complex even with a moderate number of detectable compounds. Second, the number of compounds can be very large. This is for example the case in biofluids or extracts of biological samples. In the spectra of mixtures, signal overlap prevents the reliable identification and accurate quantification of signals. The assignment of each signal in the spectrum to a specific compound, even resolved one, is also not trivial. Note that samples such as natural organic matter, which comprise tens of thousands of compounds that are mostly unknown, and call for the use dedicated methods, are outside the scope of the review.⁴

An array of methods is available to address overlap and assignment issues in NMR spectra.^5–10 These methods may aim at simplification, meaning that the number of peaks in the spectrum is reduced, separation, meaning that the spectra of different components in the mixture are separated, or dispersion/correlation, meaning that the signals are distributed in additional dimensions, as well as combinations of these three features. Classic 2D experiments such as COSY, TOCSY and HSQC are dispersion/correlation methods. By spreading signals along two dimensions rather than one, they make it possible to resolve signals that overlap in 1D ¹H spectra.¹⁰ In addition, since they correlate two signals or more from the same components, they can help to assign these signals to a known compounds with more confidence. In this section we describe other methods that were specifically developed to address the complexity of mixtures, and can complement or replace the use of 2D NMR.

2.1. Pure-shift NMR

Signal overlap in 1D ¹H NMR spectra is due in part to the effect of ¹H–¹H J couplings, because of which signals appear as multiplets with a total width that is given by the number and sizes of the J couplings, rather than the natural linewidth of a peak. Broadband homonuclear decoupling, which refers to the complete suppression of the effects of J couplings in 1D ¹H spectra, has been a long-standing goal of NMR spectroscopists. One of the earliest methods to achieve broadband decoupling consists of taking the 45° projection of a J-resolved 2D spectrum.¹¹ While this approach has found some applications in metabolomics,¹² it requires magnitude processing of the data, resulting in unfavourable lineshapes that defeat in part the purpose of homonuclear decoupling.

More recently, several strategies have been described to select a subset of nuclear spins, the active spins, and decouple them from their coupling partners, the passive spins. Two of these methods were actually first described several decades ago. In the BIRD approach, the active spins are all the protons that are bound to a carbon-13, while the passive spins are all the other protons.¹³ In the Zangger–Sterk (ZS) method,¹⁴ the 1D ¹H spectrum is mapped onto the spatial length of the tube, such that for each signal, there exists a thin slice in the sample in which only the spins contributing to the signal are active. These methods were revived, updated and expanded in the 2010s.^15–18

The most recent method for broadband homonuclear decoupling is the pure shift yielded by chirp excitation (PSYCHE) method.¹⁹ With PSYCHE, the separation between active and passive spins is based on the application of two consecutive pulses with a small tip angle β, as in the anti-z COSY pulse sequence.²⁰ The active spins are the statistical fraction of the spins that are refocused by the pair of pulses. Their contribution of decoupled spins to the signal (for small angles) scales as β², while that of undecoupled spins scales as β⁴.

Homonuclear broadband decoupling methods can give excellent resolution for 1D ¹H spectra. For this reason, they can help to distinguish peaks that overlap in an undecoupled 1D ¹H spectrum.¹⁷ The BIRD, ZS and PSYCHE broadband decoupling methods all come with a sensitivity penalty. For BIRD, since only ¹³C-bound protons contribute to the signal, the penalty is almost 100-fold. For the ZS methods, there exists a compromise between sensitivity losses and the minimum frequency difference between decoupled spins, and it results in a sensitivity loss of 10 to 50-fold. For PSYCHE, there is a trade-off between sensitivity and the size of decoupling artefacts, which is controlled through the flip angle of the frequency-swept pulses. A sensitivity loss of about a factor of 5 to 10-fold is typically reported.

Homonuclear decoupling is also possible for 2D experiments. BIRD-based decoupling can notably be incorporated into 2D HSQC experiments, with no sensitivity penalty for experiments at natural ¹³C abundance.¹⁸ This was exploited for the quantitative analysis of biological mixtures.^21,22

Another feature of these pure-shift methods is that the data are most often not acquired in a single scan, but rather a series of chunks that are concatenated before Fourier transformation. This is because J refocusing is only exact at a single time point, and approximately valid over a surrounding chunk. The consequences are two-fold. First, the sensitivity per square root of measurement time is reduced if only one chunk is acquired with each scan. Methods to alleviate this limitation have been described.^15,23,24 Second, chunking artefacts appear in the decoupled spectrum, mostly because of J evolution during the chunk time. These artefacts reduce the range of concentrations that can be simultaneously characterised with a pure-shift spectrum. Moutzouri et al. have reported a multi-scan implementation of a pure-shift pulse sequence in which chunking artefacts are suppressed by cycling their phase across multiple scans.²⁵ This makes it possible to restore the dynamic range for mixture analysis. This is illustrated in Fig. 2, where the use of pure-shift NMR with sideband suppression makes it possible to detect unambiguously a minor component in a mixture, with a concentration that is 3% of that of the major component. The relevance of 1D pure-shift NMR methods for the analysis of biological complex mixtures is also being evaluated.^26,27 it was notably found that the reduced overlap of PSYCHE spectra helped to identify metabolites, such as glutamine, that could not be reliably identified from conventional 1D ¹H spectra.²⁷

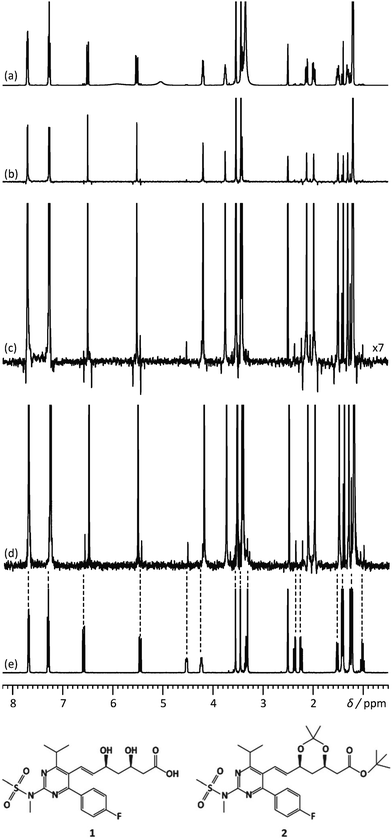Fig. 2 500 MHz (a) 1D ¹H spectrum, (b) ¹H pure shift spectrum recorded using the unmodified Zangger–Sterk pulse sequence, (c) vertical expansion of the spectrum (b and d) ¹H pure shift spectrum acquired with the pulse sequence modified to remove sidebands, for a mixture containing rosuvastatin (1) and 2.8% of its precursor BEM (2). (e) 1D ¹H spectrum of BEM. Spectra c and d were acquired in approximately 9 h with an sw1 of 39.0625 Hz and 16 chunks using an RSNOB spatially selective spin inversion element with a peak RF amplitude of 47 Hz. Reproduced from ref. 25 with permission from the Royal Society of Chemistry.

An efficient alternative to broadband homonuclear decoupling is the use of band-selective decoupling.^5,6 In this approach, the active spins are those within a selected frequency region of the spectrum, and the passive spins are all those outside that region. The main advantage of band-selective decoupling methods is that they have virtually no sensitivity penalty, in contrast to other pure-shift methods. Also, they are more straightforward to implement in a single scan. When the properties of the mixture of interest allow it, they are a method of choice to resolve the signals of structurally similar compounds. Band-selective pure-shift NMR was for example used, in 2D spectra, to distinguish diastereoisomers with near-identical ¹H and ¹³C spectra,²⁸ or enantiomers in chiral solvating agents.²⁹

The pure-shift NMR methodology has recently been extended to suppress also the effect of heteronuclear couplings. This is particularly important in the case of compounds that contain fluorine atoms, such as many pharmaceutical compounds.³⁰

2.2. Diffusion-ordered spectroscopy

Diffusion-ordered NMR spectroscopy, or DOSY, aims to separate the spectra of components in a mixture, without physical separation of the components themselves.⁷ In DOSY experiments, the separation is made according to the translational diffusion coefficients of the molecules. A pair of pulsed-field gradients (PFGs) separated by a delay is used to induce a diffusion-dependent attenuation of the peaks in the spectrum,^31,32 and the resulting diffusion weighted signal is analysed to extract both the component spectra and the diffusion coefficients. The concept of “size-resolved NMR spectrometry” was introduced as early as 1981 by Stilbs.³³ It was popularised by Johnson and co-workers who introduced the DOSY representation of the data, which consists of a 2D graphical display of the estimated diffusion coefficients for selected peaks or region in the spectrum.³⁴ Conceptually, the 1D spectrum of each component can be found by simply drawing a line at the corresponding diffusion coefficient in the 2D DOSY display.

PFG NMR and DOSY have found numerous applications to the analysis of mixtures.³⁵ Note that while the term DOSY originally refers to a specific data processing and display method, it can refer nowadays also to the experiment itself. One class of applications consists of studying interactions in solution, for aggregates and oligomers formed by, e.g., organometallic species.³⁶ DOSY is also largely used in supramolecular chemistry, to characterise the size and shape of supramolecular objects.³⁷ Virtual separation by DOSY NMR has been assessed for different classes of samples, such as dietary supplements and pharmaceuticals, as a tool to detect counterfeit products.³⁸

The virtual separation of NMR spectra with standard DOSY methods, however, is limited by the difficulty to resolve overlapping signals. The most common method for data analysis consists of a non-linear least square fit of the data with one or several exponential functions. When mono-exponential fitting is used, the resulting peak in the DOSY display appears at an intermediate value, that cannot be immediately assigned to one component. Multi-exponential fitting can resolve overlapping peaks,³⁹ but only with excellent SNR and a sufficient difference in diffusion coefficients between the two compounds. As a result, standard DOSY methods are useful for assignment and identification, but they do not increase signal dispersion.

A possible approach to improve the separation of overlapping spectra is to use multivariate processing methods. They consist of algorithmically solving the problem:

x = CP^T, (1)

where X is the data set, C is a matrix of component decays, and P is a matrix of component spectra. One of the first multivariate analysis method for PFG NMR data was CORE NMR (component resolved NMR), described by Stilbs.⁴⁰ It was significantly accelerated by Nilsson et al., who noted that one of the optimisation steps in CORE can be cast as a linear rather than non-linear problem, resulting in the SCORE (speedy CORE) algorithm.⁴¹ The fastest algorithm for multivariate processing of PFG NMR data is DECRA (direct exponential curve resolution algorithm), described by Antalek.^42,43 It relies on the existence of an exact solution to eqn (1), when the diffusion data is acquired with quadratic spacing of the PFG amplitude. In contrast to (S)CORE and DECRA, blind-source separation methods make no assumption of the form of the diffusion decay. They were also successfully used to process PFG NMR data.⁴⁴ With multivariate processing method, regions of the spectrum where peaks are well resolved help to “drive” the separation of peaks that overlap in other regions. Most method take as an input the number of components in the spectrum, which may also be adjusted by trial and error. The separation for similar spectra/compounds can be further enhanced by concurrent the use of relaxation properties.⁴⁵

Another approach to address overlap issues it to use broadband homonuclear decoupling methods, so that fewer peaks, if any, overlap in the 1D ¹H spectrum. Virtual separation with DOSY can then work very well. This was illustrated for a variety of pure-shift methods.^46,47

A third possibility to improve spectral separation is to use the DOSY method to separate the 2D spectra of components in a mixture, with the so-called 3D DOSY family of methods (2 spectral dimensions and 1 diffusion dimension).^34,48–50 Since signal dispersion is improved in 2D spectra, 3D DOSY can help to address the overlap issues of 2D DOSY. In addition, with 3D DOSY structural information is obtained for all the separated components. This is illustrated in Fig. 3, with the separation of HSQC spectra of five B vitamins. Importantly, in this case the ¹H spectra could not be separated by regular 2D DOSY because of peak overlap.⁵¹ Conveniently, a large variety of methods to analyse PFG NMR data have been implemented in the open-source GNAT package.⁵²

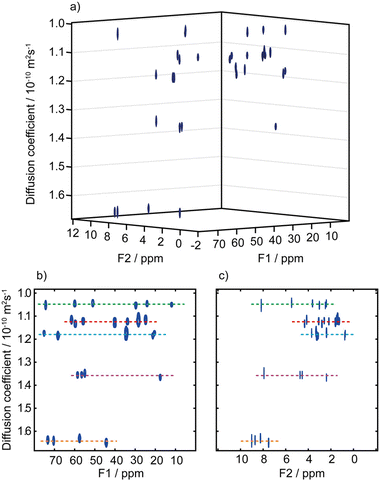Fig. 3 (a) Pseudo-3D DOSY plot of the Oneshot–HSQC spectrum of mixture of five B vitamins (biotin, B7; pyridoxine hydrochloride, B6; pantothenic acid calcium complex, B5; niacin, B3; and thiamine hydrochloride, B1) in DMSO-d₆. (b) 2D projection along F₂, and (c) 2D projection along F₁. F₁ and F₂ are the ¹³C and ¹H dimensions, respectively. Dashed lines are used to aid visualization and indicate the peaks of biotin, B7 (red); pyridoxine hydrochloride, B6 (purple); pantothenic acid, B5 (blue); niacin, B3 (orange); and thiamine hydrochloride, B1 (green). The spectra from the five components are easily distinguished, with diffusion coefficients of (1.05, 1.12, 1.18, 1.36, and 1.64) × 10⁻¹⁰ m² s⁻¹ for vitamins B1, B7, B5, B6, and B3, respectively. Data acquisition took 45 h, but a much shorter acquisition would have sufficed. Reproduced with permission from ref. 51, © 2018 American Chemical Society.

The separation power of diffusion NMR can be increased by adding macromolecules that have different exchange or binding properties with the different analytes. Using such “matrix-assisted DOSY” approach, spectra that could not be separated without the matrix can become well resolved in the diffusion dimension.^53,54 When solid matrices are used for that purpose, high-resolution magic-angle spinning (HRMAS) is employed to remove magnetic susceptibility broadening. This approach was coined “NMR chromatography”.^55,56 Interestingly, when small molecules are bound to nanoparticles, they can be distinguished from unbound small molecules with a diffusion filter. This forms the basis of a chemosensing strategy that was developed by Rastrelli and co-workers, and applied to the detection and, together with NMR chromatography, the identification of small organic molecules.^57–59

2.3. Maximum-quantum NMR

Maximum quantum (MaxQ) NMR refers to the use of a series of 2D multiple-quantum/single-quantum correlation spectra to analyse complex mixtures of small molecules. MaxQ NMR was described by Reddy and Caldarelli in 2010.^8,60 It is based on the observations that (i) a spin system comprising N spins can form only one N-quantum coherence (N is named the maxQ order) and (ii) in an NQ/1Q 2D correlation experiments, that coherence will result in a series of peaks that are uncoupled in the indirect dimension, and that correspond to the 1D spectrum for the spin system in the direct dimension. NQ/1Q 2D correlation experiments can thus provide increased dispersion and spectral separation.

In the MaxQ approach, a series of nQ/SQ correlation spectra is acquired, with n ranging from 1 to 5. The spectra are then analysed in decreasing order of the coherence order, with 1D spectra of molecular fragments obtained by taking traces in the 2D spectra, at positions that corresponds to singlets in the indirect dimension. The knowledge of the chemical shifts for the compounds identified on the pQ/SQ spectrum helps to identify the corresponding signals in the (p − 1)Q/SQ spectrum, and thus focus on the compounds for which (p − 1) is the maxQ value. With this method, Reddy and Caldarelli were able to separate the spectra of 16 polycyclic aromatic compounds identified as primary pollutants.⁶¹ Maximum quantum NMR was also combined with DOSY NMR to benefit from the separation power of the two methods simultaneously.^62,63

2.4. Polarisation transfer experiments

Polarisation transfer experiment make it possible to simultaneously address the overlap and assignment issues of mixture analyses by NMR. The most popular polarisation transfer scheme for such applications is the TOCSY (total correlation spectroscopy) block, which drives polarisation transfer among all the spins that belong to the same spin system. In 2D TOCSY spectra, the spectrum of molecular fragment can be extracted from the data, provided that a peak is well resolved for at least one chemical site in the corresponding spin system. This strategy was used by Brüschweiler and co-workers, together with a database of fragment spectra, to help identify compounds in complex metabolic mixtures.^64,65

Since the TOCSY block only correlates nuclear spins within the same spin systems, it cannot in general reveal the entire 1D spectrum of a mixture component. This can be achieved using the NOESY (nuclear Overhauser effect spectroscopy) experiment in a viscous solvent. Because the nuclear Overhauser effect is a through space transfer, polarisation can propagate across all the ¹H spins in a molecule, provided that it tumbles sufficiently slowly (the NOE for fast-tumbling molecules does not result in efficient spin diffusion). This concept was first demonstrated by Simpson and co-workers, who showed that the 1D ¹H spectra of component mixtures could be extracted from a 2D NOESY spectrum acquired in an oil–chloroform mixture, for a three-component mixture.⁶⁶ This approach requires a resolved ¹H resonance for each compound. Interestingly, when sufficient time and sensitivity are available to record a 2D HSQC NOESY spectrum, the 1D spectrum of a compound can be extracted with the less stringent requirement of having a well resolved ¹³C signal. This approach has been generalised by Lameiras and co-workers, who dubbed it ViscY, for mixture analysis in viscous solvent by NMR spin diffusion spectroscopy.^67–69 They have described several solvents (such as glycerol and glycerol carbonate) and solvent mixtures (such as blends of dimethylsulfoxide with glycerol or water), as well as band-selective 2D experiments, that make it possible to separate the 1D spectra of structurally similar compounds.

Polarisation transfer blocks are also useful in selective 1D experiment.^70–72 In this approach, the signal of a chemical site is selectively excited, and a polarisation transfer block is used such that the resulting spectrum contains also, and exclusively, the signals from correlated chemical sites. Selective 1D experiments may be advantageous compared to 2D experiments when only a subset of compounds is of interest, and when achieving the resolution needed in the indirect dimension of a 2D experiments would require a prohibitive experiment duration. They are also useful to address dynamic range issues.

This was illustrated, for example, by Sandusky et al., who showed that selective TOCSY experiments could be used for the quantitative analysis of compounds that were 1000 times less concentrated than the most abundant compounds in the mixture.⁷⁰ Selective experiments were also used by Lameiras and co-workers for ViscY experiments. Fig. 4 shows an example of ViscY experiments, in which the spectra of four phosphorus-based compounds are separated, using selective 1D NOESY experiments in a sulfolane/DMSO-d₆ mixture.⁶⁹

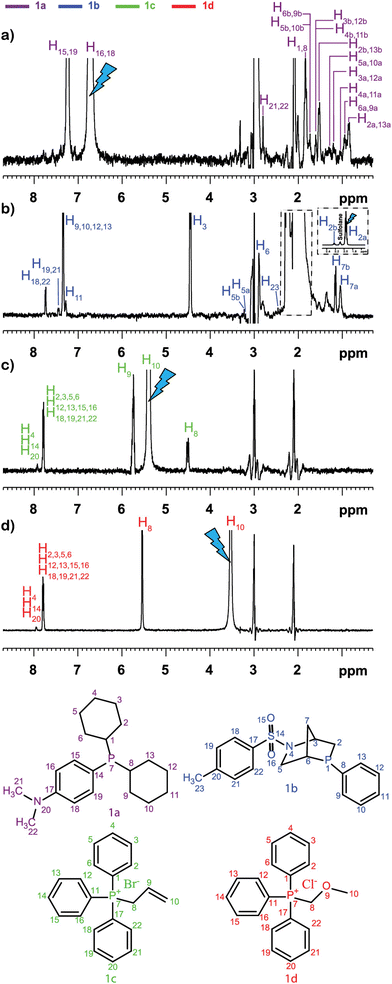Fig. 4 Multiplet selective excitation 1D ¹H NOESY spectra of a phosphorus-based compound test mixture (20 mM) dissolved in sulfolane/DMSO-d₆ (7 : 3 v/v) (a–d), t_m = 1 s, at 258 K, at 500 MHz (¹H). The initial selective inversion pulses excite: (a) H_16,18(1a), (b) H_2a(1b), (c) H₁₀(1c), and (d) H₁₀(1d) proton resonances. Reproduced with permission from ref. 69, © 2020 American Chemical Society.

Selective experiment can also be combined with broadband homonuclear decoupling, to yield pure-shift spectra of selected components in mixtures. One advantage of this approach is that the spectra of the minor components are not contaminated by the decoupling artefacts of the major components.⁷¹

A limitation of standard selective experiments is that they rely on a well-resolved signal for the component(s) of interest. This may not always be available, especially for mixtures of stereoisomers or mixtures with a high number of components. Several methods have been developed, that make it possible to select a single ¹H multiplet, even when it overlaps with other signals.^73–78 Conceptually, these pulse sequences rely on a pure-shift evolution for the spectral selection block. The chemical-shift selective filter (CSSF) described by Hall and Norwood is a multi-scan implementation of such type of selective experiment, which relies on an incremented delay to eliminate off-resonance signals.^77,78 An improved CSSF method, was used by Robinson et al. together with a TOCSY block to separate the 1D ¹H spectra of a trisaccharide and its unknown degradation product.⁷³ The GEMSTONE approach, recently described by Adams et al., replaces the incremented delay of the original CSSF by a spatial parallelisation method.⁷⁵ It makes it possible to collect selective TOCSY for overlapped multiplets in a single scan.⁷⁶

In the case of compounds that contain fluorine atom, another possible approach for polarisation transfer experiment is to select a signal of interest in the ¹⁹F spectrum, which usually has good resolution, followed by polarisation transfer to a neighbouring proton, and TOCSY-type transfer within the targeted ¹H spin system.⁷⁹

3. Concentrations

Despite its many advantages for mixture analysis, NMR spectroscopy is often limited in terms of applications by its modest sensitivity. Limits of detection and quantification may be usefully improved by increasing the magnetic field, or using a cryogenically cooled probe, but they remain orders of magnitude less favourable than with, e.g., mass spectrometry, even for 1D ¹H experiments, that are the most sensitive. For experiments involving low-abundant heteronuclei such as carbon-13, the required duration to have enough SNR is often prohibitive for time-resolved or high-throughput studies. The limited sensitivity of NMR spectroscopy originates from the low population differences between nuclear spin energy levels at natural abundance, expressed as the polarisation level (with 1 corresponding to fully polarised spins). At a magnetic field of 11.7 T and a temperature of 298 K, the polarisation level for ¹H is only 0.004%.

Hyperpolarisation methods make it possible to increase the polarisation levels of nuclear spins by several orders of magnitude,^80–85 approaching full polarisation in some cases. Several hyperpolarisation methods are now well established for applications in solution-state NMR spectroscopy, and are being assessed for mixture analysis applications. These are based on dynamic nuclear polarisation (DNP), and parahydrogen (pH₂). These methods rely on very different physical principles and instrumentation, and they have very different features in terms of molecules and nuclei that can be polarised, polarisation levels that can be reached, and types of NMR experiments that can be recorded. In this section we describe how DNP and pH₂ can help to lower the concentrations that can be accessed with NMR. Note that for mass-limited samples, sensitivity can also be increased by using tailored coils and probes (e.g., ref. 86), that will not be covered in this article.

3.1. Dynamic nuclear polarisation

Dissolution dynamic nuclear polarisation (D-DNP) consists of polarising a sample in the solid state, dissolving it with a hot solvent, and transferring it to a spectrometer to acquire NMR data with enhanced sensitivity.^80,87 The polarisation step is typically carried out in a cryostat at a temperature of 1.2 to 4 K and a magnetic field of 3.4 to 10 T, by microwave irradiation of a sample doped with molecules that bear unpaired electrons. At such temperature and magnetic field, electron spins have almost unity polarisation, and the microwave irradiation results in polarisation transfer from the spins of unpaired electrons to nuclear spins. Polarisation levels in excess of 50% can be achieved in the solid state for a variety of nuclei, with carbon-13 being by far the most used. The high relevance of D-DNP for solution-state NMR stems from the fact that the nuclear spin polarisation can be preserved to a certain extent through the dissolution and transfer process. As a result, signal enhancements of 10 000 or more can be routinely obtained for ¹³C NMR in solution.

One of the key features of D-DNP is that it is a single-shot method, because the dissolution step is irreversible. In addition, once the sample is dissolved, the nuclear spin polarisation decays irreversibly on a time scale given by the longitudinal relaxation times of the polarised nuclei. In many systems, the dissolution, transfer and stabilisation times add up to more than 10 s.⁸⁷ This is why most applications of D-DNP rely on the hyperpolarisation of quaternary carbons, which have relaxation time constants that can be larger than 20 s. Several groups have also reported instrumentation developments that make is possible to reduce the delay between dissolution and detection to less than 5 seconds.^88–91 With such devices, a broader range of chemical sites can be observed.

D-DNP is used extensively for kinetic studies based on the injection of hyperpolarised compounds in a mixture containing other reactants and/or catalysts, or in cell cultures.^92–101 In such applications, hyperpolarisation methods make it possible to acquire ¹³C NMR spectra with a time resolution of a few seconds, which would be impossible to achieve at thermal equilibrium. They also make it possible to observe intermediate species that would be invisible with conventional NMR methods. For example, Hilty and co-workers have described a series of studies of polymerisation reactions using DNP-hyperpolarised monomers.^93,95,97 They used time-series of 1D ¹³C NMR spectra at natural abundance to measure and compare reaction rates for different monomers, and also observe polymer products and side products, during a time of 10 to 30 s after the start of the reaction. Lerche, Meier and co-workers have used DNP-hyperpolarised ¹³C-labelled substrates to track the metabolic fate of molecules such as glucose and fructose in biological systems such as cancer cell or yeast cultures.^98,100 Time-series of 1D ¹³C NMR spectra were used to track intermediates in metabolic pathways.

D-DNP is also investigated as a method to increase sensitivity in NMR metabolomics.^91,102–105 Lerche and co-workers have used D-DNP for sensitivity enhanced stable-isotope resolved analysis (SIRA).^91,103 In this approach, a biological system is fed with ¹³C-labelled sugars for a period of time, before undergoing metabolic quenching and extraction. DNP-enhanced ¹³C-NMR spectra of the extracts are then quantitatively analysed to classify sample types and identify potential biomarkers. Giraudeau and co-workers have shown that D-DNP can also be used to for hyperpolarised ¹³C NMR of complex metabolic extracts at natural abundance.¹⁰² This involved the use of polarisation method in the solid state that consists of first polarising ¹H spins by DNP, and then transferring their polarisation to ¹³C spins by cross-polarisation (CP).¹⁰⁶ This CP-based approach gives high ¹³C polarisation levels even for natural-abundance samples, as illustrated in Fig. 5 in the case of a tomato extract. Importantly, it was also shown that D-DNP experiments can have a repeatability of better than 4% for the relative area of peaks above the limit of quantification (SNR ≥ 10).¹⁰⁴ This paved the way to the first implementation of hyperpolarised ¹³C NMR in an untargeted metabolomics workflow.¹⁰⁵ Interestingly, the expected limit of detection for of hyperpolarised ¹³C NMR using D-DNP is not significantly higher than that of ¹H NMR at thermal equilibrium. The goal is instead to benefit from the significantly higher dispersion of ¹³C 1D NMR spectra compared to 1D ¹H NMR, with realistic experiment durations.

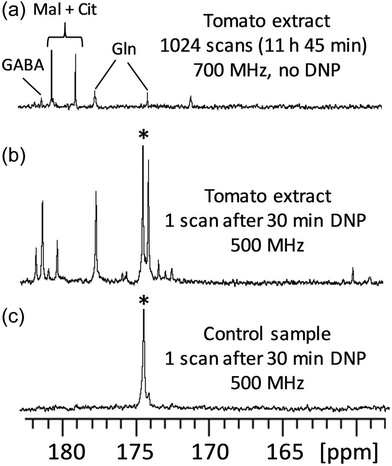Fig. 5 ¹³C NMR spectra (quaternary region) of mature green tomato fruit pericarp extracts. (a) Conventional (non-hyperpolarised) spectrum of 20 mg extract (prepared from 20 mg lyophilized grounded tissue) dissolved in 700 μL D₂O, recorded with 1024 scans (11 h 45 min) at 700 MHz with a cryogenic probe. (b) Spectrum of an identical extract recorded with D-DNP combined with CP. The extract was first dissolved in a 200 μL mixture of H₂O/D₂O/glycerol-d₈ (2 : 3 : 5) doped with 25 mM TEMPOL, then polarized for 30 min at 1.2 K and 6.7 T, and finally dissolved with 5 mL of hot D₂O and transferred in about 10 seconds to a 500 MHz spectrometer equipped with a cryogenic probe. (c) Same as (b), but the tomato extract was replaced by a control sample prepared under strictly identical conditions without any biological material. The hyperpolarized spectra result from the sum of six consecutive acquisitions using 30° pulses spaced by 7.7 s. *Indicates the signal of a ¹³C-labeled pyruvate impurity from the D-DNP setting. Cit: citrate; GABA: γ-aminobutyrate; Gln: glutamine; Mal: malate. Reproduced from ref. 102 with permission from the Royal Society of Chemistry.

Overall, the main advantage of D-DNP for mixture analysis is that it is a broadband method, that can yield high polarisation levels for virtually arbitrary molecules and chemical sites. The single-shot nature of the method however limits the type of NMR experiments that can be recorded, while the fast-decaying nature of the spin polarisation restricts the chemical site that can actually observed. Fast-injection systems, and fast 2D NMR experiments described in Section 4, have the potential to increase the information content of DNP-enhanced spectra for mixture analysis.

Several hyperpolarisation methods based on dynamic nuclear polarisation make it possible to perform multi-shot experiments. This is for example the case of Overhauser DNP,^84,85 which was recently shown to provide enhancements of up to 1000 for ¹³C NMR at high field⁸⁵ and which can also be implemented with flow,¹⁰⁷ and rapid-melt DNP.¹⁰⁸ These and related methods do not yet provide high-resolution spectra, that would be suitable for mixture analysis, but they have the potential to become analytical methods that are both broadband in terms of compounds that can be observed, and versatile in terms of spectra that can be acquired. Intriguing possibilities are also opened by the injection of highly polarised molecules prepared with DNP or pH₂, followed by intermolecular cross-relaxation, which may become relevant for mixture analysis.^109,110 Interestingly, such broadband hyperpolarisation methods will raise important dynamic range questions, as actual limits of detection will only be improved if dilute components can be detected in the presence of much more concentrated compounds.

3.2. Parahydrogen-based hyperpolarisation

Signal amplification by reversible exchange (SABRE) is a hyperpolarisation method that relies on a reversible interaction between a substrate, a metal centre, and dissolved dihydrogen enriched in its para form.⁸¹ In SABRE, the source of polarisation is parahydrogen. Dihydrogen exists in the form of two spin isomers, named ortho and para, that correspond to different spin and rotational states of the molecule. The equilibrium distribution between the two forms at room temperature is 75% ortho and 25% para. Dihydrogen gas can be enriched in its para form simply by cooling it in the presence of a metal oxide, reaching 50% parahydrogen at 77 K (liquid nitrogen temperature) and close to 100% at 20 K. The gas enriched in its para form can be stored for extended periods of time, as the two forms interconvert very slowly in the absence of a catalyst. Para-hydrogen is thus a reservoir of spin order. In SABRE, that reservoir is exploited through: (i) the addition of parahydrogen to a metal centre, often in an iridium complex; (ii) a transfer of polarisation from the hydride protons to nuclear spins in the substrates bound to the metal centre.

SABRE was initially demonstrated with a single substrate of interest.⁸¹ Shortly afterwards, the potential of SABRE-based hyperpolarisation for analytical applications was illustrated by Lloyds et al.¹¹¹ A key feature of SABRE is the reversible nature of the hyperpolarisation process, which can occur multiple times for a given substrate. As a result, an array of classic 2D NMR experiments can be used with little modifications to record spectra with enhanced sensitivity. Experimental complications, however, result from the fact that the polarisation transfer occurs spontaneously only at low magnetic field (in the milliTesla range of ¹H and in the microTesla range for ¹⁵N). The sample thus has to be moved between a polarisation region and the NMR spectrometer. The most used methods consist of dropping the sample in the magnet after shaking, or using a flow system to shuttle the sample between a polarisation region (where parahydrogen gas is bubbled) and the detection region.¹¹²

The potential of SABRE for mixture analysis has been explored by Tessari and co-workers, who showed that the method can be applied to complex mixtures of molecules with concentrations in the micromolar range, provided that an appropriate co-substrate is also added to the mixture.^113,114 They also showed that the signal intensity changes linearly with concentration in that regime. With a standard-addition method, they were able to quantify several analytes in an artificial mixture.¹¹⁵ Also working with a co-substrate, they recorded 2D DOSY data with a flow shuttle.¹¹⁶ The transfer of polarisation between the hydride ligands, which results from pH₂ addition to a metal centre, to the substrate, can also be performed with pulse sequences. This is exploited in several pulse sequences developed by Tessari and co-workers, who designed 2D experiments that correlate hydride signals with signals from, e.g., the ortho proton of a heterocycle in the target substrate.¹¹⁷ The resulting 2D spectre provide excellent signal dispersion, and can also be used for quantitative analysis by standard addition.

One key feature of SABRE hyperpolarisation is that it is a selective method, in the sense that not all molecules, and not all the spins within these molecules, can be polarised. This can be seen as a limitation in the perspective of fully untargeted analyses. It can also be turned into an advantage for the analysis of selected classes of compounds. This was demonstrated with the development of a “chemosensing” strategy based on SABRE, which was used to analyse coffee extracts after methanol extraction,¹¹⁸ and urine samples after solid-phase extraction (SPE).^119,120 Using zero-quantum/single quantum correlation experiments, Sellies et al. were able to detect and quantify analytes in urine.¹²⁰ Reimets et al. further showed that quantification of metabolites in urine using SABRE and a standard addition process was also possible without SPE, using 2D spectra such as the one shown in Fig. 6.¹²¹ One of the challenges of this approach is the identification of the observed compounds.

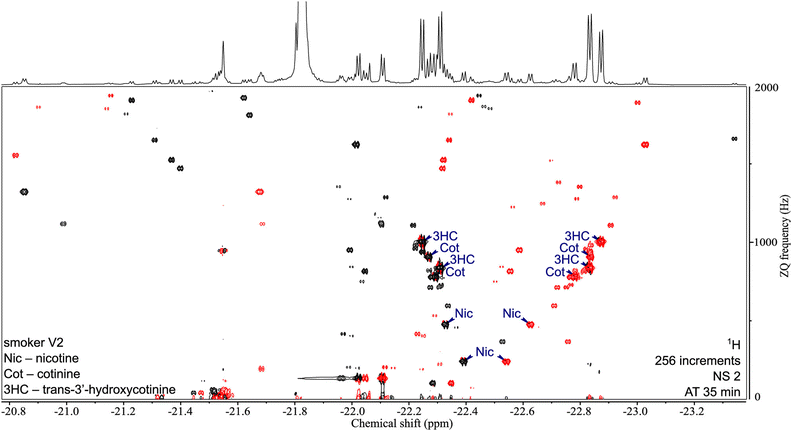Fig. 6 2D ZQ pH₂ HP spectrum of a urine extract in CDCl₃. Each complex of an analyte and the active catalyst [Ir(H₂)(IMes)(mtz)₃] gives rise to two opposite phase doublets at the same ZQ frequency. Chiral analytes (i.e., Nic, Cot, and 3HC) can combine with the catalyst in two ways due to the stereogenic center on iridium in the complex, forming two diastereomers with different physical properties. Signals were assigned by internal standard addition during method development. Upper 1D trace recorded separately with the 1D SEPP sequence. Reproduced with permission from ref. 121, © 2021 American Chemical Society.

The scope of molecules that can be polarised with SABRE keeps on expanding through the development of new chemical systems and pulse sequences.^122–125 Duckett and co-workers have for example introduced a relay strategy that can be used to polarise molecules with exchangeable protons.¹²² They for example used benzylamine, that both binds to the metal centre and has exchangeable protons.¹²⁴ Using this approach, they were able to polarise different sugar molecules, with a response that varies linearly with concentration if the sample is sufficiently dilute.

SABRE is also being used for reaction monitoring applications.^126–128 This was illustrated by Halse, Duckett and co-workers, who monitored the activation of the SABRE catalyst and proton-deuterium exchange in a SABRE hyperpolarised substrate.¹²⁶ This was achieved with single-shot measurement of hyperpolarisation lifetimes for several protons in the substrates, which reflect both the extent of catalyst activation and the degree of substrate deuteration. SABRE was also used to produce hyperpolarised substrates for reaction monitoring. In a different approach, Norcott has combined SABRE hyperpolarisation with selective experiments to analyse the reaction mixtures produced by the methanolysis of an amide, at different stages of the reactions.¹²⁹

The spin order of parahydrogen can also be released by hydrogenation of the target substrate, using a metal catalyst. This concept, named para-hydrogen induced polarisation (PHIP), was first described by Bowers and Weitekamp in 1986, and reported experimentally a year later.^82,83 PHIP requires the presence of an unsaturation that can be hydrogenated in the target molecule, or the use of a cleavable side-arm. It has been used to produce hyperpolarised substrates, that are subsequently injected in either an enzymatic solution or cell culture.^130–132 In order to extend the hyperpolarisation lifetime, and benefit from higher signal dispersion, the spin order is transfer to a neighbouring carbon-13 that has a long longitudinal relaxation time. As in the D-DNP case, the enhanced polarisation makes it possible to monitor (bio)chemical reactions with high time resolution, but with much more accessible instrumentation.

4. Change

Multidimensional experiments are essential for many applications of NMR, and mixture analysis is no exception. For mixture analysis, 2D experiments are the most frequently used multidimensional experiments, and higher-dimensional spectra are seldom recorded. The increased signal dispersion and correlation information provided by 2D spectra are essential to address overlap issues, assign signals, and obtain structural information. The duration of 2D experiments, however, is in many cases a limitation. While 1D spectra can be acquired in less than 1 second, conventional 2D experiments typically last 10 minutes at least, sometimes much more, even when sensitivity is not a limitation. This is an obstacle for the time-resolved analysis of samples that evolve in time, found in reaction monitoring applications, as well as for applications that require a high sample throughput, such as metabolomics, in which one is interested in changes in concentration over large sets of samples. Conventional 2D experiments are also not generally compatible with single-shot hyperpolarisation methods such as dissolution DNP, and this restricts the information content of the sensitivity enhanced spectra.

Several complementary concepts have been introduced to accelerate multidimensional experiments.^133–140 The duration of conventional 2D experiments originates from the point-by-point sampling of the additional dimension, which requires the consecutive acquisition of multiple scans with an incremented parameter. This is compounded by the inter-scan delays required for magnetisation recovery. Experiments may notably be accelerated by reducing the number of data points required to reconstruct the indirect dimension,^134,135 by reducing the delay that separates consecutive scans,^137–140 and by spatial parallelisation.^133,136 These three types of methods have been tailored for mixture analysis and exploited for a variety of applications. This section describes examples of fast 2D methods used for the analysis of mixtures.

4.1. Ultrafast 2D NMR

Ultrafast (UF) 2D NMR is the fastest method to collect 2D NMR data. In UF 2D NMR, the scan-to-scan incrementation of a parameter value found in classic 2D NMR (e.g., of the t₁ evolution time) is replaced by a spatial parallelisation approach, in which the parameter value varies as a function of position in the sample.^141,142 This is achieved with the combined application of a frequency-swept pulse and a magnetic field gradient. Together with magnetic-resonance imaging methods that make it possible to effectively collect separate free-induction decay (FID) signal per sample slice, such spatial encoding provides a full 2D data set in a single scan of less than 1 second. This corresponds to an acceleration by up to three orders of magnitude. UF 2D NMR was first introduced for 2D spectroscopy in 2002,¹³³ and related concepts were concurrently described for the acceleration of 2D DOSY experiments.¹³⁶

The potential of UF 2D NMR for mixture analysis was recognised early on, with the use of UF implementations of 2D correlation experiments such as TOCSY.^143,144 Examples were reported of reaction monitoring, including the detection of a short-lived intermediates,¹⁴⁵ and of the in-line acquisition of 2D spectra for a liquid chromatography type setup.¹⁴³ A series of examples of reaction monitoring applications were then described by Herrera and co-workers who, for example, obtained mechanistic insights into the synthesis of pyrimidines.^{144,146–149} They notably made use of a rapid-injection device, to capture intermediate species with a half-life of a few minutes.

Interestingly, the relevance of UF 2D NMR for mixture analysis is not limited to single-scan implementations. In fact, UF 2D NMR spectra acquired in a single scan have limitations in terms of spectral width, resolution and sensitivity. These limitations can be alleviated through the acquisition of a few (typically 2 to 8) scans, that makes it possible to increase the accessible spectral width and/or the sensitivity.¹⁵⁰ Such hybrid UF 2D NMR experiments have proven particularly useful for quantitative analyses of complex mixtures for, e.g., metabolomics applications.^151–155 UF 2D NMR spectra are virtually free of t₁ noise, and this was found to improve the limit of quantification of signal-averaged UF 2D spectra compared to conventional 2D spectra.¹⁵¹

Some of the 2D methods specifically designed for mixture analysis, described in Section 2, have also been implemented in an ultrafast fashion. This is notably the case of multiple-quantum/single quantum correlation experiments.^156–158 Le Guennec et al. showed that the spatial encoding process used in UF 2D NMR is applicable to multiple-quantum coherences, and this made it possible to collect double-quantum spectroscopy (DQS) experiments in one or a few scans.¹⁵⁶ Compared to COSY spectra, DQS results have the advantage of not displaying “diagonal” peaks, which helps to address overlap issues, as illustrated in Fig. 7. UF DQS spectra were then shown to be useful for quantification,¹⁵⁷ as well as for experiments performed in magic-angle spinning conditions.¹⁵⁹ The method was further extended by Concilio et al., who demonstrated the spatial encoding of multiple-quantum coherences of order up to 5, and used the resulting approach for a maximum-quantum analysis of a mixture of aromatic compounds.¹⁵⁸

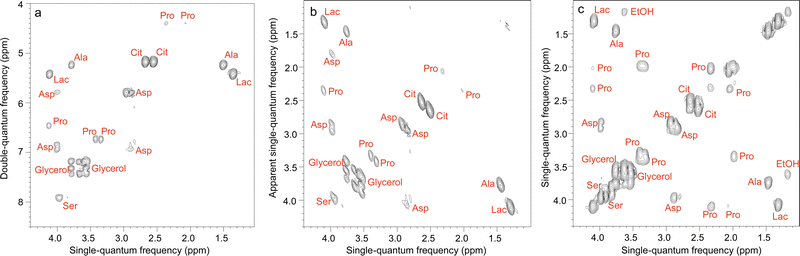Fig. 7 Ultrafast NMR spectra of a mixture of 7 metabolites in H₂O/D₂O (90/10): (a) DQS (c) COSY. All spectra were recorded in four interleaved scans to increase the observable spectral width, and four dummy scans resulting in an acquisition time of 41 s, using a double-quantum build-up delay τ = 25 ms. Spectrum (b) was obtained from spectrum (a) by a shearing transformation at a processing stage. All spectra were recorded with a 600 MHz spectrometer equipped with a cryogenic probe. Reproduced from ref. 156 with permission from the Royal Society of Chemistry.

Diffusion NMR experiments can also be accelerated by spatial parallelisation. In this case, different slices in the sample undergo magnetic-field gradient pulses of different effective duration.^136,160,161 This was first demonstrated by Thrippleton et al.,¹³⁶ and later revisited by Shrot et al.,¹⁶⁰ who used a more general detection scheme. More recently, Guduff et al. showed that UF (also called spatially encoded or SPEN) DOSY NMR can be extended to higher dimensional experiments, in order to acquire 3D DOSY data set (as described in Section 2.2) in a few minutes instead of a few hours.¹⁶¹Fig. 8 shows the result of the separation of 2D COSY spectra for a mixture of three short-chain alcohols and one amino acid, based on data that was acquired in 12 min. This approach relies on one spatially encoded diffusion dimension and one conventional chemical shift dimension. The reverse, one conventional diffusion dimension and one spatially encoded chemical shift dimension is also possible, and provides a different trade-off between acceleration and sensitivity.¹⁶² Like their conventional counterparts, UF DOSY experiments can be made more robust against convection effects, and this has proven useful for experiments carried out in organic solvents, notably for reaction monitoring applications.¹⁶³ Multivariate processing algorithms may also be exploited to improve the separation of component spectra achieved with UF DOSY experiments. For DECRA, this required the design of alternative frequency swept pulses, and resulted in a duration of just a few second for both the acquisition and the processing/analysis steps.¹⁶⁴

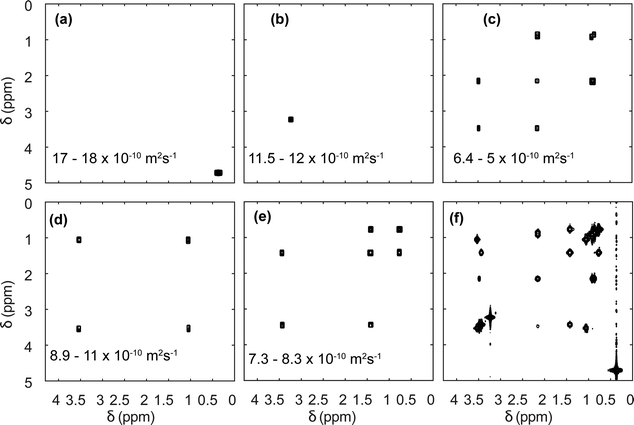Fig. 8 SPEN 3D DOSY of a mixture of 3 alcohols (methanol, ethanol, propanol) and an amino-acid (L-valine), at a concentration of ∼100 mM in D₂O. (a–e) COSY-type spectra obtained as slabs of the 3D (D, δ_direct, δ_indirect) dataset resulting from DOSY processing. The selected range in D is shown in each panel. The slice of the (z, δ_direct, δ_indirect) dataset with the lowest diffusion gradient area is shown in (f). The experiment was carried out with a 600 MHz spectrometer equipped with a triple-axis gradient high-resolution probe, and lasted 12 min. Adapted from ref. 161 with permission from the Royal Society of Chemistry.

The combination of UF 2D NMR and single-shot hyperpolarisation methods is particularly promising for mixture analysis.^{102,165–169} This is notably the case for dissolution DNP, which provides high polarisation levels for a broad range of molecules, but which is also not generally compatible with multi-scan pulse sequences. For example, the mixing step of a COSY pulse sequence would completely deplete the enhanced polarisation. Interestingly, even for experiments that may be recorded in multiple-scans with dissolution-DNP, the sensitivity of the UF implementation may be more favourable. Frydman and Blazina first reported the acquisition of UF 2D spectra for DNP-hyperpolarised substrates, using heteronuclear 2D correlation pulse sequences.¹⁷⁰ These experiments were later adapted for a variety of substrates.^102,165,171 Provided that the delay between dissolution and detection can be made sufficiently short, homonuclear 2D spectra can also be recorded in a single scan with ¹H hyperpolarisation.^169,172 This combination is not limited to 2D spectroscopy, and Guduff et al. have shown that reliable 2D DOSY spectra can also be recorded in a single-scan from DNP-hyperpolarised substrates.¹⁶⁷

4.2. Non-uniform sampling

Multidimensional NMR experiments classically rely on the discrete Fourier transform to go from time-domain to frequency-domain representations. For the indirect dimension of 2D spectra, N₁ time points are collected on a regular time grid with spacing Δt₁, and this provides N₁ spectral points with a spectral width of 1/Δt₁ after FT. While this is very robust and general, it is also unnecessarily inefficient in most cases. Non uniform sampling (NUS) refers to a family of methods that consist of (i) collecting only a fraction of the points from those that would form a regular grid, (ii) using an algorithm that depart from the classic Fourier transform to reconstruct the spectrum.^134,135,173 These methods rely on the assumption that multidimensional spectra are sparse. This means that among all the possible spectra that would be compatible with the collected data, the algorithm reconstructs the one that is the sparsest. The degree of undersampling is usually expressed as the NUS level, defined as the number of acquired points divided by the number of points that would be needed to achieve the same spectral width and digital resolution with uniform sampling.

NUS has proven useful for the 2D experiments that are typically used for mixture analysis.^{153,174–176} The number of points used to obtain a 2D spectrum with NUS cannot be taken arbitrarily low. Empirically, it was found that at least 64 points were needed in the case of HSQC and DQF-COSY experiments applied on an artificial mixture of 30 metabolites, designed to mimic the composition of human serum.¹⁵³ In this example, the resulting durations were of about 30 min for each experiment. This corresponds to an acceleration by a factor of 2 to 3 compared to the conditions that would typically have been used for such experiments. The quantitative information required for the subsequent statistical analysis was found to be preserved at such NUS levels, which makes them a relevant option for metabolomics applications.^153,176,177

Interestingly, a given number of t₁ points can be distributed over a time grid that spans a much larger range of values than that of the corresponding uniformly sampled experiments. In other words, from a practical point of view NUS is also very useful to increase the resolution of 2D spectra of complex mixtures. This was illustrated by Le Guennec et al., with the acquisition of HSQC and TOCSY spectra of an artificial mixture of metabolites.¹⁷⁸ They found that, using 256 points in the HSQC case and 512 in the TOCSY case (corresponding to experiment duration of 2 h and 1 h), resolution could be increased by a factor of up to 8 using non uniform sampling. Importantly, they also showed that successful reconstruction for such NUS levels was not successful with the so-called “exponential sampling” strategy, which consists of selecting the acquired t₁ points with an exponentially weighted probability (short t₁ values are more likely to be acquired). They used instead “Poisson-gap” sampling,¹⁷⁹ which is designed to avoid large gaps in sampling schedule, and was found to give reduced artefact levels.

Non-uniform sampling is also relevant for the analysis of mixtures that evolve in time.^{173,180–183} In this case, it can be implemented in a so-called “time-resolved” fashion by: (i) acquiring a long series of t₁ points, with repetition time T_R, according to a randomised non-uniform sampling schedule, and (ii) using a sliding-window processing, that consists of taking N_w consecutive points to reconstruct a spectrum, then moving the range of selected points by one or several units to reconstruct the next spectrum. While each spectrum is effectively acquired over a duration of N_w × T_R, and represents an average sample composition over that duration, the time resolution is improved compared to the processing of non-overlapping data sets. TR-NUS was used by Dass et al. to monitor the fermentation of wheat flour.¹⁸⁰ They collected a series of points of 2D HSQC experiments, randomly sampled from a full grid of 200 points. From this data, a times series of 2D HSQC spectra was obtained, and analysed by integration of selected peaks to track the concentration of ethanol and glycerol during fermentation, as illustrated in Fig. 9. The use of TR-NUS was recently made easier by the release of a software package for data processing and analysis.¹⁸¹

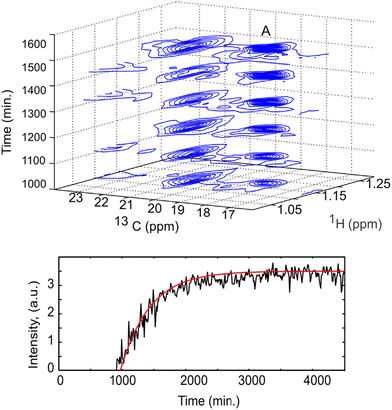Fig. 9 Fermentation of milk monitored using a TR-NUS ¹³C HSQC experiment. The top panel shows a stack of reconstructed ¹³C HSQC spectra that correspond to different time points in the fermentation process. The extra ¹³C dimension separates the ethanol cross peak (A), enabling simple determination of fermentation kinetics. The reaction rate, assuming first-order kinetics (fitted red line), was calculated from the change in ethanol cross peak intensity with (bottom panel). Reprinted with permission from ref. 180, © 2015 American Chemical Society.

The “time-resolved” approach is also applicable to diffusion NMR/DOSY experiments.^184–186 In this case a randomised list of gradient amplitudes is generated, and used to collect a time series of diffusion-attenuated spectra. As in the TR-NUS case, N_w consecutive spectra are analysed to estimate diffusion coefficients, and the window of processed spectra can then be moved by one or a few units. In contrast to TR-NUS, TR-DOSY does not necessarily require specific reconstruction algorithms, because the non-linear least-square fit used in conventional DOSY experiments can be applied to arbitrary grids of gradient values. For both TR-NUS and TR-DOSY, the window size for the processing can be chosen and adjusted after the data is acquired. Its value governs a trade-off between time resolution on the one hand, and SNR and artefact levels on the other hand.

Several time-resolved 2D experiments can be acquired simultaneously, by acquiring points for different 2D experiments in an interleaved fashion. This was recently used by Urbańczyk and co-workers to monitor a photo-polymerisation reaction in situ, with a combination of TR-NUS, to obtain a series of 2D HSQC spectra, and TR-DOSY.¹⁸⁷

4.3. Fast-pulsing and concatenated experiments

A third possible route to accelerate 2D NMR experiments consists of reducing the time T_R that separates two consecutive scans.^137–140 In most conventional 2D experiments, the majority of this delay is dedicated to the return of longitudinal magnetisation from nearly zero to its equilibrium value, through nuclear spin relaxation. In order to reduce the repetition time without sacrificing too much sensitivity, some magnetisation has to be preserved along the longitudinal axis, or the recovery of longitudinal magnetisation has to be accelerated. A combination of the two approaches is also possible.

The classic implementation of the HSQC pulse sequence entirely depletes the ¹H longitudinal magnetisation at each scan. Its modified “ALSOFAST” version, however, can return a controlled fraction of the magnetisation along the z axis at the end of each scan.^188,189 This makes it possible to operate in a “fast-pulsing” regime, in which short repetition times and small-angle excitation are combined to obtain 2D spectra in a few seconds with good sensitivity (measured as the signal to noise ration per square root of total experiment time). The ALSOFAST HSQC pulse sequence was used by Schaetlein et al. for metabolomics and fluxomics studies on a ¹³C-enriched cancer cell model.¹⁸⁹ The authors showed that the experiment could be used to obtain “low-resolution” 2D spectra in 2 seconds, that were suitable to statistical analysis, or “high-resolution” spectra in one minute, that could be used for fluxomics analysis. For samples at natural abundance, the sensitivity of this fast HSQC experiment can be increased by replacing the relaxation delay by a spin-lock, that distributes the polarisation of ¹²C-bound protons to ¹³C-bound protons.¹³⁷ The resulting ASAP (acceleration by sharing adjacent polarisation) was also shown to be compatible with the statistical analyses for series of spectra from complex samples.¹⁹⁰

The concepts of NMR supersequences and no relaxation delay NMR spectroscopy (NORD) make it possible to reduce the total time required to collect multiple 2D spectra for a given sample.^139,191 The corresponding pulse sequences are concatenated, such that each block taps into a different pool of magnetisation. A single recovery delay can then be used for the combined pulse sequence. Promising results were notably obtained by Hansen et al. for the analysis of complex mixtures with NOAH supersequences. They obtained HSQC, HSQC-TOCSY and TOCSY spectra of mouse urine with an acceleration by a factor of 2.¹⁹²

5. Conditions of operation

Virtually all of the methods described so far in this feature article were developed and applied with samples placed in a classic NMR tube of 5 mm outer diameter. While this is a powerful approach, as attested by the breadth and depth of chemical information obtained with these experiments, it can also be a limitation for mixture analysis. Sometimes the experimental conditions of interest cannot be replicated faithfully in a high-field NMR spectrometer. This is particularly true for reaction monitoring applications.¹⁹³ Flow NMR is a powerful approach to benefit from the information content of NMR spectra while analysing, in real time, a system in its usual operating conditions.¹⁹⁴ Flow NMR is becoming widespread notably through the use of benchtop NMR spectrometers. These have been reviewed recently¹⁹⁵ and will not be covered here. In parallel, the development of devices for flow NMR at high field has provided access to experimental conditions that could previously be probed only in a more indirect manner, while keeping the resolution and sensitivity offered by high-field magnets.^196–198 This also raises challenges in terms of pulse sequence development, as some important pulse sequences that address the limitations of 1D NMR experiments are not compatible with continuous flow conditions.

As outlined in Section 2, diffusion-ordered NMR spectroscopy (DOSY) is a particularly powerful approach for mixture analysis. It is based on the measurement of translational diffusion coefficients, using pulsed magnetic-field gradients. Since typical diffusion lengths in DOSY NMR experiments on small molecules are of 10 μm or less, DOSY NMR may appear to be incompatible with measurements carried out on a sample that undergoes a bulk displacement over an average length of more than 100 μm during the “diffusion” delay. Indeed, when classic DOSY pulse sequences are used, with diffusion encoding along the main direction of the flow, the estimated diffusion coefficients are highly inaccurate. Marchand et al. recently showed that, using a convection compensated pulse sequences, and a diffusion-encoding axis that is orthogonal to the main direction of the flow, accurate diffusion coefficients can be measured for samples flowing at up to 3 mL min⁻¹.¹⁹⁹ In addition, they showed that the use of multiple orthogonal axes in convection-compensated diffusion NMR pulse sequences also made it possible to reduce the number of scans to just one per value of the diffusion-encoding gradient. This “one-shot” implementation makes it possible to collect a complete data set in less than 90 s, thus giving a useful tool for reaction monitoring application, as illustrated in Fig. 10. Concurrently to this work, Thomlinson et al. showed that, using a low pulsation pump, or an empirical correction for flow effects, consistent values of diffusion coefficients could also be obtained with a single-axis gradient probe.²⁰⁰

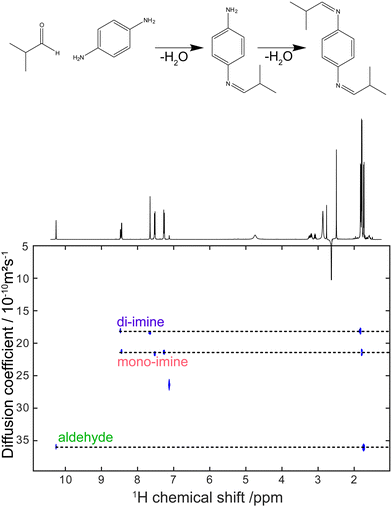Fig. 10 DOSY spectrum obtained during a di-imination reaction monitored by online NMR at a flow rate of 3 mL min⁻¹. The experiment duration was 80 s. Adapted with permission from ref. 199. © 2022 Wiley-VCH GmbH.

Ultrafast 2D NMR experiments are also built on specific assumptions on molecular positions, that may appear not to be verified in continuous flow conditions. When the spatial encoding axis is parallel to the main direction of the flow, interferences between spatial encoding and bulk sample motion result in significant signal attenuation. This can be compounded by the pulsatile nature of the flow, that results in non-repeatable values of the peak volume, thus preventing the use of UF 2D NMR for reaction monitoring in continuous flow.²⁰¹ These issues can be addressed with the use of a spatial encoding axis that is orthogonal to the main direction of the flow. This was probably key to the success of UF 2D NMR experiments in continuous flow on a benchtop spectrometer, for which the field gradient was transverse.²⁰² At high field, Jacquemmoz et al. recently showed that a transverse axis of a triple-axis gradient probe had to be used for spatial encoding, in order to obtain good-quality UF 2D NMR. In both cases, the resulting peak volumes can be used for accurate reaction monitoring.

6. Outlook

The development and applications of NMR methods for the analysis of mixtures forms a dynamic area of research. Methods are being developed, updated or refined to tackle the challenges of reaching the resolution, sensitivity and speed that are required for specific applications. It is striking to note that, while a paper entitled “Mixture analysis by NMR spectroscopy” was published more than 25 years ago,²⁰³ powerful methods are still reported today, for which the novelty lies in the way in which nuclear spins are handled. In fact, some of the most recent developments in the field might have been implemented on hardware available at the time, but the corresponding ideas were not mature yet.

From a user's point of view, NMR pulse sequences usually become available relatively fast as updates to commercial vendor software, or through online libraries. This also means that there is a wealth of options to choose from. When faced with a resolution or assignment problem, should one go for a pure-shift experiment, a selective experiment, a 2D experiment. The answer is usually problem dependent, and can often be a combination of several methods, tailored for a specific sample. Similarly, for an application that requires fast multidimensional experiments, should one choose spatial parallelisation or non-uniform sampling? And should it be combined with fast-pulsing methods? In some cases, the timescale or interest or the available sensitivity will answer the question. In cases were all the options are available, careful comparisons are needed to establish the relative merits of each approach. Tutorials are for example available, that compare the features of several fast methods.¹⁷⁴ The uptake of new NMR methods beyond a circle of experts also depends on the ease with which these methods can be implemented. Efforts to distribute implementation guides are clearly helping in this respect. Most methods can likely have impact only if they become usable as a “black box”. One can expect that, within a few years, this will become true of approaches such as ultrafast 2D NMR and time-resolved non-uniform sampling.

Several of the methods described here require the installation of new hardware. This is especially true for the hyperpolarisation methods described in Section 3. At this stage, these approaches are more exploratory, and it remains to be seen whether they will become widely used. Many striking examples were reported for applications of D-DNP to reaction monitoring, and more recent results on the use of hyperpolarised NMR for the analysis of “static” complex mixtures are very promising. The increasing availability of commercial instrumentation for these methods will also probably help to reveal the usefulness of hyperpolarised NMR for mixture analysis. Interestingly, improved limits of detection automatically result in increased complexity of the spectra, and this exacerbates the need for NMR methods that address this complexity. Similarly, the short-lived nature of the enhanced spin polarisation produced with single-shot hyperpolarisation calls for the development of fast 2D NMR methods.

An increasing number of development and applications is also observed in the emerging and fast-growing area of benchtop NMR, which was not covered in this article. Compact instruments provide access to previously inaccessible samples. This is the case for profiling application, which in principle are possible also at high field, but in practice are precluded by cost and availability reasons. This is also true for monitoring applications, which can now be implemented in the fume hood, on in industrial plants. Flow NMR at low and high field also significantly broaden the scope or reactions and processes that can be analysed.

Overall, NMR methods for the analysis of mixtures are expected to keep on growing, through the introduction of novel concepts and hardware. An increasing role of digital chemistry concepts can also be expected, which will blend with current spin dynamics concept to further increase the information content of NMR experiments.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

I am very grateful to the many colleagues with whom I have add the chance to work on these topics. I would particularly like to thank Patrick Giraudeau for useful critical feedback on the manuscript. This work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreements no 801774/DINAMIX) the Region Pays de la Loire (Connect Talent HPNMR), the Agence Nationale de la Recherche (ANR-21-CE07-0056-02), and the I-SITE NExT (iChem4.0). The NExT initiative is supported by Nantes Université, the Région des Pays de la Loire and Nantes Métropole in the frame of the Programme d’Investissement d’Avenir (PIA). The author also acknowledges the French National Infrastructure for Metabolomics and Fluxomics MetaboHUB-ANR-11-INBS-0010 (http://www.metabohub.fr) and the Corsaire metabolomics core facility (Biogenouest).

Notes and references

1. J. V. Duynhoven, E. V. Velzen and D. M. Jacobs, Annu. Rep. NMR Spectrosc., 2013, 80, 181.
2. R. Novoa-Carballal, E. Fernandez-Megia, C. Jimenez and R. Riguera, Nat. Prod. Rep., 2011, 28, 78.
3. R. Freeman, Spin Choreography: Basic Steps in High Resolution NMR, Oxford University Press, 1998.
4. N. G. Bell, L. Murray, M. C. Graham and D. Uhrin, Chem. Commun., 2014, 50, 1694.
5. L. Castanar and T. Parella, Magn. Reson. Chem., 2015, 53, 399.
6. L. Castanar, Magn. Reson. Chem., 2017, 55, 47.
7. G. A. Morris, eMagRes, 2009 DOI:10.1002/9780470034590.emrstm0119.pub2.
8. G. N. M. Reddy and S. Caldarelli, Chem. Commun., 2011, 47, 4297.
9. P. Lameiras and J. M. Nuzillard, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 123, 1.
10. P. Giraudeau, Magn. Reson. Chem., 2014, 52, 259.
11. W. P. Aue, J. Karhan and R. R. Ernst, J. Chem. Phys., 1976, 64, 4226.
12. C. Ludwig and M. R. Viant, Phytochem. Anal., 2010, 21, 22.
13. J. R. Garbow, D. P. Weitekamp and A. Pines, Chem. Phys. Lett., 1982, 93, 504.
14. K. Zangger and H. Sterk, J. Magn. Reson., 1997, 124, 486.
15. N. H. Meyer and K. Zangger, Angew. Chem., Int. Ed., 2013, 52, 7143.
16. N. H. Meyer and K. Zangger, Chem. Phys. Chem., 2014, 15, 49.
17. J. A. Aguilar, S. Faulkner, M. Nilsson and G. A. Morris, Angew. Chem., Int. Ed., 2010, 49, 3901.
18. L. Paudel, R. W. Adams, P. Kiraly, J. A. Aguilar, M. Foroozandeh, M. J. Cliff, M. Nilsson, P. Sandor, J. P. Waltho and G. A. Morris, Angew. Chem., Int. Ed., 2013, 52, 11616.
19. M. Foroozandeh, R. W. Adams, N. J. Meharry, D. Jeannerat, M. Nilsson and G. A. Morris, Angew. Chem., Int. Ed., 2014, 53, 6990.
20. A. J. Pell, R. A. Edden and J. Keeler, Magn. Reson. Chem., 2007, 45, 296.
21. I. Timari, C. Wang, A. L. Hansen, G. Costa Dos Santos, S. O. Yoon, L. Bruschweiler-Li and R. Bruschweiler, Anal. Chem., 2019, 91, 2304.
22. J. Farjon, C. Milande, E. Martineau, S. Akoka and P. Giraudeau, Anal. Chem., 2018, 90, 1845.
23. P. Sakhaii, B. Haase, W. Bermel, R. Kerssebaum, G. E. Wagner and K. Zangger, J. Magn. Reson., 2013, 233, 92.
24. J. Mauhart, S. Glanzer, P. Sakhaii, W. Bermel and K. Zangger, J. Magn. Reson., 2015, 259, 207.
25. P. Moutzouri, Y. Chen, M. Foroozandeh, P. Kiraly, A. R. Phillips, S. R. Coombes, M. Nilsson and G. A. Morris, Chem. Commun., 2017, 53, 10188.
26. G. Bertho, L. Lordello, X. Chen, C. Lucas-Torres, I. E. Oumezziane, C. Caradeuc, M. Baudin, S. Nuan-Aliman, C. Thieblemont, V. Baud and N. Giraud, J. Proteome Res., 2022, 21, 1041.
27. J. M. Lopez, R. Cabrera and H. Maruenda, Sci. Rep., 2019, 9, 6900.
28. L. Castanar, R. Roldan, P. Clapes, A. Virgili and T. Parella, Chemistry, 2015, 21, 7682.
29. L. Castanar, M. Perez-Trujillo, P. Nolis, E. Monteagudo, A. Virgili and T. Parella, Chem. Phys. Chem., 2014, 15, 854.
30. C. Mycroft, M. Nilsson, G. A. Morris and L. Castanar, Chem. Phys. Chem., 2022 DOI:10.1002/cphc.202200495.
31. D. Sinnaeve, eMagRes, 2016, 967–980.
32. W. S. Price, Concepts Magn. Reson., 1997, 9, 299.
33. P. Stilbs, Anal. Chem., 2002, 53, 2135.
34. C. S. Johnson, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 34, 203.
35. G. Pagès, V. Gilard, R. Martino and M. Malet-Martino, Analyst, 2017, 142, 3771.
36. D. Li, I. Keresztes, R. Hopson and P. G. Williard, Acc. Chem. Res., 2009, 42, 270.
37. L. Avram and Y. Cohen, Chem. Soc. Rev., 2015, 44, 586.
38. S. Balayssac, S. Trefi, V. Gilard, M. Malet-Martino, R. Martino and M. A. Delsuc, J. Pharm. Biomed. Anal., 2009, 50, 602.
39. M. Nilsson, M. A. Connell, A. L. Davis and G. A. Morris, Anal. Chem., 2006, 78, 3040.
40. P. Stilbs and K. Paulsen, Rev. Sci. Instrum., 1996, 67, 4380.
41. M. Nilsson and G. A. Morris, Anal. Chem., 2008, 80, 3777.
42. B. Antalek and W. Windig, J. Am. Chem. Soc., 1996, 118, 10331.
43. W. Windig and B. Antalek, Chemom. Intell. Lab. Syst., 1997, 37, 241.
44. I. Toumi, B. Torrésani and S. Caldarelli, Anal. Chem., 2013, 85, 11344.
45. G. Dal Poggetto, L. Castanar, R. W. Adams, G. A. Morris and M. Nilsson, J. Am. Chem. Soc., 2019, 141, 5766.
46. S. Glanzer and K. Zangger, Chemistry, 2014, 20, 11171.
47. M. Nilsson and G. A. Morris, Chem. Commun., 2007, 933.
48. S. Viel and S. Caldarelli, Chem. Commun., 2008, 2013.
49. M. Nilsson, A. M. Gil, I. Delgadillo and G. A. Morris, Chem. Commun., 2005, 1737.
50. J. M. Newman and A. Jerschow, Anal. Chem., 2007, 79, 2957.
51. G. Dal Poggetto, L. Castanar, M. Foroozandeh, P. Kiraly, R. W. Adams, G. A. Morris and M. Nilsson, Anal. Chem., 2018, 90, 13695.
52. L. Castañar, G. D. Poggetto, A. A. Colbourne, G. A. Morris and M. Nilsson, Magn. Reson. Chem., 2018, 56, 546.
53. J. Cassani, M. Nilsson and G. A. Morris, J. Nat. Prod., 2012, 75, 131.
54. N. V. Gramosa, N. Ricardo, R. W. Adams, G. A. Morris and M. Nilsson, Magn. Reson. Chem., 2016, 54, 815.
55. T. Gonzalez-Garcia, T. Margola, A. Silvagni, F. Mancin and F. Rastrelli, Angew. Chem., Int. Ed., 2016, 55, 2733.
56. G. Pages, C. Delaurent and S. Caldarelli, Angew. Chem., Int. Ed., 2006, 45, 5950.
57. M. V. Salvia, F. Ramadori, S. Springhetti, M. Diez-Castellnou, B. Perrone, F. Rastrelli and F. Mancin, J. Am. Chem. Soc., 2015, 137, 886.
58. M. Diez-Castellnou, M. V. Salvia, S. Springhetti, F. Rastrelli and F. Mancin, Chemistry, 2016, 22, 16957.
59. F. De Biasi, F. Mancin and F. Rastrelli, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 117, 70.
60. G. N. Manjunatha Reddy and S. Caldarelli, Anal. Chem., 2010, 82, 3266.
61. G. N. Reddy and S. Caldarelli, Analyst, 2012, 137, 741.
62. G. N. Manjunatha Reddy, M. Yemloul and S. Caldarelli, Magn. Reson. Chem., 2017, 55, 492.
63. E. Piersanti, C. Righetti, D. Ribeaucourt, A. J. Simaan, Y. Mekmouche, M. Lafond, J. G. Berrin, T. Tron and M. Yemloul, Analyst, 2022, 147, 2515.
64. F. Zhang and R. Brüschweiler, Angew. Chem., Int. Ed., 2007, 46, 2639.
65. F. Zhang, S. L. Robinette, L. Bruschweiler-Li and R. Bruschweiler, Magn. Reson. Chem., 2009, 47(suppl 1), S118.
66. A. J. Simpson, G. Woods and O. Mehrzad, Anal. Chem., 2008, 80, 186.
67. P. Lameiras and J. M. Nuzillard, Anal. Chem., 2016, 88, 4508.
68. P. Lameiras, S. Patis, J. Jakhlal, S. Castex, P. Clivio and J. M. Nuzillard, Chemistry, 2017, 23, 4923.
69. F. Pedinielli, J. M. Nuzillard and P. Lameiras, Anal. Chem., 2020, 92, 5191.
70. P. Sandusky and D. Raftery, Anal. Chem., 2005, 77, 2455.
71. G. Dal Poggetto, L. Castañar, G. A. Morris and M. Nilsson, RSC Adv., 2016, 6, 100063.
72. N. MacKinnon, P. T. While and J. G. Korvink, J. Magn. Reson., 2016, 272, 147.
73. P. T. Robinson, T. N. Pham and D. Uhrin, J. Magn. Reson., 2004, 170, 97.
74. S. J. Duncan, R. Lewis, M. A. Bernstein and P. Sandor, Magn. Reson. Chem., 2007, 45, 283.
75. P. Kiraly, N. Kern, M. P. Plesniak, M. Nilsson, D. J. Procter, G. A. Morris and R. W. Adams, Angew. Chem., Int. Ed., 2021, 60, 666.
76. P. Kiraly, M. Nilsson, G. A. Morris and R. W. Adams, Chem. Commun., 2021, 57, 2368.
77. L. D. Hall and T. J. Norwood, J. Magn. Reson., 1988, 78, 582.
78. L. D. Laurance and T. J. Norwood, J. Magn. Reson., 1988, 76, 548.
79. L. Castanar, P. Moutzouri, T. M. Barbosa, C. F. Tormena, R. Rittner, A. R. Phillips, S. R. Coombes, M. Nilsson and G. A. Morris, Anal. Chem., 2018, 90, 5445.
80. J. H. Ardenkjaer-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acd. Sci. U. S. A., 2003, 100, 10158.
81. R. W. Adams, J. A. Aguilar, K. D. Atkinson, M. J. Cowley, P. I. P. Elliott, S. B. Duckett, G. G. R. Green, I. G. Khazal, J. Lopez-Serrano and D. C. Williamson, Science, 2009, 323, 1708.
82. C. R. Bowers and D. P. Weitekamp, Phys. Rev. Lett., 1986, 57, 2645.
83. C. R. Bowers and D. P. Weitekamp, J. Am. Chem. Soc., 1987, 109, 5541.
84. D. Dai, X. Wang, Y. Liu, X. L. Yang, C. Glaubitz, V. Denysenkov, X. He, T. Prisner and J. Mao, Nat. Commun., 2021, 12, 6880.
85. G. Liu, M. Levien, N. Karschin, G. Parigi, C. Luchinat and M. Bennati, Nat. Chem., 2017, 9, 676.
86. J. N. Thomas, V. Ramaswamy, I. M. Litvak, T. L. Johnston, A. S. Edison and W. W. Brey, IEEE Trans. Appl. Supercond., 2021, 31, 20210222.
87. S. J. Elliott, Q. Stern, M. Ceillier, T. El Daraï, S. F. Cousin, O. Cala and S. Jannin, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 126–127, 59.
88. H.-Y. Chen and C. Hilty, Chem. Phys. Chem., 2015, 16, 2646.
89. M. Ceillier, O. Cala, T. El Daraï, S. F. Cousin, Q. Stern, S. Guibert, S. J. Elliott, A. Bornet, B. Vuichoud, J. Milani, C. Pages, D. Eshchenko, J. G. Kempf, C. Jose, S. A. Lambert and S. Jannin, Journal of Magnetic Resonance Open, 2021, 8–9, 100017.
90. S. Katsikis, I. Marin-Montesinos, M. Pons, C. Ludwig and U. L. Günther, Appl. Magn. Reson., 2015, 46, 723.
91. A. B. Frahm, D. Hill, S. Katsikis, T. Andreassen, J. H. Ardenkjaer-Larsen, T. F. Bathen, S. A. Moestue, P. R. Jensen and M. H. Lerche, Talanta, 2021, 235, 122812.
92. S. Bowen and C. Hilty, Angew. Chem., Int. Ed., 2008, 47, 5235.
93. Y. Lee, G. S. Heo, H. Zeng, K. L. Wooley and C. Hilty, J. Am. Chem. Soc., 2013, 135, 4636.
94. C. H. Chen, W. C. Shih and C. Hilty, J. Am. Chem. Soc., 2015, 137, 6965.
95. Y. Kim, C. H. Chen and C. Hilty, Chem. Commun., 2018, 54, 4333.
96. J. Kim, Y. Kim, Q. S. Luu, J. Kim, C. Qi, C. Hilty and Y. Lee, Chem. Commun., 2020, 56, 15000.
97. Y. Kim, H. Samouei and C. Hilty, Chem. Sci., 2021, 12, 2823.
98. P. R. Jensen, S. Meier, J. H. Ardenkjaer-Larsen, J. O. Duus, M. Karlsson and M. H. Lerche, Chem. Commun., 2009, 5168.
99. P. R. Jensen and S. Meier, Chem. Commun., 2020, 56, 6245.
100. P. R. Jensen, F. Sannelli, L. T. Stauning and S. Meier, Chem. Commun., 2021, 57, 10572.
101. C. Kjeldsen, J. H. Ardenkjaer-Larsen and J. O. Duus, J. Am. Chem. Soc., 2018, 140, 3030.
102. J.-N. Dumez, J. Milani, B. Vuichoud, A. Bornet, J. Lalande-Martin, I. Tea, M. Yon, M. Maucourt, C. Deborde, A. Moing, L. Frydman, G. Bodenhausen, S. Jannin and P. Giraudeau, Analyst, 2015, 140, 5860.
103. M. H. Lerche, D. Yigit, A. B. Frahm, J. H. Ardenkjaer-Larsen, R. M. Malinowski and P. R. Jensen, Anal. Chem., 2018, 90, 674.
104. A. Bornet, M. Maucourt, C. Deborde, D. Jacob, J. Milani, B. Vuichoud, X. Ji, J. N. Dumez, A. Moing, G. Bodenhausen, S. Jannin and P. Giraudeau, Anal. Chem., 2016, 88, 6179.
105. A. Dey, B. Charrier, E. Martineau, C. Deborde, E. Gandriau, A. Moing, D. Jacob, D. Eshchenko, M. Schnell, R. Melzi, D. Kurzbach, M. Ceillier, Q. Chappuis, S. F. Cousin, J. G. Kempf, S. Jannin, J.-N. Dumez and P. Giraudeau, Anal. Chem., 2020, 92, 14867.
106. A. Bornet, R. Melzi, A. J. Perez Linde, P. Hautle, B. van den Brandt, S. Jannin and G. Bodenhausen, J. Phys. Chem. Lett., 2013, 4, 111.
107. R. Kircher, H. Hasse and K. Munnemann, Anal. Chem., 2021, 93, 8897.
108. M. Sharma, G. Janssen, J. Leggett, A. P. Kentgens and P. J. van Bentum, J. Magn. Reson., 2015, 258, 40.
109. T. R. Eichhorn, A. J. Parker, F. Josten, C. Muller, J. Scheuer, J. M. Steiner, M. Gierse, J. Handwerker, M. Keim, S. Lucas, M. U. Qureshi, A. Marshall, A. Salhov, Y. Quan, J. Binder, K. D. Jahnke, P. Neumann, S. Knecht, J. W. Blanchard, M. B. Plenio, F. Jelezko, L. Emsley, C. C. Vassiliou, P. Hautle and I. Schwartz, J. Am. Chem. Soc., 2022, 144, 2511.
110. S. Korchak, L. Kaltschnee, R. Dervisoglu, L. Andreas, C. Griesinger and S. Gloggler, Angew. Chem., Int. Ed., 2021, 60, 20984.
111. L. S. Lloyd, R. W. Adams, M. Bernstein, S. Coombes, S. B. Duckett, G. G. Green, R. J. Lewis, R. E. Mewis and C. J. Sleigh, J. Am. Chem. Soc., 2012, 134, 12904.
112. R. E. Mewis, K. D. Atkinson, M. J. Cowley, S. B. Duckett, G. G. Green, R. A. Green, L. A. Highton, D. Kilgour, L. S. Lloyd, J. A. Lohman and D. C. Williamson, Magn. Reson. Chem., 2014, 52, 358.
113. N. Eshuis, N. Hermkens, B. J. van Weerdenburg, M. C. Feiters, F. P. Rutjes, S. S. Wijmenga and M. Tessari, J. Am. Chem. Soc., 2014, 136, 2695.
114. R. Fraser, F. Rutjes, M. C. Feiters and M. Tessari, Acc. Chem. Res., 2022, 55, 1832.
115. N. Eshuis, B. J. A. van Weerdenburg, M. C. Feiters, F. P. J. T. Rutjes, S. S. Wijmenga and M. Tessari, Angew. Chem., Int. Ed., 2015, 54, 1481.
116. I. Reile, R. Aspers, J. M. Tyburn, J. G. Kempf, M. C. Feiters, F. Rutjes and M. Tessari, Angew. Chem., Int. Ed., 2017, 56, 9174.
117. N. Eshuis, R. L. E. G. Aspers, B. J. A. van Weerdenburg, M. C. Feiters, F. P. J. T. Rutjes, S. S. Wijmenga and M. Tessari, Angew. Chem., Int. Ed., 2015, 54, 14527.
118. N. K. Hermkens, N. Eshuis, B. J. van Weerdenburg, M. C. Feiters, F. P. Rutjes, S. S. Wijmenga and M. Tessari, Anal. Chem., 2016, 88, 3406.
119. I. Reile, N. Eshuis, N. K. Hermkens, B. J. van Weerdenburg, M. C. Feiters, F. P. Rutjes and M. Tessari, Analyst, 2016, 141, 4001.
120. L. Sellies, I. Reile, R. Aspers, M. C. Feiters, F. Rutjes and M. Tessari, Chem. Commun., 2019, 55, 7235.
121. N. Reimets, K. Ausmees, S. Vija and I. Reile, Anal. Chem., 2021, 93, 9480.
122. W. Iali, P. J. Rayner and S. B. Duckett, Sci. Adv., 2018, 4, eaao6250.
123. P. M. Richardson, R. O. John, A. J. Parrott, P. J. Rayner, W. Iali, A. Nordon, M. E. Halse and S. B. Duckett, Phys. Chem. Chem. Phys., 2018, 20, 26362.
124. P. M. Richardson, W. Iali, S. S. Roy, P. J. Rayner, M. E. Halse and S. B. Duckett, Chem. Sci., 2019, 10, 10607.
125. L. Sellies, R. Aspers, M. C. Feiters, F. Rutjes and M. Tessari, Angew. Chem., Int. Ed., 2021, 60, 26954.
126. O. Semenova, P. M. Richardson, A. J. Parrott, A. Nordon, M. E. Halse and S. B. Duckett, Anal. Chem., 2019, 91, 6695.
127. B. J. Tickner, P. J. Rayner and S. B. Duckett, Anal. Chem., 2020, 92, 9095.
128. P. J. Rayner, M. Fekete, C. A. Gater, F. Ahwal, N. Turner, A. J. Kennerley and S. B. Duckett, J. Am. Chem. Soc., 2022, 144, 8756.
129. P. L. Norcott, Phys. Chem. Chem. Phys., 2022, 24, 13527.
130. E. Cavallari, C. Carrera, S. Aime and F. Reineri, Chemistry, 2017, 23, 1200.
131. J. Eills, E. Cavallari, C. Carrera, D. Budker, S. Aime and F. Reineri, J. Am. Chem. Soc., 2019, 141, 20209.
132. Y. Ding, S. Korchak, S. Mamone, A. P. Jagtap, G. Stevanato, S. Sternkopf, D. Moll, H. Schroeder, S. Becker, A. Fischer, E. Gerhardt, T. F. Outeiro, F. Opazo, C. Griesinger and S. Glöggler, Chem.: Methods, 2022, 2, e202200023.
133. L. Frydman, T. Scherf and A. Lupulescu, Proc. Natl. Acd. Sci. U. S. A., 2002, 99, 15858.
134. K. Kazimierczuk and V. Y. Orekhov, Angew. Chem., Int. Ed., 2011, 50, 5556.
135. D. J. Holland, M. J. Bostock, L. F. Gladden and D. Nietlispach, Angew. Chem., Int. Ed., 2011, 50, 6548.
136. M. J. Thrippleton, N. M. Loening and J. Keeler, Magn. Reson. Chem., 2003, 41, 441.
137. D. Schulze-Sunninghausen, J. Becker and B. Luy, J. Am. Chem. Soc., 2014, 136, 1242.
138. E. Kupce and R. Freeman, Magn. Reson. Chem., 2007, 45, 2.
139. E. Kupce and T. D. W. Claridge, Angew. Chem., Int. Ed., 2017, 56, 11779.
140. K. Motiram-Corral, M. Perez-Trujillo, P. Nolis and T. Parella, Chem. Commun., 2018, 54, 13507.
141. J. N. Dumez, Prog. Nucl. Magn. Reson. Spectrosc., 2018, 109, 101.
142. C. Lhoste, B. Lorandel, C. Praud, A. Marchand, R. Mishra, A. Dey, A. Bernard, J.-N. Dumez and P. Giraudeau, Prog. Nucl. Magn. Reson. Spectrosc., 2022, 130–131, 1.
143. B. Shapira, A. Karton, D. Aronzon and L. Frydman, J. Am. Chem. Soc., 2004, 126, 1262.
144. A. Herrera, E. Fernandez-Valle, E. M. Gutierrez, R. Martinez-Alvarez, D. Molero, Z. D. Pardo and E. Saez, Org. Lett., 2010, 12, 144.
145. M. Gal, M. Mishkovsky and L. Frydman, J. Am. Chem. Soc., 2006, 128, 951.
146. A. Herrera, E. Fernandez-Valle, R. Martinez-Alvarez, D. Molero, Z. D. Pardo, E. Saez and M. Gal, Angew. Chem., Int. Ed., 2009, 48, 6274.
147. Z. D. Pardo, G. L. Olsen, M. E. Fernandez-Valle, L. Frydman, R. Martinez-Alvarez and A. Herrera, J. Am. Chem. Soc., 2012, 134, 2706.
148. I. Fernandez, M. E. Fernandez-Valle, R. Martinez-Alvarez, D. Molero-Vilchez, Z. D. Pardo, E. Saez-Barajas, A. Sanchez and A. Herrera, J. Org. Chem., 2014, 79, 8086.
149. M. E. Fernandez-Valle, R. Martinez-Alvarez, D. Molero-Vilchez, Z. D. Pardo, E. Saez-Barajas and A. Herrera, J. Org. Chem., 2015, 80, 799.
150. L. Frydman, A. Lupulescu and T. Scherf, J. Am. Chem. Soc., 2003, 125, 9204.
151. M. Pathan, S. Akoka, I. Tea, B. Charrier and P. Giraudeau, Analyst, 2011, 136, 3157.
152. A. Le Guennec, I. Tea, I. Antheaume, E. Martineau, B. Charrier, M. Pathan, S. Akoka and P. Giraudeau, Anal. Chem., 2012, 84, 10831.
153. A. L. Guennec, P. Giraudeau and S. Caldarelli, Anal. Chem., 2014, 86, 5946.
154. T. Jézéquel, C. Deborde, M. Maucourt, V. Zhendre, A. Moing and P. Giraudeau, Metabolomics, 2015, 11, 1231.
155. J. Marchand, E. Martineau, Y. Guitton, B. Le Bizec, G. Dervilly-Pinel and P. Giraudeau, Metabolomics, 2018, 14, 60.
156. A. Le Guennec, P. Giraudeau, S. Caldarelli and J.-N. Dumez, Chem. Commun., 2015, 51, 354.
157. L. Rouger, B. Gouilleux, M. Pourchet-Gellez, J. N. Dumez and P. Giraudeau, Analyst, 2016, 141, 1686.
158. M. G. Concilio, C. Jacquemmoz, D. Boyarskaya, G. Masson and J. N. Dumez, Chem. Phys. Chem., 2018, 19, 3310.
159. M. Andre, M. Piotto, S. Caldarelli and J. N. Dumez, Analyst, 2015, 140, 3942.
160. Y. Shrot and L. Frydman, J. Magn. Reson., 2008, 195, 226.
161. L. Guduff, I. Kuprov, C. Van Heijenoort and J. N. Dumez, Chem. Commun., 2017, 53, 701.
162. C. Jacquemmoz and J. N. Dumez, Chem. Phys. Chem., 2018, 19, 3204.
163. G. Hamdoun, L. Guduff, C. van Heijenoort, C. Bour, V. Gandon and J.-N. Dumez, Analyst, 2018, 143, 3458.
164. R. Mishra, A. Marchand, C. Jacquemmoz and J.-N. Dumez, Chem. Commun., 2021, 57, 2384.
165. P. Giraudeau, Y. Shrot and L. Frydman, J. Am. Chem. Soc., 2009, 131, 13902.
166. V. Daniele, F.-X. Legrand, P. Berthault, J.-N. Dumez and G. Huber, Chem. Phys. Chem., 2015, 16, 3413.
167. L. Guduff, D. Kurzbach, C. van Heijenoort, D. Abergel and J.-N. Dumez, Chem. – Eur. J., 2017, 23, 16722.
168. L. Guduff, P. Berthault, C. van Heijenoort, J.-N. Dumez and G. Huber, Chem. Phys. Chem., 2019, 20, 392.
169. K. Singh, C. Jacquemmoz, P. Giraudeau, L. Frydman and J. N. Dumez, Chem. Commun., 2021, 57, 8035.
170. L. Frydman and D. Blazina, Nat. Phys., 2007, 3, 415.
171. M. Mishkovsky and L. Frydman, Chem. Phys. Chem., 2008, 9, 2340.
172. R. Panek, J. Granwehr, J. Leggett and W. Köckenberger, Phys. Chem. Chem. Phys., 2010, 12, 5771.
173. D. Golowicz, P. Kasprzak, V. Orekhov and K. Kazimierczuk, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 116, 40.
174. E. Martineau, J. N. Dumez and P. Giraudeau, Magn. Reson. Chem., 2020, 58, 390.
175. E. Martineau, S. Akoka, R. Boisseau, B. Delanoue and P. Giraudeau, Anal. Chem., 2013, 85, 4777.
176. T. V. Schlippenbach, P. J. Oefner and W. Gronwald, Sci. Rep., 2018, 8, 4249.
177. P. N. Reardon, C. L. Marean-Reardon, M. A. Bukovec, B. E. Coggins and N. G. Isern, Anal. Chem., 2016, 88, 2825.
178. A. Le Guennec, J. N. Dumez, P. Giraudeau and S. Caldarelli, Magn. Reson. Chem., 2015, 53, 913.
179. P. C. Aoto, R. B. Fenwick, G. J. Kroon and P. E. Wright, J. Magn. Reson., 2014, 246, 31.
180. R. Dass, W. Kozminski and K. Kazimierczuk, Anal. Chem., 2015, 87, 1337.
181. M. Urbanczyk, A. Shchukina, D. Golowicz and K. Kazimierczuk, Magn. Reson. Chem., 2019, 57, 4.
182. D. Golowicz, M. Kazmierczak and K. Kazimierczuk, Magn. Reson. Chem., 2021, 59, 213.
183. Y. Wu, C. D'Agostino, D. J. Holland and L. F. Gladden, Chem. Commun., 2014, 50, 14137.
184. M. Urbanczyk, D. Bernin, A. Czuron and K. Kazimierczuk, Analyst, 2016, 141, 1745.
185. T. S. C. MacDonald, W. S. Price and J. E. Beves, Chem. Phys. Chem., 2019, 20, 926.
186. L. L. Fillbrook, M. D. Nothling, M. H. Stenzel, W. S. Price and J. E. Beves, ACS Macro Lett., 2022, 11, 166.
187. K. Kristinaityte, A. Mames, M. Pietrzak, F. F. Westermair, W. Silva, R. M. Gschwind, T. Ratajczyk and M. Urbańczyk, J. Am. Chem. Soc., 2022, 144, 13945.
188. D. Schulze-Sunninghausen, J. Becker, M. R. M. Koos and B. Luy, J. Magn. Reson., 2017, 281, 151.
189. M. P. Schatzlein, J. Becker, D. Schulze-Sunninghausen, A. Pineda-Lucena, J. R. Herance and B. Luy, Anal. Bioanal. Chem., 2018, 410, 2793.
190. R. Sharma, N. Gogna, H. Singh and K. Dorai, RSC Adv., 2017, 7, 29860.
191. T. M. Nagy, K. E. Kover and O. W. Sorensen, Angew. Chem., Int. Ed., 2021, 60, 13587.
192. A. L. Hansen, E. R. Kupce, D. W. Li, L. Bruschweiler-Li, C. Wang and R. Bruschweiler, Anal. Chem., 2021, 93, 6112.
193. Y. Ben-Tal, P. J. Boaler, H. J. A. Dale, R. E. Dooley, N. A. Fohn, Y. Gao, A. Garcia-Dominguez, K. M. Grant, A. M. R. Hall, H. L. D. Hayes, M. M. Kucharski, R. Wei and G. C. Lloyd-Jones, Prog. Nucl. Magn. Reson. Spectrosc., 2022, 129, 28.
194. A. M. R. Hall, J. C. Chouler, A. Codina, P. T. Gierth, J. P. Lowe and U. Hintermair, Catal. Sci. Technol., 2016, 6, 8406.
195. T. Castaing-Cordier, D. Bouillaud, J. Farjon and P. Giraudeau, in Annual Reports on NMR Spectroscopy, ed. G. A. Webb, Academic Press, 2021, pp. 191–258.
196. A. M. R. Hall, R. Broomfield-Tagg, M. Camilleri, D. R. Carbery, A. Codina, D. T. E. Whittaker, S. Coombes, J. P. Lowe and U. Hintermair, Chem. Commun., 2017, 54, 30.
197. A. M. R. Hall, P. Dong, A. Codina, J. P. Lowe and U. Hintermair, ACS Catal., 2019, 9, 2079.
198. A. S. H. Ryder, W. B. Cunningham, G. Ballantyne, T. Mules, A. G. Kinsella, J. Turner-Dore, C. M. Alder, L. J. Edwards, B. S. J. McKay, M. N. Grayson and A. J. Cresswell, Angew. Chem., Int. Ed., 2020, 59, 14986.
199. A. Marchand, R. Mishra, A. Bernard and J. N. Dumez, Chemistry, 2022, e202201175.
200. I. A. Thomlinson, M. G. Davidson, C. L. Lyall, J. P. Lowe and U. Hintermair, Chem. Commun., 2022, 58, 8242.
201. C. Jacquemmoz, F. Giraud and J.-N. Dumez, Analyst, 2020, 145, 478.
202. B. Gouilleux, B. Charrier, S. Akoka, F.-X. Felpin, M. Rodriguez-Zubiri and P. Giraudeau, TrAC, Trends Anal. Chem., 2016, 83, 65.
203. M. Lin and M. J. Shapiro, Anal. Chem., 1997, 69, 4731.

---