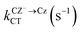Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Excited state mechanisms in crystalline carbazole: the role of aggregation and isomeric defects†
Federico J.
Hernández
 and
Rachel
Crespo-Otero
and
Rachel
Crespo-Otero
 *
*
Department of Chemistry, Queen Mary University of London, London, UK. E-mail: r.crespo-otero@qmul.ac.uk
First published on 3rd August 2021
Abstract
The molecule of carbazole (Cz) is commonly used as a building block in organic materials for optoelectronic applications, acting as a light-absorbing, electron donor and emitting moiety. Crystals from Cz and its derivatives display ultralong phosphorescence at room temperature. However, different groups have reported inconsistent quantum efficiencies for the same compounds. In a recent experimental study by Liu et al. (Nat. Mater. 2021, 20, 175–180), the ultralong phosphorescence properties of Cz have been associated with the presence of small fractions of isomeric impurities from commercially available Cz. In this paper, we use state-of-the-art computational approaches to investigate light-induced processes in crystalline and doped Cz. We revisit the role of aggregation and isomeric impurities on the excited state pathways and analyse the mechanisms for exciton, Dexter energy transfer and electron transport based on Marcus and Marcus–Levich–Jortner theories. Our excited state mechanisms provide a plausible interpretation of the experimental results and support the formation of charge-separated states at the defect/Cz molecular interface. These results contribute to a better understanding of the factors that enhance the excited state lifetimes in organic materials and the role of doping with organic molecules.
1 Introduction
The field of organic optoelectronics has experienced significant growth in the last few decades. The development of novel organic luminophores, commonly, aggregated structures of π-conjugated materials in the solid phase, has boosted the design of new materials for technologies such as photovoltaics, solid-state lasers, phototherapy, molecular sensing, optical imaging, and spintronics, amongst others.1–6 Since some of these applications benefit from long-lived excited states, achieving high populations of triplet states presents significant advantages.Metal-free organic chromophores have low spin–orbit couplings (SOCs) limiting the efficiency of intersystem crossing (ISC). However, different strategies can be implemented to promote ISC including designing donor–acceptor systems with small singlet–triplet gaps and molecules with electron transitions that involve a change in the character of the states such as n-π* transitions (El-Sayed rule).7 Other pathways include heavy-atom and halogen substitution as well as crystal engineering.8–10
The discovery of several pure organic room-temperature phosphorescence (RTP) materials, displaying excited state lifetimes of over 100 ms in the crystalline phase, has attracted significant attention due to their promising applications.11–17 Despite the recent experimental and theoretical efforts in this direction, the mechanisms behind ultralong organic phosphorescence (UOP) are yet to be fully understood.
Because of its extensive π-conjugation and easy derivatisation, Cz is a common building block in molecular materials for optoelectronic applications, acting as a light-absorbing, electron donor and emitting moiety.1,8,18 Molecular crystals from pure Cz and its derivatives display UOP at room temperature.8,19 However, there are inconsistencies in the values of the lifetimes and quantum yields reported by different groups.20 In a recent study, Liu et al. explored the role of isomeric defects in the UOP mechanism of Cz. The authors detected that the small fractions of 1H-benzo[f]indole (Bd, Fig. 1) found in commercial Cz are responsible for the ultralong lifetimes of the excited states. The isomeric defects serve as microplanar heterojunctions facilitating the formation of charge-separated states.20
In organic semiconductors, defects enable the formation of localised carrier states acting as traps for electrons and holes.21 The controlled use of defects to tune excited state lifetimes represents a promising opportunity in the field of functional electronic materials, which has been recently exploited for other organic systems demonstrating that this phenomenon is not exclusive to Cz.22 To better understand the mechanism of formation of long-lived triplets in Cz crystals, we investigate the processes activated by light and the role of isomeric defects. We start by examining the mechanism following a localised excitation on the embedded monomers. We analyse the exciton states and transport and evaluate the role of H-dimerisation in deactivation processes. We then investigate the formation of charge-transfer states in pure and doped crystalline Cz and the effect of isomeric defects of Bd on the excited state pathways. Our simulations help understand light-activated processes in crystalline Cz with implications in the design of new electronic materials for a broad range of applications.
2 Computational methods
The crystal structure of Cz, obtained from the CCDC (CCDC number: 1525166), was optimised with periodic DFT using Quantum Espresso.23 These calculations were done using the PBE-D2 functional with a plane wave cut-off of 40 Ry and ensuring Monkhorst–Pack k-point convergence (2 × 1 × 2).To simulate the excited states in the molecular crystal, we created cluster models of Cz and applied the QM–QM′ ONIOM schemes implemented in fromage.24,25 The QM regions included either one or two molecules of Cz simulated at the (TD-)B3LYP/6-311++G(d,p) level of theory using Gaussian 16.26 We tested different functionals including long-range corrected functionals with optimal tuning. The B3LYP functional showed the best agreement with the experiments (Section S1, ESI†). The cluster models considered 16 molecules for the case of one molecule in the QM region and 27 or 28 molecules for the QM regions including dimers. The QM′ region was described using the density functional tight-binding formalism as implemented in the DFTB+ package.27
The minima for the S0, S1, S2 and T1 states were optimised using the ONIOM Embedded Cluster model (OEC). The geometries of the T3/T2 and S2/S1 crossings were optimised with a penalty function28 with the condition of a zero energy gap. To explore the excited state mechanisms, we generated linear interpolated pathways based on the Cartesian coordinates of the stationary points (for example, between FC and S1min, T3min, T3/T2, T2min and T1min).
The effect of the long-range electrostatic interactions was addressed using the ONIOM Ewald Embedded Cluster (OEEC) model.24 For the electrostatic embedding at the higher level of theory, we use RESP charges obtained at the same level of theory. For the embedding of the lower level of theory, the charges were obtained with PBE/6-31G(d). Because long-range Coulomb interactions (model OEEC) do not have a significant effect on the energies (see Section S3, ESI†), we focus our discussion on the results obtained using the OEC model.
The probability of a radiative transition kif (and the corresponding radiative lifetime from state i, τi) between an initial state |Ψi〉 and a final state |Ψf〉 can be calculated using Fermi's Golden rule:29
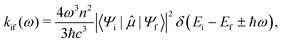 | (1) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i→f = 〈Sn|
i→f = 〈Sn|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |S0〉, where Sn is the emitting state, and in most cases n = 1 (Kasha's rule).
|S0〉, where Sn is the emitting state, and in most cases n = 1 (Kasha's rule).
In the case of phosphorescence, 〈Tm|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |S0〉 can be approximated using the first-order perturbation theory to include the spin–orbit coupling operator ĤSOC allowing intensity borrowing from spin-allowed transitions.31 This approximation converges slowly with the number of excited states and significant errors can be obtained even when hundreds of excited states are included.32,33 In this work, we use instead the multiconfigurational quadratic response (MCQR) method, which provides reliable values for μTm→S0.33 These calculations were performed at the TD-B3LYP/6-311++G(d,p) level of theory using the Dalton software.34,35
|S0〉 can be approximated using the first-order perturbation theory to include the spin–orbit coupling operator ĤSOC allowing intensity borrowing from spin-allowed transitions.31 This approximation converges slowly with the number of excited states and significant errors can be obtained even when hundreds of excited states are included.32,33 In this work, we use instead the multiconfigurational quadratic response (MCQR) method, which provides reliable values for μTm→S0.33 These calculations were performed at the TD-B3LYP/6-311++G(d,p) level of theory using the Dalton software.34,35
Herein, we estimate the rate constants for nonradiative electron transfer (ET) processes as intersystem crossing (ISC), and transport processes like exciton and charge transfer using the semiclassical Marcus theory as
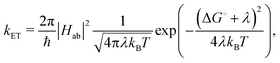 | (2) |
For ISC, Hab = 〈Sn|HSOC|Tm〉, where Sn and Tm are the singlet and triplet states involved in the Sn → Tm nonradiative transition. The reorganisation energy was approximated as λ ≈ ETm (Rmin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn) − ETm(Rmin
Sn) − ETm(Rmin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tm), as it has been done in previous studies.36 The spin–orbit couplings (SOCs) were evaluated at the TD-B3LYP/6-311++G(d,p) level of theory adopting the Breit–Pauli spin–orbit Hamiltonian with effective charge approximation as implemented in the PySOC package.37
Tm), as it has been done in previous studies.36 The spin–orbit couplings (SOCs) were evaluated at the TD-B3LYP/6-311++G(d,p) level of theory adopting the Breit–Pauli spin–orbit Hamiltonian with effective charge approximation as implemented in the PySOC package.37
The ET rate coefficients were also calculated using the Marcus–Levich–Jortner (MLJ) equation as implemented in ref. 38 and 39:
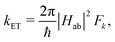 | (3) |
For the calculation of the fluorescence time constant (τf) and quantum yield (Φf), we analysed the processes depleting the population of S1 including internal conversion (kIC) and intersystem crossing (kISC). Experiments showed that internal conversion to the ground state is negligible with respect to kISC (kIC ≪ kISC).41,42 This is in line with the large gap between S1 and S0. We calculated the rates of intersystem crossing from S1 considering the transitions to T4, T3, T2 and T1. However, the transition S1 → T3 accounted for 99.9% of the total value. More information about the calculations of τf and Φf can be found in Section S4 of the ESI†.
For the calculation of the exciton hopping rates of the singlet and triplet states, the coupling terms (Hab = JSij and Hab = JTij) were evaluated using the half energy splitting method. The coupling terms used to evaluate the energy transfer rates of triplets (HTab) or charge hopping rates (HCTab) were computed using constrained DFT with configuration interactions (CDFT-CI) as implemented in Q-Chem.43 The active space considered for the CDFT-CI calculations of the couplings between the triplets was {|S0S0〉,|S0T1〉,|T1S0〉}. For the calculation of the charge transfer between negatively charged (Cz−) and neutral molecules, the active space compromised the following states: {|S0Cz−〉,|Cz−S0〉}. To analyse the performance of these methods, additional single point calculations were performed using the ADC(2)/TZVP level of theory with point charge embedding as implemented in Turbomole.44
We have also estimated the diffusion constant in the singlet or triplet state as
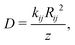 | (4) |
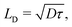 | (5) |
3 Results and discussion
Given the weak nature of intermolecular interactions in molecular organic crystals, localised excitations and incoherent exciton transfer are common mechanisms at room temperature.46 We have considered the formation of excited species localised on monomers and dimers in the Cz crystal as the initial step in the excited state mechanism. In the next section, we explore the excited state mechanism following the excitation of a single monomer in the crystal environment.3.1 The molecule centred mechanism
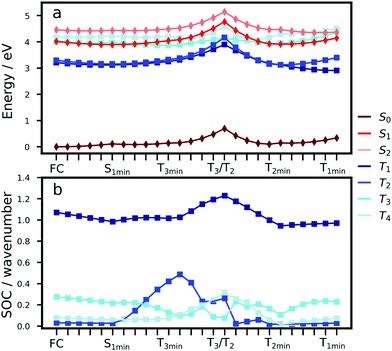
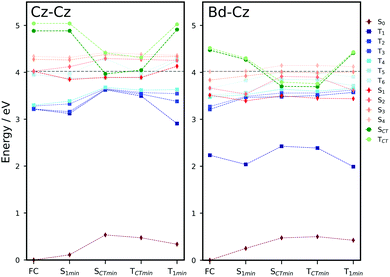
To understand the excited state processes, we explored the linear interpolated pathway between the ground state and the excited state minima and also evaluated the SOCs between the triplets and S1 (Fig. 2). There is a good agreement between the calculated energies at the TD-B3LYP/6-311++G(d,p) level of theory and the experimental data (Table S3, ESI†).18,19,20,47 A value of 3.73 eV is obtained for the S0 → S1 absorption energy of a cluster including 6 molecules of Cz in contrast with the experimental value of 3.62 eV.The experimental oscillator strength for the S0 → S2 transition in the gas phase is an order of magnitude greater than that for S0 → S1.41 A similar trend is observed in the solid state.18,19 Depending on the initial energy, either the S1 or the brightest S2 state can be populated. Provided initial excitation to S1, the system will follow vibrational relaxation in the picosecond scale to S1min from which fluorescence can compete with non-radiative mechanisms and processes like exciton transfer (see Section 3.2). Experiments in the gas phase using jet-cooled molecular beams do not show phosphorescence or nonradiative decay to S0 (ϕf ≈ 1).41 However, ISC is the main non-radiative pathway from S1 in the condensed phases.19,20,42
The fluorescence lifetime (τf) of Cz in solution under an inert atmosphere or dispersed in a solid matrix is around 14–15 ns, with a quantum yield of Φf = 0.4–0.6. When Cz is dissolved in organic media under an air saturated atmosphere, τf = 7.7–8.8 ns with Φf = 0.28–0.48.42 In the crystalline phase, τf = 8.2 ns at 300 K with a Φf = 0.78.18 For the pure crystal, we obtained fluorescence lifetimes of 11.1 and 7.9 ns and fluorescence quantum yields of 0.76 and 0.55 considering the Marcus and MLJ models, respectively. These values are in excellent agreement with the experimental ones (Table 1), which indicates that ISC is the most important competing pathway.
At the S1 minimum, the SOCs are smaller than 1 cm−1, which is not surprising in the light of the El-Sayed rule given the π–π* character of all states involved. However, if the energy gaps between the states of different multiplicities are small, ISC can happen even for small SOCs.48 Our values are in line with those reported by Ma et al. for Cz.49 The SOCs between S1 and Tn=1,2,3 remain almost unaltered between the FC and S1min geometries (Fig. 2b). Due to the similar energies of S1 and T3 (ΔES1–T3 = 0.07 eV), direct intersystem crossing is likely to occur (Fig. 2a). While the SOC values with T1 are almost 4 times greater than those with T3, a large energy gap (0.77 eV) prevents the occurrence of ISC to T1. The rates for the S1 → T3 transition calculated using the Marcus and MLJ equations are 2.14 107 s−1 and 5.75 × 107 s−1, respectively. These values are in line with the ISC rate of 3.87 × 107 s−1 obtained in a solid matrix of iso-propanol-ethyl ether and the rates obtained for Cz derivatives in the solid state (Table 1).18,42
The existence of a region for the crossing between both surfaces (T3/T2) promotes internal conversion from T3 to T2. The optimised geometry of the crossing shows a slight out-of-plane distortion from one of the aromatic rings (Fig. S6, ESI†). After the crossing, the population can split into two branches (right or left, Fig. 2), resulting in either phosphorescence or nonradiative decay. The band associated with phosphorescence from T1min appears at 2.25 eV18 (calculated value: 2.57 eV).
Crystalline Cz also shows a phosphorescence sideband at 2.95 eV, in very good agreement with the predicted emission from T2 found at 2.98 eV.19 This band becomes more intense when the crystal is electronically excited at energies over the S1 excitation energy (3.62 eV).19 Initial excitation to S2 could be followed by either IC to S1, the most likely pathway, or ISC to T4. The linear interpolated pathway considering relaxation from S2 is shown in Fig. S5 (ESI†). An appreciable vibronic coupling has been observed between S2 and S1 states in the gas-phase41 and solid state as well.50 We have also located an accessible S2/S1 crossing, which can help facilitate IC (Fig. S5 and S6, ESI†). Once in S1, the system can explore the relaxation pathways described before. Our estimated value of the ISC rate for the S2 → T4 transition is 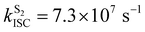 which is just 3.3 times greater than
which is just 3.3 times greater than 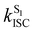 . At the S2min structure, S2 and T4 have very similar energies (ΔES2–T4 = −0.008 eV).
. At the S2min structure, S2 and T4 have very similar energies (ΔES2–T4 = −0.008 eV).
Once the system is in the lowest energy triplet manifold, provided the excess of vibrational energy, the molecule will be able to explore the left brand for a longer time allowing phosphorescence emission at higher energies (2.98 eV), which explains the sideband in the phosphorescence spectrum. The energies of T1 and T2 are almost degenerate and very close to the energy of the T2 minimum. Non-Kasha phosphorescence has been also observed for analogue systems based on dibenzothiophene, where a sideband shifted to blue from the T1 emission band was unambiguously assigned to the emission from T2.51
3.2 Exciton processes
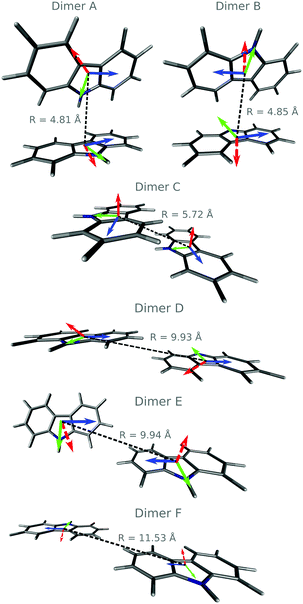
We have identified six different dimers (A–F, Fig. 3). Dimers A, B, and C have been previously reported.19,20 Dimers A, B, and E show edge-to-face arrangements commonly found in herringbone crystals, while dimers C and D are slipped π-stacking face-to-face structures. Dimer F is planar displaying a close H…H contact at 3.19 Å. Table 2 displays the splitting of the first excited state into the excitonic states S1 and S2. A very small red-shift of the absorption energy is predicted. For the singlet states, S1 and S2 are excitonic states. The largest exciton couplings are obtained for dimers B (4 × 10−3 eV) and C (2.3 × 10−2 eV) (Tables 2 and 3).
| Dimer | E S1 (eV) | f S1 | E S2 (eV) | f S2 | Aggregate | θ | |
|---|---|---|---|---|---|---|---|
| Mon 1 | Mon 2 | ||||||
| A | 4.010 | 0.032 | 4.011 | 0.016 | J | 28.9° | 79.7° |
| B | 4.001 | 0.032 | 4.009 | 0.012 | J | 26.5° | 77.1° |
| C | 3.972 | 0.077 | 4.019 | 0.001 | J | 27.8° | 26.7° |
| D | 4.021 | 0.000 | 4.023 | 0.058 | H | 83.0° | 83.1° |
| E | 4.018 | 0.018 | 4.020 | 0.044 | H | 72.0° | 77.6° |
| F | 4.019 | 0.000 | 4.020 | 0.063 | H | 57.1° | 57.1° |
| Singlets | ||||
|---|---|---|---|---|
| Dimer | J S ij (eV) | k S ij (s−1) | D S (cm2 s−1) | L SD (nm) |
| A | 1.0 × 10−3 | 7.8 × 108 (4.5 × 109) | 9.0 × 10−7 (5.2 × 10−6) | 1 (2) |
| B | 4.0 × 10−3 | 5.0 × 1010 (2.9 × 1011) | 5.9 × 10−5 (3.4 × 10−4) | 8 (20) |
| C | 2.3 × 10−2 | 1.7 × 1012 (9.5 × 1012) | 2.7 × 10−3 (1.6 × 10−2) | 56 (134) |
| D | 1.0 × 10−3 | 3.1 × 109 (1.8 × 1010) | 1.5 × 10−5 (8.9 × 10−5) | 4 (10) |
| E | 1.0 × 10−3 | 3.1 × 109 (1.8 × 1010) | 1.5 × 10−5 (8.9 × 10−5) | 4 (10) |
| F | 1.0 × 10−3 | 7.8 × 108 (4.5 × 109) | 5.2 × 10−6 (3.0 × 10−5) | 2 (6) |
| Triplets | ||||
|---|---|---|---|---|
| Dimer | H Tab (eV) | k T ij (s−1) | D T (cm2 s−1) | L TD (nm) |
| A | ≈0 | ≈0 | ≈0 | ≈0 |
| B | 4.2 × 10−4 | 7.4 × 106 (1.3 × 108) | 8.7 × 10−9 (1.6 × 10−7) | 979 (4179) |
| C | 2.3 × 10−3 | 2.3 × 108 (4.1 × 109) | 3.7 × 10−7 (6.8 × 10−6) | 6390 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 282) 282) |
| D | 1.2 × 10−4 | 6.0 × 105 (1.1 × 107) | 2.9 × 10−9 (5.4 × 10−8) | 569 (1399) |
| E | ≈0 | ≈0 | ≈0 | ≈0 |
| F | ≈0 | ≈0 | ≈0 | ≈0 |
Using the spectroscopic classification based on the oscillator strength values, the dimers can be classified as H- (D, E and F) or J-aggregates (A, B and C). The H-aggregates are obtained when fS2 > fS1 and J-aggregates when fS1 > fS2. Previous studies on the effect of H-aggregation in UOP organic materials have considered the classical Kasha's exciton model,19,52 which is based on the analysis of Coulombic interactions between two chromophores:
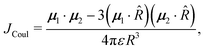 | (6) |
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) = R
= R![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) is the intermolecular displacement vector connecting the centres of mass of the monomers, and ε is the optical dielectric constant of the medium. For co-planar TDM vectors, the angle θ is defined as the angle between
is the intermolecular displacement vector connecting the centres of mass of the monomers, and ε is the optical dielectric constant of the medium. For co-planar TDM vectors, the angle θ is defined as the angle between ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) and the TDM vector of any of the chromophores, and JCoul is given by
and the TDM vector of any of the chromophores, and JCoul is given by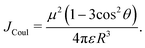 | (7) |
The exchange interactions not considered in Kasha's model could be relevant for these dimers with intermolecular distances of around 3 Å (Fig. S8, ESI†). Close packing arrangements are susceptible to experiencing a significant wave function overlap and therefore short-range interactions as exchange or superexchange. The magnitude of the short-range coupling can be comparable to or even exceed the Coulomb coupling. These interactions can promote a different exciton behaviour than normally associated with Kasha's H/J-aggregates,54 and thus the conventional geometric classification is incomplete at best.
In the case of the triplet states for the dimers A, B, C and E, the lowest energy states are localised and we could not find exciton states. For the dimers D and F, where the states T1–T6 are excitonic, the values of J are smaller than 2.5 × 10−4 eV except for the T5–T6 splitting with JT5T6 = 1.0 × 10−3 eV. We optimised the geometries of the T1 and S1 states of all dimers in the crystal environment. In line with the experimental observations, the predicted phosphorescence from T1 is an out-of-plane polarised transition (Fig. 3).55 Dimerisation has a minimal effect on the energy of the T1 → S0 transition and the corresponding phosphorescence lifetimes (see Table S7, ESI†). The SOC values between S1 and triplet states with lower or similar energies are not considerably increased with respect to the monomer (Tables S4 and S6, ESI†). Hence, no increase in the ISC rate constant is expected via direct SOC due to the presence of dimers though the number of ISC channels could be greater.
For embedded dimers, the T1 → S0 transition densities are localised on single molecules. A significant degree of localisation is also found for a cluster of six Cz molecules, all of them being treated quantum mechanically (Fig. S10, ESI†). Our calculations show that H/J-aggregation does not have a relevant effect on the energies or lifetimes of the triplet states of Cz. In the next section, we analyse the implications of the localisation of the excitations for different transport regimes for singlets and triplets in pure crystalline Cz.
To evaluate the rates of singlet exciton transport and triplet energy transfer in Cz crystals, we have considered the exciton coupling rates between adjacent molecules using the Marcus and MLJ models (eqn (2) and (3)). Table 3 shows the exciton hopping rates kij, diffusion coefficients D and diffusion lengths LD for S1 and T1 at 298 K. D and LD are obtained with eqn (4) and (5), respectively, using the distances between monomers shown in Fig. 3 and the experimental radiative lifetimes (Table 1). For both singlets and triplets, the hopping rate coefficients are systematically greater when the MLJ model is used. This shows the active role of vibrations in the exciton hopping process because the process is accompanied by a concomitant molecular distortion, i.e. the motion should have a polaronic character and thermally activated diffusion could be important.
The total reorganisation energy for exciton transfer in S1 is λ = 0.246 eV, which corresponds to an approximate barrier of λ/4 = 0.062 eV for the exciton hopping between adjacent molecules. This barrier is larger than the values of exciton couplings for all dimers. Thus, a significant localisation of the singlet excitation is expected and exciton transport should proceed through an incoherent hopping mechanism. In our calculations, six modes with frequencies of 670, 1035, 1307, 1337, 1371 and 1661 cm−1 associated with in-plane bending and stretching vibrations of the C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C
C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds of the π conjugated ring had the highest Huang–Rhys factors and were treated as quantum modes (see Section S2 and Fig. S7, ESI†). The largest value of J is obtained for dimer C due to its π-stacking structure. For dimer C, kij is comparable to the value obtained for the analogue slipped π-stacked dimer of anthracene, which also features a herringbone structure and an incoherent exciton transport mechanism.39
N bonds of the π conjugated ring had the highest Huang–Rhys factors and were treated as quantum modes (see Section S2 and Fig. S7, ESI†). The largest value of J is obtained for dimer C due to its π-stacking structure. For dimer C, kij is comparable to the value obtained for the analogue slipped π-stacked dimer of anthracene, which also features a herringbone structure and an incoherent exciton transport mechanism.39
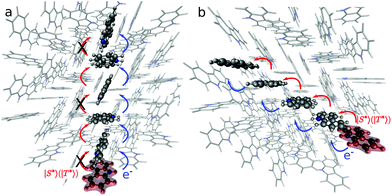
Fig. 4 shows possible exciton transfer paths through the dimers with the shortest intermolecular distances (A, B and C). The predicted exciton rate coefficients (Table 3) indicate that the only process likely to compete with vibrational relaxation to S1min (taking hνvib = 103 cm−1 leads to 2π/νvib = 2 × 10−13 s) is exciton transport along dimer C. Exciton hopping through dimer B involves further transfer through dimer A (Fig. 4a), which has a very small exciton coupling and hence a small hopping rate coefficient. The 1-D diffusion coefficients and diffusion lengths obtained considering exciton transport in S1 for dimer C are 2.7 × 10−3 cm2 s−1 and 134 nm, respectively, in qualitative agreement with the experimentally and computationally reported values for pure anthracene crystals.39 Exciton transport is also anisotropic in anthracene, where the slipped π-stacked dimer similar to dimer C also shows higher diffusion constant and length.39
In the case of T1, the rates were calculated considering λ = 0.643 eV and the normal mode with ωk = 1661 cm−1 with the highest Huang–Rhys factor (Fig. S7, ESI†), which involves the in-plane stretching vibration of the C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C
C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds of the ring. Due to their lower couplings and higher reorganisation energies, dimers B, C, and D show hopping rates three orders of magnitude smaller in T1 than in S1 (see Table 3). The small couplings in dimers A, E and F are caused by a small overlap between the constituent monomers, preventing any energy transfer in these directions (see Fig. 4a).
N bonds of the ring. Due to their lower couplings and higher reorganisation energies, dimers B, C, and D show hopping rates three orders of magnitude smaller in T1 than in S1 (see Table 3). The small couplings in dimers A, E and F are caused by a small overlap between the constituent monomers, preventing any energy transfer in these directions (see Fig. 4a).
Due to the spin-forbidden nature of phosphorescence, triplets exhibit lifetimes on the order of milliseconds for many of the pure organic materials with potential use in optoelectronics, or even longer as it is the case of Cz (1.1 s).18 The longer lifetime compensates the slow velocity yielding a much longer diffusion length for triplet excitons reaching lengths of tens of μm as shown in Table 3. Taking dimer C as an example, the diffusion constant in T1 is D = 6.8 × 10−6 cm2 s−1, 4 orders lower than that in S1, and two orders lower than the reported value for anthracene D = (0.5–2) × 10−4 cm2 s−1. However, the diffusion length estimated for dimer C is 27 μm, 200 times greater than LD in S1 and comparable to the value measured in anthracene crystals (LD = 7–20 μm).56 This huge increase comes from the long phosphorescence lifetime of T1 for Cz (see eqn (5)) (for anthracene τp = 23 ms).58
The long lifetime of triplets in Cz enables delayed fluorescence via triplet–triplet annihilation (TTA). Considering the kij of dimer C and no trapping or quenching, a triplet can visit 4.5 × 109 molecules in its lifetime period (1.1 × 105 for a singlet). However, the generation of triplets is limited by the slower kISC which is three times lower than kf (Table 1). Dopants can be used to facilitate ISC, for example, N,N-di(9H-fluoren-2-yl)phenanthrene-3-amine (DFAP) has been successfully used to increase triplet–triplet annihilation delayed fluorescence (TTADF) in fluorene crystals.59
The rate equation of the concentration of triplets [T] is
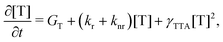 | (8) |
| γTTA = 4πRaD, | (9) |
Under the condition of a continuous generation of triplets (GT = const), the steady-state solution of eqn (8) produces two different regimes.56 At a low excitation power density (kr + knr)[T] ≫ γTTA[T]2 and [T] ∝ GT, the spontaneous decay governs the dynamics of excitons, whereas for high densities more triplet excitons are produced, γTTA[T]2 ≫ (kr + knr)[T] and 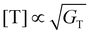 . Especially interesting is the power density at which (kr + knr)[T] = γTTA[T]2 because it represents the threshold at which the TTA process starts dominating the exciton dynamics. This power density threshold can be estimated from the material photophysical constants as
. Especially interesting is the power density at which (kr + knr)[T] = γTTA[T]2 because it represents the threshold at which the TTA process starts dominating the exciton dynamics. This power density threshold can be estimated from the material photophysical constants as
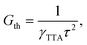 | (10) |
Eqn (10) indicates that exciton–exciton annihilation becomes more important as the exciton lifetime is longer. Considering dimer C, the bimolecular annihilation constant estimated for Cz is γTTA = 4.9 × 10−12 cm3 s−1. This value is comparable with the reported value for anthracene crystals γTTA = 2.1–2.4 × 10−11 cm3 s−1.60 Despite the low bimolecular annihilation constant, Cz presents a remarkably long phosphorescence lifetime which can yield a small Gth to produce TTADF using relatively low powers. Delayed fluorescence has been observed for pure Cz crystals,20 but no systematic investigation of the effect of the temperature or the light power density has been reported so far.
3.3 Isomeric impurities
Liu et al. showed that very low concentrations of Bd (even 0.1 mol%), an impurity commonly present in commercial Cz, display UOP at room temperature.20 Direct excitation and transport of singlets and triplets in the Cz crystal can enable the charge separation at Cz/Bd molecular junctions. Herein, we evaluate how the presence of Bd isomeric defects can affect the excited state mechanism of Cz in the solid state.In our calculations, we considered Bd-Cz dimers created by substituting a Cz molecule by a Bd molecule and reoptimised the geometries of the ground and excited states using the OEC method. The inclusion of long-range interactions (OEEC model) has a minimal effect on the energies of the excited states (Table S10, ESI†). Because of the alignment of the energy levels of Cz and Bd, the CT state where Cz acts as an electron acceptor from Bd (Cz−Bd+) is more stable than the (Cz+Bd−) state (Tables S9 and S11, ESI†).20 To analyse the role of the Cz−Bd+ states in the electron transfer process, we optimised these states using the CDFT method for dimers with smaller distances between the centres of mass (A–C).
Our calculations show that the presence of the Bd impurities redshifted the fluorescence emission energy of Cz around 33 nm (Table 4) which is in line with the 54 nm obtained experimentally. Both the S1 and T1 minima of the embedded Cz–Bd dimers show a significant localisation of the excitation on the Bd moiety (Fig. S12–S14, ESI†). The calculated absorption of the Cz–Bd dimers at 3.5 eV agrees with the onset absorption signal observed after HPLC of commercial Cz, which has been attributed to Bd.20
| Transition | Dimer A | Dimer B | Dimer C |
|---|---|---|---|
| S0 → S1 | 3.51 | 3.50 | 3.50 |
| S1 → S0 | 3.14 | 3.16 | 3.16 |
| T1 → S0 | 1.58 | 1.60 | 1.60 |
The predicted fluorescence band of the Cz–Bd dimers appeared at 3.14–3.16 eV within the region where delayed emission of Cz doped with Bd has been observed (354–543 nm).20 For dimers A and B, the energy gap between the Cz−Bd+ state and the ground state is around 3 eV, which is also in the same region. We explored the mechanism of formation of Cz−Bd+ states at the Cz–Bd molecular junction using the energy profiles based on different excited state minima for dimers A–C. Herein, we focus on the analysis of dimer A (Fig. 5), and the energy profiles for dimers A–C are shown in Fig. S12–S14 (ESI†), respectively.
For pure crystalline Cz, we have already discussed the monomer-centred mechanism in Section 3.1. Based on the localisation of the excitations and the energy profiles for the Cz dimers, we expect similar deactivation mechanisms. In this section, we analysed these decay pathways in doped dimers (Cz–Bd) contrasting them with the behaviour of pure Cz. The mechanism for the Cz dimers starts with the excitation to one of the exciton states (S1–S4), and analogously to the molecule-centred mechanism, vibrational relaxation is likely to stabilise the excitation in S1. For all dimers, S1 is clearly localised on one of the Cz monomers. In the case of Cz–Bd, for all dimers, the excitations obtained for the Franck–Condon and S1 minima are localised on Bd. Once in S1, the systems will emit light or nonradiative decay processes will be activated including exciton transport (Section 3.2.2) and charge transfer.
Decay to the triplet manifold through ISC is highly likely. For pure Cz, given the proximity in energy with T5 and T6 and their similar SOCs (0.36 and 0.26 cm−1, respectively) the transition could occur to any of these states (Table S6, ESI†). For doped Cz, at the S1 geometry, the T2, T3 and T4 states are almost resonant with S1 making ISC very likely. For B and C, the largest SOCs are obtained for T3 (0.53 and 0.45 cm−1, respectively) and in the case of A for T4 (0.92 cm−1). The SOCs are slightly larger than those obtained for pure Cz, which suggests that the impurity could help ISC. Following the population of the triplets, internal conversion will take the system to the localised T1 state.
How does the picture change for the Cz–Bd molecular junctions? Both the singlet and triplet Cz−Bd+ states are significantly more stable than in pure Cz. For the Bd doped dimers A and B, the energies of the Cz−Bd+ states at their optimised geometry are below the reference excitation energy for any of the S1–S4 states. Small amplitude vibrational distortions allowed in the crystalline phase facilitate the access to Cz−Bd+ states swiftly when an isomeric defect is nearby. For dimer C, Cz−Bd+ singlets and triplets are above the initial excitation energy and will require additional energy to become accessible. Given the longer lifetime of triplet states, it is highly probable for the electron transfer to happen from the triplet state.
While the energy of the optimised geometry for the Cz−Bd+ state is slightly higher than that for S1, charge separation can occur because the rate of charge transfer involving Cz− for dimers A–D is in the order of vibrational relaxation (Table 5). The mechanism involves the formation of Cz−Bd+ states associated with dimer A or B, followed by charge separation. The Bd+ radical cations can get trapped by the defects but Cz− can transport across the crystal (Cz−+ Cz = Cz + Cz−). Our calculated rates (Table 5) indicate that charge separation is faster for dimer C (1.7 × 1015 s−1, MLJ value), followed by dimer A (4.1 × 1014 s−1) and dimers D and B (4.1 × 1014 and 7.9 × 1013 s−1, respectively). Fig. 4 shows some possible pathways for electron transfer after the formation of the Cz− polarons. These processes keep the excitation alive for longer times contributing to the UOP.
The overall energy makeup indicates that the presence of isomeric impurities helps charge separation allowing the formation of negatively charged polarons (Cz−). In the experimental work, the absorption band at 460–472 nm (2.6–2.7 eV) has been assigned to the Cz− species.20 Our calculations of the embedded Cz− have the excitation with a higher oscillator strength predicted around 2.1 eV (2.3 eV with ADC(2)/TZVP, Table S12, ESI†).
For dimer A embedded in point charges, we compared the energy levels of the Cz−Cz+ and Cz−Bd+ geometries optimised at CDFT-B3LYP/6-311++G(d,p) with those calculated with ADC(2)/TZVP (Table S11, ESI†). For example, the energy gaps between the optimised Cz−Bd+ state and the ground state are 3.87 and 3.85 eV for ADC(2)/TZVP and CDFT-B3LYP/6-311++G(d,p), respectively. Both methods confirm that both the singlets and triplets of the Cz−Bd+ state are accessible provided initial excitation energy to S1. In the case of Cz–Cz dimers, these states are higher in energy, which explain why charge transfer states have not been observed in pure crystalline Cz.
4 Conclusions
Carbazole and its derivatives have applications in organic functional materials with long-lived excited states and ultralong phosphorescence. Due to the contradictory values of efficiencies and quantum yields obtained for materials synthesised by different groups, the interpretation of the processes underlying the UOP in Cz has been under debate.20 In this paper, we explore in detail the light-activated pathways in pure crystalline carbazole and Cz doped with Bd. In contrast with previously proposed mechanisms based on H-aggregation,19,52 we found that H- or J-aggregation does not affect appreciably the excited state deactivation pathways or the triplet lifetimes.In crystalline Cz, because of the small values of exciton couplings with respect to the reorganisation energies, the excited states are localised (1.0 × 10−3 eV < JSij < 2.3 × 10−2 eV, λ = 0.246 eV for S1). This is in line with the behaviour of most semiconducting organic crystals.21,39,61 Light-activated mechanisms centred on molecular Cz initiate a cascade of processes starting with the initial population of singlet states, which rapidly decay to S1 or the triplet manifold. These processes are essential to describe the excited state properties. This is supported by the excellent agreement between the predicted values of quantum yields only based on molecule centred processes and the experimental ones (0.76 (0.55) vs. 0.78). Our estimation of the intersystem crossing rates is also in excellent agreement with the experimental value, highlighting that ISC is the main nonradiative decay process depleting the singlet population.
Triplet states are clearly localised on independent Cz molecules and their main transport mechanism is the Dexter energy transfer. Based on the estimation of hopping rates, we analysed possible singlet exciton and triplet transfer pathways. In the Cz crystal, exciton transport is very effective along C dimers, with a π-stacking structure. Because of the less effective couplings between triplet and singlet states, the Dexter energy transport involving triplets is slower. However, due to the long lifetimes of triplets, their diffusion lengths are longer. Bimolecular processes such as triplet–triplet annihilation are limited by the concentration of triplets. In line with experimental observations, our calculations indicate that delayed fluorescence can occur using low powers.20
We analyse the effect of isomeric defects and the formation of charge transfer states in Cz doped with Bd. Our results are in line with the experimental observations by Liu et al.20 Triplets (and singlets) can travel to the Bd defects or they can be directly excited at the molecular Cz–Bd junctions. The (Cz−Bd+) states are appreciably more stable than the (Cz−Cz+) states. Because of this, charge separation occurs at the Cz–Bd molecular interfaces generating Cz− polarons. These calculations indicate that the presence of impurities, even at small concentrations, is essential to allow the formation of charge separated states. The effective charge transfer (1014 s−1) from Cz− to neutral Cz helps keep the excited states alive increasing the lifetimes in commercial or doped samples of crystalline Cz.
We hope that our results contribute to a better understanding of light-activated mechanisms in crystalline Cz and the role of isomeric defects on the long-lived excited states. Controlling the functionality of organic materials by isomeric doping seems to be a promising strategy with plenty of applications in the field of optoelectronics.20 Our simulations provide a plausible explanation for the generation of charge-separated states in line with the experimental observations. In a recent study, Ding et al. explored the concept of defect incorporation in crystals of 1-(4-bromophenyl)-1H-imidazole (1BBI) achieving a yield of 74.2% with a lifetime of 430 ms for one of the bicomponent systems.22 This research shows that this phenomenon is not limited to Cz highlighting the potential of the use of organic impurities to achieve efficient RTP systems. We hope our work can help support further advances in this exciting field.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has been supported by the EPSRC (EP/R029385/1) and Leverhulme Trust (RPG-2019-122). We utilized Queen Mary's Apocrita HPC facility, supported by QMUL Research-IT and the ARCHER UK National Supercomputing Service (EP/L000202/1) via the Materials Chemistry Consortium and the Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/T022213/1). The authors acknowledge the support from the School of Biological and Chemical Sciences at the Queen Mary University of London.References
- J. Mei, N. L. Leung, R. T. Kwok, J. W. Lam and B. Z. Tang, Chem. Rev., 2015, 115, 11718–11940 CrossRef CAS PubMed.
- S. Hirata, Adv. Opt. Mater., 2017, 5, 1700116 CrossRef.
- Y. Chen, J. W. Lam, R. T. Kwok, B. Liu and B. Z. Tang, Mater. Horiz., 2019, 6, 428–433 RSC.
- R. Crespo-Otero, Q. Li and L. Blancafort, Chem. – Asian J., 2019, 14, 700–714 CrossRef CAS PubMed.
- J. Li and K. Pu, Chem. Soc. Rev., 2019, 48, 38–71 RSC.
- I. Bergenti, V. Dediu, M. Prezioso and A. Riminucci, Philos. Trans. R. Soc., A, 2011, 369, 3054–3068 CrossRef CAS PubMed.
- J. Gierschner, S. Varghese and S. Y. Park, Adv. Opt. Mater., 2016, 4, 348–364 CrossRef CAS.
- W. Jia, Q. Wang, H. Shi, Z. An and W. Huang, Chem. – Eur. J., 2020, 26, 4437–4448 CrossRef CAS PubMed.
- Y. Gong, L. Zhao, Q. Peng, D. Fan, W. Z. Yuan, Y. Zhang and B. Z. Tang, Chem. Sci., 2015, 6, 4438–4444 RSC.
- T. Zhang, H. Gao, A. Lv, Z. Wang, Y. Gong, D. Ding, H. Ma, Y. Zhang and W. Z. Yuan, J. Mater. Chem. C, 2019, 7, 9095–9101 RSC.
- X. Wang, H. Ma, M. Gu, C. Lin, N. Gan, Z. Xie, H. Wang, L. Bian, L. Fu, S. Cai, Z. Chi, W. Yao, Z. An, H. Shi and W. Huang, Chem. Mater., 2019, 31, 5584–5591 CrossRef CAS.
- K. Jiang, L. Zhang, J. Lu, C. Xu, C. Cai and H. Lin, Angew. Chem., Int. Ed., 2016, 55, 7231–7235 CrossRef CAS PubMed.
- Y. Su, Y. Zhang, Z. Wang, W. Gao, P. Jia, D. Zhang, C. Yang, Y. Li and Y. Zhao, Angew. Chem., Int. Ed., 2020, 59, 9967–9971 CrossRef CAS PubMed.
- X. Zhen, Y. Tao, Z. An, P. Chen, C. Xu, R. Chen, W. Huang and K. Pu, Adv. Mater., 2017, 29, 1606665 CrossRef PubMed.
- Kenry, C. Chen and B. Liu, Nat. Commun., 2019, 10, 1–15 CrossRef CAS PubMed.
- H. A. Collins, M. Khurana, E. H. Moriyama, A. Mariampillai, E. Dahlstedt, M. Balaz, M. K. Kuimova, M. Drobizhev, V. X. Yang, D. Phillips, A. Rebane, B. C. Wilson and H. L. Anderson, Nat. Photonics, 2008, 2, 420–424 CrossRef CAS.
- R. Kabe, N. Notsuka, K. Yoshida and C. Adachi, Adv. Mater., 2016, 28, 655–660 CrossRef CAS PubMed.
- W. Zhao, T. S. Cheung, N. Jiang, W. Huang, J. W. Lam, X. Zhang, Z. He and B. Z. Tang, Nat. Commun., 2019, 10, 1595 CrossRef PubMed.
- C. Sun, X. Ran, X. Wang, Z. Cheng, Q. Wu, S. Cai, L. Gu, N. Gan, H. Shi, Z. An, H. Shi and W. Huang, J. Phys. Chem. Lett., 2018, 9, 335–339 CrossRef CAS PubMed.
- C. Chen, Z. Chi, K. C. Chong, A. S. Batsanov, Z. Yang, Z. Mao, Z. Yang and B. Liu, Nat. Mater., 2020, 4–10 Search PubMed.
- A. Troisi, Chem. Soc. Rev., 2011, 40, 2347 RSC.
- B. Ding, L. Ma, Z. Huang, X. Ma and H. Tian, Sci. Adv., 2021, 7, eabf9668 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- M. Rivera, M. Dommett and R. Crespo-Otero, J. Chem. Theory Comput., 2019, 15, 2504–2516 CrossRef CAS PubMed.
- M. Rivera, M. Dommett, A. Sidat, W. Rahim and R. Crespo-Otero, J. Comput. Chem., 2020, 41, 1045–1058 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684 CrossRef CAS PubMed.
- B. G. Levine, J. D. Coe and T. J. Martínez, J. Phys. Chem. B, 2008, 112, 405–413 CrossRef CAS PubMed.
- G. C. Schatz and M. A. Ratner, Quantum mechanics in chemistry, 1998.
- W. J. Kusto and J. W. Rohleder, Mol. Cryst. Liq. Cryst., 1979, 55, 151–161 CrossRef CAS.
- G. Baryshnikov, B. Minaev and H. Ågren, Chem. Rev., 2017, 117, 6500–6537 CrossRef CAS PubMed.
- H. Ågren, O. Vahtras and B. Minaev, Adv. Quantum Chem., 1996, 27, 71–162 CrossRef.
- B. Minaev, G. Baryshnikov and H. Agren, Phys. Chem. Chem. Phys., 2014, 16, 1719–1758 RSC.
- O. Vahtras, H. Ågren, P. Jørgensen, H. J. A. Jensen, T. Helgaker and J. Olsen, J. Chem. Phys., 1992, 97, 9178–9187 CrossRef CAS.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. Aa Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, WIREs Comput. Mol. Sci., 2014, 4, 269–284 CrossRef CAS PubMed.
- R. Liu, X. Gao, M. Barbatti, J. Jiang and G. Zhang, J. Phys. Chem. Lett., 2019, 10, 1388–1393 CrossRef CAS PubMed.
- X. Gao, S. Bai, D. Fazzi, T. Niehaus, M. Barbatti and W. Thiel, J. Chem. Theory Comput., 2017, 13, 515–524 CrossRef CAS PubMed.
- R. P. Fornari, J. Aragó and A. Troisi, J. Chem. Phys., 2015, 142, 184105 CrossRef PubMed.
- J. Aragó and A. Troisi, Adv. Funct. Mater., 2016, 26, 2316–2325 CrossRef.
- J. R. Reimers, J. Chem. Phys., 2001, 115, 9103–9109 CrossRef CAS.
- A. R. Auty, A. C. Jones and D. Phillips, Chem. Phys., 1986, 103, 163–182 CrossRef CAS.
- S. M. Bonesi and R. Erra-Balsells, J. Lumin., 2001, 93, 51–74 CrossRef CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available fromhttp://www.turbomole.com.
- R. C. Powell and Z. G. Soos, J. Lumin., 1975, 11, 1–45 CrossRef CAS.
- V. Stehr, R. F. Fink, B. Engels, J. Pflaum and C. Deibel, J. Chem. Theory Comput., 2014, 10, 1242–1255 CrossRef CAS PubMed.
- Y. Gu, K. Wang, Y. Dai, G. Xiao, Y. Ma, Y. Qiao and B. Zou, J. Phys. Chem. Lett., 2017, 8, 4191–4196 CrossRef CAS PubMed.
- C. M. Marian, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 187–203 CAS.
- H. Ma, Q. Peng, Z. An, W. Huang and Z. Shuai, J. Am. Chem. Soc., 2019, 141, 1010–1015 CrossRef CAS PubMed.
- H. J. Haink and J. R. Huber, J. Mol. Spectrosc., 1976, 60, 31–42 CrossRef CAS.
- Z. He, W. Zhao, J. W. Lam, Q. Peng, H. Ma, G. Liang, Z. Shuai and B. Z. Tang, Nat. Commun., 2017, 8, 1–8 CrossRef CAS PubMed.
- Z. An, C. Zheng, Y. Tao, R. Chen, H. Shi, T. Chen, Z. Wang, H. Li, R. Deng, X. Liu and W. Huang, Nat. Mater., 2015, 14, 685–690 CrossRef CAS PubMed.
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CAS.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed.
- H. Haink and J. Huber, J. Mol. Spectrosc., 1976, 60, 31–42 CrossRef CAS.
- O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888 RSC.
- S. R. Yost, E. Hontz, S. Yeganeh and T. Van Voorhis, J. Phys. Chem. C, 2012, 116, 17369–17377 CrossRef CAS.
- V. Ern, Phys. Rev. Lett., 1969, 22, 343–345 CrossRef CAS.
- S. Hirata, H. Hara and I. Bhattacharjee, J. Chem. Phys., 2020, 124, 25121–25132 CAS.
- A. Monguzzi, J. Mezyk, F. Scotognella, R. Tubino and F. Meinardi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 195112 CrossRef.
- J. Aragó and A. Troisi, Phys. Rev. Lett., 2015, 114, 026402 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc02019f |
| This journal is © The Royal Society of Chemistry 2021 |