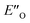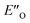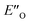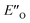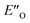Open Access Article
Open Access ArticleTernary complexes of chiral disulfonimides in transfer-hydrogenation of imines: the relevance of late intermediates in ion pair catalysis†
Matej
Žabka
 and
Ruth M.
Gschwind
and
Ruth M.
Gschwind
 *
*
Institute of Organic Chemistry, University of Regensburg, D-93053 Regensburg, Germany. E-mail: ruth.gschwind@chemie.uni-regensburg.de
First published on 17th November 2021
Abstract
In ion pairing catalysis, the structures of late intermediates and transition states are key to understanding and further development of the field. Typically, a plethora of transition states is explored computationally. However, especially for ion pairs the access to energetics via computational chemistry is difficult and experimental data is rare. Here, we present for the first time extensive NMR spectroscopic insights about the ternary complex of a catalyst, substrate, and reagent in ion pair catalysis exemplified by chiral Brønsted acid-catalyzed transfer hydrogenation. Quantum chemistry calculations were validated by a large amount of NMR data for the structural and energetic assessment of binary and ternary complexes. In the ternary complexes, the expected catalyst/imine H-bond switches to an unexpected O–H–N structure, not yet observed in the multiple hydrogen-bond donor–acceptor situation such as disulfonimides (DSIs). This arrangement facilitates the hydride transfer from the Hantzsch ester in the transition states. In these reactions with very high isomerization barriers preventing fast pre-equilibration, the reaction barriers from the ternary complex to the transition states determine the enantioselectivity, which deviates from the relative transition state energies. Overall, the weak hydrogen bonding, the hydrogen bond switching and the special geometrical adaptation of substrates in disulfonimide catalyst complexes explain the robustness towards more challenging substrates and show that DSIs have the potential to combine high flexibility and high stereoselectivity.
Introduction
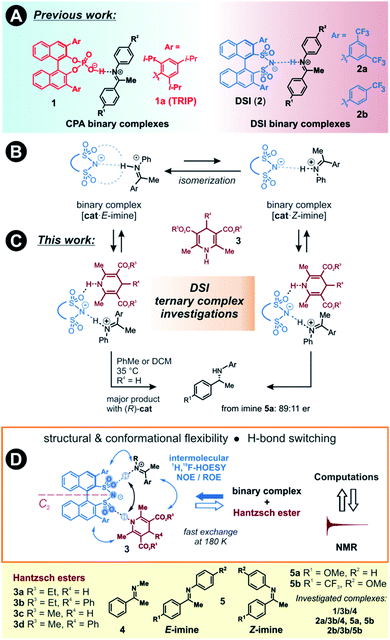
The detection and identification of reaction intermediates in asymmetric catalysis still poses considerable challenges to the experimental setup as well as to the computational elucidation of possible structures. This quest is even more difficult in the area of noncovalent organocatalysis, where well-defined hydrogen-bonded or ion-pair intermediates are rather scarcely detected and offsets between experimental and computational populations limit the explanatory power of calculations.1,2 One of the central model systems for mechanistic investigations in ion pair catalysis is the enantioselective Brønsted acid-catalysed transfer-hydrogenation of imines.3–5 This reaction represents a general and mild route to the synthesis of chiral amines, which are valuable structural units found in many bioactive compounds.6–8 The early intermediates in the corresponding catalytic cycle, the binary complexes of the catalysts and imines as well as their dimers, have already been experimentally detected.9,10 Even the dynamic behaviour of these species could be followed by NMR.11 However, later intermediates and transition states were proposed for the purely organocatalytic chiral phosphoric acid (CPA)-catalysed reaction only by theoretical calculations.12–16 The computed active transition states suggested that the reaction proceeds via the bifunctional binding of both the substrate and the reagent by the catalyst.17–19So far mechanistic studies have focused mainly on popular catalysts employed for the transfer-hydrogenation such as chiral phosphoric acids e.g. TRIP 1, and the more acidic disulfonimides 2 (see Fig. 1A).20–26 These widely used catalysts benefit from the axially chiral BINOL backbone, whose 3,3′-substituents can be fine-tuned for the desired reactivity and selectivity.14 The role of the catalysts in the catalytic cycle was studied using experimental and computational methods. The first step of the proposed catalytic cycle is the formation of an E-imine binary complex. Given sufficient thermal energy, the catalyst is capable of isomerizing the E-complex into a Z-imine complex, which are in slow exchange at 180 K, as shown by NMR studies by our group (Fig. 1B).27
We have also reported that for the complexes of CPAs, a strong, charge-assisted hydrogen bond is formed, as evidenced by the detection of 1JNH and 3JPH scalar couplings across the H-bond, with additional noncovalent CH–π and π–π interactions. This evidence is supported by the correlation of hydrogen bond strength and NMR parameters such as 1H and 15N chemical shifts in the Steiner–Limbach plot.9 In contrast, chiral DSIs form rather weak hydrogen bonds with imines and the complexes have more ion-pair character, allowing some additional structural flexibility.28,29
The reducing agent then approaches the binary complex. The reaction utilizes a sacrificial hydrogen donor, such as Hantzsch ester, to transfer a hydride ion to the LUMO-activated imine.30–32
The chiral catalyst in the complex is proposed to establish a new hydrogen bond to the reducing agent due to its bifunctional nature, thus enhancing the thermodynamic driving force for the hydride transfer (see Fig. 1C for principal arrangements in case of DSI).33 An analogous activation has been suggested in a bifunctional thiourea-catalysed transfer hydrogenation.34 With such dual activation offering an opportunity for efficient chirality transfer, a ternary complex is formed and chiral information is transmitted. The catalyst is then liberated from the complex and a proton transfer from the formed pyridinium ion ensures the regeneration of the catalyst, which can enter a new catalytic cycle. Based on extensive experimental evidence, the E/Z-isomerization and the ternary complex formation have been proposed to be the potential rate-determining steps in the cycle.35 As a result, the availability and detectability of the ternary complex in the reaction mixture is extremely limited.
Moreover, the bifunctional binding mode is a crucial factor for the reactivity, often overriding the acidity of the catalyst towards faster reaction rates. This has been demonstrated by comparing the reaction rates of DSI or its simple analogues compared to HCl as the monofunctional catalyst.36 Moreover, we have shown that a very acidic bis(sulfonic) acid catalyst gave the slowest reaction most likely due to the intramolecular H-bond stabilization of the resulting monosulfonate.28
However, the bifunctional binding of the substrate and reducing agent to the classical CPAs has not been experimentally disclosed so far. This topic is even more pressing with the far more complex situations in multiple H-bond acceptors present in the recently developed, highly-acidic ion pair catalysts. To the best of our knowledge, NMR based experiments – without extensive NOE map and the geometries proposed only by semi-empirical methods – were obtained exclusively for an organometallic Ir-catalyst and imine.37 In addition, many computational methods reproduce geometries of ion pair complexes reliably. However, the relative experimental populations of the binary complexes could not be reproduced by computations without large deviations so far, which raises questions about the correct evaluation of transition states.
Here, we present the first experimental proof for H-bonded ternary complexes of chiral disulfonimides (DSI) with imines and Hantzsch ester based on detailed NOE analysis, H-bond detection, relaxation and diffusion studies, and chemical shift perturbation analysis. The combination of these experimental data allowed us to select a computational method, which reproduced the experimental populations of the complexes. The NMR and computational analyses revealed the switching of weak H-bonds in multi-acceptor situations from the expected N–H–N pattern to an O–H–N binding in ternary complexes (see Fig. 1D). This unexpected feature has not yet been considered in the design stage of catalyst development so far. Moreover, the data showed that the inclusion of ground states is indispensable when assessing transition states of reactions where isomerization of intermediates is a slow process.
Results and discussion
Model systems and experimental setup
Two catalysts, (R)-TRIP (1) and (R)-DSI (2) were tested as model systems. Our previous efforts in establishing the ternary complex of TRIP (1) have been hampered by the extremely low solubility of the Hantzsch ester 3a.35 Furthermore, the inevitable formation of reaction products during the sample preparation complicated the analysis of 1D 1H NMR spectra at low temperatures. To solve both issues, we employed ester 3b which contains an additional phenyl group, distant from the potential binding site, and is also fully soluble at 180 K (see Fig. 1D). As imine we chose the small-sized N-Me imine 4 to minimize the impact of the steric interactions, since previous studies with larger imines were unfruitful.35Only for DSIs 2, homogenous solutions at 180 K are formed, relatively sharp peaks are present and even intermolecular NOEs/HOEs are detected between signals of iminium, catalysts 2 and Hantzsch ester 3b. Similar intermolecular NOEs/HOEs hinting at ternary complex formation were observed using N-aryl imines [15N]-5a and 5b (Fig. 1D). Generally, the binary complex of DSI and imine is in fast exchange with the ternary complex and only average signals are observed (e.g., δH-bond (E) 14.53/(Z) 15.06 ppm in 2b/3b/5b, signals are split by 1JNH in the 15N-labelled imines and Hantzsch ester) (for further discussion and exclusion of other possibilities see ESI Chapter 6.2†).
The NMR spectra generally show the major E- and minor Z-iminium ions, with the hydrogen bond in slow mutual exchange. No free imines are detected in the samples, because the imines are protonated by the acidic catalysts. There is one set of signals for the Hantzsch ester with split 2,6-dimethyl group signal; and only one set of signals for the catalyst, accompanied by averaging of the signals of its two naphthyl groups (Fig. 1D). This averaging suggests a fast equilibrium with the binary complex coupled to a fast rotation around the catalyst's C2-axis. Interestingly, the rotation of the 3,3′-substituents is hindered in DSI complexes. For example, two distinct 19F signals are present for the catalyst 2a, and two 1H AB systems for catalyst 2b. Thus, we could confirm the presence of the ternary complex with DSI catalysts by NMR and exclude the possibility of the Overhauser effects stemming from separate Hantzsch ester complexes.
Hantzsch ester binding and Z-imine complex
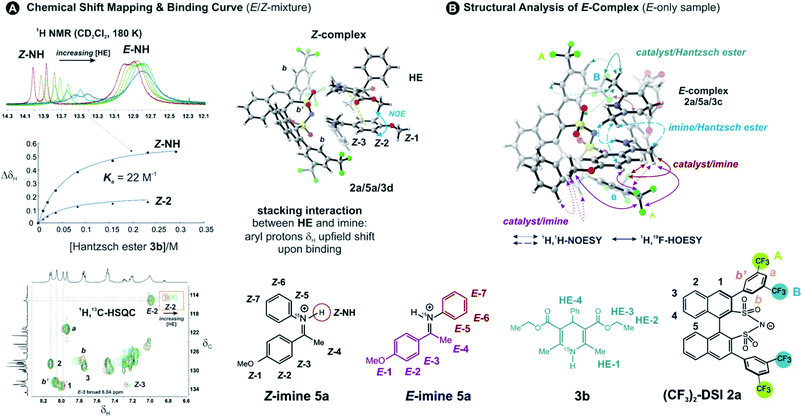
To address the binding site and the binding constant, the chemical shift perturbation upon the binding of Hantzsch ester to the binary complex was investigated. Therefore, 3b (0.5–15 eq.) was sequentially added to the binary complex 2a/5a (20 mM) and 1H and 1H,13C-HSQC spectra were recorded at 180 K to allow for chemical shift mapping (Fig. 2A). In general, the signals of the Z-complex showed significantly larger chemical shift perturbations than the E-complex (see 1D spectrum in Fig. 2A). For the Z-complex the iminium 15NH was shifted followed by protons Z-1/Z-2 (see Fig. 2A and ESI Chapter 8†). Fitting these data for two distinct sites (Z-NH and Z-2 CH) revealed a binding constant Ka = ∼22, indicating a weak binding of the Hantzsch ester to the binary Z-complex. For the E-complex, only the iminium NH and the methoxy group showed small chemical shift differences (see E-NH and E-1 in Fig. 2A and in the 1H,13C-HSQC spectrum ESI Chapter 8†). The nearly linear change suggests a much weaker binding of the E-complex.The population of Z-complexes was then doubled from 15% to 31% by photoisomerisation (back isomerization is stopped at 180 K). One intermolecular NOE contact between Z-2 of the iminium and the Hantzsch ester could be detected (see structure in Fig. 2A), which fits perfectly to the chemical shift perturbation and the calculated bifunctional structure of the ternary Z-complex. Thus, the chemical shift perturbation study in combination with the NOE detected corroborates the bifunctional binding of both imine and Hantzsch ester in the ternary complex for the first time spectroscopically.
NMR structural investigations of E-ternary complexes
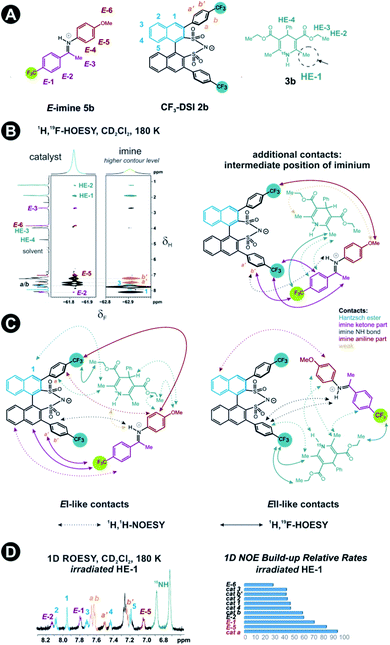
Next, structural insights about the E-ternary complex were gained. Here, we prepared exclusively E-iminium complexes to reduce chemical shift overlap and to compensate for the smaller binding constant by increased concentrations. These samples were prepared by mixing solutions of imines and catalysts/Hantzsch ester mixtures at −80 °C to avoid any acid-promoted, thermal E/Z isomerization. Despite the low binding constant, 2D 1H,1H-NOESY spectra (CD2Cl2, 180 K) with short mixing times (50–100 ms) showed unexpectedly many intermolecular NOEs and (and HOEs) especially between the Hantzsch ester 3b, the catalyst 2a and the E-imine 5a signals (see Fig. 2B) proving again the existence of a ternary complex. To exclude potential spin diffusion artifacts,38,39 we collected 2D 1H,1H-ROESY data, which confirmed the observed contacts as genuine. A relevant population of a ternary complex is indicated by the significant intensity of the ROESY and 1H,19F-HOESY crosspeaks between the catalyst and the Hantzsch ester, as well as between the Hantzsch ester and the imine. The NOE/HOE signals to the Hantzsch ester are thus decisive about the ternary structure (Fig. 2B).To get further insight about this potential conformational flexibility within the ternary complex, we utilized imine 5b with an additional CF3 group as a spectroscopic sensor together with catalyst CF3-DSI 2b. The three CF3 groups allowed us to observe 1H,19F-HOESY signals between both the catalyst and Hantzsch ester as well as imine and Hantzsch ester (Fig. 3A and B), originating from the transiently formed ternary complex. Additionally, DOSY experiment at 180 K showed the three components – Hantzsch ester, imine, and the catalyst – diffuse together, corroborating the formation of a supramolecular complex (see ESI Chapter 11†). The estimated molecular mass matches the mass of the ternary complex. Typical NOE contacts were found for the two different conformations of the previously established E-imine binary complex (see Fig. 3C): EI (EN/EOI) which has the imine aryl next to the naphthyl group of the catalyst; and EII, which has the N-aryl ring close to the catalyst naphthyl ring. Since NOE contacts between the catalyst and the imine observed in the ternary mixtures originate from both binary and ternary complexes, we used only the contacts of the Hantzsch ester to the catalyst or the imine to reveal the ternary complex conformations (see ESI Chapter 7†). However, it seems that a new conformation, not populated in binary complexes is adopted which can accommodate all the observed NOE/HOE contacts. This anticipated structure could have an intermediate position of the imine between EI and EII structures, as was already observed for CPAs, namely in the CPA/imine dimeric species10 and in calculated transition state structures.18 The Hantzsch ester would be stacked above or below the imine. The evidence for this conformation comes from the NOE/HOE contacts that could not be assigned to EI and EII structures (Fig. 3B, right).
With the data in hand, we addressed the orientation of the bound Hantzsch ester in the ternary complex. The NOE/ROEs network detected indicates a bifunctional binding of the Hantzsch ester (via a very weak H-bond) and the imine to the catalyst as proposed previously for the CPAs by theoretical calculations and is already shown in Fig. 2B. In the case of the bifunctional binding mode, the Hantzsch ester interacts via its NH group. Indeed, only the neighboring 2,6-dimethyl groups show a significant diastereotopic splitting upon binding in the ternary mixture and show the largest reduction in T2 relaxation time (further details see ESI Chapter 10†). In addition, these 2,6-dimethyl groups show the strongest intermolecular NOE/ROEs (see ESI Chapter 6.2.3 and 6.2.4†). Thus, the bifunctional binding mode is confirmed and further insight into the position of the Hantzsch ester is exemplified by the relative NOE build-up rates upon selective irradiation of these Hantzsch ester methyl groups (Fig. 3D, right) and a 1D ROESY spectrum (Fig. 3D, left). The close proximity between the two hydrogen bonds in the ternary complex was further confirmed by a selective NOE experiment from the proton of the catalyst/imine hydrogen bond (δH 14.53 ppm) to the Hantzsch ester methyl protons and vice versa.
For the first time, direct spectroscopic evidence is provided for the bifunctional binding mode of a Brønsted acid catalyst with the substrate and the reagent. In addition, the investigated ternary complexes might show conformational flexibility that reflects the situation in the binary complexes, or a single new conformation with intermediate imine/Hantzsch ester position.
Conformational screening by computational methods
The NMR investigations provided qualitative insight about the contacts within the ternary complex. However, the fast exchange between the binary and the ternary complexes and any potential ternary complex conformational exchange allowed only a qualitative analysis of the NOE patterns discussed above. Therefore, the conformational space of the ternary complex was investigated by computational methods so that the resulting 3D structures could be compared with the experimental data.Quantitative assessment of binary complexes
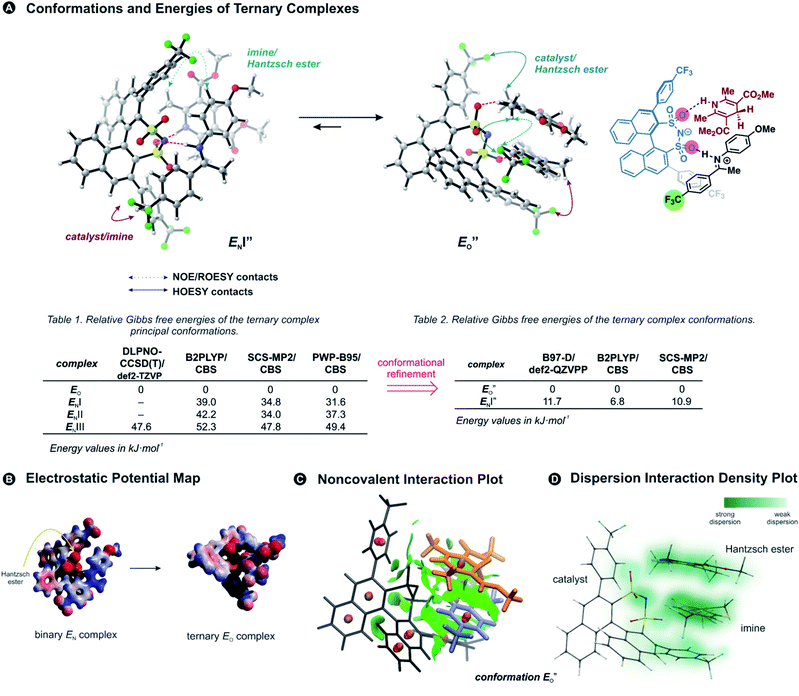
Previously, five hydrogen-bonded DSI binary complex conformations have been identified in agreement with the NMR data.28 These structures correspond to the type EN, with iminium bound to nitrogen; EOI, and EOII-types bound to the oxygen; and ZI and ZII. Type I structures bring the parent ketone part of the imine closer to the binaphthyl backbone of the catalyst, whereas in type II structures the N-aryl substituent is located near the binaphthyl core (for principal contacts see Fig. 3C). Out of these five binary complexes, the previous computational approaches always favoured the EN-complex while the experiments revealed a significant population of the Z-complexes.28This large energetic overestimation of the E-imine binary complexes in Brønsted acid catalysis by the applied theoretical methods has been a general problem so far.10 Since hydrogen bonds and π,π-interactions dominate the interaction mode revealed by NMR, we tested the B97-D functional, as it was developed to adequately describe hydrogen-bonded DNA base pairs.40,41 Indeed, calculating the Gibbs free energies of the binary complexes by the B97-D/def2-QZVPP/SMD//TPSS-D3(BJ)/def2-SVP/SMD level of theory correctly reproduces for the first time the experimental E/Z ratio (2a/5a exp. E/Z = 88%/12% at 180 K; calc. E/Z = 87%/13%). Out of the five conformations for (CF3)2-DSI 2a/5a the major structures are EN (∼87% population), and ZII (12%). Furthermore, from 8 tested methods using ORCA computational software,42 the next best energetic estimation was provided by a more advanced, robust double hybrid B2PLYP/CBS (EN ∼ 93% population, ZI ∼ 6.5%; see ESI Chapter 14.7†).43,44 Moreover, the reaction Gibbs free energy of the Hantzsch ester 3d binding to the binary complex (CF3)2-DSI 2a/Z-5a was best reproduced also by this method (exp. −4.6 kJ mol−1; calc. −9.9 kJ mol−1; see ESI Chapter 14.10†). Thus, an almost quantitative assessment of both relative energies of binary complexes and the binding of the Hantzsch ester could be achieved by selected computational methods.
Ternary complexes
Having established the methods required, we addressed the E-ternary complexes because only for those sufficiently detailed structural information was available from the NMR experiments (see above). First, we identified the principal conformers by a conformational search of the ternary complex containing CF3-DSI 2b, simplified dimethylester 3c, and imine E-5b using GFN2-xTB metadynamics.45 This search resulted in EN structures containing an NHN-hydrogen bond to the imine as well as an OHN hydrogen bond to the Hantzsch ester. Additionally, these EO structures have the iminium bound to a catalyst oxygen. Next, we performed a more extensive search to cover full conformational space – starting from the previous lowest energy structure (EO) with a more stable conformation of 3c – and generated 300 conformers (annotated with quotation mark). Then, we optimized the most stable structures with TPSS-D3(BJ)/def2-SVP method (with implicit solvation model) and obtained exclusively conformers containing hydrogen-bonded species (EN as well as EO structures for both the imine and the Hantzsch ester). The most energetically favorable candidates from the conformational analyses are the ENI′′ structure and the structure presented in Fig. 4A (for energetic assessment see discussion below). The structure ENI′′ resembles in principle the relative position of the imine towards the catalyst in the EI transition states calculated for CPAs.18 In addition, the special binding site of the DSI allows for the new conformation
structure presented in Fig. 4A (for energetic assessment see discussion below). The structure ENI′′ resembles in principle the relative position of the imine towards the catalyst in the EI transition states calculated for CPAs.18 In addition, the special binding site of the DSI allows for the new conformation  . In the conformation ENI′′ the Hantzsch ester is far away from the imine, making the hydride transfer event unfavourable. In contrast, in the
. In the conformation ENI′′ the Hantzsch ester is far away from the imine, making the hydride transfer event unfavourable. In contrast, in the 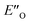 conformation, both the imine and the Hantzsch ester occupy central positions in close proximity, making this conformation a prospective candidate for the transition state.
conformation, both the imine and the Hantzsch ester occupy central positions in close proximity, making this conformation a prospective candidate for the transition state.
However, the ENI′′ conformation cannot accommodate all of the experimental NOE contacts alone in contrast to the conformation 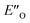 . Its presence at 180 K is corroborated experimentally by all the NOE and HOE contacts. Indeed, this EO complex is easily accessible at ambient temperature reaction conditions with the reactive form of 3 such as 3a and is a direct precursor to the E-transition state. Detailed structural analysis is given below. To our knowledge, this is the first complex in ion pair catalysis, in which an O–H–N hydrogen bond is preferred over an N–H–N hydrogen bond in presence of a multiple H-bond donor–acceptor system. So far, only for a free IDPi catalyst dimer dynamic structure,46 and our DSI binary complexes,28 the possibility of switching between oxygen and nitrogen atoms was proposed.
. Its presence at 180 K is corroborated experimentally by all the NOE and HOE contacts. Indeed, this EO complex is easily accessible at ambient temperature reaction conditions with the reactive form of 3 such as 3a and is a direct precursor to the E-transition state. Detailed structural analysis is given below. To our knowledge, this is the first complex in ion pair catalysis, in which an O–H–N hydrogen bond is preferred over an N–H–N hydrogen bond in presence of a multiple H-bond donor–acceptor system. So far, only for a free IDPi catalyst dimer dynamic structure,46 and our DSI binary complexes,28 the possibility of switching between oxygen and nitrogen atoms was proposed.
Next, we calculated the Gibbs free energies of the ternary complexes with different methods for the single-point energy calculation: B97-D and B2PLYP discussed above, one additional double hybrid functional,47 and SCS-MP2 used previously for CPA complexes in our group (Fig. 4A).27
We evaluated the methods based on the experimental data in which substantial populations of some EN conformers or a substantial population of 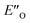 are required to potentially detect the distinct NOE contacts and especially the NOE build-up rates discussed above (Fig. 3C and D). However, based on the optimized ternary complex structures and a thorough NOE analysis, it then became clear that the
are required to potentially detect the distinct NOE contacts and especially the NOE build-up rates discussed above (Fig. 3C and D). However, based on the optimized ternary complex structures and a thorough NOE analysis, it then became clear that the 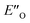 structure fits all the NOE and HOE data (see ESI Chapter 7.2†). For instance, the 2a/E-5b/3b complex showed intermolecular HOE contact between methyl group of the imine parent ketone and the 3-substituent of the catalyst, which cannot be found in any of the EN structures (Fig. 4A).
structure fits all the NOE and HOE data (see ESI Chapter 7.2†). For instance, the 2a/E-5b/3b complex showed intermolecular HOE contact between methyl group of the imine parent ketone and the 3-substituent of the catalyst, which cannot be found in any of the EN structures (Fig. 4A).
This 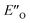 conformation develops considerable dispersion areas between the imine (parent ketone part aromatic ring), the 3,3′-substituent and the Hantzsch ester that compensate for the lack of interactions of the N-substituent with the catalyst (for NCI plot see Fig. 4C and ESI Chapter 14.8.7†). This may explain high enantioselectivities of N-methyl and N-unsubstituted imines. Therefore, appropriate computational methods should reflect a high population of the
conformation develops considerable dispersion areas between the imine (parent ketone part aromatic ring), the 3,3′-substituent and the Hantzsch ester that compensate for the lack of interactions of the N-substituent with the catalyst (for NCI plot see Fig. 4C and ESI Chapter 14.8.7†). This may explain high enantioselectivities of N-methyl and N-unsubstituted imines. Therefore, appropriate computational methods should reflect a high population of the 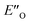 complex.
complex.
All the computational methods predict 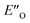 as the most stable conformation for the solution-phase geometry-optimized structures from both conformational searches (see Fig. 4A). In addition, after the principal conformational search, we conducted a DLPNO-CCSD(T) calculation that confirms the energetic bias between the principal EO and a similar EN conformation towards the EO structure. This was in agreement with the other computational methods used in the principal conformational search (see ESI 14.8†).48,49 Local energy decomposition at DLPNO-CCSD(T)/def2-TZVP level of theory shows the dispersion, electrostatics and exchange contribution in two complexes compared to binary EN complex (see ESI 14.9.1†).50–52 A stabilizing dispersion interaction develops between the imine and the Hantzsch ester in the ternary complex.
as the most stable conformation for the solution-phase geometry-optimized structures from both conformational searches (see Fig. 4A). In addition, after the principal conformational search, we conducted a DLPNO-CCSD(T) calculation that confirms the energetic bias between the principal EO and a similar EN conformation towards the EO structure. This was in agreement with the other computational methods used in the principal conformational search (see ESI 14.8†).48,49 Local energy decomposition at DLPNO-CCSD(T)/def2-TZVP level of theory shows the dispersion, electrostatics and exchange contribution in two complexes compared to binary EN complex (see ESI 14.9.1†).50–52 A stabilizing dispersion interaction develops between the imine and the Hantzsch ester in the ternary complex.
Moreover, the binding energy was decomposed, confirming larger binding energy of the EO complex. The energy decomposition showed that the electron preparation (destabilization by geometrical strain) is compensated by the gain in electrostatic energy (presumably including the hydrogen bond), and the extra stabilization which is provided by dispersion and exchange energy can aid in the ternary complex formation. Indeed, for the EO conformation, the electron preparation penalty is lower than in the EN complex and less geometrical distortion is thus required in the binding process. The dispersion interaction density plot of the 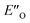 complex shows the interaction between the CF3-DSI catalyst 2b and imine 5b, where the strongest dispersion is at the catalyst O and N atoms constituting the hydrogen bond (Fig. 4D). Dispersion is thus vital in stabilization of the pre-reacting complexes.
complex shows the interaction between the CF3-DSI catalyst 2b and imine 5b, where the strongest dispersion is at the catalyst O and N atoms constituting the hydrogen bond (Fig. 4D). Dispersion is thus vital in stabilization of the pre-reacting complexes.
In line with the energy decomposition, the electrostatic potential surface map of CF3-DSI 2b/imine 5b/Hantzsch ester 3c revealed the potential binding sites as the sites providing electrostatic or hydrogen-bond interactions with the Hantzsch ester. This map shows significant negative charge located at the nitrogen and oxygens of the DSI catalyst in its EN binary complex (Fig. 4B), attracting the Hantzsch ester to develop a hydrogen bond resulting in the bifunctional activation. The negative charge is slightly reduced upon the binding of the Hantzsch ester to form the ternary complex.
The energetic preference of conformation 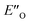 , which matches the NMR data, is given by the B2PLYP method and is in line with the binary complex energetics and Z-binding equilibrium calculations. Therefore, this method seems to be universal to describe the energetics in this study, in contrast to other methods which over- or underestimate some of the species.
, which matches the NMR data, is given by the B2PLYP method and is in line with the binary complex energetics and Z-binding equilibrium calculations. Therefore, this method seems to be universal to describe the energetics in this study, in contrast to other methods which over- or underestimate some of the species.
Overall, for the first time the ratio of E- and Z-imine binary complexes were correctly reproduced by computational methods. The calculations for the DSI E-ternary complexes revealed the major conformation 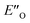 and disfavored ENI′′ conformation. The
and disfavored ENI′′ conformation. The 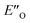 conformation has an intermediate position of both the imine and the Hantzsch ester; and resembles a precursor for the transition state. In addition,
conformation has an intermediate position of both the imine and the Hantzsch ester; and resembles a precursor for the transition state. In addition, 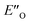 provides exclusively dispersion areas to the 3,3′-substituents and the Hantzsch ester, which may explain the high enantioselectivities for N-Me imines and NH imine hydrochloride salts.36
provides exclusively dispersion areas to the 3,3′-substituents and the Hantzsch ester, which may explain the high enantioselectivities for N-Me imines and NH imine hydrochloride salts.36
DFT computations of NMR spectra
The binary complexes of the DSIs and imines are in fast exchange with the ternary complex. Therefore, we computed NMR data to distinguish between the binary and ternary complex contributions. To calibrate the computed NMR parameters (δH, δN) on direct experimental data, first a set of DSI E- and Z-imine binary complexes as well as free imines and Hantzsch ester were selected as model systems. We plotted the computed chemical shifts at the TPSS/pcSseg-3/SMD level of theory against the experimental chemical shifts to derive a linear scaling factor.53 Then, this computed NMR scaling was applied to the calculated NMR parameters (δH, δN) of ternary structures (see ESI Chapters 14.11–14.13 for details†). Indeed, these conformations do not show significantly different chemical shifts. Thus, calculations corroborate the small chemical shift difference for the E-complexes upon binding of the Hantzsch ester.From ternary complexes to transition states
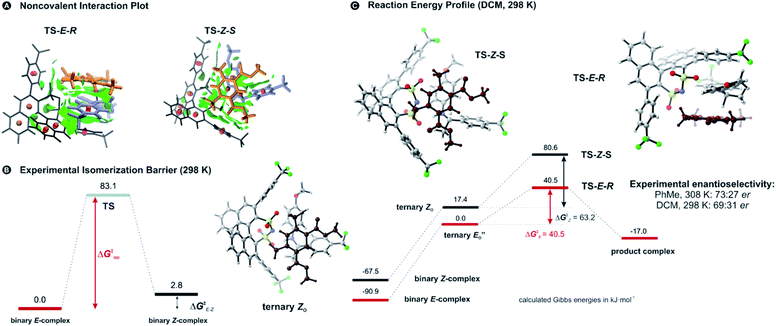
Two transition state structures, TS-E-R and TS-Z-S (+40.1 kJ mol−1), were found based on the most stable E- and Z-ternary complexes. Interestingly, all the transition state complexes are O,O-bonded transition structures (Fig. 5A and C). The structures of TS-E-R and TS-Z-S and their noncovalent interactions (NCI) plots are given in Fig. 5A.54,55 There is no notable dispersion area in the TS-Z-S structure, similar to the situation in the ternary Z-complex. In contrast, the TS-E-R reveals a very prominent interaction area – a triple-stacked π–π-complex – where imine is stacked between a catalyst 3,3′-substituent and Hantzsch ester (see ESI Chapter 14.8.7†). These attractive interactions compensate for the steric repulsion which is prominent in the non-compact E-ternary complexes and transition states. Both interactions seem to be negligible in the more compact Z-complexes which explains the comparable energies of E- and Z-complexes. The relative energetics of the transition states are in accordance with the major product, the (R)-enantiomer. However, the high energetic difference would predict its exclusive formation, which is in contrast with the experimentally observed enantioselectivity (er 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31). Recently, an exceptional example was reported of the conformational search and energetics' evaluation of hundreds of transition structures in ion-pair catalysis.52 However, in our investigated transfer-hydrogenation reaction the high activation barriers prohibit the reverse reactions or equilibration.
31). Recently, an exceptional example was reported of the conformational search and energetics' evaluation of hundreds of transition structures in ion-pair catalysis.52 However, in our investigated transfer-hydrogenation reaction the high activation barriers prohibit the reverse reactions or equilibration.
This means the transfer hydrogenation is under kinetic control and the reaction barriers from the intermediate complexes to the transition states determine the stereoselectivity.56 Moreover, additional photoisomerization/back-isomerization experiments show that the thermal E/Z-isomerization barrier within the binary complex is higher than the hydride step at 298 K (see Fig. 5B and ESI Chapter 12†). As a result, this very slow isomerization of the binary complexes cannot be regarded as a fast E/Z pre-equilibrium. Thus, the classic Curtin–Hammett principle cannot be applied,57 as “the product composition is formally related to relative concentrations of the conformation isomers”.58
Therefore, for the ΔG‡ values, not only individual transition states energies but also the stabilities of the intermediates have to be considered. In addition, in this study multiple experimental data are available about the ground states and the energetics of late intermediates.
The calculated reaction energy profile (Fig. 5C) allows for the energetic barrier assessment from 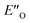 to TS-E-R (ΔG‡DCM,298 40.5 kJ mol−1). Compared to that, the energetic barrier from the lowest energy ZO-ternary complex to the transition state TS-Z-S is higher in energy (ΔG‡DCM,298 63.2 kJ mol−1). While this energetic offset still suggests the exclusive formation of the major R-enantiomer (experimental er 69
to TS-E-R (ΔG‡DCM,298 40.5 kJ mol−1). Compared to that, the energetic barrier from the lowest energy ZO-ternary complex to the transition state TS-Z-S is higher in energy (ΔG‡DCM,298 63.2 kJ mol−1). While this energetic offset still suggests the exclusive formation of the major R-enantiomer (experimental er 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 R
31 R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S), the inclusion of the intermediate energetics shifts the theoretical values towards the correct experimental enantioselectivity.
S), the inclusion of the intermediate energetics shifts the theoretical values towards the correct experimental enantioselectivity.
Within this combined analysis of experimental and computational data, each step of computational level was backed by experimental data and used for the selection of the theoretical method. Overall, this approach shows the importance of ground states and their energetics when investigating stereoselectivity in kinetically controlled reactions without fast pre-equilibration of the intermediates.
Conclusions
In summary, we present detailed experimental data about 6 E- and Z-ternary complexes between DSI catalysts, imines and a Hantzsch ester. This is to our knowledge the first detailed experimental data of ternary complexes in ion pairing catalysis at all. Extensive intermolecular NOE and HOE contacts at low temperatures, chemical shift mapping, diffusion and relaxation data were used as the experimental basis for the structure elucidation. In this study, experiments and calculations together indicate the unexpected energetic preference of the iminium binding to an oxygen in the presence of a nitrogen as an H-bond acceptor. This is reflected in the higher population of the ternary complex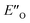 compared to the EN-complexes which is typical for the binary complexes. Furthermore, this is to our knowledge the first detailed spectroscopic proof for a bifunctional binding mode proposed earlier for CPAs by theoretical work and thermodynamic arguments.
compared to the EN-complexes which is typical for the binary complexes. Furthermore, this is to our knowledge the first detailed spectroscopic proof for a bifunctional binding mode proposed earlier for CPAs by theoretical work and thermodynamic arguments.
Moreover, this study convincingly demonstrates that the combination of experimental and computational analyses of late intermediates in ion pair catalysis is necessary for the interpretation of transition states. The correct energetic assessment of ion pairs is most critical in computational chemistry, so in this study, the complexes and binding events were used as key to select computational tools and to validate the essential calculations. This approach allowed us for the first time to reproduce correct populations of the binary complexes. Furthermore, the consideration of the reaction barriers from the ternary complexes to TSs showed the importance of structures and energetics of late intermediates in case of high isomerization barriers.
Overall, this study shows that ternary complex formation is favoured for catalysts with an open binding site and that in case of multiple hydrogen-bond donors the hydrogen bond can switch between the binary and ternary complexes leading to more favourable conformers resembling the transition states. The rather weak binding of the second substrate and the preferential stabilization of the transitions states by hydrogen bonding resembles enzymatic catalysis. In contrast to the CPAs, in which the strong hydrogen bond, rigid complexes and specific noncovalent interactions govern the stereoselectivity, the DSIs can adopt a more favourable conformation by hydrogen bond switching in the ternary complexes. For DSIs a strong and rigid hydrogen bond as adopted in CPAs would be detrimental to the stereoselectivity. In the dynamic system of the DSIs the substrate position in the TS provides mainly interactions of the parent ketone part of the imine with catalyst 3,3′-substituent. This explains the enhancement in enantioselectivity for N-methyl imines with no additional stabilization from the N-substituent. On the other hand, decrease in enantioselectivity with the electronic variation of the aryl imines corroborates a demand for a weak hydrogen bond. Thus, DSIs have the potential to combine high flexibility and high stereoselectivity, which offers an advantage over enzymatic catalysis, where more flexible and promiscuous enzymes are also less selective.59 It may also confirm the concept of structural flexibility as a vital point in asymmetric catalysis.60
Author contributions
M. Ž. and R. M. G. conceived and conceptualised the project. M. Ž. performed the experiments, DFT calculations, and visualisations. R. M. G. supervised the project and acquired funding. Both authors analysed the data, prepared and revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial and intellectual support was provided by the European Research Council (ERC-CoG 614182 – IonPairsAtCatalysis) and the DFG (SPP 1807 Control of London Dispersion Interactions in Molecular Chemistry). Additional intellectual support from DFG (RTG 2620 Ion Pair Effects in Molecular Reactivity) is acknowledged.Notes and references
- P. Renzi, J. Hioe and R. M. Gschwind, Acc. Chem. Res., 2017, 50, 2936–2948 CrossRef CAS PubMed.
- M. Žabka and R. Šebesta, Molecules, 2015, 20, 15500–15524 CrossRef PubMed.
- D. Parmar, E. Sugiono, S. Raja and M. Rueping, Chem. Rev., 2014, 114, 9047–9153 CrossRef CAS PubMed.
- M. Terada, Synthesis, 2010, 1929–1982 CrossRef CAS.
- M. Rueping, A. Kuenkel and I. Atodiresei, Chem. Soc. Rev., 2011, 40, 4539–4549 RSC.
- M. Rueping, E. Sugiono, C. Azap, T. Theissmann and M. Bolte, Org. Lett., 2005, 7, 3781–3783 CrossRef CAS.
- R. I. Storer, D. E. Carrera, Y. Ni and D. W. C. Macmillan, J. Am. Chem. Soc., 2006, 128, 84–86 CrossRef CAS PubMed.
- A. M. Faísca Phillips and A. J. L. Pombeiro, Org. Biomol. Chem., 2017, 15, 2307–2340 RSC.
- N. Sorgenfrei, J. Hioe, J. Greindl, K. Rothermel, F. Morana, N. Lokesh and R. M. Gschwind, J. Am. Chem. Soc., 2016, 138, 16345–16354 CrossRef CAS PubMed.
- M. Melikian, J. Gramüller, J. Hioe, J. Greindl and R. M. Gschwind, Chem. Sci., 2019, 10, 5226–5234 RSC.
- N. Lokesh, J. Hioe, J. Gramüller and R. M. Gschwind, J. Am. Chem. Soc., 2019, 141, 16398–16407 CrossRef CAS PubMed.
- L. Simón and J. M. Goodman, J. Am. Chem. Soc., 2008, 130, 8741–8747 CrossRef PubMed.
- L. Simón and J. M. Goodman, J. Org. Chem., 2011, 76, 1775–1788 CrossRef PubMed.
- J. P. Reid and J. M. Goodman, J. Am. Chem. Soc., 2016, 138, 7910–7917 CrossRef CAS PubMed.
- J. P. Reid and J. M. Goodman, Chem.–Eur. J., 2017, 23, 14248–14260 CrossRef CAS PubMed.
- R. Maji, S. C. Mallojjala and S. E. Wheeler, Chem. Soc. Rev., 2018, 47, 1142–1158 RSC.
- T. Marcelli, P. Hammar and F. Himo, Chem.–Eur. J., 2008, 14, 8562–8571 CrossRef CAS PubMed.
- P. Renzi, J. Hioe and R. M. Gschwind, J. Am. Chem. Soc., 2017, 139, 6752–6760 CrossRef CAS PubMed.
- L. Simón and J. M. Goodman, J. Am. Chem. Soc., 2009, 131, 4070–4077 CrossRef PubMed.
- P. García-García, F. Lay, P. García-García, C. Rabalakos and B. List, Angew. Chem., Int. Ed., 2009, 48, 4363–4366 CrossRef PubMed.
- T. James, M. Van Gemmeren and B. List, Chem. Rev., 2015, 115, 9388–9409 CrossRef CAS PubMed.
- V. N. Wakchaure, P. S. J. Kaib, M. Leutzsch and B. List, Angew. Chem., Int. Ed., 2015, 54, 11852–11856 CrossRef CAS PubMed.
- M. Hatano and K. Ishihara, Asian J. Org. Chem., 2014, 3, 352–365 CrossRef CAS.
- T. Akiyama and K. Mori, Chem. Rev., 2015, 115, 9277–9306 CrossRef CAS PubMed.
- M. Benda and S. France, Org. Biomol. Chem., 2020, 18, 7485–7513 RSC.
- V. N. Wakchaure and B. List, Angew. Chem., Int. Ed., 2016, 55, 15775–15778 CrossRef CAS PubMed.
- J. Greindl, J. Hioe, N. Sorgenfrei, F. Morana and R. M. Gschwind, J. Am. Chem. Soc., 2016, 138, 15965–15971 CrossRef CAS PubMed.
- K. Rothermel, M. Žabka, J. Hioe and R. M. Gschwind, J. Org. Chem., 2019, 84, 13221–13231 CrossRef CAS PubMed.
- A. Galván, A. B. González-Pérez, R. Álvarez, A. R. de Lera, F. J. Fañanás and F. Rodríguez, Angew. Chem., Int. Ed., 2016, 55, 3428–3432 CrossRef PubMed.
- C. Zheng and S. L. You, Chem. Soc. Rev., 2012, 41, 2498–2518 RSC.
- G.-B. Shen, Y.-H. Fu and X.-Q. Zhu, J. Org. Chem., 2020, 85, 12535–12543 CrossRef CAS PubMed.
- M. Rueping, J. Dufour and F. R. Schoepke, Green Chem., 2011, 13, 1084–1105 RSC.
- J. D. Yang, J. Xue and J. P. Cheng, Chem. Soc. Rev., 2019, 48, 2913–2926 RSC.
- J. F. Schneider, M. B. Lauber, V. Muhr, D. Kratzer and J. Paradies, Org. Biomol. Chem., 2011, 9, 4323–4327 RSC.
- K. Rothermel, M. Melikian, J. Hioe, J. Greindl, J. Gramüller, M. Žabka, N. Sorgenfrei, T. Hausler, F. Morana and R. M. Gschwind, Chem. Sci., 2019, 10, 10025–10034 RSC.
- V. N. Wakchaure, C. Obradors and B. List, Synlett, 2020, 1707–1712 CAS.
- W. Tang, S. Johnston, J. A. Iggo, N. G. Berry, M. Phelan, L. Lian, J. Bacsa and J. Xiao, Angew. Chem., Int. Ed., 2013, 52, 1668–1672 CrossRef CAS PubMed.
- M. P. Williamson, in Encyclopedia of Analytical Science, ed. P. Worsfold, C. Poole, A. Townshend and M. Miró, Elsevier, Amsterdam, 3rd edn, 2019, pp. 264–271 Search PubMed.
- T. D. W. Claridge, High-Resolution NMR Techniques in Organic Chemistry, Elsevier, Boston, 3rd edn, 2016, pp. 315–380 Search PubMed.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 5287–5293 RSC.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 4–9 Search PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 34108 CrossRef PubMed.
- B. Schirmer and S. Grimme, in Frustrated Lewis Pairs I, ed. G. Erker and D. W. Stephan, Springer, Heidelberg, 2013, pp. 213–230 Search PubMed.
- S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- H. Kim, G. Gerosa, J. Aronow, P. Kasaplar, J. Ouyang, J. B. Lingnau, P. Guerry, C. Farès and B. List, Nat. Commun., 2019, 10, 1–6 CrossRef PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- M. Sparta and F. Neese, Chem. Soc. Rev., 2014, 43, 5032–5041 RSC.
- W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778–4792 CrossRef CAS PubMed.
- G. Bistoni, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1442 CAS.
- D. Yepes, F. Neese, B. List and G. Bistoni, J. Am. Chem. Soc., 2020, 142, 3613–3625 CrossRef CAS PubMed.
- M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839–1862 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- R. Laplaza, F. Peccati, R. A. Boto, C. Quan, A. Carbone, J. P. Piquemal, Y. Maday and J. Contreras-García, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 1–18 Search PubMed.
- Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093–6107 RSC.
- J. Burés, A. Armstrong and D. G. Blackmond, J. Am. Chem. Soc., 2012, 134, 6741–6750 CrossRef PubMed.
- P. Muller, Pure Appl. Chem., 1994, 66, 1077–1184 Search PubMed.
- A. J. T. Smith, R. Müller, M. D. Toscano, P. Kast, H. W. Hellinga, D. Hilvert and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 15361–15373 CrossRef CAS PubMed.
- J. M. Crawford and M. S. Sigman, Synthesis, 2019, 51, 1021–1036 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc03724b |
| This journal is © The Royal Society of Chemistry 2021 |