Discovery of cryptic allosteric sites using reversed allosteric communication by a combined computational and experimental strategy

Abstract

Allostery, which is one of the most direct and efficient methods to fine-tune protein functions, has gained increasing recognition in drug discovery. However, there are several challenges associated with the identification of allosteric sites, which is the fundamental cornerstone of drug design. Previous studies on allosteric site predictions have focused on communication signals propagating from the allosteric sites to the orthosteric sites. However, recent biochemical studies have revealed that allosteric coupling is bidirectional and that orthosteric perturbations can modulate allosteric sites through reversed allosteric communication. Here, we proposed a new framework for the prediction of allosteric sites based on reversed allosteric communication using a combination of computational and experimental strategies (molecular dynamics simulations, Markov state models, and site-directed mutagenesis). The desirable performance of our approach was demonstrated by predicting the known allosteric site of the small molecule MDL-801 in nicotinamide dinucleotide (NAD⁺)-dependent protein lysine deacetylase sirtuin 6 (Sirt6). A potential novel cryptic allosteric site located around the L116, R119, and S120 residues within the dynamic ensemble of Sirt6 was identified. The allosteric effect of the predicted site was further quantified and validated using both computational and experimental approaches. This study proposed a state-of-the-art computational pipeline for detecting allosteric sites based on reversed allosteric communication. This method enabled the identification of a previously uncharacterized potential cryptic allosteric site on Sirt6, which provides a starting point for allosteric drug design that can aid the identification of candidate pockets in other therapeutic targets.

---

Introduction

Protein allostery, which is considered as the second secret of life, has paved a novel avenue for modern drug discovery. Allostery involves fine-tuning the functions of conserved orthosteric sites by topologically distinct allosteric sites. Allosteric ligands exhibit higher selectivity and better physio-chemical properties than orthosteric ligands, which offers a new paradigm for innovative therapeutic development.^1–6 Allostery has enabled the successful modulation of intractable drug targets, such as oncoprotein Ras, recalcitrant kinases, and G-protein-coupled receptors (GPCRs).^5–13 The prerequisite for allosteric drug design is the precise identification of allosteric sites. However, most characterized allosteric sites were serendipitously discovered through exhaustive and tedious experimental approaches, such as high-throughput screening and alanine-scanning mutagenesis.^2,14–16 Computational tools, such as AlloFinder and Ohm can overcome the limitations associated with allosteric site identification.^17,18 However, the computational methods generate artifacts due to the use of potentially biased structural data for model training and non-physiological dummy atoms or ligands for site detection and docking.^14,15,19,20 Moreover, the detection of cryptic allosteric sites, which can expand the repertoire of allosteric drug discovery, is not possible using these computational methods. The cryptic allosteric sites are exclusively detected in specific intermediate states within protein conformational ensemble.^21–23

In addition to the classical allosteric communication theory according to which the signals propagate from the allosteric sites to the orthosteric sites, a bidirectional allosteric communication theory has recently been proposed.^24–27 According to this theory, the communication signals can also propagate from the orthosteric sites to the allosteric sites, which is referred to as reversed allostery or reversed allosteric communication. Several studies have validated this theory by examining a set of classical allosteric proteins. For example, novel allosteric sites on 15-lipoxygenase and allosteric modulators targeting phosphoinositide-dependent protein kinase 1 (PDK1) were successfully identified based on the bidirectional allosteric communication theory.^24,28,29 The reversed allosteric communication model facilitates the ab initio identification of allosteric sites without prior knowledge of the orthosteric sites. However, the limitation of this model is the artificial nature of manually introduced orthosteric perturbations. Following a similar stream, we propose a computational framework for allosteric site predictions through the reversed allostery model. This framework is based on orthosteric ligand binding, which is the most common and natural orthosteric perturbation, to minimize the generation of potential artifacts. The developed framework can facilitate unbiased detection of allosteric sites under physiological conditions and delineate the crosstalk between orthosteric and allosteric sites. This model was further applied to investigate Sirt6, a key member of the sirtuin deacetylase family for which there are limited regulatory molecules.

Sirtuins, which are nicotinamide adenine dinucleotide (NAD⁺)-dependent class III histone deacetylases (HDACs), deacetylate histones and mediate various cellular events ranging from maintenance of genomic stability to metabolic activities.^30–34 Sirt6, a member of the sirtuin family (Sirt1–7), catalyzes the removal of acetyl groups from the lysine residues 9, 18, and 56 on histone 3 (H3K9, H3K18, and H3K56) and transfers them to NAD⁺ cofactor. This reaction yields nicotinamide and a combination of 2′- and 3′-O-acetyl-ADP ribose as products.^31,34–37 Sirt6, which is involved in various biological processes, such as DNA repair and aging, is expressed in different mammalian organs. Thus, Sirt6 is a potential therapeutic target.^32–34,38 There are limited selective compounds for drugging Sirt6 owing to the highly conserved structural architecture among its paralogues. This has prompted the development of Sirt6 allosteric modulators for specific therapeutic applications.^34,39–41

Sirt6 shares an evolutionarily conserved catalytic core with other sirtuin members, which comprise eight α-helices and nine β-sheets with a large Rossmann fold and a small zinc-binding domain (ZBD) (Fig. 1).^40,42 These two domains flank the Sirt6 active cleft, where a long hydrophobic channel loads acetylated substrates and NAD⁺. Recently, we identified an allosteric site behind the orthosteric site of Sirt6 and discovered a first-in-class Sirt6 allosteric activator (MDL-801) for this site (Fig. 1).^43,44 Biochemical analysis of this activator revealed that it is robustly suppressed in cancer models and that it improves the quality of induced pluripotent stem cells derived from aging mice.^45–47 These findings highlight the potential of Sirt6 allosteric drug development.

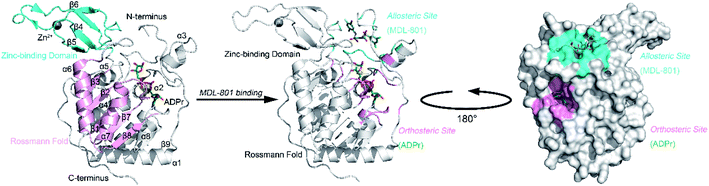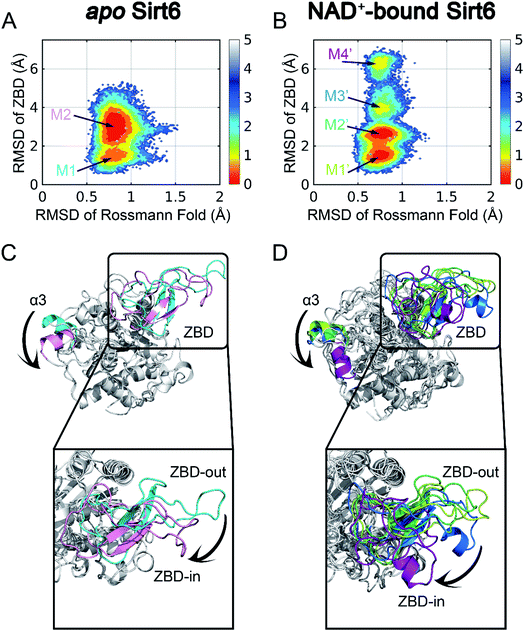
Fig. 1 Structural overview of Sirt6 with major secondary structural elements and functional domains specified. The zinc-binding domain (ZBD) and Rossmann fold (PDB ID: 5X16) are shown in cyan and pink, respectively (left panel). Structural overview of the allosteric activator (MDL-801)-bound Sirt6 with highlighted ADPr orthosteric site (pink) and MDL-801 allosteric site (cyan) (PDB ID: 5Y2F) (middle). Structural overview of MDL-801-bound Sirt6 showing the distal binding pocket of MDL-801 to orthosteric ADPr pocket. This confirmed its allosteric nature (PDB ID: 5Y2F) (right).

In this study, we developed a novel hybrid computational pipeline based on reversed allosteric communication and successfully implemented it for the prediction of Sirt6 allosteric sites. We hypothesized that orthosteric ligand binding shifts the conformational ensemble of Sirt6 and fine-tunes the conformation of the surface cavities that do not overlap with its orthosteric site, which results in the emergence of cryptic allosteric sites. Large-scale molecular dynamics (MD) simulations and Markov state model (MSM) analysis revealed that the dynamic landscape of Sirt6 is markedly altered upon binding of NAD⁺ to the orthosteric site with the emergence of two novel intermediate substrates. Structural analysis revealed that the orthosteric NAD⁺ site modulates the known allosteric MDL-801 site, which supported the rationale of our model. Importantly, NAD⁺-loaded Sirt6 exhibits a novel potential cryptic allosteric site (Pocket X) with marked allosteric effects in its intermediate conformation. The allosteric crosstalk between Pocket X and the orthosteric NAD⁺ site was elucidated using energetic calculations and correlation analysis.^18,48 Furthermore, the results of site-directed mutagenesis demonstrated that mutations in Pocket X allosterically affect the deacetylation activity of Sirt6, which confirmed the accuracy and reliability of our proposed computational framework. Thus, we propose a combined computational framework based on reversed allosteric communication for allosteric site prediction. The method developed in this study revealed a potential cryptic allosteric site on Sirt6, which can aid future rational allosteric drug design.

Results

Orthosteric NAD⁺ binding alters Sirt6 dynamic ensemble and generates new intermediate substrates

To initiate our computational pipeline for reversed allosteric communication, a 500 ns accelerated MD (aMD) simulation was performed for apo- and holo-Sirt6 in five replicas to enhance sampling and cover broader conformational spaces (see Materials and methods). The Rossmann fold and the ZBD are critical for the functions of Sirt6.⁴² Hence, they were selected as two structural features to capture the conformational dynamics of Sirt6 throughout the simulations. The root-mean-square deviations (RMSDs) in these two domains were calculated and projected onto a two-dimensional (2D) space to visualize the overall free energy landscapes (Fig. 2). The apo-Sirt6 form exhibited two dominant conformations (Fig. 2A) with RMSDs of approximately 0.8 Å in the Rossmann fold and 1.5 Å and 3 Å in the ZBD. Orthosteric NAD⁺ binding markedly altered the Sirt6 conformational ensemble (Fig. 2B). The basins for conformational clusters in NAD⁺-bound holo-Sirt6 slightly shifted along the X-axis. The RMSDs (approximately 0.7 Å) in the Rossmann fold of NAD⁺-bound holo-Sirt6 were lower than those in the Rossmann fold of the apo-protein. Two novel intermediate states were observed with RMSDs of approximately 4 Å and 6.5 Å in the ZBD. The high RMSD values in the ZBD of the holo-protein suggested conformational rearrangements and indicated that orthosteric binding triggered reversed allosteric communication.

Fig. 2 Conformational landscapes of apo- (A) and holo- (B) Sirt6. Structural comparisons of dominant intermediate state structures of apo- (C) and holo- (D) Sirt6. The highlighted regions show dominant conformational rearrangements.

To examine the key conformational states of Sirt6 during simulations, MSM, which has been widely used to probe protein conformational dynamics,^22,49,50 was constructed for our simulated systems using PyEMMA⁵¹ (see Materials and methods). The results of the implied timescale test (Fig. S1†) and the Chapman–Kolmogorov test (Fig. S2†) confirmed that our models were Markovian (see Materials and methods). Conformational ensembles for apo- and holo-Sirt6 were then clustered into 2 (M1 and M2) and 4 (M1′, M2′, M3′, and M4′) MSM metastable states, respectively (Fig. 2A and B). Comparative analysis of these dominant conformations revealed that the overall Sirt6 backbone structure was stable throughout the simulations irrespective of NAD⁺ binding. However, the α3-helix in both systems underwent remodeling (Fig. 2C and D). The most prominent conformational rearrangements were observed in the ZBD, which was consistent with our conformational landscape analysis. The structural feature of ZBD, which mainly comprises coils, loops, and three β-sheets (β4–β6), indicated its high plasticity during simulations. In apo-Sirt6, the MSM metastable states M1 and M2 positioned ZBD with outward and inward orientations relative to the overall protein (hereafter designated as ZBD-out and ZBD-in conformations, respectively) (Fig. 2C), respectively. In holo-Sirt6, the conformations of M1′ and M2′ were similar to those of M1 in apo-protein with both exhibiting a ZBD-out conformation. The newly formed substates M3′ and M4′ exhibited ZBD-in conformation but projected ZBD further inward. The loop connecting β5 and β6 was transformed into a short α-helix (Fig. 2D). The conformational landscapes and MSM analyses highlighted that orthosteric NAD⁺ binding induced marked conformational changes in the Sirt6 ensemble with predominant changes in the ZBD.

Detecting potential allosteric pockets using the reverse allosteric communication model

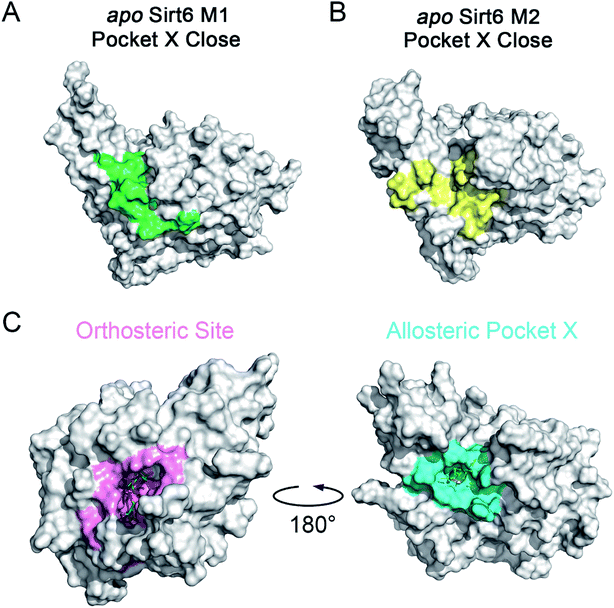
The motions and dynamics of the orthosteric and allosteric sites are highly correlated.^26,27 Perturbations at orthosteric sites can fine-tune the overall protein conformational dynamics and influence distal regions, which may result in the emergence of novel allosteric sites.^26,27,52 As the conformational ensemble of Sirt6 was markedly altered upon orthosteric NAD⁺ binding, we investigated its surface cavities to identify potential allosteric sites. Fpocket was used for pocket prediction on all six MSM metastable state structures (i.e., M1, M2 and M1′–M4′)^53,54 to retrieve novel binding cavities. In NAD⁺-bound Sirt6, we first identified the previously reported pocket for the allosteric activator MDL-801 (ref. 43) (Fig. 3A). Surprisingly, this pocket, which was detected as Pocket 1, was not completely formed during the simulations (Fig. 3B). The entrance of the pocket was partially blocked by the flexible N-terminus, which may be only displaced upon allosteric modulator loading through an “induced-fit” mechanism. These observations underscored the dynamic nature of the MDL-801 allosteric site, which underwent structural rearrangement through ligand–pocket interaction and was transformed into a suitable conformation to accommodate its corresponding allosteric ligands.^55–59 These results also demonstrate the rationale of our prediction model. Interestingly, a novel binding site, named Pocket X, was identified, which emerged because of conformational remodeling caused due to NAD⁺ binding (Fig. 3C). This novel cavity mainly comprises α5-helix, a loop linking α3- and α4-helixes, and ZBD residues. This new pocket was not visible in the Sirt6 crystal structure in which a part of the C-terminus was covered above the pocket that hindered its formation (Fig. 3D, S3B and C). Pocket X was detected only in the newly emerging M4′ MSM metastable state but not in the M1′–M3′ metastable states of holo-Sirt6. The C-terminal coil structure was induced into an α-helix and displaced, which resulted in the exposure of this novel pocket. This indicated the dynamic nature of Pocket X (Fig. 3C, D and S3D–F). Pocket X was also not detected in the apo-Sirt6 MSM metastable structures (M1 and M2), which indicated that orthosteric binding was a prerequisite for the formation of this pocket (Fig. 4A and B). This further provided evidence for the reversed allostery theory. Pocket X, which is situated behind the orthosteric pocket for NAD⁺, exerted allosteric effects (Fig. 4C). The dynamic behavior of Pocket X emphasizes the feasibility of reversed allosteric communication triggered by orthosteric ligand–protein interactions. Additionally, reversed allosteric communication resulted in the emergence of novel cryptic allosteric sites, whose formation was induced by conformational rearrangements resulting from reversed allosteric communication caused by orthosteric NAD⁺ binding.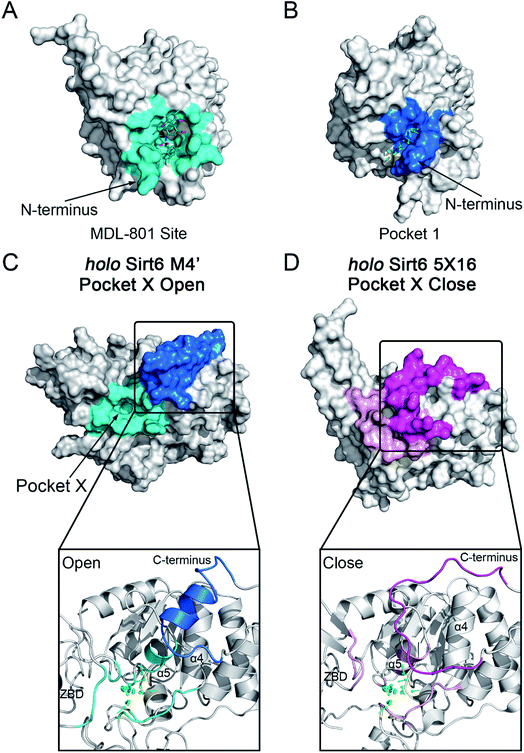

Fig. 3 (A) Structural overview of the binding site (cyan) for the allosteric activator MDL-801 on Sirt6 (PDB ID: 5Y2F). (B) Structural overview of the partial reproduction of the MDL-801 site on Sirt6 as Pocket 1 in our reversed allostery model with the N-terminus partly blocking the entrance of the pocket. Structural overview of the newly identified cryptic allosteric site (Pocket X) in its open (C) and closed (D) conformations with the C-terminus blocking the entrance of the pocket.

Fig. 4 (A) Closed conformation of Pocket X in the Markov state model (MSM) metastable state M1 of apo Sirt6 (Pocket X residues are highlighted in green). (B) Closed conformation of Pocket X in the MSM metastable state M2 of apo-Sirt6 (Pocket X residues are highlighted in yellow). (C) Novel allosteric Pocket X (cyan) located at the opposite side of Sirt6, which is distal to the orthosteric NAD⁺ binding site (pink). This confirmed its allosteric nature.

Characterizing the coupling between orthosteric and allosteric sites

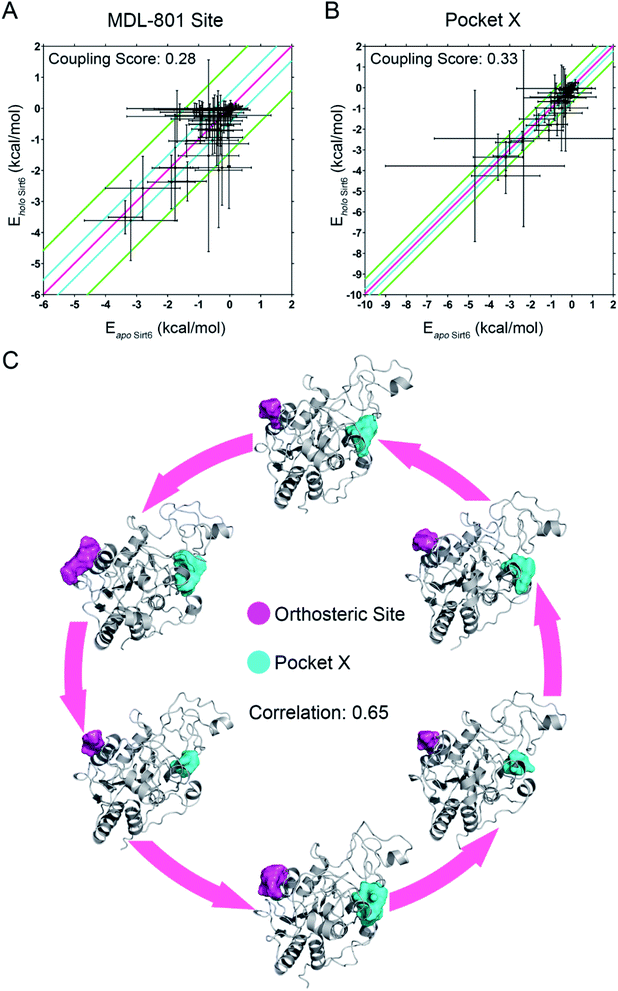
Next, we established a computational scheme to quantify the reversed allosteric communication caused by orthosteric binding and confirmed the coupling between the orthosteric site and the predicted allosteric sites. A previous study established the residue–residue interaction model in which some residue pairs within the allosteric sites exhibited substantial interaction energy changes upon ligand binding.^52,60 Based on this model, we derived a quantitative model to evaluate allosteric coupling between the orthosteric and allosteric sites. In the reversed allostery model, we speculated that the potential allosteric sites exhibited similar energetic properties in response to orthosteric ligand binding. The residue–residue interaction free energy of a proportion of residue pairs within the allosteric sites would undergo considerable changes before and after orthosteric loading, which suggested reversed allosteric communication due to orthosteric perturbations.

To utilize the differences in residue interaction energy as predictors of potential allosteric sites, a quantitative measurement was needed to set up the threshold to differentiate between the allosteric and non-allosteric sites. Based on a previous workflow,^52,60 we divided all residue pairs within a given pocket into the following three groups according to their interaction energy differences before and after orthosteric binding: small energy difference (I), medium energy difference (II), and large energy difference (III). The energy differences between the residue pairs in the small energy difference (I) group are within one standard deviation of the overall average value (between pink and cyan lines in Fig. 5A and B), whereas those in the medium energy difference (II) group were within three standard deviations (between cyan and green lines in Fig. 5A and B). In the large energy difference group (III), the energy differences between the residue pairs were distributed at least three standard deviations away from the average interaction energy changes (outside the green lines in Fig. 5A and B). The ratio of the number of residue pairs in the (III) group to that in the (II) and (III) groups was calculated as the energy coupling score, which indicated the coupling between orthosteric and allosteric sites through energetic terms. The energy coupling score was used to identify potential allosteric sites with 0.25 as the threshold, which was selected based on previous studies.^52,60 Pockets with energy coupling scores higher than 0.25 were considered as allosteric sites, while those with scores lower than 0.25 were considered as non-allosteric sites.

Fig. 5 Energy coupling analysis for the MDL-801 site (A) and Pocket X (B) in apo- and holo-Sirt6. Each dot represents one residue pair and its crosses indicate the corresponding standard deviations. The pink line reflects the average interaction energy changes between apo- and holo-protein. Regions between pink and cyan lines indicate small energy difference (one standard deviation, group I), regions between cyan and green lines indicate medium energy difference (three standard deviations, group II), and regions outside green lines indicate large energy difference (higher than three standard deviations, group III). (C) Correlation analysis using D3Pocket for orthosteric NAD⁺ site (magenta) and allosteric Pocket X (cyan).

Among the prediction results from Fpocket based on the conformational ensemble obtained after orthosteric binding, we tested our method with the recently reported MDL-801 allosteric site on Sirt6. The energy coupling score for the allosteric MDL-801 site was 0.28, which was higher than the cutoff score of 0.25 (Fig. 5A). This was consistent with the results of a previous experimental study that reported the allosteric nature of the MDL-801 binding site.⁴³ Thus, our findings demonstrating the reliability and accuracy of our “energy coupling” approach for identifying novel allosteric sites and quantifying reversed allosteric communication. This approach was further applied to analyze the newly predicted Pocket X. The energy coupling score for Pocket X was 0.33 (Fig. 5B), which was higher than the threshold score for the allosteric site. This confirmed that Pocket X was strongly coupled with the orthosteric NAD⁺ binding site and that Pocket X is allosterically regulated. Most cavities predicted by Fpocket had an energy coupling score lower than the threshold score (0.25) and thus were excluded from further analyses (Fig. S4†). This indicated the sensitivity of our approach.

The energy coupling score only deciphered the crosstalk between orthosteric and allosteric sites through energetics. Next, we delineated the structural basis underlying the reversed allosteric communication between the allosteric Pocket X and the orthosteric NAD⁺ binding site. Several cutting-edge computational algorithms were applied for allosteric analyses of Pocket X. Among them, Ohm, a newly developed network-based method,¹⁸ was used to characterize the allosteric signals originating from Pocket X. The allosteric coupling intensity of the residues in Pocket X was high (0.7866 ± 0.02609). Thus, these residues were considered allosteric hotspots. This indicated that Pocket X exerted a marked allosteric effect on the orthosteric NAD⁺ cavity, which concurred with our results. Furthermore, D3Pocket, a webserver for cavity dynamic analysis,⁴⁸ was employed for structure-based evaluation of allosteric coupling. During the simulations, a strong positive volume correlation (0.65) was observed between the orthosteric NAD⁺ site and Pocket X. The dynamics of Sirt6 involving increased volume of the orthosteric NAD⁺ site were associated with a concomitant increase in the volume of allosteric Pocket X (Fig. 5C). This was consistent with our thermodynamic analysis of the energy coupling score. Additionally, this finding indicated the correlation between the orthosteric binding site and allosteric Pocket X, which suggested bidirectional allosteric communication.

Pocket X negatively modulates the activity of Sirt6

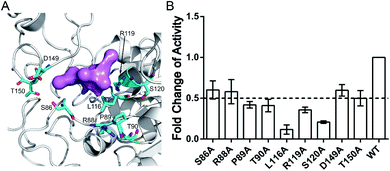
The aforementioned computational analysis of reversed allosteric communication from an orthosteric NAD⁺ site identified Pocket X as a novel allosteric site on Sirt6. To further corroborate the allosteric regulation of Sirt6 deacetylation, we performed site-directed mutagenesis experiments. The Fluor de Lys (FDL) assay^36,61 was conducted to quantify the effect of different single mutations (S86A, R88A, P89A, T90A, L116A, R119A, S120A, D149A, and T150A; Fig. 6A) on the Sirt6 deacetylation activity on the acetylated substrate peptide (RHKK-ack-AMC). Sirt6 with mutant Pocket X exhibited approximately two-fold lower deacetylation activity than wild-type Sirt6 (Fig. 6B). Additionally, Sirt6 with mutations at the L116, R119, and S120 residues in Pocket X exhibited 4–8-fold lower deacetylation activity than wild-type Sirt6 (Fig. 6A and B). These results validated that Pocket X was an allosteric pocket that negatively modulates the deacetylation activity of Sirt6. Thus, Pocket X can be potentially utilized for designing Sirt6 allosteric modulators in the future. Moreover, these experimental findings demonstrated the desirable predictive efficacy of our computational reversed allostery model, which represents a novel promising methodology for allosteric site identification and allosteric drug design.

Fig. 6 (A) Structural overview of critical residues within Pocket X. Overall backbone of Sirt6 is colored in white. The computational prediction probe for Pocket X is shown in pink, while the critical residues are displayed in cyan. (B) Mutagenesis experiments for critical residues within Pocket X. The deacetylation activity of different Sirt6 variants was measured and the relative activities of each mutant are expressed as fold changes relative to the wild-type enzyme, which is represented as 1. All assays were performed in at least triplicate and the results are presented as average ± standard deviation.

Discussion

In this study, we proposed a novel computational pipeline based on reversed allosteric communication for allosteric site prediction. HDAC Sirt6 was used to demonstrate the ability of the computational pipeline to predict the previously reported allosteric MDL-801 site. Additionally, a potential novel cryptic allosteric pocket was identified, which only formed within a newly induced MSM metastable state upon orthosteric NAD⁺ binding. Bidirectional signals between orthosteric and allosteric sites were confirmed using both energetic and structural dynamics computations, as well as site-directed mutagenesis. This approach provides evidence for the protein allostery theory and enables allosteric drug discovery for intractable drug targets, including Sirt6.

Modern medicine is based on improved selectivity and enhanced pharmacological performances. Thus, allosteric modulators are applied for drug discovery^1,4,20,62,63 with multiple allosteric candidates targeting the historically “undruggable” targets, such as K-Ras, and Src homology 2 phosphatase (SHP-2), which may have clinical applications.^{8,9,11,64–67} Previously, allosteric drugs were identified mainly through serendipitous discovery due to difficulties in the identification and characterization of their binding sites.^2,14,15,20 The rapid development of computational tools to predict allosteric sites partially enabled overcoming these limitations.^17,68–70 However, most sites predicted using these computational tools were associated with several limitations due to the nature of their computational models or algorithms. For example, data-driven prediction methods are frequently limited due to the use of biased training datasets in which most allosteric sites are identified from kinases and GPCRs, which hinders the performance of the prediction methods. Normal mode analysis-based approaches are restricted by their relatively coarse analysis procedures with limited accuracy and specificity during approximations.^{2,15,17,19,69,70} Traditionally, the allosteric effect is defined as the modulation of the orthosteric sites by the allosteric sites. Recently, a bidirectional model for allostery was proposed^24–27 according to which the signals propagate from the orthosteric sites to the allosteric sites. This theory has been validated through various studies that discovered a novel allosteric site on 15-lipoxygenase and designed allosteric modulators for PDK1.^24,28,29 The possibility of generating artifacts from non-physiological orthosteric perturbations and other ligand–pocket interactions cannot be ruled out.

To address these issues, we developed a combined computational framework exploiting the reversed allosteric communication triggered by natural orthosteric ligand binding to detect potential allosteric sites within the protein dynamic ensembles. As shown in Fig. 7, we began with the apo- and holo-protein structures. MD simulations and MSM analysis were performed to probe the conformational ensemble of proteins in the absence and presence of orthosteric ligand binding. The dominant metastable state conformations were clustered and extracted. Potential allosteric sites can be predicted based on the holo-protein conformations, and their correlations with orthosteric sites can be further quantified through both structural and energetic analyses. Finally, the computational predictions were experimentally validated through site-directed mutagenesis. Compared with the previous reports, the workflow of this study precludes most artifacts by physiologically manipulating orthosteric sites through their corresponding ligand binding instead of mutations or manual perturbations. Additionally, large-scale MD simulations and cutting-edge techniques, such as MSM analysis, facilitated the identification of subtle metastable states within a protein dynamic ensemble. Thus, this approach can provide comprehensive insights into protein conformations. The detailed analysis of the alterations of protein conformation upon orthosteric ligand binding can reveal cryptic allosteric sites, which are not detected in most crystal structures and are present only in some conformational metastable states. The identification of cryptic allosteric sites, which are potential targets for allosteric drug discovery,^21,23,71 will expand the spectrum of available druggable targets.

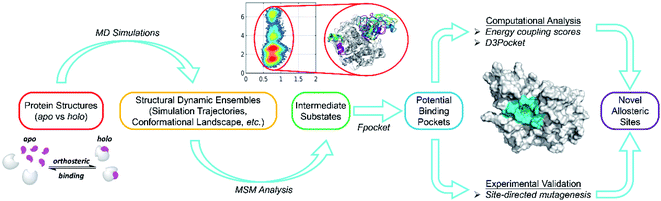Fig. 7 Overall workflow for our hybrid computational and experimental pipeline for allosteric site prediction based on reversed allosteric communication.

Our approach successfully predicted a cryptic allosteric site on Sirt6, a critical target that is involved in various physiological and pathological processes, such as longevity and carcinogenesis. However, there is a lack of specific therapeutic agents for Sirt6.^32–34,38 Sirt6 belongs to the “magnificent seven” sirtuin family (Sirt1 to Sirt7). The major challenge to identify drugs for Sirt6 is to achieve specificity among the seven different isoforms. Thus, the identification of selective Sirt6 allosteric modulator has piqued the interest of the scientific community.^34,39–41 Previous studies have achieved, limited success in identifying allosteric drugs targeting Sirt6. In this study, we identified a potential new exosite Pocket X with allosteric potential based on reversed allosteric communication. This will enable the identification of Sirt6 allosteric modulators in the future. Previous studies have demonstrated that Sirt6 inhibitors can be used to treat metabolic syndromes, such as diabetes, whereas Sirt6 activators can be used to treat cancers and aging-related diseases.^{33,34,43,45–47} The novel allosteric site discovered in this study markedly regulated the deacetylation activity of Sirt6. This indicated that this site could be a potential target for Sirt6 allosteric drug design. These findings illustrate the potential of the novel Sirt6 allosteric regulatory site identified using the reversed allosteric communication model for allosteric drug discovery.

Although the novel pocket identified using the workflow developed in this study exhibited allosteric activity, the corresponding allosteric ligands for this site were not identified. Hence, further studies on the allosteric site structure and therapeutic agents that target this site using compound screening and crystallography are needed for allosteric modulator discovery. This will complement the other half of allosteric drug design and enhance its translational significance.

Conclusions

Here, we described a novel computational workflow using the reversed allosteric communication model based on orthosteric ligand binding to predict the allosteric sites from the protein conformational ensemble. The accuracy of this methodology was validated using the previously known allosteric site for MDL-801 on Sirt6. A potential new allosteric site for Sirt6 was identified for further investigation. The method described in this study represents an up-to-date advance for protein allostery, which has potential applications in designing novel therapeutics. Moreover, the exosite on Sirt6 is a potential starting point for future rational allosteric drug design.

Materials and methods

Construction of simulated systems

The co-crystal structure (2.53 Å) of human Sirt6 in complex with cofactor ADPR, substrate H3K9 myristoyl peptide, and allosteric activator MDL-801, which was previously solved by our research group, was downloaded from the RCSB Protein Data Bank (PDB ID: 5Y2F).⁴³ The myristoylated substrate peptide in 5Y2F was truncated to represent the acetylated substrate peptide after removing its 12-carbon long aliphatic chain. To model the active reactant NAD⁺-bound Sirt6, the atomic coordinates of NAD⁺, which were extracted from the crystal structure of the Sirt1-NAD⁺ complex (PDB ID: 4I5I),⁷² were docked to replace the ADPR coordinates in 5Y2F.

Docking simulations

Molecular docking was performed using AutoDockFR–AutoDock.⁷³ Briefly, the structures of Sirt6-acetylated substrate complex and NAD⁺ were converted to PDBQT files using AutoDock Tools and loaded into AutoGridFR separately. The centroids of ADPr were set as the grid center with a search space of 60 × 60 × 60 Å using a spacing value of 0.375 Å between every two grids. The atomic affinity maps, which were generated using AutoGridFR, were used as input into AutoDockFR for protein–ligand docking. Fifty independent docking runs were performed to obtain multiple binding modes. During these docking simulations, the side chain of acetylated Lys9 (K9Ac) in the substrate peptide was set as a flexible receptor residue. The resulting docking poses were clustered with an RMSD threshold of 2 Å. The lowest energy-docking pose from each cluster was then visually determined by comparing the distance of the anomeric carbon of the nicotinamide ribose group from NAD⁺ and the acetyl oxygen atom of K9Ac. Additionally, the conformational arrangement was assumed necessary for promoting an S_N2 nucleophilic substitution reaction.

Conventional MD (cMD) simulations

The Amber ff14SB force field was employed to model the Sirt6 structure⁷⁴ and revised parameters were assigned for the Sirt6-binding Zn²⁺.⁷⁵ A TIP3P truncated octahedral water box (10 Å) was then applied for solvation, while the counterions were added for neutralization.⁷⁶ To mimic the physiological conditions for proteins, 0.15 mol L⁻¹ NaCl was randomly added to the complex system.

Complex systems underwent two rounds of energy minimization after preparation. The energies of water and counterions were minimized in 5000 steps (2000 steepest descent and 3000 conjugate gradient minimization steps) with a position restraint of 500 kcal (mol⁻¹ Å⁻²) on the protein backbone. Next, 4000 steepest descent and 6000 conjugate gradient cycles of minimization were applied to the whole system without any position restraint. Subsequently, under NVT condition and restraint of 10 kcal (mol⁻¹ Å⁻²) on Sirt6, each system was heated to 300 K in 300 ps after which 700 ps equilibration runs were performed. Finally, to obtain the energy data for aMD, 50 ns cMD simulations with a timestep of 2.0 fs were performed under 1 atm and 300 K. Langevin dynamics with a collision frequency of 1 ps⁻¹ were applied to regulate the system temperature, while the system pressure was regulated by a Berendsen barostat with isotropic position scaling. During cMD, the particle mesh Ewald method was used to model the long-range electrostatic interactions,⁷⁷ whereas a cutoff value of 10 Å was set for short-range electrostatic interactions and van der Waals force calculations. Additionally, the SHAKE algorithm was applied to restrain all covalent bonds containing hydrogen atoms.⁷⁸

aMD simulations

The aMD simulations were performed after a 50 ns cMD simulation to enhance sampling. The principle of aMD is that “boost energy” was introduced into the system potential energy surface when the corresponding potential energy is lower than the predetermined threshold. The boosting energy decreases energy barriers between conformations and flattens the free energy landscape, which accelerates the conversions between different stable conformers.⁷⁹ As shown in eqn (1) and (2), the system potential energy was V(r) and E_thresh was the threshold determined by the system size and normal energy value. If the instantaneous potential energy was lower than E_thresh, it would increase by ΔV(r) and reach V*(r). In other cases, the origin value V(r) was used as V*(r) in aMD simulation.

V*(r) = V(r); V(r) ≥ E_thresh (1)

V*(r) = V(r) + ΔV(r), V(r) < E_thresh (2)

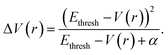where ΔV(r) is defined in eqn (3) depending on E_thresh and the acceleration parameter α

During aMD simulation, both potential energy and dihedral energy surfaces were boosted, which is referred to as the “dual boost” protocol.⁸⁰Eqn (4)–(7) determined the parameters of potential and dihedral energy. Among them, E_threshP denotes the energy threshold for potential energy, while E_threshD represents the energy threshold for dihedral energy. The α_P and α_D values represent the acceleration parameters for potential and dihedral energy, respectively. cMD simulations retrieved the average total energy (E_{tot avg}) and the average dihedral energy (E_{dih avg}) for aMD. N_atoms and N_residues represent the number of atoms and residues in the systems, respectively.

E_threshP = E_{tot avg} + N_atoms × 0.16 kcal mol⁻¹ (4)

α_P = N_atoms × 0.16 kcal mol⁻¹ (5)

E_threshD = E_{dih avg} + N_residues × 4 kcal mol⁻¹ (6)

α_D = N_residues × 4/5 kcal mol⁻¹ (7)

The last structures of the cMD simulations were set as the starting structure of the aMD simulations. Five independent aMD replicas of 500 ns with random initial velocity were performed for each system (apo versus holo Sirt6), which resulted in a cumulative timescale of 5 μs. The calculation of electrostatic interaction and van der Waals forces, as well as other systemic environmental parameter settings, such as the thermostat and barostat values were consistent with those used during cMD processes. After simulations, trajectory analysis was performed using CPPTRAJ.

Construction of MSM

Based on the coordinates of apo Sirt6, we calculated the RMSDs in the Rossmann fold and ZBD during the apo and holo Sirt6 simulations, which were then used as inputs for the PyEMMA MSM analyses.⁵¹ After validating the Markovian property (please see next part), we used the “coordinates.cluster_kmeans” method to cluster our structural data into 200 microstates with a maximum k-means iteration number of 200. Next, MSMs for apo and holo Sirt6 were constructed using the “msm.estimate_markov_model” function with a lag time of 2 ns. These 200 microstates were further clustered into multiple metastable states using the Perron cluster analysis (PCCA+) algorithm, which was further confirmed by the Chapman–Kolmogorov test (please see next part).

In each metastable state, the “coordinates.save_traj” algorithm was used to extract trajectories comprising more than 50% snapshots for the corresponding state. Next, the MDTraj package was applied to capture the representative structures corresponding to each intermediate state according to the similarity score S_ij. As shown in eqn (8), d_ij is the RMSD between structures i and j, while d_scale is the standard deviation of d.⁸¹ After iterating each pair of structures in the trajectory, the structure with the highest S_ij was considered as the most representative conformation.

S_ij = e^{−d_ij/d_scale} (8)

Validation of the MSM

Based on our 2D free energy landscape depicting the conformation distributions throughout the simulations, an implied timescale test was applied to validate the Markovian properties of our simulation systems. First, we specified the number of k-means centers and maximum iteration and then constructed the corresponding multiple transition probability matrixes (TPMs) with different lag times, which represent the time interval between transitions. TPMs account for the possibility of transition between all pairs of microstates and determine the implied timescale (also known as relaxation timescale) through eqn (9).

τ_i = −τ/ln λ_i (9)

where τ is the lag time for the construction of TPMs, λ_i represents the i^th eigenvalue of TPM with a lag time τ.

When the transition of microstates relaxes for i^th time, the implied timescale τ_i is calculated using eqn (9).

Under practical conditions, the implied timescale comes from the eigen decomposition of TPMs, and the sequence of eigenvalues corresponds to the sequence of transition. Thus, the first eigenvalue (λ₁) represents the slowest transition. To verify the Markovian properties, we must calculate different τ_i based on increasing τ. If τ_i (notably for τ₁) starts to become steady as τ increases, the transitions between microstates become independent of the lag times, which concurs with the Markovian model.⁸²

As shown in Fig. S1,† we calculated the changes in the implied timescale of apo (Fig. S1A†) and holo (Fig. S1B†) Sirt6 with lag time. Both the k-means cluster centers and the maximum iteration times were set to 200. In Fig. S1A,† the τ_i curves of apo Sirt6 converge to reach the platform from a lag time of approximately 1.25 ns, while those for holo Sirt6 are flattened from a lag time of approximately 0.5 ns (Fig. S1B†). Hence, the lag times longer than 1.25 ns will guarantee the Markovian properties of our systems. We used 2 ns as the lag time for further analysis.

According to the Sirt6 conformation landscape distributions, we clustered the microstates of apo Sirt6 into 2 MSM metastable states, while those of holo Sirt6 were clustered into 4 MSM metastable states using the PCCA+ method. The Chapman–Kolmogorov test shown in Fig. S2† demonstrated that the transition probability estimated based on MSM is highly similar to the practical transition process.⁸³ Thus, our MSM estimation was also validated.

Energy coupling score calculation

Based on the MD simulation trajectories, molecular mechanics generalized Born surface area (MM-GBSA) energy calculation was performed for the corresponding cavities on Sirt6 in both apo and holo systems. The interaction free energy with a pocket was calculated for energy residues separated by at least three amino acids in the sequence based on the following eqn (10):

E = E_int + E_eel + E_vdw + G_pol + G_sas (10)

where E_int represents internal energy, E_eel denotes electrostatic energy, E_vdw indicates van der Waals energy, and G_pol and G_sas are the polar solvation energy and solvent-accessible surface energy, respectively.

Energy differences, which were calculated for pockets in the NAD⁺-bound (holo) and NAD⁺-unbound (apo) systems, were used to evaluate the energy coupling scores.

Mutant plasmid construction and protein purification

The full-length wild type (1–355 amino acids) human Sirt6 was cloned into the PET28a vector to express the fusion protein with an N-terminal His-tag. Site-directed mutagenesis (S88A, R90A, P91A, T92A, L118A, R121A, S122A, D151A, and T152A) was performed using the In-Fusion® HD Cloning Kit (Takara), following the manufacturer's instructions. All recombinant plasmids were transfected into the Escherichia coli DH5α cells and extracted using the TIANprep Rapid Mini Plasmid Kit (TianGen). The quantity and quality of the plasmids were measured based on the absorbances at 260 and 280 nm using NanoDrop (Thermo). The plasmid sequences were further confirmed using DNA sequencing.

The recombinant plasmids were transformed into Escherichia coli Rosetta (DE3) chemically competent cells (Weidi Biotechnology) for protein purification. The recombinant colony was inoculated in ×2xYT medium with 50 μg mL⁻¹ kanamycin at 37 °C. The expression of the recombinant protein was induced using 0.5 mM isopropyl-beta-D-thiogalactopyranoside when the optical density of the culture at 600 nm (OD600) reached 0.6–0.8. The induction was continued at 16 °C for 16–18 h. Next, the cells were lysed at high pressure using Sirt6 lysis buffer (1× phosphate-buffered saline [pH 7.5], 300 mM NaCl, and 5% glycerol). The lysate was loaded onto a nickel column (GE Healthcare) with 1 mM dithiothreitol. A protein inhibitor cocktail was added before high-pressure crushing. After washing with 20, 40, 100 mM of imidazole, the protein was eluted using 250 mM imidazole. The elution was dialyzed into Sirt6 assay buffer (50 mM Tris–HCl, pH 8.0, 137 mM NaCl, 2.7 mM KCl, and 1 mM MgCl₂) and used in all in vitro assays in this study.

FDL assay

To measure the deacetylation activity of both wild-type and mutant Sirt6, 5 μM purified proteins were incubated in a 50 μL reaction mixture (75 μM RHKK-ack-AMC, 2.5 mM NAD⁺, 10% dimethyl sulfoxide, and Sirt6 assay buffer) at 37 °C for 2 h. The reaction mixture was incubated with 50 μL stop buffer mixture (40 mM nicotinamide, 6 mg mL⁻¹ trypsin, and Sirt6 assay buffer) at 25 °C for 30 min to quench the reaction. The fluorescence intensity was quantified using a microplate reader (Synergy H4 Hybrid Reader, Bio Tek) at excitation and emission wavelengths of 360 nm and 460 nm, respectively. Each experiment was independently repeated at least three times.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported partly by grants from the National Natural Science Foundation of China (22077082, 21778037, 81925034, 91753117, and 81721004), the Innovation Program of Shanghai Municipal Education Commission (2019-01-07-00-01-E00036, China), the Shanghai Science and Technology Innovation (19431901600, China), and the Shanghai Health and Family Planning System Excellent Subject Leader and Excellent Young Medical Talents Training Program (2018BR12, China).

References

1. S. Lu, Q. Shen and J. Zhang, Acc. Chem. Res., 2019, 52, 492–500.
2. S. Lu, X. He, D. Ni and J. Zhang, J. Med. Chem., 2019, 62, 6405–6421.
3. D. Ni, S. Lu and J. Zhang, Med. Res. Rev., 2019, 39, 2314–2342.
4. D. Ni, N. Liu and C. Q. Sheng, Adv. Exp. Med. Biol., 2019, 1163, 313–334.
5. R. Nussinov and C. J. Tsai, Cell, 2013, 153, 293–305.
6. J. Liu and R. Nussinov, PLoS Comput. Biol., 2016, 12, e1004966.
7. S. Lu and J. Zhang, J. Med. Chem., 2019, 62, 24–45.
8. J. Canon, K. Rex, A. Y. Saiki, C. Mohr, K. Cooke, D. Bagal, K. Gaida, T. Holt, C. G. Knutson, N. Koppada, B. A. Lanman, J. Werner, A. S. Rapaport, T. San Miguel, R. Ortiz, T. Osgood, J. R. Sun, X. Zhu, J. D. McCarter, L. P. Volak, B. E. Houk, M. G. Fakih, B. H. O'Neil, T. J. Price, G. S. Falchook, J. Desai, J. Kuo, R. Govindan, D. S. Hong, W. Ouyang, H. Henary, T. Arvedson, V. J. Cee and J. R. Lipford, Nature, 2019, 575, 217–223.
9. D. Ni, X. Li, X. He, H. Zhang, J. Zhang and S. Lu, Pharmacol. Ther., 2019, 202, 1–17.
10. J. M. Ostrem, U. Peters, M. L. Sos, J. A. Wells and K. M. Shokat, Nature, 2013, 503, 548–551.
11. F. McCormick, Cancer Cell, 2020, 37, 3–4.
12. R. Nussinov, C. J. Tsai and P. Csermely, Trends Pharmacol. Sci., 2011, 32, 686–693.
13. S. Lu, H. Jang, S. Muratcioglu, A. Gursoy, O. Keskin, R. Nussinov and J. Zhang, Chem. Rev., 2016, 116, 6607–6665.
14. S. Lu, Y. Qiu, D. Ni, X. He, J. Pu and J. Zhang, Drug Discovery Today, 2020, 25, 177–184.
15. X. Daura, Adv. Exp. Med. Biol., 2019, 1163, 141–169.
16. M. J. Latallo, G. A. Cortina, S. Faham, R. K. Nakamoto and P. M. Kasson, Chem. Sci., 2017, 8, 6484–6492.
17. M. Huang, K. Song, X. Y. Liu, S. Y. Lu, Q. C. Shen, R. X. Wang, J. Z. Gao, Y. Y. Hong, Q. Li, D. Ni, J. R. Xu, G. Q. Chen and J. Zhang, Nucleic Acids Res., 2018, 46, W451–W458.
18. J. Wang, A. Jain, L. R. McDonald, C. Gambogi, A. L. Lee and N. V. Dokholyan, Nat. Commun., 2020, 11, 3862.
19. S. Lu, W. Huang and J. Zhang, Drug Discovery Today, 2014, 19, 1595–1600.
20. S. J. Wodak, E. Paci, N. V. Dokholyan, I. N. Berezovsky, A. Horovitz, J. Li, V. J. Hilser, I. Bahar, J. Karanicolas, G. Stock, P. Hamm, R. H. Stote, J. Eberhardt, Y. Chebaro, A. Dejaegere, M. Cecchini, J. P. Changeux, P. G. Bolhuis, J. Vreede, P. Faccioli, S. Orioli, R. Ravasio, L. Yan, C. Brito, M. Wyart, P. Gkeka, I. Rivalta, G. Palermo, J. A. McCammon, J. Panecka-Hofman, R. C. Wade, A. Di Pizio, M. Y. Niv, R. Nussinov, C. J. Tsai, H. Jang, D. Padhorny, D. Kozakov and T. McLeish, Structure, 2019, 27, 566–578.
21. V. Oleinikovas, G. Saladino, B. P. Cossins and F. L. Gervasio, J. Am. Chem. Soc., 2016, 138, 14257–14263.
22. S. Lu, D. Ni, C. Wang, X. He, H. Lin, Z. Wang and J. Zhang, ACS Catal., 2019, 9, 7188–7196.
23. S. Lu, M. Ji, D. Ni and J. Zhang, Drug Discovery Today, 2018, 23, 359–365.
24. J. O. Schulze, G. Saladino, K. Busschots, S. Neimanis, E. Suss, D. Odadzic, S. Zeuzem, V. Hindie, A. K. Herbrand, M. N. Lisa, P. M. Alzari, F. L. Gervasio and R. M. Biondi, Cell Chem. Biol., 2016, 23, 1193–1205.
25. A. E. Leroux and R. M. Biondi, Trends Biochem. Sci., 2020, 45, 27–41.
26. W. Zhang, J. Xie and L. Lai, Adv. Exp. Med. Biol., 2019, 1163, 89–105.
27. X. Ma, H. Meng and L. Lai, J. Chem. Inf. Model., 2016, 56, 1725–1733.
28. H. Meng, C. L. McClendon, Z. Dai, K. Li, X. Zhang, S. He, E. Shang, Y. Liu and L. Lai, J. Med. Chem., 2016, 59, 4202–4209.
29. H. Meng, Z. Dai, W. Zhang, Y. Liu and L. Lai, Phys. Chem. Chem. Phys., 2018, 20, 14785–14795.
30. H. Jiang, S. Khan, Y. Wang, G. Charron, B. He, C. Sebastian, J. Du, R. Kim, E. Ge, R. Mostoslavsky, H. C. Hang, Q. Hao and H. Lin, Nature, 2013, 496, 110–113.
31. X. Tian, D. Firsanov, Z. Zhang, Y. Cheng, L. Luo, G. Tombline, R. Tan, M. Simon, S. Henderson, J. Steffan, A. Goldfarb, J. Tam, K. Zheng, A. Cornwell, A. Johnson, J. N. Yang, Z. Mao, B. Manta, W. Dang, Z. Zhang, J. Vijg, A. Wolfe, K. Moody, B. K. Kennedy, D. Bohmann, V. N. Gladyshev, A. Seluanov and V. Gorbunova, Cell, 2019, 177, 622–638.
32. S. Naiman and H. Y. Cohen, Nature, 2018, 560, 559–560.
33. A. R. Chang, C. M. Ferrer and R. Mostoslavsky, Physiol. Rev., 2020, 100, 145–169.
34. M. S. Bonkowski and D. A. Sinclair, Nat. Rev. Mol. Cell Biol., 2016, 17, 679–690.
35. E. Michishita, R. A. McCord, L. D. Boxer, M. F. Barber, T. Hong, O. Gozani and K. F. Chua, Cell Cycle, 2009, 8, 2664–2666.
36. P. Kokkonen, M. Rahnasto-Rilla, P. Mellini, E. Jarho, M. Lahtela-Kakkonen and T. Kokkola, Eur. J. Pharm. Sci., 2014, 63, 71–76.
37. T. L. Kawahara, E. Michishita, A. S. Adler, M. Damian, E. Berber, M. Lin, R. A. McCord, K. C. Ongaigui, L. D. Boxer, H. Y. Chang and K. F. Chua, Cell, 2009, 136, 62–74.
38. S. Kugel, C. Sebastian, J. Fitamant, K. N. Ross, S. K. Saha, E. Jain, A. Gladden, K. S. Arora, Y. Kato, M. N. Rivera, S. Ramaswamy, R. I. Sadreyev, A. Goren, V. Deshpande, N. Bardeesy and R. Mostoslavsky, Cell, 2016, 165, 1401–1415.
39. P. Kokkonen, M. Rahnasto-Rilla, P. H. Kiviranta, T. Huhtiniemi, T. Laitinen, A. Poso, E. Jarho and M. Lahtela-Kakkonen, ACS Med. Chem. Lett., 2012, 3, 969–974.
40. M. A. Klein and J. M. Denu, J. Biol. Chem., 2020, 295, 11021–11041.
41. X. Chen, W. Sun, S. Z. Huang, H. Zhang, G. Lin, H. Li, J. Qiao, L. Li and S. Yang, J. Med. Chem., 2020, 63, 10474–10495.
42. P. W. Pan, J. L. Feldman, M. K. Devries, A. Dong, A. M. Edwards and J. M. Denu, J. Biol. Chem., 2011, 286, 14575–14587.
43. Z. Huang, J. Zhao, W. Deng, Y. Chen, J. Shang, K. Song, L. Zhang, C. Wang, S. Lu, X. Yang, B. He, J. Min, H. Hu, M. Tan, J. Xu, Q. Zhang, J. Zhong, X. Sun, Z. Mao, H. Lin, M. Xiao, Y. E. Chin, H. Jiang, Y. Xu, G. Chen and J. Zhang, Nat. Chem. Biol., 2018, 14, 1118–1126.
44. S. Lu, Y. Chen, J. Wei, M. Zhao, D. Ni, X. He and J. Zhang, Acta Pharm. Sin. B, 2020 DOI:10.1016/j.apsb.2020.09.010.
45. J. L. Shang, S. B. Ning, Y. Y. Chen, T. X. Chen and J. Zhang, Acta Pharmacol. Sin., 2020 DOI:10.1038/s41401-020-0442-2.
46. J. Shang, Z. Zhu, Y. Chen, J. Song, Y. Huang, K. Song, J. Zhong, X. Xu, J. Wei, C. Wang, L. Cui, C. Y. Liu and J. Zhang, Theranostics, 2020, 10, 5845–5864.
47. Y. Chen, J. Y. Chen, X. X. Sun, J. Y. Yu, Z. Qian, L. Wu, X. J. Xu, X. P. Wan, Y. Jiang, J. Zhang, S. R. Gao and Z. Y. Mao, Aging Cell, 2020, 19, e13185.
48. Z. Chen, X. Zhang, C. Peng, J. Wang, Z. Xu, K. Chen, J. Shi and W. Zhu, J. Chem. Inf. Model., 2019, 59, 3353–3358.
49. M. M. Sultan, G. Kiss and V. S. Pande, Nat. Chem., 2018, 10, 903–909.
50. D. Shukla, Y. L. Meng, B. Roux and V. S. Pande, Nat. Commun., 2014, 5, 3397.
51. M. K. Scherer, B. Trendelkamp-Schroer, F. Paul, G. Perez-Hernandez, M. Hoffmann, N. Plattner, C. Wehmeyer, J. H. Prinz and F. Noe, J. Chem. Theory Comput., 2015, 11, 5525–5542.
52. Y. Qi, Q. Wang, B. Tang and L. Lai, J. Chem. Theory Comput., 2012, 8, 2962–2971.
53. P. Schmidtke, V. Le Guilloux, J. Maupetit and P. Tuffery, Nucleic Acids Res., 2010, 38, W582–W589.
54. V. Le Guilloux, P. Schmidtke and P. Tuffery, BMC Bioinf., 2009, 10, 168.
55. R. Nussinov, B. Ma and C. J. Tsai, Biophys. Chem., 2014, 186, 22–30.
56. P. Csermely, R. Palotai and R. Nussinov, Trends Biochem. Sci., 2010, 35, 539–546.
57. C. J. Tsai and R. Nussinov, PLoS Comput. Biol., 2014, 10, e1003394.
58. J. Liu and R. Nussinov, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7480–7482.
59. G. Kar, O. Keskin, A. Gursoy and R. Nussinov, Curr. Opin. Pharmacol., 2010, 10, 715–722.
60. X. Ma, Y. Qi and L. Lai, Proteins, 2015, 83, 1375–1384.
61. J. Hu, B. He, S. Bhargava and H. Lin, Org. Biomol. Chem., 2013, 11, 5213–5216.
62. D. Ni, Y. Li, Y. R. Qiu, J. Pu, S. Y. Lu and J. Zhang, Trends Pharmacol. Sci., 2020, 41, 336–348.
63. E. Guarnera and I. N. Berezovsky, Curr. Opin. Struct. Biol., 2016, 37, 1–8.
64. X. Sun, Y. Ren, S. Gunawan, P. Teng, Z. Chen, H. R. Lawrence, J. Cai, N. J. Lawrence and J. Wu, Leukemia, 2018, 32, 1246–1249.
65. Y. N. Chen, M. J. LaMarche, H. M. Chan, P. Fekkes, J. Garcia-Fortanet, M. G. Acker, B. Antonakos, C. H. Chen, Z. Chen, V. G. Cooke, J. R. Dobson, Z. Deng, F. Fei, B. Firestone, M. Fodor, C. Fridrich, H. Gao, D. Grunenfelder, H. X. Hao, J. Jacob, S. Ho, K. Hsiao, Z. B. Kang, R. Karki, M. Kato, J. Larrow, L. R. La Bonte, F. Lenoir, G. Liu, S. Liu, D. Majumdar, M. J. Meyer, M. Palermo, L. Perez, M. Pu, E. Price, C. Quinn, S. Shakya, M. D. Shultz, J. Slisz, K. Venkatesan, P. Wang, M. Warmuth, S. Williams, G. Yang, J. Yuan, J. H. Zhang, P. Zhu, T. Ramsey, N. J. Keen, W. R. Sellers, T. Stams and P. D. Fortin, Nature, 2016, 535, 148–152.
66. M. Zhang, H. Jang and R. Nussinov, Chem. Sci., 2020, 11, 5855–5865.
67. S. Kannan, G. Venkatachalam, H. H. Lim, U. Surana and C. Verma, Chem. Sci., 2018, 9, 5212–5222.
68. Y. Xu, S. Wang, Q. Hu, S. Gao, X. Ma, W. Zhang, Y. Shen, F. Chen, L. Lai and J. Pei, Nucleic Acids Res., 2018, 46, W374–W379.
69. X. Liu, S. Lu, K. Song, Q. Shen, D. Ni, Q. Li, X. H. He, H. Zhang, Q. Wang, Y. Y. Chen, X. Li, J. Wu, C. Sheng, G. Chen, Y. Liu, X. Lu and J. Zhang, Nucleic Acids Res., 2020, 48, D394–D401.
70. A. Panjkovich and X. Daura, Bioinformatics, 2014, 30, 1314–1315.
71. S. A. Hollingsworth, B. Kelly, C. Valant, J. A. Michaelis, O. Mastromihalis, G. Thompson, A. J. Venkatakrishnan, S. Hertig, P. J. Scammells, P. M. Sexton, C. C. Felder, A. Christopoulos and R. O. Dror, Nat. Commun., 2019, 10, 3289.
72. X. Zhao, D. Allison, B. Condon, F. Zhang, T. Gheyi, A. Zhang, S. Ashok, M. Russell, I. MacEwan, Y. Qian, J. A. Jamison and J. G. Luz, J. Med. Chem., 2013, 56, 963–969.
73. P. A. Ravindranath, S. Forli, D. S. Goodsell, A. J. Olson and M. F. Sanner, PLoS Comput. Biol., 2015, 11, e1004586.
74. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713.
75. Y. P. Pang, J. Mol. Model., 1999, 5, 196–202.
76. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
77. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
78. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
79. D. Bucher, L. C. T. Pierce, J. A. McCammon and P. R. L. Markwick, J. Chem. Theory Comput., 2011, 7, 890–897.
80. Y. L. Miao, S. E. Nichols, P. M. Gasper, V. T. Metzger and J. A. McCammon, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10982–10987.
81. R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernandez, C. R. Schwantes, L. P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532.
82. B. E. Husic and V. S. Pande, J. Am. Chem. Soc., 2018, 140, 2386–2396.
83. J. H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schutte and F. Noe, J. Chem. Phys., 2011, 134, 244108.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05131d

‡ These authors contributed equally to this work.

---