Open Access Article
Open Access ArticleMechanistic insights into rhodium-catalyzed enantioselective allylic alkylation for quaternary stereogenic centers†
Monika
Pareek
and
Raghavan B.
Sunoj
 *
*
Department of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India. E-mail: sunoj@chem.iitb.ac.in
First published on 15th December 2020
Abstract
Installing quaternary stereogenic carbon is an arduous task of contemporary importance in the domain of asymmetric catalysis. To this end, an asymmetric allylic alkylation of α,α-disubstituted aldehydes by using allyl benzoate in the presence of Wilkinson's catalyst [Rh(Cl)(PPh3)3], (R)-BINOL–P(OMe) as the external ligand, and LiHMDS as the base has been reported to offer high enantioselectivity. The mechanistic details of this important reaction remain vague, which prompted us to undertake a detailed density functional theory (SMD(THF)/B3LYP-D3) investigation on the nature of the potential active catalyst, energetic features of the catalytic cycle, and the origin of high enantioselectivity. We note that a chloride displacement from the native Rh-phosphine [Rh(Cl)(PPh3)3] by BINOL–P(OMe) phosphite and an ensuing MeCl elimination can result in the in situ formation of a Rh-phosphonate [Rh(BINOL–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)(PPh3)3]. A superior energetic span (δE) noted with such a Rh-phosphonate suggests that it is likely to serve as an active catalyst. The uptake of allyl benzoate by the active catalyst followed by the turnover determining C–O bond oxidative addition furnishes a Rh-π-allyl intermediate, which upon interception by (Z)-Li-enolate (derived from α,α-disubstituted aldehyde) in the enantiocontrolling C–C bond generates a quaternary stereogenic center. The addition of the re prochiral face of the (Z)-Li-enolate to the Rh-bound allyl moiety leading to the R enantiomer of the product is found to be 2.4 kcal mol−1 more preferred over the addition through its si face. The origin of the stereochemical preference for the re face addition is traced to improved noncovalent interactions (NCIs) and less distortion in the enantiocontrolling C–C bond formation transition state than that in the si face addition. Computed enantioselectivity (96%) is in very good agreement with the experimental value (92%), so is the overall activation barrier (δE of 17.1 kcal mol−1), which is in conformity with room temperature reaction conditions.
O)(PPh3)3]. A superior energetic span (δE) noted with such a Rh-phosphonate suggests that it is likely to serve as an active catalyst. The uptake of allyl benzoate by the active catalyst followed by the turnover determining C–O bond oxidative addition furnishes a Rh-π-allyl intermediate, which upon interception by (Z)-Li-enolate (derived from α,α-disubstituted aldehyde) in the enantiocontrolling C–C bond generates a quaternary stereogenic center. The addition of the re prochiral face of the (Z)-Li-enolate to the Rh-bound allyl moiety leading to the R enantiomer of the product is found to be 2.4 kcal mol−1 more preferred over the addition through its si face. The origin of the stereochemical preference for the re face addition is traced to improved noncovalent interactions (NCIs) and less distortion in the enantiocontrolling C–C bond formation transition state than that in the si face addition. Computed enantioselectivity (96%) is in very good agreement with the experimental value (92%), so is the overall activation barrier (δE of 17.1 kcal mol−1), which is in conformity with room temperature reaction conditions.
Introduction
The significant progress in the field of asymmetric catalysis in the last few decades helped in realizing complex organic target molecules of practical significance. The presence of quaternary carbon stereogenic centers in natural products, drugs, and biologically active molecules has been an inspiration toward developing asymmetric synthesis for such structural motifs.1 For a long time, molecules containing quaternary carbon stereogenic centers have mostly been derived from natural product precursors such as terpenoids rather than building them through chemical synthesis.2 Traditional chemical synthesis relying on Diels–Alder reactions, asymmetric allylic alkylation of chiral carbon nucleophiles, and intramolecular Heck reactions has also found interesting use.3 Over the years, there have been a remarkable number of efforts in installing quaternary carbon stereogenic centers on cyclic systems by using a myriad of protocols such as biocatalysis, organocatalysis, and transition metal catalysis.4 The enantioselective synthesis of quaternary carbon stereogenic centers in acyclic systems has been regarded as far more challenging.5 Recent trends in this front indicate the use of transition metal catalysis for effectively engaging achiral as well as racemic substrates as the starting material.The Tsuji–Trost reaction continues to be the most common choice for the generation of acyclic quaternary carbon stereogenic centers.6 Direct asymmetric allylic alkylation of enolates derived from aldehydes can also provide direct access to quaternary stereogenic centers. In particular, the List group reported an enantioselective α-allylation of α-branched aldehydes by employing a chiral phosphate anion as a source for chiral induction.7 In a related Tsuji–Trost allylation by the Yoshida group, a chiral α-amino acid derived enamine of α-branched aldehydes is used in conjunction with allyl esters activated by an achiral Pd catalyst toward realizing quaternary stereogenic carbon centers in high enantioselectivity.8 Most recently, the Stoltz as well as the Marek groups have reported an interesting decarboxylative Tsuji–Trost allylation of substituted amide enolates to afford acyclic quaternary carbon stereogenic centers.9 In 2013, the Carreira group reported an iridium-catalyzed stereodivergent Tsuji–Trost allylation of α,α-disubstituted aldehydes in which axially chiral phosphoramidite ligands are used in combination with chiral cinchona amines. By changing the configurations of phosphoramidite and cinchona amine, all four stereoisomers of the product could be generated with high enantio- and diastereo-selectivities.10 The Dong and the Stoltz groups have also reported important protocols for quaternary carbon stereogenic centers using α,α-disubstituted aldehydes.11 The various transition metal catalysts have been found to be effective for asymmetric allylic alkylation and arylation reactions.12
Recently, Evans and co-workers have demonstrated the value of Rh-catalyzed allylic alkylation of prochiral α,α-disubstituted aldehydes by using allyl benzoate to generate acyclic products bearing quaternary stereogenic centers with high enantioselectivity (Scheme 1). This reaction offers a direct method for the enantioselective alkylation of aldehydes.13 It should be noted that direct enantioselective alkylation of aldehydes generally presents challenges in the form of (i) the difficulty in controlling the configuration of the enolate and (ii) suppressing the formation of self-aldol as well as O-alkylation products.
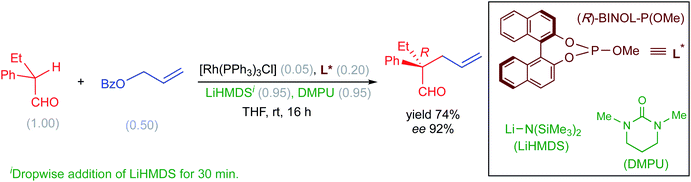 | ||
| Scheme 1 Asymmetric allylic alkylation of α,α-disubstituted aldehydes with allyl benzoate. The numbers given in parentheses refer to the concentration in mmol. | ||
The nucleophilic partner in this reaction is derived from the aldehyde in the form of an enolate by the action of the base LiHMDS. It has been proposed that the E/Z configuration of the enolate, thus produced, would have a direct impact on the stereochemical outcome of the reaction.14 However, it is not apparent whether the formation of an E-enolate or a Z-enolate would be more preferred under the given reaction conditions. In addition, the nature of the likely active catalyst and the molecular origin of how the base and the additive (DMPU) influence the energetic course of the reaction are not readily available. Given the importance of asymmetric allylic alkylations and the above-mentioned lack of clarity on key mechanistic details promoted us to undertake a detailed computational investigation by using density functional theory.15
Computational methods
All computations were performed using the Gaussian16 (Rev. B.01) suite of quantum chemical program.16 The geometry optimization of all the stationary points (reactants, intermediates, transition states, and products) was carried out by using B3LYP-D3 hybrid density functional theory17 in conjunction with the 6-31G** basis set18 for C, H, N, O, P, Li, and Cl, and the SDD basis set for Rh that consists of an effective core potential for the 28 core electrons and explicit basis sets for the 17 valence electrons.19 The transition states were verified by examining the presence of unique imaginary frequency, in addition to the Intrinsic Reaction Coordinate (IRC) calculations20 toward either side of the transition state geometry performed at the same level of theory. The geometries obtained at the end points of the IRC runs were separately subjected to further optimization to connect to the desired minima on both the sides of the transition state, thereby serving as an additional verification tool for the authenticity of the transition state. The solvent effect was taken into account by using the SMD solvation model, developed by the Truhlar and Cramer groups.21 As the experimental study employed tetrahydrofuran (THF) as the solvent, the dielectric constant of THF (ε = 7.58) was used in our SMD continuum solvation model computations. Experimental studies involved the use of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of LiHMDS as the base and DMPU as the additive. The explicit inclusion of LiHMDS and DMPU was therefore considered in our mechanistic models along with bound THF molecules, wherever deemed necessary. The vibrational entropy contributions were computed by using free-rotor approximation for all those frequency modes, which were found to be <100 cm−1.22 The discussions in this manuscript are presented on the basis of the Gibbs free energies, corrected for a standard state of 1 mol L−1, obtained at the SMD(THF)/B3LYP-D3/6-31G**,SDD(Rh) level of theory.
1 ratio of LiHMDS as the base and DMPU as the additive. The explicit inclusion of LiHMDS and DMPU was therefore considered in our mechanistic models along with bound THF molecules, wherever deemed necessary. The vibrational entropy contributions were computed by using free-rotor approximation for all those frequency modes, which were found to be <100 cm−1.22 The discussions in this manuscript are presented on the basis of the Gibbs free energies, corrected for a standard state of 1 mol L−1, obtained at the SMD(THF)/B3LYP-D3/6-31G**,SDD(Rh) level of theory.
Topological analysis of electron density distribution in various intermediates and transition states was performed using Bader's atoms in molecule (AIM) formalism by using the AIM2000 program,23 by making use of the wave function generated at the SMD(THF)/B3LYP-D3/6-31G**,SDD(Rh) level of theory. This analysis was employed to identify the noncovalent interactions (NCIs) present in the stereocontrolling transition states. Additionally, noncovalent interactions were analyzed using the graphical plots created using the noncovalent interaction (NCI) analysis program.24 The activation strain analysis was performed to compute the distortion and interaction in the stereocontrolling transition states, particularly to assess the relative distortion and interaction energies between the competing diastereomeric transition states.25 The efficiency of the catalytic cycle was computed by using the Shaik-Kozuch energetic span model.26
Results and discussion
A careful examination of the reported experimental protocol is pertinent to various mechanistic scenarios considered in this study. The procedure involves combining Wilkinsons's catalyst (1A) with the chiral ligand (R)-BINOL–P(OMe) (L*) in tetrahydrofuran (THF) solvent, which could lead to the formation of a number of analogs of Wilkinsons's catalyst. The additive N,N′-dimethylpropyleneurea (DMPU) and the substrates (2-phenylbutanal (5) and allyl benzoate (2)) were sequentially introduced, which was followed by drop-wise addition of lithium bis(trimethylsilyl)amide (LiHMDS) in THF.27 Given this, we have examined the energetic feasibilities of the formation of different variants of Wilkinson's catalyst by exchanging the labile Rh-bound triphenylphosphines (PPh3) with other ligands such as the chiral BINOL-phosphite. We note that the use of modified Wilkinson's catalyst has gained recent popularity, including that in asymmetric allylic alkylation reactions.14c,dShown in Scheme 2 are different species that could possibly be generated through ligand exchange with Wilkinson's catalyst and the corresponding relative Gibbs free energies of their formation with respect to 1A and L*. Some of these species could serve as a potential active catalyst in this reaction. The species denoted as A1–A4 can be formed by exchanging the native phosphine(s) with the chiral BINOL phosphite (L*) ligand(s), where the latter is used four times more than 1A. The substitution of two of the phosphine ligands by L*, leading to A3, is found to be the most favorable possibility in this series (Scheme 2(a)).28 Another interesting alternative arises when the chiral BINOL-phosphite displaces the native chloride instead of the phosphine ligands, leading to an ion-pair intermediate (1A⋯1) as shown in Scheme 2(b). An SN2 type rebound of the displaced chloride on the –OMe moiety can then facilitate a Rh-catalyzed Arbuzov rearrangement (analogous to Michaelis–Arbuzov rearrangement involving alkyl halides), wherein the release of MeCl can result in the in situ formation of a phosphonate B1.29 We note that the barrier for the MeCl expulsion, computed with respect to the preceding ion-pair intermediate, is 16.4 kcal mol−1, which is affordable under room temperature conditions.30 Since an excess of BINOL-phosphite (L*) was used in the experiments, the initially formed B1 could also undergo further ligand exchanges to form species such as B2–B6.
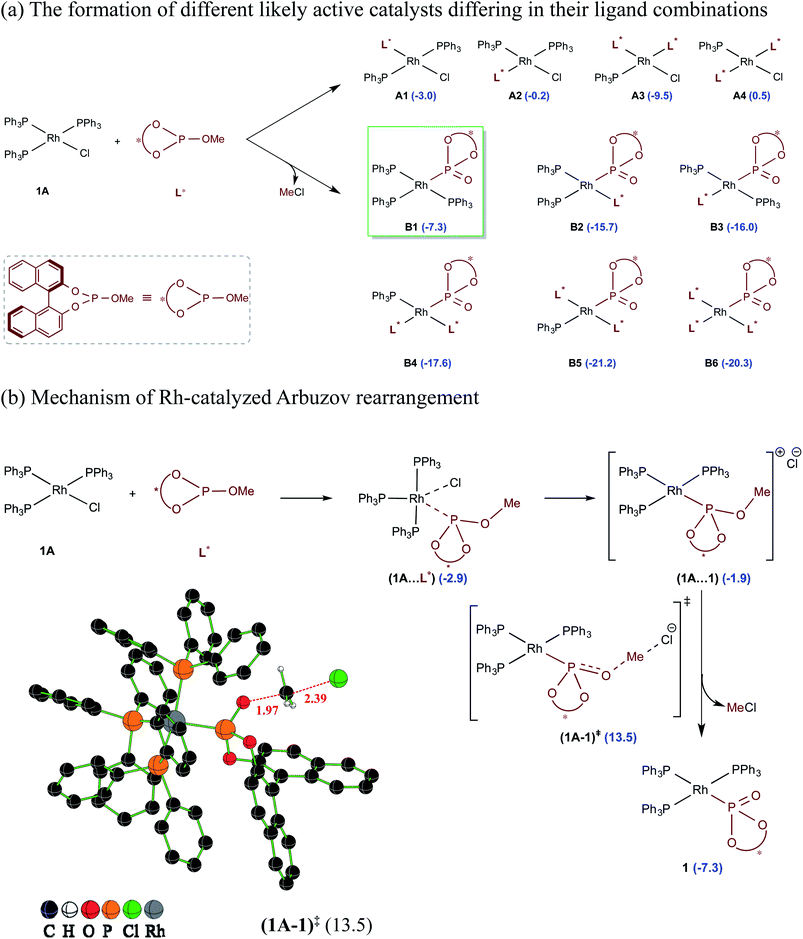 | ||
| Scheme 2 (a) The relative Gibbs free energies of the formation (in kcal mol−1) of different likely active species computed with respect to the separated reactants. (b) Important steps in the conversion of Rh-bound BINOL-methyl phosphite to the corresponding phosphonate ligand through the Rh-Arbuzov rearrangement and a representative example of an optimized geometry for the expulsion of methyl chloride. Any of the active catalysts listed here is assigned a general notion 1 when it is considered in the catalytic cycle as shown in Scheme 3. | ||
The relative Gibbs free energies provided in Scheme 2 suggest that the formation of most of the mixed ligand combinations of the Rh-phosphonates is thermodynamically feasible, hinting at their simultaneous existence and potential participation in the reaction. For ease of discussion on the broad mechanistic features shown in Scheme 3, we shall consider that the active catalyst entering the catalytic cycle is denoted as 1, which could potentially be any variant of Wilkinson's catalyst. The active species 1 can bind to one of the substrates, namely, allyl benzoate (2), through an η2 coordination to form a catalyst–substrate complex 3. Intermediate 3 can then undergo C–O bond oxidative addition via a transition state (3–4)‡ to form an η3-Rh-π-allyl intermediate 4.31 In a concurrent event, the action of LiHMDS on the pro-nucleophilic 2-phenylbutanal (5) helps in generating the desired lithium enolate (6). The next step is enantioselective C–C bond formation through a transition state (4–7)‡, wherein the nucleophilic lithium enolate 6 adds to the electrophilic Rh-π-allyl intermediate 4 to form an η2 catalyst–product complex (7). In the last step, ligand exchange with PPh3 can help release the final product (8) besides regenerating the active species 1 so as to continue the catalytic cycle with the fresh uptake of a new substrate molecule.
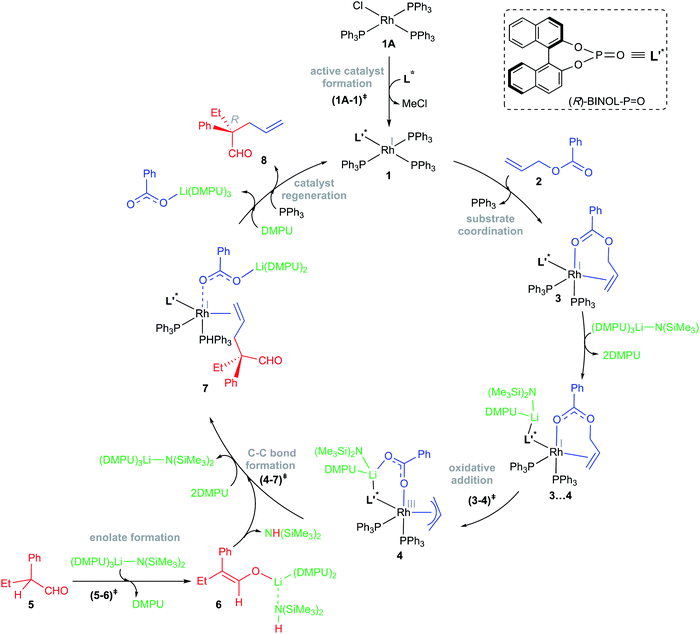 | ||
| Scheme 3 The key mechanistic steps involved in the Rh-catalyzed asymmetric allylic alkylation of 2-phenylbutanal by allyl benzoate. | ||
The overall catalytic cycle, as shown in Scheme 3, is examined in greater detail to identify the energetically most preferred pathway. Since the formation of several likely active species is found to be exoergic (Scheme 2), we have considered different ligand combinations around the Rh in the vital C–O bond oxidative addition transition state (3–4)‡. The elementary step barriers for the oxidative addition compiled in Table 1 suggest that active species such as A1 and A3 bearing the native ligands on the Rh center are quite unlikely to serve as the actual catalytic entity under the given reaction conditions. An active engagement of the base, in the form of LiHMDS·3DMPU, is therefore examined to see whether it is likely to lower the transition state energies through explicit coordination to the allyl benzoate oxygen. It is instructive to draw certain parallels between our mechanistic model and the experimental procedure such as the use of an equimolar amount (0.95 mmol) of the base and the additive (DMPU). In the THF solvent, LiHMDS is known to exist in equilibrium between its dimer and monomer, with 3 coordinated THF on the Li.32 Although the role of DMPU is typically to prevent the aggregation of Li-enolates,33 the improved yield observed upon the inclusion of DMPU alludes to a more active molecular role. In view of this, explicit coordination of DMPU by displacing the Li-bound THF molecules is considered to find that the formation of species such as LiHMDS·3DMPU is energetically feasible.32f The role of the base and its mode of participation in the C–O bond oxidative addition transition state can now be better understood. The relative Gibbs free energies of these transition states, given in Table 1, suggest that a direct participation of both the base and the additive in the OA transition state is energetically more beneficial as compared to the corresponding base-free mode.34
| (3–4)‡ | Absence of the base | LiHMDS·1DMPU | ||
|---|---|---|---|---|
| ΔGrel | ΔGbarrier | ΔGrel | ΔGbarrier | |
| a The lowest energy ligand combinations of the potential active catalyst series A (A1 and A3 as shown in Scheme 2) have been considered in the C–O bond oxidative addition transition state. In the case of series B, the incoming substrate is likely to displace the PPh3 ligand to form the catalyst–substrate complex, which would therefore be similar for both B4 and B5. Similarly, the substrate uptake by B6 by displacing one of the BINOL-phosphite ligands (L*) would make it similar to the substrate–catalyst complex derived from B4/B5. Hence, only B4 is presented here. b The transition state failed to converge even after repeated attempts. | ||||
| A1 | 24.5 | 27.5 | 20.7 | 23.7 |
| A3 | 26.9 | 36.4 | 20.2 | 29.7 |
| B1 | 21.6 | 28.9 | 9.8 | 17.1 |
| B2 | 5.4 | 21.1 | ||
| B3 | 20.8 | 36.8 | 2.0 | 18.0 |
| B4 | 16.2 | 33.8 | 2.0 | 19.6 |
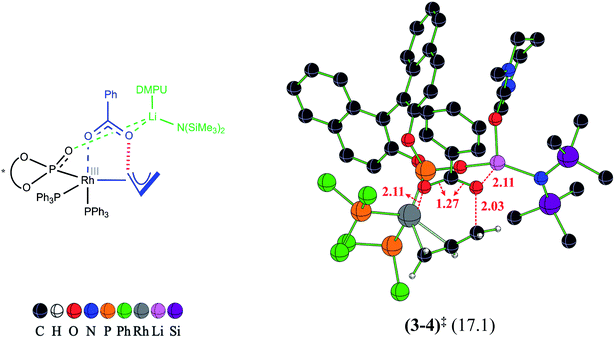
In our attempts to find various possibilities for the Li-bound OA TS (3–4)‡ it is identified that the displacement of two DMPU molecules from LiHDMS·3DMPU by the oxygen atoms of the benzoate and BINOL phosphonate is quite likely. In Table 1, such binding modes are listed as LiHMDS·1DMPU against each of the likely active species (A1 through B4). The exoergic formation of different likely active catalysts (Scheme 2) prompted us to consider their participation in the catalytic cycle. Since the C–O bond oxidative addition is the first key step wherein the active catalyst comes in contact with the substrate such as the allyl benzoate (2), we have evaluated the role of all these active catalysts in the C–O bond oxidative addition transition state (3–4)‡. These possibilities differ in terms of the number of Rh-bound phosphine/phosphonate ligands and their relative geometric dispositions in (3–4)‡. In order to afford a direct comparison between the OA TSs involving different active catalysts, the activation barrier is calculated with respect to the respective active catalyst (Table 1). The active catalyst (denoted as 1 in Scheme 3) that provides the lowest elementary step barrier for (3–4)‡ is considered for the next stereoselective C–C bond formation step in this study. We note that the lower energy ligand combinations in the potential active catalysts belonging to the A series exhibit higher elementary step barriers (23.7 and 29.7 kcal mol−1 respectively for A1 and A3) for the oxidative addition transition state (3–4)‡.35 Similarly, in the case of potential active catalysts in the B series, the lowest elementary step barrier for oxidative addition is found to be 17.1 kcal mol−1 with B1, which is therefore considered as the most likely active catalyst that follows the minimum energy path.36 The optimized geometry of the most likely OA transition state (3–4)‡ with B1 is shown in Fig. 1. The C–O bond oxidative addition transition state leads to the formation of an η3-Rh-π-allyl intermediate (4).
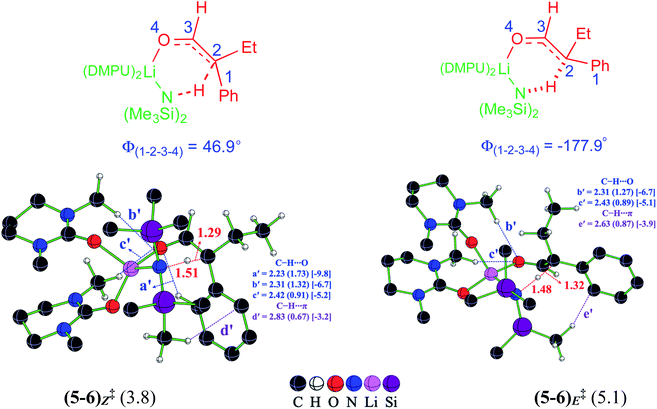
Once the electrophilic partner 4 (η3-Rh-π-allyl intermediate) is available, it can be intercepted by the Li-enolate (6). It is important to pay careful attention to the energetics of the formation of E and Z configurations of 6 as the stereochemical outcome of the reaction could have a critical dependence on the enolate configuration involved in the ensuing C–C bond formation with the Rh-π-allyl intermediate (vide infra). In an acyclic α-branched aldehyde, the free rotation along the Cα–C(carbonyl) bond, shown as C2–C3 in Fig. 2, presents two important modes for deprotonation, one leading to 6E and the other to 6Z enolate.37 The relative Gibbs free energy barriers for the LiHMDS promoted deprotonation indicate that the Z enolate is kinetically more favored by 1.3 kcal mol−1 than the E enolate.38 Interesting differences in the pattern of the intramolecular noncovalent interactions between (5–6)Z‡ and (5–6)E‡ are noted as a key contributor to Z-selectivity.39 The C–H⋯O (a′) interaction between the phenyl and the carbonyl oxygen noted in (5–6)Z‡ leading to the Z enolate is absent in the E enolate. The C–H⋯O noncovalent interactions (b′ and c′) are also noted between the methyl group on the DMPU and the carbonyl oxygen in both the Z and E enolates. The C–H⋯π interaction is also found between the methyl group on the LiHMDS and the phenyl of the α,α-disubstituted aldehyde in both the Z (d′) and E (e′) enolates.
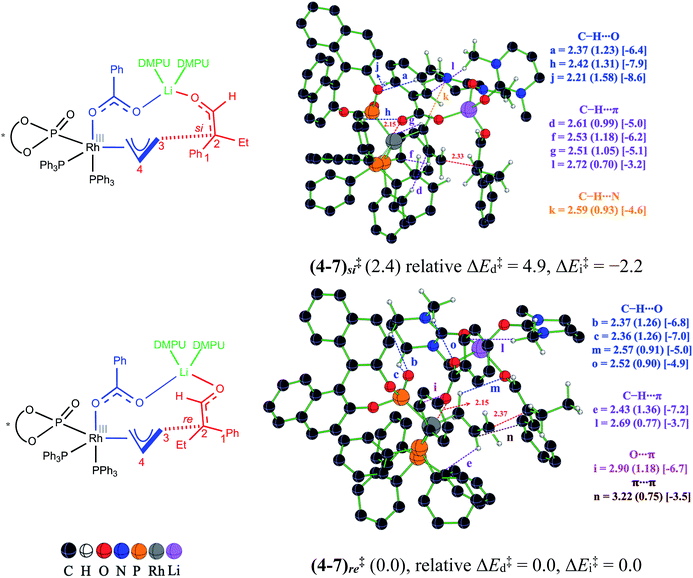
Until now, the formation of the electrophilic partner in the form of a Rh-π-allyl intermediate (4) and Li-enolate (6) as the nucleophilic counterpart is presented. When both of these key reactants become available, the next vital event, i.e., the C–C bond formation, can take place. To locate the most preferred C–C bond formation transition state, generally denoted as (4–7)‡ in this manuscript, we have considered the addition of the Li-enolate 6Z through its si and re prochiral faces and examined various conformational possibilities that differ in the dihedral angle along the incipient C–C bond.40 Certain general features of these stereoinducing TSs are (a) the anchoring role of the tetracoordinate Li in holding both the enolate and Rh-π-allyl moieties together, latter through the benzoate oxygen, and (b) the changes in the noncovalent interactions (NCIs) depending on the prochiral face of the enolate involved in the bond formation. More importantly, the enolate addition through its re face is found to be energetically more preferred over the si face addition. The relative Gibbs free energy difference of 2.4 kcal mol−1 between these diastereomeric transition states corresponds to a 96% enantiomeric excess.41 The optimized geometry for the lowest energy transition state (4–7)re‡ and its diastereomeric counterpart, along with the mapping of the NCIs, are shown in Fig. 3.
We sought additional details on the factors that contribute to the energy difference between the C–C bond formation transition states (4–7)re‡ and (4–7)si‡ by analyzing the NCIs as deciphered using the AIM analysis.42 An approximate measure of NCI is deduced from the electron density at the bond critical point (ρbcp) along various bond paths noticed in the topological analysis of the electron density.43 In addition, the quantification of the NCIs is performed by using Espinosa's formulation that employs the topological parameters of the electron density distribution as obtained from the atoms in molecule formalism.44 The strength of the individual interactions that contribute to the cumulative effect could therefore be estimated. It can be noted that the transition states (4–7)re‡ and (4–7)si‡ shown in Fig. 3 are well decorated with NCIs such as C–H⋯π, C–H⋯O, π⋯π, C–H⋯N and lone pair(O)⋯π. A comparison of the geometries of (4–7)re‡ and (4–7)si‡ reveals important differences in the NCIs depending on the prochiral face of the Li-enolate that participates in the C–C bond formation. In the lower energy diastereomeric transition state (4–7)re‡, a C–H⋯O contact (denoted as a) is noted between the phenyl ring of the benzoate and the BINOL phosphonate oxygen. Additional two C–H⋯O contacts are also identified in (4–7)re‡, which are between the equatorial PPh3 ligand and the benzoate oxygen (h) as well as one between the phenyl ring of the benzoate and the BINOL phosphonate oxygen (j). The key differences in the NCIs found in the higher energy transition state (4–7)si‡ are as follows: the C–H⋯O contacts between DMPU and (i) phosphonate oxygen (b and c) and (ii) the benzoate oxygen (o) and one between the Rh-π-allyl moiety and the enolate oxygen (m). Besides the C–H⋯O interactions, there are more number of C–H⋯π contacts in the lower energy transition state (4–7)re‡ as compared to that in (4–7)si‡. The three C–H⋯π contacts (d, f, and g) are noted in (4–7)re‡, whereas only one such interaction (e) is found in (4–7)si‡ between the axial PPh3 ligand and the Rh-π-allyl moiety. One C–H⋯π contact (l) is also found between the methyl of DMPU and the phenyl ring of the benzoate group. This interaction is present in both (4–7)re‡ and (4–7)si‡. The two different NCIs, a lone pair(O)⋯π (i) (involving the benzoate oxygen and the equatorial PPh3 ligand) and a π⋯π (n) interaction (between the Rh-π-allyl and the phenyl of the Li-enolate), are found in the higher energy transition state (4–7)si‡, whereas a C–H⋯N (k) interaction is noted in the lower energy transition state (4–7)re‡ (between Rh-π-allyl and the DMPU nitrogen). The estimated strength of NCIs in the lower energy transition state (4–7)re‡ is found to be −46.9 kcal mol−1, while that in the higher energy transition state (4–7)si‡ is −44.8 kcal mol−1, indicating an additional 2.1 kcal mol−1 stabilization in the former. The noncovalent interaction plots (NCI plots) are also generated to analyze the broader regions of NCIs between the interacting atoms/groups in these enantiocontrolling transition states.45
In addition to the NCI based analysis presented above, the origin of the energy difference between (4–7)re‡ and (4–7)si‡ is probed in greater detail by using activation strain analysis. The activation energy (ΔE‡) is considered as the sum of destabilizing distortion (ΔE‡d) and stabilizing interaction (ΔE‡i) energies in the transition state, calculated with respect to the lower energy transition state (4–7)re‡. The distortion ΔE‡d is found to be 4.9 kcal mol−1 higher in the higher energy transition state (4–7)si‡ than the corresponding value in (4–7)re‡. However, the stabilizing ΔE‡i in the higher energy transition state (4–7)si‡ is found to be 2.2 kcal mol−1 more than that in the lower energy diastereomeric counterpart (4–7)re‡.46 It is noted that in the higher energy transition state (4–7)si‡, the Rh-π-allyl fragment experiences 4.2 kcal mol−1 more distortion as compared to that found in (4–7)re‡. The net effect of ΔE‡d and ΔE‡i provides the transition state (4–7)re‡ 2.7 kcal mol−1 lower activation energy (ΔE‡) than that for (4–7)si‡.
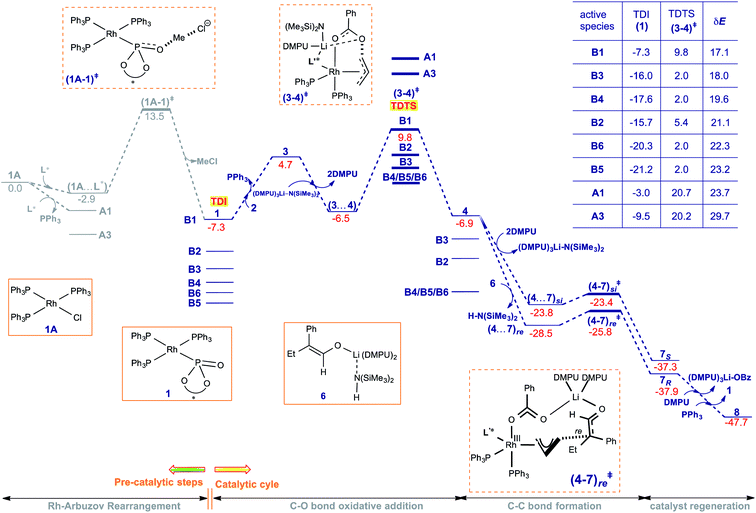
After having examined each elementary step in the catalytic cycle and shedding light on the origin of enantioselectivity in the formation of the quaternary stereogenic center, we turned our attention to the overall energetic features. The Gibbs free energy profile, as provided in Fig. 4, is employed to assess the catalytic efficiency of different potential active catalysts by calculating the energetic span (δE).26 The elementary step barrier for the C–O bond oxidative addition of the allyl benzoate is notably larger than that of other steps.47 It is interest to note that energetically the most preferred mode for the C–O bond oxidative addition involves the explicit participation of the base LiHMDS and the additive DMPU in the transition state (3–4)‡. More importantly, the transition state (3–4)‡ is identified as the TDTS (turnover-determining transition state) and intermediate 1 as the TDI (turnover-determining intermediate), with an energetic span (δE) ranging from 17.1 kcal mol−1 to 29.7 kcal mol−1 depending on the nature of the active catalyst considered. A few points of significance related to the potential involvement of different active catalysts (as shown in Scheme 2(a)), which differ in terms of the Rh-bound ligands, need attention. The formation of various active catalysts, from Wilkinson's catalyst employed as the catalyst precursor, is found to be exoergic, thus alluding to their likely availability under the reaction conditions.48 It is to be noted that the active catalyst, denoted using a general representation 1, is the TDI in the catalytic cycle (Fig. 4). This situation also implies that the catalytic efficiency predicted using δE would be different for different active catalysts (1 = A1/A3/B1–B6) that enter the catalytic cycle and bind with substrate 2 for the onward steps. For instance, the lowest δE of 17.1 kcal mol−1 is noted with B1 as the TDI and (3–4)‡ as the TDTS, whereas the corresponding value with A3 is 29.7 kcal mol−1. Similarly, another lower energy active catalyst such as B5 results in a span of 23.2 kcal mol−1. The most likely scenario under room temperature conditions employed for this reaction is to follow the minimum energy path with a given active catalyst such as B1 that offers the lowest energetic span. However, the participation of other active catalysts with comparable or even higher δEs cannot be discounted and should be considered potentially viable at elevated temperatures. An interesting lead worth considering here is to develop an empirical method to suppress the participation of active catalysts with higher δEs. Such an approach might possibly help improve the catalytic efficiency and perhaps offer higher product conversion.
The catalytic steps, post the Rh-π-allyl intermediate 4 formation, are found to be much less energy demanding as revealed by the presence of low energy intermediates and lower elementary step barriers. In the enantio-controlling C–C bond formation step, Li-enolate (6Z) can add to 4 either through its re face via the transition state (4–7)re‡ or through the si face through (4–7)si‡. It can be noticed that (4–7)re‡ leading to the R-enantiomer of the product is 2.4 kcal mol−1 lower in energy than the diastereomeric (4–7)si‡. The formation of the product is exoergic, suggesting an additional thermodynamic drive for this Rh-catalyzed asymmetric allylic alkylation reaction. The computed energetics, such as the δE of 17.1 kcal mol−1, is what is expected for room temperature conditions employed for this reaction. This can be considered as an indicator of a good correlation between the computed mechanism and the experimental observations.
Extension of the enantiocontrolling transition state models to other substrates
It would be of interest to examine whether our transition state model for the enantiocontrolling C–C bond formation between the Li-enolate and the Rh-π-allyl moiety holds well with other substrates. To this end, we have considered a range of para-substituted aryls on the pro-nucleophilic α,α-arylalkyl aldehyde. In addition to evaluating whether good predictions of % ee with substrates other than what was used for in-depth investigation, we intend to predict the likely performance of additional substrates hitherto not exploited in Rh-catalyzed asymmetric allylic alkylation. One set of substrates thus chosen consists of electron donating groups, while another set consists of electron withdrawing substituents in the α,α-arylalkyl aldehyde. The predicted % ee and the corresponding experimental values, wherever available, are provided in Table 2 for an easy comparison.| p-Substituent in the substrate | C–C bond distance (in Å) | ΔG, G((4–7)si‡ − (4–7)re‡) | Predicted % ee | Experimental % ee | |
|---|---|---|---|---|---|
| (4–7)re‡ | (4–7)si‡ | ||||
| a Not available. | |||||
| NH2 | 2.35 | 2.46 | 2.1 | 94 | |
| OH | 2.33 | 2.42 | 4.8 | >99 | |
| OMe | 2.33 | 2.40 | 4.8 | >99 | 91 |
| Me | 2.31 | 2.35 | 3.2 | 99 | 92 |
| H | 2.33 | 2.37 | 2.4 | 96 | 92 |
| F | 2.29 | 2.38 | 4.9 | >99 | 86 |
| Br | 2.26 | 2.33 | 1.5 | 85 | 77 |
| COCH3 | 2.21 | 2.27 | 2.3 | 96 | |
| CF3 | 2.26 | 2.30 | 3.7 | 99 | |
| CN | 2.20 | 2.24 | 3.1 | 99 | |
The predicted % ee obtained using our transition state model as given in Table 2 indicates good agreement with the experimental values for the known systems. Also, of interest is to note that the difference in the relative Gibbs free energies of the transition state for the re face addition of the Li-enolate to the Rh-π-allyl moiety and that of the si face addition remain consistently above 2.0 kcal mol−1 for all aryl substituents, except that in the para-Br aryl case. In other words, the influence of a para substituent located farther from the site of the C–C bond formation appears quite similar for both the re and si face addition of the Li-enolate, thereby offering consistently high enantioselectivities with most such substituents. Interestingly, the change in the nature of the para substituent does bring about a notable difference in the reaction coordinate that appears in the form of incipient C–C bond distances in the transition states (Table 2). With respect to the unsubstituted aryl aldehyde (X = H), the electron donating substituents (NH2, OMe etc.) exhibit a longer distance between the enolate carbon and the Rh-π-allyl moiety in the transition state, whereas shorter distances are noticed in the case of electron withdrawing substituents (CN or CF3). A Hammett type analysis on these substrates revealed a positive slope (i.e., reaction constant ρ), which is consistent with the mechanism, wherein an accumulation of negative charge in the transition state is the most likely scenario.49 The predictions that certain electronically active para substituents are likely to offer high enantioselectivity allude to potential room for the expansion of the substrate scope for the title reaction. It is also important to note that the modified aryl aldehydes are likely to offer similar efficacies (overall yield and duration of the reaction), given that the catalytic turn-over is determined by the generation of the electrophilic Rh-π-allyl species in the early part of the mechanism.
Conclusions
Mechanistic insights derived using density functional theory computations on Rh-catalyzed asymmetric allylic alkylation of an α,α-disubstituted aldehyde with allyl benzoate to form an acyclic quaternary stereogenic center are gathered through this study. The use of Wilkinson's catalyst [Rh(PPh3)3Cl] in conjunction with an axially chiral BINOL-based methyl phosphite (BINOL–P(OMe)) ligand is found to initiate an energetically feasible substitution of the native chloride ligand by the BINOL methyl phosphite first, which is followed by a Rh-Arbuzov rearrangement to form a BINOL phosphonate (BINOL–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and expulsion of MeCl. The consideration of various likely ligand combinations around the Rh center suggests that a Rh-phosphonate [Rh(PPh3)3(BINOL–P
O) and expulsion of MeCl. The consideration of various likely ligand combinations around the Rh center suggests that a Rh-phosphonate [Rh(PPh3)3(BINOL–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)] is energetically more likely to serve as the active catalyst than [Rh(BINOL–P(OMe))(Cl)(PPh3)2], which is an anticipated modification of the conventional Wilkinson's catalyst [Rh(PPh3)3Cl] employed here as the catalyst precursor. Additional credence to the likelihood of Rh-phosphonate participation in the catalytic cycle is obtained from energetic span (δE) calculations. The δE with [Rh(BINOL–P(OMe))(Cl)(PPh3)2] as the active catalyst is found to be 23.7 kcal mol−1, while that with [Rh(PPh3)3(BINOL–P
O)] is energetically more likely to serve as the active catalyst than [Rh(BINOL–P(OMe))(Cl)(PPh3)2], which is an anticipated modification of the conventional Wilkinson's catalyst [Rh(PPh3)3Cl] employed here as the catalyst precursor. Additional credence to the likelihood of Rh-phosphonate participation in the catalytic cycle is obtained from energetic span (δE) calculations. The δE with [Rh(BINOL–P(OMe))(Cl)(PPh3)2] as the active catalyst is found to be 23.7 kcal mol−1, while that with [Rh(PPh3)3(BINOL–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)] is only 17.1 kcal mol−1.
O)] is only 17.1 kcal mol−1.
The computed lower energy pathway indicates that the overall mechanism begins with the formation of a catalyst–substrate complex, wherein allyl benzoate (substrate) displaces one of the labile PPh3 ligands from the Rh. The C–O bond oxidative addition of the allyl benzoate results in a Rh-π-allyl intermediate that acts as the electrophilic species in the reaction. A direct participation of both the LiHMDS and the additive DMPU in the oxidative addition transition state is found to help lower the activation barrier of this important step. While the Li of LiHMDS assists the C–O cleavage by binding to the benzoate oxygen, DMPU helps in maintaining a tetracoordinate environment around the Li. As its primary role, LiHMDS deprotonates the pro-nucleophilic α,α-disubstituted aldehyde, which in the present study is 2-phenylbutanal, to generate a Li-enolate in a Z-selective manner. A similar involvement of both the base and the additive is noted as beneficial to the enantioselective C–C bond formation as well. The computed enantioselectivity (96%) is found to be in good agreement with the experimentally reported value (92%). The energetic origin of why the addition of the re prochiral face of the Li-enolate to the Rh-π-allyl moiety in the enantiocontrolling C–C bond formation step is more preferred over the si-face addition, leading to high enantioselectivity, is traced to the presence of lower distortion in the Rh-π-allyl fragment and a better interaction between the Rh-π-allyl and Li-enolate moieties in the lower energy transition state. The difference in the interaction energies, in turn, is found to stem from differences in the C–H⋯π and C–H⋯O noncovalent interactions in the enantiocontrolling transition states for the C–C bond formation. On the basis of the enantiocontrolling transition state model for the C–C bond formation, we endeavored to predict the enantioselectivities for substrates hitherto not tried in the title reaction. The predicted high % ee might motivate the expansion of the substrate scope and additional experiments focused on the mechanistic aspects of this important reaction leading to quaternary stereogenic carbon atoms.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Generous computing time from SpaceTime supercomputing at IIT Bombay and CSIR (New Delhi) for a senior research fellowship (M. P.) is gratefully acknowledged.Notes and references
- For selected reviews on enantioselective construction of quaternary carbon stereogenic centers, see:
(a) E. J. Corey and A. Guzman-Perez, Angew. Chem., Int. Ed., 1998, 37, 388–401 CrossRef
; (b) J. Christoffers and A. Mann, Angew. Chem., Int. Ed., 2001, 40, 4591–4597 CrossRef CAS
; (c) J. P. Das and I. Marek, Chem. Commun., 2011, 47, 4593–4623 RSC
; (d) K. W. Quasdorf and L. E. Overman, Nature, 2014, 516, 181–191 CrossRef CAS
; (e) Y. Liu, S.-J. Han, W.-B. Liu and B. M. Stoltz, Acc. Chem. Res., 2015, 48, 740–751 CrossRef CAS
; (f) J. Feng, M. Holmes and M. J. Krische, Chem. Rev., 2017, 117, 12564–12580 CrossRef CAS
; (g) Z.-X. Wang and B.-J. Li, J. Am. Chem. Soc., 2019, 141, 9312–9320 CrossRef
.
-
(a) H. X. Ding, K. K.-C. Liu, S. M. Sakya, A. C. Flick and C. J. O'Donnell, Bioorg. Med. Chem., 2013, 21, 2795–2825 CrossRef CAS
; (b) D. J. Newman and G. M. Cragg, J. Nat. Prod., 2016, 79, 629–661 CrossRef CAS
; (c) M. Bartholow, Pharmatimes, 2012, 48–51 Search PubMed
.
-
(a) A. Y. Hong and B. M. Stoltz, Eur. J. Org. Chem., 2013, 2745–2759 CrossRef CAS
; (b) E. J. Corey, Angew. Chem., Int. Ed., 2002, 41, 1650–1667 CrossRef CAS
; (c) C. J. Douglas and L. E. Overman, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5363–5367 CrossRef CAS
.
-
(a)
Z. G. Hajos and D. R. Parrish, German PatentDE 2102623, Jul 29, 1971 Search PubMed
; (b) U. Eder, G. Sauer and R. Wiechert, Angew. Chem., Int. Ed., 1971, 10, 496–497 CrossRef CAS
; (c) A. Nakamura, A. Konishi, Y. Tatsuno and S. Otsuka, J. Am. Chem. Soc., 1978, 100, 3443–3448 CrossRef CAS
; (d) A. Nakamura, A. Konishi, R. Tsujitani, M. Kudo and S. Otsuka, J. Am. Chem. Soc., 1978, 100, 3449–3461 CrossRef CAS
.
- I. Marek, Y. Minko, M. Pasco, T. Mejuch, N. Gilboa, H. Chechik and J. P. Das, J. Am. Chem. Soc., 2014, 136, 2682–2694 CrossRef CAS
.
-
(a) A. G. Doyle and E. N. Jacobsen, Angew. Chem., Int. Ed., 2007, 46, 3701–3705 CrossRef CAS
; (b) J. Tsuji, H. Takahashi and M. Morikawa, Tetrahedron Lett., 1965, 6, 4387–4388 CrossRef
; (c) B. M. Trost and C. Jiang, J. Am. Chem. Soc., 2001, 123, 12907–12908 CrossRef CAS
; (d) M. Sawamura, M. Sudoh and Y. Ito, J. Am. Chem. Soc., 1996, 118, 3309–3310 CrossRef CAS
; (e) S. A. Asad, J. Ulicki, M. Shevyrev, N. Uddin, E. Alberch and M. M. Hossain, Eur. J. Org. Chem., 2014, 5695–5699 CrossRef CAS
; (f) B. List, I. Čorić, O. O. Grygorenko, P. S. J. Kaib, I. Komarov, A. Lee, M. Leutzsch, S. C. Pan, A. V. Tymtsunik and M. van Gemmeren, Angew. Chem., Int. Ed., 2014, 53, 282–285 CrossRef CAS
; (g) X. Xie, Y. Chen and D. Ma, J. Am. Chem. Soc., 2006, 128, 16050–16051 CrossRef CAS
; (h) L. Yin, M. Kanai and M. Shibasaki, J. Am. Chem. Soc., 2009, 131, 9610–9611 CrossRef CAS
; (i) K. Tsuchida, Y. Senda, K. Nakajima and Y. Nishibayashi, Angew. Chem., Int. Ed., 2016, 55, 9728–9732 CrossRef CAS
; (j) H. Qiu, M. Li, L.-Q. Jiang, F.-P. Lv, L. Zan, C.-W. Zhai, M. P. Doyle and W.-H. Hu, Nat. Chem., 2012, 4, 733–738 CrossRef CAS
; (k) S. Jia, D. Xing, D. Zhang and W. Hu, Angew. Chem., Int. Ed., 2014, 53, 13098–13101 CrossRef CAS
.
-
(a) B. G. Jellerichs, J.-R. Kong and M. J. Krische, J. Am. Chem. Soc., 2003, 125, 7758 CrossRef CAS
; (b) S. Mukherjee and B. List, J. Am. Chem. Soc., 2007, 129, 11336–11337 CrossRef CAS
; (c) G. Jiang and B. List, Angew. Chem., Int. Ed., 2011, 50, 9471–9474 CrossRef CAS
; (d) G. Jindal and R. B. Sunoj, J. Org. Chem., 2014, 79, 7600–7606 CrossRef CAS
.
-
(a) M. Yoshida, T. Terumine, E. Masaki and S. Hara, J. Org. Chem., 2013, 78, 10853–10859 CrossRef CAS
; (b) M. Yoshida, E. Masaki, T. Terumine and S. Hara, Synthesis, 2014, 46, 1367–1373 CrossRef
; (c) T. Kanayama, K. Yoshida, H. Miyabe and Y. Takemoto, Angew. Chem., Int. Ed., 2003, 42, 2054–2056 CrossRef CAS
.
- P. Starkov, J. T. Moore, D. C. Duquette, B. M. Stoltz and I. Marek, J. Am. Chem. Soc., 2017, 139, 9615–9620 CrossRef CAS
.
-
(a) S. Krautwald, D. Sarlah, M. A. Schafroth and E. M. Carreira, Science, 2013, 340, 1065–1068 CrossRef CAS
; (b) A detailed mechanistic study of this reaction was earlier reported by our group, see: B. Bhaskararao and R. B. Sunoj, J. Am. Chem. Soc., 2015, 137, 15712–15722 CrossRef CAS
.
-
(a) F. A. Cruz and V. M. Dong, J. Am. Chem. Soc., 2017, 139, 1029–1032 CrossRef CAS
; (b) W.-B. Liu, C. M. Reeves and B. M. Stoltz, J. Am. Chem. Soc., 2013, 135, 17298–17301 CrossRef CAS
; (c) S. E. Shockley, J. C. Hethcox and B. M. Stoltz, Angew. Chem., Int. Ed., 2017, 56, 11545–11548 CrossRef CAS
; (d) A. Lumbroso, P. Koschker, N. R. Vautravers and B. Breit, J. Am. Chem. Soc., 2011, 133, 2386–2389 CrossRef CAS
.
- For selected reviews, see:
(a) B. M. Trost and D. L. Van Vranken, Chem. Rev., 1996, 96, 395–422 CrossRef CAS
; (b) B. M. Trost and M. L. Crawley, Chem. Rev., 2003, 103, 2921–2944 CrossRef CAS
; (c) Z. Lu and S. Ma, Angew. Chem., Int. Ed., 2008, 47, 258–297 CrossRef CAS
; (d) J. D. Weaver, A. Recio, A. J. Grenning and J. A. Tunge, Chem. Rev., 2011, 111, 1846–1913 CrossRef CAS
; (e) N. A. Butt and W. Zhang, Chem. Soc. Rev., 2015, 44, 7929–7967 RSC
; (f) Q. Cheng, H.-F. Tu, C. Zheng, J.-P. Qu, G. Helmchen and S.-L. You, Chem. Rev., 2019, 119, 1855–1969 CrossRef CAS
; (g) For a book, see: Transition Metal Catalyzed Enantioselective Allylic Substitution in Organic Synthesis, ed. U. Kazmaier, Springer, Heidelberg, 2012 Search PubMed
; (h) B. W. H. Turnbull and P. A. Evans, J. Org. Chem., 2018, 83, 11463–11479 CrossRef CAS
; (i) J. F. Hartwig and L. M. Stanley, Acc. Chem. Res., 2010, 43, 1461–1475 CrossRef CAS
; (j) S. T. Madrahimov, Q. Li, A. Sharma and J. F. Hartwig, J. Am. Chem. Soc., 2015, 137, 14968–14981 CrossRef CAS
.
- T. B. Wright and P. A. Evans, J. Am. Chem. Soc., 2016, 138, 15303–15306 CrossRef CAS
.
-
(a) Y. Minko and I. Marek, Chem. Commun., 2014, 50, 12597–12611 RSC
; (b) U. Kazmaier and D. Stolz, Angew. Chem., Int. Ed., 2006, 45, 3072–3075 CrossRef CAS
; (c) B. W. H. Turnbull and P. A. Evans, J. Am. Chem. Soc., 2015, 137, 6156–6159 CrossRef CAS
; (d) T. B. Wright, B. W. H. Turnbull and P. A. Evans, Angew. Chem., Int. Ed., 2019, 58, 9886–9890 CrossRef CAS
; (e) Z. Jiao, K. W. Chee and J. Zhou, J. Am. Chem. Soc., 2016, 138, 16240–16243 CrossRef CAS
.
- For DFT studies on finding the likely active species and role of additives, see:
(a) G. Jindal and R. B. Sunoj, J. Am. Chem. Soc., 2014, 136, 15998–16008 CrossRef CAS
; (b) Y. Reddi and R. B. Sunoj, ACS Catal., 2017, 7, 530–537 CrossRef CAS
; (c) C. Athira, A. Changotra and R. B. Sunoj, J. Org. Chem., 2018, 83, 2627–2639 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc.: Wallingford, CT, 2016 Search PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119 CrossRef
.
-
(a) P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS
; (b) V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS
.
-
(a) H. Stoll, P. Fuentealba, P. Schwerdtfeger, J. Flad, L. V. Szentpaly and H. Preuss, J. Chem. Phys., 1984, 81, 2732–2736 CrossRef CAS
; (b) M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS
; (c) D. Andrae, U. Haussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS
.
-
(a) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS
; (b) C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS
; (c) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS
.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS
.
-
(a)
I. Funes-Ardoiz and R. S. Paton, GoodVibes, v1.0.1, DOI:10.5281/zenodo.56091
; (b) S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS
.
-
(a) R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS
; (b) AIM2000 Version 2.0; Buro fur Innovative Software, SBK-Software, Bielefeld, Germany, 2002 Search PubMed
; (c) C. F. Matta and R. J. Boyd, Quantum Theory of Atoms in Molecules: Recent Progress in Theory and Application, Wiley-VCH, Weinheim, 2007 CrossRef
.
-
(a) E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS
; (b) J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef
.
-
(a) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS
; (b) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS
; (c) F. Liu, Y. Liang and K. N. Houk, Acc. Chem. Res., 2017, 50, 539–543 CrossRef
.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS
.
- The LiHMDS base exists as a trisolvated monomer in THF solvent, see:
(a) B. L. Lucht and D. B. Collum, Acc. Chem. Res., 1999, 32, 1035–1042 CrossRef CAS
; (b) P. F. Godenschwager and D. B. Collum, J. Am. Chem. Soc., 2007, 129, 12023–12031 CrossRef CAS
.
- (a) The cumulative strength of the NCIs in A3 is found to be more efficient in making the cis disposition of the chiral ligands energetically more favorable over the corresponding trans arrangement in A4; (b) The details of the AIM analysis on A3 and A4 are provided in Fig. S1 and Table S1 in the ESI.†.
- The conversion of a phosphite ligand such as BINOL–P(OMe) to the corresponding phosphonate was suggested to occur in a Rh-catalyzed allylic alkylation of acyclic α-alkoxy substituted ketones, see: P. A. Evans, E. A. Clizbe, M. J. Lawler and S. Oliver, Chem. Sci., 2012, 3, 1835–1838 RSC
.
-
(a) The details of the Rh-Arbuzov rearrangement with the other likely active catalyst from the A series are provided in Scheme S1 in the ESI;†For metal-catalyzed Arbuzov rearrangement reactions, see:
(b) T. B. Brill and S. J. Landon, Chem. Rev., 1984, 84, 577–585 CrossRef CAS
; (c) T. B. Brill and S. J. Landon, Inorg. Chem., 1984, 23, 4177–4181 CrossRef
; (d) J. Ballester, J. Gatignol, G. Schmidt, C. Alayrac, A.-C. Gaumont and M. Taillefer, ChemCatChem, 2014, 6, 1549–1552 CrossRef CAS
.
- An alternative mode of coordination through the phosphonate oxygen for the active catalyst 1 as well as in the Rh(III) intermediate (4) is respectively found to be 10.0 kcal mol−1 and 4.5 kcal mol−1 higher in energy as compared to the corresponding P-coordination.
- For more details on lithium-based reagents in organic synthesis, see:
(a) D. B. Collum, A. J. McNeil and A. Ramirez, Angew. Chem., Int. Ed., 2007, 46, 3002–3017 CrossRef CAS
Lithium reagent in a 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of THF and DMPU, see:
(b) M. Ellwart, I. S. Makarov, F. Achrainer, H. Zipse and P. Knochel, Angew. Chem., Int. Ed., 2016, 55, 10502–10506 CrossRef CAS
1 mixture of THF and DMPU, see:
(b) M. Ellwart, I. S. Makarov, F. Achrainer, H. Zipse and P. Knochel, Angew. Chem., Int. Ed., 2016, 55, 10502–10506 CrossRef CAS ; (c) X. Sun and D. B. Collum, J. Am. Chem. Soc., 2000, 122, 2452–2458 CrossRef CAS
For more details on enolate formation using LiHMDS, see: (d) P. Zhao, A. Condo, I. Keresztes and D. B. Collum, J. Am. Chem. Soc., 2004, 126, 3113–3118 CrossRef CAS
; (e) A. J. McNeil and D. B. Collum, J. Am. Chem. Soc., 2005, 127, 5655–5661 CrossRef CAS
; (f) For more details, see Scheme S2 in the ESI.†.
-
(a) J. Clayden, F. E. Knowles and C. J. Menet, Tetrahedron Lett., 2003, 44, 3397–3400 CrossRef CAS
; (b) J. Clayden, F. E. Knowles and C. J. Menet, Synlett, 2003, 1701–1703 CrossRef CAS
; (c) J. Clayden, S. Parris, N. Cabedo and A. H. Payne, Angew. Chem., Int. Ed., 2008, 47, 5060–5062 CrossRef CAS
; (d) J. Clayden, W. Farnaby, D. M. Grainger, U. Hennecke, M. Mancinelli, D. J. Tetlow, I. H. Hillier and M. A. Vincent, J. Am. Chem. Soc., 2009, 131, 3410–3418 CrossRef CAS
; (e) A. M. Fournier, R. A. Brown, W. Farnaby, H. Miyatake-Ondozabal and J. Clayden, Org. Lett., 2010, 12, 2222–2225 CrossRef CAS
.
- (a) All the likely combinations of oxidative addition were considered with A1 as the potential active catalyst, where we found that the THF coordination to Li results in higher energy than the pathway without the inclusion of LiHMDS. The active participation of LiHMDS·1DMPU is found to lower the relative Gibbs free energies and hence LiHMDS·1DMPU has been considered explicitly for the computations for other potential active catalysts.For more details, see Table S2 in the ESI;† (b) Although the formation of (DMPU)3LiHMDS from (THF)3LiHMDS is found to be feasible, when the former binds to the catalyst–substrate complex (3), only one DMPU can remain coordinated. Attempts to locate transition state geometries with (DMPU)2LiHMDS resulted in immediate de-coordination of one of the DMPUs.
- The Gibbs free energy profile for the C–O bond oxidative addition with various likely active catalysts is provided in Fig. S2 in the ESI.†.
-
(a) Different Rh-phosphonates with varying combinations of ligands could serve as the active catalyst. In the case of B3, the elementary step barrier for the C–O bond oxidative addition as well as the activation span is 0.9 kcal mol−1 higher than that with B1;
(b) In an interesting report, it was noted that the dissociation of one of the PPh3 ligands resulted in a lower energy pathway, see X. Deng, L.-Y. Shi, J. Lan, Y.-Q. Guan, X. Zhang, H. Lv, L. W. Chung and X. Zhang, Nat. Commun., 2019, 10, 949–959 CrossRef
; (c) However, in the present system, the dissociative mechanism for the C–O bond oxidative addition with B1 is found to be more than 30 kcal mol−1 higher. See Fig. S3 in the ESI† for additional details.
- For DFT studies on Li-enolates, see:
(a) M. B. Gillies, J. E. Tønder, D. Tanner and P.-O. Norrby, J. Org. Chem., 2002, 67, 7378–7388 CrossRef CAS
; (b) S. Essafi, S. Tomasi, V. K. Aggarwal and J. N. Harvey, J. Org. Chem., 2014, 79, 12148–12158 CrossRef CAS
; (c) I. Chogii, P. Das, J. S. Fell, K. A. Scott, M. N. Crawford, K. N. Houk and J. T. Njardarson, J. Am. Chem. Soc., 2017, 139, 13141–13146 CrossRef CAS
; (d) X. Zhang, B. Tutkowski, A. Oliver, P. Helquist and O. Wiest, ACS Catal., 2018, 8, 1740–1747 CrossRef CAS
; (e) M. Patil and W. Thiel, Chem.–Eur. J., 2012, 18, 10408–10418 CrossRef CAS
; (f) In the present case, since the enolization is without any chiral catalyst, both R and S enantiomers from the racemic substrate will be enolized by the action of the base to an achiral planar Li-enolate. The different possible arrangements for the generation of enolates and role of the base are shown in Fig. S4 in the ESI.†.
- For preference toward the formation of a Z-enolate over an E-enolate, see:
(a) K. A. Mack, A. McClory, H. Zhang, F. Gosselin and D. B. Collum, J. Am. Chem. Soc., 2017, 139, 12182–12189 CrossRef CAS
; (b) F. A. Davis and J. Deng, Org. Lett., 2004, 6, 2789–2792 CrossRef CAS
; (c) F. A. Davis, Y. Zhang and H. Qiu, Org. Lett., 2007, 9, 833–836 CrossRef CAS
; (d) H. Y. Kim and K. Oh, Org. Lett., 2017, 19, 4904–4907 CrossRef CAS
; (e) P. F. Godenschwager and D. B. Collum, J. Am. Chem. Soc., 2008, 130, 8726–8732 CrossRef CAS
.
- The details of the AIM analysis on the lower energy transition state (5–6)‡ are provided in Fig. S5 and Table S3 in the ESI.†.
- The details of conformational sampling are provided in Fig. S6, Tables S4 and S5 in the ESI.†.
- An alternative dissociative mechanism, devoid of one of the PPh3 ligands in the enantiocontrolling C–C bond formation transition states, is found to be 12.7 kcal mol−1 higher in energy. See Fig. S7 in the ESI† for additional details.
- The details of the AIM analysis on the enantiocontrolling C–C bond formation are given in Fig. S8 and Table S6 in the ESI.†.
- The use of atoms in molecule (AIM) in studying various kinds of noncovalent interactions can be found in the following representative studies,
(a) R. Parthasarathi, V. Subramanian and N. Sathyamurthy, J. Phys. Chem. Lett., 2006, 110, 3349–3351 CAS
; (b) M. Prakash, G. K. Samy and V. Subramanian, J. Phys. Chem. A, 2009, 113, 13845–13852 CrossRef CAS
.
-
(a) E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS
; (b) A. Unnikrishnan and R. B. Sunoj, Chem. Sci., 2019, 10, 3826–3835 RSC
; (c) A. Changotra, B. Bhaskararao, C. M. Hadad and R. B. Sunoj, J. Am. Chem. Soc., 2020, 142, 9612–9624 CAS
.
- The details of the NCI plot are provided in Fig. S9 in the ESI.†.
-
(a) I. Fernandez and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967 RSC
; (b) L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324–343 CAS
; (c) The details of activation strain analysis are provided in Fig. S10 and Table S7 in the ESI;†; (d) The geometric deviation is expressed in terms of root mean square deviation (RSMD) for a particular stereoselective mode with respect to the corresponding pre-reacting complexes. The RMSD value for the transition state (4–7)re‡ is 0.63 Å and that for the transition state (4–7)si‡ is 0.73 Å; see Fig. S11 in the ESI† for more details.
- As noted earlier, the barrier of 16.4 kcal mol−1 for (1A–1)‡, for the generation of the active catalyst 1 from its precursor, is quite affordable under room temperature conditions employed for this reaction.
- Although not directly applicable to the present reaction, in some situations where the pre-catalytic events such as the formation of the active catalyst, exterior to the catalytic cycle, involves an energy-demanding step, it is recommended that δE computation includes such steps. See:
(a) A. Comas-Vives, C. Gonzalez-Arellano, A. Corma, M. Iglesias, F. Sanchez and G. Ujaque, J. Am. Chem. Soc., 2006, 128, 4756–4765 CrossRef CAS
; (b) S. Kozuch, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 795–815 CAS
; (c) S. Kozuch and J. M. L. Martin, ACS Catal., 2011, 1, 246–253 CrossRef CAS
; (d) The details of energetic span calculation are provided in Table S8 in the ESI.†.
- Although the C–C bond formation is not a kinetically significant step in this reaction and hence not necessarily a good candidate for the Hammett analysis, we wanted to examine whether the enantiocontrolling transition states (4–7)re‡ and (4–7)si‡ would exhibit similar or different sensitivities to the presence of electronically active para substituents. The correlations between the substituent constants (σ) and log(kx/kH) for the enolate additions through its re face and the si face are found to be different. See Table S9 and Fig. S12 in the ESI† for more details on the Hammett analysis.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc04959j |
| This journal is © The Royal Society of Chemistry 2021 |