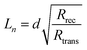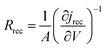DOI:
10.1039/D1RA01043C
(Paper)
RSC Adv., 2021,
11, 9086-9097
Theoretical and experimental study of solar cells based on nanostructured films of TiO2 sensitized with natural dyes extracted from Zea mays and Bixa orellana
Received
7th February 2021
, Accepted 18th February 2021
First published on 1st March 2021
Abstract
Natural dyes were extracted from Zea mays and Bixa orellana, products from Peru, for the sensitization of nanoporous titanium dioxide (TiO2) films. The manufactured DSSCs were studied from the theoretical and experimental point of view in two main stages. In the first, the computational simulation of the dye molecules was carried out using the DFT and TD-DFT method. The analysis was complemented with UV-visible characterization. In the second stage, the transport and recombination processes that occur in the solar cell were studied. For this, the methods of small-modulation transient measurements, extraction of charges and impedance spectroscopy were used. Computational simulations determined that cyanidin-3-glucoside (C3G), the main component of Zea mays, sensitizes the TiO2 film by means of a monodentate anchor through one of the hydroxyl groups. For its part, bixin, which makes up Bixa orellana, anchors through the carboxyl group and also showed a tendency to form agglomerates on TiO2. The charge extraction technique allowed establishing the distribution of trap states of the sensitized films. Small-modulation transient measurements provided information on time constants and diffusion coefficient. It was concluded that the film sensitized with C3G presented a higher density of trap states and a lower level in the conduction band, which resulted in shorter electron life times. The bixin-sensitized film presented better diffusion for its free charge carriers. This was corroborated with impedance spectroscopy, in which the diffusion length parameters pointed to the bixin cell with better charge collection efficiency. All the results were in agreement with the characteristic curves of current–voltage and with the spectral curve of efficiency of conversion of incident photons to electrons (IPCE).
Introduction
Dye Sensitized Solar Cells (DSSC) are attractive solar-to-electric energy conversion devices due to their low-cost and flexible manufacturing.1 They are based on the sensitization of a wide bandgap semiconductor consisting of a nanoporous film with a large surface area. The colorant, located on the surface of the film, fulfills the important role of absorbing light and injecting electrons into the conduction band of the semiconductor. Typically, inorganic compounds based on ruthenium complexes are employed as sensitizing molecules for DSSC.2,3 However, the use of these synthetic colorants has disadvantages such as high cost and toxicity. In contrast, natural dyes are easily extracted and their organic components, which also absorb sunlight, can be used as sensitizers for DSSC. The compounds that make up these dyes have been developed by natural evolution and it is difficult to control their structural arrangement so that they fulfill their role as sensitizers in the best way. That is why it is important to know in depth the nature of the compounds contained in the different natural products from which the dyes are extracted.
Natural colorants can be grouped, according to a common structure and their biosynthetic basis, into four main groups: Flavonoids, whose main subgroup are anthocyanins, betalains, chlorophylls and carotenoids, all of them with a history of having been used as sensitizers.4 DSSCs made with natural colorants are not yet commercially important due to low efficiencies. The limited light absorption capacity and the weak bond of natural colorants with the nanoporous network of the semiconductor are the main drawbacks. That is why it is important to study the interaction with the components of the solar cell as well as their capacities for the absorption of sunlight and subsequent conduction of charges in order to be able to propose new proposals in the way of incorporating these colorants in the device and achieve better performance.
In this article, anthocyanins from Zea mays (purple corn) and bixin from Bixa orellana (achiote) will be studied. These products are widely produced in Peru and the colorants derived from them would have all the potential to replace the artificial colorants widely used in the manufacture of solar cells. Previous works have already reported the manufacture of cells based on these natural dyes.5–7 However, they only focused on optimizing the dye extraction process and did not deepen the understanding of the processes that occur in the cell. The strategy followed in this paper consists of two different and at the same time complementary routes. The first one focuses on analyzing the properties of dyes and how they can be adapted to the solar cell system, the interaction between the dye and titanium dioxide is mainly investigated. The dyes will be modeled using the TD-DFT method8,9 to explore their optical and energetic qualities as sensitizers. The second, from a broader perspective, analyzes the complete device and investigates the transport and recombination processes of charge carriers originated from and by the excitation of the dyes. The cells will be characterized by measurements of transient signals of small modulation, charge extraction and electrochemical impedance10 to obtain the main characteristic parameters of the different electronic processes that involve the transport and recombination of electrons in the sensitized film.
Experimental
Extraction of natural dyes
The purple corn was first shelled and dehydrated at 80 °C overnight. Then the crown of the corn was scratched to obtain floccules from the surface layer, which were crushed with a mortar to obtain a fine powder. The obtained product was diluted in water in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 ratio by weight. After one hour of heating at 80 °C, the solution was filtered and centrifuged. The powder obtained from achiote seeds was diluted in acetonitrile in a 1
500 ratio by weight. After one hour of heating at 80 °C, the solution was filtered and centrifuged. The powder obtained from achiote seeds was diluted in acetonitrile in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ratio by weight. After thirty minutes of vigorous agitation, the solution was filtered.
100 ratio by weight. After thirty minutes of vigorous agitation, the solution was filtered.
Preparation of solar cells sensitized with natural dye
Glasses coated with fluorine-doped tin dioxide (FTO) with a resistance of 15 Ω cm−2 were used, which were previously washed and rinsed in an ethanolic solution of 0.1 M HCl. A paste of titanium dioxide nanoparticles DSL 30NR-D provided by the Solaronix Company was deposited on the conductive substrate using doctor-blade method in a circular area delimited by 3 mm radius. The film was consolidated by a heat treatment at 450 °C for 45 min. After cooling, the electrodes were immersed in the corresponding solutions containing the natural colorant in a period of 18 hours. On the other hand, a chloroplatinic acid solution was prepared to obtain platinum films by heat treatment at 450 °C for 15 min. The solar cells were assembled into redox electrolyte, constituted by TBAI (tetra-n-butylammonium iodide) 0.6 M and 0.05 M I2 (iodine) in acetonitrile,11 in the middle of the sensitized conductive glass/FTO electrode and the platinum counter electrode.
Characterization
Natural colorants solutions and sensitized TiO2 films were characterized using a UV-Visible USB4000 spectrophotometer from Ocean Optics. The Fourier-transform infrared (FTIR) spectra were obtained by a Nicolet iS10 team from Thermo Fisher. The recording of the standard curves of current–voltage (I–V), the transient measurements of small modulation and the measurements of charge extraction were carried out in the dyenamo toolbox (DN-AE01) under standard illumination of an LED diode S42182H whose intensity simulates white light. Incident photon-to-current conversion efficiency (IPCE) was measured by an IPCE station consisting mainly of 175 W xenon lamp source, a Monochromator CM110 (Spectral Products) and a digital acquisition board Labjack U6. Electrochemical impedance measurements were performing using a Uniscan Instruments PG580 potentiostat with a bias voltage set to corresponding open circuit voltage values. The frequency range was from 10 mHz to 100 kHz.
Computational methods
The optimization of geometries of the ground state of the molecules was carried out employing density functional theory (DFT) calculations method with B3LYP functional and the basis set 6-31+G(d) using a code GAMESS.12 The theoretical evaluation of the electron density in the HOMO and LUMO level of the dye molecules at the excited state were calculated using the time-dependent density functional theory (TDDFT) with B3LYP functional and the same basis set mentioned above. The TDDFT calculations consider the solvent effect on the dye structures by using the Polarizable Continuum Model (PCM) corresponding to water for C3G and acetonitrile for bixin.
Results
Electronic structures of sensitizing molecules
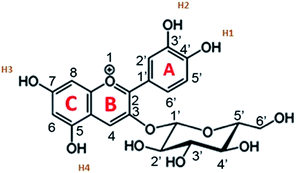
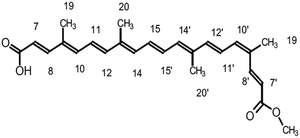
Cyanidin-3-glucoside (C3G) has been reported as the main anthocyanin with the highest concentration present in Zea mays.13 While the main component of Achiote powder, extracted from the pericarp of the seeds, is the carotenoid bixin, which represents more than 80% of the pigments present.14 The molecular structures of C3G and bixin are shown in Table 1. The energy levels of the main molecular orbitals (MO) of C3G and bixin, calculated using the TD-DFT method, are shown in Fig. 1. In the same diagram we can find the levels of the conduction band of TiO2 and the redox potential of I−/I3−. An important thermodynamic requirement in DSSCs is that the lowest unoccupied MO (LUMO) of the dye must be high enough in energy for efficient charge injection into the TiO2, while the highest occupied MO (HOMO) must be low enough for efficient regeneration of the dye oxidized by the redox couple.15 The calculated HOMO levels for both molecules are approximately −6.07 eV. On the other hand, the LUMO level for C3G is at −3.24 eV, while for bixin it is at −1.93 eV. When comparing these energy levels in the diagram we note that, indeed, both molecules fulfill this important condition to carry out the role of sensitizer in DSSC.
Table 1 Molecular structure of cyanidin-3-glucoside and bixin
| Compound |
Structure |
| Cyanidin-3-glucoside |
 |
| Bixin |
 |
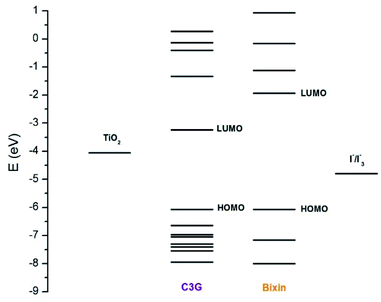 |
| | Fig. 1 Energy levels of the molecular orbitals of C3G and bixin. The energy levels of the redox couple I−/I3− (−4.9 eV) and of the conduction bank of TiO2 (−4.0 eV) are also shown in the diagram. | |
Fig. 2 shows the isodensity plots of the border OMs. For C3G, the ground state energy levels (HOMO, HOMO−1, HOMO−2) are delocalized π orbitals over the entire molecule, except in the glycoside branch. At the HOMO−2 level, the molecular orbital is located mainly in the benzene-diol unit. The LUMO of C3G is of the π* type and the molecular orbital is delocalized over the entire molecule, except in the glucoside branch and in the H2 hydroxyl group (see Table 1). After absorption of sunlight, the C3G molecule must generate current by injecting electrons from its excited state into the conduction band of the semiconductor. This injection is most likely from the densest molecular orbital in the π* state. Therefore, it follows that the anchoring groups of the C3G molecule that can inject electrons efficiently into TiO2 are the hydroxyl groups H1, H3 and H4.
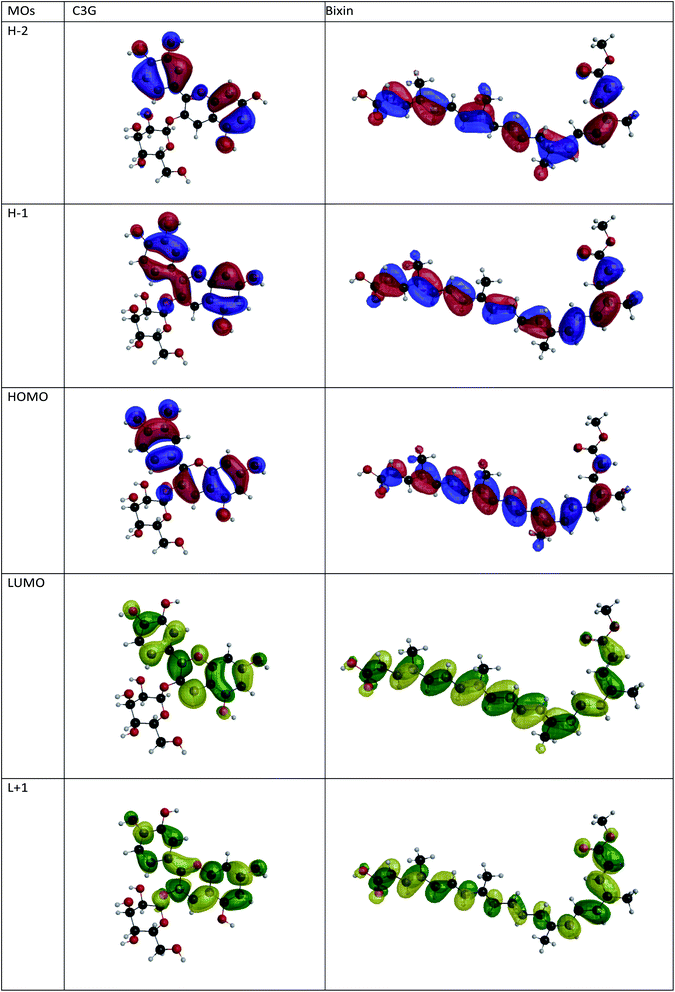 |
| | Fig. 2 Isopotential graphs of the energy levels of the molecular orbitals of C3G and bixin. | |
The electronic distribution of the HOMO level of bixin reveals a conjugation through the polyene chain, with the exception of the terminal substituent carboxyl and methyl. The electronic distribution of LUMO and LUMO+1 indicates a higher density of molecular orbitals, reaching the carboxylic terminal. It follows that electronic excitation would cause the electronic distribution to move from the center of the molecule towards the terminals, mainly favoring injection through the carboxylic terminal.
Optical properties
Table 2 shows the values calculated by the TD-DFT method of the maximum absorption wavelengths (λmax), the excitation energies, the singlet–singlet transitions in the absorption bands and the corresponding oscillatory forces. Fig. 3 and 4 show the theoretical absorption spectra of the molecules in comparison with the experimental spectra of natural dyes.
Table 2 Main theoretical parameters for electronic transitions in C3G and bixin molecules obtained by TD-DFT
| Molecule |
Excited state |
λmax |
Configuration |
Excitation energy |
Oscillator strength |
| C3G |
1 |
486.1 |
H → L (0.968) |
2.551 |
0.609 |
| 3 |
394.4 |
H−2 → L (0.967), H → L (−0.229) |
3.144 |
0.235 |
| 10 |
282.3 |
H → L+1 (−0.804); H−1 → L+1 (0.270) |
4.392 |
0.104 |
| Bixin |
1 |
468.1 |
H → L (−0.969), H−1 → L+1 (−0.226) |
2.649 |
2.565 |
| 2 |
341.3 |
H → L+1 (−0.965), H−1 → L+2 (−0.215) |
3.633 |
0.329 |
| 3 |
322.0 |
H−1→ L (0.963), H−2 → L+1 (0.228) |
3.851 |
0.316 |
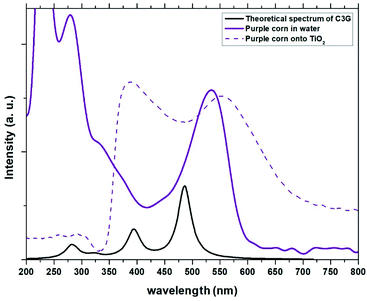 |
| | Fig. 3 Experimental absorption spectra of the dye obtained from Zea mays in solution and adhered to TiO2 compared with the theoretical spectrum obtained for C3G. | |
 |
| | Fig. 4 Experimental absorption spectra of the dye obtained from Bixa orellana in solution and adhered to TiO2 compared with the theoretical spectrum obtained for bixin. | |
The absorption peaks in the visible region at 510 nm and the peak in the UV region at 280 nm shown in the spectrum of the Zea mays solution (Fig. 3), are associated with the cinnamoyl groups (ring A) and benzoyl (ring C), respectively.16,17 The theoretical analysis of C3G found that the main absorption peak is at 486.1 nm and is mainly affected by the H → L configuration, while the second theoretical peak is at 394.4 nm and is mainly affected by the H−2 → L configuration. As seen in Fig. 2, the HOMO−2 delocalization are occupying the benzoyl groups, therefore, we can associate this theoretical absorption band with the experimental band that is in the UV region (280 nm). It can also be seen that the experimental absorption bands of the dye adsorbed on the TiO2 film widen and their corresponding maxima are redshifted. The visible absorption band can change to a lower energy due to the formation of complexes with metal ions18 and the enlargement is an indication of a charge transfer interaction.19 Based on the above, the charge transfer would be carried out through links with any of the hydroxyl groups of the A or C rings of C3G.
The conjugated double bond system of bixin, which constitutes the chromophore of the molecule, results in a strong absorption band between 420 and 510 nm, which is observed in Fig. 4.20 The typical shape of the three peaks of the main absorption band arises from transitions from the lower vibratory level of the electronic ground state to the lower vibratory levels of the electronic excited states.21 Vibration resolution methods allow obtaining accurate spectra of bixin but it is not the main objective of this study. In the theoretical calculation, the main absorption band of bixin originates mainly from a single HOMO → LUMO transition calculated at 468.1 nm, which is close to the experimental value (460 nm). Once adhered to the surface of TiO2, the absorption spectrum is broader and the intensity of the absorption peaks increases, indicating a strong interaction between bixin and the surface of TiO2.22 This interaction occurs through a bond with the carboxylic group located at the end of the molecule because delocalized π* states can be found in it. It can also be observed that the peaks have shifted towards the blue in the spectra of the bixin absorbed on the TiO2. This is attributed to the formation of aggregates and/or the disarray of the dye molecules on the surface of the TiO2 film.23
Photoelectric response of solar cells
The current–voltage characteristic curves of the devices made with natural colorants obtained under standard AM 1.5 lighting (1000 W m−2) are shown in Fig. 5. The main parameters calculated from these curves are summarized in Table 3. Here it can be seen that the cell manufactured with Bixa orellana is the one with the highest values, which is translated into greater efficiency. Fig. 6 shows the IPCE spectra of cells made with natural dyes. It is observed that the values begin to increase from 650 nm for the case of Zea mays and from 550 nm for the Bixa orellana, keeping in agreement with the UV visible absorption spectra of the sensitized films. The higher efficiencies in the Bixa orellana spectrum are also in accordance with the higher photocurrent achieved in the current–voltage curves.
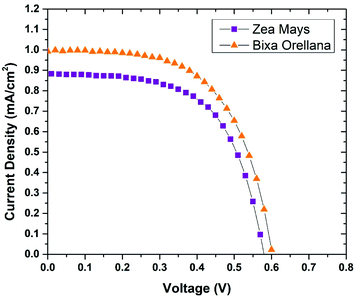 |
| | Fig. 5 Current–voltage curves of the devices manufactured with Zea mays and Bixa orellana. | |
Table 3 Characteristic parameters of current–voltage curves
| Dye |
JSC (mA cm−2) |
VOC (V) |
FF |
%η |
| Zea mays |
0.885 ± 0.003 |
0.586 ± 0.009 |
0.592 ± 0.014 |
0.307 ± 0.003 |
| Bixa orellana |
0.993 ± 0.132 |
0.600 ± 0.078 |
0.611 ± 0.021 |
0.357 ± 0.003 |
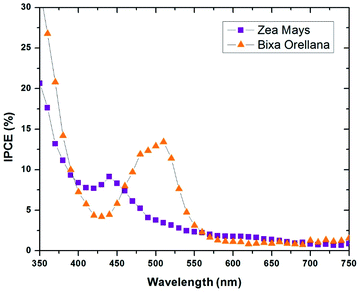 |
| | Fig. 6 IPCE spectra of the devices manufactured with Zea mays and Bixa orellana. | |
Electron lifetime and trap state distribution in sensitized film
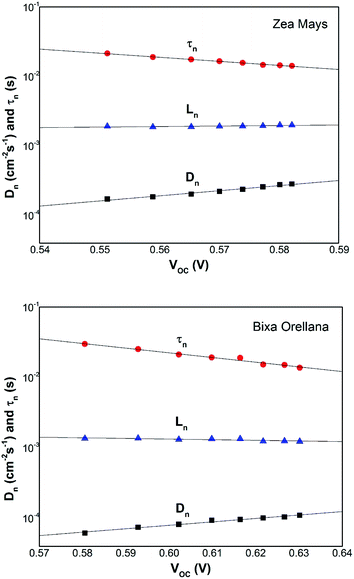
Fig. 7 shows the electron lifetimes on a logarithmic scale as a function of photovoltage for cells manufactured with Zea mays and Bixa orellana. These are the time constants for which the system regains equilibrium, after a small disturbance of the steady state, removing excess charge carriers by recombination towards the electrolyte acceptors. Although the measurements show a greater speed for the recombination of electrons by the cell manufactured with Zea mays, the values of the time constants are very similar when they approach the open circuit voltage value corresponding to normal operating conditions (0.586 V for Zea mays and 0.635 V for Bixa orellana). The trend in both cases is the decrease in the time constant as the open circuit voltage increases caused by increased light intensity. The decrease in life time is explained by a model of multiple traps located below the conduction band.24 This same model can explain the difference between the slopes of both graphs, which are related to the way in which these trap states are distributed.
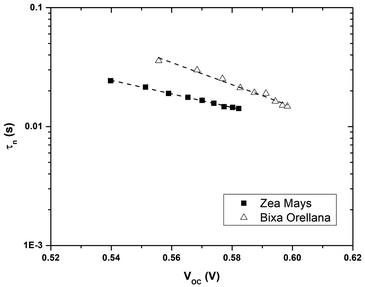 |
| | Fig. 7 Electron life time (τn) as a function of the open circuit potential for devices manufactured with Zea mays and Bixa orellana. | |
Fig. 8 shows the relationship between the extracted charge and the open circuit potential of the cells made with both colorants. The extracted charge-voltage characteristic curves of the DSSCs are attributed to the electrons “trapped” in the distribution of trap states. It can be seen that the load extracted from the cell with Zea mays is clearly greater than the load extracted from the cell with Bixa orellana. However, this higher charge does not contribute to electronic conduction, since it is trapped charges, but rather to recombination with the electrolyte acceptors. This is in agreement with the shorter lifetimes reported in the cell with Zea mays.
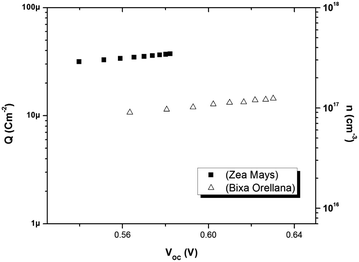 |
| | Fig. 8 Extracted charge and electron density obtained as a function of the open circuit voltage in the cells manufactured with Zea mays and Bixa orellana. | |
The electron density in TiO2, shown on the right-hand side of the y-axis, was calculated from the extracted charge and the thickness of the TiO2 film. The estimation of the electron density obtained by the charge extraction method allows obtaining information on the total density of delocalized NL trap states below the TiO2 conduction band.25 The profile of the concentration of trapped electrons can be obtained from an exponential density distribution of states gT(ET) of the form:26,27
| |
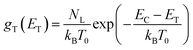 | (1) |
where
EC is the energy of the conduction band,
kB is the Boltzmann constant, and
T0 is the characteristic temperature of the trap states. Through an integration that goes from the Fermi redox energy
EF,redox of the electrolyte to the Fermi energy of the semiconductor
EF, we obtain the approximate concentration of trapped electrons
nL:
| |
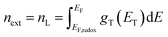 | (2) |
| |
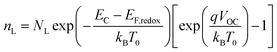 | (3) |
The data obtained from the electronic concentration as a function of the open circuit voltage can be fitted to exponential curves in the form of eqn (3) as shown in Fig. 9. The parameters to be evaluated are the characteristic temperature (T0), the density of trap states (NL) and the level of the conduction band (EC). While T0 can be calculated directly from the fit, the value of EC must be approximated from the intercept of the graph of density of states (DOS) versus energy (Fig. 10), with which we also obtain the value by NL. Table 4 shows the values obtained using the aforementioned procedure.
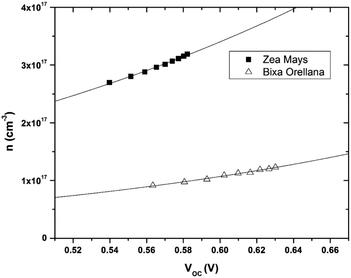 |
| | Fig. 9 Electronic density extracted as a function of open circuit voltage with its corresponding adjustment curves according to eqn (3). | |
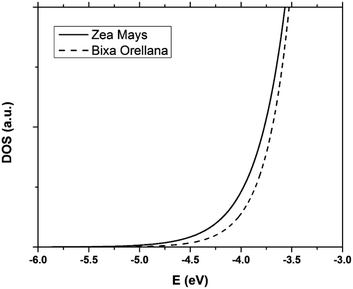 |
| | Fig. 10 Distribution of the density of trap states of TiO2 in cells manufactured with Zea mays and Bixa orellana. | |
Table 4 Values for the characteristic temperature (T0), density of trap states (NL) and energy of the conduction band (EC) of TiO2 obtained from the load data extracted from the cells
| |
T0 |
NL |
EC |
| Zea mays |
3414.6 K |
9.14 × 1017 cm−3 |
−4.05 eV |
| Bixa orellana |
2791.6 K |
4.79 × 1017 cm−3 |
−3.96 eV |
The results show that there is a higher density of trap states for the film with Zea mays, and also that these are not distributed in the same way as in the case of Bixa orellana since it has a different characteristic temperature. Another important aspect that can be observed is that the levels of the conduction band differ approximately 0.09 eV between one case and another. The change in the level of the conduction band is an effect that accompanies the sensitization process due to the modifications in the surface of TiO2.28 The closer proximity of the conduction band to the Fermi Redox level can also translate into a lower open circuit voltage. Whereas, a higher density of trap states would involve less charge available for conduction, obtaining lower values for the photocurrent.
Electronic diffusion in sensitized films
Fig. 11 shows the electron concentration extracted under short-circuit conditions as a function of the illumination intensity on a logarithmic scale for both axes. The load increases as the lighting intensity increases and, in general, the loads are higher in the case of the cell made with Zea mays. It should be noted that these load measurements have limited precision. The integration period that is carried out for the calculation of the charge is limited and does not take into account the totality of electrons extracted. Furthermore, the recombination of a part of the electrons must be taken into account before reaching the substrate. Therefore, the results underestimate the true value of the extracted electron concentrations. For the analysis of the electronic transport in the film of the solar cell, the transient photocurrent method was used, in which the response to a small square wave modulation of light is recorded. The resulting transport times, shown in Fig. 12, are then used to obtain the diffusion coefficients by relating them to the square of the film thickness (d) through eqn (4).29,30 The results are shown in Fig. 9.| |
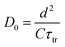 | (4) |
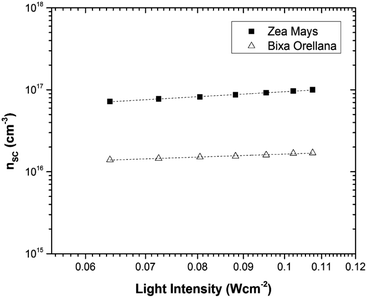 |
| | Fig. 11 Charge extracted under short-circuit conditions as a function of lighting intensity for cells manufactured with Zea mays and Bixa orellana. | |
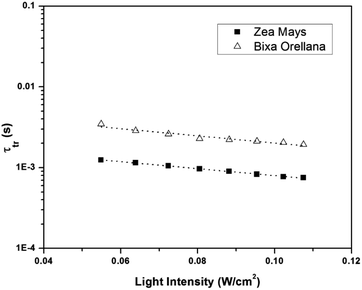 |
| | Fig. 12 Electronic transport time as a function of the intensity of illumination of the devices manufactured with Zea mays and Bixa orellana. | |
The graph of Fig. 13 does not correspond to the simple electronic transport model proposed by eqn (4) in which the diffusion of electrons from the conduction band is represented with a constant diffusion coefficient in an effective medium, D0, but rather it deals with a Dn coefficient dependent on the concentration of electrons called the apparent chemical diffusion coefficient.31,32 The multiple traps model allows us to adjust to the experimental data through an equilibrium consideration called “quasi-static assumption” (see eqn (5)). From this expression and using the load extraction data, it is obtained that the effective diffusion coefficient is 1.53 × 10−5 cm−2 s−1 for the case of the cell with Zea mays and 2.65 × 10−4 cm−2 s−1 for the case of the cell with Bixa orellana.
| |
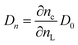 | (5) |
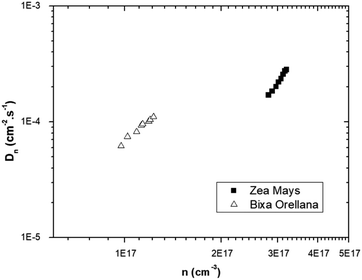 |
| | Fig. 13 Apparent chemical diffusion coefficient as a function of the electronic concentration corresponding to the cells manufactured with Zea mays and Bixa orellana. | |
The competitive recombination and diffusion processes can be conveniently described by the diffusion length parameter, 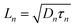 , which is the average distance (normal to the plane of the film) that an injected electron can travel through the film before recombination. If Ln > d, (where d is the thickness of the TiO2 film), only a small fraction of the injected charge will be lost before it is collected, making long diffusion lengths desirable. Fig. 14 compare the parameters of the electron life time and the diffusion coefficient, obtained experimentally, to estimate the diffusion length values of the sensitized cells as a function of the open circuit voltage. On average, the results obtained are 19.4 μm for the Zea mays case, and 13.1 μm for the Bixa orellana case, with the adjustment curve having a positive slope for the first case and a negative slope for the second. These values, compared to the 7.3 μm of thickness that the active layer of the film has on average, are sufficiently greater to achieve the formation of the photocurrent but they are not so far apart that there are still considerable losses, and this can be seen reflected in the efficiencies obtained. However, direct comparisons cannot be made between one colorant and another based on these diffusion length values because they are still close to the thickness of the film, which makes it more difficult to resort to a simplified model of diffusion.33
, which is the average distance (normal to the plane of the film) that an injected electron can travel through the film before recombination. If Ln > d, (where d is the thickness of the TiO2 film), only a small fraction of the injected charge will be lost before it is collected, making long diffusion lengths desirable. Fig. 14 compare the parameters of the electron life time and the diffusion coefficient, obtained experimentally, to estimate the diffusion length values of the sensitized cells as a function of the open circuit voltage. On average, the results obtained are 19.4 μm for the Zea mays case, and 13.1 μm for the Bixa orellana case, with the adjustment curve having a positive slope for the first case and a negative slope for the second. These values, compared to the 7.3 μm of thickness that the active layer of the film has on average, are sufficiently greater to achieve the formation of the photocurrent but they are not so far apart that there are still considerable losses, and this can be seen reflected in the efficiencies obtained. However, direct comparisons cannot be made between one colorant and another based on these diffusion length values because they are still close to the thickness of the film, which makes it more difficult to resort to a simplified model of diffusion.33
 |
| | Fig. 14 Diffusion length of the solar cell calculated from the electron lifetime and the chemical diffusion coefficient. | |
Comparison with electrochemical impedance measurements
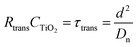
Electrochemical impedance measurements are commonly used to obtain information similar to what can be obtained from transient measurements, as well as information about other components of the solar cell. Impedance measurement involves applying a small periodic voltage disturbance to the device, keeping it in steady state conditions. The phase and response amplitude of the resulting current are measured to give an impedance spectrum. The data were analyzed adjusting them to the model described in Fig. 15. The model considers the resistance of the substrate (RS), the resistance to electronic transport at the interface of the counter electrode (Rct_EE, CPE_CE), a Warburg element for electrolytic diffusion (W) and the heart of the model is the transmission line (TL_PE) that represents the electronic interaction at the TiO2/electrolyte interface based on the works of Bisquert et al.34,35 This includes the recombination resistance, Rrec, (or charge transfer), the charge transport (or diffusion) resistance, Rtrans, and the chemical capacitance, CTiO2, of the TiO2 film. Capacitive elements are replaced by constant phase elements to account for the dispersion observed in this type of measurement.24,26 Taking into account an approximately exponential distribution of the trapped charges (eqn (A.8)), the model parameters are related to the relaxation time of small disturbances, or time constants, and the diffusion coefficient by means of expressions (6) and (7). While the diffusion length of the electron is given by the expression (8).| |
 | (7) |
| |
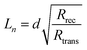 | (8) |
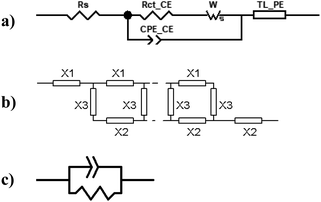 |
| | Fig. 15 (a) Equivalent circuit used to adjust the impedance spectra of the manufactured DSSCs. The transmission line TL_PE follows the scheme shown in (b), where each element X1, X2 and X3 becomes a resistor and a phase element in parallel, as shown in (c). | |
Fig. 16 presents the impedance spectra of the cells made with Zea mays and Bixa orellana. Table 5 shows the parameters obtained from these spectra by means of the equivalent circuit described above. The results show a good concordance with the values obtained by the transient signal measurements for the cases of recombination and transport times, as well as for the chemical diffusion coefficient. However, a considerable difference can now be observed between the diffusion lengths. Although the Ln values may be overestimated because the impedance measurements do not quantify the collection of charges (considered in the transient measurements), we can affirm that the cell prepared with Bixa orellana presents a greater diffusion length.
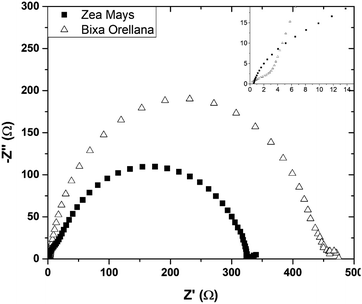 |
| | Fig. 16 Complex plane graphs of impedances obtained from cells manufactured with Zea mays and Bixa orellana. | |
Table 5 Parameters obtained from the adjustment of the graphs of Fig. 13 using the model described in Fig. 11
| Dye |
Zea mays |
Bixa orellana |
| τn |
0.0167 s |
0.0604 s |
| τtr |
0.0003 s |
0.0006 s |
| Dn |
1.94 × 10−3 cm−2 s−1 |
8.51 × 10−4 cm−2 s−1 |
| Ln |
56.8 μm |
71.3 μm |
Discussion
Sensitization of the TiO2 film by natural dyes
The topology of the electronic distribution of the HOMO and LUMO levels of the C3G molecule revealed a high probability that the electronic transition towards TiO2 would occur through hydroxyl groups, mainly those labeled as H1, H3 and H4 (see Table 1). Observing the structure of C3G, an anchoring through the two hydroxyl groups of the benzene-diol of the molecule is expected,36 following the bidentate mechanism of typical ruthenium-based molecules.37 However, according to the DFT results, LUMO doesn't occupied in H2. This indicates that hydroxyl group in H1 would form a simple bond with the Ti+ on the surface after his deprotonation. Chaiamornnugool et al. obtained similar results in their theoretical study of anthocyanins. They also mentioned that the direction of electron transfer is generated from benzopyrilium ring to 2-phenyl ring, so it is highly unlikely that anchoring occurs through H3 and H4.
With respect to bixin, the TD-DFT analysis indicated that the electronic jumps go in the direction of the carboxylic terminal which is the main anchoring group of the sensitizing molecules. The increase in intensity and widening of the UV-visible spectrum of bixin after adhering to TiO2 indicates a large number of molecules available for electron transfer. However, the blueshift indicates a stacking effect. Therefore, the formation of aggregates should be energetically preferable to the formation of the bixin/TiO2 complexes. This turns out to be an unfavorable point for this molecule since intermolecular processes decrease the electron injection efficiency from excited states.38
Distribution of trap states in sensitized films
The average concentration of the electrons in the semiconductor gives us quite useful information about the energy of the solar cell. Thus, the results suggest a trap state distribution for the TiO2 crystal lattice as shown in Fig. 17. The scheme shows us that sensitization with C3G brings with it a higher density of trap states compared to bixin, in addition to a greater proximity of the conduction band to the Fermi redox level of the electrolyte. The position of the conduction band of TiO2 depends mainly on the surface charge and also on the absorbed dipolar molecules.39 The proton release that occurs after absorption of the dye molecules results in passivation of the surface for conduction. This causes a change in the dipole potential of the surface, decreasing the level of the conduction band with respect to the Fermi redox level.40,41 Based on this, the surface of the TiO2 would be more passivated with the C3G molecules than with those of bixin. This being an indication of a better sensitization related to a better dipole moment of C3G compared to the tendency to aggregation that bixin has due to its symmetry.42 Calogero et al., in their theoretical study of anthocyanins, showed that the increment of the dipole moment results in an increase of the sensitizing performance of the dye.43 However, the polarity of the C3G also generates a greater electrostatic interaction with the cations of the electrolyte causing the appearance of more trap states for the electron.44,45
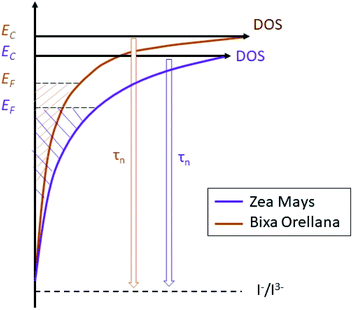 |
| | Fig. 17 Schematic diagram of the trap state distribution of films sensitized with natural dyes and their effect on the electron lifetime. | |
The model outlined in Fig. 18 provides a description of the disorder that exists in the transport and recombination of electrons of the nanostructured TiO2 due to the distribution of trap states that will help us to differentiate both parameters. The coefficient of chemical diffusion determines the speed with which equilibrium in transport is restored when excess charge carriers are injected; while the effective diffusion coefficient determines the speed of flow of the free charge carriers in the steady state. It should be noted that, in this simplified model, a distinction is being made between internal traps and surface states, in which not all electron traps act as recombination centers.31 Referring to the results for Dn obtained from the transient signal measurements, we can observe that the diffusion is greater in the case of Zea mays, that is, it presents a better recovery of its stable flow. This despite having a higher density of trap states. However, the values of D0 obtained through the calculation referred to in eqn (5), shows us a greater diffusion of free electrons in the case of the Bixa orellana. This makes us indicate that there would be a greater presence of surface trap states in the case of the film with Zea mays. That is, the sensitization with C3G has caused a greater modification in the surface of TiO2 compared to bixin.
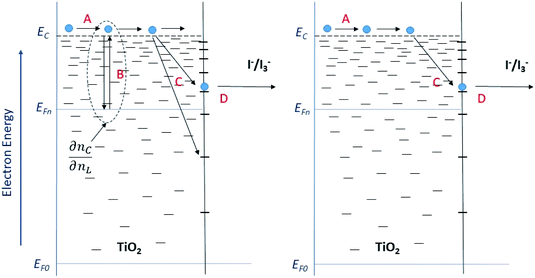 |
| | Fig. 18 Diagram of the steps involved in the transport and recombination of the excess photoinduced electrons (left) and in steady state (right). The levels of the conduction band (EC) and the Fermi levels of the electrons under illumination (EF,n) and in the dark (EF,0) are indicated. The Fermi redox level (EF,redox) and the level of the unoccupied states (Eox) are also indicated within the state distribution of the electrolytic species. (A) Transport of electrons through extended states (located at the lower edge of EC). (B) Electron capture and thermal release within an exponential distribution of states located in the band gap. (C) Capture by and (D) transfer through surface states to fluctuating levels of redox oxidized species. | |
Diffusion length and recombination resistance
Diffusion length is closely related to charge collection efficiency, so we could correlate the fact of having a longer diffusion length with obtaining a better photocurrent. However, we have found a trade-off between the results provided by transient signal measurements and those of electrochemical impedance. If we observe the graphs of Fig. 10, we can see that, in practice, the diffusion length has presented slight variations with the voltage, when, in theory, this should be a constant parameter. In the context of the multiple trap model, these variations can be explained as a consequence of non-linear transport and recombination of the cargo population.46–48 One aspect of this non-linearity is that the diffusion length is normally observed to be shorter at low electron concentrations.49,50 Such is the case of the cell with Bixa orellana, which has presented a lower electron concentration compared to the cell with Zea mays, so the diffusion length must actually be underestimated.
The parameters obtained from the electrochemical impedance spectra resulted in diffusion lengths greater than those obtained with transient measurement techniques, and this time the greatest diffusion length was assigned to the cell with Bixa orellana. The semicircles in the impedance spectra provide information about the corresponding charge transfer processes. Depending on the Rrec/Rtr relationship, we will obtain different types of spectra.51 If Rrec ≫ Rtr, as is the case of the cell with Bixa orellana, the recombination resistance forms a large arc at low frequency, and the transport resistance forms a small Warburg characteristic curve at high frequency (Fig. 12). This type of spectrum makes it possible to immediately recognize a DSSC with good collection efficiency. The cell with Zea mays also presents a high Rrec/Rtr value, although lower than in the case of the Bixa orellana.
| |
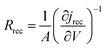 | (9) |
Regarding the short-circuit current of curve I–V, this is obtained from JSC = Jgen − Jrec. Where, Jgen, is the generation current, which is constant and depends on the intensity of the light, while, Jrec, is the recombination current. It should be noted that curve I–V shows an exponential variation whose fall informs us about the recombination rate in all conditions of the solar cell.52 The recombination resistance, Rrec, obtained from the impedance measurements, turns out to be a derivative of the current in which the variation with voltage is considered53,54 (see eqn (9)). Therefore, Rrec, gives us a magnitude that allows us to make comparisons between one cell and another, which can be defined unambiguously, even in the case of non-linear recombination. In this sense, the greater resistance to recombination presented by the cell with Bixa orellana confirms the best performance obtained in curves I–V.
Conclusions
A theoretical and experimental study was carried out to have a better understanding of the sensitization mechanisms and the main transport and recombination processes of DSSC made with natural dyes obtained from Zea mays and Bixa orellana native to Peru. The theoretical study DFT and TD-DFT focused on C3G and bixin, which are the main components of Zea mays and Bixa orellana, respectively. The results indicated that the sensitization of C3G was carried out by means of a monodentate anchor through one of the hydroxyl groups of the benzene-diol of the molecule. For its part, bixin showed greater affinity with the surface of TiO2, folding over it and forming bonds through the carboxylic group of the molecule. However, it also shows a great tendency to agglomerate, showing signs of stacking molecules in the film.
Transient signal measurements reported shorter electron lifetimes for the cell sensitized with Zea mays, which is consistent with the higher density of trap states exhibited by this film and with the lower open circuit voltage observed in the characteristic current–voltage curves. On the other hand, the highest chemical diffusion values corresponded to the film sensitized with Zea mays. However, this did not translate into better free electron transport due to a greater presence of surface trap states, indicating greater surface modification of TiO2 by C3G.
Finally, the electrochemical impedance spectra revealed a greater diffusion length for the film sensitized with Bixa orellana as a consequence of presenting a greater resistance to recombination. Likewise, this parameter made it possible to verify that the cell with Bixa orellana presented a better capture efficiency, which was translated into the highest short-circuit photocurrent of the current–voltage curves. It should be noted that the diffusion lengths calculated from the transient signal measurements were not taken into account because they presented variations with respect to voltage due to the non-linear recombination that the devices presented.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors gratefully acknowledge support from the PhD program in Physics of the National University of Engineering financed by CONCYTEC through Resolution No. 197-2015.
References
- B. O’Regan and M. Grätzel, Nature, 1991, 353, 737–740 CrossRef.
- S. Ito, in Solar Cells - Dye-Sensitized Devices, 2012 Search PubMed.
- F. Gao, Y. Wang, D. Shi, J. Zhang, M. Wang, X. Jing, R. Humphry-Baker, P. Wang, S. M. Zakeeruddin and M. Grätzel, J. Am. Chem. Soc., 2008, 130(32), 10720–10728 CrossRef CAS.
- A. K. Pandey, M. S. Ahmad, N. A. Rahim, V. V. Tyagi and R. Saidur, Natural Sensitizers and Their Applications in Dye-Sensitized Solar Cell, ed. R. C. Sobti, N. K. Arora and R. Kothari, Springer Singapore, Singapore, 2019, pp. 375–401 Search PubMed.
- K. Phinjaturus, W. Maiaugree, B. Suriharn, S. Pimanpaeng, V. Amornkitbamrung and E. Swatsitang, Appl. Surf. Sci., 2016, 380, 101–107 CrossRef CAS.
- N. M. Gómez-Ortíz, I. A. Vázquez-Maldonado, A. R. Pérez-Espadas, G. J. Mena-Rejón, J. A. Azamar-Barrios and G. Oskam, Sol. Energy Mater. Sol. Cells, 2010, 94, 40–44 CrossRef.
- D. A. Haryanto, S. Landuma and A. Purwanto, AIP Conf. Proc., 1586, 104–108 Search PubMed.
- C. ME, C. Jamorski, C. KC and S. DR, J. Chem. Phys., 1998, 108, 4439–4449 CrossRef.
- R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 109, 8218–8224 CrossRef.
- P. R. F. Barnes, K. Miettunen, X. Li, A. Y. Anderson, T. Bessho, M. Gratzel and B. C. O'Regan, Adv. Mater., 2013, 25, 1881–1922 CrossRef CAS.
- N. T. R. N. Kumara, P. Ekanayake, A. Lim, L. Y. C. Liew, M. Iskandar, L. C. Ming and G. K. R. Senadeera, J. Alloys Compd., 2013, 581, 186–191 CrossRef CAS.
- M. E. Lasinski, N. A. Romero, S. T. Brown and J. P. Blaudeau, J. Comput. Chem., 2012, 33, 723–731 CrossRef CAS.
- S. De Pascual-Teresa, C. Santos-Buelga and J. C. Rivas-Gonzalo, J. Sci. Food Agric., 2002, 82, 1003–1006 CrossRef CAS.
- C. H. Avendaño-Arrazate, L. L. Pinzón-López, A. Mendoza-López, E. Campos-Rojas, P. J. Correa-Navarro, G. Godoy-Hernández, J. O. Mijangos-Cortés and R. Rivera-Madrid, AGROProductividad, 2012, 5, 3–9 Search PubMed.
- A. Calzolari, D. Varsano, A. Ruini, A. Catellani, R. Tel-Vered, H. B. Yildiz, O. Ovits and I. Willner, J. Phys. Chem. A, 2009, 113(30), 8801–8810 CrossRef CAS.
- D. Syukri, D. Darwis and A. Santoni, J. Chem. Pharm. Res., 2013, 1276–1282 Search PubMed.
- D. Dwilistiani, D. Darwis and A. Santoni, J. Chem. Pharm. Res., 2015, 7, 519–523 CAS.
- G. Calogero and G. Di Marco, Sol. Energy Mater. Sol. Cells, 2008, 92, 1341–1346 CrossRef CAS.
- K. Vinodgopal, X. Hua, R. L. Dahlgren, A. G. Lappin, L. K. Patterson and P. V. Kamat, J. Phys. Chem., 1995, 99, 10883–10889 CrossRef CAS.
- W. Rahmalia, J. F. Fabre, T. Usman and Z. Mouloungui, Spectrochim. Acta, Part A, 2014, 131, 455–460 CrossRef CAS.
- M. Scotter, Food Addit. Contam., Part A: Chem., Anal., Control, Exposure Risk Assess., 2009, 26, 1123–1145 CrossRef CAS.
- T. Ma, K. Inoue, H. Noma, K. Yao and E. Abe, J. Photochem. Photobiol., A, 2002, 152, 207–212 CrossRef CAS.
- A. Ehret, L. Stuhl and M. T. Spitler, Electrochim. Acta, 2000, 45, 4553–4557 CrossRef CAS.
- J. Halme, P. Vahermaa, K. Miettunen and P. Lund, Adv. Mater., 2010, 22, 210–234 CrossRef.
- A. Zaban, M. Greenshtein and J. Bisquert, ChemPhysChem, 2003, 4(8), 859–864 CrossRef CAS.
- N. W. Duffy, L. M. Peter, R. M. G. Rajapakse and K. G. U. Wijayantha, Electrochem. Commun., 2000, 2, 658–662 CrossRef CAS.
- J. R. Jennings, A. Ghicov, L. M. Peter, P. Schmuki and A. B. Walker, J. Am. Chem. Soc., 2008, 130, 13364–13372 CrossRef CAS.
- M. K. Nazeeruddin, S. M. Zakeeruddin, R. Humphry-Baker, M. Jirousek, P. Liska, N. Vlachopoulos, V. Shklover, C.-H. Fischer and M. Grätzel, Inorg. Chem., 1999, 38, 6298–6305 CrossRef CAS.
- J. van de Lagemaat, N.-G. Park and A. J. Frank, J. Phys. Chem. B, 2000, 104(9), 2044–2052 CrossRef CAS.
- S. Nakade, Y. Saito, W. Kubo, T. Kitamura, Y. Wada and S. Yanagida, J. Phys. Chem. B, 2003, 107(33), 8607–8611 CrossRef CAS.
- J. Bisquert and V. S. Vikhrenko, J. Phys. Chem. B, 2004, 108, 2313–2322 CrossRef CAS.
- A. C. Fisher, L. M. Peter, E. A. Ponomarev, A. B. Walker and K. G. U. Wijayantha, J. Phys. Chem. B, 2000, 104(5), 949–958 CrossRef CAS.
- J. Bisquert and I. An Mora-Ser, J. Phys. Chem. Lett., 2010, 1, 450–456 CrossRef CAS.
- J. Bisquert, G. Garcia-Belmonte, F. Fabregat-Santiago and A. Compte, Electrochem. Commun., 1999, 1, 429–435 CrossRef CAS.
- J. Bisquert, Phys. Chem. Chem. Phys., 2000, 2, 4185–4192 RSC.
- Z. Liu, J. Mol. Struct.: THEOCHEM, 2008, 862, 44–48 CrossRef CAS.
- P. G. Bomben, K. D. Thériault and C. P. Berlinguette, Eur. J. Inorg. Chem., 2011, 2011, 1806–1814 CrossRef.
- H. Ozawa, M. Awa, T. Ono and H. Arakawa, Chem.–Asian J., 2012, 7, 156–162 CrossRef CAS.
- A. Hagfeldt, U. B. Cappel, G. Boschloo and L. Sun, Dye-Sensitized Photoelectrochemical Cells, Elsevier Ltd, 2012 Search PubMed.
- T. T. O. Nguyen, L. M. Peter and H. Wang, J. Phys. Chem. C, 2009, 113, 8532–8536 CrossRef CAS.
- A. K. Chandiran, S. M. Zakeeruddin, R. Humphry-Baker, M. K. Nazeeruddin, M. Grätzel and F. Sauvage, ChemPhysChem, 2017, 18, 2724–2731 CrossRef CAS.
- S. Tay-Agbozo, S. Street and L. D. Kispert, J. Photochem. Photobiol., A, 2018, 362, 31–39 CrossRef CAS.
- G. Calogero, A. Sinopoli, I. Citro, G. Di Marco, V. Petrov, A. M. Diniz, A. J. Parola and F. Pina, Photochem. Photobiol. Sci., 2013, 12, 883–894 CrossRef CAS.
- L. Peter, Acc. Chem. Res., 2009, 42, 1839–1847 CrossRef CAS.
- E. Hendry, M. Koeberg, B. O'Regan and M. Bonn, Nano Lett., 2006, 6, 755–759 CrossRef CAS.
- J. Villanueva-Cab, H. Wang, G. Oskam and L. M. Peter, J. Phys. Chem. Lett., 2010, 1, 748–751 CrossRef CAS.
- P. R. F. Barnes and B. C. O'Regan, J. Phys. Chem. C, 2010, 114, 19134–19140 CrossRef CAS.
- A. Gagliardi, S. Mastroianni, D. Gentilini, F. Giordano, A. Reale, T. M. Brown and A. D. Carlo, IEEE J. Sel. Top. Quantum Electron., 2010, 16, 1611–1618 CAS.
- P. R. F. Barnes, A. Y. Anderson, S. E. Koops, J. R. Durrant and B. C. O’Regan, J. Phys. Chem. C, 2009, 113(3), 1126–1136 CrossRef CAS.
- H. K. Dunn and L. M. Peter, J. Phys. Chem. C, 2009, 113, 4726–4731 CrossRef CAS.
- J. Bisquert, J. Phys. Chem. B, 2002, 106, 325–333 CrossRef CAS.
- R. Guliani, Open Renewable Energy J., 2012, 5, 49–60 CrossRef CAS.
- F. Fabregat-Santiago, J. Bisquert, G. Garcia-Belmonte, G. Boschloo and A. Hagfeldt, Sol. Energy Mater. Sol. Cells, 2005, 87, 117–131 CrossRef CAS.
- Q. Wang, S. Ito, M. Grätzel, F. Fabregat-Santiago, I. Mora-Seró, J. Bisquert, T. Bessho and H. Imai, J. Phys. Chem. B, 2006, 110, 25210–25221 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Michael R. Celestino and
María E. Quintana
,
Michael R. Celestino and
María E. Quintana *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 ratio by weight. After one hour of heating at 80 °C, the solution was filtered and centrifuged. The powder obtained from achiote seeds was diluted in acetonitrile in a 1
500 ratio by weight. After one hour of heating at 80 °C, the solution was filtered and centrifuged. The powder obtained from achiote seeds was diluted in acetonitrile in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ratio by weight. After thirty minutes of vigorous agitation, the solution was filtered.
100 ratio by weight. After thirty minutes of vigorous agitation, the solution was filtered.





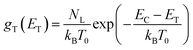
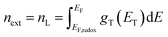
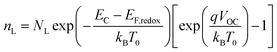


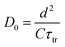


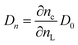

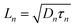 , which is the average distance (normal to the plane of the film) that an injected electron can travel through the film before recombination. If Ln > d, (where d is the thickness of the TiO2 film), only a small fraction of the injected charge will be lost before it is collected, making long diffusion lengths desirable. Fig. 14 compare the parameters of the electron life time and the diffusion coefficient, obtained experimentally, to estimate the diffusion length values of the sensitized cells as a function of the open circuit voltage. On average, the results obtained are 19.4 μm for the Zea mays case, and 13.1 μm for the Bixa orellana case, with the adjustment curve having a positive slope for the first case and a negative slope for the second. These values, compared to the 7.3 μm of thickness that the active layer of the film has on average, are sufficiently greater to achieve the formation of the photocurrent but they are not so far apart that there are still considerable losses, and this can be seen reflected in the efficiencies obtained. However, direct comparisons cannot be made between one colorant and another based on these diffusion length values because they are still close to the thickness of the film, which makes it more difficult to resort to a simplified model of diffusion.33
, which is the average distance (normal to the plane of the film) that an injected electron can travel through the film before recombination. If Ln > d, (where d is the thickness of the TiO2 film), only a small fraction of the injected charge will be lost before it is collected, making long diffusion lengths desirable. Fig. 14 compare the parameters of the electron life time and the diffusion coefficient, obtained experimentally, to estimate the diffusion length values of the sensitized cells as a function of the open circuit voltage. On average, the results obtained are 19.4 μm for the Zea mays case, and 13.1 μm for the Bixa orellana case, with the adjustment curve having a positive slope for the first case and a negative slope for the second. These values, compared to the 7.3 μm of thickness that the active layer of the film has on average, are sufficiently greater to achieve the formation of the photocurrent but they are not so far apart that there are still considerable losses, and this can be seen reflected in the efficiencies obtained. However, direct comparisons cannot be made between one colorant and another based on these diffusion length values because they are still close to the thickness of the film, which makes it more difficult to resort to a simplified model of diffusion.33