Open Access Article
Open Access ArticleProbing the secrets of hydrogen bonding in organic salt phase change materials: the origins of a high enthalpy of fusion†
Samantha L.
Piper
 a,
Craig M.
Forsyth
a,
Craig M.
Forsyth
 a,
Mega
Kar
a,
Mega
Kar
 b,
Douglas R.
MacFarlane
b,
Douglas R.
MacFarlane
 a,
Karolina
Matuszek
a,
Karolina
Matuszek
 *a and
Jennifer M.
Pringle
*a and
Jennifer M.
Pringle
 *b
*b
aSchool of Chemistry, Monash University, Clayton, Victoria 3800, Australia. E-mail: karolina.matuszek@monash.edu
bInstitute for Frontier Materials, Deakin University, Burwood Campus, Burwood, Victoria 3125, Australia. E-mail: jenny.pringle@deakin.edu.au
First published on 12th October 2021
Abstract
The development of new phase change materials that can store large amounts of renewable thermal energy will aid the decarbonisation of the energy sector that is crucial for future generations. For substantial development of these materials, understanding the relationships that underpin the enthalpy of fusion (ΔHf) is critical. In the present work, the role of hydrogen bonding in the energy storage mechanism is elucidated by single-crystal X-ray diffraction and Hirshfeld surface analyses on a range of novel and known protic organic salts based on the guanidinium, acetamidinium, and formamidinium cations. Bonding motifs and strengths are probed through the steric and electronic properties of the anions, specifically with the use of the methanesulfonate ([CH3SO3]−), trifluoromethanesulfonate ([CF3SO3]−), para-toluenesulfonate ([C7H7SO3]−), trifluoroacetate ([CF3COO]−) and chloride (Cl−) anions. We consider entropic contributions to melting thermodynamics, and the results highlight the importance of strong hydrogen bonds in the solid state, finding an increased density of hydrogen bonds can be detrimental to ΔHf if the result is non-geometrically favoured or bifurcated interactions. The results propose a new rationale for the design of these systems through matching the number of hydrogen bond donor and acceptor sites. As well as increasing the linearity and strength of hydrogen bonds, such matching aids in the formation of predictable, energetically favourable supramolecular motifs, that contribute to ΔHfvia the energetic cost of their dislocation upon melting. These insights should inform the design of future high-performance phase change materials that can efficiently store sustainable energy, helping to overcome the intermittency issues typically associated with renewable energy systems.
Introduction
Solar energy has attracted tremendous attention as a renewable energy source in recent years, and deservedly so; the sun provides as much thermal energy in one hour as humankind needs in one year.1 Yet despite the abundance of solar and other sustainable energy sources around us (e.g. wind, hydro, etc.), we are yet to overcome the issue of intermittency. Discrepancies between peak demand and availability of supply, on hourly, daily, and even seasonal timescales, mean that inexpensive and efficient energy storage systems need to be incorporated into the design of renewable systems. In the absence of these integrated systems, we still rely on coal.Thermal energy storage systems are desirable as they are able to directly provide thermal energy in industrial, domestic and agricultural contexts; the requirement for heat energy in these settings constitutes ∼50% of the total global energy demand and is responsible for ∼40% of total global CO2 emissions.2 Thermal storage systems vary in type and complexity, from storing sensible heat in water, to thermochemical heat in reversible thermal decompositions.3 Particularly appealing are latent energy storage systems utilising phase change materials (PCMs), as they are non-complex systems that can store large amounts of energy within a narrow temperature range. Solid to liquid PCMs store and release latent energy in their melting/freezing phase transitions, allowing facile uptake and release of energy. The energy storage capacity of a PCM is dictated by its enthalpy of fusion (ΔHf), which describes the amount of energy required to achieve the solid to liquid phase change.
We postulate two key reasons for the lack of realisation of latent heat storage systems in a renewable energy context. First, conventionally used materials (e.g. inorganic salt hydrates,4 paraffins,5 polymers,6 metals and alloys,7etc.) typically suffer from prohibitive drawbacks (e.g. inappropriate melting temperatures, flammability,8 corrosivity,9 phase separation,10etc.). Secondly, the mechanism of storage at the molecular level (e.g. the balance between inter- and intra-molecular interaction contributions) is poorly understood, and this leads to barriers in designing new materials with high ΔHf that evade these drawbacks.
Critical to the development of new materials for thermal energy storage is an understanding of the structure–property relationships that underpin ΔHf. ΔHf originates from the change in the internal energy of a system during melting, and thus depends chiefly on the change in interaction energies that are affected by the melting process.11 Materials that experience significant disruption to their solid state interactions upon melting will consequently exhibit high ΔHf. This disruption is also reflected in a large entropy of fusion (ΔSf), as the reduced binding energy allows more conformational freedom of molecules.12 Thus, this parameter also gives important information on the entropic consequences of melting and is used here to gain additional insights into the effect of different ion structures on the melting transitions.
The enthalpy (ΔHf) and entropy (ΔSf) of fusion are proportionate at a given temperature of melting, allowing calculation of ΔSf with experimental values of ΔHf from the first law of thermodynamics:
| ΔSf = ΔHf/Tm |
The influence of H-bonds in high ΔHf materials is evident in metal-salt hydrates, the oldest and most extensively studied type of PCM, which have high ΔHf owing to dense H-bond networks between water molecules and the ions.18 Shortcomings of salt-hydrates arise from the fact that their solid to liquid phase change thermodynamics differ to conventional melting; the phase change occurs when the salt is thermally dehydrated and liberated water molecules dissolve the remaining anhydrous (or lower degree hydrate) salt. When the volume of water liberated is insufficient to fully dissolve the salt, differences in densities leads to separation of phases, hindering cyclability.19 Despite this different mechanism of phase-change, the high enthalpies of fusion likely originate from disruption of their dense H-bond networks upon dehydration.18,20 A recent study by McGillicuddy et al.,21 inspired by the metal-salt hydrate model, used metal–organic compounds with extended H-bond networks to investigate the influence of structure and composition on ΔHf and ΔSf. This study found that density and strength of both hydrogen bonds and coordination bonds were the most important contributors to stored thermal energy density.
Ionic liquids (ILs) (and organic salts, which are effectively ionic liquids with above ambient melting points) are gaining increasing attention in the field of thermal energy storage as they have inherent properties (non-volatility, non-flammability, chemical inertness, etc.) that are advantageous for the application of PCMs. Furthermore, they have typically high densities (allowing compact energy storage capacities), and structural tunability of cations and anions theoretically allows tailoring of Tm and ΔHf. Such tunability of Tm has been demonstrated by Terasawa et al.,22 and the viability of systemically altering ΔHf was demonstrated in a study by Zhu et al.15 that increased ΔHf across a family of alkylimidazolium bromide ionic liquids by increasing the alkyl chain length of the substituted imidazolium cation.
Protic organic salts, which are readily formed via a facile synthesis involving a proton transfer reaction between a Brønstead acid and a Brønstead base, are especially appealing as they provide an opportunity to harness the desirable properties of ILs, while having H-bonds as the primary interaction between ions. In doing so, they draw parallels to metal-salt hydrates, with similar fundamental properties (e.g. high density, high thermal conductivity, etc.) due to their ionic nature, but without the propensity to undergo phase-separation. The doubly charge-assisted nature of the H-bonds in these systems achieves strength, resulting in greater charge transfer,23 as well as increasing the electrostatic component of the interaction by bringing the donor and acceptor groups closer together.24 Studies on guanidine/guanidium complexes show that a negative charge on the H-bond acceptor is an especially beneficial component in these systems for enhancing H-bond strength.25 We recently demonstrated the potential of protic organic salts as PCMs, reporting a range of guanidinium26 and pyrazolium27 organic salts with ΔHf values competitive for intermediate temperature (100–220 °C) thermal energy storage (e.g. [gdm][CH3SO3]: ΔHf = 190 J g−1, 29 kJ mol−1, Tm = 208 °C), and attributed the high enthalpies of fusion to extensive hydrogen bonding in the crystal lattice.28 Furthermore, we have shown that these materials are cyclable, with no decrease in ΔHf observed for guanidinium methanesulfonate after 400 heating/cooling cycles.29 Building on this, we were interested in how manipulating the H-bond strengths and motifs between ions could be used to tailor thermal properties of organic salts, probing the role of hydrogen bonding in the elusive relationship between chemical structure and ΔHf.
Herein, we report an extensive study of a range of novel and known small organic salts, utilising three cations with varying levels of hydrogen bonding potential. Specifically, we use the guanidinium (gdm), acetamidinium (aca), and formamidinium (fa) cations (Fig. 1) to synthesise salts with methanesulfonate (mesylate), trifluoromethanesulfonate (triflate), p-toluenesulfonate (p-Tos, tosylate), trifluoroacetate and chloride anions. While most of the guanidinium salts have been studied in the literature previously, including by us,26–29 most of the formamidinium and acetamidinium salts are reported here for the first time (with the exception of the chlorides and acetamidinium tosylate). By replacing one of the –NH2 groups of guanidinium with a –CH3 group (the acetamidinium series), the size, weight, and shape of the cation is effectively retained while removing two hydrogen bond donors and one hydrogen bond acceptor. In the formamidine series, the –NH2 group is replaced with a single proton. The acidity of the proton at this position leads to another kind of hydrogen bond, comparable to those observed in imidazolium-based ionic liquids.30,31 The replacement thus results in a smaller cation that is structurally analogous to guanidinium but with five H-bond donors and two H-bond acceptors. As differences in hydrogen bonding in protic organic salts are reflected in macroscopic properties particularly for salts with a common ion,32 we group salts by their anions, and use single-crystal X-ray crystallography and Hirshfeld surface analyses to probe structure–property relationships and highlight common structural features among the highest ΔHf materials, with a particular focus on H-bonding in the solid state. These insights will help to inform the future design of high-performance PCMs, contributing to the formulation of design rules that allow a rational approach to the development of new, high-performance hydrogen bonding systems for thermal energy storage.
 | ||
| Fig. 1 Structures of the substituted methylene diamine cations investigated: guanidinium [gdm]+, acetamidinium [aca]+, and formamidinium [fa]+. | ||
Results and discussion
The thermal properties of 14 salts with [gdm], [aca] and [fa] cations are detailed in Table 1. This includes enthalpies (ΔHf) and temperatures (Tm) of fusion and enthalpies (ΔHs–s) and temperatures (Ts–s) of any solid–solid transitions. We note that the crystal structures used in this study were collected at −150 °C, and as such take enthalpies of any solid–solid transitions into consideration by calculating the total enthalpy of the solid to liquid phase transition, ΔHtotal, for comparison with crystal structures. Although enthalpies of fusion are often reported on a mass or volume basis, which is especially relevant for energy storage applications, the fundamental nature of this study means that comparing energies on a kJ mol−1 basis allows us to better understand the effects of the different hydrogen bond geometries and motifs at the molecular level, without density considerations. Furthermore, it is noted that while the strengths of hydrogen bonds in the solid state cannot be directly measured, the correlation between bond length and linearity with strength is well-documented, with shorter and more linear H-bonds typically being the strongest.33,34 Thus, as our best guide in this study, we use these parameters to infer hydrogen bond strengths. Details of solid–solid transitions are discussed as the compounds are evaluated. Due to the ambiguity surrounding solid–solid transitions and their tendency to not be reproducible, particularly at a consistent temperature, only solid–solid transitions that are reproducibly observed are discussed.| Anion | Cation | T m (°C) ± 2 °C | T s–s (°C) ± 2 °C | ΔHf (kJ mol−1) ± 5% | ΔHs–s (kJ mol−1) ± 5% | ΔHtotal (kJ mol−1) | ΔStotal (J mol−1 K−1) |
|---|---|---|---|---|---|---|---|
| [CH3SO3] | [gdm]26 | 208 | — | 29 | — | 29 | 60 |
| [fa] | 94 | — | 21 | — | 21 | 57 | |
| [aca] | 97 | — | 15.4 | — | 15.4 | 42 | |
| [CF3SO3] | [gdm]26 | 160 | 115 | 27 | 1 | 28 | 65 |
| [fa] | 103 | −3 | 5.8 | 7.0 | 12.8 | 41 | |
| [aca] | 96 | — | 15.0 | — | 15.0 | 41 | |
| [p-Tos] | [gdm]26 | 227 | 175 | 21 | 1 | 22 | 44 |
| [fa] | 118 | — | 17.7 | — | 17.7 | 45 | |
| [aca] | 186 | 129 | 21 | 1.0 | 22 | 49 | |
| [CF3COO] | [gdm] | 154 | 64 | 14.4 | 3.2 | 17.6 | 43 |
| [fa] | 111 | 43, 67, 77, 90 | 12.8 | 1.0, 0.5, 0.7, 1.5 | 16.5 | 44 | |
| [aca] | 149 | — | 21 | — | 21 | 50 | |
| Cl | [fa] | 93 | 56, 75 | 3.4 | 1.8, 1.8 | 7.1 | 20 |
| [aca] | 171 | — | 15.7 | — | 15.7 | 35 |
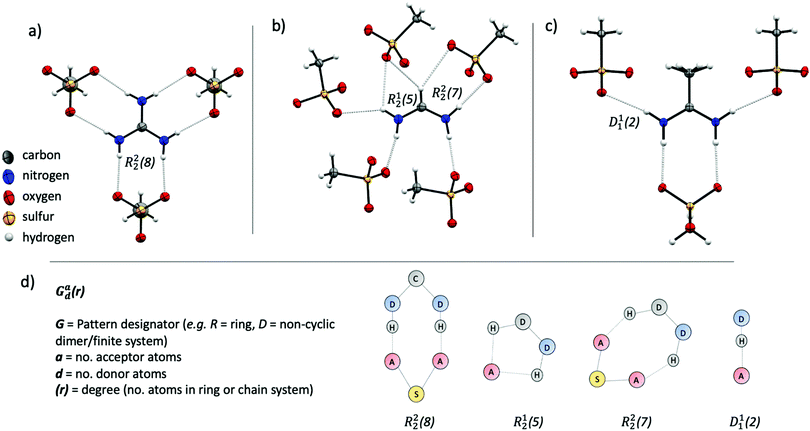
The methanesulfonate series follow a trend of increasing enthalpy of fusion with increased hydrogen bonding ability of the cation ([gdm][CH3SO3] ΔHf = 29 kJ mol−1, [fa][CH3SO3] ΔHf = 21 kJ mol−1, [aca][CH3SO3] ΔHf = 15.4 kJ mol−1). [gdm][CH3SO3] crystallises in the I2/m space group, with a mirror plane through the centre of the ion pair to give three unique and six overall hydrogen bonds per cation (av. d(D⋯A) 2.92 Å, ∠(D–H⋯A) 169°) (Fig. 2a). These hydrogen bonds exist as bidentate R22(8) motifs (by graph set notation,35 conventionally used to describe H-bond arrays in organic crystals). This 8-membered cyclic motif, which describes a ring of eight atoms including two H-bond donors and two H-bond acceptors, is prolific in systems containing –NH2 donor and –SO3 acceptor groups, being reported to have a 55% chance of occurring in systems with these donor and acceptor groups.36 This persistence suggests that it is an energetically favourable conformation that is presumably energetically costly to disrupt upon melting, facilitating the observed high enthalpy of fusion and high melting point. The predictability of the supramolecular interactions in [gdm][CH3SO3] is aided by a matching of hydrogen bond donors (HBD) of the guanidinium cation to hydrogen bond acceptors (HBA) of the methanesulfonate anion. In contrast, [fa][CH3SO3] has a deficit of donors, resulting in the formation of some bifurcated H-bonds. [fa][CH3SO3] crystallises in the Pca21 space group, with no centre of symmetry through the ion pair and consequently all seven H-bonds are crystallographically unique. Of the seven H-bonds, three are canonical (av. d(D⋯A) 2.89 Å, ∠(D–H⋯A) 173°) and four come from bifurcated donors (a single H interacting with two oxygens) (av. d(D⋯A) 3.15 Å, ∠(D–H⋯A) 139°) (Fig. 2b). Bifurcated H-bonds, which are common in systems with a surplus of H-bond donors, are comparatively weaker than non-bifurcated,37 likely accounting for the lower ΔHf of [fa][CH3SO3] compared to [gdm][CH3SO3], despite the increased total number of H-bonds in the structure.
[aca][CH3SO3] crystallises in the Cmc21 space group with a mirror plane through the centre of the ion pair, resulting in two unique H-bonds. An R22(8) motif is formed between the two central protons of the [aca]+ cation (one from each –NH2) with two oxygen atoms from one methanesulfonate anion (d(D⋯A) 2.95 Å, ∠(D–H⋯A) 170°) (Fig. 2c). The two outer protons form D11(2) linkages with one oxygen atom of the methanesulfonate anion (d(D⋯A) 3.02 Å, ∠(D–H⋯A) 169°). There is a third potential interaction from these protons with a second oxygen atom of the methanesulfonate anion (d(N⋯O) 3.44 Å, ∠(N–H⋯O) 126°), which almost appears to be an asymmetric bifurcation of these outer protons. We note that the general consensus amid the literature is that a precise description of hydrogen bonding is elusive, with strict definitions and criteria often doing an injustice to the complexity and variability of the phenomena.23,33 As such, we do not have a distinct cut-off distance beyond which we disregard the potential for H⋯O interactions to be considered hydrogen bonds, and a level of discretion is sometimes required, particularly when considering bifurcated interactions, in determining the importance of interactions relative to others in the structure. In this case, the pronounced asymmetry and obvious dominance of the first H⋯O interaction suggests that the proximity of the second oxygen atom to the donor proton likely arises from geometric convenience and is primarily electrostatic in nature,38 discounting us from crediting it as a hydrogen bonding interaction. Nonetheless, as well as these fewer interactions in [aca][CH3SO3] likely facilitating its lesser heat of fusion, the methyl group of the cation is also disordered in the structure, indicating rotational freedom in the solid state that likely contributes to the lower ΔSf of [aca][CH3SO3] (42 J mol−1 K−1).13
Hirshfeld surface analysis can provide additional insight into crystal packing by highlighting and quantifying interactions between adjacent molecules. The Hirshfeld surface, described by Spackman and co-workers and calculable via CrystalExplorer,39,40 is derived from the region of space surrounding a molecule in a crystal where the contribution of electron density from the molecule exceeds that from all neighbouring molecules in the crystal. Hence, at the surface, the electron density contribution from the molecule is equal to that from the rest of the crystal. This is an extremely valuable tool for examining supramolecular interactions in crystals, especially when quantifying subtle similarities and differences between structures. The Hirshfeld surface is colour coded to show the distance of nuclei from the surface, both internal and external, with larger distances shown to the blue end of the colour scale and shorter distances nearer to the red end. These interactions can be mapped onto a fingerprint plot, which is a two-dimensional histogram with axes representing the distance of nuclei internal (di) and external (de) to the surface, allowing for rapid comparison of structures. Hirshfeld surfaces and corresponding fingerprint plots of [gdm][CH3SO3], [fa][CH3SO3] and [aca][CH3SO3] are shown in Fig. 3. The dominance of short H-bonding interactions in [gdm][CH3SO3] is seen in the two sharp spikes in the bottom left quarter of the fingerprint plot (Fig. 3d), as we have previously reported.28 These peaks are less pronounced in [fa][CH3SO3] (Fig. 3e) and also less in [aca][CH3SO3] (Fig. 3f). The two longer H⋯O interactions between the outer protons of the acetamidinium cation and an oxygen atom of the methanesulfonate anion in [aca][CH3SO3] are observed as the two smaller spikes nearer to the centre of the plot.
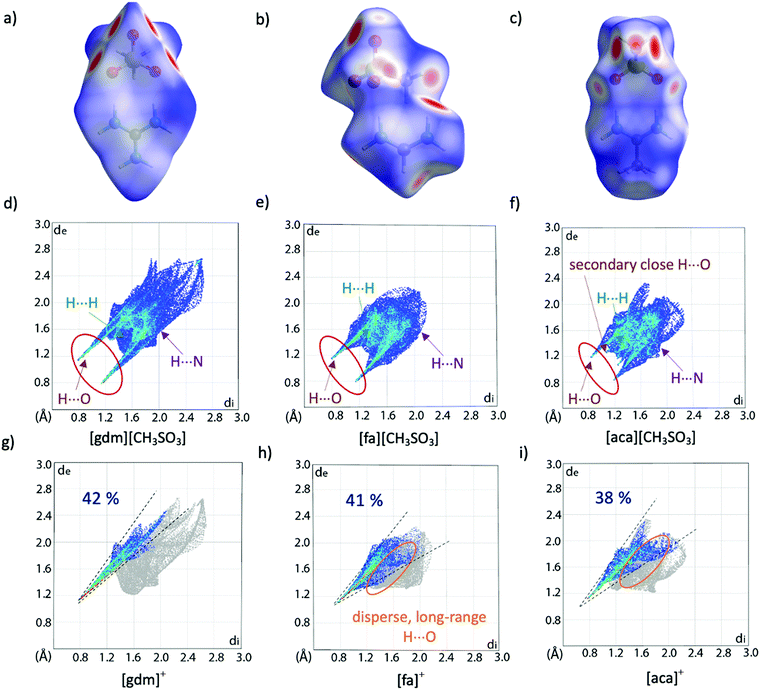 | ||
| Fig. 3 Hirshfeld surfaces (a)–(c) and corresponding fingerprint plots (d)–(f) of [gdm][CH3SO3], [fa][CH3SO3] and [aca][CH3SO3]. Fingerprint plots mapping the Hirshfeld surfaces of the cations are shown in (g)–(i), with only interactions between an internal hydrogen atom and external oxygen atom shown in colour. The percentage of these O⋯H interactions contributing to the overall surface interactions are shown as percentages on the plots. Other interaction types are annotated with arrows, with only interactions that make up >2% of the surface shown. A breakdown of non-O⋯H interactions can be found in Table S20 (ESI†). | ||
Probing the influence of anion electronics on H-bonding motifs: triflate, [CF3SO3]−
In light of the relationship emerging here between ΔHf and H-bond density and strength (inferred from length and linearity), we were interested in the possibility of using this feature to exercise control over ΔHf. By retaining the fundamental structure of the anion but replacing the methyl group with a trifluoromethyl group (the triflate anion), we were interested to see if the bonding motifs would persist with elongation of the bonds due to the inductive electron withdrawing effect of the fluorine atoms. From first principles, such a withdrawing effect should limit the hydrogen bond acceptor ability of the trifluoromethanesulfonate anion by limiting the Lewis basicity of the oxygen atoms.Crystallographic analysis of the triflate salts show that the R22(8) motif persists in [gdm][CF3SO3] and [aca][CF3SO3], with slight elongation in both compared to the mesylate structures ([gdm][CF3SO3] av. d(D⋯A) 2.99 Å, [aca][CF3SO3] av. d(D⋯A) 2.92 Å) (Fig. S1a and S1c, ESI†). Interestingly, the asymmetry of the two H⋯O interactions of the outer protons in [aca][CF3SO3] becomes more pronounced, with the long-range interaction at an increased length of 3.54 Å, and the dominant H-bonding interaction now shorter and more linear than in the methanesulfonate analogue (av. d(D⋯A) 2.91 Å, ∠(D–H⋯A) 171°). This is likely a secondary effect of the reduced basicity of the oxygen atoms of the anion, as the longer H⋯O interaction is weakened further, resulting in a strengthening of the primary interaction. The decrease in relative significance of these longer H⋯O interactions is seen in the fingerprint plot of [aca][CF3SO3] (Fig. S17f, ESI†), which does not have a second set of spikes attributed to these longer interactions, as was observed in the fingerprint plot of [aca][CH3SO3].
Bonding in [fa][CF3SO3] is the most affected of the three triflate salts by the change of anion, with the cation now not participating in any bifurcated interactions, but one bond from each donor, yielding five H-bonds with an average length of 2.99 Å and angle of 167° (Fig. S1b, ESI†). The extent of changes in H-bonding across the series is reflected in the total ΔH of the compounds. H-bonding in [gdm][CF3SO3] and the accompanying fingerprint plot of the ion pair (Fig. S1a and S17d, ESI†) most resembles its methanesulfonate analogue, and perhaps unsurprisingly [gdm][CF3SO3] retains a high ΔHf, decreasing by only 2 kJ mol−1 (ΔHtotal decreases by only 1 kJ mol−1, with a solid–solid transition of 1 kJ mol−1 observed prior to melting at 115 °C). Conversely, the substantial decrease in hydrogen bonding interactions in [fa][CF3SO3] (reflected in the fingerprint plot, Fig. S17e, ESI†) accompanies the greatest decrease in ΔHtotal when compared to its methanesulfonate analogue (8.2 kJ mol−1). ΔHtotal decreases the least for [aca][CF3SO3] compared to its methanesulfonate analogue (0.4 kJ mol−1). The ΔSf of [aca][CF3SO3] and [aca][CH3SO3] are both low, at 41 J mol−1 K−1 and 42 J mol−1 K−1 respectively. We note that both of these ΔStotal values are substantially less than the 50–60 J mol−1 K−1 typical increase in entropy for non-spherical molecules upon melting,12 indicating that both [aca][CF3SO3] and [aca][CH3SO3] undergo low temperature solid–solid transitions that are not observed in the temperature range of the DSC, and that these lower temperature transitions lower the ΔS of the melting transitions.
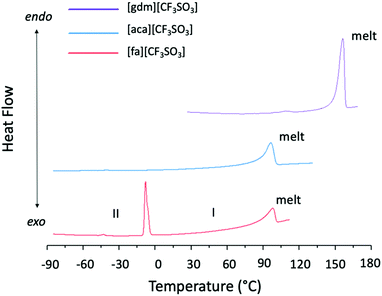
Solid–solid transitions are observed prior to melting in both [gdm][CF3SO3] and [fa][CF3SO3] (Table 1 and Fig. 4). While the solid–solid transition in [gdm][CF3SO3] is energetically small (1 kJ mol−1), the solid–solid transition of [fa][CF3SO3] from Phase II to Phase I‡ at −3 °C (phase numbering shown in Fig. 4) is energetically less than its melting enthalpy at 103 °C (5.8 kJ mol−1), and has a greater entropic change than that of the melting transition (26 J mol−1 K−1 and 15 J mol−1 K−1 respectively). Interestingly, the thermal behaviour of [fa][CF3SO3] varies among different runs of the material on the DSC, for both the same and different samples, with the enthalpy of the solid–solid transition ranging between 6 kJ mol−1 and 8 kJ mol−1, and the melting transition observed with an enthalpy between 3 kJ mol−1 and 8 kJ mol−1. We note that the ΔS of melting is below the 20 J mol−1 K−1 required by Timmerman's criterion for plastic crystal behaviour in molecular materials.41
Due to the poor quality of the crystallographic data collected at > 0 °C for this material, which is typical for plastic crystals in Phase I (the most disordered phase), as yet we have been unable to fully refine a model of Phase I to determine the structural change that occurs between the two solid phases of [fa][CF3SO3]. However, solid–solid phase transitions in plastic crystals often represent the onset of rotational motion of certain parts of the crystal upon slight expansion of the lattice.42 This is a likely explanation here as a comparison of the unit cell data of Phase II and Phase I suggests that there is no substantial structural change between the two phases, with the unit cell dimensions remaining relatively consistent (slight expansion is expected due to increased thermal motion at higher temperatures) (Table S5, ESI†). The slight increase in volume may generate more space for the ion pairs, potentially facilitating the ability of ions to engage in rotation or other movement.
It is noted that solid–solid transitions are typically undesirable in solid–liquid PCMs as some of the total enthalpy of melt is consumed at a lower temperature than the storing range, and, furthermore, that crystals with “plastic” characteristics have fundamentally different thermal properties to those we are intending to study. As such, while interesting, we omit materials with ΔSf < 35 J mol−1 K−1 from later analyses that involve the grouping of data to identify broader trends in bonding and ΔSf/ΔHf (specifically Fig. 7c and d).
Probing the influence of steric factors on H-bonding and competing alkyl interactions on ΔHf: [p-Tos]−
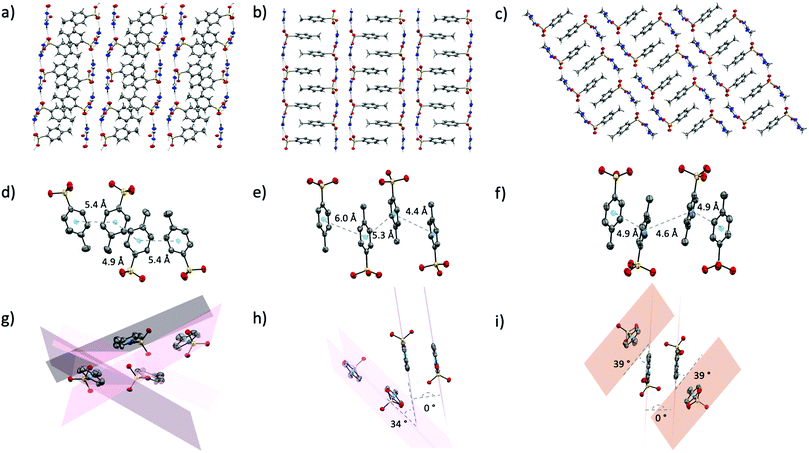
p-Toluenesulfonic acid has a pKa of −2.8, slightly lower than methanesulfonic acid (−1.9) but still significantly higher than triflic acid (−15). As such, the hydrogen bond acceptor ability of the p-toluenesulfonate (tosylate, p-Tos) anion (based on proton affinity of oxygen atoms38) should sit just below that of the methanesulfonate anion. It is surprising, then, that the crystal structures of the tosylate salts are more similar to the triflate salts than the methanesulfonate salts. The tosylate salts all form the same H-bond motifs as the triflate salts (Fig. S2, ESI†), and all also form extended networks of two-dimensional sheets where hydrophobic and hydrophilic moieties from neighbouring sheets pack together (Fig. 5a–c). The thermal properties are also somewhat semblant of the triflate series, with solid–solid transitions observed prior to melting in both [gdm][p-Tos] and [aca][p-Tos] (Table 1). Nonetheless, in contrast to the triflate series and attesting to the complexities of the latent heat of fusion, a vastly different trend in ΔH is observed, with [aca][p-Tos] and [gdm][p-Tos] both having the equal highest total solid–liquid enthalpies among the series (22 kJ mol−1). Both of these salts display solid–solid transitions of 1 kJ mol−1 prior to their melting transitions, which are again of equal energy (21 kJ mol−1, Table 1). [fa][p-Tos] has a lower total enthalpy of solid–liquid phase-transition, melting with an ΔHf of 17.7 kJ mol−1 at 118 °C and no solid–solid transitions observed prior. When comparing these enthalpies to those observed in the triflate analogues, an increase is observed for [aca][p-Tos] and [fa][p-Tos], while a decrease is seen for [gdm][p-Tos].This new trend in ΔHf can be explained by analysis of the interactions between toluene moieties in the extended structures, alongside the changes to hydrogen bonding lengths and geometries. While the six H-bonds in [gdm][p-Tos] are 0.6 Å shorter than their equivalents in [gdm][CF3SO3], they are 7° less linear (av. d(D⋯A) 2.93 Å, ∠(D–H⋯A) 166°). In the crystal structure of [gdm][p-Tos], packing of the toluene moieties does not occur in the form of π–π stacking, as the planes of neighbouring toluene rings are non-parallel (the shortest centroid–centroid distance between toluene rings is 4.8 Å, with an angle between ring planes of 52°) (Fig. 5g). Interactions between neighbouring toluene moieties in this case appear to be of van der Waals nature. Conversely, both van der Waals and π–π stacking interactions are observed between toluene moieties in the structures of [fa][p-Tos] and [aca][p-Tos] (Fig. 5h and i). These stacking interactions resemble prototypical assembly in toluene structures, stacking off-centred and parallel, with apparent π–π interactions between the offset rings, and methyl groups of adjacent molecules appearing have σ–π interactions with π-clouds of neighbouring rings (Fig. 4e, f, h and i).43 In the crystal structures, each toluene moiety has one π–π stacking interaction with a toluene moiety from an adjacent sheet, with other surrounding toluenes appearing to interact in a van der Waals nature. The average length of the H-bonds in these structures are both reduced compared to their triflate analogues, with a reduction of 0.8 Å for [aca][p-Tos] and 0.5 Å for [fa][p-Tos]. The shortening of H-bonds in [aca][p-Tos] comes with a decrease in angle of 9°, while [fa][p-Tos] displays an increase in average bond angle by 2°. It is postulated that the additional, directional π–π and σ–π interactions, which are stabilised by both electrostatic and dispersive interactions,44 likely explain the increased enthalpy of fusion observed for [fa][p-Tos] and [aca][p-Tos] when compared to their triflate analogues. The shortening of length and increased angle of the H-bonds in [fa][p-Tos] likely explains the absence of the large solid–solid transition that was observed in [fa][CF3SO3], as well as contributing to the increased ΔHtotal for [fa][p-Tos]. It is noted, as well, that toluene moieties do not have the same propensity for rotational disorder that is often observed for CF3 groups, and that π–π interactions between rings likely “hold” the rings in place to limit such a motion in the solid state.
Analysis of the Hirshfeld surfaces and corresponding fingerprint plots support this explanation of the new trend in ΔH. The plots (Fig. 6d–f) are all similarly shaped and have similar frequencies of interactions (as indicated by the colours of the pixels on the histogram). The central, thicker spike in the plots is unique to the tosylate series and corresponds to H⋯H interactions between the toluene moieties. Comparing these plots to those of the triflate analogues, it is evident that the density of strong H-bonds decreases for [gdm][p-Tos] compared to [gdm][CF3SO3], while remaining relatively consistent for [aca][p-Tos] and [fa][p-Tos] compared to [aca][CF3SO3] and [fa][CF3SO3]. As such, the additional interactions between toluene moieties of neighbouring sheets adds to the enthalpy of fusion of [aca][p-Tos] and [fa][p-Tos], while the new alkyl interactions in [gdm][p-Tos] are insufficient to compensate for the loss of H-bond density in the structure.
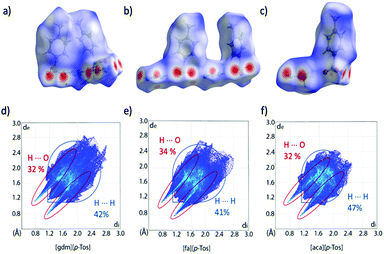 | ||
| Fig. 6 Hirshfeld surfaces and corresponding fingerprint plots of [gdm][p-Tos] (a) and (d), [fa][p-Tos] (b) and (e) and [aca][p-Tos] (c) and (f). The Hirshfeld surface exists around two ion pairs for [gdm][p-Tos] and [fa][p-Tos] as the crystal structures contain two ion pairs in the asymmetric unit (ASU). Percentages of H⋯O and H⋯H reciprocal contacts are shown on the plots alongside a guideline of where these interactions are found on the fingerprint plot. A more detailed breakdown can be found in Table S22 (ESI†). | ||
Probing the importance of H-bond strength over H-bond density: trifluoroacetate, [CF3COO]−
Alkyl interactions between neighbouring toluene moieties in the tosylate series demonstrably influence ΔHf, highlighting the potential for competing interactions to have considerable effects on ΔHf, even when H-bonding appears to be the dominant interaction. While interesting, additional non-hydrogen bonding interactions limit our capacity to observe the direct effects of H-bonds on ΔHf. In the mesylate and triflate series, an emerging trend suggests that fewer but stronger H-bonds can be more important than increased H-bond density for materials with high ΔHf. To test this, we next chose the trifluoroacetate anion for study, as it has a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 HBD
1 HBD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBA ratio with the acetamidinium cation.§
HBA ratio with the acetamidinium cation.§
In line with our prior observations, the matching of HBA to HBD of the trifluoroacetate anion and acetamidinium cation results in [aca][CF3COO] having the highest ΔHf among the trifluoroacetate series (21 kJ mol−1), despite participating in the least number of H-bonds. [aca][CF3COO] has four non-bifurcated H-bonds per cation that, over the four ion pairs of the ASU, average to be the shortest and most linear of the trifluoroacetate series (av. d(D⋯A) 2.86 Å, ∠(D–H⋯A) 168°) (Fig. S3c, ESI†). The dominance of these strong H-bonds as the primary interaction in the crystal is observed in the sharpness of the spikes in the fingerprint plot (Fig. S18f, ESI†). [fa][CF3COO] and [gdm][CF3COO] both have six hydrogen bonds per cation (2 of which are bifurcated in [fa][CF3COO]). These H-bonds have more geometric strain, with average angles of 154° in [gdm][CF3COO] and 156° in [fa][CF3COO]. Acceptor bifurcation is present in both structures, with each trifluoroacetate oxygen atom of [gdm][CF3COO] accepting three bonds, and one accepting four and the other accepting two in [fa][CF3COO] (Fig. S4, ESI†). The prevalence of weaker H-bonds in [gdm][CF3COO] and [fa][CF3COO] compared to the strong H-bonds of [aca][CF3COO] is confirmed by the fingerprint plots of their Hirshfeld surfaces, with sharp spikes (corresponding to H-bonding interactions) on the plot of [aca][CF3COO] (Fig. S18f, ESI†), less defined spikes on the plot of [fa][CF3COO] (Fig. S18e, ESI†) and even less definition in the spikes on the plot of [gdm][CF3COO] (Fig. S18d, ESI†).
Interestingly, solid–solid transitions are observed prior to melting in both [gdm][CF3COO] and [fa][CF3COO]. One solid–solid transition with an energy 3.2 kJ mol−1 is seen in [gdm][CF3COO] (64 °C), while four lower energy solid–solid transitions are observed in the DSC trace of [fa][CF3COO]. Reviewing all of the salts studied so far, it can be seen that solid–solid transitions appear to be more prevalent in materials with H-bond bifurcation. This may be explained by the weaker bifurcated interactions requiring less energy to slightly expand and liberate minor motional freedoms (e.g. rotations), although without a more thorough analysis (and confirmation of trend over a greater sample size) we note that such a conclusion is speculative in specific reference to bifurcation. Furthermore, immediately challenging this hypothesis, the crystal structure of [aca][CF3COO] refines with a disordered –CF3 group, indicating there may be a solid–solid transition below the temperature of crystal data collection (−150 °C). It is noted, however, that due to the large ASU of [aca][CF3COO], only ¼ of all CF3 groups in the structure are disordered. As a result, this disorder appears to have a limited effect on the ΔSf of [aca][CF3COO], which is the highest of the three trifluoroacetate salts (50 J mol−1 K−1).
The entropies of fusion of the trifluoroacetate salts can be rationalised with respect to the nature of the H-bonds present in the structures. As mentioned above, the stronger H-bonds in [aca][CF3COO] are likely to restrict motion more than those in [gdm][CF3COO] and [fa][CF3COO] (ΔSf = 34 J mol−1 K−1 and 33 J mol−1 K−1 respectively, ΔStotal = 43 J mol−1 K−1 and 44 J mol−1 K−1). Weaker H-bonds allow for more soft vibrations in the crystal structure and hence less vibrational motion is introduced by the melting process.13
The hypothesis that weaker H-bonds correlate with lower ΔSf is supported by analysis of the chloride salts. While [gdm]Cl decomposes upon melting and is consequently omitted from the comparison, the ΔSf of [fa]Cl and [aca]Cl are low, with total solid–liquid entropies of 35 J mol−1 K−1 for [aca]Cl and just 20 J mol−1 K−1 for [fa]Cl. Both cations participate in four H-bonds with chloride anions, with average H-bond distances of 3.21 Å for [aca]Cl and 3.23 Å for [fa]Cl (Fig. S5, ESI†). The H-bonds of [aca]Cl are more linear than those of [fa]Cl, with average bond angles of 165° and 160° for the salts respectively. These distances and angles suggest that the hydrogen bonds are weak, which is expected; while the chloride anion is a good hydrogen bond acceptor when acting as a single donor (of electrons), it can be expected that the acceptor ability of the anion decreases with increasing number of hydrogen bonds.21 It is noted that [fa]Cl has a fifth potential H-bond interaction from the proton of the central carbon, however it is long (3.43 Å) and non-linear (124°), and given that the acceptor Cl− anion is already participating in four H-bonding interactions, it is unlikely that this interaction is comparatively significant. Interestingly, [fa]Cl has two solid–solid transitions just prior to melting, one at 56 °C and one at 75 °C, both with ΔHs–s of 1.8 kJ mol−1. The orientation of the cations mean that [aca]Cl packs in an extended three-dimensional network while [fa]Cl packs in two-dimensional sheets (Fig. S15 and S16, ESI†). It is postulated that this third dimension of order in the structure of [aca]Cl increases its rigidity, limiting vibrational motion and resulting in a ΔS of solid–liquid phase transition almost double that of [fa]Cl. While it is challenging to see the effects of packing on the thermal properties of the salts in this study, as most of the other salt families with a common anion pack with the same dimensionality (Fig. S6–S14, ESI†), it is possible that as there are a range of factors that contribute to ΔHf (number of hydrogen bonds, as well as their lengths and angles), when these other factors are similar, packing can become the most significant contributor.
Trends in ΔHf and ΔSf across all series of anions
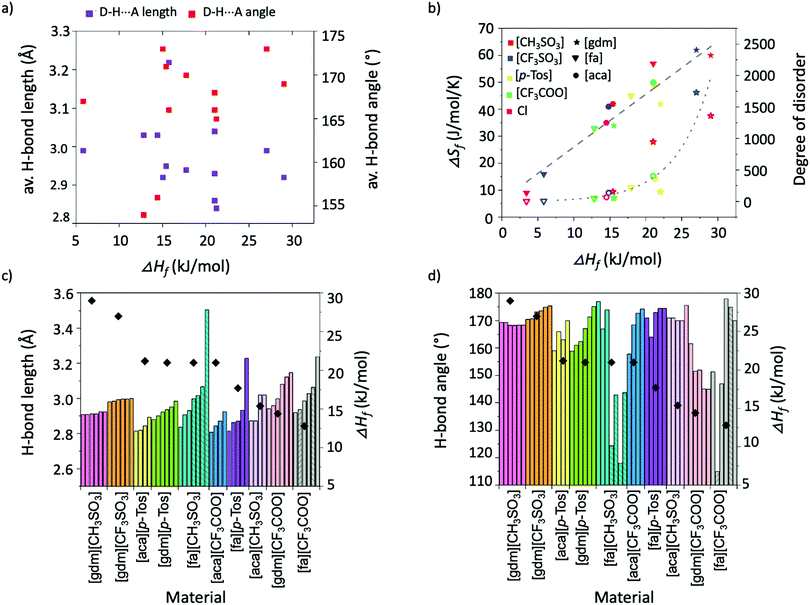
Individual analysis of the salt systems investigated in this study has demonstrated the complexities of the factors that influence ΔHf. For example, while the results support the hypothesis that short, linear H-bonds are favourable interactions for achieving high ΔHf materials, a plot of average H-bond lengths and angles in materials against their ΔHf shows no correlation between angles and ΔHf, and at best only a rough correlation between lengths and ΔHf (Fig. 7a). The favourability of shorter, linear interactions is better seen in Fig. 7c and d, which plot the length and angle of all individual H-bonds alongside the ΔHf of each material. The information about H-bonds given in these graphs is adequate to rationalise trends in ΔHf across the materials. For example, Fig. 7d shows [gdm][CH3SO3] has a higher ΔHf than [gdm][CF3SO3], despite [gdm][CF3SO3] having more linear H-bonds. Fig. 7c, however, shows the increased lengths of the H-bonds in [gdm][CF3SO3], which account for its slightly lower ΔHf.The relationship between ΔSf and ΔHf in the salt systems investigated in this study is plotted in Fig. 7b (solid shapes). The roughly linear correlation (R2 = 0.91) indicates that the compounds approximately adhere to the model of entropy–enthalpy compensation.45 The model postulates that for similar processes in similar systems, a graph plotting ΔSf and ΔHf will show a roughly linear correlation. In the context of melting, an explanation for this trend is that materials with a high ΔHf typically have tighter association of molecules in the solid state. This tighter association reduces the entropy of a system by restricting molecular motion and thus the ability for molecules to be multi-conformational and “disordered”.12 Upon melting, the degree of disorder introduced to these tightly-bound systems is thus correspondingly larger than in those with conformational freedom in the solid state. This disorder can be better conceptualised by estimating the degree of disorder introduced to the system upon melting, found by rearrangement of the Boltzmann equation (ΔSf = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (N)) to get N = eΔSf/R, where R is the ideal gas constant, and the introduced disorder, N, describes the ratio of the number of possible arrangements/conformations per molecule in the liquid state over the number of possible arrangements/conformations per molecule in the solid-state.46 For the salt systems studied here, the values of introduced disorder (N), and thus a representation of the extent to which the materials gain conformational freedom upon melting, are plotted in Fig. 7b (hollow shapes). Unsurprisingly, the chloride salts, which have the least possibility of being multi-conformational, hold two of the four lowest values of introduced disorder. Such insights into liquid state structures through relationships between ΔSf and ΔHf are extremely valuable, as an increased understanding of the liquid state is paramount to probing the origins of the thermal properties of PCMs, which will allow a better-informed design approach.
(N)) to get N = eΔSf/R, where R is the ideal gas constant, and the introduced disorder, N, describes the ratio of the number of possible arrangements/conformations per molecule in the liquid state over the number of possible arrangements/conformations per molecule in the solid-state.46 For the salt systems studied here, the values of introduced disorder (N), and thus a representation of the extent to which the materials gain conformational freedom upon melting, are plotted in Fig. 7b (hollow shapes). Unsurprisingly, the chloride salts, which have the least possibility of being multi-conformational, hold two of the four lowest values of introduced disorder. Such insights into liquid state structures through relationships between ΔSf and ΔHf are extremely valuable, as an increased understanding of the liquid state is paramount to probing the origins of the thermal properties of PCMs, which will allow a better-informed design approach.
Further insight into the liquid phase of these materials could, in the future, be gained from analysis such as neutron diffraction experiments. This technique has previously been used to investigate the liquid phase of protic ionic liquid materials, showing that they form bicontinuous sponge-like nanostructures, where the nature of the hydrogen bonding in the systems varies, and the variations are reflected in the macroscopic properties of the materials.31 These experiments have shown that ion arrangements in these liquid systems depends on both the physical dimensions of ions and the intermolecular forces between them, and that ILs with high proportions of linear H-bonds yield more solid-like properties. This is presumably reflected in a lower entropy of fusion for those systems.
One strategy to achieving high ΔHf in organic ionic materials thus lies in the presence of strong, directional H-bonds in the solid state that are significantly disrupted in the liquid state. Understanding how these key interactions and their energies change between the solid and liquid state is paramount to understanding how these interactions can be used to design new materials with high ΔHf. As such, future work will involve simulating the liquid state interactions to enhance our understanding of the structural features that underpin this property. Furthermore, a yet deeper understanding of the solid state interactions presented here could be gained from computational modelling of the solid state, providing energetic information to complement the geometric information obtained in this crystallographic study. For example, quantum mechanical calculations could be used to investigate the sensitivity of the hydrogen bonds to angular deformations or bifurcation.47 This would encourage a deeper understanding the thermodynamic consequences of these parameters, again providing valuable information that can be used as a tool in the design of new PCM materials. We expect to be able to report the results from such studies in future publications.
Conclusions
An increased understanding of the structure–property relationships that underpin ΔHf is critical to the design of new materials with high energy storage densities that can be implemented in renewable thermal energy storage systems. The results presented here demonstrate the importance of strong hydrogen bonds in materials with high ΔHf, showing that increasing the number of hydrogen bonds in a system can be detrimental to ΔHf if the result is their cumulative weakening, for example by inducing bifurcation. The formation of predictable supramolecular motifs provides scope to approach rationally the design phase, with energetically favourable motifs appearing to increase ΔHf. The formation of such motifs can allow prediction of linearity of H-bonds; for example, the R22(8) motif is geometrically suited to yield linear H-bonds, whereas R21(4) motifs yield bifurcated (and consequently non-linear) H-bonds. Specifically in protic organic salts but presumably also in neutral materials where hydrogen bonding is the main interaction, the predictability of supramolecular motifs is aided by matching the number of H-bond donor and acceptor sites. This has been shown to limit bifurcation and result in solid state structures with shorter and more linear H-bonds, leading to materials with high ΔHf.It is noted that substantial disorder may exist in crystals and that liquids typically have a high range of order, and that these together hinder our ability to reliably predict phase-change enthalpies. Deeper understanding of the liquid state structure/interactions in particular is needed to enable the realisation of materials with desirable thermal properties.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge funding from the Australian Research Council through its Linkage Project scheme (LP190100522) and collaborating organisation Energy Storage Pty Ltd.Notes and references
- L. Dong, Y. Feng, L. Wang and W. Feng, Chem. Soc. Rev., 2018, 47, 7339–7368 RSC.
- International Energy Agency (IEA), Renewables 2019, Paris.
- C. Prieto, P. Cooper, A. I. Fernández and L. F. Cabeza, Renewable Sustainable Energy Rev., 2016, 60, 909–929 CrossRef CAS.
- S. Höhlein, A. König-Haagen and D. Brüggemann, Materials, 2017, 10, 444 CrossRef PubMed.
- R. S. Abdulrahman, F. A. Ibrahim and S. F. Dakhil, Appl. Therm. Eng., 2019, 150, 193–199 CrossRef CAS.
- H. Weingrill, K. Resch-Fauster, T. Lucyshyn and C. Zauner, Polym. Test., 2019, 76, 433–442 CrossRef CAS.
- R. Fukahori, T. Nomura, C. Zhu, N. Sheng, N. Okinaka and T. Akiyama, Appl. Energy, 2016, 170, 324–328 CrossRef CAS.
- I. Sarbu and C. Sebarchievici, Sustainability, 2018, 10, 191 CrossRef.
- E. Emmons and P. J. Shamberger, Mater. Corros., 2019, 70, 877–887 CrossRef CAS.
- N. Kumar, J. Hirschey, T. J. LaClair, K. R. Gluesenkamp and S. Graham, J. Energy Storage, 2019, 24, 100794 CrossRef.
- H. Mehling, Sol. Energy, 2013, 88, 71–79 CrossRef CAS.
- A. S. Gilbert, Thermochim. Acta, 1999, 339, 131–142 CrossRef CAS.
- M. S. Searle and D. H. Williams, J. Am. Chem. Soc., 1992, 114, 10690–10697 CrossRef CAS.
- B. D. Rabideau, K. N. West and J. H. Davis, Chem. Commun., 2018, 54, 5019–5031 RSC.
- J. Zhu, L. Bai, B. Chen and W. Fei, Chem. Eng. J., 2009, 147, 58–62 CrossRef CAS.
- L. Bai, J. Zhu and B. Chen, Fluid Phase Equilib., 2011, 312, 7–13 CrossRef CAS.
- T. Inagaki and T. Ishida, J. Phys. Chem. C, 2016, 120, 7903–7915 CrossRef CAS.
- J. S. Ricci, R. C. Stevens, R. K. McMullan and W. T. Klooster, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 381–386 CrossRef CAS PubMed.
- P. A. J. Donkers, L. Pel and O. C. G. Adan, J. Energy Storage, 2016, 5, 25–32 CrossRef.
- H. A. Levy and G. C. Lisensky, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 3502–3510 CrossRef.
- R. D. McGillicuddy, S. Thapa, M. B. Wenny, M. I. Gonzalez and J. A. Mason, J. Am. Chem. Soc., 2020, 142, 19170–19180 CrossRef CAS PubMed.
- N. Terasawa, S. Tsuzuki, T. Umecky, Y. Saito and H. Matsumoto, Chem. Commun., 2010, 46, 1730 RSC.
- P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 1257–1288 RSC.
- D. Braga, L. Maini, F. Grepioni, A. De Cian, O. Félix, J. Fischer and M. Wais Hosseini, New J. Chem., 2000, 24, 547–553 RSC.
- I. Rozas, I. Alkorta and J. Elguero, Struct. Chem., 2008, 19, 923–933 CrossRef CAS.
- R. Vijayraghavan, U. A. Rana, G. D. Elliott and D. R. MacFarlane, Energy Technol., 2013, 1, 609–612 CrossRef CAS.
- K. Matuszek, R. Vijayaraghavan, C. M. Forsyth, S. Mahadevan, M. Kar and D. R. MacFarlane, ChemSusChem, 2020, 13, 159–164 CrossRef CAS PubMed.
- K. Matuszek, R. Vijayaraghavan, M. Kar and D. R. MacFarlane, Cryst. Growth Des., 2019, 20, 1285–1291 CrossRef.
- K. Matuszek, R. Vijayaraghavan, M. Kar, S. Mahadevan and D. R. MacFarlane, ChemSusChem, 2021, 14, 2757–2762 CrossRef CAS PubMed.
- E. I. Izgorodina and D. R. MacFarlane, J. Phys. Chem. B, 2011, 115, 14659–14667 CrossRef CAS PubMed.
- T. Takamuku, T. Tokuda, T. Uchida, K. Sonoda, B. A. Marekha, A. Idrissi, O. Takahashi, Y. Horikawa, J. Matsumura and T. Tokushima, Phys. Chem. Chem. Phys., 2018, 20, 12858–12869 RSC.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., 2013, 125, 4721–4725 CrossRef.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- W. W. Cleland, P. A. Frey and J. A. Gerlt, J. Biol. Chem., 1998, 273, 25529–25532 CrossRef CAS PubMed.
- M. C. Etter, J. C. MacDonald and J. Bernstein, Acta Crystallogr., Sect. B: Struct. Sci., 1990, 46, 256–262 CrossRef PubMed.
- F. H. Allen, G. P. Shields, R. Taylor, F. H. Allen, P. R. Raithby, G. P. Shields and R. Taylor, Chem. Commun., 1998, 1043–1044 RSC.
- E. S. Feldblum and I. T. Arkin, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 4085–4090 CrossRef CAS PubMed.
- P. Gilli, L. Pretto, V. Bertolasi and G. Gilli, Acc. Chem. Res., 2009, 42, 33–44 CrossRef CAS PubMed.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
- J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627–668 CrossRef PubMed.
- J. Timmermans, J. Phys. Chem. Solids, 1961, 18, 1–8 CrossRef CAS.
- H. Zhu, U. Ali Rana, V. Ranganathan, L. Jin, L. A. O’Dell, D. R. MacFarlane and M. Forsyth, J. Mater. Chem. A, 2014, 2, 681–691 RSC.
- C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191 RSC.
- F. L. Gervasio, R. Chelli, P. Procacci and V. Schettino, J. Phys. Chem. A, 2002, 106, 2945–2948 CrossRef CAS.
- P. Walden, Z. Elektrochem., 1908, 14, 713–728 CrossRef CAS.
- C. Shi, B. Wei and W. Zhang, Cryst. Growth Des., 2014, 14, 6570–6580 CrossRef CAS.
- K. Wendler, J. Thar, S. Zahn and B. Kirchner, J. Phys. Chem. A, 2010, 114, 9529–9536 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplemental figures, synthesis and experimental methods, summary of literature data, X-ray crystallographic information, DSC data, NMR spectra. CCDC 2090743–2090753. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ma00603g |
| ‡ Conventional nomenclature is used to describe phases of plastic crystals, with Phase I labelled as the highest temperature phase before melt, and lower temperature phases labelled successively thereon. |
| § The acetate anion was initially chosen but led to decomposition upon melting for all salts. |
| This journal is © The Royal Society of Chemistry 2021 |