Open Access Article
Open Access ArticleThe determination of the HOR/HER reaction mechanism from experimental kinetic data†
Hector
Prats
 *ab and
Karen
Chan
*ab and
Karen
Chan
 a
a
aCatalysis Theory Center, Department of Physics, Technical University of Denmark, 2800 Kogens Lyngby, Denmark. E-mail: h.garcia@ucl.ac.uk
bDepartment of Chemical Engineering, University College London, Roberts Building, Torrington Place, London WC1E 7JE, UK
First published on 25th November 2021
Abstract
Hydrogen oxidation and evolution are important processes from both a fundamental and applied perspective. In interpreting experimental kinetic data, few studies have explicitly accounted for the impact of H* coverage and mass transport, which lead to discrepancies in the kinetic parameters and the resultant reaction mechanism. Here, we present how to determine the kinetic parameters accounting for both effects. We discuss the use of the kinetic parameters towards mechanistic interpretations for HOR/HER and show that, in general, knowledge of the coverage of H* or activation energies may be required to assign a reaction mechanism. We apply these ideas to activity data of several HOR and HER electrocatalysts, such as Au, Pt, MoS2, and CoP.
1. Introduction
Hydrogen evolution and oxidation (HOR and HER) are, respectively, key reactions in PEM-based electrolysers1 and H2 fuel cells,2 which can play a critical role in a sustainable energy landscape. These reactions have been the subject of hundreds of studies in the past few decades,3–5 on catalysts both new and old. In interpreting experimental activity data, few studies have explicitly accounted for both the impact of the H* coverage and its dependence on potential, and mass transport. The variation of H* coverage with potential translates to a change in effective transfer coefficient,6,7 while mass transport limitations completely dominate the current response for HOR and HER Pt in acid, due to the extremely facile kinetics.8,9 Without accounting for these effects, the intrinsic kinetics are not considered and can lead to incorrect assignments of the mechanism and the kinetic parameters.Microkinetic models of HER on various catalysts have been derived on the basis of reaction and activation energies from ab initio simulations.7,10,11 While the determination of the H* binding energy is straightforward,12 challenges remain in methods to determine the electrochemical barriers. The effect of the structure of the static water layers,13 co-adsorption of spectator species,14 and the effect of the capacitances15 in the charging components all compound the uncertainties in the energetics associated with workhorse density functional theory (DFT) methods. Therefore, the interpretation of measured kinetics with effective rate expressions remains a relevant step in mechanistic studies.
In this Perspective, we (1) present how to determine kinetic parameters and make mechanistic interpretations of experimental HER/HOR data accounting for the effects of coverage and mass transport, (2) discuss common pitfalls in the determination and mechanistic interpretation of kinetic parameters and (3) apply these ideas to transition metal and novel HER catalysts such as sulfides and phosphides. We show that, in general, kinetic parameters are not sufficient to assign a reaction mechanism and that in some cases knowledge of the coverage of active H* species, or the relative differences in activation energies of elementary steps are required. We apply these ideas to Au, Ag, Pt, MoS2, and CoP catalysts. We suggest that the Heyrovsky step is rate limiting on Pt in both acid and basic conditions. The presented principles are generally applicable to the analysis of HER/HOR on other electrocatalysts.
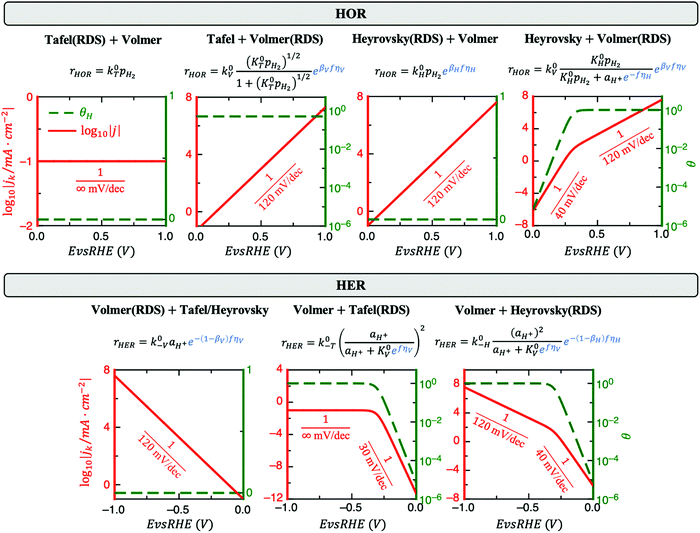
2. H Saturation can modify the Tafel slope
HOR and HER consist of at least two elementary steps, e.g., Tafel + Volmer or Heyrovsky + Volmer. Under acidic conditions, these steps are:| Tafel: H2 + 2* ↔ 2H* | (1a) |
| Heyrovsky: H2 + * ↔ H* + H+ + e− | (1b) |
| Volmer: H* ↔ H+ + e− + * | (1c) |
3. How to determine kinetic parameters from experimental activity data
(3a) The appropriate constraints on the Butler Volmer equation that account for the effective coverage
Without a detailed microkinetic model, we evaluate the experimentally determined current density jk against an effective Butler Volmer equation. In highly active catalysts where there is a significant current (i.e., >1 mA cm−2) at low overpotentials both HER and HOR contribute to the total current density. In these cases, both reactions would share the same rate-determining step (RDS) – i.e., satisfy the reversibility condition − and the corresponding kinetic parameters can be obtained from the following equation:| jk = j0[eαaFη/RT − e−αcFη/RT] | (2) |
For slower HOR/HER catalysts where the kinetic current starts to be significant only at |η| > 59 mV, the contribution of either HOR or HER to the total current is negligible and the reversibility condition cannot be applied. Then, the transfer coefficients for HOR and HER must be evaluated separately as follows:
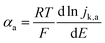 | (3a) |
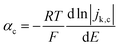 | (3b) |
In practice, the reversibility condition only holds for Pt-based catalysts, while all other catalysts (including the novel sulphide and phosphide HER catalysts discussed below) show negligible current at |η| < 59 mV and must be evaluated using eqn (3a) and (3b). Note that these equations should also be used for fast catalysts if there is a shift in the intrinsic Tafel slope at higher η, since in that case eqn (2) is not applicable in all overpotential range.
(3b) How to account for mass transport limitations
Acidic HOR/HER current densities recorded on Pt-based catalysts are generally limited by mass transport even when rotating-disk electrodes (RDEs) operating at fast rotation rates are used, especially in the HOR branch.8,9 When the kinetics of the reaction are so facile relative to mass transport, the measured activities give no information about the intrinsic kinetics, even at low overpotentials of ±10 mV. In such cases, the measured current follows the concentration overpotential curve when a slow scan rate is used (derived from the Nernstian equilibrium, see Section S2 in the ESI†):| jd = jl,a(1 − e−2Fη/RT) | (4) |
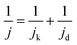 | (5) |
Note that the applicability of the above equation is limited to those systems where jl,a is known. In RDE setups, jl,a can simply be determined from the Levich equation:16
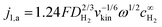 | (6) |
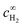 is the bulk concentration of H2.
is the bulk concentration of H2.
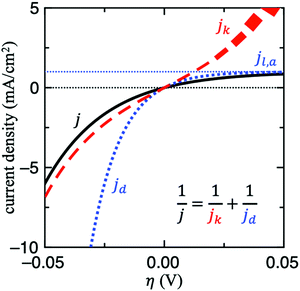
For this reason, the RDE method is widely employed in kinetic studies of electrochemical reactions, owing to its well-defined mass transport behaviour. For other techniques, it might be difficult to determine this value without mass transport modelling and thus it is not trivial to decouple jk from mass transport. Fig. 2 shows the contributions of jk and jd to j for HER/HOR reaction on an arbitrary system with j0 = jl,a = 1 mA cm−2 and αa = αc = 1. Note that when j ≈ jd, the current response is completely dominated by mass transport (see right upper corner of Fig. 2). In this scenario, jk cannot be determined since its uncertainty becomes too large. If this issue holds for a wide potential range, mass transport of the experimental setup simply needs to be optimized to obtain any estimate of jk, for instance by using floating electrodes17,18 or the H2-pump method.19–21 In the former technique, the reactant is supplied in gas-phase to the porous electrode, which is floating on aqueous electrolyte. The gaseous diffusion leads to a three order of magnitude increase in mass transport of reactant gases to the catalyst layer. In the latter, membrane electrode assemblies (MEAs) with asymmetric Pt loadings of the electrodes are used in a proton exchange membrane fuel cell (PEMFC) at pH = 0. The measured exchange current density of HOR/HER on Pt/C in acid in this configuration is about 2 orders of magnitude higher compared to full-sized Pt disk in a RDE configuration.21
To assess whether mass transport is an issue for a particular system, one can compare the measured current with jd in all the potential range explored. Another strategy to do so would be to modify the mass transport coefficient of H2, for example by increasing the rotation rate on a RDE setup. A more general strategy to evaluate and mitigate mass transport effects would be to decrease the loading, which would decrease the geometric activity vs. relative to the rate of transport.8 If the measured turnover frequency (TOF) increases in doing so, then the system is at least partially limited by diffusion.
(3c) How to make mechanistic interpretations of the fitted kinetic parameters
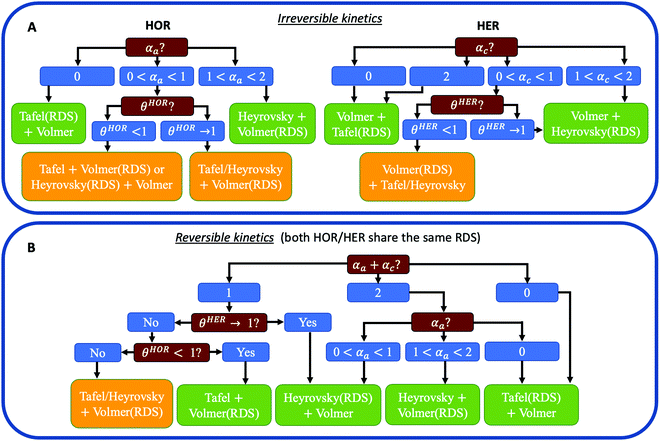
Fig. 1 reveals that the values of αa and αc alone are, in general, not enough to determine the reaction mechanism, and knowledge of the hydrogen coverage θ or activation energies may be required. Fig. 3 shows flowcharts for possible mechanisms from the RDS analysis from Fig. 1 to interpret experimentally determined HOR and/or HER transfer coefficients on any electrocatalyst for the case of irreversible (Fig. 3A) or reversible kinetics (Fig. 3B).For irreversible kinetics (Fig. 3A), where 0 < α < 1, identification of the dominant reaction mechanism is in general not possible, even when θ is known, and knowledge of the activation energies of the elementary steps from DFT simulations would be required. Where the reversibility condition holds (Fig. 3B), the dominant reaction mechanism can almost always be uniquely identified by knowing the transfer coefficients, and θ is only required if αa + αc = 1.
In a simple Sabatier picture, catalysts with where the active sites bind H* weakly will have low θ (Volmer is limiting) and ones that bind H* strongly (Heyrovsky/Tafel limiting) θ → 1. This picture is consistent with computed coverages from microkinetic modelling, developed on the basis of scaling relationships in activation energies of elementary steps.10θ could therefore be estimated from a computed H* binding energy, and it can also be estimated experimentally from cyclic voltammetry (CV) and linear sweep voltammetry (LSV) experiments.22 At close to neutral binding energies or where there are multiple possibilities in active sites, however, the assignment of this binding strength is not trivial, as we discuss for the case of Pt below. In this analysis we also have not considered the possibility of shifts in the RDS, which would also change the Tafel slopes, as overpotential increases.
4. Pitfalls in interpreting experimental polarization curves
We now discuss below some common pitfalls in interpreting experimentally measured activity.(4a) When fitting experimental polarization curves, don’t constrain αa + αc to 1
As shown in the previous section, αa + αc can range from 0 to 2. However, a very common practice in the literature to obtain the kinetic parameters for HOR/HER on Pt is to fit jk to the Butler–Volmer equation (i.e., eqn (2)) imposing αa + αc = 1.9,20,21,23–26 In the specific case of Pt, this constraint does not affect the final result, since the sum of the transfer coefficients for HOR/HER on Pt is 1 (see Section 5, below). Despite that, it should not be imposed as a general constrain to any electrocatalyst. A risk of using this constrain in other non-Pt catalysts is that, in the typical low overpotential range considered in HOR/HER, the resulting fit looks always good, even when the true sum of transfer coefficients is not 1 (see Fig. S2, ESI†). This might lead to the incorrect conclusion that αa + αc= 1 is always valid, which can ultimately result in very different kinetic parameters and wrong mechanistic interpretation. Finally, different assumptions in the value of αa + αc can lead to discrepancies in the values of j0 when it is obtained from the slope of the micropolarization region. Since the slope is proportional to 1/j0(αa + αc), j0 cannot be determined from the slope alone and the Butler–Volmer equation must be used. These issues are illustrated in more detail in Section S4 in the ESI.†(4b) Consider coverage effects when making mechanistic interpretations
Some HOR/HER studies on Pt suggest that if the sum of alphas is equal to 1 then it must correspond to Tafel + Volmer mechanism, with Volmer step being rate-limiting.3,19,21,26,27 As shown in Fig. 3B, this will be correct for where θ < 1 in all potential range considered, but the reaction pathways involving Heyrovsky + Volmer with either of the two steps being RDS are also compatible with αa + αc = 1. This statement has been justified sometimes by saying that the sum of transfer coefficients must be equal to n/vRDS,26 where n is the total number of transferred electrons (for HOR/HER n = 2) and vRDS is a stoichiometric factor accounting for the number of times the RDS has to proceed in order for the complete reaction to take place once (i.e., for Volmer(RDS) + Tafel, vRDS = 2). However, this statement is only valid for outer-sphere multi-electron transfer reactions such as the self-exchange reaction Tl(aq)3+ + 2e− ↔ Tl(aq)+ in acidic media,28 but it is not valid for HOR/HER where H* coverage might play a role.(4c) Account for mass transport limitations
A major challenge in evaluating the activity of Pt-based materials for acidic HOR/HER is that the kinetics of the reaction are so facile that the measured currents are always limited by mass transport. On RDEs, the measured polarization curves overlap with the concentration overpotential curve (i.e., eqn 4).9,23 Furthermore, the presence of mass transport limitations has also been suggested recently in fast mass transport setups.8 Still, in most experimental studies on acidic HOR/HER on Pt-based electrodes, Tafel slopes (TSs) of ∼30 mV dec−1 for HER are reported.29–35 Since the transfer coefficients are frequently estimated from TSs, incorrect interpretation of measured TS could lead to misleading mechanistic interpretations. For instance, if the 30 mV dec−1 TS is interpreted as a kinetic TS, then an apparent αc ∼ 2 would be obtained, leading to the conclusion that the dominant pathway is Volmer + Tafel(RDS) (see Fig. 3A).7 However, this value is just the apparent Tafel slope of a two-electron reaction governed by mass transport (also known as nernstian reaction) at room temperature and does not reflect any kinetic information. In Section S3 in the ESI† we show the derivation of this effective slope. We speculate that the reason why this TS has been misinterpreted in several studies is because of the incorrect but spread idea that for HER/HOR mass transport effects are only present at high anodic overpotentials where the polarization curve flattens out. This idea, however, is only valid for irreversible electrochemical reactions. For highly reversible reactions such as HER/HOR, jd increases exponentially in the HER branch, as shown in Fig. 2.(4d) If possible, do not use jl,a instead of jd
A common approach found in the literature to correct alkaline HOR/HER currents on Pt for mass transport is to use jl,a instead of jd in eqn (5) and apply it only to the HOR branch, while the HER branch is assumed to be free of mass transport limitations.20,21,23–26 This variation in eqn (5) is known as the irreversible Koutecky–Levich equation and, as its name indicates, in principle it is valid only for irreversible reactions. For the highly reversible HER/HOR reaction, the irreversible Koutecky–Levich equation might underestimate the true jk especially when jd ≪ jl,a, which can lead to lower j0 and higher transfer coefficients e.g., for RDE measurements of alkaline HOR/HER on Pt/C (0.1 M KOH, 293 K), j0 and αc values of 1.9 (1.0) mA cmdisk−2 and 0.6 (0.97) are obtained, respectively, from the reversible (irreversible) Koutecky–Levich equation, as shown in Section S5 in the ESI.† At high η both equations provide the same results, since jd ≈ jl,a. Moreover, mass transport effects can also be present in the HER branch at low η due to slow diffusion of evolved H2 away from the electrode surface. Therefore, it is more advisable to use the reversible Koutecky–Levich equation and apply it to the whole potential range considered.(4e) Choose an appropriate scan rate
In polarization curve measurements, the electrode potential changes over time at a speed determined by the scan rate. The same applies to CV experiments, which are typically performed as a first step to detect small levels of anions impurities in the supporting electrolytes and to determine the specific surface area. An appropriate value for the scan rate must be chosen for each one of these experiments, as detailed below.Conventional CV or LSV experiments assume homogeneous concentrations at the start of the scan, and only diffusional mass transport throughout the scan due to the formation of a diffusion layer with variable thickness that grows over time. In a slow scan the diffusion layer will grow much further from the electrode in comparison to a fast scan. Consequently, the flux to the electrode surface is smaller at slow scan rates. Since the current is proportional to the flux towards the electrode, the magnitude of the current decreases as the scan rate is slower.36 In fact, for electrochemically reversible electron transfer processes involving freely diffusion redox species, the peak current increases linearly with the square root of the scan rate, as described by the Randles–Sevcik equation.37 The lower limit for the scan rate is determined by the mass transport boundary layer. As described in Section S6 in the ESI,† for a scan of 1 V and assuming a diffusion coefficient of 10−9 m2 s−1, the scan rate should be faster than ∼16 mV s−1. Thus, scan rates between 50–200 mV s−1 are commonly used to study the electrochemical behaviour of the electrolytes and catalyst in HOR/HER measurements,9,23,26 but ultimately choosing the scan rate in CV or LSV experiments depends on the information one wants to obtain. The upper is limited by the capacitance. Capacitive current scales linearly with scan rate, so at fast scans, the faradaic current will ultimately end up being lost in comparison with the capacitive current (also called double-layer current or non-faradaic current).38
In contrast, polarization curve measurements should be independent of the scan rate, as the system must be in steady-state at any measured potential. To that end, HOR/HER polarization curves are typically recorded in a RDE setup and with a H2-saturated electrolyte (instead of Ar-saturated, which is the case for the previous CV experiment), in order to increase the rate of mass transport. In a RDE setup, the movement of ions or molecules is completely dominated by a diffusion layer with constant thickness, arising from the stirring generated by the rotating disk, which can be approximated as follows:36
| δi = 1.61Di1/3vkin1/6ω−1/2 | (7) |
The fact that the diffusion layer is constant implies that the measured current is independent of the scan rate, provided that the diffusion layer is always equilibrated.
The upper limit for the scan rate can be calculated as follows. When this diffusion layer is disturbed from an initial state of equilibrium by a sudden change in boundary conditions (e.g., change of the electrode potential), it takes a finite amount of time τdif,i for the system to effectively reach a new equilibrium state. In planar diffusion, τdif,i ∼ δi2/Di.39 Thus, thinner diffusion layers and faster diffusion coefficients lead to a faster equilibration. If the scan rate vscan is too fast, the steady-state current at a given potential is never reached, giving rise to significant hysteresis in CV experiments,8 which will prevent any subsequent kinetic analysis. The degree of hysteresis depends on the ratio between τdif,i and the scan rate. Specifically, if the time for reaching the steady-state (τdif,i) is short compared to the time for sweeping the voltammogram (∼RT/Fvscan) then steady-state like behaviour will be seen:40
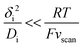 | (8) |
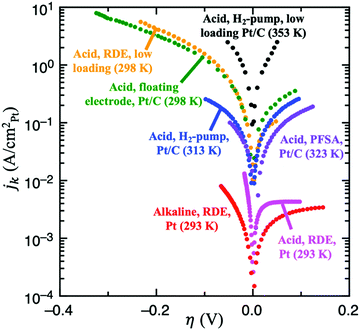 | ||
| Fig. 4 Experimental results for HOR/HER utilizing several different experimental techniques. From lowest to highest specific current: full sized Pt RDE in H2-saturated 0.1 M KOH, 10 μgPt cmdisk−2, 3600 rpm, 10 mV s−1 (red, ref. 9); full sized Pt RDE in H2-saturated 0.1M HClO4, 3600 rpm (pink, ref. 9); Pt/C dispersed on an Au grid in contact with a perfluorsulfonic acid (PFSA) membrane, 90 m2 gPt−1, 5 mV s−1 (purple, ref. 46); Pt/C using the H2-pump approach in a proton exchange fuel cell (PEMFC) setup, 2 mV s−1 (blue, ref. 21); Pt/C in 4M HClO4 using the floating electrode technique, 0.84 μgPt cm−2, 10 mV s−1 (green, ref. 18); low loading Pt/C RDE in 0.5M H2SO4, 13 ngPt cm−2, 1600 rpm, 50 mV s−1 (yellow, details in ref. 8); and low loading Pt/C using the H2-pump approach in a PEMFC, 3 μgPt cm−2 (black, details in ref. 19). | ||
Finally, if the precise rates of mass transport are not known, it must be verified that the measured polarization curve is independent of the scan rate. This can be done by conducting polarization curve measurements at slower scan rates and comparing the results obtained. Ideally, an infinitely slow scan rate should be used. However, too slow scan rate can be problematic due to trace contamination with transition metals of the electrolyte solutions. These metallic impurities can get adsorbed on the electrode surface at low potentials and get stripped from it at higher potentials, implying that at the beginning of each negative-going scan the electrode surface would be cleaner and more active than in the subsequent positive-going scan.26 This effect will be of course more pronounced if the scan rate is very slow.
5. Example: using the principles above to determine the kinetic parameters and mechanism of HER and HOR for various catalysts
In this section we use the procedure described in Section 3 to obtain the kinetic parameters and dominant reaction mechanism for HOR/HER on several transition metals and novel HER catalysts, with particular focus to the controversial case of Pt in both acid and alkaline conditions.(5a) Transition metals
Weak binding transition metal catalysts such as Au or Ag exhibit Tafel slopes of 121 and 147 mV dec−1, respectively, for HER in acid,44,45 and 168 and 134 mV dec−1 in alkaline,25 which corresponds to 0 < αc < 1. The HER activity of these materials is 2–3 orders of magnitude smaller than the concentration overpotential curve (e.g., for a RDE experiment in 0.5M H2SO4 and ω = 1600 rpm, the limiting HER current is about −1700 mV cm−2, as shown in Fig. S1 (ESI†), while these catalysts exhibit current densities of −1 to −10 mV cm−2), and therefore we can assume that mass transport effects are negligible. Because these catalysts only exhibit significant HER activity at |η| > 300 mV, the reversibility condition cannot be applied. Also, due to their weak binding strength for H, we can assume that θ < 1 in all overpotential range. Then, the flowchart in Fig. 3A indicates that Volmer is the RDS in these materials, followed by either the Heyrovsky or Tafel steps. DFT-based kinetic models suggest the predominance of the Heyrovsky over the Tafel step.10We now consider in detail the case of Pt. At low pH values, RDE experiments using full-sized Pt disks only give the concentration overpotential curve,9,23 so fast mass transport setups must be used. There are few studies on HOR and/or HER using H2-pump PEMFC setup,21 Au grid in contact with a perfluorsulfonic acid (PFSA) membrane46 and floating electrode technique18 at room or near-room temperature (i.e., <324 K), which report much higher activities than conventional RDE measurements. However, a recent work suggests the presence of mass transport limitations even in these systems, since they do not exceed the apparent activity found for RDE of Pt nanoparticles at low loadings, where mass transport limitations are still present.8 The activities from these studies are shown in Fig. 4.
There is, however, one H2-pump study19 on HOR/HER carried out at 353 K and using a low loading Pt/C sample (3 μgPt cm−2) which, due to the increased temperature, reports activities much higher than those of any study at room temperature. This work is the only one to our knowledge that shows an exponential increase in the HOR current with potential, which suggests that it is not limited by mass transport. We assume that this H2-pump study reports the least mass transport limited current for acidic HOR/HER on Pt and a fit of the reported current to Eqn 2 results in αa ≈ αc ≈ 0.5 (see Fig. S5 in the ESI†). Note that, in this study, the authors argue that the only reaction mechanism compatible with αa ≈ αc ≈ 0.5 is Tafel + Volmer(RDS). However, as illustrated in Fig. 3B, there are other pathways compatible with this result, and θ must be considered to truly determine the dominant reaction mechanism.
In the literature, two types of H* species have been distinguished, namely underpotential deposited (UPD) and overpotential deposited (OPD) H*, where H* is adsorbed above the HER/HOR equilibrium potential at 0 V vs. RHE (e.g. on hollow sites), or below 0 V (e.g. on top sites), and the nature of the active H* species at HER conditions has been debated in the last decade.7,47 It has been concluded from experimental CVs on Pt(111) in 0.1M HClO4 that the H* coverage at Eeq is higher than 2/3 ML and a full monolayer is reached at more negative potentials.22 Moreover, DFT calculations on Pt(111) have shown that H* adsorbs on hollow sites up to a coverage of 1 ML, and that the subsequent H* adsorption on top sites is energetically unfavourable due to strong lateral interactions.10,48 Thus, we assume that at least in the small overpotential range |η| < 0.05 V the experimental data was measured, UPD H* is the only active H* species with θHER → 1, indicating that HOR/HER follows a Heyrovsky(RDS) + Volmer pathway (see Fig. 3B). This conclusion agrees with the recent work by Tang et al.10 who also determined this mechanism to be the most favourable for HER on Pt(111) and UPD H* to be the active H* species, based on DFT calculations of the energy barriers for the different steps and kinetic modelling.
To our knowledge, there are no HOR/HER studies on Pt in alkaline conditions using fast mass transport setups, and only RDE data is available.9,23,24 However, at high pH values the kinetics are at least two orders of magnitude more sluggish (see Fig. 4), and the polarization curves obtained from RDE experiments only overlap the concentration overpotential curve at high anodic potentials. Thus, it is possible to obtain kinetic parameters for both HOR and HER by correcting for mass transport using eqn (5). Similar to acidic HOR/HER, αa ≈ αc ≈ 0.5 is obtained (see Fig. S7 in the ESI†) and H* binding on Pt is only slightly strong. Assuming that the relative differences between the barriers on the UPD and OPD H* are similar with both H2O and H3O+ as proton donors, the hollow, UPD sites would remain the active sites. The CV profiles in acid (0.1 M HClO4) and in alkaline (0.05 M NaOH) overlap well,49 indicating that the coverage of the UPD H* should be similar to that in acid, θHER → 1. Therefore Heyrovsky(RDS) + Volmer would be the dominant reaction mechanism for HOR/HER alkaline conditions like in acid, consistent with previous DFT-based kinetic models.14
(5b) Novel HER catalysts
Metal sulfides and phosphides have proven to be promising non-precious acidic HER catalysts.44,50,51 On MoS2 basal planes, the binding strength of H can be increased by straining the surface or incorporating S vacancies,44 yielding the optimum catalytic activity for neutral H binding. The Tafel slopes exhibited by these catalysts range from 60 to 98 mV dec−1 (i.e., 0 < αc < 1), depending on the degree of strain and number of S vacancies. According to Fig. 3A, θ is required to identify Volmer or Heyrovsky as the RDS. Non-strained MoS2 basal planes with no S vacancies binds H very weakly, leading to θ < 1 and therefore the dominant reaction mechanism must be Volmer being rate-limiting followed by either Tafel or Heyrovsky. On the other hand, strained MoS2 basal planes with a high number of S vacancies binds H strongly (i.e., θ → 1), meaning that HER follows a Volmer + Heyrovsky(RDS) reaction mechanism. As for MoS2 nanoparticles, edge sites are responsible for the HER activity, which present Tafel slopes of 56 mV dec−1.50 Very similar Tafel slopes are exhibited by CoP nanoparticles supported on Ti, which are around 50 mV dec−1, independent of mass loading. The only reaction pathway compatible with these result is Volmer + Heyrvosky(RDS), as shown in Fig. 3A, and knowledge of θ is not required in these cases.6. Conclusions
In this Perspective, we illustrate how to determine the dominant reaction mechanism for HOR/HER from experimental activity data accounting for the impact of H* coverage and mass transport. In summary, mass transport effects can be corrected by using the reversible Koutecky–Levich equation whenever they contribute only partially to the measured current, to obtain the kinetic current and kinetic parameters. The reaction mechanism in general cannot be determined only with kinetic parameters, and in some cases the coverage of the active H* species or even the relative activation energies of elementary steps are required. For systems where the reversibility condition can be applied (e.g., Pt), the transfer coefficients can be obtained by fitting the kinetic current to an effective Butler–Volmer equation with the only constraint that their sum must range from 0 to 2. The reaction mechanism can be determined by using the flowchart presented in Fig. 3B, which may require information about the coverage of H* species at reaction conditions. On the other hand, for less active catalysts where the reversibility condition does not hold (e.g., Au), the transfer coefficients for HOR and HER should be evaluated separately by using eqn (3a) and/or eqn (3b), and the determination of the dominant reaction mechanism can be done by following the flowchart in Fig. 3A. We also discuss some common pitfalls in interpretating HOR/HER activity and their consequences. Finally, we apply this recipe to several electrocatalysts, with careful attention to Pt, and suggest that Heyrovsky step is rate limiting for HOR/HER on Pt in both acid and basic conditions. We hope that this Perspective will contribute to solve the existing discrepancies on the kinetic analysis of HOR/HER on Pt and that the presented recipe will be useful to make mechanistic interpretations of HOR/HER on any electrocatalyst.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support was provided by V-Sustain: The VILLUM Centre for the Science of Sustainable Fuels and Chemicals (#9455) from VILLUM FONDEN. We thank Dr Nitish Govindarajan and Dr Georg Kastlunger for useful discussions.References
- J. A. Turner, Science, 2004, 305, 972–974 CrossRef CAS PubMed.
- I. Staffell, D. Scamman, A. V. Abad, P. Balcombe, P. E. Dodds, P. Ekins, N. Shah and K. R. Ward, Energy Environ. Sci., 2019, 12, 463–491 RSC.
- X. Tian, P. Zhao and W. Sheng, Adv. Mater., 2019, 31, 1808066 CrossRef PubMed.
- N. Dubouis and A. Grimaud, Chem. Sci., 2019, 10, 9165–9181 RSC.
- E. S. Davydova, S. Mukerjee, F. Jaouen and D. R. Dekel, ACS Catal., 2018, 8, 6665–6690 CrossRef CAS.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Sci. Rep., 2015, 5, 13801 CrossRef PubMed.
- P. Lindgren, G. Kastlunger and A. A. Peterson, ACS Catal., 2020, 10, 121–128 CrossRef CAS.
- J. J. Hansen, H. Prats, K. K. Toudahl, N. M. Secher, K. Chan, J. Kibsgaard and I. Chorkendorff, ACS Energy Lett., 2021, 6, 1175–1180 CrossRef CAS PubMed.
- J. Zheng, Y. Yan and B. Xu, J. Electrochem. Soc., 2015, 162, F1470–F1481 CrossRef CAS.
- M. T. Tang, X. Liu, Y. Ji, J. K. Nørskov and K. Chan, J. Phys. Chem. C, 2020, 124, 28083–28092 CrossRef CAS.
- Z. Wang, M. Tang, A. Cao, K. Chan and J. K. Nørskov, ChemRxiv DOI:10.26434/chemrxiv.14679084.v1.
- J. K. Nørskov, T. Bligaard, A. Logadottier, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef.
- A. M. Patel, S. Vijay, G. Kastlunger, J. K. Nørskov and K. Chan, J. Phys. Chem. Lett., 2021, 12, 5193–5200 CrossRef CAS PubMed.
- P. S. Lamoureux, A. R. Singh and K. Chan, ACS Catal., 2019, 9, 6194–6201 CrossRef CAS.
- J. A. Gauthier, C. F. Dickens, H. H. Heenen, S. Vijay, S. Ringe and K. Chan, J. Chem. Theory Comput., 2019, 15, 12 CrossRef PubMed.
- C. M. A. Brett and A. M. O. Brett, Electrochemistry. Principles, Methods, and Applications, Oxford University Press, New York, 1st edn, 1993 Search PubMed.
- C. M. Zalitis, D. Kramer and A. R. Kucernak, Phys. Chem. Chem. Phys., 2013, 15, 4329 RSC.
- C. M. Zalitis, D. Kramer, J. Sharman, E. Wright and A. R. Kucernak, ECS Trans., 2013, 58, 39–47 CrossRef.
- K. C. Neyerlin, W. Gu, J. Jorne and H. A. Gasteiger, J. Electrochem. Soc., 2007, 154, B631–B635 CrossRef CAS.
- J. Durst, A. Siebel, C. Simon, F. Hasché, J. Herranz and H. A. Gasteiger, Energy Environ. Sci., 2014, 7, 2255–2260 RSC.
- J. Durst, C. Simon, F. Hasché and H. A. Gasteiger, J. Electrochem. Soc., 2015, 162, F190–F203 CrossRef CAS.
- D. Strmcnick, D. van der Vliet, V. Stamenkovic and N. M. Markovic, Electrochem. Commun., 2008, 10, 1602–1605 CrossRef.
- W. Sheng, H. A. Gasteiger and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, B1529–B1536 CrossRef CAS.
- P. J. Rheinländer, S. Henning, J. Herranz and H. A. Gasteiger, ECS Trans., 2012, 50, 2163–2174 CrossRef.
- W. Sheng, M. Myint, J. C. Chen and Y. Yan, Energy Environ. Sci., 2013, 6, 1509–1512 RSC.
- P. J. Rheinländer, J. Herranz, J. Durst and H. A. Gasteiger, J. Electrochem. Soc., 2014, 161, F1448–F1457 CrossRef.
- J. Durst, C. Simon, A. Siebel, P. Rheinländer, T. Schuler, M. Hanzlik, J. Herranz, F. Hasché and H. A. Gasteiger, ECS Trans., 2014, 64, 1069–1080 CrossRef CAS.
- L. D. Zusman and D. N. Beratan, J. Phys. Chem. A, 1997, 101, 4136–4141 CrossRef CAS.
- E. J. Popczun, J. R. McKone, C. G. Read, A. J. Biacchi, A. M. Wiltrout, N. S. Lewis and R. E. Schaak, J. Am. Chem. Soc., 2013, 135, 9267–9270 CrossRef CAS PubMed.
- J. Deng, P. Ren, D. Deng, L. Yu, F. Yang and X. Bao, Energy Environ. Sci., 2014, 7, 1919–1923 RSC.
- M. A. Lukowski, A. S. Daniel, C. R. English, F. Meng, A. Forticaux, R. J. Hamers and S. Jin, Energy Environ. Sci., 2014, 7, 2608–2613 RSC.
- M.-R. Gao, J.-X. Liang, Y.-R. Zheng, Y.-F. Xu, J. Jiang, Q. Gao, J. Li and S.-H. Yu, Nat. Commun., 2015, 6, 5982 CrossRef CAS PubMed.
- D.-Y. Wang, M. Gong, H.-L. Choud, C.-J. Pan, H.-A. Chen, Y. Wu, M.-C. Lin, M. Guan, J. Yang, C.-W. Chen, Y.-L. Wang, B.-J. Hwang, C.-C. Chen and H. Dai, J. Am. Chem. Soc., 2015, 137, 1587–1592 CrossRef CAS PubMed.
- M. Tavakkoli, T. Kallio, O. Reynaud, A. G. Nasibulin, C. Johans, J. Sainio, H. Jiang, E. I. Kauppinen and K. Laasonen, Angew. Chem., Int. Ed., 2015, 54, 4535–4538 CrossRef CAS PubMed.
- I. Ledezma-Yanez, W. D. Z. Wallace, P. Sebastián-Pascual, V. Climent, J. M. Feliu and M. T. M. Koper, Nat. Energy, 2017, 2, 17031 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods. Fundamentals and Applications, John Wiley & Sons, Inc,New York, 2nd edn, 2001 Search PubMed.
- N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart and J. L. Dempsey, J. Chem. Educ., 2018, 95, 197 CrossRef CAS.
- O. Gharbi, M. T. T. Tran, B. Tribollet, M. Turmine and V. Vivier, Electrochim. Acta, 2020, 343, 136109 CrossRef CAS.
- R. I. Hickson, S. I. Barry and G. N. Mercer, Critical Times in Multilayer Diffusion. Part 1: Exact Solutions., Int. J. Heat Mass Transfer, 2009, 52, 5776 CrossRef CAS.
- R. G. Compton and C. E. Banks, Understanding Voltammetry, Imperial College Press, 2nd edn, 2010, ch. 5 Search PubMed.
- R. M. Q. Mello and E. A. Ticianelli, Electrochim. Acta, 1997, 42, 1031 CrossRef CAS.
- N. M. Marković, B. N. Grgur and P. N. Ross, J. Phys. Chem. B, 1997, 101, 5405 CrossRef.
- C. Sandford, M. A. Edwards, K. J. Klunder, D. P. Hickey, M. Li, K. Barman, M. S. Sigman, H. S. White and S. D. Minteer, Chem. Sci., 2019, 10, 6404 RSC.
- H. Li, C. Tsai, A. L. Koh, L. Cai, A. W. Contryman, A. H. Fragapane, J. Zhao, H. S. Han, H. C. Manoharan, F. Abild-Pedersen, J. K. Nørskov and X. Zheng, Nat. Mater., 2016, 15, 48–53 CrossRef CAS PubMed.
- R. Tölle and A. Otto, Surf. Sci., 2005, 597, 110–118 CrossRef.
- A. R. Kucernak and E. Toyoda, Electrochem. Commun., 2008, 10, 1728–1731 CrossRef CAS.
- K. S. Exner, Angew. Chem., Int. Ed., 2020, 59, 10236–10240 CrossRef CAS PubMed.
- E. Skúlason, V. Tripkovic, M. E. Björketun, S. Gudmundsdóttir, G. Karlberg, J. Rossmeisl, T. Bligaard, H. Jónsson and J. K. Nørskov, J. Phys. Chem. C, 2010, 114, 18182–18197 CrossRef.
- M. J. T. C. van der Niet, N. Garcia-Araez, J. Hernández, J. M. Feliu and M. T. M. Koper, Catal. Today, 2013, 202, 105–113 CrossRef CAS.
- T. F. Jaramillo, K. P. Jørgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102 CrossRef CAS PubMed.
- E. J. Popczun, C. G. Read, C. W. Roske, N. S. Lewis and R. E. Schaak, Angew. Chem., Int. Ed., 2014, 53, 5427–5430 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04134g |
| This journal is © the Owner Societies 2021 |