Open Access Article
Open Access ArticleCorrelated disorder in metal–organic frameworks
Emily G.
Meekel
and
Andrew L.
Goodwin
 *
*
Department of Chemistry, Inorganic Chemistry Laboratory, University of Oxford, South Parks Road, Oxford OX1 3QR, UK. E-mail: andrew.goodwin@chem.ox.ac.uk; Tel: +44 (0)1865 272137
First published on 1st March 2021
Abstract
We survey the importance of correlated—as opposed to random—disorder in metal–organic frameworks (MOFs), focussing on correlations in vacancy arrangements, composition, and linker orientations in some canonical systems. We explore the link to physical and chemical properties, and highlight the various experimental and computational tools available for characterising and interpreting correlated disorder in MOFs.
1 Introduction
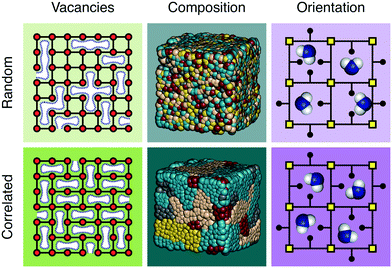
The discovery of disordered,1 defective,2,3 amorphous,4 and even liquid5,6 metal–organic frameworks (MOFs) has forced a paradigm shift in our collective understanding of MOF structural chemistry.7 Having long focused on the elegant control possible over crystalline network structures,8,9 the field is now increasingly exploiting the presence and nature of disorder in MOFs as an important design tool with which to tune their physical and chemical properties.10,11Disorder is sometimes random; more often it is correlated.12 A vacancy at one linker site in an otherwise crystalline MOF, for example, may affect the likelihood for neighbouring linkers also to be vacant. Such vacancy correlations can propagate throughout a structure, collectively determining a variety of bulk properties—including porosity.2,13 Likewise, mixed-metal and/or mixed-linker MOFs can have non-statistical distributions that determine their corresponding chemistry; such is the basis, after all, of the ‘multivariate’ MOF approach which exploits compositional heterogeneity to improve functionality.14 And in orientationally-disordered MOFs, correlations in linker orientations can also affect mechanical and host/guest responses.15 These various distinctions are illustrated schematically in Fig. 1. It is no accident then that controlling the correlations within disordered MOFs—whether involving vacancy, composition, or linker orientation distributions—is an essential aspect of defect engineering.2,16–18
Distinguishing correlated disorder from random disorder is often a nontrivial experimental and computational challenge. Conventional crystallography, which has played such an important historical role in MOF science, probes only the average structure of materials: it is demonstrably insensitive to correlations within disordered states.19 Yet a number of developments have now converged to equip us, as a community, with the tools needed to probe correlated disorder in MOFs. Experimentally, recent advances in solid-state NMR, X-ray diffuse scattering, pair distribution function (PDF), and electron microscopy measurements are providing valuable empirical insight into MOF defect structures.13,20–22 At the same time, ab initio density functional theory (DFT) calculations of a sufficient scale to interrogate non-crystalline MOF architectures are becoming increasingly tractable.6,23 The development of efficient high-quality MOF force-field methodologies extend these approaches beyond the nanometre scale.24,25
With these recent developments in mind, we survey in this Highlight article the phenomenology of correlated disorder in MOFs. Our focus is on disorder of three primary types—correlated vacancies, compositional disorder, and orientational disorder—and we place our discussion in the context of the behaviour of a small selection of canonical systems. Our emphasis is also threefold: (i) the nature of correlated disorder in these MOFs; (ii) the use of experimental and computational tools to characterise correlations; and (iii) the implications for physical and chemical properties. Our article concludes with a forward-looking discussion of the future challenges and opportunities in the field.
2 Vacancy correlations
UiO-66 and its variants are the canonical example of MOFs in which vacancy defects occur in a correlated—rather than random—manner.26–28 With a chemical composition of Zr6O4(OH)4(BDC)6 (H2BDC = 1,4-benzenedicarboxylic acid), the parent compound UiO-66 adopts a face-centred cubic structure based on the 12-connected fcu net.26 Not only does the high connectivity confer thermal, chemical and mechanical stability,29 but it renders the framework tolerant to both missing-linker and missing-cluster defects.30 The first signs of correlations in vacancy arrangements came from the appearance of structured diffuse scattering in the powder X-ray diffraction patterns of UiO-66(Hf) samples synthesised under high modulator concentrations.31 Diffuse scattering is featureless in the case of random disorder,19,32 and so its modulation in these patterns is characteristic of correlations in cluster vacancies—the specific form indicating nanodomains with the 8-connected reo topology [Fig. 2(a)].27 With the advent of low-dose high-resolution transmission electron microscopy (HRTEM), it has since been possible to image directly these nanodomains, which are found to coexist with related missing-linker variants [Fig. 2(b)].33 Very recently, scanning electron diffraction (SED) has also been used to image reo nanodomain distributions within individual crystallites at a spatial resolution of about 5 nm.22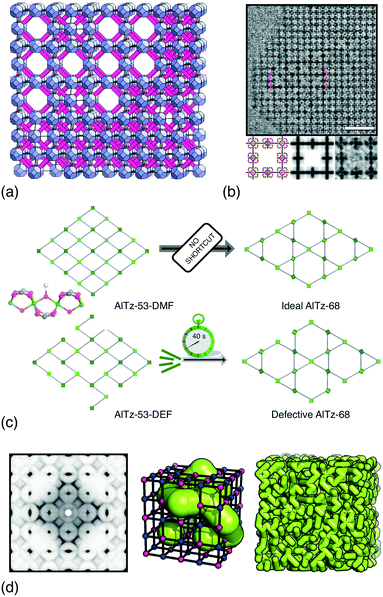 | ||
| Fig. 2 Correlated vacancies in MOFs. (a) Nanodomain model for UiO-66(Hf) developed in ref. 27: cluster vacancies are correlated to give domains of reo topology embedded within the parent fcu framework. Reproduced from ref. 27 with permission from Springer Nature. (b) High-resolution transmission electron microscopy images of missing-cluster/missing-linker nanodomains in UiO-66.33 The scale bar measures 5 nm. The lower panels denote (left–right) atomistic model, calculated potential map, and observed potential map. Adapted from ref. 33 with permission from Springer Nature. (c) Comparison of sql–kgm transformation mechanisms (left–right) in non-defective AlTz-53-DMF (top) and defective AlTz-53-DEF (bottom); the coordinating strength of included solvent plays a key role in facilitating network rearrangement.34 The green nodes denote aluminium hydroxide/carboxylate columns (illustrated on left). Adapted from ref. 34 with permission from Springer Nature. (d) The single-crystal X-ray diffuse scattering pattern of Zn3[Co(CN)6]2 PBA is characteristic of non-random correlations in the underlying pore network structure (green tubes) that permeates the cubic transition-metal cyanide framework. As disordered as the pore network is, it is not random.13 Adapted from ref. 13 with permission from Springer Nature. | ||
The driving force for correlated disorder in the UiO-66 family is thought to be the mechanical stability of reo-type connectivity within the fcu net.35 Other, lower symmetry, vacancy distributions are mechanically unstable with respect to shear and so do not survive during crystal growth; this biases the system away from purely statistical vacancy arrangements. An additional consideration is the structure-directing interaction between the UiO-66 framework and both counterions and solvent in the reaction mixture.36 The picture that emerges is one in which vacancy incorporation in UiO-66 is a kinetic effect—and hence why defect density can be controlled by e.g. synthesis temperature,37 solvent,38 or modulator concentration or pKa.16
From a functional perspective, there are a number of implications of random vs. correlated vacancy defects is this family. Perhaps the most obvious is the effect on sorption behaviour, because this depends on the nature of the pore network generated by connected vacancies.16 Related is the dramatic increase in proton conductivity observed for UiO-66 samples with high linker-vacancy concentrations—although the specific link between missing-linker arrangements and efficiency of proton transport in this system remains to be explored in detail.39 Correlated cluster absences affect mechanical properties, such as thermal expansivity40 and compressibility.10 And DFT calculations show the distribution of both linker and cluster vacancies control the spatial localisation of frontier orbitals, in turn affecting both electronic and catalytic behaviour.36,41
The importance of vacancy correlations in other MOF systems is also increasingly apparent. In the aluminium carboxylate MOF AlTz-53-DEF, for example, correlated linker vacancies facilitate a remarkable reversible switching between sql and kgm network topologies during desolvation/resolvation cycles [Fig. 2(c)].34 Even for the well-known MOF-5, adsorption isotherms are sensitive to the distribution of linker vacancies—a result demonstrated using grand canonical Monte Carlo (GCMC) simulations.42 A similar link between linker vacancy arrangements and water adsorption behaviour has been made particularly clear in the case of MOF-801—a fumarate-containing relative of UiO-66.43 And in DUT-49, a MOF famous for its negative gas adsorption (NGA) behaviour,44 cluster vacancies in its fcu network quench the NGA effect, with vacancy correlations thought to play a key role.45
Dense coordination networks can harbour disordered correlated vacancy distributions, the form and origin of which we expect may prove relevant in due course to the behaviour of MOFs. For example, Prussian blue analogues (PBAs) are heavily defective cyanide frameworks with the pcu topology.46,47 Single-crystal X-ray diffraction measurements of PBAs reveal highly structured diffuse scattering,13,48,49 which has recently been interpreted using the three-dimensional difference pair distribution function (3D-ΔPDF) approach [Fig. 2(d)].13 The scattering arises from correlated hexacyanometallate vacancies, which avoid occupying neighbouring sites. A key point is that the precise correlations—which control the sorption and transport characteristics of the resulting pore network—can be tuned by variation in PBA composition and synthesis route.13 Conceptually similar vacancy patterns are found in the thiocyanate analogues, albeit with long-range order.50 And in formate perovskites, cation vacancies again interact by avoiding neighbouring sites; this leads to a disorder/order transition in [GUA] Mn1−x2+Fe2x/33+□x/3(HCOO)3 (GUA+ = guanidinium cation) at xord ≃ 0.6.51
3 Compositional disorder
It is now well established that many MOF architectures are tolerant to the incorporation of multiple different metals and/or linkers within the one material.7,11,52,53 In such cases an obvious consideration is whether composition is homogeneously distributed or varies in some nonstatistical way—e.g. domain formation or core–shell architectures.54 The multivariate MOF (MTV-MOF) paradigm,55 and strategies such as sequential linker installation (SLI),56 have at their heart the concept that the spatial arrangement of different linkers or metals within a given MOF architecture is key to function.The sense one gets is that, other than for very dilute mixtures, truly-random compositional distributions are conspicuously rare in MOFs. Clearly, kinetics of crystallisation play an important role here; for example, the different nucleation rates of Zn- and Co-containing imidazolate frameworks allow the one-port formation of mixed-metal frameworks with core–shell architectures.57 Likewise, precursors with different kinetic stabilities can be chosen cleverly to control the degree of mixing during synthesis of mixed-metal coordination polymers.58 But there are thermodynamic considerations at play too: a comprehensive DFT study has highlighted the dual roles of charge distribution and size-mismatch in determining the balance between mixing and segregation.59,60 Such considerations may rationalise the preferential formation of CeZr5 clusters in mixed-Ce/Zr UiO-66 samples, as evidenced by X-ray absorption fine structure (EXAFS) measurements and as implicated in their catalytic behaviour.61
In addition to DFT calculations and EXAFS measurements, a variety of techniques offer sensitivity to the spatial distribution of components in compositionally disordered MOFs. Electron microscopy allows direct visualisation of compositional gradients on the micron scale [Fig. 3(a)]; so too does fluorescence imaging microscopy.64 Even peak asymmetry in synchrotron powder X-ray diffraction measurements has some indirect sensitivity to this microstructure.65 Rotational-echo double-resonance (REDOR) NMR measurements are sensitive to the through-space distance between nuclear spins; by selective labelling of different linkers it is possible to differentiate random, clustered and anti-clustered mixed-linker arrangements on the unit-cell lengthscale. A particularly elegant REDOR-NMR study of a multivariate MOF-5 family showed how different linker mixtures favoured different substitutional correlation types [Fig. 3(b)].54 Very recently, atom probe tomography (APT) has even been used to ‘sequence’ metals in mixed-metal MOF-74 rods [Fig. 3(c)], demonstrating that both random and correlated sequence types emerge naturally from different metal combinations and different synthesis temperatures.62 While both REDOR-NMR and APT provide very detailed information, they are nonetheless demanding techniques. By contrast, we have found that humble infrared spectroscopy can offer a surprisingly straightforward measure of cation distributions in mixed-metal MOFs and coordination polymers [Fig. 3(d)].63
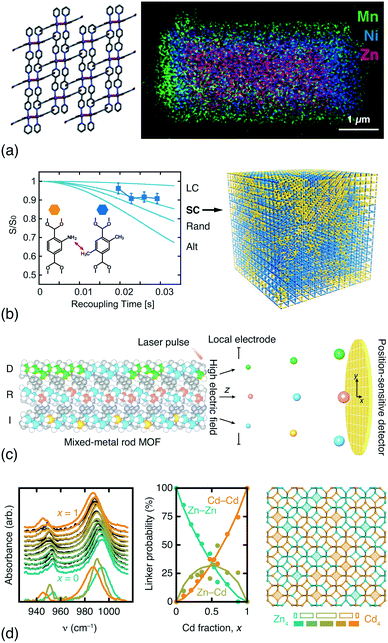 | ||
| Fig. 3 Determining compositional correlations in compositionally disordered MOFs. (a) STEM-EDX images of transition-metal segregation in the mixed-metal Zn/Ni/MnCID-5 ⊃ G MOF.58 Adapted from ref. 58 with permission from the American Chemical Society. (b) REDOR-NMR decay curves are sensitive to the degree of clustering/anticlustering of individual linkers in mixed-linker MOFs (LC = large clusters, SC = small clusters, Alt = alternating).54 Adapted from ref. 54 with permission from the American Association for the Advancement of Science. (c) Atom probe tomography allows the sequencing of metal-oxide rods in multivariate MOF-74.62 Here the method is shown to differentiate ‘duplicate’ (D), random (R), and ‘insertion’ (I) sequences. Adapted from ref. 62 with permission from the American Association for the Advancement of Science. (d) The in-plane methylimidazolate (mIm) stretching region of the IR spectra of mixed-metal (Zn/Cd) ZIF-8 derivatives is sensitive to the relative populations of Zn–mIm–Zn, Zn–mIm–Cd and Cd–mIm–Cd linkages. These populations can be extracted using non-negative matrix factorisation and used to derive models of the Zn/Cd distribution, which is found to involve clustering.63 Note the greater-than-statistical population of Zn4/Cd4 four-rings (experimental ZnnCd4−n populations as solid bars; statistical populations as open bars). Adapted from ref. 63 with permission from the Royal Society of Chemistry. | ||
Just as enzymes derive their function from the precise spatial arrangement of different components—e.g. the amino-acids of their protein backbone—the vision with compositionally complex MOFs has always been one of controlling heterogeneity to optimise a particular chemical or physical property.11 A simple but effective example is the recent demonstration of correlation-dependent photocatalysis in a mixed-linker UiO-68 derivative.66 But this vision is not unique to the MOF field: indeed, conventional solid-state chemistry has long exploited the use of solid solutions and inhomogeneity in this general way. A good example is that of the relaxor ferroelectrics, such as PbMg1/3Nb2/3O3, where the structural complexity responsible for their useful dielectric properties emerges naturally from an interplay between composition and lattice geometry.67 We anticipate the design rules developed to control complexity in these inorganic materials may yet have a role to play in MOF science.12
4 Orientational disorder
Whenever the nodes or linkers of a MOF have lower point symmetry than that of the corresponding site in the MOF lattice, the issue of orientational disorder arises.12,68 A longstanding example is that of the IRMOF series, where orientational disorder follows from asymmetric substitution of terephthalate linkers.69 Because the pores of MOFs are surrounded by multiple neighbouring linkers, the chemical and physical pore environments are affected by the presence or absence of correlations in linker orientations. Hence the distinction between random and correlated disorder in such systems may be crucial for interpreting a variety of host/guest phenomena. Such is the case in the CAU-1 family, for example, for which hyperpolarised 129Xe NMR spectroscopy has been used to identify correlations in side-chain orientations, in turn reflected in the experimental Ar sorption isotherms.70 So too in the IRMOF-3-AMPh system (AMPh denotes a phenylamide substituent), where linker orientations can be ordered or disordered according to a clever choice of synthesis approach; the two polymorphs have profoundly different H2 sorption profiles [Fig. 4(a)].71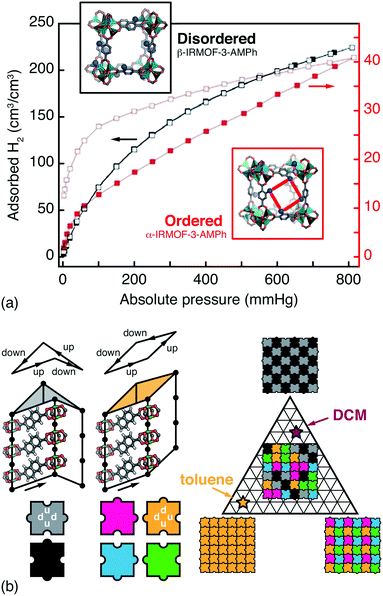 | ||
| Fig. 4 Orientational disorder in MOFs. (a) The α- and β-polymorphs of the substituted MOF-5 derivative IRMOF-3-AMPh have different linker orientation correlations and H2 (de)sorption profiles. Using the fully substituted AMPh-terephthalate linker during MOF synthesis gives the ordered α phase, with reduced and hysteretic H2 uptake is sorption profile. By contrast, post-synthetic modification of an aminoterephthalate MOF-5 derivative gives the disordered β phase, which has a greater accessible pore volume.71 Adapted from ref. 71 with permission from the Royal Society of Chemistry. (b) In the pillared MOF DUT-8(Ni), naphthalenedicarboxylate linkers introduce a ‘step-up’/‘step-down’ between neighbouring columns (exaggerated for effect here). There are six feasible NDC arrangements—i.e. two steps up and two steps down—around the lozenge-shaped pores. These arrangements give pores with either D2d or C2v point symmetry (grayscale and coloured tiles, respectively) that propagate according to a set of simple rules (jigsaw pairings shown here). Different guest molecules have different affinities for these two pore geometries, which allows a guest-induced transition between complex phases; for example, toluene and dichloromethane (DCM) favour configurations with C2v- and D2d-rich pore geometries, respectively.15 | ||
Just as linker orientations influence pore chemistry, so is it that guest adsorption can affect the correlations in linker orientations. Perhaps the clearest example in a disordered MOF is found in DUT-8(Ni), a pillared paddle-wheel MOF with 2,6-naphthalenedicarboxylate (NDC) linkers.72 The origin of disorder in this system is the existence of two degenerate NDC orientations.73 Each orientation introduces an offset—either up or down—in the positions of the neighbouring paddlewheel pillars. Since the lozenge-shaped pores of DUT-8(Ni) are flanked by four NDCs, there is a natural constraint that two must step up and two step down—after all, the total offset on traversing a loop around the pore must vanish to zero.68 The six possible NDC arrangements satisfying this rule partition into a set of four with a C2v-symmetric pore structure, and a set of two with a D2d pores. Neighbouring pores share edges, such that a large and complex configurational landscape emerges, characterised by different spatial arrangements of pore geometries.15 Remarkably, the adsorption and desorption of different solvent molecules drives the system reversibly across this landscape—the strength of host/guest interactions overcoming the ∼20 kJ mol−1 barrier to NDC ‘flips’ [Fig. 4(b)]. The recent development of efficient and accurate MOF force fields24,25 may allow computational insight into the mechanism for this unusual disorder–disorder switching.
The extent to which orientational disorder is static or dynamic depends on the reorientation barrier height, and if this barrier is commensurate with the available thermal energy then one expects to observe an order/disorder transition.12 There are plenty of examples in the literature, but we focus here on the case of the hybrid perovskite [NPr4][Mn(N(CN)2)3]—not technically a MOF but relevant nonetheless because its MOF-like framework structure exhibits a particularly useful barocaloric effect exploitable in solid-state cooling.74 The conformations of the flexible [NPr4]+ extra-framework cations and orientations of the dicyanamide linkers couple: they are disordered at temperatures above 331 K and ordered below. The transition between the two states is accompanied by a large change in both entropy and volume. The latter confers sensitivity to pressure—the disordered state can be re-ordered by squeezing, which is the basis for a barocaloric heating/cooling cycle [Fig. 5].75 Correlations within the disordered state, although still poorly understood, influence the barocaloric entropy change and reduce the critical pressure needed for each cooling cycle.12,74 In the parallel field of magnetocalorics—based on the order and disorder of magnetic spins—correlated disorder and the geometric frustration from which it arises are well-known to increase cooling efficiency.76–78 We therefore anticipate that similar design principles will prove valuable in exploiting orientational disorder in hybrid frameworks and MOFs alike.
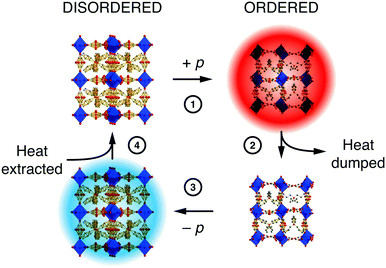 | ||
| Fig. 5 A simple barocaloric cooling strategy that exploits the pressure-dependence of the order/disorder transition in [NPr4][Mn(N(CN)2)3]. Starting at ambient conditions where the system is orientationally disordered (top left), ordering is induced by (1) application of pressure (note the change in unit cell dimensions is exaggerated here for effect). The loss of configurational entropy results in heating, and this excess heat (2) is dumped to the environment. (3) Removing the applied pressure forces the system to disorder; the concomitant increase in entropy now requires the system to cool. The cold solid (4) extracts heat from its environment.74,75 Adapted from ref. 74 with permission from Springer Nature. | ||
5 Conclusions and outlook
Perhaps our central thesis is that MOFs are fundamentally predisposed to correlated disorder. On the one hand, they have many compositional and configurational degrees of freedom79—so there will always be a strong entropic driving force for disordered states.80 And, on the other hand, interactions between neighbouring nodes, or neighbouring linkers, or between host and guest are rarely negligible, such that disorder is unlikely to be random. Sometimes this distinction between random and correlated disorder will be unimportant, but we hope to have identified in this brief review a range of physical and chemical properties for which the distinction is crucial.An historical barrier to studying and exploiting correlated disorder in MOFs has been the ostensible insensitivity of experimental techniques to its presence and nature: conventional crystallography is the obvious culprit here. But there are now many different experimental and computational tools available with the relevant capabilities. The hurdle that unquestionably remains is that of developing rigorous strategies for exercising synthetic control over correlated disorder. To this end we have flagged the interplay between composition and network geometry, and also the role of local-symmetry lowering as potential mechanisms for driving very specific types of correlated disordered states. The balance of kinetic and thermodynamic control during synthesis is clearly also to be decisive in many cases.
Looking forward, the field shares much of its aims with those of multivariate MOF chemistry: ultimately, correlated disorder is a form of structural complexity that might be exploited in e.g. catalysis or information storage or selective host/guest chemistry.11,68 An intriguing recent development along similar lines is the concept of using correlated disordered states as intermediates in materials synthesis to target low-dimensional phases.17 But we note in conclusion the possible additional importance of different types of correlated disorder in MOFs to those outlined here—involving e.g. frustrated magnetism,78 local charge ordering,81 or cooperative spin-state transitions.82 We see enormous potential in combining the unconventional physics of correlated disordered states with the scope for exquisite control over geometry for which MOFs are renowned.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the E.R.C. for funding (Advanced Grant 788144), and E. M. Reynolds, M. J. Cliffe, and J. M. Bulled for useful discussions.References
- A. K. Cheetham, T. D. Bennett, F.-X. Coudert and A. L. Goodwin, Dalton Trans., 2016, 45, 4113–4126 RSC.
- Z. Fang, B. Bueken, D. E. De Vos and R. A. Fischer, Angew. Chem., Int. Ed., 2015, 54, 7234–7254 CrossRef CAS PubMed.
- D. S. Sholl and R. P. Lively, J. Phys. Chem. Lett., 2015, 6, 3437–3444 CrossRef CAS PubMed.
- T. D. Bennett, A. L. Goodwin, M. T. Dove, D. A. Keen, M. G. Tucker, E. R. Barney, A. K. Soper, E. G. Bithell, J.-C. Tan and A. K. Cheetham, Phys. Rev. Lett., 2010, 104, 115503 CrossRef PubMed.
- D. Umeyama, S. Horike, M. Inukai, T. Itakura and S. Kitagawa, J. Am. Chem. Soc., 2015, 137, 864–870 CrossRef CAS PubMed.
- R. Gaillac, P. Pullumbi, K. A. Beyer, K. W. Chapman, D. A. Keen, T. D. Bennett and F.-X. Coudert, Nat. Chem., 2017, 16, 1149–1154 CAS.
- H. Furukawa, U. Müller and O. M. Yaghi, Angew. Chem., Int. Ed., 2015, 54, 3417–3430 CrossRef CAS PubMed.
- O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714 CrossRef CAS PubMed.
- M. O'Keeffe, Chem. Soc. Rev., 2009, 38, 1215–1217 RSC.
- T. D. Bennett, A. K. Cheetham, A. H. Fuchs and F.-X. Coudert, Nat. Chem., 2017, 9, 11–16 CrossRef CAS PubMed.
- W. Xu, B. Tu, Q. Liu, Y. Shu, C.-C. Liang, C. S. Diercks, O. M. Yaghi, Y.-B. Zhang, H. Deng and Q. Li, Nat. Rev. Mater., 2020, 5, 764–779 CrossRef CAS.
- A. Simonov and A. L. Goodwin, Nat. Rev. Chem., 2020, 4, 657–673 CrossRef CAS.
- A. Simonov, T. De Baerdemaeker, H. L. B. Boström, M. L. Ríos Gómez, H. J. Gray, D. Chernyshov, A. Bosak, H.-B. Bürgi and A. L. Goodwin, Nature, 2020, 578, 256–260 CrossRef CAS PubMed.
- A. Helal, Z. H. Yamani, K. E. Cordova and O. M. Yaghi, Natl. Sci. Rev., 2017, 4, 296–298 CrossRef CAS.
- S. Ehrling, E. M. Reynolds, V. Bon, I. Senkovska, T. E. Gorelik, J. D. Evans, M. Rauche, M. Mendt, M. S. Weiss, A. Pöppl, E. Brunner, U. Kaiser, A. L. Goodwin and S. Kaskel, Adaptive response of a metal–organic framework through reversible disorder–disorder transitions, 2021, DOI:10.26434/chemrxiv.12326165.v1.
- G. C. Shearer, S. Chavan, S. Bordiga, S. Svelle, U. Olsbye and K. P. Lillerud, Chem. Mater., 2016, 28, 3749–3761 CrossRef CAS.
- F. C. N. Firth, M. J. Cliffe, D. Vulpe, M. Aragones-Anglada, P. Z. Moghadam, D. Fairen-Jimenez, B. Slater and C. P. Grey, J. Mater. Chem. A, 2019, 7, 7459–7469 RSC.
- J. Wang, L. Liu, C. Chen, X. Dong, Q. Wang, L. Alfilfil, M. R. AlAlouiin, K. Yao, J. Huang, D. Zhang and Y. Han, J. Mater. Chem. A, 2020, 8, 4464–4472 RSC.
- D. A. Keen and A. L. Goodwin, Nature, 2015, 521, 303–309 CrossRef CAS PubMed.
- B. E. G. Lucier, S. Chen and Y. Huang, Acc. Chem. Res., 2018, 51, 319–330 CrossRef CAS PubMed.
- D. Zhang, Y. Zhu, L. Liu, X. Ying, C.-E. Hsiung, R. Sougrat, K. Li and Y. Han, Science, 2018, 359, 675–679 CrossRef CAS PubMed.
- D. N. Johnstone, F. C. N. Firth, C. P. Grey, P. A. Midgley, M. J. Cliffe and S. M. Collins, J. Am. Chem. Soc., 2020, 142, 13081–13089 CrossRef CAS PubMed.
- S. Ling, R. I. Walton and B. Slater, Mol. Simul., 2015, 41, 1348–1356 CrossRef CAS.
- J. P. Dürholt, R. Galvelis and R. Schmid, Dalton Trans., 2016, 45, 4370–4379 RSC.
- S. M. J. Rogge, Faraday Discuss., 2021, 225, 271–285 RSC.
- J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850–13851 CrossRef PubMed.
- M. J. Cliffe, W. Wan, X. Zou, P. A. Chater, A. K. Kleppe, M. G. Tucker, H. Wilhelm, N. P. Funnell, F.-X. Coudert and A. L. Goodwin, Nat. Commun., 2014, 5, 4176 CrossRef CAS PubMed.
- Y. Feng, Q. Chen, M. Jiang and J. Yao, Ind. Eng. Chem. Res., 2019, 58, 17646–17659 CrossRef CAS.
- H. Wu, T. Yildirim and W. Zhou, J. Phys. Chem. Lett., 2013, 4, 925–930 CrossRef CAS PubMed.
- H. Wu, Y. S. Chua, V. Krungleviciute, M. Tyagi, P. Chen, T. Yildirim and W. Zhou, J. Am. Chem. Soc., 2013, 135, 10525–10532 CrossRef CAS PubMed.
- S. Jakobsen, D. Gianolio, D. S. Wragg, M. H. Nilsen, H. Emerich, S. Bordiga, C. Lamberti, U. Olsbye, M. Tilset and K. P. Lillerud, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125429 CrossRef.
- T. R. Welberry and B. D. Butler, Chem. Rev., 1995, 95, 2369–2403 CrossRef CAS.
- L. Liu, Z. Chen, J. Wang, D. Zhang, Y. Zhu, S. Ling, K.-W. Huang, Y. Belmabkhout, K. Adil, Y. Zhang, B. Slater, M. Eddaoudi and Y. Han, Nat. Chem., 2019, 11, 622–628 CrossRef CAS PubMed.
- S.-H. Lo, L. Feng, K. Tan, Z. Huang, S. Yuan, K.-Y. Wang, B.-H. Li, W.-L. Liu, G. S. Day, S. Tao, C.-C. Yang, T.-T. Luo, C.-H. Lin, S.-L. Wang, S. J. L. Billinge, K.-L. Lu, Y. J. Chabal, X. Zou and H.-C. Zhou, Nat. Chem., 2020, 12, 90–97 CrossRef PubMed.
- A. W. Thornton, R. Babarao, A. Jain, F. Trousselet and F.-X. Coudert, Dalton Trans., 2016, 45, 4352–4359 RSC.
- K. L. Svane, J. K. Bristow, J. D. Gale and A. Walsh, J. Mater. Chem. A, 2018, 6, 8507–8513 RSC.
- G. C. Shearer, S. Chavan, J. Ethiraj, J. G. Vitillo, S. Svelle, U. Olsbye, C. Lamberti, S. Bordiga and K. P. Lillerud, Chem. Mater., 2014, 26, 4068–4071 CrossRef CAS.
- G. Ye, D. Zhang, X. Li, K. Leng, W. Zhang, J. Ma, Y. Sun, W. Xu and S. Ma, ACS Appl. Mater. Interfaces, 2017, 9, 34937–34943 CrossRef CAS PubMed.
- J. M. Taylor, S. Dekura, R. Ikeda and H. Kitagawa, Chem. Mater., 2015, 27, 2286–2289 CrossRef CAS.
- M. J. Cliffe, J. A. Hill, C. A. Murray, F.-X. Coudert and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 11586–11592 RSC.
- M. Taddei, G. M. Schukraft, M. E. A. Warwick, D. Tiana, M. J. McPherson, D. R. Jones and C. Petit, J. Mater. Chem. A, 2019, 7, 23781–23786 RSC.
- L. Sarkisov, Dalton Trans., 2016, 45, 4203–4212 RSC.
- J. Choi, L.-C. Lin and J. C. Grossman, J. Phys. Chem. C, 2018, 122, 5545–5552 CrossRef CAS.
- S. Krause, V. Bon, I. Senkovska, U. Stoeck, D. Wallacher, D. M. Többens, S. Zander, R. S. Pillai, G. Maurin, F.-X. Coudert and S. Kaskel, Nature, 2016, 532, 348–352 CrossRef CAS PubMed.
- S. Krause, F. S. Reuter, S. Ehrling, V. Bon, I. Senkovska, S. Kaskel and E. Brunner, Chem. Mater., 2020, 32, 4641–4650 CrossRef CAS PubMed.
- A. Ludi, H.-U. Güdel and M. Ruegg, Inorg. Chem., 1970, 9, 2224–2227 CrossRef CAS.
- S. S. Kaye and J. R. Long, J. Am. Chem. Soc., 2005, 127, 6506–6507 CrossRef CAS PubMed.
- P. Franz, C. Ambrus, A. Hauser, D. Chernyshov, M. Hostettler, J. Hauser, L. Keller, K. Krämer, H. Stoeckli-Evans, P. Pattison, H.-B. Bürgi and S. Decurtins, J. Am. Chem. Soc., 2004, 126, 16472–16477 CrossRef CAS PubMed.
- D. Chernyshov and A. Bosak, Phase Transitions, 2010, 83, 115–122 CrossRef CAS.
- M. J. Cliffe, E. N. Keyzer, A. D. Bond, M. A. Astle and C. P. Grey, Chem. Sci., 2020, 11, 4430–4438 RSC.
- H. L. B. Boström, J. Bruckmoser and A. L. Goodwin, J. Am. Chem. Soc., 2019, 141, 17978–17982 CrossRef PubMed.
- S.-Y. Zhang, S. Jensen, K. Tan, L. Wojtas, M. Roveto, J. Cure, T. Thonhauser, Y. J. Chabal and M. J. Zaworotko, J. Am. Chem. Soc., 2018, 140, 12545–12552 CrossRef CAS PubMed.
- S. Abednatanzi, P. G. Derakhshandeh, H. Depauw, F.-X. Coudert, H. Vrielinck, P. Van Der Voort and K. Leus, Chem. Soc. Rev., 2019, 48, 2535–2565 RSC.
- X. Kong, H. Deng, F. Yan, J. Kim, J. A. Swisher, B. Smit, O. M. Yaghi and J. A. Reimer, Science, 2013, 341, 882–885 CrossRef CAS PubMed.
- H. Deng, C. J. Doonan, H. Furukawa, R. B. Ferreira, J. Towne, C. B. Knobler, B. Wang and O. M. Yaghi, Science, 2010, 327, 846–850 CrossRef CAS PubMed.
- S. Yuan, W. Lu, Y.-P. Chen, Q. Zhang, T.-F. Liu, D. Feng, X. Wang, J. Qin and H.-C. Zhou, J. Am. Chem. Soc., 2015, 137, 3177–3180 CrossRef CAS PubMed.
- W. Guo, W. Xia, K. Cai, Y. Wu, B. Qiu, Z. Liang, C. Qu and R. Zou, Small, 2017, 13, 1702049 CrossRef PubMed.
- T. Fukushima, S. Horike, H. Kobayashi, M. Tsujimoto, S. Isoda, M. L. Foo, Y. Kubota, M. Takata and S. Kitagawa, J. Am. Chem. Soc., 2012, 134, 13341–13347 CrossRef CAS PubMed.
- F. Trousselet, A. Archereau, A. Boutin and F.-X. Coudert, J. Phys. Chem. C, 2016, 120, 24885–24894 CrossRef CAS.
- M. Taddei, D. Tiana, N. Casati, J. A. van Bokhoven, B. Smit and M. Ranocchiari, Phys. Chem. Chem. Phys., 2017, 19, 1551–1559 RSC.
- K. A. Lomachenko, J. Jacobsen, A. L. Bugaev, C. Atzori, F. Bonino, S. Bordiga, N. Stock and C. Lamberti, J. Am. Chem. Soc., 2018, 140, 17379–17383 CrossRef CAS PubMed.
- Z. Ji, T. Li and O. M. Yaghi, Science, 2020, 369, 674–680 CrossRef CAS PubMed.
- A. F. Sapnik, H. S. Geddes, E. M. Reynolds, H. H.-M. Yeung and A. L. Goodwin, Chem. Commun., 2018, 54, 9651–9654 RSC.
- W. Schrimpf, J. Jaing, Z. Ji, P. Hirschle, D. C. Lamb, O. M. Yaghi and S. Wuttke, Nat. Commun., 2018, 9, 1647 CrossRef PubMed.
- K. W. P. Orr, S. M. Collins, E. M. Reynolds, F. Nightingale, H. L. B. Boström, S. J. Cassidy, D. M. Dawson, S. E. Ashbrook, O. V. Magdysyuk, P. A. Midgley, A. L. Goodwin and H. H.-M. Yeung, Chem. Sci., 2021 10.1039/D0SC03940C.
- B. Lerma-Berlanga, C. R. Ganivet, N. Almora-Barrios, S. Tatay, Y. Peng, J. Albero, O. Fabelo, J. González-Platas, H. García, N. M. Padial and C. Martí-Gastaldo, J. Am. Chem. Soc., 2021, 143, 1798–1806 CrossRef CAS PubMed.
- M. Paściak, T. R. Welberry, J. Kulda, M. Kempa and J. Hlinka, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 224109 CrossRef.
- E. M. Reynolds, E. H. Wolpert, A. R. Overy, L. Mizzi, A. Simonov, J. N. Grima, S. Kaskel and A. L. Goodwin, Faraday Discuss., 2021, 225, 241–254 RSC.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472 CrossRef CAS PubMed.
- T. W. Kemnitzer, C. B. L. Tschense, T. Wittmann, E. A. Rössler and J. Senker, Langmuir, 2018, 34, 12538–12548 CrossRef CAS PubMed.
- P. V. Dau and S. M. Cohen, Chem. Commun., 2014, 50, 12154–12157 RSC.
- N. Klein, C. Kerzog, M. Sabo, I. Senkovska, J. Getzschmann, S. Paasch, M. R. Lohe, E. Brunner and S. Kaskel, Phys. Chem. Chem. Phys., 2010, 12, 11778–11784 RSC.
- P. S. Petkov, V. Bon, C. L. Hobday, A. B. Kuc, P. Melix, S. Kaskel, T. Düren and T. Heine, Phys. Chem. Chem. Phys., 2019, 21, 674–680 RSC.
- J. M. Bermúdez-García, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga and M. A. Señarís-Rodgríguez, Nat. Commun., 2017, 8, 15715 CrossRef PubMed.
- P. Lloveras, E. Stern-Taulats, M. Barrio, J.-L. Tamarit, S. Crossley, W. Li, V. Pomjakushin, A. Planes, L. Mañosa, N. D. Mathur and X. Moya, Nat. Commun., 2015, 6, 8801 CrossRef CAS PubMed.
- P. Schiffer, A. P. Ramirez, D. A. Huse and A. J. Valentino, Phys. Rev. Lett., 1994, 73, 2500–2503 CrossRef CAS PubMed.
- P. J. Saines, J. A. M. Paddison, P. M. M. Thygesen and M. G. Tucker, Mater. Horiz., 2015, 2, 528–535 RSC.
- J. M. Bulled, J. A. M. Paddison, A. Wildes, E. Lhotel, B. Pato-Doldan, L. C. Gomez-Aguirre, P. J. Saines and A. L. Goodwin, 2021, arXiv:2012.10361.
- H. L. B. Boström and A. L. Goodwin, Acc. Chem. Res., 2021, 54, 1288–1297 CrossRef PubMed.
- K. T. Butler, A. Walsh, A. K. Cheetham and G. Kieslich, Chem. Sci., 2016, 7, 6316–6324 RSC.
- S. Leubner, V. E. G. Bengtsson, A. K. Inge, M. Wahiduzzaman, F. Steinke, A. Jaworski, H. Xu, S. Halis, P. Rönfeldt, H. Reinsch, G. Maurin, X. Zou and N. Stock, Dalton Trans., 2020, 49, 3088–3092 RSC.
- J. Cruddas and B. J. Powell, J. Am. Chem. Soc., 2019, 141, 19790–19799 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |