From a P4 butterfly scaffold to cyclo- and catena-P4 units†
Julian
Müller
,
Gábor
Balázs
and
Manfred
Scheer
 *
*
Institut für Anorganische Chemie, Universität Regensburg, Regensburg 93040, Germany. E-mail: manfred.scheer@ur.de; Web: http://www.uni-regensburg.de/chemie-pharmazie/anorganische-chemie-scheer/
First published on 25th January 2021
Abstract
The reactivity of [{Cp′′′Fe(CO)2}2(μ,η1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-P4)] (1) towards half-sandwich complexes of Ru(II), Rh(III), and Ir(III) is studied. The coordination of these Lewis acids leads to a rearrangement of the P4 butterfly unit to form complexes with either an aromatic cyclo-P4R2 unit (R = Cp′′′Fe(CO)2) or a catena-tetraphosphaene entity.
1-P4)] (1) towards half-sandwich complexes of Ru(II), Rh(III), and Ir(III) is studied. The coordination of these Lewis acids leads to a rearrangement of the P4 butterfly unit to form complexes with either an aromatic cyclo-P4R2 unit (R = Cp′′′Fe(CO)2) or a catena-tetraphosphaene entity.
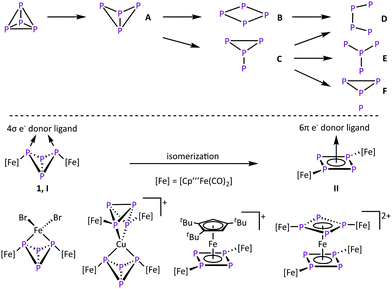
The activation of small molecules is an active research topic. This research area focuses mainly on inert molecules such as H2,1,2 N2,1,3 CO2,4 and CH41 since their functionalisation might be important to solve e.g. energy problems. However, this research area also includes highly reactive compounds such as white phosphorus (P4) where the focus is to control its reactivity. In industrial applications, P4 is an important starting material for the synthesis of organophosphorus derivatives. However, their synthesis proceeds via multistep reactions with low atom economic efficiency. To increase the sustainability, a direct and selective functionalization is desired. Therefore, the degradation of tetrahedral P4 in the presence of reactive main group compounds5 and transition metal complexes6 is investigated (Scheme 1, top). Typically, harsh reaction conditions are needed to generate these reactive metal species.7–12 In the field of P4 conversion, work was done by the Scherer group, e.g. by showing that the photolysis of [Cp′′Fe(CO)2]2 (Cp′′ = η5-C5H3tBu2) in the presence of P4 leads to [Cp′′2Fe2(CO)nP4] (n = 3, 4 type A, n = 2 type B, n = 1 and n = 0 type D) by successive decarbonylation (Scheme 1, top).8 Comparable results were obtained via thermolytic reactions of P4 with [Cp′′′Fe(CO)2]29 (Cp′′′ = η5-C5H2tBu3), [Cp*Co(CO)2]13 (Cp* = η5-C5Me5) and [Cp*Co(iPr2Im)(η2-C2H4)]10,14 (iPr2Im = 1,3-di-isopropylimidazolein-2-ylidene), respectively. The thermolysis of [Cp*Ni(CO)]2 leads to complexes of the type E.15 In molten GaCl3, P4 can also be converted by in situ generated Ph2P+,12 leading to the insertion of phosphonium cations into several P–P bonds to form cationic P4(PPh2) (type A), P4(PPh2)2 (type C) and P4(PPh2)3 (type F) compounds.
Conversions of P4 at mild conditions is an overall goal in this chemistry, which can be achieved with coordinative unsaturated complexes,16,17 like the triple-decker complex [(Cp′′′Co)2(μ-C7H8)].18 In solution it dissociates into the 14-valence-electron (VE) fragment [Cp′′′Co] and reacts readily with complexes bearing intact tetrahedral P4 units to cyclo-P4 (type B) containing derivatives.16 On the other hand we showed that the formation of the butterfly complex [{Cp′′′Fe(CO)2}2(μ,η1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-P4)]9 (1) by the reaction of [Cp′′′Fe(CO)2]2 with P4 does not need thermal activation and already occurs quantitatively at room temperature.19 The reactivity of 1 is very versatile, since the reaction with PhC
1-P4)]9 (1) by the reaction of [Cp′′′Fe(CO)2]2 with P4 does not need thermal activation and already occurs quantitatively at room temperature.19 The reactivity of 1 is very versatile, since the reaction with PhC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CPh or P
CPh or P![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CtBu gives access to triphospholyl- and tetraphospholyl-containing iron complexes.20 We could also show that 1 has the properties of a chelate ligand (Scheme 1, bottom, coordination type I).21,22 Here, the P4 butterfly scaffold coordinates to various transition metal-based Lewis acids via the two “wing tip” phosphorus atoms. However, in the presence of a d6 metal Lewis acid like Fe(II) that bears ligands that can easily be substituted, an unusual isomerisation of the butterfly unit (4σ e− donor, coordination type I) to an aromatic cyclo-P4R2 unit (6π e− donor, R = [Cp′′′Fe(CO)2], coordination type II) is observed, giving access to the unique homoleptic octaphosphorus sandwich complex [{(Cp′′′Fe(CO)2)2(μ3,η4
CtBu gives access to triphospholyl- and tetraphospholyl-containing iron complexes.20 We could also show that 1 has the properties of a chelate ligand (Scheme 1, bottom, coordination type I).21,22 Here, the P4 butterfly scaffold coordinates to various transition metal-based Lewis acids via the two “wing tip” phosphorus atoms. However, in the presence of a d6 metal Lewis acid like Fe(II) that bears ligands that can easily be substituted, an unusual isomerisation of the butterfly unit (4σ e− donor, coordination type I) to an aromatic cyclo-P4R2 unit (6π e− donor, R = [Cp′′′Fe(CO)2], coordination type II) is observed, giving access to the unique homoleptic octaphosphorus sandwich complex [{(Cp′′′Fe(CO)2)2(μ3,η4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-P4)}2Fe][PF6]2.22a To obtain deeper insight into the isomerisation reaction of 1, it was reacted with various 3d metal Lewis acids to give mainly coordination as a chelating ligand, but in one case an isomerisation via a redoxreaction to Co(III) occurred.22b Since the availability of 3d6 metal-based Lewis acids like Fe(II) and Co(III) is limited, the question to use 4d and 5d transition metal complexes, which typically yield products with a higher stability, came into mind. This might alter the reaction outcome in general. Herein, we report on the reactivity of 1 towards Ru(II)-, Rh(III)-, and Ir(III)-based Lewis acids, surprisingly leading exclusively to an isomerisation to form cyclo- and also catena-P4 containing complexes.
1-P4)}2Fe][PF6]2.22a To obtain deeper insight into the isomerisation reaction of 1, it was reacted with various 3d metal Lewis acids to give mainly coordination as a chelating ligand, but in one case an isomerisation via a redoxreaction to Co(III) occurred.22b Since the availability of 3d6 metal-based Lewis acids like Fe(II) and Co(III) is limited, the question to use 4d and 5d transition metal complexes, which typically yield products with a higher stability, came into mind. This might alter the reaction outcome in general. Herein, we report on the reactivity of 1 towards Ru(II)-, Rh(III)-, and Ir(III)-based Lewis acids, surprisingly leading exclusively to an isomerisation to form cyclo- and also catena-P4 containing complexes.
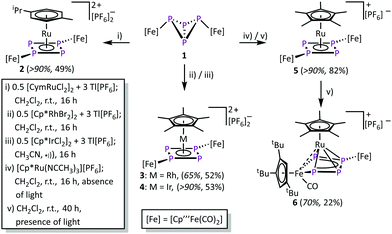
A method to generate unsaturated transition metal fragments in solution is to treat the corresponding metal halide precursor with an excess of a thallium(I) salt that bears a weakly coordinating anion to eliminate poorly soluble thallium(I) halides. This was used to generate the solvent-stabilized (CH3CN or CH2Cl2) species “[CymRu][PF6]2” (Cym = para-cymene) and “[Cp*M][PF6]2” (M = Rh, Ir) in situ. These metal fragments react smoothly with 1 leading to [{Cp′′′Fe(CO)2}2(μ3,η4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
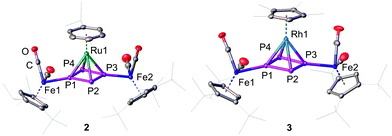
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-P4)(LM)][PF6]2 (2: LM = CymRu; 3: LM = Cp*Rh; 4: LM = Cp*Ir; Scheme 2). Complexes 2–4 feature all cyclo-P4R2 units that coordinate the central [LM]2+ fragments. This finding reveals that the isomerisation of the P4 butterfly moiety (4σ e− donor, coordination type I) to a cyclo-P4R2 ligand (6π e− donor, coordination type II) is a general feature, not only bound to 3d metals, if the 18 VE rule can be fulfilled and a d6 metal is present. The molecular structures of 2–4 shows, that the central metal atom is coordinated in an η4 fashion by the cyclo-P4R2 unit (Fig. 1). The similar covalent radii of Ru (rRu = 1.25 Å), Rh (rRh = 1.25 Å), and Ir (rIr = 1.22 Å) lead to similar M–P4,cent. distances of 1.8890(2) Å in 2, 1.8939(3) Å in 3 and 1.8915(2) Å in 4.23 Compared to [{Cp′′′Fe(CO)2}2(μ3,η4
1-P4)(LM)][PF6]2 (2: LM = CymRu; 3: LM = Cp*Rh; 4: LM = Cp*Ir; Scheme 2). Complexes 2–4 feature all cyclo-P4R2 units that coordinate the central [LM]2+ fragments. This finding reveals that the isomerisation of the P4 butterfly moiety (4σ e− donor, coordination type I) to a cyclo-P4R2 ligand (6π e− donor, coordination type II) is a general feature, not only bound to 3d metals, if the 18 VE rule can be fulfilled and a d6 metal is present. The molecular structures of 2–4 shows, that the central metal atom is coordinated in an η4 fashion by the cyclo-P4R2 unit (Fig. 1). The similar covalent radii of Ru (rRu = 1.25 Å), Rh (rRh = 1.25 Å), and Ir (rIr = 1.22 Å) lead to similar M–P4,cent. distances of 1.8890(2) Å in 2, 1.8939(3) Å in 3 and 1.8915(2) Å in 4.23 Compared to [{Cp′′′Fe(CO)2}2(μ3,η4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-P4)(Cp′′′Fe)][PF6], the distances are approx. 0.13 Å longer (1.7609(5) Å) which is attributed to the smaller covalent radius of Fe (rFe = 1.16 Å).22a The P–P bond lengths are with 2.1356(7)–2.1481(7) Å (2), 2.1433(8)–2.1459(8) Å (3), and 2.1488(6)–2.1518(6) Å (4) in the range between a P–P single (2.20–2.25 Å) and a P
1-P4)(Cp′′′Fe)][PF6], the distances are approx. 0.13 Å longer (1.7609(5) Å) which is attributed to the smaller covalent radius of Fe (rFe = 1.16 Å).22a The P–P bond lengths are with 2.1356(7)–2.1481(7) Å (2), 2.1433(8)–2.1459(8) Å (3), and 2.1488(6)–2.1518(6) Å (4) in the range between a P–P single (2.20–2.25 Å) and a P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bond (2.00–2.05 Å). These bond lengths are in good agreement with the determined P–P distances in the isolated cyclo-P42− anion (2.146(1) and 2.1484(9) Å) in Cs2P4·2NH324 as well as in other complexes with formal P42− ligands.16,22,25 The cyclo-P4 units exhibit similar diamond-shaped geometries in all three complexes, which was also found in the other complexes derived from 1.22
P double bond (2.00–2.05 Å). These bond lengths are in good agreement with the determined P–P distances in the isolated cyclo-P42− anion (2.146(1) and 2.1484(9) Å) in Cs2P4·2NH324 as well as in other complexes with formal P42− ligands.16,22,25 The cyclo-P4 units exhibit similar diamond-shaped geometries in all three complexes, which was also found in the other complexes derived from 1.22
The 1H NMR spectrum of 2 in CD2Cl2 shows two singlets at δ = 1.33 and 1.45 ppm and a multiplet at δ = 5.66 ppm with an integral ratio of 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 for the two Cp′′′ ligands. The signals at δ = 1.35, 2.59, and 6.71 ppm can be assigned to the Cym ligand. The 1H NMR spectra of 3 and 4 show similar signals for the Cp′′′ ligands while the singlet of the Cp* signal can be detected at δ = 2.46 (3, CD2Cl2) and 2.64 ppm (4, CD3CN), respectively. The 31P{1H} NMR spectra of 2 and 4 show each an AA′XX′ spin system for the cation (2 in CD2Cl2: δ = 148.9 and 102.9 ppm; 4 in CD3CN: δ = 102.3 and 62.7 ppm).‡ The cation of 3 shows two signals at δ = 169.8 and 121.1 ppm that are part of an AA′MM′X spin system (X corresponds to Rh) caused by the NMR-active 103Rh nuclei (I = 1/2, 100% natural abundance).‡ However, the 31P{1H} NMR spectrum of the reaction solution of 3 reveals an additional set of signals at δ = 201.7, 157.7 and 125.7 ppm corresponding to a byproduct (AA′MNX spin system, X corresponds to Rh),‡ in a ratio of 3 to the byproduct of approximately 2
4 for the two Cp′′′ ligands. The signals at δ = 1.35, 2.59, and 6.71 ppm can be assigned to the Cym ligand. The 1H NMR spectra of 3 and 4 show similar signals for the Cp′′′ ligands while the singlet of the Cp* signal can be detected at δ = 2.46 (3, CD2Cl2) and 2.64 ppm (4, CD3CN), respectively. The 31P{1H} NMR spectra of 2 and 4 show each an AA′XX′ spin system for the cation (2 in CD2Cl2: δ = 148.9 and 102.9 ppm; 4 in CD3CN: δ = 102.3 and 62.7 ppm).‡ The cation of 3 shows two signals at δ = 169.8 and 121.1 ppm that are part of an AA′MM′X spin system (X corresponds to Rh) caused by the NMR-active 103Rh nuclei (I = 1/2, 100% natural abundance).‡ However, the 31P{1H} NMR spectrum of the reaction solution of 3 reveals an additional set of signals at δ = 201.7, 157.7 and 125.7 ppm corresponding to a byproduct (AA′MNX spin system, X corresponds to Rh),‡ in a ratio of 3 to the byproduct of approximately 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Despite several attempts, the exact structure of the byproduct could not be clarified yet, but, according to the NMR features, the presence of a cyclo-P4 unit bound to a 103Rh core is very likely.
1. Despite several attempts, the exact structure of the byproduct could not be clarified yet, but, according to the NMR features, the presence of a cyclo-P4 unit bound to a 103Rh core is very likely.
The reaction of 1 and [Cp*Ru(NCCH3)3][PF6] in the absence of light yields [{Cp′′′Fe(CO)2}2(μ3,η4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-P4)(Cp*Ru)][PF6] (5). During this reaction, all acetonitrile ligands are substituted by 1, while the P4 core isomerises to a cyclic P4 unit. Despite numerous attempts, it was not possible to isolate 5 in crystalline form. However, the 31P{1H} NMR spectrum of 5 in CD2Cl2 shows an AA′XX′ spin system at δ = 82.0 and 51.6 ppm unambiguously confirms its identity.‡ The chemical shift values as well as the spin system compare well to that found for 2–4 and [{Cp′′′Fe(CO}2)2(μ3,η4
1-P4)(Cp*Ru)][PF6] (5). During this reaction, all acetonitrile ligands are substituted by 1, while the P4 core isomerises to a cyclic P4 unit. Despite numerous attempts, it was not possible to isolate 5 in crystalline form. However, the 31P{1H} NMR spectrum of 5 in CD2Cl2 shows an AA′XX′ spin system at δ = 82.0 and 51.6 ppm unambiguously confirms its identity.‡ The chemical shift values as well as the spin system compare well to that found for 2–4 and [{Cp′′′Fe(CO}2)2(μ3,η4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-P4)(Cp′′′Fe)][PF6]22 (δ = 78.9, 56.8 and 45.6 ppm).
1-P4)(Cp′′′Fe)][PF6]22 (δ = 78.9, 56.8 and 45.6 ppm).
Performing the reaction of 1 with [Cp*Ru(NCCH3)3][PF6] in the presence of light, a different reaction outcome is observed. Surprisingly, the main product is not 5, but a subsequent CO elimination, followed by the insertion of the [Cp′′′Fe(CO)] fragment into one of the adjacent P–P bonds, leads to [{Cp′′′Fe(CO)2}{Cp′′′Fe(CO)}(μ3,η4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-P4)(Cp*Ru)][PF6] (6) in moderate yield (22%, 70% according to 31P NMR spectroscopy). Complex 6 features a metallo-tetraphosphaene unit and represents a formally twofold activated P4 butterfly complex 1. The formation of 6 also highlights the high diversity in different binding modes of the P4 unit in 1. Furthermore, 6 should be handled with caution, as further treatment with UV light leads to subsequent transformations and finally to decomposition.
1-P4)(Cp*Ru)][PF6] (6) in moderate yield (22%, 70% according to 31P NMR spectroscopy). Complex 6 features a metallo-tetraphosphaene unit and represents a formally twofold activated P4 butterfly complex 1. The formation of 6 also highlights the high diversity in different binding modes of the P4 unit in 1. Furthermore, 6 should be handled with caution, as further treatment with UV light leads to subsequent transformations and finally to decomposition.
The insertion of Fe1 into the P1–P4 bond leads to the formation of the 1S-2R-3R-4R-5S configuration (Fig. 2) while insertion into the P3–P4 bond leads to the formation of the 1R-2S-3S-4S-5R configuration (Fig. S5, ESI†). The two enantiomers form a racemate and are both present in the solid state structure. The central FeP4 metallacycle reveals an envelope conformation with an almost planar catena-P4 unit (dihedral angle P1-P2-P3-P4 of 7.73(3)°). The three Fe–P distances vary from 2.2413(6) to 2.2539(6) Å and are in the range of typical Fe–P single bonds.21–23 The P–P bond distances vary from 2.1335(8) to 2.1446(8) Å and are in a range between a P–P single and a P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bond. The [Cp*Ru] fragment is located over the center of the metallocycle with two shorter Ru–P distances (Ru1–P1
P double bond. The [Cp*Ru] fragment is located over the center of the metallocycle with two shorter Ru–P distances (Ru1–P1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.3592(5); Ru1–P4
2.3592(5); Ru1–P4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.3513(6) Å) and two longer Ru–P distances (Ru1–P2
2.3513(6) Å) and two longer Ru–P distances (Ru1–P2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.4454(5); Ru1–P3 2.4469(6) Å). This results in a shift of the ruthenium fragment towards the [Cp′′′Fe1(CO)] fragment and raises the question of a Ru–Fe interaction. While the Ru1–Fe1 distance of 2.9052(4) Å is longer than a predicted single bond (2.41 Å),23 the distance is still significantly smaller than the sum of the van der Waals radii (4.90 Å).26 A complex similar to 6 is for example the dirhodium complex [(Cp+Rh(CO))(μ,η4
2.4454(5); Ru1–P3 2.4469(6) Å). This results in a shift of the ruthenium fragment towards the [Cp′′′Fe1(CO)] fragment and raises the question of a Ru–Fe interaction. While the Ru1–Fe1 distance of 2.9052(4) Å is longer than a predicted single bond (2.41 Å),23 the distance is still significantly smaller than the sum of the van der Waals radii (4.90 Å).26 A complex similar to 6 is for example the dirhodium complex [(Cp+Rh(CO))(μ,η4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-P4){Cp+Rh}] (III, Cp+ = η5-C5Me4Et).11 Although, III has two electrons more than 6, the P–P bond lengths (2.150(3)–2.160(3) Å) are comparable. However, in III, no metal–metal interaction was observed since the η4-coordinated [Cp+Rh] fragment is located over the center of the P4 chain. The complex [K(dme)2][(MesBIAN)Co(μ,η4
2-P4){Cp+Rh}] (III, Cp+ = η5-C5Me4Et).11 Although, III has two electrons more than 6, the P–P bond lengths (2.150(3)–2.160(3) Å) are comparable. However, in III, no metal–metal interaction was observed since the η4-coordinated [Cp+Rh] fragment is located over the center of the P4 chain. The complex [K(dme)2][(MesBIAN)Co(μ,η4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-P4)Ga(nacnac)]27 (IV, dme = dimethoxyethane, MesBIAN = 1,2-bis(2,4,6-dimethylphenylimino)acenaphthene, nacnac = CH[CMeN(2,6-iPr2C6H3)]2) exhibits a similar, however main group-based, heteroatomic core, but without significant metal–metal interaction. The bond lengths (2.1198(7)–2.1286(7) Å) are comparable to the ones in 6. A similar carbon-based complex is [{CpFe(CO)}{μ,η4
2-P4)Ga(nacnac)]27 (IV, dme = dimethoxyethane, MesBIAN = 1,2-bis(2,4,6-dimethylphenylimino)acenaphthene, nacnac = CH[CMeN(2,6-iPr2C6H3)]2) exhibits a similar, however main group-based, heteroatomic core, but without significant metal–metal interaction. The bond lengths (2.1198(7)–2.1286(7) Å) are comparable to the ones in 6. A similar carbon-based complex is [{CpFe(CO)}{μ,η4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-(CR-(CH)2-CR)}(Cp*Ru)] (R = CMe2OH) where the [Cp*Ru] fragment is η5-coordinated by the cyclopentadiene ring of iron.28 The reported Ru–Fe distances of 2.6688(7)/2.6743(7) Å are shorter compared to the one in 6 and are described as Ru–Fe single bonds.
2-(CR-(CH)2-CR)}(Cp*Ru)] (R = CMe2OH) where the [Cp*Ru] fragment is η5-coordinated by the cyclopentadiene ring of iron.28 The reported Ru–Fe distances of 2.6688(7)/2.6743(7) Å are shorter compared to the one in 6 and are described as Ru–Fe single bonds.
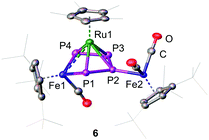 | ||
| Fig. 2 Cationic part of the 1S-2R-3R-4R-5S enantiomer of 6 in the solid state. Hydrogen atoms are omitted for clarity. A.d.p. are shown at 50% probability level. | ||
The 1H NMR as well as the 31P{1H} NMR spectrum (CD2Cl2) of a crystalline sample of 6 points to the presence of two conformers in solution which are formed in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.7. At room temperature, both conformers are involved in dynamic processes leading to signal broadening. This is most likely caused by the rotation of either one of the Cp′′′ ligands or the whole [Cp′′′Fe(CO)2] fragment. At lower temperatures, the rotation is slowed down resulting in sharp signals.‡ The 31P{1H} NMR spectrum shows an AMXY spin system for both isomers which resonate at similar chemical shifts so that they mainly overlap. The signals at δ = 501.1, 465.5, 144.1 and 126.0 ppm can be assigned to the main species while the signals at δ = 500.9, 457.0, 145.2 and 126.5 ppm correspond to the minor species. With chemical shifts and coupling constants (Table S7, ESI†) being almost identical, the structure of the two species must be very similar.‡ However, these findings compare well to [(Cp′′Fe)(μ,η5
1.7. At room temperature, both conformers are involved in dynamic processes leading to signal broadening. This is most likely caused by the rotation of either one of the Cp′′′ ligands or the whole [Cp′′′Fe(CO)2] fragment. At lower temperatures, the rotation is slowed down resulting in sharp signals.‡ The 31P{1H} NMR spectrum shows an AMXY spin system for both isomers which resonate at similar chemical shifts so that they mainly overlap. The signals at δ = 501.1, 465.5, 144.1 and 126.0 ppm can be assigned to the main species while the signals at δ = 500.9, 457.0, 145.2 and 126.5 ppm correspond to the minor species. With chemical shifts and coupling constants (Table S7, ESI†) being almost identical, the structure of the two species must be very similar.‡ However, these findings compare well to [(Cp′′Fe)(μ,η5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-P4){Cp′′Fe(CO)}]8 (δ = 567.2 and 169.1 ppm) and IV27 (δ = 74.0 and −125.4 ppm) showing both an AA′XX′ spin system for the catena-P4 unit. The dirhodium complex III11 (δ = 201.4 and 150.8 ppm) reveals an AA′NMXX′ spin system (N and M correspond to Rh).
2-P4){Cp′′Fe(CO)}]8 (δ = 567.2 and 169.1 ppm) and IV27 (δ = 74.0 and −125.4 ppm) showing both an AA′XX′ spin system for the catena-P4 unit. The dirhodium complex III11 (δ = 201.4 and 150.8 ppm) reveals an AA′NMXX′ spin system (N and M correspond to Rh).
To obtain deeper insight into the electronic structure of 6, DFT calculations at the BP86/def2-TZVP level were performed which show the absence of a direct Ru1–Fe1 bond. Instead, a multi-center bond with bond contributions of Ru1 = 40%, Fe1 = 25% and P1 = P4 = 17.5% is present. The Wiberg Bond Index of the Ru1–Fe1 bond of only 0.32 is in good agreement with the multi-center bond description. The corresponding localised molecular orbital, which contains 41% Ru, 24% Fe and 35% P atomic orbital contribution, is depicted in Fig. 3 (left). We could not locate a bond-critical point between Ru and Fe1 by the analysis of the topology of the electron density of 6 by means of the Atoms in Molecules (AIM) approach. However, a ring-critical point could be detected, situated in the plane spanned by Ru, Fe1, P1 and P4. The frontier orbitals in 6 are depicted on the right hand side in Fig. 3. The highest occupied molecular orbital (HOMO) shows mainly the lone pairs of the phosphorus atoms while both HOMO−1 and HOMO−2 show mainly bonding interaction within the P4Fe unit. The lowest unoccupied molecular orbital (LUMO) shows mainly nonbonding orbitals at the phosphorus as well as the metal atoms.
 | ||
| Fig. 3 Left: The localised molecular orbital of 6 showing the interaction between Ru, Fe and P. Right: Frontier orbitals in 6 at the BP86/def2-TZVP level. | ||
Furthermore, we were interested in why 5 transforms into 6, while the transformation from 2 to the hypothetical complex [{Cp′′′Fe(CO)2}{Cp′′′Fe(CO)}(μ3,η4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-P4)(CymRu)]2+ (7) is not observed under the same conditions. Therefore, we determined the natural charge distribution of the four complexes.‡ According to this, the [CymRu]2+ fragments act as weak electron acceptors, while [Cp*Ru]+ act as strong electron acceptors. In contrast, the cyclo-P4R2 (R = Cp′′′Fe(CO)2) units in 2 and 5 act as strong electron donors. During the transformation from cyclo-P4R2 units to catena-P4 units, this effect is even enhanced. Therefore, it is suggested that the further transformation is dependent on the nature of the ligands that are attached to the central Lewis acid.
1-P4)(CymRu)]2+ (7) is not observed under the same conditions. Therefore, we determined the natural charge distribution of the four complexes.‡ According to this, the [CymRu]2+ fragments act as weak electron acceptors, while [Cp*Ru]+ act as strong electron acceptors. In contrast, the cyclo-P4R2 (R = Cp′′′Fe(CO)2) units in 2 and 5 act as strong electron donors. During the transformation from cyclo-P4R2 units to catena-P4 units, this effect is even enhanced. Therefore, it is suggested that the further transformation is dependent on the nature of the ligands that are attached to the central Lewis acid.
The disfavored formation of 7 in comparison to 6 is also highlighted by the calculated reaction energies at the B3LYP level (solvation effects incorporated by the COSMO model). The calculations showed that the formation of 6 starting from 5 is endothermic by 95.87 kJ mol−1. However, these calculations do not take into account the terms of entropy which should have a mayor impact due to the release of CO gas during this process. The formation of 7 starting from 2 would be endothermic by 150.87 kJ mol−1 which shows that, in principle, the formation of 6 in comparison to 7 would be energetically less disfavored.
In summary, we could show that the P4 butterfly complex 1 can easily be activated by a vast variety of different d6 metal-based Lewis acids, leading to the formation of 2–5 bearing cyclo-P4R2 units. However, by using [Cp*Ru(NCCH3)3][PF6] in the presence of light 6 is formed. Complex 6 exhibits an iron-tetraphosphaene unit which is formed via CO elimination and the subsequent insertion of the iron fragment into a P–P bond. However, this second activation step is not observed for complexes 2–4 under the same reaction conditions. DFT calculations confirmed that the transformation is strongly dependent on the nature of the ligand at the Lewis acid. The formation of different complexes under mild conditions highlights the high diversity of binding modes of the P4 unit in 1.
This work was supported by the Deutsche Forschungsgemeinschaft (Sche 384/38-1).
Conflicts of interest
There are no conflicts to declare.Notes and references
- C. Chow, M. Taoufik and E. A. Quadrelli, Eur. J. Inorg. Chem., 2011, 1349 CrossRef CAS.
- (a) D. W. Stephan, Dalton Trans., 2009, 3129 RSC; (b) G. C. Welch, R. R. S. Juan, J. D. Masuda and D. W. Stephan, Science, 2006, 314, 1124 CrossRef CAS.
- (a) D. M. Ermert and L. J. Murray, Dalton Trans., 2016, 45, 14499 RSC; (b) N. Hazari, Chem. Soc. Rev., 2010, 39, 4044 RSC.
- (a) M. Behrens, Angew. Chem., Int. Ed., 2014, 53, 12022 CrossRef CAS; (b) V. P. Indrakanti, J. D. Kubicki and H. H. Schobert, Energy Environ. Sci., 2009, 2, 745 RSC.
- (a) M. Scheer, G. Balázs and A. Seitz, Chem. Rev., 2010, 110, 4236 CrossRef CAS; (b) N. A. Giffin and J. D. Masuda, Coord. Chem. Rev., 2011, 255, 1342 CrossRef CAS.
- (a) B. M. Cossairt, N. A. Piro and C. C. Cummins, Chem. Rev., 2010, 110, 4164 CrossRef CAS; (b) M. Caporali, L. Gonsalvi, A. Rossin and M. Peruzzini, Chem. Rev., 2010, 110, 4178 CrossRef CAS.
- (a) S. Heinl, A. Y. Timoshkin, J. Müller and M. Scheer, Chem. Commun., 2018, 54, 2244 RSC; (b) M. Scheer, K. Schuster and U. Becker, Phosphorus, Sulfur Silicon Relat. Elem., 1996, 109, 141 Search PubMed.
- O. J. Scherer, G. Schwarz and G. Wolmershäuser, Z. Anorg. Allg. Chem., 1996, 622, 951 CrossRef CAS.
- O. J. Scherer, T. Hilt and G. Wolmershäuser, Organometallics, 1998, 17, 4110 CrossRef CAS.
- S. Dürr, D. Ertler and U. Radius, Inorg. Chem., 2012, 51, 3904 CrossRef.
- O. J. Scherer, M. Swarowsky, H. Swarowsky and G. Wolmershäuser, Angew. Chem., Int. Ed. Engl., 1988, 27, 694 CrossRef.
- J. J. Weigand, M. Holthausen and R. Fröhlich, Angew. Chem., Int. Ed., 2009, 48, 295 CrossRef CAS.
- O. J. Scherer, M. Swarowsky and G. Wolmershaeuser, Organometallics, 1989, 8, 841 CrossRef CAS.
- B. Zarzycki, F. M. Bickelhaupt and U. Radius, Dalton Trans., 2013, 42, 7468 RSC.
- O. J. Scherer, T. Dave, J. Braun and G. Wolmershäuser, J. Organomet. Chem., 1988, 350, C20–C24 CrossRef CAS.
- M. Modl, S. Heinl, G. Balázs, F. Delgado Calvo, M. Caporali, G. Manca, M. Keilwerth, K. Meyer, M. Peruzzini and M. Scheer, Chem. – Eur. J., 2019, 25, 6300 CrossRef CAS.
- (a) D. Yakhvarov, P. Barbaro, L. Gonsalvi, S. Mañas Carpio, S. Midollini, A. Orlandini, M. Peruzzini, O. Sinyashin and F. Zanobini, Angew. Chem., Int. Ed., 2006, 45, 4182 CrossRef CAS; (b) M. Di Vaira, M. P. Ehses, M. Peruzzini and P. Stoppioni, Eur. J. Inorg. Chem., 2000, 2193 CrossRef CAS; (c) A. P. Ginsberg and W. E. Lindsell, J. Am. Chem. Soc., 1971, 93, 2082 CrossRef CAS.
- J. J. Schneider, D. Wolf, C. Janiak, O. Heinemann, J. Rust and C. Krüger, Chem. – Eur. J., 1998, 4, 1982 CrossRef CAS.
- C. Schwarzmaier, A. Y. Timoshkin, G. Balázs and M. Scheer, Angew. Chem., Int. Ed., 2014, 53, 9077 CrossRef CAS.
- (a) O. J. Scherer, T. Hilt and G. Wolmershäuser, Angew. Chem., Int. Ed., 2000, 39, 1425 CrossRef; (b) M. Scheer, S. Deng, O. J. Scherer and M. Sierka, Angew. Chem., Int. Ed., 2005, 44, 3755 CrossRef CAS.
- C. Schwarzmaier, S. Heinl, G. Balázs and M. Scheer, Angew. Chem., Int. Ed., 2015, 54, 13116 CrossRef CAS.
- (a) J. Müller, S. Heinl, C. Schwarzmaier, G. Balázs, M. Keilwerth, K. Meyer and M. Scheer, Angew. Chem., Int. Ed., 2017, 56, 7312 CrossRef; (b) J. Müller and M. Scheer, Chem. – Eur. J., 2021, 26, DOI:10.1002/chem.202005025.
- P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2009, 15, 186 CrossRef.
- F. Kraus, J. C. Aschenbrenner and N. Korber, Angew. Chem., Int. Ed., 2003, 42, 4030 CrossRef CAS.
- (a) C. Anthony, S.-M. Nathalie, N. Noel, F.-B. Marie and M. Nicolas, Angew. Chem., Int. Ed., 2018, 57, 1874 CrossRef; (b) U. Chakraborty, J. Leitl, B. Muhldorf, M. Bodensteiner, S. Pelties and R. Wolf, Dalton Trans., 2018, 47, 3693 RSC; (c) F. Dielmann, A. Timoshkin, M. Piesch, G. Balázs and M. Scheer, Angew. Chem., Int. Ed., 2017, 56, 1671 CrossRef CAS; (d) M. Piesch, S. Reichl, M. Seidl, G. Balázs and M. Scheer, Angew. Chem., Int. Ed., 2019, 58, 16563 CrossRef CAS; (e) O. J. Scherer, R. Winter and G. Wolmershäuser, Z. Anorg. Allg. Chem., 1993, 619, 827 CrossRef CAS.
- S. Alvarez, Dalton Trans., 2013, 42, 8617 RSC.
- C. G. P. Ziegler, T. M. Maier, S. Pelties, C. Taube, F. Hennersdorf, A. W. Ehlers, J. J. Weigand and R. Wolf, Chem. Sci., 2019, 10, 1302 RSC.
- J. N. L. Dennett, S. A. R. Knox, K. M. Anderson, J. P. H. Charmant and A. G. Orpen, Dalton Trans., 2005, 63 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2051733–2051736. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0cc08328c |
| ‡ See ESI† for further information. |
| This journal is © The Royal Society of Chemistry 2021 |