Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring the thermoelectric properties of oligo(phenylene-ethynylene) derivatives†
Hang
Chen‡
a,
Sara
Sangtarash‡
 *bc,
Guopeng
Li‡
a,
Markus
Gantenbein
d,
Wenqiang
Cao
a,
Afaf
Alqorashi
b,
Junyang
Liu
*bc,
Guopeng
Li‡
a,
Markus
Gantenbein
d,
Wenqiang
Cao
a,
Afaf
Alqorashi
b,
Junyang
Liu
 a,
Chunquan
Zhang
e,
Yulong
Zhang
e,
Lijue
Chen
a,
Yaorong
Chen
a,
Gunnar
Olsen
a,
Chunquan
Zhang
e,
Yulong
Zhang
e,
Lijue
Chen
a,
Yaorong
Chen
a,
Gunnar
Olsen
 d,
Hatef
Sadeghi
d,
Hatef
Sadeghi
 c,
Martin R.
Bryce
c,
Martin R.
Bryce
 *d,
Colin J.
Lambert
*d,
Colin J.
Lambert
 *b and
Wenjing
Hong§
*b and
Wenjing
Hong§
 *a
*a
aState Key Laboratory of Physical Chemistry of Solid Surfaces, College of Chemistry and Chemical Engineering, iChEM, Xiamen University, 361005, Xiamen, China. E-mail: whong@xmu.edu.cn
bDepartment of Physics, Lancaster University, LA1 4YB, Lancaster, UK. E-mail: c.lambert@lancaster.ac.uk; s.sangtarash@lancaster.ac.uk
cSchool of Engineering, University of Warwick, Coventry CV4 7AL, UK
dDepartment of Chemistry, Durham University, DH1 3LE, Durham, UK. E-mail: m.r.bryce@durham.ac.uk
ePen-Tung Sah Institute of Micro-Nano Science and Technology, Xiamen University, Xiamen, 361005, China
First published on 13th July 2020
Abstract
Seebeck coefficient measurements provide unique insights into the electronic structure of single-molecule junctions, which underpins their charge and heat transport properties. Since the Seebeck coefficient depends on the slope of the transmission function at the Fermi energy (EF), the sign of the thermoelectric voltage will be determined by the location of the molecular orbital levels relative to EF. Here we investigate thermoelectricity in molecular junctions formed from a series of oligophenylene-ethynylene (OPE) derivatives with biphenylene, naphthalene and anthracene cores and pyridyl or methylthio end-groups. Single-molecule conductance and thermoelectric voltage data were obtained using a home-built scanning tunneling microscope break junction technique. The results show that all the OPE derivatives studied here are dominated by the lowest unoccupied molecular orbital level. The Seebeck coefficients for these molecules follow the same trend as the energy derivatives of their corresponding transmission spectra around the Fermi level. The molecule terminated with pyridyl units has the largest Seebeck coefficient corresponding to the highest slope of the transmission function at EF. Density-functional-theory-based quantum transport calculations support the experimental results.
Introduction
Thermoelectric materials enable direct conversion between thermal energy and electrical energy and open a new way to harvest new environmentally-friendly energy for energy-savings and recycling. Nanoscale organic molecular thermoelectric materials are promising due to their tunable electronic structure and the feasibility of large-scale production through chemical synthesis.1,2 Thus, studies of charge and heat transport in single-molecule junctions, formed by trapping an individual molecule between two electrodes, are of great fundamental importance to developing molecular electronics and energy-conversion devices.3–9 Intensive experimental and theoretical studies have tried to reveal the fundamental mechanisms of charge and thermal transport at the nanoscale, and recent progress has suggested that organic materials at the single-molecule scale can show enhanced thermoelectric properties by adjusting their charge transport properties.10–13 The measurement of the Seebeck coefficient allows us to determine the ability of heat-to-electricity conversion at the organic junction. Furthermore, theory indicates that electrical transport through molecular junctions can be described by the Landauer formula14,15 and the Seebeck coefficient is given in the scattering formalism by16,17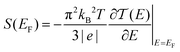 | (1) |
 is the energy-dependent transmission function, T is the average temperature of the leads, EF is the Fermi level of the leads and kB is the Boltzmann constant. The Seebeck coefficient is proportional to the energy derivative of the transmission coefficient in eqn (1).16 This fact indicates that the Seebeck coefficient can also be used to determine the dominant channel of a molecular junction. The sign of the coefficient will establish which molecular energy level is closer to EF, either the highest occupied molecular orbital (HOMO) (if the measured value is positive) or the lowest unoccupied molecular orbital (LUMO) (if it is negative).15 Therefore, the single-molecule electronics techniques offer a unique opportunity to investigate the thermoelectric properties of organic materials, which allows further promotion of organic energy conversion devices.
is the energy-dependent transmission function, T is the average temperature of the leads, EF is the Fermi level of the leads and kB is the Boltzmann constant. The Seebeck coefficient is proportional to the energy derivative of the transmission coefficient in eqn (1).16 This fact indicates that the Seebeck coefficient can also be used to determine the dominant channel of a molecular junction. The sign of the coefficient will establish which molecular energy level is closer to EF, either the highest occupied molecular orbital (HOMO) (if the measured value is positive) or the lowest unoccupied molecular orbital (LUMO) (if it is negative).15 Therefore, the single-molecule electronics techniques offer a unique opportunity to investigate the thermoelectric properties of organic materials, which allows further promotion of organic energy conversion devices.
Since the thermoelectric properties of a molecular junction were investigated through the STM break-junction (STM-BJ),18 scanning thermal microscopy (SThM),19 mechanically controlled break junction (MCBJ)20 and electromigration21 techniques, those advances have transformed studies of thermal and thermoelectric properties at the single-molecule scale and even enabled fabrication of single-molecule energy conversion devices, thermal rectifiers or transistors.19,22–27 The thermoelectric properties of molecules can be tuned by molecular length,28–30 electrode coupling,31–33 quantum interference effects,34–36 intermolecular interactions,37 substituent effects,38 variations of the end group,24 and also by using pi-stacked systems to increase the heat current, controlling the molecular energy levels relative to the Fermi energy of the electrodes.12 Further investigation of the thermoelectric properties of a family of molecules with varying electronic structures will provide the experimental and theoretical insights into the correlation between the transmission function and the Seebeck coefficient based on eqn (1).
Here we investigate the Seebeck coefficient of four oligo(phenylene-ethynylene) (OPE) derivatives shown in Fig. 1a using a home-built scanning tunnelling microscope break junction technique (STM-BJ).18 All the molecules have 1,4-difunctionalized pyridyl39 or methylthio28 terminals at both ends and the OPE cores in their backbone.40 The choice of these four molecules is motivated by their expected different energy derivatives in electron-transmission characteristics. Seebeck coefficient measurements show that the transport through all the four molecules is dominated by their LUMO channels. The Seebeck coefficients for these molecules follow the same trend as the energy derivatives of their corresponding transmission spectra around the Fermi level and are supported by our Seebeck coefficient calculations.
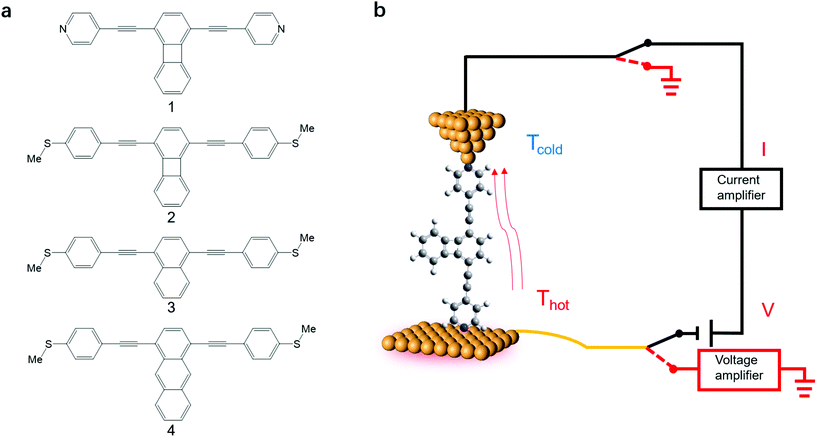 | ||
| Fig. 1 (a) The structures of OPE derivatives 1–4 studied in this work. (b) Schematic of the experimental setup. | ||
Experimental section
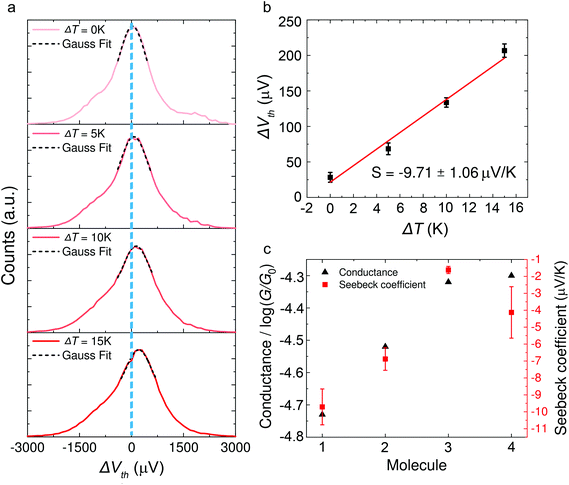
The synthesis of molecules 1–4 has been reported previously.40 Their single-molecule charge transport properties have been determined at room temperature using a home-built scanning tunnelling microscope break junction technique (STM-BJ).18 The target molecule was self-assembled onto a 30 mm × 10 mm silicon substrate (with a 200 nm thick gold film on it), a fixed bias voltage of 100 mV was applied between the gold tip and the substrate (see ESI† for details). ∼2000 individual conductance–distance traces without any selection were recorded for each molecule for further statistical analysis. A blank control experiment was performed using a clean gold substrate without any molecule assembled, which suggested that the background noise was around 10−6G0. In order to prevent the contact between the tip and the substrate to avoid direct heat transfer during the thermoelectric experiment, a soft contact mode was chosen to measure the molecular conductance and thermopower (see ESI† for details).41,42 A high-threshold conductance value of 0.01G0 (where G0 is the quantum conductance, which equals 2e2/h) was chosen as the high trigger to control the Au tip approaching and withdrawing, so that only single-molecule junctions are formed.To investigate the Seebeck coefficient of single-molecule devices, we incorporated a home-built temperature control unit into the STM-BJ setup.23,34 The scheme of the home-built STM-BJ set-up is shown in Fig. 1b, and the set-up incorporated a conductance mode (conductance mode: only current amplifier switched on) and a thermoelectricity mode (thermoelectricity mode: only voltage amplifier switched on). To create a stable temperature difference between the tip and the substrate, the substrate was heated via a Peltier device, and the temperature difference was modulated by a thermocouple mounted under the substrate with feedback control. Meanwhile, the tip was kept at room temperature.23,43 A series of temperature differences (ΔT = ΔTsubstrate − ΔTtip ≈ 0, 5, 10 to 15 K) between the tip and the substrate were set respectively in the air. During the thermoelectric measurements, the tip, controlled by a piezoelectric actuator, was withdrawn from the substrate until a stable molecular junction was formed. Once the plateau was created, the circuit was switched from conductance mode to thermoelectricity mode through a relay switch. The thermoelectric voltage (ΔVth = ΔVsubstrate − ΔVtip) across a single-molecule junction was directly recorded using a voltage amplifier for a period of 100 ms, which was induced by the corresponding temperature difference. Then, the molecular junction broke down, and the set-up switched back to conductance mode. Histograms of the thermoelectric voltage were used to estimate the variation of the Seebeck coefficient and then normalized to make sure each temperature difference contains the same number of counts. Gaussian fitting gave the most probable thermoelectric voltage ΔVth. The heated substrate was connected to the voltage amplifier using copper wires, which contribute an additional thermoelectric voltage to the system. Therefore, the Seebeck coefficient of the molecular junction function is given by34
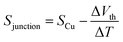 | (2) |
Results and discussion
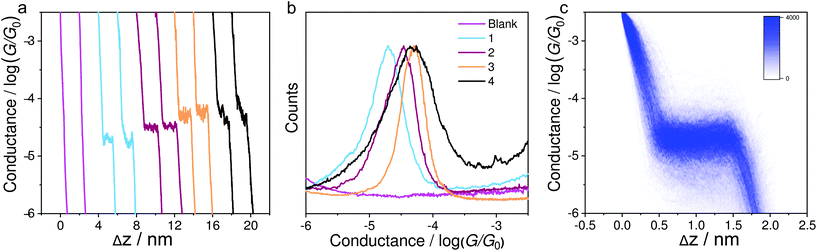
Fig. 2a shows the typical individual traces of conductance (G) versus stretching distance (Δz) plotted in a semi-logarithmic scale. The single-molecule conductance plateaus of molecules 1–4 using the soft-contact mode vary from 10−4.73 to 10−4.30G0. It can be clearly seen from Table 1 that these values are very similar to the results reported previously40 using a previous MCBJ method in their corresponding molecular solutions with hard contact of electrodes. Similar molecules with alkynyl spacers within the backbone exhibit similar conductance data in MCBJ or STM-BJ experiments in previous work.39,45 This is because the electrode coupling has little influence on the molecular backbone. We thus confirmed that the present method of soft contact to measure the assembled molecules in the air was reliable. To quantitatively determine the most probable conductance values, Fig. 2b indicates the one-dimensional (1D) conductance histograms of the four molecules, which reveal that the most probable conductance values for molecules 1–4 were 10−4.73G0, 10−4.52G0, 10−4.32G0, and 10−4.30G0, respectively. The plateaus and peaks were further confirmed by a clear density cloud in the corresponding 2D conductance–distance histograms, as shown in Fig. 2c for compound 1. It can be clearly seen that the molecule 2 with methylthio anchoring groups shows a higher conductance value than pyridyl-terminated molecule 1, as observed previously.40 The similar conductance values of molecules 2 to 4 reveal that the pendant cyclobutadiene unit of 2 has no significant impact on charge transport. Moreover, in contrast to our previous MCBJ results,40 we observed only a high conductance peak of molecule 4, suggesting that the signal is from single molecules.| Compounds | Seebeck coefficienta (μV K−1) | Measured conductance/log(G/G0)b-STM-BJ | Measured conductance/log(G/G0)b-MCBJ40 |
|---|---|---|---|
| a The error bars are based on the standard deviation in the linear fitting of the most probable thermoelectric voltage as a function of ΔT. b Most probable conductance values and the error bars are based on the standard deviation in the Gaussian fitting of the 1D conductance histograms. | |||
| 1 | −9.71 ± 1.06 | −4.73 ± 0.22 | −4.6 ± 0.41 |
| 2 | −6.88 ± 0.67 | −4.52 ± 0.23 | −4.4 ± 0.52 |
| 3 | −1.62 ± 0.21 | −4.32 ± 0.18 | −4.2 ± 0.46 |
| 4 | −4.13 ± 1.52 | −4.30 ± 0.33 | −4.1 ± 0.49 |
Typical histograms of the thermoelectric voltage for molecule 1 are shown in Fig. 3a. Since the fluctuation of molecular junction configurations is inevitable during the measurement process in ambient environment, the fluctuation of the molecular configuration and the electrode contact coupling is likely to lead to the fluctuation of the Seebeck coefficient.46,47 Therefore, the thermoelectric voltage from different molecular junctions might exhibit different distributions. Thus the thermoelectric voltage values of more than 1000 junctions were recorded and summarized into histograms during the thermovoltage measurement. The histogram peaks, which are based on the Gaussian fitting, representing the most probable measured Vpeak were chosen and plotted as a function of ΔT, and the Seebeck coefficient was obtained from the thermoelectric slope as shown in Fig. 3b. These values are plotted in Fig. 3c and summarized in Table 1. The Seebeck coefficients for molecules 1–4 are −9.71 ± 1.06 μV K−1, −6.88 ± 0.67 μV K−1, −1.62 ± 0.21 μV K−1 and −4.13 ± 1.52 μV K−1, respectively (see ESI, Fig. S5† for more details). It can be clearly seen that the sign of the Seebeck coefficients for all four OPE derivatives is negative, which means that EF is closer to the lowest unoccupied molecular orbital (LUMO) level and their transport properties are electron-dominated. The Seebeck coefficient value for molecule 1 was found to be the largest, followed by molecules 2 > 4 > 3. Moreover, the methylthio-terminal was found to impart HOMO-dominated transport28 or LUMO-dominated transport48 in the previous studies, whereas in these molecular systems, molecules 1–4 all show LUMO-dominated transport (negative Seebeck coefficient). The only difference between 1 and 2 is the anchor group, but the magnitude of the Seebeck coefficient of molecule 1 is much higher (more negative) than molecule 2. Considering the above-mentioned factor, we suppose such a difference in the thermoelectric performance of the two molecules is caused by destructive quantum interference in molecule 1.
In order to confirm the hypothesis that the destructive quantum interference occurred in molecule 1, we used density functional theory (DFT) to obtain the mean field Hamiltonian from the relaxed ground state geometry of the junctions (see Methods in the ESI†) and calculated the transmission coefficient T(E) of electrons with energy E passing from one electrode to the other. From the calculated T(E) value shown in Fig. 4a, an antiresonance peak is observed between the HOMO and LUMO of molecule 1, which causes a steeper slope around the Fermi level of the electrode. However, the transmission functions of molecule 2 show a typical feature of constructive quantum interference, suggesting that the significant difference between molecules 1 and 2 is due to the quantum interference effect.
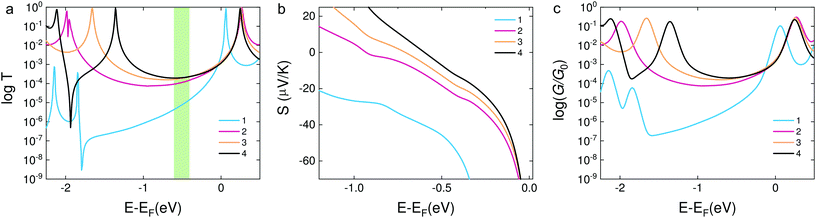 | ||
| Fig. 4 (a) DFT results of the transmission coefficients for compounds 1–4. (b) Seebeck coefficients of the corresponding molecules. The highlighted area shows the Fermi energy at which the calculated transmission and Seebeck coefficient are in qualitative agreement with the experimental findings. The relaxed structures are shown in Fig. S8 in the ESI.† (c) Calculated electrical conductance of molecules 1–4. | ||
Calculations show that the conductance of 4 ≈ 3 > 2 is in good agreement with the experiment for a wide energy range around E − EF = −0.5 eV. From the transmission functions in Fig. 4a, we can attribute the trend to the reduction of the HOMO–LUMO gap. The LUMO is closer to the Fermi level, suggesting that the transport channels of all three molecules are dominated by the LUMO which is consistent with the negative Seebeck coefficient measured in our experiments. The LUMOs of molecules 2–4 show no obvious changes with the different pendant units on the central phenylene ring. However, the HOMO of the three molecules is sequentially shifted towards the Fermi level, and this phenomenon was also observed in the investigation of a series of thiophene-1,1-dioxide derivatives.28 Thus, the conductance increased and the Seebeck coefficient decreased caused by the LUMO moving closer to the Fermi level.
We used the calculated T(E) value to obtain the Seebeck coefficients shown in Fig. 4b and the corresponding electrical conductance shown in Fig. 4c. We considered that all the Fermi energies of the electrodes in the case of each molecule are in the same range, as indicated by a green band in Fig. 4a. This yields the correct trend for molecules 1, 2 and 4. Molecule 3 is an outlier and has a smaller Seebeck coefficient than expected, which indicates that the Fermi energy in this case is closer to the middle of the HOMO–LUMO gap. However, the predicted values of the Seebeck coefficient were higher than the measured values. In order to correct the level alignment obtained from DFT, a scissor correction was performed using the method described in ref. 49 and 50. This leads to a better agreement between the theory and the experiment as shown in Fig. S8 in the ESI.† We found that the Seebeck coefficient of 1 is about two times higher than that of 2 for a wide energy range. Furthermore, the Seebeck coefficient of 4 is higher than that of 3; both of the above results are in agreement with the experiment. The higher overall values obtained from calculations when compared to the experimental results can be induced by different binding configurations to the electrodes in the experiment which lead to energy level broadening. The values of the Seebeck coefficient are sensitive to the slope of T(E) as shown in eqn (1), and therefore are more sensitive to the broadening of resonances compared to the electrical conductance.
Conclusions
In conclusion, we studied the thermoelectric properties of OPE derivatives using a modified STM-BJ technique, and we demonstrated the importance of the anchor groups in the OPE derivatives. We further established that the increase in pendant unit conjugation of OPE derivatives would lead to a decrease in the Seebeck coefficient. The ab initio calculations are in good agreement with the experimental results. Furthermore, since the three-terminal configurations with a gating voltage can actively tune the transmission behaviours of molecular junctions, this should be a good strategy for the design of future organic molecular devices with efficient thermoelectric energy conversion.Author contributions
W. H., M. R. B. and C. J. L. conceived the concept and co-supervised the project. STM-BJ setup was constructed by H. C. and G. L. in W. H.'s group. H. C. and G. L. carried out single-molecule conductance and thermoelectric experiments. S.S., A. A. and H. S. performed theoretical simulations. M. G. and G. O. completed synthesis of molecules used in this work. C. Z. and Y. Z. helped to fabricate the substrate. W. C., J. L., L. C. and Y. C. helped to analyse data. H. C. and S. S. wrote the manuscript. H. C., S. S., J. L., G. O., M. R. B., C. J. L. and W. H. helped to revise and polish the manuscript. All authors gave approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 21722305, 21673195, 21703188, 21933012, and 31871877), National Key R&D Program of China (2017YFA0204902), the China Postdoctoral Science Foundation (No. 2017M622060). Support from the UK EPSRC is acknowledged, through grants EP/N017188/1, EP/N03337X/1 and EP/P027156/1. S. S. acknowledges the Leverhulme Trust (Leverhulme Early Career Fellowship no. ECF-2018-375) for funding. H. S. acknowledges the UKRI for Future Leaders Fellowship no. MR/S015329/1. This work was supported by the EC H2020 FET Open project 767187 “QuIET” and 766853 “EFINED”. M. R. B. thanks the EPSRC grant EP/K0394/23/1 for funding. G. O. thanks the Danish Council for Independent Research, Technology and Production Sciences for funding (grant FTP, 8027-00005B).Notes and references
- B. Russ, A. Glaudell, J. J. Urban, M. L. Chabinyc and R. A. Segalman, Nat. Rev. Mater., 2016, 1, 16050 CrossRef CAS.
- Y.-J. Zeng, D. Wu, X.-H. Cao, W.-X. Zhou, L.-M. Tang and K.-Q. Chen, Adv. Funct. Mater., 2020, 30, 1903873 CrossRef CAS.
- A. R. Nitzan and M. A. Ratner, Science, 2003, 300, 1384–1389 CrossRef CAS PubMed.
- D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440 CrossRef CAS PubMed.
- S. V. Aradhya and L. Venkataraman, Nat. Nanotechnol., 2013, 8, 399–410 CrossRef CAS PubMed.
- E. Leary, A. La Rosa, M. T. González, G. Rubio-Bollinger, N. Agraït and N. Martín, Chem. Soc. Rev., 2015, 44, 920–942 RSC.
- R. J. Nichols and S. J. Higgins, Annu. Rev. Anal. Chem., 2015, 8, 389–417 CrossRef CAS PubMed.
- M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252–254 CrossRef CAS.
- F. Chen, J. Hihath, Z. Huang, X. Li and N. J. Tao, Annu. Rev. Phys. Chem., 2007, 58, 535–564 CrossRef CAS PubMed.
- C. M. Finch, V. M. García-Suárez and C. J. Lambert, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 033405 CrossRef.
- Q. H. Al-Galiby, H. Sadeghi, L. A. Algharagholy, I. Grace and C. Lambert, Nanoscale, 2016, 8, 2428–2433 RSC.
- G. Kiršanskas, Q. Li, K. Flensberg, G. C. Solomon and M. Leijnse, Appl. Phys. Lett., 2014, 105, 233102 CrossRef.
- Q. H. Al-Galiby, H. Sadeghi, D. Z. Manrique and C. J. Lambert, Nanoscale, 2017, 9, 4819–4825 RSC.
- M. Buttiker, Y. Imry, R. Landauer and S. Pinhas, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6207–6215 CrossRef PubMed.
- M. Paulsson and S. Datta, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 241403 CrossRef.
- U. Sivan and Y. Imry, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 551–558 CrossRef CAS PubMed.
- P. N. Butcher, J. Phys. Chem., 1990, 2, 4869–4878 Search PubMed.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- L. Cui, W. Jeong, S. Hur, M. Matt, J. C. Klockner, F. Pauly, P. Nielaba, J. C. Cuevas, E. Meyhofer and P. Reddy, Science, 2017, 355, 1192–1195 CrossRef CAS PubMed.
- T. Morikawa, A. Arima, M. Tsutsui and M. Taniguchi, Nanoscale, 2014, 6, 8235–8241 RSC.
- Y. Kim, W. Jeong, K. Kim, W. Lee and P. Reddy, Nat. Nanotechnol., 2014, 9, 881–885 CrossRef CAS PubMed.
- L. Cui, R. Miao, K. Wang, D. Thompson, L. A. Zotti, J. C. Cuevas, E. Meyhofer and P. Reddy, Nat. Nanotechnol., 2017, 13, 122–127 CrossRef PubMed.
- P. Reddy, S.-Y. Jang, R. A. Segalman and A. Majumdar, Science, 2007, 315, 1568–1571 CrossRef CAS PubMed.
- J. R. Widawsky, P. Darancet, J. B. Neaton and L. Venkataraman, Nano Lett., 2012, 12, 354–358 CrossRef CAS PubMed.
- L. Cui, S. Hur, Z. A. Akbar, J. C. Klockner, W. Jeong, F. Pauly, S. Y. Jang, P. Reddy and E. Meyhofer, Nature, 2019, 572, 628–633 CrossRef CAS PubMed.
- N. Mosso, U. Drechsler, F. Menges, P. Nirmalraj, S. Karg, H. Riel and B. Gotsmann, Nat. Nanotechnol., 2017, 12, 430–433 CrossRef CAS PubMed.
- N. Mosso, H. Sadeghi, A. Gemma, S. Sangtarash, U. Drechsler, C. Lambert and B. Gotsmann, Nano Lett., 2019, 19, 7614–7622 CrossRef CAS PubMed.
- E. J. Dell, B. Capozzi, J. Xia, L. Venkataraman and L. M. Campos, Nat. Chem., 2015, 7, 209–214 CrossRef CAS PubMed.
- T. Meier, F. Menges, P. Nirmalraj, H. Holscher, H. Riel and B. Gotsmann, Phys. Rev. Lett., 2014, 113, 060801 CrossRef CAS PubMed.
- J. R. Widawsky, W. Chen, H. Vazquez, T. Kim, R. Breslow, M. S. Hybertsen and L. Venkataraman, Nano Lett., 2013, 13, 2889–2894 CrossRef CAS PubMed.
- S. K. Yee, J. A. Malen, A. Majumdar and R. A. Segalman, Nano Lett., 2011, 11, 4089–4094 CrossRef CAS PubMed.
- R.-N. Wang, G.-Y. Dong, S.-F. Wang, G.-S. Fu and J.-L. Wang, J. Appl. Phys., 2016, 120, 184303 CrossRef.
- Y.-X. Zhen, M. Yang and R.-N. Wang, Front. Phys., 2019, 14, 23603 CrossRef.
- R. Miao, H. Xu, M. Skripnik, L. Cui, K. Wang, K. G. L. Pedersen, M. Leijnse, F. Pauly, K. Warnmark, E. Meyhofer, P. Reddy and H. Linke, Nano Lett., 2018, 18, 5666–5672 CrossRef CAS PubMed.
- C. J. Lambert, H. Sadeghi and Q. H. Al-Galiby, C. R. Phys., 2016, 17, 1084–1095 CrossRef CAS.
- C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888 RSC.
- C. Evangeli, K. Gillemot, E. Leary, M. T. Gonzalez, G. Rubio-Bollinger, C. J. Lambert and N. Agrait, Nano Lett., 2013, 13, 2141–2145 CrossRef CAS PubMed.
- K. Baheti, J. A. Malen, P. Doak, P. Reddy, S. Y. Jang, T. D. Tilley, A. Majumdar and R. A. Segalman, Nano Lett., 2008, 8, 715–719 CrossRef CAS PubMed.
- W. Hong, D. Z. Manrique, P. Moreno-Garcia, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 2292–2304 CrossRef CAS PubMed.
- M. Gantenbein, X. Li, S. Sangtarash, J. Bai, G. Olsen, A. Alqorashi, W. Hong, C. J. Lambert and M. R. Bryce, Nanoscale, 2019, 11, 20659–20666 RSC.
- P. Moreno-García, A. La Rosa, V. Kolivoška, D. Bermejo, W. Hong, K. Yoshida, M. Baghernejad, S. Filippone, P. Broekmann, T. Wandlowski and N. Martín, J. Am. Chem. Soc., 2015, 137, 2318–2327 CrossRef PubMed.
- W. Haiss, H. van Zalinge, S. J. Higgins, D. Bethell, H. Höbenreich, D. J. Schiffrin and R. J. Nichols, J. Am. Chem. Soc., 2003, 125, 15294–15295 CrossRef CAS PubMed.
- L. Shi and A. Majumdar, J. Heat Transfer, 2002, 124, 329–337 CrossRef CAS.
- F. J. Blatt, Thermoelectric Power of Metals, Plenum Press, New York, 1976 Search PubMed.
- P. Duan, J. Liu, J.-Y. Wang, K. Qu, S. Cai, F. Wang, L. Chen, X. Huang, R. Li, J. Shi, Q.-C. Zhang, W. Hong and Z.-N. Chen, Sci. China: Chem., 2020, 63, 467–474 CrossRef CAS.
- L. Rincon-Garcia, A. K. Ismael, C. Evangeli, I. Grace, G. Rubio-Bollinger, K. Porfyrakis, N. Agrait and C. J. Lambert, Nat. Mater., 2016, 15, 289–293 CrossRef CAS PubMed.
- R.-N. Wang, G.-Y. Dong, S.-F. Wang, G.-S. Fu and J.-L. Wang, Phys. Chem. Chem. Phys., 2016, 18, 28117–28124 RSC.
- R. J. Davidson, D. C. Milan, O. A. Al-Owaedi, A. K. Ismael, R. J. Nichols, S. J. Higgins, C. J. Lambert, D. S. Yufit and A. Beeby, RSC Adv., 2018, 8, 23585–23590 RSC.
- H. Sadeghi, Nanotechnology, 2018, 29, 373001 CrossRef PubMed.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 093029 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental technique and computational methods for calculating the transmission coefficients. See DOI: 10.1039/d0nr03303k |
| ‡ These authors contributed equally to this work. |
| § W. H. coordinated the writing of the manuscript with contributions from all authors. All authors have given approval to the final version of the manuscript. |
| This journal is © The Royal Society of Chemistry 2020 |