‘Blind time’ – current limitations on laser ablation multi-collector inductively coupled plasma mass spectrometry (LA-MC-ICP-MS) for ultra-transient signal isotope ratio analysis and application to individual sub-micron sized uranium particles
Grant
Craig
 *ab,
Matthew S. A.
Horstwood
*ab,
Matthew S. A.
Horstwood
 c,
Helen J.
Reid
a and
Barry L.
Sharp
c,
Helen J.
Reid
a and
Barry L.
Sharp
 a
a
aCentre for Analytical Science, Department of Chemistry, Loughborough University, Loughborough, Leicestershire LE11 3TU, UK. E-mail: grant.craig@thermofisher.com
bThermo Fisher Scientific Bremen GmbH, Hanna-Kunath Str. 11, 28359 Bremen, Germany
cNERC Isotope Geosciences Laboratory, British Geological Survey, Nicker Hill, Keyworth, Nottinghamshire NG12 5GG, UK
First published on 17th April 2020
Abstract
The application of laser ablation multi-collector inductively coupled plasma mass spectrometry (LA-MC-ICP-MS) to the isotope ratio analysis of UOx particles has the potential to improve the isotopic determination of these particles when compared to currently utilised ICP-MS techniques. To investigate this a high-speed, integrated ablation cell and dual concentric injector design was tested in the expectation that the resulting increase in signal to noise ratio and sample ion yield would improve the determination of 234U/238U, 235U/238U and 236U/238U for such materials. However, when compared to a slower washout, more established low-volume cell design, the highly transient signals of the new design proved challenging for the mixed detector array of the multi-collector mass spectrometer, introducing a new bias. We describe a major component of this bias, referred to as ‘blind time’, and model its impact on UOx particle analysis. After accounting for blind time, average precisions for the uranium isotopic composition of sub-micron sized UOx particles using LA-MC-ICP-MS were 3% 1RSD for 235U/238U and 8% 1RSD for 234U/238U. When ablating a glass rather than a UOx particle, uncertainties of 1.3% 1RSD for 235U/238U were achieved for 150 nm equivalent particle sizes using LA-MC-ICP-MS.
Introduction
International governmental agencies have introduced safeguards designed to ensure the compliance of nuclear facilities (e.g. nuclear reactors, enrichment facilities or test sites) to stated declarations and to detect undeclared, unauthorised activities.1 A prime concern of these safeguards are microparticles (down to a few hundred nanometres in diameter) containing perhaps only picograms of actinide material. Such actinide-bearing particles are also vital to nuclear forensics2,3 (the study of intercepted nuclear material) and to environmental studies of previously contaminated locations.4,5 For all three areas of interest the isotopic composition can give a wealth of information including but not limited to the sample age, intended use and place of manufacture.3,6–8 Routine inspections for safeguards analysis use cotton swipes to collect particles which are then extracted to determine the uranium (U) or plutonium (Pu) isotopic composition by mass spectrometry.9 Dissolution of the collected particles for analysis by inductively coupled plasma mass spectrometry (ICP-MS) is routine,10 however the isotope ratios recovered are for the bulk of the material: analysing each particle individually could reveal a strong deviation from the bulk.11 Separation and dissolution of individual U particles has been successfully implemented for ICP-MS,12–14 and successfully compared to secondary ion mass spectrometry (SIMS) analysis of the same material.15 For routine analysis thermal ionisation mass spectrometry (TIMS) and SIMS are commonly used for uranium particles, with SIMS predominant.1 However other forms of mass spectrometry, including laser ablation (LA-)ICP-MS, have been investigated as complimentary techniques.LA-ICP-MS is a promising technique for nuclear safeguards, requiring less sample preparation than either TIMS or SIMS. The primary advantages of LA-ICP-MS are speed of analysis, more widespread instrumentation and therefore accessibility and ease of use. Over time, sample size for LA-ICP-MS has varied from pressed powder pellets16 to 10–30 μm particles11,17,18 and smaller.19 Recently the scale has shifted from the micron to submicron,20–24 attention being focussed by recent inter-laboratory comparisons.25–27 To date, several studies have analysed micron and sub-micron uranium particles by LA-ICP-MS. Pointurier et al.21 compared a 213 nm laser system coupled with a quadrupole-based ICP-MS, to TIMS and SIMS for 235U/238U isotope ratio analysis. Kappel et al.22 analysed 235U/238U by LA-MC-ICP-MS as part of an evaluation of data handling strategies for single particles and Claverie et al.28 applied LA-MC-ICP-MS to micron-sized uranium particles, measuring both 235U/238U and 234U/238U to a precision of 2.0% 1RSD using a multiple Faraday configuration. Critically, the flexibility of ICP-MS allows modification of signal to noise ratios (SNR) by adapting conventional analysis approaches. Increasing the SNR improves the limit of detection and limit of quantification, important when considering the lack of material in sub-micron uranium particles. The SNR can be improved by compressing the transient signals generated into a shorter time frame. Short transient signals are challenging in ICP-MS, in terms of data acquisition and handling by both the ICP-MS instrument and the user,29 requiring changes in methodology. One such change has been calculating isotope ratios from entire integrated transient signals rather than by each mass spectrometer cycle.18,30,31 Isotope ratio analysis of transient signals has already been pioneered for single shot laser ablation of larger materials30,32 as well as single particles. Spectral skew is a known problem for transient signal analysis with single collector ICP-MS, whereby inaccuracies are introduced due to differential delays in signal acquisition.33 Adopting pseudo-simultaneous detection to overcome spectral skew with LA-ICP-TOF-MS for uranium particle analysis has been investigated but was limited in detector linearity and sample ion yield.23 Multi-collector inductively coupled plasma mass spectrometers (MC-ICP-MS) achieves full simultaneous measurement by collecting each isotope on separate detectors as well as high ion yield (>7%, Craig et al.34) and as such should be ideally suited for highly transient signals. However, although isotopes signals are detected simultaneously on MC-ICP-MS, the isotope signals need not be output simultaneously. For Faraday cup detectors the signal output is reliant on the first order tau constant of the resistor in the associated amplifier.35,36 As such, differential decay of the signal on different Faraday detectors can lead to variation in transient signal isotope ratio analysis. For highly transient signals, this can introduce bias in isotope ratio measurements e.g. Krupp and Donard37 This differential detector response is at its most extreme when comparing output signals from transient pulses recorded on mixed detector arrays (e.g. Faradays and ion counters).
We set out to investigate the utility of LA-MC-ICP-MS for analysis of individual submicron UOx particles for U isotope ratio determination. Given the small quantity of material to be analysed and the low abundance of 234U and 236U in many samples it was hypothesised that a high detection efficiency and signal to noise ratio would be required. To this end we determined to apply an ultrafast combined ablation cell and torch injector design, the prototype DCI,38 to the LA-MC-ICP-MS system. This system built on a key area of development in laser ablation cell design, “two-volume” cells, where a smaller cell is housed inside a larger casing. These cells have better flow dynamics than previous generations of ‘single volume’ ablation cells and are now standard issue from most manufacturers.39 Ultrafast laser ablation sample introduction systems aim to reduce elemental fractionation, improve signal to noise, remove memory effects and achieve higher transport efficiency with sub-100 ms washout times.40 As well as the DCI, similar systems first described by Wang et al.41 and van Malderen et al.42 have become commercially available. Applications for these ultrafast laser ablation cells have primarily focussed on elemental analyses and their potential utility for isotope ratio analysis by MC-ICP-MS has not yet been fully investigated.34
Experimental
An ESI® (New Wave Research™) UP193FX 193 nm excimer laser system was coupled to a Thermo Scientific™ Neptune Plus™ MC-ICP-MS. The MC-ICP-MS was equipped with a multiple ion counting (MIC) array to simultaneously measure 234U, 235U and 236U. 238U was collected on a Faraday cup (Table 1) coupled to a 1011 Ω amplifier.| Cup | IC 5 | IC 3 | IC 2 | IC 1 | L4 | C |
| Detector | CDD | SEM | SEM | SEM | FAR (1011 Ω) | FAR (1011 Ω) |
| Mass | 234U | 235U | 236U | 237.05 | 238U | 255.5 |
Two different laser ablation configurations were used to transport the laser plume from the ablation site to the plasma. The first, more established configuration used a low-volume single-volume cell, the Zircon Cell, developed by Horstwood et al.43 which followed the work of Bleiner and Günther44 by restricting the internal volume to a flat-sided teardrop shape of ca. 3 cm3. The helium ablation gas exited the cell along 1/8′′ ID Teflon-lined Tygon tubing. Ar make-up gas and N2 sourced from the outlet of an Aridus™ desolvating nebuliser system (CETAC Technologies, Omaha, Nebraska) was mixed with the ablation gas via a Y-piece halfway between the cell and the injector. The total length of tubing used was 1.5 m and as a result the total internal volume of the configuration was ca. 15 cm3.
The second configuration, incorporating a high speed, integrated ablation cell and dual concentric injector (DCI) developed at Loughborough University45 (Fig. 1) was first described in Douglas et al.38 It consisted of three main components, an inner cell, an outer cell and the DCI. The inner cell, the micro “Sniffer” cell, sat about 100 μm above the sample surface within the larger holding “Enterprise” outer cell. The inner cell had to remain stationary relative to the laser head and therefore the sample moves within the outer cell, and under the floating inner cell, by magnetic coupling. From the inner cell, a 250 μm i.d. thin fused silica tube transported the ablated material to the injector. In the DCI the fused silica line was passed down the centre of a 2.0 mm quartz injector, hence acting as a secondary internal injector. Around the fused silica line was added the Ar make-up gas and N2, again sourced from an Aridus, creating a “sheath” around the He ablation gas. The DCI system was intended to work in a close-coupled configuration in which the fused silica tubing was kept straight and did not exceed 30 cm in length, restricting the total volume to 0.015 cm3. Due to the size of the MC-ICP-MS such a close coupling was impossible and as a result in our configuration the fused silica tubing was both curved and increased in length to 150 cm, resulting in a total volume of 0.075 cm3.
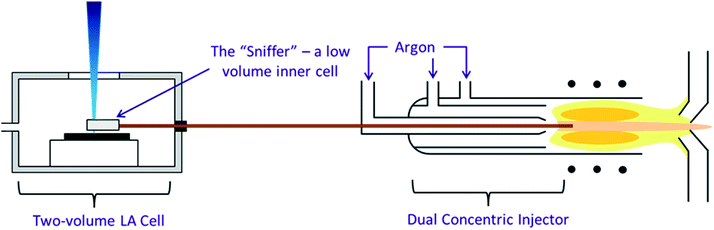 | ||
| Fig. 1 The three components of the high speed, integrated ablation cell and DCI, reproduction from Douglas D. N., Managh A. J., Reid H. J., Sharp B. L., Anal. Chem., 2015, 87(22), 11285–11294. | ||
Correction factors were determined from solutions of known uranium isotopic composition introduced via the Aridus desolvating nebulizer prior to LA analysis. Certified reference material (CRM) 112A (New Brunswick Laboratory, US Department of Energy, Washington DC, USA)46 with concentration <15 ppb in no more than 2% (m m−1) HNO3, was used to calculate the UH+/U+ and abundance sensitivity. CRM U010 (New Brunswick Laboratory, US Department of Energy, Washington DC, USA)47 was used to determine correction factors for mass bias and relative detector gain.
Laser ablation of a single solid reference material, NIST SRM®611 (National Institute of Standards and Technology, Gaithersburg, Maryland, USA, 461.5 ± 1.1 ppm U)48 was used to compare the different instrumental configurations.
The European Joint Research Center Geel (Belgium, formerly IRMM) have so far carried out eight Nuclear Signatures Inter-Laboratory Measurement Evaluation Programme (NUSIMEP) inter-laboratory comparisons (ILC). Two of these, NUSIMEP-6 and NUSIMEP-7, took the form of sub-micron uranium oxide particles of known composition coated onto carbon planchets25,27 and as such are useful reference materials to evaluate the ability of LA-ICP-MS to analyse such samples. The particles analysed in this study, composed of U3O8, were from both NUSIMEP-6 and NUSIMEP-7. NUSIMEP-6 consisted of a single graphite planchet with particles of a single isotopic composition condensed onto it. NUSIMEP-7 used two planchets, one containing particles of a single isotopic composition and another containing particles of two different compositions, the ‘double composition’ planchet. Reference uranium isotope ratios for the particles on each planchet are given in Table 3.
Due to the dynamic range required to detect and appropriately measure all uranium isotopes, a mixed detector array of Faraday cups and ion counters was required. Across the acquisition period of a transient signal (generated by either laser ablation or gas chromatography) using MC-ICP-MS, systematic isotope ratio drift has been observed.36,37,49,50 The cause of the isotope ratio drift in such cases has been identified as different tau response rates on the associated Faraday detector amplifiers,49 and approaches to correct for the different amplifier tau response rates have been developed.31,50–53 For our analysis the difference in response rate was expected to be more pronounced; without a high resistance amplification circuit, the ion counter response is near instantaneous (Table 2).
| Zircon Cell | DCI | |
|---|---|---|
| ESI® New Wave Research™ UP-193FX excimer laser | ||
| Ablation mode | Single spot | Single spot |
| Fluence | 11 J cm−2 | 11 J cm−2 |
| Repetition rate | 1 Hz | 1 Hz |
| Spot size | 5 μm (UOx) | 5 μm (UOx) |
| 20 μm (SRM611) | 20 μm (SRM611) | |
| He carrier gas | 0.8 L min−1 | 9 mL min−1 |
| Cell pressure | ≈0 kPa | 77 kPa |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| CETAC Aridus™ I | ||
| Nebulizer | PFA 50 | PFA 50 |
| Sweep gas | 3.5 L min−1 | 5.3 L min−1 |
| N2 add gas | 9 mL min−1 | 9 mL min−1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Thermo Scientific™ Neptune Plus™ MC-ICP-MS | ||
| RF power | 1170 W | 1170 W |
| Cool gas | 15 L min−1 | 15 L min−1 |
| Aux. gas | 0.9 L min−1 | 0.9 L min−1 |
| Skimmer cone | X | X |
| Sampler cone | Jet | Jet |
| Sample gas | 0.82 L min−1 | 0.82 L min−1 |
| 234U/238U | 235U/238U | 236U/238U | |
|---|---|---|---|
| SRM611 (ref. 54) | 9.45(05) × 10−6 | 2.3855(47) × 10−3 | 4.314(04) × 10−5 |
| NUSIMEP-6 (ref. 25) | 4.9817(48) × 10−5 | 7.0439(35) × 10−3 | 5.2048(86) × 10−7 |
| NUSIMEP-7 (1)26 | 7.4365(60) × 10−5 | 9.0726(45) × 10−3 | 8.0205(71) × 10−6 |
| NUSIMEP-7 (2)26 | 7.4365(60) × 10−5 | 9.0726(45) × 10−3 | 8.0205(71) × 10−6 |
| 3.4514(24) × 10−4 | 3.4148(17) × 10−2 | 1.03268(70) × 10−4 |
We adopted the approach of Cottle et al.30 who measured a response delay of ca. 0.2 s between ion counter and Faraday cup signals during single shot LA-MC-ICP-MS. This response delay strongly affected the accuracy of the isotope ratio when calculated on a time-slice (cycle-by-cycle) basis. As a consequence, the integrated area for each individual isotope was used to calculate the ratios for each pulse; that is total signal integration (TSI).
Results
Uranium isotope ratio measurement of SRM 611
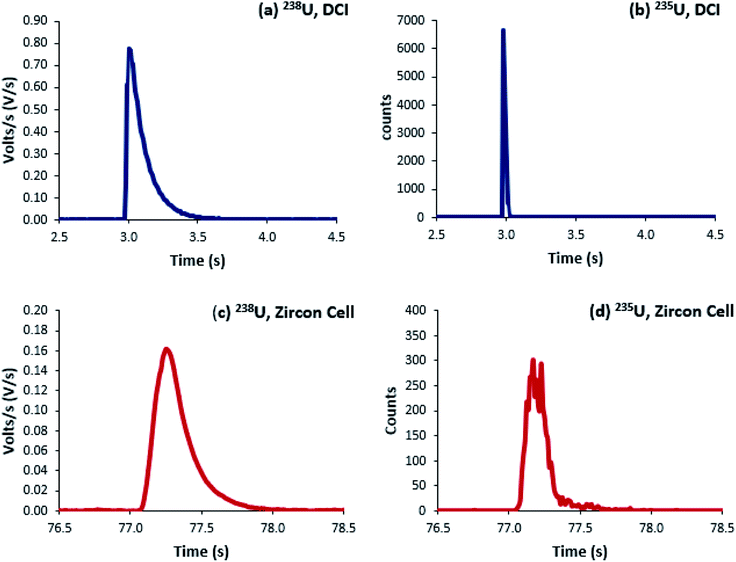
Uranium isotope ratios of SRM 611 were calculated for each of 300 single shot ablations. For the ion counters total peak width averaged 510 ms for the Zircon Cell and 110 ms for the Enterprise Cell and DCI (Fig. 2). The reduction in peak width using the DCI increased the signal-to-noise ratio by a factor of 25 and improved the definition of the minor (234U and 236U) isotopes. However, due to the slow Faraday amplifier response an average peak width significantly greater than 110 ms was measured for 238U (Fig. 4). To calculate an isotope ratio from such divergent peak profiles proved the necessity of the TSI data evaluation strategy. The three uranium isotope ratios, 234U/238U, 235U/238U and 236U/238U, were determined for the 300 ablation shots collected with both laser ablation systems (Table 4).| Zircon Cell | DCI | |||||
|---|---|---|---|---|---|---|
| 234U/238U | 235U/238U | 236U/238U | 234U/238U | 235U/238U | 236U/238U | |
| a Geometric mean: non-symmetric log-normal distribution, confidence intervals either side of the mean are not identical. b Relative difference = (geometric mean/reference value) − 1. | ||||||
| Mean | 1.04 × 10−5 | 2.35 × 10−3 | 4.55 × 10−5 | 1.05 × 10−5 | 2.34 × 10−3 | 4.56 × 10−5 |
| −SD (%)a | 15.7 | 1.33 | 7.38 | 13.2 | 2.89 | 7.62 |
| +SD (%)a | 18.6 | 1.35 | 7.96 | 15.2 | 2.97 | 8.24 |
| Relative difference (%)b | 9.64 | −1.50 | 5.29 | 10.4 | −1.93 | 5.53 |
| RSDPoisson, counting statistics (%) | 16.8 | 1.11 | 8.18 | 15.1 | 0.99 | 7.28 |
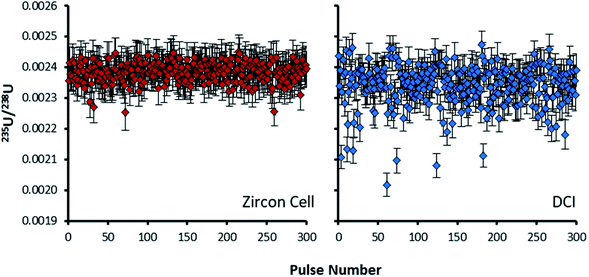
For the Zircon Cell the three uranium isotope ratios were accurate, within uncertainty, to the reference values and the precision closely tracked the values predicted from counting statistics. The increased detection efficiency and signal-to-noise ratio of the DCI and Enterprise Cell did not however, translate into a comparative improvement in precision. The 235U/238U SD of 2.9–3.0% was three times larger than counting statistics (0.99%). Plots of 235U/238U for each pulse (Fig. 3) confirmed the wider distribution of ratios with the DCI, with outliers biased towards a more depleted 235U composition. Given the broadly similar count rates with both laser ablation systems, results suggested the introduction of the DCI had introduced a new source of imprecision. A possible source of the additional uncertainty (‘blind time’) was investigated.
‘Blind time’ – undetected ions between integrations
In the Neptune MC-ICP-MS software there is a discrepancy between how different integration times are identified, e.g. ‘66 ms’, and the integration time of the data output, e.g. ‘68–69 ms’. For the example 66 ms integration time, the output of each integration is divided into three sections; a main 59 ms section; a secondary 7 ms section and the final 2 or 3 ms (average 2.37 ms over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 integrations) residual time. The three sections are a legacy of the data acquisition system for the Faraday cups, which was developed with the collection of continuous signals in mind.37 During operation the Faraday cups generate an analogue current. The analogue current is subsequently digitized using voltage to frequency conversion (by an analogue-to-digital converter). In this application rather than encoding the size of the signal, the change in the signal is encoded instead (removing any quantisation error). The current from the Faraday is therefore converted into a stream of digital pulses. For volt level signals on the Faraday the pulses occur at a frequency in the kHz range. If measured within a fixed time window in the kHz (ms) range the next pulse could occur either inside or outside of the window, limiting the precision to ≈1‰. To achieve precision levels in the ppm range, requires the timing to a subsequent pulse to be measured against a fast, MHz, clock. It is this fast clock measurement which occurs in the secondary section (7 ms) of the integration. At the end of the integration the system resets to the slower, kHz, clock. Once reset, the detector system waits until the next digital pulse is detected before beginning the next integration. It is the delay in waiting for the next pulse on each channel which is responsible for the extra time, known here as “blind time”.55 During blind time the mass spectrometer is effectively dead; no signal is recorded, on either the Faraday cups or ion counters. With the 66 ms integration time, only 96.4% of a continuous signal is being detected (Table 5). Interestingly, this indicates that due to the tau decay constant being longer than the integration time and therefore, encompassing multiple blind time events, 100% of the signal is never detected using Faraday detection and maximum precision is degraded using shorter integrations times where proportionately more of the signal is lost during the ‘blind time’.
000 integrations) residual time. The three sections are a legacy of the data acquisition system for the Faraday cups, which was developed with the collection of continuous signals in mind.37 During operation the Faraday cups generate an analogue current. The analogue current is subsequently digitized using voltage to frequency conversion (by an analogue-to-digital converter). In this application rather than encoding the size of the signal, the change in the signal is encoded instead (removing any quantisation error). The current from the Faraday is therefore converted into a stream of digital pulses. For volt level signals on the Faraday the pulses occur at a frequency in the kHz range. If measured within a fixed time window in the kHz (ms) range the next pulse could occur either inside or outside of the window, limiting the precision to ≈1‰. To achieve precision levels in the ppm range, requires the timing to a subsequent pulse to be measured against a fast, MHz, clock. It is this fast clock measurement which occurs in the secondary section (7 ms) of the integration. At the end of the integration the system resets to the slower, kHz, clock. Once reset, the detector system waits until the next digital pulse is detected before beginning the next integration. It is the delay in waiting for the next pulse on each channel which is responsible for the extra time, known here as “blind time”.55 During blind time the mass spectrometer is effectively dead; no signal is recorded, on either the Faraday cups or ion counters. With the 66 ms integration time, only 96.4% of a continuous signal is being detected (Table 5). Interestingly, this indicates that due to the tau decay constant being longer than the integration time and therefore, encompassing multiple blind time events, 100% of the signal is never detected using Faraday detection and maximum precision is degraded using shorter integrations times where proportionately more of the signal is lost during the ‘blind time’.
| Selected integration time (ms) | Measured total time (ms) | Blind time (ms) | % lost |
|---|---|---|---|
| 8 | 11.50 | 3.50 | 30.4% |
| 66 | 68.47 | 2.47 | 3.61% |
| 131 | 134.3 | 3.28 | 2.44% |
| 262 | 265.3 | 3.31 | 1.25% |
| 524 | 527.8 | 3.82 | 0.72% |
| 1049 | 1051 | 2.44 | 0.23% |
The 8 ms integration time apart, it can be assumed that such short interruptions in data collection will have a negligible effect on either continuous or semi-continuous signal responses. However, for transient signals collected on a mixed detector array, ‘blind time’ may have a significant impact on isotope ratio analysis.
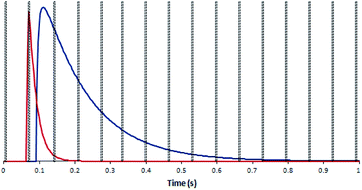
In order to test the effect of blind time on isotope ratio measurement with the DCI, a model was created. 30 single shot laser ablation pulses on SRM 611, collected with both laser ablation configurations, were merged to produce an ‘average’ single shot ablation profile for each type of detector. To these average response profiles exponential modified Gaussian functions were fitted using the software package Igor Pro™ (version 6.36, Wavemetrics, Oregon, USA) and the Multipeak Fitting function.38 The parameters generated were used in conjunction with the exponential-Gaussian hybrid function56 to produce four model laser ablation pulses, one for each combination of laser ablation configuration and detector type (Fig. 4). Now that model curves had been constructed based on real data, some modelling calculations could now be carried out to demonstrate the effect of a ‘blind time’ component on the total amount of signal recorded within each peak area using different integration times. The ‘blind time’ used in the model curves was 3 ms, a value close to the average measured blind time of the detector system. By removing 3 ms integrations every 66 ms for each of the possible full integer start times (65 in this case), the range of signal which could potentially be lost on each detector was calculated for each integration period option in the Neptune software.
In the plot of a model DCI pulse (Fig. 4), the signal collected on the IC is interrupted by two blind time events, in contrast to the 9 blind time events which interrupt the output of the Faraday signal. If the proportion of signal lost is different between the two detectors this would introduce a bias to the determined isotope ratio.
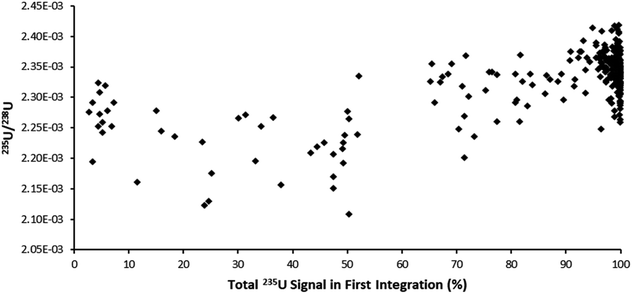
The ultrafast single shot profiles of the DCI more strongly affected the percentage of total signal which could be lost to blind time on the ion counters compared to the Faraday detector. Using the model, it was estimated, with 66 ms integration (Table 6), blind time could be responsible for at most 0.15% RSD 235U/238U on the mean single shot ablation pulses collected with the Zircon Cell, but up to 2.76% RSD with the DCI. The model supported the hypothesis that blind time was responsible for the additional 235U/238U uncertainty with the DCI. To further bolster the blind time hypothesis more single shot ablation pulses were collected on NIST 611, this time using a 262 ms integration time instead of 66 ms. As the average peak width on the SEM was only 110 ms, the 235U signal collected could either be contained within a single integration or split between two integrations with blind time in between. The model suggested for a 262 ms integration time 238U, collected on a Faraday detector, would lose between 0.34 to 2.16% of signal due to blind time events. 235U would either lose no counts, resulting in a slightly enriched 235U/238U ratio, or lose up to 10.7% and give a depleted 235U/238U ratio. For our experimental particle data, the 235U/238U ratio was plotted against the percentage of the total 235U signal captured in the first integration (Fig. 5). According to our model, particle data with approximately 50% of the total signal in the first integration would be most likely to exhibit blind time effects. This is indeed what Fig. 5 appears to show. In the plot most pulses with 100% of the 235U signal in a single integration also have a higher 235U/238U ratio, than those pulses where the 235U signal was interrupted by blind time, consistent with the theoretical model.
| Faraday – 238U | SEM – 235U | 235U/238U | |||||
|---|---|---|---|---|---|---|---|
| Min signal lost (%) | Max signal lost (%) | Range (%) | Min signal lost (%) | Max signal lost (%) | Range (%) | Estimated RSD (%) | |
| Zircon Cell | 4.21 | 4.44 | 0.23 | 4.13 | 4.55 | 0.42 | 0.15 |
| DCI | 3.50 | 5.00 | 1.50 | 0.67 | 11.20 | 10.53 | 2.76 |
Strategies to reduce ‘blind time’ for ultrafast transient signal analysis
Increasing the integration time from 66 ms to 262 ms reduced the proportion of pulses with significantly depleted 235U/238U ratios. By reducing the number of blind time events the likelihood of blind time occurring at the maxima of 235U counts was also reduced. However, increasing the integration time did not eliminate blind time completely and furthermore opened up the possibility of enriched 235U/238U ratios by capturing the entire SEM output within a single integration. For particle analysis, where a single particle could represent the entire population of one composition, any bias due to blind time could seriously bias data interpretation.The existence of blind time in some models of MC-ICP-MS may prevent the successful analysis of ultrafast transient signals. Until such time as next-generation instrumentation is developed, it is important to understand the minimum transient signal duration required in order for every ratio to be unaffected by blind time in LA-MC-ICP-MS set-ups. To estimate this value the parameters of the blind time model were modified to create results for pulses of approximately 50, 100, 200 and 300 ms duration. Each increase in pulse duration reduced the impact of blind time on the isotope ratio precision (Fig. 6). From this figure we can conclude that reducing the transient signal duration much below the 0.5 s achieved by the Zircon Cell will lead to blind time effects on ultrafast transient isotope ratio analyses. As such the reported washout times of most commercially available two-volume laser ablation cells (≤1 s)57 may represent the best compromise for particle analysis with current MC-ICP-MS systems.
Effect of blind time on isotope ratio measurement of sub-micron uranium particles
From the 235U/238U ratios obtained it was observed that particles, regardless of laser ablation configuration, seemed to be affected by blind time effects. This had been expected for the ultrafast DCI, but not the Zircon Cell. Those particles affected with the Zircon Cell were those single-shot ablation peak profiles which were interrupted with spikes in signal, of single integration duration (Fig. 7). The occurrence of such spikes was very strongly correlated with bias towards depleted uranium isotope ratios. Each spike was thought to represent the entrainment of a whole particle, or large fragment, into the plasma. Unlike the rest of the signal profile, these highly transient spikes would be susceptible to blind time effects.
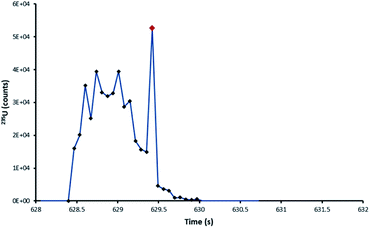 | ||
| Fig. 7 235U pulse profile of the ablation of a NUSIMEP-6 particle, Zircon Cell. The standard profile is interrupted by a large single integration spike in the signal. | ||
To filter out the biased signals the application Flexmix, a software package in R, described by Kappel et al.22 was used to assign strongly biased signals to a separate cluster. The particles isolated in the separate cluster were not used to determine the average uranium isotope ratios (Table 7).
| Zircon Cell | DCI | |||
|---|---|---|---|---|
| 234U/238U | 235U/238U | 234U/238U | 235U/238U | |
| Mean | 4.92 × 10−5 | 6.76 × 10−3 | 4.76 × 10−5 | 6.80 × 10−3 |
| −RSD (%) | 7.66 | 2.93 | 9.54 | 2.79 |
| +RSD (%) | 8.29 | 3.01 | 10.6 | 2.87 |
| RD (%) | −1.21 | −4.05 | −4.49 | −2.84 |
| Zircon Cell | DCI | |||||
|---|---|---|---|---|---|---|
| 234U/238U | 235U/238U | 236U/238U | 234U/238U | 235U/238U | 236U/238U | |
| Mean | 7.97 × 10−5 | 8.97 × 10−3 | 1.18 × 10−5 | 7.78 × 10−5 | 8.86 × 10−3 | 9.59 × 10−6 |
| −RSD (%) | 21.5 | 3.63 | 44.0 | 21.6 | 4.77 | 43.8 |
| +RSD (%) | 27.4 | 3.76 | 78.6 | 27.6 | 5.01 | 78.0 |
| RD (%) | 6.91 | −1.19 | 38.3 | 4.47 | −2.36 | 17.8 |
| 1st composition | Zircon Cell | DCI | ||||||
|---|---|---|---|---|---|---|---|---|
| n = 73 | 234U/238U | 235U/238U | 236U/238U | n = 104 | 234U/238U | 235U/238U | 236U/238U | |
| Mean | 7.43 × 10−5 | 8.72 × 10−3 | 1.12 × 10−5 | 7.75 × 10−5 | 9.05 × 10−3 | 1.40 × 10−5 | ||
| −RSD (%) | 8.49 | 3.27 | 30.0 | 12.8 | 6.80 | 35.6 | ||
| +RSD (%) | 9.27 | 3.38 | 42.1 | 14.7 | 7.30 | 55.3 | ||
| RD (%) | −0.04 | −3.97 | 33.10 | 4.14 | −0.23 | 55.83 | ||
| 2nd composition | Zircon Cell | DCI | ||||||
|---|---|---|---|---|---|---|---|---|
| n = 119 | 234U/238U | 235U/238U | 236U/238U | n = 70 | 234U/238U | 235U/238U | 236U/238U | |
| Mean | 3.35 × 10−4 | 3.12 × 10−2 | 1.10 × 10−4 | 3.57 × 10−4 | 3.10 × 10−2 | 1.20 × 10−4 | ||
| −RSD (%) | 16.7 | 6.76 | 26.9 | 22.4 | 7.73 | 37.9 | ||
| +RSD (%) | 20.1 | 7.25 | 36.9 | 28.9 | 8.37 | 60.9 | ||
| RD (%) | −2.96 | −8.99 | 6.02 | 3.25 | −9.52 | 14.72 | ||
Discussion
Sub-micron and micron-sized uranium particles are a challenging sample material for LA-MC-ICP-MS. A possible way forward for 235U/238U ratio measurements is measuring both isotopes on Faraday detectors.22,24,28 In doing so three of the limitations imposed by the ion counter are removed: the automatic protection system which deflects away ion beams greater than 2000 cpms, the limited dynamic range and now, significant blind time effects which are minor on Faraday detector systems due to their long and largely equivalent tau decay times. In our study the data from many of the largest, most valuable, particles had to be rejected due to at least one of these effects. Although the automatic protection could potentially be altered, the limited dynamic range cannot, and it would seem for LA-MC-ICP-MS analysis of uranium particles both 235U and 238U should be measured on Faraday detectors. However, for small or depleted uranium particles, the resulting small ion beam would be close to the Johnson noise of the 1011 Ω amplifier. A recent instrumental development available for MC-ICP-MS, high gain 1013 Ω amplifiers, have been applied to the LA-MC-ICP-MS analysis of similar small ion beams,53 and have been used for uranium isotope ratio analysis by TIMS.58 Unless TSI data processing is adopted, using high gain amplifiers for LA-MC-ICP-MS of uranium particles does require correcting for the different amplifier tau.59 Claverie et al.28 used the time-shift method developed by Gourgiotis et al.50 to correct for differences in detector response when analysing 1–3.5 μm uranium particles by LA-MC-ICP-MS. For the population of particles analysed RSD's were 2.1% 235U/238U (expected composition 7.248 × 10−3) and 2.5% 234U/238U (expected composition 6.1 × 10−5). Furthermore, by using the time-shift correction they were able to use a point-by-point data reduction strategy to assign an uncertainty to each individual particle.In our study the NUSIMEP-6 population, with a similar isotopic composition, was determined to ≈3% RSD 235U/238U and ≈8% RSD 234U/238U, for a particle size distribution of 0.64 ± 0.43 μm. An RSD of 1.3% was achieved with the Zircon Cell on SRM 611, for an amount of uranium material equivalent to a 150 nm uranium particle. The solid glass matrix of SRM 611 was significantly less likely to produce large discrete particulate and hence was less susceptible to blind time.
For mixed detector arrays the results obtained from the ultrafast DCI suggest the washout time which will give the best signal to noise ratio, without introducing compromising blind time effects, is ca. 0.5 s. As 234U and 236U will still need to be measured on ion counters, using the ultrafast DCI or other rapid washout systems for LA-MC-ICP-MS of uranium particles cannot be recommended, unless either the precision and accuracy required is less than the uncertainty due to blind time, or blind time is removed in MC-ICP-MS instrumentation. Such an improvement would be welcome outside uranium particle analysis as currently the efficiency of any analysis with a small integration time is reduced by the multiple blind time events experienced. For an 8 ms integration time 30% of the introduced ions are currently undetected and ironically, the only time when 100% of a signal is detected is on an ion counter when the input signal pulse is shorter than the integration time. Even with the >5% detection efficiency of the ultrafast laser ablation configuration,34 the average number of counts of 234U and 236U detected for each sub-micron particle was still too low to reach the precision required by the nuclear safeguards community. This also rules out the use of a pseudo-simultaneous LA-ICP-TOF-MS (where blind time would not be a factor) for particle analysis as the sensitivity of ICP-TOF-MS is orders of magnitude less than MC-ICP-MS.23 For LA-MC-ICP-MS to be a viable tool for minor isotope ratio determination in uranium particle analysis, the particles analysed must either be larger, micron sized and above, or be enriched in the minor isotopes.
Conclusions
Despite significantly improving the signal to noise ratio of the sample introduction set-up for LA-MC-ICP-MS using an ultrafast washout laser ablation cell and torch design, expected improvements in isotope ratio precision were not realized. The highly transient data resulting from the adoption of the ultrafast LA-MC-ICP-MS has introduced an additional source of bias and scatter, here termed ‘blind time’ which recognizes a fundamental time limit in some MC-ICP-MS systems where data are not recorded. For highly transient data significant components of time and therefore data can be missed, indicating that accurate determination of such analyses may not be achievable with some MC-ICP-MS instruments equipped with mixed detector arrays. Possible exceptions, such as the 234U/238U and 236U/238U compositions investigated in this study, are where counting statistic limitations dominate the uncertainty budget, masking the blind time effects on the isotope ratios. The improvement in signal to noise ratio provided by ultrafast washout laser ablation cell systems was of great benefit in resolving the minor uranium isotopes from the baseline and may yet have a role in future analytical methods if the observed biases and scatter due to blind time could be eliminated. For the Neptune Series MC-ICP-MS, modelling of blind time suggested a minimum signal duration of 500 ms is required to eliminate blind time effects when using a mixed detection array. We would therefore recommend that commercially available two-volume cells with washout times of 0.5–1 s are currently most appropriate to use in conjunction with MC-ICP-MS instruments for uranium particle analysis. The Zircon Cell (average pulse duration 0.5 s) measured an uncertainty of 1.3% 1RSD for 235U/238U for a population of single-shot ablations of SRM 611: the ablated material from each shot was equivalent to a 150 nm uranium particle.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was made possible through the Natural Environment Research Council-Royal Society of Chemistry Analytical Chemistry Trust Fund (NERC-ACTF), Analytical Science & Technology research programme, funding NE/I019786/1. Work at the NERC Isotope Geosciences Laboratory (NIGL), British Geological Survey was funded through IP-1315-0512. The authors would also like to thank the two anonymous reviewers for their helpful and constructive reviews.References
- M. Betti, L. A. de las Heras and G. Tamborini, Appl. Spectrosc. Rev., 2006, 41, 491–514 CrossRef CAS.
- M. May, R. Abedin-Zadeh, D. Barr and A. Carnesale, Nuclear Forensics. Role, State of the Art, Program Needs, 2008 Search PubMed.
- K. Mayer, M. Wallenius and Z. Varga, Chem. Rev., 2013, 113, 884–900 CrossRef CAS PubMed.
- R. R. Parrish, M. Horstwood, J. G. Arnason, S. Chenery, T. Brewer, N. S. Lloyd and D. O. Carpenter, Sci. Total Environ., 2008, 390, 58–68 CrossRef CAS PubMed.
- N. S. Lloyd, S. R. N. Chenery and R. R. Parrish, Sci. Total Environ., 2009, 408, 397–407 CrossRef CAS PubMed.
- Z. Varga, M. Wallenius and K. Mayer, J. Anal. At. Spectrom., 2010, 25, 1958–1962 RSC.
- F. E. Stanley, J. Anal. At. Spectrom., 2012, 27, 1821–1830 RSC.
- G. R. Eppich, R. W. Williams, A. M. Gaffney and K. C. Schorzman, J. Anal. At. Spectrom., 2013, 28, 666–674 RSC.
- E. Kuhn, D. Fischer and M. Ryjinski, Environmental Sampling for IAEA Safeguards: A Five Year Review, 2001 Search PubMed.
- R. C. B. Pestana, J. E. S. Sarkis, R. C. Marin, C. H. Abreu-Junior and E. F. U. Carvalho, J. Radioanal. Nucl. Chem., 2013, 298, 621–625 CrossRef CAS.
- T. M. Witte, PhD thesis, Iowa State, 2011.
- X. Z. Zhang, F. Esaka, K. T. Esaka, M. Magara, S. Sakurai, S. Usuda and K. Watanabe, Spectrochim. Acta, Part B, 2007, 62, 1130–1134 CrossRef.
- T. Shinonaga, F. Esaka, M. Magara, D. Klose and D. Donohue, Spectrochim. Acta, Part B, 2008, 63, 1324–1328 CrossRef.
- F. Esaka, M. Magara and T. Kimura, J. Anal. At. Spectrom., 2013, 28, 682–688 RSC.
- F. Esaka, M. Magara, C. G. Lee, S. Sakurai, S. Usuda and N. Shinohara, Talanta, 2009, 78, 290–294 CrossRef CAS PubMed.
- Z. Stefánka, R. Katona and Z. Varga, J. Anal. At. Spectrom., 2008, 23, 1030–1033 RSC.
- N. S. Lloyd, R. R. Parrish, M. Horstwood and S. R. N. Chenery, J. Anal. At. Spectrom., 2009, 24, 752–758 RSC.
- Z. Varga, Anal. Chim. Acta, 2008, 625, 1–7 CrossRef CAS.
- J. S. Becker, H. Sela, J. Dobrowolska, M. Zoriy and J. S. Becker, Int. J. Mass Spectrom., 2008, 270, 1–7 CrossRef CAS.
- F. Pointurier, A. Pottin and A. Hubert, Anal. Chem., 2011, 83, 7841–7848 CrossRef CAS PubMed.
- F. Pointurier, A. Hubert and A.-C. Pottin, J. Radioanal. Nucl. Chem., 2012, 296, 609–616 CrossRef.
- S. Kappel, S. F. Boulyga, L. Dorta, D. Günther, B. Hattendorf, D. Koffler, G. Laaha, F. Leisch and T. Prohaska, Anal. Bioanal. Chem., 2013, 405, 2943–2955 CrossRef CAS.
- A.-L. Ronzani, F. Pointurier, M. Rittner, O. Borovinskaya, M. Tanner, A. Hubert, A.-C. Humbert, J. Aupiais and N. Dacheux, J. Anal. At. Spectrom., 2018, 33, 1892–1902 RSC.
- Z. Varga, M. Krachler, A. Nicholl, M. Ernstberger, T. Wiss, M. Wallenius and K. Mayer, J. Anal. At. Spectrom., 2018, 33, 1076–1080 RSC.
- Y. Aregbe, J. Truyens, R. Kips, S. Richter, E. Stefaniak, H. Kühn and M. Kraiem, NUSIMEP-6: uranium isotope amount ratios in uranium particles, 2008 Search PubMed.
- J. Truyerns, E. Stefaniak, S. Mialle and Y. Aregbe, NUSIMEP-7: uranium isotope amount ratios in uranium particles, 2011 Search PubMed.
- J. Truyens, E. a Stefaniak and Y. Aregbe, J. Environ. Radioact., 2013, 125, 50–55 CrossRef CAS PubMed.
- F. Claverie, A. Hubert, S. Berail, A. Donard, F. Pointurier and C. Pécheyran, Anal. Chem., 2016, 88, 4375–4382 CrossRef CAS PubMed.
- M. Tanner and D. Günther, Anal. Chim. Acta, 2009, 633, 19–28 CrossRef CAS PubMed.
- J. M. Cottle, M. S. A. Horstwood and R. R. Parrish, J. Anal. At. Spectrom., 2009, 24, 1355–1363 RSC.
- T. Pettke, F. Oberli, A. Audétat, U. Wiechert, C. R. Harris and C. a. Heinrich, J. Anal. At. Spectrom., 2011, 26, 475–492 RSC.
- L. Allen, H. Pang and A. Warren, J. Anal. At. Spectrom., 1995, 10, 267–271 RSC.
- M. Wiedenbeck, R. Bugoi, M. J. M. Duke, T. Dunai, J. Enzweiler, M. Horan, K. P. Jochum, K. Linge, J. Košler, S. Merchel, L. F. G. Morales, L. Nasdala, R. Stalder, P. Sylvester, U. Weis and A. Zoubir, Geostand. Geoanal. Res., 2012, 36, 337–398 CrossRef CAS.
- G. Craig, A. J. Managh, C. Stremtan, N. S. Lloyd and M. S. A. Horstwood, Anal. Chem., 2018, 90, 11564–11571 CrossRef CAS PubMed.
- A. Gourgiotis, G. Manhès, P. Louvat, J. Moureau and J. Gaillardet, J. Anal. At. Spectrom., 2015, 30, 1582–1589 RSC.
- A. Gourgiotis, G. Manhès, P. Louvat, J. Moureau and J. Gaillardet, Rapid Commun. Mass Spectrom., 2015, 29, 1617–1622 CrossRef CAS PubMed.
- E. M. Krupp and O. F. X. Donard, Int. J. Mass Spectrom., 2005, 242, 233–242 CrossRef CAS.
- D. N. Douglas, A. J. Managh, H. J. Reid and B. L. Sharp, Anal. Chem., 2015, 87, 11285–11294 CrossRef CAS PubMed.
- W. Müller, M. Shelley, P. Miller and S. Broude, J. Anal. At. Spectrom., 2009, 24, 209–214 RSC.
- S. J. M. van Malderen, A. J. Managh, B. L. Sharp and F. Vanhaecke, J. Anal. At. Spectrom., 2016, 31, 423–439 RSC.
- H. A. O. Wang, D. Grolimund, C. Giesen, C. N. Borca, J. R. H. Shaw-Stewart, B. Bodenmiller and D. Günther, Anal. Chem., 2013, 85, 10107–10116 CrossRef CAS PubMed.
- S. J. M. Van Malderen, J. T. van Elteren and F. Vanhaecke, J. Anal. At. Spectrom., 2015, 30, 119–125 RSC.
- M. S. A. Horstwood, G. L. Foster, R. R. Parrish, S. R. Noble and G. M. Nowell, J. Anal. At. Spectrom., 2003, 18, 837–846 RSC.
- D. Bleiner and D. Günther, J. Anal. At. Spectrom., 2001, 16, 449–456 RSC.
- D. N. Douglas, PhD thesis, Loughborough University, 2013.
- J. Neuhoff, Certificate of Analysis CRM 112-A Uranium (normal) Metal Assay and Isotopic Standard, New Brunswick Laboratory, Argonne IL, 2010 Search PubMed.
- J. Neuhoff, Certificate of Analysis CRM U010 Uranium Isotopic Standard (5 mg Uranium as U3O8), New Brunswick Laboratory, Argonne IL, 2008 Search PubMed.
- S. A. Wise and R. L. Watters, National Institute of Standards & Technology Certificate of Analysis Standard Reference Material® 611 Trace Elements in Glass, NIST, Gaithersburg MD, 2012 Search PubMed.
- M. Dzurko, D. Foucher and H. Hintelmann, Anal. Bioanal. Chem., 2009, 393, 345–355 CrossRef CAS PubMed.
- A. Gourgiotis, S. Bérail, P. Louvat, H. Isnard, J. Moureau, A. Nonell, G. Manhès, J.-L. Birck, J. Gaillardet, C. Pecheyran, F. Chartier and O. F. X. Donard, J. Anal. At. Spectrom., 2014, 29, 1607–1617 RSC.
- T. Hirata, Y. Hayano and T. Ohno, J. Anal. At. Spectrom., 2003, 18, 1283–1288 RSC.
- T. Iizuka and T. Hirata, Chem. Geol., 2005, 220, 121–137 CrossRef CAS.
- J.-I. Kimura, Q. Chang, N. Kanazawa, S. Sasaki and B. S. Vaglarov, J. Anal. At. Spectrom., 2016, 31, 790–800 RSC.
- M. Zimmer, W. Kinman, A. Kara and R. Steiner, Minerals, 2014, 4, 541–552 CrossRef.
- A. J. Managh, D. N. Douglas, K. Makella Cowen, H. J. Reid and B. L. Sharp, J. Anal. At. Spectrom., 2016, 31, 1688–1692 RSC.
- K. Lan and J. W. Jorgenson, J. Chromatogr. A, 2001, 915, 1–13 CrossRef CAS PubMed.
- J. M. Cottle, A. R. Kylander-Clark and J. C. Vrijmoed, Chem. Geol., 2012, 332–333, 136–147 CrossRef CAS.
- A. Trinquier and P. Komander, J. Radioanal. Nucl. Chem., 2016, 307, 1927–1932 CrossRef CAS.
- G. Craig, Z. Hu, A. Zhang, N. S. Lloyd, C. Bouman and J. Schwieters, Thermo Fish. Sci. Tech. Note 30396, 2017 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |