Interfacial reactions of Cu(II) adsorption and hydrolysis driven by nano-scale confinement†
Andrew W.
Knight
a,
Poorandokht
Ilani-Kashkouli
 b,
Jacob A.
Harvey
b,
Jacob A.
Harvey
 c,
Jeffery A.
Greathouse
c,
Jeffery A.
Greathouse
 c,
Tuan A.
Ho
c,
Tuan A.
Ho
 c,
Nadine
Kabengi
bd and
Anastasia G.
Ilgen
c,
Nadine
Kabengi
bd and
Anastasia G.
Ilgen
 *c
*c
aStorage and Transportation Technology Department, Sandia National Laboratories, Albuquerque, NM 87185-0754, USA
bDepartment of Geosciences, Georgia State University, Atlanta, 30303 Georgia
cGeochemistry Department, Sandia National Laboratories, Albuquerque, NM 87185-0754, USA. E-mail: agilgen@sandia.gov; Tel: +1 (505) 284 1393
dDepartment of Chemistry, Georgia State University, Atlanta, 30303 Georgia
First published on 31st October 2019
Abstract
Spatial confinement is prevalent in sedimentary rocks and can lead to changes in the chemical behavior at mineral–water interfaces. This includes both deviations in the physico-chemical properties of confined water, when compared to the bulk liquid phase, and subsequent alterations in adsorption chemistry of ions inside nano-scale mineral pores. Here we document contrasting adsorption mechanisms and differences in local coordination environments of copper (Cu2+), depending on whether the ion is adsorbed on non-porous silica surfaces, versus inside 8 nm and 4 nm pores in silica. X-ray absorption spectroscopy, flow micro-calorimetry, and batch adsorption methods together with molecular modeling are used to thoroughly describe the dependence of these adsorption processes on the pore size. We show that confinement within silica pores promotes Cu–Cu interactions and increases the formation of Cu–Cu polynuclear surface complexes. We also demonstrate that the mechanism of Cu2+ adsorption on non-porous versus porous silica is vastly different. The adsorption of Cu2+ on non-porous silica is an endothermic process, whereby Cu2+ undergoes dehydration prior to surface complexation. In contrast, adsorption within nano-scale pores is preceded by only partial dehydration, and significant formation of Cu–Cu polynuclear complexes, which leads to an overall exothermic signal. Interfacial confinement leads to dramatic changes in the adsorption mechanism and speciation, which in turn controls the fate and transport of chemical species in natural environments.
Environmental significanceReactions at mineral–water interfaces control the fate and transport of elements in aqueous and soil environments, as well as in sedimentary rocks. In tightly compacted soils and rocks, mineral–water interfaces are spatially confined, with the confined reactive domains having nm-scale dimensions. The reactivity of mineral–water interfaces is affected by this spatial confinement. Namely, the dielectric constant and density of water decrease when the domain size approaches less than 5 nm. These changes in the properties of solvent (water) lead to the changes in hydration and coordination chemistry of ions, and, as a result, changes in the complexation of ions with the mineral surfaces. We discovered that adsorption of copper Cu2+ aqueous species onto silica surface depends on spatial confinement. Here we show that adsorption mechanisms of Cu2+ onto confined (8 nm and 4 nm pores) vs. non-confined silica surfaces are vastly different. The confinement within silica pores increases the formation of Cu–Cu polynuclear surface complexes, and changes the sign of the overall heat of adsorption. Identifying the reactivity changes and chemical mechanisms active under nano-scale confinement further expands our understanding of interfacial chemistry in environmentally-relevant systems. |
Introduction
Mineral–water interfaces provide reactive surfaces for the adsorption of ions and act as mineral nucleation sites.1 The chemical identity of ions (i.e. which ions are present), and surface reactivity, play integral roles in controlling the fate and transport of chemical species in the environment.1,2 An additional factor—nano-scale confinement—has recently been recognized to affect interfacial chemical reactions.2–11 Here we show that chemical pathways, products, and energetics of partitioning reactions are sensitive to spatial confinement at the silica–water interfaces.Nano-scale pores are ubiquitous in nature and have large surface area to volume ratios, thus the physical and chemical processes occurring within this reactive porous media can control the macroscopic behavior of water and ions, including solute hydration, chemical and physical sorption processes, stable isotope fractionation, and nucleation.3,12,13 Currently, a fundamental understanding of nano-scale confinement effects on interfacial processes is inadequate, and therefore cannot be incorporated into continuum models for predicting macroscopic chemical behavior. Recent studies have used systematic approaches to quantify chemical changes in incrementally smaller pores.4,6,9 These studies are critical for the development of fundamental frameworks for predicting geochemical reactions in the subsurface.
Nano-scale confinement induces shifts in water's physical properties, which drives enhanced cation adsorption and electron transfer reactions on mineral surfaces.5–9,14–16 Nano-scale confinement alters intermolecular water–water interactions, leading to changes in the dielectric constant, density, viscosity, and surface tension of water in pores with diameter less than 5 nm.8,14,15 Driven by changes in water properties, cation hydration energies decrease, shifting the equilibrium of the solvation and dehydration reactions, the structure and influence of the electrical double layer, and changes in the interfacial energies between the surface and solution.3,4,9 Previously, we demonstrated an increased adsorption maximum and faster reaction kinetics when Cu2+ is adsorbed on mesoporous silica (SBA-15) with a 4 nm pore diameter, compared to SBA-15 materials with 6 and 8 nm pore diameters.4 Similarly, Kim et al. reported enhanced adsorption of arsenic (As) on ordered mesoporous alumina when compared to its non-porous counterpart.17 Additionally, Mantha et al. 2019 demonstrated that Cu-bearing nano-particles can form in confined pore spaces present in organic matter of soils, and that these Cu-bearing nano-particles play an important role in the transport of metals within the soil column.2
Congruently, calorimetry studies presented thermodynamic evidence for enhanced inner-sphere adsorption inside nano-scale pores.18 Sodium, for example, forms inner-sphere adsorption complexes when confined inside zeolite pores (0.51 nm pore diameter), while mostly forming outer-sphere complexes on unconfined surfaces.19 Anomalous adsorption behavior was observed for sodium, nickel, potassium and calcium in nano-scale pores of zeolite.18,20 These studies reported that adsorption of cations is enhanced in incrementally smaller pores in zeolite (all examined pores were <1 nm diameter). The proposed explanation for the enhanced adsorption is that in the pores between 0.3–0.5 nm (where the hydrated ion diameter is larger than the pore diameter) ions have to dehydrate to enter the pore, and these dehydrated ions form inner-sphere complexes.18,20
While efforts have been made to understand thermodynamic changes of nano-scale confined systems, few datasets quantify the microstructure (i.e. local coordination environment) around ions adsorbed on confined surfaces. Recently, Nelson et al. investigated coordination environment of zinc (Zn2+) confined inside controlled pore glasses (CPGs), where Zn2+ adsorbed predominantly as a tetrahedral complex inside 10 nm pores (the smallest pore evaluated), while inside larger pores (up to 330 nm pore diameters) the coordination environment varied between tetrahedral and octahedral.9 Their study provides valuable analyses to improve our understanding of Zn2+ adsorption on siliceous materials, however it is critical to interrogate the confinement effects in pores with <10 nm diameter, since significant changes in the solvent (water) properties were only observed for spatial confinement of 10 nm and less. While few studies indicate confinement effects inside pores that are >10 nm in diameter,9,21 the research overwhelmingly suggests that these effects are most pronounced in pores that are <10 nm.5,22–24 Therefore, it is imperative to investigate the coordination chemistry of adsorbed ions confined within materials with pore sizes less than 10 nm, as these nano-scale domains are ubiquitous in the environment.3,4,11,12
In this study we address the scientific gap in understanding changes in the coordination environment and reaction pathway for Cu2+ by using X-ray absorption fine structure spectroscopy (XAFS), flow micro-calorimetry, and molecular dynamics (MD) simulations to decipher the systematic changes as a function of decreasing pore size of adsorbing silica. We interrogate the impact of nano-scale confinement on the coordination chemistry and heat of adsorption during Cu2+ partitioning onto non-porous silica and within nano-scale pores in mesoporous (SBA-15) silica with 8 and 4 nm pores. The sum of our findings provides a complete understanding of the pathways, products and thermodynamics of Cu2+ adsorption reaction onto silica surface under nano-scale confinement.
Experimental and computational methods
General
All reagents used for batch adsorption experiments, for the preparation of XAFS samples, and for calorimetric adsorption analyses were ACS reagent grade or higher, including copper(II) nitrate trihydrate (Cu(NO3)2·3H2O), ammonium nitrate (NH4NO3), nitric acid (HNO3), and ammonium hydroxide (NH4OH). Ultrapure nitric acid (HNO3) was used for dilutions prior to aqueous analysis and for aqueous sample preservation. Aqueous concentrations of Cu2+ were quantified via inductively coupled plasma mass spectrometry (ICP-MS) (NexION 350D). All gasses and cryogenic liquids used for ICP-MS analysis and Brunauer–Emmett–Teller (BET) surface area analysis were ultra-high-purity grade, including liquid and gaseous argon (Ar) and nitrogen (N2), along with gaseous helium (He). All silica materials were purchased from Sigma Aldrich. These materials included non-porous fumed silica as well as mesoporous silica; SBA-15-8, SBA-15-4 correspond to hexagonally ordered cylindrical pores with diameters of 4.4 ± 0.3 and 7.0 ± 0.1 nm. Milli-Q H2O (Barnstead NANOpure Diamond) with the resistivity of 18.2 MΩ × cm, 0.2 μm filtered and UV irradiated was used in the preparation of all solutions and suspensions.Substrate conditioning and surface area analysis
We used chemically-pure commercially available silica substrates. Besides chemical purity, the difference between amorphous SiO2 phases in natural environments, and the substrates used in our work, is the hydroxyl (–OH) site density on their surfaces. Both fumed silica and SBA-15 phases are treated at elevated temperatures during synthesis, and the –OH surface densities are lower than the theoretical maximum.25 We anticipate that amorphous silica precipitating at lower temperatures in soils and river sediments has fully hydroxylated surfaces. Purchased silica materials were conditioned by cleaning and hydrating, as described previously.4 Briefly, silica was added to a centrifuge bottle along with Milli-Q distilled deionized water in a solid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) liquid mass ratio of 2
liquid mass ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and mixed on a shaker table for 24 hours. Following the mixing step, the silica materials were filtered using 0.45 μm nylon filter membrane and rinsed with Milli-Q water and suspended in 200 mL of Milli-Q water. This process was repeated two additional times, and following the final rinse, the silica materials were transferred to a scintillation vial and placed in the oven (45 °C) for at least 48 h to dry. Rinsed, hydrated, and dried silica materials were split for further specific preparation procedures required for each subsequent experiment.
1, and mixed on a shaker table for 24 hours. Following the mixing step, the silica materials were filtered using 0.45 μm nylon filter membrane and rinsed with Milli-Q water and suspended in 200 mL of Milli-Q water. This process was repeated two additional times, and following the final rinse, the silica materials were transferred to a scintillation vial and placed in the oven (45 °C) for at least 48 h to dry. Rinsed, hydrated, and dried silica materials were split for further specific preparation procedures required for each subsequent experiment.
The surface area was quantified using a Brunauer–Emmett–Teller (BET) surface area analyzer, as reported previously.4 Briefly, approximately 200 mg of dried fumed silica was transferred to a tarred BET tube equipped with an airtight cap and loaded onto an ASAP 2020 to be degassed for 4 hours at 300 °C and backfilled with inert He gas. Following sample degas, any mass change resulting from the degas step was noted and adjusted. To start the analysis, a dewar was filled with liquid N2 and the BET tube was equipped with a thermal jacket and placed in the sample holder. The BET surface area and the non-local density functional theory (NLDFT) method was used to determine the average pore diameter and pore volume of fumed silica.26,27
Adsorption samples for XAFS analysis
XAFS samples were prepared via adsorption reactions of Cu(NO3)2 with silica (SBA-15-8, SBA-15-4, and fumed silica). Prior to adsorption, roughly 200 mg of dried silica material (as described above) was mixed and equilibrated with 50 mL of NH4NO3 for 24 hours. As we noted in previous work, NH4NO3 was selected as the background electrolyte to prevent introducing competing metal species to the system.4 Next, Cu(NO3)2 was added (0.1 mM, 0.2 mM, and 0.3 mM) along with enough Milli-Q water to bring the total volume to 100 mL. The pH was adjusted to pH = 6.0 ± 0.1 using dilute HNO3 or NH4OH. The samples were placed on the mixing table and mixed overnight. The reaction was terminated by phase separation via centrifugation at 3000 rpm for 10 minutes. The supernatant was decanted and collected to be quantified through analysis by ICP-MS. For XAFS analysis, as described previously,13 the solid pastes were mounted onto a Teflon sample holder, sealed with Kapton tape, and immediately immersed in a transportable dry shipper (N2 atmosphere, liquid nitrogen temperature).XAFS data were collected at the undulator beamline sector 20-ID (XOR) at the Advanced Photon Source (APS) at Argonne National Laboratory. As described previously, the uncollimated beam was used with a Si(111) monochromator that was detuned by 15% for harmonic rejection.13 The monochromator was tuned to the Cu K-edge at approximately 9200 eV via a Cu metal foil, similar to Cheah et al.28,29 The monochromator step size was 10 eV in the pre-edge, with a counting time of 0.5 seconds per point, 0.3 eV step size in the near edge region with 0.5 second counting time, and 0.05 eV in the XAFS region with a counting time of 0.5 seconds per point. The fluorescence points for Cu were collected on a Vortex Si Drift solid state 4 element detector. During the analysis, the sample chamber was kept at 22 K using a Displex liquid helium cryostat to avoid beam damage. For each sample, a minimum of 3 XAFS scans were collected to achieve an appropriate signal to noise ratio. The Cu standards used to determine the amplitude reduction factor (S0) were copper(II) acetate, copper(II) hydroxide, copper(II) oxide, and copper(I) oxide. The S0 value was determined to be 0.89 by fitting Cu XAFS standards. This S0 value was used for fitting all Cu XAFS data collected during this analytical run.
The Cu K-edge XAFS data was processed and analyzed using Athena and Artemis30 interface to the IFEFFIT software.31 The background subtraction, normalization, and conversion into k-space using Athena are described in detail elsewhere.31,32 A Fourier transform (Hanning Window, dk = 2) was applied to Cu K-edge XAFS data over the k-range from approximately 3–12 (Table 1). The Fourier transformed data was imported to Artemis to be analyzed by IFEFFIT30 with a shell-by-shell fitting of theoretical single scattering (SS) paths approach.33 For analysis and calculation of theoretical phase and amplitude functions for Cu–O, Cu–Cu, and Cu–Si, paths were generated using FEFF6 code33 from the crystal structure of dioptase reported in Ribbe et al.34
| Sample | Surface loading (μmol m−2) | k-Range | R-Range (Å) | Shell | CN | R (Å) | σ 2 (Å2) | ΔE0 eV | R-Factor | Red χ2 | Ind. Pts. |
|---|---|---|---|---|---|---|---|---|---|---|---|
Notes:a Usable k-range.b Coordination number.c Bond length.d Debye–Waller factors: mean-square amplitude reduction factor, including thermal and static disorder components.e Energy shift between the theoretical and measured spectrum.f R-Factor (mean square misfit) 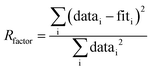 .g Reduced chi-square .g Reduced chi-square 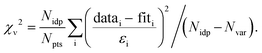 h Independent points (number of data points minus number of variable parameters) Nidp = Npts − Nvar. h Independent points (number of data points minus number of variable parameters) Nidp = Npts − Nvar. |
|||||||||||
| Fumed silica-hCu | 0.18 (3) | 3.0–11.83 | 1.0–5.0 | Cu–Oeq | 4.3 (3) | 1.94 (7) | 0.007 | 2.6 (9) | 0.020 | 31.40 | 22.05 |
| Cu–Oax | 0.6 (1) | 2.29 (1) | 0.002 | ||||||||
| Cu–Cu | 0.9 (6) | 2.94 (2) | 0.009 | ||||||||
| Cu–Si | 0.1 (3) | 3.52 (3) | 0.009 | ||||||||
| SBA-15-8-hCu | 0.09 (1) | 2.6–10.7 | 1.0–5.0 | Cu–Oeq | 3.7 (7) | 1.94 (6) | 0.003 | −1.0 (7) | 0.026 | 48.07 | 22.02 |
| Cu–Oax | 1.2 (6) | 2.84 (3) | 0.007 | ||||||||
| Cu–Cu | 1.7 (2) | 2.96 (6) | 0.005 | ||||||||
| Cu–Si | 0.3 (3) | 2.99 (6) | 0.008 | ||||||||
| SBA-15-8-mCu | 0.06 (1) | 3.0–11.85 | 1.0–5.0 | Cu–Oeq | 3.4 (3) | 1.94 (7) | 0.002 | −1 (1) | 0.021 | 28.60 | 22.05 |
| Cu–Oax | 0.8 (4) | 2.82 (2) | 0.005 | ||||||||
| Cu–Cu | 1.7 (2) | 2.96 (7) | 0.008 | ||||||||
| Cu–Si | 0.2 (3) | 3.5 (1) | 0.004 | ||||||||
| SBA-15-4-hCu | 0.09 (2) | 3.0–11.86 | 1.0–5.0 | Cu–Oeq | 3.9 (2) | 1.94 (2) | 0.003 | 1 (3) | 0.009 | 34.14 | 22.04 |
| Cu–Oax | 0.7 (5) | 2.90 (3) | 0.003 | ||||||||
| Cu–Cu | 1.6 (5) | 2.96 (9) | 0.008 | ||||||||
| Cu–Si | 0.9 (2) | 3.03 (2) | 0.009 | ||||||||
| SBA-15-4-mCu | 0.06 (1) | 3.0–11.84 | 1.0–5.0 | Cu–Oeq | 3.5 (5) | 1.95 (1) | 0.002 | 1.8 (9) | 0.024 | 59.04 | 22.05 |
| Cu–Oax | 1.2 (5) | 2.86 (2) | 0.005 | ||||||||
| Cu–Cu | 1.9 (4) | 2.97 (5) | 0.009 | ||||||||
| Cu–Si | 0.6 (4) | 3.53 (7) | 0.003 | ||||||||
Calorimetric adsorption studies
The flow microcalorimeter (FMC) used in this study was custom-designed and fabricated in the Kabengi laboratory at Georgia State University. Descriptions of the instrumentation and basic operational procedures have been detailed previously.35 Here we include a brief description summarizing the experimental protocols relevant to this study. The system to quantify the thermodynamic signals of Cu2+ adsorption is summarized in Table 2. To obtain the thermal signatures and subsequently the heats of Cu2+ adsorption, a 20.0 ± 0.5 mg sample of silica particles (either SBA-15-8, SBA-15-4, or fumed silica) was homogeneously packed into the sample holder of the FMC's microcolumn, and equilibrated with a 0.01 M NH4NO3 solution at a flow rate of 0.30 ± 0.03 mL min−1 until thermal equilibrium was reached as indicated by a steady baseline. The input solution was then switched to one in which 0.3 mM NH4NO3 had been replaced with 0.3 mM Cu(NO3)2. The concentration of NH4NO3 was kept at 9.25 mM to keep the ionic strength (I) constant. The calorimetric signal corresponding to the interaction of Cu2+ with the silica sample was thus obtained. Once the thermal signal returned to the original baseline, after about 15–30 min, indicating that the reaction between the sample and Cu2+ had ended, we switched the input solution back to 0.01 M NH4NO3. During the Cu2+ treatment and the subsequent NH4NO3 exposure, effluent samples were collected for chemical analysis. The total aqueous concentration of Cu2+ in the outflow samples was determined using ICP-MS. The mass of Cu2+ retained and subsequently desorbed from the surface was determined by a mass balance calculation between the mass of Cu2+ injected and that recovered in all effluents.| Material | BET surface area (m2 g−1) | Mesopore diameter (nm) | OH− density (OH−/nm2) | Mass (mg) | Normalized energy (mJ m−2) | Normalized adsorption (kJ mol−1) | Normalized adsorption (μmol m−2) |
|---|---|---|---|---|---|---|---|
| a This study. b From Knight et al. (2018).4 | |||||||
| Fumed silica | 192 ± 7a | N/A | 2.15a | 20 ± 0.5 | 0.429 | 1.165 | 0.369 |
| SBA-15-8 | 661 ± 5b | 7.0 ± 0.3b | 1.8 ± 0.2b | 20 ± 0.5 | −0.128 | −1.349 | 0.095 |
| SBA-15-4 | 580 ± 13b | 4.4 ± 0.1b | 2.3 ± 0.2b | 20 ± 0.5 | −0.253 | −2.168 | 0.117 |
The heats of reactions (Qads in mJ m−2) and molar enthalpies (ΔH in kJ mol−1) were calculated by integrating the calorimetric peaks and were converted to energy units (Joules) by calibration with calorimetric peaks of known energy inputs generated from a calibrating resistor. The solution pH was adjusted daily using dropwise addition of 0.1 M HNO3 and 0.1 M NH4OH to achieve a final pH of 6.0 ± 0.1. Changes in total concentration and ionic strength resulting from pH adjustments were determined to be negligible.
ICP-MS analyses of copper
The amount of Cu2+ adsorbed onto silica surfaces was determined for all samples by ICP-MS. All XAFS samples and all calorimetric samples were quantified as we have described previously.4,36 For XAFS samples, following phase separation, the eluent was diluted using ultrapure 2% HNO3 to a concentration range adequate for quantification via ICP-MS. For calorimetric samples, the effluents of flow-through experiments were collected during both Cu2+ adsorption and desorption on silica and were also diluted with ultrapure 2% HNO3. Copper standards were prepared with concentration ranges from 10 to 2000 ppb and were used to generate a calibration curve. All reference solutions were prepared in an identical experimental matrix to account for any matrix interferences in the analysis. The amount of Cu2+ adsorbed was normalized by surface area and calculated from eqn (1):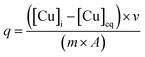 | (1) |
MD simulation details
MD simulations of silica nanopores filled with aqueous phase were performed using the LAMMPS code38 under constant volume conditions with a thermostat temperature of 300 K. Timesteps used were 0.5 fs for short-range interactions (10.0 Å cutoff radius) and 1.0 fs for long-range electrostatic interactions, which were evaluated with a particle–particle particle-mesh algorithm.39 Temperature was controlled using a Nose–Hoover thermostat with a relaxation time of 100 fs. Potential parameters for silica atoms were taken from ClayFF,40 which relies on nonbonded interactions (i.e., van der Waals and electrostatics) with an additional harmonic bond stretch term for surface hydroxyl groups and an additional angle bending term for surface silanol groups,41 which was recently validated against experimental infrared spectroscopy.42 ClayFF has been used previously to model the interaction of aqueous fluids with similar surfaces, including amorphous silica43–48 and quartz.49–55 The flexible simple point charge (SPC) water model was used, which includes harmonic OH bond stretch and HOH angle bending terms.56 SPC parameters were also used for the OH− ion, with the O charge adjusted to −1.41e for a net ion charge of −1.0e.57,58 Parameters for Cu2+ were taken from a general set for aqueous divalent cations that accurately reproduce experimental hydration free energies.59 Lennard-Jones (LJ) parameters for unlike atom pairs were generated using arithmetic mixing rules. All interaction parameters are provided in ESI.†Details for the construction of the silica surface model, composition of pore fluids, and pre-equilibrium simulation methodology are described in detail in the ESI.† MD trajectories for analysis were generated from a 10 ns production simulation. Number densities were calculated by determining the distance from each Cu atom to the nearest pore oxygen divided by the available volume at that distance determined from a Monte-Carlo insertion code. Insertions were accepted if the distance from the attempted insert to any other atom was greater than 65% of the interatomic LJ sigma value. The 0.65 factor was chosen to accept all distances that were observed in the MD simulations.
Results and discussion
Confinement promotes formation of copper dimer species on the silica surface
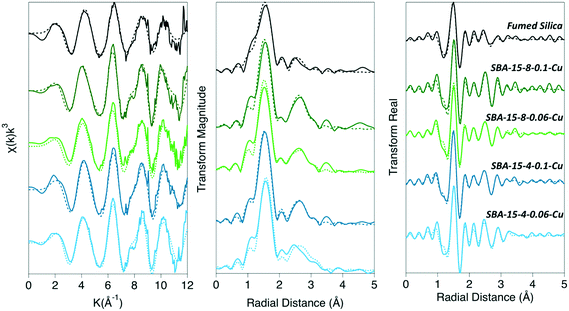
We quantified the coordination environment around the adsorbed Cu2+ cation with XAFS spectroscopy, as a function of both pore size and density of adsorbed Cu2+ on the silica surface. The data were fit to a model suggested by Cheah et al.,28,29 where Cu2+ formed predominantly monodentate inner-sphere complexes. We observed a larger proportion of polymeric Cu species when confined inside mesopores, compared to the non-porous silica surface. Adsorbed polymeric Cu species were reported in earlier work for Cu2+ adsorbed on non-porous silica.28,29 In our samples, Cu–Cu backscattering is much more pronounced in the porous silica samples, compared to non-porous silica. We attribute this effect to the decrease in the dielectric constant of confined water,8,14 which leads to a decrease in the hydration energy of Cu2+, and therefore enhanced formation of surface complexes.Previous XAFS data analyses indicates that Cu2+ experiences strong Jahn–Teller effects due to its d9 election configuration, and therefore forms a distorted (elongated) octahedron; where the Cu–Oeq (bonds with four equatorial oxygen neighbors) are shorter than the Cu–Oax bonds (axial direction).28,29,60–63 Current experimental evidence is inconclusive and has led to a debate regarding the distorted octahedron as the preferred aqueous species: four-, five-, and six-coordinate complexes have been hypothesized,62 and the aqueous complex is likely to be a dynamic distribution of five- and six-coordinated complexes.60–62 For our XAFS analysis we are aware of this challenge and have maintained a consistent and rigorous fitting protocol in an attempt to isolate differences between samples, rather than proposing a specific coordination geometry. Therefore, in our model we simply considered the lowest energy conformation, with a coordination number (CN) of 6, consisting of four equidistance equatorial O atoms and two elongated axial O atoms. The second shell in our model consisted of Cu–Si and Cu–Cu backscattering paths. The average CN and bond distance (R) for each coordination shell are summarized in Table 1.
The XAFS data of adsorbed Cu2+ was fit using the paths for a distorted octahedral coordination environment, as described in the previous XAFS studies and simulations.28,29,61,63 The average measured CN for Cu–Oeq was ∼ 3.76 ± 0.36 (Table 1); while the CN for Cu–Oax was ∼0.9 ± 0.28 for non-porous and porous silica samples. Based upon these CN numbers, the local coordination around Cu is likely to contain 5 or 6 oxygen atoms. Likewise, the bond distances for Cu–Oeq were determined to be nearly identical for all silica samples (Table 1). The Cu–Oax bond distances are similar for all porous silica samples (2.82 ± 0.02–2.90 ± 0.03 Å); however, the Cu–Oax distance for non-porous silica is significantly shorter (2.29 ± 0.01 Å). The Cu–O distances for non-porous silica agreed well with the model and other previously reported values for a distorted octahedral complex, where Cu–Oeq = 1.94–1.96 Å, and Cu–Oax = 2.15–2.65 Å.34,61–63 However, not all previous research fit the Cu–Oax shell due to either large σ2 values indicating that no reasonable CN or bond distance could be obtained or the data were fit with a different coordination environment.28,29,62 Our σ2 for Cu–O shells did not exceed 0.008, and therefore the bond distances are quantified accurately for all samples, with an error of 0.1 Å.
The second coordination shell involves interactions between Cu with nearest Cu atoms (i.e., Cu–O–Cu) as well as coordination with Si (i.e., Cu–O–Si) at the surface. We observed the presence of Cu–Cu backscattering in all porous and non-porous silica samples. This observation agrees with previous studies, which report Cu2+ forming dimeric or polymeric complexes on the surface of non-porous silica, while maintaining a monomeric coordination when adsorbed on alumina.28,29 However, in our work we observed more dimeric complexes in porous silica, compared to non-porous silica, as evidenced by the amplitude of the Cu–Cu backscattering feature. When Cu2+ was adsorbed to non-porous silica, the CNCu–Cu = 0.9 ± 0.6, and RCu–Cu = 2.94 ± 0.02 Å (Table 1). Whereas the CNCu–Cu for the porous SBA-15 silicas was 1.7 ± 0.2 for both high- and medium-surface coverage inside the 8 nm pores, and 1.6 ± 0.5 and 1.9 ± 0.4 for the high- and medium-surface coverage inside the 4 nm pore, respectively. The CNCu–Cu on the SBA-15 samples did not significantly differ between 4 nm and 8 nm pore diameters and did not depend on the surface coverage of adsorbed Cu2+. The intensity of the Cu–Cu backscattering feature for SBA-15 samples was significantly higher than for non-porous silica (Fig. 1), and further suggests that, in confinement, Cu2+ has a greater tendency to form dimeric to multimeric complexes. The determined Cu–Cu distances in all samples were approximately the same in the mesoporous silica samples, where RCu–Cu ranged from 2.96–2.97 Å. These RCu–Cu and CNCu–Cu values correspond to the formation of a Cu2(OH)2-like adsorption complex on the surface (where one Cu is in inner-sphere surface coordination), as the CNCu–Cu was determined to be 1.9 ± 0.2 and RCu–Cu = 2.96 ± 0.002 Å, which agrees with the previous studies reporting Cu polymerization on non-porous silica.28,29 However, our complexes on mesoporous silica appear to differ from those described by Cheah et al. for amorphous silica, in which the authors observed an adsorption complex that was distinctly different from Cu(OH)2, with a lower CN and shorter bond length (CN = 0.5–0.9 and RCu–Cu = 2.58–2.59 Å).
The Cu–Si backscattering feature of adsorbed Cu2+ was fit with low (<1) CN numbers in all analyzed samples. Due to silicon's low mass, the backscattering signal from the Cu–Si shell is weaker, compared to Cu–Cu backscattering signal. Since Cu–Si and Cu–Cu shells overlap, the Cu–Si becomes nearly invisible. We fit all data including and excluding Cu–Si shell, and a statistically significant improvement of the fit was only seen for the SBA-15-4-hCu sample (ESI†). Because the XAFS signal is an average of all the Cu2+ species in the system, we conclude that copper forms both inner- and outer-sphere complexes on silica surface. Additionally, the presence of Cu-oxide nano-particles cannot be ruled out for the samples containing oligomeric Cu2+ species within confined silica pores. Based on the qualitative trends in the Cu–Si CNs, there may be a greater probability of Cu2+ to form inner-sphere complexes with Si in smaller pores, and that proportion of these complexes may decrease as the pore sizes increases. The Cu–Si bond length for the porous silicas with surface loadings of approximately 0.05 μmol m−2 were about 3.5 Å, while for the silicas with a higher Cu2+ surface loading, approximately 0.1 μmol m−2 for porous silica and 0.2 μmol m−2 for nonporous silica, the Cu–Si distance was determined to be approximately 3.0–3.5 Å (Table 1, Fig. 2).
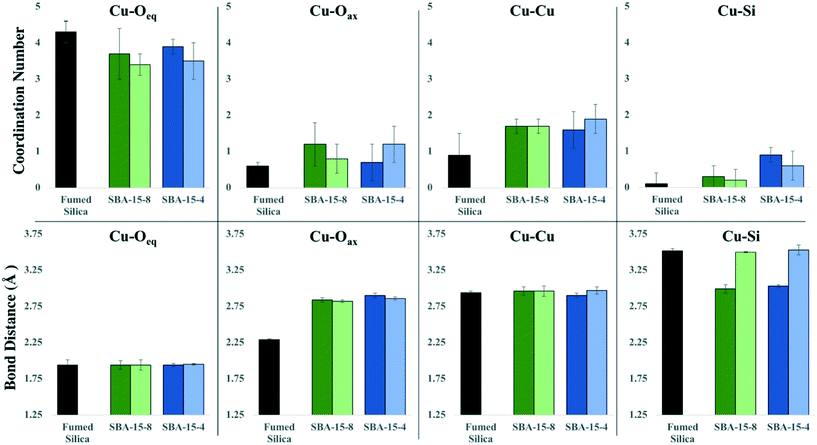 | ||
| Fig. 2 The distribution of average bond distances and coordination numbers of each shell for fumed silica, SBA-15-8, and SBA-15-4 for high Cu2+ surface loading. | ||
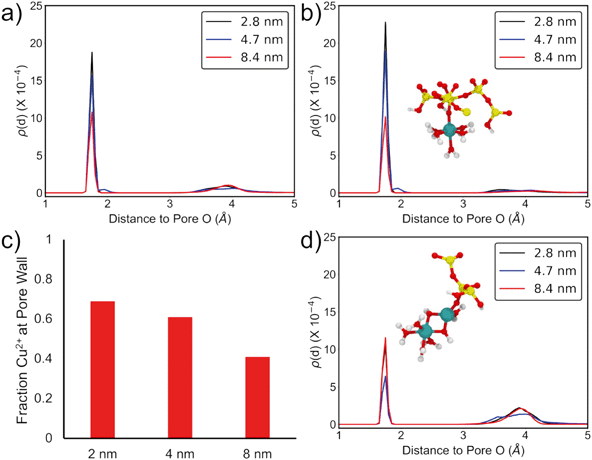
This effect of confinement on Cu2+ adsorption was explored further by examining the results of MD simulations of Cu-hydroxide complexes in 2, 4, and 8 nm amorphous silica slit pores (Fig. 3, see ESI† for full computational details). Cu2+ is least likely to be found at the pore wall in the 8 nm pore and that probability increases monotonically to 2 nm as evidenced by the increasing intensity of the <2 Å peak (Fig. 3a). By integrating the area under the curve in this region we find that 69% of the Cu2+ in the simulation is found at the pore wall for the 2 nm pore, compared to just 41% in the 8 nm pore, indicating increased adsorption with increasing degree of spatial confinement. Moreover, the CNCu–Si, calculated from the simulated radial distribution functions (RDFs), increases from 0.41 to 0.69 going from 8 nm to 2 nm pores, qualitatively agreeing with the experimentally observed trend of enhanced Cu–Si backscattering feature in XAFS (Table 3, Fig. 3).
| Sample | Shell | CN | R (Å) |
|---|---|---|---|
| 8 nm pore | Cu–Odep | 0.42 | 1.75 |
| Cu–O | 1.88 | 1.78 | |
| Cu–Ow | 2.74 | 1.98 | |
| Cu–Cu | 0.59 | 2.65 | |
| Cu–Si | 0.41 | 3.15 | |
| 4 nm pore | Cu–Odep | 0.58 | 1.75 |
| Cu–O | 1.17 | 1.75 | |
| Cu–Ow | 3.36 | 1.98 | |
| Cu–Cu | 0.26 | 2.68 | |
| Cu–Si | 0.58 | 3.15 | |
| 2 nm pore | Cu–Odep | 0.69 | 1.78 |
| Cu–O | 1.05 | 1.78 | |
| Cu–Ow | 3.58 | 1.98 | |
| Cu–Cu | 0.35 | 2.65 | |
| Cu–Si | 0.69 | 3.12 |
Calorimetric evidence for different adsorption pathways on confined vs. non-confined silica surfaces
Calorimetric data for the heats of adsorption for Cu2+ on non-porous silica, and mesoporous silica are shown in Table 2 and Fig. 4. The heats of adsorption were monitored by the resulting calorimetric signal, as seen in Fig. 4. It is immediately obvious in Fig. 4, that the adsorption pathway of Cu2+ on non-porous silica is different than on the mesoporous SBA-15 materials. The measured calorimetric signal associated with the adsorption of Cu2+ is endothermic for non-porous silica, while the adsorption process is primarily exothermic on the porous silicas. The normalized adsorption energies were determined to be 1.165, −1.349, and −2.168 kJ mol−1 for non-porous silica, SBA-15 with 8 nm, and SBA-15 with 4 nm pores, respectively. The surface-area-normalized adsorption maximum values were determined to be 0.369 μmol m−2, 0.095 μmol m−2, and 0.117 μmol m−2 for non-porous silica, SBA-15 with 8 nm pores, and SBA-15 with 4 nm pores, respectively. These surface coverage values are close to those for samples examined with XAFS analysis (Fig. S1†) and our previously reported adsorption maximum values for SBA-15 with 4 nm and SBA-15 with 8 nm pores.4 These flow-through experiments are therefore complimentary and capture similar adsorption surface coverages, as examined in our XAFS analysis.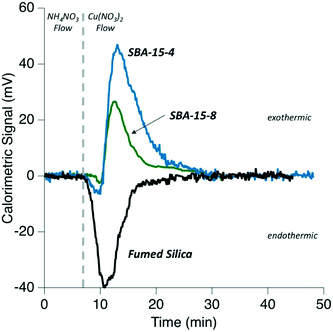 | ||
| Fig. 4 Comparison of calorimetric heats measured during Cu2+ flow through experiment (adsorption) for fumed silica, SBA-15-8, and SBA-15-4 versus time. | ||
Adsorption of copper under nano-scale confinement
Through coupled spectroscopy, micro-calorimetry, and MD simulations, we develop a detailed understanding of the nano-scale confinement impact on the energetics of adsorption, reaction pathway, and coordination chemistry of Cu2+ on silica surfaces. The results indicate dramatic differences in the reaction pathway between porous and non-porous silicas, as seen from the calorimetric signals. Spectroscopic analyses show measurable differences in the average local coordination environment of adsorbed Cu2+, driven by nano-scale confinement effects. In summary, the effects of confinement result in (i) distortion of the first coordination shell of Cu2+, seen as elongation of the Cu–Oax bond distances relative to Cu–Oeq bond distances, (ii) increased proportion of dimer/oligomer Cu2+ surface complexes, and (iii) changes to the surface complexation modes.Based upon our measurements, the average Cu2+ coordination on the surface could either be considered a distorted octahedron or distorted square pyramid. In either case, the average local coordination environment of Cu2+ adsorbed onto the porous SBA-15 samples is more distorted compared to non-porous silica, as evidenced by the Cu–Oax and Cu–Oeq bond distances. Longer Cu–Oax bond distances, less similar to Cu–Oeq distances, represent a more disordered complex, where the Cu–Oax were 0.5–0.6 Å longer when confined within pores than adsorbed to non-porous silica. Additionally, within the confined porous SBA-15 samples, Cu–Oax distances for 4 nm pores were longer than those for 8 nm pores, suggesting that as confinement increases, distortion of the first coordination shell of Cu2+ also increases. Additionally, this may suggest that Cu–Oax elongation occurs in confinement due to Cu–O bond weakening as a result of increased oligomerization. We note that calculated Cu–Owater bonds (1.98 Å) are longer than both the Cu–OH and Cu–O− bonds (1.78 Å) in the simulations, indicating that both increased adsorption and dimerization lead to some Cu–O bonds that are shorter than others. In the experiments we also observed that these effects are sensitive to the density of adsorbed Cu2+ on the surface. While the overall surface coverage remains low (i.e. most OH available on the SiO2 surface are free of Cu2+), the Cu–Oax distances became longer with increased surface density of adsorbed Cu2+. With increasing surface coverage of Cu2+ on the surfaces in silica pores, the effects of spatial confinement become more pronounced. In both mesoporous silicas with 4 nm and 8 nm pores, increased surface Cu2+ coverage led to an increase in the average Cu–Oax distance of 0.2–0.4 Å. Therefore, we observe that the least distorted Cu2+ complexes exist on non-porous silica, and as surface coverage increases inside the pores of mesoporous silicas, disorder increases. Unlike some studies, where changes in the CN were observed,9 we did not see any significant changes in CNCu–O in the XAFS data, at least within the uncertainty of ∼10–20% typical for CNs derived from XAFS data. The subtle differences between Cu–O distances suggest that nano-scale confinement distorts the coordination geometry of Cu2+. This phenomenon could be a result of steric effects of a hydrated Cu2+ complex entering an incrementally smaller pore. The ion–water interactions inside nano-scale pore are weaker, compared to the non-confined phase, due to water's dielectric constant decreasing with increasing degree of confinement8,14 and, therefore, the hydration sphere of Cu2+ may become distorted inside the pores.
In addition to the elongation of the Cu–Oax bonds, confinement increased the propensity for Cu2+ to undergo dimerization or oligomerization. While bond distances in all samples remained nearly the same, the amplitude of Cu–Cu backscattering (CNCu–Cu) was nearly double for mesoporous samples, compared to non-porous silica. As simulation snapshots demonstrate, Cu–Cu species all exist in a distribution, however when confined, the average CNCu–Cu is greater than in the non-confined system. This finding is confirmed by preliminary MD simulation results on a non-porous silica surface where a vacuum gap is applied above the liquid layer (data not shown). In this system no Cu2+ dimers are observed, in stark contrast to the results observed in the confined simulations. Previous studies investigating Cu2+ adsorption on amorphous silica demonstrated that Cu2+ forms dimers on silica surfaces.28 Our findings on non-porous silica confirm these earlier reports, while we also show that in confinement Cu–Cu backscattering is more pronounced. This polymerization reaction explains the difference in calorimetric trends between porous and non-porous silicas. Adsorption of Cu2+ in confinement was exothermic, while it was endothermic for non-porous silica. The endothermic response for the adsorption of Cu2+ on non-porous silica is likely a result of dehydration of the Cu2+ ion prior to adsorption.18–20 This suggests that when Cu2+ displaces NH4+ at the silica adsorption sites, the Cu2+ ions dehydrate and form inner-sphere adsorption complexes on the surface, which has been shown to be an endothermic reaction.19,64 Similar results were previously noted for Na+ and Ca+ on zeolite surfaces. When Na+ replaced Ca2+ at an adsorption site, there was a small exothermic peak followed by large endothermic peak. This process was described as follows; Na+ enters the pore, displacing Ca2+, and Ca2+ rehydrates (exothermic). Then, in order to adsorb to the surface as an inner-sphere complex, Na+ dehydrates (endothermic).19
Our XAFS and calorimetry data indicate that Cu2+ forms inner-sphere adsorption complexes on non-porous silica (CNCu–Si = 0.1 and RCu–Si = 3.52 Å). Previous work has illustrated Cu–Si complexes and provided estimated Cu–Si bond distances reflecting different surface adsorption complexes. It was determined that, Cu2+ can form a corner-sharing mono-dentate (RCu–Si = 2.6–3.5 Å), edge-sharing bi-dentate (RCu–Si = 2.2–2.4 Å), or corner sharing bi-dentate complex (RCu–Si = 3.0–3.5 Å).28,29 From these values, we cannot definitively say which complex is present in our systems, however it is unlikely that the edge-sharing bi-dentate complex is occurring as the expected bond distances are too short. The formation of an inner-sphere mono-dentate complex is consistent with other reports of Cu2+ adsorbed onto amorphous non-porous silica.28 Based upon the assumption that the Si–O bond length (∼1.61 Å)65,66 remains unchanged in confinement, we can assess the likelihood of Cu2+ adsorption through Cu–Oeq or Cu–Oax based upon estimated bond angles.
Conversely, the adsorption of Cu2+ on the SBA-15 materials responded with a weak endothermic feature, followed by a strong exothermic peak. The magnitude of both the endothermic and exothermic signals were stronger as the pore size decreased from 8 nm to 4 nm in diameter. This observed magnitude change could be a result of known changes to water properties.67 Because the H-bonding network and dielectric constant of water are altered when confined inside mesoporous silica, it is likely that the hydration energy of Cu2+ decreases with decreasing pore diameter – thus changing the magnitude of the calorimetric signal. The small endothermic peak is likely attributed to dehydration of Cu2+, similar to the adsorption process on non-porous silica. However, as the Cu2+ surface loading increases over time, and additional adsorption occurs, dimerization is promoted. The dimerization reaction is an exothermic process, and thus would result in an exothermic signal. A possible mechanism for the dehydration and dimerization (assuming 6-coordiantated) process for Cu2+ inside the mesopores of the SBA-15 materials is:
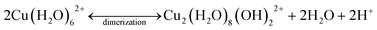 | (2) |
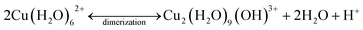 | (3) |
The weak endothermic signal, coupled with XAFS results, indicates that Cu2+ forms an inner-sphere complex with silica in the pores of mesoporous silicas which is confirmed by MD simulations. Interestingly, the Cu–Si distance (∼3.0 Å) is shorter for porous silicas with high surface loadings, relative to non-porous silica and porous silicas with medium surface loadings (∼3.5 Å). In porous samples, it seems most likely that Cu forms a surface complex with Si through the Oeq bond, as the bond angles for Cu–Oax–Si are ∼100°. However, for non-porous silica, Cu coordination through either Oax or Oeq results in a Cu–O–Si bond angle that is >130 °. Furthermore, there seems to be a systematic increase in the CNCu–Si as a function of decreasing pore diameter and increasing surface loading (Fig. 1, Table 1). While we do observe systematic changes, a Cu–Si distance of 3.0 Å falls within the hypothesized range for a corner sharing mono-dentate surface complex (2.6–3.5 Å), and the CNCu–Si never exceeds 1.0. Therefore, the XAFS data are insufficient to identify the exact geometry (mono- or bi-dentate) of Cu–Si coordination on the examined silica surfaces.
Conclusions
Our experimental and MD simulation results illustrate that the mechanism and reaction products of Cu2+ adsorption on silica surfaces are pore-size-dependent. Nano-scale confinement leads to an increase in the distortion of the coordination complex when Cu2+ is confined to the pores of SBA-15 samples when compared to non-porous silica. Additionally, the Cu–Si bond lengths suggest that the coordination environment around Cu2+ depends on both pore diameter, as well as Cu2+ density on silica surfaces. On mesoporous silicas with high surface coverage, Cu–Si distances are shorter than for non-porous silica and mesoporous silicas with medium surface coverage. Lastly, we have demonstrated that nano-scale confinement promotes Cu2+ dimerization, as supported by XAFS, MD simulation, and calorimetric studies. The increase in the Cu–Cu backscattering amplitude for mesoporous samples, compared to non-porous silica, combined with a small endothermic signal followed by a strong exothermic signal, suggests that Cu2+ undergoes dehydration during the dimerization process.These results provide the first assessment into the impact of nano-scale confinement on adsorption process of Cu2+ on silica with controlled pore sizes. The adsorption process, including adsorption pathway and surface speciation, is pore-size dependent, which has significant implications on ion adsorption, and, therefore, fate and transport in geologically relevant mesopores. The reported findings will aid in the development of more realistic understanding of fate and transport of chemical species in tight, porous geologic media, such as sedimentary rocks.
Author contributions
AGI led the project and hypothesis development. AGI and AWK designed experimental program, collected and analyzed XAFS data. AWK performed adsorption experiments and aqueous sample analysis. PIK and NK executed adsorption flow through micro-calorimetry experiments and data interpretation. JAH, JAG, and TAH constructed MD models and analyzed MD data. The manuscript was written in collaboration with all the authors.Disclaimer
This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-NA-0003525. Additional support for NK and PIK came from Award Number DE-SC0012186. All X-ray absorption experiments were performed at Sector 20-ID at the Advanced Photon Source (APS), an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science by Argonne National Laboratory. The authors thank Dr. Chengjun Sun and Austen B. Tigges for their help with data collection at APS. The authors thank Dr. Louise Criscenti for reviewing the manuscript prior to submission, and multiple helpful discussions of our findings.References
- W. L. Huang, M. A. Schlautman and W. J. Weber, A distributed reactivity model for sorption by soils and sediments: 5. The influence of near-surface characteristics in mineral domains, Environ. Sci. Technol., 1996, 30, 2993–3000 CrossRef CAS.
- H. Mantha, M. Schindler and M. F. Hochella, Occurrence and formation of incidental metallic Cu and CuS nanoparticles in organic-rich contaminated surface soils in timmins, ontario, Environ. Sci.: Nano, 2019, 6, 163–179 RSC.
- Y. F. Wang, Nanogeochemistry: Nanostructures, emergent properties and their control on geochemical reactions and mass transfers, Chem. Geol., 2014, 378, 1–23 CrossRef.
- A. W. Knight, A. B. Tigges and A. G. Ilgen, Adsorption of copper (II) on mesoporous silica: The effect of nano-scale confinement, Geochem. Trans., 2018, 19, 13 CrossRef.
- J. B. Brubach, A. Mermet, A. Filabozzi, A. Gerschel, D. Lairez, M. P. Krafft and P. Roy, Dependence of water dynamics upon confinement size, J. Phys. Chem. B, 2001, 105, 430–435 CrossRef CAS.
- S. LeCaer, S. Pin, S. Esnouf, Q. Raffy, J. P. Renault, J. B. Brubach, G. Creff and P. Roy, A trapped water network in nanoporous material: The role of interfaces, Phys. Chem. Chem. Phys., 2011, 13, 17658–17666 RSC.
- N. E. Levinger, Water in confinement, Science, 2002, 298, 1722–1723 CrossRef CAS.
- J. Marti, G. Nagy, E. Guardia and M. C. Gordillo, Molecular dynamics simulation of liquid water confined inside graphite channels: Dielectric and dynamical properties, J. Phys. Chem. B, 2006, 110, 23987–23994 CrossRef CAS.
- J. Nelson, J. R. Bargar, L. Wasylenki, G. E. Brown and K. Maher, Effects of nano-confinement on Zn(II) adsorption to nanoporous silica, Geochim. Cosmochim. Acta, 2018, 240, 80–97 CrossRef CAS.
- J. Zachara, S. Brantley, J. Chorover, R. Ewing, S. Kerisit, C. X. Liu, E. Perfect, G. Rother and A. G. Stack, Internal domains of natural porous media revealed: Critical locations for transport, storage, and chemical reaction, Environ. Sci. Technol., 2016, 50, 2811–2829 CrossRef CAS.
- M. Schindler and D. M. Singer, Mineral surface coatings: Environmental records at the nano-scale, Elements, 2017, 13(3), 159–164 CrossRef CAS.
- A. G. Ilgen, J. E. Heath, I. Y. Akkutlu, L. T. Bryndzia, D. R. Cole, Y. K. Kharaka, T. J. Kneafsey, K. L. Milliken, L. J. Pyrak-Nolte and R. Suarez-Rivera, Shales at all scales: Exploring coupled processes in mudrocks, Earth-Sci. Rev., 2017, 166, 132–152 CrossRef CAS.
- A. G. Ilgen, R. K. Kukkadapu, D. R. Dunphy, K. Artyushkova, J. M. Cerrato, J. N. Kruichak, M. T. Janish, C. J. Sun, J. M. Argo and R. E. Washington, Synthesis and characterization of redox-active ferric nontronite, Chem. Geol., 2017, 470, 1–12 CrossRef CAS.
- S. Senapati and A. Chandra, Dielectric constant of water confined in a nanocavity, J. Phys. Chem. B, 2001, 105, 5106–5109 CrossRef CAS.
- T. Takei, K. Mukasa, M. Kofuji, M. Fuji, T. Watanabe, M. Chikazawa and T. Kanazawa, Changes in density and surface tension of water in silica pores, Colloid Polym. Sci., 2000, 278, 475–480 CrossRef CAS.
- A. R. Zimmerman, J. Chorover, K. W. Goyne and S. L. Brantley, Protection of mesopore-adsorbed organic matter from enzymatic degradation, Environ. Sci. Technol., 2004, 38, 4542–4548 CrossRef CAS.
- Y. H. Kim, C. M. Kim, I. H. Choi, S. Rengaraj and J. H. Yi, Arsenic removal using mesoporous alumina prepared via a templating method, Environ. Sci. Technol., 2004, 38, 924–931 CrossRef CAS.
- C. P. Schulthess, R. W. Taylor and D. R. Ferreira, The nanopore inner sphere enhancement effect on cation adsorption: Sodium and nickel, Soil Sci. Soc. Am. J., 2011, 75, 378–388 CrossRef CAS.
- D. R. Ferreira, C. P. Schulthess and N. J. Kabengi, Calorimetric evidence in support of the nanopore innersphere enhancement theory on cation adsorption, Soil Sci. Soc. Am. J., 2012, 77, 94–99 CrossRef.
- D. R. Ferreira and C. P. Schulthess, The nanopore inner sphere enhancement effect on cation adsorption: Sodium, potassium, and calcium, Soil Sci. Soc. Am. J., 2011, 75, 389–396 CrossRef CAS.
- R. Musat, J. P. Renault, M. Candelaresi, D. J. Palmer, S. Le Caer, R. Righini and S. Pommeret, Finite size effects on hydrogen bonds in confined water, Angew. Chem., Int. Ed., 2008, 47, 8033–8035 CrossRef CAS.
- J. L. Skinner, P. A. Pieniazek and S. M. Gruenbaum, Vibrational spectroscopy of water at interfaces, Acc. Chem. Res., 2012, 45, 93–100 CrossRef CAS.
- V. Crupi, S. Interdonato, F. Longo, D. Majolino, P. Migliardo and V. Venuti, New insight on the hydrogen bonding structures of nanoconfined water: A raman study, J. Raman Spectrosc., 2008, 39, 244–249 CrossRef CAS.
- X. F. Huang, Q. Wang, X. X. Liu, S. H. Yang, C. X. Li, G. Sun, L. Q. Pan and K. Q. Lu, Vibrational dynamics of water within mesoporous materials at different hydration levels during adsorption and desorption processes, J. Phys. Chem. C, 2009, 113, 18768–18771 CrossRef CAS.
- L. T. Zhuravlev, The surface chemistry of amorphous silica. Zhuravlev model, Colloids Surf., A, 2000, 173, 1–38 CrossRef CAS.
- M. M. L. R. Carrott, A. J. E. Candeias, P. J. M. Carrott, P. I. Ravikovitch, A. V. Neimark and A. D. Sequeira, Adsorption of nitrogen, neopentane, n-hexane, benzene and methanol for the evaluation of pore sizes in silica grades of MCM-41, Microporous Mesoporous Mater., 2001, 47, 323–337 CrossRef.
- P. I. Ravikovitch and A. V. Neimark, Characterization of micro- and mesoporosity in SBA-15 materials from adsorption data by the NLDFT method, J. Phys. Chem. B, 2001, 105, 6817–6823 CrossRef CAS.
- S. F. Cheah, G. E. Brown and G. A. Parks, Xafs spectroscopy study of Cu(II) sorption on amorphous SiO2 and gamma-Al2O3: Effect of substrate and time on sorption complexes, J. Colloid Interface Sci., 1998, 208, 110–128 CrossRef CAS PubMed.
- S. F. Cheah, G. E. Brown and G. A. Parks, Xafs study of cu model compounds and cu2+ sorption products on amorphous sio2, gamma-al2o3, and anatase, Am. Mineral., 2000, 85, 118–132 CrossRef CAS.
- B. Ravel and M. Newville, Athena, Artemis, Hephaestus: Data analysis for X-ray absorption spectroscopy using IFEFFIT, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS.
- M. Newville, IFEFFIT: Interactive XAFS analysis and FEFF fitting, J. Synchrotron Radiat., 2001, 8, 322–324 CrossRef CAS PubMed.
- S. Kelly, D. Hesterberg and B. Ravel, in Methods of soil analysis: Part 5 - mineralogical methods, ed. A. Ulery and L. Drees, Soil Science Society of America, Madison, Wisconsin, 2008 Search PubMed.
- S. I. Zabinsky, J. J. Rehr, A. Ankudinov, R. C. Albers and M. J. Eller, Multiple-scattering calculations of X-ray-absorption spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 2995–3009 CrossRef CAS PubMed.
- P. H. Ribbe, G. V. Gibbs and M. M. Hamil, Refinement of structure of dioptase, Cu6[Si6O18]:6H2O, Am. Mineral., 1977, 62, 807–811 CAS.
- R. D. Rhue, C. Appel and N. Kabengi, Measuring surface chemical properties of soil using flow calorimetry, Soil Sci., 2002, 167, 782–790 CrossRef CAS.
- J. Creed, C. Brockhoff and T. Martin, EPA method 200.8, Revision 5.4, Determination of trace elements in waters and wastes by inductively coupled plasma-mass spectrometry, 1994, https://www.epa.gov/sites/production/files/2015-08/documents/method_200-8_rev_5-4_1994.pdf Search PubMed.
- M. L. Ojeda, J. M. Esparza, A. Campero, S. Cordero, I. Kornhauser and F. Rojas, On comparing BJH and NLDFT pore-size distributions determined from N2 sorption on SBA-15 substrata, Phys. Chem. Chem. Phys., 2003, 5, 1859–1866 RSC.
- S. J. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- M. E. Tuckerman, G. J. Martyna and B. J. Berne, Molecular dynamics algorithms for condensed systems with multiple time scales, J. Chem. Phys., 1990, 93, 1287–1291 CrossRef CAS.
- R. T. Cygan, J.-J. Liang and A. G. Kalinichev, Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field, J. Phys. Chem. B, 2004, 108, 1255–1266 CrossRef CAS.
- M. Pouvreau, J. A. Greathouse, R. T. Cygan and A. G. Kalinichev, Structure of hydrated gibbsite and brucite edge surfaces: DFT results and further development of the clayFF classical force field with metal–O–H angle bending terms, J. Phys. Chem. C, 2017, 121, 14757–14771 CrossRef CAS.
- J. A. Harvey, C. T. Johnston, L. J. Criscenti and J. A. Greathouse, Distinguishing between bulk and edge hydroxyl vibrational properties of 2:1 phyllosilicates via deuteration, Chem. Commun., 2019, 55, 3453–3456 RSC.
- J. M. Rimsza, R. E. Jones and L. J. Criscenti, Surface structure and stability of partially hydroxylated silica surfaces, Langmuir, 2017, 33, 3882–3891 CrossRef CAS PubMed.
- S. Leroch and M. Wendland, Simulation of forces between humid amorphous silica surfaces: A comparison of empirical atomistic force fields, J. Phys. Chem. C, 2012, 116, 26247–26261 CrossRef CAS PubMed.
- C. D. Daub, N. M. Cann, D. Bratko and A. Luzar, Electrokinetic flow of an aqueous electrolyte in amorphous silica nanotubes, Phys. Chem. Chem. Phys., 2018, 20, 27838–27848 RSC.
- M. Collin, S. Gin, B. Dazas, T. Mahadevan, J. C. Du and I. C. Bourg, Molecular dynamics simulations of water structure and diffusion in a 1 nm diameter silica nanopore as a function of surface charge and alkali metal counterion identity, J. Phys. Chem. C, 2018, 122, 17764–17776 CrossRef CAS.
- I. C. Bourg and C. I. Steefel, Molecular dynamics simulations of water structure and diffusion in silica nanopores, J. Phys. Chem. C, 2012, 116, 11556–11564 CrossRef CAS.
- T. A. Ho, D. Argyris, D. V. Papavassiliou, A. Striolo, L. L. Lee and D. R. Cole, Interfacial water on crystalline silica: A comparative molecular dynamics simulation study, Mol. Simul., 2011, 37, 172–195 CrossRef CAS.
- Z. Brkljaca, D. Namjesnik, J. Lutzenkirchen, M. Predota and T. Preocanin, Quartz/aqueous electrolyte solution interface: Molecular dynamic simulation and interfacial potential measurements, J. Phys. Chem. C, 2018, 122, 24025–24036 CrossRef CAS.
- M. Bouhadja and A. A. Skelton, Dynamical properties of water and ions at the quartz (101)–water interface at a range of solution conditions: A classical molecular dynamics study, J. Phys. Chem. C, 2018, 122, 1535–1546 CrossRef CAS.
- O. Kroutil, Z. Chval, A. A. Skelton and M. Predota, Computer simulations of quartz (101)-water interface over a range of pH values, J. Phys. Chem. C, 2015, 119, 9274–9286 CrossRef CAS.
- G. R. Quezada, R. E. Rozas and P. G. Toledo, Molecular dynamics simulations of quartz (101)-water and corundum (001)-water interfaces: Effect of surface charge and ions on cation adsorption, water orientation, and surface charge reversal, J. Phys. Chem. C, 2017, 121, 25271–25282 CrossRef CAS.
- A. A. Skelton, D. J. Wesolowski and P. T. Cummings, Investigating the quartz (10
![[1 with combining overline]](https://www.rsc.org/images/entities/char_0031_0305.gif) 0)/water interface using classical and ab initio molecular dynamics, Langmuir, 2011, 27, 8700–8709 CrossRef CAS.
0)/water interface using classical and ab initio molecular dynamics, Langmuir, 2011, 27, 8700–8709 CrossRef CAS. - A. A. Skelton, P. Fenter, J. D. Kubicki, D. J. Wesolowski and P. T. Cummings, Simulations of the quartz(10
![[1 with combining overline]](https://www.rsc.org/images/entities/char_0031_0305.gif) 1)/water interface: A comparison of classical force fields, ab initio molecular dynamics, and X-ray reflectivity experiments, J. Phys. Chem. C, 2011, 115, 2076–2088 CrossRef CAS.
1)/water interface: A comparison of classical force fields, ab initio molecular dynamics, and X-ray reflectivity experiments, J. Phys. Chem. C, 2011, 115, 2076–2088 CrossRef CAS. - Y. M. Ma, H. Zhang and B. J. Zhang, Structure of sodium sulphate aqueous solution/quartz interface: A molecular dynamics simulation, Mol. Simul., 2014, 40, 634–639 CrossRef CAS.
- O. Teleman, B. Jonsson and S. Engstrom, A molecular dynamics simulation of a water model with intramolecular degrees of freedom, Mol. Phys., 1987, 60, 193–203 CrossRef CAS.
- E. Brodskaya, A. P. Lyubartsev and A. Laaksonen, Investigation of water clusters containing OH− and H3O+ ions in atmospheric conditions. A molecular dynamics simulation study, J. Phys. Chem. B, 2002, 106, 6479–6487 CrossRef CAS.
- E. N. Brodskaya, A. V. Egorov, A. P. Lyubartsev and A. Laaksonen, Computer modeling of melting of ionized ice microcrystals, J. Chem. Phys., 2003, 119, 10237–10246 CrossRef CAS.
- C. S. Babu and C. Lim, Empirical force fields for biologically active divalent metal cations in water, J. Phys. Chem. A, 2006, 110, 691–699 CrossRef CAS PubMed.
- P. Frank, M. Benfatto, R. K. Szilagyi, P. D'Angelo, S. Della Longa and K. O. Hodgson, The solution structure of [Cu(aq)]2+ and its implications for rack-induced bonding in blue copper protein active, Inorg. Chem., 2005, 44, 1922–1933 CrossRef CAS PubMed.
- V. S. Bryantsev, M. S. Diallo, A. C. T. van Duin and W. A. Goddard, Hydration of copper(II): New insights from density functional theory and the cosmo solvation model, J. Phys. Chem. A, 2008, 112, 9104–9112 CrossRef CAS PubMed.
- J. Chaboy, A. Munoz-Paez, P. J. Merkling and E. S. Marcos, The hydration of Cu2+ : Can the Jahn-Teller effect be detected in liquid solution?, J. Chem. Phys., 2006, 124, 064509 CrossRef.
- I. Persson, P. Persson, M. Sandstrom and A. S. Ullstrom, Structure of jahn-teller distorted solvated copper(II) ions in solution, and in solids with apparently regular octahedral coordination geometry, J. Chem. Soc., Dalton Trans., 2002, 1256–1265 RSC.
- G. C. Bye, M. Mcevoy and M. A. Malati, Adsorption of copper(II) ions from aqueous-solution by 5 silica samples, J. Chem. Technol. Biotechnol., 1982, 32, 781–789 CrossRef CAS.
- J. Du and A. N. Cormack, The medium range structure of sodium silicate glasses: A molecular dynamics simulation, J. Non-Cryst. Solids, 2004, 349, 66–79 CrossRef CAS.
- J. M. Rimsza and J. Du, Structural and mechanical properties of nanoporous silica, J. Am. Ceram. Soc., 2013, 97, 772–781 CrossRef.
- A. W. Knight, N. G. Kalugin, E. Coker and A. G. Ilgen, Water properties under nano-scale confinement, Sci. Rep., 2019, 9, 8246 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting information contains Fig. S1 showing the surface loading of Cu for the XAFS samples; Table S1 presents the hydration energy, ionic and hydrated radii, as well as hydration number of species involved in calorimetric studies; Fig. S2 showing the adsorption and desorption profiles of the samples used in the calorimetric analysis; details on the preparation of the nano-pore silica models for MD simulation along with Fig. S3 showing the density of silica surface as a function of position, Fig. S4 showing the Cu number density from MD simulations with initial configurations of all monomers or all dimers in solution, Table S2 showing the CN and bond distances from MD simulations comparing Cu coordination chemistry with initial configurations of all monomers or all dimers in solution, Table S3 presenting the fluid composition and pore diameters, and lastly the interaction parameters used in the MD simulation. See DOI: 10.1039/c9en00855a |
| This journal is © The Royal Society of Chemistry 2020 |