Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Two-dimensional eclipsed arrangement hybrid perovskites for tunable energy level alignments and photovoltaics†
Zhenyu
Wang
 abc,
Alex M.
Ganose
abc,
Alex M.
Ganose
 bcd,
Chunming
Niu
a and
David O.
Scanlon
bcd,
Chunming
Niu
a and
David O.
Scanlon
 *bcd
*bcd
aXi'an Jiaotong University, Center of Nanomaterials for Renewable Energy, State Key Lab of Electrical Insulation and Power Equipment, School of Electrical Engineering, 99 Yanxiang Road, Xi’an 710054, China
bDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: d.scanlon@ucl.ac.uk
cThomas Young Centre, University College London, Gower Street, London WC1E 6BT, UK
dDiamond Light Source Ltd, Diamond House, Harwell Science and Innovation Campus, Didcot, Oxfordshire OX11 0DE, UK
First published on 3rd April 2019
Abstract
Excellent long-term durability and moisture tolerance, low cost synthesis routes, and the possibility of flexible tuning of electronic properties have meant that the two-dimensional (2D) hybrid halide perovskites have recently attracted much attention, and have been successfully used as light absorbers in efficient photovoltaic devices. 2D hybrid halides perovskites which feature long chain alkylammonium cations, however, are generally suggested for light emitting diode (LED) applications, due to their strong photoluminescence (PL), but none have been applied thus far for photovoltaic (PV) applications. Additionally, it has been shown that luminescence quenching occurs in the Pb-based analogues, (AEQT)PbX4 (X = Cl, Br, I), however, energy transfer and charge separation between organic and inorganic components of the structures are still not fully understood. Herein, we investigate the geometrical, electronic and optical properties of the semiconducting 2D perovskites (AEQT)BX4 (B = Pb, Sn; X = Cl, Br, I), using relativistic hybrid density functional theory calculations. We demonstrate that unlike the traditional 2D perovskites, the choice of the organic ammonium cation has a considerable effect on the carrier transport properties. Our calculations reveal that optical transitions between the organic and inorganic components is disallowed. The electronic structures of the series are flexibly tailored by different halides and metal cations, with band gaps ranging from 2.06 to 2.68 eV. Energy level alignments greatly hinder the electron–hole recombination in (AEQT)PbCl4, (AEQT)PbBr4, (AEQT)PbI4 and (AEQT)SnBr4, and thereby should enhance their PL efficiencies. With a moderate fundamental band gap (2.06 eV) and strong direct valence band to conduction band transition, (AEQT)SnI4 is the only composition that shows intense and broad optical absorption, and as expected displays a high spectroscopic limited maximum efficiency (SLME) of 20.8%. Our results indicate the (AEQT)SnI4 is a stable and efficient light-absorbing material for application as a top absorber of the tandem solar cell.
Introduction
Organic–inorganic lead halide perovskites have emerged as remarkable photovoltaic absorber materials in recent years.1–6 To date, polycrystalline thin-film perovskite photovoltaic devices have reached power conversion efficiencies of 23.7%,7 largely exceeding most of emerging PV devices, including quantum dot cells, organic tandem cells, dye-sensitized solar cells.8 Although three-dimensional (3D) organic–inorganic halide perovskite solar cells have experienced tremendous development in the past few decades, the involvement of toxic lead and long-term instability are preventing large scale commercialisation.9–13Two-dimensional (2D) hybrid halide perovskites, a subclass of the organic–inorganic perovskites, were first synthesised by Mitzi et al. in 1994.14 In 2014, Smith et al. reported that 2D perovskites display more resistance to moisture than their 3D counterparts,15 opening a new path in the investigation of solar cell absorbers. One route to addressing the problem of toxicity is to replace lead with the less toxic Sn and Ge cations.16–18 With appealing environmental stability and less toxic components, the Ruddlesden–Popper 2D tin perovskites have been introduced in solar cell devices, however with limited success in terms of efficiencies.15,18–21 So far, general improvements in perovskite solar cell efficiency have primarily achieved by better control over thin film morphology, the choice of solvent treatment, and manipulation of the stoichiometry or chemistry of halide precursors (BX2 or MAX, B = divalent metal, MA = CH3NH3+, X = Cl, Br, I).22,23 In this way, power conversion efficiencies have risen to 15.4% during the past two years.24 In general, the fundamental band gap is determined mostly by the composition of the inorganic layer, which provides an effective route to tune their electronic properties. With regard to the well-known 3D perovskite, MAPI (CH3NH3PbI3), changing halide composition allows tuning of the band gap from 1.6 to 3.1 eV.25,26 Alternatively, replacing metal cation allows tuning from 1.6 to 2.0 eV.27,28
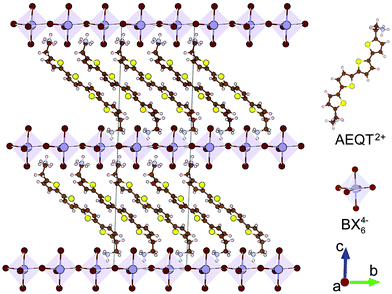
Classified by the position of metal atoms (B) from one inorganic layer over those in the adjacent ones, the 2D hybrid perovskites are generally sorted into “staggered” ((R-NH3)2BX4) and “eclipsed” arrangement ((H3N-R-NH3)BX4) (Fig. S1, ESI†), where R-NH3+ is an aliphatic or single ring aromatic ammonium cation, B is a divalent metal, and X is a halogen.29,30 They both have multi-quantum-well structures of which semiconducting inorganic perovskite-like sheets are alternatively arranged with dye organic layers. Due to the large exciton binding energies and excitonic oscillator strengths of the materials, both types of layered systems have efficient photoluminescence and electroluminescence.29,31–33 Additionally, the perovskite-like framework in the alternating structure will reduce the quenching interactions between dye molecules, and therefore further improve the luminescence efficiency.34 To our knowledge, “staggered” arrangement perovskites and their analogues generally consist of small organic moieties, and the corresponding conduction band maximum (CBM) valence band minimum (VBM) are derived from the inorganic component. Recent evidence suggests that most of “staggered” arrangement perovskites have strong absorption in the visible light region and can be applied in visible light harvesting applications. However, the studies of the “eclipsed” arrangement perovskites are limited to the Pb- or Ge-based systems and the majority concentrate on the luminescence properties instead of their photovoltaic capabilities.34–36
In 1999, Mitzi and co-workers synthesised a series of “eclipsed” arrangement layered materials, (AEQT)PbX4 (AEQT = H3NC2H4C16H8S4C2H4NH32+; X = Cl, Br, I), and found the offsets between the energy levels of organic and inorganic components from distinct layers, of which the organic cation could play a role in the determination of band gaps and carrier mobility.33,34 Recent theoretical research into the electronic structure of the analogues of (AEQT)PbX4 (AE4TPbX4) has revealed that due to the quantum-well-like behaviour of layered perovskites, the states associated with inorganic and organic components are possibly spatially well-separated,37 thereby allowing for an additional degree of electronic structure tuning and effectively impeding the electron–hole recombination.
To date, an understanding of the Sn-based analogues is missing, and a non-toxic 2D hybrid halide would be of huge interest to the materials community and PV industry which deserves further study. Flexibly tunable energy level alignments and restricted energy loss from electron–hole recombination could enable these materials to be solar absorbers with the potential for high PV efficiencies. Studying electron transfer between different components during the photoelectric effect would be of great significance to understand whether the unique behaviour will enhance the PV or carrier transport performance. With these in mind, in this study, we report the crystal structures, electronic properties and optical properties of three Pb-based and three Sn-based layered perovskites, (AEQT)BX4 (B = Pb, Sn; X = Cl, Br, I), using relativistic hybrid density functional theory. We provide an insight into the band offset of these series, shed light on the transition possibility between the inorganic framework and organic components, and how the selection of organic molecules affects the PV performance. With the evaluation of the thin-film PV ability, we demonstrate that (AEQT)SnI4 holds promise for PV applications.
Computational details
First-principles calculations were carried out using the Vienna ab initio simulation package (VASP),38–41 with the scalar relativistic projector augmented-wave (PAW) pseudopotentials applied to describe the interactions between core and valence electrons.42,43 The plane wave cutoff energy was set to 580 eV, and k-point meshes of Γ-centered 4 × 4 × 2 were employed for the geometry optimisation, electronic structure and optical property calculations. These parameters enable the total energy of each system converge within 10 meV per atom.Lattice relaxations were tested via using the Perdew–Burke–Ernzerhof functional44 (PBE), with dispersion interactions included via Grimme's D3 dispersion correction45 (PBE-D3), and the PBEsol functional,46 a version of PBE revised for solids. Both functionals are generally able to accurately reproduce the structural parameters of layered materials and containing weak long-range forces.18,47–50 During geometry optimisation, the atomic positions, lattice shape and cell volume were allowed to relax, and were considered converged when all forces totalled less than 0.02 eV Å−1.
In order to obtain an accurate description of the electronic structure of our systems, hybrid density functional theory was employed. Herein, we used the Heyd–Scuseria–Ernzerhof (HSE) functional51,52 incorporating 43% HF exact exchange and 100% of the correlation energy from PBE. This has been shown to reproduce the band gap of MAPI and BASnI4 ((CH3(CH2)3NH3)2SnI4),18,53 and therefore we expect that it will perform well here. Explicit treatment of spin–orbit coupling (SOC) effects is considered in all electronic structure calculations, due to the relativistic effects present on the heavy elements Pb, Sn and I.54–57 This combination of HSE43 + SOC was used for all band structure, density of states, optical absorption and charge density calculations. The high-frequency dielectric response was calculated from the optical transition matrix elements within the transversal approximation.58,59 The ionic dielectric contribution was calculated using density functional perturbation theory (DFPT),60 using the PBE-D3 functional. Atom-projected band structure diagrams were plotted used the sumo package.69
Discussion and results
Crystal structure
Fig. 1 displays the crystal structures of the series, where each of the inorganic layers consists of sheets of corner-sharing metal halide octahedra ([BX6]4−). The B site cation (Pb2+ or Sn2+) is generally a divalent metal that can adopt an octahedral coordination. The inorganic layers are separated by a long-chain bipolar AEQT2+ dye molecule cation, where the cation spans the distance between adjacent inorganic layers, with both sides of ammonium head ionically bonding to the halogens in the inorganic layers.All geometry relaxations were started from the experimental structures or from modifying the existing structures by swapping elements in the same group of the periodic table. Although (AEQT)PbCl4, (AEQT)PbBr4 and (AEQT)PbI4 have been synthesized, only (AEQT)PbBr4 has been structurally characterised.34 Additionally, none of the Sn-based analogues have been reported thus far. Thus, only (AEQT)PbBr4 is optimized from its experimental structure,34 while the rest of the series ((AEQT)PbCl4, (AEQT)PbI4, (AEQT)SnCl4, (AEQT)SnBr4, and (AEQT)SnI4) were created based on the structure of (AEQT)PbBr4via replacing Pb with Sn, and Br with Cl or I. Both PBE-D3 and PBEsol were tested for the geometry relaxations. The optimized lattice constants and available experimental data on the (AEQT)BX4 structures are given in Table 1. The results indicated PBE-D3 gives better agreement with experiment for (AEQT)PbBr4, and therefore PBE-D3 has been used for all of the structural analysis employed for the rest of the calculations. As a general trend, the metal–halogen bond lengths increase down Group VIIA, as is expected.61 As shown in Table 1, we also see an enlargement of lattice parameters a and b, going from chloride to bromide and then to iodide, which is in agreement with the variation of the halogen ionic radii.
| Compounds | Functional | a | b | c | α | β | γ | ΔdH1 | ΔdH2 |
|---|---|---|---|---|---|---|---|---|---|
| (AEQT)PbCl4 | PBE-D3 | 5.596 | 11.346 | 39.976 | 92.5 | 90.0 | 90.0 | 4.32 | 6.90 |
| (AEQT)PbBr4 | PBE-D3 | 5.762 | 11.824 | 39.037 | 91.9 | 90.0 | 90.0 | 4.26 | 7.38 |
| PBEsol | 5.751 | 11.864 | 40.104 | 93.2 | 90.0 | 90.0 | — | — | |
| Ref. 34 | 5.842 | 11.573 | 39.741 | 92.4 | 90.0 | 90.0 | — | — | |
| (AEQT)PbI4 | PBE-D3 | 6.054 | 12.589 | 38.072 | 92.2 | 90.0 | 90.0 | 3.81 | 7.19 |
| (AEQT)SnCl4 | PBE-D3 | 5.677 | 11.175 | 39.803 | 92.8 | 90.0 | 90.0 | 4.34 | 6.93 |
| (AEQT)SnBr4 | PBE-D3 | 5.847 | 11.608 | 38.989 | 91.9 | 90.0 | 90.0 | 4.28 | 7.40 |
| (AEQT)SnI4 | PBE-D3 | 6.087 | 12.355 | 38.018 | 91.9 | 90.0 | 90.0 | 4.05 | 7.43 |
It is worthwhile mentioning that we obtained a different symmetry of 2D perovskites (Cc) to those in a recent computational study (P21/c).37 As compared with the recent study in the Table S1 (ESI†),37 we found our structures showed slightly contracted lattice parameters and were lower in energy, indicating they are the ground state structures at the level of theory used in this study. These differences could result from the different methodology for the relaxation. Although both studies used the PBE functional with dispersion corrections, in our work we have employed Grimme's corrections, whereas in the work by Blum and co-workers, the Tkatchenko–Scheffler.37
To test the stability of (AEQT)BX4 (B = Pb, Sn; X = Cl, Br, I) in respect of stable compounds, we have tested two decomposition routes:
| (AEQT)BX4 → (AEQT)X2 + BX2, | (1) |
| (AEQT)BX4 → (AEQT–2H) + BX2 + 2HX, | (2) |
The enthalpies of decomposition for the pathways shown in eqn (1) and (2) are given as ΔdH1 and ΔdH2, respectively, and are provided in Table 1. Across all decomposition routes, all series showed positive enthalpies of decomposition, indicating that spontaneous decomposition is unfavourable.
Electronic properties
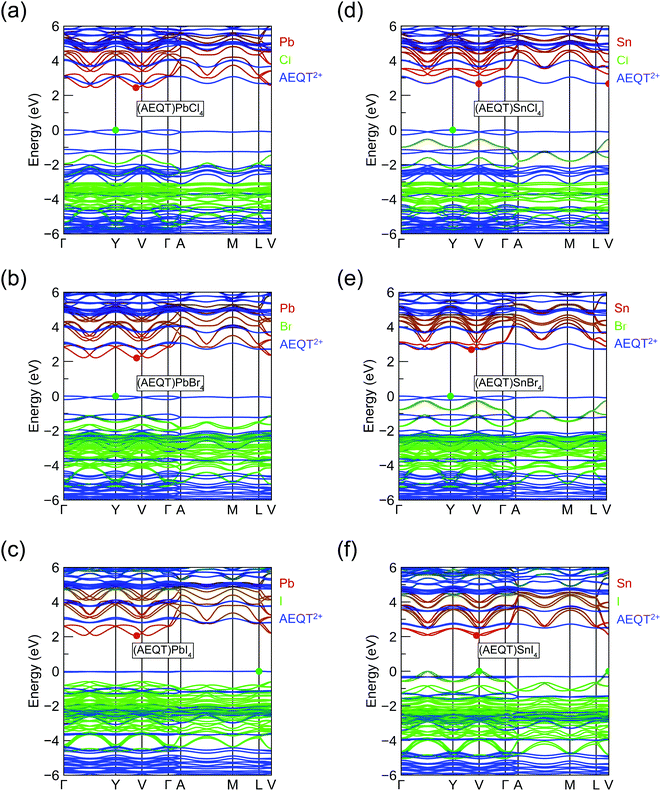
To assess the nature of the band gap in (AEQT)BX4 (B = Pb, Sn; X = Cl, Br, I) series, and better understand the effects of the AEQT2+ cation on the electronic structure of the layered perovskite, the band structures and the density of states (DOS) were calculated by HSE43 + SOC shown in Fig. S2 of the ESI.† The orbital-projected band structures are displayed in Fig. 2, and the fundamental band gaps and in-plane effective masses are listed in Table 2.| Compounds | E Indg | E Dirg | m ‖h | m ‖e | ε ‖r | ε ⊥r | SLMEa |
|---|---|---|---|---|---|---|---|
| a Thickness: 0.5 μm. | |||||||
| (AEQT)PbCl4 | 2.45 | 2.50 | 27.30 | 0.47 | 4.84 | 3.34 | 9.5 |
| (AEQT)PbBr4 | 2.20 | 2.24 | 46.60 | 0.47 | 4.79 | 3.13 | 12.5 |
| (AEQT)PbI4 | 2.06 | 2.07 | 105.21 | 0.43 | 4.92 | 3.08 | 7.7 |
| (AEQT)SnCl4 | 2.67 | 2.77 | 15.45 | 1.38 | 10.29 | 4.37 | 7.9 |
| (AEQT)SnBr4 | 2.68 | 2.73 | 19.34 | 0.80 | 12.04 | 3.64 | 7.8 |
| (AEQT)SnI4 | 2.06 | 2.07 | 0.63 | 0.50 | 12.37 | 5.09 | 20.8 |
The fundamental band gaps of the Pb-based series increase from 2.06 eV (X = I) to 2.20 eV (X = Br), then to 2.45 eV (X = Cl), which shows the same trend in 3D lead halide perovskites.25,26 Unlike the work by Blum and co-workers,37 the Pb-based series we calculated were all indirect in nature, of which average energy difference between the direct and indirect band gaps is 0.04 eV across the series. In addition, the calculated band gaps were slightly larger by an average of 0.29 eV, though similar functionals were applied for geometry optimization and electronic property calculations. It is expected that these differences result from the different relaxed structures obtained by the different methodologies.37 Both studies, however, found that the CBM of Pb-based series were composed of the p orbital of Pb and halogens, and their VBM originated from the AEQT2+ cations. This induces the small electron effective mass (<0.5 m0) and heavy hole effective mass (>27 m0).
In terms of the Sn-based systems, the fundamental band gaps increase from 2.06 (X = I) to 2.67 (X = Cl) eV, and although indirect, they are only slightly indirect, with the direct band gaps only a maximum of 0.1 eV higher in energy across all cases. The frontier orbitals of the Sn-based series are derived from different components. The CBMs in (AEQT)SnCl4 and (AEQT)SnBr4 are determined by the molecular cation and inorganic framework, respectively, whereas their VBMs are both composed of the orbitals of AEQT2+ cation. Particularly, the conduction band edges of (AEQT)SnBr4 nearly consists solely of AEQT2+ orbitals, because the energy difference between its CBM and lowest unoccupied molecular orbital (LUMO) of AEQT2+ cation is less than 20 meV. In contrast, like the majority of 3D perovskites, the frontier orbitals of (AEQT)SnBr4 are composed of the inorganic components, of which CBM are derived from the Sn's p orbital, and VBM from Sn's s and I's p orbitals. For these reasons, (AEQT)SnI4 exhibits dispersive VBM and CBM and relatively light effective masses (≈0.6 m0). (AEQT)SnCl4 and (AEQT)SnBr4 share large hole effective mass (>15 m0), while (AEQT)SnBr4 possess a much smaller electron effective mass than (AEQT)SnCl4. The atomic orbital contributions of the series at the VBM and CBM are further characterised by the electron density isosurfaces in Fig. S3 (ESI†).
As shown in Fig. 2, the highest occupied molecular orbital (HOMO) of AEQT2+ cation exhibits a very small variation amongst the series (<0.2 eV), and the maximum energy differences of their LUMO are 0.4 eV. Across the series, the organic HOMO–LUMO gaps exhibit a narrow range (2.66 to 2.80 eV), which is in agreement with 2.7 eV measured by the singlet transition of the organic chromophore in (AEQT)PbCl4via a photoluminescence measurement.33 The minor variation of HOMO–LUMO gap is also confirmed by the recent theoretical study with energy of 2.2 to 2.4 eV.37
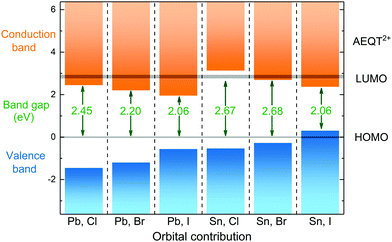
To illustrate the relative positions of band edges of organic and inorganic components from each series, each of their energy level is calculated with respect to the HOMO of AEQT2+ cations, respectively. It is found that their HOMO–LUMO gaps of AEQT2+ cation are similar, and thus their energy level schemes could be aligned together. To simplify the whole diagram, all separate schemes are merged relative to the same HOMO of AEQT2+ cation and depicted in Fig. 3. It is noted that this diagram does not indicate that the frontier orbitals of AEQT2+ cation with reference to the vacuum level stay the same across all series.
As displayed in the energy level diagram, the energy differences between the lead halide sheets in (AEQT)PbCl4 and (AEQT)PbI4 is 3.89 and 2.65 eV, respectively, which are close to the energy of the excitation band transition of the inorganic perovskite-like sheets (3.7 and 2.4 eV) measured by experiment.33 Our calculations show excellent agreement with the experiment, and illustrate that except for (AEQT)SnCl4 and (AEQT)SnI4, the fundamental band gaps (green numbers in Fig. 3) of the other series are smaller than the HOMO–LUMO gap of either inorganic or organic components.
Blum and co-workers recently sorted the hybrid organic–inorganic perovskites into four subgroups by comparing the positions in the band edges of the different components.37 Using the same notation, we found three types across the series: Type Ia, where the low-energy electrons and holes are localized on the organic components, such as (AEQT)SnCl4; Type Ib, where the low-energy electrons and holes are localized on the inorganic components, like (AEQT)SnI4; Type IIb, where the electrons and holes are localized on the inorganic and organic components, respectively, for example, (AEQT)PbCl4, (AEQT)PbBr4, (AEQT)PbI4 and (AEQT)SnBr4. In the third group, due to the separation of electron and holes, the electron–hole recombination is expected to be reduced.
Optical properties
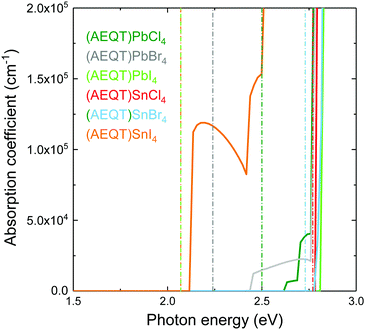
Fig. 4 shows the HSE43 + SOC calculated absorption spectra for (AEQT)BX4 (B = Pb, Sn; X = Cl, Br, I). Uniquely, the trend of decreasing band gap as the halide ion increases is not observed in the optical absorption spectra. There are large differences between the fundamental direct band gaps and the adsorption edges in both the Pb-based and Sn-based series. We note large difference between the fundamental direct band gaps and the absorption edges in the Type IIb series, indicating the direct VB–CB optical transition from organic to inorganic component may be unfavourable. The optical transition matrix elements were calculated using the transversal approximation including explicit treatment of SOC effects.63 Allowed and disallowed transitions were judged by the square of magnitude of matrix element, |M|2.64In all cases, the |M|2 of the transition between the AEQT2+ cation and the perovskite-like framework is less than 10−3 eV−2 Å−2, revealing this transition is unfavourable. This likely results from the limited orbital overlap of the organic and inorganic wavefunctions. In other words, only the transition from inorganic to inorganic components or from organic to organic components are allowed. Since the electrons and the holes are located separately across the alternative layers in the inorganic and organic hybrid components, in addition to the unfavourable transition between the two components, such unique energy level alignments therefore enable the electron–hole recombination to be suppressed among (AEQT)PbCl4, (AEQT)PbBr4, (AEQT)PbI4 and (AEQT)SnBr4, and find broad applications in the LED industry.
To evaluate the hypothetical photovoltaic performance of the series, a metric proposed by Yu and Zunger,65 the spectroscopic limited maximum efficiency (SLME) with a thin film thickness of 0.5 μm, has been calculated and shown in Table 2. As (AEQT)SnI4 exhibits strong and broad absorption in the visible light region, it possesses the highest SLME (20.8%). This is comparable to other Sn-based layered perovskites, such as (BA)2(MA)Sn2I7 (BA = (CH3(CH2)3NH2)2+) (22.6%).18 For the rest of the series, the unfavourable inorganic–organic optical transition, coupled with large optical band gaps (>2.4 eV), results in very poor optical absorption in the visible light region and corresponding low SLMEs.
One of the distinct features of the 2D perovskites is their quantum-well-like structure, in which dielectric constant varies across the inorganic sheets (“wells”) to the organic layers (“barriers”) due to their different polarizability.66,67 The dielectric constants for the full range of analogues are provided in Table 2. The dielectric constants in the direction parallel to the perovskite-like sheets (ε‖r) are larger than those in the direction perpendicular to the sheets (ε⊥r), which is in agreement with studies of other layered perovskite systems.18,50 Both the in-plane and out-of-plane dielectric constants for Sn-based series are larger than those in the Pb-based ones, which can be explained by the larger Born effective charges of Sn-based series (Table S2, ESI†). Particularly, among both Pb- and Sn-based series, (AEQT)SnI4 exhibit the largest dielectric constants with ε‖r = 12.37 and ε⊥r = 5.09, in which the in-plane one is comparable to (MA)2Sn(SeCN)2Cl2 (ε‖r = 11.7) while the out-of-plane one is comparable to (BA)2SnI4 (ε⊥r = 4.5).18,50 Furthermore, large dielectric constants are proposed to be an indicator of defect tolerance, and so these systems could be insensitive to lattice imperfections and can achieve a relatively high optoelectronic energy.68
Conclusions
In conclusion, we have demonstrated that the electronic properties of (AEQT)BX4 (B = Pb, Sn; X = Cl, Br, I) can be tuned through incorporation of different halides and metal cations, with band gaps varying from 2.06–2.68 eV. The location of frontier orbitals varies according to the halide and metal. Such tunability of electronic properties, especially the energy level alignments of organic and inorganic components, opens up the possibility to theoretically tailor charge separation or recombination, which is important to suppress the PL quenching caused by electron–hole recombination. The unique energy alignments of (AEQT)PbCl4, (AEQT)PbBr4, (AEQT)PbI4 and (AEQT)SnBr4 may make them of use in the LED industry. The transition between the organic and inorganic components is confirmed to be unfavourable, resulting in poor absorption of light in the visible spectrum for most of the series. However, we identify a novel 2D perovskite material, (AEQT)SnI4, in which the VBM and CBM are composed of contributions from the inorganic sheets. Due to its broad absorption in the visible light region, reasonably large dielectric constants and SLME of 20.8%, (AEQT)SnI4 shows a promise as a potential solar absorber. (AEQT)SnI4 thus presents an exciting prospect because of its earth abundance, and possible enhanced moisture stability and defect tolerance. Experimental verification of our computational predictions are welcomed.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work made use of the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk), via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202). DOS acknowledges support from the EPSRC (EP/N01572X/1). DOS acknowledges membership of the Materials Design Network. CN acknowledges the financial support from the National Natural Science Foundation of China (Grant No. 21773182). AMG acknowledges Diamond Light Source for the co-sponsorship of a studentship on the EPSRC Centre for Doctoral Training in Molecular Modelling and Materials Science (EP/L015862/1). ZW acknowledges the China Scholarship Council (CSC) for supporting a visit to University College London. VB (Volker Blum) is acknowledged for giving us the structures from his paper.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal halide perovskites as visible-light sensitizers for photovoltaic cells, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- H.-S. Kim, C.-R. Lee, J.-H. Im, K.-B. Lee, T. Moehl, A. Marchioro, S.-J. Moon, R. Humphry-Baker, J.-H. Yum, J. E. Moser, M. Grätzel and N.-G. Park, Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%, Sci. Rep., 2012, 2, 591 CrossRef.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Sequential deposition as a route to high-performance perovskite-sensitized solar cells, Nature, 2013, 499, 316–319 CrossRef CAS PubMed.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, The emergence of perovskite solar cells, Nat. Photonics, 2014, 8, 506–514 CrossRef CAS.
- A. Polman, M. Knight, E. C. Garnett, B. Ehrler and W. C. Sinke, Photovoltaic materials: present efficiencies and future challenges, Science, 2016, 352, aad4424 CrossRef.
- W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. I. Seok, Iodide management in formamidinium-lead-halide-based perovskite layers for efficient solar cells, Science, 2017, 356, 1376–1379 CrossRef CAS PubMed.
- https://www.nrel.gov/pv/assets/pdfs/best-reserch-cell-efficiencies.pdf (Access 10 March 2019).
- M. A. Green, Y. Hishikawa, W. Warta, E. D. Dunlop, D. H. Levi, J. Hohl-Ebinger and A. W. Ho-Baillie, Solar cell efficiency tables (version 50), Prog. Photovoltaics, 2017, 25, 668–676 Search PubMed.
- G. Niu, X. Guo and L. Wang, Review of recent progress in chemical stability of perovskite solar cells, J. Mater. Chem. A, 2015, 3, 8970–8980 RSC.
- S. Ahmad, P. K. Kanaujia, H. J. Beeson, A. Abate, F. Deschler, D. Credgington, U. Steiner, G. V. Prakash and J. J. Baumberg, Strong Photocurrent from Two-Dimensional Excitons in Solution-processed Stacked Perovskite Semiconductor Sheets, ACS Appl. Mater. Interfaces, 2015, 7, 25227–25236 CrossRef CAS PubMed.
- G. Nagabhushana, R. Shivaramaiah and A. Navrotsky, Direct calorimetric verification of thermodynamic instability of lead halide hybrid perovskites, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7717–7721 CrossRef CAS PubMed.
- T. W. Kasel and C. H. Hendon, Electronic implications of organic nitrogen lone pairs in lead iodide perovskites, J. Mater. Chem. C, 2018, 6, 4765–4768 RSC.
- L. Meng, J. You and Y. Yang, Addressing the stability issue of perovskite solar cells for commercial applications, Nat. Commun., 2018, 9, 5265 CrossRef PubMed.
- D. B. Mitzi, C. A. Feild, W. T. A. Harrison and A. M. Guloy, Conducting tin halides with a layered organic-based perovskite structure, Nature, 1994, 369, 467–469 CrossRef CAS.
- I. C. Smith, E. T. Hoke, D. Solis-Ibarra, M. D. McGehee and H. I. Karunadasa, A Layered Hybrid Perovskite Solar-Cell Absorber with Enhanced Moisture Stability, Angew. Chem., Int. Ed., 2014, 126, 11414–11417 CrossRef.
- D. H. Cao, C. C. Stoumpos, T. Yokoyama, J. L. Logsdon, T.-B. Song, O. K. Farha, M. R. Wasielewski, J. T. Hupp and M. G. Kanatzidis, Thin Films and Solar Cells Based on Semiconducting Two-Dimensional Ruddlesden–Popper (CH3(CH2)3NH3)2(CH3NH3)n−1SnnI3n+1 Perovskites, ACS Energy Lett., 2017, 2, 982–990 CrossRef.
- P. Cheng, T. Wu, J. Zhang, Y. Li, J. Liu, L. Jiang, X. Mao, R.-F. Lu, W.-Q. Deng and K. Han, (C6H5C2H4NH3)2GeI4: A Layered Two-Dimensional Perovskite with Potential for Photovoltaic Applications, J. Phys. Chem. Lett., 2017, 8, 4402–4406 CrossRef CAS PubMed.
- Z. Wang, A. M. Ganose, C. Niu and D. O. Scanlon, First-principles insights into tin-based two dimensional hybrid halide perovskites for photovoltaics, J. Mater. Chem. A, 2018, 6, 5652–5660 RSC.
- D. H. Cao, C. C. Stoumpos, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, 2D homologous perovskites as light-absorbing materials for solar cell applications, J. Am. Chem. Soc., 2015, 137, 7843–7850 CrossRef CAS PubMed.
- H. Tsai, et al., High-efficiency two-dimensional Ruddlesden-Popper perovskite solar cells, Nature, 2016, 536, 312–316 CrossRef CAS PubMed.
- L. N. Quan, M. Yuan, R. Comin, O. Voznyy, E. M. Beauregard, S. Hoogland, A. Buin, A. R. Kirmani, K. Zhao, A. Amassian, D. H. Kim and E. H. Sargent, Ligand-stabilized reduced-dimensionality perovskites, J. Am. Chem. Soc., 2016, 138, 2649–2655 CrossRef CAS PubMed.
- J. S. Manser, M. I. Saidaminov, J. A. Christians, O. M. Bakr and P. V. Kamat, Making and breaking of lead halide perovskites, Acc. Chem. Res., 2016, 49, 330–338 CrossRef CAS PubMed.
- Y. Hu, L. M. Spies, D. Alonso-Álvarez, P. Mocherla, H. Jones, J. Hanisch, T. Bein, P. R. F. Barnes and P. Docampo, Identifying and controlling phase purity in 2D hybrid perovskite thin films, J. Mater. Chem. A, 2018, 6, 22215–22225 RSC.
- A. M. Ganose, C. N. Savory and D. O. Scanlon, Beyond Methylammonium Lead Iodide: Prospects for the Emergent Field of ns2 Containing Solar Absorbers, Chem. Commun., 2017, 53, 20–44 RSC.
- A. Sadhanala, F. Deschler, T. H. Thomas, S. E. Dutton, K. C. Goedel, F. C. Hanusch, M. L. Lai, U. Steiner, T. Bein, P. Docampo, D. Cahen and R. H. Friend, Preparation of single-phase films of CH3NH3Pb(I1−xBrx)3 with sharp optical band edges, J. Phys. Chem. Lett., 2014, 5, 2501–2505 CrossRef CAS PubMed.
- A. Sadhanala, S. Ahmad, B. Zhao, N. Giesbrecht, P. M. Pearce, F. Deschler, R. L. Z. Hoye, K. C. Goödel, T. Bein, P. Docampo, S. E. Dutton, M. F. L. De Volder and R. H. Friend, Blue-green color tunable solution processable organolead chloride–bromide mixed halide perovskites for optoelectronic applications, Nano Lett., 2015, 15, 6095–6101 CrossRef CAS PubMed.
- F. Hao, C. C. Stoumpos, D. H. Cao, R. P. Chang and M. G. Kanatzidis, Lead-free solid-state organic-inorganic halide perovskite solar cells, Nat. Photonics, 2014, 8, 489–494 CrossRef CAS.
- T. Krishnamoorthy, H. Ding, C. Yan, W. L. Leong, T. Baikie, Z. Zhang, M. Sherburne, S. Li, M. Asta, N. Mathews and S. G. Mhaisalkar, Lead-free germanium iodide perovskite materials for photovoltaic applications, J. Mater. Chem. A, 2015, 3, 23829–23832 RSC.
- D. B. Mitzi, K. Chondroudis and C. R. Kagan, Organic-inorganic electronics, IBM J. Res. Dev., 2001, 45, 29–45 CAS.
- D. B. Synthesis Mitzi, structure, and properties of organic-inorganic perovskites and related materials, Prog. Inorg. Chem., 2007, 1–121 Search PubMed.
- M. Era, S. Morimoto, T. Tsutsui and S. Saito, Organic–inorganic heterostructure electroluminescent device using a layered perovskite semiconductor (C6H5C2H4NH3)2PbI4, Appl. Phys. Lett., 1994, 65, 676–678 CrossRef CAS.
- D. B. Mitzi, Synthesis, Crystal Structure, and Optical and Thermal Properties of (C4H9NH3)2MI4 (M = Ge, Sn, Pb), Chem. Mater., 1996, 8, 791–800 CrossRef CAS.
- D. B. Mitzi, K. Chondroudis and C. R. Kagan, Design, structure, and optical properties of organic–inorganic perovskites containing an oligothiophene chromophore, Inorg. Chem., 1999, 38, 6246–6256 CrossRef CAS PubMed.
- K. Chondroudis and D. B. Mitzi, Electroluminescence from an organic–inorganic perovskite incorporating a quaterthiophene dye within lead halide perovskite layers, Chem. Mater., 1999, 11, 3028–3030 CrossRef CAS.
- T. Ishihara, J. Takahashi and T. Goto, Exciton state in two-dimensional perovskite semiconductor (C10H21NH3)2PbI4, Solid State Commun., 1989, 69, 933–936 CrossRef CAS.
- S. Ahmad and G. V. Prakash, Strong room-temperature ultraviolet to red excitons from inorganic organic-layered perovskites, (R-NH3)2MX4 (M = Pb2+, Sn2+, Hg2+; X = I−, Br−), J. Nanophotonics, 2014, 8, 083892 CrossRef.
- C. Liu, W. Huhn, K.-Z. Du, A. Vazquez-Mayagoitia, D. Dirkes, W. You, Y. Kanai, D. B. Mitzi and V. Blum, Tunable Semiconductors: Control over Carrier States and Excitations in Layered Hybrid Organic-Inorganic Perovskites, Phys. Rev. Lett., 2018, 121, 146401 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. Grimme, Accurate description of van der Waals complexes by density functional theory including empirical corrections, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- F. Brivio, A. B. Walker and A. Walsh, Structural and Electronic Properties of Hybrid Perovskites for High-Efficiency Thin-Film Photovoltaics from First-Principles, APL Mater., 2013, 1, 042111 CrossRef.
- K. T. Butler, J. M. Frost and A. Walsh, Band alignment of the hybrid halide perovskites CH3NH3PbCl3, CH3NH3PbBr3 and CH3NH3PbI3, Mater. Horiz., 2015, 2, 228–231 RSC.
- A. M. Ganose, K. T. Butler, A. Walsh and D. O. Scanlon, Relativistic electronic structure and band alignment of BiSI and BiSeI: candidate photovoltaic materials, J. Mater. Chem. A, 2016, 4, 2060–2068 RSC.
- A. M. Ganose, C. N. Savory and D. O. Scanlon, Electronic and defect properties of (CH3NH3)2Pb(SCN)2I2 analogues for photovoltaic applications, J. Mater. Chem. A, 2017, 5, 7845–7853 RSC.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum: Hybrid functionals based on a screened Coulomb potential, [J. Chem. Phys., 2003, 118, 8207] J. Chem. Phys. 2006124219906 Search PubMed.
- M. H. Du, Efficient carrier transport in halide perovskites: theoretical perspectives, J. Mater. Chem. A, 2014, 2, 9091–9098 RSC.
- P. Umari, E. Mosconi and F. De Angelis, Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 perovskites for solar cell applications, Sci. Rep., 2014, 4, 4467 CrossRef.
- C. Bernal and K. Yang, First-principles hybrid functional study of the organic–inorganic perovskites CH3NH3SnBr3 and CH3NH3SnI3, J. Phys. Chem. C, 2014, 118, 24383–24388 CrossRef CAS.
- J. Im, C. C. Stoumpos, H. Jin, A. J. Freeman and M. G. Kanatzidis, Antagonism between Spin–Orbit Coupling and Steric Effects Causes Anomalous Band Gap Evolution in the Perovskite Photovoltaic Materials CH3NH3Sn1−xPbxI3, J. Phys. Chem. Lett., 2015, 6, 3503–3509 CrossRef CAS PubMed.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, DFT and k·p modelling of the phase transitions of lead and tin halide perovskites for photovoltaic cells, Phys. Status Solidi RRL, 2014, 8, 31–35 CrossRef CAS.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223 CrossRef.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Linear Optical Properties in the Projector-Augmented Wave Methodology, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- R. Sanderson, Chemical bonds and bonds energy, Elsevier, 2012, vol. 21 Search PubMed.
- A. M. Ganose, C. N. Savory and D. O. Scanlon, (CH3NH3)2Pb(SCN)2I2: A More Stable Structural Motif for Hybrid Halide Photovoltaics?, J. Phys. Chem. Lett., 2015, 6, 4594–4598 CrossRef CAS PubMed.
- J. Paier, M. Marsman and G. Kresse, Dielectric properties and excitons for extended systems from hybrid functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 121201 CrossRef.
- A. E. Maughan, A. M. Ganose, M. M. Bordelon, E. M. Miller, D. O. Scanlon and J. R. Neilson, Defect Tolerance to Intolerance in the Vacancy-Ordered Double Perovskite Semiconductors Cs2SnI6 and Cs2TeI6, J. Am. Chem. Soc., 2016, 138, 8453–8464 CrossRef CAS PubMed.
- L. Yu and A. Zunger, Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials, Phys. Rev. Lett., 2012, 108, 068701 CrossRef PubMed.
- T. Ishihara, Optical properties of PbI-based perovskite structures, J. Lumin., 1994, 60, 269–274 CrossRef.
- J. Even, L. Pedesseau and C. Katan, Understanding quantum confinement of charge carriers in layered 2D hybrid perovskites, ChemPhysChem, 2014, 15, 3733–3741 CrossRef CAS.
- A. Zakutayev, C. M. Caskey, A. N. Fioretti, D. S. Ginley, J. Vidal, V. Stevanovic, E. Tea and S. Lany, Defect Tolerant Semiconductors for Solar Energy Conversion, J. Phys. Chem. Lett., 2014, 5, 1117–1125 CrossRef CAS PubMed.
- A. M. Ganose, A. J. Jackson and D. O. Scanlon, sumo: Command-line tools for plotting and analysis of periodic ab initio calculations, Journal of Open Source Software, 2018, 3, 717 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9tc01325c |
| This journal is © The Royal Society of Chemistry 2019 |