Combining electronic and structural features in machine learning models to predict organic solar cells properties†
Daniele
Padula
 *,
Jack D.
Simpson
*,
Jack D.
Simpson
 and
Alessandro
Troisi
and
Alessandro
Troisi
 *
*
Department of Chemistry, University of Liverpool, Liverpool L69 7ZD, UK. E-mail: dpadula@liverpool.ac.uk; atroisi@liverpool.ac.uk
First published on 30th October 2018
Abstract
We present a translation of the chemical intuition in materials discovery, in terms of chemical similarity of efficient materials, into a rigorous framework exploiting machine learning. We computed equilibrium geometries and electronic properties (DFT) for a database of 249 Organic donor–acceptor pairs. We obtain similarity metrics between pairs of donors in terms of electronic and structural parameters, and we use such metrics to predict photovoltaic efficiency through linear and non-linear machine learning models. We observe that using only electronic or structural parameters leads to similar results, while considering both parameters at the same time improves the predictive capability of the models up to correlations of r ≈ 0.7. Such correlation allows for reliable predictions of efficient materials, and lends to be coupled with combinatorial of evolutionary approaches for a more reliable virtual screening of candidate materials.
Conceptual insightsThe great diversity of physical phenomena occuring in a Solar Cell upon light absorption makes very difficult the unification of knowledge in a single theoretical framework that would allow to predict Photovoltaic Efficiency from molecular details of the components. Moreover, the chemical properties of the materials are often not explicitly taken into account. With applicative purposes in mind, we explored the use of machine learning models taking in input information regarding the similarity of Organic Seminconducting Donors in terms of chemical topology and electronic structure. We discovered that considering both chemical and physical information improves the predictivity of the models (up to r ≈ 0.7), which makes them usable in the discovery of new Organic Materials. |
The design of new organic semiconductors for bulk heterojunction solar cells1–4 has attracted many research initiatives5–7 highlighting the relevance and interest of any method enabling the prediction of power conversion efficiency (PCE) of a solar cell from the knowledge of its constituents.8–12 From the theoretical point of view, the landscape is very complicated due to the many physical processes occurring within a Photovoltaic Cell upon light absorption, such as exciton formation13 and migration,14 charge transport15 and recombination.16,17 For this reason, a microscopic modelling of each heterojunction is not a viable route for discovering new materials and materials prediction and can be limited to a few benchmark systems. Prediction for new semiconductors can become efficient through models depending on a limited number of easily computable parameters. One of the best known models of this type is Scharber's model,18 which relies on a few reasonable assumptions and exploits only a few electronic parameters of a donor–acceptor pair to obtain a prediction of photovoltaic efficiency. However, it is difficult to extend the model to include additional electronic parameters,8,12,19,20 other descriptors of various nature (structural,9,21 topological,22,23 thermodynamic24–26), or other phenomena27 without formulating a completely new theory.
Adopting Machine Learning (ML) frameworks bypasses the step of theoretical development, creating a “black box” connection to properties otherwise inaccessible, at the cost of physical insight. Many different parameters of various nature can be included in the models, no hypotheses on the way the parameters are related among themselves or with the target property have to be made, and unexpected correlations can be highlighted.20 In other words, given a set of examples and input parameters, these algorithms fit an unknown function that mixes the parameters and returns an estimate of the target data. The great flexibility and variety of ML algorithms are beginning to be applied to materials discovery problems,6,8,10,28–33 although no consolidated methodology is emerging yet.9 Other groups reported ML approaches to screen for materials for photovoltaic applications through Artificial Neural Networks (ANN) and Random Forest (RF),32 to refine computed photovoltaic parameters through Gaussian Process Regression (GPR),29 assuming the validity of Scharber's model or bypassing any existing theory and including a wide range of electronic parameters, ignoring topological ones through ANN or RF,8 or using complex structural representations to feed Deep Tensor Neural Networks (DTNN)34 to predict orbital energies.35 In recent work published by some of us8 a large number of descriptors related to different physical phenomena was included. Each additional descriptor increases the computational cost related to obtaining the input, with the additional downside of missing elements connected to the chemistry of the material, in terms of structure, morphology, topology etc. Here we include a description of the chemical structure, which is less easy to correlate to the physical origin of the PCE, but implicitly includes the effects of chemical properties such as solubility, morphology etc. The definition of similarity in terms of both chemical and/or electronic parameters allowed us to obtain a set of highly predictive models targeting the photovoltaic efficiency of a donor–acceptor pair. Additionally, the small set of electronic parameters required in this model makes input data much easier to obtain. The main disadvantage, instead, is that kernel based methods scale with the square of examples in the data set, thus the reported method is feasible for data sets up to a few thousands entries.31 The proposed approach mimics in a mathematically rigorous fashion the empirical exploration of new donors based on small chemical modifications of efficient molecules, providing new molecules with similar energy levels. Our results are important for applicative purposes, meaning that they provide reasonable predictions that can be coupled with combinatorial10 or evolutionary36 approaches to discover new materials.
Dataset
We built a database of 249 Organic donor–acceptor pairs that have been characterised in the literature between 2013 and 2017 (see ESI† for details on the search), mostly BHJ cells with a few (8) bilayer cells. We have gathered the experimental photovoltaic parameters (VOC, JSC, FF, η), and we have computed equilibrium geometries and four electronic properties at DFT level (HOMO energy for the donor EHOMOD, LUMO energy for the donor ELUMOD, LUMO energy for the acceptor ELUMOA, the total internal reorganisation energy λ in vacuo for the oxidation of the donor and the reduction of the acceptor). The data set contains only photovoltaic pairs where the acceptor is a fullerene acceptor, namely C60, PC61BM or PC71BM. The choice of the low variability of the acceptors was consistent with similar studies in the literature,8,10,29 and reflects the experimental way of scanning for new donors, when the acceptor is kept fixed (or vice versa). In other words, the available experimental data do not explore uniformly the space of donor–acceptor pairs, but only a cross section with either few donors or few acceptors. Additionally, we would require much more complicated models to take into account also various acceptors, which we will explore in forthcoming work. Despite the low variability of acceptors, including in the input the ELUMOA parameter allows to take into consideration the same donor more than once, effectively increasing the size of the data set and allowing the model to “learn” the importance of energy level alignment. To consider structural similarities between donors, we relied on fingerprinting procedures commonly adopted in drug discovery,37,38 which associate a structural fingerprint (i.e. a vector) to each compound. We performed the analysis using both the Daylight and the Morgan fingerprinting algorithms.38 More details on the level of calculation, software and strategies used are described in the ESI.† The data set is freely available to download as ESI.†Scharber's model results
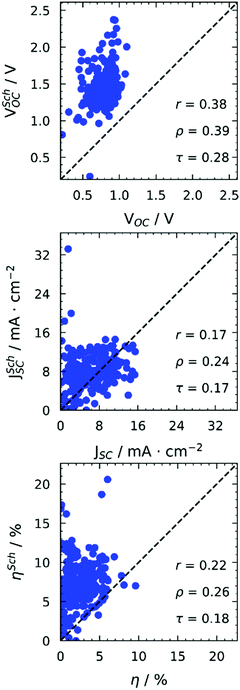
Before discussing several machine learning algorithms, we report the predictions obtained with Scharber's model, which is the most commonly used model for screening potential candidates on the basis of a few physical assumptions (described in ref. 18). According to this model, the open circuit voltage (VOC), short circuit current (JSC), and power conversion efficiency (PCE or η) can be computed from the frontier orbital energies of a donor–acceptor pair and the solar irradiance spectrum, according to eqn (1).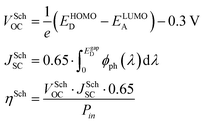 | (1) |
All properties are predicted very poorly by this model. For Fig. 1, we used Scharber's model taking as input orbitals computed on gas phase optimised structures. However, we checked the effect of solvation by including an implicit solvation model39 (PCM) with two solvents (toluene, chloroform) in our geometry optimisations, obtaining excellent correlations between orbital energies from gas phase and solvent geometries (see Fig. S11 in the ESI†). It is worth noticing that the energies of frontier orbitals of the studied molecules span a very small energy window of about 1.5 eV. Very good correlations between experimental and computed orbital energies are often reported in the literature.40–42 However, they span much bigger energy windows or include much less data points. Our observations are in line with what already reported by others on similar molecules,29 and highlight the limitations of DFT in the accurate discrimination of properties of molecules with “comparable” electronic structure, even when adopting more detailed descriptions including environmental effects.
Distance/similarity metrics
Measures of similarity between compounds will be used as input for the ML algorithms to be described below. Similarity measures are broadly used in cheminformatics and drug discovery and can help to detect overfitting, to establish a baseline for predictive methods thanks to zero cost procedures such as similarity-based regressions, or to mimic experimental discovery procedures.43 In our case, the properties defining each example xi are a set of electronic properties (xeli) and a molecular fingerprint (xfpi) and the distance is measured differently along these two sets of dimensions.The distance between two examples xi and xj in terms of electronic parameters (in this case EHOMOD, ELUMOD, ELUMOA, λ) can be computed as a Euclidean distance between the portions of the vectors containing electronic properties, namely xeli and xelj, as in
| Del(xi,xj) = ‖xeli − xelj‖2 | (2) |
| Dfp(xi,xj) = 1 − T(xfpi,xfpj) | (3) |
In Fig. 2 we report a graphical representation of the distances among pairs of donors in the data set. The distances in terms of electronic parameters show low variability across the data set. Concerning structural distance, Morgan fingerprints appear to perform better concerning selectivity, as there are less zones with a low value of the distance metric.
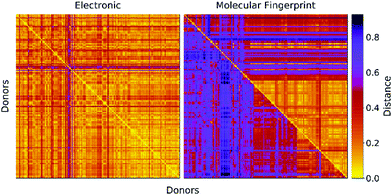 | ||
| Fig. 2 Distance matrices for the donors in the data set. Left: Euclidean distance between electronic parameters (see eqn (2)). Right: Structural distance in terms of molecular fingerprints computed with two fingerprinting algorithms (Upper triangular: Daylight fingerprints. Lower triangular: Morgan fingerprints). | ||
Prediction of photovoltaic parameters and efficiency with k-NN regression
A very simple prediction of a property is based only on similarity: if two molecules are similar, they will likely show similar behaviour. This algorithm reflects the way experimental trial and error research occurs: once a molecule with good properties is found, functionalisation allows the preparation of similar molecules in the hope they will have better properties.43 We computed the predicted values of the properties as a weighted average of the experimental values for the k most similar molecules, with weights and proximity determined by the distances expressed in eqn (2) and (3). The algorithm is known as k-NN (nearest neighbours) regression.44 The predictions were computed using a leave-one-out (LOO) procedure, meaning that the training set used to compute distances is constituted by the whole data set except the point to be predicted. In other words, the experimental data relative to a certain point have not been used for its calculation, resulting in a truly predictive procedure. At the same time, the availability of experimental data makes the quality of models quantifiable through correlation metrics. We also considered a k-fold cross-validation scheme, but LOO was preferred because it is expected to give better results45 due to the bigger size of training sets, and to give a lower variance of predictions because models will be trained on almost the same data.We used the distances reported in eqn (2) and (3) (with both Daylight and Morgan fingerprinting algorithms, where fingerprints are needed), and used various values of k. In Fig. 3 we report as an example the results for the predictions of photovoltaic cell parameters, for k = 3 (results for other values of k are quantitatively similar as discussed in the ESI†). The algorithm can be used to predict directly VOC, JSC, η and its results are illustrated in Fig. 3 using various definitions of distance.
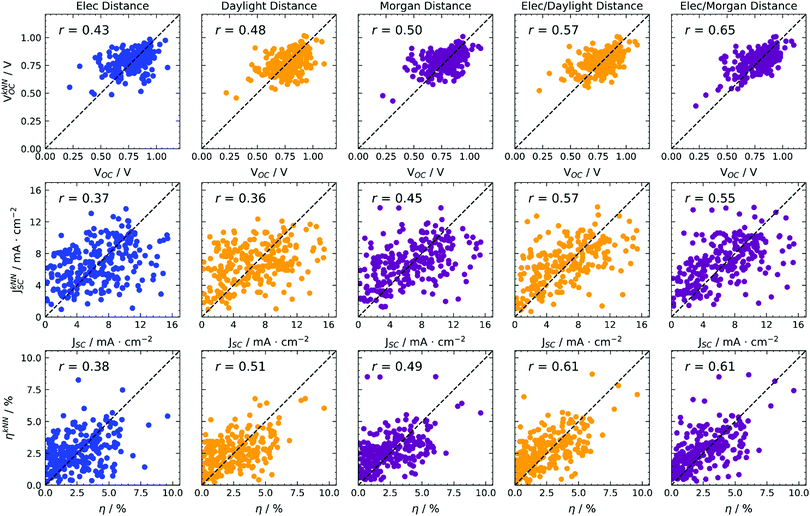 | ||
| Fig. 3 k-NN (k = 3) regression predictions of photovoltaic parameters based on various distances, indicated at the top of each column. Colours encode electronic properties only (blue), or the type of molecular fingerprint used (Daylight in yellow, Morgan in magenta). RMSE data available in Table S1 (ESI†). | ||
Considering a distance in terms of electronic parameters only (first column of Fig. 3) results in moderate correlation coefficients for the predictions, likely because the electronic properties are relatively homogeneous across the whole data set. Switching to a structural distance metric (second and third columns of Fig. 3), improves predictions sensibly, with little dependence on the fingerprinting algorithm, as both Daylight and Morgan fingerprints give comparable results. In this case, we must stress the advantage that no quantum chemical calculations have to be run at all, as the distance metric results exclusively from a 2-D representation of molecules, i.e. the ability to draw them.
As a step forward we can consider a linear combination of the two distances
| D = γ1Del(xi,xj) + γ2Dfp(xi,xj) | (4) |
Prediction of photovoltaic efficiency with kernel ridge regression
An algorithm such as k-NN is extremely rigid in considering only a fixed number of neighbours, regardless of the density of data points and ignoring the non-linear relation between positions in the parameter space and property. A much more flexible algorithm, known as Kernel Ridge Regression (KRR),30,31 will be considered next. This algorithm can be seen as a generalised version of the least squares procedure, where non-linearity and regularisation have been introduced, and it is treated extensively in the ESI† and other literature contributions.30,31 More formally, we define a training set of N examples {(xi,yi)}Ni=1, with xi a vector containing the inputs for the i-th example (e.g. electronic and/or structural fingerprints), and the outputs yi (i.e. the target experimental property like η), are gathered in a vector y. Given an arbitrary scalar function f(xi,xj), known as the kernel function,31 the predicted property y′ for a new element with input property x′ is expressed by the KRR algorithm as| y′ = yT(K + αI)−1κ′ | (5) |
| f(xi,xj) = e−(γ1Del2(xi,xj)+γ2Dfp2(xi,xj)) | (6) |
We obtained predictions of photovoltaic parameters to be used as input for Scharber's model (see ESI†) and direct predictions of photovoltaic efficiencies using the kernels reported in eqn (6) (with both Daylight and Morgan fingerprinting algorithms, where fingerprints are needed), using electronic input data standardised to zero average and unit standard deviation. Predictions were obtained adopting a LOO scheme as described previously, taking advantage of the possibility that, for KRR, the LOO scheme can be implemented analytically,46 and thus results in a computationally cheaper procedure with respect to k-fold cross-validation.
The direct predictions of efficiency in Fig. 4 allow one to obtain better predictions with respect to refining the input for Scharber's model (see ESI†), and improve with respect to direct predictions adopting the simpler k-NN regression, as can be observed in the summary of correlation coefficients reported in Table 1. Adopting electronic distance only (first column of Fig. 4), we notice a significant improvement when using KRR, passing from r = 0.38 to r = 0.49. We tried to estimate the importance of each electronic feature for this model. Since for kernel-based methods feature importance cannot be defined, as the problem is formulated in the examples space, we decided to adopt a feature elimination procedure (see Table S3 in the ESI†), observing a little influence of the reorganisation energy λ, and a considerable importance for the ELUMOD. Adopting structural distance only (second and third columns of Fig. 4), we obtain a significant improvement with Morgan fingerprints (r = 0.49 to r = 0.57) and a worse result with Daylight fingerprints (r = 0.51 to r = 0.43). Finally, when both distances are considered within KRR (fourth and fifth columns of Fig. 4), we again obtain a significant improvement with respect to using one distance only. Adopting a linear combination of distances with KRR, we also obtain better results with respect to the simpler k-NN algorithm, especially with Morgan fingerprints (r = 0.61 to r = 0.68).
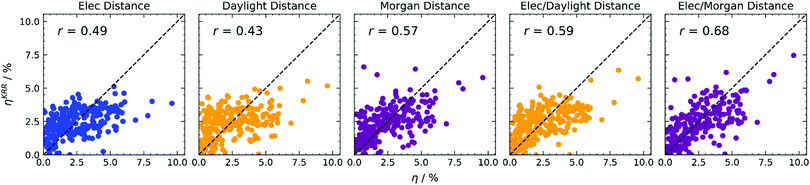 | ||
| Fig. 4 KRR predictions of photovoltaic efficiency based on various distance-based kernels, indicated at the top of each column. Colours encode electronic properties only (blue), or the type of molecular fingerprint used (Daylight in yellow, Morgan in magenta). RMSE data available in Table S1 (ESI†). | ||
| Fig. | Model | Input | Target property | r |
|---|---|---|---|---|
| 3 | k-NN | Elec | V OC | 0.43 |
| 3 | k-NN | Elec | J SC | 0.37 |
| 3 | k-NN | Elec | η | 0.38 |
| 3 | k-NN | Daylight | V OC | 0.48 |
| 3 | k-NN | Daylight | J SC | 0.36 |
| 3 | k-NN | Daylight | η | 0.51 |
| 3 | k-NN | Morgan | V OC | 0.50 |
| 3 | k-NN | Morgan | J SC | 0.45 |
| 3 | k-NN | Morgan | η | 0.49 |
| 3 | k-NN | Elec/Daylight | V OC | 0.57 |
| 3 | k-NN | Elec/Daylight | J SC | 0.57 |
| 3 | k-NN | Elec/Daylight | η | 0.61 |
| 3 | k-NN | Elec/Morgan | V OC | 0.65 |
| 3 | k-NN | Elec/Morgan | J SC | 0.55 |
| 3 | k-NN | Elec/Morgan | η | 0.61 |
| 4 | KRR | Elec | η | 0.49 |
| 4 | KRR | Daylight | η | 0.43 |
| 4 | KRR | Morgan | η | 0.57 |
| 4 | KRR | Elec/Daylight | η | 0.59 |
| 4 | KRR | Elec/Morgan | η | 0.68 |
For the best model, we obtain strong correlations (r ≈ 0.7, see Table 1, and Table S2 reporting additional correlation coefficients, ESI†) that are comparable to the best reported so far in the literature,6,8 improve significantly over naïve prediction strategies, and thus are good enough to obtain reliable predictions of efficiencies, aimed at accelerating the discovery of new efficient materials. To assess the effect of specific structural features on our best model, we checked, through a Kruskal–Wallis test,47 that the distribution of errors did not change significantly upon removal of entries containing a specific structural feature of interest. As an example, we report in the ESI† the distribution of errors obtained for our best model trained only on entries that do not contain Halogen atoms.
In conclusion, we have verified that Scharber's model has very limited predictive power when used in conjunction with DFT calculations. We have therefore explored a range of machine learning algorithms combining electronic properties and topological information, obtaining highly predictive models. A simple k-NN model already yields correlations of ∼0.6 between experiment and predictions, which can be improved up to ∼0.7 by exploiting non-linear kernel methods. The introduction of structural similarity metrics mimics the approach adopted in experimental research, i.e. it can be seen as an implementation of “artificial chemical intuition”. Various improvements can be foreseen: analysis of larger data sets in terms of molecules and properties included, identification of figures of merit better than RMSE for the optimisation of hyperparameters, and coupling with combinatiorial or genetic searches to propose new high efficiency candidates.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the ERC through Grant No. 615834. We are grateful to Dr Stefano Caprasecca (Open University, Verizon Connect) for fruitful discussions.References
- G. J. Hedley, A. Ruseckas and I. D. Samuel, Chem. Rev., 2017, 117, 796–837 CrossRef CAS PubMed.
- S. Antohe, S. Iftimie, L. Hrostea, V. A. Antohe and M. Girtan, Thin Solid Films, 2017, 642, 219–231 CrossRef CAS.
- K. Wang, C. Liu, T. Meng, C. Yi and X. Gong, Chem. Soc. Rev., 2016, 45, 2937–2975 RSC.
- L. Lu, T. Zheng, Q. Wu, A. M. Schneider, D. Zhao and L. Yu, Chem. Rev., 2015, 115, 12666–12731 CrossRef CAS PubMed.
- S. A. Lopez, E. O. Pyzer-Knapp, G. N. Simm, T. Lutzow, K. Li, L. R. Seress, J. Hachmann and A. Aspuru-Guzik, Sci. Data, 2016, 3, 160086 CrossRef PubMed.
- E. O. Pyzer-Knapp, K. Li and A. Aspuru-Guzik, Adv. Funct. Mater., 2015, 25, 6495–6502 CrossRef CAS.
- J. Hachmann, R. Olivares-Amaya, A. Jinich, A. L. Appleton, M. A. Blood-Forsythe, L. R. Seress, C. Román-Salgado, K. Trepte, S. Atahan-Evrenk, S. Er, S. Shrestha, R. Mondal, A. Sokolov, Z. Bao and A. Aspuru-Guzik, Energy Environ. Sci., 2014, 7, 698–704 RSC.
- H. Sahu, W. Rao, A. Troisi and H. Ma, Adv. Energy Mater., 2018, 1801032, DOI:10.1002/aenm.201801032.
- D. C. Elton, Z. Boukouvalas, M. S. Butrico, M. D. Fuge and P. W. Chung, Sci. Rep., 2018, 8, 9059 CrossRef PubMed.
- S. A. Lopez, B. Sanchez-Lengeling, J. de Goes Soares and A. Aspuru-Guzik, Joule, 2017, 1, 857–870 CrossRef CAS.
- Y. Liu, T. Zhao, W. Ju and S. Shi, J. Materiomics, 2017, 3, 159–177 CrossRef.
- C. Schober, K. Reuter and H. Oberhofer, J. Phys. Chem. Lett., 2016, 7, 3973–3977 CrossRef CAS PubMed.
- V. Janković and N. Vukmirović, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 235208 CrossRef.
- O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888 RSC.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J. L. Bredas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- C. M. Proctor, M. Kuik and T.-Q. Nguyen, Prog. Polym. Sci., 2013, 38, 1941–1960 CrossRef CAS.
- N. A. Ran, J. A. Love, M. C. Heiber, X. Jiao, M. P. Hughes, A. Karki, M. Wang, V. V. Brus, H. Wang, D. Neher, H. Ade, G. C. Bazan and T.-Q. Nguyen, Adv. Energy Mater., 2018, 8, 1701073 CrossRef.
- M. C. Scharber, D. Mühlbacher, M. Koppe, P. Denk, C. Waldauf, A. J. Heeger and C. J. Brabec, Adv. Mater., 2006, 18, 789–794 CrossRef CAS.
- R. P. Fornari, P. Rowe, D. Padula and A. Troisi, J. Chem. Theory Comput., 2017, 13, 3754–3763 CrossRef CAS PubMed.
- A. Kuzmich, D. Padula, H. Ma and A. Troisi, Energy Environ. Sci., 2017, 10, 395–401 RSC.
- M. Rupp, A. Tkatchenko, K. R. Muller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- S. Bibi and J. Zhang, New J. Chem., 2016, 40, 3693–3704 RSC.
- J. Mai, T.-K. Lau, J. Li, S.-H. Peng, C.-S. Hsu, U. S. Jeng, J. Zeng, N. Zhao, X. Xiao and X. Lu, Chem. Mater., 2016, 28, 6186–6195 CrossRef CAS.
- S. Torabi, F. Jahani, I. Van Severen, C. Kanimozhi, S. Patil, R. W. A. Havenith, R. C. Chiechi, L. Lutsen, D. J. M. Vanderzande, T. J. Cleij, J. C. Hummelen and L. J. A. Koster, Adv. Funct. Mater., 2015, 25, 150–157 CrossRef CAS.
- J. Li, G. Zhang, D. M. Holm, I. E. Jacobs, B. Yin, P. Stroeve, M. Mascal and A. J. Moulé, Chem. Mater., 2015, 27, 5765–5774 CrossRef CAS.
- F. Machui, S. Abbott, D. Waller, M. Koppe and C. J. Brabec, Macromol. Chem. Phys., 2011, 212, 2159–2165 CrossRef CAS.
- G. Sini, M. Schubert, C. Risko, S. Roland, O. P. Lee, Z. Chen, T. V. Richter, D. Dolfen, V. Coropceanu, S. Ludwigs, U. Scherf, A. Facchetti, J. M. J. Fréchet and D. Neher, Adv. Energy Mater., 2018, 8, 1702232 CrossRef.
- O. A. von Lilienfeld, Angew. Chem., Int. Ed. Engl., 2018, 57, 4164–4169 CrossRef CAS PubMed.
- E. O. Pyzer-Knapp, G. N. Simm and A. Aspuru Guzik, Mater. Horiz., 2016, 3, 226–233 RSC.
- K. Vu, J. C. Snyder, L. Li, M. Rupp, B. F. Chen, T. Khelif, K.-R. Müller and K. Burke, Int. J. Quantum Chem., 2015, 115, 1115–1128 CrossRef CAS.
- M. Rupp, Int. J. Quantum Chem., 2015, 115, 1058–1073 CrossRef CAS.
- S. Nagasawa, E. Al-Naamani and A. Saeki, J. Phys. Chem. Lett., 2018, 9, 2639–2646 CrossRef CAS PubMed.
- R. Visini, J. Arus-Pous, M. Awale and J. L. Reymond, J. Chem. Inf. Model., 2017, 57, 2707–2718 CrossRef CAS PubMed.
- K. T. Schutt, F. Arbabzadah, S. Chmiela, K. R. Muller and A. Tkatchenko, Nat. Commun., 2017, 8, 13890 CrossRef PubMed.
- P. B. Jorgensen, M. Mesta, S. Shil, J. M. Garcia Lastra, K. W. Jacobsen, K. S. Thygesen and M. N. Schmidt, J. Chem. Phys., 2018, 148, 241735 CrossRef PubMed.
- I. Y. Kanal, S. G. Owens, J. S. Bechtel and G. R. Hutchison, J. Phys. Chem. Lett., 2013, 4, 1613–1623 CrossRef CAS PubMed.
- D. Bajusz, A. Racz and K. Heberger, J. Cheminf., 2015, 7, 20 Search PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- D. D. Méndez-Hernández, P. Tarakeshwar, D. Gust, T. A. Moore, A. L. Moore and V. Mujica, J. Mol. Model., 2013, 19, 2845–2848 CrossRef PubMed.
- C.-G. Zhan, J. A. Nichols and D. A. Dixon, J. Phys. Chem. A, 2003, 107, 4184–4195 CrossRef CAS.
- G. Zhang and C. B. Musgrave, J. Phys. Chem. A, 2007, 111, 1554–1561 CrossRef CAS PubMed.
- Q. Wang, J. J. van Franeker, B. J. Bruijnaers, M. M. Wienk and R. A. J. Janssen, J. Mater. Chem. A, 2016, 4, 10532–10541 RSC.
- N. S. Altman, Am. Stat., 1992, 46, 175–185 Search PubMed.
- Y. Zhang and Y. Yang, J. Econom., 2015, 187, 95–112 CrossRef.
- Y. Zhao and K. Kwoh Chee, Proceedings of the 17th International Conference on Pattern Recognition, 2004. ICPR 2004, 2004, 3, 494–497, vol. 493.
- K. Claridge, D. Padula and A. Troisi, Phys. Chem. Chem. Phys., 2018, 20, 17279–17288 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: An archive containing the coordinates of the optimised geometries of analysed molecules and a database of the properties gathered from quantum chemical calculations used as input for electronic distance calculations, details on the procedures adopted for data gathering and calculations, a detailed theoretical treatment of Kernel Ridge Regression, values of hyperparameters and metrics for the models used, additional figures and tables. See DOI: 10.1039/c8mh01135d |
| This journal is © The Royal Society of Chemistry 2019 |