Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Defect chemistry and electrical properties of sodium bismuth titanate perovskite
F.
Yang
 *a,
M.
Li
*a,
M.
Li
 b,
L.
Li
b,
L.
Li
 a,
P.
Wu
a,
E.
Pradal-Velázquez
a and
D. C.
Sinclair
a,
P.
Wu
a,
E.
Pradal-Velázquez
a and
D. C.
Sinclair
 *a
*a
aDepartment of Materials Science & Engineering, University of Sheffield, Sheffield, S1 3JD, UK. E-mail: fan.yang@sheffield.ac.uk; d.c.sinclair@sheffield.ac.uk
bDepartment of Mechanical, Materials and Manufacturing Engineering, University of Nottingham, NG7 2RD, UK
First published on 28th November 2017
Abstract
The ferroelectric perovskite Na0.5Bi0.5TiO3, NBT, can exhibit three types of electrical behaviour, i.e. oxide-ion conduction (type I), mixed ionic–electronic conduction (type II) and insulating/dielectric (type III) based on various defect mechanisms. Here we review how to tune the electrical properties of NBT via several mechanisms, including A-site Na or Bi non-stoichiometry, isovalent substitution, and acceptor- and donor-doping. The diversity of the electrical behaviour in the NBT lattice is attributed to the high level of oxide-ion conductivity originating from highly mobile oxygen ions which can be fine-tuned to optimise or suppress ionic conduction. High oxide-ion conductivity can be obtained by manipulating the starting Na/Bi ≥1 and by acceptor-doping to make NBT a potential electrolyte material for intermediate temperature solid oxide fuel cells (IT-SOFCs). In contrast, the oxide-ion conduction can be partially or fully suppressed by having a starting (nominal) composition with Na/Bi <1, donor-doping, or utilising the trapping effect between oxygen vacancies and some B-site acceptor dopants. This significantly reduces the dielectric loss and makes NBT-based materials excellent candidates as high-temperature dielectrics for capacitor applications.
Introduction
Sodium bismuth titanate, Na0.5Bi0.5TiO3 (NBT), is considered as one of the most promising lead-free piezoelectric materials to replace lead zirconate titanate (PZT) because of its high Curie temperature (∼325 °C), relatively high remnant polarization (38 μC cm−2) and piezoelectric constant (73 pC N−1).1–3 NBT was first reported in the 1960s and has received increasing attention in recent years driven by the surge in developing lead-free materials.4 There has been extensive research on the crystal structure and phase transformation of NBT,5–10 and numerous efforts have been devoted to improving its piezoelectric properties.4,11–20One major drawback of NBT as a piezoelectric/dielectric material is its high electrical conductivity which leads to high and unacceptable dielectric loss and leakage currents at elevated temperatures.1 To solve this problem improved understanding of the electrical conductivity and the conduction mechanism(s) of NBT is essential. Hiruma et al.21 and Sung et al.22,23 have shown that the electrical properties of NBT are highly sensitive to A-site cation nonstoichiometry and that small deviations in nominal A-site cation stoichiometry can result in more than 3 orders of magnitude difference in the room temperature dc resistivity. Although it is widely accepted that the mobility of oxygen vacancies plays an important role22,23 and that Bi2O3 loss during ceramic processing is a likely source of the oxygen vacancies,21,22,24 the origin of the dramatic dependence of electrical conductivity with such small variations in the nominal starting compositions, as well as the conduction mechanism(s) of NBT, remain challenging issues.
Recently, we used a combination of impedance spectroscopy, electromotive force (EMF) and 18O Time-of-Flight Secondary Ion Mass Spectroscopy (ToF SIMS) to clarify the electrical conduction mechanisms in NBT and revealed the significant change in the electrical conductivity induced by small variations of Na or Bi nonstoichiometry being related to a switch between oxide-ion and electronic conduction.25,26 The nominally stoichiometric NBT (nominal Na0.5Bi0.5TiO3; NB0.50T), presents high conductivity with an oxide-ion transport number tion ∼ 0.9 at 600–800 °C, suggesting that the electrical conduction is dominated by oxide-ions. The predominance of oxide-ion conduction (as opposed to sodium ion or electronic conduction) in NB0.50T has been further confirmed by 18O tracer diffusion measurements. The high oxide-ion conductivity in NB0.50T is attributed to the oxygen vacancies generated through low levels of Bi2O3 loss during ceramic processing according to the Kroger–Vink equation,
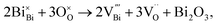 | (1) |
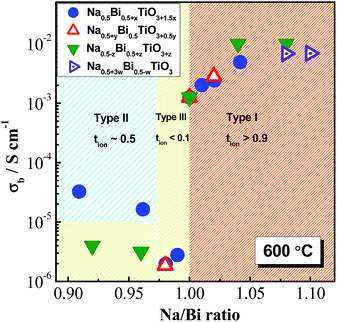
Based on the magnitude of bulk conductivity σb and tion values, we have concluded that NBT can exhibit three types of electrical behaviour by tailoring the A-site Na/Bi non-stoichiometry (Fig. 1a): type I, predominant oxide-ion conduction, high σb, tion ∼ 0.9; type II, mixed ionic–electronic conduction, intermediate σb, tion ∼ 0.5; type III, predominant electronic conduction, low σb, tion < 0.1. These three types of electrical behaviour can also be clearly distinguished from the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T relationship, Fig. 1b. Type I NBT shows a sharp rise of tan
δ–T relationship, Fig. 1b. Type I NBT shows a sharp rise of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ with increasing temperature and tan
δ with increasing temperature and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ exceeds 0.2 at ∼350 °C. In contrast, type III NBT presents low tan
δ exceeds 0.2 at ∼350 °C. In contrast, type III NBT presents low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ in a wide temperature range (<0.02 from 300 to 600 °C), making it an excellent high temperature dielectric material. In between type I and III, type II shows low tan
δ in a wide temperature range (<0.02 from 300 to 600 °C), making it an excellent high temperature dielectric material. In between type I and III, type II shows low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ in a narrow temperature range and a steep rise above ∼500 °C to exceed 0.1 at 600 °C.
δ in a narrow temperature range and a steep rise above ∼500 °C to exceed 0.1 at 600 °C.
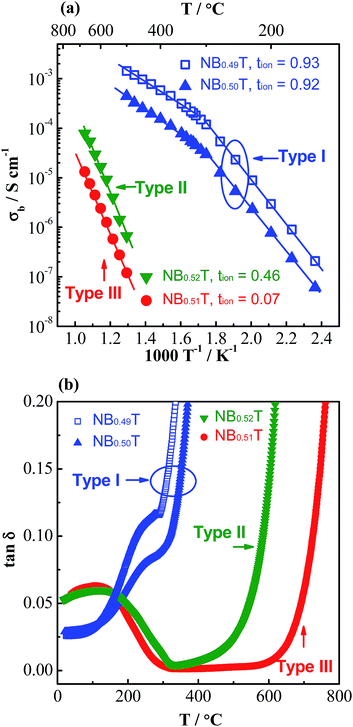 | ||
Fig. 1 (a) Arrhenius plot of bulk conductivity, σb and (b) dielectric loss, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, at 1 MHz versus temperature for NBT with various A-site Bi nonstoichiometry: Na0.5Bi0.49TiO2.985, NB0.49T; Na0.5Bi0.5TiO3, NB0.50T; Na0.5Bi0.51TiO3.015, NB0.51T; Na0.5Bi0.52TiO3.03, NB0.52T. Replotted after ref. 29. δ, at 1 MHz versus temperature for NBT with various A-site Bi nonstoichiometry: Na0.5Bi0.49TiO2.985, NB0.49T; Na0.5Bi0.5TiO3, NB0.50T; Na0.5Bi0.51TiO3.015, NB0.51T; Na0.5Bi0.52TiO3.03, NB0.52T. Replotted after ref. 29. | ||
The above findings not only reveal the electrical conduction behaviour of NBT but also show the flexibility in tailoring the electrical conductivity and conduction mechanisms in NBT and expand the potential application of NBT-based materials from piezoelectric/dielectric devices to oxide-ion and mixed ionic–electronic conductors. They also highlight the importance of defect chemistry in the electrical properties of NBT. Here we review how to tune the electrical properties of NBT by various defect mechanisms including; A-site Na or Bi non-stoichiometry; isovalent substitution; and acceptor- and donor-doping. In particular, we focus on controlling the oxide-ion conduction in NBT to switch the conduction mechanism and conductivity among types I, II and III according to the requirements for different applications.
The structure of this review is as follows. First, we review the defect chemistry and electrical properties of undoped NBT, which consists only of Na, Bi, Ti and O without any other dopant and therefore rules out any possible influence from foreign ions. Second, the results from isovalent doping which does not introduce any oxygen vacancies into NBT are discussed to unveil the important parameters that may affect oxide-ion conduction in NBT. Third, possible compensation mechanism(s) from acceptor-doping in NBT are discussed with an attempt to enhance the bulk conductivity and to explore the potential of NBT-based materials as electrolytes in IT-SOFCs. We also demonstrate the possibility of suppressing the oxide-ion conduction in NBT using the trapping effect between B-site acceptor-dopants and oxygen vacancies. Finally, the influence of donor-doping on the electrical properties is reviewed to demonstrate the dielectric/insulating behaviour, thus making NBT-based materials potential candidates for high temperature dielectric/piezoelectric applications. The article concludes with a summary to highlight the important findings, to date.
Defect chemistry and electrical properties of NBT
Undoped NBT
Our earlier studies25,26 showed that the electrical conductivity and conduction mechanisms are highly sensitive to the A-site Na or Bi non-stoichiometry. For nominal Na/Bi ratios ≥1, NBT exhibits high oxide-ion conductivity; nominal Na/Bi ratios <1 dramatically suppress the oxide-ion conduction and ‘switch’ NBT to a predominant n-type electronic semiconductor/insulator. In recent follow-on studies, three different mechanisms were employed to manipulate the A-site Na or Bi non-stoichiometry in attempts to fully establish the mechanism(s) and levels of nonstoichiometry in NBT and to improve our understanding of the oxide-ion conducting to semiconducting/insulating switch over.First, we investigated finer increments of A-site non-stoichiometry with two series of materials, Bi non-stoichiometry based on the general formula Na0.5Bi0.5+xTiO3+1.5x (x = −0.02, −0.01, −0.005, 0, 0.005, 0.01, 0.02 and 0.05) and Na non-stoichiometry based on Na0.5+yBi0.5TiO3+0.5y (y = −0.01, 0 and 0.01). The phase purity and the electrical properties in these ceramics were examined using various techniques. Second, a Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi 1
Bi 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 substitution mechanism (Na+ → Bi3+) based on Na0.5−zBi0.5+zTiO3+z (z = −0.02, −0.01, 0, 0.01, 0.02) was studied. This substitution mechanism aimed to alter the Na/Bi ratio while ensuring that the A-site of the perovskite is fully occupied. Third, a Na
1 substitution mechanism (Na+ → Bi3+) based on Na0.5−zBi0.5+zTiO3+z (z = −0.02, −0.01, 0, 0.01, 0.02) was studied. This substitution mechanism aimed to alter the Na/Bi ratio while ensuring that the A-site of the perovskite is fully occupied. Third, a Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi 3
Bi 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 substitution mechanism (3Na+ → Bi3+) based on Na0.5+3wBi0.5−wTiO3 (w = −0.05, −0.02, −0.01, 0, 0.05) was investigated. This mechanism maintains A-site charge neutrality without introducing any oxygen deficiency. The results of the above three non-stoichiometry mechanisms are summarised in this section.
1 substitution mechanism (3Na+ → Bi3+) based on Na0.5+3wBi0.5−wTiO3 (w = −0.05, −0.02, −0.01, 0, 0.05) was investigated. This mechanism maintains A-site charge neutrality without introducing any oxygen deficiency. The results of the above three non-stoichiometry mechanisms are summarised in this section.
Bi or Na non-stoichiometry
| Nonstoichiometry | x or y | Na/Bi | Electrical behaviour | Phase purity | ||
|---|---|---|---|---|---|---|
| XRD | SEM | TEM | ||||
| Bi, Na0.5Bi0.5+xTiO3+1.5x | −0.02 | 1.04 | I | Na2Ti6O13 | Na2Ti6O13 | — |
| −0.01 | 1.02 | I | Clean | Na2Ti6O13 | TiO2 | |
| −0.005 | 1.01 | I | Clean | Na2Ti6O13 | TiO2 | |
| 0 | 1.00 | I | Clean | Clean | TiO2 | |
| 0.005 | 0.99 | III | Clean | Clean | Clean | |
| 0.01 | 0.98 | III | Clean | Clean | Bi2O3 | |
| 0.02 | 0.96 | II | Clean | Clean | Bi2O3 | |
| 0.05 | 0.91 | II | Bi2O3, Na0.5Bi4.5Ti4O15 | Bi2O3, Na0.5Bi4.5Ti4O15 | Bi2O3 | |
| Na, Na0.5+yBi0.5TiO3+0.5y | −0.01 | 0.98 | III | Clean | Clean | TiO2 |
| 0 | 1.00 | I | Clean | Clean | TiO2 | |
| 0.01 | 1.02 | I | Clean | Na-rich phase | — | |
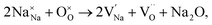 | (2) |
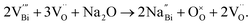 | (3) |
However, the observed electrical properties of the NBT series with Na non-stoichiometry are not consistent with eqn (2) and (3), therefore suggesting that these mechanisms are inappropriate for this series.
XRD, SEM and TEM analysis on Na non-stoichiometric NBT reveals that the observed electrical behaviour originates from changes in the composition of the main phase in these ceramics. For example, for Na-deficient NBT, i.e., y = −0.01, STEM HAADF Z-contrast images revealed the presence of a TiO2 secondary phase. Thus the bulk composition is deficient in both Na and Ti, and therefore the chemical formula Na0.49Bi0.50TiO2.99 can be rewritten as Na0.5Bi0.51Ti1.02−δO3.055−2δ where δTiO2 is the secondary phase observed by TEM. Therefore, the bulk composition of y = −0.01 was essentially Bi-rich to make NBT insulating (type III). For Na-rich NBT, a Na-rich secondary phase was detected under SEM, indicating that the excess Na in the starting material does not enter into the lattice. The bulk composition is Bi-deficient due to the Bi-loss during ceramic processing. Consequently, oxygen vacancies are generated according to eqn (1) and make the NBT oxide-ion conducting (type I).
Na+ → Bi3+ (ref. 31)
As Na or Bi deficiency will introduce vacancies on the A-site, a Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi 1
Bi 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 substitution mechanism (Na+ → Bi3+) with a nominal composition of Na0.5−zBi0.5+zTiO3+z (z = −0.02, −0.01, 0, 0.01, 0.02), which ensures that the A-site of the perovskite lattice is fully occupied, was investigated. The phase purity and electrical behaviour of this series are summarised in Table 2.
1 substitution mechanism (Na+ → Bi3+) with a nominal composition of Na0.5−zBi0.5+zTiO3+z (z = −0.02, −0.01, 0, 0.01, 0.02), which ensures that the A-site of the perovskite lattice is fully occupied, was investigated. The phase purity and electrical behaviour of this series are summarised in Table 2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi 1
Bi 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 substitution: Na0.5−zBi0.5+zTiO3+z (z = −0.02, −0.01, 0, 0.01, 0.02)
1 substitution: Na0.5−zBi0.5+zTiO3+z (z = −0.02, −0.01, 0, 0.01, 0.02)
| z | Nominal composition | Na/Bi | Electrical behaviour | Phase purity | |
|---|---|---|---|---|---|
| XRD | SEM | ||||
| −0.02 | Na0.52Bi0.48TiO2.98 | 1.08 | I | Clean | Na2Ti3O7 |
| −0.01 | Na0.51Bi0.49TiO2.99 | 1.04 | I | Clean | Clean |
| 0 | Na0.5Bi0.5TiO3 | 1.00 | I | Clean | Clean |
| 0.01 | Na0.49Bi0.51TiO3.01 | 0.96 | III | Clean | Clean |
| 0.02 | Na0.48Bi0.52TiO3.02 | 0.92 | III | Na0.5Bi4.5Ti4O15 | Na0.5Bi4.5Ti4O15 |
With this defect mechanism, single phase NBT (based on SEM) can be obtained for −0.01 ≤ z ≤ 0.01. A Na2Ti3O7 secondary phase was detected for z = −0.02 and a Na0.5Bi4.5Ti4O15 secondary phase was detected for z = 0.02. Similar to Na or Bi non-stoichiometry, NBT also exhibits a type I behaviour with starting Na/Bi ratios ≥1 and type III with Na/Bi ratios <1.
The effect of Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi 1
Bi 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 substitution on the electrical conduction behaviour is similar to Bi-deficient NBT where oxygen vacancies are generated to induce oxide-ion conduction (for z < 0) or Bi-rich NBT where oxygen vacancies are filled to exhibit n-type semi-conduction (for z > 0). As this defect mechanism does not introduce any A-site vacancies, it confirms the importance of oxygen vacancies (as opposed to the A-site cation vacancies) in the electrical conduction of NBT.
1 substitution on the electrical conduction behaviour is similar to Bi-deficient NBT where oxygen vacancies are generated to induce oxide-ion conduction (for z < 0) or Bi-rich NBT where oxygen vacancies are filled to exhibit n-type semi-conduction (for z > 0). As this defect mechanism does not introduce any A-site vacancies, it confirms the importance of oxygen vacancies (as opposed to the A-site cation vacancies) in the electrical conduction of NBT.
3Na+ → Bi3+ (ref. 32)
A Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi 3
Bi 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 substitution mechanism (3Na+ → Bi3+) with a nominal composition of Na0.5+3wBi0.5−wTiO3 (w = −0.05, 0, 0.01, 0.02, 0.05) has also been investigated. This mechanism maintains a neutral charge at the A-site without introducing any oxygen deficiency. The phase purity and electrical behaviour of this series are summarised in Table 3.
1 substitution mechanism (3Na+ → Bi3+) with a nominal composition of Na0.5+3wBi0.5−wTiO3 (w = −0.05, 0, 0.01, 0.02, 0.05) has also been investigated. This mechanism maintains a neutral charge at the A-site without introducing any oxygen deficiency. The phase purity and electrical behaviour of this series are summarised in Table 3.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bi 3
Bi 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 substitution: Na0.5+3wBi0.5−wTiO3 (w = −0.05, −0.02, −0.01, 0, 0.05)
1 substitution: Na0.5+3wBi0.5−wTiO3 (w = −0.05, −0.02, −0.01, 0, 0.05)
| w | Nominal composition | Na/Bi | Electrical behaviour | Phase purity |
|---|---|---|---|---|
| XRD | ||||
| −0.05 | Na0.35Bi0.55TiO3 | 0.63 | — | NBT + Bi4Ti3O12 |
| 0 | Na0.5Bi0.5TiO3 | 1.00 | I | Clean |
| 0.01 | Na0.53Bi0.49TiO3 | 1.08 | I | Clean |
| 0.02 | Na0.56Bi0.48TiO3 | 1.17 | I | Na-rich phase |
| 0.05 | Na0.65Bi0.45TiO3 | 1.44 | I | Na-rich phase |
Based on XRD, large amounts of Bi4Ti3O12 can be detected for w = −0.05 and a small amount of a Na-rich secondary phase for w = 0.05. Phase pure NBT is only obtained for w = 0.01 based on XRD. However, according to the nominal composition of w = 0.01, A-site occupancy is >1, which is unlikely to happen. Normalising the A-site occupancy to 1 gives the formula Na0.52Bi0.48Ti0.98O2.94 and would therefore generate a Na,Ti-rich secondary phase that has not been detected by XRD.
These results suggest that this substitution mechanism does not yield an extensive single phase NBT solid solution. NBT with w > 0 exhibits a type I behaviour which is a result of Bi-deficient bulk NBT with the presence of a Na,Ti-rich secondary phase.
Summary
In this section, three different A-site defect mechanisms have been applied to NBT and their effects on the electrical properties are summarised in Fig. 2. In general, NBTs with Na/Bi ratios ≥1 exhibit high oxide-ion conductivity (type I) and those with Na/Bi ratios <1 show low conductivity which is dominated by low levels of electronic conduction (type III). NBTs with significant levels of Bi-rich secondary phases can present mixed-conduction with comparable contributions from electronic and oxide-ion conduction (type II). It should be stressed that the level of allowed non-stoichiometry within NBT is extremely low, usually below the detection limit of most readily available analytical methods. But such low levels of non-stoichiometry can result in more than three orders of magnitude difference in the bulk conductivity, and therefore electrical measurements are the most sensitive and reliable method to detect the predominant type of non-stoichiometry in NBT.Isovalent doping33
Nominally stoichiometric NBT exhibits high oxide-ion conductivity, which originates from the oxygen vacancies generated through a small amount of Bi2O3 loss during ceramic processing. A previous study34 showed that 0.5–1 at% Nb doping on the B-site can fill up the oxygen vacancies and significantly decrease the electrical conductivity. Therefore, the bismuth and oxygen nonstoichiometry in NBT can be estimated to be in the range of 0.0017–0.0033 for Bi and 0.0025–0.005 for oxygen, corresponding to a formula of Na0.5Bi0.4967−0.4983TiO2.995−2.9975.34 The fact that such a low level of oxygen vacancy concentration can result in such high oxide-ion conductivity implies that the mobility of oxygen ions in NBT is very high. In perovskites, the oxygen ion migration is through a saddle point which is a triangle formed by two A-site cations and one B-site cation.35 In NBT, first-principles calculations36,37 showed that the lowest energy barriers for oxygen ion migration occur in the saddle points between Bi–Bi–Ti ions (0.22 eV), whereas higher barriers are observed for Na–Bi–Ti (0.6–0.85 eV) and Na–Na–Ti (1.0–1.3 eV) saddle points, as shown in Fig. 3. Experimentally, there is no evidence for long-range ordering of the A-site cations in NBT, and therefore the Na–Bi–Ti saddle points are considered as the rate-limiting step in the overall oxide-ion migration in NBT. It is generally accepted that the high polarisability of Bi3+ and weak Bi–O bonds on the A-site are critical to the high mobility of oxygen ions.27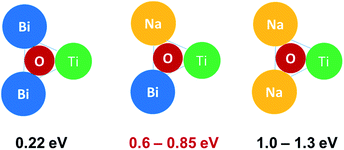 | ||
| Fig. 3 Saddle-point configuration and associated activation energies for oxygen ion migration in NBT. Values taken from ref. 37. | ||
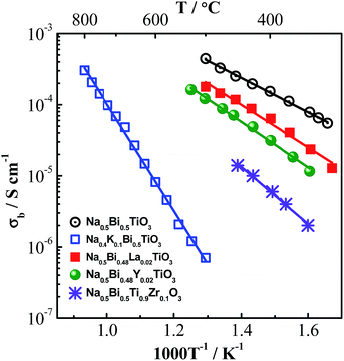
To further understand the local configuration and properties of cations on the oxide-ion conduction in NBT, isovalent doping, such as K+ to replace Na+, Y3+ or La3+ to replace Bi3+ and Zr4+ to replace Ti4+, have been carried out. The Arrhenius plot of the bulk conductivity, σb, of K-doped, Y-doped, La-doped and Zr-doped NBT obtained from impedance spectroscopy is shown in Fig. 4. The ionic radius, polarisability and bonding strength with oxygen of these elements are listed in Table 4.
| Dopant | Ionic radius (Å) | Polarisability (Å3) | Bonding strength with oxygen (kJ mol−1) |
|---|---|---|---|
| Na+ | 1.39 (12-fold) | 1.80 | 257 |
| K+ | 1.64 (12-fold) | 3.83 | 239 |
| Bi3+ | 1.39 (12-fold) | 6.12 | 343 |
| La3+ | 1.36 (12-fold) | 4.82 (ref. 40) | 799 |
| Y3+ | 1.06 (12-fold) | 3.81 | 719 |
| Ti4+ | 0.605 (6-fold) | 2.93 | 672 |
| Zr4+ | 0.72 (6-fold) | 3.25 | 801 |
Partial replacement of Na+ by K+ significantly decreases the bulk conductivity, which is surprising as K+ has higher polarisability and weaker bonding strength with oxygen compared to Na+, which should be beneficial for oxide-ion conduction. Here the suppressed conductivity is attributed to compositional variations associated with the higher volatility of K compared to Na. The K loss is more significant than Bi-loss during sintering, and therefore makes KNBT Bi-rich on the A-site. Partial replacement of Bi3+ by Y3+ or La3+ on the A-site decreases the bulk conductivity of NBT, which can be attributed to the lower polarisability of Y and La compared to Bi, as well as the much stronger Y–O or La–O bond compared to the Bi–O bond. Although the polarisability of Zr is higher than that of Ti, partial replacement of Ti4+ by Zr4+ also decreases the bulk conductivity of NBT, which suggests that the bonding strength with oxygen plays a key role in the oxide-ion migration. The high cation–oxygen bond strength limits the mobility of oxygen ions in NBT and therefore suppresses the oxide-ion conduction. It can be predicted that these isovalent doped NBTs have much lower dielectric loss and can be excellent high-temperature dielectric materials with appropriate doping levels.
Acceptor-doping41–43
Nominally stoichiometric NBT exhibits high oxide-ion conductivity. It is very promising to develop a family of oxide-ion conductors based on NBT. Enhancement of conductivity can be achieved by inducing a low level of Bi-deficiency in undoped NBT. However, the Bi-deficiency level in NBT is very low. Alternative approaches are required to enhance the oxide-ion conductivity of NBT. Acceptor doping is a commonly employed strategy to enhance ionic conductivity in fluorite-type and perovskite-type oxide-ion conductors by creating oxygen vacancies. In this section, the defect mechanism of acceptor doping in NBT and its effect on the oxide-ion conductivity are reviewed. Acceptor dopants are limited to fixed valency metals such as K+, Ca2+, Sr2+, and Ba2+ (to replace Bi3+ on the A-site) and Mg2+, Zn2+, Sc3+, Al3+, and Ga3+ (to replace Ti4+ on the B-site). Transition metal ions such as Fe3+, Co3+, Ni2+ and Mn3+ on the B-site may introduce electronic conduction into NBT and are therefore not included in this review.NBT has an ABO3 perovskite structure where the A-site is shared by randomly distributed Na+ and Bi3+ ions and the B-site is occupied by Ti4+ ions. Depending on the ionic size, acceptor-type dopants can be doped either on the A-site to replace Bi3+ (larger dopant ions) or on the B-site to replace Ti4+ (smaller dopant ions). In each case, doping may occur by either an ionic or electronic compensation mechanism. In the case of the former, acceptor doping would create oxygen vacancies. A summary of the defect reactions investigated for a range of A- and B-site acceptor dopants in this study (given in brackets) is described by the following Kroger–Vink equations:
A-site:
 | (4a) |
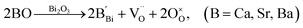 | (4b) |
B-site:
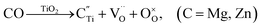 | (4c) |
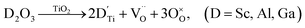 | (4d) |
However, the influence of acceptor-doping on the electrical properties in many perovskite titanates, e.g., BaTiO3 (BT) and SrTiO3 (ST) is often more complex with either n-type, p-type or oxide ion conductivity being dominant depending on a combination of the oxygen-partial-pressure, annealing temperature and cooling rate conditions employed.44–46 Furnace cooled, acceptor-doped BT and ST ceramics processed in air usually exhibit p-type hole conduction (h˙) based on the uptake of oxygen (on cooling) as given by the following mechanism
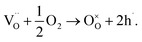 | (5) |
Therefore, acceptor-doping in NBT can either enhance oxide-ion conductivity by creating oxygen vacancies as described by eqn (4) or enhance p-type hole conduction as described by eqn (5). Electrical property measurements on 2% Mg-doped and 2% Sr-doped NB0.49T show enhanced bulk conductivity, enhanced oxide-ion transport numbers and higher oxygen diffusion coefficients compared to undoped NB0.49T, as listed in Table 5. These electrical properties prove that acceptor-doping of NB0.49T on both sites is predominantly by an ionic compensation mechanism to create oxygen vacancies. Acceptor-doping is therefore effective to enhance the oxide-ion conduction of NB0.49T without introducing any significant electronic contribution.
Based on the above understanding, various acceptor-type dopants have been selected to dope NBT and NB0.49T in an attempt to optimise the oxide-ion conductivity in this perovskite. Among all the dopants and doping levels, a maximum enhancement of σb by less than 1 order of magnitude compared to NB0.49T is achieved by 2% Sr-doping on the A-site or 1% Mg-doping on the B-site, as shown in Fig. 5. With other dopants and doping levels the bulk conductivity values are all within the shaded region.
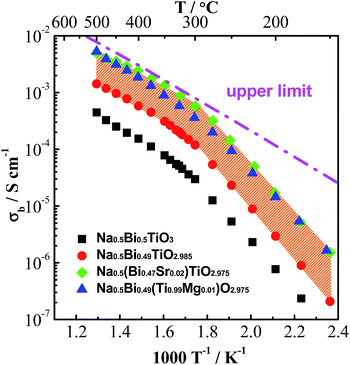 | ||
| Fig. 5 An Arrhenius plot of bulk conductivity, σb, for undoped and acceptor-doped NBT ceramics.41 The dash-dot line represents the upper limit of σb based on the oxygen-vacancy diffusion coefficient predicted in ref. 45, see text. | ||
Possible reasons for the limited enhancement of bulk conductivity by acceptor-doping in NBT are: (1) a low solid solution limit of these acceptor dopants (typically <2 at%) and (2) trapping of oxygen vacancies especially by B-site acceptor dopants, which decreases the mobility of charge carriers.37 More fundamentally, R. A. De Souza45 recently reviewed oxygen vacancy diffusion in a wide variety of ABO3-type perovskites ranging from ferroelectric dielectrics such as BaTiO3 and mixed ionic–electronic conductors such as (Ba0.5Sr0.5)(Co0.8Fe0.2)O3−δ to electrolytes such as (La0.9Sr0.1)(Ga0.8Mg0.2)O2.85. He reported a surprising result that regardless of the level of oxygen vacancies in these materials, the oxygen vacancy diffusivity is very similar and considered the possibility of a fundamental limit to oxygen-vacancy diffusivity in the ABO3 perovskite lattice. Using this oxygen vacancy diffusivity limit for cubic perovskites proposed by De Souza, an upper limit for σb of NBT with an oxygen deficiency of 0.025, calculated from the Nernst–Einstein equation, is predicted, as shown by the dashed line in Fig. 5. Above 300 °C, the highest bulk conductivity obtained by either Sr- or Mg-doping is consistent with the value calculated from this upper limit, therefore suggesting that optimisation of oxide-ion conductivity in the NBT lattice may have been achieved.
Nevertheless, these acceptor-doped NBTs show attractive bulk conductivity. Compared with the two best known δ-Bi2O3 oxide-ion conductors used in intermediate-temperature solid oxide fuel cells (IT-SOFCs), (BiO1.5)0.8(ErO1.5)0.2, 20ESB, and (BiO1.5)0.88(DyO1.5)0.08(WO3)0.04, 8D4WSB, although σb of doped NB0.49T is initially lower than those of 20ESB and 8D4WSB, it shows no appreciable degradation with time contrary to the rapid conductivity degradation of 20ESB and 8D4WSB.42 They also have the advantage over these δ-Bi2O3 phases as a more sustainable (rare-earth free) material. With excellent ionic conductivity, extremely low levels of degradation and reasonable stability in reducing atmospheres,25,42,43 acceptor-doped NBTs can be promising electrolyte materials for IT-SOFCs.
It is worth mentioning that the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σb–1/T relationship of undoped and acceptor-doped NBTs show a change in activation energy, Ea from ∼0.4 eV above 300 °C to ∼0.9 eV below 300 °C (Fig. 5). The reason(s) for a change of Ea around this temperature has not been fully established but the possibility of a change in the charge carrier from oxygen ions to electrons, holes or protons has been excluded by previous studies.41 A plausible explanation for the change of Ea is the coexistence of rhombohedral (R) and tetragonal (T) phases in the temperature range from 250 to 400 °C, which was revealed by variable temperature neutron diffraction and TEM studies.41,42 An estimation of σb from the Maxwell model for a two-phase composite showed good agreement with the experimental data of σb, suggesting that the coexistence of R and T phases may be a plausible explanation for the change in Ea at ∼300 °C.42 Other possible reasons for the change of Ea are dissociation of defect clusters and/or changing of conduction paths associated with the various NBT polymorphs as recently proposed by Meyer and Albe.47
σb–1/T relationship of undoped and acceptor-doped NBTs show a change in activation energy, Ea from ∼0.4 eV above 300 °C to ∼0.9 eV below 300 °C (Fig. 5). The reason(s) for a change of Ea around this temperature has not been fully established but the possibility of a change in the charge carrier from oxygen ions to electrons, holes or protons has been excluded by previous studies.41 A plausible explanation for the change of Ea is the coexistence of rhombohedral (R) and tetragonal (T) phases in the temperature range from 250 to 400 °C, which was revealed by variable temperature neutron diffraction and TEM studies.41,42 An estimation of σb from the Maxwell model for a two-phase composite showed good agreement with the experimental data of σb, suggesting that the coexistence of R and T phases may be a plausible explanation for the change in Ea at ∼300 °C.42 Other possible reasons for the change of Ea are dissociation of defect clusters and/or changing of conduction paths associated with the various NBT polymorphs as recently proposed by Meyer and Albe.47
It is interesting to note that many B-site acceptor-doped NBT materials exhibit significantly lower bulk conductivity when compared to A-site acceptor-doped materials with the same nominal oxygen vacancy concentration, Fig. 6. This suggests a strong tendency for the trapping of oxygen vacancies by B-site acceptor dopants, which is supported by first-principles calculations.37 Trapping of oxygen vacancies decreases their mobility and therefore is detrimental to the oxide-ion conduction. However, it provides an opportunity to control the oxide-ion conduction in NBT using this trapping effect. As the solid solution limit of B-site acceptor dopants in NBT is rather low, some Bi-based high-pressure phases such as BiAlO3, BiGaO3 and BiScO3 were used to form solid solutions with NBT to expand the B-site acceptor-dopant level. For example, with BiAlO3, 8% Al3+ can be incorporated into NBT to replace Ti4+ (ref. 20 and 48) compared to <3% by single B-site doping with Al3+. Impedance spectroscopy measurements show a systematic decrease of bulk conductivity with increasing x in (NBT)1−x(BiAlO3)x solid solutions, Fig. 7a and electromotive force measurements show a continuous decrease of oxide-ion transport number with increasing x, Fig. 7b. As incorporation of BiAlO3 into NBT does not induce any additional oxygen vacancies or create any additional oxygen ions, it can therefore be considered as a ‘stoichiometric’ doping mechanism.
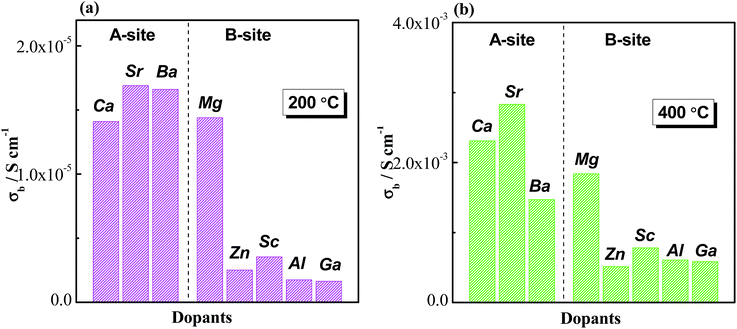 | ||
| Fig. 6 Comparison of bulk conductivity, σb, with A-site and B-site acceptor-dopants at (a) 200 °C and (b) 400 °C. | ||
 | ||
| Fig. 7 (a) Arrhenius plots of the bulk conductivity and (b) oxide-ion transport number at 600 °C for the (NBT)1−x(BiAlO3)x (0 ≤ x ≤ 0.08) solid solutions.48 | ||
The suppressed oxide-ion conductivity by BiAlO3 incorporation can be attributed mainly to a decrease in oxygen vacancy mobility associated with Al acceptor trapping. A simple calculation suggests 7% Al3+ can trap all the oxygen vacancies in the solid solution,48 which is consistent with the σb–x and tion–x relationships shown in Fig. 7. Therefore, using the trapping effect between oxygen vacancies and B-site acceptor dopants, it is possible to fine tune the electrical conduction mechanism from predominant ionic to mixed ionic–electronic to predominant (but low level) electronic conduction.
To summarise this section, low levels of acceptor-type dopants can be introduced to either the A-site to replace Bi3+ or to the B-site to replace Ti4+ to generate oxygen vacancies to enhance the bulk conductivity of NBT. However, the bulk conductivity of acceptor-doped NBT (above 300 °C) seems to approach an upper limit which is restrained by the oxygen vacancy diffusivity in the perovskite lattice. These acceptor-doped NBTs can be promising electrolyte materials for IT-SOFCs. Comparison between A- and B-site dopants suggests that some B-site dopants are more effective at trapping oxygen vacancies to decrease their mobility. This is detrimental for oxide-ion conduction but it provides an opportunity to fine tune the electrical conductivity and conduction mechanism of NBT using the trapping effect between B-site acceptor dopants and oxygen vacancies to create excellent dielectric materials.
Donor-doping29,34
Donor-dopants such as Nb can be incorporated into NBT to replace Ti on the B-site. The doping limit of Nb in Na0.5Bi0.5Ti1−xNbxO3+0.5x is low with the presence of small amounts of Bi2Ti2O7- or Na0.5Bi4.5Ti4O15-related secondary phases for x ≥ 0.02.34 However, extremely low levels of Nb doping can significantly change the electrical conductivity and conduction mechanism of NBT, as summarised below.When Nb is introduced to replace Ti in NBT, there are at least two possible compensation mechanisms: (a) electronic compensation, described by
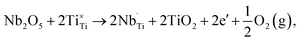 | (6) |
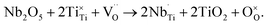 | (7) |
The electronic compensation mechanism is commonly adopted by BT or ST-based perovskites, which induces high levels of n-type semi-conductivity to the materials. For example, Nb doping on the Ti-site can transform BT from a dielectric material to an n-type semiconductor with room temperature conductivity >0.01 S cm−1;49 10% Nb-doped ST can achieve an electronic conductivity of ∼500 S cm−1,50 which makes it a promising oxide-based thermoelectric material. However, the fact that Nb-doping reduces the bulk conductivity of NBT significantly (Fig. 8) indicates that the electronic compensation mechanism is not applicable to NBT. This is attributed to the different band structure of NBT compared with BT or ST. NBT has a high conduction band minimum (ECB) and a high valence band maximum (EVB),44 which makes it less favourable for electronic donor-doping. Therefore, Nb-doping in NBT occurs via an ionic compensation mechanism described by eqn (6). The excess positive charge from Nb5+ ions is compensated by filling oxygen vacancies with oxygen. As a result, the oxide-ion conductivity is suppressed due to a decrease in the charge carrier concentration. Consequently the ionic transport number, tion, decreases from 0.93 for NBT to 0.57 for 0.2 at% Nb-doping, further down to 0.47 for 0.3 at% Nb-doping and finally below 0.1 for ≥0.5 at% Nb-doping (Table 6).
 | ||
| Fig. 8 Arrhenius plot of the bulk conductivity, σb, of Nb-doped NBT with a nominal composition Na0.5Bi0.5Ti1−xNbxO3+0.5x. Activation energy for each composition is indicated in the figure. Replotted after ref. 29 and 34. | ||
| Doping level (%) | Nominal composition | t ion | tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 600 °C δ at 600 °C |
Type | ||
|---|---|---|---|---|---|---|
| 600 °C | 700 °C | 800 °C | ||||
| 0 | Na0.5Ti0.5TiO3 (ref. 25) | 0.93 | 0.93 | 0.85 | ≫0.2 | I |
| 0.2 | Na0.5Bi0.5Ti0.998Nb0.002O3.001 (ref. 29) | 0.57 | 0.63 | 0.63 | 0.083 | II |
| 0.3 | Na0.5Bi0.5Ti0.997Nb0.003O3.0015 (ref. 29) | 0.47 | 0.49 | 0.53 | 0.016 | II |
| 0.5 | Na0.5Bi0.5Ti0.995Nb0.005O3.0025 (ref. 30) | 0.06 | 0.06 | 0.06 | <0.01 | III |
| 1 | Na0.5Bi0.5Ti0.99Nb0.01O3.005 (ref. 31) | Not available | <0.01 | III | ||
| 5 | Na0.5Bi0.5Ti0.95Nb0.05O3.025 (ref. 29) | 0.04 | 0.03 | 0.03 | <0.01 | III |
The continuous decrease in oxide-ion conduction in NBT by Nb doping originates from a decrease in the number of oxygen vacancies. It is expected that similar effects can be observed by Ta-, Mo- and W-doping. This mechanism is different from those of the NBT–BiAlO3 solid solutions where the suppression of oxide-ion conduction is attributed to a decrease in the oxygen vacancy mobility via trapping by the acceptor-dopants.
Concluding remarks
The ferroelectric perovskite NBT can present three types of electrical behaviour based on oxide-ion conduction (type I), mixed ionic–electronic conduction (type II) and insulator/dielectric (type III) by controlling the defects introduced by various mechanisms. The flexibility in fine tuning the electrical properties of NBT makes it an attractive material to be applied in various technologically important devices such as SOFCs (type I) and electronic components such as capacitors and piezoelectric sensors/actuators (type III). To date, the major findings include:(1) The A-site Na or Bi non-stoichiometry level in NBT is very low. The electrical conductivity of NBT is dependent on the starting Na/Bi ratio. Based on our current processing conditions, Na/Bi ≥1 is required to obtain high oxide-ion conductivity. Na/Bi <1 switches the electrical conduction mechanism from predominant oxide-ion conduction to predominant (but low level) electronic conduction. NBT ceramics with a considerable amount of a Bi-rich secondary phase can exhibit mixed ionic–electronic conduction.
(2) The local configuration at the saddle point is critical to the oxide-ion conduction in NBT. Polarisability and bonding strength with oxygen of the cations, especially the latter, are the most important factors that influence the oxide-ion migration. Due to the high polarisability and weak Bi–O bond, it can be predicted that most isovalent dopants on the A-site to replace Bi3+ are detrimental to the oxide-ion conduction.
(3) Low levels of acceptor dopants can be introduced to either the A-site to replace Bi3+ or to the B-site to replace Ti4+ to create oxygen vacancies and consequently enhance the oxide-ion conductivity. Acceptor-doped NBTs have high oxide-ion conductivity, extremely low levels of conductivity degradation and reasonable stability in reducing atmospheres (at least below 550 °C) and are therefore promising electrolyte materials for IT-SOFCs. Comparison between A- and B-site dopants suggests a stronger tendency for trapping of oxygen vacancies by B-site acceptor-dopants. Using this trapping effect, it is possible to control the level of oxide-ion conduction and therefore fine-tune the electrical conductivity and conduction mechanism of NBT according to the requirements of different applications.
(4) Low levels of donor-dopants can be introduced at the B-site to replace Ti4+. Donor doping fills the oxygen vacancies in NBT and therefore suppresses the oxide-ion conductivity. Depending on the doping level, NBT can present mixed ionic–electronic conduction (type II) and finally an insulating/dielectric behaviour based on a low level of electronic conduction (type III).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the EPSRC for funding EP/L027348/1. E. Pradal-Velázquez thanks CONACYT for his scholarship under “Becas CONACYT al extranjero (registro 327115)”.References
- E. Aksel and J. L. Jones, Sensors, 2010, 10, 1935 CrossRef CAS PubMed.
- D. Damjanovic, N. Klein, J. Lin and V. Porokhonskky, Funct. Mater. Lett., 2010, 3, 5 CrossRef CAS.
- K. Reichmann, A. Feteira and M. Li, Materials, 2015, 8, 8467 CrossRef PubMed.
- M. Davies, E. Aksel and J. L. Jones, J. Am. Ceram. Soc., 2011, 94, 1314 CrossRef CAS.
- G. O. Jones and P. A. Thomas, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 168 CAS.
- S. Gorfman and P. A. Thomas, J. Appl. Crystallogr., 2010, 43, 1409 CrossRef CAS.
- E. Aksel, J. S. Forrester, J. L. Jones, P. A. Thomas, K. Page and M. R. Suchomel, Appl. Phys. Lett., 2011, 98, 152901 CrossRef.
- I. Levin and I. M. Reaney, Adv. Funct. Mater., 2012, 22, 3445 CrossRef CAS.
- B. N. Rao, R. Datta, S. S. Chandrashekaran, D. K. Mishra, V. Sathe, A. Senyshyn and R. Ranjan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 224103 CrossRef.
- E. Aksel, J. S. Forrester, B. Kowalski, P. A. Thomas and J. L. Jones, Appl. Phys. Lett., 2011, 99, 222901 CrossRef.
- E. Aksel, H. Foronda, K. Calhoun, J. L. Jones, S. Schaab and T. Granzow, Funct. Mater. Lett., 2010, 3, 45 CrossRef CAS.
- E. Aksel, E. Erdem, P. Jakes, J. L. Jones and R. A. Eichel, Appl. Phys. Lett., 2010, 97, 012903 CrossRef.
- E. Aksel, J. S. Forrester, B. Kowalski, M. Deluca, D. Damjanovic and J. L. Jones, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 024121 CrossRef.
- D. Q. Xiao, D. M. Lin, J. G. Zhu and P. Yu, J. Electroceram., 2008, 21, 34 CrossRef CAS.
- T. Takenaka, K. Maruyama and K. Sakata, Jpn. J. Appl. Phys., 1991, 30, 2236 CrossRef CAS.
- J. R. Gomah-Pettry, S. Said, P. Marchet and J. P. Mercurio, J. Eur. Ceram. Soc., 2004, 24, 1165 CrossRef CAS.
- E. Venkata Ramana, B. V. Bahuguna Saradhi, S. V. Suryanarayana and T. Bhima Sankaram, Ferroelectrics, 2005, 324, 55 CrossRef.
- Y. Hiruma, K. Yoshii, H. Nagata and T. Takenaka, Ferroelectrics, 2007, 346, 114 CrossRef CAS.
- Y. Hiruma, H. Nagata and T. Takenaka, J. Appl. Phys., 2008, 104, 124106 CrossRef.
- H. Yu and Z. Ye, Appl. Phys. Lett., 2008, 93, 112902 CrossRef.
- Y. Hiruma, H. Nagata and T. Takenaka, J. Appl. Phys., 2009, 105, 084112 CrossRef.
- Y. S. Sung, J. M. Kim, J. H. Cho, T. K. Song, M. H. Kim, H. H. Chong, T. G. Park, D. Do and S. S. Kim, Appl. Phys. Lett., 2010, 96, 022901 CrossRef.
- Y. S. Sung, J. M. Kim, J. H. Cho, T. K. Song, M. H. Kim and T. G. Park, Appl. Phys. Lett., 2011, 98, 012902 CrossRef.
- H. Nagata, J. Ceram. Soc. Jpn., 2008, 116, 271 CrossRef CAS.
- M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31 CrossRef CAS PubMed.
- M. Li, H. Zhang, S. N. Cook, L. Li, J. A. Kilner, I. M. Reaney and D. C. Sinclair, Chem. Mater., 2015, 27, 629 CrossRef CAS.
- D. Schütz, M. Deluca, W. Krauss, A. Feteira, T. Jackson and K. Reichmann, Adv. Funct. Mater., 2012, 22, 2285 CrossRef.
- M. Bousquet, J. R. Duclère, E. Orhan, A. Boulle, C. Bachelet and C. Champeaux, J. Appl. Phys., 2010, 107, 104107 CrossRef.
- L. Li, M. Li, H. Zhang, I. M. Reaney and D. C. Sinclair, J. Mater. Chem. C, 2016, 4, 5779 RSC.
- L. Li, Oxide ion conduction in A-site Bi-containing perovskite-type ceramics, PhD thesis, University of Sheffield, 2016.
- P. Wu and D. C. Sinclair, unpublished results.
- F. Yang and D. C. Sinclair, unpublished results.
- L. Li, F. Yang, E. Pradal-Venazque and D. C. Sinclair, unpublished results.
- M. Li, L. Li, J. Zang and D. C. Sinclair, Appl. Phys. Lett., 2015, 106, 102904 CrossRef.
- M. S. Islam, J. Mater. Chem., 2000, 10, 1027 RSC.
- J. A. Dawson, H. Chen and I. Tanaka, J. Mater. Chem. A, 2015, 3, 16574 CAS.
- X. He and Y. Mo, Phys. Chem. Chem. Phys., 2015, 17, 18035 RSC.
- N. M. Gimes and R. W. Grimes, J. Phys.: Condens. Matter, 1998, 10, 3029 CrossRef.
- Y. R. Luo, Compressive Handbook of Chemical Bond Energies, CRC Press, Boca Raton, FL, 2017 Search PubMed.
- C. Vineis, P. K. Davies, T. Negas and S. Bell, Mater. Res. Bull., 1996, 31, 431 CrossRef CAS.
- F. Yang, M. Li, L. Li, P. Wu, E. Pradal-Velázquez and D. C. Sinclair, J. Mater. Chem. A, 2017, 5, 21658 CAS.
- F. Yang, H. Zhang, L. Li, I. M. Reaney and D. C. Sinclair, Chem. Mater., 2016, 28, 5269 CrossRef CAS.
- F. Yang, P. Wu and D. C. Sinclair, Solid State Ionics, 2017, 299, 38 CrossRef CAS.
- S. Li, J. Morasch, A. Klein, C. Chirila, L. Pintilie, L. Jia, K. Ellmer, M. Naderer, K. Reichmann, M. Gröting and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045428 CrossRef.
- R. A. De Souza, Adv. Funct. Mater., 2015, 25, 6326 CrossRef CAS.
- D. M. Symth, J. Electroceram., 2003, 11, 89 CrossRef.
- K.-C. Meyer and K. Albe, J. Mater. Chem. A, 2017, 5, 4368 CAS.
- F. Yang, P. Wu and D. C. Sinclair, J. Mater. Chem. C, 2017, 5, 7243 RSC.
- B. Huybrechts, K. Ishizaki and M. Takata, J. Mater. Sci., 1995, 30, 2463 CrossRef CAS.
- B. Zhang, J. Wang, T. Zou, S. Zhang, X. Yaer, N. Ding, C. Liu, L. Miao, Y. Li and Y. Wu, J. Mater. Chem. C, 2015, 3, 11406 RSC.
| This journal is © The Royal Society of Chemistry 2018 |