Simulation-guided engineering of an enzyme-powered three dimensional DNA nanomachine for discriminating single nucleotide variants

Abstract

Single nucleotide variants (SNVs) are important both clinically and biologically because of their profound biological consequences. Herein, we engineered a nicking endonuclease-powered three dimensional (3D) DNA nanomachine for discriminating SNVs with high sensitivity and specificity. Particularly, we performed a simulation-guided tuning of sequence designs to achieve the optimal trade-off between device efficiency and specificity. We also introduced an auxiliary probe, a molecular fuel capable of tuning the device in solution via noncovalent catalysis. Collectively, our device produced discrimination factors comparable with commonly used molecular probes but improved the assay sensitivity by ∼100 times. Our results also demonstrate that rationally designed DNA probes through computer simulation can be used to quantitatively improve the design and operation of complexed molecular devices and sensors.

---

Introduction

Nature has evolved highly complicated and hierarchical machines that perform diverse biological functions in living systems with remarkably high efficiency and precision. Inspired by nature, various artificial molecular machines have also been created with DNA as a primary choice of building blocks.¹ In particular, DNA-based walking devices that convert chemical energy to mechanical motions hold great promises for smart drug delivery, biocomputing, and diagnostics.^2–9 Despite the extraordinary nanometer precision in transporting payload along well-designed one-dimensional (1D),² two-dimensional (2D),³ or three-dimensional (3D) tracks,⁴ the real-world applicability of current DNA walking devices is challenged by the slow kinetics and low processivity.⁵ Recent effort in designing stochastic DNA walkers that traverse on 3D tracks made of micro- or nanoparticles has greatly enhanced the walking speed and processivity and thus promoted their uses in biosensing and biodiagnostic applications.^5–9 For example, Ellington group introduced a series of 3D stochastic DNA walkers that could take more than 30 continuous steps by integrating catalytic hairpin assembly (CHA) with microparticles.⁵ Our group developed a nicking endonuclease-powered stochastic 3D DNA walker that moves rapidly on a 20 nm gold nanoparticle (AuNP).⁶ A few other nanoparticle-based high-processive stochastic 3D DNA walkers that were propelled by DNAzymes,⁷ nucleases,⁸ and enzyme-free DNA catalysis,⁹ have also been recently created and found unique applications in amplified biosensing and imaging. Despite the recent advances for biomolecular analysis,^5–9 assays making use of DNA walking devices often involve iterative empirical sequence-based optimization to achieve the desired analytical performance. So far, there is no simulation tool available to guide the design and operation of DNA walking devices for bioanalytical applications. Herein, we introduce a simulation-guided strategy that programs the sensitivity and specificity of a 3D DNA walking device for discriminating single nucleotide variants (SNVs).

SNVs are important biomarkers both clinically and biologically, as single base differences in nucleic acid sequences can lead to profound biological and clinical consequences.¹⁰ The discrimination of a single nucleotide mismatch in a given nucleic acid sequence can be technically very challenging. Although the hybridization with a fully complementary sequence is energetically more favourable than a SNV, the thermodynamic gain of many correctly paired bases can easily override the thermodynamic penalty of a single mismatch.¹¹ Similarly, the high processivity of most stochastic 3D DNA walking devices relies on the high energy input through newly paired bases or enzymatic cleavage, and thus are generally not favourable systems to discriminate SNVs.⁶ To ensure the sequence specificity, the hybridization has to be performed at or near the melting temperature, where the free energy of the reaction is close to zero.¹¹ However, commonly used tuning strategies including high assay temperatures and chemical denaturation are not practically feasible and difficult to be predicted for complexed dynamic DNA systems, such as DNA walkers. Here, we aim to address this challenge by engineering a 3D DNA nanomachin (3DDN) with frustrated complementary probes that are operated by the toehold-exchange. Such probes hybridize less favourably to their intended targets than the standard hybridization probes and thus can enhance sequence specificity at the cost of the hybridization yield.^11–13 Therefore, guided by our simulation tool, we perform an in silico sequence design and optimization to balance the device sensitivity and specificity. Facilitated by the simulation, we also develop a new in-solution tuning strategy that enhances both sensitivity and specificity of 3DDN through non-covalent DNA catalysis.

Results and discussion

Device design and theoretical considerations

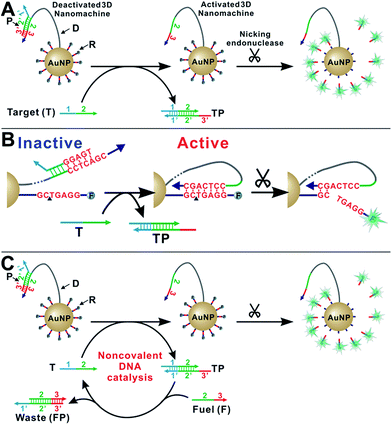
As shown in Scheme 1A, our enzyme-powered 3D DNA nanomachine (3DDN) is engineered by co-conjugating ∼20 DNA walkers (D) carrying a nicking recognition site and ∼400 fluorescently labelled signal reporters (R) carrying a nicking cleavage site on a single 20 nm AuNP. In the presence of nicking endonuclease, D rapidly walks along the surface of AuNP and cleaves R to generate amplified fluorescence signals. To be used for nucleic acid sensing, D is first deactivated using a protecting DNA (P) through hybridization. P deactivates the 3DDN by partially sequestering the nicking recognition sequence on D, and thus D is unable to hybridize with R (Scheme 1B). The target (T) activates the DNA walker by freeing D from DP duplex through a toehold exchange reaction. The reaction can be written as DP + T ↔ TP + D and has a reaction standard free energy ΔG⁰_rxn. DP with more negative ΔG⁰_rxn value binds with T with higher hybridization yield, but it also spuriously binds SNVs. Conversely, DP with less negative ΔG⁰_rxn value binds T with low yield but high selectivity. So far, there are generally two ways to tune the thermodynamics of a toehold-exchange reaction to achieve a reasonable trade-off between hybridization yield (assay sensitivity) and sequence selectivity (assay specificity), including (1) the discrete sequence-level tuning through the length of toehold domains,¹¹ and (2) the continuous in-solution tuning by controlling the stoichiometry between the probe strand and the protector strand.¹² The tuning of both parameters can be performed in silico, which has been successfully demonstrated in the design of ultraspecific conditional molecular probes.^11–13 We reason that such powerful simulation tools can also guide the design and applications of more complexed, multi-component, multi-step DNA machinery systems. Herein, we perform a simulation-guided engineering of the 3DDN for discriminating SNVs. We also introduce a new auxiliary probe, a molecular fuel (F) that tunes both assay sensitivity and specificity in-solution via noncovalent DNA catalysis (Scheme 1C).

Scheme 1 (A) Schematic illustration of the enzyme-powered 3D DNA nanomachine (3DDN). (B) Mechanisms of deactivation of 3DDN by sequestering D with P and activation by T through toehold exchange. (C) Schematic illustration of the in-solution tuning of 3DDN via noncovalent DNA catalysis.

Simulation-guided sequence-level tuning of 3DDN for discriminating SNVs

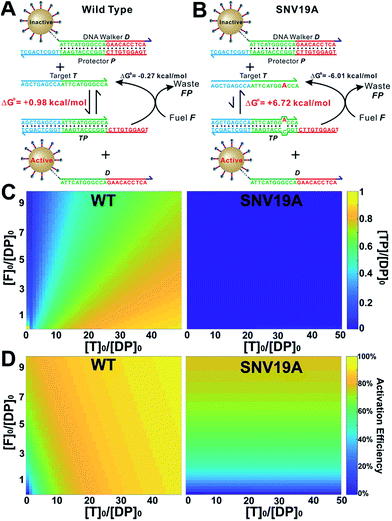
As a proof-of-principle, we designed a 3DDN responsive to a subsequence of the Mycobacterium tuberculosis rpoB gene (Fig. 1). The sequence design and optimization was guided by simulation, where reaction yield (Fig. 1C) or sequence selectivity (Fig. 1D) was plotted as a function of ΔG⁰_rxn. ΔG⁰ values for all sequences were determined using NuPack under a condition (37 °C, 100 mM Na⁺, 10 mM Mg²⁺) nearly identical to the actual experiments (Table S2†). The reaction yield equals to the ratio between [TP] and [T]₀, theoretical values of which were estimated using MATLAB (details in the ESI S2†), where [T]₀ was fixed at 1 nM (Fig. 1C and S1†). The activation efficiency (AE), defined as the ratio between target-activated D over the total, can be further estimated theoretically by plotting [D]/[DP]₀ as a function of [T]₀ and ΔG⁰_rxn (Fig. S2†). [DP]₀ was estimated to be 2 nM for all experiments, as 100 pM devices were used for all experiments and ∼20 DP per device was estimated. The sequence selectivity was determined as the ratio between the reaction yield of a wild type (WT) target and that of a single nucleotide variant at a given ΔG⁰_rxn. By comparing WT with SNV19A and 8 other SNVs (Table S4†), we determined that the optimal lengths of forward (f) and reverse toeholds (r) were both 10 nt (Fig. 1 and S2†). Using this sequence design, the reaction yield is ∼50% for the WT and less than 10% for all SNVs.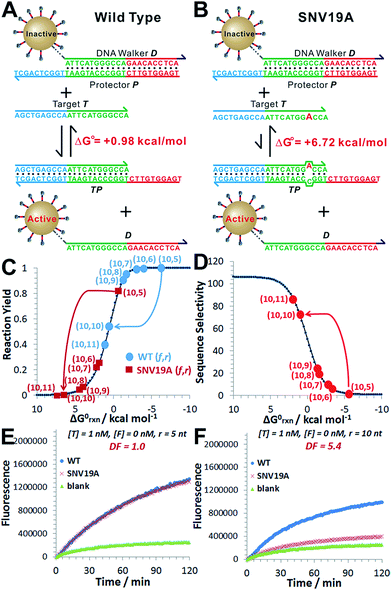

Fig. 1 Sequence-level tuning of the 3D DNA nanomachine (3DDN) for discriminating SNVs. (A and B) The toehold-exchange motif (DP) of the 3DDN consists of a DNA walker (D) and pre-hybridized protecting strand (P). This motif can react with an intended target (T) to release D for the subsequent stochastic walking along the AuNP track. Under the optimal sequence design (f = 10 nt, r = 10 nt), the standard free energy (ΔG⁰) of the forward reaction is +0.98 kcal mol⁻¹ for the wild type target (WT) but is +6.72 kcal mol⁻¹ for the spurious target (SNV19A). (C and D) In silico analyses of the 3DDN. Reaction yields (C) and sequence selectivity (D) as a function of ΔG⁰_rxn. The forward toehold was fixed at f = 10 nt and the lengths of the reverse toehold (r) vary from 5 to 11 nt. Details of the theoretical framework and computer simulation are shown in ESI S2.† (E and F) experimental time-based fluorescence response of 100 pM 3DDN to 1 nM WT or SNV target. The discrimination factor (DF) was determined using the equation that: DF = (F_WT − F_blank)/(F_SNV − F_blank). All the reactions were performed at 37 °C in 1× NEB CutSmart Buffer containing 20 U Nb.BbvCI. Each data point is an average of triplicated analyses.

The in silico sequence optimization was further verified experimentally by detecting 1 nM WT and SNV19A using the 3DDN (Fig. 1E and F). The discrimination factor (DF) that quantifies the single-base specificity as the ratio of the hybridization yields (net fluorescence) generated by equal concentrations of the intended and SNV targets, was improved by 5.4 times after the sequence optimization (r = 10 nt vs. r = 5 nt). However, this improvement is at the cost of a signal reduction by nearly 1.5 times.

Simulation-guided in-solution tuning of 3DDN via noncovalent catalysis

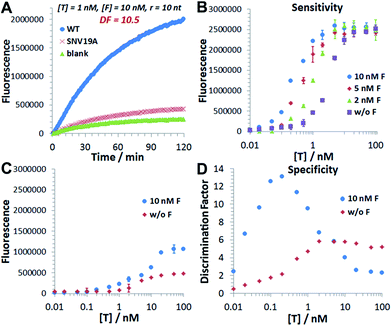
We then introduce F as an auxiliary probe for tuning the sensitivity and selectivity of 3DDN in solution (Scheme 1C). The addition of F to the system offers an alternative activation pathway through a strand exchange reaction: DP + F ↔ FP + D. This reaction is kinetically inert but can be accelerated by T. As a catalyst, each T activates multiple DNA walkers and thus can enhance the assay sensitivity. Meanwhile, each elementary reaction involving in the DNA catalysis is a toehold exchange with ΔG⁰_rxn to be near zero, and the overall reaction thus remains sensitive to SNVs, ensuring high assay specificity (Fig. 2A and B). To quantitatively evaluate the possibility of using F to enhance the discrimination of SNVs, we simulated the catalytic activation of the 3DDN using a two-step reaction model (details in the ESI S3†). Our simulation results reveal remarkable differences between WT and SNV19A in terms of the level of the intermediate TP (Fig. 2C) and the device AE (Fig. 2D). In particular, our model suggests that SNV19A and other 8 representative SNVs were much less sensitive to the noncovalent catalysis comparing to WT, evidenced by the low level or absence of the reaction intermediate TP (Fig. 2C and S3†) and the lack of correlation between T and F in terms of activating the 3DDN (Fig. 2D and S4†). Therefore, F holds the potential to selectively activate the 3DDN for WT over SNVs and thus can potentially enhance the assay sensitivity without significantly compromising the sequence selectivity. The effectiveness of the F-mediated non-covalent DNA catalysis was further confirmed using polyacrylamide gel electrophoresis (Fig. S5†). Moreover, our simulation also quantitatively predicts that the catalytic enhancement of 3DDN using F is most effective when [F]₀/[DP]₀ ranges from 0 to 5 and [T]₀/[DP]₀ ranges from 0 to 10 (Fig. 2D).

Fig. 2 In-solution tuning of the 3D DNA nanomachine via noncovalent DNA catalysis. (A and B) Catalytic enhancement of the toehold-exchange between T and DP using a molecular fuel (F) through noncovalent catalysis. (C) Simulation of the level of the intermediate TP for WT and SNV19A as a function of [F]₀ and [T]₀. (D) Simulation of device activation efficiency for WT and SNV19A as a function of [F]₀ and [T]₀.

We then experimentally examine the effect of F on the 3DDN. The results in Fig. 3A show that 10 nM F achieves a 2-fold enhancement for both assay sensitivity and specificity when discriminating 1 nM WT from 1 nM SNV19A. We further challenged our strategy by detecting WT and SNV19A with concentrations ranging from 10 pM to 100 nM. The addition of F with concentrations varying from 0 nM to 10 nM quantitatively shifts the overall detection range of 3DDN towards lower target concentrations by as much as 1 order of magnitude (Fig. 3B). Further increases in [F] did not significantly shift the dynamic range (Fig. S6†). This observation is highly consistent with the theoretical prediction using our two-step reaction model (Fig. 2D). SNV19A was also found to be insensitive to F at the concentration range below 5 nM (Fig. 3C). Collectively, the non-covalent catalysis enhances both assay sensitivity (Fig. 3B) and specificity (Fig. 3D) of the 3DDN at a target concentration range below 5 nM. As the fluorescence signal was fully saturated when target concentration is above 5 nM (Fig. 3B), the device becomes less specific at this higher concentration range (Fig. 3D).

Fig. 3 Catalytic enhancement of the 3D DNA nanomachine in terms of both assay sensitivity and assay specificity. (A) Experimental time-based fluorescence response of 100 pM device to 1 nM WT or SNV19A in the presence of 10 nM F. (B) Background-corrected fluorescence as a function of target concentrations in the presence of varying concentrations of F from 0 nM to 10 nM. (C) Background-corrected fluorescence as a function of target concentrations in the presence (w F) or absence (w/o F) of 10 nM F. (D) Discrimination factor against SNV19A as a function of target concentrations in the presence (w F) or absence (w/o F) of 10 nM F. All the reactions were performed at 37 °C in 1× NEB CutSmart Buffer containing 20 U Nb.BbvCI for 1 h. Each error bar represents one standard deviation from triplicated analyses.

Predictable discrimination of SNVs using catalytic 3DDN

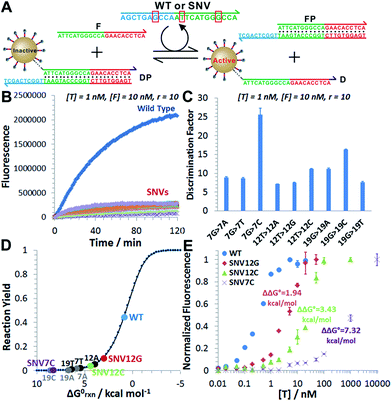
We next challenged our catalytic 3DDN with nine SNVs of varying base identities and positions (Fig. 4A). Our system discriminates all SNVs at 1 nM with DF ranging from 7 to 26, with a median of 12 (Fig. 4B and C). The obtained specificity is comparable with commonly used molecular probes, such as molecular beacons,¹⁴ triple-stem DNA probes,¹⁵ and toehold-strand displacement beacons.^13,16 However, because of the intrinsic signal amplification capability, our 3DDN improves the detection limit by ∼100 times.

Fig. 4 (A) Sequence of the wild type target (WT) and positions/identities of base changes that lead to the 9 SNV targets. The red circles denote the positions of the mismatch. (B) Time-based fluorescence responses of 100 pM device to 1 nM WT or SNVs in the presence of 10 nM F. (C) Discrimination factors determined for 9 SNVs at 1 nM concentrations. (D) The distribution of the WT and the 9 SNVs on the standard Gibbs free energy landscape. (E) Dose-response curves of WT and three representative SNVs obtained by plotting the normalized fluorescence as a function of target concentrations. The fluorescence for each sample was normalized against the background fluorescence for the blank (set to 0) and maximum fluorescence when all DNA walkers are released (set to 1). Each error bar represents one standard deviation from triplicate analyses.

It is also possible to predict the reactivity of our 3DDN system towards varying SNVs based on their thermodynamic parameters. As the overall specificity is generally determined by the toehold-exchange between T and DP, an intuitive way to predict the sequence selectivity can be on the basis of the thermodynamic change (ΔΔG⁰_rxn) associated with a given single-nucleotide mismatch (Fig. 4D). The measured fluorescence responses of our device against three representative SNVs (SNV12G, 12C, and 7C) across a concentration range from 10 pM to 10 μM were consistent with their trends in ΔΔG⁰_rxn (Fig. 4E). The predictive reactivity of F-enhanced 3DDN was further confirmed using SNVs at different locations and base identities (Fig. S7†). Here, the tuning of 3DDN enabled by non-covalent DNA catalysis offers an alternative on-the-fly approach to fine-tune the assay performance. This approach is critical in our system, as the ratio between D and P has been locked at 1 : 1 and it is hence not possible to fine-tune the sequence selectivity using the stoichiometry strategy previously described by Wu, et. al.¹²

Towards the practical uses of our strategy in biological or clinical samples, we finally challenged the catalytic 3DDN system for discriminating SNVs in complicated sample matrix. To do so, we spiked 1 nM of target DNA (WT or SNV19A) into two types of sample matrixes commonly seen in nucleic acid testing, including high concentrations of background DNA (0.1 mg mL⁻¹ salmon sperm genome fragments) and 10-time diluted human serum samples. As shown in Fig. S8,† the 3DDN remains fully active in both sample matrixes and its ability to discriminate SNVs was not affected either. The noticeable high background fluorescence observed in Fig. S8B† was a result of the autofluorescence of the human serum sample. Another concern for the practical uses of the 3DDN is the long-term colloidal and chemical stability of the DNA-AuNP motif during storage. We further monitored the activity and specificity of the 3DDN over a period of 1 month. As shown in Fig. S9,† no apparent losses in activity were observed for 3DDN during the 1 month storage at 4 °C. Similarly, no significant changes in specificity of the catalytic 3DDN system were observed either. Collectively, these observations suggest that our 3DDN is a chemically robust system for discriminating SNVs against varying sample matrix and long-time storage.

Conclusions

Herein, we have engineered a nicking endonuclease-powered 3D DNA nanomachine for discriminating SNVs with simulation-guided optimization at both sequence-level and operational level. We have also introduced a new in-solution tuning strategy that tunes both assay sensitivity and specificity using a single molecular fuel through noncovalent catalysis. Despite its critical roles in DNA logic circuits (e.g., seesaw gates)¹⁷ and for characterizing the thermodynamics of nucleic acid motifs,¹⁸ noncovalent DNA catalysis finds very few applications in regulating DNA devices or sensors. Our work opens the possibility to use this reaction as an on-the-fly approach for tuning the analytical performance of DNA devices or sensors. Collectively, we have developed a detection system that offers the specificity for SNVs comparable to commonly used molecular probes, but a much higher sensitivity. It is also possible to predict the reactivity of our detection system towards different SNVs in silico on the basis of their thermodynamic parameters. As thermodynamic parameters of any hybridization reaction can be easily obtained using DNA analysing software, such as NuPack, our simulation strategy can be generalized to any nucleic acid target or sequence of interest. As such, our simulation-guide tuning strategy will be a useful addition to the existing simulation tools, such as the coarse-grained simulation recently introduced by Nir and coworkers,¹⁹ for the design and operation of DNA motors and walking devices with better performance and functionality towards biosensing applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Natural Sciences and Engineering Research Council of Canada, the Brock University Advancement Fund, and the Brock University Start-Up Fund for financial support.

Notes and references

1. J. M. Abendorth, O. S. Bushuyev, P. S. Weiss and C. J. Barrett, ACS Nano, 2015, 9, 7746–7768; J. Bath and A. J. Turberfield, Nat. Nanotechnol., 2007, 2, 275–284.
2. W. B. Sherman and N. C. Seeman, Nano Lett., 2004, 4, 1203–1207; P. Yin, H. Yan, X. G. Daniell, A. J. Turberfield and J. H. Reif, Angew. Chem., Int. Ed., 2004, 43, 4906–4911; M. You, Y. Chen, X. Zhang, H. Liu, R. Wang, K. Wang, K. R. Williams and W. Tan, Angew. Chem., Int. Ed., 2012, 51, 2457–2460.
3. K. Lund, A. J. Manzo, N. Dabby, N. Michelotti, A. Johnson-Buck, J. Nangreave, S. Taylor, R. Pei, M. N. Stojanovic, N. G. Walter, E. Wingree and H. Yan, Nature, 2010, 465, 206–209; S. F. J. Wickham, J. Bath, Y. Katsuda, M. Endo, K. Hidaka, H. Sugiyama and A. J. Turberfield, Nat. Nanotechnol., 2012, 7, 169–173; A. J. Thubagere, W. Li, R. F. Johnson, Z. Chen, S. Doroudi, Y. L. Lee, G. Izatt, S. Wittman, N. Srinivas, D. Woods, E. Wingree and L. Qian, Science, 2017, 357, eaan6558; T. E. Tomov, R. Tsukanov, M. Liber, R. Masoud, N. Plavner and E. Nir, J. Am. Chem. Soc., 2013, 135, 11935–11941; T. E. Tomov, R. Tsukanov, Y. Glick, Y. Berger, M. Liber, D. Avrahami, D. Gerber and E. Nir, ACS Nano, 2017, 11, 4002–4008; D. Wang, C. Vietz, T. Schroder, G. Acuna, B. Lalkens and P. Tinnefeld, Nano Lett., 2017, 17, 5368–5374.
4. C. Zhou, X. Duan and N. Liu, Nat. Commun., 2015, 6, 8102.
5. C. Jung, P. B. Allen and A. D. Ellington, Nat. Nanotechnol., 2016, 11, 157–163; C. Jung, P. B. Allen and A. D. Ellington, ACS Nano, 2017, 11, 8047–8054.
6. X. Yang, Y. Tang, S. D. Mason, J. Chen and F. Li, ACS Nano, 2016, 10, 2324–2330.
7. J. Chen, A. Zuehlke, B. Deng, H. Peng, X. Hou and H. Zhang, Anal. Chem., 2017, 89, 12888–12895; H. Peng, X. F. Li, H. Zhang and X. C. Le, Nat. Commun., 2017, 8, 14378; K. Wang, M.-Q. He, F.-H. Zhai, J. Wang, R.-H. He and Y.-L. Yu, Biosens. Bioelectron., 2018, 105, 159–165.
8. H. Zhang, M. Lai, A. Zuehlke, H. Peng, X. F. Li and X. C. Le, Angew. Chem., Int. Ed., 2015, 54, 14326–14330; X. Qu, D. Zhu, G. Yao, S. Su, J. Chao, H. Liu, X. Zuo, L. Wang, J. Shi, L. Wang, W. Huang, H. Pei and C. Fan, Angew. Chem., Int. Ed., 2017, 56, 1855–1858; M.-Q. He, K. Wang, W.-J. Wang, Y.-L. Yu and J.-H. Wang, Anal. Chem., 2017, 89, 9292–9298.
9. C. P. Liang, P. Q. Ma, H. Liu, X. Guo, B. C. Yin and B. C. Ye, Angew. Chem., Int. Ed., 2017, 56, 9077–9081.
10. S. Kim and A. Misra, Annu. Rev. Biomed. Eng., 2007, 9, 289–320.
11. D. Y. Zhang, S. X. Chen and P. Yin, Nat. Chem., 2012, 4, 208–214; S. Ohta, D. Glancy and C. W. Chan, Science, 2016, 351, 841–845.
12. L. R. Wu, J. S. Wang, J. Z. Fang, E. R. Evans, A. Pinto, I. Pekker, R. Boykin, C. Ngouenet, P. J. Webster, J. Beechem and D. Y. Zhang, Nat. Methods, 2015, 12, 1191–1196.
13. J. S. Wang and D. Y. Zhang, Nat. Chem., 2015, 7, 545–553.
14. S. Tyagi, D. P. Bratu and F. R. Kramer, Nat. Biotechnol., 1998, 1, 49–53.
15. Y. Xiao, K. J. I. Plakos, X. Lou, R. J. White, J. Qian, K. W. Plaxco and H. T. Soh, Angew. Chem., Int. Ed., 2009, 48, 4354–4358.
16. Q. Li, G. Luan, Q. Guo and J. Liang, Nucleic Acids Res., 2002, 30, e5; S. X. Chen and G. Seelig, J. Am. Chem. Soc., 2016, 138, 5076–5086.
17. L. Qian and E. Winfree, Science, 2011, 332, 1196–1201; L. Qian, E. Winfree and J. Bruck, Nature, 2011, 475, 368–372.
18. C. Wang, J. H. Bae and D. Y. Zhang, Nat. Commun., 2016, 7, 10319.
19. D. C. Khara, J. S. Schreck, T. T. Tomov, Y. Berger, T. E. Ouldrdge, J. P. K. Doye and E. Nir, Nucleic Acids Res., 2018, 46, 1553–1561.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc02761g

‡ Y. Li and A. G. Wang contributed equally to this work.

---