Possible relations between supercooled and glassy confined water and amorphous bulk ice

Abstract

In this paper we discuss apparent contradictions in the literature between dynamical results on supercooled confined water obtained by different experimental methods. The reason for the lack of a clear glass transition of confined water is also discussed. Dielectric relaxation data and results from differential scanning calorimetry measurements provide a consistent picture, but it is still unclear why the glass transition related structural (α) relaxation disappears before the normal time-scale of a calorimetric glass transition (i.e. about 100 s) is reached. From recent results on amorphous bulk ice we propose that this anomalous phenomenon may not be an effect of confinement, but an intrinsic property of water when it transforms to a crystal-like glassy state, probably around 225 K. Thus, the results from the studies of confined water in the so-called no man's land (the temperature range 150–235 K) where bulk water rapidly crystallizes may be of more relevance for supercooled and glassy bulk water than previously thought. Furthermore, the structural difference between glassy water (or amorphous ice) and crystalline ice is likely to be rather small, due to the large degree of disorder in crystalline ice.

---

Jan Swenson

Jan Swenson earned his PhD in Physics at Chalmers University of Technology, Sweden, in 1996. He was thereafter a postdoctoral fellow at University College London, UK, before he returned to Chalmers for an assistant professorship and employment with the Royal Swedish Academy of Sciences. In 2005 he got a full professorship at NTNU, Norway, and since 2006 he has been professor in physics at Chalmers. His current research interests concern supercooled and confined water, the role of water in biological materials, and how biological materials can be stabilized and cryopreserved by a cryoprotective substance, such as trehalose.

---

1. Introduction

We all know that we need water for our survival.¹ In our bodies, as well as in most animals, plants and types of nature, the main fraction of the water is confined in restricted areas between other materials or molecules. There is no clear definition of what is required for water to be considered as confined, but commonly the term confined is used when the structural and dynamical properties of the water can be distinguished from bulk water. Typically, this requires that the size of a water cavity be of the order of 10 nm or less (although the flow of water is affected by substantially less severe confinement). In our bodies this requirement is more than well met, since most of this water is never more than about 5 Å from other different types of biomolecules, such as nucleic acids, proteins and lipids.² This highly confined water is essential for the structure and function of these “molecules of life”, and therefore controls many of the biological processes occurring in our bodies.^3–5 In other types of systems, e.g. of relevance for geology and modern technology, the water may be confined in hard materials, such as rocks, metals and glasses. The water in all these types of confinement behaves differently depending on the nature and geometry of the water-filled cavities. The size and dimensionality of the cavity as well as the structure, hydrophobicity and roughness of its inner surface all affect the structure and dynamics of the confined water.^6–16 However, in the deeply supercooled regime, experimental results have shown that the dynamics of confined water is rather universal, irrespective of whether the water is located in a solid porous material, hydrating a biomolecule or in a solution below or close to the glass transition temperature, T_g, of the entire system.¹⁷

In this paper we will mainly discuss results obtained from differential scanning calorimetry (DSC), dielectric spectroscopy, quasielastic neutron scattering (QENS) and relaxation nuclear magnetic resonance (NMR) measurements. However, before we discuss the physical nature of experimentally observed results it is valuable to make some common definitions and distinctions. With dielectric spectroscopy it is possible to measure dipole relaxations. However, such a process can have different natures, depending on whether it is directly related to the viscosity of the liquid or is of more local character. The former relaxation process is called the structural α-relaxation and the latter is a so-called secondary β-relaxation. A homogeneous liquid only exhibits one α-relaxation, but may show several β-relaxations. In a dielectric experiment on a bulk liquid the α-relaxation is given by an asymmetric peak in the imaginary part of the permittivity, in contrast to β-relaxations, which have a symmetric peak shape.¹⁸ Furthermore, the dielectric strength of the α-relaxation increases with decreasing temperature, while the β-relaxation exhibits the opposite behavior.¹⁸ Moreover, since the α-relaxation is cooperative in character, it exhibits a super-Arrhenius temperature dependent relaxation time, in contrast to the thermally activated β-relaxations with Arrhenius temperature dependent relaxation times. Due to all these different characteristics it is often easy to distinguish between α- and β-relaxations, but in confinement these general “rules” may be altered. At higher temperatures, around room temperature, rotational and diffusional motions, as well as the viscosity related structural α-relaxation and the more local β-relaxations, are generally coupled and occur on the same time scale. Therefore, even if different experimental techniques probe different types of motions, the time-scale of the measured water dynamics is basically the same irrespective of the method used. However, at lower temperatures all these kinds of motions tend to decouple in all types of deeply supercooled liquids, which implies that rotational motions decouple from translational motions and local β-relaxations decouple from the cooperative α-relaxation.¹⁸ The glass transition temperature, T_g, is usually defined as the temperature at which the relaxation time of the α-relaxation is about 100 s.¹⁸ This relaxation time corresponds to a macroscopic viscosity of about 10¹² N s m⁻² and the material appears solid-like. Hence, below T_g the α-relaxation can be regarded as frozen, but β-relaxations and local rotational motions as well as long-range translational motions can still exist far below T_g. This fact can actually make it difficult to determine whether a liquid is below or above its glassy state. Normally, T_g is most easily determined by differential scanning calorimetry (DSC), but in this case confined water behaves oddly and no clear calorimetric T_g can be observed.^19,20 This is puzzling, as will be discussed, but it also makes it less obvious how dynamical data obtained by e.g. QENS, dielectric relaxation spectroscopy and relaxation NMR should be interpreted. The advantage with QENS from this perspective is that it is possible to distinguish between localized, rotational and long-range translational motions by measuring how the relaxation time depends on the momentum transfer (Q) of the scattering event.^21,22 In the case of hydrogen-rich materials, such as H₂O, the total scattering is strongly dominated by the large incoherent scattering of hydrogen, and it measures the self-motions of these atoms.^21,22 Finally, there are different types of NMR measurements, where particularly ²H stimulated echo (STE) experiments are useful to provide information about the overall amplitude and jump angles of a reorientational motion, which can be used to distinguish between α- and β-relaxations.²³ Nevertheless, it is clear from the literature that it is far from trivial to distinguish between different types of motions and to understand their physical nature.

Although most studies of confined water have been driven by the many applied problems in life science, medicine, pharmacology, geology and technology, there has also been a growing interest in studying confined water due to the possibility to enter into the so called no man's land from 150 K to 235 K, where bulk water is difficult to study due to almost instantaneous crystallization.²⁴ However, with recent advances of fast measurements it has been possible to enter into this no man's land and study the structure of water down to 227 K,^25,26 as well as the diffusivity of water up to 159 K.²⁷ In fact, measurements of the structural and dynamical properties of water in the no man's land temperature range are very important for the possibility to explain the many anomalous properties of water. For instance, a liquid–liquid phase transition with a liquid–liquid critical point at some pressure has been proposed to explain the peculiarities of water.^25,28–30 It has also been proposed that the transition from a high temperature high density liquid (HDL) to a low temperature low density liquid (LDL) is associated with a so-called fragile-to-strong transition at about 225 K.³¹ A supercooled liquid is classified as fragile when the temperature dependence of its viscosity or related α-relaxation time (τ_α) exhibits a highly non-Arrhenius temperature dependence.³² This behaviour is typical for ionic and van-der-Waals systems, but also for bulk water, which above 235 K is known as one of the most fragile liquids that ever have been studied.^31,33 In contrast, a strong supercooled liquid shows a temperature dependence close to the Arrhenius law, and this is typically observed for materials with network structures of strong covalent bonds, such as SiO₂.³² Hence, it is proposed that the HDL is a very fragile liquid due to the absence of a complete network structure, whereas the LDL is supposed to be a strong liquid because of its expected tetrahedral network structure.³¹ Therefore, it is of great interest to perform measurements on water in no man's land and although bulk water can partly be studied in this temperature range it is evident that its rapid crystallization puts serious limitations on such studies. Instead, many attempts have been made to use confined water to understand the properties of bulk water in this difficult temperature range. However, the question is whether the studies of confined water are of relevance for bulk water, so we can actually learn something about the structure and dynamics of deeply supercooled bulk water by avoiding crystallization of water in severe confinement. For cylindrical pores, calorimetric studies have indicated that crystallization can be avoided for pore diameters of 21 Å or less (at least in the case of hydrophilic silica pores, such as MCM-41).^{19,20,34–37} However, recently this interpretation of the results has been questioned since an ice-like formation of the central water molecules may occur even in pores with a size of about 20 Å.^38,39 The possible similarity of this water structure to rapidly quenched bulk water will be discussed. We will also discuss recent interpretations⁴⁰ of the structure and dynamics of bulk water above the most accepted glass transition temperature of 136 K (for hyperquenched water and low-density amorphous ice),⁴¹ which suggest that bulk water in the main temperature range of no man's land behaves very similarly to confined water below a temperature of about 180 K.^{36,38,39,42–44} Thus, an interesting question arises of whether the properties of deeply supercooled and glassy confined water are of more relevance for bulk water than previously thought.

2. The possibility of a fragile-to-strong transition of confined water

It has been known for a long time³³ that bulk water behaves as a so-called fragile liquid down to about 235 K, where rapid crystallization occurs. As mentioned above, a fragile liquid exhibits a highly non-Arrhenius temperature dependence, and for bulk water this becomes particularly evident close to 235 K, where the dynamical properties become rapidly slower with decreasing temperature. In fact, the temperature dependence of the dynamical properties, such as viscosity, of bulk water is best described by a power law that diverges at 228 K.⁴⁵ This singularity is consistent with the second critical point scenario, and if the viscosity of bulk water extrapolates to infinity at 228 K it further implies that the glass transition temperature, T_g, of bulk water must be slightly higher than 228 K. However, T_g of bulk water is commonly accepted to be located at 136 K,⁴¹ and the only possibility to resolve this inconsistency is to introduce a fragile-to-strong transition of water close to 228 K, i.e. before the viscosity at the glass transition (10¹² N s m⁻²) is reached, as first proposed by Ito et al.³¹ The temperature dependence of the viscosity or related structural α-relaxation time would then exhibit a crossover similar to the crossover from the red to the blue curve shown in Fig. 1. Since the rapid crystallization of bulk water in the temperature range around 228 K makes a verification of this possible crossover very difficult in the case of bulk water it is natural that confined water, where crystallization can be avoided at all temperatures, has been used to elucidate whether a fragile-to strong transition seems to occur.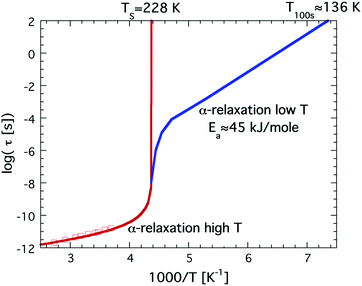

Fig. 1 Schematic illustration of a possible fragile-to-strong transition scenario of bulk water, given by the red to blue crossover. This illustration is consistent with the high temperature power law behavior diverging at 228 K and a T_g at 136 K. Dielectric relaxation data at high temperatures are shown as red open squares.⁴⁶

The first study in favor of a fragile-to-strong transition of, at least, confined water was published in the year 2000,⁴⁷ where Bergman and Swenson studied water confined in a Na-vermiculite clay and observed an Arrhenius temperature dependence (as typical for the structural α-relaxation of very strong glass forming liquids) of the observed main relaxation in the temperature range from 215 K down to 130 K, where a relaxation time of approximately 100 s was obtained,⁴⁷ as shown in Fig. 2. Thus, although the actual crossover from fragile to strong could not be observed, a quasi-elastic neutron scattering (QENS) study showed⁴⁸ that the water in this clay exhibited a fragile behavior at higher temperatures above 254 K, suggesting that a fragile-to-strong transition occurred somewhere between 215 K and 254 K.

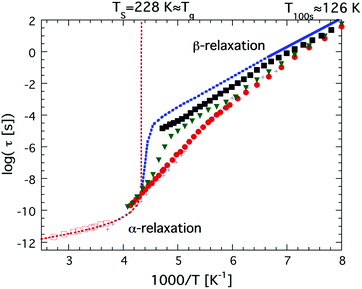Fig. 2 Temperature dependences of water relaxation times, τ, obtained by dielectric spectroscopy and ²H NMR. Dielectric relaxation data are shown for bulk water (red open squares),⁴⁶ low density amorphous (LDA) ice (or LDL) (solid blue line in the temperature range 126–151 K),⁶⁸ water confined in MCM-41 C10 (red solid circles),³⁶ water confined in the molecular sieve X13 (green solid triangles),⁶⁰ and water confined in a fully hydrated Na-vermiculite clay (black solid squares).⁴⁷²H NMR relaxation data are shown for water in MCM-41 C10 (black crosses).^38,39 The high temperature power law dependence of supercooled bulk water is indicated by the red dotted line, reaching a singularity at T_s = 228 K. The low temperature Arrhenius dependence of bulk water in the temperature range 126–151 K⁶⁸ has been extrapolated to higher temperatures and the crossover to the high temperature power law dependence has been sketched (blue dotted line).

The first direct observation of a claimed fragile-to-strong transition of confined water was obtained by Faraone et al.⁴⁹ from a QENS study of supercooled water confined in MCM-41. They observed a very pronounced dynamic crossover at about 225 K, and since it occurred at basically exactly the same temperature as the predicted fragile-to-strong transition of bulk water³¹ it was natural to believe that the observed crossover is of relevance also for bulk water, although the Arrhenius temperature dependent relaxation time below the crossover temperature extrapolates to 100 s below 100 K^43,50 and therefore indicates a T_g below 100 K, as shown in Fig. 3. It should here be noted that the same MCM-41 (C12) as Faraone et al.⁴⁹ used was also used by Soper^7,8 in a neutron diffraction and EPSR modeling study. However, while Faraone et al.⁴⁹ measured the pore diameter of this MCM-41 as 14 Å by nitrogen adsorption–desorption experiments, Soper⁸ obtained a pore diameter of 24 Å from neutron diffraction. Therefore, Soper suggested⁷ that the observed fragile-to-strong transition could be due to partial crystallization of the water, as also suggested in ref. 38 to occur for this MCM-41 sample. Anyhow, irrespective of the physical origin of this first observation of the dynamic crossover it did not take many years until similar crossovers were observed in a wide range of water containing systems, such as hydrated proteins,⁵¹ DNA⁵² and RNA,⁵³ as well as different types of solutions^54,55 and other types of solid materials.^56,57 All these studies were based on QENS measurements, but also diffusion NMR measurements⁵⁸ suggested the same scenario. In e.g.ref. 17 this fragile-to-strong crossover scenario is discussed in more detail including how it is considered related to the crossing of the Widom line, i.e. the pressure at a given temperature where there are maximum correlation lengths of the HDL and LDL.

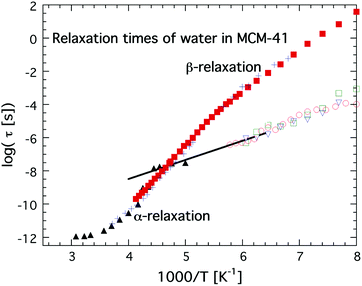Fig. 3 Temperature dependences of relaxation times, τ, of water in MCM-41 obtained from QENS (C12, black solid triangles),⁴⁹ dielectric spectroscopy (C10, red solid squares)³⁶ and ²H NMR (C10, blue crosses).^38,39 These relaxation times of water in MCM-41 are compared with a faster and more local dielectric relaxation process of water confined in a fully hydrated Na-vermiculite clay (red open circles),⁴⁷ myoglobin⁴³ (green open squares) and phospholipid membrane DMPC⁶⁴ (open blue triangles). The approximate low temperature Arrhenius dependence of the low QENS data has been indicated by a black line. Note the excellent agreement over the whole measured temperature ranges between the dielectric and ²H NMR data on water confined in MCM-41 C10, and also the excellent agreement between the extrapolated QENS data below 225 K and the fast local dielectric relaxation of water in clay, myoglobin and DMPC.

Simultaneously, dielectric relaxation spectroscopy was used to study the dynamics of supercooled water confined in the same or similar systems^{20,42,43,47,59–63} (see also ref. 17 for a large number of other references). These studies showed often also a dynamic crossover of the main relaxation process, see e.g.ref. 17. However, this crossover was found to be much weaker and occurred generally at 180 ± 10 K, but this does not imply that the QENS and dielectric results are fully inconsistent since a weaker and faster dielectric process was generally observed at lower temperatures and this process shows the same temperature dependence as the relaxation process observed by QENS below the crossover temperature at 225 K.⁴³ This is shown in Fig. 3, where an extrapolation of the QENS data below 225 K coincides with dielectric data of water in a clay⁴⁷ (note here that this is a faster and more local process than the main relaxation shown in Fig. 2), a phospholipid membrane⁶⁴ and myoglobin.⁴³ It is also shown in dielectric data of water in MCM-41, but it is very weak there and therefore it is difficult to determine its temperature dependence with high accuracy. Since this dielectric relaxation process is faster than the main process, from which it seems to decouple at about 225 K, it is clear that it cannot be associated with the structural α-relaxation.⁴³ In fact, Bergman and Swenson et al. realized^42,43,60,64 that their original interpretation of the dielectric main relaxation of supercooled confined water below the crossover temperature is not correct, and that also this relaxation should be assigned as a more local β-relaxation. Since it has been shown to be pressure dependent,^61,62 it indicates that this relaxation is of Johari-Goldstein type.⁶⁵ This type of relaxation is of a local and non-cooperative character, but it involves all atoms in the water molecule and it is also coupled to translational motions. Also this crossover scenario around 180 K from a believed α-like high temperature relaxation to a low temperature β-relaxation is further discussed in ref. 17, but the important point to note is that the dielectric and QENS results are fully consistent provided that the relaxation process exhibiting an Arrhenius temperature dependence below 225 K is assigned as a β-relaxation, rather than the structural α-relaxation. Further support for this alternative assignment of the relaxation process comes from Doster et al.,⁶⁶ where they studied the dynamics of protein hydration water with QENS and came to the conclusion that a dynamic crossover is either observed or not observed at 225 K, depending on how the data are analyzed. They favored an analysis where no dynamic crossover was obtained. Anyhow, the important conclusion of this study⁶⁶ is that also slower water dynamics exists below 225 K, consistent with the dielectric data. Also ²H NMR relaxation studies of both water in MCM-41 C10^38,39 (also shown in Fig. 3) and protein hydration water⁴⁴ gave the same temperature dependence of the water dynamics as the dielectric data, and thus contrasted with the temperature dependence of the diffusion NMR data⁵⁸ mentioned above. Finally, it was observed in a neutron-spin echo study of an aqueous LiCl solution that a dynamic crossover at 225 K was only obtained at high momentum transfer (Q) values, whereas at Q = 0.1 Å⁻¹ the high temperature non-Arrhenius temperature dependence continued far below 225 K,⁶⁷ in agreement with dielectric and ²H NMR relaxation data. Hence, this neutron scattering study by Mamontov et al.⁶⁷ is consistent with both ordinary QENS data as well as dielectric and ²H NMR relaxation data, and, more importantly, the authors provide a simple explanation for why the two techniques seem to give different results, by making the following statement: “The main relaxation component continues to follow a non-Arrhenius power law below T_c, as evidenced by the data collected at low Q that show no dynamic crossover. At higher Q, the crossover marks the temperature below which a localized component with apparently Arrhenius temperature dependence splits from the main component. It is this localized component that is likely observed in QENS measurements, whereas the relaxation times of the main component become too long for the experimental resolution.” This statement confirms that there is no disagreement or conflict between QENS, dielectric and NMR data provided that the crossover observed at about 225 K for most QENS data on confined water is interpreted to arise from a crossover from an α-like high temperature relaxation to a local low temperature relaxation. Since a true fragile-to-strong transition refers to the temperature dependence of the viscosity related α-relaxation it is clear that the crossover to a local relaxation process should not be denoted as a fragile-to-strong transition.

Also MD simulation studies have claimed that a fragile-to-strong transition occurs for both confined and bulk water around 225 K, and that it seems to be a general characteristics of supercooled water irrespective of the used interaction potential.⁶⁹ In the case of water, this fragile-to-strong crossover has been directly related to a liquid–liquid transition.⁶⁹ However, this crossover in the MD simulations is very weak, and becomes almost insignificant if the temperature dependence of the relaxation time is not described by a power law above the crossover temperature, but instead by the Vogel–Fulcher–Tammann (VFT) equation, as commonly used to describe the temperature dependent dynamics of supercooled liquids.⁷⁰ In fact, a similar weak fragile-to-strong transition is commonly found in different types of supercooled liquids,^71,72 where no liquid–liquid transition occurs. Hence, according to the MD simulations, supercooled water, in bulk or confined, exhibits a surprisingly normal dynamic behavior of supercooled liquids. This further implies that the crossover in the MD simulations at about 225 K is substantially different from the crossover observed by QENS. As for other types of supercooled liquids it seems to be related to a crossover from a normal liquid diffusion behavior at high temperatures to a more hopping-like diffusion process below the crossover temperature.⁷³

As mentioned above, both dielectric relaxation data and ²H NMR relaxation data have shown that there is a dynamic crossover at about 180 K, as shown in Fig. 2. However, the ²H NMR relaxation data on water confined in MCM-41 of different pore sizes have shown that there is also a weak crossover at about 225 K.^38,39 This crossover from a highly fragile behavior to a more strong behavior was most pronounced for larger pore sizes where it has been established that partial crystallization of the pore water occurs at about the same temperature,^35,37 but a weak crossover was also observed for a pore diameter of 21 Å, where no evident crystallization is seen in DSC measurements.^34–37 Due to the similarity with the behavior of the larger pores this crossover was interpreted to be a result of crystallization or some kind of solidification of the inner pore water, leaving only the surface water in a supercooled state.^38,39 Since more severely confined water exhibits a less fragile behavior, such a crystallization or solidification is expected to give rise to a more strong behavior of the remaining unfrozen water. Hence, these ²H NMR relaxation data on water confined in MCM-41 show that neither the crossover at about 180 K nor the crossover at 225 K can be interpreted as a fragile-to-strong crossover.^38,39 However, the physical origin of the crossover at about 180 K is not obvious, and has therefore been widely debated, as further discussed in the next chapter. Also chapter 4 is related to this crossover, since we are there discussing the nature of the relaxation process below the crossover temperature and suggest that this process is similar to what has been observed for amorphous bulk ices.⁴⁰

3. No glass transition of confined water?

Many previous studies of confined water^{19,20,34–37,74} have shown that no glass transition is clearly observable in an ordinary DSC measurement. Only by more sensitive adiabatic calorimetry it has been claimed that also confined water exhibits a glass transition.⁷⁵ Oguni et al.⁷⁵ found two T_g-values; one at about 115 K for the single molecular layer of surface water and one for the remaining water, which increased from about 165 K for small pores with a diameter up to 17 Å to 210 K for 21 Å diameter pores. However, the interpretations of their data have been questioned by Johari et al.^76,77 who claim that the calorimetric feature assigned to T_g of the central water is rather due to a gradual conversion to distorted ice-like structures. In this paper we argue that the difference between these two viewpoints may be very small. The “transition” can probably be considered as a crystallization process in the sense that it involves some structural changes, which do not normally occur at a glass transition. On the other hand, the structure of the supercooled water is likely to be rather ice-like, simultaneously with the “crystalline” structure below the transition temperature being highly disordered, making the structural difference rather small and a distinction between a glass transition and a crystallization process difficult. Here it should furthermore be noted that authors are claiming very different pore diameters for MCM-41 produced in similar, although not identical, ways. For instance, MCM-41 produced with C₁₂ chains as a template has a diameter of 23.8 Å according to Kittaka et al.^35,37 who are producing the material themselves. This value is consistent with the value Soper obtained from neutron scattering,³⁶ but considerably larger than the value 14 Å given in e.g.ref. 49, 58 and 77 for the same type of MCM-41-S sample. Thus, these differences in claimed pore diameters can at least partly explain why a more clear crystallization process occurs for pore sizes less than 20 Å in some studies, but not in other studies.

Further support for a vanishing of the glass transition related dynamics, i.e. the structural α-relaxation, before the typical time scale (about 100 s) of the glass transition is reached comes from dielectric relaxation data^{17,20,36,42,60} (see also Fig. 2), where no continuation of the high temperature α-relaxation can be observed below the crossover temperature. This lack of a clear calorimetric glass transition and the apparent vanishing of its related dynamics at the crossover temperature is puzzling and an anomalous observation for confined water, since no such behavior has been observed for any other confined liquids where the structural α-relaxation can be observed at high temperatures. One explanation that has been proposed for the dynamic crossover and the anomalous behavior of confined water is that the molecular rearrangements responsible for the glass transition and its associated α-relaxation in deeply supercooled bulk water require a large network of hydrogen bonded water molecules,⁷⁸ which simply cannot be formed in pore sizes of about 20 Å or less. In support of this explanation is that a hydrogen bonded tetrahedral network structure may be completed in bulk water already at about the homogenous nucleation temperature around 235 K.³¹ Hence, it is possible that the α-relaxation below this temperature is due to molecular rearrangements of volumes considerably larger than the pore size where crystallization of confined water can be avoided (i.e. about 20 Å). If this interpretation of the dynamic crossover of confined supercooled water is correct it is furthermore possible that the extraordinary large volume of cooperatively rearranging regions in bulk water below the homogenous nucleation temperature leads to a very rapid slowing down of the α-relaxation below this temperature, leading to a glass transition close to the proposed singularity point at about 228 K,⁷⁹ where dynamical quantities, such as viscosity and the diffusion constant, seem to extrapolate to infinity.^33,45,80 Here it is interesting to note that the percolation model developed for supercooled bulk water by Stanley and Teixeira⁷⁸ acually predicts that not even bulk water should exhibit any glass-to-liquid transition.

4. Possible implications for bulk water

In 2004 the low temperature dielectric main relaxation with an Arrhenius temperature dependence was assigned to a local β-relaxation,⁶³ as mentioned above, and in 2010 it was proposed that this low temperature process might be the same also for bulk water.⁷⁹ Since it seems to be basically universal for all kinds of confined water, as shown in ref. 17, and since it seems to be local in character, there is no reason to believe that it should be much different in bulk water. Indeed, Amann-Winkel et al.⁶⁸ observed a relaxation process of low-density amorphous ice (LDA) that is similar to the process observed for confined water, see Fig. 2. It reached a relaxation time of 100 s at 126 K, only a slightly lower temperature than commonly observed for confined water, but exhibited a slightly lower activation energy, as seen in Fig. 2 (however, it has not as low activation energy as incorrectly plotted in Fig. 1 of ref. 17), although the error bars in the determination of this activation energy should be relatively large due to the limited temperature range in which it could be observed before crystallization to ice occurred above 150 K. However, the authors of ref. 68 assigned this process in bulk water to the structural α-relaxation, fairly consistent with the widely accepted glass transition temperature of bulk water at 136 K.⁴¹ In fact, for many years the scientific community working on glassy and supercooled bulk water has been confident in the assignment of the calorimetric feature at about 136 K to a true glass transition in the sense that water is a viscous liquid above this temperature. Thus, the interpretation that this low temperature Arrhenius activated process is due to a local β-relaxation rather than the structural α-relaxation is in conflict with the belief that the calorimetric feature observed for bulk water at 136 K⁴¹ is a true glass-to-liquid transition. However, this new interpretation with a true glass-to-liquid transition instead close to 228 K, as first suggested in ref. 79, has gained further support in recent years by e.g. McCartney and Sadtchenko⁸¹ from fast scanning calorimetry, Qvist et al.⁸² from QENS and MD simulations and Shephard and Salzmann⁴⁰ from DSC studies of amorphous ices where they compare the believed glass transition of these amorphous phases with the calorimetric feature observed for hydrogen disordered crystalline ice phases. Experimental data from the latter study are shown in Fig. 4, where it is evident that LDA exhibits a basically identical calorimetric feature to the hydrogen disordered crystalline phases at its believed glass transition. Furthermore, the fact that the exact temperature of the endothermic peak is not affected by isotope substitution of ¹⁶O to ¹⁸O, but significantly shifted for D₂O, implies that this feature is due to an unfreezing of molecular reorientation dynamics, rather than related to translational motions of the oxygen atoms, which should be the case if it were a true glass-to-liquid transition. Thus, the natural conclusion from their study is that the amorphous phase LDA undergoes the same unfreezing of local molecular reorientations as the orientationally disordered crystalline ice phases.⁴⁰ This interpretation of the calorimetric feature at about 136 K for glassy bulk water also explains its anomalously small change in heat capacity. The step in heat capacity has a typical magnitude of disordered crystals, including the hydrogen-disordered ices,⁸³ but is only 2% of for example (H₂O)₂–H₂O₂ and H₂O–N₂H₄,⁸⁴ which exhibit a glass-to-liquid transition. This implies that the interpretations made in ref. 40, 79, 81 and 82 are consistent and that the true glass-to-liquid transition occurs at the crossover from this amorphous ice phase to the ordinary supercooled liquid water phase. This crossover should be associated with an apparent strong-to-fragile transition (going from low temperatures) similar to what we observe for confined water at about 180 K. However, for bulk water this crossover should occur at a higher temperature due to the fact that an ice-like tetrahedral network structure is more easily formed without any geometrical constraints, and therefore completed at a higher temperature, leading to a higher liquid-to-glass transition temperature, as also shown by fast scanning calorimetry,⁸⁵ likely close to 228 K as indicated in Fig. 2. If this scenario is correct it is evident that the dynamical scenarios of supercooled bulk water and supercooled confined water are very similar, and that the proposed fragile-to-strong transition of bulk water should rather be considered as a liquid-to-glass transition, but with a structure not far from crystalline ice. Probably, the glassy phase can almost be considered as a polycrystalline material, which then leads to another possible explanation for the vanishing of the structural α-relaxation at the crossover temperature of supercooled confined water, namely that it is an intrinsic property of supercooled water rather than caused by confinement effects, as discussed above. Hence, a vanishing of the structural α-relaxation may occur even for supercooled bulk water (as predicted in ref. 78) at the crossover temperature, due to the completion of a very ice-like network structure, leaving only motions typical of glasses and disordered crystals below the crossover temperature. In fact, a crossover from a high temperature α-relaxation to a low temperature β-relaxation as the origin of a “fragile-to-strong” transition has been suggested to be a universal phenomenon for glass-forming liquids when there is a large comparability in the structural units relaxing through the α-relaxation and β-relaxation, respectively.⁸⁶ If this is correct, it implies that the crossover scenario observed for supercooled confined water is not even limited to water, but universal for all supercooled liquids exhibiting a “fragile-to-strong” transition.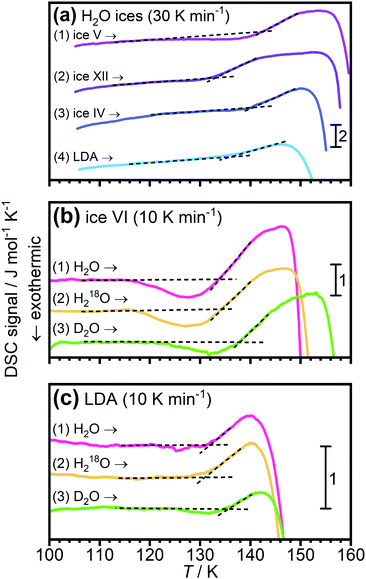

Fig. 4 DSC scans of LDA and hydrogen disordered ice phases. (a) shows data from ref. 83 for ice IV, V and XII, as well as for LDA. In (b and c) data are shown for isotopically different samples of ice VI and LDA, respectively. These data are taken from ref. 41 and indicate that for both the ice phase and LDA the endothermic peak is due an unfreezing of hydrogen motions, rather than oxygen motions.

However, although this crossover scenario to a low temperature β-relaxation is consistent with most experimental observations it should be noted that there are also results in the literature that contradict the possibility that water becomes a solid material only slightly below 228 K. Attempts have been made to measure the viscosity of LDA in the temperature range between the believed glass transition temperature at 136 K and the crystallization temperature at 150 K,⁸⁷ and more long-range diffusional motions, typical of liquids, have been claimed to occur in this temperature range.^27,88–90 However, these results are neither uncontroversial nor internally consistent since they predict different temperature dependences of the viscosity or diffusivity of the claimed deeply supercooled water. There seem to be two main problems to distinguish between a true glass-to-liquid transition and an unfreezing of local molecular reorientations. The first reason is that even for equilibrated high density amorphous ice (eHDA) at 89 K the structure is fully relaxed (i.e. the intermediate scattering function has decayed to zero) on a 1000 s time scale, due to viscoelastic relaxation and stress release from nanometer-sized heterogeneities.⁹⁰ The second problem is that the amorphous ice is in a metastable state and that both the crystallization process and an irreversible structural relaxation⁹¹ may start already around the transition temperature during slow heating. Thus, different types of dynamical processes occur already in the amorphous ice and therefore it is difficult to distinguish these motions from the motions in an ultra-viscous liquid around T_g.

Regarding the relevance of the ice phases for the behavior of both the amorphous phases of ice and liquid water, it is interesting to note the recently discovered⁹² special properties of ice II, which is a hydrogen ordered phase of ice at high pressures. In ref. 92 it was found that this ice phase completely disappeared, and instead was replaced by the hydrogen disordered phases III and V, if a small amount of ammonium fluoride was added to the ice. The very special properties of ice II were even suggested to be the reason for the anomalies of the phase diagram of water.⁹²

5. Conclusion

The dynamics of confined water in the deeply supercooled regime and its possible implications for bulk water have been discussed in this work. We question both a fragile-to-strong transition of supercooled water at about 225 K³¹ and a liquid-to-glass transition at 136 K,⁴¹ and we base this on how the observed dynamic crossovers of confined water should be interpreted. The relevance for bulk water of the observations for confined water is further supported by recent results on amorphous ice.^40,68 Firstly, DSC measurements in comparison with disordered ice phases suggest that the calorimetric feature at 136 K is not due to a glass-to-liquid transition, but rather due to an unfreezing of local molecular reorientations,⁴⁰ and secondly, dielectric relaxation measurements show that LDA exhibits an almost identical relaxation process to confined water below its crossover temperature at about 180 K.⁶⁸ Therefore, we propose a link between the data obtained for deeply supercooled and glassy confined water and amorphous ice of bulk water, which implies that the believed glass transition at 136 K⁴¹ is rather due to the freezing-in of a local β-relaxation and instead the suggested dynamic crossover around 225 K is due to a liquid-to-glass transition and an associated crossover from a high temperature α-relaxation to a low temperature β-relaxation.⁷⁹

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author wants to thank Christoph Salzmann and Silvina Cerveny for valuable discussions and comments on the manuscript. CS is further acknowledged for providing Fig. 4. This work was financially supported by the Swedish Research Council (grant no. 2015-05434).

References

1. J. A. Rupley and G. Careri, in Advances in Protein Chemistry, ed. C. B. Anfinsen, F. M. Richards, J. T. Edsall and D. S. Eisenberg, Academic Press, 1991, 41, 37–172.
2. H. D. Middendorf, Physica B, 1996, 226, 113–127.
3. Biophysics of Water, ed. F. Franks and S. Mathias, Wiley, London, 1983.
4. K. Luby-Phelps, F. Lanni and D. L. Taylor, Annu. Rev. Biophys. Biomol. Struct., 1988, 17, 369–396.
5. S. B. Zimmerman and A. P. Minton, Ann. Rev. Biophys. Biomol. Struct., 1993, 22, 27.
6. S. Chakraborty, H. Kumar, C. Dasgupta and P. K. Maiti, Confined Water: Structure, Dynamics and Thermodynamics, Acc. Chem. Res., 2017, 50, 2139–2146.
7. A. K. Soper, J. Phys.: Condens. Matter, 2012, 24, 064107.
8. A. K. Soper, Chem. Phys. Lett., 2013, 590, 1–15.
9. M. Antognazzi, A. D. L. Humphris and M. J. Miles, Appl. Phys. Lett., 2001, 78, 300–302.
10. U. Raviv, P. Laurat and J. Klein, Nature, 2001, 413, 51–54.
11. P. Gallo, M. A. Ricci and M. Rovere, J. Chem. Phys., 2002, 116, 342–346.
12. A. A. Milischuk and B. M. Ladanyi, J. Chem. Phys., 2011, 135, 174709.
13. P. A. Bonnaud, B. Coasne and R. J. Pellenq, J. Phys.: Condens. Matter, 2010, 22, 284110.
14. J. R. Grigera, S. G. Kalko and J. Fischbarg, Langmuir, 1996, 12, 154–158.
15. M. F. Harrach, F. Klameth, B. Drossel and M. Vogel, J. Chem. Phys., 2015, 142, 034703.
16. H.-J. Wang, X.-K. Xi, A. Kleinhammes and Y. Wu, Science, 2008, 322, 80–83.
17. S. Cerveny, F. Mallamace, J. Swenson, M. Vogel and L. Xu, Chem. Rev., 2016, 116, 7608–7625.
18. F. Kremer and A. Schönhals, Broadband Dielectric Spectroscopy, Springer, Berlin Heidelberg, 2002.
19. J. Swenson, K. Elamin, H. Jansson and S. Kittaka, Chem. Phys., 2013, 424, 20–25.
20. K. Elamin, H. Jansson, S. Kittaka and J. Swenson, Phys. Chem. Chem. Phys., 2013, 15, 18437–18444.
21. M. Bee, Quasielastic neutron scattering, Adam Hilger, Bristol, 1988.
22. T. Springer, Quasielastic neutron scattering for the investigation of diffusive motions in solids and liquids, Springer, Berlin, 1972.
23. R. Böhmer, G. Diezemann, G. Hinze and E. Rössler, Prog. Nucl. Magn. Reson. Spectrosc., 2001, 39, 191–267.
24. O. Mishima and H. E. Stanley, Nature, 1998, 396, 329–335.
25. K. H. Kim, et al. , Science, 2017, 358, 1589–1593.
26. J. A. Sellberg, Nature, 2014, 510, 381–384.
27. R. S. Smith and B. D. Kay, Nature, 1999, 398, 788–791.
28. J. C. Palmer, F. Martelli, Y. Liu, R. Car, A. Z. Panagiotopoulos and P. G. Debenedetti, Nature, 2014, 510, 385–388.
29. P. H. Poole, F. Sciortino, U. Essmann and H. E. Stanley, Nature, 1992, 360, 324–328.
30. V. Holten and M. A. Anisimov, Sci. Rep., 2012, 2, 713.
31. K. Ito, C. T. Moynihan and C. A. Angell, Nature, 1999, 398, 492–495.
32. C. A. Angell, Science, 1995, 267, 1924–1935.
33. J. Hallet, Proc. Phys. Soc., 1963, 82, 1043.
34. S. Takahara, et al. , J. Phys. Chem. B, 1999, 103, 5814–5819.
35. S. Kittaka, S. Ishimaru, M. Kuranishi, T. Matsuda and T. Yamaguchi, Phys. Chem. Chem. Phys., 2006, 8, 3223–3231.
36. J. Sjöström, J. Swenson, R. Bergman and S. Kittaka, J. Chem. Phys., 2008, 128, 154503.
37. K. Yoshida, T. Yamaguchi, S. Kittaka, M.-C. Bellisent-Funel and P. Fouquet, J. Chem. Phys., 2008, 129, 054702.
38. M. Sattig and M. Vogel, J. Phys. Chem. Lett., 2014, 5, 174–178.
39. M. Sattig, S. Reutter, F. Fujara, M. Werner, G. Buntkowsky and M. Vogel, Phys. Chem. Chem. Phys., 2014, 16, 19229–19240.
40. J. J. Shephard and C. G. Salzmann, J. Phys. Chem. Lett., 2016, 7, 2281–2285.
41. G. P. Johari, A. Hallbrucker and E. Mayer, Nature, 1987, 330, 552–553.
42. J. Swenson, H. Jansson and R. Bergman, Phys. Rev. Lett., 2006, 96, 247802.
43. J. Swenson, H. Jansson, J. Hedström and R. Bergman, J. Phys.: Condens. Matter, 2007, 19, 205109.
44. M. Vogel, Phys. Rev. Lett., 2008, 101, 225701.
45. R. J. Speedy and C. A. Angell, J. Chem. Phys., 1976, 65, 851–858.
46. C. Rønne, P.-O. Åstrand and S. R. Keiding, Phys. Rev. Lett., 1999, 82, 2888–2891.
47. R. Bergman and J. Swenson, Nature, 2000, 403, 283–286.
48. J. Swenson, R. Bergman and S. Longeville, J. Chem. Phys., 2001, 115, 11299–11305.
49. A. Faraone, L. Liu, C.-Y. Mou, C.-W. Yen and S.-H. Chen, J. Chem. Phys., 2004, 121, 10843.
50. J. Swenson, Phys. Rev. Lett., 2006, 97, 189801.
51. S.-H. Chen, L. Liu, E. Fratini, P. Baglioni, A. Faraone and E. Mamontov, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9012–9016.
52. S.-H. Chen, et al. , J. Chem. Phys., 2006, 125, 171103.
53. X.-Q. Chu, P. Baglioni, A. Faraone and S.-H. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 011908.
54. E. Mamontov, J. Phys. Chem., 2009, 113, 14073.
55. F. Mallamace, et al. , J. Phys. Chem. B, 2010, 114, 1870–1878.
56. E. Mamontov, J. Chem. Phys., 2005, 123, 171101.
57. X.-Q. Chu, A. I. Kolesnikov, A. P. Moravsky, V. Garcia-Sakai and S.-H. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 021505.
58. F. Mallamace, et al. , J. Chem. Phys., 2006, 124, 161102.
59. M. Nakanishi, P. Griffin, E. Mamontov and A. P. Sokolov, J. Chem. Phys., 2012, 136, 124512.
60. H. Jansson and J. Swenson, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, S51–S54.
61. S. Cerveny, A. Algria and J. Colmenero, J. Chem. Phys., 2008, 128, 044901.
62. N. Shinyashiki, et al. , J. Phys. Chem. B, 2009, 113, 14448–14456.
63. S. Cerveny, G. A. Schwartz, R. Bergman and J. Swenson, Phys. Rev. Lett., 2004, 93, 245702.
64. C. Svanberg, P. Berntsen, A. Johansson, T. Hedlund, E. Axén and J. Swenson, J. Chem. Phys., 2009, 130, 035101.
65. G. P. Johari and M. Goldstein, J. Chem. Phys., 1970, 53, 2372–2388.
66. W. Doster, S. Busch, A. M. Gasper, M.-S. Appavou, J. Wuttke and H. Scheer, Phys. Rev. Lett., 2010, 104, 098101.
67. E. Mamontov, A. Faraone, E. W. Hagaman, K. S. Han and E. Fratini, J. Phys. Chem. B, 2010, 114, 16737–16743.
68. K. Amann-Winkel, et al. , Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17720–17725.
69. M. De Marzio, G. Camisasca, M. Rovere and P. Gallo, Front. Phys., 2018, 13, 136103.
70. C. A. Angell, Chem. Rev., 2002, 102, 2627–2650.
71. D. V. Matyushov and C. A. Angell, J. Chem. Phys., 2007, 126, 094501.
72. D. Corradini, P. Gallo, S. V. Buldyrev and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051503.
73. M. De Marzio, G. Camisasca, M. Rovere and P. Gallo, J. Chem. Phys., 2017, 146, 084502.
74. S. Kittaka, K. Sou, T. Yamaguchi and K. Tozaki, Phys. Chem. Chem. Phys., 2009, 11, 8538–8543.
75. M. Oguni, Y. Kanke, A. Nagoe and S. Namba, J. Phys. Chem. B, 2011, 115, 14023–14029.
76. G. P. Johari, J. Chem. Phys., 2009, 130, 124518.
77. E. Tombari, G. Salvetti and P. G. Johari, J. Phys. Chem. C, 2012, 116, 2702–2709.
78. H. E. Stanley and J. Teixeira, J. Chem. Phys., 1980, 73, 3404.
79. J. Swenson and J. Teixeira, J. Chem. Phys., 2010, 132, 14508.
80. I. M. Hodge and C. A. Angell, J. Chem. Phys., 1978, 68, 1363–1368.
81. S. A. McCartney and V. Sadtchenko, J. Chem. Phys., 2013, 138, 084501.
82. J. Qvist, H. Schober and B. Halle, J. Chem. Phys., 2011, 134, 144508.
83. C. G. Salzmann, P. G. Radaelli, B. Slater and J. L. Finney, Phys. Chem. Chem. Phys., 2011, 13, 18468–18480.
84. C. A. Angell, Science, 2008, 319, 582–587.
85. D. Bhattacharya, C. N. Payne and V. Sadtchenko, J. Phys. Chem. A, 2011, 115, 5965–5972.
86. Q. Sin, C. Zhou, Y. Yue and L. Hu, J. Phys. Chem. Lett., 2014, 5, 1170–1174.
87. G. P. Johari, J. Phys. Chem. B, 1998, 102, 4711–4714.
88. C. H. Hill, C. Mitterdorfer, T. G. A. Youngs, D. T. Bowron, H. J. Fraser and T. Loerting, Phys. Rev. Lett., 2016, 116, 215501.
89. F. Löw, K. Amann-Winkel, T. Loerting, F. Fujara and B. Geil, Phys. Chem. Chem. Phys., 2013, 15, 9308–9314.
90. F. Perakis, et al. , Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8193–8198.
91. J. J. Shephard, J. S. O. Evans and C. G. Salzmann, J. Phys. Chem. Lett., 2013, 4, 3672–3676.
92. J. J. Shephard, B. Slater, P. Harvey, M. Hart, C. L. Bull, S. T. Bramwell and C. G. Salzmann, Nat. Phys., 2018, 14, 569–573.

---