Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Where's water? The many binding sites of hydantoin†
Sébastien
Gruet
 *abc,
Cristóbal
Pérez
*abc,
Cristóbal
Pérez
 abc,
Amanda L.
Steber
abc,
Amanda L.
Steber
 abc and
Melanie
Schnell
abc and
Melanie
Schnell
 *abc
*abc
aDeutsches Elektronensychrotron, Notkestrasse 85, D-22607 Hamburg, Germany
bInstitut für Physikalische Chemie, Christian-Albrechts-Universität zu Kiel, Max-Eyth-Strasse 1, D-24118 Kiel, Germany
cMax-Planck-Institut für Struktur und Dynamic der Materie and The Hamburg Centre for Ultrafast Imaging at the Universität Hamburg, Luruper Chaussee 149, D-22761 Hamburg, Germany. E-mail: melanie.schnell@mpsd.mpg.de
First published on 28th November 2017
Abstract
Prebiotic hydantoin and its complexes with one and two water molecules are investigated using high-resolution broadband rotational spectroscopy in the 2–8 GHz frequency range. The hyperfine structure due to the nuclear quadrupole coupling of the two 14N atoms is analysed for the monomer and the complexes. This characteristic hyperfine structure will support a definitive assignment from low frequency radioastronomy data. Experiments with H218O provide accurate experimental information on the preferred binding sites of water, which are compared with quantum-chemically calculated coordinates. In the 2-water complexes, the water molecules bind to hydantoin as a dimer instead of individually, indicating the strong water–water interactions. This information provides first insight on how hydantoin interacts with water on the molecular level.
1 Introduction
The search for prebiotic molecules in the interstellar medium (ISM) has been an ongoing effort of astronomy, astrochemistry, and laboratory spectroscopy for several decades. There is particular interest in simple organic molecules like sugars, amino acids, and their derivates as they will reveal important information about the origin and formation of life. Recently, ground-based observatories have been updated and new ones brought online, such as the Atacama Large Millimeter/submillimeter Array (ALMA), the Robert C. Byrd Greenbank Telescope, and the Institute for Radio Astronomy in the Millimeter Range (IRAM), which provide high-spatial and high-frequency resolution radioastronomic data. This data can be used not only to identify new molecular species in the ISM but also to investigate molecular reaction pathways of previously detected molecules. Once a chemical reaction, by which the discovered molecule can be formed, is proposed, spatial maps of the components of this reaction can be examined in order to judge its likelihood as a contributor to the molecule's occurrence. By systematically checking the feasibility of these reactions through this manner, much insight about the chemistry occurring in interstellar environments can be gleamed.1,2 In order to identify new molecules and create molecule specific maps, knowledge of the rotational transition frequencies of the molecules of interest is a prerequisite. These can be provided by high-resolution laboratory experiments in the microwave (mw) up to the terahertz regime, using techniques such as THz absorption spectroscopy using solid-state frequency multiplier chains,3 Fabry–Perot cavity Fourier transform microwave spectroscopy,4 and chirped pulse Fourier transform microwave (CP-FTMW) spectroscopy.5The cyclic amide hydantoin, or glycolylurea, has many interesting qualities, one of them being its tie to prebiotic chemistry. Hydantoin is a heterocyclic organic compound with the sum formula C3H5N2O2 (CH2C(O)NHC(O)NH) that arises from the reaction of the prebiotic molecules glycolic acid and urea. As urea has already been detected in the interstellar medium (ISM),6 it is likely that hydantoin could be present, as reactions of urea in the gas phase or on ice grain surfaces with glycolic acid would give rise to the formation of hydantoin. So far, hydantoin has been detected in carbonaceous chondrites together with several amino acids by gas chromatography combined with mass spectrometry.7 This finding points to reaction pathways connecting hydantoin and amino acids. More recently, laboratory studies on interstellar ice analogues revealed that the hydrolysis of hydantoin, under acidic conditions, can produce small amino acids such as glycine, which is one of the building blocks of life.8
Studies providing spectroscopic and structural information on hydantoin are rather limited and mostly dedicated to experiments in the solid phase. These experiments include the previously mentioned studies on ice analogues, a matrix isolation study in which the photochemistry of hydantoin was investigated,9 and a X-ray crystallography study in which its structure was determined.10 The vibrational spectra of the normal and enriched isotopologues were also recorded at low resolution in the infrared regime.11,12 The first high-resolution laboratory spectroscopy study of hydantoin in the gas phase was reported in 2017 using millimeter-wave (mmw) spectroscopy in the frequency range 90 to 370 GHz.13 Molecular constants for the ground state and two low-lying vibrationally excited states were reported, which can be useful for high frequency radio astronomical observations where molecular vibrationally excited states can be observed. Spectral line catalogues for these states provide useful rest frequencies for searches of hydantoin in interstellar space. Due to rotational transitions corresponding to high J rotational quantum numbers, the unique hyperfine splitting pattern expected for hydantoin, which arises from the nuclear quadrupole coupling of the two nitrogen atoms (14N), was not observed.
In the present work, we investigate hydantoin and its complexes with one and two water molecules using high-resolution broadband rotational spectroscopy. We use the low frequency range (2–8 GHz) of our COMPACT spectrometer to analyse and provide accurate molecular parameters of the nuclear quadrupole coupling hyperfine structure, which can also be useful for the identification of hydantoin in space.14,15 Every low-J rotational transition will exhibit this uniquely identifying hyperfine splitting. We are also interested in understanding the interactions between hydantoin and water. Indeed, the knowledge of how water binds to such prebiotic precursors is relevant for modeling chemical processes on interstellar ice grains.
2 Experimental and computational details
Rotational spectroscopic measurements were performed with the Hamburg COMPACT spectrometer covering the 2–8 GHz frequency range, which has been described in detail elsewhere.16 Hydantoin (C3N2O2H4, purchased from Sigma-Aldrich, purity >99%) was placed in a heatable reservoir (a modified Parker General Valve, Series 9) close to the valve orifice and heated to ∼180 °C. The resulting vapor pressure was picked up by the backing gas neon and supersonically expanded into the chamber. The jet temperature is estimated to be close to 2 K. For the clusters with water, the neon flowed over an external reservoir containing water, to seed the neon with water. It then passed over the heated hydantoin, before being supersonically expanded into the vacuum chamber. In both cases, the valve operated at a repetition rate of 9 Hz, and 3 bars of neon were used as the backing gas. After the expansion, the molecular jet was polarized with a 4 μs chirp pulse spanning 2–8 GHz. This chirp was generated with an arbitrary waveform generator, amplified with a 300 W traveling wave tube amplifier, and transmitted into the vacuum chamber via a horn antenna. Following each excitation pulse, the free induction decay (FID) of the macroscopic ensemble of polarized molecules was recorded for 40 μs. In order to increase the data collection speed and reduce sample consumption, the fast frame capability17 of the Tektronix digital oscilloscope DPO 71254C was used to collect eight consecutive FIDs in the time domain per gas pulse. This resulted in an effective repetition rate of 72 Hz. For the spectrum of the hydantoin monomer as well as for the hydantoin–H216O spectrum, 2 million FIDs were coadded. In the hydantoin–H218O measurements, in which a H216O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H218O mixture (2
H218O mixture (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio) was used, 4 million FIDs were coadded. Fourier transformation of the averaged time domain FID, recorded at point spacings of 10 ps, resulted in the frequency domain rotational spectrum with frequency resolution of 25 kHz.
1 ratio) was used, 4 million FIDs were coadded. Fourier transformation of the averaged time domain FID, recorded at point spacings of 10 ps, resulted in the frequency domain rotational spectrum with frequency resolution of 25 kHz.
The transition frequency assignments were carried out using the AABS package,18 after which the fits were further refined using the SPFIT/SPCAT programs, including parameters to treat the hyperfine structure for the molecule.19 Comparisons with the quantum-chemical calculations were helpful for predicting the hyperfine splitting due to the two 14N nuclei of hydantoin. A series of programs available on the PROSPE website20 was used to aid in the assignment of the spectra and determine the experimental structures. The program CORSCL was used to estimate the rotational constants for 18O isotopologues of each complex, while the KRA program was to determine the experimental oxygen-atom positions in the principal axis system (rs) through the Kraitchman equations, and STRFIT was used to compute the r0 fits.21,22 Complementary to the rs structure, we performed a structural least-squares fit of the experimental moments of inertia of the isotopologues to determine the effective ground state structure (r0). The initial geometry for the r0 fits of each complex was taken from ab initio calculations.
The experimental results were complemented by and compared with electronic structure calculations. Computations at the B3LYP-D3(BJ)/aug-cc-pVTZ level of theory, which includes dispersion corrections and Becke–Johnson damping,23 were performed using the Gaussian 09, rev. D.0124 program suite.
3 Results and discussion
3.1 Rotational spectroscopy of hydantoin
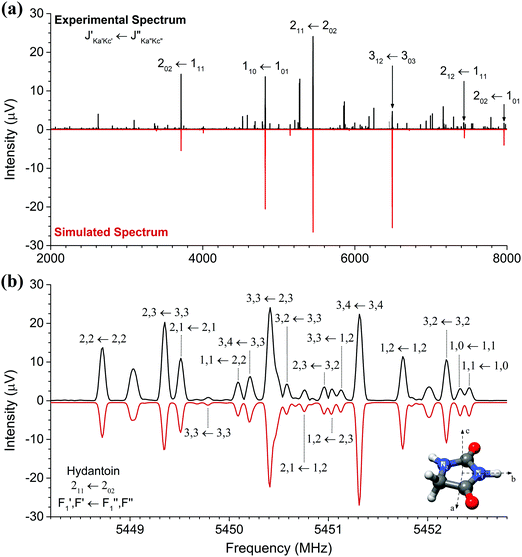
The high-resolution broadband rotational spectrum of the hydantoin monomer is displayed in Fig. 1(a). A limited number of rotational transitions is present in the 2–8 GHz frequency range due to the comparatively large rotational constants of hydantoin. These, among other effects, result in large spacings between the individual groups of transitions. However, hydantoin is an asymmetric-top molecule (near-prolate, with an asymmetry parameter of κ = −0.76) containing two nitrogen atoms (I = 1), which results in rich hyperfine substructure. The bottom panel of Fig. 1(b) shows the hyperfine pattern for the 211 ← 202 b-type rotational transition. The hyperfine structure was modeled with the χii (i = a, b, or c) diagonal components of the nuclear quadrupole coupling tensor of each nitrogen atom, taking into account that χaa + χbb + χcc = 0.25 A I2 coupling scheme was used: the spin I1 of one nucleus (here the N1 atom) couples to J to form F1 = I1 + J, which couples to the vector sum I2 of the two equivalent spins (N1 and N2 atoms) to form F = F1 + I2.25 Line splittings due to nuclear quadrupole coupling are inversely proportional to the rotational quantum number J. Because of this, the hyperfine splitting eventually collapses for rotational transitions with increasing J value. In the millimeter-wave study on hydantoin by Ozeki et al.,13 no hyperfine structure was observed because of the high J rotational quantum numbers involved. The low-frequency range of the COMPACT spectrometer probes the lowest rotational transitions, so that, together with the high resolution of the spectrometer, the hyperfine structure is well resolved. We performed a joint fit of the rotational and hyperfine transitions using the SPFIT/SPCAT programs.The rotational parameters obtained from this fit are summarized in Table 1 and compared with results obtained in the recent mmw spectroscopy study and from quantum-chemical calculations (B3LYP-D3(BJ)/aug-cc-pVTZ). We were unable to perform a global fit of our mw and the previously reported mmw data as only a selected few line frequencies were published in the mmw study. Line lists of the mw rotational transitions including hyperfine structure are given in the ESI.† In our study, inclusion of centrifugal distortion constants into the asymmetric rotor fit were unnecessary. This is different from the mmw study in which high rotational transitions were probed, leading to their use. Even though this is the case, there is very little variation between the two sets of experimental rotational constants. A, B, and C agree to within 10 kHz. The calculated rotational constants agree to within 1% of both experimental methods. This is particularly good considering that the quantum-chemical calculations provide rotational constants for a molecule without considering vibrational zero-point energy corrections. Moreover, good agreement was expected because hydantoin is a decent-size rigid molecule without conformational flexibility.
| Parameters | Parent fit (this work) | Parent fit (mmw)13 | Calc. |
|---|---|---|---|
| A (MHz) | 6537.73154(80) | 6537.73998(70) | 6570.35 |
| B (MHz) | 2291.37309(21) | 2291.37582(57) | 2289.88 |
| C (MHz) | 1716.47119(31) | 1716.471265(67) | 1716.35 |
| Δ J (kHz) | 0.095338(167) | ||
| Δ JK (kHz) | 0.15923(69) | ||
| Δ K (kHz) | 2.25266(83) | ||
| δ J (kHz) | 0.025701(83) | ||
| δ K (kHz) | 0.28008(144) | ||
| χ aa (1) (MHz) | 1.6316(57) | 1.671 | |
| χ bb–cc(1) (MHz) | 5.227(20) | 5.370 | |
| χ ab (1) (MHz) | [0.092] | 0.092 | |
| χ aa (2) (MHz) | 2.5927(43) | 2.753 | |
| χ bb–cc(2) (MHz) | 6.935(16) | 7.439 | |
| χ ab (2) (MHz) | [−0.223] | −0.223 | |
| N lines | 114 | 161 | |
| RMS (kHz) | 5.3 | 39 | |
| μ a /μb/μc (D) | 0.2/2.7/0 | ||
| No. of lines (a/b/c) | 27/87/0 |
The nuclear quadrupole coupling constants for the two nitrogen atoms N1 and N2 were determined and are shown in Table 1. For a given nucleus, the magnitude of the nuclear quadrupole coupling constants depends on the interaction of the nucleus with the electric field gradient. It thus provides useful information on the character of neighboring chemical bonds. For the two nitrogen atoms N1 and N2 (Fig. 1), the nuclear quadrupole coupling constants are different, which points to a difference in their chemical environment. This is indeed the case: N1 has two adjacent electron withdrawing carbonyl groups, while N2 has only one neighboring CO group and a CH2 group. This results in N2 having a higher electron density than N1 and thus larger χii values.
3.2 Hydantoin–water complexes
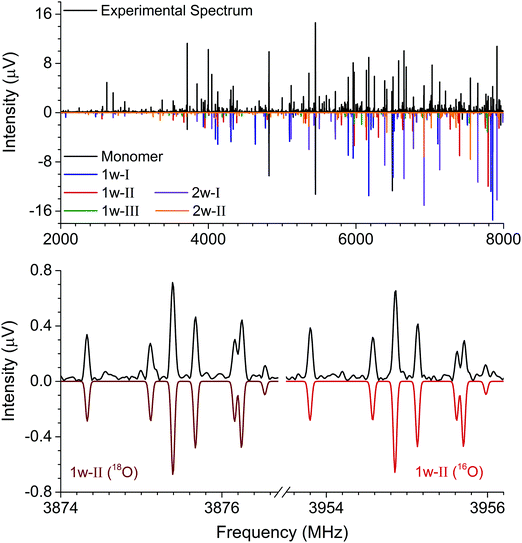
The rotational constants of the experimentally observed complexes 1w-I, 1w-II, and 1w-III are summarized in Table 2. Their values are sufficiently different to unambiguously differentiate and assign the individual complexes based solely on a comparison between the experimental and ab initio rotational constants. For further elucidation of the assignments, the types of rotational transitions assigned (a-, b-, or c-type) were compared with the calculated dipole moment components. Complexes 1w-I and 1w-II are predicted to have a strong μb value as well as a μa component, and both types of transitions were assigned for the two complexes. Complex 1w-III, however, is predicted to only have a μb component, which agrees with our experimental observations. Note that for all three complexes, we do not observe an indication of c-type transitions or internal motion of the water molecule. The formation of two relatively strong hydrogen bonds prevents the water monomer from exhibiting internal dynamics.
| Parameters | 1w-I | Calc. | 1w-II | Calc. | 1w-III | Calc. |
|---|---|---|---|---|---|---|
| A (MHz) | 5029.76179(63) | 5077.85 | 2944.64549(47) | 2969.01 | 2956.01125(78) | 2987.27 |
| B (MHz) | 1135.03113(20) | 1140.42 | 1520.96485(56) | 1527.09 | 1507.54475(93) | 1510.23 |
| C (MHz) | 932.88647(16) | 938.13 | 1010.39251(44) | 1016.37 | 1005.70153(76) | 1010.68 |
| Δ J (kHz) | 0.1305(62) | 0.300(23) | 0.305(42) | |||
| δ J (kHz) | — | 0.1039(54) | — | |||
| χ aa (1) (MHz) | 1.7100(73) | 1.763 | 1.4634(59) | 1.457 | 1.541(23) | 1.641 |
| χ bb–cc(1) (MHz) | 5.185(10) | 5.309 | 4.873(11) | 4.892 | 4.488(27) | 4.462 |
| χ ab (1) (MHz) | [0.136] | 0.136 | [0.327] | 0.327 | [−0.251] | −0.251 |
| χ aa (2) (MHz) | 2.0814(62) | 2.177 | 2.5916(44) | 2.715 | 2.137(10) | 2.365 |
| χ bb–cc(2) (MHz) | 6.7832(76) | 7.070 | 6.7080(92) | 7.247 | 7.346(14) | 7.870 |
| χ ab (2) (MHz) | [−0.595] | −0.595 | [0.161] | 0.161 | [−0.249] | −0.249 |
| N lines | 179 | 181 | 86 | |||
| RMS (kHz) | 5.0 | 7.5 | 9.2 | |||
| |μa|/|μb|/|μc| (D) | 1.1/1.2/0.9 | 1.0/3.0/0.8 | 0.7/3.1/0.8 | |||
| No. of lines (a/b/c) | 89/90/0 | 32/149/0 | 0/87/0 |
To obtain experimental structure information and to further support the assignment, we performed a series of experiments in which the water sample was comprised of a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of H216O
1 ratio of H216O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H218O. The analysis of this new dataset yielded three additional rotational assignments (one per cluster). The tables reporting rotational parameters for these three new complexes are provided in the ESI.† By isotopically substituting the H216O with an H218O, induced changes in the moments of inertia of the cluster can be used for determining the oxygen-atom positions in the principal axis system through the Kraitchman equations.21 This renders the so-called substitution structure (rs). Although the rs structure is of common application in rotational spectroscopy, it presents limitations when determining structural parameters. This is particularly limiting when the isotopic information is sparse and the substituted atom lies near an inertial axis where vibrational contributions can play an important role. Theoretical calculations for the three observed complexes show that the water monomer is located near or in the hydantoin ab inertial plane. This was corroborated through the imaginary values of the c coordinate for the oxygen atom upon isotopic substitution, which were set to zero for structural comparisons.
H218O. The analysis of this new dataset yielded three additional rotational assignments (one per cluster). The tables reporting rotational parameters for these three new complexes are provided in the ESI.† By isotopically substituting the H216O with an H218O, induced changes in the moments of inertia of the cluster can be used for determining the oxygen-atom positions in the principal axis system through the Kraitchman equations.21 This renders the so-called substitution structure (rs). Although the rs structure is of common application in rotational spectroscopy, it presents limitations when determining structural parameters. This is particularly limiting when the isotopic information is sparse and the substituted atom lies near an inertial axis where vibrational contributions can play an important role. Theoretical calculations for the three observed complexes show that the water monomer is located near or in the hydantoin ab inertial plane. This was corroborated through the imaginary values of the c coordinate for the oxygen atom upon isotopic substitution, which were set to zero for structural comparisons.
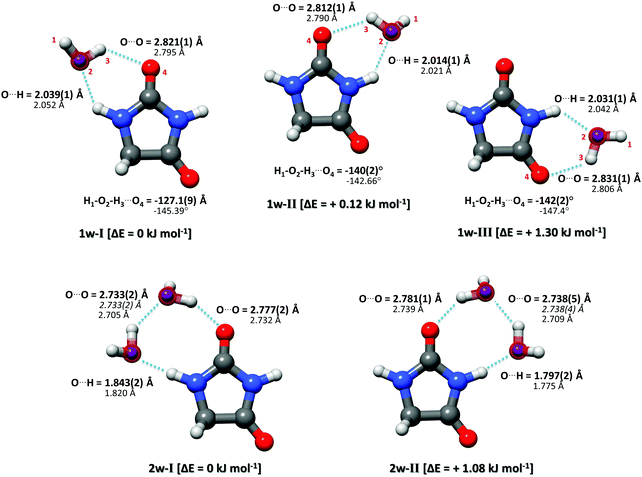
Complementary to the rs structure, we performed a structural least-squares fit of the experimental moments of inertia of the isotopologues to determine the effective ground state structure (r0). The initial geometry for the r0 fits of each complex was taken from ab initio calculations. The relevant structural parameters are shown in Fig. 3 for all three clusters. An important feature to consider is the degree of planarity the structures exhibit upon water complexation. A first indication of the non-planarity of the clusters comes from the inertial defect, defined as Δc = Ic − Ia − Ib. This parameter quantifies the mass distribution out of the ab inertial plane. For the hydantoin monomer this value is −3.430102(58) uÅ2. This indicates that even in the monomer, there are small contributions from the out-of-plane atoms: the hydrogen atoms in the CH2 group. The inertial defect for the water complexes are −3.99647(12) uÅ2, −3.72083(25) uÅ2 and −3.68579(43) uÅ2 for 1w-I, 1w-II and 1w-III respectively. These values are slightly larger than those for the monomer indicating more non-planarity in the structure. These values essentially remain unchanged upon H218O substitution showing that the oxygen atoms lie in the ab inertial plane, thus indicating that the increased non-planarity must be due to at least one proton of the water. This is indeed the case, and the r0 structural fit allowed us to determine that the dangling hydrogen orientation is out of the plane. By fitting the dihedral angle corresponding to this non-planarity (H1–O2–H3–O4), our results show that the structure for complex 1w-I has the smallest dihedral angle at −127.1(9)°, while complex 1w-III has the largest angle at −142.2(2)°. This agrees with the changes in the inertial defects for each of these structures. This is also in good agreement with the calculated structures. For a set of similar systems (i.e. uracil–water and thymine–water complexes), the authors were forced to fix this dihedral to 140° in order to obtain a r0 fit.26
In our broadband spectra, we observed rotational signatures of two species with rotational constants that fit to what we would expect for the size of hydantoin–(H2O)2 complexes. One spectrum is dominated by a-type transitions, while the second mainly consists of b-type transitions. Both spectra could be fit individually to asymmetric rotor Hamiltonians including the nuclear quadrupole coupling of two nitrogen nuclei. Again, no indication of water tunneling in the complexes was observed. The resulting rotational and nuclear quadrupole coupling constants are summarized in Table 3. The energy difference between the two structures amounts to ∼1 kJ mol−1. Our calculations predicted an additional 2-water complex involving the “water–dimer” unit, which binds to the NH group containing N1 and the CO group neighboring the CH2 group, similar to the 1w-III complex. This is predicted to be about 4.6 kJ mol−1 higher in energy than complex I, and it was not observed in our spectrum. A fourth complex, where the two water molecules bind separately to the NH and CO groups of hydantoin, is more than 11 kJ mol−1 higher in energy.
| Parameters | 2w-I | Calc. | 2w-II | Calc. |
|---|---|---|---|---|
| A (MHz) | 2938.0518(12) | 2977.06 | 2120.22255(63) | 2125.42 |
| B (MHz) | 754.55686(17) | 765.55 | 946.67424(56) | 969.57 |
| C (MHz) | 604.47571(17) | 613.12 | 658.71724(43) | 670.81 |
| Δ J (kHz) | 0.0621(31) | 0.1959(77) | ||
| Δ JK (kHz) | — | −0.689(37) | ||
| Δ K (kHz) | 4.05(28) | 2.408(87) | ||
| δ J (kHz) | — | 0.0529(66) | ||
| χ aa (1) (MHz) | 1.7000(73) | 1.771 | 1.2380(73) | 1.167 |
| χ bb–cc(1) (MHz) | 5.181(13) | 5.287 | 4.625(14) | 4.620 |
| χ ab (1) (MHz) | [0.154] | 0.154 | [0.565] | 0.565 |
| χ aa (2) (MHz) | 1.5713(66) | 1.828 | 2.5276(57) | 2.638 |
| χ bb–cc(2) (MHz) | 6.500(10) | 6.730 | 6.750(11) | 7.272 |
| χ ab (2) (MHz) | [−0.792] | −0.792 | [0.188] | 0.188 |
| N lines | 218 | 135 | ||
| RMS (kHz) | 5.9 | 7.5 | ||
| |μa|/|μb|/|μc| (D) | 1.4/0.8/0 | 1.0/2.9/0.1 | ||
| No. of lines (a/b/c) | 131/87/0 | 22/115/0 |
Like in the case of the hydantoin–H2O complexes, we also investigated the 2-water complexes with H218O. Unlike the 1-water complexes where there is only one position for the insertion of H218O, here we have two possibilities, H216O–H218O and H218O–H216O. Due to their different location with respect to the cluster's center of mass, their single substitution gives rise to two new, separated rotational spectra. The rotational parameters for these four new spectra, two per cluster, are shown in the ESI.† The r0 experimental parameters were also obtained in both cases from a fit to nine moments of inertia from three different isotopologues. The relevant experimental structural parameters are compared with results from B3LYP-D3(BJ)/aug-cc-pVTZ calculations (lower values) in Fig. 3. The structural analysis for both complexes revealed that the two water molecules form a unit (similar to the water dimer) in which one water moiety forms a hydrogen bond with a CO group and the second water monomer forms a hydrogen bond with the neighboring NH group. This results in hydrogen bonded eight-membered rings that further stabilize the cluster and involve the formation of three hydrogen bonds.
Interesting structural differences are observed when comparing the bonding distances of our clusters to those of the bare water dimer and/or other molecular clusters that include two water molecules. These are dictated by cooperative effects. The presence of one hydrogen bond increases the unequal charge distribution in water and leads to further polarisation. This can make the remaining part of water more susceptible to additional hydrogen bonds, especially when polar groups are present and substantially modify the strength of a given hydrogen bond. In the case of hydantoin, a clear indication of cooperativity can be observed when looking at the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Owater distances. While for the 1-water clusters the distances are all above 2.8 Å, a clear shortening to 2.777(2) Å and 2.781(1) Å for 2w-I and 2w-II respectively is seen. Furthermore, it is interesting to compare the Owater–Owater distance of the two water molecules of complexes I and II with the Owater–Owater distances observed for the free water dimer and other 2-water molecule complexes. At 2.733(2) Å (complex I) and 2.738(4) Å (complex II), the O–O distances are significantly shorter than in the isolated (H2O)2 (2.98(4) Å).30 They are also about 0.1 Å shorter than the O–O distances for a number of other molecular complexes with two water molecules: biphenyl 2-carboxaldehyde–(H2O)2 (2.852(2) Å),31 camphor–(H2O)2 (2.821(2) Å for complex 2w(I) and 2.837(1) Å for complex 2w(II)),27 β-propiolactone–(H2O)2 (2.85(1) Å),28 or the 12-crown-4 ether with 2.779(3) Å.29 The observed shortening can be attributed to a larger donor character of the –NH group of hydantoin with respect to aliphatic hydrogens as those in the systems mention above. This marked acidity contributes to the strengthening of the stability of the overall hydrogen network, which manifests itself as shorter interaction distances.
O⋯Owater distances. While for the 1-water clusters the distances are all above 2.8 Å, a clear shortening to 2.777(2) Å and 2.781(1) Å for 2w-I and 2w-II respectively is seen. Furthermore, it is interesting to compare the Owater–Owater distance of the two water molecules of complexes I and II with the Owater–Owater distances observed for the free water dimer and other 2-water molecule complexes. At 2.733(2) Å (complex I) and 2.738(4) Å (complex II), the O–O distances are significantly shorter than in the isolated (H2O)2 (2.98(4) Å).30 They are also about 0.1 Å shorter than the O–O distances for a number of other molecular complexes with two water molecules: biphenyl 2-carboxaldehyde–(H2O)2 (2.852(2) Å),31 camphor–(H2O)2 (2.821(2) Å for complex 2w(I) and 2.837(1) Å for complex 2w(II)),27 β-propiolactone–(H2O)2 (2.85(1) Å),28 or the 12-crown-4 ether with 2.779(3) Å.29 The observed shortening can be attributed to a larger donor character of the –NH group of hydantoin with respect to aliphatic hydrogens as those in the systems mention above. This marked acidity contributes to the strengthening of the stability of the overall hydrogen network, which manifests itself as shorter interaction distances.
4 Summary and conclusions
In summary, we used broadband rotational spectroscopy to study the prebiotic molecule hydantoin and its complexes with up to two water molecules. Hydantoin is a cyclic molecules, offering two amide groups and thus a number of possibilities for the formation of hydrogen bonds with water molecules. We observed three qualitatively different complexes of hydantoin with one water molecule, all within relative energies less than 1.5 kJ mol−1 of each other. Each water molecule forms two hydrogen bonds, one with the CO and one with the NH group, resulting in a hydrogen-bonded six-membered ring. For the complexes with two water molecules, there is evidence to suggest that water forms a dimer which then binds to one of the amide groups, forming an hydrogen-bonded eight-membered ring. This illustrates the dominance of water–water interactions. The structural assignment of the water complexes was supported by using H218O-enriched samples to determine both the substitution (rs) and the effective ground state (r0) structures as well as by analysis of the hyperfine structure arising from the two amide nitrogen atoms in hydantoin. This structural analysis allowed an accurate characterization of the structure of the clusters that were compared to other water aggregates where structural information was available. Cooperativity effects explain the significantly shorter O–O distances observed for the 2-water complexes compared to those observed in the free water dimer or in other complexes of polar molecules with two water molecules. This showcases the hydrogen bond donor character of the –NH in amides.Due to its unique hyperfine patterns, hydantoin offers itself as a likely candidate to be identified in the ISM, as no other molecule would exhibit the same hyperfine splitting pattern. As a consequence, a small number of rotational transitions would be sufficient for its unambiguous assignment. The identification of this molecule in the ISM has larger implications than just the discovery of another molecule. Its formation is dependent upon urea, which has already been identified in the ISM, and it can go on to form the amino acid glycine which is an important step to the evolution of life. Interactions of hydantoin with water have been shown. These are an important first step to understanding how water would impact the chemistry that hydantoin would be involved in, if it were created through chemical reactions on ice grains.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed as part of our activities within the framework of the ERC Starting grant 'Astrorot', grant agreement number 638027. It has also been supported by the Deutsche Forschungsgemeinschaft within the priority program SPP1807 (SCHN1280/4-1) and by the excellence cluster 'The Hamburg Centre for Ultrafast Imaging – Structure, Dynamics and Control of Matter at the Atomic Scale' of the Deutsche Forschungsgemeinschaft via a Louise Johnson Fellowship for A. L. S. Open Access funding provided by the Max Planck Society.References
- E. Herbst and E. F. van Dishoeck, Annu. Rev. Astron. Astrophys., 2009, 47, 427–480 CrossRef CAS.
- M. Bonfand, A. Belloche, K. M. Menten, R. T. Garrod and H. S. P. Müller, Astron. Astrophys., 2017, 604, A60 CrossRef.
- G. Chattopadhyay, E. Schlecht, J. S. Ward, J. J. Gill, H. H. S. Javadi, F. Maiwald and I. Mehdi, IEEE Trans. Microwave Theory Tech., 2004, 52, 1538–1547 CrossRef CAS.
- T. J. Balle and W. H. Flygare, Rev. Sci. Instrum., 1981, 52, 33–45 CrossRef CAS.
- G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103 CrossRef PubMed.
- A. J. Remijan, L. E. Snyder, B. A. McGuire, H.-L. Kuo, L. W. Looney, D. N. Friedel, G. Y. Golubiatnikov, F. J. Lovas, V. V. Ilyushin, E. A. Alekseev, S. F. Dyubko, B. J. McCall and J. M. Hollis, Astrophys. J., 2014, 783, 77 CrossRef.
- A. Shimoyama and R. Ogasawara, Origins Life Evol. Biospheres, 2002, 32, 165–179 CrossRef CAS.
- P. de Marcellus, M. Bertrand, M. Nuevo, F. Westall and L. Le Sergeant d'Hendecourt, Astrobiology, 2011, 11, 847–854 CrossRef CAS PubMed.
- G. O. Ildiz, C. M. Nunes and R. Fausto, J. Phys. Chem. A, 2013, 117, 726–734 CrossRef CAS PubMed.
- F.-L. Yu, C. H. Schwalbe and D. J. Watkin, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2004, 60, o714–o717 Search PubMed.
- Y. Saito and K. Machida, Bull. Chem. Soc. Jpn., 1978, 51, 108–112 CrossRef CAS.
- G. O. Ildiz, I. Boz and O. Unsalan, Opt. Spectrosc., 2012, 112, 665–670 CrossRef CAS.
- H. Ozeki, R. Miyahara, H. Ihara, S. Todaka, K. Kobayashi and M. Ohishi, Astron. Astrophys., 2017, 600, A44 CrossRef.
- D. P. Zaleski, N. A. Seifert, A. L. Steber, M. T. Muckle, R. A. Loomis, J. F. Corby, J. Oscar Martinez, K. N. Crabtree, P. R. Jewell, J. M. Hollis, F. J. Lovas, D. Vasquez, J. Nyiramahirwe, N. Sciortino, K. Johnson, M. C. McCarthy, A. J. Remijan and B. H. Pate, Astrophys. J., Lett., 2013, 765, L10 CrossRef.
- B. A. McGuire, A. M. Burkhardt, C. N. Shingledecker, S. V. Kalenskii, E. Herbst, A. J. Remijan and M. C. McCarthy, Astrophys. J., Lett., 2017, 843, L28 CrossRef.
- D. Schmitz, V. A. Shubert, T. Betz and M. Schnell, J. Mol. Spectrosc., 2012, 280, 77–84 CrossRef CAS.
- C. Perez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Chem. Phys. Lett., 2013, 571, 1–15 CrossRef CAS.
- Z. Kisiel, L. Pszczółkowski, I. R. Medvedev, M. Winnewisser, F. C. De Lucia and E. Herbst, J. Mol. Spectrosc., 2005, 233, 231–243 CrossRef CAS.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS.
- Z. Kisiel, in Spectroscopy from Space, ed. J. Demaison, K. Sarka and E. A. Cohen, Springer, Dordrecht, 2001, pp. 91–106 Search PubMed.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17–24 CrossRef CAS.
- Z. Kisiel, J. Mol. Spectrosc., 2003, 218, 58–67 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- W. Gordy and R. L. Cook, Microwave Molecular Spectra, Wiley, 1984 Search PubMed.
- J. C. López, J. L. Alonso, I. Peña and V. Vaquero, Phys. Chem. Chem. Phys., 2010, 12, 14128–14134 RSC.
- C. Pérez, A. Krin, A. L. Steber, J. C. López, Z. Kisiel and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 154–160 CrossRef PubMed.
- C. Pérez, J. L. Neill, M. T. Muckle, D. P. Zaleski, I. Peña, J. C. Lopez, J. L. Alonso and B. H. Pate, Angew. Chem., Int. Ed., 2015, 54, 979–982 CrossRef PubMed.
- C. Pérez, J. C. López, S. Blanco and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 4053–4058 CrossRef PubMed.
- T. R. Dyke, K. M. Mack and J. S. Muenter, J. Chem. Phys., 1977, 66, 498–510 CrossRef CAS.
- S. R. Domingos, C. Pérez and M. Schnell, J. Chem. Phys., 2016, 145, 161103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06518c |
| This journal is © the Owner Societies 2018 |