Open Access Article
Open Access ArticleSinglet fission in thin films of metallo-supramolecular polymers with ditopic thiophene-bridged terpyridine ligands†
David
Rais
 *a,
Jiří
Pfleger
a,
Miroslav
Menšík
a,
Alexander
Zhigunov
a,
Pavla
Štenclová‡
b,
Jan
Svoboda
ab and
Jiří
Vohlídal
b
*a,
Jiří
Pfleger
a,
Miroslav
Menšík
a,
Alexander
Zhigunov
a,
Pavla
Štenclová‡
b,
Jan
Svoboda
ab and
Jiří
Vohlídal
b
aInstitute of Macromolecular Chemistry, Academy of Sciences of the Czech Republic, Heyrovského nám. 2, 162 06, Prague, Czech Republic. E-mail: rais@imc.cas.cz
bCharles University, Faculty of Science, Department of Physical and Macromolecular Chemistry, Hlavova 2030, 128 40 Prague 2, Czech Republic
First published on 23rd June 2017
Abstract
The singlet fission (SF) phenomenon is currently investigated for its potential to overcome the Shockley–Queisser energy conversion efficiency limit of single-junction photovoltaic (PV) cells. One of the hurdles of using SF for PV cells is the limited choice among the presently available SF materials. We compare the photophysical behavior of thin solid films of two novel compounds: a ditopic ligand bis(terpyridine-4′-yl)terthiophene (T) and a metallo-supramolecular polymer (MSP), prepared by the coordination of T to Zn2+ ions (PT). The transient absorption kinetics in PT after photoexcitation into its second electronic excited state was consistent with an ultrafast (SF) process with a time constant of 160 fs. The lifetime of such a formed triplet state reached only 1 ns, due to mutual bimolecular annihilation, which also hindered the determination of the yield of the triplet state formation. In contrast, the metal-free thin films of T showed no signs of SF, but rather profound exciton relaxation through an excimer formation. Powder WAXS diffractograms pointed out a lower degree of structural order in the PT than that in the T – which may be the probable reason for differences in energy relaxation pathways of these two materials. To the best of our knowledge, singlet fission has not yet been reported in the MSP class of materials.
Introduction
The process of singlet fission (SF) was first postulated in 1965 to explain the photophysical phenomena observed in anthracene crystals.1 In the SF process, one directly photogenerated singlet exciton S1 (with spin number S = 0) splits into two triplet excitons T1 (each with S = 1). It is currently believed that SF proceeds through an intermediate correlated triplet pair state 1(TT) (with total spin S = 0):2| S1 + S0 ⇌ 1(TT) ⇌ T1 + T1 | (1) |
As proposed by Hanna and Nozik in 2006, SF could be exploited for raising the top limit for the efficiency of PV solar cells5 up to 44.4% by reducing the thermalization losses. The majority of the experimental work until now has been focussing on the SF phenomenon in crystalline aromatic hydrocarbons of the acene type, mainly tetracene and pentacene, and their derivatives, where the yield of the reported triplet excitons reached 200%.2 Nevertheless, the limited choice of the presently available SF materials is a recurrent hurdle for the device development and points out the importance for the search of new materials.
The novel π-conjugated metallo-supramolecular polymers (MSPs)6 presented in this work are composed of molecules reversibly linked into chains via coordination of their end-groups to metal ions; they are also referred to as dynamers.7 They are designed to address the requirements for manufacturing mass electronic devices by wet processes, such as rotogravure printing8 or nanoimprinting.9 A specific configuration of nitrogen atoms allows for the defined tridentate facial–meridian coordination of terpyridine end-groups to the ion couplers10–15 giving MSPs with a well-defined stereochemistry, which is important for the reproducible preparation of functional materials, such as molecular wires.16 This feature is absent in many other MSPs.17
This study focuses on a femtosecond time-resolved transient optical absorption spectroscopy of thin films of α,ω-bis(tpy)terthiophene, T, and its MSP with Zn2+ ion-couplers. In our previous work,18 we have found by transient optical absorption experiments that these two materials, when dissolved in dimethyl sulfoxide, display similar spectroscopic features. Reversible binding of the T molecules with Zn2+ ions in solution resulted in a decrease in the intersystem crossing time constant from a value of 0.5 ns in metal-free solution to 0.13 ns in the presence of an equimolar amount of Zn2+. However, it remained unclear as to why the singlet and triplet photoexcited species in the MSP solution apparently relaxed in concert with a time constant of 1.5 ns.
As we will show in the present report, the spectroscopic features of the singlet and triplet states previously observed in the T/Zn2+ MSP solution were also found in the solid phase. This finding has given us the possibility to identify the nature of the excitations in the MSP in solid state. We present evidence that the singlet and triplet excitations in the solid MSP are coupled through the singlet fission process. The thin films of metal-free T have shown different evolution of excited states, leading to an excimer formation. We will discuss the effect of the supramolecular structure on the outcome of the evolution of the excited states in these two materials.3,19,20
The formation of excimers usually leads to an energy dissipation which in turn decreases the yield of the triplet states from the singlet fission process.21 We will show how the conditions in the MSP solid phase can possibly restrict structural relaxation associated with the excimer formation and therefore allows the singlet fission process to occur. This may be applicable in third-generation photovoltaic devices,22 where the high triplet yield is highly desirable.
Materials and methods
Tetrahydrofuran (THF, Sigma-Aldrich Cat. No 401757-1L, septa sealed bottle, tested for the peroxide content with an indicator paper <2 mg per liter H2O2 equivalent) and zinc acetate (Aldrich, Cat. No. 383317, 99.99% trace metals basis) were used as obtained without further purification. The compound T and its zinc-supramolecular polymer PT (see Fig. 1) were synthesized in a powder form using the synthetic procedure described in our previous papers.23,24Thin film preparation
Films of T and its metallo-supramolecular polymer with Zn (PT) were spin cast at 3000 rpm onto 4 × 5 cm rectangular quartz-glass slide substrates from a hexafluoroisopropanol solution of T and an equimolar mixture of T and zinc acetate, respectively. The solution concentration was 11 mM in both these cases. The films were dried in air and stored in the dark. The film thickness of about 35 nm was determined using a Taylor–Hobson surface profilometer.Wide-angle X-ray diffraction (XRD)
Wide-angle X-ray diffraction (XRD) patterns were obtained from samples deposited by smearing powders of the respective material onto glass substrates. The patterns were acquired in a reflection mode using a Explorer high-resolution diffractometer (GNR Analytical Instruments, Italy). The instrument was equipped with a CuKα radiation source (wavelength λ = 1.54 Å) monochromatized with Ni foil (β filter) and a one-dimensional silicon strip detector, Mythen 1K (Dectris, Switzerland). The measurements were carried out in the range 2θ = 2–50° with steps of 0.1°. The exposure time at each step was 10 seconds. The signal from the substrate was subtracted from the diffraction data. A peak deconvolution procedure was made using a Fityk software.25Transient absorption (TA) spectroscopy
The transient absorption (TA) spectroscopy experiment was described in detail in our previous work.18 In contrast to the previously described apparatus, in this study we used a linearly polarized excitation and detection laser pulses with an adjustable angle α between the polarization directions. Unless otherwise stated, the TA experiments were done with an angle α = 54.7° (so-called “magic angle”) to eliminate the effects of the photoinduced anisotropy decay on the recorded kinetics.26 This approach allowed us to use a polarization filter in the probe light collection optics placed in between the sample and photodetector, to minimize the artifacts caused by the stray light from the pump beam.Quantum-chemical calculations
Quantum-chemical calculations were performed using the Gaussian 09 package.27 We employed the Becke three-parameter Lee–Yang–Parr (B3LYP) method with the 6-31G(d) basis set. The density functional theory (DFT) framework was applied to find the optimized configuration of the ground state of the molecule T in vacuum. Then, the parameters of predicted optical transitions (energies – hνDFT, symmetries, and oscillator strengths – fDFT) from the ground state of the molecule T in the optimized geometry to the excited states were calculated using the time-dependent DFT (TD-DFT) method. The predicted transitions were calculated without a spin preservation requirement, revealing the position of a triplet state that may play role in the singlet fission process.Results
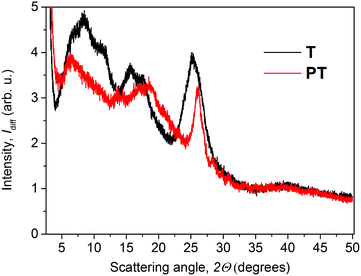
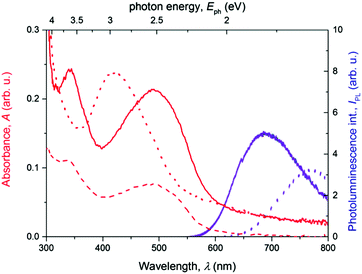
The XRD diffractograms of the as-prepared powder samples of T and PT are shown in Fig. 2. Taking into account the character of the patterns, we can only discuss the basic features to compare these two materials. In the case of the PT sample, the analysis of the diffractograms showed overlapping peaks in the case of the PT sample, resulting in a number of broad diffraction bands. The diffraction peak of PT at around 26°, corresponding to the inter-planar distance of 3.4 Å, coincides with the diffraction peak obtained for T samples. Overall, the PT shows lower number of diffraction peaks compared to T, indicating a relatively lower supramolecular ordering in PT. Areas of amorphous halo were negligible for both samples. Thus we assume a good chance of the substance to be found in a highly ordered state if prepared under suitable conditions. However, we had no goal to improve the crystallization process but only to describe here the internal structure of the powders as they were obtained by synthesis. In further discussion, we assume that the morphologic features observed for powder samples are also applicable to the thin films that were used in photophysical experiments. When we attempted to characterize the thin films using grazing-incidence angle XRD, we only obtained too weak signals for conclusive analysis of the structural differences between these two materials. Additionally, we found no post-synthesis residual traces of zinc acetate in either of its polymorph states28,29 in the PT, which indicates that all Zn2+ ions present in the sample are built in the T/Zn2+ MSP chains.The steady-state optical absorption and luminescence spectra of the T and PT films are shown in Fig. 3. The absorption band of T located at around 420 nm is associated with transitions from HOMO that is spread over the central block of T and the adjacent central rings of tpy end-groups. This band was observed at the same position in the tetrahydrofuran (THF) solution,24 which indicates the lack of specific interactions between π-electronic systems of individual molecules in the ground-state of the solid phase. In the spectrum of PT, the HOMO–LUMO transition band appears at 490 nm, which is red-shifted with respect to T. According to the quantum chemical calculations,24 it is due to the increased delocalization of electrons in polymer chains, as a direct consequence of the MSP formation. The band is red-shifted by 21 nm against its position observed in the THF solution. This indicates that the PT allows significant interactions of π-conjugated electronic systems in their ground-states, differing strongly from the solid T. As in the THF solution, a new band of the solid PT appears at about 332 nm. This band is associated with the transition of tpy end-groups from anti to syn conformation of nitrogen atoms, which accompanies their coordination to Zn2+ ions.10
 | ||
| Fig. 3 The steady-state absorbance (red lines) and fluorescence (magenta lines) spectra of the thin films of free ligand T (dotted lines) and PT (full lines). | ||
As can be seen, the photoluminescence spectra of both T and PT samples show a single structureless band centered at 770 nm and 690 nm, respectively. The apparent Stokes shift, particularly for T, is extremely large for both materials, indicating a deep relaxation of emissive excited states. The lack of structure in the emission bands together with the weak photoluminescence quantum yield suggests that excimers30,31 are formed from the initially photoexcited states in the thin films of T. In the solid PT, a similar energy relaxation of the emissive excited state could also produce a strongly red-shifted emission. But due to the presence of a significant intermolecular interaction in the ground state, we invoke a hypothesis that it is rather a relaxed exciton emission. The low emission yields could be also caused by the formation of non-emissive triplet states32 in a parallel pathway, as we reported previously for solutions of these materials.18
The apparent Stokes shift of PT is much lower than that found for T. This can be explained by steric hindrances caused by the tpy-Zn2+-tpy linkages, which enforce a more rigid molecular structure. The lowered flexibility for supramolecular ordering in PT was apparent also in the WAXS experiments yielding a lower number of diffraction peaks (vide supra) for PT compared to T.
Transient absorption spectroscopy
We will describe here the spectrotemporal evolutions of the differential absorbance ΔA(λpr,t) signal in the samples of solid thin films of the metal-free compound T and its zinc-containing MSP counterpart PT, which we observed in TA experiments. We used various photoexcitation conditions (pulse central wavelength, λex, and its total energy) to stimulate various energy relaxation pathways, in order to map the energetic landscape of the systems under study.Thin solid film of T
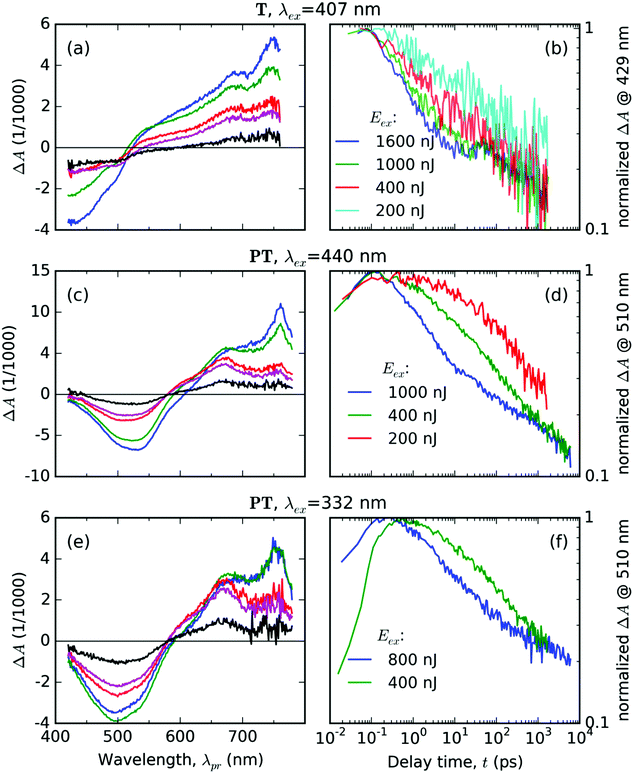
Excitation of the T solid thin film with pulses of the central wavelength λex = 407 nm resulted in the evolution of the transient absorption (TA) spectra as shown in Fig. 4a and b. The early delay time spectrum displayed in Fig. 4a shows two broad spectral features with opposite signs: a negative signal in the range of probe wavelengths 420–520 nm, and a positive signal in the range 520–760 nm. The former overlaps well with the ground-state absorption spectrum as shown in Fig. 3, thus we interpret it as a ground-state bleaching signal (GSB). The positive excited-state absorption (ESA) feature appears structured with two local maxima at the positions about 690 and 750 nm. Further evolution of the TA signals with the increasing delay time can be summarized as an initial rapid partial decay of both GSB and ESA features within the first picoseconds, followed by a period of slower decay rates with the lifetimes exceeding the experimental time window. The TA spectra and kinetics recorded with various pump energies are summarized in Fig. S1 and S2 in the ESI.†The most dramatic evolution occurs at the probe wavelength around 500 nm, i.e., in the area where the ΔA(λpr) signal sign is changing – the isosbestic point (IP), in which the absorbances of the photoexcited sample is the same as in unexcited one. During the first 1.2 ps, the IP progressively blue drifts from its early position at 525 nm down to 515 nm, where it “sits” until 4.8 ps. Then IP gradually red drifts to 545 nm within 57 ps, where it remains for the next 100 ps. Eventually, it again begins to drift to the red – to 590 nm at 1500 ps delay. These IP drifts indicate manifold changes in the electronic configuration of the T molecules in the excited state.
The temporal evolution of the normalized TA signal intensity at the probe wavelength λpr = 429 nm (in the GSB band, see Fig. 4b) exhibits a dependence on the excitation pulse energy; it shows an increase in the initial decay rate with an increase in the pump energy. In the delay time ranging from 10 to 30 ps, the GSB signal decay slowed down, most prominently in the case of the highest total pump energy. At still longer delay times above 30 ps, the rates of the TA signal decay at the GSB probe wavelength are practically identical for all the tested pump energies (see Fig. 4b). This is an evidence for the decay mode transition from a mode driven by mutual interactions between the excited states at early delay times (e.g., annihilation by bimolecular reactions) to a mode driven by spontaneous transitions that do not depend on the concentration of the excited states.
Thin solid film of PT
Excitation of the PT solid film using pulses with central wavelength of λex = 440 nm resulted in the following features of the TA spectra (Fig. 4c and d): (i) a single negative GSB band ranging from 400 to 570 nm and (ii) two positive ESA bands peaking at 760 nm and 670 nm, respectively. The temporal evolution of the normalized TA signal intensity at the probe wavelength λpr = 510 nm (GSB band of PT, see Fig. 4d) exhibits a dependence on the excitation pulse energy – showing a faster decay at an increased pump energy. The relative intensities of the two ESA bands change with the delay time (Fig. 4c). The TA spectra and kinetics recorded using different pump energies are summarized in Fig. S4 and S5 in the ESI.†The TA spectra taken after the UV pulse excitation at λex = 332 nm show similar features (see Fig. 4e and f) as those taken with λex = 440 nm (compare Fig. 4c and e). The positions of the ESA bands are the same and the time evolution of the GSB band also depends on the pump energy (see plots of the normalized GSB time profile at λpr = 510 nm – Fig. 4f). However, the TA signal evolution upon excitation at λex = 332 nm shows a different time profile of the signal onset than the TA signal profile observed upon excitation at λex = 440 nm (Fig. 4d). The kinetics obtained for λex = 332 nm shows a rather slow increase in the GSB band intensity that extends up to delay time t = 0.5 ps observed for the pump energy of 400 nJ. One can see that this increase occurs in the whole range of probe wavelengths of the GSB region (compare the blue curve for the early time delay with the green curve for the later time delay in Fig. 4e). In addition, this increase is accompanied by an increase in the intensity of the ESA band centered at 670 nm, while the intensity of the ESA band at 760 nm does not change. This is a particularly significant observation, because the excitation pulse lasts only for about 70 fs for both values of λex. Hence it is clear that the increase lasting about 500 fs is not driven by the direct absorption of the laser field in this material.
DFT calculations
Our DFT calculations predict that the geometry of the ground state of the T molecule in vacuum possesses the symmetry of the CS point group. A table listing the Cartesian coordinates of atoms in the ground state can be found in the ESI.† The TD-DFT calculations have revealed the number of optical transitions from the CS ground state to higher electronic excited states (see Table 1). The predicted transition to the S1 state was found at an energy of 2.67 eV, which is about 0.15 eV lower than the observed peak in the steady-state absorption (2.82 eV). The latter value was derived from the absorbance spectrum plotted in the linear photon energy scale with the respective Jacobian matrix for the transformation of the absorbance data from Fig. 3 (the photon energy scale plot is not shown).| No. | Symmetry | hν DFT (eV) | λ DFT (nm) | f DFT |
|---|---|---|---|---|
| 1 | A′′ | 1.6631 | 746 | 0 |
| 2 | A′ | 2.3434 | 529 | 0 |
| 3 | A′′ | 2.6739 | 464 | 1.9479 |
| 4 | A′′ | 2.8688 | 432 | 0 |
| 5 | A′ | 3.0074 | 412 | 0 |
| 6 | A′ | 3.135 | 395 | 0 |
| 7 | A′′ | 3.1357 | 395 | 0 |
| 8 | A′′ | 3.1978 | 388 | 0 |
| 9 | A′ | 3.2244 | 385 | 0 |
| 10 | A′ | 3.2249 | 384 | 0.0029 |
| 11 | A′′ | 3.2314 | 384 | 0 |
| 12 | A′ | 3.2377 | 383 | 0 |
| 13 | A′′ | 3.3172 | 374 | 0.0001 |
| 14 | A′ | 3.3196 | 373 | 0.0002 |
| 15 | A′ | 3.6131 | 343 | 0 |
| 16 | A′′ | 3.6211 | 342 | 0 |
| 17 | A′ | 3.6276 | 342 | 0 |
| 18 | A′′ | 3.646 | 340 | 0 |
| 19 | A′ | 3.6474 | 340 | 0.0858 |
| 20 | A′′ | 3.6477 | 340 | 0.0046 |
Interestingly, the calculations also revealed an allowed transition to the S2 state at 3.22 eV, and a spin-forbidden transition with an energy of 1.66 eV to the T1 triplet state. This leads us to the hypothesis that the energy of the S2 state could be sufficient for the production of two T1 states in the singlet fission process.
The electron density topologies for the HOMO and LUMO orbitals in the T molecule are shown in Fig. S7 in the ESI.† Unfortunately, we were not able to perform similar DFT calculations for the PT molecule due to its strongly increased complexity and corresponding increase of required computation resources.
Discussion
Spectral analysis of the time-resolved TA spectra
We performed the decomposition of the spectrotemporal evolution of the TA signals, ΔA(λpr,t), into a time-invariant spectral model of the excited-state species, which is composed of two spectral components: εX(λpr) and εY(λpr), and their respective temporal evolutions: aX(t) and aY(t). We constructed the spectral model functions33εX(λpr) and εY(λpr) based on the result of global analysis, from the shapes of the EADS (see the section Global analysis of the time-resolved TA spectra in the ESI†). The optimization of the aX(t) and aY(t) values was done with the help of the linear least squares method by minimizing the residual function δ(λpr,t) in the following equation at each experimental delay time t separately:| ΔA(λpr,t) = aX(t)εX(λpr) + aY(t)εY(λpr) + δ(λpr,t) | (2) |
Thin solid films of T
In the case of thin films of T, we chose two EADS shown in Fig. 5 and decomposed the signal ΔA(λpr,t) directly into the respective components εX(λpr) and εY(λpr) with the weight factors aX(t) and aY(t) as fitting parameters (see eqn (2)) for each experimental delay time t. As can be seen from Fig. 6a–d, this approach gives good fits for t > 2 ps for all three representative probe wavelengths and all experiments with the varying pump energy. At earlier times, our spectral model does not incorporate the spectral evolution caused by the internal vibronic relaxation (IVR) processes.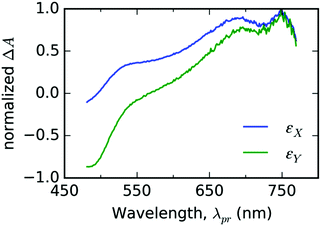 | ||
| Fig. 5 The fit bases εX(λpr) (blue line color) and εY(λpr) (green line color) used for spectral analysis of TA spectrotemporal data measured with thin solid film of free ligand T. | ||
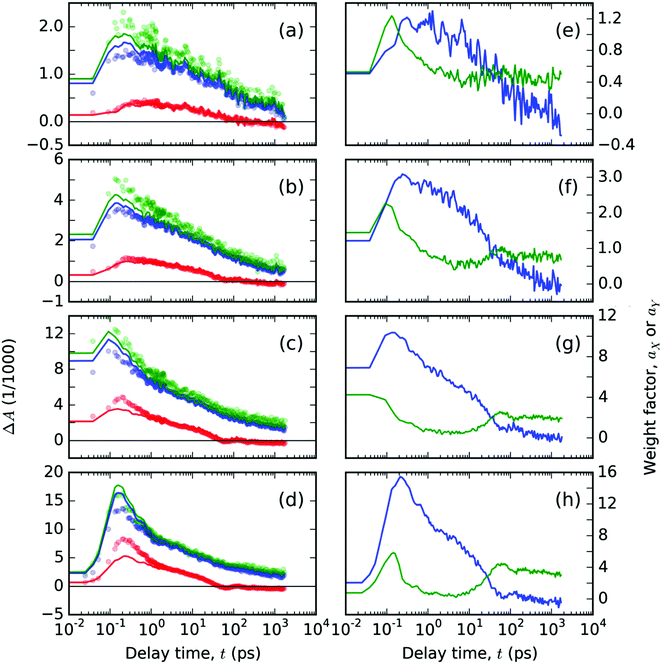 | ||
| Fig. 6 Spectral analysis of TA signals, ΔA(λ,t), free ligand T thin solid film: (a–d) the temporal evolutions of the ΔA(λ,t) plotted with circles at the representative probe wavelengths λ: (red) 550, (blue) 680 and (green) 740 nm. Full lines in panels (a–d) represent the best-fitting curves obtained from spectral analysis with eqn (2) using the base functions as shown in Fig. 5, with the respective time-dependent weight factors, (blue) aX and (green) aY, as shown in panels (e–h). The two panels in each row contain the data from experiments with a pump at 407 nm with varying pulse energies 200, 400, 1000 and 1600 nJ, respectively, in the order from top to bottom. | ||
The obtained evolutions of aX(t) and aY(t) parameters (Fig. 6e–h) show that the onset of the aY(t) parameter occurs at a uniform delay time interval from 10 to 50 ps for all the pump intensity values. This result indicates that the photochemical species associated with the spectral profile εY(λpr) emerge spontaneously at a delay time that does not depend on the concentration of the excited states.
The longest lifetimes derived from our TA experiments on the thin films of T were in the range 2.6–4.0 ns (Fig. S3 in the ESI†). This agrees well with the reported longest lifetime of 2.73 ns obtained from the multiexponential fit of the photoluminescence decay data.24 Thus we can conclude that the longest living excited state is of the excimer type. Evidence supporting the formation of excimers in the solid T has been recently obtained also from the luminescence spectra of the solid T diluted in the solid KBr.37 The excimer formation also explains the extraordinary large Stokes shift observed for the solid T. The difference between the Stokes shifts of T observed for the thin film and diluted solution, respectively,18,24 which is equal to ca. 0.8 eV, can be regarded as the stabilization energy of the excimer according to ref. 31. Such a stabilization energy of the excimer is quite large to prevent it from diffusional motion and thus also from mutual excimer interactions. The long delay time kinetics are then governed by spontaneous transitions, which also explains why the GSB kinetics at t > 30 ps are no longer dependent on the excitation pulse energy (see Fig. 4b).
Formation of excimers38 can also be responsible for an increase in the negative signal in the spectral region 470–550 nm (GSB band) observed for T (see Fig. 4a, curves for 20–21 ps and 50–55 ps delay times). A coherent coupling of the isolated singlet states S1 and S0 of the two molecules within the excimer leads to the transformation of the isolated states into two excimer states, |EM+〉 and |EM−〉, which are split by the interaction energy, denoted as |J1|. The optical transitions from the new excimer states differ in the intensity due to the selection rules: only the ESA from |EM+〉 can be probed in the TA experiment in the spectral range of GSB (for details please see the section Optical transitions in excimers using dipole approximation in the ESI†). At the instant of excimer formation, the two new states exchange population through coherent coupling, but the relaxation leads to a population transfer from |EM+〉 to the lower-lying and optically dark |EM−〉. If we assume that the transition energy from |EM+〉 falls within the long-wavelength shoulder of the GSB band of the T, we can assign the brief strengthening of the negative signal in that region to the excimer relaxation associated with the reduction of the positive ESA signal from the |EM+〉 population. This is because both molecules forming the excimer are screened from absorption from the ground state after its relaxation to the state |EM−〉 (cf. the corresponding section in the ESI†). At the same delay time range, we also observe a negative signal decay plateau at a probe wavelength of 429 nm, being most prominent for the high pump intensities (Fig. 4b). We assume that the ESA from |EM+〉 is negligible in this spectral region and that we observe the prevailing GSB signal, which remains intact by the excimer relaxation process. From the result of global analysis (see Fig. S3 in the ESI†), we have determined the range of 20–30 ps for the time constant of the spontaneous excimer relaxation.
Thin solid film of PT
In the following part, let us assume that the ESA features of the PT thin film found at λpr = 760 nm and λpr = 670 nm each belongs to a different distinguishable excited state. Due to their good correspondence with the singlet and triplet excited states found for T in DMSO solution (cf.Fig. 7), we can assign those features to the singlet and triplet excitons, respectively. In the results of global analysis (Fig. S6 in the ESI†), we could distinguish the presence of the singlet and triplet features in varying proportions in the individual EADS. It allowed us to construct a new set of two spectral components: εS(λpr) for the singlet and εT(λpr) for the triplet excitons, using a linear combination of the selected pairs of EADS, εi and εj. As a guide for the desirable shapes of the components, we have used the individual EADS obtained in our previous paper on the DMSO solutions of the same material:18| εS = εi − qεj | (3) |
| εT = εi − kεj |
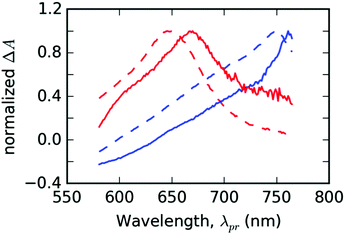 | ||
| Fig. 7 The fit bases used for the spectral analysis of PT thin solid films (full lines) compared with the species-associated differential spectra (SADS) obtained by the global analysis of TA solution of ligand T in DMSO (dashed lines). Spectral profiles of singlet (εS) and triplet (εT) states are plotted in the blue and red colors, respectively. The data from solutions were taken from ref. 18. | ||
In the GSB region, the transformation according to eqn (3) failed in assigning the correct weights to contributions of the respective photochemical species. Thus, we did not evaluate the correspondence of the spectral shapes in the GSB probe wavelength region.
Using the time-invariant spectral profiles εS(λpr) and εT(λpr), we could decompose the experimental TA signal, ΔA(λpr,t), in the probe spectral range of 600–800 nm into the temporal evolutions of the respective weight factors aS(t) and aT(t) using eqn (2) and identities εX = εS, εY = εT, aX = aS and aY = aT. The Beer–Lambert law predicts the proportionality of the weight factors aS(t) and aT(t) to the concentration of the proposed singlet and triplet excited states, cS(t) and cT(t), respectively. However, due to the unknown values of absorption cross-sections of the respective excited states, the calculation of instantaneous relative concentrations (or fractions) required further scaling. We utilized the TA signal in the range of GSB for scaling, with an explicit assumption of equal contributions of both excited states in this probe wavelength range (495–505 nm) denoted as ΔAGSB(t):
| ΔAGSB(t) = wSaS(t) + wTaT(t) + δ′(λpr,t), | (4) |
Using the linear least squares minimization method, we have found the best-fitting time invariant scaling factors wS and wT, for which the residual function δ′(λpr,t) reached a minimal value. The representative fitted kinetic profiles (Fig. 8) show that the spectral model eqn (2) fits the data quite well, and that there are no significant contributions from the photochemical species other than the two considered in eqn (4). One can observe slight underestimation of the TA signal at 745 nm (dominant feature assigned above to the singlet excited species) and slight overestimation of the signal at 670 nm. The only exceptions are the data obtained with the highest pump energy at early delay times: 1000 nJ for 440 nm (Fig. 8c) and 800 nJ for 332 nm pump wavelengths (Fig. 8e). At the delay times above 1 ps, the error of the fit was always sufficiently low.
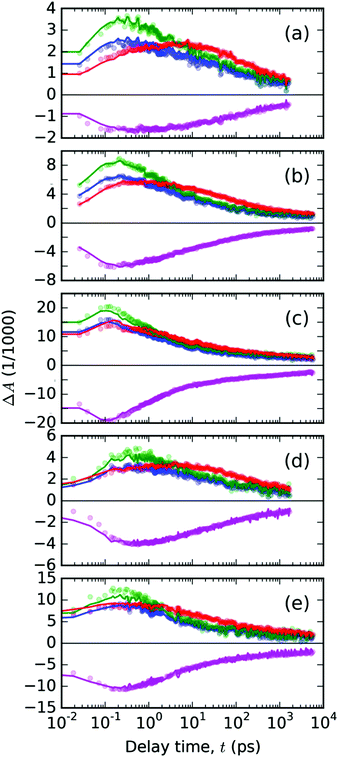 | ||
| Fig. 8 The temporal evolutions of the ΔA(λ,t) in the PT thin solid film plotted with points at the representative probe wavelengths λpr (color of points denotes λpr in nm: 720 – blue, 745 – green, 670 – red, 500 – magenta). The panels (a–c) contain the data from experiments with pump at 440 nm with varying pulse energies 200, 400 and 1000 nJ, respectively. The data from pump at 332 nm are shown in panels (d) – 400 nJ and (e) – 800 nJ. Full lines with the positive signals in the spectral range of 600–800 nm represent the best-fitting curves obtained from the spectral analysis with eqn (2); the full magenta lines with the negative TA signal in the GSB region were used to fit the scaling weight factors in eqn (4). | ||
In Fig. 9a and b we show the obtained evolutions crS(t) and crT(t). Their values are normalized to the maximum value of the singlet excited state concentration. This representation allowed us to compare the singlet exciton population decay rates as well as the relative triplet exciton yields (value of the maximum at the respective crT(t) curve) under varying pump conditions. At the first glance, one can see that the evolution of the singlet as well as triplet exciton population depends on the pump conditions and that each kind of excitation follows a different kinetic profile. This observation strongly supports the hypothesis that the spectral features used in the performed analysis (see Fig. 7) indeed represent two distinguishable photochemical species; because if they belonged to the same species, they should emerge and decay in concert. A second glance at the double-log plots tells us that all the decay kinetics are non-exponential, following rather apparently linear (i.e. power-law) time dependencies. It suggests that the kinetics is dominated by a bimolecular reaction such as exciton–exciton annihilation, which is the usual reason for the observed increase in the exciton population decay rate at the increased intensity of the photoexcitation.39,40 This is consistent with our hypothesis on the mutual annihilation of either excited species. In our case, the singlet exciton population decayed at the timescale of tens of picoseconds, whereas the triplets at the nanosecond timescale. This can be understood in the frame of the mutual annihilation hypothesis as a result of a much lower interaction rate of triplet excitons arising from a slower energy transfer when the non-zero spin value must be preserved, when compared to the singlet exciton energy transfer case.32
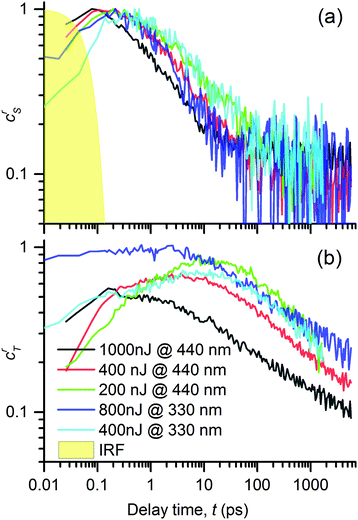 | ||
| Fig. 9 Time evolutions of the excited states in the PT thin film: (a) concentration of singlet excitons, crS, and (b) concentrations of triplet exciton, crT, obtained by the spectral analysis of TA signals, ΔA(λ,t), using eqn (2) and (4). Excitation with light pulses centered at 440 and 332 nm and varying pulse energies (see the legends). | ||
Let us now discuss the detailed relations between the decay of singlet excitons and the onset of triplet excitons, as shown in Fig. 9, under varying pump conditions. In the case of a pump at 440 nm, we observed that the faster the singlet decay, the faster the rise in triplet exciton population. The population of the singlet species had fallen to 50% of its maximum value in 1, 2.5 and ≈4.5 ps, for the pump energies of 1000, 400 and 200 nJ, respectively, whereas the population of the triplet excitons reached the peak values at 0.2, 4 and 10 ps, respectively. This correspondence suggests that the triplet excitons are created as a product of mutual interactions of the singlet excitons.
For λex = 332 nm, we obtained a rather similar behavior like that for λex = 440 nm. However, the most significant difference was the high fraction of triplets practically instantly after the excitation (roughly equal to the singlet population for a pump energy of 800 nJ). This generation of the triplet states is particularly fast if it is compared to the characteristic time of the intersystem crossing (ISC), τISC = (130 ± 3) ps, as observed in DMSO solution of the PT.18 It led us to the conclusion that the triplet state T1 was generated via a process of singlet fission1,2 (SF) from the higher excited state S2 that was directly photoexcited by light of 332 nm (cf. the absorbance spectrum in Fig. 3).
The SF phenomenon could also explain the apparent post-pulse increase of the GSB signal upon UV excitation (see Fig. 4e and f), because it accounts for two triplet excited states from each singlet photoexcited state. We observed this effect at both tested pump intensities; it was stronger for the lower intensity. Such intensity dependence complements well with the observed kinetic symptoms of mutual exciton annihilation processes: at lower photoexcitation densities, the annihilation is less pronounced giving more significance to other competing processes. Unfortunately, the annihilation and competing non-resonant internal conversion process (such as exciton relaxation, or self-trapping) prevented us from the estimation of the yield of the triplet excitons. Using the known value of the instrument response function τIRF = 70 fs, we used the early kinetics of the GSB for the excitation at 332 nm to estimate that the SF process time constant could be as fast as τSF = 160 fs (as obtained from the time constant of the early GSB signal rise).
The overall lifetime of the triplet excitons is probably limited either by their mutual annihilation or by an interaction with atmospheric oxygen molecules. The oxygen molecule readily accepts the energy as well as the spin.41 The morphology of thin films provides a good access for the oxygen molecules.
Fig. 10 shows the Jablonski diagram of the proposed transitions of the excited states in both the T and PT thin films.
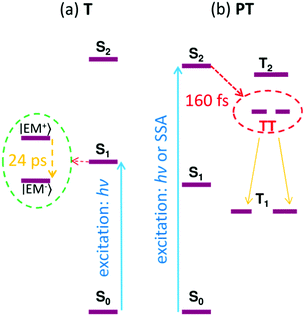 | ||
| Fig. 10 The Jablonski diagram reconstructed for the thin films of compounds T (a) and PT (b), respectively. SSA = singlet–singlet annihilation; hν = energy of the absorbed photons. | ||
Conclusions
The time-resolved transient absorption spectroscopic experiments with thin solid films of T have revealed a spontaneous formation of excimers upon photoexcitation. The excimer relaxation time constant is in the range of 20–30 ps, and the excimer lifetime was found to be about 3 ns. The stabilization energy of the excimers is quite large ∼0.8 eV, which prevents their diffusional motion and the excimers are trapped instead. Prior to the exciton relaxation, the observed excited state decay can be attributed to the mutual excimer annihilation by the Förster energy transfer mechanism due to its power-law temporal profile and dependence of the corresponding time constant on the excitation intensity. This process is blocked after the formation of an optically inactive relaxed excimer state. We have observed no evidence of a triplet state formation in the solid thin films of T.In contrast, in thin films of PT, the triplet excitons are created immediately after the 70 fs excitation pulse at a wavelength of 332 nm corresponding to excitation of S2 (higher excited singlet state). This process is too fast to be explained by an intersystem crossing for which we have earlier determined the time constants τISC in range of 130–500 ps in DMSO solution of the same material.18 Moreover, the rise of the triplet exciton population strongly depends on the excitation pulse energy, which indicates a bimolecular interaction mechanism such as singlet–singlet annihilation. With the excitation at λex = 332 nm, the total population of the excited states, as obtained from the GSB signal, continued to increase even after the excitation pulse impact. This indicates that the population of the excited states was increasing even at delay times after the photoexcitation had been completed. An intensity increase of the signal of triplet excitons has been found to be synchronized with the post-excitation increase in the GSB signal, which indicates that excess of excitons are produced in the triplet form from the singlet fission process. The singlet and triplet exciton populations interact mutually through bimolecular reactions (annihilations), giving rise to a complicated pump-energy dependent non-exponential kinetics, and unfortunately hinders the estimation of the triplet exciton yield from the SF process.
We can thus conclude that the singlet fission occurs in the PT thin solid films, when the material is excited to the S2 state. We estimated the time constant of the SF process to be as fast as 160 fs. The excited state S2 could be reached either directly using the UV excitation at λex = 332 nm, or by the annihilation of two singlet excitons in the S1 state. To the best of our knowledge, this is the first time that the singlet fission was observed in metallo-supramolecular coordination polymers.
The details of the singlet fission process in our materials are similar to those reported on the photophysical phenomenon for an amorphous solid film of polythiophene derivatives,42 in which the process was mediated through mutual exciton annihilations. Some similarity can be found also with carotenoid aggregates,43 where the singlet fission process competes with another ultrafast internal conversion quenching process involving a lower-lying excited state.
The reported results are also of general importance for research in the field of singlet fission materials: the ground-state-bleaching (GSB) signal in TA spectroscopy is often used as a scaling parameter to determine the triplet yield from singlet fission44 by the so-called singlet depletion method.45 Thus, a special care must be undertaken if one wants to distinguish whether the observed GSB increase originates from an excimer formation or from the singlet fission. Both processes lead to additional bleaching of absorption of molecules that remained in the ground state after the excitation pulse impact.
Author contributions
The manuscript was written by contributions from all authors. All authors have given approval to the final version of the manuscript.Acknowledgements
This work was supported by the Czech Science Foundation (project P108/12/1143) and the Ministry of Education, Youth and Sports of the Czech Republic, under grants LD14011 and LO1507 (National Sustainability Program I (NPU I), Project POLYMAT) as well as by the COST Actions CM1302 (SIPS) European Network on Smart Inorganic Polymers and MP1202 (HINT) Rational Design of Hybrid Interfaces. Access to the computing and storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum provided under the programme “Projects of Large Research, Development, and Innovations Infrastructures” (CESNET LM2015042) is greatly appreciated.References
- S. Singh, W. J. Jones, W. Siebrand, B. P. Stoicheff and W. G. Schneider, J. Chem. Phys., 1965, 42, 330–342 CrossRef CAS.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- H. L. Stern, A. J. Musser, S. Gelinas, P. Parkinson, L. M. Herz, M. J. Bruzek, J. Anthony, R. H. Friend and B. J. Walker, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7656–7661 CrossRef CAS PubMed.
- N. R. Monahan, D. Sun, H. Tamura, K. W. Williams, B. Xu, Y. Zhong, B. Kumar, C. Nuckolls, A. R. Harutyunyan, G. Chen, H.-L. Dai, D. Beljonne, Y. Rao and X.-Y. Zhu, Nat. Chem., 2017, 9, 341–346 CrossRef CAS PubMed.
- M. C. Hanna and A. J. Nozik, J. Appl. Phys., 2006, 100, 074510 CrossRef.
- D. Cram, Science, 1988, 240, 760–767 CAS.
- J.-M. Lehn, Prog. Polym. Sci., 2005, 30, 814–831 CrossRef CAS.
- J. Sheats, J. Mater. Res., 2004, 19, 1974–1989 CrossRef CAS.
- S. Franssila, Polymer Microprocessing, John Wiley & Sons, Ltd, 2010, pp. 203–223 Search PubMed.
- U. S. Schubert, H. Hofmeier and G. R. Newkome, Modern Terpyridine Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 2006 Search PubMed.
- A. M. Cargill Thompson, Coord. Chem. Rev., 1997, 160, 1–52 CrossRef.
- V. Duprez, M. Biancardo, H. Spanggaard and F. Krebs, Macromolecules, 2005, 38, 10436–10448 CrossRef CAS.
- A. Wild, A. Winter, F. Schlutter and U. S. Schubert, Chem. Soc. Rev., 2011, 40, 1459–1511 RSC.
- E. C. Constable, Chem. Soc. Rev., 2007, 36, 246–253 RSC.
- F. Schlütter, G. Pavlov, J.-F. Gohy, A. Winter, A. Wild, M. Hager, S. Hoeppener and U. Schubert, J. Polym. Sci., Part A: Polym. Chem., 2011, 49, 1396–1408 CrossRef.
- R. Sakamoto, K.-H. Wu, R. Matsuoka, H. Maeda and H. Nishihara, Chem. Soc. Rev., 2015, 44, 7698–7714 RSC.
- D. Gates, Annu. Rep. Prog. Chem., Sect. A: Inorg. Chem., 2006, 102, 449–468 RSC.
- D. Rais, M. Menšík, P. Bláhová, J. Svoboda, J. Vohlídal and J. Pfleger, J. Phys. Chem. A, 2015, 119, 6203–6214 CrossRef CAS PubMed.
- H. Liu, V. M. Nichols, L. Shen, S. Jahansouz, Y. Chen, K. M. Hanson, C. J. Bardeen and X. Li, Phys. Chem. Chem. Phys., 2015, 17, 6523–6531 RSC.
- B. J. Walker, A. J. Musser, D. Beljonne and R. H. Friend, Nat. Chem., 2013, 5, 1019–1024 CrossRef CAS PubMed.
- D. Beljonne, H. Yamagata, J. L. Bredas, F. C. Spano and Y. Olivier, Phys. Rev. Lett., 2013, 110, 226402 CrossRef CAS PubMed.
- M. A. Green, Third generation photovoltaics advanced solar energy conversion, Springer, Berlin, New York, 2006, vol. 12 Search PubMed.
- J. Svoboda, P. Štenclová, F. Uhlík, J. Zedník and J. Vohlídal, Tetrahedron, 2011, 67, 75–79 CrossRef CAS.
- P. Bláhová, J. Zedník, I. Šloufová, J. Vohlídal and J. Svoboda, Soft Mater., 2014, 12, 214–229 CrossRef.
- M. Wojdyr, J. Appl. Crystallogr., 2010, 43, 1126–1128 CrossRef CAS.
- G. Fleming, J. Morris and G. Robinson, Chem. Phys., 1976, 17, 91–100 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian Inc., Wallingford CT, 2010 Search PubMed.
- W. Clegg, I. R. Little and B. P. Straughan, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 1701–1703 CrossRef.
- H. He, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m3291–m3292 CAS.
- J. B. Birks, Nature, 1967, 214, 1187–1190 CrossRef CAS.
- S. A. Jenekhe and J. A. Osaheni, Science, 1994, 265, 765–768 CAS.
- A. Köhler and H. Bässler, Mater. Sci. Eng., R, 2009, 66, 71–109 CrossRef.
- I. H. van Stokkum, D. S. Larsen and R. van Grondelle, Biochim. Biophys. Acta, Bioenerg., 2004, 1657, 82–104 CrossRef CAS PubMed.
- Y. Ogata, D. Kawaguchi and K. Tanaka, Sci. Rep., 2015, 5, 8436 CrossRef PubMed.
- S. T. Roberts, R. E. McAnally, J. N. Mastron, D. H. Webber, M. T. Whited, R. L. Brutchey, M. E. Thompson and S. E. Bradforth, J. Am. Chem. Soc., 2012, 134, 6388–6400 CrossRef CAS PubMed.
- S. Lukman, A. J. Musser, K. Chen, S. Athanasopoulos, C. K. Yong, Z. Zeng, Q. Ye, C. Chi, J. M. Hodgkiss, J. Wu, R. H. Friend and N. C. Greenham, Adv. Funct. Mater., 2015, 25, 5452–5461 CrossRef CAS.
- T. Vitvarová, J. Svoboda, M. Hissler and J. Vohlídal, Organometallics, 2017, 36, 777–786 CrossRef.
- J. B. Birks, Rep. Prog. Phys., 1975, 38, 903 CrossRef CAS.
- E. Engel, K. Leo and M. Hoffmann, Chem. Phys., 2006, 325, 170–177 CrossRef CAS.
- O. Kühn and S. Lochbrunner, Semicond. Semimetals, 2011, 85, 47–81 Search PubMed.
- C. Schweitzer and R. Schmidt, Chem. Rev., 2003, 103, 1685–1758 CrossRef CAS PubMed.
- J. Guo, H. Ohkita, H. Benten and S. Ito, J. Am. Chem. Soc., 2009, 131, 16869–16880 CrossRef CAS PubMed.
- A. J. Musser, M. Maiuri, D. Brida, G. Cerullo, R. H. Friend and J. Clark, J. Am. Chem. Soc., 2015, 137, 5130–5139 CrossRef CAS PubMed.
- P. E. Hartnett, E. A. Margulies, C. M. Mauck, S. A. Miller, Y. Wu, Y.-L. Wu, T. J. Marks and M. R. Wasielewski, J. Phys. Chem. B, 2016, 120, 1357–1366 CrossRef CAS PubMed.
- I. Carmichael and G. L. Hug, J. Phys. Chem. Ref. Data, 1986, 15, 1–250 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7tc00484b |
| ‡ Present address: Institute of Physics of the Czech Academy of Sciences, Cukrovarnická 10/112, 162 00 Praha 6, Czech Republic. |
| This journal is © The Royal Society of Chemistry 2017 |