 Open Access Article
Open Access ArticleAuxetic mechanical metamaterials
H. M. A. Kolken
 * and
A. A. Zadpoor
* and
A. A. Zadpoor
Department of Biomechanical Engineering, Delft University of Technology, Delft, The Netherlands. E-mail: h.m.a.kolken@student.tudelft.nl; Tel: +31-653258953
First published on 17th January 2017
Abstract
The surge of interest in so-called “designer materials” during the last few years together with recent advances in additive manufacturing (3D printing) techniques that enable fabrication of materials with arbitrarily complex nano/micro-architecture have attracted increasing attention to the concept of mechanical metamaterials. Owing to their rationally designed nano/micro-architecture, mechanical metamaterials exhibit unusual properties at the macro-scale. These unusual mechanical properties could be exploited for the development of materials with advanced functionalities, with applications in soft robotics, biomedicine, soft electronics, acoustic cloaking, etc. Auxetic mechanical metamaterials are identified by a negative Poisson's ratio and are perhaps the most widely studied type of mechanical metamaterials. Similar to other types of mechanical metamaterials, the negative Poisson's ratio of auxetics is generally a direct consequence of the topology of their nano/micro-architecture. This paper therefore focuses on the topology–property relationship in three main classes of auxetic metamaterials, namely re-entrant, chiral, and rotating (semi-) rigid structures. While the deformation mechanisms in the above-mentioned types of structures and their relationship with the large-scale mechanical properties receive most attention, the emerging concepts in design of auxetics such as the use of instability in soft matter and origami-based structures are discussed as well. Furthermore, the data available in the literature regarding the elastic properties of auxetic mechanical metamaterials are systematically analyzed to identify the spread of Young's modulus–Poisson's ratio duos achieved in the auxetic materials developed to date.
1. Introduction
Mechanical metamaterials1,2 have emerged during the last few years as an exciting paradigm for developments of materials with unusual mechanical properties and advanced functionalities. The unusual mechanical properties include negative Poisson's ratio, negative elasticity and negative compressibility.3 The term “metamaterials” was initially used within the context of optics and electromagnetism,4–6 but today refers to all materials engineered to exhibit novel properties not usually found in nature. The macro-scale properties of metamaterials originate from their small-scale topology (i.e. nano/micro-architecture). The small-scale topology of metamaterials can therefore be designed to obtain specific mechanical or physical properties.3,7 That is why metamaterials are sometimes referred to as “designer materials”. Recent advances in additive manufacturing (AM) have enabled the fabrication of structures with arbitrarily complex nano/micro-architecture, which has attracted increasing attention to the concept of mechanical metamaterials.3,8Study of the relationship between the small-scale topology and macro-scale mechanical properties of mechanical metamaterials is therefore highly relevant. In this paper, we will review several decades of research on topology–property relationship in a specific class of mechanical metamaterials collectively referred to as auxetic materials. The term “auxetics” was introduced by Evans in 1991.9 It is derived from the Greek word “auxetikos” and refers to “what tends to increase”.10 Stretching a piece of auxetic material results in a lateral expansion instead of contraction. The ratio of lateral contraction (transverse strain) to that of axial stretch (longitudinal strain) is named after Siméon Denis Poisson11 and ranges between −1.0 and +0.5 for isotropic materials. According to Greaves et al. (2011), “the Poisson's ratio describes the resistance of a material to distort under mechanical load rather than to alter in volume”.12 First proof of these negative Poisson's ratio (NPR) materials dates back to the 1870s,13 while Lakes was the first one to intentionally design such a material in 1987.14,15
The existence of natural auxetic materials remains controversial from the perspective of traditional mechanics,16 but some researchers have reported the auxetic behavior in cancellous bone, living cow skin, tendons, certain minerals and some zeolites.17–23 Their Poisson's ratio was found to originate from its geometry or microstructure and the way it deforms under uniaxial loading.24 The latter, so-called deformation mechanism can operate at any scale, due to the Poisson's ratio being scale-independent. This allows NPR materials to be classified by their geometry or deformation mechanism(s).24–27 Three well-established basic structures can be identified, which aid in the explanation of these mechanisms: re-entrant structures, chiral structures, and rotating rigid structures.27 Other mechanisms exist as well, but fall beyond the scope of this review. Examples include the triangular network of shock-absorbers, which axially deform and maintain their relative angles,28 as well as the inherently auxetic double-helix yarn presented by Miller et al. (2009), which deforms through a reversal of the stiff, outer wrap and the more compliant, thicker core.29
Auxetic structures have since been widely applied in the development of novel products, such as running shoes, shape memory foams, and bioprostheses.30–32 This is not only for their unusual mechanical response, but auxetics also offer a route to attaining extreme values of other material properties, like a higher indentation resistance, shear resistance, energy absorption, hardness and fracture toughness.16,24,30,33 The ability to design a material with a structure that exhibits a desired set of mechanical properties, including a negative Poisson's ratio, has led to the development of auxetic mechanical metamaterials.
In what follows, we will present an overview of the auxetic structures. We will compare the mechanical properties of different auxetic structures to indicate which topological features give rise to certain types of mechanical behavior. The mechanical properties of different geometries of auxetic structures will be presented according to their deformation mechanism(s). The paper has therefore been divided into three main sections, each handling a different set of deformation mechanism(s), named after the corresponding basic structure. Special attention has been paid to the geometrical parameters of the structures, and their role in attaining a negative Poisson's ratio.
2. Re-entrant structures
Re-entrant refers to something “directed inward” or having a negative angle,34 which directly applies to the ribs of the “bow-tie” honeycomb in Fig. 1.25 The deformation of re-entrant structures is dominated by the re-alignment of cell ribs (hinging), although deflection and axial deformation (stretching) of the cell ribs are also among the mechanisms responsible for the auxetic behavior.35,36 | ||
| Fig. 1 Re-entrant bow-tie structure with θ being the re-entrant angle, h/l being the cell rib length ratio and w being the thickness of the ribs. (1) In rest. (2) Tensile loading in y-direction.25 | ||
2.1 Foams
The development of intentionally designed auxetic materials dates back to 1987,14,15 when Lakes proposed his foam transformation procedure. This process involved the transformation of conventional, open-cell thermoplastic foams to foams that exhibit re-entrant structures. The foam was triaxially compressed (compression factor of between 1.4 and 4) in a mold and subsequently heated to a temperature slightly above its softening temperature. The mold was then cooled to room temperature, after which the foam could be extracted to undergo relaxation.14 This procedure will transform conventional polyhedral unit cells into their re-entrant siblings, where the cell ribs of each cell permanently protrude inward. Triaxial compression during the foaming process enables the transformation of thermosetting foams,37 whereas sequential triaxial plastic compression is used to obtain re-entrant metallic foams.14,37In 1997, Chan & Evans proposed a multi-stage heating and compression method for production of large auxetic foam blocks.38 Recently, Quadrini et al. (2015) proposed a fabrication method for auxetic epoxy foams based on solid state foaming.39 Unlike Lakes' transformation method, this process leaves the cell structure intact.39 Unfortunately, the resulting materials are usually anisotropic, making it hard to determine a relationship between the elastic constants. Several experiments have therefore been performed to examine the properties of various foam specimens.37,40–46
Shortly after Lakes's introduction, Friis et al. (1988) studied transformed polymeric and metallic foams.37 All foams were found to exhibit a negative Poisson's ratio and smaller elastic moduli as compared to the initial foaming material.37 This can be explained by the presence of buckled ribs in the auxetic foams, which are far easier to deform.40 Subsequently, the resulting foams appear to be more resilient in all three orthogonal directions, showing a nearly linear stress–strain relation up to 40% strain.14,37 Other studies demonstrated the non-linear dependency of the Poisson's ratio on axial strain.40,42,43 This can be explained by the alignment of cell ribs at large strains, inducing multiple deformation mechanisms. The Poisson's ratio reached a relative minimum of −0.7 for polymeric foams at 2–5% strain42 and −0.8 for metallic foams at 0.1% strain.43
Most of the differences between conventional and auxetic foams have been attributed to a change in the cell geometry, governed by the volumetric compression ratio.45 Increasing the volumetric compression ratio gives rise to a relative minimum in Poisson's ratio, a decrease in Young's modulus (by a factor of 2)40,45 and an increase in shear modulus41 and toughness.42,43 However, polymeric foam in tension may experience an increase in Young's modulus at high volumetric compression ratios due to cell rib adhesion or interference.45
Indentation tests performed by Lakes & Elms (2000) revealed that re-entrant foams have higher yield strengths and energy absorptions than conventional foams of identical original density.44 The reconversion of a returned shape memory foam into a second auxetic phase even enhanced the energy dissipation.46 Fig. 2 schematically illustrates the response of auxetic materials when subjected to indentation.25
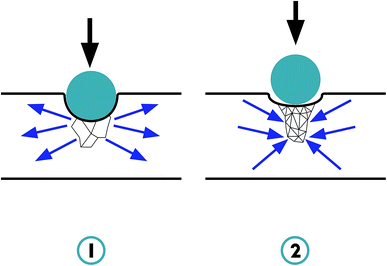 | ||
| Fig. 2 Deformation profile of (1) non-auxetic material and (2) auxetic material.25 | ||
Besides the thermo-mechanical conversion processes used in the above experiments, several chemo-mechanical processes have been proposed to avoid high temperatures and improve product quality. Grima et al. (2009) placed their triaxially compressed PU foam in acetone for an hour, after which it was air-dried in its compressed state.47 The resulting foam showed similar properties to those obtained from the thermo-mechanical process, and could be re-converted to conventional foam using the same organic solvent.47 Li et al. (2016) recently introduced the use of CO2 as a processing agent, eliminating the need for a volatile organic solvent.48 CO2 strongly reacts with polymers possessing electron-donating groups, like the styrene acrylonitrile copolymer (SAN) found in PU foams, and enhances the polymer chain mobility, which significantly reduces the glass transition temperature. The process, involving the compression of a foam specimen into a CO2 fed pressure reactor, can therefore be executed at ambient temperatures.48 After equilibrium, the pressure can be released and the SAN particles resume their glassy state, fixing the inwardly buckled structure.48 This process is not only efficient, economical and environmentally benign, it also realizes the large scale manufacturing of auxetic foams exhibiting a strain-independent Poisson's ratio (up till 50% strain).48
Several theoretical models were created to analyze and predict the mechanical properties of auxetic foams. Two-dimensional hexagonal honeycombs were initially used to model the behavior of conventional foams, as proposed by Gibson & Ashby (1988).49 A re-entrant three-dimensional elongated dodecahedron was later used to adequately model a foam.50 Choi & Lakes (1995) used a strain energy technique45 and later included rotation due to plastic hinge formation,51 while previous models solely focused on the deflection of cell ribs. Masters & Evans (1996) finally combined all three deformation mechanisms to form a general model in 2D.35
Broken cell ribs were observed in processed foams by Smith et al. (2000), who proposed a two-dimensional missing rib foam model.36 The model was found to be superior to the existing two-dimensional models in predicting the strain-dependent Poisson's ratio.
According to Grima et al. (2005), neither of the above-mentioned structural modifications has been experimentally justified as the main initiator of the auxetic effect.52 They therefore proposed a model that is based on the hypothesis that major deformations take place along the length of the ribs, whereas the geometry at the joints and the topology of the system are conserved. The rigid joints are proposed to behave like rigid triangles, which will rotate relative to each other to generate the auxetic effect (see Section 4.2).52 Although presented as the predominant mechanism underlying the auxetic effect, they properly state that other mechanisms, like the ones presented above, may work in parallel.52
2.2 Honeycombs
A honeycomb usually refers to the regular array of prismatic hexagonal cells of the bee. This section will, however, deal with auxetic honeycombs, referring to any array of identical re-entrant cells which nest together to fill a plane or 3D space and exhibit a negative Poisson's ratio.While regular hexagonal cells show in-plane isotropy, re-entrant hexagonal cells were found to be highly anisotropic.35 They do, however, offer increased transverse Young's moduli and shear moduli as compared to regular hexagonal honeycombs.53 The transverse shear modulus showed significant dependence on the rib slenderness ratio (w/l), approaching the upper bound at small rib slenderness ratios.54
The effect of density variations on the in-plane Poisson's ratios and Young's moduli of conventional and re-entrant honeycombs was studied by Whitty et al. (2002).55 Their Finite Element (FE) models showed excellent agreement with the experimental values presented by Alderson et al. (2000).56 A reduction in vertical rib thickness was shown to reduce the stiffness, Ey, and Poisson's ratio, νyx, (becomes less negative).55 Since the vertical ribs do not deform when loaded in the x-direction, they are redundant with respect to the mechanical properties in the x direction. Reducing the diagonal rib thickness, however, leads to a decrease in the Young's moduli.55 The in-plane Poisson's ratios both increase in magnitude (become more negative) when reducing the diagonal rib thickness, whereas νxy also increases when both thicknesses are simultaneously reduced.55 The study confirmed that flexing of the diagonal ribs dominates the deformation once their thickness is similar or lower than the vertical rib thickness. However, when subject to a load in the y direction, stretching of the vertical ribs can become the dominant deformation mechanism once their thickness is significantly lower than the diagonal rib thickness.55
Yang et al. (2003) presented an extension of the homogenization FE model by Lee et al. (1996),57 applying the Eringen's micropolar elasticity theory to derive a FE model of the re-entrant hexagonal honeycomb.58 The degree of auxeticity was found to be dependent on the re-entrant angle and the cell rib length ratio h/l (Fig. 1). A relative minimum of −0.99382 was reached with a re-entrant angle of 14.47° and a cell rib length ratio of 0.5.58 The stiffness of these honeycombs was found to decrease with the increase of the re-entrant angle, increasing the structure's auxeticity.57 The auxeticity of this structure was shown to increase with increasing cell rib length ratio, until it began to decrease past the optimum value of 0.5.58,59
The above-mentioned geometry parameters have been applied in a second study, to examine the effects of micropolar material constants.60 Variation in the micropolar Young's modulus did not affect the structural Poisson's ratio, whereas an increase in micropolar Poisson's ratio led to a decrease in the structural Poisson's ratio (becomes more negative).60 A relative minimum (−9.2682) was found when the structural dimension of the honeycomb became smaller than the characteristic length.60
Bezazi et al. (2005) slightly changed the conventional centresymmetric unit cell, with the introduction of base walls.59 The elimination of sharp edges complies with possible manufacturing constraints and stress concentration effects. The new design exhibited a significantly lower NPR compared to a commercially available centresymmetric version.59 Increasing the length of the base wall resulted in a lower in-plane stiffness, and thereby a more flexible structure, whereas the Poisson's ratio remained virtually unmodified. An increase in base angle, however, caused a significant increase in NPR.59 Adding a narrow rib in the re-entrant hexagonal honeycombs was shown to significantly improve the Young's modulus.61 A linear relation could be obtained between the Young's modulus and Poisson's ratio, by changing the thickness of the added rib under small strain tension. The Poisson's ratio could even be tuned to positive values by changing the force constant of the added rib.61
Many of the above-mentioned studies focused on the deformation and properties in the elastic range. However, when used in load bearing applications, large deformations may occur. A theoretical approach was therefore formulated to predict negative Poisson's ratios of re-entrant hexagonal honeycombs, based on the large deflection model.62 According to Wan et al. (2004), the Poisson's ratios are non-linearly dependent on strain at large deformation and vary from positive to negative in response to the geometrical changes presented by Yang et al. (2003).58,62
Whereas classical continuum theory predicts auxetic materials to have enhanced shear properties, a study by Fu et al. (2016) shows that this strongly depends on the geometry of the cell structures.63 The non-linear shear modulus of re-entrant hexagonal honeycombs was found to increase with the re-entrant angle and decrease with the increase of cell rib length ratio.63
Re-entrant hexagonal honeycombs have been successfully applied in the fabrication of filters with enhanced defouling properties and a Poisson's ratio of −1.82.56 Others used soft lithography for the micro-production of re-entrant hexagonal honeycombs, reaching a Poisson's ratio of −1.08.64 Mizzi et al. (2015) used a fairly new, but promising perforation method to emulate the re-entrant honeycomb mechanism. The resulting structure, made with I-shaped slits, not only exhibits a large initial NPR, but also remains highly auxetic at large strains.65
 | ||
| Fig. 3 Re-entrant honeycomb structures. (A) Arrowhead.66 (B) Lozenge grid and square grid (from top to bottom).67(C) 3-STAR, 4-STAR and 6-STAR systems (from top to bottom).26 | ||
The missing rib foam model introduced two auxetic geometries referred to as the Lozenge grid and the square grid (Fig. 3B).36 Both structures exhibited an in-plane negative Poisson's ratio, with relative minima at −0.43 and −0.6 respectively.67
Since the re-entrant hexagonal honeycomb can be considered as a structure made from “arrow-shaped building blocks”, the auxetic potential of other such periodic structures was explored by Grima et al. (2005).26 When the arrows are connected in such a way that their arms form “stars”, structures with rotational symmetry of order n = 3, 4 and 6 may be built (forming STAR-3, -4 and -6 systems, respectively) (Fig. 3C). Opening of the stars under uniaxial loading drives the auxetic effect, whereas the stiffness is governed by the applied force constants.26 The STAR-3 systems were found to exhibit both auxetic and conventional behaviors depending on the magnitude of the applied force constants, with Poisson's ratios ranging from 0.872 to −0.163.26 The STAR-4 and STAR-6 systems exhibited on-axis auxeticity for most combinations of force constants, with relative minima of −0.845 and −0.451, respectively.26 Despite the “lower” on-axis NPR, the STAR-4 systems were found to be “less” auxetic than STAR-6 systems due to their anisotropic nature.26
An extension of the concept of re-entrant structures was explored with the introduction of an elastic instability.68 This instability was shown to induce a reversible, buckling-driven pattern transformation at a critical value of the applied compressive strain. The studied system comprised a molded elastomeric square lattice with circular holes, which after the critical strain value transformed into mutually orthogonal ellipses.68 The observed deformation shows both re-entrant and rotational mechanisms, approaching the deformation found in the perforated systems studied by Grima et al. (2010)69 (Section 4.1). This critical eigenmode was found to decrease the system's Poisson's ratio until it finally reached an asymptotic negative minimum.68 The results suggest that maximum auxeticity can be reached for samples with the highest possible void fraction (i.e. −0.904 for Φ = 0.70).68 The same research group investigated the effects of pore shape and porosity on the structural response.70 The pore shape was found to effectively alter the lateral contraction and compaction of the structure under uniaxial compression.70 Where microscopic instabilities lead to a significant increase in compaction for the A- and B-type voids (Fig. 4A and B), macroscopic instabilities were found to induce a buckling mode with a significantly lower area change and positive Poisson's ratio in structures with C-type voids (Fig. 4C).70 The B-type voids initiated the greatest auxetic response, whereas the structure with A-type voids showed the highest stiffness.70 Changing the porosity of the structure was also found to considerably alter the stiffness, critical buckling strain, Poisson's ratio and compaction properties of the structure.70 Another study explored the influence of initial architecture on the overall buckling behavior, by varying the periodic distribution of circular holes.71 Circular holes were placed on the vertices of square, triangular, trihexagonal, and rhombi-trihexagonal tessellations to form periodic porous structures. All structures exhibited the aforementioned buckling-induced pattern transformation beyond the critical strain value.71 The latter two were found to buckle into a reversible chiral pattern, with an asymptotic incremental Poisson's ratio of −0.78 and −0.75, respectively.71 This behavior will occur once the structure is preloaded beyond the instability point, with a minimum NPR of −0.39 found for the triangular-based structure and a maximum NPR of −0.95 for the square lattice.71
 | ||
| Fig. 4 Void shapes in 2D soft materials. (A) Exhibiting the highest stiffness. (B) Exhibiting the biggest auxetic response. (C) Showing the least compaction with positive Poisson's ratio.70 | ||
Inspired by the buckling-induced elastic and elastoplastic metamaterials of the Bertoldi group, Ghaedizadeh et al. (2016) developed a general approach to designing auxetic metallic metamaterials undergoing large plastic deformations.72 However, with the application of a metallic base material, the square lattice lost its auxetic behavior, which was attributed to the localization of plastic collapse in the representative volume element.72 Moving a small portion of the connecting ribs to the proximity of the connecting joints and altering the geometry of the microstructure resulted in a specific deformation pattern that led to auxetic behavior. The Poisson's ratio remained relatively constant (around −0.90) while changing the elastoplastic properties of the base material.72 Without the aforementioned alterations, the auxetic behavior of conventional square lattices may be restored through enhancement of the plastic-hardening ratio.72
2.3 Three-dimensional re-entrant structures
Despite its excellent production of simple auxetic foams, Lakes' conversion method14,15 does not enable the tuning of properties and unit cell geometry. Many researchers have therefore build their 3D re-entrant structures using additive manufacturing techniques, to ensure repeatability. Yang et al. (2012) manufactured a Ti–6A1–4V idealized re-entrant structure using Electron Beam Melting (EBM) (comparable to Fig. 5A).73 EBM is a powder-based printing process in which an electron beam is used to selectively melt powder particles. After building each layer, the powder bed is lowered and a fresh layer of material (i.e. powder) is added. In such powder bed fusion systems, the parts may later be sintered or fused layer by layer to create the final structure.74,75 The study showed that the compressive strength of highly auxetic structures could be many times higher than those of conventional foams.73 By maintaining the relative density of the structure and making its Poisson's ratio more negative, a higher strength and stiffness can be achieved.73 Bückmann et al. (2012) successfully fabricated the same kind of structure using direct laser writing optical lithography.76 Inkjet printing was used to manufacture 3D idealized polymeric re-entrant structures.77 This liquid-based AM technique involves the on demand dispensing of curable polymer.74,78,79 All samples exhibited a negative Poisson's ratio at small strain, with −1.18 being the lowest value recorded.77 | ||
| Fig. 5 (A) A typical re-entrant structure made of 3D re-entrant hexagonal unit cells and (B) a 6-hole Bucklicrystal presented by the Bertoldi group.83 | ||
The auxeticity of a unit cell structure with re-entrant hollow skeleton was found to increase with an increased re-entrant angle.80 Similar to 2D re-entrant honeycombs, a variation in geometric variables will enable the tuning of the unit cell's Poisson's ratio within isotropic limits. The Poisson's ratio of this structure reached a relative minimum of −0.84.80 The same behavior was observed in the 3D star shaped structure of Shokri Rad et al. (2015).81 For re-entrant angles between 20° and 45°, the model exhibited an increasing NPR in all directions.81 The Young's modulus and density were found to decrease once the structure became “less” re-entrant, in accordance with the study by Yang et al. (2012).73,81
Unlike most theoretical models, the above structures contain stiff cell walls and stiff joints that will initiate buckling at large deformations. Dual-material auxetic metamaterials (DMAMs) aim to deliver what theoretical models assume, stiff cell walls and elastic joints. Wang et al. (2015) modeled and built 3D auxetic structures using dual-material PolyJet technology.82 This technology simultaneously prints two types of materials in the same part. The controlled deformation at the elastic joints prevents the stiff walls from buckling, which keeps the Poisson's ratio relatively stable (at −0.04) as the strain increases past the “run-in” phase of 0–5% strain (ε = 0.2).82 This behavior can be improved during the run-in phase by the use of relatively stiffer material at the elastic joints, which also yields a higher equivalent Young's modulus.82 The same effects can be achieved by increasing the length fraction of the stiff sections. Since these changes do not affect the Poisson's ratio after the “run-in” phase, the Young's modulus can be tuned independently.82
The buckling-induced pattern transformation seen in 2D soft structures has been extended to 3D in the form of “Bucklicrystals” (Fig. 5B).83 This term refers to the periodic arrangement of patterned spherical shells, which in response to a stimulus undergo an isotropic volume reduction.83,84 For this to happen, all ligaments should undergo a uniform first buckling mode. This implies patterns comprising of 6, 12, 24, 30, and 60 holes to be implemented in the building blocks.84 The 6-hole Bucklicrystal fabricated by Babaee et al. (2013) clearly showed an isotropic volume reduction, indicating a 3D NPR.83 Given the excellent agreement with experimental measurements, FE simulations were used to model the auxetic behavior of 6-, 12- and 24-hole Bucklicrystals. The Poisson's ratios showed a non-linear response to strain: initially starting positive, but finally reaching a negative plateau at large strains (−0.4, −0.2 and −0.5, respectively).83 Except for the 6-hole Bucklicrystal, all crystals retain their transversely symmetric behavior at large strains (ε = 0.3).83
Inspired by the 2D soft metamaterials in Section 3.2.2, Shen et al. (2014) developed a series of 3D-printed elastomeric NPR structures based on simple initial geometries.85 The structure containing simple spherical cells exhibited obvious auxetic behavior (NPR around −0.40), with a non-linear relation between the Poisson's ratio and strain.85 A buckling analysis was done to indicate whether the structure follows a desired deformation mode, this mode was subsequently introduced as an initial imperfection in the FE model. Changing the magnitude of this imperfection resulted in a series of simple cubic 3D auxetic metamaterials in which the auxetic behavior can be retained over a wide range of strain (ε = 0.3).85
Lim (2016) extended the arrowhead structure proposed by Larsen et al. (1997)66 to a 3D anisotropic material based on intersecting double arrowheads.86 It was found that a change in length ratios of the linkage as well as their subtending angles could alter the Poisson's ratio significantly.86 An auxetic structure in which the Poisson's ratio is of opposite signs on different planes may very well be tailor-made using the intersecting double-arrowhead configuration.86
On top of the aforementioned approaches, Rad et al. (2014) presented a successful analytical and finite element approach for the modeling of 3D re-entrant structures.87 However, to enable the application of a model in various loading and material cases, large deflection beam theory should be utilized. Yang et al. (2015) successfully established such an analytical model, which was later verified by FE modeling and experiments to be relatively accurate at predicting the performance of the auxetic structure beyond the elastic limit.88
2.4 Microporous polymers
Shortly after the introduction of Lakes's foam conversion technique, Caddock et al. (1989) presented the auxetic potential of expanded polytetrafluoroethylene (PTFE).89 Polytetrafluoroethylene is usually processed by sintering, but to achieve an extremely porous microstructure the sintered material is rapidly heated and drawn. Subsequent expansion will eventually result in a microporous material with negative Poisson's ratios.89 The material was shown to be highly anisotropic, with reported Poisson's ratios as low as −12.89 A schematic representation of the microstructure has been shown in Fig. 6, showing an interconnected network of disc-shaped particles and fibrils. Tensile tests were performed to see which microstructural changes give rise to such a large NPR.89,90 Starting with a nearly fully densified material, the fibrils will cause a first expansion as they become taut and translate the particles (Fig. 6B). Secondly, the disc-shaped particles will start to rotate leading to the fully expanded form (Fig. 6C and D). A maximum NPR was observed at small strain values, primarily caused by the translation of the particles.89,90 The Poisson's ratio and stiffness were subsequently found to increase with strain, upon rotation of the particles.89,90 These results confirm that expanded PTFE exhibits auxetic behavior solely because of its microstructure and not because of any intrinsic mechanical property. | ||
| Fig. 6 Structural changes observed in microporous PTFE undergoing tensile loading in the x-direction.90 (A) Nearly fully densified state. (B) Tension in fibrils causes particle displacement. (C) Rotation of the disc-shaped particles. (D) Fully expanded condition.89 | ||
For the production of auxetic ultra-high molecular weight polyethylene (UHMWPE), three distinct stages can be identified: compaction of polymer powder, sintering and extrusion through a die.91 This novel thermoforming route enabled the reproduction of the nodule-fibril microstructure observed in expanded PTFE.91,92 The theoretical model presented by Evans et al. (1989)90 was slightly adjusted to fit the compression test of Neale et al. (1993).93 The model successfully predicted the strain dependent behavior of the Poisson's ratio up to 4% strain.93 A Poisson's ratio of −1.24 was measured at small strain in a radial compression test, indicating a nearly isotropic fibrillar network,94 whereas an approximate value of −6 was found for low modulus extrudates.95 In 2005, a novel processing route was developed, excluding the extrusion stage and thereby enabling the production of more complex auxetic parts.92
The same production route was used to attain the auxetic effect in polypropylene (PP).91 It was concluded that to do this successfully, one should use a finely divided powder (size up to 300 μm) with a rough particle surface. A relatively small NPR of −0.22 was obtained, which can be increased by creating more spherical nodules and increasing the radial expansion during processing.91
3. Chiral structures
A typical chiral unit comprises a central cylinder encapsulated in tangentially attached ligaments, which is not superimposable on its mirror image (Fig. 7).96 The described basic unit can either be constructed right-handed or left-handed, creating chiral or anti-chiral structures.97 Anti-chiral structures exhibit reflective symmetry, since their nodes are attached on the same side of the connecting ligaments (Fig. 8C and D).98 | ||
| Fig. 7 Deformation of a hexachiral unit. (1) In rest. (2) Completely deformed due to folding of the ligaments and rotation of the cylinders in response to compression in the y-direction. | ||
 | ||
| Fig. 8 Chiral structures based on hexagonal and re-entrant hexagonal honeycombs.102 (A) Trichiral honeycomb. (B) Re-entrant trichiral honeycomb. (C) Anti-trichiral honeycomb. (D) Re-entrant anti-trichiral honeycombs. | ||
The cylinders will rotate under mechanical loading, causing the ligaments to flex. This results in folding or unfolding of the ligaments under tensile or compressive loadings, respectively. Depending on the geometrical features of the structure, this may result in a negative Poisson's ratio close to −1.98
To create periodic chiral structures, one should obey the constraints of rotational symmetry. The number of ligaments attached to each node should therefore be equal to the order n of rotational symmetry.97 Unless this constraint is relaxed, only five such structures can exist: trichirals, anti-trichirals, tetra-chirals, anti-tetrachirals, and hexachirals.97,98 Meta-chiral structures may be created once this constraint is relaxed.97
3.1 Two-dimensional chiral lattices
Unlike re-entrant cells, the Poisson's ratio of chiral cells is not dependent on any structural angle. Their ability to “wind” in upon themselves under compression, allows them to maintain their Poisson's ratio over a significant range of strain (25%).99,100 Subsequently, increasing the number of ligaments per node may increase the stiffness of these cylinder-ligament systems.98 Chiral honeycombs were also found to exhibit higher moduli than their anti-chiral counterparts having the same number of ligaments,98 although contradictory results were presented by Lorato et al. (2010).101 The presence of cylinders tends to decrease the in-plane stiffness of such structures as compared to re-entrant hexagonal honeycombs.102Logically, nodes in a tetrachiral structure are each connected by four tangential ligaments. Both chiral and anti-chiral honeycombs displayed a Poisson's ratios close to −1 according to Alderson et al. (2010),98 whereas the tetrachiral honeycomb was found to be non-auxetic by Mousanezhad et al. (2016).103 The anti-tetrachiral honeycomb, however, simultaneously exhibited anisotropy, auxeticity, and a lower than usual shear modulus (decreasing with r/R).103 Altering the ligament lengths along the x- and y-direction may cause large variations in the Poisson's ratio, whereas equal lengths evoke an isotropic Poisson's ratio of −1.104 Mizzi et al. (2015) even found values as low as −13 in sheets with I-shaped perforations, emulating the anti-tetrachiral mechanism.65 Although always negative, the Poisson's ratio did show variations in response to changing ligament ratios. Upon increasing L/r, the NPR and stiffness remained relatively constant, whereas the Young's modulus significantly increased with ligament thickness ratio.98,104 An increasing NPR was observed with increasing r/R, resulting in reduced structural rigidity.103 Careful selection of such parameters will enable the design of structures with minimum density, but maximum in-plane stiffness and shear strength without affecting the Poisson's ratio.104,105
A hexachiral structure possesses hexagonal symmetry, since each node has six tangentially attached ligaments (Fig. 7). These honeycombs have been found to display in-plane mechanical isotropy, with Poisson's ratios close to −1.98,99 The nodes (cylinders) give the structure an enhanced out-of-plane buckling and compressive strength,106,107 whereas the in-plane Young's modulus decreases with L/r and increases with ligament thickness ratio.98 While all of the aforementioned structures include straight ligaments, Dirrenberger et al. (2011) proposed a hexachiral structure with circular ligaments.108 This rotachiral honeycomb can exhibit highly negative Poisson's ratios up to −17, when loaded out-of-plane.108 Unfortunately, its in-plane elastic moduli appear to be one order of magnitude lower than those found in conventional hexachiral honeycombs.108
Although all of the above-mentioned experimental data have been obtained using additively manufactured samples, chiral systems may also be obtained by gluing the ligaments to the nodes.104,109 Gatt et al. (2015) studied the effects of the gluing material on the overall mechanical properties of an anti-tetrachiral system.110 The Poisson's ratio of the system was found to be unaffected by the amount and position of the glue, while the Young's modulus showed an increase by increasing the amount of glue applied on the connecting end of the ligament.110 In systems with relatively “soft” glue hinging is observed, whereas systems with relatively “hard” glue deform through the typical ligament-flexure mechanism.110
3.2 Three-dimensional chiral lattices
Ha et al. (2016) analyzed several 3D lattice structures, made out of cubes and numerous deformable ribs.100 The effective Young's modulus and effective shear modulus were found to depend on the number of unit cells per side, while finally converging to a constant value.100 Increasing this number led to a decrease in stiffness, whereas an opposite effect is achieved by increasing the rib slenderness ratio.100 The Poisson's ratio could be tuned to negative values (−0.1393) with a sufficient number of cells. The model's anisotropy seems to depend on the parity of the number of cells on each side, where an even distribution leads to less anisotropy.100The small strain properties of a cubic auxetic structure composed of 3D antitetrachiral lattices were numerically analyzed and experimentally verified by Huang et al. (2016).111 The model showed isotropy when being compressed in the z-direction, whereas anisotropy was observed for compressive loading in the x- and y-directions.111 A parametric study was conducted to examine the relation between geometry and mechanical properties of such structures. The Poisson's ratio showed a nearly linear increase (became less negative) with rib slenderness ratio, whereas a non-linear relation was observed between this ratio and the normalized effective Young's modulus.111
4. Rotating (semi-) rigid structures
An idealized rotating structure contains rigid squares connected through simple hinges. When loaded, the squares will rotate at the vertices, either expanding or contracting depending on the loading type.112 The concept has been widely implemented using squares, rectangles, triangles, rhombi, and parallelograms.4.1 Squares and rectangles
Although it had been observed in inorganic crystalline materials, Grima et al. (2000) were the first to explore the auxetic potential of rotating rigid squares.112 They used the principle of conservation of energy to model this behavior, showing that this idealized system will always maintain its aspect ratio and therefore exhibits constant Poisson's ratios of −1.112 If the rotating units were assumed to be semi-rigid, the Poisson's ratios would become dependent on the relative rigidity of these units with respect to the rigidity of the hinges, as well as the direction of loading.112Replacing the squares by rigid rectangles resulted in a very different behavior. These structures were found to exhibit both positive and negative Poisson's ratios, depending on the angle between the rectangles (θ as depicted in Fig. 9).113 They may exhibit NPRs beyond the isotropic limit, but only for a specific range of θ.113 Subsequently, the Poisson's ratios were found to depend on the shape of the rectangles, which means the Poisson's ratios are strain-dependent and dependent on the direction of loading.113 The range of θ showing NPRs may be increased by decreasing the difference between a and b (Fig. 9), although it will occur on the expense of the structure's auxeticity.113 The Young's modulus was also shown to vary, increasing towards infinity and subsequently decreasing with θ.113
 | ||
| Fig. 9 Deformation of a rotating rigid rectangles structure. (1) In rest. (2) Tensile loading in x-direction.140 | ||
The same group identified two distinct connectivity schemes, which enable the formation of a tessellating structure of rectangles.114 These structures are referred to as Type I and Type II networks, in which Type I networks show rhombi-shaped empty spaces and the Type II networks show parallelograms (Fig. 10).114 The Type I structures have been studied extensively (see the previous paragraph) and were shown to exhibit anisotropic behavior. The Type II structures, however, were shown to exhibit very different mechanical properties. They were found to mimic the behavior of the rotating rigid squares structure with an isotropic Poisson's ratio of −1.114
 | ||
| Fig. 10 Type I and Type II rotating rectangles. Type I showing rhombi in their empty space and Type II showing parallelograms.114 | ||
Adding to the earlier presented rigid systems, Grima et al. (2011) predicted the behavior of systems comprising different-sized squares and rectangles.115 The model allows the fine-tuning of mechanical properties through careful selection of the geometric parameters a, b, c, d and θ (in which c and d refer to the height and width of the added geometry). The model showed that these kind of systems exhibit auxeticity in both planer directions.115 The auxeticity may be increased, if the sides of the rectangles satisfy ad3 + cb3 < bd(ab + cd) for loading in the X1-direction and ad3 + cb3 > bd(ab + cd) for loading in the X2-direction.115 A Type II structure made of different-sized rectangles (a × b, c × d) exhibited an on-axis Poisson's ratio of −1, but was shown to be anisotropic. A different-sized square structure did show analogous mechanical properties to that of the “parent” case, i.e. two-dimensional isotropy with a Poisson's ratio of −1.115
The auxetic effect is often overestimated, since most models tend to idealize the situation and thereby fail to predict the dependence of the Poisson's ratios on the direction of loading. Grima et al. (2007) simulated the behavior of zeolite crystals under axial and shear loading and proposed a new semi-rigid square model, which allows the squares to deform and become rectangles.116 The introduction of an extra degree of freedom was found to provide a better representation of the Poisson's ratio in rotating squares nanostructures, but further improvement remains necessary since the auxeticity is still being overestimated.116
Grima et al. (2010) simulated the response of three planar systems, each involving a different arrangement of rhomboidal perforations, in both tension and compression.69 The perforations were arranged in such a way to create rotating rigid unit mechanisms. Resembling either square or rectangular rotating units, all of the systems were found to exhibit a wide range of Poisson's ratios.69 The data also suggested that as the material in between the perforations increases(s), the conformations lose their resemblance and become less auxetic. In contrast, the system will become more auxetic once the length of these perforations is increased.69 The system's isotropy was found to be controlled by the degree of rotational symmetry of the cut-pattern.117 Straight line slits have also been proven successful in emulating these rotating rigid structures.65 Slann et al. (2015) numerically modeled and experimentally confirmed the auxetic behavior of planar cellular structures with rectangular (1) and rhomboidal (2) perforations (Fig. 11).118 The samples were manufactured by Fused Deposition Modeling (FDM), a process which involves the deposition of a thread of molten polymer filament onto a substrate using a movable head.74,75 They were mechanically tested and the numerical model was used to perform a parametric study. Geometry 1 exhibited a higher degree of auxeticity and resistance to strain, whereas geometry 2 showed higher in-plane stiffness (both uniaxial and shear).118 This can partially be explained by the generation of thin, high aspect ratio intercellular regions in geometry 1, which reduce the stiffness but consequently increase the auxeticity.118 Rhomoboidal perforations have since been successfully applied in the fabrication of esophageal stents using laser cutting and die casting techniques.78
 | ||
| Fig. 11 Cellular plates with (1) rectangular perforations and (2) rhomboidal perforations.118 | ||
The abovementioned 2D concepts were translated to 3D by Attard et al. (2012), to model the auxetic behavior of a cuboidal shaped network.119 Through analytical modeling it was shown that the system might simultaneously exhibit auxetic behavior in all three directions. The presented model forms a basis for other three-dimensional systems involving the relative rotation of their units.119
Gatt et al. (2014) proposed a new class of hierarchical auxetics based on the rotating rigid units mechanism.120 Systems with hierarchy levels 0 and 1 were simulated with varying stiffness constants of the hinges between level 0 (kθ) and level 1 (kϕ) squares. In the case of stiff θ-hinges and soft ϕ-hinges, the system primarily deformed through rotation of the level 1 squares.120 The location of these “effective” hinges strongly influenced the system's mechanical properties, making them either behave as Type I rotating rectangles or as Type I β rotating parallelograms.120 Similar behavior was observed in systems with both hinge-types being soft. The level 0 deformations could not occur independently from the level 1 deformations, which resulted in a very rigid and stiff construct when kϕ > kθ.120 The results verify the promising nature of these systems, which may be engineered to exhibit a variable pore size and/or shape.120
4.2 Triangles
Although the rotating rigid triangles system has been proposed to exhibit negative Poisson's ratios,52 Grima et al. (2006) were the first to derive a full description of its mechanical properties.121 A system of hinged equilateral rigid triangles was found to be isotropic with a constant Poisson's ratio of −1 irrespective of triangle size, θ, and the direction of loading.121 Tessellates made from isosceles triangles were found to exhibit both positive and negative Poisson's ratio, depending on the shape of the triangles and the angle (θ) between them.122 The onset of NPR values could be advanced by decreasing θ, thereby increasing the range of aspect ratios for which auxeticity can be observed.122In addition, Grima et al. (2010) modeled the behavior of rectangular sheets with star- or triangular-shaped perforations in both compression and in tension.122 With s approaching zero, these systems reduce to a rotating (equilateral or isosceles) triangles structure. The loss of auxeticity was observed in both tension and compression as s increases,122 which may enhance the stiffness of the hinge and therefore hinders the rotating triangles mechanism. Larger positive and negative Poisson's ratios were found for the systems mimicking the rotating isosceles triangles.122
4.3 Rhombi
The rhombi can be arranged in two different ways to give rise to Type α and Type β rotating rigid rhombi systems (Fig. 12). In the Type α system, the obtuse angle of one rhombus is connected to the acute angle of its neighbor, whereas the rhombi in a Type β system are connected through the same angle (acute–acute, obtuse–obtuse).123 The mathematical models of Attard et al. (2008) show that both systems can exhibit auxetic behavior.123 The Type α system was found to be highly anisotropic, with the Poisson's ratio being dependent on ϕ, θ, and the direction of loading (Fig. 12).123 Just like the Type I rotating rectangles structure, this system exhibited both positive and negative Poisson's ratios depending on θ. Giant Poisson's ratios may be observed in the transition region, showing a symmetrical distribution of ν12 and ν21 around θ = π/2.124 In contrast, the Type β system showed in-plane isotropy with a Poisson's ratio of −1 irrespective of strain (or angles ϕ and θ) and the direction of loading.123 The Type β system was not found to be space filling in the fully closed conformation, unlike the Type α system.124 | ||
| Fig. 12 Rotating rigid rhombi systems, Type α and Type β.124 | ||
In the special case where ϕ = 90°, the Type α system also reduces to the isotropic rotating squares system with a Poisson's ratio of −1 (except for ϕ = θ = 90°).123 The opposite behavior may be observed when θ = 90° and the empty spaces become squares. In this case, the system exhibits an isotropic Poisson's ratio of +1 (except for ϕ = θ = 90°).123
4.4 Parallelograms
The aforementioned connectivity schemes of the rotating rectangles and rotating rhombi have been combined to describe the way in which rigid parallelograms can be connected. This resulted in Type I α, Type I β, Type II α and Type II β systems (Fig. 13).125 Mathematical expressions were derived for each of the mechanical properties of the system. The Type II β parallelograms showed in-plane isotropy with a constant Poisson's ratio of −1, similar to the Type β rhombi.125 This is very different from what is observed in the Type I α, Type I β and Type II α systems. The on-axis Poisson's ratios of these systems were found to be highly dependent on ϕ, θ (Fig. 13), and the direction of loading.124,125 The Poisson's ratio of Type I systems was also found to depend on the aspect ratio a/b.125 They all exhibited a wide variation of Poisson's ratios depending on θ, with a maximum of four transitions while stretching from a fully closed to a fully open configuration. The Type I α and Type II α always showed auxetic behavior in the fully closed conformation, whereas the initial behavior of the Type I β system appeared to be highly dependent on the relative magnitude of the aspect ratio and ϕ.124,125 | ||
| Fig. 13 Rotating rigid parallelograms systems, Type I α, Type I β, Type II α and Type II β.124 | ||
Just like the rhombi, something special happens when ϕ = 90°. The Type I systems become equivalent to Type I rectangles and may reduce even further to the isotropic rotating squares system when a = b.125
The Type II α system was found to behave much more similar to the Type I rotating rectangles system, despite its structural resemblance with Type II rotating rectangles at ϕ = π/2.124 Only in the special case of θ ≠ ϕ = π/2, the Poisson's ratio of this system reduces to −1 as expected from the Type II rotating rectangles system. The same holds for the Type α rotating rhombi, since the mathematical model for these two structures is similar in terms of the Poisson's ratio and only differs by a multiplication factor in terms of their moduli.124
The perforated systems modeled by Mizzi et al. (2015) were found to behave similarly to the Type I α and the Type α rotating rhombi system upon increasing the tilt of the straight line slits.65
5. Discussion and conclusions
5.1 Topology–property relationship in auxetic structures
The most important geometrical features identified in the literature to influence the mechanical behavior of the three main classes of auxetic metamaterials have been highlighted in the following paragraphs of the current section.The re-entrant structures mainly deform through hinging of the cell ribs. This may be enhanced by a reduction in diagonal rib thickness (or all ribs), an increase in re-entrant angle θ, and an increase in cell rib length ratio h/l (up to a certain optimum value).55,58,59 The thickness of the ribs directly affects the rigidity of structure, and, thus, its overall stiffness. The Young's modulus was therefore found to decrease as the cell rib thickness decreased and the re-entrant angle increased.55,57 The non-linear shear modulus was found to increase with re-entrant angle and decreasing rib slenderness ratio w/l and h/l.54,63 The anisotropic nature of most re-entrant structures allows the Poisson's ratio to have an arbitrarily large negative value while not violating the thermodynamic requirements.35 Although little data is available on non-hexagonal re-entrant structures, the above-mentioned geometrical features are expected to have similar effects on the mechanical properties of those type of structures. The same parameters have been shown to dictate the mechanical response of three-dimensional re-entrant structures. For example, the NPRs were found to increase with increasing re-entrant angle. In contrast to 2D re-entrant structures, the same trend was also observed for the Young's moduli.73,80,81 This observation has been made in multiple studies and suggests that three-dimensional re-entrant structures can simultaneously exhibit an NPR and high stiffness. As for the soft re-entrant structures, the buckling-induced auxetic response has been shown to depend on the void fraction, void shape and void arrangement.68,70,71,83 The latter shows that even though the material in-between the perforations is increased, auxeticity can be enhanced when pursuing another buckling pattern.71 Even though instability-based soft auxetics exhibit interesting behaviors, their NPR is generally limited to compression.68,83
The Poisson's ratio of chiral systems has been shown to depend on several geometrical features, but can be considered independent of strain.99,100 Their deformation is guided by the rotation of the nodes and the subsequent flexion of the ligaments. A reduction in the cell rib thickness and an increase in r/R can enhance ligament flexion, and, thus, the auxetic effect.98,103,104 The stiffness of these structures has been found to increase with the number of ligaments, their length to thickness ratio and the quantity of glue used at the connecting end of the ligament in conventionally obtained structures, which in turn makes node rotation and ligament flexion more difficult.98,103,104,110 The Poisson's ratio was found to be independent of L/r in the anti-tetrachiral and hexachiral structures, whereas a decrease in NPR was observed for the anti-trichiral structure.98 The same trends could be observed in three-dimensional chiral auxetic metamaterials,100,111 but more research is needed to explore the auxetic potential of these three-dimensional structures, as well as the contradictory information regarding the stiffness of chiral structures vs. their anti-chiral counterparts.98,101
A very distinct relation has been observed between the Poisson's ratio and the geometrical variables of rotating rigid structures. These structures deform through rotation of the rigid units, thereby changing the angles between them.112 This directly relates to the rigidity of the joints, which has been shown to negatively influence the auxetic effect.65,122 The rotating rigid squares, Type II rectangles, equilateral triangles, Type β rhombi and Type II β parallelograms show in-plane isotropy with Poisson's ratios close to −1, whereas the Poisson's ratio of other systems is highly dependent on ϕ, θ, the direction of loading, and sometimes even the aspect ratio of its units.112,114,121,123–125 All the anisotropic rotating systems can be reduced to one of the abovementioned isotropic systems by carefully selecting the aspect ratio, ϕ, and θ. These insights suggest that no matter what initial unit geometry you pick, the mechanical properties can be steered by the aspect ratio, ϕ, and θ.
It has been shown that the parametrical changes that improve the stiffness of the structure often reduce its auxeticity. The number of ligaments in chiral structures and the re-entrant angle in three-dimensional re-entrant structures are an exception to this rule. The lack of information regarding the rotating rigid structures does not allow conclusions to be drawn on this matter. The abovementioned topology–property relationships may provide guidance when designing auxetic mechanical metamaterials.
5.2 Design recommendations
When designing an auxetic metamaterial, several aspects may play a role in deciding which type of structure to proceed with. It is often desirable to design a structure that can simultaneously exhibit a high NPR and high stiffness. Since the above-mentioned parametrical changes show that almost any kind of geometry can be tuned to exhibit certain mechanical properties, the geometries have been compared based on their normalized stiffness. This limits the effects of the solid material properties and therefore enables a proper geometrical evaluation.Fig. 14A visualizes the highest reported negative in-plane Poisson's ratio vs. normalized Young's modulus for two-dimensional auxetic structures, using the data presented in the reviewed literature. This graph suggests that re-entrant structures outperform the chiral and rotating rigid structures in terms of Poisson's ratio and corresponding stiffness. The relatively low stiffness of chiral structures may be explained by the extra degree of freedom introduced by the rotation of the cylinders. In contrast, rotating rigid structures seem to offer a relatively high Young's modulus. This may be explained by the amount of bulk material incorporated, which in turn decreases the NPR. In light of these arguments, the re-entrant structures seem to offer the perfect balance between structural rigidity and NPR. This does, however, come with a significant degree of anisotropy, which may not be desirable in certain applications.
 | ||
| Fig. 14 (A) In-plane Poisson's ratio vs. normalized Young's modulus for two-dimensional auxetic metamaterials. Data has been retrieved from ref. 56, 57, 59, 60, 70, 71, 98, 102, 103, 105, 108, 118, 141 and 142. (B) In-plane Poisson's ratio vs. normalized Young's modulus for three-dimensional auxetic metamaterials. Data has been retrieved from ref. 37, 43, 50, 73, 76, 81, 100 and 111. (C) In-plane Poisson's ratio vs. normalized Young's modulus in re-entrant structures. Data has been retrieved from ref. 56, 57, 59, 60, 70, 71, 73, 76, 81, 141 and 142. | ||
Fig. 14B visualizes this relation for three-dimensional auxetic structures. Again, the objective seems to be achieved by the re-entrant structures. Although auxetic foams actually belong to the re-entrant structures, they have been highlighted separately. Their ultimate micro-architecture cannot be closely predicted or controlled, which makes their use in metamaterials less likely.
The idealized re-entrant structures were therefore more closely studied in Fig. 14C. This graph shows that the re-entrant hexagonal unit cells cover a wide range of Poisson's ratios at relatively high stiffness. Some of the soft materials studied by the Bertoldi group show the highest normalized stiffness, but only exhibit small values of NPR in compression. The other re-entrant geometries do not show any extraordinary values compared to the re-entrant hexagonal structures. Based on this graph one may state that the easiest and cheapest way of attaining a stiff NPR structure is to adjust the parameters of a re-entrant hexagonal unit cell.
The other structures may need to be chosen in light of other mechanical, physical, or financial requirements. As far as chiral structures are concerned, the anti-tetrachiral structure has the biggest potential of exhibiting highly negative Poisson's ratio due to its anisotropic nature. The trichiral structures can be considered the least auxetic, whereas in-plane mechanical isotropy can be achieved with hexachiral unit cells. The rotating rigid unit structures can be easily manufactured with the help of perforations. They may therefore offer a cheap solution to those in need of an (isotropic) NPR structure. Microporous polymers can be applied as a material, rather than a structure, which means they can be used in any geometrical configuration. An increased understanding of the microporous polymer processing route will enable the production of auxetic polymers with specifically tailored properties. Their use has already been suggested in coronary angioplasty, in which an expanded PTFE rod can be used to open up the artery.126
5.3 Challenges and limitations
Fig. 14A and B clearly show that most research has been done on the re-entrant structures, especially the re-entrant hexagonal honeycombs. Although chiral and rotating rigid structures have been modeled extensively, experimental data have not yet been widely reported. Most of the reported data are based on the parametric studies done using analytical derivations or Finite Element Modeling (FEM), since little effort has been put into the actual fabrication of the proposed geometries (Fig. 14A and B). Due to some simplifying assumptions, FE models are not guaranteed to present accurate estimation of the mechanical properties of auxetics. It is therefore not clear whether the extremely high NPRs found for re-entrant structures can be observed in actual experiments. Some of the AM techniques currently used to fabricate these complex auxetic geometries have been known to introduce anisotropy; see e.g.127 Moreover, the effects of the parameters of the AM process on the resulting mechanical properties are often not taken into account.The rotating rigid structures are by far the least studied, especially in three dimensions. Besides lack of experimental data, there is no direct information available regarding the topology–stiffness relationship in this type of auxetics. Since rotating rigid structures have been shown to exhibit fluctuating Poison's ratios, it is even more challenging to predict the stiffness of the system. It is therefore not possible to perform a well-founded comparison between the three basic types of auxetic structures.
Another point is that most studies concentrate on small strain deformations. Some large deflection models have been proposed, but experimental data is scarce. Potential applications often require a material that exhibits the auxetic effect over the full range of strain. Development of structures proven to be auxetic beyond the small deformation range both in tension and compression is one of the important challenges in design of auxetics.
This review has primarily been focusing on the relationship between geometrical features and the Young's modulus and Poisson's ratio of auxetic structures. Other mechanical properties could also play important roles in determining whether one of the presented types of auxetic structures is used for development of materials with advanced functionalities.
5.4 Other types of auxetic structures
The most common types of auxetic mechanical metamaterials were reviewed before. Three basic structures were identified to distinguish between the deformation mechanisms observed in the different geometries of auxetic structures. There are, however, other types of structures of recent interest for development of auxetic metamaterials that were not reviewed here. One of the most important types of such structures are those based on the origami concept (the ancient Japanese art of paper folding). Origami structures naturally qualify as mechanical metamaterials as systems whose mechanical behavior is largely driven by the crease patterns, folding sequences, and other parameters describing the geometry of a typical origami structure. In addition, the mechanical behavior of folded sheets could be entirely different from those of the paper from which they are made. Indeed, some of the mechanical properties of certain origami structures may be entirely independent from those of the paper and entirely dependent on the geometry of the origami structure.128 Perhaps the most widely studied origami structures are the Miura-ori configurations. The mechanical behavior of the original Miura-ori origami configurations and some of their variations are studied in multiple recent studies. For example, the Poisson's ratio of Miura-ori origami structures are shown to take negative or positive values depending on their design parameters.129 Miura-ori origami structures with negative Poisson' ratio are just some of the examples of auxetic materials130 that could be created using the origami concepts.The mechanical properties of other origami structures have also been studied including zigzag-base folded sheets that combine origami and kirigami concepts,131 three-dimensional origami configurations based on the Tachi–Miura polyhedron (TMP),132 and origami structures based on non-periodic Ron Resch folding.129 Some of these systems are based on the same type of structures as discussed above. For example, the configurations based on the Tachi–Miura polyhedron132 could be considered some type of re-entrant structures. Techniques such as origami could therefore be simply considered manufacturing techniques in certain cases and not necessarily new types of auxetic structures.
5.5 Potential applications and future research
Auxetic materials have thus far been applied in many novel applications including soft robotics,133 biomedicine,32 soft electronics,134 and acoustics.135 With the ongoing development of AM techniques even more complex NPR structures may soon be fabricated. Initially, designs were adjusted to accommodate the production process.59 Nowadays the roles have been reversed and the design constraints seem to vanish.79 These changes facilitate the production of more advanced NPR materials with tailored properties.Auxetic materials are currently used to achieve improved shock-absorbance, synclastic curvature, and improved shear performance. These properties are especially useful in the automotive, defense, sports, and aerospace industries.30,46,136,137 However, their potential in the (bio)medical field remains relatively unknown. Several years ago, “smart bandages” were introduced as a novel way of facilitating and monitoring the wound-healing process. A swelling may induce fiber stretching, which not only increases the breathability of the bandage, but may also open up pores for the release of active pharmaceutical ingredients (APIs). The same concept could be applied to the design of smart stents,78 for the release of APIs during the “blow-up” phase. Gatt et al. (2015) emphasize the potential of hierarchical rotating rigid structures, which could be engineered to exhibit a variable pore size/shape upon loading.120 This behavior is of course not limited to stents and bandages, but could very well be applied in scaffolds and prostheses too. Even the agricultural industry could benefit from the controlled delivery of substances such as fertilizers. Since rotating rigid structures lend themselves to this kind of applications, the importance of more real-time (3D) experimental data on the mechanical behavior of rotating rigid auxetics is once more highlighted.
Although the auxetic effect is not limited to porous microstructures, it does offer great opportunities for the orthopedic industry where additively manufactured porous structures138,139 are often used. Their resemblance to cancellous bone17 enables their use as bone-substituting materials. When applied in prosthetic limbs or joints, they may counteract the variations in bone volume, and hence prevent loosening. Subsequently, their synclastic curvature will allow the prosthesis to conform to the shape of the bone cavity. This may potentially improve the survival rate of prostheses and hence postpone the need for revision surgery.
In conclusion, lots of research has been done on re-entrant structure and to a lesser extent on chiral and rotating rigid structures. More actual experimental data also in the large range of deformations will be needed to fully compare the mechanical potential of each of the basic structures. In addition to the Young's modulus and Poisson's ratio, other properties should be included to create an overall impression of the geometrical features affecting the mechanical performance of auxetics. Combining these basic structures may be another way of creating tailored auxetic mechanical metamaterials, which has not been explored yet.
References
- Z. G. Nicolaou and A. E. Motter, Mechanical metamaterials with negative compressibility transitions, Nat. Mater., 2012, 11(7), 608–613 CrossRef CAS PubMed.
- J. N. Grima and R. Caruana-Gauci, Mechanical metamaterials: materials that push back, Nat. Mater., 2012, 11(7), 565–566 CrossRef CAS PubMed.
- A. A. Zadpoor, Mechanical meta-materials, Mater. Horiz., 2016, 3, 371–381 RSC.
- W. Cai, U. K. Chettiar, A. V. Kildishev and V. M. Shalaev, Optical cloaking with metamaterials, Nat. Photonics, 2007, 1(4), 224–227 CrossRef CAS.
- V. M. Shalaev, Optical negative-index metamaterials, Nat. Photonics, 2007, 1(1), 41–48 CrossRef CAS.
- D. R. Smith, J. B. Pendry and M. C. Wiltshire, Metamaterials and negative refractive index, Science, 2004, 305(5685), 788–792 CrossRef CAS PubMed.
- J. H. Lee, J. P. Singer and E. L. Thomas, Micro-/Nanostructured Mechanical Metamaterials, Adv. Mater., 2012, 24(36), 4782–4810 CrossRef CAS PubMed.
- L. Yang, O. Harrysson, D. Cormier, H. West, H. Gong and B. Stucker, Additive manufacturing of metal cellular structures: design and fabrication, JOM, 2015, 67(3), 608–615 CrossRef CAS.
- K. E. Evans, M. A. Nkansah, I. J. Hutchinson and S. C. Rogers, Molecular network design, Nature, 1991, 353, 124 CrossRef CAS.
- M. Quinion, Auxetic, http://www.worldwidewords.org/turnsofphrase/tp-aux1.htm, accessed 05-09-2016.
- S. Poisson, Note sur l'extension des fils et des plaques élastiques, Ann. Chim. Phys., 1827, 384–387 Search PubMed.
- G. N. Greaves, A. Greer, R. Lakes and T. Rouxel, Poisson's ratio and modern materials, Nat. Mater., 2011, 10(11), 823–837 CrossRef CAS PubMed.
- A. E. H. Love, A treatise on the mathematical theory of elasticity, Cambridge University Press, 2013 Search PubMed.
- R. Lakes, Foam structures with a negative Poisson's ratio, Science, 1987, 235(4792), 1038–1040 CAS.
- R. Lakes, Negative Poisson's ratio materials, Science, 1987, 238, 551 CAS.
- Y. Prawoto, Seeing auxetic materials from the mechanics point of view: a structural review on the negative Poisson's ratio, Comput. Mater. Sci., 2012, 58, 140–153 CrossRef CAS.
- J. Williams and J. Lewis, Properties and an anisotropic model of cancellous bone from the proximal tibial epiphysis, J. Biomech. Eng., 1982, 104(1), 50–56 CrossRef CAS PubMed.
- C. Lees, J. F. Vincent and J. E. Hillerton, Poisson's ratio in skin, Bio-Med. Mater. Eng., 1991, 1(1), 19–23 CAS.
- R. Gatt, M. V. Wood, A. Gatt, F. Zarb, C. Formosa, K. M. Azzopardi, A. Casha, T. P. Agius, P. Schembri-Wismayer and L. Attard, Negative Poisson's ratios in tendons: an unexpected mechanical response, Acta Biomater., 2015, 24, 201–208 CrossRef PubMed.
- N. R. Keskar and J. R. Chelikowsky, Negative Poisson ratios in crystalline SiO2 from first-principles calculations, Nature, 1992, 358, 222–224 CrossRef CAS.
- H. Kimizuka, H. Kaburaki and Y. Kogure, Mechanism for negative poisson ratios over the alpha–beta transition of cristobalite, SiO2: a molecular-dynamics study, Phys. Rev. Lett., 2000, 84(24), 5548–5551 CrossRef CAS PubMed.
- J. N. Grima, R. Gatt, V. Zammit, J. J. Williams, K. E. Evans, A. Alderson and R. I. Walton, Natrolite: a zeolite with negative Poisson's ratios, J. Appl. Phys., 2007, 101(8), 086102 CrossRef.
- A. Yeganeh-Haeri, D. J. Weidner and J. B. Parise, Elasticity of a-cristobalite: a silicon dioxide with a negative Poisson's ratio, Science, 1992, 257(5070), 650–652 CAS.
- A. Alderson, A triumph of lateral thought, Chem. Ind., 1999, 17, 384–391 Search PubMed.
- K. E. Evans and A. Alderson, Auxetic materials: functional materials and structures from lateral thinking!, Adv. Mater., 2000, 12(9), 617–628 CrossRef CAS.
- J. N. Grima, R. Gatt, A. Alderson and K. Evans, On the potential of connected stars as auxetic systems, Mol. Simul., 2005, 31(13), 925–935 CrossRef CAS.
- X. Hou and V. V. Silberschmidt, Metamaterials with negative poisson's ratio: a review of mechanical properties and deformation mechanisms, Mechanics of Advanced Materials, Springer, 2015, pp. 155–179 Search PubMed.
- L. Rothenburg, A. A. Berlin and R. J. Bathurst, Microstructure of isotropic materials with negative Poisson's ratio, Nature, 1991, 354, 470–472 CrossRef.
- W. Miller, P. Hook, C. W. Smith, X. Wang and K. E. Evans, The manufacture and characterisation of a novel, low modulus, negative Poisson's ratio composite, Compos. Sci. Technol., 2009, 69(5), 651–655 CrossRef CAS.
- M. Sanami, N. Ravirala, K. Alderson and A. Alderson, Auxetic materials for sports applications, Procedia Eng., 2014, 72, 453–458 CrossRef.
- L. Santo, Shape memory polymer foams, Prog. Aeronaut. Sci., 2016, 81, 60–65 CrossRef.
- F. Scarpa, Auxetic materials for bioprostheses, IEEE Signal Process Mag., 2008, 25(5), 125–126 CrossRef.
- J. Schwerdtfeger, P. Heinl, R. Singer and C. Körner, Auxetic cellular structures through selective electron-beam melting, Phys. Status Solidi B, 2010, 247(2), 269–272 CrossRef CAS.
- Reentrant, Merriam-Webster.comn.d.
- I. Masters and K. Evans, Models for the elastic deformation of honeycombs, Compos. Struct., 1996, 35(4), 403–422 CrossRef.
- C. W. Smith, J. Grima and K. Evans, A novel mechanism for generating auxetic behaviour in reticulated foams: missing rib foam model, Acta Mater., 2000, 48(17), 4349–4356 CrossRef CAS.
- E. Friis, R. Lakes and J. Park, Negative Poisson's ratio polymeric and metallic foams, J. Mater. Sci., 1988, 23(12), 4406–4414 CrossRef CAS.
- N. Chan and K. Evans, Fabrication methods for auxetic foams, J. Mater. Sci., 1997, 32(22), 5945–5953 CrossRef CAS.
- F. Quadrini, D. Bellisario, L. Ciampoli, G. Costanza and L. Santo, Auxetic epoxy foams produced by solid state foaming, J. Cell. Plast., 2015, 0021955X15579456 Search PubMed.
- N. Chan and K. Evans, The mechanical properties of conventional and auxetic foams. Part I: compression and tension, J. Cell. Plast., 1999, 35(2), 130–165 CAS.
- N. Chan and K. Evans, The mechanical properties of conventional and auxetic foams. Part II: shear, J. Cell. Plast., 1999, 35(2), 166–183 CAS.
- J. Choi and R. Lakes, Non-linear properties of polymer cellular materials with a negative Poisson's ratio, J. Mater. Sci., 1992, 27(17), 4678–4684 CrossRef CAS.
- J. Choi and R. Lakes, Non-linear properties of metallic cellular materials with a negative Poisson's ratio, J. Mater. Sci., 1992, 27(19), 5375–5381 CrossRef CAS.
- R. Lakes and K. Elms, Indentability of conventional and negative Poisson's ratio foams, J. Compos. Mater., 1993, 27(12), 1193–1202 CrossRef.
- J. Choi and R. Lakes, Analysis of elastic modulus of conventional foams and of re-entrant foam materials with a negative Poisson's ratio, Int. J. Mech. Sci., 1995, 37(1), 51–59 CrossRef.
- M. Bianchi, F. Scarpa and C. Smith, Shape memory behaviour in auxetic foams: mechanical properties, Acta Mater., 2010, 58(3), 858–865 CrossRef CAS.
- J. N. Grima, D. Attard, R. Gatt and R. N. Cassar, A Novel Process for the Manufacture of Auxetic Foams and for their Re-Conversion to Conventional Form, Adv. Eng. Mater., 2009, 11(7), 533–535 CrossRef CAS.
- Y. Li and C. Zeng, Room-Temperature, Near-Instantaneous Fabrication of Auxetic Materials with Constant Poisson's Ratio over Large Deformation, Adv. Mater., 2016, 28(14), 2822–2826 CrossRef CAS PubMed.
- L. J. Gibson and M. F. Ashby, Cellular solids: structure and properties, Cambridge university press, 1999 Search PubMed.
- K. Evans, M. Nkansah and I. Hutchinson, Auxetic foams: modelling negative Poisson's ratios, Acta Metall. Mater., 1994, 42(4), 1289–1294 CrossRef.
- J. Choi and R. Lakes, Nonlinear analysis of the Poisson's ratio of negative Poisson's ratio foams, J. Compos. Mater., 1995, 29(1), 113–128 CrossRef.
- J. N. Grima, A. Alderson and K. E. Evans, An alternative explanation for the negative Poisson's ratios in auxetic foams, J. Phys. Soc. Jpn., 2005, 74(4), 1341–1342 CrossRef CAS.
- F. C. Smith, F. L. Scarpa and G. Burriesci, Simultaneous optimization of the electromagnetic and mechanical properties of honeycomb materials, SPIE's 9th Annual International Symposium on Smart Structures and Materials, International Society for Optics and Photonics, 2002, pp. 582–591 Search PubMed.
- F. Scarpa and P. Tomlin, On the transverse shear modulus of negative Poisson's ratio honeycomb structures, Fatigue Fract. Eng. Mater. Struct., 2000, 23(8), 717–720 CrossRef CAS.
- J. Whitty, F. Nazare and A. Alderson, Modelling the Effects of Density Variations on the In-Plane Poisson's Ratios and Young's Moduli of Periodic Conventional and Re-Entrant Honeycombs – Part 1: Rib Thickness Variations, Cell. Polym., 2002, 21(2), 69–98 Search PubMed.
- A. Alderson, J. Rasburn, S. Ameer-Beg, P. G. Mullarkey, W. Perrie and K. E. Evans, An auxetic filter: a tuneable filter displaying enhanced size selectivity or defouling properties, Ind. Eng. Chem. Res., 2000, 39(3), 654–665 CrossRef CAS.
- J. Lee, J. Choi and K. Choi, Application of homogenization FEM analysis to regular and re-entrant honeycomb structures, J. Mater. Sci., 1996, 31(15), 4105–4110 CrossRef CAS.
- D. Yang, S. Lee and F. Huang, Geometric effects on micropolar elastic honeycomb structure with negative Poisson's ratio using the finite element method, Finite Elem. Anal. Des., 2003, 39(3), 187–205 CrossRef.
- A. Bezazi, F. Scarpa and C. Remillat, A novel centresymmetric honeycomb composite structure, Compos. Struct., 2005, 71(3), 356–364 CrossRef.
- F.-Y. Huang, B.-H. Yan and D.-U. Yang, The effects of material constants on the micropolar elastic honeycomb structure with negative Poisson's ratio using the finite element method, Eng. Computation, 2002, 19(7), 742–763 CrossRef.
- Z.-X. Lu, X. Li, Z.-Y. Yang and F. Xie, Novel structure with negative Poisson's ratio and enhanced Young's modulus, Compos. Struct., 2016, 138, 243–252 CrossRef.
- H. Wan, H. Ohtaki, S. Kotosaka and G. Hu, A study of negative Poisson's ratios in auxetic honeycombs based on a large deflection model, J. Mec. Theor. Appl., 2004, 23(1), 95–106 Search PubMed.
- M. Fu, O. Xu, L. Hu and T. Yu, Nonlinear shear modulus of re-entrant hexagonal honeycombs under large deformation, Int. J. Solids Struct., 2016, 80, 284–296 CrossRef.
- B. Xu, F. Arias, S. T. Brittain, X.-M. Zhao, B. Grzybowski, S. Torquato and G. M. Whitesides, Making negative Poisson's ratio microstructures by soft lithography, Adv. Mater., 1999, 11(14), 1186 CrossRef CAS.
- L. Mizzi, K. M. Azzopardi, D. Attard, J. N. Grima and R. Gatt, Auxetic metamaterials exhibiting giant negative Poisson's ratios, Phys. Status Solidi RRL, 2015, 9(7), 425–430 CrossRef CAS.
- U. D. Larsen, O. Signund and S. Bouwsta, Design and fabrication of compliant micromechanisms and structures with negative Poisson's ratio, J. Microelectromech. Syst., 1997, 6(2), 99–106 CrossRef.
- N. Gaspar, X. Ren, C. W. Smith, J. Grima and K. E. Evans, Novel honeycombs with auxetic behaviour, Acta Mater., 2005, 53(8), 2439–2445 CrossRef CAS.
- K. Bertoldi, P. Reis, S. Willshaw and T. Mullin, Novel negative Poisson's ratio behavior induced by an elastic instability, Am. Phys. Soc., 2010, 11002 Search PubMed.
- J. N. Grima and R. Gatt, Perforated sheets exhibiting negative Poisson's ratios, Adv. Eng. Mater., 2010, 12(6), 460–464 CrossRef.
- J. T. B. Overvelde, S. Shan and K. Bertoldi, Compaction through buckling in 2D periodic, soft and porous structures: effect of pore shape, Adv. Mater., 2012, 24(17), 2337–2342 CrossRef CAS PubMed.
- J. Shim, S. Shan, A. Košmrlj, S. H. Kang, E. R. Chen, J. C. Weaver and K. Bertoldi, Harnessing instabilities for design of soft reconfigurable auxetic/chiral materials, Soft Matter, 2013, 9(34), 8198–8202 RSC.
- A. Ghaedizadeh, J. Shen, X. Ren and Y. M. Xie, Tuning the performance of metallic auxetic metamaterials by using buckling and plasticity, Materials, 2016, 9(1), 54 CrossRef.
- L. Yang, O. Harrysson, H. West and D. Cormier, Compressive properties of Ti–6Al–4V auxetic mesh structures made by electron beam melting, Acta Mater., 2012, 60(8), 3370–3379 CrossRef CAS.
- N. Guo and M. C. Leu, Additive manufacturing: technology, applications and research needs, Front. Mech. Eng., 2013, 8(3), 215–243 CrossRef.
- T. Wohlers and T. Gornet, History of additive manufacturing, Wohlers Report: Additive Manufacturing and 3D Printing State of the Industry Annual Worldwide Progress Report, 2011 Search PubMed.
- T. Bückmann, N. Stenger, M. Kadic, J. Kaschke, A. Frölich, T. Kennerknecht, C. Eberl, M. Thiel and M. Wegener, Tailored 3D mechanical metamaterials made by dip-in direct-laser-writing optical lithography, Adv. Mater., 2012, 24(20), 2710–2714 CrossRef PubMed.
- R. Critchley, I. Corni, J. A. Wharton, F. C. Walsh, R. J. Wood and K. R. Stokes, The Preparation of Auxetic Foams by Three-Dimensional Printing and Their Characteristics, Adv. Eng. Mater., 2013, 15(10), 980–985 CAS.
- M. N. Ali and I. U. Rehman, Auxetic polyurethane stents and stent-grafts for the palliative treatment of squamous cell carcinomas of the proximal and mid oesophagus: a novel fabrication route, J. Manuf. Syst., 2015, 37, 375–395 CrossRef.
- M. Vaezi, S. Chianrabutra, B. Mellor and S. Yang, Multiple material additive manufacturing – Part 1: a review: this review paper covers a decade of research on multiple material additive manufacturing technologies which can produce complex geometry parts with different materials, Virtual Phys. Prototyp., 2013, 8(1), 19–50 CrossRef.
- D. Li, L. Dong and R. S. Lakes, A unit cell structure with tunable Poisson's ratio from positive to negative, Mater. Lett., 2016, 164, 456–459 CrossRef CAS.
- M. Shokri Rad, Z. Ahmad and A. Alias, Computational approach in formulating mechanical characteristics of 3D star honeycomb auxetic structure, Adv. Mater. Sci. Eng., 2015, 2015 Search PubMed.
- K. Wang, Y.-H. Chang, Y. Chen, C. Zhang and B. Wang, Designable dual-material auxetic metamaterials using three-dimensional printing, Mater. Des., 2015, 67, 159–164 CrossRef.
- S. Babaee, J. Shim, J. C. Weaver, E. R. Chen, N. Patel and K. Bertoldi, 3D Soft metamaterials with negative Poisson's ratio, Adv. Mater., 2013, 25(36), 5044–5049 CrossRef CAS PubMed.
- J. Shim, C. Perdigou, E. R. Chen, K. Bertoldi and P. M. Reis, Buckling-induced encapsulation of structured elastic shells under pressure, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(16), 5978–5983 CrossRef CAS PubMed.
- J. Shen, S. Zhou, X. Huang and Y. M. Xie, Simple cubic three-dimensional auxetic metamaterials, Phys. Status Solidi B, 2014, 251(8), 1515–1522 CrossRef CAS.
- T. C. Lim, A 3D auxetic material based on intersecting double arrowheads, Phys. Status Solidi B, 2016, 253(7), 1252–1260 CrossRef CAS.
- M. S. Rad, Y. Prawoto and Z. Ahmad, Analytical solution and finite element approach to the 3D re-entrant structures of auxetic materials, Mech. Mater., 2014, 74, 76–87 CrossRef.
- L. Yang, O. Harrysson, H. West and D. Cormier, Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing, Int. J. Solids Struct., 2015, 69, 475–490 CrossRef.
- B. Caddock and K. Evans, Microporous materials with negative Poisson's ratios. I. Microstructure and mechanical properties, J. Phys. D: Appl. Phys., 1989, 22(12), 1877 CrossRef CAS.
- K. Evans and B. Caddock, Microporous materials with negative Poisson's ratios. II. Mechanisms and interpretation, J. Phys. D: Appl. Phys., 1989, 22(12), 1883 CrossRef CAS.
- A. Pickles, K. Alderson and K. Evans, The effects of powder morphology on the processing of auxetic polypropylene (PP of negative Poisson's ratio), Polym. Eng. Sci., 1996, 36(5), 636–642 CAS.
- K. Alderson, R. Webber, A. Kettle and K. Evans, Novel fabrication route for auxetic polyethylene. Part 1. Processing and microstructure, Polym. Eng. Sci., 2005, 45(4), 568–578 CAS.
- P. Neale, K. Alderson, A. Pickles and K. Evans, Negative Poisson's ratio of microporous polyethylene in compression, J. Mater. Sci. Lett., 1993, 12(19), 1529–1532 CAS.
- K. Alderson and K. Evans, The fabrication of microporous polyethylene having a negative Poisson's ratio, Polymer, 1992, 33(20), 4435–4438 CrossRef CAS.
- K. Alderson, A. Kettle, P. Neale, A. Pickles and K. Evans, The effect of the processing parameters on the fabrication of auxetic polyethylene, J. Mater. Sci., 1995, 30(16), 4069–4075 CrossRef CAS.
- R. Lakes, Deformation mechanisms in negative Poisson's ratio materials: structural aspects, J. Mater. Sci., 1991, 26(9), 2287–2292 CrossRef.
- J. N. Grima, R. Gatt and P. S. Farrugia, On the properties of auxetic meta-tetrachiral structures, Phys. Status Solidi B, 2008, 245(3), 511–520 CrossRef CAS.
- A. Alderson, K. Alderson, D. Attard, K. Evans, R. Gatt, J. Grima, W. Miller, N. Ravirala, C. Smith and K. Zied, Elastic constants of 3-, 4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading, Compos. Sci. Technol., 2010, 70(7), 1042–1048 CrossRef.
- D. Prall and R. Lakes, Properties of a chiral honeycomb with a Poisson's ratio of—1, Int. J. Mech. Sci., 1997, 39(3), 305–314 CrossRef.
- C. S. Ha, M. E. Plesha and R. S. Lakes, Chiral three-dimensional lattices with tunable Poisson's ratio, Smart Mater. Struct., 2016, 25(5), 054005 CrossRef.
- A. Lorato, P. Innocenti, F. Scarpa, A. Alderson, K. Alderson, K. Zied, N. Ravirala, W. Miller, C. Smith and K. Evans, The transverse elastic properties of chiral honeycombs, Compos. Sci. Technol., 2010, 70(7), 1057–1063 CrossRef.
- A. Alderson, K. Alderson, G. Chirima, N. Ravirala and K. Zied, The in-plane linear elastic constants and out-of-plane bending of 3-coordinated ligament and cylinder-ligament honeycombs, Compos. Sci. Technol., 2010, 70(7), 1034–1041 CrossRef.
- D. Mousanezhad, B. Haghpanah, R. Ghosh, A. M. Hamouda, H. Nayeb-Hashemi and A. Vaziri, Elastic properties of chiral, anti-chiral, and hierarchical honeycombs: a simple energy-based approach, Theor. Appl. Mech. Lett., 2016, 6(2), 81–96 CrossRef.
- R. Gatt, D. Attard, P. S. Farrugia, K. M. Azzopardi, L. Mizzi, J. P. Brincat and J. N. Grima, A realistic generic model for anti-tetrachiral systems, Phys. Status Solidi B, 2013, 250(10), 2012–2019 CAS.
- Y. Chen, F. Scarpa, Y. Liu and J. Leng, Elasticity of anti-tetrachiral anisotropic lattices, Int. J. Solids Struct., 2013, 50(6), 996–1004 CrossRef.
- A. Spadoni, M. Ruzzene and F. Scarpa, Global and local linear buckling behavior of a chiral cellular structure, Phys. Status Solidi B, 2005, 242(3), 695–709 CrossRef CAS.
- F. Scarpa, S. Blain, T. Lew, D. Perrott, M. Ruzzene and J. Yates, Elastic buckling of hexagonal chiral cell honeycombs, Composites, Part A, 2007, 38(2), 280–289 CrossRef.
- J. Dirrenberger, S. Forest, D. Jeulin and C. Colin, Homogenization of periodic auxetic materials, Procedia Eng., 2011, 10, 1847–1852 CrossRef.
- H. Abramovitch, M. Burgard, L. Edery-Azulay, K. Evans, M. Hoffmeister, W. Miller, F. Scarpa, C. Smith and K.-F. Tee, Smart tetrachiral and hexachiral honeycomb: sensing and impact detection, Compos. Sci. Technol., 2010, 70(7), 1072–1079 CrossRef CAS.
- R. Gatt, J. P. Brincat, K. M. Azzopardi, L. Mizzi and J. N. Grima, On the Effect of the Mode of Connection between the Node and the Ligaments in Anti-Tetrachiral Systems, Adv. Eng. Mater., 2015, 17(2), 189–198 CrossRef.
- H. H. Huang, B. L. Wong and Y. C. Chou, Design and properties of 3D-printed chiral auxetic metamaterials by reconfigurable connections, Phys. Status Solidi B, 2016, 253(8), 1557–1564 CrossRef CAS.
- J. Grima and K. Evans, Auxetic behavior from rotating squares, J. Mater. Sci. Lett., 2000, 19(17), 1563–1565 CrossRef CAS.
- J. N. Grima, A. Alderson and K. E. Evans, Negative Poisson's ratios from rotating rectangles, CMST, 2004, 10, 137–145 CrossRef.
- J. N. Grima, R. Gatt, A. Alderson and K. E. Evans, On the Auxetic Properties of Rotating Rectangles' with Different Connectivity, J. Phys. Soc. Jpn., 2005, 74(10), 2866–2867 CrossRef CAS.
- J. N. Grima, E. Manicaro and D. Attard, Auxetic behaviour from connected different-sized squares and rectangles, Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, The Royal Society, 2011, pp. 439–458 Search PubMed.
- J. Grima, V. Zammit, R. Gatt, A. Alderson and K. Evans, Auxetic behaviour from rotating semi-rigid units, Phys. Status Solidi B, 2007, 244(3), 866–882 CrossRef CAS.
- S. Shan, S. H. Kang, Z. Zhao, L. Fang and K. Bertoldi, Design of planar isotropic negative Poisson's ratio structures, Extreme Mechanics Letters, 2015, 4, 96–102 CrossRef.
- A. Slann, W. White, F. Scarpa, K. Boba and I. Farrow, Cellular plates with auxetic rectangular perforations, Phys. Status Solidi B, 2015, 252(7), 1533–1539 CrossRef CAS.
- D. Attard and J. N. Grima, A three-dimensional rotating rigid units network exhibiting negative Poisson's ratios, Phys. Status Solidi B, 2012, 249(7), 1330–1338 CrossRef CAS.
- R. Gatt, L. Mizzi, J. I. Azzopardi, K. M. Azzopardi, D. Attard, A. Casha, J. Briffa and J. N. Grima, Hierarchical auxetic mechanical metamaterials, Sci. Rep., 2015, 5, 8395 CrossRef CAS PubMed.
- J. N. Grima and K. E. Evans, Auxetic behavior from rotating triangles, J. Mater. Sci., 2006, 41(10), 3193–3196 CrossRef CAS.
- J. N. Grima, R. Gatt, B. Ellul and E. Chetcuti, Auxetic behaviour in non-crystalline materials having star or triangular shaped perforations, J. Non-Cryst. Solids, 2010, 356(37), 1980–1987 CrossRef CAS.
- D. Attard and J. N. Grima, Auxetic behaviour from rotating rhombi, Phys. Status Solidi B, 2008, 245(11), 2395–2404 CrossRef CAS.
- J. N. Grima, P. S. Farrugia, R. Gatt and D. Attard, On the auxetic properties of rotating rhombi and parallelograms: a preliminary investigation, Phys. Status Solidi B, 2008, 245(3), 521–529 CrossRef CAS.
- D. Attard, E. Manicaro and J. N. Grima, On rotating rigid parallelograms and their potential for exhibiting auxetic behaviour, Phys. Status Solidi B, 2009, 246(9), 2033–2044 CrossRef CAS.
- B. Caddock and K. Evans, Negative Poisson ratios and strain-dependent mechanical properties in arterial prostheses, Biomaterials, 1995, 16(14), 1109–1115 CrossRef CAS PubMed.
- B. E. Carroll, T. A. Palmer and A. M. Beese, Anisotropic tensile behavior of Ti–6Al–4V components fabricated with directed energy deposition additive manufacturing, Acta Mater., 2015, 87, 309–320 CrossRef CAS.
- Z. Y. Wei, Z. V. Guo, L. Dudte, H. Y. Liang and L. Mahadevan, Geometric mechanics of periodic pleated origami, Phys. Rev. Lett., 2013, 110(21), 215501 CrossRef CAS PubMed.
- C. Lv, D. Krishnaraju, G. Konjevod, H. Yu and H. Jiang, Origami based mechanical metamaterials, Sci. Rep., 2014, 4, 5979 CAS.
- M. Schenk and S. D. Guest, Geometry of Miura-folded metamaterials, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(9), 3276–3281 CrossRef CAS PubMed.
- M. Eidini and G. H. Paulino, Unraveling metamaterial properties in zigzag-base folded sheets, Sci. Adv., 2015, 1(8), e1500224 Search PubMed.
- H. Yasuda and J. Yang, Reentrant Origami-Based Metamaterials with Negative Poisson's Ratio and Bistability, Phys. Rev. Lett., 2015, 114(18), 185502 CrossRef CAS PubMed.
- A. Lazarus and P. M. Reis, Soft actuation of structured cylinders through auxetic behavior, Adv. Eng. Mater., 2015, 17(6), 815–820 CrossRef.
- Y. Tang and J. Yin, Design of cut unit geometry in hierarchical kirigami-based auxetic metamaterials for high stretchability and compressibility, Extreme Mechanics Letters, 2016 DOI:10.1016/j.eml.2016.07.005.
- S. Krödel, T. Delpero, A. Bergamini, P. Ermanni and D. M. Kochmann, 3D Auxetic Microlattices with Independently Controllable Acoustic Band Gaps and Quasi-Static Elastic Moduli, Adv. Eng. Mater., 2014, 16(4), 357–363 CrossRef.
- C. Lira, F. Scarpa and R. Rajasekaran, A gradient cellular core for aeroengine fan blades based on auxetic configurations, J. Intell. Mater. Syst. Struct., 2011, 22(9), 907–917 CrossRef.
- Q. Liu, Literature review: materials with negative Poisson's ratios and potential applications to aerospace and defence, DTIC Document, 2006 Search PubMed.
- S. A. Yavari, S. Ahmadi, J. van der Stok, R. Wauthlé, A. Riemslag, M. Janssen, J. Schrooten, H. Weinans and A. A. Zadpoor, Effects of bio-functionalizing surface treatments on the mechanical behavior of open porous titanium biomaterials, J. Mech. Behav. Biomed. Mater., 2014, 36, 109–119 CrossRef PubMed.
- S. A. Yavari, S. Ahmadi, R. Wauthle, B. Pouran, J. Schrooten, H. Weinans and A. Zadpoor, Relationship between unit cell type and porosity and the fatigue behavior of selective laser melted meta-biomaterials, J. Mech. Behav. Biomed. Mater., 2015, 43, 91–100 CrossRef PubMed.
- Z. Wang and H. Hu, Auxetic materials and their potential applications in textiles, Text. Res. J., 2014, 84(15), 1600–1611 CrossRef.
- J. C. Á. Elipe and A. D. Lantada, Comparative study of auxetic geometries by means of computer-aided design and engineering, Smart Mater. Struct., 2012, 21(10), 105004 CrossRef.
- P. Theocaris, G. Stavroulakis and P. Panagiotopoulos, Negative Poisson's ratios in composites with star-shaped inclusions: a numerical homogenization approach, Arch. Appl. Mech., 1997, 67(4), 274–286 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |


