Enhanced magnetic anisotropy in a tellurium-coordinated cobalt single-ion magnet†
Xiao-Nan
Yao
,
Mu-Wen
Yang
,
Jin
Xiong
,
Jia-Jia
Liu
,
Chen
Gao
,
Yin-Shan
Meng
,
Shang-Da
Jiang
,
Bing-Wu
Wang
 * and
Song
Gao
*
* and
Song
Gao
*
Beijing National Laboratory of Molecular Science, College of Chemistry and Molecular Engineering, State Key Laboratory of Rare Earth Materials Chemistry and Applications, Peking University, Beijing, 100871, P. R. China. E-mail: wangbw@pku.edu.cn; gaosong@pku.edu.cn
First published on 8th February 2017
Abstract
A series of tetrahedral Co(II) complexes with chalcogen donors were prepared, which exhibited strong magnetic uniaxial anisotropies and slow relaxations as SIMs. By substituting donors from S to Te, we realized the fine-tuning of the ligand field while keeping the coordination geometry virtually unchanged, yielding the first tellurium-coordinated SIM.
Single-ion magnets (SIMs), also known as mononuclear single-molecule magnets, have garnered considerable interest since the reports of slow magnetic relaxations in isolated neodymium systems and phthalocyanine terbium double-decker complexes in the early 2000s.1,2 The slow magnetic relaxation of a lanthanide ion stems from its quite large spin–orbit coupling (SOC) and a suitable ligand environment, which stabilizes the largest |±MJ> state and leads to an Ising-type ground state.3–6 Generally, lanthanide based SIMs show much larger relaxation barriers than transition metal based ones due to the unquenched orbital angular momentums of 4f electrons, contrary to those of 3d electrons. And for the same reason, transition metal based SIMs did not show up until 2010.7–9
Over the years, efforts to find high-spin transition metal complexes with unquenched orbital angular momentums have never ceased. It is believed that constructing a uniaxial ligand field around transition-metal ions is an effective way.10 Consequently, many complexes with various coordination geometries were synthesized, including square pyramidal,11 tetrahedral,12 trigonal planar,13 triangular prismatic,14,15 linear,16 and pentagonal bipyramidal17 complexes. In practice, tailoring the magnetic anisotropy of transition metal complexes by constructing a suitable ligand environment was our primary goal. In particular, in 2013, Zadrozny et al. reported a linear two-coordinate complex of Fe(I), [Fe(C(SiMe3)3)2]2−, which exhibits magnetic blocking below 4.5 K with an effective relaxation barrier of 226 cm−1, comparable to outstanding lanthanide SIMs.2,18–20 Another excellent example reported by Rechkemmer et al. sets the record for relaxation barriers of four-coordinate Co(II)-based SIMs with Ueff = 118 cm−1.21
In most cases, due to the quenched orbital angular momentums of 3d electrons, the SOC of a transition-metal ion is so weak that it should be considered as a perturbation on the interelectronic repulsion and ligand field effect, and thus the total spin quantum number S is a good quantum number to describe the multiplets. It could be described using zero-field splitting (ZFS) and ZFS parameters D and E.22,23 The corresponding Hamiltonian is expressed as
| HZFS = D[Sz2 − S(S + 1)/3] + E(Sx2 − Sy2). | (1) |
There were some studies on how different donors from the same main group influence the magnetic anisotropy of SMMs,24–27 but similar studies on elements in period five remains a blank. For one thing, heavy donors could enhance the SOC of the complexes, in favor of improving the magnetic anisotropy; for the other, the accompanying suppression of the vibronic coupling was also expected in constructing better SMMs.28 Herein, we report a series of four-coordinate Co(II) complexes Co[(EPR2)2N]2 (R = phenyl or isopropyl) with donor atoms E = S (1), Se (2) and Te (3). The structures of 1 and 2 have been reported previously29 and 3 was obtained by a modified method.30 These three complexes exhibit moderate distortion from Td to D2d symmetries mostly because of the absence of counterions.
Isothermal evaporation of their THF or hexane solutions under an Ar atmosphere affords single crystals for 1–3. All the three complexes crystallize in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , and share a similar molecular structure (Fig. 1). There are two slightly different molecules in an asymmetric unit in 1, which are labeled as 1a and 1b, respectively. Selected structural information of 1–3 is listed in Tables S1 and S2 (ESI†).
, and share a similar molecular structure (Fig. 1). There are two slightly different molecules in an asymmetric unit in 1, which are labeled as 1a and 1b, respectively. Selected structural information of 1–3 is listed in Tables S1 and S2 (ESI†).
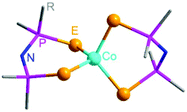 | ||
| Fig. 1 Molecular structure diagram of Co[(EPR2)2N]2 (E = S, Se, Te; R = Ph, iPr). The hydrogen atoms and the R groups are not shown for clarity. | ||
Variable-temperature dc magnetic susceptibility was measured on crystalline powders embedded in capsules at a field of 1 kOe over 2 to 300 K as shown in Fig. 2. The χmT values at 300 K of 1, 2 and 3 are 2.59, 2.66 and 3.06 emu mol−1 K respectively, which are significantly larger than the spin-only value of 1.875 emu mol−1 K for a high spin Co(II) ion, as a result of the contribution of the orbital angular momentum. The χmT–T plots of 1 and 2 are quite similar: the χmT values decrease gradually on cooling due to depopulation of excited states above 35 K, and then drop rapidly to 1.45 and 1.66 emu mol−1 K at 2 K. The sudden drop could be attributed to the magnetic anisotropy of Co(II) ions, given that the nearest Co–Co distance (∼9 Å) is too large for long-range antiferromagnetic interactions.16 For 3, the inflection point increases to 60 K, probably suggesting a larger magnetic anisotropy as described below. These χmT plots are typical for complexes with spin-only magnetic anisotropy, where the ZFS parameters D and E introduce magnetic anisotropy to the ground states by mixing them with the excited states.21,31 The low-temperature magnetization was measured at different dc fields of 1–5 T (Fig. S1–S3, ESI†). The non-superposition of the M vs. H/T plots also implies the magnetic anisotropy. Moreover, a fit to the data using Anisofit 2.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 gave the ZFS parameters D and E, as well as the effective isotropic g factors giso (Table S3, ESI†). All the obtained D values are negative, and relatively small |E/D| ratios (∼0.1) indicate that all the three complexes exhibit easy axis anisotropy with the ground state |MS = ± 3/2> lying below the |MS = ±1/2> state by ∼2|D|. It is worth noting that for 1, detailed EPR studies were performed before,33,34 and the resulting D values for 1 were −11.9 cm−1 and |E/D| ≈ 0.05, very close to what we obtained from magnetic measurements. Similar parameters (D = −15.8 cm−1 and |E/D| = 0.102, giso = 2.37) are obtained for 2, suggesting that it may show similar dynamic magnetic behaviors. But for 3, much larger D (−45.1 cm−1) and giso (2.94) make it special in this series as a very good SIM candidate. High-frequency electron paramagnetic resonance (HFEPR) measurement was performed on 2 and 3. Unfortunately, very little information was obtained because of a quite weak signal–noise ratio especially at a higher field. For 2, we could identify peaks corresponding to transitions between |MS = ±3/2> along the z axis by comparing experimental data with simulations (Fig. S4–S6, ESI†). By contrast, complex 3 did not show useful EPR signals in our measurement because of the lower s/n ratio and relatively smaller |E/D| value, which made those forbidden transitions even harder to observe.
32 gave the ZFS parameters D and E, as well as the effective isotropic g factors giso (Table S3, ESI†). All the obtained D values are negative, and relatively small |E/D| ratios (∼0.1) indicate that all the three complexes exhibit easy axis anisotropy with the ground state |MS = ± 3/2> lying below the |MS = ±1/2> state by ∼2|D|. It is worth noting that for 1, detailed EPR studies were performed before,33,34 and the resulting D values for 1 were −11.9 cm−1 and |E/D| ≈ 0.05, very close to what we obtained from magnetic measurements. Similar parameters (D = −15.8 cm−1 and |E/D| = 0.102, giso = 2.37) are obtained for 2, suggesting that it may show similar dynamic magnetic behaviors. But for 3, much larger D (−45.1 cm−1) and giso (2.94) make it special in this series as a very good SIM candidate. High-frequency electron paramagnetic resonance (HFEPR) measurement was performed on 2 and 3. Unfortunately, very little information was obtained because of a quite weak signal–noise ratio especially at a higher field. For 2, we could identify peaks corresponding to transitions between |MS = ±3/2> along the z axis by comparing experimental data with simulations (Fig. S4–S6, ESI†). By contrast, complex 3 did not show useful EPR signals in our measurement because of the lower s/n ratio and relatively smaller |E/D| value, which made those forbidden transitions even harder to observe.
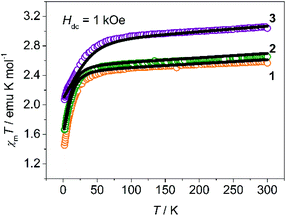 | ||
| Fig. 2 Temperature dependence of χmT between 2 and 300 K for crystalline powder samples of 1–3 (dots are values obtained in SQUID; lines correspond to ab initio calculations and scaled by 0.92). | ||
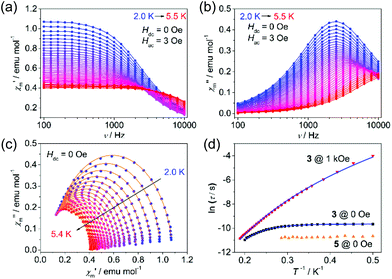
To probe the dynamic magnetic behavior, the ac susceptibility at various frequencies was measured at low temperatures. Under zero applied dc field, no out-of-phase ac susceptibility (χ′′m) peaks were observed for both 1 and 2 within 10 kHz, indicating a very fast quantum tunneling of the magnetism (QTM) (τQTM < 0.016 ms), while complex 3 exhibited slow magnetic relaxations below 5.5 K (Fig. 3a and b). The relatively larger relaxation time compared with 1 and 2 may be ascribed to the smaller QTM probability between the ground states |MS = ±3/2>, which results from larger SOC, smaller |E/D| values and thus smaller excited states component mixed into the ground states. Relaxation times (τ) could be extracted by fitting χ′m and χ′′m to a generalized Debye model (Fig. 3c) and the distribution of the corresponding α values is very narrow (0.01 < α < 0.07). It is obvious from the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. T−1 plot (Fig. 3d) that the QTM process dominates below 3 K as indicated by the temperature independence of the relaxation times. At higher temperatures, thermal processes dominate. If we fit the five data points of the highest temperatures to the Arrhenius expression [τ = τ0
τ vs. T−1 plot (Fig. 3d) that the QTM process dominates below 3 K as indicated by the temperature independence of the relaxation times. At higher temperatures, thermal processes dominate. If we fit the five data points of the highest temperatures to the Arrhenius expression [τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ueff/kBT)], we could obtain the ‘effective relaxation energy barrier’ Ueff = 16(2) cm−1 (Fig. S15, ESI†). This barrier is much smaller than what we expected (2|D| = 90.2 cm−1). Applying a dc field of 1 kOe could prominently suppress the QTM process (Fig. S13–S15, ESI†), in which case, the ‘effective barrier’ extracted from the Arrhenius fitting does not change much (22(1) cm−1) for 3 (Table S3, ESI†). Both 1 and 2 exhibit slow magnetic relaxations under 1 kOe dc field, with energy barriers of 25.3(2) and 29.2(7) cm−1 respectively (Fig. S7–S12, ESI†). The energy barrier comes from the splitting of the ground S = 3/2 multiplets for high-spin d7 ions. Thus, the large discrepancy between 2|D| and Ueff for 3 indicates that other relaxation processes like Raman or direct processes may be included.16,27,35 Thus, we used the multi-process equation:
exp(Ueff/kBT)], we could obtain the ‘effective relaxation energy barrier’ Ueff = 16(2) cm−1 (Fig. S15, ESI†). This barrier is much smaller than what we expected (2|D| = 90.2 cm−1). Applying a dc field of 1 kOe could prominently suppress the QTM process (Fig. S13–S15, ESI†), in which case, the ‘effective barrier’ extracted from the Arrhenius fitting does not change much (22(1) cm−1) for 3 (Table S3, ESI†). Both 1 and 2 exhibit slow magnetic relaxations under 1 kOe dc field, with energy barriers of 25.3(2) and 29.2(7) cm−1 respectively (Fig. S7–S12, ESI†). The energy barrier comes from the splitting of the ground S = 3/2 multiplets for high-spin d7 ions. Thus, the large discrepancy between 2|D| and Ueff for 3 indicates that other relaxation processes like Raman or direct processes may be included.16,27,35 Thus, we used the multi-process equation:
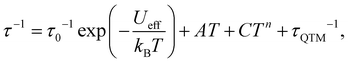 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz).17 In order to exclude the potential influence of the intermolecular interactions, a diamagnetic zinc analogue Zn[(TePiPr2)2N]2 (4) and a magnetic diluted sample Co0.06Zn0.94[(TePiPr2)2N]2 (5) were prepared. Both 4 and 5 crystallize in the P21/n space group, in contrast with the P
000 Hz).17 In order to exclude the potential influence of the intermolecular interactions, a diamagnetic zinc analogue Zn[(TePiPr2)2N]2 (4) and a magnetic diluted sample Co0.06Zn0.94[(TePiPr2)2N]2 (5) were prepared. Both 4 and 5 crystallize in the P21/n space group, in contrast with the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group of 1–3. This difference is quite unfavorable for a dynamic magnetic study because the QTM process is very sensitive to subtle structural distortion. As a result, unlike most of other reported diluted examples,38,39 the QTM process of 5 is not only preserved, but also faster than the pure sample (Fig. 3d and S16, ESI†). That means the QTM of 3 may originate from the molecule itself, and the variation of τQTM may be attributed to the slight structural distortion of Co[(TePiPr2)2N]2 molecules in 5.
space group of 1–3. This difference is quite unfavorable for a dynamic magnetic study because the QTM process is very sensitive to subtle structural distortion. As a result, unlike most of other reported diluted examples,38,39 the QTM process of 5 is not only preserved, but also faster than the pure sample (Fig. 3d and S16, ESI†). That means the QTM of 3 may originate from the molecule itself, and the variation of τQTM may be attributed to the slight structural distortion of Co[(TePiPr2)2N]2 molecules in 5.
To deeply understand the magnetism of these complexes, ab initio calculations of CASSCF/CASPT2 were performed on 1–3 using the obtained crystal structures (see the ESI† for more details). The calculations reproduce the magnetic susceptibility data well with a scale factor 0.92, as indicated by the solid lines in Fig. 2. What is more, all the calculated D (Table S4, ESI†) agree well with the fitting values listed in Table S3 (ESI†), verifying the absence of the Orbach process in the ac susceptibility measurements.
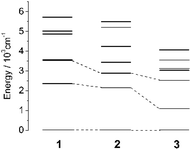
As reported in the literature,21 the large D parameter of a tetrahedral Co(II) complex comes from the splitting of the 4T2 (F) term when the complex bears a structural distortion from the Td to the D2d symmetry. We summarized the geometries of the reported four-coordinate homoleptic Co(II) complexes with the Td or D2d symmetry and easy axis magnetic anisotropy. Shape 2.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40,41 was used to analyze the distortion of the CoE4 core from an ideal tetrahedron (Table S5, ESI†), in which the resulting S value characterizes the degree of deviation from the Td symmetry for the complex (i.e. the closer the S is to zero, the less distortion from the Td symmetry the complex bears). 1–3 have much smaller S (<0.3) than the reported four-coordinate Co(II) complexes (1–10), leading to relatively small D. At the same time, complexes with similar S values have larger magnetic anisotropies as the donors grow heavier. The result indicates that the donor influences the magnetic anisotropy as much as the structural distortion, which could be ascribed to two ways: (1) the softness of the heavier donors lead to a weaker ligand field, thus lowering the energy of excited states with magnetic anisotropy; (2) larger SOC of heavier donors contributes to improving the magnetic anisotropy of the complexes.24–27 To confirm this, we also compared the splitting of the ground 4F term for a free Co(II) ion in complexes 1–3. Under the ligand field of Td, the 4F term was split into 4A2, 4T2, and 4T1 terms, and a structural distortion led to further splitting of the orbital multiplets (Fig. 4). The actual geometry of the complexes, which is in fact the C1 symmetry, breaks down the orbital degeneracy. According to the nature of the tetrahedral ligand field, the ground state and the first excited state could be connected by the matrix element <L = 3, ML = ±2|Lz| L = 3, ML = ±2>.23,27,42 Thus, |D| is proportional to the reciprocal of the energy splitting of the first two states (1
40,41 was used to analyze the distortion of the CoE4 core from an ideal tetrahedron (Table S5, ESI†), in which the resulting S value characterizes the degree of deviation from the Td symmetry for the complex (i.e. the closer the S is to zero, the less distortion from the Td symmetry the complex bears). 1–3 have much smaller S (<0.3) than the reported four-coordinate Co(II) complexes (1–10), leading to relatively small D. At the same time, complexes with similar S values have larger magnetic anisotropies as the donors grow heavier. The result indicates that the donor influences the magnetic anisotropy as much as the structural distortion, which could be ascribed to two ways: (1) the softness of the heavier donors lead to a weaker ligand field, thus lowering the energy of excited states with magnetic anisotropy; (2) larger SOC of heavier donors contributes to improving the magnetic anisotropy of the complexes.24–27 To confirm this, we also compared the splitting of the ground 4F term for a free Co(II) ion in complexes 1–3. Under the ligand field of Td, the 4F term was split into 4A2, 4T2, and 4T1 terms, and a structural distortion led to further splitting of the orbital multiplets (Fig. 4). The actual geometry of the complexes, which is in fact the C1 symmetry, breaks down the orbital degeneracy. According to the nature of the tetrahedral ligand field, the ground state and the first excited state could be connected by the matrix element <L = 3, ML = ±2|Lz| L = 3, ML = ±2>.23,27,42 Thus, |D| is proportional to the reciprocal of the energy splitting of the first two states (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.10
1.10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.16 for complexes 1 to 3). However, the ratio of the obtained |D| values is 1
2.16 for complexes 1 to 3). However, the ratio of the obtained |D| values is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.34
1.34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.82, exhibiting a much larger growth rate from 1 to 3, revealing that heavier donors indeed play an important part through bringing in larger SOC to the complexes.
3.82, exhibiting a much larger growth rate from 1 to 3, revealing that heavier donors indeed play an important part through bringing in larger SOC to the complexes.
In summary, we prepared a series of four-coordinate complexes 1–3 bearing a relatively small distortion from the Td symmetry. The ligand field of these compounds was fine-tuned by changing the donor atoms from S and Se to Te, in which the magnetic anisotropy of the latter was seldom investigated before. The magnetic anisotropy was enhanced with heavier donors because of the softness and stronger SOC for heavier donors. Both 1 and 2 are field-induced SIMs, while 3 exhibits a slow magnetic relaxation under zero dc field, which is characteristic of SIMs. A high Ueff of ∼2|D| was not obtained for 3 even under a 1 kOe dc field due to the dominance of relaxation pathways other than the Orbach process. Ab initio calculations gave a clearer description of the energy levels and agreed well with experimental measurements.
This research was funded by the National Natural Science Foundation of China (21222208, 21321001, 91422302, 21421091 and 21432001) and the National Key Basic Research Program of China (2013CB933401 and 2011CB808705). We also thank Prof. Wei Tong for his help in the EPR measurement.
Notes and references
- B.-Q. Ma, S. Gao, G. Su and G.-X. Xu, Angew. Chem., Int. Ed., 2001, 40, 434–437 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- P. Zhang, L. Zhang, C. Chao, S.-F. Xue, S.-Y. Lin and J.-K. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487 CrossRef CAS PubMed.
- Y.-N. Guo, L. Ungur, G. E. Granroth, A. K. Powell, C. Wu, S. E. Nagler, J.-K. Tang, L. F. Chibotaru and D. Cui, Sci. Rep., 2014, 4, 5471 CAS.
- Y.-S. Ding, N. F. Chilton, R. E. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS PubMed.
- D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224–1225 CrossRef CAS PubMed.
- W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115–18126 CrossRef CAS PubMed.
- J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491 RSC.
- M. Dey and N. Gogoi, Angew. Chem., Int. Ed., 2013, 52, 12780–12782 CrossRef CAS PubMed.
- T. Jurca, A. Farghal, P.-H. Lin, I. Korobkov, M. Murugesu and D. S. Richeson, J. Am. Chem. Soc., 2011, 133, 15814–15817 CrossRef CAS PubMed.
- J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732–20734 CrossRef CAS PubMed.
- P.-H. Lin, N. C. Smythe, S. I. Gorelsky, S. Maguire, N. J. Henson, I. Korobkov, B. L. Scott, J. C. Gordon, R. T. Baker and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 15806–15809 CrossRef CAS PubMed.
- Y.-Y. Zhu, C. Cui, Y.-Q. Zhang, J.-H. Jia, X. Guo, C. Gao, K. Qian, S.-D. Jiang, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802–1806 RSC.
- Y.-Y. Zhu, Y.-Q. Zhang, T.-T. Yin, C. Gao, B.-W. Wang and S. Gao, Inorg. Chem., 2015, 54, 5475–5486 CrossRef CAS PubMed.
- J. M. Zadrozny, M. Atanasov, A. M. Bryan, C. Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138 RSC.
- X. C. Huang, C. Zhou, D. Shao and X. Y. Wang, Inorg. Chem., 2014, 53, 12671–12673 CrossRef CAS PubMed.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581 CrossRef CAS PubMed.
- S. D. Jiang, B. W. Wang, H. L. Sun, Z. M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733 CrossRef CAS PubMed.
- S. Demir, J. M. Zadrozny and J. R. Long, Chem. – Eur. J., 2014, 20, 9524–9529 CrossRef CAS PubMed.
- Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 10467 CrossRef CAS PubMed.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford Univ. Press, Oxford, 2006 Search PubMed.
- O. Kahn, Molecular Magnetism, VCH Pub., New York, 1993 Search PubMed.
- H. Andres, R. Basler, H. U. Gudel, G. Aromi, G. Christou, H. Buttner and B. Ruffle, J. Am. Chem. Soc., 2000, 122, 12469–12477 CrossRef CAS.
- H. I. Karunadasa, K. D. Arquero, L. A. Berben and J. R. Long, Inorg. Chem., 2010, 49, 4738–4740 CrossRef CAS PubMed.
- M. R. Saber and K. R. Dunbar, Chem. Commun., 2014, 50, 12266–12269 RSC.
- J. M. Zadrozny, J. Telser and J. R. Long, Polyhedron, 2013, 64, 209–217 CrossRef CAS.
- M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2013, 4, 139–156 RSC.
- L. M. Gilby and B. Piggott, Polyhedron, 1999, 18, 1077–1082 CrossRef CAS.
- J. S. Ritch, T. Chivers, K. Ahmad, M. Afzaal and P. O'Brien, Inorg. Chem., 2010, 49, 1198–1205 CrossRef CAS PubMed.
- S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018 CrossRef CAS PubMed.
- M. P. Shores, J. J. Sokol and J. R. Long, J. Am. Chem. Soc., 2002, 124, 2279–2292 CrossRef CAS PubMed.
- S. Sottini, G. Mathies, P. Gast, D. Maganas, P. Kyritsis and E. J. J. Groenen, Phys. Chem. Chem. Phys., 2009, 11, 6727–6732 RSC.
- D. Maganas, S. Milikisyants, J. M. A. Rijnbeek, S. Sottini, N. Levesanos, P. Kyritsis and E. J. J. Groenen, Inorg. Chem., 2010, 49, 595–605 CrossRef CAS PubMed.
- E. Carl, S. Demeshko, F. Meyer and D. Stalke, Chem. – Eur. J., 2015, 21, 10109–10115 CrossRef CAS PubMed.
- E. R. King, G. T. Sazama and T. A. Betley, J. Am. Chem. Soc., 2012, 134, 17858–17861 CrossRef CAS PubMed.
- M.-E. Boulon, G. Cucinotta, J. Luzon, C. Degl'Innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem., Int. Ed., 2013, 52, 350–354 CrossRef CAS PubMed.
- J. Liu, Y. C. Chen, J. L. Liu, V. Vieru, L. Ungur, J. H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X. M. Chen and M. L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678 CrossRef CAS PubMed.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, Shape 2.0, Universitat de Barcelona, Barcelona, 2010 Search PubMed.
- Z. Qiu, Electron Spin Resonance Spectroscopy (in Chinese), Xinhua Press, Beijing, 1980 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Syntheses and calculation details; crystallographic and geometric information; and additional magnetic data. CCDC 1479883 for 3. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6qi00543h |
| This journal is © the Partner Organisations 2017 |