Accurate representations of the physicochemical properties of atmospheric aerosols: when are laboratory measurements of value?

Abstract

Laboratory studies can provide important insights into the processes that occur at the scale of individual particles in ambient aerosol. We examine the accuracies of measurements of core physicochemical properties of aerosols that can be made in single particle studies and explore the impact of these properties on the microscopic processes that occur in ambient aerosol. Presenting new measurements, we examine here the refinements in our understanding of aerosol hygroscopicity, surface tension, viscosity and optical properties that can be gained from detailed laboratory measurements for complex mixtures through to surrogates for secondary organic atmospheric aerosols.

---

1. Introduction

The size, composition and phase of ambient aerosol particles evolve through complex processes occurring at the microscale and are governed, at their core, by such physicochemical properties as component vapour pressures, hygroscopicities, solubilities, viscosities and surface tensions.^1–4 Variations in environmental conditions (temperature and relative humidity, RH), gas phase concentrations (of volatile and semi-volatile compounds), and interactions with radiation (both solar and terrestrial) drive these microscopic processes. Collectively, changes in the aerosol ensemble are manifested at the macroscopic scale through, for example, observed variabilities in the aerosol mass concentration,^5,6 the activity of aerosol as cloud condensation and ice nuclei (CCN and IN, respectively),^2,7,8 and the single scattering albedo.⁹ Thus, properties and processes at the microscale influence the factors that govern the impact of aerosols on the broader areas of climate,¹⁰ air quality^5,6 and human health.¹¹ Although an authentic representation in regional and global scale models of the complexity of aerosol processes occurring at the microscale is presently intractable with current numerical and computational technologies, it remains unclear what level of detail is even required when addressing these global challenges. To quantify the importance of this complexity, representing the microphysical processes with physically realistic and informed models is central to constraining robust, traceable and justifiable simplifications of processes in large scale frameworks.^12–15

Laboratory measurements provide a route to explore the complexity of aerosol processes, providing the necessary resolution and control of system parameters (e.g. particle and gas phase composition, temperature, RH, particle size) to resolve the microphysical details. Measurements can span from single particles to ensembles and can provide fine resolution of the changes in properties such as particle size, composition, mixing state, phase, and refractive index.¹⁶ In essence, they can allow a “bottom-up” approach to addressing the atmospheric role of aerosols, contrasting to the “top-down” approach of making field or remote observations and the application of large scale models. The top-down approach can lead to ambiguity when trying to infer and establish simple principles and derive general rules; conversely, the bottom-up approach resulting from the combination of laboratory measurements and models at the microscale becomes intractable when dealing with complex reality. Laboratory measurements have been central to understanding and quantifying reaction rates, absorption cross-sections of molecules and the quantum yields for photochemical processes, successfully providing the underpinning for understanding the atmospheric gas phase and interpreting ambient measurements. Similarly, laboratory measurements of aerosol processes can help underpin or challenge the interpretation of ambient measurements, provide insights into previously unexpected phenomena and constrain predictive models.¹⁷ In addition, they can and should seek to bridge the complexity divide between simple benchmark systems and the hugely mixed and multicomponent world of ambient aerosols.

Up to this point, increasing the level of complexity that can be addressed in laboratory studies has been constrained by the challenges of developing appropriate microphysical frameworks to improve our understanding of key processes. Not only are models needed to better exploit the sensitivity, resolution and accuracy of information now available from lab studies,¹⁶ but they are essential to address the challenge of defining the level of complexity and resolution at the microscopic level that must be included when predicting the evolution of ambient aerosol and their roles in climate, air pollution and health. If bottom-up lab measurements can begin to address more complex systems (e.g. the couplings between multiple processes and the properties of highly multicomponent mixtures such as secondary organic aerosol, SOA) while retaining the rigour and resolution achieved for benchmark systems, there should appear a convergence with the increasing level of resolution and detail available from top-down measurements and models of ambient aerosol.

Indeed, there are many areas where laboratory measurements continue to be important for improving our understanding of the complexities of ambient aerosol through a refined bottom-up approach. The developing picture of nucleation and new particle formation in the atmosphere has benefited considerably from the carefully controlled measurements made in the laboratory^18,19 or by the CLOUD project^13,14 of nucleation rates, the influence of cosmic rays, and the role of amines and highly oxygenated molecules. Our understanding of the hygroscopic response of aerosols has benefited from many decades of studies of the response of particles of known composition to water vapour, providing data for validation of widely used thermodynamic models for predicting equilibrium properties^20,21 and leading to clarity in interpreting data from reduced parameter analyses such as κ-Köhler theory.²² The critical supersaturation required for the activation of cloud condensation nuclei is dependent on surface tension; recent laboratory measurements have brought clarity in quantifying the dynamic changes in surface tension that control the critical supersaturation during activation.²³ Laboratory-based studies have often taken a lead in identifying the heterogeneous chemistry that occurs in the atmosphere including the rate of the reaction between HCl and ClONO₂ on ice particles leading to Cl₂,²⁴ the formation of high molecular weight oligomers in secondary organic aerosol (SOA),²⁵ and the formation of Criegee intermediates in the gas phase and their role in the oxidation of SO₂ as a route to sulphate.^26,27 Much of our understanding of ice nucleation and the efficiencies of different ice nuclei has come from laboratory measurements using simple benchmark systems,^28,29 often supplemented by studies with complex ambient samples studied in the laboratory, a prime example of bridging the gap in complexity.³⁰ Finally, the condensation kinetics of water on growing cloud droplets has received considerable attention in the laboratory over decades,³¹ which now provide a robust picture of the differences and similarities between pure water droplets and droplets coated in organic components.^32,33 Although debate about the global significance of achieving a detailed microphysical representation of some of these properties may continue, laboratory studies have been important in providing an underpinning framework for interpreting ambient data. They have also led to development of numerous new analytical tools that are widely used in the field.^34–37

Lab studies also allow the identification of previously unexpected phenomena that require further evaluation to quantify their significance for atmospheric aerosol. The importance of liquid–liquid phase separation between hydrophobic and hydrophilic phases remains uncertain, with consequences for equilibrium composition, morphology, optical properties and reaction kinetics.^38,39 Topping et al. concluded that phase separation could reduce the predicted mass of condensed organic material by between 10 and 50%, dependent on the concentration of semi-volatile components and ambient conditions.⁴⁰ A further uncertainty in the role of aerosol phase arises from the recognition that SOA can exist in a glassy phase; this possibility was first identified from a survey of the glass transition temperatures of a range of organic compounds provided by lab measurements⁴¹ and only later confirmed by direct observations of glassy SOA in boreal forests.⁴² Lab measurements have been crucial in showing that water transport remains “fast” in glassy aerosol for typical atmospheric particle sizes,⁴³ including in surrogates of SOA.^44,45 The potential significance of slow equilibration of volatile organic compounds between the gas and condensed viscous/glassy SOA and delayed heterogeneous chemistry remains unclear.^46–49

The whole realm of understanding photochemical reactions in aerosols remains at an early stage of exploration; laboratory methods are ideally poised to address many of the uncertainties.⁵⁰ Recent laboratory work has suggested that photocatalysed chemistry at the surfaces of mineral dust particles can lead to ˙OH formation, the oxidation of SO₂ to H₂SO₄, and nucleation events, consistent with observations in the field.⁵¹ Laboratory studies have also shown that dissolved organic matter, such as humic acids, can act as photosensitisers, leading to the production of unsaturated functionalised compounds from saturated fatty acids, typical precursors for SOA.⁵² Indeed, recent work has even suggested that carboxylic acids at a water surface are photochemically active, leading to the production of highly oxygenated products.⁵³ More generally, recent laboratory studies have suggested that chemical reactions can proceed in confined volumes at rates that are considerably faster than in the bulk phase, sometimes by many orders of magnitude.^54–57 This may lead to a re-evaluation of our understanding of the chemical transformations that can occur in aerosol, with much of our understanding of organic reaction mechanisms based on bulk studies.

The discussion provided here is not intended to be exhaustive, but to highlight some key themes. Laboratory measurements have been successful in imposing constraints on the physicochemical processes that undoubtedly are important at a microscale in the atmosphere using benchmark systems, for identifying new phenomena through direct observation, and for providing a route to test inferences from field data. They could continue to contribute to a wide range of ongoing unresolved issues spanning predictions of gas–particle partitioning of organic components (e.g. refined models of component vapour pressures, mass accommodation coefficients),^1,58 the role of processes such as co-condensation during cloud droplet growth,⁵⁹ the optical properties of absorbing aerosol⁹ and the role of aerosol pH. However, they should also continue to build on the level of complexity that can be addressed, narrowing the gap with the ever improving resolution achieved from field studies, and exploiting the considerable improvements that have come about in experimental techniques. In parallel, the continued development of microphysical models is essential to provide a framework for interpreting measurements and improving pragmatic simplifications used in large scale models to assess and predict aerosol impacts.

Here, we present new data for a range of physicochemical properties to illustrate the accuracy in laboratory measurements that can be achieved through recent instrumental advances in single particle approaches. We also illustrate how laboratory measurements can access the properties of aerosols of increasing chemical complexity through studies on SOA surrogates, illustrating some of the clear insights that can be gained into ambient aerosol that are not available from more conventional laboratory or field instruments.

2. Hygroscopic growth of aerosol

2.a Context

Aerosol particles act as CCN, governing cloud droplet number concentrations and size distributions, and influencing cloud albedo and lifetime.⁸ The fraction of the aerosol population that activates is determined by the supersaturation of water vapour as a rising air parcel cools, the particle size distribution and the composition and hygroscopicity of the aerosol,^8,60,61 with the larger, more hygroscopic fraction of CCN activating at lower critical supersaturation (S_c). The response of aerosol particles to water vapour can be predicted from Köhler theory for an involatile solute, which equates the gas phase RH to a product of the water activity at the solution composition of the particle, the solute term, and a surface curvature term, the Kelvin term.² The interplay of the solute and Kelvin effects determines the value of S_c that must be reached for the aerosol to activate to form a cloud droplet.

The molecular complexity of SOA precludes an explicit treatment of hygroscopic growth based on measurements for individual components. Instead, parameterisations (e.g. κ-Köhler theory)⁶² that exploit the potential of correlating the hygroscopicity with representative measures of composition (e.g. variation in κ with O : C ratio)^63,64 offer a pragmatic solution. However, an inherent assumption of a constant osmotic coefficient in κ-Köhler theory necessarily limits the generality of the hygroscopicity parameter, κ, when applied to conditions which differ from the RH of the measurement. Subsaturated measurements of κ made at RHs < 98% are difficult to reconcile with supersaturated determinations⁶⁵ and measurements of κ are often compromised by the challenge of accessing high RH.⁶⁶ Indeed, most hygroscopicity measurements for organic aerosol (both in coarse and accumulation mode studies) have been made under subsaturated conditions (RH < 90%) at a single temperature with uncertainties in RH and growth factor of typically ±1.5% and ±5%, respectively, and larger inter-instrument variabilities.^66,67

When assessing the importance of uncertainties in the solute and Kelvin terms, it should be remembered that the current best estimate of the aerosol–cloud radiative⁶⁸ forcing is −0.9 W m⁻² and an increase in cloud droplet number by 20% can lead to a change in radiative forcing of −1 W m⁻².⁶⁹ Indeed, a recent investigation on the impact of including more realistic variations in κ-Köhler values found that, given a reasonable range in values between 0.15 and 0.05, radiative forcing predictions vary from −1.02 W m⁻² to −0.25 W m⁻² depending on the choice of model framework.⁷⁰

Here, we present measurements of hygroscopicity with a new technique that allows a full growth curve to be determined from dry conditions up to >99.9% RH over a wide temperature range (250–320 K), yielding novel and extensive data for constraining predictive equilibrium state models. Such an approach can be used to provide an extensive survey of the hygroscopic properties of benchmark compounds or to probe SOA samples.

2.b Method description

The hygroscopic response of droplets is retrieved from comparative kinetics measurements of the evaporation of a droplet of known hygroscopic response (the probe droplet) and the sample droplet of interest using an electrodynamic balance, referred to as the CK-EDB. Thorough descriptions of the experimental technique and data analysis procedures are provided elsewhere.^71,72 Probe and sample droplets are injected sequentially into the CK-EDB from droplet-on-demand generators and their evolving sizes measured. Typical volumes required to load the dispensers can be <20 μL. The gas phase RH and temperature are held constant and the instantaneous mass flux of water from evaporating droplets is used to retrieve the variation in vapour pressure and, thus, water activity with change in droplet composition, i.e. the equilibrium state curve is retrieved from the kinetic measurement. Measurements are averaged over 40–100 evaporation events.

The droplet hygroscopicity is represented as the variation in the mass fraction of solute (MFS) or growth factor (GF) with water activity. Typical accuracies are better than <±0.2% in water activity at a_w > 0.9 and <±0.01 in κ (<2%) at 95% RH, comparing favourably with more conventional instruments measuring sub-saturated growth (±1% in a_w below 95% RH and ±0.1% for high humidity instruments at >99% RH)^8,63,67 and CCN activation (10–30% for S_c values between 0.1 and 1%, a_w > 0.99).⁷³ An entire growth curve can be measured in <10 s, avoiding the ambiguities arising from volatilisation of semi-volatile components. The large droplet sizes studied avoid the additional ambiguity that arises when correction must be made for the Kelvin effect for accumulation mode aerosol.

2.c Results and discussion

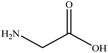
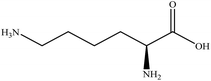
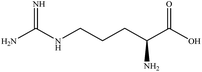
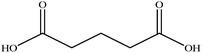
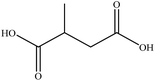
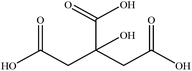
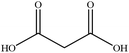
In this section we present hygroscopicity measurements for two five-component mixtures designated Mixture 1 (glycine, lysine, glutaric, malonic acid and water) and Mixture 2 (citric acid, methyl succinic acid, arginine, glutaric acid and water), all organic solute components present in equal mole fractions (see Table 1 for structures and properties), as well as for the individual binary aqueous solutions. Essential to interpret CK-EDB measurements and valuable in their own right for assessing the mixing rules for treating the properties of multicomponent aerosol, we report bulk measurements and parametrisations for density and RI as a function of mass fraction of solute (MFS) in Fig. 1a and b for Mixture 1.⁷² The measurements are compared with predictions of density (using ideal mixing) and RI (using molar refraction) for the mixtures based on the properties of all binary solutions and with a direct fitting of the bulk mixture RI data to molar refraction and of density measurements to a 3^rd order polynomial. Predictions from the binary solutions are in reasonable agreement with the measured mixture points and the fit to the mixture data: for example, the predicted n-RI of 1.5200 at MFS = 1 for Mixture 1 from the four binary solutions is in good agreement with the fit to molar refraction for the mixture, 1.5242 (see Table 1). However, it must be noted that the density and n-RI are marginally underestimated in predictions from the binary solutions alone. These data are presented as a first test of the molar refraction mixing rule for five component mixtures and may not be fully representative for other systems. We use below the parameterisations for density and n-RI based on the binary solution fits, previously showing that an error of 2% in pure component density introduces uncertainties on the calculated hygroscopicity that are comparable or even smaller than other experimental uncertainties.⁷¹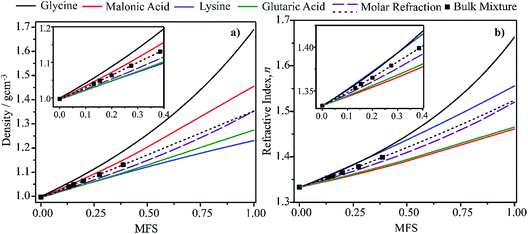

Table 1 Compounds present in Mixture 1 and 2. Pure component densities and refractive indices of the single compounds⁷² and of the two mixtures are reported (^#calculated applying the molar refraction mixing rule and ideal mixing to the four single components; *obtained from the fit of measured bulk densities and refractive indices). Single component experimental κ values from Marsh et al.,¹¹⁰ the measured κ and a calculated mass fraction weighted κ for Mixture 1 and 2 are shown. All κ values refer to a_w = 0.95

Compound	Molecular structure	Pure component density (g cm^−3)	Pure component refractive index	Experimental kappa, κ	Mass fraction weighted calculated kappa, κ
Glycine		1.6905	1.6634	0.408	—
Lysine		1.2362	1.5575	0.219	—
Arginine		1.3995	1.6370	0.147	—
Glutaric acid		1.2745	1.4655	0.144	—
Methyl succinic acid		1.3035	1.4779	0.16	—
Citric acid		1.5500	1.5087	0.189	—
Malonic acid		1.4558	1.4611	0.281	—
Mixture 1	Glycine, lysine, malonic acid, glutaric acid (O : C = 0.75)	1.3526^#	1.5200^#	0.215	0.242
		1.3530*	1.5242*
Mixture 2	Arginine, glutaric acid, methyl succinic acid, citric acid (O : C = 0.77)	1.3850^#	1.5264^#	0.090	0.162

---

Fig. 1 Density (a) and refractive index (b) parameterisations as a function of solute mass fraction in binary solutions of the four organic components in Mixture 1 (solid lines).⁷² Calculations for Mixture 1 from the single components properties (purple dashed line) and from the fitting (black dotted line) of measured bulk data (squares) are also shown.

In Fig. 2, we report the hygroscopicity measurements of Mixtures 1 and 2 at 20 °C. Immediately it is clear that hygroscopicity of Mixtures 1 and 2 do not behave in the simple additive way that would be expected from ideal mixing, even when we consider the data at the highest water activities (i.e., below the solubility limits) where the bulk measurements of n-RI and density carry little error in interpreting the CK-EDB data. Below these water activities, the considerably lower degree of hygroscopic growth for the mixtures should be interpreted with caution until a fuller analysis has been achieved. In addition, when performing the measurements for Mixture 2 it became clear that there was a kinetic limitation to water loss at water activities below 0.8, with variations from measurement-to-measurement. Given that the binary solutions for these organic components do not show appreciable viscosities at such high water activities,⁷⁴ this similarly suggests that the viscosity of the mixture does not simply relate to the binary solutions in an additive way.

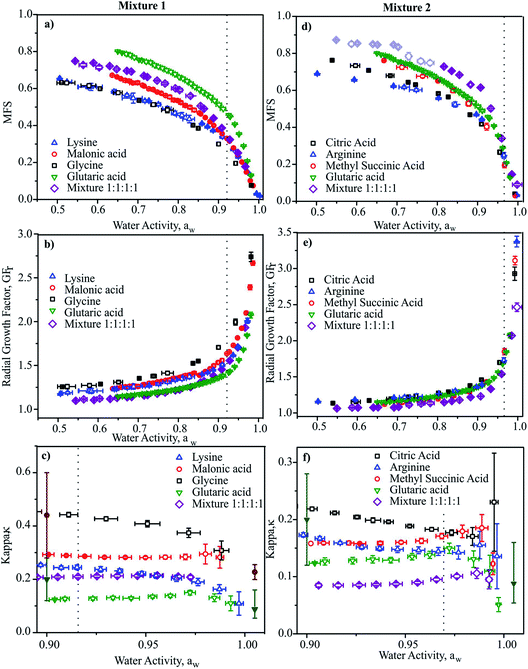Fig. 2 Mass fractions (a and d), radial growth factor (b and e) and κ (c and f) vs. a_w for Mixture 1 and 2, respectively at 20 °C. Data for the four binary aqueous solutions are also shown for comparison.¹¹⁰ Dotted lines indicate the bulk solubility limits. In (d) the light shaded purple open diamonds represent data where water transport was limited by droplet viscosity. In (c) and (f), literature data are shown (filled symbols) for glutaric acid^111,112 and malonic acid^112,113 from subsaturated (at a_w = 0.9) and supersaturated measurements (a_w > 1.0) for comparison.

In Fig. 2c and f we report values of κ retrieved at discrete a_w values. Values show clear trends with a_w as expected, illustrating the importance of stating the water activity/RH at which κ is reported and the need to report values as close to the dilute limit (a_w = 1) as practical.⁶⁶ Again, it is clear that the value of κ for the mixture is not well represented by considering the properties of the binary solutions, even at water activities above the solubility limits. This is confirmed by comparing with mass fraction weighting of κ, as reported in Table 1 with κ over predicted for both mixtures by a factor of 2. It should be noted that the values of κ reported for the binary solutions are in agreement with previous reports, although the uncertainties are generally smaller than literature sub-saturated data and comparable to super-saturated measurements.

2.d Recommendations

Although this comparison is not intended as a comprehensive evaluation of mixing rules for hygroscopicity and κ, it provides an important example that such mixing rules need to be tested against increasingly complex systems. In addition, it illustrates that aerosols containing the same O : C ratio (0.75 and 0.77 for Mixtures 1 and 2), can have very different hygroscopic properties and can vary significantly from expectations based on ideal mixing. This suggests that reporting simple measures of aerosol composition (such as O : C) fails to capture the diversity of components forming the aerosol, and it is perhaps unsurprising that such attempts at providing correlations can be highly variable in their level of success.⁶⁴ To accurately represent the hygroscopic growth of the aerosol, these data suggest that a metric must be found that provides a measure of the molecular diversity within the aerosol as well as a simple average value. In summary, the CK-EDB enables extremely accurate determinations of hygroscopic growth. It is also ideally suited to examining the kinetics of co-condensation of SVOCs and the effect hygroscopic growth,⁵⁹ as well as liquid–liquid phase separation and the influence of surface composition on condensational kinetics.³²

3. Surface tensions of aerosol

3.a Context

The surface tension of a growing droplet with increasing water activity towards 1 plays a critical role in determining the magnitude of the supersaturation required for a particle to activate as a CCN and become a cloud droplet. Nenes et al.⁷⁵ showed that disregarding surface tension suppression by organic components can lead to changes in cloud droplet number by as much as 40%; indeed, the effect of surface tension on cloud droplet number can be more significant than the Twomey effect, the sensitivity of cloud droplet number to aerosol concentration. However, Prisle et al. concluded that including only surface tension depression can lead to significantly larger effects on cloud droplet number than when including the full bulk/surface partitioning of surface active species; instead, they recommended ignoring surface tension effects in climate models.¹⁵ Typically, the CCN diameter at activation is of order 1 μm with S_c ∼ 0.2% (100.2% RH).⁷⁶ In many instances, measurements of S_c have been found to be consistent with surface tension values equal to pure water; however, numerous studies have concluded that the surface tension must be significantly depressed.^77–79 To interpret measurements of S_c made with accumulation mode aerosol, surface-bulk partitioning of the organic components must be correctly accounted for.⁸⁰ Even then, resolving the Kelvin effect is challenging and limited by typical uncertainties in a_w of ±0.1%.⁷⁶

As additional complexities, it has been suggested that the adsorption of gas phase organic components can promote cloud droplet formation by reducing the surface tension,⁸¹ surface partitioning of organic components to the droplet surface can change during growth²³ and dynamic surface tension may be more important than equilibrium spreading pressures.⁸² We present here a new method that allows direct and refined measurement of droplet surface tension for droplets of ∼5 μm radius over a wide range in water activity.

3.b Method description

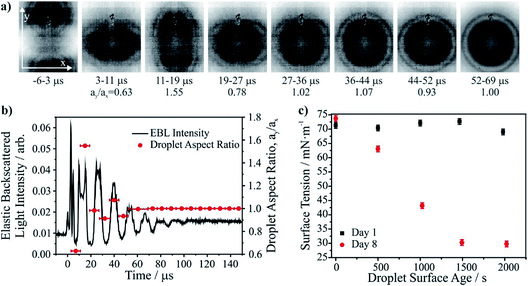
As described in more detail in previous work,^83,84 the surface tension of a droplet is inferred from the coalescence dynamics of two low viscosity (<20 mPa s) droplets in a holographic optical tweezers.^83,85 Droplet contact is followed by a damped oscillation in droplet shape monitored from brightfield imaging and the time-dependent backscattered light recorded by a photodiode (Fig. 3a and b). Due to the short timescale of coalescence and shape oscillation, even 8 μs time resolution in imaging is insufficient to fully capture the dynamic shape changes. Thus, the frequencies of the oscillating modes are inferred from a Fourier transform of the light scattering signal, allowing the determination of the surface tension.

Fig. 3 Coalescence of two optically trapped droplets can be monitored using (a) droplet aspect ratios derived from high frame rate camera images or (b) using elastic backscattered light in order to resolve the damped oscillatory motion of the coalescence event. Droplet aspect ratios in (b) are from the images shown in (a). (c) Measured surface tensions as a function of time for droplets experiencing a flow of 300 mL min⁻¹ wet air purified with a zero air generator.

3.c Results and discussion

Precise measurement of droplet surface tension allows resolution of the impacts of the surrounding gas phase on droplet surface properties. In Fig. 3c we compare the surface tensions of droplets at varying times after generation and trapping. The air for the humidified gas flow was provided by a zero air generator (Precision Zero Air 1.5, Peak Scientific, stated purity 0.05 ppm) to attempt to provide high purity air to the droplet, recognising that even low levels of contamination can impact on surface tension measurements. Although the measurements taken on Day 1 in Fig. 3c indicate a gas flow of sufficient purity to maintain a time-invariant surface tension, measurements taken just a week later (Day 8) under exactly the same conditions (300 mL min⁻¹ wet flow) result in rapid contamination of the droplet surface to a value consistent with a surfactant coating. These measurements highlight the challenge of maintaining a clean droplet surface during the timescale of an experiment. Indeed, we have previously shown that high purity gas cylinders have sufficient levels of trace contaminants to impact droplet surface properties on even shorter timescales.⁸³

3.d Recommendations

We have highlighted a new method that allows direct measurements of surface tension of aqueous aerosol droplets. The measurements reported here highlight the rapid contamination of aerosol droplet composition that must occur in ambient air, leading to suppression in surface tension. Given that the characteristic time for equilibration in droplet composition with a soluble component in the gas phase scales with radius, a time of ∼1500 s shown here for droplets of ∼5 μm radius would correspond to a surface contamination time of only ∼19 s for a 100 nm radius particle. The approach is sufficiently versatile that it can be used to examine changes in surface composition/tension driven by gas adsorption or photochemistry as well as providing a route to investigate some of the dynamic factors that control the kinetics of surface adsorption on aerosol droplets.

4. Viscous aerosol

4.a Context

The impact of aerosol phase state on ambient SOA properties has largely been addressed through laboratory studies of benchmark systems and SOA samples produced in chamber studies,^{44,45,74,86–88} the identification of particle phase and equilibration timescales directly in chamber studies,^89–91 or models of ambient aerosol that are constrained by data from laboratory studies.^49,86,92 Indeed, ambient data with the required resolution are virtually impossible to acquire to address such a complex problem. Measurements of the water activity dependence of particle viscosity for a wide range of organic–aqueous systems extending over a wide range in viscosity (10⁻³ to 10⁹ Pa s) have been achieved, leading to improvements and validation of predictive tools for estimating particle viscosity based on composition.⁷⁴ In the same work, by combining these predictive tools with GECKO-A simulations of α-pinene oxidation generating ∼50 000 compounds, a viscosity distribution can be predicted: ∼1500 compounds were predicted to have pure component viscosities >10⁶ Pa s. Laboratory measurements of viscosities of α-pinene derived SOA⁹³ suggest that the viscosity under dry conditions may be in the range 10⁷ to 10⁹ Pa s or larger.⁴⁷ Viscosities of isoprene derived SOA and toluene SOA have been shown to be lower and higher, respectively.⁸⁶ In all cases, water acts as a plasticiser, reducing the viscosity of the aerosol.

Water diffusion in viscous particles has been shown to occur more rapidly than would be expected based on the Stokes–Einstein relationship between viscosity and diffusion.^44,45,84,94 Although this implies that the equilibration of ambient aerosols to changes in RH occurs on timescales considerably shorter than the time-resolution in most atmospheric models, it is often frequently argued that mass transport limitations and dissolution timescales could impact on hygroscopic growth and CCN measurements. In contrast to water, diffusion of semi-volatile and involatile organic components has been shown to more closely follow Stokes–Einstein,^88,95 suggesting the possibility of a kinetic limitation in the gas–particle partitioning of semi-volatile components. Most models that have investigated this kinetic limitation assume a compositionally independent (e.g. no a_w dependence) single value of the diffusion constant based on the expected viscosity (or a threshold value, e.g. 10⁶ Pa s)⁴⁹ rather than fully accounting for the microphysical detail and inhomogeneities in particle composition that develop.⁹² It is still uncertain if this is a reasonable simplification. Further, although some recent chamber measurements have suggested that the scrambling of deuterated and un-deuterated toluene SOA sample compositions by gas–particle exchange occurs completely on a timescale of <2.5 h at all but the lowest RHs (<20%), these measurements were at room temperature and the dependence on temperature remains uncertain.⁸⁹

In summary, refined measurements of microphysical processes are required to understand the influence of slow diffusional mixing and mass transport on aerosol equilibration timescales. Here we present new measurements that resolve the dissolution timescale of viscous aerosol.

4.b Method description

We use the CK-EDB approach as described in Section 2.b. In addition, we take advantage of the rapid timescale that can be achieved in introducing a step in the RH between two constant values. By switching between two gas flows, we can increase the RH experienced by the particle from <20% to >80% in less than 0.5 s.³²

4.c Results and discussion

We compare the condensation kinetics of water on aqueous droplets of sodium nitrate, sucrose, Mixture 1 and Mixture 2 (Section 2) in Fig. 4a. For the binary systems, the RH is increased from ∼20 to ∼80%; for the mixtures, the RH change is from ∼40 to ∼70%. In all cases, the temperature is 0 °C. The time-dependencies in size are shown relative to the initial radius, examples of exact sizes are shown in Fig. 4b and c. For these RH changes, the sodium nitrate droplet changes in radius by a larger fraction than sucrose, reflecting the larger hygroscopicity of the salt. Similarly, the droplet of Mixture 1 changes in size by a larger fraction than Mixture 2. All particles equilibrate to the new gas phase RH in <10 s; fits to an exponential rise are shown in Fig. 4a with the time constant specified. The exact time constants are strongly dependent on the RH change, the size change and absolute particle size and so variations in time constant should not be considered significant.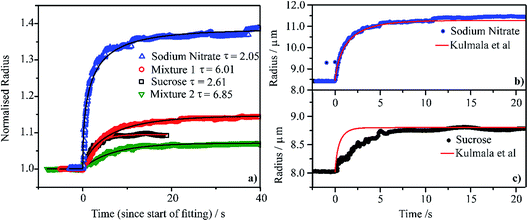

Fig. 4 (a) Water condensation kinetics at 0 °C onto single aqueous droplets containing sodium nitrate (RH stepped from 24% to 80%), sucrose (from 25% to 80% RH), Mixture 1 (from 46% to 81% RH) and Mixture 2 (from 46% to 81% RH). A fitting of each measured curve with a stretched exponential function (y = r_high − (r_high − r_low)exp[−(t/τ)]) is shown and τ values are also reported. The measured radii are normalised on each droplet’s radius before the RH step. (b) and (c) Comparison of the measured radius response to the step in RH (same as in panel (a)) with a condensation kinetics simulation from the model of Kulmala et al.⁹⁶

In Fig. 4b and c, we compare the measured condensation kinetics with predictions using the analytic model of Kulmala et al.⁹⁶ Here, we use the known responses in the equilibrium solution properties from our previous measurements. We assume that the particle remains homogeneous throughout (i.e., is uniform in composition) and that the mass accommodation coefficient for water is unity (i.e., there is no surface kinetic limitation). We have used this approach previously to simulate water condensation and evaporation kinetics.^32,33 The predicted condensation kinetics of water on an aqueous sodium nitrate droplet follow very closely the measurement. This suggests that the condensation process is limited by the diffusion of water in the gas phase, with the kinetics characteristic of the continuum regime. The simulated condensation kinetics for the sucrose particle are faster than measured, suggesting a mild kinetic limitation imposed on condensation. The sucrose particle starts at a viscosity of >10¹² Pa s at t = 0 s ending at a viscosity of >1 Pa s once equilibrated. However, even for such large particles the condensation process is over in <10 s. This suggests that the condensation kinetics of water on any accumulation mode aerosol of high viscosity in the atmosphere is likely to be complete in ≪1 s.

4.d Recommendations

Laboratory measurements will continue to be central in better defining the impact of aerosol phase on the processes occurring in ambient aerosol. Here, we show that water condensation kinetics on viscous and glassy particles and dissolution remain fast, with only a marginal delay with respect to the gas diffusion limit even for particles of ∼10 μm radius. Already laboratory studies are attempting to bridge the complexity gap. Simple benchmark systems have allowed us to identify when the Stokes–Einstein equation breaks down, allowing a constraint to be placed on the timescales of atmospheric processes. Studies of surrogates of SOA have yielded important insights into the limits of viscosities achieved by ambient SOA. Future studies must better constrain gas–particle equilibration timescales particularly at low temperatures, the impact of the complex microphysical structuring/heterogeneities in individual particles on the behaviour of whole populations of particles, and the relationship between the kinetics of heterogeneous chemistry and particle viscosity.

5. Optical properties of aerosol

5.a Context

The real and imaginary parts of the refractive index (n-RI and k-RI, respectively) govern the light scattering and absorption cross-sections of aerosol particles. Cavity ring-down spectroscopy (CRDS) and photoacoustic spectroscopy (PAS) have become common approaches for determining n-RI and k-RI in situ.⁹⁷ Analyses of the instrumental noise, systematic errors and calibration uncertainties in ensemble CRDS measurements have shown that n-RI can only be retrieved with an accuracy of ±0.02,^97,98 an accuracy that prevents rigorous testing of mixing rules.⁹⁹ Uncertainties in k-RI from ensemble CRD extinction measurements can be as large as ±50%, principally because of the compounding errors from already significant uncertainties in n-RI.⁹⁷ Combined measurements of absorption by PAS and extinction by CRDS can be challenging to reconcile and mass-specific absorption cross-sections from CRDS/PAS and UV-visible spectrometry agree to at best ±25%.^100,101 In addition, most measurements of optical properties report values for RI only under dry conditions.⁹

A 7% change in n-RI (from 1.4 to 1.5) has been estimated to increase the radiative forcing of aerosol by 12% through a change in the asymmetry parameter. By comparison, measured ranges of n-RI for anthropogenic SOA from a single precursor (e.g. toluene) can span from 1.36 to 1.66.⁹ Potentially even larger uncertainties in measurements and predictions can exist for SOA from mixed precursors (e.g. toluene and phenol).¹⁰² The Hadley Centre Global Environment climate model HadGEM3 assumes a value of n-RI of 1.50. The impacts of uncertainties in k-RI on radiative forcing are even more severe: recent studies have suggested that the k-RI of brown carbon (BrC) aerosol is the third most significant source of uncertainty for aerosol–radiation interactions after biomass burning emissions and cloud brightness. Measurements of the absorbing aerosol optical depth (AAOD) can be rationalised only if absorption previously attributed to black carbon (BC) is instead attributed to BrC.¹⁰³ Indeed, recent studies suggest that BrC could contribute 27 to 70% of black carbon absorption globally.¹⁰⁴

In summary, refined tools and detailed measurements of optical properties are required to better constrain the optical properties of SOA; laboratory measurements on single particles could provide a route to reducing current uncertainties.

5.b Method description

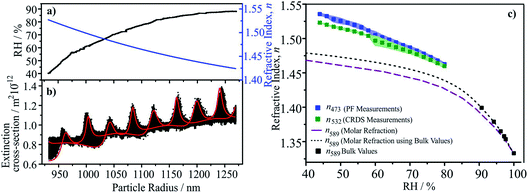
We have described in detail previously the retrieval of n-RI for single particles captured by a Bessel beam trap and probed by light scattering and CRDS.^105–107 The geometric cross-section of the particle is determined through fitting the angularly-resolved light scattering, retrieving size and size/RH-dependence of RI over the complete measurement.¹⁰⁷ The optical cross-section from concurrent CRD measurements is compared with simulations to infer the size/RH-dependence of the RI at the CRD wavelength.^105,107 Thus, n-RI at multiple wavelengths (405, 473, 532 nm) over a wide range in RH is retrieved for each particle.

5.c Results and discussion

As an illustration of the accuracy of this approach, we report measurements of n-RI for Mixture 1. In Section 2 we demonstrated that the molar refraction mixing rule provides an accurate representation of the bulk solution RIs below the solubility limit at 589 nm. Here we consider the n-RIs at 532 and 473 nm for supersaturated solutions. A typical data set is shown in Fig. 5. Initially starting at >80%, the RH was gradually reduced to 40% leading to a decrease in size and an increase in n-RI, Fig. 5a. The evolving radius and n-RI were obtained from fitting the angular scattering at 473 nm. At each time point (i.e. each radius), the optical cross-section was inferred from CRD at 532 nm, Fig. 5b, and is characterised by peaks in extinction as the size evolves. The envelope in cross-section arises from Brownian motion of the particle across the nodes and anti-nodes in the standing wave formed by the optical cavity. This must be compared with predictions from cavity standing wave Mie theory to enable the retrieval of n-RI as a function of size/RH.^105,107 The values of n-RI retrieved at 473 and 532 nm compared well with predictions from the molar refraction mixing rule at 589 nm in Fig. 5c. As anticipated, the trends of n-RI with RH increase with increasing solute concentration and an increase with decreasing wavelength.

Fig. 5 (a) Relative humidity and refractive index variations as a function of the size of an evaporating Mixture 1 solution droplet. (b) Extinction cross-section (black dots) from measured cavity ring-down times for the same droplet as in panel (a), together with Mie theory calculations (red lines). (c) Wavelength dependence of n-RI vs. RH for Mixture 1 (measurements are averaged over 3 droplet measurements, envelope shows standard deviation).

5.d Recommendations

The measurements shown here illustrate that optical measurements can now be made on single particles over a wide range of RH and at multiple wavelengths with low uncertainties in n-RI of ±0.002 (±0.15%), at least an order of magnitude improvement on previous techniques. Previously, we have also shown that k-RI can be retrieved with accuracies of <±20% when between 10⁻³ to 2 × 10⁻², improving to <±5% at larger k-RI values.¹⁰⁸ Achieving such accuracy is crucial to reducing instrument uncertainties to a level that robust conclusions about the optical properties of scattering and absorbing organic aerosol can be made and the current range of values understood.⁹ Indeed, the role of particle morphology (e.g. shape, surface roughness, liquid–liquid phase separation) and mixing state (e.g. internal mixtures of BrC and BC) may only be finally elucidated from such accurate measurements.

6. Extending single-particle measurements to α-pinene SOA

To conclude, it is valuable to show the direction in which such measurements can be taken; we briefly remark on a limited set of measurements of the properties of SOA samples from the oxidation of α-pinene. SOA was generated in an in-house built photo-chemical flow reactor (PFR) at the University of York. Technical details regarding the PFR design can be found in Pereira et al. (2017, in preparation). Briefly, the PFR consists of a 300 L polyvinyl fluoride bag. UV irradiation is achieved using an Hg pen-ray located in the centre of the PFR. Temperature and humidity were continually measured, and maintained at 23.9 °C and 51.0% respectively, in the experiment described here. α-Pinene and water vapour were continuously introduced into the PFR. Initial VOC concentration was determined using SYFT-MS, and NO_x and O₃ concentrations were measured as 19.7 ppbv and 594.8 ppbv, respectively. High (27.4 ppmv) concentrations of α-pinene were used to generate sufficient SOA mass (>10² mg) for offline analysis and single particle work. SOA mass was collected using an electrical low pressure impactor and transferred into vials, wrapped in foil to prevent photolysis degradation and stored in a freezer at −20 °C. One vial was used for compositional analysis and the second for single particle measurements. An extensive range of techniques has been used to characterise SOA composition and a full description will be provided in a subsequent publication. The SOA sample examined here consisted of 58.46% carbon, 8.15% hydrogen and 0.03% nitrogen by weight. The remaining 33.4% was attributed to elemental oxygen, resulting in an O : C ratio of 0.43 and an average carbon oxidation state of −0.81.¹⁰⁹ It should be noted that these values refer to the whole α-pinene SOA sample, whereas here we present measurements for the water soluble fraction of the sample alone, which accounts for 58.4 ± 1.4% of the total organic sample mass.

CK-EDB measurements of the evolving size of dilute aqueous solution droplets of the water soluble fraction are shown in Fig. 6a. The time-dependent evaporation kinetics can be used by comparison with a probe droplet to retrieve the hygroscopic growth of the SOA sample (see Section 2 and Fig. 6d). Drying the droplet at lower RH leads to more rapid water loss and a smaller equilibrium size. The kinetics of water evaporation remain fast, even when drying to 10% RH (<5 s). This is consistent with previous diffusion constants estimated for water in α-pinene SOA, i.e. there is no kinetic impairment to water loss at 20 °C.^44,45 Over long time frames (>15 000 s), there is continued slow loss of SVOCs from the dried particle. When the radius-squared time-dependence is examined,¹⁶ the diminishing gradient implies that the higher volatility compounds evaporate leaving compounds of lower volatility. Although not shown here, the volatilisation at 10% RH is slower than at intermediate RHs, suggesting a kinetic limitation on the volatilisation kinetics of semi-volatile organic components and the formation of a viscous SOA matrix at low RH. Fig. 6b shows that the value of n-RI continues to rise during this time period as the evaporation rate slows, suggesting that the lower volatility components, which are likely more oxygenated and higher in molecular weight, have higher n-RI than the higher volatility components. The value of n-RI tends towards values previously reported for α-pinene SOA as the more volatile components evaporate,⁹ although it should be clear that the value strongly depends on composition/age and on RH.

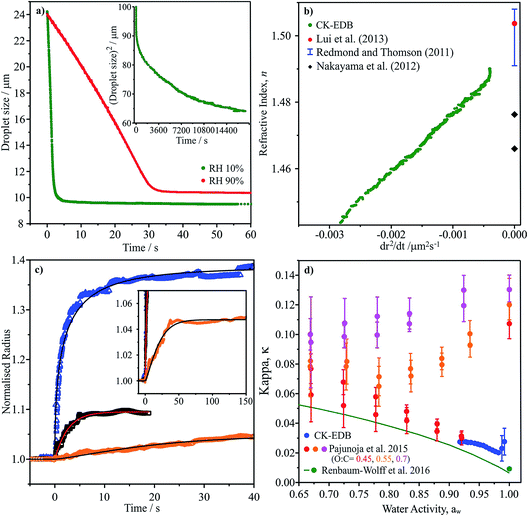Fig. 6 (a) Evaporation profile of aqueous α-pinene SOA (O : C of 0.43) droplet at two RHs, inset shows long time evaporation (radius²vs. time). (b) CK-EDB refractive index variation with dr²/dt plotted with literature SOA measurements (dry).⁹ (c) Water condensation kinetics on sodium nitrate, sucrose and aqueous α-pinene SOA at 0 °C, showing normalised radius. Inset shows long time condensation profile for aqueous α-pinene SOA. (d) κ vs. a_w for CK-EDB aqueous α-pinene SOA at 20 °C compared with literature values.^65,114

In Fig. 6c we report measurements of the condensation kinetics of water on α-pinene SOA at 0 °C for an increase in RH from 35 to 80%. The equilibration time requires almost 50 s, consistent with slower water transport than during the evaporation process due to the lower temperature and slower diffusion. However, this timescale still suggests rapid equilibration of accumulation mode particles. Using this approach, it will be straightforward to examine both the water and SVOC transport kinetics at temperatures down to ∼250 K. Finally in Fig. 6d, we report the a_w dependence of the value of κ. Intriguingly, the values are remarkably close to those reported by Pajunoja et al. for α-pinene SOA with an O : C of 0.45, although their measurements were reportedly for the whole soluble and insoluble mass.⁶⁵

In summary, we have used a variety of single particle studies to illustrate the accuracy that can now be achieved in measurements of aerosol hygroscopicity, surface tension, kinetics and optical properties for systems of increasing chemical complexity from mixtures to SOA. Indeed, it is now even routine to determine the hygroscopicity of the aerosol, the kinetics of water transport, the vapour pressures/volatilities of the organic components and the RH dependence of the refractive index on the same particle, providing a comprehensive account of properties that more commonly can only be accessed by separate measurements and on different samples. The temperature dependence of these properties can also be interrogated. In combination, such highly accurate measurements could allow access to comparisons/correlations between these properties that have not been previously possible, as well as providing highly refined data for expanding and benchmarking models of aerosol microphysics. Such measurements should provide important insights into the processes that ambient aerosol undergo and yield accurate parameterisations of aerosol properties.

Acknowledgements

JPR, AM and BRB acknowledge support from EPSRC for studentship funding and grant EP/L010569/1. REW acknowledges NERC support from the DTP GW4+ NE/L002434/1. JPR and GR acknowledge NERC through funding from grant NE/N013700/1; JPR, YCS, KLP, JFH and DOT acknowledge NERC through support from NE/M004600/1. We thank Nicolas Rothfuss for python code for fitting condensation measurements. The experimental data are provided through the University of Bristol data repository at Reid, J. P. (2017): Accurate representations of the physicochemical properties of atmospheric aerosols, University of Bristol, DOI: 10.5523/bris.1tu9y4ue9vzfx27hnzz9ch5zu7

References

1. M. Bilde, et al. , Chem. Rev., 2015, 115, 4115–4156.
2. D. K. Farmer, C. D. Cappa and S. M. Kreidenweis, Chem. Rev., 2015, 115, 4199–4217.
3. S. N. Pandis, et al. , Faraday Discuss., 2013, 165, 9.
4. H. Vehkamäki, I. Riipinen and H. Vehkamaki, Chem. Soc. Rev., 2012, 41, 5160–5173.
5. M. Hallquist, et al. , Atmos. Chem. Phys., 2009, 9, 5155–5236.
6. R. Zhang, et al. , Chem. Rev., 2015, 115, 3803–3855.
7. B. J. Murray, D. O’Sullivan, J. D. Atkinson and M. E. Webb, Chem. Soc. Rev., 2012, 41, 6519–6554.
8. G. Mcfiggans, et al. , Atmos. Chem. Phys., 2006, 6, 2593–2649.
9. T. Moise, J. M. Flores and Y. Rudich, Chem. Rev., 2015, 115, 4400–4439.
10. A. R. Ravishankara, Y. Rudich and D. J. Wuebbles, Chem. Rev., 2015, 115, 3682–3703.
11. U. Pöschl and M. Shiraiwa, Chem. Rev., 2015, 115, 4440–4475.
12. R. A. Zaveri, R. C. Easter, J. E. Shilling and J. H. Seinfeld, Atmos. Chem. Phys., 2014, 14, 5153–5181.
13. J. Kirkby, et al. , Nature, 2011, 476, 429–433.
14. J. Kirkby, et al. , Nature, 2016, 533, 521–526.
15. N. L. Prisle, et al. , Geophys. Res. Lett., 2012, 39, L05802.
16. U. K. Krieger, C. Marcolli and J. P. Reid, Chem. Soc. Rev., 2012, 41, 6631–6662.
17. J. Abbatt, C. George, M. Melamed, P. Monks, S. Pandis and Y. Rudich, Atmos. Environ., 2014, 84, 390–391.
18. C. N. Jen, P. H. McMurry and D. R. Hanson, J. Geophys. Res.: Atmos., 2014, 119, 7502–7514.
19. B. R. Bzdek, D. P. Ridge and M. V. Johnston, Atmos. Chem. Phys. Discuss., 2010, 10, 45–68.
20. A. Zuend, C. Marcolli, B. P. Luo and T. Peter, Atmos. Chem. Phys., 2008, 8, 4559–4593.
21. A. S. Wexler and S. L. Clegg, J. Geophys. Res.: Atmos., 2002, 107, 4207.
22. S. R. Suda, et al. , Environ. Sci. Technol., 2014, 48, 10182–10190.
23. C. R. Ruehl, J. F. Davies and K. R. Wilson, Science, 2016, 351, 1447–1450.
24. M. J. Molina, T. L. Tso, L. T. Molina and F. C. Wang, Science, 1987, 238, 1253–1257.
25. M. Kalberer, et al. , Science, 2004, 303, 1659–1662.
26. C. J. Percival, et al. , Faraday Discuss., 2013, 165, 45.
27. O. Welz, et al. , Science, 2012, 335, 204–207.
28. B. J. Murray, D. A. Knopf and A. K. Bertram, Nature, 2005, 434, 202–205.
29. B. J. Murray, et al. , Nat. Geosci., 2010, 3, 233–237.
30. T. W. Wilson, et al. , Nature, 2015, 525, 234–238.
31. C. E. Kolb, et al. , Atmos. Chem. Phys., 2010, 10, 10561–10605.
32. J. F. Davies, R. E. H. Miles, A. E. Haddrell and J. P. Reid, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8807–8812.
33. J. F. Davies, R. E. H. Miles, A. E. Haddrell and J. P. Reid, J. Geophys. Res.: Atmos., 2014, 119, 10931–10940.
34. B. R. Bzdek, M. R. Pennington and M. V. Johnston, J. Aerosol Sci., 2012, 52, 109–120.
35. R. C. Flagan, Aerosol Sci. Technol., 1998, 28, 301–380.
36. J. Laskin, A. Laskin and S. A. Nizkorodov, Int. Rev. Phys. Chem., 2012, 32, 128–170.
37. R. C. Sullivan and K. A. Prather, Anal. Chem., 2005, 77, 3861–3885.
38. M. Song, C. Marcolli, U. K. Krieger, A. Zuend and T. Peter, Geophys. Res. Lett., 2012, 39, 3016–3036.
39. L. Mitchem, J. Buajarern, A. D. Ward and J. P. Reid, J. Phys. Chem. B, 2006, 110, 13700–13703.
40. D. Topping, M. Barley and G. McFiggans, Faraday Discuss., 2013, 165, 273–288.
41. B. Zobrist, C. Marcolli, D. A. Pedernera and T. Koop, Atmos. Chem. Phys., 2008, 8, 5221–5244.
42. A. Virtanen, et al. , Nature, 2010, 467, 824–827.
43. D. L. Bones, J. P. Reid, D. M. Lienhard and U. K. Krieger, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11613–11618.
44. H. C. Price, et al. , Chem. Sci., 2015, 6, 4876–4883.
45. D. M. Lienhard, et al. , Atmos. Chem. Phys., 2015, 15, 13599–13613.
46. V. Perraud, et al. , Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2836–2841.
47. L. Renbaum-Wolff, et al. , Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8014–8019.
48. M. Shiraiwa, M. Ammann, T. Koop and U. Poeschl, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11003–11008.
49. M. Shiraiwa and J. H. Seinfeld, Geophys. Res. Lett., 2012, 39, L24801.
50. C. George, M. Ammann, B. D’Anna, D. J. Donaldson and S. A. Nizkorodov, Chem. Rev., 2015, 115, 4218–4258.
51. Y. Dupart, et al. , Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20842–20847.
52. R. Ciuraru, L. Fine, M. van Pinxteren, B. D’Anna, H. Herrmann and C. George, Sci. Rep., 2015, 5, 12741.
53. S. Rossignol, et al. , Science, 2016, 353, 699–702.
54. J. K. Lee, S. Kim, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2015, 201503689.
55. M. Girod, E. Moyano, D. I. Campbell and R. G. Cooks, Chem. Sci., 2011, 2, 501.
56. A. Fallah-Araghi, et al. , Phys. Rev. Lett., 2014, 112, 28301.
57. R. M. Bain, C. J. Pulliam and R. G. Cooks, Chem. Sci., 2015, 6, 397–401.
58. G. McFiggans, D. O. Topping and M. H. Barley, Atmos. Chem. Phys., 2010, 10, 10255–10272.
59. D. Topping, P. Connolly and G. McFiggans, Nat. Geosci., 2013, 6, 1–4.
60. U. Dusek, et al. , Science, 2006, 312, 1375–1378.
61. P. Reutter, et al. , Atmos. Chem. Phys., 2009, 9, 7067–7080.
62. M. D. Petters and S. M. Kreidenweis, Atmos. Chem. Phys., 2007, 7, 1961–1971.
63. J. Duplissy, et al. , Atmos. Chem. Phys., 2011, 11, 1155–1165.
64. A. M. J. Rickards, R. E. H. Miles, J. F. Davies, F. H. Marshall and J. P. Reid, J. Phys. Chem. A, 2013, 117, 14120–14131.
65. A. Pajunoja, et al. , Geophys. Res. Lett., 2015, 42, 3063–3068.
66. S. R. Suda and M. D. Petters, Aerosol Sci. Technol., 2013, 47, 991–1000.
67. N. Good, et al. , Atmos. Chem. Phys., 2010, 10, 2577–2593.
68. T. F. Stocker, et al., Technical Summary, Cambridge University Press, Cambridge, UK, New York, USA, 2013.
69. M. C. Facchini, M. Mircea, S. Fuzzi and R. J. Charlson, Nature, 1999, 401, 257–259.
70. D. O. Topping, Priv. Commun., 2017.
71. G. Rovelli, R. E. H. Miles, J. P. Reid and S. L. Clegg, J. Phys. Chem. A, 2016, 120, 4376–4388.
72. C. Cai, et al. , J. Phys. Chem. A, 2016, 120, 6604–6617.
73. D. Rose, et al. , Atmos. Chem. Phys., 2008, 8, 1153–1179.
74. Y. C. Song, et al. , J. Phys. Chem. A, 2016, 120, 8123–8137.
75. A. Nenes, R. J. Charlson, M. C. Facchini, M. Kulmala, A. Laaksonen and J. H. Seinfeld, Geophys. Res. Lett., 2002, 29, 1848.
76. C. R. Ruehl, P. Y. Chuang and A. Nenes, Atmos. Chem. Phys., 2010, 10, 1329–1344.
77. V. F. Mcneill, N. Sareen and A. N. Schwier, Top. Curr. Chem., 2013, 339, 201–259.
78. M. D. Petters and S. M. Kreidenweis, Atmos. Chem. Phys., 2013, 13, 1081–1091.
79. C. R. Ruehl, P. Y. Chuang, A. Nenes, C. D. Cappa, K. R. Kolesar and A. H. Goldstein, Geophys. Res. Lett., 2012, 39, L23801.
80. N. L. Prisle, T. Raatikainen, A. Laaksonen and M. Bilde, Atmos. Chem. Phys., 2010, 10, 5663–5683.
81. N. Sareen, A. N. Schwier, T. L. Lathem, A. Nenes and V. F. McNeill, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 2723–2728.
82. B. Nozière, C. Baduel and J.-L. Jaffrezo, Nat. Commun., 2014, 5, 3335.
83. B. R. Bzdek, R. M. Power, S. H. Simpson, J. P. Reid and C. P. Royall, Chem. Sci., 2016, 7, 274–285.
84. R. M. Power, S. H. Simpson, J. P. Reid and A. J. Hudson, Chem. Sci., 2013, 4, 2597–2604.
85. B. R. Bzdek, L. Collard, J. E. Sprittles, A. J. Hudson and J. P. Reid, J. Chem. Phys., 2016, 145, 54502.
86. M. Song, et al. , Atmos. Chem. Phys. Discuss., 2016, 1–34.
87. N. A. Hosny, et al. , Chem. Sci., 2016, 7, 1357–1367.
88. H. C. Price, J. Mattsson and B. J. Murray, Phys. Chem. Chem. Phys., 2016, 18, 19207–19216.
89. Y. Qing, E. S. Robinson, X. Ding, P. Ye, R. C. Sullivan and N. M. Donahue, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(45), 12649–12654.
90. E. Järvinen, et al. , Atmos. Chem. Phys., 2016, 16, 4423–4438.
91. A. P. Bateman, A. K. Bertram and S. T. Martin, J. Phys. Chem. A, 2015, 119, 4386–4395.
92. S. O’Meara, D. Topping and G. McFiggans, Atmos. Chem. Phys., 2016, 16, 5299–5313.
93. Y. Zhang, et al. , Atmos. Chem. Phys., 2015, 15, 7819–7829.
94. F. H. Marshall, et al. , Chem. Sci., 2016, 7, 1298–1308.
95. Y. Chenyakin, D. A. Ullmann, E. Evoy, L. Renbaum-Wolff, S. Kamal and A. K. Bertram, Atmos. Chem. Phys. Discuss., 2016, 38, 1–29.
96. M. Kulmala, T. Vesala and P. E. Wagner, Proc. R. Soc. London, Ser. A, 1993, 441, 589–605.
97. K. J. Zarzana, C. D. Cappa and M. A. Tolbert, Aerosol Sci. Technol., 2014, 48, 1133–1144.
98. R. E. H. Miles, S. Rudić, A. J. Orr-Ewing, J. P. Reid and S. Rudic, Aerosol Sci. Technol., 2011, 45, 1360–1375.
99. B. J. Mason, et al. , J. Phys. Chem. A, 2012, 116, 8547–8556.
100. A. T. Lambe, et al. , Environ. Sci. Technol., 2013, 47, 6349–6357.
101. M. Shiraiwa, Y. Kondo, T. Iwamoto and K. Kita, Aerosol Sci. Technol., 2010, 44, 46–54.
102. J. Liu, et al. , Atmos. Chem. Phys., 2016, 16, 12815–12827.
103. X. Wang, et al. , Atmos. Chem. Phys., 2014, 14, 10989–11010.
104. G. Lin, J. Penner, M. Flanner, S. Sillman, L. Xu and C. Zhou, J. Geophys. Res.: Atmos., 2014, 119, 7453–7476.
105. B. J. Mason, M. I. Cotterell, T. C. Preston, A. J. Orr-Ewing and J. P. Reid, J. Phys. Chem. A, 2015, 119, 5701–5713.
106. B. J. Mason, J. S. Walker, J. P. Reid and A. J. Orr-Ewing, J. Phys. Chem. A, 2014, 118, 2083–2088.
107. M. Cotterell, B. J. Mason, T. C. Preston, A. Orr-Ewing and J. P. Reid, Phys. Chem. Chem. Phys., 2015, 17, 15843–15856.
108. M. I. Cotterell, T. C. Preston, A. J. Orr-Ewing and J. P. Reid, Aerosol Sci. Technol., 2016, 50, 1077–1095.
109. J. H. Kroll, et al. , Nat. Chem., 2011, 3, 133–139.
110. A. Marsh, et al. , Atmos. Chem. Phys. Discuss., 2016, 1–30.
111. K. E. Huff Hartz, J. E. Tischuk, M. N. Chan, C. K. Chan, N. M. Donahue and S. N. Pandis, Atmos. Environ., 2006, 40, 605–617.
112. K. A. Koehler, et al. , Atmos. Chem. Phys., 2006, 6, 795–809.
113. P. P. Kumar, K. Broekhuizen and J. P. D. Abbatt, Atmos. Chem. Phys., 2003, 3, 509–520.
114. L. Renbaum-Wolff, et al. , Atmos. Chem. Phys., 2016, 16, 7969–7979.

---