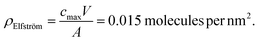Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Field-effect sensors – from pH sensing to biosensing: sensitivity enhancement using streptavidin–biotin as a model system†
Benjamin M.
Lowe
 a,
Kai
Sun
a,
Kai
Sun
 a,
Ioannis
Zeimpekis
a,
Ioannis
Zeimpekis
 a,
Chris-Kriton
Skylaris
b and
Nicolas G.
Green
a,
Chris-Kriton
Skylaris
b and
Nicolas G.
Green
 *a
*a
aDepartment of Electronics and Computer Science, Nano Research Group, University of Southampton, UK. E-mail: ng2@ecs.soton.ac.uk
bSchool of Chemistry, University of Southampton, UK
First published on 6th October 2017
Abstract
Field-Effect Transistor sensors (FET-sensors) have been receiving increasing attention for biomolecular sensing over the last two decades due to their potential for ultra-high sensitivity sensing, label-free operation, cost reduction and miniaturisation. Whilst the commercial application of FET-sensors in pH sensing has been realised, their commercial application in biomolecular sensing (termed BioFETs) is hindered by poor understanding of how to optimise device design for highly reproducible operation and high sensitivity. In part, these problems stem from the highly interdisciplinary nature of the problems encountered in this field, in which knowledge of biomolecular-binding kinetics, surface chemistry, electrical double layer physics and electrical engineering is required. In this work, a quantitative analysis and critical review has been performed comparing literature FET-sensor data for pH-sensing with data for sensing of biomolecular streptavidin binding to surface-bound biotin systems. The aim is to provide the first systematic, quantitative comparison of BioFET results for a single biomolecular analyte, specifically streptavidin, which is the most commonly used model protein in biosensing experiments, and often used as an initial proof-of-concept for new biosensor designs. This novel quantitative and comparative analysis of the surface potential behaviour of a range of devices demonstrated a strong contrast between the trends observed in pH-sensing and those in biomolecule-sensing. Potential explanations are discussed in detail and surface-chemistry optimisation is shown to be a vital component in sensitivity-enhancement. Factors which can influence the response, yet which have not always been fully appreciated, are explored and practical suggestions are provided on how to improve experimental design.
Introduction
Chemical sensors are important in a wide range of applications such as medical diagnostics,1 explosives detection,2 food safety3 and environmental monitoring.4 A promising class of chemical sensors are Field-Effect Transistor-sensors (FET-sensors). FET-sensors have been receiving increasing interest over the last two decades, motivated by the need for low-cost biosensors capable of direct and rapid detection of analyte molecules without the need for expensive and time-consuming labelling steps. As a medical diagnostic tool, this would increase survival rates of patients by reducing load on centralised-diagnostic facilities. FET-sensors have the potential to offer ultrahigh sensitivity, low-cost production, portability and facile miniaturisation as part of a ‘Lab-on-a-Chip’. FET-sensors present several advantages in comparison with currently available label-free biosensors which operate via mass-detection,5,6 the electrical detection offered by FET-sensors provides additional information on, for example, conformational changes7 or extracellular potentials.8 In contrast to many other biosensing methodologies, FET-sensors do not require bulky optical measurement equipment.FET-based pH sensors were initially popularised as far back as the 1970s with the work of Bergveld,9,10 and have been successfully commercialised.11 However, the extension of these devices to sensitive and reliable detection of biomolecular analytes (‘BioFET’ devices) has proved more difficult than initially expected. These problems have resulted in research providing a range of novel FET-sensor architectures12–14 and methods of operation,15–17 however advances in the field of BioFET research are obstructed by a lack of consensus on which quantitative metrics (i.e. figure-of-merit) should be used to compare devices. As a result, most published studies can only be compared qualitatively. By focusing on a single biomolecule analyte, this review provides the first comprehensive quantitative analysis of the FET-sensor response. Streptavidin-sensing was primarily chosen as a model system due to its general wide spread usage and well-understood (bio)chemistry. This is compared with pH sensing, which is a better understood application of FET sensors, and has already been well-characterised. This review also highlights factors that can influence the response yet have not always been fully appreciated, thereby resulting in sub-optimal experimental design.
One particular design aspect in pH sensing using FET-sensors18–20 is that the oxide material plays a dominant role in determining the magnitude of the response. An important motivation for this work was therefore to investigate whether similar trends holds for biomolecular-sensing BioFET experiments.
This review is divided into three main sections. First, the operating principle of FET-sensors and relevant physiochemical properties of streptavidin are introduced. Then relevant metrics for comparing device performance are critically reviewed, and finally, a quantitative analysis of streptavidin-sensing and pH-sensing literature is presented.
Operation of field-effect sensors
FET-sensors are similar to Metal–Oxide–Semiconductor Field-effect Transistors (MOSFETs) wherein the gate is replaced by an electrolyte resulting in an oxide–electrolyte interface. An example setup is shown in Fig. 1.21 A voltage can be applied via a reference electrode in the liquid and operated similarly to the gate in a MOSFET, with gate voltage: Vg. For an n-channel device, an increasingly positive gate voltage will result in the formation of the conductive channel beneath the interface between the semiconductor and the gate insulator (oxide). In contrast, for a p-channel device, an increasingly negative gate voltage will result in the formation of the conductive channel. A typical MOSFET is a bulk transistor with a source/channel/drain configuration like n+/p/n+ or p+/n/p+. In contrast, the small thickness of nanowire-based or ultra-thin SOI FET-sensors facilitates complete depletion of the channel. This allows these devices to operate in junctionless (i.e. n/n/n, p/p/p) or even undoped (i.e. n/i/n or p/i/p) configurations. FET-sensors can also be operated in a MOSFET-like configuration (n/p/n, p/n/p). FET-sensor designs vary, with the source–drain contacts not necessarily being highly doped. For a setup like that in Fig. 1 featuring an insulating oxide layer, FET-sensor response is driven by changes in the electric field at the oxide surface due to analyte molecules binding to the surface. In the case of pH sensors, the FET-sensor is usually termed an Ion-Sensitive FET (IS-FET), and the surface is an oxide material in which pH-induced changes in the protonation state of the surface hydroxyl groups result in a change in the surface charge and therefore the surface potential. For sensing molecular analytes such as biomolecules, the surface is usually functionalised to provide receptor sites which are specific to the analyte and the device is usually termed a BioFET. The change in the interfacial electric field on binding of analyte causes a change in the concentration of charge carriers in the channel region of the device, with a corresponding measurable change in the source–drain conductivity.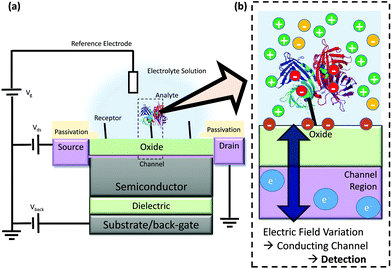 | ||
| Fig. 1 Schematic diagram of FET operation (not to scale) (a) Example structure of a FET-sensor, a back-gate within this text refers to an electrode applied to the substrate for which a bias can be applied, note that not all devices have a back-gate and Vback can instead simply be grounded. (b) Binding of analyte such as streptavidin (shown as ribbons from its X-ray crystal structure21) results in a change in electric field at the interface and a resulting change in the carrier concentration within the conducting channel. This induces a measurable change in current/potential between the source and the drain. The source and drain connections are protected from contact with the analyte solution, and only the gate surface (shown in green) is functionalised for specific binding of analyte. | ||
Whilst Fig. 1 shows a simple planar device geometry akin to a single-gate MOSFET, a plethora of device geometries have been developed such as nanogap,22–24 nanobelt,25,26 nanoribbon18,27–32 and nanowire15,29,33–37,38 structures. The application of additional lateral gates has been shown useful in tuning the carrier concentration of the device and pursuit of an optimal gate configuration is an active area of research.39–41 There is also significant interest in the development of carbon-based devices which do not have an oxide layer such as graphene or carbon-nanotube devices.14,42 The advantage of these devices is stated to be potential sensitivity enhancement via (i) direct contact with analyte (ii) the size of the material being comparable to the size of the analyte.43 It should be noted that the lack of a band-gap in graphene produces a limitation in the ability of the transistor to transduce a change in surface potential to a change in current response.44
The mechanism of operation of devices without an oxide layer, such as graphene and carbon nanotube devices, is expected to be different to those with an oxide layer due to the possibility of direct charge transfer from the analyte to the semiconducting carbon layer.45,46 Due to the different mechanism of gating, these carbon-based devices are not the focus of this review. Under certain conditions discussed later, the transistor component has the capability of transducing a change in surface potential to an exponential change in current. While, in principle, changes in surface potential due to analyte binding can be measured directly without a transistor similarly to a conventional glass pH sensing electrode,47 this approach requires potentially large and expensive measurement equipment (high impedance amplifier). The FET-component facilitates miniaturisation of the device, providing smaller sample volumes and faster response times.20
The reference electrode
Reference electrodes are used to provide a potential within the FET-sensor system to which other potentials can be referenced. Through the reference electrode, a gate voltage (Vg) can be applied in the sample and is sometimes referred to as a ‘top-gate’ voltage or ‘liquid-gate’ voltage in analogy to MOSFET operation. An ideal reference electrode ensures that the potential at the electrode–electrolyte interface is insensitive to changes in the electrolyte solution.33 FET-sensors can be used to quantitatively measure binding of analyte as the response is a function of the electrolyte–oxide surface potential. The reference electrode provides a stable potential in the bulk electrolyte which is used to reference the measurement.A stable reference potential requires a redox reaction in which there is constant thermodynamic activity of each participant in the reaction. In a conventional reference electrode, for example as used in electrochemistry or traditional glass-electrode pH sensors, this is achieved by placing a reference metal inside a compartment with a high concentration of salt solution connected to the analyte sample by a liquid junction which can only exchange ions.48 Miniaturisation of this system is problematic and results in reference electrodes with reduced lifetimes48 and a common alternative in the field of FET-sensing is the pseudo-reference electrode in which a bare metal or chlorinated silver wire is used. Unlike conventional reference electrodes, the interfacial potential is not known a priori, but under controlled conditions can still maintain a stable potential.
Noble metal pseudo-reference electrodes such as gold (Au) and platinum (Pt) are sometimes used but cause issues with current instability and pH dependency.34 Although Pt-pseudo reference electrodes have been used in various streptavidin-sensing experiments,35,49–51 many research groups have reported that Pt pseudo-reference electrodes are unreliable and should not be used due to issues such as unstable potentials, transient noise and changes in electrical potential due to non-specific binding of biomolecules (‘bio-fouling’).27,33,52,53
The most common pseudo-reference electrodes used in FET-sensors are silver–silver chloride (Ag/AgCl) electrodes which consist of a silver wire usually treated by either chemical or electrochemical chlorination.54 Rajan demonstrated experimentally that Ag/AgCl pseudo-reference electrodes are a suitable alternative to a conventional reference electrode,52 with the proviso that, due to the strong interaction with chloride in the buffer, the chloride content of the buffer is kept constant throughout the sensing experiment. Both Rajan52 and Rim et al.34 measured the open-circuit voltage between a Ag/AgCl pseudo-reference and conventional reference electrode to investigate bio-fouling and found the open-circuit voltage to be small, suggesting that pseudo-reference electrodes can be suitable for biosensing. For a more detailed review of pseudo-reference electrode validation experiments, see ESI section 1.†
The reference electrode setups used in the literature are broadly diverse; based on 37 publications identified in this review, 11% used Pt pseudo-reference electrodes, 19% used Ag/AgCl pseudo-reference electrodes, 11% used Ag/AgCl conventional reference electrodes, 21% did not publish their setup or it was ambiguously presented and 27% utilised only a back-gate. Of these setups, only Ag/AgCl pseudo-reference electrodes have consistently been proven to be capable of providing a reliable reference potential versus a conventional reference electrode.
Regions of operation – linear, saturation and subthreshold
The current flowing through a FET is controlled by the gate voltage, Vg and the drain voltage, Vds. Depending on the particular choice of these two parameters, the device is said to be operating in one of three main regions: sub-threshold, linear and saturation. These regions are summarised graphically in Fig. 2 and explained below.58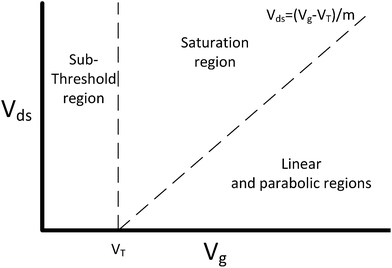 | ||
| Fig. 2 FET regions of operation. m is the body-effect coefficient (m ≥ 1). Adapted from figure by Taur and Ning (2013).58 | ||
The threshold voltage (VT) is important in defining the region of operation and can qualitatively be described as the minimum gate voltage (Vg) for which the device conducts a significant current and is therefore ‘on’. More precisely, it describes the value of the gate voltage required to form an inverted channel, in which the induced carrier concentration in the inversion layer reaches the carrier concentration in the channel (bulk carrier concentration).58 A detailed description of the threshold voltage and its significance to sensing is provided in ESI section 2.†
In a traditional Metal–Oxide–Semiconductor FET (MOSFET), when the gate voltage is low (i.e. Vg < VT), the drain current (I) is referred to as the ‘subthreshold current’ and the device is operated in the ‘subthreshold region’. This region is often used for FET-sensors because the response upon analyte addition can be enhanced29,38,52 with the drain current increasing exponentially rather than linearly dependent upon changes in the gate voltage.59 This is described by
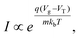 | (1) |
If a larger gate voltage is used and the drain voltage is low (i.e. Vg > mVds + VT, where m is an the empirical body-effect coefficient and m ≥ 1 (ref. 58)) then the device is operating in the ‘linear’ region. If the drain current is high (i.e. mVds + VT > Vg), then the saturation region is reached.
Device characterisation
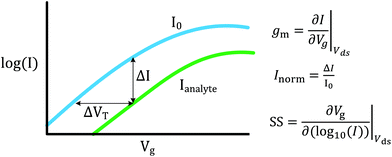
FET-sensors operate on the principle that binding of analyte to the sensor surface results in a change in surface potential (Δψs) via electrostatic gating. This induces a change in the device threshold voltage, which can be measured via the transistor as an amplified signal in the form of a change in the drain current. By measuring the variation in drain current (I) as a function of the reference electrode potential, the shift in threshold voltage (ΔVT) and the change in drain current (ΔI) can be measured. Either of these properties are termed device ‘response’ in this work. From these measurements, metrics important for characterising FET-sensors can be calculated. Commonly used metrics to characterise the sensor are the Subthreshold Slope (SS) for the subthreshold region of operation and the transconductance (gm) for the linear region of operation. Common metrics for characterising sensor response to analyte are the normalised change in current (Inorm) and the shift in threshold voltage (ΔVT). These four metrics are illustrated in Fig. 3 and are defined as follows.The subthreshold slope is constant in the subthreshold region and therefore provides a straightforward quantification of device response in this region. The value of the Subthreshold Slope is a measure of transistor quality in terms of its response to changes in the gate potential. It is defined as the change in gate voltage (Vg) needed to change the subthreshold current (I) by one decade60 and is determined from measurements as the inverse of the slope of the linear region on a (log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I) versus Vg graph at constant Vds:
I) versus Vg graph at constant Vds:
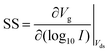 | (2) |
When Vds is greater than a few kbT/q (where kb is the Boltzmann constant and T is the temperature), the subthreshold slope is independent of Vds because the current is diffusion-dominated.58 The subthreshold slope can be modulated by a back-gate voltage, Vg,back.30 The reciprocal of the subthreshold slope is also called the ‘gate voltage swing’ or ‘subthreshold swing’.60
The subthreshold slope can also be defined as:
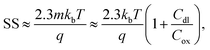 | (3) |
The transconductance, gm, is constant in the linear region and is therefore particularly useful for describing the properties of the device in this region. Similar to the subthreshold slope, the transconductance measures the slope of the I versus Vg plot:
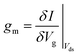 | (4) |
The sensor response metrics are related to the effect of analyte binding producing a horizontal shift in the I–Vg curve,45 corresponding to a change in ΔVT and a change in current, ΔI. The current-response (ΔI) can be used as the performance metric, in which case it is common practice to normalise the current (Inorm) as the change in current divided by the initial current.
Alternatively, ΔVT can be used as a direct measure. Assuming an electrostatic gating mechanism, ΔVT is equal to the change in surface potential, a direct indication that this parameter can be used for quantitative biosensing.45,61
In some cases, however, the assumption of electrostatic gating is not valid. For example, if the metal contacts to the semiconductor are not well-passivated and therefore insufficiently protected from direct interaction with the analyte, analyte-induced changes to the metal–semiconductor work function produce a signal not originating from an electrostatic gating mechanism.20,45,62,63 Another important example is if the reference electrode potential is modified by the analyte. A detailed description of this can be found in the literature: Heller et al. describe how the I–Vg graph (transfer characteristics) can be used to diagnose the mechanism of FET response (e.g. electrostatic gating, work function change etc.).45
Streptavidin biochemistry
Streptavidin is one of the most common model proteins used in biosensing studies64 and its detection is often used as the initial proof-of-concept for new biosensor designs.28,37,65 The relevance of streptavidin is much broader; for example, Gupta et al. have shown that streptavidin has direct clinical relevance in capturing biotinylated interferon γ (MIG), which is a biomarker for several inflammatory and autoimmune disease states.66 Streptavidin is also commonly used in enzyme-linked immunosorbent assays (ELISA), a standard biochemical assay. As BioFETs can, in principle, detect the electric field generated by a single elementary charge,67,68 even small changes in the electrodynamic properties of streptavidin should be detectable, making an understanding of the charge properties of streptavidin important. Surprisingly, despite its common usage in BioFET experiments and most other biosensors,64 a rigorous description of its expected charge as a function of pH is not available. Furthermore, many publications do not report the commercial origin of their streptavidin samples under the assumption that it is not relevant to its charging-properties.49,69–71 In this section, based on analysis of published biochemical literature, this assumption is proposed to be false.Streptavidin is a tetrameric protein composed of four identical subunits each with a high-affinity binding site for its ligand, biotin.72 Strong chaotropic agents (6 M urea) result in its dissociation into a dimeric form.73 It is commonly used as a model protein in sensing studies for a variety of reasons. First, streptavidin has an extremely high affinity for biotin which can be quantified by its affinity constant (Kd) of approximately 10−15 M.21 Fast binding kinetics are evident from the association rate constant of greater than 107 M−1 s−1.35 A sensor surface can be given high streptavidin selectivity and affinity by functionalising it with biotin. Second, the ionic strength of the buffer affects the binding affinity and protein stability of many proteins but not streptavidin–biotin affinity.74 As discussed later, buffer dilution does still strongly affect sensor response due to screening effects. Third, it is well characterised, widely commercially available and there is an abundance of literature on chemical-functionalisation of biotin to sensor surfaces.42,72,75 Finally, the isoelectric point (pI) of streptavidin76–80 results in a near-neutral protein under physiological conditions, which reduces its propensity for non-specific binding. Despite these advantages, it should be noted that the unusually high affinity of streptavidin for biotin makes it unrepresentative of binding characteristics of most biomolecules.
The full sequence of streptavidin, as encoded by the native gene which is naturally expressed in the bacterium Streptomyces avidinii, is shown in Fig. 4, with residues that are often charged shown as coloured and underlined. The blue highlighted region is unlikely to be present in any commercial sample of streptavidin used for biosensing experiments as it is a signalling region that is removed in vivo.81 The structure of streptavidin can vary between commercial preparations due to processing steps which result in artificial truncation of the protein, for example, in order to increase the protein solubility.82 In 1990, Green stated that most, but not all, commercial samples of streptavidin were truncated.76 Since 1990, residues 15–159 of the native gene were used to express a recombinant form (i.e. artificially expressed in a non-natural bacterium) of streptavidin with increased solubility in the bacterium Escherichia coli, and some modern commercial preparations of streptavidin are this recombinant form,‡ adding further possibilities for variability between different commercial preparations.
 | ||
| Fig. 4 Full sequence of streptavidin from the work of Argarana et al.81 the blue region (1–24) corresponds to the N-terminus signalling region that is likely removed in vivo.76 The green highlighted region (37–157) corresponds to the truncated-structure that was resolved in the X-ray crystal structure published by Weber et al.21 (PBD ID: 1STP) and used in the simulation of net charges presented here. Pähler et al.82 truncated streptavidin such that residues residues 37–163 were present (i.e. green and yellow regions). At pH 7, residues that based on the intrinsic pKa of the individual amino acid are usually positively charged (red) or negatively charged (purple, black box outline) are both underlined. This analysis shows, for example, that the streptavidin used by Weber et al. is likely to be 1q more negative than the net charge of the streptavidin of Pähler et al., due to the positive lysine residue (K) labelled 160 in the figure. Weber et al. comment that the termini are likely flexible or disordered,21 suggesting that the intrinsic pKa of the amino acids for the non-highlighted regions are reliable as they are not buried within the protein. | ||
In X-ray crystallography studies, Weber et al. reported that they were unable to crystallise non-truncated streptavidin, but successfully crystallised a truncated form of streptavidin,21 the sequence of which is highlighted in green in Fig. 4 together with the full sequence for the protein. The pH-dependent charging properties of this structure were modelled, with a calculated charge of −7.20q at pH 7.4 (ESI section 4†).
Examination of the sequence shows that, depending on where in the sequence streptavidin is truncated in different preparations, it is likely to differ in net charge by several elementary charge units. As high sensitivity sensors, BioFETs could in principle detect even small changes in the electrodynamic properties of streptavidin.67 A detailed analysis of streptavidin biochemistry literature (ESI section 4†) revealed that both the molecular weight and pI values can vary between different preparations with molecular weights in the range of between 53 and 66 kDa and pI values between 5 and 7.5.76–80 This variation in pI and molecular weight is likely due to both variation in the biomolecular structure, and difficulty in obtaining accurate measurements of these properties. The resulting variability in electrodynamic properties (charge, kinetics etc.) will affect the reproducibility and comparability of experiments performed using different commercial preparations, and it is therefore recommended that the origin of the protein used in experiments is reported. This is not currently common practice; of the publications identified within this review (tabulated in ESI section 5†), 45% did not report the origin of their streptavidin sample.
In addition, surface-bound streptavidin has been measured with different properties to the free protein. The pI of surface-bound streptavidin has been measured using Surface Force Apparatus (SFA) and Atomic Force Microscopy which demonstrated a pI of 5.0 ± 0.5.79,83 Experimental determination of streptavidin pI is discussed further in ESI section 4.†
Another biomolecule commonly used in BioFET experiments is prostate-specific antigen (PSA) due to biomedical applications as a prostate cancer biomarker, however the biomolecular capture step is more complex than streptavidin, requiring the use of a complex biomolecule such as an antibody or aptamer.86 The most well-studied biomolecule in BioFETs is undoubtedly nucleic acid-based systems such as DNA. However, as summarised in a review by Poghossian et al.,87 experiments are rarely performed using the same DNA-sequence or polynucleotide length, making their structural and electrical characteristics not easily comparable. Furthermore, in the DNA-sensing community there is high variability in experimental design, for example, the choice of buffer composition.87
Buffer solution
The buffer solution maintains the pH and the stability of the biomolecule, the system and the measurements. Its composition, the concentration and ratios of ions in solution, can have a significant effect on the bio-sensitivity of the sensor. Even in absence of biomolecules, ions in the buffer can modulate the surface chemistry or be selectively adsorbed to the surface, generating a detectable response. Accurate reporting of the composition of this solution is therefore essential to any biosensor experiment.| pH = −log10(aH+) | (5) |
Phosphate buffer is often used for biosensing experiments; a convention is to define 10 mM ionic strength phosphate buffer as 1× NaPi = Na2HPO4 (8.1 mM) and NaH2PO4 (1.9 mM). The most common buffer for protein sensing is Phosphate-Buffered Saline, PBS, which is composed of 1× NaPi mixed with 138 mM NaCl and 2.7 mM KCl.74 The ionic strength of 1× PBS is 162.7 mM.74 Some confusion can arise where authors use the acronym PBS for ‘Phosphate Buffered Solution’, as it becomes ambiguous whether they are reporting NaPi or PBS.70 This distinction is often critical since, as discussed in ESI section 1,† when a Ag/AgCl pseudo-reference electrode is used, then the chloride content of the buffer can significantly change the reference potential.52
The dilution notation (×) is often used in this field due to the relevance of ionic strength and because dilution is often required for larger signals, as discussed later. Dilution can introduce a variety of issues, for example, at high dilutions (e.g. 0.01× PBS) the buffering capacity of the solution is reduced meaning that the system can become highly sensitive to small pH changes. For example, even the experimentalist breathing near the sample can result in elevated CO2(g) dissolved into the sample and being detected88 as per:
| CO2(g) + H2O(l) ⇌ CO2(aq) + H2O(l) ⇌ HCO3−(aq) + H+(l) | (6) |
This introduces a potential source of noise to the measurement.
A related issue arises upon addition of large amounts of biomolecule to a solution. Adsorption or release of protons to/from the biomolecules themselves can affect the pH of the bulk solution. Lloret et al. measured the bulk change in pH using a pH microelectrode in response to addition of streptavidin and found that for 1 µM streptavidin in 0.01× PBS (a common dilution), there was a change of 0.5 pH units.74 In contrast, at 1× PBS the shift in pH was negligible due to the high buffering capacity. The significance of this cannot be understated; for a typical PBS concentration of 0.01×, and a typical SiO2 surface in the pH 5 to 9 region (ΔVT,pH ≈ 30 mV per pH response), this would correspond to a non-specific response of ΔVT = 15 mV due to bulk pH change; which is of the same order of magnitude as most measured streptavidin signals.
A simple experimental control is to ensure that only low concentrations of analyte are used. This is more relevant to medical diagnostic applications in which biomolecules often must be detected at low-concentrations from blood samples.
Proper controls can reduce variability due to non-specific binding and lack of buffering capacity. Fully washing the surface with the analyte buffer (without analyte) can remove signal due to non-specifically bound streptavidin, however washing is not solely sufficient for specific biomolecule detection. One strategy to isolate non-specific binding response is to perform an experiment in which streptavidin pre-saturated with biotin is added and then the device is washed; in the case of specific-binding, this should show no significant response.49 To demonstrate that the signal is due to specific biomolecule binding, Stern et al. utilised a cleavable-biotin molecule and confirmed that the device response could be restored to baseline by biotin-cleavage.36 Lloret et al. suggested tailoring the buffer to have the highest possible buffering capacity whilst both remaining suitable for biomolecule stability and at a sufficiently low ionic strength to allow analyte sensing. For example, using NaPi rather than PBS.
The Debye length is the characteristic length scale for charge screening of electrolytes under the Debye–Hückel model.89 This concept can be useful when considering BioFET operation on large biomolecules which may contain charges located several Debye lengths away from the surface. In high ionic strength solutions, the Debye length is short so that distant charges would be screened and have no significant effect on the surface potential. Dilution reduces the ionic strength of the solution and extends the Debye length; however, this can cause ancillary issues such as a reduction in buffering capacity and instability of the biomolecule in solution,90 or reduced affinity of the biomolecule–target interaction, although the latter is not the case for streptavidin.74 For PBS dilutions of 1×, 0.1× and 0.01×, the calculated Debye lengths are 0.76 nm, 2.41 nm and 7.61 nm respectively.74 Stern et al. demonstrated a significant BioFET response for binding of streptavidin in solution to biotin on the sensor at 0.01× PBS, but no significant response at 1× PBS. Approximating streptavidin as ∼5 nm from the surface,21 they found that this result agrees with the Debye–Hückel model.91
Whilst the concept of Debye screening is useful in explaining reduced response in high ionic strength systems, caution must be taken in its use. For example, Bergveld92 used the Debye–Hückel model of the electrical double layer to argue that charged biomolecules cannot be detected at high ionic strengths, having written:
‘The resulting double layer, with a thickness of the Debye length, is of the order of 1 nm thick in moderate electrolyte concentrations. Beyond this distance no external electric field exists. Hence the idea that a layer of charged molecules at the surface of an ISFET modulates the electric field in the gate oxide should definitely be forgotten’ (emphasis added) – Bergveld (1996).92
In the Debye–Hückel model, the Debye length is ∼1 nm at ∼160 mM ionic strength and yet streptavidin has been detected at this ionic strength by various authors66,70,93 and similar observations can be found for other biomolecules.66,94
Even under the assumption that the Debye–Hückel model describes the system accurately, there are several misapprehensions which should be highlighted. First, the Debye length is not a hard cut-off beyond which no electrostatic effect is felt, because the screened Coulombic interactions reach to infinity. This can be seen from the expressions from the Debye–Hückel model at an electrode–electrolyte interface:
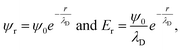 | (7) |
Second, it is also assumed that molecules are rigid and bound in a fixed orientation, whereas in reality they are flexible and dynamic and therefore some orientation of the analyte can bring the molecular charges closer to the surface than other orientations.95
A further consideration is that the surface chemistry itself can change at different ionic strengths, resulting in alteration of the sensor response. For example, the FET-sensor of Tarasov et al. showed a shift in threshold voltage of 59 mV for every 10-fold increase in KCl concentration.96 They attributed this effect to pH independent selective adsorption of anions. Similarly, a non-linear FET-sensor response to increasing NaCl concentration was measured by Maekawa et al.97 This empirical observation has also been observed in molecular dynamics simulation studies.97,98
The electronic device and signal drift
Physical and structural characteristics of the transistor device, particularly the choice of semiconducting material, can affect both the amplification ability of the transistor and its performance in terms of drift. Silicon is commonly used as the semiconductor material rather than more exotic materials, as its ubiquitous presence in the semiconductor industry means that fabrication is simple, well-understood and low cost. Silicon-based FET sensors can, however, suffer from long-term unidirectional drift in signal. Various mechanisms for this action have been proposed99 yet this remains an important research question within the field as it is a key factor limiting commercialisation efforts and/or, in the case of Si3N4 films, via aqueous hydration of the surface to SiO2 or an oxynitride.99–103 While SiO2 surfaces are rapidly hydrated, Si3N4 surfaces and other common oxide materials such as Al2O3 and Ta2O5 are known to be more resistant to hydration101 and show reduced drift rates at pH 7.104Given the timescale of the drift often observed in SiO2 surfaces (hours) device noise or drift could be due to ions from the aqueous solution diffusing into the insulating material101,105 which would show a corresponding change in the threshold voltage of the device.101 As an alternative material to SiO2 which is impermeable to ions,95 AlGaN/GaN-based FETs have been demonstrated with significantly reduced drift in physiological buffers and various groups have successfully utilised AlGaN/GaN-based devices for streptavidin sensing.49,50,66,106,107
Understanding and modelling drift characteristics of FET-sensors remains a vital challenge in the field. As an illustration of this, there remains no physical model capable of accurate quantitative modelling of experimental signal drift for gas-based FET-sensors.108
Recent developments
For successful commercialisation of BioFETs in biomedical applications, operation in high ionic strength environments remains a key engineering challenge. An alternative mode-of-operation for sensing FETs has been proposed, first by Schasfoort et al.109,110 and recently demonstrated for detection of poly-L-lysine.17 This mode relies on making a sudden change in ionic strength change (‘ion-step’) and measuring the initial non-equilibrium response before the system fully equilibrates. More recently, Krivitsky et al. detected biomarkers from untreated blood samples using a similar strategy in which the transient response from specific-binding is compared to a non-specifically bound control.111 By measuring the transient response of the system, biomolecules can potentially be detected in higher ionic strength buffers than conventional ‘equilibrium’ sensing experiments. This also potentially offers better sensitivity to the analyte and reduced sensitivity to the background drift in the drain current.Other methods have shown promise at circumventing Debye screening limitations. For example, FET nanogap-devices operate on a different mechanism to conventional BioFETs, where the dielectric constant of the gate is modified by analyte binding and the device is operated after drying.22,23,112 Another example for conventional FET-sensors is that the surface layer could be modified with a biomolecule-permeable polymer layer which is proposed to operate by extending the effective distance over which charges are screened within the layer.113 A final example of particular interest is the use of frequency-mode detection,15,46,114–117 where the current response is measured in the frequency domain instead of the time-domain (details can be found in ESI 6†).
The lack of wide-spread adoption of alternative operating methods may be due to: complexity, with the additional required steps required making them less commercially appealing; a lack of awareness in a rapidly changing field; or lack of reproducibility. Given the variety of strategies which have shown some efficacy at circumventing the limitations arising from charge screening, it is likely that this will successfully be surmounted in a commercial device.
Device performance metrics
Given the lack of maturity of FET-sensor technology, it is understandable that this field has not yet converged upon a set of standards, both in terms of well-defined nomenclature or usable engineering parameters. Such nomenclature and parameters are required to rigorously compare the performance of BioFET sensors, particularly the metrics involved in the detection and quantification of analytes.IUPAC definitions
IUPAC defines ‘sensitivity’ as a metric of the specific response as a function of the analyte concentration. More specifically, it is defined by IUPAC as ‘the slope of the calibration curve’. IUPAC defines the calibration curve as:‘The functional (not statistical) relationship for the chemical measurement process, relating the expected value of the observed (gross) signal or response variable to the analyte amount. The corresponding graphical display for a single analyte is referred to as the calibration curve’.118
The IUPAC definition of sensitivity is not a measure of the ability to detect the minimal amount of an analyte, and therefore a second relevant metric is the limit of detection which IUPAC defines as the smallest measure that can be reasonably detected for a given analytical procedure, and is expressed as a concentration or quantity. More specifically:
‘The limit of detection, expressed as the concentration, cL, or the quantity, qL, is derived from the smallest measure, xL, that can be detected with reasonable certainty for a given analytical procedure. The value of xL is given by the equation xL = ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) bi − ksbi, where
bi − ksbi, where ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) bi is the mean of the blank measures, sbi is the standard deviation of the blank measures, and k is a numerical factor chosen according to the confidence level desired’.118
bi is the mean of the blank measures, sbi is the standard deviation of the blank measures, and k is a numerical factor chosen according to the confidence level desired’.118
Analysis of sensitivity
The IUPAC definition of sensitivity incorporates two elements: the measurement of a specific response, and its dependence upon analyte concentration. Some BioFET publications have quantified sensor performance using a definition of ‘sensitivity’ which differs from the IUPAC definition. For example, some authors refer to the absolute change in current (ΔI) or, more frequently, the change in current divided by the initial current is referred to as the ‘sensitivity’. To avoid confusion and for comparison, a clear set of nomenclature is defined in this section for use in this review.The symbol Inorm is used to refer to the normalised change in current, which is defined as:
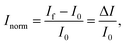 | (8) |
Some publications simply refer to the absolute measured change in current from the device (ΔI) as the metric however, this results in a large device-to-device variation. The normalised change in current has become common practise as it reduces this variation.119 The reason for this reduction in device-to-device ratio is that the absolute current is directly dependent upon geometric parameters and threshold voltage of the device, whereas the normalised change in current is only subject to device-to-device variation from differences in the device threshold voltage.119 Further, the change in current (ΔI) can either be positive or negative and consequently the normalised change in current, Inorm, also has an associated sign. Some authors have reported the normalised change in current without this sign which makes the polarity of the measured change ambiguous.49
This can be explored using the MOSFET drift-diffusion equations and the shift in threshold voltage (due to analyte binding) can be related to the normalised change in current using the following equation:18,44
| ΔVT = SS(log10(Inorm + 1)). | (9) |
This equation can be used to calculate the expected magnitude of Inorm for a given analyte. For example, considering the case of an ideal n-channel transistor with a subthreshold slope of 59 mV dec−1 and an analyte that induces a change in threshold voltage of 10 mV, the calculated Inorm is approximately −33%. For the equivalent analyte and a p-channel device, the calculated change in Inorm is approximately +50%.
This important distinction between a negative Inorm and a positive Inorm can be emphasised as a qualitative difference; a current which decreases is ‘bounded’ by zero and therefore has a maximum possible value of −100%, whereas an current which increases has no mathematical upper limit for Inorm. In this paper, this is referred to as ‘unbounded’ to indicate that is always positive and can reach large positive values. In the subthreshold region, a direct comparison between an unbounded signal from one device (negative molecule on an n-channel semiconductor) and the bounded signal of another (i.e. with a p-channel device) is uninformative. This is particularly relevant for ambipolar devices (e.g. the devices of Nam et al.120); ambipolar devices can operate in either an n-branch or a p-branch depending on the choice of gate voltage, requiring a metric which can compare the response of the unlike branches.
In order to compare the signal between devices with different channel types, the change in current can be normalised by the current obtained either before the response (I0) or after the response (If), whichever is lower. These lowest and highest values are referred to as Ilow and Ihigh respectively. This results in an Inorm which is always positive and ‘unbounded’ with no mathematical upper limit. This ‘unbounded’ metric is herein referred to as Inorm+ or the ‘unbounded normalised change in current’:
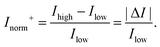 | (10) |
The differences between the unbounded and bounded Inorm are illustrated schematically in Fig. 5. For consistency with our previous quantitative analysis of the literature performed for pH sensing,18Inorm+ was used in this analysis. As an example, for streptavidin (negatively charged analyte at pH 7.4) on an n-channel device, the drain current would decrease and therefore Ilow would be the drain current after addition of streptavidin and Ihigh high before addition. Alternatively, it would be possible to compare the ‘bounded’ change in current, where the current is normalised by the higher of the current (Inorm−) before or after binding.
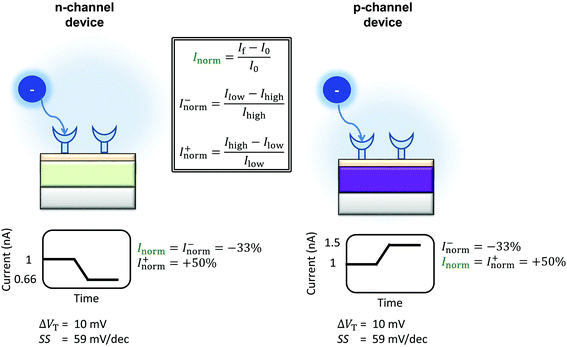 | ||
| Fig. 5 Schematic of the change in current upon sensing a negatively charged analyte by an n-channel device (left) and p-channel device (right) is shown. The device is assumed to operate in the subthreshold region. The values shown are calculated using eqn (9), operating in the subthreshold region, assuming an ideal device (SS = 59 mV dec−1) and an analyte which can induce a change in the threshold voltage of 10.39 mV. The polarity of the response is reversed between the two types of device, and therefore the normalised change in current. The normalised change in current is obtained by Inorm = ΔI/I0, where I0 is the initial current prior to analyte addition. In a sensing experiment, the lowest value of the current recorded is referred to here as Ilow and the highest value as Ihigh. The change in current can be instead normalised by Ilow instead of I0, resulting in the ‘unbounded’ normalised change in current (Inorm+). An alternative method would be to normalise by Ihigh (Inorm−). Inspection of the above figure illustrates that in order to compare the sensing results for a particular analyte between devices of different semiconductor, the normalised change in current must be calculated consistently i.e. Inorm+ cannot be directly compared to |Inorm−| as different values are expected from the same stimulus. | ||
Other than as a figure-of-merit, there are important scientific reasons for the measurement of the response as a function of analyte concentration. The affinity (i.e. equilibrium dissociation constant, Kd) of an analyte binding to a sensor can be estimated by fitting the concentration-dependent response data to an appropriate binding model.35 Further, the concentration at which the response saturates can be used to estimate the density of bound molecules.28,121 Note that at concentrations much greater than the Kd of the binding reaction, sensor saturation occurs, along with increased levels of non-specific binding.122
Performance metrics have also been discussed by Rajan et al.,29,52 who highlighted a few examples from the literature of concentration-response curves for BioFETs over different analytes and stressed the importance of considering, not only the IUPAC sensitivity, but also the Signal-to-Noise Ratio (SNR). At this time, unfortunately, most BioFET data is reported without noise analysis or sufficient repeats to obtain an estimate of the statistical uncertainty of measurements, and so quantitative estimation of this SNR or IUPAC Limit of detection is rare. Given these limitations, the analysis presented in this analysis uses the normalised change in current per 10-fold increase in analyte concentration (e.g. % per unit pH or % per 10-fold increase in streptavidin concentration) as a performance metric to compare sensing results between different experiments. This metric will be referred to as ‘Sensitivity’ due to its similarity to the IUPAC definition and will be discussed in more detail later and in ESI 7.3.†
The largest shift in threshold voltage for a pH sensor can be calculated based on the Nernstian response of 59 mV per pH. The steepest subthreshold slope for a classical transistor is approximately 59 mV dec−1.44 From eqn (9), the largest normalised change in current is obtained when the subthreshold slope is steepest and the shift in threshold voltage is largest, resulting in an upper theoretical Sensitivity limit of 900% pH. Lee et al. used additional circuitry intended to amplify the FET-signal beyond this value but did not provide quantitative evidence to support that it had improved the signal-to-noise ratio or limit of detection.126
Relationship between surface potential and current response
I norm is a measure of the amplification of the current response. By contrast, ΔVT is a measurement of the changes in the electrostatic potential at the surface and therefore can be used both to provide quantitative detection of analyte and also to supress device-to-device variation.119,127 The change in threshold voltage due to analyte binding can either be measured directly from the shift in the I–Vg curve, or calculated using MOSFET drift-diffusion equations (ESI sections 3 and 8†). The analytical relationship between current change and the change in threshold voltage is dependent upon the region of operation of the FET as follows.For FET-sensors operated in the subthreshold region, this relationship is given by eqn (9)18,38,44 and has a logarithmic dependence on Inorm. In the subthreshold region, the transconductance is variable as a function of gate voltage and therefore cannot be treated as a constant.
For FET-sensors operated in the linear regime, ΔVT can be extracted experimentally by simply dividing the current-response data (ΔI) by the device transconductance, gm:29,61,119,128
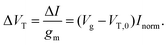 | (11) |
This expression is only valid if the analyte does not change the operating regime of the device61 and providing that gm is the same before and after binding35 (i.e. electrostatic gating mechanism of FET operation45). Alternatively, the threshold voltage prior to analyte addition, VT,0 and Inorm can be used to calculate the shift in threshold voltage.52 Derivation of these equations can be found in ESI section 8.†
Signal-to-noise ratio enhancement
This section presents common methodologies to obtain, optimise and understand the Signal-to-Noise Ratio (SNR) properties of FET-sensors as a figure-of-merit for biosensors.An important relevant question is: what gate voltage and region of operation is best for SNR and IUPAC limit of detection, given that the noise varies between devices and as a function of gate voltage? For the current response, the SNR is defined as the ratio of the change in current ΔI to the noise in the measurement (δi) response.
Empirically, there are various methods for determining the noise component. Given the low-frequency noise is of interest for biosensing, and that the most common noise source of FET-transistors is of the form 1/f (flicker noise), a common approach46,52,107,129,130 utilises the following expression:
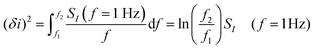 | (12) |
where SI(f = 1 Hz) is the drain current noise power spectral density at 1 Hz and the integral is between the largest and smallest frequencies sampled. Given that ln(f2/f1) is only weakly dependent upon the choice of bandwidth in most sensing experiments, this can be neglected to give a simplified calculated metric for SNR:
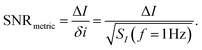 | (13) |
Sometimes ΔI is converted into the voltage regime using ΔI = gmΔVT, however care must be taken with this equality as transconductance is constant only in the linear region (eqn (11)) or can only be accurately treated as such for small changes in threshold voltage.
There is experimental evidence from a number of authors demonstrating that the subthreshold region has better SNR. Operating in the subthreshold regime improved the SNR for the BioFET device of Gao et al. who measured prostate-specific antigen (PSA) binding and found the optimum Inorm agreed well with the maximum in SNR, but did not explain how SNR was calculated.38 They explained their result giving resistive noise as the dominant noise source, which is proportional to carrier density and therefore greatly decreased in the subthreshold region. Tarasov et al., who performed noise analysis of an ion-sensitive FET both in air and at pH 7 and defined the SNR as the reciprocal of the equivalent noise power of the threshold voltage, also demonstrated improved SNR in the subthreshold region.31 Heller et al. performed charged-molecule sensing and salt concentration-change sensing experiments and remarked that for their device, measurement at peak transconductance provided poorer SNR than measurement in the subthreshold region.45
Contradictory evidence also exists. Rajan et al.130 performed noise analysis upon various systems with different buffers and showed peak SNR in the linear region close to the point of peak transconductance. The disagreement with other devices in the literature was explained as the device having a different regime of mobility fluctuation noise.131 Rajan also investigated the SNR due to binding of streptavidin to biotin functionalised surfaces, over a range of gate voltages.52 A high concentration of D-biotin in the bulk could displace surface-biotin-bound streptavidin so that the same sensor could be reused at various gate voltages. Increased SNR was then observed as the gate voltage was moved from the subthreshold region into the linear region.52 In summary, the evidence suggests that although operation in the subthreshold region often improves SNR, its ability to improve SNR may be system dependent.
A related question is therefore what region of operation is optimal for sensor Sensitivity (e.g. Inorm per pH). In the linear region (eqn (11)), Inorm increases as the gate voltage Vg approaches the threshold voltage VT, i.e. as the subthreshold region is approached. Inorm is always optimised in the Subthreshold Region. Once the subthreshold region is reached, eqn (11) becomes invalid and an alternative expression (eqn (9)) for the normalised change in current is recovered, which is a function of the subthreshold slope and is independent of gate voltage. To demonstrate that these theoretical relations hold experimentally, Fig. 6 shows the results from the BioFET streptavidin binding experiment of Wen et al.49 with all the relevant parameters plotted (Inorm, ΔI, I and gm).
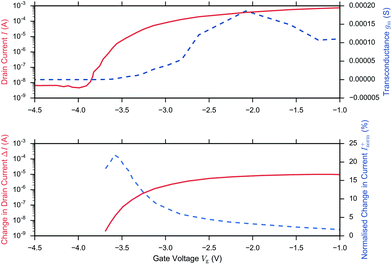 | ||
| Fig. 6 I–Vg device characterisation (upper figure) and corresponding streptavidin sensing data (lower figure) from Wen et al.49 on addition of 4.73 pm streptavidin in 0.25× PBS and Vd = 0.5 V. The upper figure shows the drain current (solid) and because ΔVT is small (0.019 V), the before/after streptavidin addition drain currents are overlaid at this scale. The drain current response was extracted from the paper and the transconductance (gm, dashed line) was calculated in the figure, presented here from the drain current response using second order and first order central differences on the interior and boundaries respectively. Peak gm and peak ΔI (dashed line, extracted from the paper) was observed in the linear region and optimum Inorm+ (dashed, line extracted from the paper) in the subthreshold region, in agreement with theory. At low drain currents, the noise may become larger than the signal and therefore the SNR is not necessarily optimal. | ||
In summary, in the subthreshold region, Sensitivity is optimised as a result of the large normalised change in current, Inorm, which occurs when the initial drain current, I0, is small, however in this region of operation, the noise of the low drain current may become larger than the signal and therefore SNR or IUPAC limit of detection are not necessarily optimal.
Lu et al. investigated low frequency noise (∼4 Hz) in devices with a bare SiO2 surface but saw that the noise was ionic strength dependent. From the paper, a 0.001 M PBS system showed a current noise power density which was 70% noisier than in 0.1 M PBS buffer, while the current noise power density showed only small pH dependence.132 Their results were partly rationalised with a number fluctuation-dominated current noise model but the authors acknowledged that the fluctuations cannot be fully explained in terms of modulation of the charge trapping probability with changes in ionic strength.
This amplification was described by Go et al. as the result of capacitive coupling within the system.134 The coupling amplified a change in top-gate voltage (ΔVT,top) which consequently results in an amplified shift in bottom-gate voltage (ΔVT,back) which depends upon the capacitance of the liquid-exposed top-gate dielectric (Ctop), the back-gate dielectric (Cback) and a factor (αSN) with a value between 0 and 1 depending on the extent of coupling due to the choice of biasing conditions:134
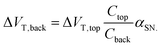 | (14) |
Further research is required in this field for the development of a general theory of back-gated operation.30 The ΔVT,back threshold voltage shift amplification strategy has been utilised for biosensing, such as the work of Duan et al.35 and Jayant et al.140–142
While there is no doubt that double-gated FET operation can amplify the measured voltage shift, an important question that remains is whether it can provide an improved SNR. Go et al. concluded that double-gated FET operation can only improve the SNR if the noise from the measurement equipment sets the lower limit of performance.134 In the double-gated FET operation of Pud et al., noise spectroscopy revealed an improved SNR.16 Regardless, the use of a back-gate voltage offers the advantage of reducing the requirements for external circuitry to amplify the signal. Go et al. derived a quantitative model of double-gated FET operation which can explain the results of some systems; in their model the response is a result of capacitive coupling between the back-gate and the top-gate oxides, and under certain gate voltage conditions, the semiconductor body capacitance.134
It has been demonstrated both experimentally28,36,143 and theoretically143,144 that increasing surface area-to-volume ratios increases normalised change in current. Operating in the subthreshold region, the improvement is attributed to the subthreshold slope improvement (i.e. decreased value) which results from the improved ratio of oxide capacitance to depletion-layer capacitance (eqn (3)). There is no evidence that nanowire or nanoribbon geometries can achieve a better subthreshold slope than the ideal value of 59 mV dec−1 through their superior surface area–volume ratio. Particularly, it is worth noting that scaling in channel length results in degradation of the subthreshold slope due to the Short Channel Effect (SCE).138 Planar devices are capable of providing comparable Sensitivity to nanoscale devices given that planar devices can be made with a subthreshold slope of ∼80 mV dec−1 for bulk,138 or ∼63 mV dec−1 for fully-depleted SOI transistor or double-gated SOI transistor devices.146 Nanocrystalline MoS2 thin films (with a HfO2 oxide surface layer) are also shown capable of obtaining a near ideal subthreshold slope of ∼60 mV dec−1.44 However, increased surface area-to-volume ratios provide other advantages such as improved biomolecule binding kinetics and therefore reduced response time.147,148 A reduced response time would improve the effective limit of detection within practical time-constraints (e.g. several minutes).147,148 For planar devices at very low concentrations of biomolecular analyte (femtomolar), the time-to-equilibration of the response may be impractically long; if measurements are taken pre-equilibration of the biomolecular surface binding reaction of the surface, the ‘effective’ Sensitivity between two devices, after the same fixed time, would be higher for the device with shorter response time. Furthermore, nanoscale geometries offer increased potential for miniaturisation.
Quantitative analysis
Methods
This analysis compares FET-sensor results for pH-sensing with streptavidin-binding to oxide-APTES-(or the methoxysilane equivalent, APTMS)-biotin-functionalised surfaces. Where available, the parameters such as the subthreshold slope and normalised change in current were directly extracted from the streptavidin literature, and where this was not reported explicitly it was extracted manually from I–Vg graphs.As discussed, when comparing normalised change in current between devices of different types (i.e. p- or n- channel device), normalisation simply using the ‘initial’ drain current, prior to analyte addition, is insufficient. The change in drain current was normalised by the lower drain current to give the ‘unbounded’ normalised change in current, Inorm+, using eqn (10). As this was used consistently through this analysis, the symbol Inorm will be used to refer to the unbounded change in the rest of this review. As an example, for streptavidin on an n-channel device, the drain current is expected to decrease after addition of streptavidin and therefore Ilow will be the drain current after addition of streptavidin and Ihigh before addition. This is consistent with our previous quantitative analysis of the literature for pH sensing.18
For publications which present streptavidin-sensing data as a function of concentration of streptavidin, it is possible to calculate the ‘normalised change in current for a 10-fold increase in streptavidin concentration’, and equivalently for pH sensing, the response due to a change of 1 pH unit was used (pH is related to the proton concentration, eqn (5)). Assuming a linear relationship between a 10-fold change in analyte concentration (e.g. a pH unit for pH sensing) and a 10-fold change in current, then Inorm per 10-fold increase in analyte concentration is expected to be a constant. Therefore, for a set of n 10-fold changes in analyte concentration, the largest current after n 10-fold changes in concentration (In) can be calculated from the lowest current (I0) and the normalised change in current (Inorm):
| In = I0(Inorm + 1)n. | (15) |
For an n-channel device with a negatively charged biomolecular analyte, In and I0 correspond to the lowest and highest concentration of analyte, respectively. Rearranging for Inorm gives an expression for the representative normalised change in current per 10-fold increase in analyte concentration:
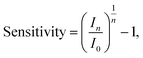 | (16) |
Note that not all published data are presented both unambiguously and with completeness. As a result, sometimes paper-specific assumptions had to be made in order to complete this analysis. These assumptions are explained in detail in ESI section 7.5.†
Surface binding reactions
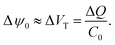 | (17) |
From this simple model it can be seen that a concentration-dependent response with increased biomolecule binding to the surface is expected, a response demonstrated by many authors for streptavidin sensing.26,28,32,36,49,51,107,120,160–166
The simplest model for biomolecule-binding reactions, is the first-order Langmuir model of surface-reactions (details in ESI section 10†). In this model the surface reaction of analyte (A) to the surface sites (S) is treated simply:
| A + S ⇌ AS. | (18) |
The resulting equilibrium constant, Kd = [AS]/([AS][S]), bears many similarities to the well-known pKa for the case of proton-binding, as illustrated in Fig. 7. Solving the rate equation for the above system and finding the steady-state solution analytically, results in the Langmuir equation, also shown in Fig. 7.
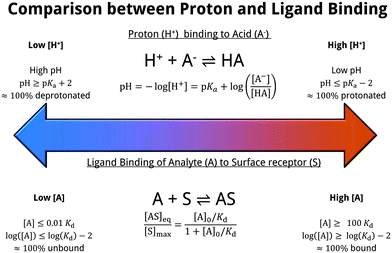 | ||
| Fig. 7 Comparison between proton affinity and ligand affinity metrics. The pKa describes the equilibrium constant of proton-binding, similarly the Kd describes the equilibrium constant of ligand-binding. The simple surface-analyte reaction modelled here (first-order langmuir isotherm) is the simplest biomolecular-surface binding scheme, and describes the fraction of bound analyte at equilibrium [AS]eq to the total binding site concentration [S]max. Various assumptions are made within this model, which are detailed within ESI 10.† | ||
The equilibrium coverage, modelled by the Langmuir equation, is related to device response. As a result, the dynamic range of the sensor (i.e. the concentration range of analyte upon which it operates) can be seen to be fundamentally limited by Kd. At bulk concentrations [A]0 ≫ Kd, the sensor is expected to be saturated. For systems in which there is a low Kd, such as streptavidin–biotin binding, based on the Langmuir equation, the high affinity means that a large proportion of the total number of sites [S]max are expected to be occupied (i.e. [AS]/[S]max ∼ 100%) even at low concentrations of bulk analyte. For surface-bound systems, there is evidence to suggest the Kd may be smaller than the solution measured Kd.167
If a finite volume of analyte is used and the ligand has a high affinity, then the effects of finite numbers of sites can become important as the bulk concentration of ligand can be depleted by reactions to the surface.168 Rajan utilised numerical simulation to demonstrate the consequences of ligand-depletion on the equilibrium coverage ([AS]/[S]max) and showed that in low Kd, small volume systems (i.e. low number of molecules available for binding), the equilibrium coverage is significantly lower than that predicted by the Langmuir isotherm, and with increasing numbers of receptors (e.g. with increased receptor-functionalised sensor area) this effect is exacerbated.52 For example, if a 50 µL solution contains 1 fM solution of biomolecule, then 301 streptavidin molecules are in solution. Assuming one biomolecule binds to one receptor, and a Kd of 1 fM, then the equilibrium coverage predicted by the Langmuir equation is 50%. For a large sensor (well functionalised sensor, ≫301 receptors) an equilibrium coverage of much less than 50% would be expected because all the biomolecule would have depleted from solution and bound to the many available receptors.
The lower limit of detection of the sensor is restricted to single-molecule binding; the critical concentration at which only one target molecule binds the sensor at equilibrium (cmin), to a sensor of area A with density of receptors [S]max is:169
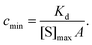 | (19) |
A simple strategy for estimating the maximum density of bound molecules can be demonstrated. When measuring the response as a function of the analyte concentration, a concentration at which response is saturated (cmax) occurs. Assuming binding occurs specifically to receptors at the surface (i.e. no multilayers) then the saturation concentration corresponds to the upper limit of the density of specifically-bound biomolecule.28 To demonstrate this analysis, various examples from streptavidin-sensing publications are used.
From the work of Elfström et al.,28 given a sample volume, V, of 200 µL solution and concentration, cmax, of 0.5 nM, the total number of molecules in the solution (= cmaxV) can be obtained. Assuming all molecules bind to the surface (valid given Kd ≪ streptavidin concentration at the surface) and that they bind homogenously, then the bound density, ρ, will simply be cmaxV divided by the functionalised area, A, exposed to analyte (10 mm2):
This can be compared with the maximum streptavidin density, ρmax, theoretically possible for streptavidin, assuming each molecule occupies ∼25 nm2.21
| ρmax = 0.04 molecules per nm2 |
This comparison suggests that the surface-bound density for the device of Elfström et al. is close to ideal. In contrast, if this is compared to Duan et al.35 who showed a cmax of 2 pM, taking into account the different sensor areas and amount of streptavidin,§ then a significantly lower surface coverage is calculated:
| ρDuan = 0.000072 molecules per nm2 |
This lower surface site density may well be explained by low levels of functionalisation of the surface. These calculations are useful as they provide an estimate of surface site density, i.e. functionalisation success rate, and ultimately dictates an upper limit for response. They can also inform experimental design when choosing sensible concentration ranges to perform experiments under. If a sensor has low functionalisation density, then it may also have a poor response time (a long time for proteins to diffuse to the binding sites).
Won Hee Lee et al.32 and Wen et al.49 did not report the volume of analyte solution utilised, making this analysis impossible. However, using the data from Stern et al., a similar calculation can be performed. Their nanowire-based FETs were selectively functionalised, in principle creating a device with very low active surface area.36,170 Fluorescence imaging confirmed that there was selective binding of streptavidin.170 Given the surface area and sample volume of their device,¶ the calculated saturation concentration cmax should be approximately 20–200 fM, however the measured signal increased up to 1 nM. A possible explanation for this disagreement would be that the high concentration response is due to longer-range interactions from streptavidin not directly bound to the nanowires (e.g. multilayer coverage) or that despite the selective-functionalisation, there is sufficient non-specifically bound streptavidin elsewhere on the device that the effective concentration at the surface of the nanowire is much lower than the initial bulk concentration.
If there were a linear relationship between analyte-binding and receptor-concentration, then it would be possible to extract the density of biotin on the surface from this simple analysis of sensor response as a function of analyte concentration. However, experiments have shown a non-linear relationship between biotin concentration at the surface and sensor response. Duan et al. showed a response saturation for polyelectrolyte films containing 30% biotin171 which agrees well with the Surface Plasmon Resonance (SPR) experiments of Jung et al. who showed saturation with an alkylthiolate monolayer containing 34% biotin.172 The non-linearity in the concentration-dependence is likely a combination of steric-constraints of the protein and the fact that streptavidin has four binding sites. Jung et al. observed that streptavidin binds to one site for low concentrations of biotin (0.34% biotin), two sites for peak saturation (approximately 30% biotin), and that for high biotin content (>40% biotin) the biotin became less available within the monolayer due to reorientation ordering, resulting in less binding to streptavidin.172 If this result is transferable to other chemical functionalisation systems, it counter-intuitively suggests that extremely high-density biotin functionalisation would be detrimental to Sensitivity.
For ultra-low concentrations of biomolecules, a lower value of the subthreshold slope can decrease the response time for a given signal change. The reason for this is that for a given change in signal, a lower subthreshold slope value requires a smaller change in surface potential. Assuming that the bound biomolecule concentration is proportional to surface potential change, a smaller number of bound molecules is required and therefore the time-to-detection is reduced.44,173
The transport of analyte to the surface of the sensor is important for setting the time-to-response and therefore the effective detection limit within a given time-frame. For example, using simple analytical arguments to describe the diffusive flux, detection of 1 fM biomolecular analyte using a 30 nm radius nanowire is expected to take an average detection time on the order of hours, compared to orders of magnitude longer using planar devices.147,148 In contrast to biomolecular sensing, pH sensing provides fast response times as the diffusion constant for H+ is orders of magnitude higher due to Grotthuss transport, in which H+ transport along hydrogen bonded networks.174,175 The theoretical detection time for an individual proton is non-trivial to calculate due to the complexity introduced by acid–base equilibria and Grotthuss transport, which cannot be described by simple Brownian motion.176 In summary, for BioFET design the limitations imposed by the mass transport, binding kinetics and geometry choices should be considered when designing for optimal response.52,147,169,177
Streptavidin sensing data
In this section, current-response data for the detection of streptavidin is presented for devices with oxide-APTES-biotin surface functionalisation and streptavidin sensing.FET-sensor data was obtained from eight publications in which streptavidin binding to oxide–APTES–biotin coated surfaces was measured in the subthreshold region, and is shown in Fig. 8.26,28,32,37,49,70,107,178,179 The normalised change in current, Inorm, is plotted against the device subthreshold slope. The data was obtained from experiments which were not all performed at the same concentration of streptavidin and at more than one ionic strength. Where experiments were performed at several concentrations of streptavidin, or at differing ionic strength, this is indicated in the figure. For experiments performed at a higher concentration of streptavidin, there is a higher density of bound analyte (until the sensor surface is saturated) and a corresponding increase in Inorm.
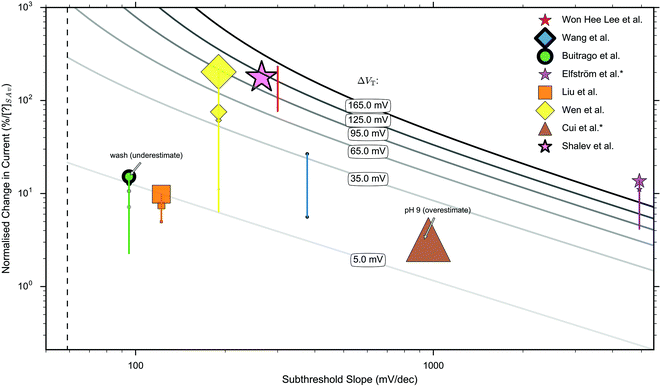 | ||
| Fig. 8 Measured ‘unbounded’ normalised change in current (Inorm) versus measured subthreshold slope for sensing operating in the subthreshold region.26,28,32,37,49,70,107,178,179 Publications indicated by an asterisk (*) have no liquid top-gate thus the plotted properties correspond to the response measured by a back-gate. The remaining publications were performed with a liquid top-gate, with corresponding subthreshold slope measured from the current response upon sweeping the liquid top-gate voltage. The shape of marker symbol corresponds to the type of device: 3D nanowire stack = ●, nanoribbon = ★, nanobelt = ■, planar = ◆, nanowire = ▲. The size of the marker symbol is proportional to the log(concentration) of streptavidin used. The vertical lines joining some markers corresponds to a series of measurements under different concentrations. A thicker outline of a marker symbol indicates an experiment made under high ionic strength, where the maximum ionic strength was 1× PBS and the minimum 0.01× PBS. The dashed line shows the theoretical lower limit of the subthreshold slope of 59 mV dec−1 available to classical FETs at room temperature. The solid grey lines are isocontours calculated by inserting the shift in threshold voltage, ΔVT, into eqn (9), the value inserted is labelled upon each line. i.e. for a data point on top of a line, it represents its calculated shift in threshold voltage and therefore the calculated change in surface potential. The results of Buitrago et al.70,178 and Cui et al.37 are likely to be an underestimate and overestimate respectively for the reasons given in ESI 7.5.† A more detailed explanation of the data extraction, the marker thickness, and a replot with a linear ×-axis can be found in ESI 7.6.† A clear relationship between Inorm+ and subthreshold slope is not apparent. | ||
If the normalised change in current was measured between several different concentrations, the normalised change in current for each is shown on the graph and the relative concentration used is indicated via the size of the marker symbol. No clear relationship between the normalised change in current and subthreshold slope was observed. High ionic strength can reduce response and therefore increasing ionic strength is indicated in Fig. 8 with a thicker marker outline.
Each solid curve shown in Fig. 8 shows the calculated shift in threshold voltage for a given subthreshold slope and Inorm (from eqn (9)), and therefore it can be seen that most measurements correspond to a shift in the threshold voltage, ΔVT, of between 5 mV and 165 mV.
Data analysis of responses in streptavidin and pH sensing
Other that the subthreshold slope, eqn (9) shows that the Sensitivity is a function of the surface potential variation induced by analyte binding. Oxide materials demonstrate a surface potential variation which is approximately linear as a function of pH (over a narrow range of pH values), which can therefore be represented as a single number, for example, a SiO2 surface typically has a pH-induced surface potential change of 33 ± 6 mV per pH.18 For this system, a maximum pH Sensitivity of between 190% to 360% is calculated assuming an optimal subthreshold slope of 59 mV dec−1 (ideal at room temperature). This is useful for the design of pH sensors as it indicates that optimal Sensitivity in the subthreshold region can be obtained by choosing a dielectric with high pH Sensitivity (e.g. HfO2 rather than SiO2) and engineering a good transistor (low subthreshold slope). An important research question is whether simple device-design strategies like these can also be developed for biosensing, which is a primary motivation for this analysis.
The precise relationship between pH Sensitivity and biomolecular Sensitivity remains an active area of research.69,74,142 Shalev et al. provided evidence to suggest that biomolecular sensing may be a result of biomolecules altering the chemical equilibria of titratable groups on the surface, and therefore for some systems pH-Sensitivity and biomolecular-Sensitivity are expected to be related.69 In this analysis pH-sensing and biomolecular-sensing Sensitivity have been considered separately.
The analysis in this section focuses upon pH-sensing and streptavidin/biotin interactions on FET devices operating in the subthreshold region.
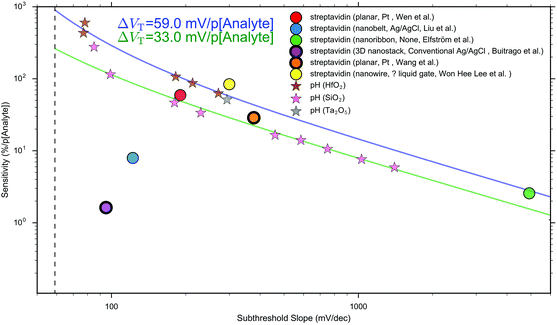 | ||
| Fig. 9 The relationship between Sensitivity and subthreshold slope, for measurements obtained within the subthreshold region. Both streptavidin sensing26,28,32,49,70,107 (●) and pH sensing data (★)18,38,44,183–190 are shown. For pH sensing, consistent surface potential changes are observed for a given oxide, resulting in the ability to predict Sensitivity accurately using eqn (9). In contrast, for biosensing, eqn (9) was insufficient to accurately predict Sensitivity, indicative of significant surface potential variation per 10-fold increase in streptavidin concentration. All biosensing and pH sensing measurements were performed using a liquid top-gate, with the exception of the biosensing measurements of Elfström et al. which utilised a fixed back-gate voltage with no liquid top-gate. For streptavidin-sensing data, the device geometry, liquid top-gate reference electrode material and authors, respectively, are shown in parenthesis within the legend. Dielectrics show a characteristic shift in threshold voltage per change in pH unit that is ∼33 mV per pH for SiO2 and ∼59 mV per pH for HfO2. Curves calculated using eqn (9) for a threshold voltage shift per 10 fold increase in analyte concentration of 33 mV and 59 mV are shown using solid lines. The dashed line indicates the theoretical lower limit of the subthreshold slope at room temperature of 59 mV dec−1 available to classical FETs. Details of method used to obtain the data and a replot of the same data but on a linear ×-axis can be found in ESI 7.6.† | ||
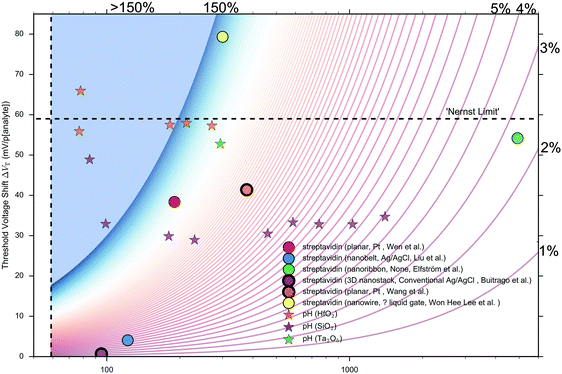 | ||
| Fig. 10 The relationship between the calculated shift in threshold voltage per 10-fold increase in analyte concentration and measured subthreshold slope, for measurements obtained within the subthreshold region. For streptavidin-sensing data, the device geometry and authors are shown in the legend. This is a replot of the experimental data shown in Fig. 9a, but in this figure, the shift in threshold voltage per 10-fold increase in analyte concentration is calculated by inserting both its subthreshold slope and Sensitivity into eqn (9). Both streptavidin sensing26,28,32,49,70,107 (●) and pH sensing (★) results18,38,44,183–190 are shown. Isocontours are drawn using eqn (9), in 1% increments, using values of the Sensitivity between 1% (red) and 150% (dark blue), with >150% being shown as a pale blue region. The theoretically optimal subthreshold slope of 59 mV dec−1 for a classical transistor at room temperature is shown as a dashed line. Eqn (9) predicts that with a subthreshold slope of 59 mV dec−1, it is impossible to obtain greater than ∼50% Sensitivity with a shift in threshold voltage <10 mV per 10-fold increase in analyte concentration, and this can be seen graphically within the figure. The Nernst limit at 300 K (59 mV per pH) is drawn as a dotted line. Details of method used to obtain the data and a copy of the plot with a linear ×-axis can be found in ESI 7.6.† | ||
As shown in Fig. 9, the Sensitivity values ranged between 3% and 84% per 10 fold increase in streptavidin, whereas the pH-sensing Sensitivity varied between 1% and 600% per pH. Therefore, on the basis of available streptavidin-sensing data, a value for Sensitivity in streptavidin-sensing comparable to optimal pH sensing has not been obtained. The pH-sensing results are consistent with a response of 33 mV per pH for SiO2 systems and 59 mV per pH for HfO2 systems. Whilst Sensitivity is a function of subthreshold slope, it is also a function of surface potential variation, and therefore a correlation is only expected when the latter is constant. For pH sensing, for a given oxide material a constant potential shift per pH was identified, such that for a given oxide, subthreshold slope alone can be used to predict Sensitivity using eqn (9). In contrast, for streptavidin-sensing data, despite the same surface functionalisation and analyte between the experiments (oxide–APTES–biotin–streptavidin), the subthreshold slope alone was not sufficient to accurately predict Sensitivity. This result is indicative of large surface potential variation per 10-fold increase in streptavidin concentration.
In order to better visualise the calculated shift in threshold voltage, the subthreshold slope of each data point and corresponding Sensitivity value was inserted into eqn (9) to obtain the calculated shift in threshold voltage per 10-fold increase in analyte concentration for that measurement. This was then used to plot Fig. 10. In this figure, isocontours calculated using eqn (9) are drawn from red to blue for values of the Sensitivity increasing in 1% increments in the range 1–150%. From Fig. 10, again it can be seen that the pH sensing data showed a shift in threshold voltage which is generally consistent for a particular oxide material (∼33 mV per pH for SiO2 with one anomaly, ∼59 mV per pH for HfO2 with one anomaly), in contrast to the streptavidin-sensing data (oxide–APTES–biotin surface chemistry) which showed no clear trend in threshold voltage shift.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32) was lower than the maximum observed in pH sensing data (up to 600%
32) was lower than the maximum observed in pH sensing data (up to 600%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44). For some devices,28,32,49,107 the Sensitivity for biomolecular analyte was similar to that expected from a pH sensor with the same subthreshold slope, however for the devices of Liu et al.26 and Buitrago et al.,70 a significantly lower Sensitivity than pH sensing results was obtained, despite the low subthreshold slopes (112 mV dec−1 and 95 mV dec−1 respectively). This can be explained as a consequence of the fact that these biosensing experiments are not obtaining both the high shift in surface potential and low subthreshold slope that is required for a high Sensitivity (shown more clearly in Fig. 10). It should be noted that the low Sensitivity of 2% seen in the study of Buitrago et al.70 may be simply a consequence of the response not being measured at equilibrium, as in Buitrago it was stated that analyte was ‘immediately washed away by PBS’.178 The high Sensitivity of Won Hee Lee et al.32 of 84% may be unreliable given a key claim of the conference paper is that subthreshold slope is changing with increased analyte concentration and this is not clearly demonstrated in the paper (as discussed in ESI section 7.5†).
44). For some devices,28,32,49,107 the Sensitivity for biomolecular analyte was similar to that expected from a pH sensor with the same subthreshold slope, however for the devices of Liu et al.26 and Buitrago et al.,70 a significantly lower Sensitivity than pH sensing results was obtained, despite the low subthreshold slopes (112 mV dec−1 and 95 mV dec−1 respectively). This can be explained as a consequence of the fact that these biosensing experiments are not obtaining both the high shift in surface potential and low subthreshold slope that is required for a high Sensitivity (shown more clearly in Fig. 10). It should be noted that the low Sensitivity of 2% seen in the study of Buitrago et al.70 may be simply a consequence of the response not being measured at equilibrium, as in Buitrago it was stated that analyte was ‘immediately washed away by PBS’.178 The high Sensitivity of Won Hee Lee et al.32 of 84% may be unreliable given a key claim of the conference paper is that subthreshold slope is changing with increased analyte concentration and this is not clearly demonstrated in the paper (as discussed in ESI section 7.5†).
Eqn (9) shows that Sensitivity is a function of both the subthreshold slope and surface potential variation induced by analyte binding. Fig. 9 and 10 showed that a consistent surface potential change per pH is evident for pH sensing but not for streptavidin-sensing. This can be explained as for biosensing, even small variations between experiments in the surface chemistry or treatment can result in drastic changes in the amount of bound protein, and thus drastic changes in the surface potential variation. As a result of these variations, the relationship between subthreshold slope and Sensitivity is not clearly seen in Fig. 9 and 10 based on the current limited data. This result demonstrates the increased importance of effective surface treatment for biosensing experiments as compared to pH sensing experiments.
The theory (eqn (9)) states that it is unlikely to obtain high Sensitivity with a high subthreshold slope value as this would require extreme changes in surface potential. In agreement with this, neither pH sensing nor streptavidin sensing data was found in the high Sensitivity/high subthreshold slope region.
Regarding the calculated shift in threshold voltage per 10-fold increase in analyte concentration (Fig. 10), for pH sensing, the results showed a shift in threshold voltage per pH which was consistent with the material of the oxide, as previously observed in the literature.18 Specifically, despite the fact that the pH sensing results are from disparate literature sources, they show highly consistent threshold voltage shifts of ∼33 mV per pH (SiO2) and ∼59 mV per pH (HfO2). Most SiO2 systems show a pH response of approximately 33 mV per pH,18,38,183,184 with some reports demonstrating a higher value of 43 mV per pH,191 46 mV per pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 97 and 42–50 mV per pH
97 and 42–50 mV per pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185 which may be due to different surface preparation procedures. Other oxides demonstrate higher values, such as Ta2O5 at 52 mV per pH
185 which may be due to different surface preparation procedures. Other oxides demonstrate higher values, such as Ta2O5 at 52 mV per pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186 and HfO2 at approximately 59 mV per pH.44,187–190 One pH sensing result44 in Fig. 10 can be seen to exceed the Nernst limit (59 mV per pH) with a calculated threshold voltage of 66 mV per pH. This result is likely due to small error in the extraction of the subthreshold slope: in the high Sensitivity, low subthreshold slope region of the plot, the effect of small errors in subthreshold slope is high. As an example, for this measurement, an error of only 8 mV dec−1 in the extraction of the subthreshold slope would place this result within the Nernst limit.
186 and HfO2 at approximately 59 mV per pH.44,187–190 One pH sensing result44 in Fig. 10 can be seen to exceed the Nernst limit (59 mV per pH) with a calculated threshold voltage of 66 mV per pH. This result is likely due to small error in the extraction of the subthreshold slope: in the high Sensitivity, low subthreshold slope region of the plot, the effect of small errors in subthreshold slope is high. As an example, for this measurement, an error of only 8 mV dec−1 in the extraction of the subthreshold slope would place this result within the Nernst limit.
The physical origin for these material-consistent surface potential shifts can be explained in terms of surface complexation models, also known as site binding models, which were first introduced by Yates et al.192 and later refined by Healy et al.193 In these models, an increased density of hydroxyl groups on the surface corresponds to an increase in surface potential shift per unit pH.123,191 This theory is supported by experimental work which has shown that blocking hydroxyl groups on the surface with organic functionality can reduce the surface potential shift per pH.123,194,195
At the lower limit, Fig. 10 shows that most oxide surfaces demonstrate surface potential shifts as a function of pH which are above approximately 25 mV per pH. As this value is a shift per 10-fold increase in analyte (pH = −log([H+])), this can be contrasted to streptavidin sensing experiments, which showed both: (a) a greater variation in possible shifts in threshold voltage per 10-fold increase in streptavidin concentration and, (b) the possibility of very low shifts of less than 10 mV (Liu et al.26 and Buitrago et al.70). If a device has a shift in threshold voltage per 10-fold increase in streptavidin concentration that is <10 mV, it can be seen in Fig. 10 that it is theoretically impossible to obtain a Sensitivity value greater than approximately 50%. This form of analysis can be used to provide information for improved BioFET design; it suggests that if a device shows a low threshold voltage shift per 10-fold increase in analyte, then design focus should be put upon enhancing the change in surface potential by optimising the surface chemistry. Below we hypothesise an explanation for this contrast in pH and biosensing data, and posit that such considerations are needed in order to design BioFETs which are as sensitive to analyte as the already commercially-successful (pH) ion-sensitive FETs.
Comparison of streptavidin and pH sensors
There are many potential factors which could explain the observed differences in the threshold voltage shifts between pH-sensing and biosensing experiments. Several of these factors relate to the surface and its chemistry. Fig. 11 shows a schematic which attempts to summarise possible differences in the surface chemistry, and therefore measured surface potential shifts, between pH and biosensing experiments. This section explores each of these factors in relation to the operation of a FET sensor system, highlighting the important implications for the understanding and design of such a sensor for biomolecules. Each section heading is labelled corresponding to the labels within Fig. 11.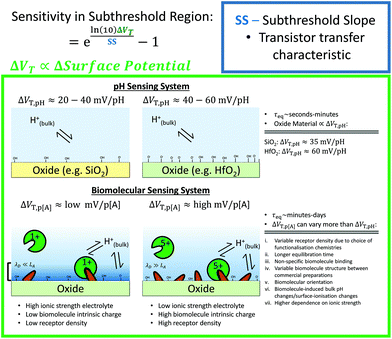 | ||
| Fig. 11 Comparison of factors influencing the surface potential in a pH sensing experiment (above) with those in a biomolecular sensing experiment (below). The systems on the left and right have a low and high receptor density, respectively. Receptors for pH sensing are hydroxide groups, whereas for biomolecular detection specific receptors (shown as yellow wedges) are required. For pH sensing, the receptor density is the determining factor the change in surface potential, and therefore the shift in threshold voltage per pH (ΔVT,pH). In contrast, for biomolecular systems, many more factors can affect the shift in threshold voltage per 10-fold increase in concentration of analyte (ΔVT,p[A]). The net charge of the biomolecular system (shown as green circles) can influence response. The debye length (λD) is compared to the distance of the analyte from the surface (LA) on the figure, which can significantly affect BIoFET signal. Here τeq is used to refer to the typical time-scale to equilibration. The equation shown is a rearranged form of eqn (9) from the main text. | ||
In order to investigate this, analysis of the concentration-dependent response curve was performed to infer the density of bound-biomolecule. As an example, the device of Elfström et al. in Fig. 10 demonstrated a surface potential shift of 52 mV per 10-fold increase in streptavidin, which is large compared to the majority of other streptavidin-sensing measurements and pH-sensing measurements. The density of streptavidin molecules upon the surface of the device of Elfström et al. was calculated to be near to the ideal density for close-packed streptavidin. It should be noted that their device was operated without a reference electrode at fixed back-gate voltage, which is generally believed to be required for a well-defined signal. This supports the hypothesis that the biosensing shift in threshold voltage per 10-fold increase in streptavidin concentration is largely determined by the density of surface receptors. Optimising the density of receptors and the sensor surface area is important in improving the device response.129
As previously discussed, signal change being directly proportional to bound-analyte is a weaker assumption for biomolecule sensing, because the bulk pH of the solution can be modified by analyte and detected by the sensor.74 The practice of using minimal buffering capacity and high biomolecule concentration (added in a single aliquot) is not uncommon26,44,66,106,119,196 leading to a solution which is not buffered adequately. Low concentrations of analyte are closer to the reality of applications in medical diagnostics in which biomolecules are often only present at low concentrations within blood samples. Alternatively a solution should be used which has the same buffering capacity as PBS at a lower ionic strength, for example, using just the sodium phosphate component of the PBS buffer.74
Summary and future outlook
Biosensor design is a highly interdisciplinary field. Understandably, this has led to a diverse range of experimental designs and varying goals, resulting in many publications focusing on some aspects of sensor characterisation in more detail than others. It is important going forward that clear standards be developed and used for the purpose of developing reliable sensors with reproducible and translatable characteristics.Reporting the drain current as a function of top-gate voltage is encouraged, as this provides information on the quality of the transistor, but also can be used to extract information regarding the change in surface potential at the sensor surface–electrolyte interface. This information can be used to quantitatively compare sensor capability.
At this stage in FET-sensor research, the focus is predominantly upon Sensitivity-enhancement. As the field moves toward commercial applications, it will become increasingly important to provide controls which evidence specificity as well as Sensitivity. In order to maximise Sensitivity, many BioFET experiments are performed at high concentration of biomolecules with low buffering capacity solution (diluted buffer), potentially resulting in a significant non-specific response due to biomolecule-induced changes in the bulk pH of the solution.
Metrics of reporting device performance have been discussed. The normalised change in current (Inorm) is currently almost ubiquitously used performance metric in the field and is useful for characterising the current response as it often reduces device-to-device variation compared to the absolute change in current. The normalised change in current is optimised in the subthreshold region, which is not necessarily the region of optimal SNR. The region of optimal SNR has been shown to be device dependent, with reports of optimum SNR both near to the region of maximum transconductance (which is usually in the linear region) and in the subthreshold region. An improved figure-of-merit that has been proposed in the literature is the SNR or IUPAC limit of detection, which involve identifying the noise levels in the signal. The importance of reporting the polarity of the normalised change in current should be emphasised, as the absolute value can lead to ambiguity in interpreting experimental results.
Reference electrodes are crucial for consistent and reliable sensing results, however, the difficulty in reference electrode miniaturisation has led to common usage of pseudo-reference electrodes in their place. Several publications suggest that Pt-based pseudo-reference electrodes are unsuitable for reliable sensing. In contrast, Ag/AgCl pseudo-reference electrodes have the potential to be a viable alternative to conventional reference electrodes. Using a back-gate as the pseudo-reference electrode without a top-gate liquid (pseudo-) reference electrode has been reported to provide unreliable results. The use of a top-gate liquid electrode together with an optimised back-gate electrode voltage which modifies the carrier concentration profile within the device can improve the subthreshold slope. By using a fixed top-gate liquid electrode voltage and sweeping the back-gate voltage, a measurement can be performed resulting in an amplified back-gate threshold voltage shift, however in this setup any SNR enhancement is expected only when the measurement equipment sets the lower limit of performance.
Streptavidin biochemistry was reviewed, and it was shown that there is a significant amount of variability for structural and electrical properties of streptavidin between different preparations of the biomolecule. An analysis of the sequence was presented which highlights that different commercial preparations are likely to have different structures, and as even small changes in electrodynamic properties of a biomolecule are in principle detectable by a BioFET, it is recommended that authors report the commercial origin of their biomolecule for reproducibility.
For pH sensing, it is known that the Sensitivity can be increased by optimising the transistor design such as to have a low value of the subthreshold slope and by choosing an oxide material which has a large shift in surface threshold voltage per pH e.g. HfO2. In contrast to Sensitivity in pH sensing, the analysis of the literature presented in this review revealed that streptavidin-sensing Sensitivity showed no clear dependence on subthreshold slope. This observation can be attributed to streptavidin-sensing demonstrating a much greater variation in the threshold voltage shift per 10-fold increase in analyte concentration between devices, even when devices shared the same oxide material. This study shows that the pH sensor design-strategy in which focus is upon subthreshold slope optimisation and oxide material choice does not directly transfer to biosensing, because, for example, a poorly functionalised biosensor surface is expected to always have negligible Sensitivity regardless of the choice of oxide. This has addressed one of the original motivations of this work to investigate whether optimisation strategies that had been employed for pH sensors would be directly transferable to optimisation of biomolecular sensing. The analysis presented suggests that subthreshold slope improvement is not likely to be as beneficial for biosensor optimisation as it is for pH sensing because the limiting factor for Sensitivity is often the surface chemistry. In conclusion, the quantitative analysis presented here suggests that in order to optimise FET-sensor Sensitivity, the device should be operated in the subthreshold region. Device design optimisation should focus upon the simultaneous optimisation of both the subthreshold slope of the device and the electrolyte-oxide surface chemistry. For example, even using an ideal classical transistor (optimal subthreshold slope of approximately 59 mV dec−1), if the surface is poorly functionalised with analyte receptors it will have a low Sensitivity.
The variability in the shift in threshold voltage per 10-fold increase in analyte concentration for biosensing responses was greater than that found for pH sensing responses. This higher variability can be explained by a variety of factors. pH models predict the most important factor in influencing this shift is the density of analyte–receptor (e.g. hydroxyl groups) at the surface, and therefore this could be an important factor determining the variability in biomolecular response. Further, the effects of ionic strength and buffering capacity in biosensing are much more pronounced than for pH sensing due to the biomolecule distance from the surface, and due to the ability of the biomolecule to change the pH of the buffer. Additional variability in biosensing threshold voltage shift per 10-fold increase in analyte concentration can originate from loss of biomolecule due to non-specific binding. This is particularly problematic for nanoscale dimension devices in which the biosensitive regions of the device can have a small surface area relative to the total exposed surface area. As discussed, a fundamental source of variability can originate from the biomolecule itself.
By measuring the response-curve as a function of analyte concentration, researchers are provided with important information for device design: the saturation point of the curve can indicate the density of bound analyte, the response per 10-fold increase in analyte concentration can provide a figure-of-merit for the device and by fitting the curve to an appropriate binding model, the binding affinity of the analyte to its receptor can be estimated. Simple calculations can be used to estimate the density of bound analyte based on the concentration at which the sensor response saturates, and both this value and measurement of the shift in threshold voltage per 10-fold increase in analyte concentration can be useful in determining whether Sensitivity enhancement efforts are limited by surface chemistry or transistor performance.
Devices even of simple (microscopic) planar geometry were shown capable of obtaining comparable Sensitivity to more elaborate nanodevice geometries (such as nanowires), suggesting nanoscale device design is not a requisite for high biomolecular Sensitivity. Due to process control constraints, the subthreshold slope is limited to ∼63 mV dec−1, with a theoretical lower limit of 59 mV dec−1 at room temperature. Therefore, it is expected that no further Sensitivity gain is obtained by further scaling of device geometry for equilibrated (with respect to the analyte binding reactions) pH sensing and biomolecular sensing experiments. This contradicts the commonly accepted claim that a high surface-to-volume ratio is a requisite for high biomolecular Sensitivity. Nanoscale device geometries are however expected to offer improved response times for biomolecular detection, and therefore improve both the effective limit of detection given practical time-constraints for a sensing experiment.
State of the art devices operate by modulating the resistance of the semiconductor (with an upper limit of 59 mV of change in gate voltage to a decade of current change) by modulating the local carrier concentration in the semiconductor. For the published nanowire sensors, the nanowire dimensions are commonly around 100 nm in width and therefore far larger than typical biomolecule dimensions, resulting in the same sensing mechanism between nanowires and conventional sheet channels. Looking to the future of the field, an interesting possibility would be the fabrication of a novel BioFET (with semiconductor insulated from electrolyte with a dielectric, i.e. operated by field-effect mechanism) such that the width scale of the device is comparable to typical biomolecular dimensions (on the order of ∼1–2 nm width and thickness). In contrast to present devices, the channel of such a device could be completely inverted by individual biomolecules, which can result in different Sensitivity and SNR characteristics. A competing challenge for such a design would be the challenge of fine dimensional control which is beyond the limit of top-down fabrication technology as well as the local variation in discrete dopant sites (discrete dopant fluctuations) within the semiconductor, which results in significant variation in device-to-device Sensitivity and, in turn, presents a significant issue for reliable detection of single molecules without the use of additional circuitry.144
Many of the current limitations which have been presented are similar to those that have been encountered for other emerging biosensing technologies. The current ‘gold standard’ for label-free biosensing is Surface Plasmon Resonance (SPR) biosensors. In a highly extensive review published in 2005, Rich and Myszka analysed 1113 articles (103 reviws, 1010 papers) and discussed common issues within the Surface Plasmon Resonance biosensor literature such as: authors only considering high concentrations of analyte, response being normalised inappropriately or the data was reported in insufficient detail.197 Surface chemistry optimisation has played an important part of Surface Plasmon Resonance biosensor development.198 In principle, BioFET devices have the potential to surpass Surface Plasmon Resonance biosensors due to their potential for low-cost fabrication, ability to detect low-mass analyte and the elimination of the requirement for additional optical equipment (which can be high cost and low throughput).
As highlighted in this review, current advances in the field of BioFET research are being obstructed by the lack of consensus upon which quantitative metrics (i.e. figure-of-merit) should be used to compare devices, with the result that most published studies can only be compared qualitatively. Despite this, BioFET research is a rapidly advancing field in which novel device design and operation methodologies are consistently being developed. Owing to the widespread capability for integration of this type of technology with the portable electronics used in Point-of-Care analysis and wearable technology, the potential for BioFET sensors to revolutionise approaches to biosensing in healthcare, security applications and sensing in the built and natural environments is prodigious.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by an EPSRC Doctoral Training Centre grant (EP/G03690X/1).Notes and references
- T. Vo-Dinh and B. Cullum, Fresenius’ J. Anal. Chem., 2000, 366, 540–551 CrossRef CAS PubMed.
- L. Senesac and T. G. Thundat, Mater. Today, 2008, 11, 28–36 CrossRef CAS.
- P. Arora, A. Sindhu, N. Dilbaghi and A. Chaudhury, Biosens. Bioelectron., 2011, 28, 1–12 CrossRef CAS PubMed.
- J. Riu, A. Maroto and F. Rius, Talanta, 2006, 69, 288–301 CrossRef CAS PubMed.
- A. Ramanavieius, F. W. Herberg, S. Hutschenreiter, B. Zimmermann, I. Lapënaitë, A. Kaušaitë, A. Finkelšteinas and A. Ramanavièienë, Acta Med. Litu., 2005, 12, 1–9 Search PubMed.
- S. G. Patching, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 43–55 CrossRef CAS PubMed.
- D. Cahen, R. Naaman and Z. Vager, Adv. Funct. Mater., 2005, 15, 1571–1578 CrossRef CAS.
- P. Bergveld, J. Wiersma and H. Meertens, IEEE Trans. Biomed. Eng., 1976, BME-23, 136–144 CrossRef.
- P. Bergveld, IEEE Trans. Biomed. Eng., 1972, BME-19, 342–351 CrossRef PubMed.
- P. Bergveld, IEEE Trans. Biomed. Eng., 1970, BME-17, 70–71 CrossRef.
- W. Oelßner, J. Zosel, U. Guth, T. Pechstein, W. Babel, J. G. Connery, C. Demuth, M. Grote Gansey and J. B. Verburg, Sens. Actuators, B, 2005, 105, 104–117 CrossRef.
- M. J. Schöning and A. Poghossian, Analyst, 2002, 127, 1137–1151 RSC.
- M. J. Schöning and A. Poghossian, Electroanalysis, 2006, 18, 1893–1900 CrossRef.
- A. Nehra and K. Pal Singh, Biosens. Bioelectron., 2015, 74, 731–743 CrossRef CAS PubMed.
- G. Zheng, X. P. A. Gao and C. M. Lieber, Nano Lett., 2010, 10, 3179–3183 CrossRef CAS PubMed.
- S. Pud, J. Li, V. Sibiliev, M. Petrychuk, V. Kovalenko, A. Offenhäusser and S. Vitusevich, Nano Lett., 2014, 14, 578–584 CrossRef CAS PubMed.
- S. Chen, J. W. van Nieuwkasteele, A. van den Berg and J. C. T. Eijkel, Anal. Chem., 2016, 88, 7890–7893 CrossRef CAS PubMed.
- K. Sun, I. Zeimpekis, C. Hu, N. M. J. Ditshego, O. Thomas, M. R. R. de Planque, H. M. H. Chong, H. Morgan and P. Ashburn, Nanotechnology, 2016, 27, 285501 CrossRef CAS PubMed.
- R. E. G. Van Hal, J. C. T. Eijkel and P. Bergveld, Sens. Actuators, B, 1995, 24, 201–205 CrossRef CAS.
- P. Bergveld, Sens. Actuators, B, 2003, 88, 1–20 CrossRef CAS.
- P. C. Weber, D. H. Ohlendorf, J. J. Wendoloski and F. R. Salemme, Science, 1989, 243, 85–88 CAS.
- H. Im, X.-J. Huang, B. Gu and Y.-K. Choi, Nat. Nanotechnol., 2007, 2, 430–434 CrossRef CAS PubMed.
- M. Im, J.-H. Ahn, J.-W. Han, T. J. Park, S. Y. Lee and Y.-K. Choi, IEEE Sens. J., 2011, 11, 351–360 CrossRef CAS.
- G. K. Iverson and J. C. Salmons, J. Engl. Linguist., 2005, 33, 207–221 CrossRef.
- Y. Cheng, K.-S. Chen, N. L. Meyer, J. Yuan, L. S. Hirst, P. B. Chase and P. Xiong, Biosens. Bioelectron., 2011, 26, 4538–4544 CrossRef CAS PubMed.
- H. H. Liu, T. H. Lin and J.-T. Sheu, Sens. Actuators, B, 2014, 192, 111–116 CrossRef CAS.
- S. Chen and S.-L. Zhang, Anal. Chem., 2011, 83, 9546–9551 CrossRef CAS PubMed.
- N. Elfström, A. E. Karlström and J. Linnros, Nano Lett., 2008, 8, 945–949 CrossRef PubMed.
- N. K. Rajan, X. Duan and M. A. Reed, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2013, 5, 629–645 CrossRef CAS PubMed.
- I. Zeimpekis, K. Sun, C. Hu, N. M. J. Ditshego, O. Thomas, M. R. R. de Planque, H. M. H. Chong, H. Morgan and P. Ashburn, Nanotechnology, 2016, 27, 165502 CrossRef CAS PubMed.
- A. Tarasov, W. Fu, O. Knopfmacher, J. Brunner, M. Calame and C. Schönenberger, Appl. Phys. Lett., 2011, 98, 012114 CrossRef.
- W. H. Lee, J.-M. Lee, M. Uhm, J. Lee, K. R. Kim, S.-J. Choi, D. M. Kim, Y.-J. Jeong and D. H. Kim, IEEE Electron Device Lett., 2014, 35, 587–589 CrossRef CAS.
- S. Chen, L. Nyholm, N. Jokilaakso, A. E. Karlström, J. Linnros, U. Smith and S.-L. Zhang, Electrochem. Solid-State Lett., 2011, 14, J34–J37 CrossRef CAS.
- T. Rim, K. Kim, N. Hong, W. Ko, C.-K. Baek, S. Jeon, M. J. Deen, M. Meyyappan, Y.-H. Jeong and J.-S. Lee, RSC Adv., 2013, 3, 7963–7969 RSC.
- X. Duan, Y. Li, N. K. Rajan, D. A. Routenberg, Y. Modis and M. A. Reed, Nat. Nanotechnol., 2012, 7, 401–407 CrossRef CAS PubMed.
- E. Stern, J. F. Klemic, D. A. Routenberg, P. N. Wyrembak, D. B. Turner-Evans, A. D. Hamilton, D. A. LaVan, T. M. Fahmy and M. A. Reed, Nature, 2007, 445, 519–522 CrossRef CAS PubMed.
- Y. Cui, Q. Wei, H. Park and C. M. Lieber, Science, 2001, 293, 1289–1292 CrossRef CAS PubMed.
- X. P. A. Gao, G. Zheng and C. M. Lieber, Nano Lett., 2010, 10, 547–552 CrossRef CAS PubMed.
- E. Buitrago, M. F.-B. Badia, Y. M. Georgiev, R. Yu, O. Lotty, J. D. Holmes, A. M. Nightingale, H. M. Guerin and A. M. Ionescu, Sens. Actuators, B, 2014, 199, 291–300 CrossRef CAS.
- J.-H. Ahn, S.-J. Choi, J.-W. Han, T. J. Park, S. Y. Lee and Y.-K. Choi, Nano Lett., 2010, 10, 2934–2938 CrossRef CAS PubMed.
- G. Shalev, G. Landman, I. Amit, Y. Rosenwaks and I. Levy, NPG Asia Mater., 2013, 5, e41 CrossRef CAS.
- M. O. Noor and U. J. Krull, Anal. Chim. Acta, 2014, 825, 1–25 CrossRef CAS PubMed.
- S. Liu and X. Guo, NPG Asia Mater., 2012, 4, e23 CrossRef.
- D. Sarkar, W. Liu, X. Xie, A. C. Anselmo, S. Mitragotri and K. Banerjee, ACS Nano, 2014, 8, 3992–4003 CrossRef CAS PubMed.
- I. Heller, A. M. Janssens, J. Männik, E. D. Minot, S. G. Lemay and C. Dekker, Nano Lett., 2008, 8, 591–595 CrossRef CAS PubMed.
- I. Heller, J. Männik, S. G. Lemay and C. Dekker, Nano Lett., 2009, 9, 377–382 CrossRef CAS PubMed.
- T. E. Edmonds, in Chemical Sensors, Springer Science & Business Media, 2013, p. 223 Search PubMed.
- J. Janata, Analyst, 1994, 119, 2275 RSC.
- X. Wen, S. Gupta, Y. Wang, T. R. N. Iii, S. C. Lee and W. Lu, Appl. Phys. Lett., 2011, 99, 043701 CrossRef.
- X. Wen, S. Gupta, T. R. Nicholson, S. C. Lee and W. Lu, Phys. Status Solidi C, 2011, 8, 2489–2491 CrossRef CAS.
- F. N. Ishikawa, M. Curreli, C. A. Olson, H.-I. Liao, R. Sun, R. W. Roberts, R. J. Cote, M. E. Thompson and C. Zhou, ACS Nano, 2010, 4, 6914–6922 CrossRef CAS PubMed.
- N. K. Rajan, Limit of Detection of Silicon BioFETs, PhD thesis, Yale University, 2013 Search PubMed.
- E. D. Minot, A. M. Janssens, I. Heller, H. A. Heering, C. Dekker and S. G. Lemay, Appl. Phys. Lett., 2007, 91, 093507 CrossRef.
- U. Guth, F. Gerlach, M. Decker, W. Oelßner and W. Vonau, J. Solid State Electrochem., 2009, 13, 27–39 CrossRef CAS.
- M. Lambrechts and W. Sansen, in Biosensors: Microelectrochemical Devices, CRC Press, 1992, p. 69 Search PubMed.
- C. Toumazou and P. Georgiou, Electron. Lett., 2011, 47, S7–S12 CrossRef.
- M. T. Martínez, Y.-C. Tseng, M. González and J. Bokor, J. Phys. Chem. C, 2012, 116, 22579–22586 Search PubMed.
- Y. Taur and T. H. Ning, Fundamentals of Modern VLSI Devices, Cambridge University Press, 2nd edn, 2013 Search PubMed.
- S. M. Sze, Semiconductor Devices: Physics and Technology, John Wiley & Sons, Inc., Hoboken, N.J, 2nd edn, 1985 Search PubMed.
- N. D. Arora, in MOSFET Models for VLSI Circuit Simulation: Theory and Practice, Springer Science & Business Media, 2012, p. 265 Search PubMed.
- A. Vacic and M. A. Reed, J. Exp. Nanosci., 2014, 9, 41–50 CrossRef CAS.
- R. J. Chen, H. C. Choi, S. Bangsaruntip, E. Yenilmez, X. Tang, Q. Wang, Y.-L. Chang and H. Dai, J. Am. Chem. Soc., 2004, 126, 1563–1568 CrossRef CAS PubMed.
- H. R. Byon and H. C. Choi, J. Am. Chem. Soc., 2006, 128, 2188–2189 CrossRef CAS PubMed.
- E. H. Williams, A. V. Davydov, A. Motayed, S. G. Sundaresan, P. Bocchini, L. J. Richter, G. Stan, K. Steffens, R. Zangmeister, J. A. Schreifels and M. V. Rao, Appl. Surf. Sci., 2012, 258, 6056–6063 CrossRef CAS.
- X. Duan, N. K. Rajan, M. H. Izadi and M. A. Reed, Nanomed., 2013, 8, 1839–1851 CrossRef CAS PubMed.
- S. Gupta, M. Elias, X. Wen, J. Shapiro, L. Brillson, W. Lu and S. C. Lee, Biosens. Bioelectron., 2008, 24, 505–511 CrossRef CAS PubMed.
- N. Clément, K. Nishiguchi, J. F. Dufreche, D. Guerin, A. Fujiwara and D. Vuillaume, Appl. Phys. Lett., 2011, 98, 014104 CrossRef.
- A. Henning, M. Molotskii, N. Swaminathan, Y. Vaknin, A. Godkin, G. Shalev and Y. Rosenwaks, Small, 2015, 11, 4931–4937 CrossRef CAS PubMed.
- G. Shalev, Y. Rosenwaks and I. Levy, Biosens. Bioelectron., 2012, 31, 510–515 CrossRef CAS PubMed.
- E. Buitrago, M. Fernández-Bolaños, Y. M. Georgiev, R. Yu, O. Lotty, J. D. Holmes, A. M. Nightingale and A. M. Ionescu, in Proceedings of Technical Program - 2014 International Symposium on VLSI Technology, Systems and Application (VLSI-TSA), 2014, pp. 1–2.
- S. Upadhyay, R. Frederiksen, N. Lloret, L. De Vico, P. Krogstrup, J. H. Jensen, K. L. Martinez and J. Nygård, Appl. Phys. Lett., 2014, 104, 203504 CrossRef.
- R. A. Sperling and W. J. Parak, Philos. Trans. R. Soc., A, 2010, 368, 1333–1383 CrossRef CAS PubMed.
- T. Sano and C. R. Cantor, J. Biol. Chem., 1990, 265, 3369–3373 CAS.
- N. Lloret, R. S. Frederiksen, T. C. Møller, N. I. Rieben, S. Upadhyay, L. D. Vico, J. H. Jensen, J. Nygård and K. L. Martinez, Nanotechnology, 2013, 24, 035501 CrossRef PubMed.
- N. A. Lapin and Y. J. Chabal, J. Phys. Chem. B, 2009, 113, 8776–8783 CrossRef CAS PubMed.
- N. M. Green, in Methods in Enzymology, ed. M. Wilchek and E. A. Bayer, Academic Press, 1990, vol. 184, pp. 51–67 Search PubMed.
- L. Chaiet and F. J. Wolf, Arch. Biochem. Biophys., 1964, 106, 1–5 CrossRef CAS PubMed.
- N. M. Green, in Advances in Protein Chemistry, ed. J. T. E. Anfinsen and F. M. R. C. B. Anfinsen, Academic Press, 1975, vol. 29, pp. 85–133 Search PubMed.
- S. Sivasankar, S. Subramaniam and D. Leckband, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 12961–12966 CrossRef CAS.
- Streptavidin Properties and Characterization, Rockland Inc Search PubMed.
- C. E. Argarana, I. D. Kuntz, S. Birken, R. Axel and C. R. Cantor, Nucleic Acids Res., 1986, 14, 1871–1882 CrossRef CAS PubMed.
- A. Pähler, W. A. Hendrickson, M. A. Kolks, C. E. Argaraña and C. R. Cantor, J. Biol. Chem., 1987, 262, 13933–13937 Search PubMed.
- L. Almonte, E. Lopez-Elvira and A. M. Baró, ChemPhysChem, 2014, 15, 2768–2773 CrossRef CAS PubMed.
- R. C. Bruch and H. B. White, Biochemistry, 1982, 21, 5334–5341 CrossRef CAS PubMed.
- D. Wild, The Immunoassay Handbook, Gulf Professional Publishing, 2005 Search PubMed.
- M. D. Sonawane, S. B. Nimse, K.-S. Song and T. Kim, RSC Adv., 2016, 6, 7599–7609 RSC.
- A. Poghossian, A. Cherstvy, S. Ingebrandt, A. Offenhäusser and M. J. Schöning, Sens. Actuators, B, 2005, 111–112, 470–480 CrossRef CAS.
- E. J. Fogt, D. F. Untereker, M. S. Norenberg and M. E. Meyerhoff, Anal. Chem., 1985, 57, 1995–1998 CrossRef CAS PubMed.
- J. O. Bockris and A. K. N. Reddy, Modern Electrochemistry 1, Kluwer Academic Publishers, Boston, 1998, vol. 1 Search PubMed.
- B. N. Dominy, D. Perl, F. X. Schmid and C. L. Brooks III, J. Mol. Biol., 2002, 319, 541–554 CrossRef CAS PubMed.
- E. Stern, R. Wagner, F. J. Sigworth, R. Breaker, T. M. Fahmy and M. A. Reed, Nano Lett., 2007, 7, 3405–3409 CrossRef CAS PubMed.
- P. Bergveld, Sens. Actuators, A, 1996, 56, 65–73 CrossRef CAS.
- H. H. Lee, M. Bae, S.-H. Jo, J.-K. Shin, D. H. Son, C.-H. Won and J.-H. Lee, Sens. Mater., 2015, 27, 575–583 Search PubMed.
- P. Estrela, D. Paul, Q. Song, L. K. Stadler, L. Wang, E. Huq, J. J. Davis, P. K. Ferrigno and P. Migliorato, Anal. Chem., 2010, 82, 3531–3536 CrossRef CAS PubMed.
- P. Casal, X. Wen, S. Gupta, T. Nicholson, Y. Wang, A. Theiss, B. Bhushan, L. Brillson, W. Lu and S. C. Lee, Philos. Trans. R. Soc., A, 2012, 370, 2474–2488 CrossRef CAS PubMed.
- A. Tarasov, M. Wipf, R. L. Stoop, K. Bedner, W. Fu, V. A. Guzenko, O. Knopfmacher, M. Calame and C. Schönenberger, ACS Nano, 2012, 6, 9291–9298 CrossRef CAS PubMed.
- Y. Maekawa, Y. Shibuta and T. Sakata, ChemElectroChem, 2014, 1, 1516–1524 CrossRef CAS.
- L. J. Criscenti, R. T. Cygan, A. S. Kooser and H. K. Moffat, Chem. Mater., 2008, 20, 4682–4693 CrossRef CAS.
- L. Bousse and P. Bergveld, Sens. Actuators, 1984, 6, 65–78 CrossRef CAS.
- S. Jamasb, IEEE Sens. J., 2004, 4, 795–801 CrossRef CAS.
- S. Jamasb, S. Collins and R. L. Smith, Sens. Actuators, B, 1998, 49, 146–155 CrossRef CAS.
- S. Jamasb, S. D. Collins and R. L. Smith, in 1997 International Conference on Solid State Sensors and Actuators, 1997. TRANSDUCERS ‘97 Chicago, 1997, vol. 2, pp. 1379–1382.
- S. Jamasb, S. D. Collins and R. L. Smith, IEEE Trans. Electron Devices, 1998, 45, 1239–1245 CrossRef CAS.
- J.-L. Chiang, J.-C. Chou, Y.-C. Chen, G. S. Liau and C.-C. Cheng, Jpn. J. Appl. Phys., 2003, 42, 4973–4977 CrossRef CAS.
- S. Kim, D. W. Kwon, R. Lee, D. H. Kim and B.-G. Park, Jpn. J. Appl. Phys., 2016, 55, 06GG01 CrossRef.
- B. S. Kang, F. Ren, L. Wang, C. Lofton, W. W. Tan, S. J. Pearton, A. Dabiran, A. Osinsky and P. P. Chow, Appl. Phys. Lett., 2005, 87, 023508 CrossRef.
- Y. Wang, P. C. Sondergaard, A. Theiss, S. C. Lee and W. Lu, ECS Trans., 2014, 61, 139–146 CrossRef CAS.
- S. Jamasb, Circ. Syst. Signal. Pr., 2016, 10, 119–125 Search PubMed.
- R. B. Schasfoort, R. P. H. Kooyman, P. Bergveld and J. Greve, Biosens. Bioelectron., 1990, 5, 103–124 CrossRef CAS PubMed.
- P. Bergveld, Biosens. Bioelectron., 1991, 6, 55–72 CrossRef CAS PubMed.
- V. Krivitsky, M. Zverzhinetsky and F. Patolsky, Nano Lett., 2016, 16, 6272–6281 CrossRef CAS PubMed.
- S. Kim, J.-Y. Kim, J.-H. Ahn, T. J. Park, S. Y. Lee and Y.-K. Choi, Appl. Phys. Lett., 2010, 97, 073702 CrossRef.
- N. Gao, W. Zhou, X. Jiang, G. Hong, T.-M. Fu and C. M. Lieber, Nano Lett., 2015, 15, 2143–2148 CrossRef CAS PubMed.
- K. Georgakopoulou, A. Birbas and C. Spathis, J. Appl. Phys., 2015, 117, 104505 CrossRef.
- I. Jokić, M. Frantlović, Z. Djurić, K. Radulović and Z. Jokić, Microelectron. Eng., 2015, 144, 32–36 CrossRef.
- G. S. Kulkarni and Z. Zhong, Nano Lett., 2012, 12, 719–723 CrossRef CAS PubMed.
- G. S. Kulkarni, W. Zang and Z. Zhong, Acc. Chem. Res., 2016, 49, 2578–2586 CrossRef CAS PubMed.
- IUPAC Compendium of Chemical Terminology: Gold Book, ed. M. Nič, J. Jirát, B. Košata, A. Jenkins and A. McNaught, IUPAC, Research Triagle Park, NC, 2.1.0., 2009 Search PubMed.
- F. N. Ishikawa, M. Curreli, H.-K. Chang, P.-C. Chen, R. Zhang, R. J. Cote, M. E. Thompson and C. Zhou, ACS Nano, 2009, 3, 3969–3976 CrossRef CAS PubMed.
- H. Nam, B.-R. Oh, M. Chen, S. Wi, D. Li, K. Kurabayashi and X. Liang, J. Vac. Sci. Technol., B, 2015, 33, 06FG01 Search PubMed.
- N. Elfström, Silicon Nanowires for Biomolecule Detection, PhD thesis, Royal Institute of Technology, 2008 Search PubMed.
- R. L. Rich and D. G. Myszka, J. Mol. Recognit., 2008, 21, 355–400 CrossRef CAS PubMed.
- S. Chen, J. G. Bomer, E. T. Carlen and A. van den Berg, Nano Lett., 2011, 11, 2334–2341 CrossRef CAS PubMed.
- K. Shoorideh and C. O. Chui, Understanding and optimization of the sensitivity of nanoscale FET-based biosensors, Proceedings Volume 9174, Nanoepitaxy: Materials and Devices VI, 2014, vol. 9174, pp. 917413–917416 Search PubMed.
- K. Shoorideh and C. O. Chui, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 5111–5116 CrossRef CAS PubMed.
- J. Lee, J. Jang, B. Choi, J. Yoon, J.-Y. Kim, Y.-K. Choi, D. M. Kim, D. H. Kim and S.-J. Choi, Sci. Rep., 2015, 5, 12286 CrossRef PubMed.
- A. Vacic, J. M. Criscione, E. Stern, N. K. Rajan, T. Fahmy and M. A. Reed, in 2014 International Conference on Microelectronic Test Structures (ICMTS), 2014, pp. 203–206.
- A. Vacic, J. M. Criscione, E. Stern, N. K. Rajan, T. Fahmy and M. A. Reed, Biosens. Bioelectron., 2011, 28, 239–242 CrossRef CAS PubMed.
- N. K. Rajan, K. Brower, X. Duan and M. A. Reed, Appl. Phys. Lett., 2014, 104, 084106 CrossRef.
- N. K. Rajan, D. A. Routenberg and M. A. Reed, Appl. Phys. Lett., 2011, 98, 264107 CrossRef PubMed.
- N. K. Rajan, D. A. Routenberg, J. Chen and M. A. Reed, Appl. Phys. Lett., 2010, 97, 243501 CrossRef PubMed.
- M.-P. Lu, E. Vire and L. Montès, Nanotechnology, 2015, 26, 495501 CrossRef PubMed.
- H.-K. Lim and J. G. Fossum, IEEE Trans. Electron Devices, 1983, 30, 1244–1251 CrossRef.
- J. Go, P. R. Nair and M. A. Alam, J. Appl. Phys., 2012, 112, 034516 CrossRef PubMed.
- J. Go, P. R. Nair, B. Reddy, B. Dorvel, R. Bashir and M. A. Alam, in Electron Devices Meeting (IEDM), 2010 IEEE International, 2010, p. 8.7.1–8.7.4.
- O. Knopfmacher, A. Tarasov, W. Fu, M. Wipf, B. Niesen, M. Calame and C. Schönenberger, Nano Lett., 2010, 10, 2268–2274 CrossRef CAS PubMed.
- G. Shalev, A. Doron, U. Virobnik, A. Cohen, Y. Sanhedrai and I. Levy, Appl. Phys. Lett., 2008, 93, 083902 CrossRef.
- H.-S. P. Wong, IBM J. Res. Dev., 2002, 46, 133–168 CrossRef CAS.
- H.-J. Jang and W.-J. Cho, Sci. Rep., 2014, 4, 5284 CrossRef CAS PubMed.
- K. Jayant, K. Auluck, M. Funke, S. Anwar, J. B. Phelps, P. H. Gordon, S. R. Rajwade and E. C. Kan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2013, 88, 012801 CrossRef PubMed.
- K. Jayant, K. Auluck, M. Funke, S. Anwar, J. B. Phelps, P. H. Gordon, S. R. Rajwade and E. C. Kan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2013, 88, 012802 CrossRef PubMed.
- K. Jayant, K. Auluck, S. Rodriguez, Y. Cao and E. C. Kan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2014, 89, 052817 CrossRef PubMed.
- N. Elfström, R. Juhasz, I. Sychugov, T. Engfeldt, A. E. Karlström and J. Linnros, Nano Lett., 2007, 7, 2608–2612 CrossRef PubMed.
- P. R. Nair and M. A. Alam, IEEE Trans. Electron Devices, 2007, 54, 3400–3408 CrossRef CAS.
- H. Ghosh, D. Kundu and C. RoyChaudhuri, IEEE Trans. Electron Devices, 2016, 63, 3241–3248 CrossRef CAS.
- J.-P. Colinge, Silicon-on-Insulator Technology: Materials to VLSI: Materials to Vlsi, Springer Science & Business Media, 2004 Search PubMed.
- P. R. Nair and M. A. Alam, Appl. Phys. Lett., 2006, 88, 233120 CrossRef.
- P. E. Sheehan and L. J. Whitman, Nano Lett., 2005, 5, 803–807 CrossRef CAS PubMed.
- Y. Maekawa, Y. Shibuta and T. Sakata, Chem. Phys. Lett., 2015, 619, 152–157 CrossRef CAS.
- L. De Vico, L. Iversen, M. H. Sørensen, M. Brandbyge, J. Nygård, K. L. Martinez and J. H. Jensen, Nanoscale, 2011, 3, 3635 RSC.
- L. De Vico, M. H. Sørensen, L. Iversen, D. M. Rogers, B. S. Sørensen, M. Brandbyge, J. Nygård, K. L. Martinez and J. H. Jensen, Nanoscale, 2011, 3, 706 RSC.
- C. Heitzinger, N. J. Mauser and C. Ringhofer, SIAM J. Appl. Math., 2010, 70, 1634–1654 CrossRef.
- P. R. Nair and M. A. Alam, Nano Lett., 2008, 8, 1281–1285 CrossRef CAS PubMed.
- S. Baumgartner, C. Heitzinger, A. Vacic and M. A. Reed, Nanotechnology, 2013, 24, 225503 CrossRef PubMed.
- T. Windbacher, V. Sverdlov, S. Selberherr, C. Heitzinger, N. Mauser and C. Ringhofer, AIP Conf. Proc., 2010, 1199, 507 CrossRef.
- M. W. Shinwari, M. J. Deen and D. Landheer, Microelectron. Reliab., 2007, 47, 2025–2057 CrossRef.
- D. Landheer, W. R. McKinnon, W. H. Jiang and G. Aers, Appl. Phys. Lett., 2008, 92, 253901 CrossRef.
- M. H. Sørensen, N. A. Mortensen and M. Brandbyge, Appl. Phys. Lett., 2007, 91, 102105 CrossRef.
- J. O. Bockris, A. K. N. Reddy and M. E. Gamboa-Aldeco, Modern Electrochemistry 2A, Kluwer Academic Publishers, Boston, 2002, vol. 2A Search PubMed.
- A. Choi, K. Kim, H.-I. Jung and S. Y. Lee, Sens. Actuators, B, 2010, 148, 577–582 CrossRef CAS.
- P. Ginet, S. Akiyama, N. Takama, H. Fujita and B. Kim, J. Micromech. Microeng., 2011, 21, 065008 CrossRef.
- C.-Y. Hsiao, C.-H. Lin, C.-H. Hung, C.-J. Su, Y.-R. Lo, C.-C. Lee, H.-C. Lin, F.-H. Ko, T.-Y. Huang and Y.-S. Yang, Biosens. Bioelectron., 2009, 24, 1223–1229 CrossRef CAS PubMed.
- P. Hu, J. Zhang, Z. Wen and C. Zhang, Nanotechnology, 2011, 22, 335502 CrossRef PubMed.
- K. A. Jeon, H. J. Son, C. E. Kim, M. S. Shon, K. H. Yoo, A. M. Choi, H. I. Jung and S. Y. Lee, IEEE, 2006, pp. 1265–1268 Search PubMed.
- J. S. Kim, W. I. Park, C.-H. Lee and G.-C. Yi, Korean Phys. Soc., 2006, 49, 1635 CAS.
- D. Khatayevich, T. Page, C. Gresswell, Y. Hayamizu, W. Grady and M. Sarikaya, Small, 2014, 10, 1505–1513 CrossRef CAS PubMed.
- I. R. Olmsted, A. Kussrow and D. J. Bornhop, Anal. Chem., 2012, 84, 10817–10822 CrossRef CAS PubMed.
- D. A. Hall and C. J. Langmead, Br. J. Pharmacol., 2010, 161, 1276–1290 CrossRef CAS PubMed.
- T. M. Squires, R. J. Messinger and S. R. Manalis, Nat. Biotechnol., 2008, 26, 417–426 CrossRef CAS PubMed.
- E. Stern, Label-free sensing with semiconducting nanowires, PhD thesis, Yale University, 2007 Search PubMed.
- X. Duan, L. Mu, S. D. Sawtelle, N. K. Rajan, Z. Han, Y. Wang, H. Qu and M. A. Reed, Adv. Funct. Mater., 2015, 25, 2279–2286 CrossRef CAS.
- L. S. Jung, K. E. Nelson, P. S. Stayton and C. T. Campbell, Langmuir, 2000, 16, 9421–9432 CrossRef CAS.
- D. Sarkar and K. Banerjee, Appl. Phys. Lett., 2012, 100, 143108 CrossRef.
- M. L. Soudijn, Proton Transport in Aqueous Ionic Solutions, PhD thesis, University of Amsterdam, 2012 Search PubMed.
- C. J. T. de Grotthuss, Ann. Chim., 1806, 58, 54–73 Search PubMed.
- B. M. Lowe, C.-K. Skylaris and N. G. Green, J. Colloid Interface Sci., 2015, 451, 231–244 CrossRef CAS PubMed.
- P. Schuck and H. Zhao, Methods Mol. Biol., 2010, 627, 15–54 CAS.
- E. Buitrago, École Polytechnique Fédérale de Lausanne, 2014 Search PubMed.
- G. Shalev, A. Cohen, A. Doron, A. Machauf, M. Horesh, U. Virobnik, D. Ullien and I. Levy, Sensors, 2009, 9, 4366–4379 CrossRef CAS PubMed.
- N. M. J. Ditshego, N. A. B. Ghazali, M. Ebert, K. Sun, I. Zeimpekis, P. Ashburn, M. R. R. de Planque and H. M. H. Chong, IEEE, 2015, pp. 801–804 Search PubMed.
- K. Sun, I. Zeimpekis, C. Hu, N. M. J. Ditshego, O. Thomas, M. R. R. de Planque, H. M. H. Chong, H. Morgan and P. Ashburn, Nanotechnology, 2016, 27, 285501 CrossRef CAS PubMed.
- M. A. Brown, Z. Abbas, A. Kleibert, R. G. Green, A. Goel, S. May and T. M. Squires, Phys. Rev. X, 2016, 6, 011007 Search PubMed.
- S. Kim, K. Kim, T. Rim, C. Park, D. Cho, C. K. Baek, Y. H. Jeong, M. Meyyappan and J. S. Lee, in 2011 IEEE International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), 2011, pp. 1233–1236.
- S. Kim, T. Rim, K. Kim, U. Lee, E. Baek, H. Lee, C.-K. Baek, M. Meyyappan, M. J. Deen and J.-S. Lee, Analyst, 2011, 136, 5012–5016 RSC.
- X. T. Vu, R. Stockmann, B. Wolfrum, A. Offenhäusser and S. Ingebrandt, Phys. Status Solidi A, 2010, 207, 850–857 CrossRef CAS.
- C.-E. Lue, T.-C. Yu, C.-M. Yang, D. G. Pijanowska and C.-S. Lai, Sensors, 2011, 11, 4562–4571 CrossRef CAS PubMed.
- A. Tarasov, N. de Rooij, C. Schönenberger and L. Linnros, Silicon nanowire field-effect transistors for sensing applications, PhD thesis, University of Basel, 2012 Search PubMed.
- S. Zafar, C. D'Emic, A. Afzali, B. Fletcher, Y. Zhu and T. Ning, Nanotechnology, 2011, 22, 405501 CrossRef PubMed.
- S. Rigante, M. Wipf, A. Bazigos, K. Bedner, D. Bouvet and A. M. Ionescu, IEEE, San Francisco, CA, USA, 2014, pp. 1063–1066 Search PubMed.
- K. Bedner, V. A. Guzenko, A. Tarasov, M. Wipf, R. L. Stoop, D. Just, S. Rigante, W. Fu, R. A. Minamisawa and C. David, et al. , Sens. Mater., 2013, 25, 567–576 CAS.
- T. Akiyama, Y. Ujihira, Y. Okabe, T. Sugano and E. Niki, IEEE Trans. Electron Devices, 1982, 29, 1936–1941 CrossRef.
- D. E. Yates, S. Levine and T. W. Healy, J. Chem. Soc., Faraday Trans., 1974, 70, 1807–1818 RSC.
- T. W. Healy and L. R. White, Adv. Colloid Interface Sci., 1978, 9, 303–345 CrossRef CAS.
- A. Tarasov, M. Wipf, K. Bedner, J. Kurz, W. Fu, V. A. Guzenko, O. Knopfmacher, R. L. Stoop, M. Calame and C. Schönenberger, Langmuir, 2012, 28, 9899–9905 CrossRef CAS PubMed.
- M.-N. Niu, X.-F. Ding and Q.-Yi Tong, IEEE, Penang, Malaysia, 1996, pp. 189–193 Search PubMed.
- A. Star, J.-C. P. Gabriel, K. Bradley and G. Grüner, Nano Lett., 2003, 3, 459–463 CrossRef CAS.
- R. L. Rich and D. G. Myszka, J. Mol. Recognit., 2006, 19, 478–534 CrossRef CAS PubMed.
- R. B. M. Schasfoort and A. J. Tudos, Handbook of Surface Plasmon Resonance, Royal Society of Chemistry, 2008 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C7AN00455A |
| ‡ E.g. Sigma-Aldrich (Product Id: S067, CAS number 9013-20-1 MDL number MFCD00082035). |
| § Gate area 10 µm2, cmax = 2 pM, analyte was exposed to the surface over two minutes, assuming all liquid came into contact with the surface (overestimate), at a flow rate of 300 µL min−1 results in volume of 600 µL. |
| ¶ A total of 100 µL sample volume exposed to the surface (with 10 µL exposed at any one point in time) which, assuming perfect selective functionalisation of just the nanowires, has an functionalised surface area of ∼3 × 107 nm−2. |
| This journal is © The Royal Society of Chemistry 2017 |