Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Preparation and characterization of primary magnesium mixtures for the ab initio calibration of absolute magnesium isotope ratio measurements†
Björn
Brandt
a,
Jochen
Vogl
*a,
Janine
Noordmann
b,
Angela
Kaltenbach
b and
Olaf
Rienitz
b
aBAM Federal Institute for Materials Research and Testing, Unter den Eichen 87, 12205 Berlin, Germany. E-mail: jochen.vogl@bam.de
bPhysikalisch-Technische Bundesanstalt (PTB), Bundesallee 100, 38116 Braunschweig, Germany. E-mail: olaf.rienitz@ptb.de
First published on 17th August 2015
Abstract
We report an appropriate preparation of binary isotope calibration mixtures of the three stable isotopes of magnesium to be used in the ab initio calibration of multicollector mass spectrometers (ICPMS and TIMS). For each of the three possible combinations of binary mixtures (“24Mg” + “25Mg”, “24Mg” + “26Mg”, and “25Mg” + “26Mg”), three individual setups have been prepared under gravimetric control, each of them with an isotope ratio close to unity, and a total magnesium mass fraction close to 20 mg kg−1. The preparation was designed to occur via an intermediate dilution of a parent solution of a highly purified specimen of the isotopically enriched magnesium materials. For the application as calibration mixtures, a complete uncertainty budget was set up, and is presented and discussed in detail, including the aspects that went into the design of the dilution and mixing approach to minimize uncertainty. The principle parameters for the purpose of the later calibration of the mass spectrometers are the absolute masses of isotopically enriched magnesium materials in the primary calibration mixtures. For the first time relative expanded uncertainties U (k = 2) for these masses of ≤0.005% could be achieved for all mixtures.
1. Introduction
Since the first mass spectrometric detection of Ne isotopes by J. J. Thompson in 1910, it has been known that most chemical elements exist in the form of more than one stable isotope.1 Mostly, the resulting isotopic composition is assumed to be invariant in nature and is taken as a quasi-constant value.2 For most elements, however, small variations of their isotopic composition do exist.Two approaches exist to denote isotopic composition:
The absolute isotopic composition of an element is expressed in either of two tautological representations: as isotope amount fractions (“isotope abundances”) for each isotope, or as isotope amount ratios. Although the expression in terms of isotope amount fractions is conceptually simpler, and directly yields the atomic weight and the molar mass of an element, the expression in terms of isotope amount ratios has found widespread use, since it is more directly connected to the experimental determination.
For many applications, however, the absolute isotopic composition is not required. In such cases, the isotopic variation is reported as the relative deviation of the isotope ratio in the sample to the isotope ratio of an internationally accepted standard. Such relative deviations are expressed as so-called “delta-values” (δ values).3
The main difference between both approaches is that for determining the absolute isotopic composition, all influencing quantities have to be considered, while for delta-measurements – where the isotope ratio measured in the sample is divided by the isotope ratio measured in the accepted standard – it is assumed that all corrections and/or calibrations are compensated for due to the assumed identical behaviour of the sample and the standard in the mass spectrometer. Consequently, measurement uncertainties for delta-values are much smaller than those for absolute measurements.
However, delta-values do not convey the full picture of the isotopic composition, and they lack absolute traceability on the basis of the international system of units (SI), and thus are burdened with a number of potential negative consequences. Additionally, difficulties may occur once the artefact used as an anchor point for the delta scale has been consumed, and thus needs to be replaced by a new material. It is for those reasons that absolute isotope ratio measurements are very desirable.
Until today, the sole universal method for high-accuracy isotope ratio determination is mass spectrometry. Practically no alternatives exist. The two most versatile methods for mass spectrometric isotope ratio determination are thermal ionization mass spectrometry (TIMS) and inductively coupled plasma-mass spectrometry (ICPMS), both exhibiting a number of peculiarities that need to be taken into account for achieving accurate isotope ratios. The most important aspect, however, is that each ion current or ion intensity measured with a mass spectrometer such as TIMS or ICPMS is biased by mass fractionation or discrimination, detector efficiency, amplifier gain, and other effects. This in turn also applies to ion current ratios measured by using TIMS and ICPMS. The correction of such bias is accomplished by various approaches, such as external correction by using correction factors (“K factors”) or by δ-measurements.4,5 For both approaches, isotope reference materials (IRMs) are required.
Absolute IRMs can only be certified by mass spectrometric measurements, which, however, are subject to mass fractionation and/or mass discrimination, which in turn require a suitable calibration to correct the results. This dilemma has been solved by A. O. Nier, who pioneered the approach to calibrate mass spectrometers using synthetic isotope mixtures in 1950.6 In this approach (see Fig. 1), isotopically enriched and chemically purified materials are used as the starting point to prepare isotope calibration mixtures in a number of steps under full gravimetric control, so that the theoretical isotope ratios in the calibration mixtures can be calculated using the weighing data and the isotope ratios of the isotopically enriched starting materials. To this point, however, the isotope ratios of the isotopically enriched materials are not yet known, and still need to be determined experimentally. Since, however, at this point the mass spectrometer is also not yet calibrated, the isotope ratios measured for the isotopically enriched materials are affected by mass fractionation and/or mass discrimination, as are the theoretically calculated isotope ratios in the isotope mixtures (which are based on those experimental determinations). This whole approach apparently gives rise to a catch-22 situation; however, although it thus may appear that the approach would not constitute an apt way to determine the calibration factors of the instrument, it turns out that, in reality, the system is overdefined, and all those unknowns can be determined from the same experiment: in the past, the corresponding equations were solved by an iterative approach, which was typically applied to mixtures of only two isotopes. The use of only two isotopes in a multi-isotope system, however, requires that the correction factors for the other isotope ratios need to be extra- or interpolated using empirical laws, which are not fully verified, and do not account for variations in detector efficiency and amplifier gain in multi-collector instruments. This changed when Pritzkow et al. used enriched materials for seven out of the eight naturally occurring cadmium isotopes to prepare isotope mixtures, yielding expanded uncertainties for the Cd isotope ratios down to 0.02%.7 More recently, the equation system describing the synthetic isotope mixture approach was solved by exact analytical equations (verified for at least three isotopes), which yields the calibration factors without the need for iteration.8 Both components together – the use of preferably all stable isotopes of an element for the mixtures, and the exact analytical equations – form the virtually ideal route for obtaining absolute isotope ratios. Moreover, it also fulfils the requirements for a primary method of measurement as defined by the CCQM.9
Magnesium has been selected as the target element of this demonstrative work since its isotope ratios are widely used in biology, cosmochemistry, geochemistry and nutrition.10–14 Until today, the only certified isotope reference material available for the calibration of absolute magnesium isotope ratio measurements is NIST SRM 980;15 this material is sold by NIST in the form of metal chips; additionally, a solution of an aliquot is available as IRMM-009.
Unfortunately, NIST SRM 980 turned out to show significant heterogeneity.16 Although this isotope heterogeneity is largely covered by the expanded uncertainty, it is too large for today's magnesium isotope research. Also, this inhomogeneity renders SRM 980 unsuitable for delta measurements; other artefacts are thus currently applied by the community (CAM-1 and DSM-3).16
Consequently, a replacement of this material is urgently needed.5,17 Such a new magnesium isotope reference material can only be characterized via the above described isotope mixture approach. The main requirements are: adequate homogeneity of the isotope amount ratio (≤0.01%), which can easily be achieved by providing the IRM in the form of a solution, and an expanded relative uncertainty < 0.02% for the isotope amount ratios, which would be small enough to serve the needs of current experimental magnesium isotope ratio analyses (relative precision of 0.01% to 0.02%).16,18
To prepare isotope mixtures with expanded uncertainties of ≤0.02% for the mass fractions, however, two primary solutions of different isotopically enriched materials – each with expanded uncertainties of ≤0.014% for the mass fractions – are required as the starting materials to produce a blend. The best mono-elemental solutions available from commercial suppliers such as Merck, however, have much larger relative expanded uncertainties of approx. 0.4%.
The challenge of producing primary solutions of isotopes with relative expanded uncertainties of ≤0.014% was taken up in this project. This paper describes the preparation of those calibration solutions, and their associated uncertainties, which are required as input parameters for the second step of the project – the calibration of the mass spectrometer, and the determination of the isotopic composition of the three IRM candidates.
2. Methods, instrumentation, and software
2.1 Uncertainty budgets
Estimations of uncertainties of all masses in the calibration mixtures are the central task in this project. All estimations of uncertainties are based strictly on the principles described in the Guide for the Expression of Uncertainty in Measurement (GUM).19 In essence, those guidelines advise us to collect all information regarding the uncertainties of all experimental input values, and then propagate the respective probability distributions all the way to the final result through the applicable evaluation formulae. For this purpose, a number of mathematical approaches can be used. Practically, uncertainties in this work are calculated using software (GUM Workbench, version 2.4, Metrodata GmbH, Weil am Rhein, Germany20). GUM Workbench uses a simplified method for the propagation of variances, which is strictly valid only if the equation that propagates those variances is sufficiently linear.This approach allows determination of the overall uncertainty of a resultant value based on the uncertainties of all input values, and to determine the largest contributors of uncertainty. If all input values are correctly represented, and the set of equations also represents all relevant “uncontrollable” systematic experimental influences (such as room temperature fluctuations), the resulting uncertainty can be assumed to adequately represent the uncertainty of the expectation value, and it can be expected that the two together span a range that contains the true value. Since the analysis allows determination of the largest contributors to the uncertainty of the final result, it can be used to reduce the uncertainty by improving the experiment and to get as close as practically possible to the true value. This work describes an improvement of experimental results based on such an analysis.
2.2 Isotopically enriched magnesium materials
Enriched specimens of the three isotopically enriched magnesium materials were obtained from Oak Ridge National Laboratory (ORNL) in March 2010. ORNL has an inventory of enriched magnesium materials that are stored in the oxidic form; for this work, those enriched magnesium oxides have been reduced by ORNL into the metallic form on our request.All three isotopically enriched materials were delivered sealed into individual glass tubes, and are accompanied by assay analysis reports covering isotopic enrichment and basic assay of metallic purity based on spark source mass spectrometry. The details of the materials are listed in Table 1.
| Parameter | “24Mg” | “25Mg” | “26Mg” | |
|---|---|---|---|---|
| a According to the data supplied by manufacturer ORNL. | ||||
| Appearance | 2 pieces | 10 pieces | 1 chip | |
| Mass of material | mg | 200 | 200 | 201 |
| 24Mg amount fractiona | mol mol−1 | 0.9992 | 0.0180 | 0.0039 |
| 25Mg amount fractiona | mol mol−1 | 0.0005 | 0.9787 | 0.0017 |
| 26Mg amount fractiona | mol mol−1 | 0.0003 | 0.0033 | 0.9944 |
The analytical data provided by ORNL, however, have an insufficient degree of accuracy for our purposes. Additionally, the purity analyses by ORNL only consider metallic impurities, leaving non-metals such as oxygen aside, which are significant impurities for the case of Mg. To remove non-metals, and to reduce metallic impurities to sufficiently low levels, the isotopes were further purified in this project using high vacuum (HV) sublimation. Since the supplied reports regarding chemical purity are extremely spotty, new purity analyses were obtained experimentally.
2.3 Laboratory containers
For storage of isotopically enriched materials in their metallic form, and for all acids and solutions, containers manufactured from the synthetic organofluorine polymer resins FEP (fluorinated ethylene propylene) or PFA (polyfluoralkoxy polymer) were used. Both FEP and PFA have a density of 2150 kg m−3.21,22Solid isotopically enriched materials were stored in 15 mL jars with screw caps (Savillex Corp.). Solutions were stored in PFA (Sanplatec Corp., Japan) or FEP (Thermo Scientific™, Nalgene™) bottles. All PFA and FEP containers have been newly purchased, and have never been used for storage of any other solutions. They were cleaned following a six-step purification protocol:
(1) Rinse inside and outside three to five times with ultrapure water (Milli-Q).
(2) Fill to 1/3 with 0.10 g g−1 HNO3 (p.a.); close bottle.
(3) Shake the filled bottle for at least 2 h.
(4) Heat the filled bottle on the hot plate (<4 h, 120 °C).
(5) After cooling: rinse five times with ultrapure water.
(6) Dry at 40 °C inside a PE storage bag with cap unplugged.
All bottles are kept individually in polyethylene (PE) re-sealable zipper storage bags for protection against dust and lint. They were either labelled directly (using transfer print stickers) or the storage PE bags have been labelled. Bottles are handled exclusively using cotton laboratory gloves to preclude fingerprints.
2.4 Purification of metals by high vacuum-sublimation
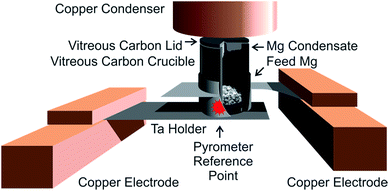
For purification of metals, we use a high-vacuum (HV) sublimation apparatus at BAM that was built by and obtained from Empa.7 In this apparatus, the feed magnesium metal is sublimated inside a small crucible system that consists of two parts – a crucible cylinder and a top lid, both machined from vitreous (“glassy”) carbon (see Fig. 2). A thermal gradient over this crucible/lid system is established from the outside by resistance heating of the tantalum frame that holds it. The complete setup is housed in a high vacuum (base pressure approx. 1 × 10−8 hPa). The feed metal at the heated base of the crucible sublimates and condenses on the cooler lid, which acts as the primary condenser. Lower-boiling metallic impurities of the feed material also condense in a chilled copper cylinder (diameter: approx. 2.7 cm) mounted approx. 0.5 cm above the top lid, acting as the secondary condenser. Higher-boiling impurities ideally remain in the residue on the bottom of the crucible. Gaseous impurities are evacuated.The vitreous carbon material used is Sigradur® G (HTW GmbH, Thierhaupten, Germany) with low impurity levels. According to communication from the manufacturer, the ash content of Sigradur® is 0.000038 g g−1; the main contents of the ash are silicon (25%) and calcium (20%); magnesium was found to be below 0.2%.
The tantalum holder systems are custom made using electrical erosion and laser beam welding by workshops at Empa, Technical University of Berlin (Germany), or DESY (Zeuthen, Germany); starting from semi-finished products: tantalum foils (0.3 mm) and tubes (O.D. 14 mm, wall 0.5 mm), obtained from Plansee SE, Reutte, Austria.
This tantalum holder is clamped onto chilled copper electrodes. Together with the chilled copper block secondary condenser, those chilled electrodes help to counter the resistance heating, and thereby establish the thermal gradient over the crucible system that is required for sublimation; the upper part of the tantalum holder is closer to the electrode, which results in the upper part of the tantalum holder getting less warm during heating than the lower base. The electrodes are mounted on chilled HV-high current feedthroughs (Trinos Vakuum-Systeme GmbH, Pfeiffer Vacuum, Göttingen, Germany).
This whole sublimation apparatus is housed in a cylindrical steel vacuum receiver (V = 53 L), topped with an O-ring-sealed flange. The base plate of the chamber is welded onto the vessel; the chilled vacuum high-current feedthroughs that carry the sublimation setup (Fig. 2) are mounted to this bottom flange. Various instruments are attached to this chamber via different flanges, typically using KF-seals. The vacuum receiver is evacuated via an air-cooled turbo-molecular drag pump (Pfeiffer Vacuum, TMU260), using a membrane pump (Pfeiffer Vacuum, MD 4T) as the first pumping stage. The pressure inside the vessel is determined by two vacuum gauges (Balzers), one Pirani thermal conductivity gauge (TPR250) and a cold cathode gauge (IKR250) for the fine vacuum and the high vacuum ranges, respectively.
The temperature of the crucible system is controlled by an intensity ratio pyrometer (model IGA 120, impact GmbH) focused at a reference point at the front of the tantalum holder from the front side of the vacuum vessel through a quartz window. In order to reach a predefined temperature inside the crucible, the temperature at the reference point must be several ten degrees higher (as an example, for one holder/crucible combination, the difference was approx. 50 °C for a sublimation temperature of 520 °C). Since the tantalum holder frame has a low resistance, a low voltage/high current galvanic power supply is used for resistance heating (power station pe2050, plating electronic GmbH, Denzlingen, Germany); a typical value for the heating is 1.0 V, 120 A to achieve a temperature approx. 510 °C inside the vitreous carbon crucible; those values also are subject to larger variations between individual tantalum holders.
After sublimations, the chamber is backfilled with oxygen-free argon (purity 99.999%, Linde; residual oxygen filter “O2-free”, Air Liquide).
Two main factors determine the ideal sublimation temperature: (1) the physical and chemical properties of the metal to be sublimated, and (2) the slightly differing geometries of the individual tantalum holders due to the manual production, which result in slightly differing heat conductivity properties; two tantalum holders showed very similar properties (sublimation of 200 mg Mg within 6 h at 560 °C at the reference point), while a third one that was used in the final sublimation rounds showed significantly different properties (sublimation of 200 mg Mg within 6 h at 615 °C measured at the reference point).
For one tantalum holder, the following limiting practical conditions to sublimate 200 mg Mg quantitatively were found: at 520 °C, quantitative sublimation required more than 24 h, while at 560 °C, the sublimation completed within 6 h. The separation quality depends on the sublimation temperature and the number of sublimation cycles. Note that sublimation may shift the isotopic enrichment due to mass fractionation effects.
2.5 Weighing procedures
Beside purity determination, the determination of absolute mass by means of weighing was the central practical exercise in this work, since all digestion, dilution and mixing steps have been controlled gravimetrically. The corresponding protocols were discussed in detail recently23 and were applied here in essence. Four analytical balances have been used for different weighing procedures, three of them electronic force compensation comparator balances at BAM with various resolutions and allowed maximum loads (Mettler Toledo UMT2, AX205 and Sartorius LC5101S); the fourth balance was a mechanical beam balance at PTB (Mettler H315):In all weighings, the electronic balances have been adjusted using the internal adjustment weights. The balances have stainless steel weights with a nominal density of 8000 kg m−3 (electronic balances) or 7950 kg m−3 (H315). Further details of the balances are listed in Table 2.
The analytical balance UMT2 was used for the determination of the magnesium masses. AX205 was used for weighing the empty PFA bottles, for weighing the filled bottles, and for difference weighing of solutions during the digestion, dilution and mixing process. LC-5101S was used for weighing the solutions, and the filled PFA bottles, particularly during the preparation of acids, and the parent solutions, while FCB12K0.1B was used only for one large setup of dilute HNO3 (5 L of 0.02 g g−1, see below). The balance H315 was used at PTB for the preparation of the first series of calibration mixtures (not further described herein).
External certified weights of OIML class E2 of various masses ranging from 20 mg to 5 kg have been used in this project. Transfer weights with masses ≤ 1 g are made from Neusilber (German silver) with a nominal density of 8600 kg m−3; those with masses > 1 g are made from stainless, non-magnetic steel with a nominal density of 7950 kg m−3. All E2 weights are certified every four years by the Berlin-Brandenburg State Office for Metrology, and had last been verified for this project on 07/11-2013.
In case of important, non-repeatable weighings on the comparator balance UMT2, E2 weights (100 mg and 500 mg) are weighed additionally as a second means to allow calibration of the balance.
As the balances show different characteristics, the weighing protocols vary slightly, but follow a general procedure: the sample to be weighed was placed in the centre of the weighing platform, and it was waited until the mass reading had stabilized; in the case of balance UMT2, this typically took 30–40 s; the first stable value (as indicated by the balance's own electronics) was always used. In the case of AX205 and LC5101S, the value was followed for a certain time, and only if it had been stable for 30 s (at the AX205), or 10–15 s (LC5101S), the reading was accepted and recorded. Then, the sample was removed, and the balance was given time to return back to the tare value, which was also recorded, and the average between zero and tare was subtracted from the weighing result. In case of UMT2 no significant difference was observed.
Weighings were typically repeated for a number of times.
Solutions in bottles are stored under full weight-control, by recording the weight as well as the climate data before and after the bottle has been opened and solution has been withdrawn. This allows correcting the mass fractions for evaporation effects.
The electronic balances are so sensitive towards electrostatic charges on the PFA/FEP containers, particularly when they are empty, that practical measures have to be taken to obtain precise and true weighing values. At BAM, we apply a nitrogen ring ionizer/blow-out gun (RI65P7187500, Haug GmbH, Leinfelden-Echterdingen, Germany) to blow ionized nitrogen (N2 5.0, Linde) over the containers, and thereby remove electrostatic charge prior to any weighing procedure. Successful removal of charges is assumed when the balance reading is stable over a period of more than 30 seconds; if charges have not been removed successfully, the weighing value tends to creep during this time frame; in this case, repeated weighing results exhibit significant scatter.
The mechanical balance H315 is less sensitive towards electrostatic charging. For its case, a piezoelectric anti-static instrument (Sigma-Aldrich ZEROSTAT 3) was sufficient to reduce electrostatic charges, and to remove dust and lint in parallel.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 kg m−3) would appear heavier on this balance by 0.088‰ under the same conditions. In order to obtain absolute masses, the weighing values need to be corrected for the influence of buoyancy of the surrounding medium, typically air. For transformation of a weighing value, W, into a true mass m, a buoyancy correction factor K has to be calculated, such that:23
300 kg m−3) would appear heavier on this balance by 0.088‰ under the same conditions. In order to obtain absolute masses, the weighing values need to be corrected for the influence of buoyancy of the surrounding medium, typically air. For transformation of a weighing value, W, into a true mass m, a buoyancy correction factor K has to be calculated, such that:23| m = KW | (1) |
This correction factor can be readily calculated once the densities of sample (ρi) and calibration weight (ρcal) are known, together with the air densities during calibration (ρair1) and weighing (ρair2):
 | (2) |
For the calculation of air densities as a function of climate data, a number of fitting functions exist. The following function is based on one of the most comprehensive data analyses to date,24 and has been applied in this work to calculate air densities from climate data:
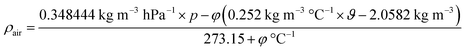 | (3) |
For determination of climate data at BAM, a calibrated device was used (Greisinger digital hydro-/thermo-/barometer GFTB200, GHM Messtechnik GmbH). At PTB, a calibrated reference measuring instrument (Testo 650 Testo AG, Lenzkirch, Germany) was used.
2.6 Determinations of solid and liquid densities
2.7 Liquid chemicals and reagents
The trace levels of the acids were later tested using ICPMS; for this purpose, the acids were concentrated by a factor of more than 10 using evaporation. The Mg blank level was determined as 19 pg g−1 for HNO3 and 48 pg g−1 for HCl. Other impurities are listed in Table S1 of the ESI.†
2.8 Analytical determination of impurities
All GDMS results shown here were obtained using the instrument “Element GD” (Thermo Fisher Scientific). This instrument is equipped with a Grimm type high flow ion source, which was used in constant current mode at an Ar+ ion current of 70 mA. Before the start of each measurement sequence, the sample was pre-sputtered to clean the sample surface from oxide layers and adsorbed impurities. A measurement sequence typically consisted of five to ten measurements in DC source mode. All mass fraction data are calculated from the ion beam ratios based on relative sensitivity factors.32 For some elements, calibrations using internal reference materials (BAM AKP207 & 208) were conducted.
Magnesium shows a tendency to spark in the GD source, which leads to material overload in the mass spectrometer and unspecific, transient signal spikes of the material that can saturate the mass spectrometer and detector, and thereby severely influence the integrated detector signal, specifically of low-content impurities.32 Such sparks, however, only show up in the signal of one isotope every tenth to hundredth sample, and can be easily spotted as outliers, since the intensity spikes are drastic.
Since the sublimated Mg samples are too small for the standard sample holder of the Element GD instrument, they were compressed into steel disk sample holders (BAM, I.D. 11 mm) using a hydraulic press (90 kN, 1 min). The steel piston of this press tool was carefully cleaned after each sample.
All ICPMS analyses were performed on sector field single collector instruments of type Element XR or Element 2 (Thermo Fisher Scientific). Instrument Element 2 is equipped with a jet interface, while the Element XR offers an additional Faraday cup detector (intensity range up to 1012 s−1). Both instruments were used in standard configuration applying an ASX-520 autosampler (CETAC Technologies), a MicroMist nebulizer (200 μL min−1), and a cyclonic spray chamber (both GlassExpansion). For external calibration, a commercial multi-element standard (ICP IV standard, Merck) and in-house prepared multi-element standards were used. Standard addition was conducted for selected elements using mono-elemental solutions of the same sources. Yttrium was used as an internal standard (Merck Certipur).
2.8.2.1 Zinc quantification by IDMS. In the case of the most abundant impurity in the isotopically enriched magnesium materials, zinc, standard calibration techniques provided insufficient degrees of uncertainty; in this case, isotope dilution mass spectrometry (IDMS) was applied as the reference method using the double IDMS calibration approach.33,34
For this purpose, an existing protocol for the quantification of zinc in aluminium was modified particularly for the separation of Zn from the metallic matrix. The analyte, Zn, is separated from the matrix, Mg, using anion exchange chromatography (mini-column AG 1-X8, chloride form, 200–400 mesh, Bio-Rad Laboratories Inc.), where Zn is retained as chloride complex in hydrochloric acid solution, while the Mg matrix runs through. The Zn was completely separated from Mg with near quantitative recovery (>90%). The IDMS analysis was conducted using a 67Zn spike, which was calibrated against an in-house primary calibration solution prepared from a high-purity material (candidate BAM-Y014). The 66Zn/67Zn isotope ratios were measured using instrument Element 2 in standard configuration and medium resolution mode. The isotope ratio reproducibility was 0.3%. Uncertainty calculations were carried out based on the double IDMS equation using GUM Workbench.
3. Design of the approach: minimize uncertainty
3.1 Uncertainty budget
The resultant values in this project are the masses (after purity-correction) of each isotopically enriched material in the binary mixtures. Those values and their uncertainties are to be calculated using GUM Workbench; they are based on the following input quantities:• Weighing values measured by calibrated balances,
• Solid and liquid densities,
• Climate data (temperature, pressure, and relative humidity), and
• Total purity of the isotopically enriched materials.
Those mass ratios of the enriched materials in the binary mixtures together with the isotopic enrichments (which need to be determined in a second project based on mass spectrometry) result in the gravimetric isotope ratios, which are required for the calibration of the mass spectrometers in the second part. At this point, the isotopic enrichments of the commercial “24Mg”, “25Mg” and “26Mg” materials will be determined using the recent analytical solutions to the underlying equation system,8 and in addition, using the established iterative approach.
This shows that the uncertainty of the mass ratios of the enriched materials in the binary mixtures predetermines the uncertainty of the gravimetric isotope ratios, and consequently the uncertainties of the K-factors obtained in the calibration approach by synthetic isotope mixtures (binary mixtures). Therefore, the uncertainties of all quantities listed above have to be minimized. This requires an optimization of the dilution and blending procedures.
3.2 Constraints
In the minimization of the relative uncertainties of the binary mixtures used for calibration, two primary constraints had to be obeyed in this project:(1) The available amount of isotopically enriched materials, and
(2) The available balances with their maximum loads, and their relative uncertainties.
The enriched magnesium materials, 200 mg each, had been purchased prior to this project. Thus, this value was considered as a fixed constraint to be used in the design of minimizing the overall uncertainty for the binary mixtures. This meant to minimize the uncertainty of the purity statement, as well as achieve the best possible weighing results for determining the absolute mass of the isotopically enriched materials and the absolute masses of all dilutions and blending. For this purpose, we have applied the best available commercial balances whenever possible: e.g. Mettler-Toledo UMT-2 for weighing the sublimated isotopes, Mettler-Toledo AX-205 for dilutions and Sartorius LC-5101S for preparing diluted acids.
Additionally, the absolute amounts and mass fractions of parent solutions and intermediate dilutions were designed to make use of the maximum possible range of the best available balance; the approach was designed not to exceed the maximum load of this best possible balance, in order not to be forced to use a balance with larger maximum load, but lower relative accuracy.
4. Results
4.1 Preparatory work
A number of preparatory steps are named briefly in this section; extended descriptions have been moved to the ESI.† Preparations of dilute acids are described in section S2 in the ESI,† including tables about the exact mass fractions of the acids used and associated uncertainties. Determinations of densities of liquids and solids (for buoyancy correction) are described in section S3 in the ESI,† including tables of results and associated uncertainties.4.2 Purification of magnesium isotopes; weighing
Approx. 200 mg of the test material was used for each round of test sublimation (the same amount as in the sublimation of the enriched materials). The test material was filled into the sublimation dish (vitreous carbon crucible with the top lid); the sublimation dish was transferred into the sublimation chamber, evacuated (<10−7 hPa), and then heated for 15 min to below 300 °C to remove adsorbed air and moisture; then, the temperature was increased to the sublimation condition, where it was held constant for a predetermined period. The purified material was collected as a condensate at the top lid of the vitreous carbon crucible, forming a disk of approx. 8 mm in diameter. Sublimation was always conducted quantitatively; the time to achieve quantitative sublimation was extrapolated from a number of incomplete sublimations in the first stage of those tests. A photo of the lid with the removed condensate disk and a microscopic image of a typical condensate disk are shown in Fig. 3.
 | ||
| Fig. 3 Sublimate disk of magnesium (approx. 8 mm in diameter). Left: after removal from the lid. Right: microscopic image. | ||
GDMS was used to determine the purity of the test material and the condensates obtained during the test sublimations; details of the GDMS analysis of magnesium specimen can be found in Section 2.8 and in ref. 32.
All data considered here are from the initial fraction of the sublimation (the fraction that condensed first, in direct contact to the vitreous carbon lid), but agree with the data observed at the flipside of the condensate disk, except for Zn (where a slight fractionation over the course of sublimation is observed); approx. 60 s pre-sputter time was allowed for the GDMS to remove possible contaminants of the compression tool from the sample. The conversion from signal intensity to mass fraction was based on Mg reference materials where certified values for the impurity were available, and based on standard-RSF otherwise. This is completely sufficient for following the purification by individual sublimation cycles.
The test material was found to contain 15 impurities at levels above 1 mg kg−1, which were focused on during the optimization. Parameters initially tested for their influence on the purification result were the sublimation temperature and the number of sublimation cycles.
4.2.2.1 Influence of sublimation temperature on purification. The practical sublimation temperature depends on the time it takes for quantitative sublimation, and on the purification result. Very high temperatures are expected to prevent the formation of a suitable temperature gradient and thus degrade the quantitative collection and the purification. On the other end of the scale, at the lowest practical sublimation temperature, 510 °C at the reference point, it needed more than 30 h to quantitatively sublimate the 200 mg Mg. With the highest tested temperature, close to 570 °C, sublimation was completed in 5 h. The recoveries of all tested conditions were typically >98%.
Fig. 4 shows the purity of the condensed magnesium as a function of sublimation temperature and compared to the raw material (at the left side). The trace levels of most impurities were reduced to ≤1 mg kg−1 after just one cycle, at any viable temperature. Very obviously, the purification result depends only marginally on the temperature; and very clearly, temperatures towards the high end of our scale, where sublimation is fastest, do not result in deterioration of the separation result compared to the low temperatures, where sublimation is slow. Therefore, it was concluded to use 560 °C at the reference point (≈510 °C inside the crucible) as a viable sublimation temperature.
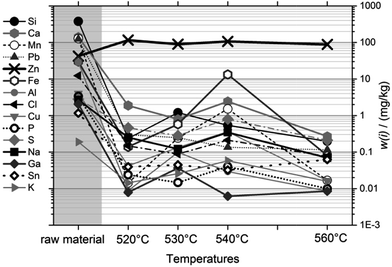 | ||
| Fig. 4 Purification, presented as the mass fractions of 15 impurities, as a function of sublimation temperature. Temperatures given were measured at the reference point. | ||
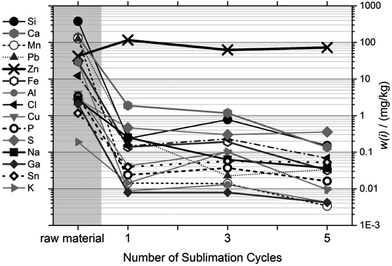
4.2.2.2 Influence of number of cycles on purification. The effect of repeated sublimation on the purity of the condensed magnesium is shown in Fig. 5. While the results indicate that additional purification cycles can improve the purification result, the effect of later sublimation cycles compared to the first cycle is small. Since, however, the recovery per cycle is close to 100%, it was decided to use five sublimation cycles at 560 °C.
The removal of zinc and cadmium in a sublimation process alone could not be improved significantly by a variation of the approaches (such as long-time tempering slightly below sublimation condition to allow the zinc and cadmium to transfer from the magnesium matrix to the surface, followed by fractional sublimation with discarding the initial 10% of material, or other such physicochemical approaches); it appears that gas phase thermodynamics of magnesium, zinc and cadmium are too similar. Also, the removal of the slightly lower-boiling zinc from the liquid phase magnesium (distillation) was not successful: magnesium was melted in the crucible in an inert (argon) atmosphere; however, the loss of magnesium was high, while the purification concerning zinc was negligible. Alternative approaches to the physical methods were briefly tested, such as the approach to capture zinc (and cadmium) using possible alloying components, which melt below the sublimation temperature, but evaporate at much higher temperatures; the metal tested is tin. While the experiments indicate that this approach could scavenge up to approx. 25% of the zinc content in one cycle, the loss of material was high (20%), and not justifiable by the performance.
As none of the tested approaches yielded a significant separation efficiency for zinc and cadmium with a good recovery in parallel, it was decided to better quantify those two levels after the purification using sufficiently precise analytical techniques: IDMS was chosen as the method to determine the zinc content, while for cadmium and all other impurities, external calibration ICPMS was considered to be sufficiently accurate.
After the last sublimation cycle, the mass of the sublimate disk was determined by using the ultra-fine balance UMT2. This value is one of the most important resultant values in this project and was determined with utmost care. The enriched magnesium materials are expected to be virtually free from oxygen and other reactive gases after the high-vacuum sublimation. In order to prevent oxygen from reacting with the magnesium, the following steps (after the sublimation) were all carried out using oxygen-free argon.
The timing of steps during sublimation, and until the finishing of weighing, was carried out using a precise time protocol; the steps following the completion of sublimation were carried out with time precision better than 1 min. After the heating had been switched off, the sample was left to cool for 60 min before the vacuum was broken. Switching off the pumps and venting the system with argon took another 14 min before the top lid of the sublimation apparatus was removed. The vitreous carbon crucible was then transferred to the operating desk in a stream of flowing argon; the top lid was lifted up and the condensate was removed from the lid using a steel forceps – all protected by a flowing argon atmosphere. The free sample was then visually inspected to be free from sublimation residue and other particles, and then transferred to a cleaned PFA jar, that was filled with argon, and closed. The whole process from opening the sublimation apparatus to the PFA jar being closed was engineered to take 2 min. The sample in the PFA jar was then transferred to the balance room, where it was put next to the balance for another 17 min to acclimatize.
Three calibration weights (20 mg, 100 mg, and 500 mg) of OIML class E2 were weighed ten times each during idle time less than one hour before the weighing of each magnesium sublimate disk. Thereafter, weighing of the sublimate disks started. Ten values were recorded in the first round, followed by a second round immediately thereafter. All twenty values exhibited no linear drift (which could be an indication either for balance instabilities or for reactions with air – e.g. oxidations). Table 3 lists the first ten values, which were used to determine the absolute mass of the three isotopically enriched materials. Those ten weighings were averaged, recalibrated using the bracketing and interpolation approach described in Section 2.5.3 (based on the E2 external weights), and finally corrected for the influence of buoyancy using the method described above to yield the physical mass. The ten individual weighing values, their average and standard deviations, the air densities calculated based on the recorded climate data, and the resultant buoyancy correction factors are compiled in Table 3; also compiled is the resultant mass of each isotope. The individual weighing values for each material do not exhibit a detectable trend, which could be due to effects such as temperature change, reactions with oxygen or moisture, possible uptake of dust, or the loss of substance due to the handling in between each weighing step. This fact is reflected in small standard deviations between the individual weighings, which are much lower than the respective balance uncertainties.
| Weighing date | “24Mg” | “25Mg” | “26Mg” |
|---|---|---|---|
| 28/01/2014 | 29/01/2014 | 27/01/2014 | |
| Weighing | Weighing values | ||
| a Conventional mass. | |||
| 1 | 177.2927 mg | 173.1579 mg | 181.7187 mg |
| 2 | 177.2928 mg | 173.1582 mg | 181.7188 mg |
| 3 | 177.2929 mg | 173.1583 mg | 181.7186 mg |
| 4 | 177.2929 mg | 173.1584 mg | 181.7181 mg |
| 5 | 177.2932 mg | 173.1587 mg | 181.7182 mg |
| 6 | 177.2934 mg | 173.1586 mg | 181.7181 mg |
| 7 | 177.2930 mg | 173.1592 mg | 181.7180 mg |
| 8 | 177.2930 mg | 173.1587 mg | 181.7179 mg |
| 9 | 177.2927 mg | 173.1586 mg | 181.7177 mg |
| 10 | 177.2925 mg | 173.1588 mg | 181.7181 mg |
| Average (N = 10) | 177.29291 mg | 173.15854 mg | 181.71822 mg |
| s (k = 1) | 0.00026 mg | 0.00036 mg | 0.00036 mg |
| W after interpolation | 177.29363 mg | 173.15923 mg | 181.71931 mg |
| Air density | 1.17625 kg m−3 | 1.18258 kg m−3 | 1.16970 kg m−3 |
| Solid density | 1707.3 kg m−3 | 1777.4 kg m−3 | 1848.7 kg m−3 |
| Correction factor K | 1.0005527 g g−1 | 1.0005282 g g−1 | 1.0004971 g g−1 |
| m after correction | 177.39162 mg | 173.25068 mg | 181.80965 mg |
| U (k = 2) after corr. | 0.0047 mg | 0.0047 mg | 0.0046 mg |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Certificate (E2) | Transfer weights, masses determined (N = 10) | ||
| m c = 20.004a mg | 20.00360 mg | 20.00385 mg | 20.00342 mg |
| U (k = 2) = 0.003 mg | |||
| m c = 99.995a mg | 99.99381 mg | 99.99370 mg | 99.99341 mg |
| U (k = 2) = 0.005 mg | |||
| m c = 500.004a mg | 499.99585 mg | 499.99629 mg | 499.99578 mg |
| U (k = 2) = 0.008 mg | |||
Table 3 also compiles uncertainties U (for k = 2) based on the UMT2 balance calibration using the E2 weights as discussed in Section 2.5.3. The weighing values, the certified conventional masses and the expanded uncertainties of the E2 weights are also listed in Table 3.
For the three masses of the enriched materials, the resulting expanded uncertainty U (k = 2) was equal or less than 0.0047 mg in all cases based on the calibration.
4.3 Dissolution, and preparation of primary stock solutions
After weighing, the purified materials were immediately transferred into PFA containers using the same PE forceps applied during weighing (to move the materials onto and away from the ultra-fine balance tray). Prior to the transfer of the materials, the empty PFA bottles had been weighed ten times using balance AX-205; climate data have been recorded and buoyancy was corrected using the published value for PFA and FEP density (2.150 kg m−3, DuPont21,22).The magnesium metal was dissolved under mild conditions using dilute nitric acid (0.06 g g−1 HNO3); the following aspects were considered: the reaction between HNO3 and magnesium follows eqn (4) under mild conditions, with virtually no alternative reactions – such as HNO3 decomposition, as confirmed in prior test runs:
| Mg + 2HNO3 → Mg(NO3)2 + H2↑ | (4) |
The magnesium is oxidized by the protons, which are reduced and are transformed into the gaseous hydrogen (H2), which leaves the reaction vessel. The other product is magnesium nitrate Mg(NO3)2. In essence, two molecules of HNO3 are consumed per magnesium atom. Consequently, this reaction changes the pH value of the solution. This has to be accounted for when aiming at a final acid strength of 0.02 g g−1 HNO3. For this purpose, the stoichiometric consumption of HNO3 according to eqn (4) is calculated, and then the additional amount of HNO3 required for achieving 0.02 g g−1 HNO3 in the final solution is added. The total mass of HNO3 is then converted into the required amount of 0.06 g g−1 HNO3 by using the exact mass fraction of the 0.06 g g−1 acid (as determined in section S2.2 in the ESI†).
This calculated amount of 0.06 g g−1 HNO3 was added to the magnesium using PFA containers by difference weighing. The mixture was left standing overnight to complete the dissolution. Slightly brownish vapours above the liquid were observed, indicating a slight decomposition of the acid; also, some droplets of liquid condensed on the inner PFA walls due to the excess reaction heat.
After the completion of the dissolution, the weights of the solutions were determined using balance AX-205 as informational values. The resulting masses are only slightly below the expected values, which is mainly due to the loss of water and eventually a minimal HNO3 decomposition. The solutions were filled up with ultra-pure water such that the target mass fraction of magnesium and of nitric acid was reached. Then, the total mass of solution was determined as an informational value using balance LC-5101S (which is not precise enough in this range of total mass to achieve results that are sufficiently accurate). Directly before the first use (1st dilution approach), the mass was determined again using balance H315 at PTB. Table 4 reflects all the steps and the associated data required to obtain those primary stock solutions of the enriched materials. Then, solution was withdrawn twice (once for analysis and once for dilutions).
| “24Mg” | “25Mg” | “26Mg” | |
|---|---|---|---|
| a Based on the mass fraction of 0.06 g g−1 HNO3: (5.9979 ± 0.0082) g cm−3. b Weighing value of solution after digestion minus the mass of magnesium contained in the solution. c Mass difference between acid filled in and mass of acid determined later minus the calculated stoichiometric mass loss due to H2 loss. | |||
| Mass PFA bottle/g, N = 10 | 68.607305 | 68.141224 | 68.271606 |
| Mass of Mg metal/g, N = 10 | 0.1773916 | 0.1732507 | 0.1818097 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Setup calculations | |||
| Target total mass/(g) | 177.392 | 173.251 | 181.810 |
| Mg target mass fraction/(μg g−1) | 1000 | 1000 | 1000 |
| HNO3 target mass fraction/(g g−1) | 0.020 | 0.020 | 0.020 |
| Required HNO3 (dissolution)/g | 0.9321 | 0.8744 | 0.8822 |
| Required HNO3 (final sol.)/g | 3.5479 | 3.4651 | 3.6363 |
| Sum required mass of HNO3/g | 4.4800 | 4.3395 | 4.5184 |
| Required mass 0.06 g g−1 HNO3a/g | 74.692 | 72.349 | 75.333 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Actual setup, HNO 3 addition | |||
| Mass of 0.06 g g−1 HNO3/g | 74.7452 | 72.3888 | 75.4209 |
| Mass HNO3 after digestionb/g | 74.7138 | 72.3562 | 75.4028 |
| Expected mass loss due to H2/g | 0.0149 | 0.0140 | 0.0141 |
| Obs. additional mass lossc/g | 0.0165 | 0.0186 | 0.0039 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Actual setup, fill-up with water | |||
| Mass of water added/g | 102.803 | 100.965 | 106.557 |
| W total, bottle + solution/g | 246.085 | 241.431 | 250.201 |
| Total mass of solution/g | 177.687 | 173.494 | 182.142 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Final solution before 1 st use | |||
| W total, bottle + solution/g | 246.0391 | 241.4227 | 250.1934 |
| Total mass of solution/g | 177.6399 | 173.4850 | 182.1342 |
| Purity, enriched material/(g g−1) | 0.999909 | 0.999740 | 0.998953 |
| Mg mass fraction/(mg kg−1) | 998.5113 | 998.3924 | 997.1760 |
| HNO3 mass fraction/(g g−1) | 0.019995 | 0.019992 | 0.019996 |
Note that the mass fraction of magnesium in the obtained solution is purely a function of the original mass of magnesium in the bottle, its purity, and the total mass of solution. The latter is subject to change due to evaporation of the solvent, and therefore, masses before and after each withdrawal were recorded carefully to allow correction for evaporation.
Table 4 lists all calculated mass and mass fraction data directly before the first withdrawal. These data show that the mass fractions of magnesium were very close to the target of 1000 mg kg−1. The nitric acid mass fraction is also very close to the target value (0.02 g g−1); since this value mainly impacts the density (and thus buoyancy correction), it is, however, of minor significance here.
The corresponding uncertainty is calculated as described in Section 2.1 considering the following factors:
• The uncertainties of weighing values used as inputs, which are based on the balance calibration protocol for all values.
• Densities used as input for buoyancy corrections are either based on measurements (pycnometry, hydrostatic weighing) with full uncertainty budgets, or on tabulated data (PFA, balance weights, water, HNO3 other than 0.02 g g−1).
• The uncertainties of air densities are based on an uncertainty budget using eqn (3), and the uncertainties for the input values (as listed in Table 5).
| Parameter | “24Mg” | U | Typeb | Source |
|---|---|---|---|---|
| a Uncertainties for values with normal (Gaussian) distribution are denoted for coverage factor k = 2; values with rectangular distribution are denoted as the rectangle function's half widths. b Type A (observation), Type B: “n” denoting normal distribution, “r” denoting rectangular distribution. Type “R”: intermediate or final result. | ||||
| Weighing, empty PFA bottle | ||||
| W (PFA bottle)/g | 68.57936 | 0.00023 | A | AX-205 |
| Temperature ϑ/°C | 21.1 | 2 | B(n) | Upper bound |
| Rel. humidity φ/% | 29.6 | 6 | B(n) | Upper bound |
| Abs. pressure p/hPa | 1014.1 | 10 | B(n) | Upper bound |
| ρ PFA/(kg m−3) | 2150 | 100 | B(r) | Upper bound |
| ρ cal/(kg m−3) | 8000 | 100 | B(r) | Upper bound |
| ρ air/(kg m−3) | 1.198 | 0.015 | R | Eqn (3) |
| Buoyancy corr. K/(g g−1) | 1.000408 | 0.000030 | R | Eqn (2) |
| m (PFA bottle)/g | 68.6073 | 0.0021 | R | Eqn (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Weighing, purified, enriched 24 Mg isotope | ||||
| W (“24Mg” material)/g | 0.17729363 | 0.00000468 | A | UMT-2 |
| Temperature ϑ/°C | 22.4 | 2 | B(n) | Upper bound |
| Rel. humidity φ/% | 18.8 | 6 | B(n) | Upper bound |
| Abs. pressure p/hPa | 999.6 | 10 | B(n) | Upper bound |
| ρ (“24Mg” material)/(kg m−3) | 1707 | 17 | B(n) | PTB meas. |
| ρ cal/(kg m−3) | 8000 | 100 | B(r) | Upper bound |
| Purity, w (Mg)/(g g−1) | 0.999906 | 0.000032 | R | Table 6 |
| ρ air/(kg m−3) | 1.176 | 0.014 | R | Eqn (3) |
| Buoyancy corr. K/(g g−1) | 1.0005423 | 0.0000098 | R | Eqn (2) |
| m (“24Mg” material)/g | 0.1773916 | 0.0000047 | R | Eqn (1) |
| m net (“24Mg” material)/g | 0.1773755 | 0.0000062 | R | Eqn (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Total mass of solution before 1 st use | ||||
| W total (bottle + sol.)/g | 246.0391 | 0.0010 | A | H315 |
| Temperature ϑ/°C | 21.7 | 2 | B(n) | Upper bound |
| Rel. humidity φ/% | 34 | 6 | B(n) | Upper bound |
| Abs. pressure p/hPa | 1004 | 10 | B(n) | Upper bound |
| ρ sol/(kg m−3) | 1014.9 | 1.5 | B(r) | Pycnometer |
| ρ cal/(kg m−3) | 7950 | 50 | B(r) | Upper bound |
| ρ air/(kg m−3) | 1.182 | 0.015 | R | Eqn (3) |
| Net W (solution)/g | 177.4593 | 0.0011 | R | Difference |
| Buoyancy corr. K/(g g−1) | 1.001017 | 0.000013 | R | Eqn (2) |
| m (solution)/g | 177.6399 | 0.0028 | R | Eqn (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Mass fraction of Mg before 1 st use | ||||
| Mg mass fraction/(mg kg−1) | 998.511 | 0.039 | R | Eqn (6) |
• Purity of the solid magnesium, based on the analytical result (see below), including uncertainty.
The net mass of a metal is based on the weighed mass and purity:
| mnet = mgross × wpur | (5) |
The mass fraction of magnesium in the solution is simply based on the net mass of magnesium metal, and the total mass of solution:
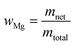 | (6) |
Table 5 lists the uncertainties used as the input to calculate the uncertainty for the parent solution of “24Mg”.
The resulting uncertainty budget for the Mg mass fraction in the parent solution of “24Mg” is exemplary displayed in Fig. 6 (left side); the uncertainty budgets for “25Mg” and “26Mg” are very similar. The Mg mass fraction in this solution has a value of 998.511 mg kg−1, and an expanded uncertainty U (k = 2) of 0.039 mg kg−1, which corresponds to 0.0039% (Table 5). The single contributors are listed in Table 5. The visualization of the budget in Fig. 6 shows clearly that the major contributor to the overall uncertainty is the uncertainty associated with the weighing of the isotopically enriched materials, which accounts for 46.7% of the overall uncertainty, followed by the uncertainty of the purity of the isotopically enriched materials accounting for 29.6% of the overall uncertainty. Thus, the weighing and the purity determination of the purified, enriched materials are the limiting factor for preparing synthetic isotope mixtures in this case. All other parameters contribute no more than 25% to the total uncertainty. The overall total value of the uncertainty is excellent, as will be discussed later.
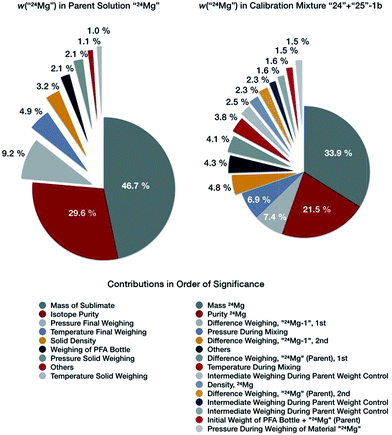 | ||
| Fig. 6 Uncertainty budgets for the mass fraction of “24Mg” in the parent solutions “24Mg” (left), and in the binary calibration mixture “24” + “25”-1b (right side). | ||
4.4 Determination of purity
To this point, the masses of the enriched magnesium materials have not been corrected for the materials' actual purity, which is smaller than 1 g g−1. Since not all the mass weighed out is, in fact, magnesium, the purity of the material needed to be determined to correct the data, and thereby establish the actual magnesium mass fractions in the primary solutions that have been created.As described above, the purity of the enriched materials can only be determined in the primary solution, as no additional material can be spared for GDMS measurements, and the integrity of the sublimated materials should not be touched. Therefore, the mass fractions of 67 elements in the primary solutions were determined by ICPMS as described in Section 2.8.2. Zinc is the dominant metallic impurity in all three isotopically enriched materials, and was determined by IDMS to achieve low enough uncertainties. The noble gases (He, Ne, Ar, Kr, and Xe) and hydrogen were not expected. For oxygen and nitrogen sound estimates were made, which are explained below. Carbon and halogens (F, Cl, Br, and I) were completely separated by the sublimation, which was verified by the GDMS measurements in the natural magnesium material; this applies also to yttrium, which was used as the internal standard in ICPMS. Radioactive elements (Tc, Pm, Po At, Rn, Fr, Ra, Ac, and Pa) – besides U and Th (which have been measured) – were not expected.
The oxygen and nitrogen mass fractions cannot be quantified by ICPMS in the solutions; GDMS and other techniques such as carrier gas hot extraction are not allowed as the integrity of the purified materials should not be touched. Therefore, sound estimates were made. Generally, oxygen and nitrogen are expected to have been removed during HV sublimation (pressure around 10−7 hPa); however, there was a risk of oxygen and nitrogen contamination by short contact to air during handling between the last sublimation and the weigh-out procedure. To preclude this, the isotopes were handled under the argon gas flow during all manipulations and were stored in argon-filled PFA jars during equilibration for weighing.
Additionally, a strictly timed protocol was adhered to, to admit all three enriched materials to the risk of coming into contact with air for the same amount of time, and thus results in similar oxygen and nitrogen uptake at trace levels, which would later cancel in their impact on the end results. The timing for all materials was as follows: backfilling the HV sublimation apparatus after cooling took 14 min; removal from the lid in flowing argon took 2 min until the sample was in the PFA jar under argon protective gas; then the jar was immediately transferred to the ultra-fine balance, and left there for 17 min for equilibration. The subsequent weighings do not indicate any systematic mass drift by a potential oxygen uptake due to the air contact during weighing (Table 3).
However, in order to account even for the small oxygen uptake during handling, data on typical oxide film thicknesses on pure magnesium in moist air were obtained from the literature, and transferred into a maximally conceivable upper limit. Nordlien and co-workers have studied the film thicknesses of magnesium oxide on freshly cleaved, pure magnesium using TEM for different conditions.36 The relevant growth condition that was chosen as comparable to this work (25–30 °C, 35–55% rel. humidity, 15–60 min exposure) led to a film thickness of 25 nm, which was composed of magnesium hydroxide (0.5 kg kg−1) and magnesium oxide (0.5 kg kg−1) according to XPS measurements.
Using the dimensions of the Mg sublimate disk (diameter 8 mm, thickness 3 mm), a total surface area of 1.76 cm2 could be estimated for it, which was increased to 3 cm2 to account for the corrugation of the surface. With the film thickness of 25 nm, an oxide film volume of 7.5 × 10−6 cm3, and a film mass of 22.2 μg using the average density of MgO and Mg(OH)2 (2.96 g cm−3) were obtained. The mass of oxygen in this film is 11 μg, which gives an oxygen mass fraction of 60 mg kg−1 for a disk of 175 mg.
Since, however, the actual conditions in this case were less harsh, and the fresh magnesium surface has been in touch only for very short moments to dilute air, the actual amount of oxygen in the sublimate disk at the time of weighing will be much lower, and not such an extensive film. Thus, it was decided to assume a quarter of the amount (15 mg kg−1) of possible film thickness, with a relative uncertainty of 100% as maximally conceivable values. For the case of nitrogen, no literature could be found on atmospheric reactions; experience with other high purity metals lets us set a conceivable limit of (3 ± 3) mg kg−1 for nitrogen.
Mass fractions of 68 elements were analysed; for 23 additional elements estimates were made, so that in total, mass fractions of 91 elements were used for calculation of purity. The complete list of results for all tested impurities is shown in Tables S7 and S8 in the ESI.†
The limit of detection (LOD) was calculated as three times the standard deviation of the blank, following the IUPAC definition; the limit of quantification (LOQ) was calculated as nine times the standard deviation of the blank. When a mass fraction below the LOD resulted from the measurements for a specific element, the value was set to the LOD value divided by two with a relative expanded uncertainty of 100%. Whenever a determined mass fraction of an element is above the LOD, but less than the LOQ, the value is taken as determined and an expanded uncertainty of LOQ/2 is added. The relative expanded uncertainties for mass fractions above LOQ are 30% for impurities determined by ICPMS; those for zinc, determined by IDMS, are calculated individually based on the double IDMS equation.
All individual impurities are summed up and are subtracted from ideal purity (1 g g−1 = 1 kg kg−1); the individual uncertainties are propagated accordingly. The resulting purity of the purified enriched materials and the five major impurities are listed in Table 6, together with the associated expanded uncertainties.
| Mass fraction/(mg kg−1) | “24Mg” | “25Mg” | “26Mg” |
|---|---|---|---|
| Nitrogen | 3(3) | 3(3) | 3(3) |
| Oxygen | 15(15) | 15(15) | 15(15) |
| Sodium | 3.6(1.1) | 8.6(2.6) | 0.38(38) |
| Zinc | 52.20(40) | 195.0(1.4) | 957.4(6.1) |
| Cadmium | 6.5(2.0) | 22.5(6.7) | 57(17) |
| Sum of all impurities | 94 | 260 | 1047 |
| U (k = 2) for impurities | 32 | 35 | 47 |
| Purity wpur/(kg kg−1) | 0.999906 | 0.999740 | 0.998953 |
| U (k = 2) for purity/(kg kg−1) | 0.000032 | 0.000035 | 0.000047 |
4.5 Dilution; blending to binary calibration mixtures
Dilution and blending was conducted in two campaigns. In the first campaign, the 2.5 g of the primary solutions of the enriched materials were diluted to 250 g yielding an approximate mass fraction of 10 μg g−1 each; those intermediate dilutions were then mixed 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, using 10 g of each stock solution, and filled up to 100 g yielding approximate magnesium mass fractions of 2 μg g−1 in the three mixtures “24” + “25”, “24” + “26” and “24” + “26”. This was repeated three times, so that nine individual mixtures (3 × “24” + “25”, 3 × “24” + “26” and 3 × “24” + “26”) resulted. The uncertainty analysis for this first campaign, however, showed that a relatively large uncertainty was introduced in the initial dilution step (where only 2.5 g of the parent solution were diluted to 250 g of intermediate dilution), which lead to an overall expanded uncertainty of 0.085% for the calibration mixtures. This uncertainty is significantly larger than the target expanded uncertainty of 0.02% aimed at in this project.
1, using 10 g of each stock solution, and filled up to 100 g yielding approximate magnesium mass fractions of 2 μg g−1 in the three mixtures “24” + “25”, “24” + “26” and “24” + “26”. This was repeated three times, so that nine individual mixtures (3 × “24” + “25”, 3 × “24” + “26” and 3 × “24” + “26”) resulted. The uncertainty analysis for this first campaign, however, showed that a relatively large uncertainty was introduced in the initial dilution step (where only 2.5 g of the parent solution were diluted to 250 g of intermediate dilution), which lead to an overall expanded uncertainty of 0.085% for the calibration mixtures. This uncertainty is significantly larger than the target expanded uncertainty of 0.02% aimed at in this project.
Also previously used densities of the solutions showed expanded uncertainties of 5% which were too large and contributed significantly to the overall uncertainty of the parent solution. Therefore, new densities of the solutions were determined, which are listed in Table S4 and described in section S3.1 (in the ESI†).
An improved dilution and mixing approach was created based on the experience obtained within the first campaign. The most important was that the first dilution step was not designed for optimum results. Instead, in the second approach, the dilution factor was set at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, and this time, 10 g of parent solution were filled up to 100 g yielding magnesium mass fractions of 100 mg kg−1. Additionally, the weighings were carried out at the AX-205 balance, which offers significantly lower uncertainties in this range than the H315 balance. Difference weighing in a PFA bottle was used for this purpose. The binary mixtures were then created using the same approach as the first time (mixing 10 g of each of two intermediate solution, and fill up to 100 g), but this time starting from the ten times more concentrated intermediate solution, which resulted in ten times higher concentrations (mass fractions) in the binary mixtures than in the first round (20 mg kg−1, instead of 2 mg kg−1 total Mg mass fraction). The complete diluting and mixing scheme of the second improved campaign is shown in Fig. 7. Tables S9 and S10 (in the ESI†) compile representative values for the preparation of the intermediate dilutions and binary mixtures, respectively. Those tables also include relevant input uncertainties for the uncertainty budgets of one intermediate dilution (Table S9†), and one binary mixture (Table S10†) as examples; they also list the resulting values for the magnesium masses in the solutions.
10, and this time, 10 g of parent solution were filled up to 100 g yielding magnesium mass fractions of 100 mg kg−1. Additionally, the weighings were carried out at the AX-205 balance, which offers significantly lower uncertainties in this range than the H315 balance. Difference weighing in a PFA bottle was used for this purpose. The binary mixtures were then created using the same approach as the first time (mixing 10 g of each of two intermediate solution, and fill up to 100 g), but this time starting from the ten times more concentrated intermediate solution, which resulted in ten times higher concentrations (mass fractions) in the binary mixtures than in the first round (20 mg kg−1, instead of 2 mg kg−1 total Mg mass fraction). The complete diluting and mixing scheme of the second improved campaign is shown in Fig. 7. Tables S9 and S10 (in the ESI†) compile representative values for the preparation of the intermediate dilutions and binary mixtures, respectively. Those tables also include relevant input uncertainties for the uncertainty budgets of one intermediate dilution (Table S9†), and one binary mixture (Table S10†) as examples; they also list the resulting values for the magnesium masses in the solutions.
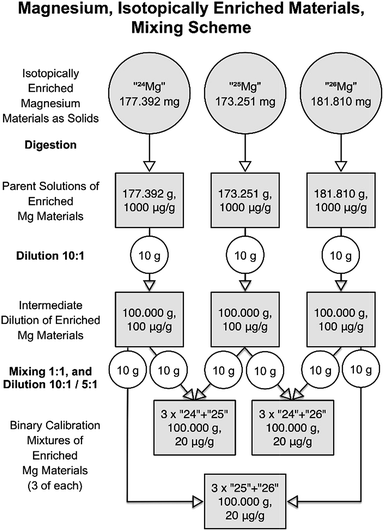 | ||
| Fig. 7 Dilution and mixing scheme of the second campaign for producing the synthetic isotope mixtures. | ||
The resulting masses and the associated uncertainties for all nine calibration solutions are compiled in Table 7. Those values are the final results of this project and form the only input quantities of the present work for the later calibration of the mass spectrometer, which will be described in a second publication.37
| Mixtures | “24Mg” | “25Mg” | “26Mg” |
|---|---|---|---|
| m/mg | m/mg | m/mg | |
| “24” + “25”-1b | 1.014057(43) | 1.033044(46) | |
| “24” + “25”-2b | 1.027357(42) | 1.029161(45) | |
| “24” + “25”-3b | 1.029404(44) | 1.116827(50) | |
| “24” + “26”-1b | 1.032338(43) | 1.006593(54) | |
| “24” + “26”-2b | 1.020895(43) | 1.073835(57) | |
| “24” + “26”-3b | 0.998705(41) | 1.028239(55) | |
| “25” + “26”-1b | 1.025770(45) | 1.084446(57) | |
| “25” + “26”-2b | 0.997086(45) | 0.995639(54) | |
| “25” + “26”-3b | 1.024665(45) | 1.008705(53) |
Using the optimized dilution and mixing approach, the relative expanded uncertainties for the masses in the mixtures could be reduced to values between 0.004% and 0.005%. Thus the relative expanded uncertainties for the total Mg masses in the mixtures and the mass ratios could be reduced to values between 0.0058% and 0.0069% compared to the 0.085% in the first campaign, demonstrating an improvement by a factor of more than 10. These relative expanded uncertainties meet the target uncertainty of 0.02% set for this project. This in turn means that the dilution and mixing scheme was successfully designed so that no additional significant uncertainty contributions were introduced; diluting and mixing thus did not contribute to the overall uncertainty.
5. Discussion
The three isotopically enriched Mg materials have been purified by high vacuum sublimation. A complete purity assessment has been applied for the first time to all three materials by using the indirect approach, where all possible impurities (91 elements) are assessed, mass fractions of the individual impurities are summed up and subtracted from ideal purity (1 kg kg−1). The determined purity was ≥0.9989 kg kg−1 for all materials. The associated relative expanded uncertainties were between 0.0032% and 0.0047%, which is on par with the relative expanded uncertainties of the best primary pure substances worldwide ranging from 0.01% to 0.001%.38–40 The weighing and dissolution of the enriched, purified materials were carried out such that relative expanded uncertainties for the Mg mass fraction between 0.0037% and 0.0050% could be achieved. As a comparison, primary solutions which were used for the CCQM key comparison K87 offer relative expanded uncertainties of ≈0.1% for elemental mass fractions of 1 g kg,41 and primary standards used as back-spike in IDMS were commonly produced with relative expanded uncertainties down to 0.02%.33 In the case of Mg the smallest relative expanded uncertainty being published is 0.018% and relates to the primary solution used for the CCQM key comparison K8.42 Thus the primary solutions of the isotopically enriched Mg materials produced in this project are unsurpassed in their expanded uncertainty. From these primary solutions the synthetic isotope mixtures were prepared offering relative expanded uncertainties for the mass ratios between 0.0058% and 0.0069%, which has not been achieved before. Such synthetic isotope mixtures, being used as calibration solutions for MC-ICPMS, should enable the characterization and certification of Mg isotope reference materials with expanded uncertainties of ≤0.02% for isotope amount ratios.Recently, an effort has been published, whose goal was to determine isotope amount ratios and the atomic weight of Mg representing bulk silicate earth via a double spike method using MC-ICPMS.43 The preparation of a double spike, i.e. a mixture of two enriched isotopes, in principle is similar to the preparation of synthetic isotope mixtures. The large difference to our own project is that we have prepared calibration mixtures from all stable Mg isotopes, but the other authors have only used two isotopes in their double spike approach. Our approach has the advantage that all isotope ratios of magnesium can be directly calibrated via isotope mixtures, while Bizzarro et al. need to rely on auxiliary assumptions (such as the validity of mass fractionation laws, which are always simplifications, and not fully understood).
The work presented by Bizzarro et al. undoubtedly show Mg isotope measurements of high quality with a strong metrological emphasis. Nevertheless, there are also some deficiencies with the preparation of the double spike and the uncertainty considerations, leaving some doubts in the accuracy of the presented “absolute” isotopic composition. Our major criticism is the purity assessment of the enriched materials, which focuses on 12 elements only, selected on the basis of the ORNL assay and measured by an inadequate procedure (MC-ICPMS) in a very dilute Mg solution. Bulk oxygen impurities are not suitably addressed; the authors seem to have applied the ORNL materials without further purification. The authors make the central assumption that the impurities in both of the applied isotopically enriched materials are very similar. However, we have worked with the exact same materials (identical batch from the same source, ORNL) in the present work – and the data presented here show clearly that those assumptions do not hold (see Tables 6, and S7 and S8†).
Also, the weighing of the enriched Mg isotopes in the cited work was denoted as “certified to the E2 level”, and resulted in uncertainties (not stated whether standard or expanded) of 0.0010 mg. These uncertainties are extremely low, considering that expanded uncertainties (k = 2) can be as much as ≈0.0053 mg for a 100 mg weight of class E2; in fact, even the better OIML class E1 allows for an expanded uncertainty of ≈0.0016 mg for a 100 mg weight,44 so that the question arises whether or not the authors actually wanted to qualify their weighing results for the magnesium isotopes as agreeing with E1 level (which would corroborate the uncertainties they state) – or more simply, whether a typing error occurred. In our work the weighing of the purified, isotopically enriched materials was carried out using the UMT2 balance, which we calibrated using E2 weights. The accordingly calculated expanded uncertainty was 0.0047 mg for masses between 170 mg and 180 mg, which is higher by a factor of nearly 5 than the uncertainties reported by Bizzarro et al. This also shows that the weighing uncertainty presented by those authors is not realistic for the E2 level.
Although Bizzarro et al. present no absolute value for the magnesium mass fraction in the double spike and its associated uncertainty, it can be assumed that the isotope mixtures presented in the present work are closer to the “true” value, because all influencing quantities have been considered and a full uncertainty budget has been calculated. Isotope amount ratios and molar mass will be compared in a follow-up publication.
We want to compare our work with a second recent work. Very recently, the determination of the atomic weight of Yb via synthetic isotope mixtures was published by Wang et al.45 Three isotopically enriched Yb materials have been chemically purified, the purity has been determined, and isotope mixtures have been prepared. Based on the measurement results, complete uncertainty budgets have been provided by those authors. The only criticism is the measurement uncertainty of 0.1 μg for the mass of the purified, isotopically enriched materials, which is far too low for a realistic uncertainty. However, this uncertainty is not important in the presented uncertainty budget, since in this case, the relatively large uncertainty of the purity determination of 0.01% dominates the overall uncertainty. This leads to a relative expanded uncertainty of ≈0.026% for the Yb mass fraction in the primary solutions of the enriched materials.
In our work, we achieved primary solutions of the enriched Mg materials with relative expanded uncertainties between 0.0032% and 0.0047%, which is better at least by a factor of 5. This is even more important, as our uncertainties are lower than the typical relative repeatability for Mg isotope ratio determination of 0.01%.
6. Conclusions
In the earliest studies only 2 isotopes were used for calibrating the mass spectrometers. In our atomic weight determination of cadmium, we applied for the first time 7 of the 8 stable isotopes of this element for calibrating the mass spectrometer. Since then the situation has changed and studies for atomic weight determinations typically use more than 2 isotopes. Nevertheless, the work presented here is one of the rare cases where all isotopes of an element were calibrated, besides the recent work on Si.46 Enriched materials for all Mg isotopes were purified, and subsequently characterized regarding their final purity. Primary solutions were prepared and blended to form binary mixtures (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio) for each of the three possible binary combinations (“24Mg” + “25Mg”, “24Mg” + “26Mg”, and “25Mg” + “26Mg”). Three individual setups have been prepared under highest gravimetric control, each of them with an isotope ratio close to unity, and a target total magnesium mass fraction close to 20 mg kg−1, resulting in a total of nine calibration solutions. For this setup, relative expanded uncertainties for the Mg mass fraction in the primary isotope solutions of ≤0.005% have been achieved, and relative expanded uncertainties for the Mg masses in the binary isotope mixtures were ≤0.007%.
1 ratio) for each of the three possible binary combinations (“24Mg” + “25Mg”, “24Mg” + “26Mg”, and “25Mg” + “26Mg”). Three individual setups have been prepared under highest gravimetric control, each of them with an isotope ratio close to unity, and a target total magnesium mass fraction close to 20 mg kg−1, resulting in a total of nine calibration solutions. For this setup, relative expanded uncertainties for the Mg mass fraction in the primary isotope solutions of ≤0.005% have been achieved, and relative expanded uncertainties for the Mg masses in the binary isotope mixtures were ≤0.007%.
This work constitutes the first demonstrated case in which relative expanded uncertainties significantly below 0.01% have been achieved for the mass fractions in the binary isotope mixtures for all isotopes of an element. These solutions in turn lay the foundation for the first isotope reference material with measurement uncertainties for the “absolute” isotope ratios (isotope amount ratios), which lie in the same range as the typical reproducibility of Mg isotope ratio and delta measurements.5
This improvement also shows that the situation described previously by Vogl and Pritzkow4 – broadly speaking, that only delta reference materials would serve the users' needs – might be changed in the future for specific elements. To enable this, the measurement uncertainties still have to be lowered, which can be realised by following the setup approach described here, in combination with a more accurate weighing of the purified isotopes, e.g. by using E1 weights, and by improving the purity assessment of the isotopically enriched materials.
Acknowledgements
Financial support by EMRP (the European Metrology Research Programme) is gratefully acknowledged (EMRP-SIB09 “Primary standards for challenging elements”).47 The EMRP is jointly funded by the EMRP participating countries within EURAMET and the European Union. The authors explicitly thank Heinrich Kipphardt and Wolfgang Pritzkow for helpful advice; Maren Koenig for assistance with the IDMS analyses; Dorit Becker, Ti Ha Le and Volker Görlitz for assistance with the preparative work; Andreas Schulz, Christian Meyer, Jens Pfeiffer, Alexei Plotnikov, Carola Pape and Christiane Niedergesäβ for assistance with ICPMS, GDMS and density measurements. The authors also thank Joachim Hinrichs from Thermo Fisher Scientific for support with GDMS measurements.Notes and references
- J. J. Thompson, Philos. Mag., 1910, 10, 752–767 CrossRef.
- J. de Laeter, J. Böhlke, P. de Bièvre, H. Hidaka, H. Peiser, K. Rosman and P. Taylor, Pure Appl. Chem., 2003, 75, 683–800 CrossRef CAS.
- T. B. Coplen, Rapid Commun. Mass Spectrom., 2011, 25, 2538–2560 CrossRef CAS PubMed.
- J. Vogl and W. Pritzkow, J. Anal. At. Spectrom., 2010, 25, 923–932 RSC.
- J. Vogl, M. Rosner and W. Pritzkow, Anal. Bioanal. Chem., 2013, 405, 2763–2770 CrossRef CAS PubMed.
- A. O. Nier, Phys. Rev., 1950, 77(2), 789–793 CrossRef CAS.
- W. Pritzkow, S. Wunderli, J. Vogl and G. Fortunato, Int. J. Mass Spectrom., 2007, 261, 74–85 CrossRef CAS.
- G. Mana and O. Rienitz, Int. J. Mass Spectrom., 2010, 291, 55–60 CrossRef CAS.
- Report of the 5th meeting of the Consultative Committee for Amount of Substance (CCQM), Bureau International des Poids et Mesures (BIPM), 1999, Online available, http://www.bipm.org/utils/en/pdf/CCQM5-EN.pdf Search PubMed.
- J. Black, Q.-Z. Yin and W. Casey, Geochim. Cosmochim. Acta, 2006, 70, 4072–4079 CrossRef CAS.
- K. Ra and H. Kitagawa, J. Anal. At. Spectrom., 2007, 22, 817–821 RSC.
- A. Galy, E. Young, R. Ash and R. O'Nions, Science, 2000, 290, 1751–1753 CrossRef CAS PubMed.
- B. Shen, J. Wimpenny, C.-T. Lee, D. Tollstrup and Q.-Z. Yin, Chem. Geol., 2013, 356, 209–214 CrossRef CAS.
- T. Bohn, T. Walczyk, L. Davidsson, W. Pritzkow, P. Klingbeil, J. Vogl and R. Hurrell, Br. J. Nutr., 2004, 91, 113–120 CrossRef CAS PubMed.
- E. J. Catanzaro, T. J. Murphy, E. L. Garner and W. R. Shields, J. Res. Natl. Bur. Stand., Sect. A, 1966, 70, 453–458 CrossRef CAS.
- A. Galy, O. Yoffe, P. Janney, R. Williams, C. Cloquet, O. Alard, L. Halicz, M. Wadhwa, I. Hutcheon, E. Ramon and J. Carignan, J. Anal. At. Spectrom., 2003, 18, 1352–1356 RSC.
- J. Vogl, W. Pritzkow and P. Klingbeil, Anal. Bioanal. Chem., 2004, 380, 876–879 CrossRef CAS PubMed.
- V. Chang, A. Makishima, N. Belshaw and R. O'Nions, J. Anal. At. Spectrom., 2003, 18, 296–301 RSC.
- Joint Committee for Guides in Metrology (JCGM/WG 1), Evaluation of measurement data – Guide to the expression of uncertainty in measurement, JCGM, 2008 Search PubMed.
- Metrodata GmbH, GUM Workbench Pro 2.4.1.375, Weil am Rhein, 2009 Search PubMed.
- Teflon FEP Fluoroplastic Film Properties Bulletin, DuPont, Wilmington, DE, USA, 2013 Search PubMed.
- Teflon PFA Fluoroplastic Film Properties Bulletin, DuPont, Wilmington, DE, USA, 2013 Search PubMed.
- A. Kaltenbach, J. Noordmann, V. Görlitz, C. Pape, S. Richter, H. Kipphardt, G. Kopp, R. Jährling, O. Rienitz and B. Güttler, Anal. Bioanal. Chem., 2015, 407, 3093–3102 CrossRef CAS PubMed.
- R. Nater, A. Reichmuth, R. Schwartz, M. Borys and P. Zervos, Dictionary of Weighing Terms, Springer, Berlin, 2009 Search PubMed.
- F. Spieweck and H. Bettin, Methoden zur Bestimmung der Dichte von Festkörpern und Flüssigkeiten, Physikalisch-technische Bundesanstalt (PTB), Braunschweig, 1998 Search PubMed.
- C. Niedergesäβ, Hydrostatische Bestimmung der Dichte von Festkörpern (Arbeitsanweisung PTB 3.43-AA-02), Physikalisch-technische Bundesanstalt (PTB), Braunschweig, 2014 Search PubMed.
- F. Küster and A. Thiel, Rechentafeln für die Chemische Analytik, Walter de Gruyter, Berlin, New York, 104th edn, 1993 Search PubMed.
- H. Bettin and F. Spieweck, Die Dichte des Wassers als Funktion der Temperatur nach Einführung der Internationalen Temperaturskala von 1990, PTB-Mitt., 1990, 100, 195–196 Search PubMed.
- W. Gorski and H. Toth, Destilliertes Wasser als Dichtereferenzmaterial – Die elektrische Leitfähigkeit als Kriterium seiner Güte, PTB-Mitt., 1988, 98, 324–325 CAS.
- O. Rienitz, A. Pramann and C. Pape, Anal. Bioanal. Chem., 2013, 405, 5627–5628 CrossRef CAS PubMed.
- O. Rienitz, A. Pramann and C. Pape, Anal. Bioanal. Chem., 2013, 405, 8691–8692 CrossRef CAS PubMed.
- A. Plotnikov, J. Pfeifer, S. Richter, H. Kipphardt and V. Hoffmann, Anal. Bioanal. Chem., 2014, 406, 7463–7471 CrossRef CAS PubMed.
- J. Vogl and W. Pritzkow, MAPAN-Journal of Metrology Society of India, 2010, 25, 135–164 Search PubMed.
- J. Vogl, Rapid Commun. Mass Spectrom., 2012, 26, 275–281 CrossRef CAS PubMed.
- S. Dushman and L. Koller, Vapor pressures and rates of evaporation, in Scientific Foundations of Vacuum Technique, 2nd edn, 1949, pp. 691–703 Search PubMed.
- J. Nordlien, S. Ono, N. Masuko and K. Nisancioglu, Corros. Sci., 1997, 39, 1397–1414 CrossRef CAS.
- B. Brandt, J. Vogl, J. Noordmann, O. Rienitz and D. Malinovskiy, J. Anal. At. Spectrom., 2015, in preparation Search PubMed.
- BAM Primary Pure Substances, Online available at, http://www.rm-certificates.bam.de/en/certificates/primary_pure_substances/index.htm.
- H. Kipphardt, R. Matschat, J. Vogl, T. Gusarova, M. Czerwensky, H.-J. Heinrich, A. Hioki, L. Konopelko, B. Methven, T. Miura, O. Petersen, G. Riebe, R. Sturgeon, G. Turk and L. Yu, Accredit. Qual. Assur., 2010, 15, 29–37 CrossRef CAS.
- T. Zhou, S. Richter, R. Matschat and H. Kipphardt, Accredit. Qual. Assur., 2013, 18, 341–349 CrossRef CAS.
- O. Rienitz, D. Schiel, V. Görlitz, R. Jährling, J. Vogl, J. V. Lara-Manzano, A. Zon, W. Fung, M. Buzoianu, R. C. de Sena, L. A. dos Reis, L. Valiente, Y.-H. Yim, S. Hill, R. Champion, P. Fisicaro, W. Bing, G. C. Turk, M. R. Winchester, D. Saxby, J. Merrick, A. Hioki, T. Miura, T. Suzuki, M. Linsky, A. Barzev, M. Máriássy, O. Cankur, B. Ari, M. Tunc, L. Konopelko, Y. A. Kustikov and M. Bezruchko, Final report on CCQM-K87: mono-elemental calibration solutions, Metrologia, 2012, 49, 08010 CrossRef.
- H. Felber, M. Weber and C. Rivier, Final report on key comparison CCQM-K8 of monoelemental calibration solution, Metrologia, 2002, 39, 08002 CrossRef.
- M. Bizzarro, C. Paton, K. Larsen, M. Schiller, A. Triniquier and D. Ulfbeck, J. Anal. At. Spectrom., 2011, 26, 565–577 RSC.
- Weights of classes E1, E2, F1, F2, M1, M1-2, M2, M2-3 and M3, Part 1: Metrological and technical requirements, OIML R 111-1 International Recommendation, 2004.
- J. Wang, T. Ren, H. Lu, T. Zhou and Y. Zhou, J. Anal. At. Spectrom., 2015, 30, 1377–1385 RSC.
- A. Pramann, O. Rienitz, D. Schiel and B. Güttler, Int. J. Mass Spectrom., 2011, 299, 78–86 CrossRef CAS.
- Online available at, http://www.ptb.de/emrp/sib09.html.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ja00284b |
| This journal is © The Royal Society of Chemistry 2016 |