Tandem ICP-mass spectrometry for Sr isotopic analysis without prior Rb/Sr separation
Eduardo
Bolea-Fernandez
a,
Lieve
Balcaen
a,
Martín
Resano
b and
Frank
Vanhaecke
*a
aGhent University, Department of Analytical Chemistry, Krijgslaan 281-S12, 9000 Ghent, Belgium. E-mail: Frank.Vanhaecke@ugent.be; Fax: +32 92644960; Tel: +32 92644848
bUniversity of Zaragoza, Aragón Institute of Engineering Research (I3A), Department of Analytical Chemistry, Pedro Cerbuna 12, 50009 Zaragoza, Spain
First published on 23rd June 2015
Abstract
The use of a mixture of 10% of CH3F and 90% of He as a reaction gas in tandem ICP-mass spectrometry (ICP-MS/MS) enables the accurate determination of the 87Sr/86Sr isotope ratio in geological materials, provided that mass discrimination is corrected for by using a combination of internal (Russell law, assuming a constant 88Sr/86Sr isotope ratio) and external correction (using the isotopic reference material NIST SRM 987 SrCO3) in a sample-standard bracketing approach. No prior Rb/Sr separation is required as the isobaric overlap at a mass-to-charge ratio of 87 is avoided by monitoring SrF+ reaction product ions instead of Sr+ ions. Rb shows no reactivity towards CH3F. The double mass selection (MS/MS mode) prevents both spectral overlap from atomic ions at the mass-to-charge ratios of SrF+ reaction product ions and a measurable effect from the matrix on the 87Sr/86Sr result. This aspect is critical, as it enables accurate results to be obtained without the need for using a matrix-matched standard to correct for mass discrimination, in contrast to previous work with a quadrupole ICP-MS instrument with a CH3F/Ne-pressurized cell, in which the use of a matrix-matched standard was compulsory. The precision attainable – 0.05% RSD external precision – suffices for making the newly developed method useful in a variety of applications.
1. Introduction
In comparison to elements with a similar atomic number, Sr shows a relatively pronounced natural variation in its isotopic composition as a result of one of its isotopes – 87Sr – being radiogenic. The consequence is a wide variety of applications for which Sr isotopic analysis is of relevance (e.g., Rb/Sr geochronological dating and other geochemical applications, provenance determination of agricultural products of plant and animal origin and migration studies).1–4Although like for every other element with ≥2 isotopes, the isotopic composition of Sr also shows natural variation as a result of isotope fractionation,3,5,6 the main process responsible for the natural variation in the isotopic composition of Sr7,8 is the β− decay of 87Rb into 87Sr (T1/2 = 4.88 × 1010 years (ref. 9)). This means that, in a closed system, sub-samples containing Rb and Sr will be enriched in 87Sr, and the degree of enrichment depends on the time during which the two elements have resided together and their elemental ratio Rb/Sr.10–12
However, accurate determination of the 87Sr/86Sr isotope ratio by means of inductively coupled plasma-mass spectrometry (ICP-MS) is not free from challenges. One of the most important problems is the spectral overlap of the signals of the isobaric ions 87Rb+ and 87Sr+, which needs a mass resolution of ∼300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to be resolved, which is beyond the capabilities of present-day commercially available ICP-MS instruments.13,14 Additional spectral interference due to the presence of polyatomic ions, such as ArCa+ and Ca2+ dimers, can also jeopardize the accuracy of the isotope ratio results. The use of high mass resolution,15 which furthermore results in a significant drop in signal intensity and deterioration in isotope ratio precision,16 is not feasible for overcoming the spectral overlap. Sr has to be isolated from the matrix, or at least separated from Rb, prior to analysis.17–19 Obviously, these isolation steps negatively affect the sample throughput and make Sr isotopic analysis labor-intensive.
000 to be resolved, which is beyond the capabilities of present-day commercially available ICP-MS instruments.13,14 Additional spectral interference due to the presence of polyatomic ions, such as ArCa+ and Ca2+ dimers, can also jeopardize the accuracy of the isotope ratio results. The use of high mass resolution,15 which furthermore results in a significant drop in signal intensity and deterioration in isotope ratio precision,16 is not feasible for overcoming the spectral overlap. Sr has to be isolated from the matrix, or at least separated from Rb, prior to analysis.17–19 Obviously, these isolation steps negatively affect the sample throughput and make Sr isotopic analysis labor-intensive.
It has been demonstrated that chemical resolution using a quadrupole-based ICP-MS (ICP-QMS) instrument equipped with a collision/reaction cell can be an elegant option to resolve spectral overlap,20 thus extending the application range of ICP-QMS to the isotopic analysis of elements that otherwise suffer from spectral interference. The use of a collision/reaction cell allows removal of spectral overlap relying on physical processes (e.g., a combination of collisions with a non-reactive gas to slow down polyatomic ions more than atomic ions, thus enabling the former to be selectively discriminated against via kinetic energy discrimination),21 or by a selective ion/molecule reaction between an interfering ion,22–24 or a target ion,25–27 and a reactive gas. The latter approach is sometimes referred to as chemical resolution and allows interference-free measurement at either the original mass-to-charge (m/z) ratio of the target nuclide or at the m/z ratio of the reaction product ion formed. In this way, the sample pretreatment can be reduced or even eliminated, also facilitating the direct analysis of solid samples via laser ablation-ICP-MS (LA-ICP-MS).
Unfortunately, the isotope ratio precision typically offered by ICP-QMS is rather modest, with values around 0.1% RSD internal precision. Pressurizing the collision/reaction cell of an ICP-QMS instrument with an inert collision gas can lead to a slight improvement in the isotope ratio precision, by damping the fluctuations in signal intensity, through the mixing of ions sampled from the plasma ion source at slightly different moments in time.28,29 However, the isotope ratio precision thus attainable is still considerably worse than that achievable with thermal ionization mass spectrometry (TIMS) or multi-collector ICP-MS (MC-ICP-MS), with an internal precision down to 0.001% RSD. Therefore, the use of ICP-QMS for the determination of isotope ratios has often been restricted to the study of induced changes in the isotopic composition of target elements in the context of tracer experiments with enriched stable isotopes,30,31 or of elemental assay using isotope dilution for calibration.32 However, it has to be stressed that the use of the more expensive MC-ICP-MS or TIMS instrumentation is not always required when natural variation in the isotopic composition of a target element needs to be studied, as for some applications, particularly those dealing with radiogenic nuclides, the precision attainable with an ICP-QMS instrument can be fit-for-purpose.11,33–35
In addition to the difficulties with spectral overlap mentioned above, every type of ICP-MS instrumentation suffers from mass discrimination,36 a term referring to the differences in the efficiencies of ion extraction, transmission and/or detection as a function of the analyte mass. This effect results in a bias between the measured isotope ratio and the corresponding true value that needs to be adequately corrected for. Different approaches have been described in the literature for this purpose (e.g., internal correction, external correction and the combination of both).37 Also, it has been demonstrated that mass discrimination effects become more pronounced in ICP-QMS when the collision/reaction cell is pressurized with a gas, as a result of slight differences in the collisional and/or chemical behavior of the isotopes as a function of their mass.26,38
In earlier work, the use of methyl fluoride (CH3F) as a selective reaction gas (in combination with Ne as a non-reactive collision gas) in an ICP-QMS instrument equipped with a dynamic reaction cell (DRC) for the direct determination of Sr isotope ratios has been described.25 In this approach, the selective reaction between CH3F and Sr+ (Rb+ does not react with CH3F) allows for circumventing the isobaric overlap at m/z = 87 by measuring the relative signal intensities of the Sr isotopes via the intensities of the corresponding SrF+ ions. Owing to the mono-isotopic character of F, SrF+ ions show the same isotopic pattern as do Sr+ ions themselves. Despite the achievements shown in the work referred to above, this did not result in a general breakthrough for Sr isotopic analysis, as it was noted that (i) interfering nuclides occurring at the m/z ratio of the selected reaction product ions (e.g., 103Rh, 106Cd, 105,106Pd and 107Ag) could not be removed, and (ii) that the matrix composition affects the mass discrimination to a large extent, such that the use of a matrix-matched isotopic standard for external mass bias correction was required. These important drawbacks have hindered routine application of this approach in real-life applications.
Recently, a new type of ICP-MS device was introduced onto the market. The so-called triple quadrupole ICP-MS instrument is equipped with a tandem mass spectrometry configuration (ICP-MS/MS), with an octopole collision/reaction cell located in-between two quadrupole analyzers. This set-up opens new possibilities for interference-free determination of ultra-trace concentrations of elements that otherwise suffer from strong spectral overlap.39,40 In MS/MS-mode, only those ions with the original m/z-ratio of the analyte element pass the first quadrupole and enter the reaction cell. This results in an enhanced control over the reactions taking place in the cell and a strong reduction in matrix effects. Because of this, highly reactive gases (e.g., NH3 and CH3F) can be used without the risk of obtaining complex mass spectra that are difficult to interpret.41 ICP-MS/MS with a CH3F/He (10% CH3F and 90% He) mixture42 as a reaction gas has recently been successfully used by the authors for the purpose of ultra-trace determination of several elements (Al, As, Co, Cr, Mn, Ni, Se, Ti and V),43,44 but the possibilities of ICP-MS/MS for isotope ratio determination have not been fully explored yet,45–49 and no work to date has reported on the use of this technique for Sr isotopic analysis.
In this work, the capabilities of tandem ICP-mass spectrometry with CH3F as a reaction gas were evaluated, with the aim to develop a method that enables the straightforward determination of the 87Sr/86Sr isotope ratio in geological materials, without previous Sr isolation or Rb/Sr separation.
2. Experimental
2.1. Reagents and standards
Only high-purity reagents were used throughout the work. Ultra-pure water (resistivity > 18.2 MΩ cm) was obtained from a Milli-Q Element water purification system (Millipore, France). Ultra-pure 28 M HF (Fisher Chemicals, Great Britain) and pro-analysis 14 M HNO3 (ChemLab, Belgium), further purified by sub-boiling distillation, were used for acid digestion. Appropriate dilutions from 1 g L−1 single-elemental standard solutions (Ag, Ca, Cd, Pd, Rb and Sr – Instrument Solutions, The Netherlands) were made for obtaining solutions used in the context of method development. The isotopic reference material NIST SRM 987 Strontium Carbonate with a certified Sr isotopic composition (87Sr/86Sr = 0.71034 ± 0.00026) and an in-house standard solution of Sr (Instrument solutions, The Netherlands), previously characterized via MC-ICP-MS (87Sr/86Sr = 0.70753 ± 0.00006), were used for optimization, method development and validation purposes.2.2. Samples
Five geological reference materials – USGS AGV1 Andesite, USGS G-2 Granite, USGS BHVO-1 Basalt, BCR CRM 141 Calcareous Loam Soil and BCR CRM 142 Light Sandy Soil – were analyzed for their 87Sr/86Sr isotope ratio and the results obtained were compared to values reported in the literature for the purpose of validation.2.3. Sample preparation
Sample digestion was carried out in Savillex® beakers that had been previously subjected to a cleaning procedure with both HNO3 and HCl and subsequent rinsing with Milli-Q water. Approximately 0.2 g of each reference material was accurately weighed and dissolved in 3 mL of 14 M HNO3 and 10 mL of 28 M HF. The mixture was heated in an open beaker on a hot plate (90 °C) until dry. For the reference materials USGS AGV1 (andesite) and USGS G-2 (granite), the residue was taken up in 1.4 M HNO3. In the case of USGS BHVO-1 (basalt), BCR CRM 141 (calcareous loam soil) and BCR CRM 142 (light sandy soil), an additional digestion process was required to obtain a clear solution. Therefore, 5 mL of 14 M HNO3 was added to the residue and the resulting mixture was heated at 110 °C in a closed beaker overnight. After digestion, the solutions thus obtained were appropriately diluted for subsequent analysis. The concentration of Sr was kept constant throughout the work (7.5 μg L−1 and 10 μg L−1 for SQ and MS/MS mode, respectively), providing approximately the same signal intensity in both modes. To avoid possible contamination, only “metal-free” tubes were used to prepare all dilutions (15 or 50 mL polypropylene centrifuge tubes, VWR, Belgium).2.4. Instrumentation
All measurements were performed using an Agilent 8800 tandem ICP-MS instrument (ICP-QQQ, Agilent Technologies, Japan), equipped with a MicroMist nebulizer (400 μL min−1) fitted onto a Peltier-cooled Scott-type spray chamber (2 °C). The octopole collision/reaction cell was pressurized with a mixture of CH3F/He (10% CH3F and 90% He, “Certified Master Class”, Air Liquide, Belgium). The CH3F/He mixture was introduced via the 4th inlet (operation range of the mass flow controller, 0–100%, corresponding to gas flow rates of 0–1 mL min−1, calibrated for O2).3. Results and discussion
3.1. Method development for interference-free determination of Sr
An important prerequisite for successful direct Sr isotopic analysis is the ability of the analytical method to monitor the signals of (at least) 86Sr, 87Sr and 88Sr free from spectral overlap. The actual isotope ratio of interest is 87Sr/86Sr, while 88Sr/86Sr is used for internal correction for mass discrimination. As measuring 84Sr provides no added value, while increasing the measurement time and potentially deteriorating the isotope ratio precision, this nuclide was not monitored. In this work, CH3F (a mixture of 10% CH3F and 90% He) was evaluated as a reaction gas in ICP-MS/MS. Via product ion scanning, with the cell pressurized with 1 mL min−1 of CH3F/He, the mass-to-charge (m/z) ratio of each of the target nuclides (86,87,88Sr+) was selected in the first quadrupole, and the entire mass spectrum was scanned using the second quadrupole for identifying the reaction product ions formed. The main reaction product ions were identified as 86,87,88SrF+. In MS/MS mode, the CH3F/He flow rate setting was evaluated in the range of 0–1.0 mL min−1, and a maximum signal-to-background ratio was found at 0.90 mL min−1. The optimum instrument settings are summarized in Table 1.| Agilent 8800 | |
|---|---|
| Reaction gas | CH3F/He (10/90) |
| Scan type | MS/MS |
| Plasma mode | Low matrix |
| RF power (W) | 1550 |
| Extract 1 (V) | −3.0 |
| Q1 bias (V) | 0 |
| Reaction gas flow rate setting (mL min−1) | 0.90 |
| Q1 → Q2 | 86 → 105 |
| 87 → 106 | |
| 88 → 107 | |
| Octopole bias (V) | −4.7 |
| Energy discrimination (V) | −8.4 |
| Extract 2 (V) | −175.0 |
| Q2 QP bias (V) | −13.1 |
| Wait time offset (ms) | 0 |
| Sweeps/replicate | 100 |
| Acquisition time/mass (s) [1 acquisition point per spectral peak] | 30 |
| Number of replicates | 10 |
| Total analysis time/sample (s) | 906 |
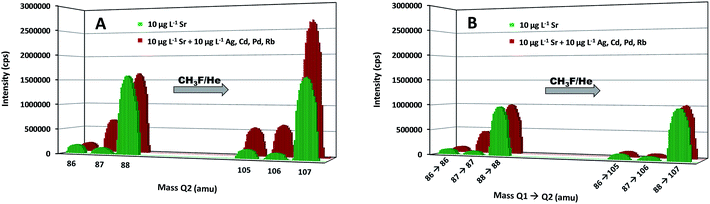
With the aim of demonstrating the capabilities of the MS/MS approach to avoid spectral overlap, two standard solutions were analyzed, the first one containing 10 μg L−1 of Sr and the second one containing the same concentration of Sr and 10 μg L−1 of Ag, Cd, Pd and Rb. These elements can give rise to spectral interference at the original m/z ratio of one of the target nuclides (87Rb) or at the m/z ratio of the selected reaction product ions (105,106Pd, 106Cd, 107Ag). Both standard solutions were measured in both single quadrupole mode (SQ, where the first quadrupole is not operating as a mass filter, but only as an ion guide) and MS/MS mode. The results are given in Fig. 1. In both modes, the isotopic pattern observed for the pure Sr solution was the same without and with the reaction, as a consequence of the mono-isotopic character of F, enabling the determination of the isotopic composition of Sr via measurement of the intensities of the SrF+ ions. A comparison between the results for both standard solutions (without and with admixed elements) shows the effect of the overlap of the signals of 87Sr and 87Rb, which was resolved in both modes owing to the reaction of Sr+ ions with CH3F, while Rb+ shows no reactivity towards this gas. Although a better sensitivity was achieved in SQ mode, the spectral interference occurring in the presence of Ag, Cd and Pd ions at the m/z ratio of the selected reaction product ions prevents accurate Sr isotopic analysis in this mode. For samples containing those elements, Sr isotopic analysis without previous Sr isolation can only be successfully accomplished in MS/MS mode.
In MS/MS mode, some figures of merit (e.g., sensitivity or limits of detection and of quantification) were characterized and the corresponding results are given in Table 2.
| Isotope | Reaction product ion | CH3F/He flow (mL min−1) | Q1 (amu) | Q2 (amu) | Sensitivitya (counts L μg−1 s−1) | Intercepta (counts s−1) | R 2 | LoDb (ng L−1) | LoQb (ng L−1) |
|---|---|---|---|---|---|---|---|---|---|
| a Uncertainties expressed as standard deviation (n = 10). b LoDs and LoQs calculated as 3 and 10 times the standard deviation of 10 consecutive measurements of a blank solution (0.14 M HNO3), divided by the slope of the calibration curve, respectively. | |||||||||
| 86Sr | 86SrF+ | 0.90 | 86 | 105 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 ± 90 660 ± 90 |
48 ± 310 | 0.999992 | 1 | 4 |
| 87Sr | 87SrF+ | 87 | 106 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690 ± 50 690 ± 50 |
68 ± 210 | 0.999993 | 1 | 4 | |
| 88Sr | 88SrF+ | 88 | 107 | 172![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 900 000 ± 900 |
340 ± 600 | 0.999998 | 0.8 | 3 | |
3.2. Optimization of instrument settings and data acquisition parameters for the accurate and precise isotope ratio determination of Sr via SrF+ monitoring
With the objective of achieving accurate and precise 87Sr/86Sr isotope ratio results via conversion of Sr+ into the corresponding SrF+ ions using CH3F/He as a reaction gas in ICP-MS/MS, the detector dead time was experimentally determined and the effect of the data acquisition parameters was checked.The detector dead time was determined according to the method proposed by Russ.50 Standard solutions of Sr with concentrations of 2.5, 5.0 and 10 μg L−1 were measured at different detector dead times in the range of 0 to 70 ns. The 88SrF+/86SrF+ ratios were plotted versus the dead time for each concentration. According to this approach, the point where the lines intersect corresponds to the correct value, which was 32.6 ± 0.3 ns in this case. Additional experiments were carried out to ascertain that the detector dead time determined using 88SrF+/86SrF+ is also valid for 87SrF+/86SrF+. For a range between 1 and 10 μg L−1, it was evaluated whether the 87SrF+/86SrF+ isotope ratio changes as a function of the Sr concentration. Values between 0.72497 and 0.72660 were obtained; no trend was observed and no significant differences were found, as indicated via ANOVA at a 95% level of significance (Fexperimental = 1.0991 < Fcritical = 2.3861). This demonstrates that the differences in concentration (covering one order of magnitude) do not affect the accuracy of the isotope ratio results, such that it can be concluded that the dead time correction is done adequately and that the extent of instrumental mass bias does not vary within the range studied. Thus, the experimentally determined detector dead time was inserted into the software and used throughout all further studies.
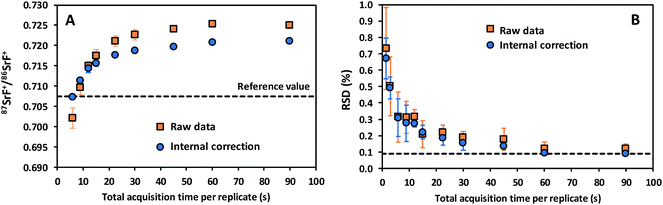
In addition, data acquisition parameters were optimized. The best performance is typically obtained when combining a sufficiently long acquisition time (cf. the role of the total number of ions detected in Poisson counting statistics) with fast scanning (to counteract the noisy character of the ICP ion source).29 Different experiments were conducted with the aim of evaluating the effect of the data acquisition parameters on the accuracy and precision of the isotope ratio results. 87SrF+/86SrF+ ratios and internal precision values, expressed as RSD (%), were determined using 10 replicates for each measurement and 100 sweeps per replicate. The results thus obtained are presented in Fig. 2 as a function of the total acquisition time per replicate, for both the raw data and the results after the use of an internal correction (vide infra). As expected, the RSD (%) decreases for longer acquisition times, down to a minimum at a total acquisition time of 90 s, corresponding with an acquisition time of 30 s for each of the isotopes selected (RSD = 0.12 and 0.09% for the raw data and the internally corrected data, respectively). It can be seen that the 87SrF+/86SrF+ ratio itself also changes with increasing total acquisition time, until a constant ratio is obtained for the highest values (Fig. 2). A similar trend was observed for the 88SrF+/86SrF+ ratio, with the deviation at low acquisition times being even more pronounced. For 88SrF+/86SrF+, however, a stable isotope ratio value is obtained as of a somewhat lower integration time than for 87SrF+/86SrF+. This leads to an over-correction via internal correction, as can be seen in Fig. 2 for the lowest acquisition times. This tendency can most probably be explained as a result of the use of chemical reactions, where the reaction product ions typically require more time to actually reach the second quadrupole and detector and give rise to a stable ion beam, which means that a minimum dwell time (selected as a function of the acquisition time per nuclide/number of sweeps) has to be used for the measurement of the isotopic composition of Sr as SrF+via ICP-MS/MS. More evidence for this hypothesis was found in additional experiments, where – for measurements with a short total acquisition time (3 s) – a wait time offset (WTO) was used. This WTO is an additional time on top of the quadrupole settling time, allowing the slowdown of the ions in the cell to be compensated for and giving the system time to arrive at steady state conditions. As can be seen in Fig. 3, a WTO in the order of a few milliseconds (∼5 ms) was sufficient to compensate for the effect seen at low acquisition times. In addition to the experiments explained above, also the number of sweeps per replicate was evaluated as a possible parameter affecting the precision in the isotope ratio measurements. However, although a wide range of number of sweeps was tested (50–1000), no reproducible effect on the accuracy or precision was noticed, probably, because longer dwell times are required when dealing with isotope ratio measurement after the chemical reaction in the cell. Based on the results of these experiments, 100 sweeps and a total acquisition time of 90 s were selected as the optimum parameters, as they provide the best possible precision and stable isotope ratio results. When using these longer acquisition times, no additional measurement time was needed to obtain a constant isotope ratio result, and thus, the WTO was set to 0 ms. The optimized instrument settings and data acquisition parameters used in all further experiments are shown in Table 1.
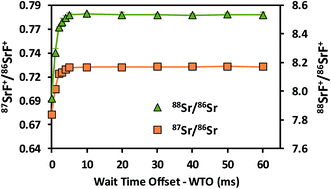 | ||
| Fig. 3 Raw 88Sr/87Sr and 87Sr/86Sr isotope ratio results (based on the corresponding SrF+ signals) as a function of the wait time offset (WTO) obtained using a total acquisition time of 3 s. | ||
3.3. Mass bias correction
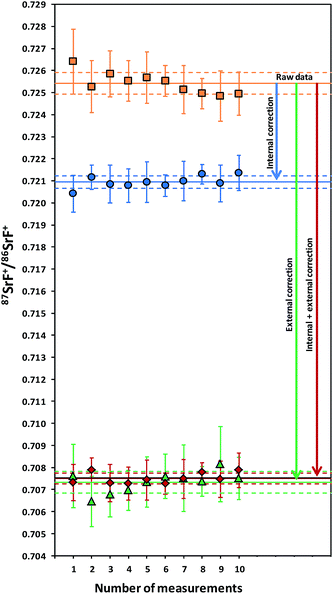
As mentioned in the introduction, ICP-MS is affected by mass discrimination, such that a measured isotope ratio differs from the corresponding true value. Several approaches have been described to correct for the mass bias thus caused. The use of internal correction, external correction and the combination of both were evaluated with the aim of obtaining better accuracy and precision. For the internal correction approach, the 88Sr/86Sr ratio is assumed to be (sufficiently) constant in nature and used to correct the 87Sr/86Sr ratio by means of the Russell law, with the assumption that f88/86 = f87/86 (see eqn (1)). Alternately, the raw data were externally corrected for the mass bias using NIST SRM 987 as an external standard, used in a sample-standard bracketing approach (SSB). Finally, also the combination of both correction methods was tested. Fig. 4 and Table 3 show the results for a sequence of 10 measurements of an in-house standard solution of Sr with an isotopic composition that was previously characterized via MC-ICP-MS (87Sr/86Sr = 0.70753 ± 0.00003). As can be seen, the raw data are biased high, and the use of internal correction using the Russell law (eqn (1)), based on an 88Sr/86Sr isotope ratio of 8.3752 does not allow us to properly correct for mass discrimination. Although internal correction leads to a significant improvement in both, internal and external precision, the results are still biased high. The bias remaining after applying internal correction most probably results from additional mass discrimination produced by collisions and reactions in the cell (not all isotopes react to exactly the same extent with the reaction gas (CH3F), neither are they equally affected by collisions with the inert He gas). Therefore, external correction with NIST SRM 987 in a SSB approach (eqn (2)) was tested. Good agreement was found between the externally corrected data and the true value, but with this correction method, the external precision was not improved beyond that of the raw data. Finally, the combination of internal and external correction was seen to provide the best results in terms of both accuracy and precision, without any significant difference between the experimentally determined isotope ratios and the true value, and with an external precision of 0.035% RSD (n = 10). Additionally, as shown in Fig. 4, also an improved internal precision (the standard deviation on 10 replicates for each measurement) was achieved when the isotope ratios were internally corrected.| Mass bias correction | 87SrF+/86SrF+ ± s | RSD (%) |
|---|---|---|
| a Results obtained for n = 10. b Results obtained for n = 50 collected from different sequences during a period of one month. | ||
| Raw data | 0.72542 ± 0.00049a | 0.067a |
| Internal correction | 0.72095 ± 0.00028a | 0.039a |
| External correction | 0.70733 ± 0.00048a | 0.068a |
| Internal + external correction (n = 10) | 0.70751 ± 0.00025a | 0.035a |
| Internal + external correction (n = 50) | 0.70756 ± 0.00028b | 0.039b |
| 87Sr/86Sr | RSD (%) | |
|---|---|---|
| Reference value (MC-ICP-MS) | 0.70753 ± 0.00003 | 0.0042 |
In order to better assess the capabilities of the last approach for the determination of isotope ratios of Sr using CH3F in ICP-MS/MS, longer-term studies were performed. The 87SrF+/86SrF+ isotope ratio results were collected for a period of one month and provided an average of 0.70756 ± 0.00028 and an external precision of 0.039% RSD (n = 50). Thus, the combination of internal and external correction was used in all further studies.
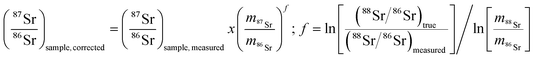 | (1) |
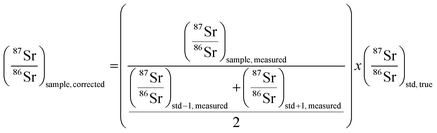 | (2) |
3.4. Influence of the sample matrix on isotope ratio results in SQ and MS/MS mode
In previous work,25 it was shown that – even when the Sr isotopes can be measured interference-free – a good accuracy and precision of the 87Sr/86Sr isotope ratio results could not be guaranteed for geological reference materials, unless matrix-matched isotopic standards were used for external mass bias correction. This leads to the conclusion that matrix effects are responsible for the deviations obtained.In this work, we assessed whether also with the newly developed ICP-MS/MS approach matrix effects necessitate the use of a matrix-matched standard. Therefore, the accuracy and precision of Sr isotopic analysis was assessed for pure Sr standard solutions, Sr standards with increasing concentrations of some matrix elements added (up to 1000 μg L−1 Ca and 200 μg L−1 Rb) and geological reference materials, both in SQ and MS/MS mode. The standards were measured on 3 different days in order to assess the robustness of the method under such conditions. No significant differences were found between the Sr standard solution and the different Rb- and Ca-containing solutions, neither between the results obtained in SQ and MS/MS-mode, which indicates that for these rather simple matrices, matrix effects can be neglected. For the geological reference materials, however, the situation is clearly different. For one of the reference materials, USGS AGV-1 Andesite, isotopic analysis in SQ mode (where all matrix ions are passing the first quadrupole and enter the collision/reaction cell) resulted in a 87Sr/86Sr isotope ratio of 0.65432 ± 0.00085 (after mass bias correction, based on a combination of both internal and external correction using NIST SRM 987). This result deviates strongly from the corresponding reference value of 0.70406 ± 0.00005. In MS/MS mode, however, where only a very limited selection of ions enter the cell, good agreement was found between the results obtained and the corresponding reference value (see the next section). This leads to the conclusion that for samples with a heavy matrix, matrix effects do have an influence on the final results. However, these effects can be overcome by operating the tandem mass spectrometer in the MS/MS mode, which is an additional proof of the strength of the method developed in this work.
3.5. Determination of the isotopic composition of Sr in geological reference materials using ICP-MS/MS
This novel method using CH3F as a reaction gas in ICP-MS/MS for the determination of the isotopic composition of Sr without prior Sr isolation from the matrix was used for the analysis of five reference materials of geological origin. The results are shown in Table 4. No significant differences were established between the experimental results and the corresponding reference values. In addition, the precision expressed as standard deviation for n = 5 was not significantly different (F < Fcritical) from that obtained for an in-house standard solution of Sr (n = 10, Table 3), except for BCR CRM 142, for which a very slight difference was found (3.66 > 3.63). Therefore, it can be stated that the approach for Sr isotopic analysis developed in this work allows accurate and precise isotope ratio results to be obtained, without the requirement of using a matrix-matched isotopic standard for mass bias correction, as was required in a similar context (CH3F/Ne-pressurized reaction cell) with a Perkin Elmer Sciex Elan DRC ICP-MS instrument.25| Sample descriptiona | Experimental result ± sb | Reference value ± uncertainty |
|---|---|---|
| a Final concentration of Sr, after appropriate dilution of the reference materials, was 10 μg L−1. b Standard deviation of 5 consecutive measurements. | ||
| USGS AGV-1 Andesite | 0.70408 ± 0.00038 | 0.70406 ± 0.00005 |
| USGS G-2 Granite | 0.70968 ± 0.00021 | 0.70983 ± 0.00006 |
| USGS BHVO-1 Basalt | 0.70337 ± 0.00029 | 0.70347 ± 0.00001 |
| BCR CRM 141 Calcareous Loam Soil | 0.70909 ± 0.00030 | 0.70924 ± 0.00007 |
| BCR CRM 142 Light Sandy Soil | 0.71513 ± 0.00048 | 0.71505 ± 0.00010 |
4. Conclusion
In this work, the capabilities of a novel approach for Sr isotopic analysis using CH3F as a reaction gas in ICP-MS/MS were demonstrated. The method developed was able to remove all interfering species that could hinder Sr isotopic analysis. The removal of matrix elements, before they enter into the reaction cell in MS/MS-mode, diminishes the influence of matrix effects on the final results, thus avoiding the necessity of using a matrix-matched standard, in contrast to the SQ-mode, where the use of a matrix-matched standard is compulsory. The method developed enables accurate and precise (external precision better than 0.05% RSD) determination of the 87Sr/86Sr isotope ratio. Via error propagation using the Kragten approach,51 it was shown that the measurement precision itself dominates the total uncertainty. Inclusion of the contribution from mass bias correction results in an RSD of 0.07%. It was shown that this approach can be successfully applied to the Sr isotopic analysis of reference materials of geological origin, without prior Rb/Sr separation. The robustness of the results obtained for these complex materials suggests that such a method could also be deployed for the analysis of other types of samples for which Sr isotopic analysis could be of scientific interest.Acknowledgements
The UGent authors acknowledge Agilent Technologies for providing them with an ACT-UR research project grant and the Special Research Fund of Ghent University (BOF-UGent) for research project funding. MR acknowledges the funding from the Spanish Ministry of Economy and Competitiveness (Project CTQ2012-33494) and from the Aragón Government (Fondo Social Europeo).References
- C. M. Almeida and M. T. S. D. J. Vasconcelos, J. Anal. At. Spectrom., 2001, 16, 607–611 RSC.
- L. Balcaen, L. Moens and F. Vanhaecke, Spectrochim. Acta, Part B, 2010, 65, 769–786 CrossRef.
- J. Irrgeher, T. Prohaska, R. E. Sturgeon, Z. Mester and L. Yang, Anal. Methods, 2013, 5, 1687–1694 RSC.
- B. Y. Song, J. S. Ryu, H. S. Shin and K. S. Lee, J. Agric. Food Chem., 2014, 62, 9232–9238 CrossRef CAS PubMed.
- J. Fietzke and A. Eisenhauer, Geochem., Geophys., Geosyst., 2006, 7, 1–6 CrossRef.
- F. Vanhaecke, L. Balcaen and D. Malinovsky, J. Anal. At. Spectrom., 2009, 24, 863–886 RSC.
- J. S. Becker, H. J. Dietze, J. A. McLean and A. Montaser, Anal. Chem., 1999, 71, 3077–3084 CrossRef CAS PubMed.
- J. S. Becker, Int. J. Mass Spectrom., 2005, 242, 183–195 CrossRef CAS.
- W. Neumann and E. Huster, Earth Planet. Sci. Lett., 1976, 33, 277–288 CrossRef CAS.
- R. C. Capo, B. W. Stewart and O. A. Chadwick, Geoderma, 1998, 82, 197–225 CrossRef CAS.
- F. Vanhaecke, G. De Wannemacker, L. Moens and J. Hertogen, J. Anal. At. Spectrom., 1999, 14, 1691–1696 RSC.
- F. Begemann, K. R. Ludwig, G. W. Lugmair, K. Min, L. E. Nyquist, P. J. Patchett, P. R. Renne, C. Y. Shih, I. M. Villa and R. J. Walker, Geochim. Cosmochim. Acta, 2001, 65, 111–121 CrossRef CAS.
- L. Moens and N. Jakubowski, Anal. Chem., 1998, 70, 251A–256A CrossRef CAS.
- N. Jakubowski, L. Moens and F. Vanhaecke, Spectrochim. Acta, Part B, 1998, 53, 1739–1763 CrossRef.
- C. Latkoczy, T. Prohaska, G. Stingeder and M. Teschler-Nicola, J. Anal. At. Spectrom., 1998, 13, 561–566 RSC.
- F. Vanhaecke, L. Moens, R. Dams, I. Papadakis and P. Taylor, Anal. Chem., 1997, 69, 268–273 CrossRef CAS.
- L. Balcaen, I. De Schrijver, L. Moens and F. Vanhaecke, Int. J. Mass Spectrom., 2005, 242, 251–255 CrossRef CAS.
- P. Galler, A. Limbeck, S. F. Boulyga, G. Stingeder, T. Hirata and T. Prohaska, Anal. Chem., 2007, 79, 5023–5029 CrossRef CAS PubMed.
- D. De Muynck, G. Huelga-Suarez, L. Van Heghe, P. Degryse and F. Vanhaecke, J. Anal. At. Spectrom., 2009, 24, 1498–1510 RSC.
- S. D. Tanner, V. I. Baranov and D. R. Bandura, Spectrochim. Acta, Part B, 2002, 57, 1361–3452 CrossRef.
- S. F. Boulyga and J. S. Becker, Fresenius' J. Anal. Chem., 2001, 370, 618–623 CrossRef CAS PubMed.
- J. J. Sloth and E. H. Larsen, J. Anal. At. Spectrom., 2000, 15, 669–672 RSC.
- Y. L. Chang and S. J. Jiang, J. Anal. At. Spectrom., 2001, 16, 1434–1438 RSC.
- F. Vanhaecke, L. Balcaen, G. D. Wannemacker and L. Moens, J. Anal. At. Spectrom., 2002, 17, 933–943 RSC.
- L. Moens, F. Vanhaecke, D. R. Bandura, V. I. Baranov and S. D. Tanner, J. Anal. At. Spectrom., 2001, 16, 991–994 RSC.
- F. Vanhaecke, L. Balcaen, I. Deconinck, I. D. Schrijver, C. M. Almeida and L. Moens, J. Anal. At. Spectrom., 2003, 18, 1060–1065 RSC.
- P. Cheng, G. K. Koyanagi and D. K. Bohme, Anal. Chim. Acta, 2008, 627, 148–153 CrossRef CAS PubMed.
- D. R. Bandura, V. I. Baranov and S. D. Tanner, J. Anal. At. Spectrom., 2000, 15, 921–928 RSC.
- M. Resano, P. Marzo, J. Pérez-Arantegui, M. Aramendía, C. Cloquet and F. Vanhaecke, J. Anal. At. Spectrom., 2008, 23, 1182–1191 RSC.
- S. Stürup, Anal. Bioanal. Chem., 2004, 378, 273–282 CrossRef PubMed.
- M. R. Flórez, M. Aramendía, M. Resano, A. C. Lapeña, L. Balcaen and F. Vanhaecke, J. Anal. At. Spectrom., 2013, 28, 1005–1015 RSC.
- P. Rodríguez-González, J. M. Marchante-Gayón, J. I. García Alonso and A. Sanz-Medel, Spectrochim. Acta, Part B, 2005, 60, 151–207 CrossRef.
- I. S. Begley and B. L. Sharp, J. Anal. At. Spectrom., 1997, 12, 395–402 RSC.
- S. F. Boulyga, J. L. Matusevich, V. P. Mironov, V. P. Kudrjashov, L. Halicz, I. Segal, J. A. McLean, A. Montaser and J. S. Becker, J. Anal. At. Spectrom., 2002, 17, 958–964 RSC.
- P. P. Coetzee and F. Vanhaecke, Anal. Bioanal. Chem., 2005, 383, 977–984 CrossRef CAS PubMed.
- C. P. Ingle, B. L. Sharp, M. S. A. Horstwood, R. R. Parrish and D. J. Lewis, J. Anal. At. Spectrom., 2003, 18, 219–229 RSC.
- L. Yang, Mass Spectrom. Rev., 2009, 28, 990–1011 CrossRef CAS PubMed.
- Q. Xie and R. Kerrich, J. Anal. At. Spectrom., 2002, 17, 69–74 RSC.
- S. Díaz Fernández, N. Sigishama, J. Ruiz Encinar and A. Sanz-Medel, Anal. Chem., 2012, 84, 5851–5857 CrossRef PubMed.
- L. Balcaen, E. Bolea-Fernandez, M. Resano and F. Vanhaecke, Anal. Chim. Acta, 2014, 809, 1–8 CrossRef CAS PubMed.
- S. D. Tanner and V. I. Baranov, J. Am. Soc. Mass Spectrom., 1999, 10, 1083–1094 CrossRef CAS.
- X. Zhao, G. K. Koyanagi and D. K. Bohme, J. Phys. Chem. A, 2006, 110, 10607–10618 CrossRef CAS PubMed.
- E. Bolea-Fernandez, L. Balcaen, M. Resano and F. Vanhaecke, Anal. Chem., 2014, 86, 7969–7977 CrossRef CAS PubMed.
- E. Bolea-Fernandez, L. Balcaen, M. Resano and F. Vanhaecke, Anal. Bioanal. Chem., 2015, 407, 919–929 CrossRef CAS PubMed.
- T. Ohno, Y. Muramatsu, Y. Shikamori, C. Toyama, N. Okabe and H. Matsuzaki, J. Anal. At. Spectrom., 2013, 28, 1283–1287 RSC.
- M. Tanimizu, N. Sugiyama, E. Ponzevera and G. Bayon, J. Anal. At. Spectrom., 2013, 28, 1372–1376 RSC.
- L. Balcaen, G. Woods, M. Resano and F. Vanhaecke, J. Anal. At. Spectrom., 2013, 28, 33–39 RSC.
- T. Ohno and Y. Muramatsu, J. Anal. At. Spectrom., 2014, 29, 347–351 RSC.
- J. Zheng, W. Bu, K. Tagami, Y. Shikamori, K. Nakano, S. Uchida and N. Ishii, Anal. Chem., 2014, 86, 7103–7110 CrossRef CAS PubMed.
- G. P. Russ, in Applications of Inductively Coupled Plasma Mass Spectrometry, ed. A. R. Date and A. L. Gray, Blackie, Glasgow, 1989 Search PubMed.
- J. Kragten, Analyst, 1994, 119, 2161–2165 RSC.
| This journal is © The Royal Society of Chemistry 2016 |