Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Detection of correlated conformational fluctuations in intrinsically disordered proteins through paramagnetic relaxation interference†
D.
Kurzbach‡
a,
A.
Vanas‡
a,
A. G.
Flamm‡
a,
N.
Tarnoczi
a,
G.
Kontaxis
a,
N.
Maltar-Strmečki
b,
K.
Widder
b,
D.
Hinderberger
b and
R.
Konrat
*a
aDepartment for Structural and Computational Biology Max F. Perutz Laboratories, University of Vienna Vienna Biocenter Campus 5, 1030 Vienna, Austria. E-mail: Robert.Konrat@univie.ac.at
bInstitute for Physical Chemistry Martin-Luther-Universität Halle-Wittenberg von-Danckelmann-Platz 4, 06120 Halle (Saale), Germany
First published on 21st September 2015
Abstract
Functionally relevant conformational states of intrinsically disordered proteins (IDPs) are typically concealed in a vast space of fast interconverting structures. Here we present a novel methodology, NMR-based paramagnetic relaxation interference (PRI), that allows for direct observation of concerted motions and cooperatively folded sub-states in IDPs. The proposed NMR technique is based on the exploitation of cross correlated electron-nuclear dipolar relaxation interferences in doubly spin-labeled proteins and probes the transient spatial encounter of electron-nucleus spin pairs.
Introduction
Intrinsically disordered proteins (IDPs) constitute important hubs in protein interaction networks.1 They play key roles in cellular regulatory linkages thus aiding to maintain the physiological equilibrium. A malfunction is frequently accompanied by severe malady like cancer or neurodegenerative diseases.2,3 However, to date IDP function and structure-function relations have been only vaguely understood.4,5 Although these highly dynamic proteins sample vast and heterogeneous conformational spaces there is evidence for short-lived preformation of binding sites in otherwise disordered structural ensembles.6,7 Paramagnetic relaxation enhancement (PRE) has been established as a powerful tool for probing these sparsely populated and conformationally dynamic states. A paramagnetic spin label is used to enhance the transverse relaxation rates, R2, of amide protons (1HN) in the protein backbone by a rate 1HN–Γ2. The magnitude of 1HN–Γ2 is dependent on the correlation function of the dipole between HN and the unpaired electron, X. It decays with a correlation time τc and the average distance between HN and X by 〈rHN–X−6〉.8–10τc denotes the effective reorientation time of the amide-electron (HN–X) vector.11,12 For two-spin HN–X systems 1HN–Γ2 quantifies the PRE as 1HN–Γ2 = (1/15)((h/2π)μ0γHgμB/4π)2S(S + 1)[4J(0) + 3J(ωL)]〈rHN–X−6〉, where all symbols have their usual meaning.8 Yet, the quantification of PREs, τc and the spectral density functions J(ω) is not straightforward for IDPs.13Several applications of IDPs have been reported demonstrating the validity of the PRE approach.8,14,15 However, since all thermally accessible sub-states contribute to the observed PRE the existence of concerted motions and cooperatively folded segments could not unambiguously be detected. To understand correlated (concerted) structural fluctuations in IDPs we propose a novel technique that exploits paramagnetic relaxation interference (PRI) effects. In our approach and in contrast to conventional PRE techniques we exploit dipole–dipole cross-correlation effects between two spin labels carrying electrons X(1) and X(2) and an amide proton 1HN.
The novel PRI methodology involves PRE measurements using single spin labels, X(1) and X(2), to determine the rates 1HN–Γ2[X(1)] and 1HN–Γ2[X(2)], and a double mutant containing spin labels at both residual positions, X(1) and X(2), to determine 1HN–Γ2[X(1) + X(2)]. The PRI effect is quantified as Δ1HN–Γ2 = 1HN–Γ2[X(1) + X(2)] − {1HN–Γ2[X(1)] + 1HN–Γ2[X(2)]}. The simultaneous presence of two unpaired electrons in spatial proximity leads to interference effects between the X(1)–1HN and X(2)–1HN dipoles. Analogous cross-correlated relaxation mechanisms have been utilized to great advantage in TROSY and Methyl-TROSY techniques to study high-molecular weight systems.16,17 Beyond that cross-correlated NMR relaxation has attracted substantial interest in the past as a powerful tool for studying structure and dynamics of proteins in solution.18 Cross-correlated relaxation arises from interference effects between the fluctuations of two different relaxation mechanisms of the same rank, which are active simultaneously and in a correlated manner. These concerted effects have been shown to be a valuable source of information about the structure and dynamics of proteins, since they are dependent on the relative geometry of the spin system. Typically cross-correlated interference effects can be observed between two different dipolar (D) interactions (D–D), two different chemical shift anisotropy (CSA–CSA) tensors or between a dipolar and a chemical shift anisotropy (D–CSA) interaction. Here a novel X(1)–1HN and X(2)–1HN electron-nucleus dipole–dipole interference term is exploited.
Results and discussion
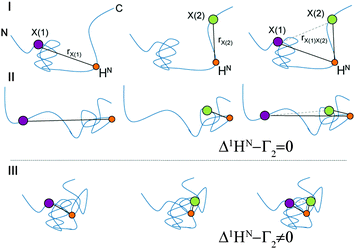
The principle of the presented technique is outlined in Fig. 1. For illustration, we consider the hypothetical case of an IDP that exists in several conformations (I, II and III) displaying differing local compaction of the polypeptide chain. In conformations I and II either the N- or the C-terminal segment is folded and long-range PRE effects are therefore separately observed only for residues located in the compacted regions. The two structured segments undergo uncorrelated folding–unfolding transitions. Thus, the observed PRE effect in the doubly labeled sample is equal to the sum of the individual single-electron (PRE) contributions. In contrast, if conformation III is significantly populated in the ensemble experimental PREs observed for the doubly labeled samples are altered due to dipole–dipole cross-correlation/interference effects. In the doubly labeled case (right side of Fig. 1) significant deviations from the additive sum, 1HN–Γ2[X(1)] + 1HN–Γ2[X(2)] (Δ1HN–Γ2 ≠ 0), are thus observed. The magnitude of Δ1HN–Γ2 is primarily dependent on a term 〈3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1〉, where θ is the angle between the X(1)–1HN and X(2)–1HN dipoles. The angle brackets indicate the effective (“rHN–X−6 filtered”) ensemble (and time) average. We want to emphasize that PRI depicts exclusively properties of the compacted state of a structurally dynamic protein, since the 〈rHN–X−6〉 dependence entails a steep distance dependence of the underlying PRE. Given that individual PRI-effects can be measured as a function of residue and spin label positions this novel technique allows for direct experimental assessment of correlated (concerted) structural fluctuations in IDPs.
θ − 1〉, where θ is the angle between the X(1)–1HN and X(2)–1HN dipoles. The angle brackets indicate the effective (“rHN–X−6 filtered”) ensemble (and time) average. We want to emphasize that PRI depicts exclusively properties of the compacted state of a structurally dynamic protein, since the 〈rHN–X−6〉 dependence entails a steep distance dependence of the underlying PRE. Given that individual PRI-effects can be measured as a function of residue and spin label positions this novel technique allows for direct experimental assessment of correlated (concerted) structural fluctuations in IDPs.
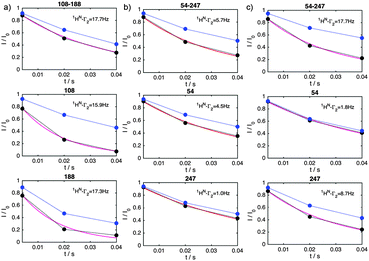
We illustrate this novel methodology with an application to the IDP Osteopontin (OPN) and the brain acid soluble protein 1 (BASP1).19 It is well-known that OPN samples are extended as well as small populations of transiently folded and compacted conformations (cf.Fig. 1).20 The latter are central to substrate interactions.14,21 For OPN we performed PRI measurements on a 220 amino acid (aa) long metastasis-associated,21 truncated form (aa 47–264 of full-length OPN). Four singly and six doubly spin-labelled OPN cysteine mutants were produced by combining four labelling sites: C54, C108, C188 and C247.20 MTSL (S-(1-oxyl-2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-3-yl)methyl methanesulfonothioate) labels were used to introduce stable unpaired electrons. Fig. 2a–c, display prototypical PRE 1HN–Γ2 data obtained for residues 68 of C108–C188, 119 of C108–C18 and 226 of C54–247. 1HN–Γ2 rates were obtained using three-point measurements as adapted from the approach of Clore and co-workers.22 We observed significantly different PRIs, Δ1HN–Γ2, between the different residues indicating significant heterogeneity of the conformational ensemble of OPN in solution. In order to rule out intermolecular PRE effects control experiments were performed using 14N-MTS-labeled and 15N wild-type (for detection) OPN. Corresponding data are given in the ESI.† To demonstrate that indeed electron-nucleus dipole–dipole interference terms constitute the relevant factors we measured PRE data at different fields (600 and 800 MHz). The obtained values were found to be independent of magnetic field strength thus corroborating the relevance of dipole–dipole cross-correlation effects (see ESI†). The latter is further validated by electron T1 times that have been exemplarily determined for the system C54–C188 at 50 K: C54: 804 ± 4 μs, C188: 710 ± 11 μs and C54–C188: 706 ± 5 μs. These values indicate the spatial proximity of the two spin labels in the double mutant allowing for significant inter-electron dipolar coupling. Finally, good agreement between experimental and theoretical 1HN–Γ2 rates was obtained employing a formalism described by Kay and co-workers23 for transverse relaxation in AMX spin systems (see Fig. 2). During the relaxation period non-vanishing dipole–dipole CCRs lead to mixtures of in-phase and doubly anti-phase coherences and thus to differential weighting of the individual multiplet components (αα, βα, αβ and ββ), depending on the sign of CCR. Most importantly, and as shown by Kay and co-workers23 the diagonal elements of the (transverse) relaxation matrix (R(αα,αα) = R(ββ,ββ) and R(αβ,αβ) = R(βα,βα)) are larger than the off-diagonal (cross-relaxation) elements (e.g., R(αα,αβ)). The only sizeable off-diagonal element is R(αβ,βα), the inter-electron NOE as it is determined by the zero-frequency spectral density function J(ωeA − ωeB), ωeA and ωeB being the (identical) electron Larmor frequencies. Contributions from electron longitudinal relaxation (T1) were estimated based on experimental electron T1 values.24,25 Taking this and published electron T1 values into account and assuming a protein correlation time of about 10 ns suggests an electron T1 for the protein-bound MTSL of several tenth of μs for the magnetic field strength used in our study. It can thus be concluded that the inter-electron dipolar cross-relaxation R(αβ,βα) plays a pivotal role and that the individual multiplet components do not uniformly interchange. Further fundamental insights can be obtained by formulating spin relaxation in the framework of singlet and triplet states in radical pairs employing product operators. In the product basis {α, β} the density operator for the singlet state is S0 = 1/√2(αβ − βα), while the triplet states are defined as {T1+ = 1/√2(αα), T1− = 1/√2(ββ) and T10 = 1/√2(αβ + βα)}. Furthermore, the singlet state can be written as a linear combination of the identity matrix E, longitudinal two-spin order SZASZB and zero-quantum coherence {ZQC}x, S0 = 1/4E − SZASZB + {ZQC}x. Likewise the triplet state T10 can be formulated as T10 = 1/4E − SZASZB − {ZQC}x. Dipole–dipole cross-correlation leads to a mixture of in-phase HX and doubly anti-phase 4HXSZASZB, which can be written as linear combination of HXS0 and HXT10.26 It is well established that singlet-states show favorable relaxation properties.27,28 For example, inter-electron dipolar interactions are not relevant for the relaxation of the singlet-state S0. Chemical shift anisotropy (or g-anisotropy) contributions are reduced, too. Therefore, we conclude that the lifetime of HXS0 will be significant and sufficiently long to be observable in the NMR experiment. Differential relaxation due to dipole–dipole cross-correlation will thus manifest itself in different (effective) transverse relaxation times Γ2–1HN.
Fig. 3 shows experimental residue plots of PRI values obtained for the six doubly labelled OPN systems (C54–C188, C54–C108, C108–C247, C108–C188, C188–C247 and C54–C247). The data clearly show that significantly different PRIs are obtained depending on the positions of the spin label(s). The observation of significant PRIs indicates the simultaneous spatial proximity of the two labelling sites in the vicinity of the observed 1HN. Thus, concerted participation of individual protein segments in the formation of a compacted state of an IDP may be deduced from the PRI-residue plots in Fig. 3.
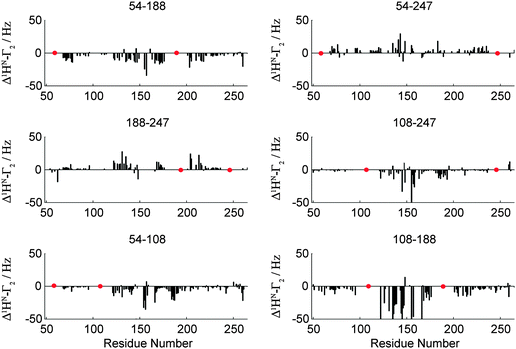 | ||
| Fig. 3 Δ1HN–Γ2 (PRI) cross-correlation rates for a set of six double mutants (indicated) of OPN. Data for all mutants and experimental details are given in the ESI.† Red dots indicate labeling sites. | ||
While largely positive PRIs were observed for the double-mutants C54–C247 and C188–C247, negative values were found when the spin labels were attached in the central (core) region 100–190 of OPN. It can thus be concluded that the conformational ensemble contains significantly compacted sub-states with distinct spatial arrangements. In these compact states conformational averaging is limited resulting in non-zero averaging of the geometric term 〈3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1〉. This is in agreement with our earlier findings that localized a compacted conformation to this region between aa 100 and 190 of OPN.20,21
θ − 1〉. This is in agreement with our earlier findings that localized a compacted conformation to this region between aa 100 and 190 of OPN.20,21
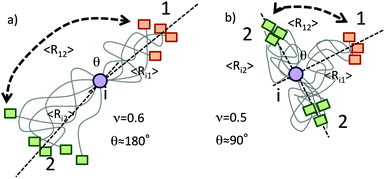
At first glance, it seems to be counterintuitive that individual segments in IDPs display significantly different conformational averaging with sizeable residue 〈3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1〉. However, it is illustrative to analyze the dipole–dipole interference terms in the framework of Flory’s theory for polymers. An outline is given in Fig. 4. Depending on the stiffness/extension of the amino acid chain (quantified by the scaling exponent, ν) the average angle inclined by the two dipole vectors X(1)–1HN and X(2)–1HN can significantly vary. The mean square end-to-end distance between two residues separated by N amino acids can be expressed as 〈r2〉 ∝ lmNν (lm being the length of the monomer unit). In extended chains (due to repulsive forces along the chain) one finds 0.5 < ν < 0.6 leading to an average projection angle θ closer to 180° and thus entailing large positive PRIs since Δ1HN–Γ2, ∝ 〈3cos2
θ − 1〉. However, it is illustrative to analyze the dipole–dipole interference terms in the framework of Flory’s theory for polymers. An outline is given in Fig. 4. Depending on the stiffness/extension of the amino acid chain (quantified by the scaling exponent, ν) the average angle inclined by the two dipole vectors X(1)–1HN and X(2)–1HN can significantly vary. The mean square end-to-end distance between two residues separated by N amino acids can be expressed as 〈r2〉 ∝ lmNν (lm being the length of the monomer unit). In extended chains (due to repulsive forces along the chain) one finds 0.5 < ν < 0.6 leading to an average projection angle θ closer to 180° and thus entailing large positive PRIs since Δ1HN–Γ2, ∝ 〈3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1〉 holds. In contrast, in globular ideal coil or collapsed segments one finds 0.3 < ν < 0.5 and θ is closer to 90°. This is accompanied by negative cross-correlation rates. The observation that the compacted core segment (100–190 of OPN)14,20,21 displays negative PRI is in good agreement with our theoretical (Flory polymer theory) considerations and points towards the reliability of the proposed method.
θ − 1〉 holds. In contrast, in globular ideal coil or collapsed segments one finds 0.3 < ν < 0.5 and θ is closer to 90°. This is accompanied by negative cross-correlation rates. The observation that the compacted core segment (100–190 of OPN)14,20,21 displays negative PRI is in good agreement with our theoretical (Flory polymer theory) considerations and points towards the reliability of the proposed method.
A second example for the applicability of our PRI method was found with the human brain acid soluble protein 1 (BASP1). Earlier studies about changes in transverse relaxation times upon variations in environmental pH on the chicken analogue of BASP1 suggest that this protein samples N-terminally compacted states between aa 1 and 60 of the primary sequence.19 A PRI analysis similar to that of OPN described above (see the ESI† for the full data set) evidently displays the N-terminal compaction of BASP1. A spin label at position C3 of the protein chain leads to strong negative PRIs for the N-terminal residues irrespective of the position of the second spin label (C92, C136, C205, see Fig. 5). Like for OPN the observed negative cross-correlation rates are in accordance with small θ values as expected for compacted polypeptide chains. For other spin label positions we observe nearly vanishing Δ1HN–Γ2. Our observations clearly indicate that the N-terminal region of BASP1 transiently samples compact substrates despite the lack of significant secondary 13C backbone chemical shifts for that regions.
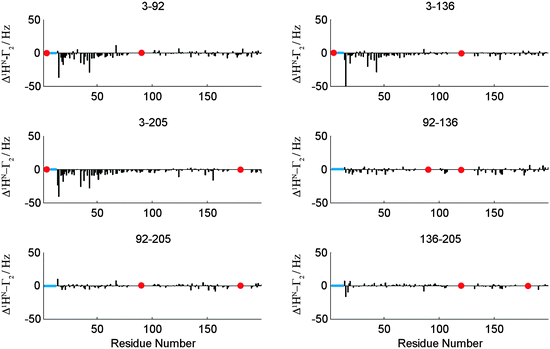 | ||
| Fig. 5 Δ1HN–Γ2 (PRI) cross-correlation rates for a set of six double mutants (indicated) of BASP1. Data for all mutants and experimental details are given in the ESI.† Note that PRI data directly around the indicated labelling sites have been removed due to very low signal intensities at these positions. However, a PRI effect directly around labeling sites would be expected if signal intensities would allow for its detection. Red dots indicate labeling sites. | ||
Conclusions
Concluding, paramagnetic relaxation interference (PRI) exploits relaxation interference between different electron-nucleus dipoles in protein samples carrying two paramagnetic spin labels and yields unique insight into correlated conformation fluctuations of IDPs thereby going beyond static pictures of protein conformations. In contrast to conventional paramagnetic (PRE) NMR techniques PRI probes (transient) triple-contacts between two electrons and 1HNs of the protein backbone and reveals unique information about folded, low-populated conformations. Information about structural dynamics of IDPs and their many different conformers is important as the associated biological processes are frequently controlled by mechanisms like protein domain exchanges/swapping, conformational adaptations or switches, induced-fit and conformational selection-type events. Given its ease of implementation, we anticipate that PRI measurements will significantly broaden the realm of NMR applications in IDP research. In addition to the applications described here the unexpected example of a long-lived spin state involving radical pairs in doubly spin-labeled proteins also offers exciting possibilities for NMR structural biology of folded (globular) proteins. Experiments exploring the possibilities of (structure-based) signal assignment and structure calculation and refinement applications are currently underway in our laboratory.Experimental
Protein preparation
The expression of recombinant natively and 15N labeled quail OPN was carried out as described previously.20,21 Human BASP1 mutants were sub-cloned into pet29b expression vectors and expressed similar to a procedure described by Geist et al.19 After purification via His-affinity chromatography His-tags were cleaved with Thrombin (4 °C, over night). Proteins were tagged with MTSL.20,21 The labeling efficiency was always >95% as determined via DTNB assays. Excess MTSL was removed through dialysis into PBS.For NMR PBS containing 10% D2O was used as a lock solvent. Concentrations were 0.7 mM for OPN and 0.3 mM for BASP1. For EPR the samples were concentrated to 0.7 mM.
For PRE determination the MTSL labels were reduced with ascorbic acid for referencing.
NMR measurements
NMR spectra were recorded at 25 °C on Varian spectrometers operating at 600 and 800 MHz. NMR spectra were processed with NMRPipe29 and analyzed using SPARKY. Spectra were recorded in the PFG sensitivity-enhanced mode for quadrature detection in the 15N indirect dimension with carrier frequencies for 1HN and 15N of 4.73 ppm and 120 ppm, respectively. A squared and 60° phase-shifted sine bell window function was applied in all dimensions for apodization. Time domain data were zero-filled to twice the data set size, prior to Fourier transformation.PRE rates of 15N-labeled OPN mutants C54, C108, C188, C247, C54–C108, C54–C188, C54–C247, C108–C188, C108–C247, C188–C247 and of BASP mutants C3, C92, C136, C205, C3–C92, C3–C136, C3–205, C92–C136, C92–C205, C136–C205 were obtained with three-point measurements as adapted from the approach by Clore and co-workers.22
EPR measurements
All experiments were carried out using a Bruker ELEXSYS E580 spectrometer operating at <9.4 GHz (X-band) with a Flexline split ring resonator ER 4118X MS3. The resonator was over-coupled giving a Q factor of approximately 100. The video bandwidth was set to be 50 MHz. All measurements were made at 50 K with the sample in a frozen glassy state, established using a closed cycle cryostat (ARS Inc.). A two-pulse electron-spin-echo (ESE) sequence (π/2–τ–π–τ–echo) with a π pulse width of 40 ns was used to detect the echo decay spectra. A-two-step phase cycle was employed to eliminate unwanted echoes. The inversion recovery technique (π–t1–π/2–τ–π–echo) was used to measure the longitudinal relaxation time, T1, using an echo detection sequence with a pulse separation time of 200 ns and a π pulse duration of 32 ns. T1 time was deduced form the magnetization recovery curves fitted to the mono exponential function. Measurements of both relaxation times were performed at the field position that respond to the maximum of field-swept ESE detected spectra. The ESE detected spectra were simulated with Matlab® using the Easy-spin routines.30,31Acknowledgements
DK thanks the Alexander von Humboldt Foundation for a Feodor-Lynen scholarship. This work was supported in part by the FWF (P26317-B21 and W-1221-B03).Notes and references
- H. J. Dyson and P. E. Wright, Nat. Rev. Mol. Cell Biol., 2005, 6, 197–208 CrossRef CAS PubMed.
- M. M. Babu, R. van der Lee, N. S. de Groot and J. Gsponer, Curr. Opin. Struct. Biol., 2011, 21, 432–440 CrossRef CAS PubMed.
- P. Tompa, Trends Biochem. Sci., 2012, 37, 509–516 CrossRef CAS PubMed.
- D. M. Korzhnev and L. E. Kay, Acc. Chem. Res., 2008, 41, 442–451 CrossRef CAS PubMed.
- K. Sugase, J. C. Lansing, H. J. Dyson and P. E. Wright, J. Am. Chem. Soc., 2007, 129, 13406–13407 CrossRef CAS PubMed.
- C. K. Fisher and C. M. Stultz, Curr. Opin. Struct. Biol., 2011, 21, 426–431 CrossRef CAS PubMed.
- M. R. Jensen and M. Blackledge, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E1557–E1558 CrossRef CAS PubMed.
- G. M. Clore and J. Iwahara, Chem. Rev., 2009, 109, 4108–4139 CrossRef CAS PubMed.
- N. Bloembergen and L. O. Morgan, J. Chem. Phys., 1961, 34, 842–850 CrossRef CAS.
- I. Solomon, Phys. Rev., 1955, 99, 559–565 CrossRef CAS.
- C. Charlier, S. N. Khan, T. Marquardsen, P. Pelupessy, V. Reiss, D. Sakellariou, G. Bodenhausen, F. Engelke and F. Ferrage, J. Am. Chem. Soc., 2013, 135, 18665–18672 CrossRef CAS PubMed.
- N. Bloembergen, J. Chem. Phys., 1957, 27, 572–573 CrossRef CAS.
- A. Soranno, B. Buchli, D. Nettels, R. R. Cheng, S. Muller-Spath, S. H. Pfeil, A. Hoffmann, E. A. Lipman, D. E. Makarov and B. Schuler, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17800–17806 CrossRef CAS PubMed.
- D. Kurzbach, T. C. Schwarz, G. Platzer, S. Hofler, D. Hinderberger and R. Konrat, Angew. Chem., Int. Ed., 2014, 53, 3840–3843 CrossRef CAS PubMed.
- M. R. Jensen, R. W. H. Ruigrok and M. Blackledge, Curr. Opin. Struct. Biol., 2013, 23, 426–435 CrossRef CAS PubMed.
- J. E. Ollerenshaw, V. Tugarinov and L. E. Kay, Magn. Reson. Chem., 2003, 41, 843–852 CrossRef CAS.
- A. Velyvis and L. E. Kay, J. Am. Chem. Soc., 2013, 135, 9259–9262 CrossRef CAS PubMed.
- D. Kurzbach, G. Kontaxis, N. Coudevylle and R. Konrat, in Intrinsically Disordered Proteins Studied by NMR Spectroscopy, ed. I. Felli and R. Pierattelli, Springer, 2015 Search PubMed.
- L. Geist, M. A. Henen, S. Haiderer, T. C. Schwarz, D. Kurzbach, A. Zawadzka-Kazimierczuk, S. Saxena, S. Zerko, W. Kozminski, D. Hinderberger and R. Konrat, Protein Sci., 2013, 22, 1196–1205 CrossRef CAS PubMed.
- D. Kurzbach, G. Platzer, T. C. Schwarz, M. A. Henen, R. Konrat and D. Hinderberger, Biochemistry, 2013, 52, 5167–5175 CrossRef CAS PubMed.
- G. Platzer, A. Schedlbauer, A. Chemelli, P. Ozdowy, N. Coudevylle, R. Auer, G. Kontaxis, M. Hartl, A. J. Miles, B. A. Wallace, O. Glatter, K. Bister and R. Konrat, Biochemistry, 2011, 50, 6113–6124 CrossRef CAS PubMed.
- J. Iwahara, C. Tang and G. M. Clore, J. Magn. Reson., 2007, 184, 185–195 CrossRef CAS PubMed.
- L. E. Kay and T. E. Bull, J. Magn. Reson., 1992, 99, 615–622 CAS.
- R. Owenius, G. R. Eaton and S. S. Eaton, J. Magn. Reson., 2013, 236, 47–56 CrossRef PubMed.
- I. V. Koptyug, S. H. Bossmann and N. J. Turro, J. Am. Chem. Soc., 1996, 118, 1435–1445 CrossRef CAS.
- G. Zwangenberg and P. J. Hore, Chem. Phys. Lett., 1993, 203, 65–74 CrossRef.
- M. Carvetta, O. G. Johannessen and M. H. Levitt, Phys. Rev. Lett., 2004, 92, 153003 CrossRef PubMed.
- R. Sarkar, P. Ahuja, P. R. Vasos and G. Bodenhausen, Phys. Rev. Lett., 2010, 104, 053001 CrossRef PubMed.
- F. Delaglio, S. Grzesiek, G. W. Vuister, G. Zhu, J. Pfeifer and A. Bax, J. Biomol. NMR, 1995, 6, 277–293 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, Biol. Magn. Reson., 2007, 27, 299–321 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp04858c |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2016 |