 Open Access Article
Open Access ArticleDesigning the structure and folding pathway of modular topological bionanostructures
A.
Ljubetič†
 a,
I.
Drobnak†
a,
H.
Gradišar
ab and
R.
Jerala
*ab
a,
I.
Drobnak†
a,
H.
Gradišar
ab and
R.
Jerala
*ab
aNational Institute of Chemistry, Hajdrihova 19, Ljubljana, Slovenia. E-mail: roman.jerala@ki.si
bExcellent NMR – Future Innovation for Sustainable Technologies, Centre of Excellence, Ljubljana, Slovenia
First published on 15th March 2016
Abstract
Polypeptides and polynucleotides are programmable natural polymers whose linear sequence can be easily designed and synthesized by the cellular transcription/translation machinery. Nature primarily uses proteins as the molecular machines and nucleic acids as the medium for the manipulation of heritable information. A protein's tertiary structure and function is defined by multiple cooperative weak long-range interactions that have been optimized through evolution. DNA nanotechnology uses orthogonal pairwise interacting modules of complementary nucleic acids as a strategy to construct defined complex 3D structures. A similar approach has recently been applied to protein design, using orthogonal dimerizing coiled-coil segments as interacting modules. When concatenated into a single polypeptide chain, they self-assemble into the 3D structure defined by the topology of interacting modules within the chain. This approach allows the construction of geometric polypeptide scaffolds, bypassing the folding problem of compact proteins by relying on decoupled pairwise interactions. However, the folding pathway still needs to be optimized in order to allow rapid self-assembly under physiological conditions. Again the modularity of designed topological structures can be used to define the rules that guide the folding pathway of long polymers, such as DNA, based on the stability and topology of connected building modules. This approach opens the way towards incorporation of designed foldamers in biological systems and their functionalization.
Introduction
The engineering of biomolecular structures has been an important goal for scientists ever since it was discovered that structure and function are largely determined by the primary sequence of building blocks in the biomolecule.1–3 The ultimate challenge for molecular engineers is to design from scratch a polypeptide or polynucleic acid sequence that would spontaneously fold into a predefined structure and perform a specific function, either in vitro or in living cells.4 This would allow us to engineer molecular machines that would be efficiently produced in cells and would be able to perform a variety of tasks at the single-molecule level. Given that all life is driven by such nano-scale machines, the potential is incredible – but so is the challenge. Two distinct problems are involved in this challenge: a structure needs to be identified that will be suitable for performing the desired function, and a primary sequence needs to be designed that will spontaneously assemble into the required structure under the physiological conditions. The target structure must therefore be the most stable (have the lowest free energy) of all possible conformations accessible to the primary sequence. Both problems are exceptionally challenging because the conformational flexibility of biomolecules is vast. The multitude of possible conformational movements far exceeds our ability to even computationally simulate the effects they can have on the stability (energy) and functional efficiency of the biomolecule.4–6 Nature has solved this problem through billions of years of evolution, selecting for functions that improved the fitness of different organisms, however not necessarily functions that are of technological interest to us.Because the problem of biopolymer design is too complex to tackle in our lifetime by a comprehensive (brute force) approach, it needs to be broken down into smaller, simplified sub-problems. An early solution has been to take a naturally occurring protein as a starting point and only tweak specific parts through point mutations or truncations in order to abolish or modify its natural structure and function.7 This represents the basis of the incremental (evolutionary) design and is reasonably straightforward, as long as only small changes are introduced; more radical changes however produce unpredictable outcomes. Taking this approach further, many larger natural proteins can be broken down into distinct structural domains that are able to fold independently from the rest of the protein. Different domains can be mixed and matched to form novel proteins either as a single polypeptide chain or as multiple chains held together by domains that specifically interact with each other.8 A more advanced strategy is to modify the existing domains to engineer specific binding interfaces for other protein domains and for small ligands, resulting in a predictable structure of the complex and potentially novel functions, including those not found in nature.9,10 This is made possible by advances in computational simulations that search a large number of possible conformations and attempt to calculate the stability of each conformation, so that the energetic minimum can be sought. Computational tools like molecular dynamics11–13 or the Rosetta structure modelling suite14,15 are by now well established and can be of great help in determining and designing structures at the atomic level. However, they can still sample only a relatively small part of the conformational space available to biomolecules, so they require some specialized knowledge in order to make the best use of their strengths while being aware of their shortcomings. Some of the most advanced examples in this field include designing protein–protein interfaces with a precise geometry that allows multiple proteins to assemble into symmetric structures like polyhedra9 (Fig. 1) or planar meshes.16
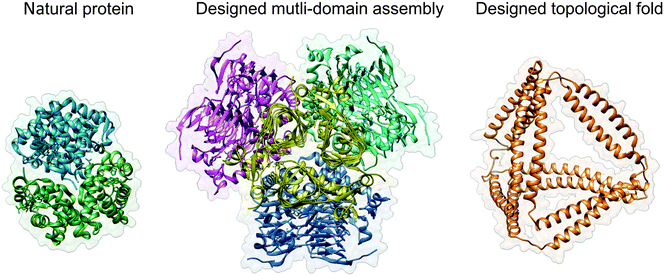 | ||
| Fig. 1 Protein design strategies. Haemoglobin (PDB ID 2DN2) is shown as a typical representative of natural globular proteins. The designed multi-domain assembly (PDB ID 4EGG) is composed of four trimeric subunits, with their contact interfaces carefully designed to produce a symmetric tetrahedral structure. The result is a large, bulky assembly with a solid core, similar in principle to most natural proteins. Designed topological protein composed of concatenated coiled-coil dimer forming modules yields a tetrahedral protein cage with a large cavity in the centre (structural model taken from ref. 24). Images were created with UCSF Chimera.61 | ||
Nucleic acids and polypeptides are the two types of linear programmable biomolecules whose sequence can be modified at will in order to guide the self-assembly of their tertiary structures. Proteins are used in nature to perform most functions as molecular machines, while nucleic acids primarily have a role in storage and translation of heritable information. Using nucleic acids instead of proteins in structure design is a way of making the design problem more tractable since simple, well understood base-pairing rules allow us to engineer very specific intra- or inter-molecular contacts. DNA also tends to adopt a predictable double helical structure whenever two complementary strands come into contact.17 As a result, designing the secondary and even tertiary structures of nucleic acids based on complementary modules is considerably easier than for proteins, but the relative simplicity also has drawbacks. The limited diversity of functional groups found in nucleic acids allows less versatile functionalization and the relatively rigid base-pairing rules allow for less structural plasticity and adaptability compared to proteins. RNA is more flexible in this regard than DNA, but as a result its structure is more difficult to predict and it is particularly susceptible to hydrolysis and degradation by ribonucleases. Additionally, nucleic acids may trigger an immune response within the cytosol of eukaryotic cells.18 Thanks to a wide array of established molecular biology tools and automated chemical synthesis, manipulation of nucleic acids is much simpler than with proteins, but it remains expensive when large quantities are desired.
Spectacular progress in designed DNA nanostructures has been achieved in the last three decades. Several different approaches, including multi-strand assembly, hierarchical assembly, scaffold-based assembly and single strand assembly (reviewed in ref. 19), have been successfully demonstrated. It is now possible to assemble almost any selected 3D shape using designed DNA with a resolution of several nm, with particle sizes ranging from 100 nm up to several micrometers in the case of periodic assemblies. The key to this approach is modularity, where the final structures are assembled from modules based on complementary antiparallel strands, whose stability and orthogonality is well understood and can be designed at will. DNA origami,20 the technique where a single long chain, typically from a bacteriophage, is shaped by a large number of shorter oligonucleotides that act as clamps, has proven to be very successful in designing a variety of 2D and 3D nano-scale structures.21 Most DNA nanostructure methods require a separate synthesis of many different oligonucleotides, followed by careful mixing and slow annealing to make sure the correct (most stable) structure is obtained.
In contrast, we focus here on the topologically constrained folding of single chain biopolymers (Fig. 2), a process that more closely mimics the way natural biomolecules fold. The advantage of a single chain design is that each unit folds independently of others, without the need for mixing and assembling different components in the correct ratio. In principle, single chain biopolymers can therefore be produced and folded in vivo, as long as we can avoid misfolding and non-specific interactions with other cellular components. In addition to the design of the structure as the unique energetic minimum, we need to design a primary sequence that will not only give the correct final structure, but will also follow a smooth and efficient folding pathway that avoids aggregation-prone intermediates and misfolded states.22,23 Designing the folding pathway represents a major challenge, both for proteins and for DNA-based nanostructures, but overcoming this challenge will open the door to efficient in vivo production of designed molecular machines and their integration with existing biological systems. This would greatly advance many technological applications, ranging from cost-effective production of biomaterials, engineering new biosynthetic pathways, to cell-based therapeutic approaches to combat diseases.
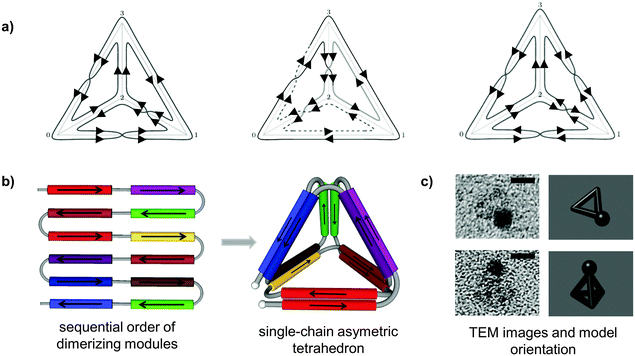 | ||
| Fig. 2 Topological design of the tetrahedral fold from a single polypeptide chain. (a) Topological solutions for double Eulerian trails assembling a single-chain tetrahedral path. Three distinct topoisomers are possible, built either from four parallel and two antiparallel, or three parallel and three antiparallel coiled-coil pairs. (b) A single chain is composed of twelve coiled-coil forming modules, linked in defined order that self-assembled into a cage-like tetrahedral nanostructure. The chain path is threaded through the edges of a tetrahedron traversing each edge exactly twice, so that the path interlocks the structure into a stable shape formed by the six coiled-coil dimers. In this particular topology, two coiled-coils edges are antiparallel and four parallel.24 (c) Representative tetrahedral particles from TEM images and projections of a tetrahedron in the matching orientation are shown. Samples on grids were stained first with 1.8 nm NiNTA-nanogold beads via His-tag followed by the uranyl positive staining. Scale bars represent 5 nm.24 | ||
Topology-based modular structure design
Topological polypeptide and polynucleic acid folds (topofolds) are based on the idea of taking several orthogonal pairs of building blocks (peptide or oligonucleotide segments that only bind to their specific cognate pair) and concatenating these modules into a single or a small number of chains. The sequence of modules in the chain is designed so that only one three-dimensional arrangement allows all modules to pair up with their partners (Fig. 2b).19,24 The resulting biomolecular structure is stabilized by specific interactions between cognate pairs of modules and their topological arrangement ensures that forming any other structure would sacrifice at least some of these stabilizing contacts, making competing structures energetically disfavoured. Topology-based structure design effectively reduces the vastly complex problem of folding several hundred amino acids or nucleotides in 3D space by balancing a large number of weak long range cooperative interactions into the much simpler problem of arranging a small number of modules into a continuous chain that describes the desired shape. Since this problem can be solved mathematically through the use of graph theory,25 designing completely novel biomolecular (topo)folds becomes in principle very simple. To translate these designs into actual structures, however, requires a careful choice of building modules (Fig. 3). The key requirement here is orthogonality: each building block should only bind to its cognate pair and not to any other part of the chain. In nucleic acids, designing orthogonal oligonucleotide duplexes is relatively straightforward, since we have reliable methods for predicting duplex stability from the oligonucleotide sequence.26,27 For protein design, such tools need to be further developed.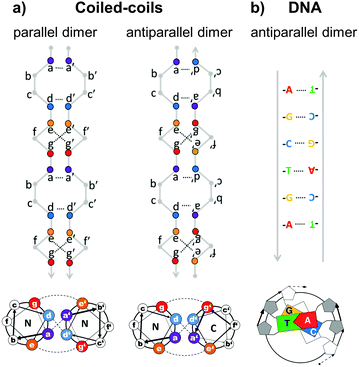 | ||
| Fig. 3 Comparison of the specificity underlying protein forming coiled-coil dimer and DNA duplex building modules. (a) Coiled-coils are characterized by a periodic heptad repeat with residue positions labelled as abcdefg. Specific association of chains is governed by hydrophobic interactions between amino acid residues at positions a and d, forming a hydrophobic spine running the length of the coiled-coil and electrostatic interactions between oppositely charged residues at positions e and g, defining either parallel or antiparallel orientation of strands.28 (b) DNA duplex specificity is determined by the Watson–Crick nucleic base complementarity (A–T, C–G). These specific pairwise interactions give rise to a stable double-helical structure in an antiparallel orientation. | ||
Coiled-coil dimers as the building blocks of designed topological protein folds
The closest approximation to the complementarity of DNA duplexes are coiled-coil dimers. Coiled-coils are ubiquitous protein structural elements and are often found in transcription factors. They are composed of alpha-helices that coil around each other with a mild twist. The basic rules governing the formation of coiled-coils, their orientation and oligomerization state, and their binding specificity have been established.28–33 The characteristic primary sequence pattern of regular coiled-coil dimers is composed seven-residue (heptad) repeats, labelled a–f, with hydrophobic amino acids at positions a and d, and charged amino acids at positions e and g (Fig. 3a). The residues at positions a and d stabilize the coiled-coil duplex through hydrophobic interactions with their opposite number from the partner chain, forming a hydrophobic spine running along the centre of the coiled-coil interface. This hydrophobic spine is flanked by electrostatic interactions between charged residues at positions e and g. By adjusting the pattern of charged and hydrophobic residues at the coiled-coil interface, researchers have designed libraries of orthogonal coiled-coils34–38 that are suitable for topofold design and have already been used to construct a single-chain topofold tetrahedron.24In contrast to DNA duplexes which are always antiparallel, coiled-coil dimers may form in either a parallel or an antiparallel orientation, which expands the number of accessible designed topologies. An additional advantage of designed coiled-coil dimers is that the specificity of pairing is defined primarily by 4 (positions a, d, e, g) out of the 7 residues of the repeat, leaving the 3 remaining residues (positions b, c, f) available for the introduction of side chains that provide different functionalities. Many coiled-coil dimer forming peptides have been experimentally tested and some of them have been specifically selected or designed for their lack of cross-reactivity.34–38 Other sets of orthogonal protein–protein binding pairs could in principle also be used to construct topofold proteins, but coiled-coils (and nucleic acid duplexes) have the advantage of being relatively thin and long, which makes them useful for constructing cage-like structures around solvent-accessible cavities (Fig. 1 and 4).
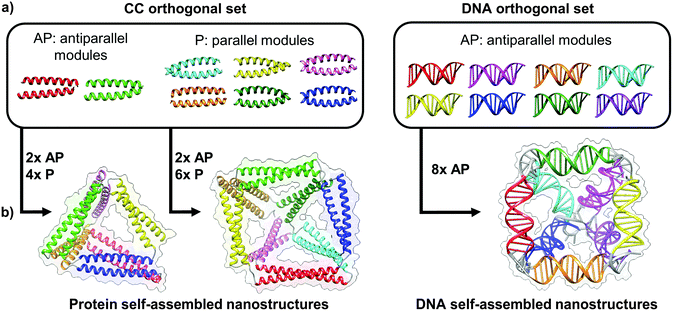 | ||
| Fig. 4 Toolbox of orthogonal dimer forming module set enables formation of designed topological polyhedral folds from a single chain. (a) The protein toolbox consists of orthogonal dimeric coiled-coils (CC), which can bind in either parallel (P) or anti parallel (AP) orientation. The DNA toolbox offers a larger number of orthogonal building blocks, though all are limited to the antiparallel orientations.39 (b) The size of the orthogonal set limits the diversity and complexity of folds that can be constructed. While antiparallel and parallel orientations of coiled-coil dimers allows in principle construction of any type of a protein polyhedron, the antiparallel only orientation of DNA building blocks restricts the selection of polyhedra, with square pyramid as the smallest single chain antiparallel polyhedron.19 | ||
Designed single-chain polypeptide polyhedra
Design of a single-chain topofold polyhedron begins by determining what topology of orthogonally dimerizing modules will give rise to the specified final shape. The desired shape of a polyhedron is deconstructed into the edges which are to be composed of rigid coiled-coil dimers (Fig. 4). The polypeptide path is then threaded as an Eulerian path through the edges of a polyhedron, traversing each edge exactly twice (Fig. 2a). The solution to this mathematical problem is a topology of pairwise interacting segments: the two chain segments that traverse the same edge of the polyhedron must form a contacting pair. Orthogonal coiled-coil dimer-forming segments are concatenated into a single polypeptide chain so that their pairwise interactions will produce the required topology in a unique way (Fig. 2b). The coiled-coil segments can be engineered independently and reused in many different topological designs. Unlike natural protein domains, this type of fold is based on topology rather than on packing of the hydrophobic protein core. This allows topological protein cages to enclose large hydrophilic cavities, whose shape and size can in principle be adjusted (Fig. 1). Another important advantage of the topology-based design in comparison to the design of cages composed of oligomerizing domains is the ability to design asymmetric structures where each edge or vertex can be addressed independently to introduce different functionalities such as introduction of binding or catalytic sites, encapsulation of small molecules etc. This approach enables the construction of entirely new protein folds unseen in nature, such as tetrahedron, square pyramid and bipyramid.The proof of principle of this strategy was experimentally demonstrated with the design and characterization of the modular self-assembled tetrahedron as the simplest three-dimensional geometric object (Fig. 2).24 The polypeptide chain for a monomeric tetrahedral structure was composed of 12 designed coiled-coil forming peptide modules, capable of forming six orthogonal coiled-coil dimers, four parallel and two antiparallel. The building modules selected from a toolbox of designed orthogonal coiled-coil dimers were concatenated into a defined order and linked by short, flexible peptide linkers that formed the vertices of the tetrahedron. The polypeptide was produced in recombinant form in E. coli and purified in the unfolded form. Self-assembly was achieved at low protein concentration by slow dialysis into denaturant-free buffer, resulting in a nanostructure with edges around 5 nm. The tetrahedral-shaped structure was confirmed by atomic force microscopy and transmission electron microscopy imaging (Fig. 2c), secondary structure content and the correct topology by the reconstitution of the split fluorescent protein linked to the N- and C-terminus of the tetrahedral polypeptide.24
Advantages and limitations of designed modular topofolds
The major advantages of topofolds over other designed protein nanostructures is that they can be made of thin building blocks, such as coiled-coils, rather than bulky globular domains. This enables the design of completely novel folds unlike any seen in nature, with cavities for accommodating extra cargo. Furthermore, as single-chain biomolecules, topofolds have the distinct advantage that they can fold spontaneously, without the need for mixing, denaturing, and slowly annealing multiple biomolecular chains as is common in the production of designed nucleic acid structures. Topology-based structure design is equally well suited to the design of proteins and nucleic acids, so the type of biomolecule can be chosen according to the requirements of the specific application.39There are, however, a number of practical limitations to topology-based structure design. The main limitation for protein-based nanostructure design is the availability of orthogonal building blocks. Although a substantial number of coiled-coil dimers has been designed and characterized, orthogonality, i.e. a lack of cross-reactivity, has only been demonstrated for a few relatively small subsets compared to the possibilities of nucleic acids.34,35,37,38 The current coiled-coil toolbox suffices for designing simple polyhedral structures such as the tetrahedron or square pyramid (Fig. 4), but a larger set of orthogonal pairs will be needed to construct more complex shapes with much larger numbers of edges. Expanding the pool of orthogonal coiled-coil pairs is therefore a priority and remains an active area of research. On the other hand, designing orthogonal duplexes is much simpler for DNA nanostructures, although nucleic acids have the disadvantage of only forming antiparallel duplexes, which imposes some limits on what single chain topologies can be designed. For example, a single-chain tetrahedron cannot be constructed without the use of parallel strands, although it is possible to construct either a two-chain tetrahedron or a square pyramid using DNA. By contrast, it has been shown that any polyhedron could in principle be constructed from a single chain if we have both parallel and antiparallel interacting modules at our diposal.24 Another limitation which has to be taken into account for the more complex structures is that due to a relatively large number of interacting modules and the possibility of forming topological knots, the biopolymer chain may have difficulty finding its energetic minimum. To avoid partially folded intermediates that are kinetically stable or even aggregation-prone, the folding pathway needs to be considered.
Design of the folding pathway
The folding problem
Correct folding, i.e. how the 3D structure is obtained from a linear chain of building blocks, underlies all functions of proteins in the cell. Misfolding of just a single type of protein, out of thousands of proteins expressed by cells, can decrease the fitness of the organism or may even be lethal.40In view of its outstanding interest to all areas of life, protein folding has been studied for more than 50 years. It was realized that a random search of all possible conformations is not a feasible folding mechanism (i.e. the Levinthal paradox5), since folding would require very long timescales, but proteins fold on the sub-second timescales. A proposed solution to Levinthal's paradox was that proteins fold through distinct intermediate states in a well-defined pathway.41 The pathways were defined in terms of abstract states based on kinetic models (i.e. how many different kinetic constants are observed in macroscopic refolding experiments). From further experimental evidence, especially hydrogen–deuterium exchange mass spectroscopy and mutational studies, emerged a more statistically oriented “new view”.42 The new view explains the folding of proteins in terms of a free energy folding funnel. The folding of proteins in this view is based on a downhill energetic bias, where the “ruggedness” of the energy landscape is the cause for the observed kinetic intermediates. The native state could in theory be reached through multiple stochastic pathways that are difficult to predict or observe and characterize experimentally.
The views are basically different aspects (the macroscopic and the microscopic) of the folding process. The Foldon hypothesis43,44 reconciles both views, by proposing that proteins are multistate objects built form small (usually ∼30 amino acids long) separately cooperative foldon units. Only a few foldons need to be found by a random search, while the formation of the subsequent foldons may be guided by those that are already formed. Multiple pathways are possible if the cooperativity between certain foldons is weak.
In protein topofold structures each coiled-coil edge could be considered a separate discrete foldon. Equally in DNA topofold structures each complementary module represents a foldon. As will be shown later, the stability of foldon units and their topology enables some degree of control over the folding pathway by changing the order in which the foldons form.
Although most attention has been aimed at the folding of proteins, in recent years there has been an increased interest in the folding of RNA,45 DNA46 (in DNA origami) and synthetic foldamers47 that aim to mimic the natural biomolecules.
Benefits of designing the folding pathway
While the folding problem of natural proteins is in itself fascinating, its complexity presents a serious constraint for designable bionanostructures. Only structures that have favourable folding kinetics would be able to fold under the physiological conditions and in the crowded cellular environment. Fast folding kinetics would have important advantages for any technological applications and particularly for the introduction of designed bionanomolecules into cells for therapeutic applications, sensors and other uses. Additionally the ability to shape the folding pathways would allow better understanding of natural folds and dynamics of molecular machines.So far most of the designed DNA nanostructures have been assembled by a slow annealing process in a narrowly defined range of temperature and concentrations of building elements, typically taking several hours or even days of slow cooling in order to achieve a reasonable folding yield.48 The ability to control the folding process would also enable the design of topologically knotted structures. Knotted structures have significant technological potential, since their thermal49 and mechanical50 properties are enhanced, similar to macroscopic knots, for example. Formation of knots is not very common in natural protein tertiary structures, due to the demanding kinetics of their folding, which usually involves slipknots. Most frequent protein knots are trefoil knots (31), although knotted structures with a crossing number of six have recently been determined.51 A knotted protein has been designed by gene fusion52 and exhibited higher thermal stability than the unknotted analogue. Folding of both proteins was reversible, but unsurprisingly the knotted protein exhibited 20 times slower folding kinetics.
Folding of knotted designed biopolymers is so challenging because the chain needs to be threaded through previously formed loops in the correct predetermined sequential order, which requires a strategy to control the folding pathway.52–54 Modular topological bionanostructures represent an excellent opportunity to simplify and manipulate the folding pathway due to the uncoupled yet well-understood and tuneable pairwise interactions that define the fold.
Circuit topology and folding
Topology studies the properties of objects that are preserved through continuous deformations. For example a circle, ellipse, and a square are all topologically equivalent, since they can be interconverted by stretching. Focusing only on the object's topology greatly condenses the structural information and makes any topological conclusions immediately applicable to a wide class of different 3D objects (such as DNA, RNA and proteins). The circuit topology55 of a linear chain with several binary contact sites can be defined by classifying the pairwise relations between any two contacts as either parallel (P), cross (X) or series (S) as shown in Fig. 5a. Such a definition is complete (in the sense that any two pairs of contacts in any linear chain can be classified), invariant to inter-contact distances and can be used to establish topological equivalence. Contact order (the average separation between contact sites in the chain) and the size of the chain are correlated to the folding rate56,57 although the deeper reasons for this connection are still emerging.58 Mashaghi et al.55 propose that topology guides the folding dynamics and therefore also affects the folding rate. Their topological simulations of folding have shown that for chains with an equal contact order, those with a higher fraction of parallel or cross relations should fold faster. The acceleration is due to the fact that parallel and cross relations exhibit cooperativity, as one formed contact brings the other segments closer together and in this way reduces the overall folding time. Some folding steps can also be topologically forbidden, for example those that would require the unbinding of previously formed contacts. Topofold structures are perfectly suited to experimentally test these predictions, as each coiled coil segment or DNA module can be considered as a single contact.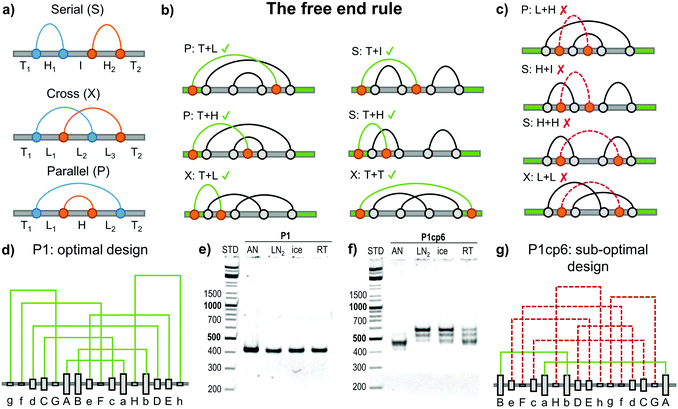 | ||
| Fig. 5 Design of the folding pathway of twisted topological polyhedra based on the “free end rule”. (a) Any two contact pairs in a linear chain (shown as blue and orange dots) can be classified either in a series (S), cross (X) or parallel (P) relation. The remaining segments can be classified either as a free terminus (T), a hairpin loop (H), an internal loop (L) or an internal segment (I).55 Subsequent contacts may form either favourable or unfavourable folding steps, where the previous connection needs to be unfolded before formation of a new contact. (b) Favourable steps include at least one segment having “free end “. (c) Unfavourable folding steps are hindered either topologically or kinetically due to the previous arrangement of the grey contacts. (d) The optimal topological design (P1) of a single chain (DNA) pyramid with a defined order of the formation of connections. Modules are formed in the alphabetical order with “Aa” being the most stable and the first contact to form. No violations of the free end rule are present. (e) Experimentally the DNA pyramid folded rapidly and with high yield under all conditions.59 AN – thermal annealing, LN2 – quenching with liquid nitrogen, ice – quenching with ice, RT – room temperature cooling. (f) Experimental folding of the sub-optimal circular permutation (P1cp6) design. (g) A circular permutation of the optimal design where the P1 sequence is circularly shifted by six positions to the left in the chain. This permutation introduces six unfavourable steps (shown with a dashed red line). This design did not fold into a DNA pyramid even by slow annealing show in panel (f). More detail is given in Kočar et al.59 | ||
Establishing the rules for designing the folding pathway of twisted linear polymers
The large majority of designed DNA nanostructures have been composed of a single very long and multiple short chains (even more than a thousand strands have been used21). Such multi-strand design removes some kinetic folding constraints, but the large number of components represents a disadvantage for many applications, introduces concentration dependence and makes in vivo implementations very difficult. Recently, design rules for folding of highly knotted single chain DNA structures were elucidated and demonstrated experimentally on a single chain DNA square pyramid.59Topofold structures constructed of twisted pairwise interacting polymers, such as a DNA double helix, may contain many kinetically or topologically disfavoured folding steps, particularly in cases where the contact segments exceed one turn of a helix (approx. 10 bp), since it may introduce topological knots. Depending on the initial folding steps (Fig. 5a) the remaining segments can be classified either as a free unstructured terminus (T), a hairpin loop (H), an internal loop (L) or an internal segment (I).59
Pairing of the remaining free modules is affected by the connections already formed. For example, paring of modules between loops (e.g. L + H, H + H and L + L, Fig. 5c) is topologically hindered, as the modules are unable to wrap around each other to form a full-length double helix without unlinking existing connections (providing each of the modules is longer than one turn of the double helix). Threading of previously formed loops through another already formed loop (e.g. I + H, Fig. 5c) is also kinetically disfavoured, as demonstrated by both simulations and experimental results.59
The most favourable folding steps are therefore those in which at least one of the interacting modules is located on a T segment. Favourable folding steps for different arrangements are shown in Fig. 5b. Since at least one of the interacting modules must reside on the free end of the chain, this design principle was named the “free end” rule. Importantly, it has been proven mathematically that at least two folding pathways that consist only of favourable steps can be constructed for every single-chain polyhedron.59 Such an optimal pathway is therefore feasible even if one of the termini is fixed, which may be particularly relevant during the biosynthesis of linear biopolymers where the growing end of the chain is not free.
The importance and feasibility of designing a favourable folding pathway for the modular single chain structures was demonstrated through several designs of a single chain square DNA pyramid.59 The square pyramid is the smallest regular polyhedron that can be composed from a single chain using only antiparallel modules to form a double Eulerian trail that traverses each edge exactly twice in an antiparallel orientation. The square pyramid is highly knotted and was not expected to fold correctly without designing a favourable folding pathway. In order to prove this experimentally, six variants of the square DNA pyramid were designed from the same set of interacting orthogonal module building blocks so that all designs should form the same final structure with equal stability.
Different interacting DNA modules were designed with different thermal stabilities, which was used to steer the folding (annealing) pathway, as more stable pairs were expected to form first. The six designs differed only in the order of the modules in the chain, where the optimal design comprised only steps in agreement with the free end rule, while in other designs one or up to six folding steps violated the free end rule. The optimal design is shown in Fig. 5d. A circular permutation of the optimal design, where each segment has been circularly shifted six modules to the right in the linear chain is shown in Fig. 5g. The circular permutation uses exactly the same modules, but the order of pairing according to the stability results in six unfavourable steps (shown in dashed red). The optimal pyramid design indeed folded correctly by slow annealing and demonstrated efficient self-assembly even when it was rapidly quenched from 90 °C to the temperature of ice or even liquid nitrogen (Fig. 5e), which demonstrates the efficiency of the rational design for the folding pathway. On the other hand, the designs containing more than five unfavourable steps did not fold efficiently even when annealed (Fig. 5e).59
The validity of the free end rule was also corroborated by simulating the folding rates using a coarse grained oxDNA60 model and Forward flux sampling. The free end rule thus represents a guiding principle for the design of modular DNA nanostructures and enables robust designs of highly knotted DNA structures that fold quickly and with high yield.
The free end rule can also be integrated with the new view on folding.43 Each DNA module can be viewed as a separate foldon. By switching the positions of the foldons in the chain the folding pathway can be manipulated.
Since these design rules depend on the topology rather than on the molecular details, they could also be transferrable to other twisted knotted single chain structures such as coiled-coil-based topofold proteins. The protein tetrahedron recently built24 using orthogonal coiled–coiled modules is not knotted, as it uses modules shorter than one superhelical turn, but for protein topofold structures constructed from longer coiled-coil modules we can expect the “free end” rule to become relevant and a tool to steer the protein folding pathway.
Conclusions
Recent advances in designed DNA and polypeptide-based modular bionanostructures represent a breakthrough in terms of our ability to rationally design their structures and folding properties by controlling the properties of individual building elements and the interactions between them. With further advances, polynucleic acids and polypeptides could be used for the rational and programmable design of smart materials with properties that have not evolved in nature.Topofold biopolymers are of particular interest as they are based on different design principles from conventional globular proteins, so there is a higher probability for providing novel structures and functions. The successful design of the folding pathway of highly knotted DNA nanostructure demonstrates that it is feasible to design the folding pathway of complex structures. It is likely that it will also be possible to design modular topofold proteins that are able to fold in vivo. The next challenge for this line of research is to investigate the limits of the structural complexity that can be achieved by this strategy, using both theoretical and experimental approach, and the possibilities of introducing functions, both similar to those of natural proteins as well as functions that are unique to topological folds.
Acknowledgements
We acknowledge the financial support of the Slovenian Research Agency to R. J. and H. G. (program P4-0176, projects N4-0037, L4-6812, J4-5528), ICGEB grant to H. G. and the ERANET SynBio (project Bioorigami, coordinated by R. J.). We thank to Dr Nino Bašić for preparing the images of mathematical topology solutions.References
- C. B. Anfinsen, E. Haber, M. Sela and F. H. White, Proc. Natl. Acad. Sci. U. S. A., 1961, 47, 1309–1314 CrossRef CAS.
- A. R. Fersht, Nat. Rev. Mol. Cell Biol., 2008, 9, 650–654 CrossRef CAS PubMed.
- K. A. Dill and J. L. MacCallum, Science, 2012, 338, 1042–1046 CrossRef CAS PubMed.
- G. A. Khoury, J. Smadbeck, C. A. Kieslich and C. A. Floudas, Trends Biotechnol., 2014, 32, 99–109 CrossRef CAS PubMed.
- C. Levinthal, J. Chim. Phys. Phys.-Chim. Biol., 1968, 65, 44–45 Search PubMed.
- T. J. Lane, D. Shukla, K. A. Beauchamp and V. S. Pande, Curr. Opin. Struct. Biol., 2013, 23, 58–65 CrossRef CAS PubMed.
- K. M. Ulmer, Science, 1983, 219, 666–671 CAS.
- R. L. Dimarco and S. C. Heilshorn, Adv. Mater., 2012, 24, 3923–3940 CrossRef CAS PubMed.
- N. P. King, W. Sheffler, M. R. Sawaya, B. S. Vollmar, J. P. Sumida, I. André, T. Gonen, T. O. Yeates and D. Baker, Science, 2012, 336, 1171–1174 CrossRef CAS PubMed.
- D. J. E. Huard, K. M. Kane and F. A. Tezcan, Nat. Chem. Biol., 2013, 9, 169–176 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 2, 1–7 Search PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, WIREs Comput. Mol. Sci., 2013, 3, 198–210 CrossRef CAS.
- A. Leaver-fay, M. Tyka, S. M. Lewis, O. F. Lange, R. Jacak, K. Kaufman, P. D. Renfrew, C. A. Smith, I. W. Davis, S. Cooper, A. Treuille, D. J. Mandell, Y. A. Ban, S. J. Fleishman, J. E. Corn and D. E. Kim, Methods Enzymol., 2011, 487, 545–574 CAS.
- R. Das and D. Baker, Annu. Rev. Biochem., 2008, 77, 363–382 CrossRef CAS PubMed.
- S. Gonen, F. DiMaio, T. Gonen and D. Baker, Science, 2015, 348, 1365–1368 CrossRef CAS PubMed.
- A. Travers and G. Muskhelishvili, FEBS J., 2015, 282, 2279–2295 CrossRef CAS PubMed.
- D. L. Burdette and R. E. Vance, Nat. Immunol., 2013, 14, 19–26 CrossRef CAS PubMed.
- V. Kočar, S. Božič Abram, T. Doles, N. Bašić, H. Gradišar, T. Pisanski and R. Jerala, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2015, 7, 218–237 CrossRef PubMed.
- P. W. K. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed.
- I. Saaem and T. H. LaBean, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2013, 5, 150–162 CrossRef CAS PubMed.
- P. Clark, Trends Biochem. Sci., 2004, 29, 527–534 CrossRef CAS PubMed.
- F. U. Hartl and M. Hayer-Hartl, Nat. Struct. Mol. Biol., 2009, 16, 574–581 CAS.
- H. Gradišar, S. Božič, T. Doles, D. Vengust, I. Hafner-Bratkovič, A. Mertelj, B. Webb, A. Šali, S. Klavžar and R. Jerala, Nat. Chem. Biol., 2013, 9, 362–366 CrossRef PubMed.
- G. Fijavž, T. Pisanski and J. Rus, MATCH, 2014, 71, 199–212 Search PubMed.
- R. Owczarzy, P. M. Vallone, F. J. Gallo, T. M. Paner, M. J. Lane and A. S. Benight, Biopolymers, 1997, 44, 217–239 CrossRef CAS PubMed.
- R. Owczarzy, A. V. Tataurov, Y. Wu, J. A. Manthey, K. A. McQuisten, H. G. Almabrazi, K. F. Pedersen, Y. Lin, J. Garretson, N. O. McEntaggart, C. A. Sailor, R. B. Dawson and A. S. Peek, Nucleic Acids Res., 2008, 36, W163–W169 CrossRef CAS PubMed.
- B. D. N. Woolfson, Adv. Protein Chem., 2005, 70, 79–112 CrossRef PubMed.
- J. M. Mason, K. M. Müller and K. M. Arndt, Methods Mol. Biol., 2007, 352, 35–70 CAS.
- P. Burkhard, J. Stetefeld and S. V. Strelkov, Trends Cell Biol., 2001, 11, 82–88 CrossRef CAS PubMed.
- A. N. Lupas and M. Gruber, Adv. Protein Chem., 2005, 70, 37–78 CrossRef CAS PubMed.
- A. W. Reinke, R. A. Grant and A. E. Keating, J. Am. Chem. Soc., 2010, 132, 6025–6031 CrossRef CAS PubMed.
- A. M. Slovic, S. E. Stayrook, B. North and W. F. Degrado, J. Mol. Biol., 2005, 348, 777–787 CrossRef CAS PubMed.
- H. Gradišar and R. Jerala, J. Pept. Sci., 2011, 17, 100–106 CrossRef PubMed.
- K. E. Thompson, C. J. Bashor, W. A. Lim and A. E. Keating, ACS Synth. Biol., 2012, 1, 118–129 CrossRef CAS PubMed.
- J. M. Fletcher, A. L. Boyle, M. Bruning, G. J. Bartlett, T. L. Vincent, N. R. Zaccai, C. T. Armstrong, E. H. C. Bromley, P. J. Booth, R. L. Brady, A. R. Thomson and D. N. Woolfson, ACS Synth. Biol., 2012, 1, 240–250 CrossRef CAS PubMed.
- C. Negron and A. E. Keating, J. Am. Chem. Soc., 2014, 136, 16544–16556 CrossRef CAS PubMed.
- V. Potapov, J. B. Kaplan and A. E. Keating, PLoS Comput. Biol., 2015, 11, e1004046 Search PubMed.
- H. Gradišar and R. Jerala, J. Nanobiotechnol., 2014, 12, 4 CrossRef PubMed.
- L. M. Luheshi, D. C. Crowther and C. M. Dobson, Curr. Opin. Chem. Biol., 2008, 12, 25–31 CrossRef CAS PubMed.
- M. Karplus, Folding Des., 1997, 2(Supplem), S69–S75 CrossRef CAS PubMed.
- K. A. Dill and H. S. Chan, Nat. Struct. Mol. Biol., 1997, 4, 10–19 CAS.
- S. W. Englander and L. Mayne, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15873–15880 CrossRef CAS PubMed.
- A. A. Nickson, B. G. Wensley and J. Clarke, Curr. Opin. Struct. Biol., 2013, 23, 66–74 CrossRef CAS PubMed.
- S. V. Solomatin, M. Greenfeld, S. Chu and D. Herschlag, Nature, 2010, 463, 681–684 CrossRef CAS PubMed.
- K. E. Dunn, F. Dannenberg, T. E. Ouldridge, M. Kwiatkowska, A. J. Turberfield and J. Bath, Nature, 2015, 525, 82–86 CrossRef CAS PubMed.
- G. Guichard and I. Huc, Chem. Commun., 2011, 47, 5933–5941 RSC.
- A. V. Pinheiro, D. Han, W. M. Shih and H. Yan, Nat. Nanotechnol., 2011, 6, 763–772 CrossRef CAS PubMed.
- T. C. Sayre, T. M. Lee, N. P. King and T. O. Yeates, Protein Eng., Des. Sel., 2011, 24, 627–630 CrossRef CAS PubMed.
- J. I. Sułkowska, P. Sułkowski, P. Szymczak and M. Cieplak, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 19714–19719 CrossRef PubMed.
- D. Bölinger, J. I. Sułkowska, H.-P. Hsu, L. A. Mirny, M. Kardar, J. N. Onuchic and P. Virnau, PLoS Comput. Biol., 2010, 6, e1000731 Search PubMed.
- N. P. King, A. W. Jacobitz, M. R. Sawaya, L. Goldschmidt and T. O. Yeates, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20732–20737 CrossRef CAS PubMed.
- P. F. N. Faísca, Comput. Struct. Biotechnol. J., 2015, 13, 459–468 CrossRef PubMed.
- A. Bucka and A. Stasiak, Nucleic Acids Res., 2002, 30, e24 CrossRef PubMed.
- A. Mugler, S. J. Tans and A. Mashaghi, Phys. Chem. Chem. Phys., 2014, 16, 22537–22544 RSC.
- D. Baker, Nature, 2000, 405, 39–42 CrossRef CAS PubMed.
- D. N. Ivankov, S. O. Garbuzynskiy, E. Alm, K. W. Plaxco, D. Baker and A. V Finkelstein, Protein Sci., 2003, 12, 2057–2062 CrossRef CAS PubMed.
- P. F. N. Faísca, R. D. M. Travasso, A. Parisi and A. Rey, PLoS One, 2012, 7, e35599 Search PubMed.
- V. Kočar, J. S. Schreck, S. Čeru, H. Gradišar, N. Bašić, T. Pisanski, J. P. K. Doye and R. Jerala, Nat. Commun., 2016, 7, 10803 CrossRef PubMed.
- J. P. K. Doye, T. E. Ouldridge, A. A. Louis, F. Romano, P. Šulc, C. Matek, B. E. K. Snodin, L. Rovigatti, J. S. Schreck, R. M. Harrison and W. P. J. Smith, Phys. Chem. Chem. Phys., 2013, 15, 20395–20414 RSC.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
Footnote |
| † Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2016 |




