Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bistren cryptands and cryptates: versatile receptors for anion inclusion and recognition in water
Giuseppe
Alibrandi
a,
Valeria
Amendola
b,
Greta
Bergamaschi
b,
Luigi
Fabbrizzi
*b and
Maurizio
Licchelli
b
aDipartimento di Scienze Chimiche, Università di Messina, Viale F. Stagno d'Alcontres 31, Villaggio S. Agata, 98166 Messina, Italy
bDipartimento di Chimica, Università di Pavia, Via Taramelli 12, 27100 Pavia, Italy. E-mail: luigi.fabbrizzi@unipv.it
First published on 20th January 2015
Abstract
Bistren cryptands can be easily synthesised through the Schiff base condensation of two molecules of tren and three molecules of a dialdehyde, followed by hydrogenation of the six C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bonds to give octamine cages, whose ellipsoidal cavity can be varied at will, by choosing the appropriate dialdehyde, in order to include substrates of varying sizes and shapes. Bistrens can operate as effective anion receptors in two ways: (i) in their protonated form, providing six secondary ammonium groups capable of establishing hydrogen bonding interactions with the anion; (ii) as dicopper(II) cryptates, in which the two coordinatively unsaturated metal centres can be bridged by an ambidentate anion. Representative examples of the two approaches, as well as the design of an anion molecular dispenser, in which a dicopper(II) bistren cryptate acts as a bottle will be illustrated.
N double bonds to give octamine cages, whose ellipsoidal cavity can be varied at will, by choosing the appropriate dialdehyde, in order to include substrates of varying sizes and shapes. Bistrens can operate as effective anion receptors in two ways: (i) in their protonated form, providing six secondary ammonium groups capable of establishing hydrogen bonding interactions with the anion; (ii) as dicopper(II) cryptates, in which the two coordinatively unsaturated metal centres can be bridged by an ambidentate anion. Representative examples of the two approaches, as well as the design of an anion molecular dispenser, in which a dicopper(II) bistren cryptate acts as a bottle will be illustrated.
Introduction
Water is the most commonly used liquid because of its large availability; it is the major constituent of the fluids in living beings, it is vital for all known forms of life and, in a more strictly chemical perspective, it dissolves more substances in greater quantities than any other common liquid. In the realm of metal coordination chemistry, since the pioneering studies of Werner,1 metal–ligand interactions have been mostly investigated in water, even though water itself is a good ligand for metal ions. In fact, in the absence of other seriously competing ligands (those higher in the spectrochemical series and chelating agents), metal ions exist in solution as aqua-complexes, usually six-coordinated, in an octahedral geometry: most of them, when crystallising as salts of poorly coordinating anions (e.g. perchlorate), maintain their six bound water molecules, according to a regular octahedral geometry: [MII(H2O)6](ClO4)2. On the other hand, in the smaller and more recently instituted realm of anion coordination chemistry, things are different: (i) in the language in use in this realm, the term ‘ligand’ has been replaced by ‘receptor’; (ii) receptor–anion interactions are in general weak, in most cases distinctly weaker than metal–ligand interactions. Thus, receptor–anion interactions, which are based on electrostatic forces and/or on a hydrogen bond (HB), usually cannot compete successfully with water molecules, present in an overwhelming amount and capable of donating HBs to negatively charged solutes. Thus, investigations on formation and stability of corresponding complexes in an aqueous solution are often precluded. In fact, most of the complexation equilibria involving anions and receptors have been and are currently being carried out in organic solvents, e.g. CHCl3, MeCN, DMSO, listed in the order of increasing polarity.2Therefore, the formation of water stable complexes requires a rather high degree of pre-organisation of the receptor; it should be rigid, concave and possibly polycyclic (a cage), with a cavity size and shape compatible with those of an anion, and it should contain multiple points of interaction, strategically placed inside its cavity. The interactions should be as strong as possible, as those provided by one or more metal ions included in the cavity or by ammonium groups (HB and electrostatic). This is the case of bistren cages or aza-cryptands, which can act as effective anion receptors in water (i) when containing two coordinatively unsaturated metal ions, and (ii) when protonated at the secondary amine groups. Representative examples of the two approaches will be discussed in the following sections. Some cryptand-related reviews have been published recently.3–5
Origin and development of bistren cryptands
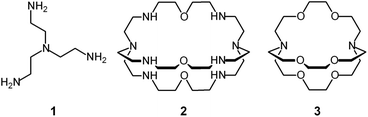
Tren – the abbreviated name for tris(2-aminoethyl)amine, 1 – is a classical tetradentate ligand in metal coordination chemistry.6 Due to its tripodal structure, tren favours the formation of five-coordinate metal complexes of trigonal bipyramidal geometry, in which four amine nitrogen atoms occupy four sites of the coordination polyhedron (three equatorial and one axial), and the fifth one (axial) is left available to a solvent molecule or to an anion. The trigonal bipyramid is generally compressed (axial bonds shorter than equatorial ones).
Lehn, in his 1977 communication,7 anticipated great expectations from dimetallic bistren cryptates of the type illustrated above: ‘Cascade complexes... may lead to selective fixation and transport of a given substrate as well as to the development of new bi- (or poly-) nuclear catalysts for multicenter-multielectronic processes (condensation of two or more included substrates held in proximity, O2 and N2 reduction, water splitting, etc.) and of models for polynuclear metalloproteins (hemocyanin, hemerythrin, oxygenases, etc.)’.7 It should be noticed that nearly 40 years later none of the above mentioned objectives has been achieved. However dimetallic bistren cryptates have shown a unique capability of selectively including anions, thus forming stable cascade complexes, and have played a significant role in anion recognition in water.
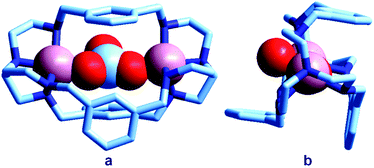
The first crystal and molecular structure of a dimetallic cascade complex was reported by Martell et al. in 1989,9 and is shown in Fig. 2.
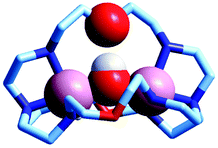 | ||
| Fig. 2 The crystal and molecular structure of the cascade complex [CuII2(2)(OH)]2+.9 All hydrogen atoms have been omitted, except those on the included OH− ion. The hydroxide anion (i) bridges the two CuII centres and (ii) it establishes a hydrogen bond with the facing ethereal oxygen atom of the bistren cryptand. The distance O–H⋯O is 201 pm, while the O⋯O distance in the same fragment is 274 pm. The O(hydroxide)⋯O(ethereal) distance for the other cryptand oxygen atoms is 433 pm. | ||
It is observed that the hydroxide anion bridges the two CuII metal ions. Moreover, it should be noted that the OH− ion points its hydrogen atom towards a facing ethereal oxygen atom of the bistren skeleton. The short O–H⋯O distance (201 pm) is indicative of the existence of a well defined HB interaction, which imparts an additional stability to the cascade complex. This is demonstrated by the fact that the constant for the anion inclusion equilibrium [CuII2L]4+ + OH− ⇄ [CuII2L(OH)]3+ (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 10.0) is much higher than that observed for the corresponding inclusion equilibrium of the isoelectronic fluoride ion (log
K = 10.0) is much higher than that observed for the corresponding inclusion equilibrium of the isoelectronic fluoride ion (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 5.5).9
K = 5.5).9
In spite of their versatile and promising behaviour as anion receptors, the development of bistren derivatives was prevented by the complexity of the synthesis, involving several steps and high dilution cyclization processes. Things changed and studies on bistren derivatives tumultuously progressed one decade later, when Lehn introduced a simple and high yielding synthetic procedure,10 based on the Schiff base condensation of 2 molecules of tren with 3 molecules of a dialdehyde, as illustrated in Scheme 1.
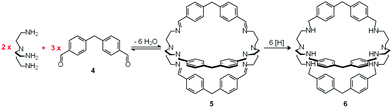 | ||
| Scheme 1 Two step synthesis of the bistren cryptand 6: (i) Schiff base condensation equilibrium involving the formation of 6 imine bonds to give 5; (ii) hydrogenation of the imine bonds (e.g. with LiAlH4) to give the robust octamine cage 6.10 | ||
In the first step, tren and dialdehyde 4, in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 molar ratio, react in MeCN to give the unsaturated macrobicyclic hexaimine 5. The reversible nature of the Schiff base condensation process, illustrated by the equilibrium in Scheme 2, allows the achievement of the in se rather complicated structure 5, through a repetitive trial and error mechanism, leading to the formation of 6 imine bonds, in a closed arrangement.
3 molar ratio, react in MeCN to give the unsaturated macrobicyclic hexaimine 5. The reversible nature of the Schiff base condensation process, illustrated by the equilibrium in Scheme 2, allows the achievement of the in se rather complicated structure 5, through a repetitive trial and error mechanism, leading to the formation of 6 imine bonds, in a closed arrangement.
 | ||
Scheme 2 Schiff base condensation equilibrium illustrating the so-called reversible nature of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N covalent bond. N covalent bond. | ||
Then, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N ‘reversible’ covalent bonds of 5 are converted and immobilized into inert single C–N bonds by hydrogenation with LiAlH4 in a THF solution, to give bistren cryptand 6 (two steps, overall yield 42%). This procedure was later extended by Jane Nelson and coworkers, who used a variety of dialdehydes to generate a series of bistren cryptands with different spacers (7–11) by linking the two tren subunits (Schiff base condensation in refluxing EtOH,11 and hydrogenation of the C
N ‘reversible’ covalent bonds of 5 are converted and immobilized into inert single C–N bonds by hydrogenation with LiAlH4 in a THF solution, to give bistren cryptand 6 (two steps, overall yield 42%). This procedure was later extended by Jane Nelson and coworkers, who used a variety of dialdehydes to generate a series of bistren cryptands with different spacers (7–11) by linking the two tren subunits (Schiff base condensation in refluxing EtOH,11 and hydrogenation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N imine bonds with NaBH4).12
N imine bonds with NaBH4).12
 | ||
| Fig. 3 The crystal and molecular structure of the [CuII2(7)(CO3)]2+ cascade complex.13 Two oxygen atoms of the carbonate ion bridge the two CuII metal ions, while the third oxygen atom points outside of the cage: (a) lateral view; (b) view of the cryptate complex along the axis defined by the bridgehead tertiary nitrogen atoms of bistren. | ||
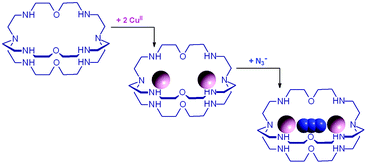
In particular, an alkaline solution containing CuBr2 and 7 was allowed to evaporate in the air through a small opening, with the purpose of crystallizing a cascade complex including a bridging hydroxide ion, as observed for the bistren complex shown in Fig. 2. Instead, over a period of 3–4 weeks, blue-green crystals formed, containing a CO32− inclusion complex. The preference of carbonate (originating from atmospheric CO2) with respect to OH− seems to be due to the impossibility of the latter anion to establish a HB interaction with m-xylyl spacers. The carbonate ion behaves as an ambidentate ligand, bridging the two metal centres with two oxygen atoms. The third oxygen atom of CO32− protrudes outside of the cage.
Anion recognition by dicopper(II) bistren cryptates
The first systematic study on selective anion inclusion by dimetallic bistren cryptates was carried out in our Laboratory in 1995.14 In particular, we considered the dicopper(II) complex of the cryptand 7 as a receptor. The crystal structure shown in Fig. 3 indicates that dicopper(II) cryptates of 7 have a cavity large enough to include polyatomic anions. Typically, in a titration experiment, a solution containing the receptor, i.e. the dimetallic cryptate, was titrated with a standard solution of the envisaged anion. However, preliminarily, the aqueous solution should be buffered to a pH that guarantees the presence of the dimetallic cryptate as a predominant species in a known and well defined form. Fig. 4 shows the percent concentration of the species present in equilibrium over the 2–9 pH range, for a solution 10−3 M in 7 and 2 × 10−3 M in CuII.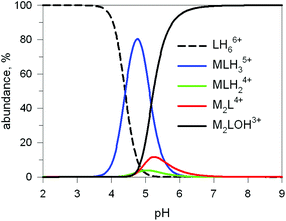 | ||
Fig. 4 Concentration profiles (%) of the species present at the equilibrium over the 2–9 pH range, for a solution 10−3 M in 7 and 2 × 10−3 M in CuII, calculated from the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values reported in ref. 13 L = 7. K values reported in ref. 13 L = 7. | ||
It is observed that [CuII2L]4+, in which probably two water molecules occupy the available axial positions of the two trigonal bipyramids, is present as a minor species at pH 5–5.5, reaching a maximum concentration of 10%, and cannot be therefore chosen as a receptor. Thus, titrations were carried out a pH = 8 (triflic acid/morpholine buffer), where the only species present (at 100%) is [CuII2L(OH)]3+, in which probably one of the two copper(II) bound water molecules has released a proton. Thus, on the addition of an anion X−, the exchanging equilibrium (1) should take place, in which the hydroxide and presumably the other included water molecule are displaced by the incoming ambidentate anion.
| [CuII2L(OH)]3+ + X− ⇄ [CuII2L(X)]3+ + OH− | (1) |
Fig. 5a shows the family of spectra obtained on titration of an aqueous solution containing Cu(CF3SO3)2 and 7 in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio, buffered at pH 8, at 25 °C, with NaN3.
1 molar ratio, buffered at pH 8, at 25 °C, with NaN3.
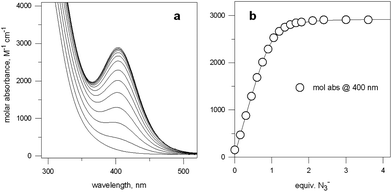 | ||
Fig. 5 (a) Spectra obtained over the course of the titration with NaN3 of an aqueous solution containing Cu(CF3SO3)2 and 7 in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio, buffered at pH 8, at 25 °C; (b) titration profile (molar absorbance at 400 nm vs. equiv. of NaN3), indicating the formation of a 1 1 molar ratio, buffered at pH 8, at 25 °C; (b) titration profile (molar absorbance at 400 nm vs. equiv. of NaN3), indicating the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 receptor–anion complex.14 1 receptor–anion complex.14 | ||
Azide addition makes the solution turn from pale blue to a blue-green colour, while a new rather intense band, centred at 400 nm, develops. Plotting of the absorbance at 400 nm vs. added equiv. of N3− generates a saturation curve, whose plateau is reached on addition of 1 anion equiv. (see Fig. 5b). This suggests the existence of an equilibrium of the type described by eqn (1), in which one azide anion is encapsulated by the cryptand and the two terminal nitrogen atoms of the N3− ion coordinate the two CuII centres. Thus, the intense absorption band centred at 400 nm which develops over the course of the titration should have a ligand-to-metal charge transfer (LMCT) nature. This hypothesis was confirmed by the determination of the crystal structure of the salt: [CuII2(7)(N3)](ClO4)3·MeCN·EtOH.15 The structure of the cryptate complex [CuII2(7)(N3)]3+, is shown in Fig. 6b.
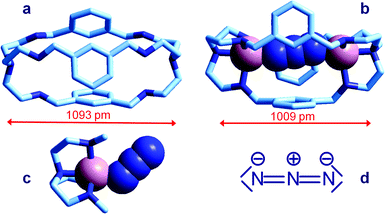 | ||
| Fig. 6 Crystal and molecular structure of (a) the bistren cryptand 7;16 (b) the corresponding cryptate including N3−: [CuII2(7)(N3)]3+,15 Cu–N–N angles are 167° and 163°; (c) the Me3tren ‘hemi-cryptate’ [CuII(Me3tren)(N3)]+,17 the Cu–N–N angle is 130.5°; (d) the structural formula of N3−. Figures over the double head arrows indicate the distances between the tertiary amine groups of each bistren cryptand framework. | ||
The anion is fully encapsulated in the cryptate and bridges the two CuII ions. Fig. 6a and 6b compare the distances between tertiary amine nitrogen atoms in the crystallographically characterized metal free cryptand 7 (1093 pm) and in the cryptate complex including N3−, [CuII2(7)(N3)]3+ (1009 pm). This indicates that complex formation requires some contraction of the cryptand framework, which should not involve a too high conformational energy cost. Such an unfavourable energy cost is more than compensated by the establishing of CuII–N coordinative bonds with the tren subunits and with azide. It should be also noticed that the unusual collinear coordinative arrangement of the N3− ion; in particular, the values of the two Cu–N–N angles are 167° and 163°, well different from the Cu–N–N value observed in the strain-free ‘hemicryptate’ [CuII(Me3tren)(N3)]+ (Fig. 6c; Me3tren: tris(2-(N-methylamino)ethyl)amine): 130.5°. The bent mode of coordination of the azide to the CuII tetramine subunits (whether branched or linear) is natural and results from the sp2 hybridization of the terminal nitrogen atoms of N3−, as shown by the structural formula in Fig. 6d.
The collinear arrangement observed in the cryptate complex is therefore unnatural and is imposed by the steric constraints of the cryptand framework. However, this does not seem to affect to a significant extent the stability of the receptor–anion complex. In fact, a non-linear least-squares treatment of the titration data over a wavelength interval 350–500 nm allowed to determine a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 4.78 ± 0.05 for the displacement equilibrium (1) Note that the determined K is a conditional constant and refers to pH 8.
K = 4.78 ± 0.05 for the displacement equilibrium (1) Note that the determined K is a conditional constant and refers to pH 8.
Analogous titration experiments were carried out with a variety of polyatomic anions. A significant result was obtained by plotting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values vs. anion bite, i.e. the distance between two consecutive donor atoms of the corresponding anions (see Scheme 3 and Fig. 7).
K values vs. anion bite, i.e. the distance between two consecutive donor atoms of the corresponding anions (see Scheme 3 and Fig. 7).
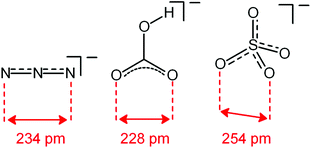 | ||
| Scheme 3 Anion bite of the selected anions: distance between two consecutive donor atoms of an anion acting as an ambidentate ligand. | ||
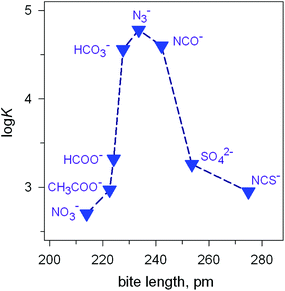 | ||
Fig. 7 Peak selectivity for the stability of the [CuII2(7)(X)]3+ complex with respect to the bite distance of the anion X− (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K of equilibria: [CuII2(7)(OH)]3+ + X− ⇄ [CuII2(7)X]3+ + OH− , at 25 °C, in a solution buffered at pH = 8.14 K of equilibria: [CuII2(7)(OH)]3+ + X− ⇄ [CuII2(7)X]3+ + OH− , at 25 °C, in a solution buffered at pH = 8.14 | ||
The plot in Fig. 7 shows the existence of a sharp selectivity in favour of azide. Therefore, the N3− ion has the right length to position its donor atoms in the two available axial positions of the two CuII centres, without inducing any endergonic conformational rearrangement of the bistren framework. When encapsulating anions of either larger (i.e. NCS−) or smaller bite lengths (e.g. NO3−), the cryptate must leave its relaxed conformation in order to position the two CuII centres at the right distance: the more important the rearrangement of the cryptand framework (either expansion or contraction), the more significant the decrease of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K value for eqn (1). Thus, the [CuII2(7)(OH)]3+ receptor neither recognises the shape of the anion nor its electrical charge: it recognises its bite length.
K value for eqn (1). Thus, the [CuII2(7)(OH)]3+ receptor neither recognises the shape of the anion nor its electrical charge: it recognises its bite length.
Noticeably, the [CuII2(7)]4+ cryptate, in any form, at any pH, is not able to include monoatomic anions like halides, which can act as ambidentate ligands, but, apparently, are too small to bridge the two metal centres. This has been ascribed to the rigidity of the bistren framework, in particular of the m-xylyl spacers linking the two tren subunits.14,18
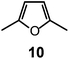
Quite surprisingly, the dicopper(II) cryptate of (10), whose spacer, a 2,5-dimethylfuran fragment, is only 13 pm shorter than that of 7 (see Scheme 4), is able to encapsulate halide ions, forming stable complexes in water. X-ray diffraction studies on the crystalline salts [CuII2(10)(Cl)](ClO4)319 and [CuII2(10)(Br)](ClO4)320 demonstrated that chloride and bromide ions are encapsulated by the cryptate and bridge the two CuII centres, as shown in Fig. 8.
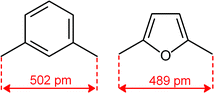 | ||
| Scheme 4 C–C distance in the spacers of cryptands 7 and 10, as observed in metal free cryptands (ref. 16). | ||
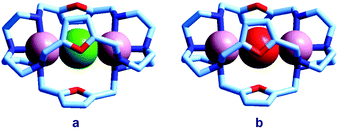 | ||
| Fig. 8 The crystal and molecular structure of: (a) [CuII2(10)(Cl)](ClO4)3,19 and (b) [CuII2(10)(Br)](ClO4)3.20 Hydrogen atoms and perchlorate ions have been omitted for clarity. | ||
The distances between the tertiary amine nitrogen atoms in the two inclusion complexes (874 pm for Cl− and 896 pm for Br−) are distinctly smaller than observed in the [CuII2(7)(N3)]3+ cryptate (1009 pm), which implies a more pronounced contraction of the bistren framework. The corresponding conformational energy cost seems to be compensated, other than by the formation of the Cu–X–Cu bonds, by an additional term associated with the interaction between the halide and the oxygen atoms of the furan rings. In fact, the X⋯O distances (317 ± 3 pm for Cl− and 319 ± 2 pm for Br−) are appreciably lower than the sum of the van der Waals radii (327 and 337 pm, respectively).21 Such interactions have a profound influence on the energy and intensity of the absorption spectra of the halide inclusion complexes, as will be discussed below.
Preliminary potentiometric titration experiments on the Cu2+/10 system in a molar ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 lead to the distribution diagram illustrated in Fig. 9.
1 lead to the distribution diagram illustrated in Fig. 9.
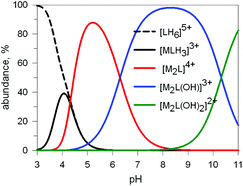 | ||
Fig. 9 Concentration (% with respect to L = 10) of the species present at the equilibrium for the system 10/CuII (ligand-to-metal ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), in an aqueous solution 0.1 M in NaClO4, at 25°. Log 2), in an aqueous solution 0.1 M in NaClO4, at 25°. Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values were obtained through a potentiometric titration.20 K values were obtained through a potentiometric titration.20 | ||
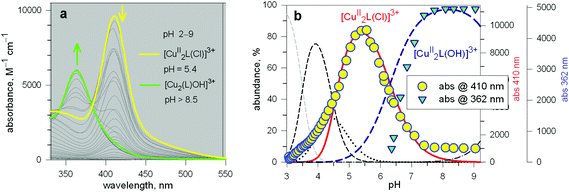
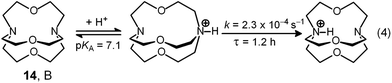
Two major dimetallic species are present over the 3–11 pH interval: the [CuII2L]4+ complex in the 4–7 pH range (maximum concentration: 85%, at pH = 5, red line in Fig. 9, pale blue colour of the solution), and the [CuII2L(OH)]3+ complex in the 5–11 pH range (maximum concentration: 97%, at pH = 8.5, blue line, with the solution exhibiting an intense emerald green colour and an absorption band centred at 362 nm; molar absorbance, ε = 6500 M−1 cm−1). The encapsulation of the small hydroxide ion should require a severe contraction of the bistren framework. This is demonstrated by the crystal and molecular structure of the complex salt [CuII2L(OH)](CF3SO3)3,22 shown in Fig. 10.
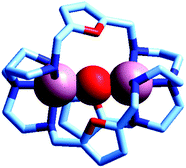 | ||
| Fig. 10 The crystal and molecular structure of the cascade complex [CuII2(10)(OH)]2+.22 All hydrogen atoms have been omitted, including those of the hydroxide ion. The oxygen atom of OH− establishes a well defined interaction with the oxygen atoms of the three furan rings of the cryptand: in particular, the O(hydroxide)⋯O(furan) distances are 289 pm, distinctly lower than twice the Van der Waals radius of oxygen (304 pm). | ||
In fact, the Ntert⋯Ntert distance (805 pm) is especially low, which should involve a rather endothermic contraction of the cryptand framework, as discussed for the dicopper(II) cryptates of 10, encapsulating chloride and bromide. Also in this case, a well defined interaction between the oxygen atom of the encapsulated hydroxide and the ethereal oxygen atoms of the furan ring seems to be present, as the measured O⋯O distance is distinctly smaller than the sum of the van der Waals radii (289 vs. 304 pm). It is then this additional interaction that probably compensates the conformational energy cost associated with the cryptand's rearrangement. Note that in the analogous complex [CuII2(3)(OH)]2+, whose structure is shown in Fig. 3, the Ntert⋯Ntert distance (768 pm) is even shorter than in the [CuII2(10)(OH)]2+. In this case, the conformational energy cost has been counterbalanced by the formation of a hydrogen bonding interaction involving the included OH− ion and one of the ethereal oxygen atoms of the ligating framework. Conversely, no interaction exists between the oxygen atom of OH− and the other ethereal oxygen atoms of 3 (O⋯O distances 433 pm). On the other hand, in the aqueous [CuII2L]4+ complex, in the absence of coordinating anions, the intermetallic cavity is thought to be ‘void’ or, more realistically, occupied by either water molecules or by the anion of the background electrolyte, i.e. ClO4−.
In order to determine the binding tendencies of the dicopper(II) cryptate towards halide ions, a solution containing 10 and two equiv. of CuII was adjusted to pH = 5.25 with an MES buffer and was titrated with a standard solution of sodium halide, NaX.20 On X− addition (X = Cl, Br, I), the pale blue solution (containing as major species, 87% of the ‘void’ complex [CuII2L]4+) turned bright yellow.
Fig. 11 reports the family of spectra recorded during titration with the chloride ion. The titration profile in the inset (molar absorbance vs. equiv. of Cl−) corresponds to the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 inclusion complex, whose structure is shown in Fig. 9a, and the log
1 inclusion complex, whose structure is shown in Fig. 9a, and the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K value (conditional constant at pH = 5.25) for the equilibrium (2),
K value (conditional constant at pH = 5.25) for the equilibrium (2),
| [CuII2(10)]4+ + Cl− = [CuII2(10)(Cl)]3+ | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 M−1 cm−1) has a LMCT nature. The interaction of chloride with the cryptand's ethereal oxygen atoms may raise the energy of the filled Cl− orbital from which the electron is excited to the half-filled d orbital of CuII, which accounts for the relatively low energy of the transition, responsible for the bright yellow colour.
600 M−1 cm−1) has a LMCT nature. The interaction of chloride with the cryptand's ethereal oxygen atoms may raise the energy of the filled Cl− orbital from which the electron is excited to the half-filled d orbital of CuII, which accounts for the relatively low energy of the transition, responsible for the bright yellow colour.
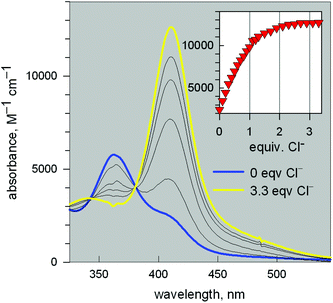 | ||
Fig. 11 Spectra recorded over the course of the titration of a solution containing the [CuII2(3)]4+ system, adjusted to pH = 5.25 with a standard solution of NaCl.20 The increasing band centred at 410 nm corresponds to the formation of the [CuII2(3)(Cl)]3+ inclusion complex. The titration profile in the inset gave a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K value of 3.98 ± 0.02 for the equilibrium: [CuII2(3)]4+ + Cl− = [CuII2(3)(Cl)]3+. K value of 3.98 ± 0.02 for the equilibrium: [CuII2(3)]4+ + Cl− = [CuII2(3)(Cl)]3+. | ||
Analogous titration profiles were obtained for bromide and iodide: Br−, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.01 ± 0.01, ε = 10
K = 3.01 ± 0.01, ε = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 M−1 cm−1; I−, 2.39 ± 0.02, 950 cm−1 M−1.17 Surprisingly, titration with NaF did not cause any development of the yellow colour. However, it must be considered that the energy of the LMCT transition increases with the increasing electronegativity of the halogen atom. Thus, the fluoride-to-copper transition, due to the high electronegativity of fluorine, is probably shifted to lower wavelengths, in particular in the UV portion of the spectrum, where it may be obscured by the strong amine-to-metal CT transitions. However, significant spectral modifications in the UV region observed during the titration of the cryptate solution with NaF, buffered at pH = 5.25, generated a saturation profile and the pertinent log
800 M−1 cm−1; I−, 2.39 ± 0.02, 950 cm−1 M−1.17 Surprisingly, titration with NaF did not cause any development of the yellow colour. However, it must be considered that the energy of the LMCT transition increases with the increasing electronegativity of the halogen atom. Thus, the fluoride-to-copper transition, due to the high electronegativity of fluorine, is probably shifted to lower wavelengths, in particular in the UV portion of the spectrum, where it may be obscured by the strong amine-to-metal CT transitions. However, significant spectral modifications in the UV region observed during the titration of the cryptate solution with NaF, buffered at pH = 5.25, generated a saturation profile and the pertinent log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K value could be determined: 3.20 ± 0.02.
K value could be determined: 3.20 ± 0.02.
The plot in Fig. 12 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K vs. halide ionic radius) shows a moderate, still defined selectivity in favour of chloride: the log
K vs. halide ionic radius) shows a moderate, still defined selectivity in favour of chloride: the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values (conditional constant at pH = 5.25) range within an interval of only 1.2 log units. However, the [CuII2(10)]4+ cryptate displays the unique capability of including anions of varying sizes and shapes. In fact, it encapsulates not only the small halides and hydroxide ions, but also linear triatomic anions like N3− and NCS−. In particular, when titrating a solution of [CuII2(10)]4+, buffered to pH = 5.25 with NaN3, the pale blue solution took an intense olive green colour: the plot of the absorbance of the band which developed at 386 nm vs. equiv. of N3− indicated the formation of a 1
K values (conditional constant at pH = 5.25) range within an interval of only 1.2 log units. However, the [CuII2(10)]4+ cryptate displays the unique capability of including anions of varying sizes and shapes. In fact, it encapsulates not only the small halides and hydroxide ions, but also linear triatomic anions like N3− and NCS−. In particular, when titrating a solution of [CuII2(10)]4+, buffered to pH = 5.25 with NaN3, the pale blue solution took an intense olive green colour: the plot of the absorbance of the band which developed at 386 nm vs. equiv. of N3− indicated the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct with a log
1 adduct with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 4.70 ± 0.06, for an equilibrium of type (2). The development of a CT band (ε = 6100 M−1 cm−1) as well as the 1
K = 4.70 ± 0.06, for an equilibrium of type (2). The development of a CT band (ε = 6100 M−1 cm−1) as well as the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry strongly suggest that the N3− ion is included within the cage. A similar behaviour was observed with NCS− (log
1 stoichiometry strongly suggest that the N3− ion is included within the cage. A similar behaviour was observed with NCS− (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 4.28 ± 0.03). Thus, it appears that the [CuII2(10)]4+ complex displays an extreme versatility, being able to contract/expand its cavity at will, in order to include anions of variable sizes and shapes, from the small hydroxide and fluoride to the large thiocyanate. It has been shown that [CuII2(10)]4+ forms its most stable inclusion complex with the azide ion, which encompass the two metal centres with a minimum conformational rearrangement of the cryptand framework. The encapsulation of monoatomic halide ions and of hydroxide involves a drastic conformational rearrangement of the cryptand, but this cost is fully paid by the interactions established by the furan oxygen atoms with the enclosed halide.
K = 4.28 ± 0.03). Thus, it appears that the [CuII2(10)]4+ complex displays an extreme versatility, being able to contract/expand its cavity at will, in order to include anions of variable sizes and shapes, from the small hydroxide and fluoride to the large thiocyanate. It has been shown that [CuII2(10)]4+ forms its most stable inclusion complex with the azide ion, which encompass the two metal centres with a minimum conformational rearrangement of the cryptand framework. The encapsulation of monoatomic halide ions and of hydroxide involves a drastic conformational rearrangement of the cryptand, but this cost is fully paid by the interactions established by the furan oxygen atoms with the enclosed halide.
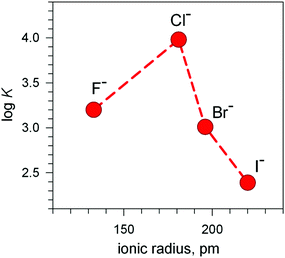 | ||
Fig. 12 Selectivity pattern for the affinity of halides towards the dimetallic cryptate receptor [CuII2(3)]4+. Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values refer to the equilibrium: [CuII2(3)]4+ + X− ⇄ [CuII2(3)(X)]3+ at pH = 5.25; (X− = halide anion).20 K values refer to the equilibrium: [CuII2(3)]4+ + X− ⇄ [CuII2(3)(X)]3+ at pH = 5.25; (X− = halide anion).20 | ||
The spectral properties illustrated above for the [CuII2(10)]4+ receptor (intense colour of the cryptates including halides, yellow, and hydroxide, emerald-green) are strictly related to the presence of 2,5-dimethylfuran spacers in the cryptand.
Fig. 13 shows the conditional constants obtained on titration with NaX (X− = halide) of an aqueous solution containing 2 equiv. of CuII(CF3SO3)2 and 1 equiv. of cryptand (10, 12 and 13), buffered to pH 5.8.24 Note that the pH is higher than that imposed for anion inclusion in the [CuII2(10)]4+ receptor, as illustrated in Fig. 11 and 12. The higher the pH, the lower the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K for the inclusion equilibrium, due to the increasing competition by OH−. In fact, iodide complexes do not form at that pH, or, more correctly, their log
K for the inclusion equilibrium, due to the increasing competition by OH−. In fact, iodide complexes do not form at that pH, or, more correctly, their log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values are lower than 2. Moreover, the log
K values are lower than 2. Moreover, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values for a given receptor, e.g. [CuII2(10)]4+ cannot be compared with those of another receptor, e.g. [CuII2(12)]4+ because at pH 5.8 they can be present in different forms. In any case, the plots in Fig. 13 provide information about the affinity trends towards halides. In particular, only [CuII2(10)]4+ displays a peak selectivity (in favour of chloride), whereas [CuII2(12)]4+ and [CuII2(13)]4+ show the affinity trend F− > Cl−.
K values for a given receptor, e.g. [CuII2(10)]4+ cannot be compared with those of another receptor, e.g. [CuII2(12)]4+ because at pH 5.8 they can be present in different forms. In any case, the plots in Fig. 13 provide information about the affinity trends towards halides. In particular, only [CuII2(10)]4+ displays a peak selectivity (in favour of chloride), whereas [CuII2(12)]4+ and [CuII2(13)]4+ show the affinity trend F− > Cl−.
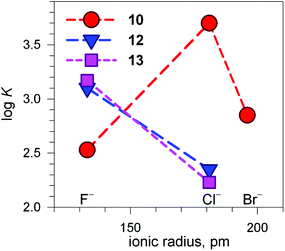 | ||
Fig. 13 Plot of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values for the equilibrium [CuII2(cry)]4+ + X− ⇄ [CuII2(cry)(X)]3+ at pH 5.8 vs. the halide ionic radius (cry = 10, 12, 13). Depending upon cry, [CuII2(cry)]4+ may include in its cavity H2O molecules or OH− in different amounts. This precludes any vertical comparison.24 K values for the equilibrium [CuII2(cry)]4+ + X− ⇄ [CuII2(cry)(X)]3+ at pH 5.8 vs. the halide ionic radius (cry = 10, 12, 13). Depending upon cry, [CuII2(cry)]4+ may include in its cavity H2O molecules or OH− in different amounts. This precludes any vertical comparison.24 | ||
An automatic molecular dispenser of chloride operating through the combined activity of a cryptand and of a cryptate
The unique properties of the [CuII2(10)(Cl)]3+ and [CuII2(10)(OH)]3+ inclusion complexes made it possible to design of a device capable of releasing chloride into a solution through a moderate variation of pH, thus generating a pH driven molecular dispenser.25 The basic mechanism can be explained on the basis of Fig. 14. In particular, Fig. 14a shows the family of spectra taken during the titration with standard NaOH of a solution 2.5 × 10−4 M in 10 (= L), 5 × 10−4 M in Cu(CF3SO3)2, 5 × 10−3 M in NaCl, adjusted to pH 2 with triflic acid: on increasing the pH, a bright yellow colour develops due to the formation of the [CuII2(10)(Cl)]3+ complex, to which an intense absorption band centred at 410 corresponds (ε = 9500 M−1 cm−1). On further pH increase, the solution turns emerald green due to the formation of the [CuII2(10)(OH)]3+ inclusion complex (band centred at 360 nm, ε = 6000 M−1 cm−1).Fig. 14b displays the distribution diagram of the species present at the equilibrium over the course of the titration. Noticeably, absorbances of the two envisaged complexes superimpose well on the corresponding concentration profiles. Most importantly, on moving from pH 5.5 to pH 8.5, the following process takes place:
| [CuII2(10)(Cl)]3+ + OH− ⇄ [CuII2(10)(OH)]3+ + Cl− | (3) |
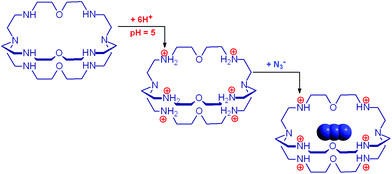
The cryptand 14 (B), in its in,in conformation, is a rather weak base (Bin,in, pKa = 7.1) and undergoes a fast external protonation equilibrium to give the BH+in,out derivative, which slowly converts to the more stable BH+in,in conformer (τ = 1.2 h, see eqn (4) in Scheme 5). On the other hand, with respect to the formation of BH+in,in, Bin,in is a very strong base (pKa ≥ 17.8). Therefore, on the dissolution of 14 in water, OH− ions are released into the solution and the pH increases according to the kinetic algorithm expressed by eqn (5):
| pH = pHinit − 10−4 × t | (5) |
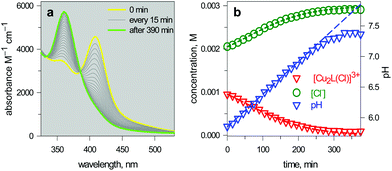 | ||
| Fig. 15 (a) Spectra taken on a 1 mm quartz cuvette containing 1.1.1 – cryptand (14, ca. 0.1 M), [Cu2(L)]4+ (L = 10, 3 × 10−3 M), KCl (3 × 10−3 M) and triflic acid to adjust the pHinit to 6; (b) symbols: values of [Cu2L(Cl)]3+ and [Cl−] obtained from the spectrophotometric titration through appropriate algorithms; lines: calculated concentration profiles when the pH increases at a rate of 1.0 × 10−4 unit s−1.25 | ||
The intensity of the absorption band at 410 nm continuously decreased and that of the band at 360 nm simultaneously increased, indicating the synchronous vanishing of [CuII2(10)Cl]3+ and the growth of [CuII2(10)OH]3+. Note the complete similarity between the dynamic spectra in Fig. 15a (pH was made to continuously increase by an internal microscopic device, which constantly produces OH−) and the static spectra in Fig. 14a (pH varied stepwise through the successive addition of aliquots of OH− from a macroscopic burette).
The device, under the chosen conditions, releases about 1 × 10−3 M of chloride ions into the solution, whose concentration changes from 2 × 10−3 M to 3 × 10−3 M. The behaviour of the molecular dispenser is encouraging in principle, but it is poorly satisfactory in practice: 2/3rd of the chloride content leaked out from the bottle before controlled release had begun! Such a performance depends mainly on the fact that pH shows a linear dependence upon time over a rather limited interval and pHinit = 6 had to be chosen as the initial pH (where the bottle is filled only 1/3rd). Probably other cryptates exist capable of being filled 100% and delivering all the chloride (or a different anion) contained in their cavity, in a restricted pH interval. It is less probable that they display the rich and versatile spectral properties of the dicopper(II) cryptate of 10.
Anion receptors derived by the protonation of bistren cryptands
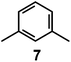
In 1978, one year after the introduction of dimetallic bistren cryptates, Lehn realized that cryptand 2, hexaprotonated in an aqueous solution adjusted at pH 5, could include a linear polyatomic anion, e.g. azide,30 according to the cascade mechanism depicted in Fig. 16.On potentiometric titration studies over the 2–12 pH interval, six pKa values could be evaluated, ranging from 9.3 to 5.7 (at 25 °C) and pertaining to the protonation of the six secondary amine groups of 2.30 The protonation of the two tertiary amine groups of 2, due to the strong electrostatic repulsions, could take place only in very acidic solutions (pH < 2). On titration of a solution of 2 with NaN3, adjusted at pH 5 with perchloric acid, 13C resonance shifts progressively increased to reach a plateau after the addition of 1 equiv. of azide, indicating the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex.30
1 complex.30
Fig. 17 shows the distribution diagram of the species at the equilibrium over the 2–12 pH range, calculated from the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kn values (n = 1–6).30 It is observed that at pH 5, at which 13C titration was performed, receptor 2 (= L) is present at ca. 80% as LH66+ and at ca. 20% as LH55+. From the titration profiles (13C NMR shift vs. anion equiv.), a conditional association constant log
Kn values (n = 1–6).30 It is observed that at pH 5, at which 13C titration was performed, receptor 2 (= L) is present at ca. 80% as LH66+ and at ca. 20% as LH55+. From the titration profiles (13C NMR shift vs. anion equiv.), a conditional association constant log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kass = 4.3 ± 0.3 was evaluated, two orders of magnitude higher than for the other investigated mono- and poly-atomic anions. It should be also noted that the titration of a solution of tren with azide at pH = 5, containing the triprotonated species trenH33+, did not cause any change in the 13C spectra, thus excluding the formation of any receptor anion-complex.30 This established the existence of a cryptate effect also in anion coordination chemistry. The formation of an inclusion complex of the formula [LH6⋯N3]5+ was confirmed later by X-ray diffraction studies on a single crystal of the salt [LH6⋯N3](Cl)(PF6)4,31 whose structure is shown in Fig. 18a. Each terminal atom of the azide ion receives three hydrogen bonds from the secondary ammonium groups of each tren subunit. The stability of the receptor anion complex is further increased by electrostatic interactions.
Kass = 4.3 ± 0.3 was evaluated, two orders of magnitude higher than for the other investigated mono- and poly-atomic anions. It should be also noted that the titration of a solution of tren with azide at pH = 5, containing the triprotonated species trenH33+, did not cause any change in the 13C spectra, thus excluding the formation of any receptor anion-complex.30 This established the existence of a cryptate effect also in anion coordination chemistry. The formation of an inclusion complex of the formula [LH6⋯N3]5+ was confirmed later by X-ray diffraction studies on a single crystal of the salt [LH6⋯N3](Cl)(PF6)4,31 whose structure is shown in Fig. 18a. Each terminal atom of the azide ion receives three hydrogen bonds from the secondary ammonium groups of each tren subunit. The stability of the receptor anion complex is further increased by electrostatic interactions.
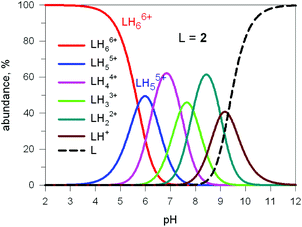 | ||
| Fig. 17 Concentration profiles of a 10−4 M bistren cryptand 2 (L) over the pH range 2–12. Curves were calculated on the basis of stepwise protonation constants from ref. 30. | ||
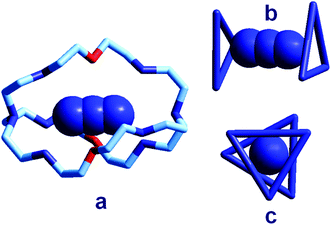 | ||
| Fig. 18 (a) The crystal and molecular structure of the receptor–anion complex [LH6⋯N3]5+ (L = 2);31 hydrogen atoms omitted, as well as PF6− counterions; the six secondary amine nitrogen atoms are protonated; (b) the same complex in which only the three secondary ammonium groups of each tren subunit are shown, linked to give a triangle, lateral view; (c) top view. | ||
In order to better illustrate the coordination geometry of the six secondary ammonium groups of LH66+, the protonated nitrogen atoms of each tren subunit have been linked together, in Fig. 18b and 18c, to give a triangle. The three ammonium groups at the three vertices of each triangle interact with one terminal nitrogen atom of the azide ion (Fig. 5b). The torsional angle between the two triangles, θ, is ca. 28°, a value intermediate between the 0°, eclipsed, and 60°, staggered conformations of the tren subunits. Since these seminal papers by Lehn were published, great attention has been devoted to studies on anion recognition by protonated bistrens in an aqueous acidic solution, documented by tens of papers, in particular from the Nelson's group.32,33
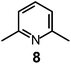
Here we will consider in detail the encapsulation by the protonated forms of bistrens 7 and 9 of the environmentally relevant anions ReO4− and 99TcO4−. The procedure of investigation is the same as described before. First the distribution of the differently protonated species is obtained through the potentiometric titration and determination of the pertinent protonation constants of the bistren cryptand; then, a convenient pH is chosen at which LH66+ is the dominant or sole species and a solution buffered at that pH is titrated with the envisaged anion, using NMR or isothermal calorimetry (ITC) as the recording technique. Fig. 19 shows the distribution diagram of the species present at the equilibrium over the 2–12 pH interval, (0.1 M NaCF3SO3, T = 25 °C), in the case of bistren cryptand 7.34
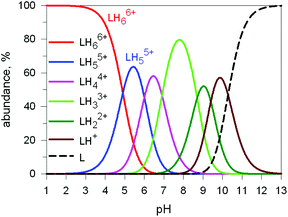 | ||
| Fig. 19 Concentration profiles of a 7 × 10−3 M solution of the bistren cryptand 7 (L) over the pH range 1–13.34 | ||
The diagram in Fig. 19 shows that at pH 2 100% LH66+ is present . Moreover, it has to be considered that a 10−2 M solution of a strong acid (e.g. triflic acid) is a buffer itself. Thus, a 1H NMR titration was carried out by adding NaReO4 to a D2O solution 7.7 × 10−3 M in 7, adjusted to pD 2 (see Fig. 20).34 Perrhenate addition induced a downfield shift of the signals corresponding to the –CH2– protons of the tren subunits of 7, which is consistent with the existence of significant electrostatic interactions between the methylene C–H protons and ReO4−, thus indicating the formation of an inclusion complex.
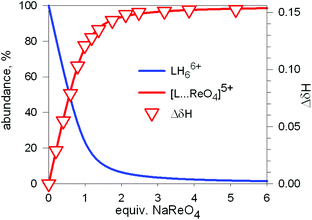 | ||
Fig. 20 Symbols: plot of the chemical shift of the –CH2– protons of the tren subunits of cryptand 7 (ΔδHb) vs. equiv. of NaReO4 over the course of an 1H NMR titration of a D2O solution 7.7 × 10−3 M in 7, adjusted to pD 2; lines: concentration profiles calculate for a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.4. L = 7.34 K = 3.4. L = 7.34 | ||
1H NMR spectra were fitted by means of a nonlinear least-squares program,35 and a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.4 ± 0.1 was determined for the equilibrium:
K = 3.4 ± 0.1 was determined for the equilibrium:
| LH66+ + ReO4− ⇄ [LH6…ReO4]5+ | (6) |
The equilibrium was investigated also through ITC titration and a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.29 ± 0.01 was determined. Same studies were extended to cryptands 8, 9 and 10, and the corresponding log
K = 3.29 ± 0.01 was determined. Same studies were extended to cryptands 8, 9 and 10, and the corresponding log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values are shown in Table 1, which contains also log
K values are shown in Table 1, which contains also log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values obtained by ITC measurements, characterised by a higher accuracy.
K values obtained by ITC measurements, characterised by a higher accuracy.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values for the equilibrium LH66+ + ReO4− ⇄ [LH6⋯ReO4]5+, in an aqueous solution adjusted to pH 2, in 0.1 M Na CF3SO3. Receptors are indicated by the structural formulae of corresponding spacers.34
K values for the equilibrium LH66+ + ReO4− ⇄ [LH6⋯ReO4]5+, in an aqueous solution adjusted to pH 2, in 0.1 M Na CF3SO3. Receptors are indicated by the structural formulae of corresponding spacers.34
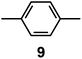
It is observed that receptor 9, containing p-xylyl spacers, in its hexaprotonated form, displays the highest affinity for ReO4−. In particular, the corresponding association constant is nearly two orders of magnitude higher than the isomeric bistren 7, which contains m-xylyl spacers. Thus, one can hypothesise that the hexaprotonated bistren 9 offers a cavity, whose size and shape is tailor made for the perrhenate anion, thus allowing the establishing of perfect hydrogen bonding interactions between the four oxygen atoms of ReO4− and the six secondary ammonium groups of the receptor. The crystal and molecular structure of the complex salt [LH6⋯ReO4](CF3SO3)5,34 shown in Fig. 21 shows that things are not exactly so.
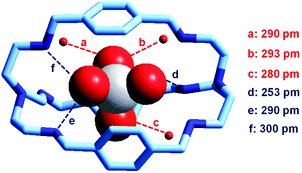 | ||
| Fig. 21 The crystal and molecular structure of the inclusion complex salt [LH6⋯ReO4)](CF3SO3)5·8H2O (L = 9). Hydrogen atoms and triflate counterions have been omitted for clarity. Only the three water molecules involved in hydrogen bonding with ReO4− are shown as small red spheres. Dashed lines: significant hydrogen bond interactions (distances N, O⋯OReO3− < 350 pm).34 | ||
It is observed that the perrhenate ion establishes strong hydrogen bond interactions only with three of the six secondary ammonium groups available. On the other hand, important HB interactions are established between ReO4− oxygen atoms and three water molecules, which are not included within the bistren cavity, but lie on the ‘faces’ defined by each macrocyclic ring of the receptor. The crystal structure does not necessarily correspond to that present in an aqueous solution, where dynamic interactions with water molecules should occur. In any case, the ReO4− ion seems well set in the middle of the receptor's cavity: Re⋯Ntert distances 474 and 512 pm.
ReO4− is often used as a structural surrogate of 99TcO4−, even if the chemical analogy is dubious.36 The isotope 99Tc (β-emitter, t1/2 = 2.1 × 105 years) represents 6% of the total fission product yield and the radioactive anion 99TcO4− is present as a major component in the nuclear waste. Because of its high solubility in water (11.3 M for the sodium salt, 20 °C), 99TcO4− easily migrates within the earth's crust and enters the food chain. The search for an artificial selective receptor for 99TcO4− capable of working in water is therefore especially important and challenging.37
In our group, we have recently obtained the crystal and molecular structure of the complex salt [LH6(TcO4)](TcO4)(CF3SO3)4·8H2O (L = 9),37 containing the inclusion complex [LH6⋯99TcO4]5+, whose structure is shown in Fig. 22.
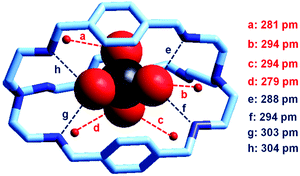 | ||
| Fig. 22 The crystal and molecular structure of the inclusion complex salt: [LH6(TcO4)](TcO4)(CF3SO3)4·8H2O. Hydrogen atoms, and counterions, including uncomplexed 99TcO4−. Of the eight solvation water molecules, only the four involved in hydrogen bonding interactions with 99TcO4− are reported. Dashed lines indicate hydrogen bond interactions with O,N⋯OTcO3− < 330 pm.37 | ||
Compared to the [LH6⋯ReO4]5+ analogue, the 99TcO4− complex presents a higher number of hydrogen bonds, with both NH2+ groups and water molecules, which may suggest a higher stability in water. Through ITC measurements thermodynamic quantities associated with the anion inclusion equilibrium were determined. They are reported in Table 2 and compared to the corresponding values for ReO4−, NO3− and Cl−.
| Anion | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
ΔG° kcal mol−1 | ΔH° kcal mol−1 | TΔS° kcal mol−1 | ΔG°hydr kcal mol−1 |
|---|---|---|---|---|---|
| 99TcO4− | 5.50 ± 0.01 | −7.63 ± 0.01 | −11.0 ± 0.1 | −3.3 ± 0.1 | −78.9 |
| ReO4− | 5.22 ± 0.01 | −7.24 ± 0.01 | −10.7 ± 0.1 | −3.5 ± 0.1 | −60.0 |
| NO3− | 3.41 ± 0.01 | −4.72 ± 0.01 | −3.36 ± 0.01 | 1.36 ± 0.01 | −71.7 |
| Cl− | 2.25 ± 0.01 | −3.14 ± 0.01 | −3.14 ± 0.01 | 1.76 ± 0.01 | −81.3 |
Indeed, the inclusion constant of 99TcO4− is twice that observed for ReO4−. However, such moderate extra-stability (ΔΔG° = −0.4 kcal mol−1) is probably to be ascribed to the much lower energy spent for dehydrating 99TcO4− compared to ReO4− (ΔGhydr (TcO4−) = −60.0 kcal mol−1; ΔGhydr (ReO4−) = −78.9 kcal mol−1: ΔΔGhydr = 19 kcal mol−1). Note that the inclusion equilibria are enthalpy driven (which reflects a favourable balance between the exothermic HB interactions of the oxoanion with the cavity and the endothermic dehydration energy terms) and contrasted by the negative entropy contribution (to be associated with the decrease of particles and to the rigidification of the receptor's framework following anion encapsulation). Very interestingly, NO3− and Cl−, present in large amounts in the acidic nuclear effluents, poorly compete with 99TcO4−, showing association constants lower by more than two and three orders of magnitude, respectively. An inspection of the thermodynamic quantities in Table 2 indicates that the rather poor affinity of nitrate and chloride vs. the hexaprotonated receptor depends upon a weakly exothermic enthalpy contribution. This should be ascribed to the poor capability of the two anions to fit the size and shape of the hexaammonium cavity and to establish effective hydrogen bonds.
The contest between a dimetallic cryptate and a hexaprotonated cryptand for the linear recognition of dicarboxylates
At the end of the story, one could ask, which among the two classes of receptors derived from bistren, whether dicopper(II) cryptates or hexaprotonated cryptands, can act as the most effective and selective receptor for anions. As a playfield, we will choose the recognition of dicarboxylates.In 1991, Lehn considered that the hexaprotonated form of the previously discussed bistren cryptand 6, LH66+, possessed an ellipsoidal, oblong cavity, suitable for the encapsulation of medium sized dicarboxylates, whether aromatic or aliphatic. In particular, he was able to crystallize the complex salt [LH6⋯C6H4(COO)2](C6H4(COO)2)2·14H2O, in which a terephthalate ion (1,4-C6H4(COO)22−) is encapsulated within a hexaprotonated receptor LH66+, (L = 6).38 The structure of the inclusion complex is reported in Fig. 23.
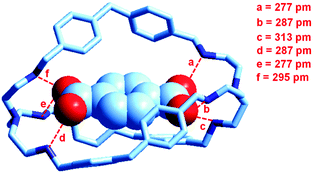 | ||
| Fig. 23 The structure of the terephthalate inclusion complex of the bistren hexaprotonated receptor LH66+ (L = 6). Hydrogen atoms, counterions and solvation water molecules of the crystalline salt [LH6⋯C6H4(COO)2](C6H4(COO)2)2·14H2O have been omitted for clarity. The encapsulated anion establishes six well defined hydrogen bonds with the six secondary ammonium groups of the receptor, indicated by dashed lines. The distance between the bridgeheads’ tertiary nitrogen atoms Ntert⋯Ntert is 1377 pm.38 | ||
The terephthalate dianion is well accommodated inside the cavity of the receptor and establishes six well defined hydrogen bonds with the six secondary ammonium groups of LH66+. The association constant of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex was determined through 1H NMR titration experiments, in a D2O solution buffered at pD 6.0, at 20 °C. In particular, the 1H NMR signals of terephthalate were found to undergo marked upfield shifts in the presence of increasing amounts of LH66+, indicating that complexation occurred. From data analysis, an association constant K = 2.5 × 104 was calculated. Then, the study was extended to a series of linear aliphatic dicarboxylates −OOC(CH2)nCOO− (n = 2–8) and the corresponding formation constants of the 1
1 complex was determined through 1H NMR titration experiments, in a D2O solution buffered at pD 6.0, at 20 °C. In particular, the 1H NMR signals of terephthalate were found to undergo marked upfield shifts in the presence of increasing amounts of LH66+, indicating that complexation occurred. From data analysis, an association constant K = 2.5 × 104 was calculated. Then, the study was extended to a series of linear aliphatic dicarboxylates −OOC(CH2)nCOO− (n = 2–8) and the corresponding formation constants of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes were determined.38 Pertinent log
1 complexes were determined.38 Pertinent log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values are reported in Table 3.
K values are reported in Table 3.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values for the equilibria on the inclusion of linear aliphatic dicarboxylates of formula −OOC(CH2)nCOO− by the hexaprotonated cryptand LH66+,a and the dicopper(II) cryptate [CuII2(L)]4+,b (L = 6)
K values for the equilibria on the inclusion of linear aliphatic dicarboxylates of formula −OOC(CH2)nCOO− by the hexaprotonated cryptand LH66+,a and the dicopper(II) cryptate [CuII2(L)]4+,b (L = 6)
| −OOC(CH2)nCOO− | LH66+ + A2− ⇄ [LH6⋯A]4+ | [CuII2(L)]4+ A2− ⇄ [CuII2(L)(A)]2+ | ||
|---|---|---|---|---|
| n | K (M−1) | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
K (M−1) | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
| a Ref. 38; in a D2O solution at 20 °C; buffered at pH = 6, with pyridine + CF3COOD, 10−2. b Ref. 39; in 50/50 (v/v) H2O–EtOH at 25 °C, pH = 7.2. | ||||
| 2 (succinate) | 1400 | 3.15 | 5.62 × 107 | 7.75 |
| 3 (glutarate) | 2300 | 3.36 | 3.16 × 108 | 8.50 |
| 4 (adipate) | 2600 | 3.41 | 1.02 × 1010 | 10.01 |
| 5 (pimelate) | 2100 | 3.32 | 2.19 × 107 | 7.34 |
| 6 (suberate) | 1900 | 3.28 | — | — |
| 7 (azelate) | 1400 | 3.15 | — | — |
| 8 (sebacate) | 1500 | 3.18 | — | — |
| Terephthalate (1,4-) | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4.40 | 6.17 × 109 | 9.79 |
| Isophthalate (1,3-) | — | — | 3.71 × 108 | 8.57 |
| Phthalate (1,2-) | — | — | 5.01 × 107 | 7.70 |
It should be noted that the association constants K for all the considered dicarboxylates are comprised within only one order of magnitude. However, the subtle differences seem to disclose a meaningful behaviour, which is illustrated in Fig. 24.
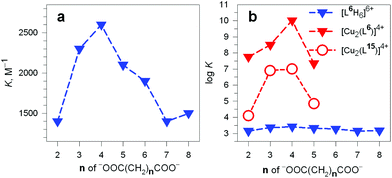 | ||
Fig. 24 (a) Plot of the constants K associated with the equilibrium: (i) LH66+ + A2− ⇄ [LH6⋯A]4+ (L = 6) vs. the number of methylene groups n of the α,ω-dicarboxylic acids −OOC(CH2)nCOO− (A2−) pH 6, 20 °C;38 (b) plot of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values associated with the dicarboxylate inclusion equilibria (i), filled blue triangles, and (ii): [CuII2(L)]4+ + A2− ⇄ [CuII2(L)(A)]2+ (L = L6 = 6) vs. n, pH 7.2, 25 °C, red filled triangles.39 Empty circles refer to eq. (ii) for L = L15 = 15.40 K values associated with the dicarboxylate inclusion equilibria (i), filled blue triangles, and (ii): [CuII2(L)]4+ + A2− ⇄ [CuII2(L)(A)]2+ (L = L6 = 6) vs. n, pH 7.2, 25 °C, red filled triangles.39 Empty circles refer to eq. (ii) for L = L15 = 15.40 | ||
In particular, the plot of K vs. the number of methylene groups in the carboxylic acid shows a well defined peak selectivity behaviour with the peak corresponding to n = 4 (adipate). It was then suggested that the hexaammonium receptor LH66+ (L = 6) performs a linear recognition of the substrate whose length probably corresponds best to the size of the intramolecular cavity.38
Very recently, Delgado et al. have investigated the formation of the corresponding dicopper(II) cryptates [CuII2(L)]4+ (L = 6) and their interaction with some medium sized linear aliphatic dicarboxylates −OOC(CH2)nCOO− (n = 2–4) and the three positional isomers of phthalate, in a water–ethanol mixture (50/50, v/v) at 25 °C. They were also able to crystallise the salts of the corresponding inclusion complexes of terephthalate and of adipate, whose molecular structures are shown in Fig. 25.
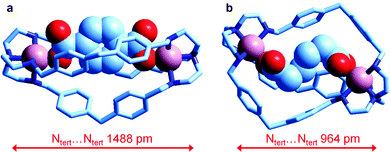 | ||
| Fig. 25 The crystal and molecular structure of the salts: (a) [CuII2(L)(terephthalate)](ClO4)2·MeOH·4H2O, and (b) [CuII2(L)(adipate)](NO3)2·10.8H2O (L = 6). Hydrogen atoms, counterions and solvational molecules have been omitted for clarity.39 | ||
It is observed that in the terephthalate inclusion complex (Fig. 25a) the bistren framework is suitably elongated in order to accommodate the rigid dianion. The distance between the bridgehead tertiary nitrogen atoms, Ntert⋯Ntert, 1488 pm, is quite large, larger than that observed for the corresponding hexaammonium terephthalate complex, which does not contain the two copper(II) ions (1377 pm). On the other hand, in the adipate complex (Fig. 25b), the Ntert⋯Ntert distance is much lower (964 pm), which indicates a great flexibility of the bistren framework. It has been suggested that such a flexible nature is associated with the presence of the –CH2– group linking the two phenyl rings of each spacer. It has been also shown by equilibrium studies that the two inclusion complexes, in spite of their very different conformational arrangements, show a high and comparable stability in solution.
Table 3 reports the values of the constants (K and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K) associated with the equilibria [CuII2(L)]4+ + A2− ⇄ [CuII2(L)(A)]2+ (L = 6) involving aliphatic α,ω-dicarboxylates. The plot in Fig. 24b (log
K) associated with the equilibria [CuII2(L)]4+ + A2− ⇄ [CuII2(L)(A)]2+ (L = 6) involving aliphatic α,ω-dicarboxylates. The plot in Fig. 24b (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K vs. the number of methylene groups in the dianion) discloses a well defined peak selectivity in favour of the adipate ions, which forms an inclusion complex 2–3 orders of magnitude more stable than the corresponding anions of shorter (succinate, glutarate) and longer (pimelate) chain lengths. The plot illustrates well the capability of the dicopper(II) cryptate to recognise the length of the dicarboxylate. Note in the same Fig. 24b that on a logarithmic scale (blue filled triangles) the selectivity of the hexaprotonated cryptand 6 practically disappears.
K vs. the number of methylene groups in the dianion) discloses a well defined peak selectivity in favour of the adipate ions, which forms an inclusion complex 2–3 orders of magnitude more stable than the corresponding anions of shorter (succinate, glutarate) and longer (pimelate) chain lengths. The plot illustrates well the capability of the dicopper(II) cryptate to recognise the length of the dicarboxylate. Note in the same Fig. 24b that on a logarithmic scale (blue filled triangles) the selectivity of the hexaprotonated cryptand 6 practically disappears.
The compared behaviours described above express definitely the pre-eminence of dimetallic bistren cryptates in anion recognition with respect to hexaammonium bistren cryptands. Such a high capability of discrimination is derived from the nature of the receptor–anion interaction. In particular, the metal–ligand interactions are much stronger than the hydrogen bonding interactions. Moreover, due to the presence of incompletely filled d orbitals, a coordinatively unsaturated transition metal ion establishes with the anionic substrate an interaction characterised by a high degree of directionality, a feature much less pronounced in the case of hydrogen bonding and totally absent for electrostatic interactions. However, one could argue that the above described comparison is not correct because the hexaammonium receptor was studied in pure water, whereas the dicopper(II) cryptate was investigated in 50/50 (v/v) ethanol–water. In the latter medium the reagents are less solvated and dehydration energy plays a significant role: in particular anion inclusion is favoured.
In order to make a homogeneous comparison, we can choose the dicopper(II) cryptate complex of the bistren derivative 15,40 whose spacers are constituted by diphenyl fragments, which should produce an ellipsoidal cavity with a slightly shorter major axis with respect to cryptand 6, whose spacers contain an additional –CH2– group, and should also impart a higher rigidity. Fig. 26 shows the crystal structure of the ‘void’ cryptate, in which the fifth coordination site of each CuII centre is occupied by a water molecule.40 The structure offers a sound representation of the cryptate receptor in water before anion inclusion. In view of the negligible steric hindrance of the coordinate water molecules, the Ntert⋯Ntert distance (1330 pm) should correspond to the receptor relaxed to its minimum energy conformation.
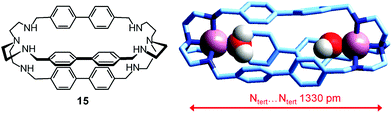 | ||
| Fig. 26 The crystal and molecular structure of the dimetallic complex salt [CuII2(15)(H2O)2](NO3)4.40 Hydrogen atoms of the bistren ligand and counterions have been omitted for clarity. | ||
Due to the poor solubility in water of the [CuII2(15)(H2O)2](NO3) complex salt (≈10−4 M), anion inclusion equilibria were investigated by following the parading of fluorescent indicator displacement.41,42 The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values associated with the [CuII2(L)]4+ + A2− ⇄ [CuII2(L)(A)]2+ (L = 6) equilibria involving aliphatic α,ω-dicarboxylates are reported in the diagram in Fig. 24b (empty circles). It is observed that the log
K values associated with the [CuII2(L)]4+ + A2− ⇄ [CuII2(L)(A)]2+ (L = 6) equilibria involving aliphatic α,ω-dicarboxylates are reported in the diagram in Fig. 24b (empty circles). It is observed that the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values are lower than those referring to the cryptate of the bistren derivative 6 (50/50 v/v, EtOH–H2O) due to the greater endothermicity of the dehydration terms, but distinctly higher (up to four orders of magnitude) than for the inclusion equilibria for the hexaprotonated version of 6. Moreover, a well defined selectivity is maintained with respect to the number of –CH2– groups of the α,ω-dicarboylates. In particular, the log
K values are lower than those referring to the cryptate of the bistren derivative 6 (50/50 v/v, EtOH–H2O) due to the greater endothermicity of the dehydration terms, but distinctly higher (up to four orders of magnitude) than for the inclusion equilibria for the hexaprotonated version of 6. Moreover, a well defined selectivity is maintained with respect to the number of –CH2– groups of the α,ω-dicarboylates. In particular, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values decrease along the series: glutarate ≈ adipate ≫ pimelate ≈ succinate. The absence of a peak selectivity may be ascribed to the fact that the cryptate of the rigid cryptand 15, containing diphenyl spacers, offers a smaller cavity than the cryptate of cryptand 6, containing a diphenylmethane spacer. The smaller cavity is not perfectly complementary in size to either glutarate (too short) or adipate (too long), which during inclusion have to rearrange and spend conformational energy.
K values decrease along the series: glutarate ≈ adipate ≫ pimelate ≈ succinate. The absence of a peak selectivity may be ascribed to the fact that the cryptate of the rigid cryptand 15, containing diphenyl spacers, offers a smaller cavity than the cryptate of cryptand 6, containing a diphenylmethane spacer. The smaller cavity is not perfectly complementary in size to either glutarate (too short) or adipate (too long), which during inclusion have to rearrange and spend conformational energy.
The receptor's rigidity effect on dicarboxylate inclusion selectivity is better illustrated by the interactions with the positional isomers of phthalate. Fig. 27 reports the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values for phthalates inclusion equilibria by cryptates [CuII2(6)]4+ and [CuII2(15)]4+. In both cases, the log
K values for phthalates inclusion equilibria by cryptates [CuII2(6)]4+ and [CuII2(15)]4+. In both cases, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values increase according to the sequence: phthalate < isophthalate < terephthalate. However, the [CuII2(15)]4+ receptors show a distinctly more pronounced selectivity towards the 1,4 isomeric anion than [CuII2(6)]4+. This may be due to the rigidity of the framework of 15, compared to the more flexible 6, which may rearrange to accommodate the different isomers at a much lower conformational cost.
K values increase according to the sequence: phthalate < isophthalate < terephthalate. However, the [CuII2(15)]4+ receptors show a distinctly more pronounced selectivity towards the 1,4 isomeric anion than [CuII2(6)]4+. This may be due to the rigidity of the framework of 15, compared to the more flexible 6, which may rearrange to accommodate the different isomers at a much lower conformational cost.
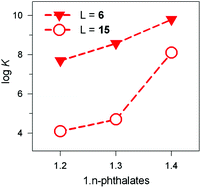 | ||
Fig. 27 Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values for the equilibria: [CuII2(L)]4+ + A2− ⇄ [CuII2(L)(A)]2+, where A2− is a 1,n-phthalate: (i) filled triangles, L = 6, 50/50 (v/v) H2O–EtOH, 25 °C;39 (ii) empty circles, L = 15, water, 25 °C.40 K values for the equilibria: [CuII2(L)]4+ + A2− ⇄ [CuII2(L)(A)]2+, where A2− is a 1,n-phthalate: (i) filled triangles, L = 6, 50/50 (v/v) H2O–EtOH, 25 °C;39 (ii) empty circles, L = 15, water, 25 °C.40 | ||
It is hypothesised that terephthalate encompasses quite well the length of the main axis of the ellipsoid. Indeed, the distance between the two oxygen atoms of the two metal bound water molecules is 736 pm, while the distance of the farthest oxygen atoms of terephthalate is 739 (as observed in its ammonium salt),43 thus granting an almost perfect fitting.
Conclusion
Cages in the everyday life are not appealing items because everybody is conscious that they have been designed for a blameworthy function: imprisoning birds or wild animals. This does not occur in the molecular world and the inventiveness and skillfulness of chemists in designing cage-shaped polycyclic hosts, for the inclusion of a variety of guests, are highly appreciated. Note that in the macroscopic world a kinetic barrier prevents the escape of a prisoner from the cage. In contrast, in the molecular world, entering–exiting of a substrate in/from a cage is not affected, in most cases, by a relevant kinetic barrier and is only thermodynamically controlled. Thus, the substrate gets in/out of the cage at will.44 Such a feature provides the basis for an effective recognition of anions by cage-shaped receptors.46Bistren cryptands are versatile cage-shaped systems which behave as efficient and selective anion receptors for several reasons: (i) they can be easily synthesised through a two step procedure: the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 Schiff base condensation of tren with a dialdehyde; tren is a commercial and cheap reagent, thus all synthetic efforts have to be converged in the preparation of the dialdehyde; (ii) any bistren cryptand can be addressed by two different modes of anion recognition, either as an hexaammonium cation or as a dimetallic complex; (iii) in both versions, cryptand derived receptors are water soluble thus providing recognition and, if desired, the sequestering of anions in aqueous media.
3 Schiff base condensation of tren with a dialdehyde; tren is a commercial and cheap reagent, thus all synthetic efforts have to be converged in the preparation of the dialdehyde; (ii) any bistren cryptand can be addressed by two different modes of anion recognition, either as an hexaammonium cation or as a dimetallic complex; (iii) in both versions, cryptand derived receptors are water soluble thus providing recognition and, if desired, the sequestering of anions in aqueous media.
In conclusion, bistren derivatives represent an interesting case in which metal coordination chemistry and anion coordination chemistry successfully meet, within the broad realm of supramolecular chemistry in water.
Acknowledgements
We are indebted to the Italian Ministry of University and Research (MIUR) for financial support (PRIN: project Infochem).Notes and references
- A. Werner, Z. Anorg. Allg. Chem., 1893, 3, 267 CrossRef.
- Anion Coordination Chemistry, ed. K. Bowman-James, A. Bianchi and E. García-Espana, John Wiley & Sons, New York, 2012 Search PubMed.
- S. O. Kang, J. M. Llinares, V. W. Day and K. Bowman-James, Chem. Soc. Rev., 2010, 39, 3980 RSC.
- P. Mateus, N. Bernier and R. Delgado, Coord. Chem. Rev., 2010, 254, 1726 CrossRef CAS PubMed.
- L. Fabbrizzi and A. Poggi, Chem. Soc. Rev., 2013, 42, 1681 RSC.
- J. E. Prue and G. Schwarzenbach, Helv. Chim. Acta, 1950, 33, 963 CrossRef CAS.
- J.-M. Lehn, S. H. Pine, E. Watanabe and A. K. Willard, J. Am. Chem. Soc., 1977, 99, 6766 CrossRef CAS.
- B. Dietrich, J.-M. Lehn and J.-P. Sauvage, Tetrahedron Lett., 1969, 10, 2889 CrossRef.
- R. J. Motekaitis, P. R. Rudolf, A. E. Martell and A. Clearfield, Inorg. Chem., 1989, 28, 112 CrossRef CAS.
- J. Jazwinski, J.-M. Lehn, D. Lilienbaum, R. Ziessel, J. Guilhem and C. Pascard, J. Chem. Soc., Chem. Commun., 1987, 1691 RSC.
- D. McDowell and J. Nelson, Tetrahedron Lett., 1988, 28, 385 CrossRef.
- M. G. B. Drew, D. McDowell and J. Nelson, Polyhedron, 1988, 7, 229 CrossRef.
- R. Menif, J. Reibenspies and A. E. Martell, Inorg. Chem., 1991, 30, 3446 CrossRef CAS.
- L. Fabbrizzi, P. Pallavicini, A. Perotti, L. Parodi and A. Taglietti, Inorg. Chim. Acta, 1995, 238, 5 CrossRef CAS.
- C. J. Harding, F. E. Mabbs, E. J. L. MacInnes, V. McKee and J. Nelson, J. Chem. Soc., Dalton Trans., 1996, 3227 RSC.
- F. Arnaud-Neu, S. Fuangswasdi, B. Maubert, J. Nelson and V. McKee, Inorg. Chem., 2000, 39, 573 CrossRef CAS.
- F. A. Mautner, C. N. Landry, A. A. Gallo and S. S. Massoud, J. Mol. Struct., 2007, 837, 72 CrossRef CAS PubMed.
- L. Fabbrizzi, A. Leone and A. Taglietti, Angew. Chem., Int. Ed., 2001, 40, 3066 CrossRef CAS.
- V. Amendola, G. Bergmaschi, M. Boiocchi, L. Fabbrizzi, A. Poggi and M. Zema, Inorg. Chim. Acta, 2008, 361, 4038 CrossRef CAS PubMed.
- V. Amendola, E. Bastianello, L. Fabbrizzi, C. Mangano, P. Pallavicini, A. Perotti, A. Manotti Lanfredi and F. Ugozzoli, Angew. Chem., Int. Ed., 2000, 39, 2917 CrossRef CAS.
- A. Bondi, J. Phys. Chem., 1964, 68, 441 CrossRef CAS.
- C. J. Harding, V. McKee, J. Nelson and Q. Lu, J. Chem. Soc., Chem. Commun., 1993, 1768 RSC.
- P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739 CrossRef CAS.
- G. Bergamaschi, M. Boiocchi, M. L. Perrone, A. Poggi, I. Viviani and V. Amendola, Dalton Trans., 2014, 43, 11352 RSC.
- G. Alibrandi, V. Amendola, G. Bergamaschi, R. Dollenz, L. Fabbrizzi, M. Licchelli and C. Lo Vecchio, Chem. – Eur. J., 2013, 19, 3729 CrossRef CAS PubMed.
- G. Alibrandi, Angew. Chem., Int. Ed., 2008, 47, 3026 CrossRef CAS PubMed; G. Alibrandi, C. Lo Vecchio and G. Lando, Angew. Chem., Int. Ed., 2009, 48, 6332 CrossRef PubMed.
- J. Cheney and J. M. Lehn, J. Chem. Soc., Chem. Commun., 1972, 487 RSC.
- J. Cheney, J. P. Kintzinger and J. M. Lehn, Nouv. J. Chim., 1978, 2, 411 CAS.
- P. B. Smith, J. L. Dye, J. Cheney and J. M. Lehn, J. Am. Chem. Soc., 1981, 103, 6044 CrossRef CAS.
- J.-M. Lehn, E. Sonveaux and A. K. Willard, J. Am. Chem. Soc., 1978, 100, 4914 CrossRef CAS.
- B. Dietrich, J. Guilhem, J.-M. Lehn, C. Pascard and E. Sonveaux, Helv. Chim. Acta, 1984, 67, 91 CrossRef CAS.
- J. Nelson and V. McKee, Prog. Inorg. Chem., 1998, 47, 167 CrossRef CAS.
- V. McKee, J. Nelson and R. M. Town, Chem. Soc. Rev., 2003, 32, 309 RSC.
- V. Amendola, G. Alberti, G. Bergamaschi, R. Biesuz, M. Boiocchi, S. Ferrito and F.-P. Schmidtchen, Eur. J. Inorg. Chem., 2012, 3410 CrossRef CAS.
- C. Frassineti, L. Alderighi, P. Gans, A. Sabatini, A. Vacca and S. Ghelli, Anal. Bioanal. Chem., 2003, 376, 1041 CrossRef CAS PubMed.
- E. A. Katayev, G. V. Kolesnikov and J. L. Sessler, Chem. Soc. Rev., 2009, 38, 1572 RSC.
- R. Alberto, G. Bergamaschi, H. Braband, T. Fox and V. Amendola, Angew. Chem., Int. Ed., 2012, 51, 9772 CrossRef CAS PubMed.
- J.-M. Lehn, R. Meric, J.-P. Vigneron, I. Bkouche-Waksman and C. Pascard, J. Chem. Soc., Chem. Commun., 1991, 62 RSC.
- P. Mateus, R. Delgado, V. André and M. T. Duarte, Inorg. Chem., 2015, 54, 229 CrossRef CAS PubMed.
- M. Boiocchi, M. Bonizzoni, L. Fabbrizzi, G. Piovani and A. Taglietti, Angew. Chem., Int. Ed., 2004, 43, 3847 CrossRef CAS PubMed.
- S. L. Wiskur, H. Ait-Haddou, J. J. Lavigne and E. V. Anslyn, Acc. Chem. Res., 2001, 34, 963 CrossRef CAS PubMed.
- M. Ansa Hortalá, L. Fabbrizzi, N. Marcotte, F. Stomeo and A. Taglietti, J. Am. Chem. Soc., 2003, 125, 20 CrossRef PubMed.
- J. A. Kaduk, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 474 Search PubMed.
- A classical example of a cage with an extremely high kinetic barrier, which prevents the guest from escaping, is given by Sargeson's cobalt(III) sepulchrate and sarcophagine complexes.45 In this case, it is the guest itself (CoIII) that has built its prison from the inside.
- (a) I. I. Creaser, J. M. Harrowfield, A. J. Herlt, A. M. Sargeson, J. Springborg, R. J. Geue and M. R. Snow, J. Am. Chem. Soc., 1977, 99, 3181 CrossRef CAS; (b) R. J. Geue, T. W. Hambley, J. M. Harrowfield, A. M. Sargeson and M. R. Snow, J. Am. Chem. Soc., 1984, 106, 5478 CrossRef CAS.
- L. Fabbrizzi, Top. Curr. Chem., 2012, 323, 127 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |