Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A thermodynamic insight into the recognition of hydrophilic and hydrophobic amino acids in pure water by aza-scorpiand type receptors†
Salvador
Blasco
a,
Begoña
Verdejo
*a,
Carla
Bazzicalupi
b,
Antonio
Bianchi
*b,
Claudia
Giorgi
b,
Concepción
Soriano
a and
Enrique
García-España
*a
aInstituto de Ciencia Molecular, C/Catedrático José Beltrán 2, 46980 Paterna, Valencia, Spain. E-mail: enrique.garcia-es@uv.es
bDipartimento di Chimica, Via Della Lastruccia 3, 50019 Sesto Fiorentino, Italy. E-mail: antonio.bianchi@unifi.it
First published on 30th October 2014
Abstract
Interactions of different hydrophilic (His, Asp, Glu,) and hydrophobic (Ala, Phe, Tyr, Trp) amino acids in water with a scorpiand aza-macrocycle (L1) containing a pyridine group in the ring and its derivative (L2) bearing a naphthalene group in the tail have been analysed by potentiometric and calorimetric measurements. Theoretical calculations corroborate that major attractive forces that hold the adduct together are hydrogen bonds and salt-bridges, even though other interactions such as π-stacking or NH+⋯π may contribute in the case of hydrophobic amino acids and L2. Calorimetric measurements indicate that the interactions between L1 and the different amino acids are principally driven by entropy, often associated with solvation/desolvation processes.
Introduction
Molecular recognition implies complementarity of electronic and structural features between the receptor and the target substrate.1 In the case of biological substrates, the forces involved in the recognition processes are mostly electrostatic attractions (charge–charge, dipole–charge, dipole–dipole, and H-bonds). Such electrostatic forces are markedly weakened in polar solvents, in particular, in water, which, apart from having high polarity, is also an efficient donor and acceptor of H-bonds. Hence, molecular recognition in water requires high complementarity between substrates and receptors and the presence of many binding sites on both, as actually occurs in biological systems. On the other hand, water favours hydrophobic association, which is another important aspect of the biological world. Accordingly, the design of synthetic receptors for the recognition of biological substrates in water is very challenging, but it is also a very attractive objective since water is the solvent of life. To obtain a clear view of the binding event in water, enthalpic and entropic contributions give fundamental information. Nonetheless, these types of data related to pure water are very scarce in the literature.2Here we report on the interactions of a selection of hydrophilic (His, Asp, Glu) and hydrophobic (Ala, Phe, Tyr, Trp) amino acids with two scorpiand aza-macrocycles (L1 and L2, see Chart 1). Amino acid recognition is of great interest in different fields like drug delivery,3 protein–nucleic acid recognition4 or amino acid sensing.5 This process is particularly challenging, since they have a zwitterionic nature over a wide pH range and often require host species having functionalities able to simultaneously interact with their positive ammonium and negative carboxylate sites. In this respect, in spite of being relatively small molecules, L1 and L2 contain different binding sites (amine and/or ammonium groups, hydrophobic moieties) and have the ability to self-adapt to the guest amino acid due to the flexibility afforded by their hanging arms. Indeed, such an induced-fit ability is a key point for successful recognition in many biological systems.
L1 and L2 have been chosen to achieve selectivity with amino acids of different hydrophobicity due to their different hydrophilic/hydrophobic balance.6 In the case of the more water soluble L1, a complete set of thermodynamic binding data is provided.
Results and discussion
Protonation of L1 and L2
The equilibrium constants for the protonation of L1 and L2 were reported in a previous paper where it was anticipated that L2 undergoes important conformational changes upon protonation.6 In the mono- and diprotonated forms, the molecule assumes a folded conformation stabilized by intramolecular hydrogen bonds, involving the amino group of the pendant arm and the ammonium group(s) of the macrocyclic moiety, and π-stacking interaction between the two aromatic units. Further protonation of L2, occurring on the amino group of the pendant arm, causes the opening of such a conformation with loss of all intramolecular interactions to form a more expanded structure where the three positive charges of [H3L2]3+ are brought as far apart as possible to minimize the electrostatic repulsion between them.7This was clearly evidenced by NMR spectra recorded for ligand solutions at different pH values and by the crystal structures obtained for L2, [H(L2)]ClO4·H2O and [H3(L2)](H2PO4)3·H2O.6 Furthermore, stacking of pyridine and naphthalene moieties for L2 was also evidenced by changes in the UV-Vis spectra as a function of pH (see Fig. 1).
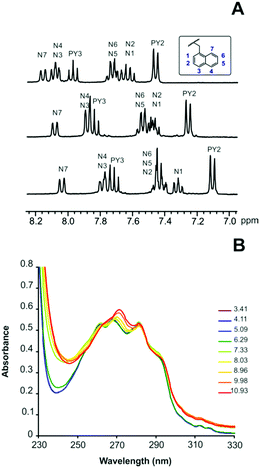 | ||
| Fig. 1 (A) 1H NMR spectra in D2O of L2 recorded from the top to the bottom at pD = 4.1, pD = 8.2 and pD = 9.4. (B) pH dependence of the absorption spectra of L2. | ||
The calorimetric study performed in this work showed that such conformational changes are clearly manifested by the enthalpic and entropic contributions to ligand protonation, in contrast to the free energy change (stability constants) which appears to be almost insensitive to these structural modifications (Table 1). As shown in Table 1, successive protonation of L1 is accompanied by invariably favourable enthalpy changes, while the entropic contributions become less and less favourable with increasing ligand protonation and consequent increasing solvation, according to a general trend observed for polyamines.8 A similar behaviour is found for the first two protonation stages of L2, while the third one is an athermic process moved by a largely favourable entropy contribution (Table 1): the breaking of intramolecular bonds, occurring at this stage, compensates the favourable enthalpy contribution coming from protonation of the amine group but gives the molecules a greater conformation freedom.
| Reaction | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
ΔG° (kcal mol−1) | ΔH° (kcal mol−1) | TΔS° (kcal mol−1) |
|---|---|---|---|---|
| a Numbers in parentheses are standard deviations in the last significant figure. | ||||
| L1 + H+ ⇄ [HL1]+ | 10.19(6)a | −13.90(8) | −10.19(7) | 3.7(1) |
| [HL1]+ + H+ ⇄ [H2L1]2+ | 9.19(7) | −12.54(9) | −12.05(9) | 0.5(1) |
| [H2L1]2+ + H+ ⇄ [H3L1]3+ | 7.94(5) | −10.83(7) | −11.46(5) | −0.6(1) |
| L2 + H+ ⇄ [HL2]+ | 10.01(1) | −13.65(1) | −8.6(4) | 5.1(4) |
| [HL2]+ + H+ ⇄ [H2L2]2+ | 8.71(1) | −11.88(2) | −13.2(6) | −1.3(6) |
| [H2L2]2+ + H+ ⇄ [H3L2]3+ | 7.27(1) | −9.92(2) | 0.1(7) | 10.0(5) |
Therefore, it appears that to achieve a closed conformation, both intramolecular hydrogen bonding and π-stacking interaction need to occur simultaneously in this kind of receptors. Taking into account that these types of intramolecular interactions are precluded to L1, it can be assumed that this receptor is not able to adopt a “closed” conformation.
Binding of amino acids by L1 and L2
The equilibrium constants for the interaction of protonated forms of L1 and L2 with Ala, Phe, Tyr, Trp, His, Asp and Glu were determined by means of pH-metric titrations in 0.15 M NaClO4 solutions at 298.1 K. Analyses of the titrations curves by means of the HYPERQUAD9 program afforded the equilibrium constants for the general reaction (1):| L + An− + mH+ ⇄ HmLA(m−n)+ | (1) |
| Reaction | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
ΔH° (kcal mol−1) | TΔS° (kcal mol−1) |
|---|---|---|---|
| a Numbers in parentheses are standard deviations in the last significant figure. | |||
| HL+ + Tyr2− ⇄ [HL(Tyr)]− | 3.27(1)a | 9.0(4) | 13.5(4) |
| HL+ + HTyr− ⇄ [HL(HTyr)] | 3.61(1) | 5.0(3) | 9.9(3) |
| H2L2+ + HTyr− ⇄ [H2L(HTyr)]+ | 3.79(1) | 7.2(4) | 12.3(4) |
| H2L2+ + H2Tyr ⇄ [H2L(H2Tyr)]2+ | 3.31(1) | 6.2(3) | 10.7(3) |
| H3L3+ + H2Tyr ⇄ [H3L(H2Tyr)]3+ | 3.39(1) | 7.0(4) | 11.6(4) |
| HL+ + Asp2− ⇄ [HL(Asp)]− | 3.2(1) | 5.1(2) | 9.5(2) |
| HL+ + HAsp− ⇄ [HL(HAsp)] | 3.48(6) | 3.4(2) | 8.2(2) |
| H2L2+ + HAsp− ⇄ [H2L(HAsp)]+ | 3.47(6) | 4.1(2) | 8.9(2) |
| H3L3+ + HAsp− ⇄ [H3L(HAsp)]2+ | 3.72(6) | 4.6(2) | 8.3(2) |
| H3L3+ + H2Asp ⇄ [H3L(H2Asp)]3+ | 4.26(6) | 4.3(2) | 10.2(2) |
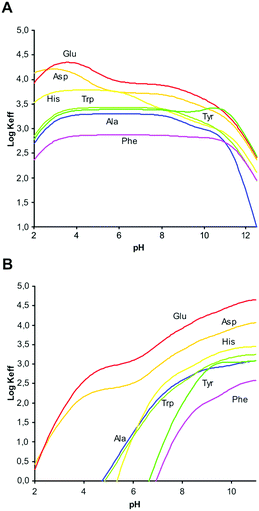
A comparison of the equilibrium information collected in these tables evidence significant differences in the binding properties of the two ligands towards amino acids. Very impressive is the ability of the neutral (not protonated and not charged) L2 ligand to form stable complexes with anionic forms of amino acids. These are the most stable complexes formed by L2, the stability of the other complex species decreasing with increasing ligand protonation. Conversely, L1 requires at least one positive charge, [HL1]+, to interact with the amino acids and the stability of its complexes generally increases with ligand protonation. Accordingly, L2 is a better receptor for amino acids in neutral-to-alkaline media while L1 extends its binding properties to the acidic region. To better visualize and quantify such differences, the stability constants reported in Tables S1 and S2† can be used to calculate effective stability constants (Keff,11eqn (2)) for complexation equilibria involving total amounts of reactants and products in the form:
| Keff = [Hx+yLA]/[(HxL)][(HyA)] | (2) |
Plots of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keff as a function of pH for all the complex systems here studied are shown in Fig. 2. As can be seen, for L1 all complexes show the same general trend with a slight increase of log
Keff as a function of pH for all the complex systems here studied are shown in Fig. 2. As can be seen, for L1 all complexes show the same general trend with a slight increase of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keff at around pH 3, where deprotonation of the carboxylic group present in the amino acid takes place.
Keff at around pH 3, where deprotonation of the carboxylic group present in the amino acid takes place.
This interaction remains constant in a wide pH range until total deprotonation of L1 occurs at around pH 9, a value from which a marked decline in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keff is observed. If the overall charge of the amino acids is considered, we observe that complex stability is not determined by merely electrostatic attractions. For instance, the equilibrium constant for the interaction of [H3L1]3+ with H2Asp (log
Keff is observed. If the overall charge of the amino acids is considered, we observe that complex stability is not determined by merely electrostatic attractions. For instance, the equilibrium constant for the interaction of [H3L1]3+ with H2Asp (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 4.26, Table 2) is higher than the constant for the interaction of the same ligand form with the more charged HAsp species (log
K = 4.26, Table 2) is higher than the constant for the interaction of the same ligand form with the more charged HAsp species (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.72, Table 2), in contrast to electrostatic expectations, while the opposite trend, obeying Coulomb's law, is observed when HTyr− and H2Tyr (log
K = 3.72, Table 2), in contrast to electrostatic expectations, while the opposite trend, obeying Coulomb's law, is observed when HTyr− and H2Tyr (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.79 and 3.31, respectively, Table 2) are considered. Other examples of this type can be found in Tables S1 and S2 (see ESI†). Evidently, other forces than charge–charge interactions contribute to determine the stability of these amino acid complexes.
K = 3.79 and 3.31, respectively, Table 2) are considered. Other examples of this type can be found in Tables S1 and S2 (see ESI†). Evidently, other forces than charge–charge interactions contribute to determine the stability of these amino acid complexes.
However, for L2 a clearly different behaviour is observed depending on the hydrophilic/hydrophobic character of the amino acids studied. As can be seen in Fig. 2B, in comparison with Ala, amino acids like Glu or Asp show an increasing interaction from acidic to basic pH values that can be attributed to the additional carboxylate group present in the side chain. Nevertheless, interaction with amino acids containing aromatic moieties (Phe, Tyr, Trp, His) is observed only for pH values above 5. This behaviour can be principally ascribed to the π-stacking interactions between the aromatic rings present in the amino acid side chain and the naphthalene moiety of L2.
1H NMR spectra recorded with solutions containing L2 and Glu showed that opening of the ligand structure upon protonation ([H2L2]2+ → [H3L2]3+) occurs also in the presence of amino acids (Fig. S1†). As already discussed for the free ligand, such a conformational change has a considerable enthalpic cost which is overcompensated by the entropic gain originating from the increased freedom achieved by the ligand when passing from closed to open conformation. Nevertheless, if the open ligand conformation is constrained by interaction with an amino acid, this favourable entropic gain vanishes and the corresponding complex loses stability. Most likely, this is the reason why the amino acid complexes with L2 in open conformation ([H3L2]3+), when formed, are the less stable complexes produced by this ligand. In contrast, L1, maintaining an open conformation in all its forms, does not experience a similar depression of complex stability in acidic solution and, instead, the greater positive charge of its highly protonated forms enhances the complex stability.
In agreement with the 1H NMR information, UV-vis spectroscopic data obtained for L2 and its Glu and Ala complexes confirm that the presence of the amino acid, in [H3L(GluH)]2+ species, forces the ligand to remain longer in its open conformation, while in the presence of Ala the effect is more reduced.12,13
Theoretical calculations
To rationalize these behaviours, we performed a modeling study on the complexes formed by L1 and L2. The modeling was performed using simulated annealing procedures based on a molecular mechanics method. The empirical force field was used as implemented in the HyperChem program.14 In all cases, the solvent effects were implicitly simulated. The minimum energy structures of the different complexes formed by L1 with Tyr and by L2 with Glu, which are used here as an example, are shown in Fig. 3 and 4, respectively, while those for the other complex systems are shown in Fig. S2–S7.†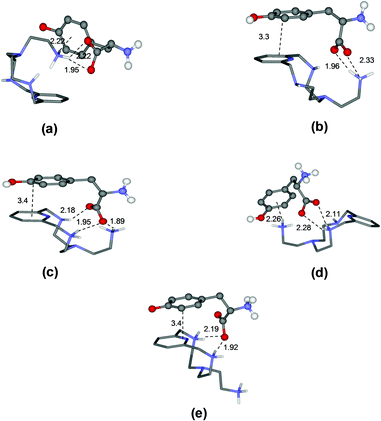 | ||
| Fig. 3 Minimum energy structures calculated for the complexes [HL1(Tyr)]− (a), [HL1(HTyr)] (b), [H2L1(HTyr)]+ (c), [H2L1(H2Tyr)]2+ (d), and [H3L1(H2Tyr)]3+ (e). | ||
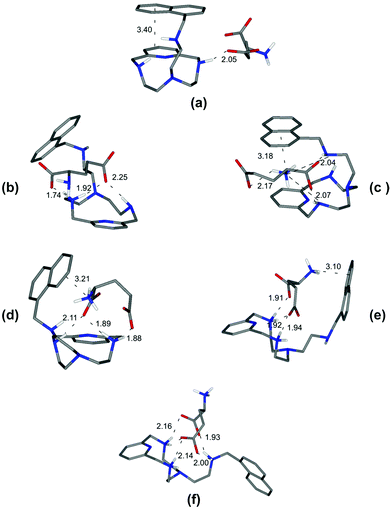 | ||
| Fig. 4 Minimum energy structures calculated for the complexes [L2(Glu)]2− (a), [HL2(Glu)]− (b), [L2(HGlu)]− (c), [HL2(HGlu)] (d), [H2L2(HGlu)]+ (e), and [H3L2(HGlu)]2+ (f). | ||
A general observation coming from the analysis of the minimum energy structures of the complexes formed with all amino acids is that when the amino acid contains an ammonium group, the interacting partners approach each other in such a way as to locate the positively charged ammonium groups as far apart as possible. Hence, although at a macroscopic level (stability constants) electrostatic forces appear not to play a fundamental role, at the molecular level they can be fundamental in regulating the mutual orientation of the interacting partners within the complex.
As a specific example, the minimum energy structures for the complexes with tyrosine are shown in Fig. 3. According to the calculated structure, the [HL1(Tyr)]− complex, formed by [HL1]+ with the completely deprotonated, 2− charged form of tyrosine, is held together by a bifurcated hydrogen bond involving the two tyrosine carboxylate oxygen atoms and a single proton of the ligand ammonium group, and by a NH+–π interaction between this ammonium group and the aromatic ring of the amino acid (Fig. 3a). Upon the protonation of the phenolate tyrosine oxygen to give [HL1(HTyr)], strengthening of the complex is observed thanks to the formation of two salt-bridges between the oxygen atoms of the carboxylate groups of tyrosine and two hydrogen atoms of the ligand ammonium groups accompanied by π-stacking interaction between the aromatic residues of the interacting partners (Fig. 3b). Such structural features are consistent with the fair increase of complex stability observed in solution (from log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.27 to log
K = 3.27 to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.61, Table 2). Protonation of the ligand to form the [H2L1(HTyr)]+ species gives rise to a modest reorganization of the complex structure (Fig. 3c), mostly consisting in a modification of the binding mode of the carboxylate tyrosine group, while the π-stacking interaction between the aromatic residues of the two partners is retained. In [H2L1(HTyr)]+, the carboxylate groups still form a couple of salt-bridges, as in [HL1(HTyr)], but this time only one oxygen atom is used, the other one being involved in a hydrogen bond with the unprotonated secondary amine group of the ligand. On the other hand, only one ammonium group was used by [HL1]+ to form salt-bridges with HTyr−. All in all, only a modest stabilization can be expected for the formation of [H2L1(HTyr)]+, relative to [HL1(HTyr)], as actually observed in solution (log
K = 3.61, Table 2). Protonation of the ligand to form the [H2L1(HTyr)]+ species gives rise to a modest reorganization of the complex structure (Fig. 3c), mostly consisting in a modification of the binding mode of the carboxylate tyrosine group, while the π-stacking interaction between the aromatic residues of the two partners is retained. In [H2L1(HTyr)]+, the carboxylate groups still form a couple of salt-bridges, as in [HL1(HTyr)], but this time only one oxygen atom is used, the other one being involved in a hydrogen bond with the unprotonated secondary amine group of the ligand. On the other hand, only one ammonium group was used by [HL1]+ to form salt-bridges with HTyr−. All in all, only a modest stabilization can be expected for the formation of [H2L1(HTyr)]+, relative to [HL1(HTyr)], as actually observed in solution (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.79, Table 2). Upon protonation of the amine group of tyrosine to form [H2L1(H2Tyr)]2+, the resulting ammonium group moves away from the protonated ligand, likely due to electrostatic repulsion, as shown in Fig. 3d. This causes breaking of the π-stacking interaction observed in the previous adduct and loss of one hydrogen bond, while a NH+⋯π interaction is formed. Such a weakening of the substrate–receptor interaction corresponds to a lower stability of the complex in solution (log
K = 3.79, Table 2). Upon protonation of the amine group of tyrosine to form [H2L1(H2Tyr)]2+, the resulting ammonium group moves away from the protonated ligand, likely due to electrostatic repulsion, as shown in Fig. 3d. This causes breaking of the π-stacking interaction observed in the previous adduct and loss of one hydrogen bond, while a NH+⋯π interaction is formed. Such a weakening of the substrate–receptor interaction corresponds to a lower stability of the complex in solution (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.31, Table 2). Successive protonation of the ligand, to form [H3L1(H2Tyr)]3+, causes the ammonium group on the ligand pendant to move away from the macrocycle, far from the substrate molecule, most likely due to the electrostatic repulsion with the two ammonium groups on the ring. As a consequence, the NH+⋯π interaction formed by these groups is broken, while the aromatic groups of the interacting partners restore the π-stacking interaction and the number of salt-bridges (2) does not change (Fig. 3e). Despite the considerable modification of the mutual arrangements of the interacting partners in the last two complexes, the strength of the interaction is not expected to change significantly, in agreement with the stability shown by these adducts in solution (log
K = 3.31, Table 2). Successive protonation of the ligand, to form [H3L1(H2Tyr)]3+, causes the ammonium group on the ligand pendant to move away from the macrocycle, far from the substrate molecule, most likely due to the electrostatic repulsion with the two ammonium groups on the ring. As a consequence, the NH+⋯π interaction formed by these groups is broken, while the aromatic groups of the interacting partners restore the π-stacking interaction and the number of salt-bridges (2) does not change (Fig. 3e). Despite the considerable modification of the mutual arrangements of the interacting partners in the last two complexes, the strength of the interaction is not expected to change significantly, in agreement with the stability shown by these adducts in solution (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.31(1) and 3.39(1), respectively, Table 2).
K = 3.31(1) and 3.39(1), respectively, Table 2).
On the other hand, and in accordance with the calculated structure, the [L2(Glu)]2− complex, formed by the completely deprotonated L2 and the 2− charged form of glutamic acid, is held together by a single hydrogen bond involving one of the glutamic carboxylate oxygen atoms and a single proton of the ligand amine group (Fig. 4a). Furthermore, L2 presents a closed conformation associated with the π–π interaction between the aromatic moieties present in the receptor.
Depending on the amino group where protonation occurs, two different closed conformations are possible. If protonation occurs over one of the amino groups of the macrocyclic core to give [HL2(Glu)]−, a rearrangement can be observed accompanied by the formation of two new salt-bridges between the oxygen atoms of the carboxylate groups of Glu and the hydrogen atoms of the receptor ammonium group (Fig. 4b). However, if protonation occurs over the Glu's amino group, a most favourable [L2(HGlu)]− complex is formed due to the presence of an additional NH+⋯π interaction between the ammonium group of amino acids and the naphthalene moiety, thereby strengthening the complex (Fig. 4c). Such structural features are consistent with the fair increase of complex stability observed in solution (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 4.44(2) and log
K = 4.44(2) and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 4.98(2) respectively, Table 3). The next protonation to form the [HL2(HGlu)] species gives rise to a reorganization of the complex structure (Fig. 4d), mostly consisting in a modification of the binding mode of the carboxylate groups, maintaining constant the NH+⋯π interaction between the naphthalene moiety and the ammonium group of Glu. In [HL2(HGlu)], one of the carboxylate groups forms a couple of salt-bridges, as in [L2(HGlu)]−, but this time only one oxygen atom is used; the other one is involved in a salt-bridge with the protonated amino group of the macrocyclic core. This fact can explain certain destabilization observed for the formation of [HL2(HGlu)] relative to [L2(HGlu)]− (log
K = 4.98(2) respectively, Table 3). The next protonation to form the [HL2(HGlu)] species gives rise to a reorganization of the complex structure (Fig. 4d), mostly consisting in a modification of the binding mode of the carboxylate groups, maintaining constant the NH+⋯π interaction between the naphthalene moiety and the ammonium group of Glu. In [HL2(HGlu)], one of the carboxylate groups forms a couple of salt-bridges, as in [L2(HGlu)]−, but this time only one oxygen atom is used; the other one is involved in a salt-bridge with the protonated amino group of the macrocyclic core. This fact can explain certain destabilization observed for the formation of [HL2(HGlu)] relative to [L2(HGlu)]− (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 4.38(2), Table 3).
K = 4.38(2), Table 3).
| Reaction | Ala | Tyr | Glu |
|---|---|---|---|
| a Numbers in parentheses are standard deviations in the last significant figure. | |||
| L + A2− ⇄ [LA]2− | — | 3.11(3) | 4.68(2) |
| L + A− ⇄ [LA]− | 3.11(5)a | — | — |
| L + HA− ⇄ [L(HA)]− | — | 3.25(5) | 4.98(2) |
| HL+ + A2− ⇄ [HLA]− | — | 3.17(5) | 4.44(2) |
| L + HA ⇄ [L(HA)] | 3.33(8) | — | — |
| HL+ + A− ⇄ [HLA] | 3.05(8) | — | — |
| HL+ + HA− ⇄ [HL(HA)] | — | 3.30(2) | 4.38(2) |
| HL+ + HA ⇄ [HL(HA)]+ | 3.01(6) | — | — |
| H2L2+ + HA− ⇄ [H2L(HA)]+ | — | 3.29(5) | 3.83(2) |
| H2L2+ + HA ⇄ [H2L(HA)]2+ | 2.5(1) | — | — |
| H3L3+ + HA− ⇄ [H3L(HA)]2+ | — | — | 2.98(2) |
Upon protonation of the secondary amino group in the macrocyclic core to form [H2L2(HGlu)]+, the ammonium group of the amino acid moves away from the protonated ligand, likely due to electrostatic repulsion, as shown in Fig. 4e. Such a weakening of the substrate–receptor interaction corresponds to the lower stability of the complex in solution (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 3.83(2), Table 3). The third protonation of L2, to form the [H3L2(HGlu)]2+ species, promotes a conformational change to a more expanded structure of the receptor to minimize the electrostatic repulsions between the three ammonium groups of [H3L2]3+ (Fig. 4f). In this sense, only the formation of salt-bridges between the two carboxylate groups of the amino acid and the ammonium groups of the receptor stabilizes the [H3L2(HGlu)]2+ species (log
K = 3.83(2), Table 3). The third protonation of L2, to form the [H3L2(HGlu)]2+ species, promotes a conformational change to a more expanded structure of the receptor to minimize the electrostatic repulsions between the three ammonium groups of [H3L2]3+ (Fig. 4f). In this sense, only the formation of salt-bridges between the two carboxylate groups of the amino acid and the ammonium groups of the receptor stabilizes the [H3L2(HGlu)]2+ species (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 2.98(2), Table 3). Through similar considerations based on modeling studies and taking into account that salt-bridges contribute to the stability of the L1 complexes more than simple hydrogen bonds and that salt-bridges involving shared atoms contribute less than salt-bridges involving non-shared ones,15 we can draw reasonable justifications for the stability trends observed for the other amino acid complexes (see ESI, Fig. S2–S7†).
K = 2.98(2), Table 3). Through similar considerations based on modeling studies and taking into account that salt-bridges contribute to the stability of the L1 complexes more than simple hydrogen bonds and that salt-bridges involving shared atoms contribute less than salt-bridges involving non-shared ones,15 we can draw reasonable justifications for the stability trends observed for the other amino acid complexes (see ESI, Fig. S2–S7†).
Enthalpic and entropic contributions to complexation
The formation of amino acid complexes with L1 was also studied by means of isothermal titration calorimetry in 0.15 M NaClO4, at 298.1 K, to obtain the enthalpy changes and derived entropic terms reported in Tables 2 and S1.† Unfortunately, an analogous study was not possible with L2, since its complexes are not enough soluble to analyse with the apparatus described in the Experimental section. As can be seen in Tables 2 and S1,† most of the complexation reactions are endothermic and promoted by favourable entropy changes, although there are a number of complexation equilibria, mostly related to the formation of histidine and alanine complexes, that are weakly exothermic or nearly athermic. The enthalpy changes associated with similar interactions result from a subtle combination of favourable and unfavourable contributions deriving from the formation of weak bonds (favourable) and desolvation effects (unfavourable) the latter being strictly related to the local neutralization of charge occurring upon substrate–receptor interaction. Desolvation effects are normally dominating when oppositely charged species are involved, leading to positive (unfavourable) enthalpy changes and positive (favourable) entropic gains.2 The favourable entropic contribution caused by the release of solvent molecules occurring upon charge neutralization is normally large enough, as in the present case, to overcome the loss of entropy due to substrate–receptors association. As shown by the thermodynamic parameters in Tables 2 and S1,† these effects give rise to some compensation between the enthalpy and entropy changes for the relevant complexation reactions. A good linear ΔH° − TΔS° correlation (correlation coefficient (R) of 0.98) is obtained for the complete set of data reported in Table S1† (Fig. 5).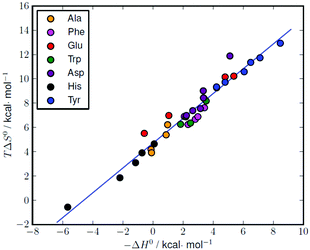 | ||
| Fig. 5 Enthalpy–entropy compensation plot for the complexation of different amino acids with L1 (see Table S1† for the original data). Correlation: TΔS° = (1.02 ± 0.04)(−ΔH°) + (4.69 ± 0.15), r = 0.98. | ||
Similar ΔH° − TΔS° compensatory relationships hold in general for complexation reactions involving weak interactions, i.e., van der Waals, hydrogen bonding, dipole–dipole, and ion–dipole interactions, and have been used to obtain quantitative estimations of ligand conformational changes resulting from complex formation, according to the general observation that the slope α of the ΔH° − TΔS° plots (TΔS° = αΔH° + I) increases with the adaptability of the ligand binding sites to the specific substrates.16 From this point of view, the high α value (1.02(4)) obtained for the amino acid complexes with L1 compares well with the values (0.89–0.92) previously obtained for the binding of phosphate and pyrophosphate anions by acyclic and macrocyclic polyammonium receptors,17 suggesting, by analogy with the latter, a good adaptability of L1 in all its protonated forms to the amino acidic substrates, despite the ligand stiffening occurring upon accumulation of positive charge on the ligand.
Experimental
EMF measurements
The potentiometric titrations were carried out at 298.1 ± 0.1 K using 0.15 M NaClO4 as the supporting electrolyte. The experimental procedure (burette, potentiometer, cell, stirrer, microcomputer, etc.) has been fully described elsewhere.18 The acquisition of the emf data was performed with the computer program PASAT.19 The reference electrode was a Ag/AgCl electrode in saturated KCl solution. The glass electrode was calibrated as a hydrogen-ion concentration probe by titration of previously standardized amounts of HCl with CO2-free NaOH solutions and the equivalent point was determined by Gran's method,20 which gives the standard potential, E°′, and the ionic product of water (pKw = 13.73(1)).The computer program HYPERQUAD was used to calculate the protonation and stability constants.8 The pH range investigated was 2.5–11.0 and the concentration of the amino acids and of the ligands ranged from 1 × 10−3 to 5 × 10−3 mol dm−3 with the A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L molar ratio 1
L molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The different titration curves for each system (at least two) were treated either as a single set or as separated curves without significant variations in the values of the stability constants. Finally, the sets of data were merged together and treated simultaneously to give the final stability constants.
1. The different titration curves for each system (at least two) were treated either as a single set or as separated curves without significant variations in the values of the stability constants. Finally, the sets of data were merged together and treated simultaneously to give the final stability constants.
Calorimetric studies
The enthalpies of ligand protonation and anion binding were determined in the same ionic media as those of potentiometric measurements by means of an automated system composed of a Thermometric AB thermal activity monitor (model 2277) equipped with a perfusion–titration device and a Hamilton Pump (model Microlab M) coupled with a 0.250 cm3 gastight Hamilton syringe (model 1750 LT). The microcalorimeter was checked by determining the enthalpy of reaction of strong base (KOH) with strong acid (HCl) solutions. The value obtained (−56.7(2) kJ mol−1) was in agreement with the literature values.21 In a typical experiment, a NaOH solution (0.10 M, addition volumes 15 μL) was added to acidic solutions of the ligand (5 × 10−3 M, 1.2 cm3), containing equimolar quantities of the amino acid in the binding experiments. Corrections for heats of dilution were applied. The corresponding enthalpies of reaction were determined from the calorimetric data by means of the AAAL program.22 ΔH° and TΔS° values for the protonation of anions were redetermined under our experimental conditions (Table S3, ESI†).Theoretical calculations
Molecular modelling investigations on the adducts formed by different protonated forms of L1 and L2 with some amino acids were performed according to the location of acidic protons on the interacting partners reported in Tables 2, 3 and S1† (tables of stability constants). The potential energy surface of all systems was explored by means of simulated annealing (empirical force field method AMBER3,23T = 600 K, equilibration time = 5 ps, run time = 10 ps and cooling time = 15 ps, time step = 1.0 fs, atomic partial charges evaluated at the PM324 semi-empirical level of theory). For each system, 80 conformations were sampled.In the case of L1, adducts formed with Ala, Asp, His, Glu, Phen, Tyr and Trp were studied using an implicit simulation of the aqueous environment (ε = 4r). In the case of ligand L2, only adducts formed with Ala and Glu were studied. Due to the formation of adducts between the amino acids and the ligand in its completely deprotonated form, calculations were preliminarily performed in a vacuum, restraining to a given value the interaction distances between donor/acceptor groups (N–H⋯O distance 2.0 Å, an additional force constant of 7 kcal mol−1 Å−2).
Conclusions
Interaction of several hydrophilic (His, Asp, Glu) and hydrophobic (Ala, Phe, Tyr, Trp) amino acids in water with two scorpiand aza-macrocycles (L1 and L2) has been analysed and two clearly differentiated behaviours have been observed. The stability of L1 complexes with all amino acids remains almost constant in a wide pH range until total deprotonation of the receptor forces it to decrease. Conversely, L2 complexes show an increasing stability at high pH values that can be attributed to the action of the naphthalene moiety attached to the pendant arm of the receptor.In all cases, theoretical calculations show that the main interactions take place through the carboxylate groups of the amino acids. In this sense, the major attractive forces that hold the adduct together are hydrogen bonds and salt-bridges, even though other interactions such as π-stacking or NH+–π may give a significant contribution, particularly for hydrophobic amino acids and L2.
Calorimetric measurements indicate that the interaction between L1 and the different amino acids is principally driven by entropy changes, often associated with solvation/desolvation processes.
Acknowledgements
Financial support by the Spanish Ministerio de Economía y Competitividad (projects CONSOLIDER INGENIO CSD-2010-00065) and Generalitat Valenciana (project PROMETEO 2011/008) is gratefully acknowledged. B.V. wishes to thank the Spanish Ministerio de Economía y Competitividad for a Juan de la Cierva Postdoctoral contract.Notes and references
- J.-M. Lehn, Supramolecular Chemistry. Concepts and Perspectives, Wiley-VCH, Weinheim, 1995 Search PubMed.
- Anion Coordination Chemistry, ed. K. Bowman-James, A. Bianchi and E. García-España, Wiley-VCH, Verlag GmbH & Co., Weinheim, Germany, 2012 Search PubMed; J. W. Steed and J. L. Atwood, Supramolecular Chemistry, Wiley-VCH, 2nd edn, 2009 Search PubMed; J. L. Sessler, P. A. Gale and W. S. Cho, Anion Receptor Chemistry, Royal Society of Chemistry, Cambridge, 2006 Search PubMed; Supramolecular Chemistry of Anions, ed. A. Bianchi, K. Bowman-James and E. García-España, Wiley-VCH Verlag, GmbH, New York, 1997 Search PubMed.
- I. Aydin, T. Aral, M. Karakaplan and H. Hosgoren, Tetrahedron: Asymmetry, 2009, 20, 179 CrossRef CAS PubMed; P. Breccia, M. V. Gool, R. Pérez-Fernández, S. Martín-Santamaría, F. Gago, P. Prados and J. de Mendoza, J. Am. Chem. Soc., 2003, 125, 8270 CrossRef PubMed; J. L. Sessler and A. Andrievsky, Chem. – Eur. J., 1998, 4, 159 CrossRef.
- C. M. Baker and G. H. Grant, Biopolymers, 2007, 85, 456 CrossRef CAS PubMed.
- A. Accetta, R. Corradini and R. Marchelli, Top. Curr. Chem., 2011, 300, 175 CrossRef CAS; R. M. Duke, E. B. Veale, F. M. Pfeffer, P. E. Kruger and T. Gunnlaugsson, Chem. Soc. Rev., 2010, 10, 3936 RSC; N. Bernier, C. V. Esteves and R. Delgado, Tetrahedron, 2012, 68, 4860 CrossRef PubMed.
- B. Verdejo, A. Ferrer, S. Blasco, C. E. Castillo, J. González, J. La torre, M. A. Máñez, M. G. Basallote, C. Soriano and E. García-España, Inorg. Chem., 2007, 46, 5707 CrossRef CAS PubMed.
- A. Bencini, A. Bianchi, E. García-España, M. Micheloni and J. A. Ramírez, Coord. Chem. Rev., 1999, 188, 97 CrossRef CAS.
- M. Micheloni, P. Paoletti and A. Vacca, J. Chem. Soc., Perkin Trans. 2, 1978, 945 RSC.
- P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739 CrossRef CAS.
- M. T. Albelda, M. A. Bernardo, E. García-España, M. L. Godino-Salido, S. V. Luis, M. J. Melo, F. Pina and C. Soriano, J. Chem. Soc., Perkin Trans. 2, 1999, 2545 RSC.
- C. Bazzicalupi, A. Bianchi, C. Giorgi, M. P. Clares and E. García-España, Coord. Chem. Rev., 2012, 256, 13 CrossRef CAS PubMed; A. Bianchi and E. García-España, J. Chem. Educ., 1999, 12, 1725 Search PubMed; J. A. Aguilar, B. Celda, E. García-España, S. V. Luis, M. Martínez, J. A. Ramírez, C. Soriano and R. Tejero, J. Chem. Soc., Perkin Trans. 2, 2000, 1323 RSC.
- P. Gans, A. Sabatini and A. Vacca, Ann. Chim., 1999, 89, 45 CAS.
- M. Inclán, M. T. Albelda, J. C. Frías, S. Blasco, B. Verdejo, C. Se rena, C. Salat-Canela, M. L. Díaz, A. García-España and E. García-España, J. Am. Chem. Soc., 2012, 134, 9644 CrossRef PubMed.
- Hyperchem release 7.51 for Windows MM System, Hypercube, Inc., Gainesville, FL, 2002 Search PubMed.
- G. Gilli and P. Gilli, The Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory, Oxford University Press, New York, 2009 Search PubMed.
- W. Tao and M. Barra, J. Chem. Soc., Perkin Trans 2, 1998, 1957 RSC; Y. Inoue, T. Hakushi, Y. Liu, L.-H. Tong, B.-J. Shen and D.-S. Jin, J. Am. Chem. Soc., 1993, 115, 475 CrossRef CAS; Y. Inoue, Y. Liu, L.-H. Tong, B.-J. Shen and D.-S. Jin, J. Am. Chem. Soc., 1993, 115, 10637 CrossRef.
- C. Bazzicalupi, A. Bencini, A. Bianchi, M. Cecchi, B. Escuder, V. Fusi, E. García-España, C. Giorgi, S. V. Luis, G. Maccagni, V. Marcelino, P. Paoletti and B. Valtancoli, J. Am. Chem. Soc., 1999, 121, 6807 CrossRef CAS.
- E. García-España, M.-J. Ballester, F. Lloret, J. M. Moratal, J. Faus and A. Bianchi, J. Chem. Soc., Dalton Trans., 1988, 1101 Search PubMed.
- M. Fontanelli and M. Micheloni, Proceedings of the I Spanish-Italian Congress on Thermodynamics of Metal Complexes, Peñíscola, Castellón, 1990; program for the automatic control of the microburette and the acquisition of the electromotive force readings (PASAT).
- G. Gran, Analyst, 1952, 77, 661 RSC; F. J. Rossotti and H. Rossotti, J. Chem. Educ., 1965, 42, 375 CrossRef CAS.
- R. M. Smith and A. E. Martell, NIST Critical Stability Constants Database, version 2, 1995 Search PubMed.
- A. Vacca, AAAL Program, University of Florence, 1997 Search PubMed.
- S. J. Weiner, P. A. Kollman, D. A. Case, U. Singh, C. Ghio, G. Alagona, S. Profeta Jr. and P. Weiner, J. Am. Chem. Soc., 1984, 106, 765 CrossRef CAS; P. Weiner and P. Kollman, J. Comput. Chem., 1981, 2, 287 CrossRef.
- J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209 CrossRef CAS; J. J. P. Stewart, J. Comput. Chem., 1989, 10, 221 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ob02092h |
| This journal is © The Royal Society of Chemistry 2015 |