Open Access Article
Open Access ArticleB-DNA structure and stability: the role of hydrogen bonding, π–π stacking interactions, twist-angle, and solvation†
Jordi
Poater
a,
Marcel
Swart
bc,
F. Matthias
Bickelhaupt
ad and
Célia
Fonseca Guerra
*a
aDepartment of Theoretical Chemistry and Amsterdam Center for Multiscale Modeling, VU University Amsterdam, De Boelelaan 1083, NL-1081 HV Amsterdam, The Netherlands. E-mail: C. FonsecaGuerra@vu.nl
bInstitut de Química Computacional i Catàlisi and Departament de Química, Universitat de Girona, 17071 Girona, Catalonia, Spain
cInstitució Catalana de Recerca i Estudis Avançats (ICREA), Pg. Lluís Companys 23, 08010 Barcelona, Spain
dInstitute of Molecules and Materials, Radboud University Nijmegen, Heyendaalseweg 135, 6525 AJ Nijmegen, The Netherlands
First published on 20th May 2014
Abstract
We have computationally investigated the structure and stability of B-DNA. To this end, we have analyzed the bonding in a series of 47 stacks consisting of two base pairs, in which the base pairs cover the full range of natural Watson–Crick pairs, mismatched pairs, and artificial DNA base pairs. Our analyses provide detailed insight into the role and relative importance of the various types of interactions, such as, hydrogen bonding, π–π stacking interactions, and solvation/desolvation. Furthermore, we have analyzed the functionality of the twist-angle on the stability of the structure. Interestingly, we can show that all stacked base pairs benefit from a stabilization by 6 to 12 kcal mol−1 if stacked base pairs are twisted from 0° to 36°, that is, if they are mutually rotated from a congruent superposition to the mutually twisted stacking configuration that occurs in B-DNA. This holds especially for stacked AT pairs but also for other stacked base pairs, including GC. The electronic mechanism behind this preference for a twisted arrangement depends on the base pairs involved. We also show that so-called “diagonal interactions” (or cross terms) in the stacked base pairs are crucial for understanding the stability of B-DNA, in particular, in GC-rich sequences.
Introduction
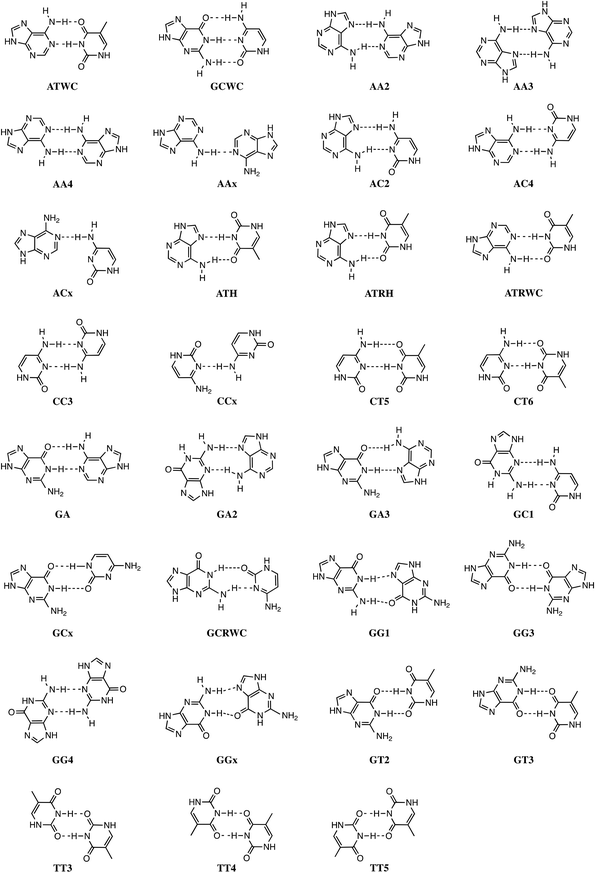
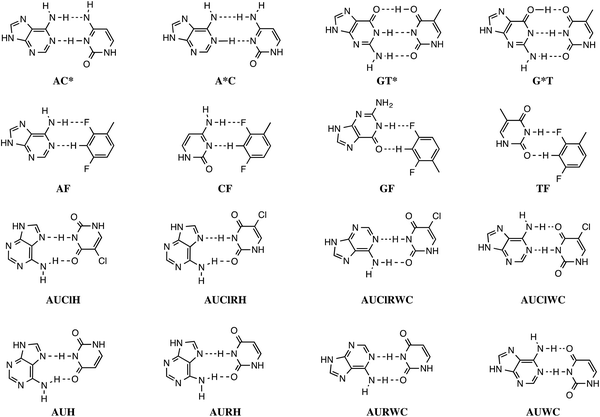
Stacking interactions play a central role in determining the structure and stability of DNA, as follows from various computational studies.1,2 Recently, we revealed the importance of π–π stacking as well solvent effects for the immensely high fidelity with which DNA replication occurs.2 This study consisted of the first high-level quantum chemical study on DNA replication covering not only the formation of DNA base pairs but also π–π stacking interactions in a model system consisting of four DNA bases. We showed that the intrinsic affinity of the template-primer complex to select the correct natural DNA base derives from the concerted action of hydrogen-bonding patterns, (de)solvation effects, twist angle and π–π stacking interactions.2 It was shown how π–π stacking plays a less pronounced role for the selectivity, but it is important for the overall stability of the aggregate of incoming nucleotide and the template-primer complex.In the present work, we wish to gain more insight in the stability of the structure of B-DNA with high-level quantum chemical computations. It is known that the stability of the double helical structure of B-DNA is supplied by the hydrogen bonds as proposed by Watson and Crick3 and by the stacking interactions. However, the relative importance of both stabilizing interactions as well as how they interfere with each other is largely unknown. The hydrogen bonds in Watson–Crick base pairs and mismatches thereof were shown to posses both electrostatic and covalent (i.e., orbital interaction) character with reinforcement by π polarization.4 More recently,5 a series of Watson–Crick base pairs and mismatched DNA base pairs were analyzed in order to obtain a better comprehension of the hydrogen-bonding mechanism under aqueous solvation (see Scheme 1). This work also considered tautomerization, which might occur in aqueous conditions.6 The lactim forms of guanine (G*) or thymine (T*), as well as the imino forms of cytosine (C*) or adenine (A*) were paired with a complementary natural base.7
In addition, the pairs formed with an isostere of T, 2,4-difluorotoluene (F) were also taken into account. Kool et al.8 demonstrated experimentally that F can be correctly incorporated into template-primer complexes, forming A–F pairs, in the presence of DNA polymerase. This finding was explained computationally with the presence of the attractive donor–acceptor interactions in the weak hydrogen bonding.9 The charge transfer interactions relieve the repulsive interaction when the A–F pair is confined to the spatial pocket of the polymerase. Finally, also the pairing of 5-chlorouracil paired with A was studied (see Scheme 2).5 This mimic of uracil has recently been found10 by Marlière et al. to correctly incorporate into an Escherichia coli strain with the posterior survival of the bacteria without the need of the initial T. From previous work, we know that in the condensed phase all hydrogen bonds of the base pairs become weaker and most of these bonds elongate. This can be explained by the stabilization of the lone pairs in the separate bases involved in hydrogen bonding.
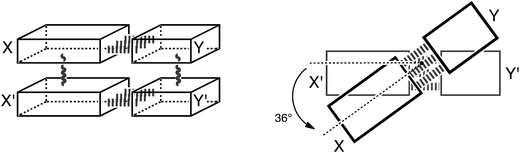
Thus, herein, we want to incorporate the stacking interactions into our computational investigations and analyze structure and bonding in the stacks of 47 base pairs, including natural, mismatched and artificial stacked base pairs. Our structural and bonding analyses are based on state-of-the-art Kohn–Sham molecular orbital theory at the BP86-D/TZ2P level. We investigate the different interactions that add to the stable structure of B-DNA: that is hydrogen-bonding, π–π stacking interactions, cross-terms (interaction between X and Y′, see Scheme 3) and the influence of these two interactions onto each other. We complement these analyses with an exploration of the role of solvation and of the twist-angle.
Computational methods
General procedure
All calculations were carried out with the ADF program11 using dispersion-corrected density functional theory (using Grimme's DFT-D correction)12 at the BP86-D/TZ2P level of theory.13 Solvent effects in aqueous solution are described with the COSMO model, which takes effectively into account cavitation, internal energy and entropy effects of the solvent and yields an estimate of the Gibbs free energies.14 The BP86-D functional was recently shown to yield hydrogen-bonding structures and energies for AT and GC Watson–Crick pairs and stacked configurations15 that agree excellently with the best ab initio CCSD(T) benchmark data.16 All systems have been optimized under Cs symmetry constraint with the aim to simulate the experimental condition B-DNA where the base pairs are nearly planar and attached to the backbone. Previously, it was shown that the difference in stability between such Cs-symmetric structures and fully optimized, non-planar geometries is very small: bond energies at the relaxed C1 and Cs conformations differ by 0.1 kcal mol−1 or less (except for the GA and GG1 systems that differ 0.6 and 0.3 kcal mol−1, respectively, because of the pyramidalization of the amino group).5,17Bonding analyses
The bonding interactions have been further analyzed by means of the energy decomposition analysis.18 The interaction energy ΔEint corresponds to the actual energy change when the separated bases are combined to form the base pair, and can be decomposed:| ΔEint = ΔVelstat + ΔEPauli + ΔEoi + ΔEdisp | (1) |
Here, ΔVelstat corresponds to the classical electrostatic interaction between the unperturbed charge distributions of the prepared bases and is usually attractive. The Pauli-repulsion ΔEPauli comprises the destabilizing interactions between occupied orbitals and is responsible for the steric repulsions. The orbital interaction ΔEoi accounts for charge transfer (donor–acceptor interactions between occupied orbitals on one moiety with unoccupied orbitals of the other, including the HOMO–LUMO interactions) and polarization (empty/occupied orbital mixing on one fragment due to the presence of another fragment). The latter can be decomposed into the contributions from each irreducible representation of the interacting system (i.e. σ and π in our planar base pairs). Finally, the ΔEdisp term (Grimme's DFT-D correction) accounts for the dispersion interactions.12,19
Model systems
In this computational investigation, stacked base pairs will be considered (see Scheme 3). Equivalent base pairs (X–Y and X′–Y′) are stacked above each other with a distance of 3.4 Å between the planes of the base pairs (see Scheme 3). The calculations were done at a twist angle of 0° and 36° to understand the role of the angle in the stabilization of B-DNA. The following nomenclature is used throughout this work: a dash “–” denotes hydrogen bonding; a slash “/” denotes stacking; the prime denotes the lower base and the fragments are put between parenthesis (see Scheme 3). Thus, ΔE(X–Y)/(X′–Y′)π–π denotes the stacking interaction between two identical base pairs X–Y, and ΔE(X/X′)–(Y/Y′)HB denotes the hydrogen bonding interaction between two stacked X bases (X/X′) with two stacked Y bases (Y/Y′). The separate terms of the interactions in the stacked base pairs are represented as: ΔEX/X′π–π is the stacking interaction between two bases X, ΔEX–YHB is the hydrogen bonding interaction between base X and base Y and ΔEX/Y′cross denotes the cross-term interaction between the diagonally opposite bases X and Y′ (see Scheme 3).The cooperativity within the hydrogen bond energy of one base pair XY due to the simultaneous occurrence of the stacking can be calculated as follows (see Scheme 3):
| ΔΔEcoop(H) = ΔE(X/X′)–(Y/Y′)HB − 2ΔEX–YHB – [ΔEX/Y′cross + ΔEX′/Ycross] | (2) |
If the value of ΔΔEcoop(H) is negative, the stacking reinforces the hydrogen bonding. The influence of the hydrogen bonds on the stacking interactions can be calculated as follows:
| ΔΔEcoop(π) = ΔE(X–Y)/(X′–Y′)π–π− ΔEX/X′π–π − ΔEY/Y′π–π − [ΔEX/Y′cross + ΔEX′/Ycross] | (3) |
If the value of ΔΔEcoop(π) is negative the hydrogen bonds reinforce the stacking interactions. It can be easily derived (see ESI†) that for the definition of cooperativity proposed above, the following holds: ΔΔEcoop(H) = ΔΔEcoop(π). Therefore we refer in the remaining text as ΔΔEcoop.
Results and discussion
The series of base pairs studied comprises the natural Watson–Crick, mismatched and artificial DNA base pairs as mentioned above (see Schemes 1 and 2). To understand the stabilizing interactions in B-DNA and supramolecular systems inspired by DNA, we have analyzed a stack of two identical base pairs at a distance of 3.4 Å, X–Y/X′–Y′ (see Scheme 3). We have used for that purpose the geometries of the base pairs obtained from BP86-D/TZ2P optimizations.5 The dimer of two base pairs is stabilized by hydrogen bonding between the bases within one layer, and stacking interactions between the bases of the different layers.Hydrogen bonding
The hydrogen-bond interaction energies, ΔE(X/X′)–(Y/Y′)HB, for all stacked systems (X–Y/X′–Y′) are calculated as the interaction between two stacked X bases and two stacked Y bases, thus X/X′ and Y/Y′ (see Tables 1 and 2). Table 1 shows the values for the series of 31 Watson–Crick and mismatched base pairs, and Table 2 encloses the values for the RNA and modified base pairs. Comparison of the calculated hydrogen bonds energies at a twist angle of 0° and 36°, reveals that they are almost equivalent with differences of less than 1.4 kcal mol−1. Furthermore, we observe that the hydrogen bonds energies are almost halved when the stack is solvated by water, which is in correspondence with our previous findings for the single base pairs.5,6,15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a
| XY | Stackingb | Hydrogen bonding | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔE(X–Y)/(X′–Y′)π–π | 2ΔEX–YHB | ΔE(X/X′)–(Y/Y′)HB | ΔEX/Y′cross + ΔEX′/Ycross | ΔΔEcoop![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
||||||||||
| 0° | 36° | Pair | 0° | 36° | 0° | 36° | 0° | 36° | ||||||
| Gas | Wat | Gas | Wat | ΔΔgas | Gas | Gas | Wat | Gas | Wat | Gas | Gas | Gas | Gas | |
| a Calculated at the BP86-D/TZ2P level of theory in the gas phase and in water (COSMO). b ΔΔgas is the difference in stacking energy between at a twist angle of 0° and 36°. c See eqn (2). | ||||||||||||||
| Watson–Crick | ||||||||||||||
| ATWC | −3.9 | −5.8 | −12.2 | −9.8 | −8.3 | −41.8 | −45.4 | −23.8 | −44.6 | −23.8 | −2.6 | −2.0 | −1.0 | −0.8 |
| GCWC | −3.0 | −7.9 | −9.8 | −9.7 | −6.8 | −73.8 | −82.0 | −33.4 | −80.8 | −34.4 | −10.0 | −8.4 | 1.8 | 1.4 |
| Mismatches | ||||||||||||||
| AA2 | −6.5 | −9.7 | −13.2 | −10.2 | −6.7 | −33.8 | −36.2 | −19.8 | −36.4 | −19.8 | −1.8 | −2.0 | −0.6 | −0.6 |
| AA3 | −6.0 | −9.4 | −13.7 | −9.7 | −7.7 | −28.6 | −30.8 | −16.2 | −31.4 | −16.4 | −1.2 | −1.6 | −1.0 | −1.2 |
| AA4 | −7.0 | −9.5 | −12.8 | −10.0 | −5.8 | −37.0 | −40.2 | −21.0 | −40.0 | −21.2 | −2.6 | −2.4 | −0.6 | −0.6 |
| AAx | −5.5 | −8.7 | −11.5 | −8.3 | −6.0 | −18.8 | −20.2 | −9.2 | −20.4 | −9.0 | −0.8 | −0.8 | −0.6 | −0.8 |
| AC2 | −2.6 | −5.8 | −9.6 | −8.0 | −7.0 | −40.6 | −44.2 | −17.2 | −43.6 | −18.2 | −2.8 | −2.0 | −0.8 | −1.0 |
| AC4 | −3.4 | −6.0 | −10.4 | −8.1 | −7.0 | −43.4 | −48.0 | −19.0 | −47.4 | −19.6 | −4.0 | −3.4 | −0.6 | −0.6 |
| ACx | −1.0 | −5.5 | −8.2 | −7.0 | −7.2 | −19.8 | −21.6 | −7.0 | −21.4 | −7.8 | −0.4 | −0.2 | −1.4 | −1.4 |
| ATH | −4.0 | −6.0 | −13.1 | −9.5 | −9.1 | −40.8 | −44.6 | −21.6 | −44.4 | −21.4 | −3.2 | −2.8 | −0.6 | −0.8 |
| ATRH | −4.0 | −5.9 | −12.7 | −8.6 | −8.7 | −39.8 | −43.6 | −20.8 | −43.2 | −20.2 | −3.2 | −2.6 | −0.6 | −0.8 |
| ATRWC | −3.8 | −6.1 | −11.9 | −9.4 | −8.1 | −40.4 | −44.0 | −23.2 | −43.2 | −22.8 | −2.4 | −1.6 | −1.2 | −1.2 |
| CC3 | −1.0 | −1.5 | −9.3 | −5.2 | −8.3 | −53.6 | −60.8 | −16.0 | −60.6 | −17.8 | −7.8 | −7.2 | 0.6 | 0.2 |
| CCx | 4.7 | −3.6 | −5.1 | −4.8 | −9.8 | −22.2 | −23.0 | −8.6 | −24.0 | −8.6 | −3.0 | −3.4 | 2.2 | 1.6 |
| CT5 | 0.9 | −0.8 | −7.6 | −5.3 | −8.6 | −35.0 | −38.6 | −13.6 | −38.2 | −14.2 | −2.0 | −2.0 | −1.6 | −1.2 |
| CT6 | 1.2 | −1.4 | −7.0 | −4.6 | −8.1 | −32.6 | −36.0 | −13.8 | −35.4 | −13.0 | −1.6 | −1.2 | −1.8 | −1.6 |
| GA | −6.0 | −10.6 | −12.8 | −10.8 | −6.8 | −46.4 | −51.8 | −22.6 | −51.8 | −22.8 | −5.6 | −5.4 | 0.2 | 0.0 |
| GA2 | −3.7 | −9.2 | −12.4 | −7.8 | −8.8 | −31.6 | −34.4 | −18.6 | −34.8 | −17.8 | −2.0 | −2.4 | −0.8 | −0.8 |
| GA3 | −5.1 | −10.1 | −12.4 | −10.0 | −7.3 | −40.4 | −44.8 | −20.2 | −44.8 | −20.0 | −3.8 | −3.6 | −0.6 | −0.8 |
| GC1 | −0.5 | −5.2 | −9.6 | −6.3 | −9.1 | −43.0 | −47.6 | −17.6 | −47.4 | −18.4 | −4.6 | −4.3 | 0.0 | −0.1 |
| GCx | −3.5 | −7.6 | −9.8 | −8.8 | −6.3 | −66.0 | −74.6 | −26.4 | −74.0 | −27.2 | −10.4 | −9.0 | 1.8 | 1.0 |
| GCRWC | 4.4 | −7.1 | −2.7 | −7.4 | −7.1 | −31.4 | −31.0 | −21.0 | −31.8 | −21.4 | −2.2 | −2.4 | 2.6 | 2.0 |
| GG1 | −1.5 | −9.0 | −10.5 | −8.8 | −9.1 | −46.2 | −50.2 | −21.0 | −50.8 | −20.6 | −6.8 | −6.6 | 2.8 | 2.0 |
| GG3 | −6.8 | −10.6 | −14.1 | −10.7 | −7.3 | −72.0 | −82.0 | −27.4 | −81.6 | −28.2 | −12.2 | −10.8 | 2.2 | 1.2 |
| GG4 | −0.9 | −8.1 | −10.5 | −5.2 | −9.6 | −32.0 | −35.0 | −18.2 | −34.8 | −17.0 | −1.6 | −1.6 | −1.4 | −1.2 |
| GGx | 1.9 | −9.3 | −6.5 | −8.1 | −8.4 | −31.8 | −32.2 | −19.0 | −33.2 | −18.0 | −3.4 | −3.8 | 3.0 | 2.4 |
| GT2 | −0.9 | −6.8 | −8.8 | −9.0 | −8.0 | −43.8 | −48.0 | −24.2 | −47.0 | −23.6 | −3.2 | −2.2 | −1.0 | −1.0 |
| GT3 | −1.1 | −6.2 | −10.0 | −9.8 | −8.8 | −47.2 | −51.4 | −23.8 | −50.8 | −23.8 | −3.8 | −3.2 | −0.4 | −0.4 |
| TT3 | 1.2 | −1.5 | −9.1 | −6.2 | −10.2 | −29.8 | −32.0 | −20.0 | −32.4 | −19.6 | −1.2 | −1.8 | −1.0 | −0.8 |
| TT4 | 0.9 | −1.7 | −10.7 | −7.4 | −11.6 | −33.4 | −35.8 | −21.4 | −36.2 | −20.4 | −1.6 | −2.2 | −0.8 | −0.6 |
| TT5 | 1.0 | −1.5 | −10.0 | −7.1 | −11.0 | −31.4 | −33.8 | −20.6 | −34.2 | −19.8 | −1.4 | −2.0 | −1.0 | −0.8 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a
| XY | Stackingb | Hydrogen bonding | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔE(X–Y)/(X′–Y′)π–π | 2ΔEX–YHB | ΔE(X/X′)–(Y/Y′)HB | ΔEX/Y′cross + ΔEX′/Ycross | ΔΔEcoop![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
||||||||||
| 0° | 36° | Pair | 0° | 36° | 0° | 36° | 0° | 36° | ||||||
| Gas | Wat | Gas | Wat | ΔΔgas | Gas | Gas | Wat | Gas | Wat | Gas | Gas | Gas | Gas | |
| a Calculated at the BP86-D/TZ2P level of theory in the gas phase and in water (COSMO). b ΔΔgas is the difference in stacking energy between at a twist angle of 0° and 36°. c See eqn (2). | ||||||||||||||
| Lactim mismatches | ||||||||||||||
| AC* | −4.3 | −6.4 | −10.7 | −9.0 | −6.5 | −44.2 | −47.4 | −26.4 | −46.8 | −26.4 | −2.0 | −1.4 | −1.2 | −1.2 |
| A*C | −3.7 | −5.7 | −10.3 | −8.0 | −6.6 | −61.0 | −67.2 | −27.0 | −66.4 | −28.2 | −6.8 | −5.6 | 0.6 | 0.2 |
| GT* | −3.4 | −7.7 | −11.5 | −11.2 | −8.1 | −94.0 | −102.2 | −46.2 | −100.8 | −46.2 | −9.4 | −7.6 | 1.2 | 0.8 |
| G*T | −2.8 | −7.0 | −10.9 | −10.7 | −8.1 | −57.6 | −60.4 | −39.4 | −59.4 | −39.4 | −2.6 | −1.2 | −0.2 | −0.6 |
| Difluorotoluene mismatches | ||||||||||||||
| AF | −4.9 | −6.2 | −11.1 | −9.7 | −6.2 | −11.2 | −13.0 | −3.6 | −13.0 | −4.0 | −1.2 | −1.2 | −0.6 | −0.6 |
| CF | −0.4 | −1.6 | −7.3 | −6.3 | −6.9 | −11.6 | −13.6 | 0.8 | −13.6 | 0.6 | −1.0 | −0.8 | −1.0 | −1.2 |
| GF | −2.8 | −6.5 | −9.4 | −9.4 | −6.6 | −16.0 | −18.6 | −4.4 | −18.6 | −4.4 | −2.4 | −2.2 | −0.2 | −0.4 |
| TF | −0.9 | −2.3 | −9.5 | −7.8 | −8.6 | −9.4 | −10.8 | −4.0 | −11.0 | −3.4 | −1.0 | −1.2 | −0.4 | −0.4 |
| Chlorouracil and uracil mismatches | ||||||||||||||
| AUClH | −4.6 | −5.9 | −13.2 | −8.9 | −8.5 | −42.4 | −46.6 | −23.2 | −46.4 | −23.4 | −3.6 | −3.2 | −0.6 | −0.6 |
| AUClRH | −4.6 | −6.0 | −12.5 | −8.1 | −7.9 | −41.8 | −45.8 | −23.0 | −45.4 | −23.0 | −3.4 | −2.8 | −1.0 | −1.2 |
| AUClRWC | −4.2 | −6.6 | −11.7 | −8.9 | −7.4 | −42.6 | −46.2 | −25.8 | −45.6 | −25.6 | −2.6 | −1.8 | −0.2 | −0.4 |
| AUClWC | −4.5 | −6.1 | −12.4 | −9.4 | −7.9 | −44.0 | −48.0 | −25.4 | −47.6 | −25.8 | −3.2 | −2.6 | −0.4 | −0.4 |
| AUH | −4.5 | −6.9 | −11.7 | −8.8 | −7.2 | −41.0 | −45.0 | −22.6 | −44.6 | −22.2 | −3.2 | −2.6 | −0.6 | −0.6 |
| AURH | −4.4 | −6.6 | −11.8 | −8.7 | −7.3 | −39.8 | −43.6 | −21.4 | −43.2 | −21.4 | −3.2 | −2.6 | −1.0 | −1.2 |
| AURWC | −4.1 | −6.9 | −10.8 | −9.1 | −6.7 | −40.2 | −43.6 | −23.8 | −42.8 | −23.2 | −2.2 | −1.6 | −0.2 | −0.4 |
| AUWC | −4.3 | −6.8 | −11.0 | −9.2 | −6.7 | −42.2 | −46.0 | −24.6 | −45.2 | −24.4 | −2.8 | −2.0 | −0.4 | −0.4 |
To investigate if the hydrogen bond interaction energies in a stack differ from the hydrogen bond interaction energies in an isolated base pair, we compared for the gas phase situation the hydrogen bond interaction energies of the stack, ΔE(X/X′)–(Y/Y′)HB, to twice the hydrogen bond interaction energies of an isolated base pair X–Y, ΔEX–YHB. The outcome is that the hydrogen bond interaction energies are always larger (in absolute value) in the stack (except GCRWC by 0.4 kcal mol−1). For the Watson–Crick base pairs the hydrogen bonds of the stacked system amounts at a twist angle of 0° in the gas phase to −45.4 kcal mol−1 for ATWC and −82.0 kcal mol−1 for GCWC, whereas twice the hydrogen bond energy of ATWC and GCWC sums up to −41.8 kcal mol−1 and −73.8 kcal mol−1, respectively. This can be rationalized as the values of the stack cannot be fully attributed to the hydrogen bonds alone. There are two bases per layer, so there are also interactions present between bases that are in a sense diagonally to each other, that is on opposite sides and in different layers, the so-called cross terms (see Scheme 3). These cross-terms also contribute to the “hydrogen-bond” interaction of these systems (ΔEX/Y′cross and ΔEX′/Ycross). For the naturally occurring Watson–Crick base pairs these cross-terms amount to −2.6 kcal mol−1 and −10.0 kcal mol−1 for stacked ATWC and GCWC respectively at a twist angle of 0° (see Tables 1 and 3). This shows the importance of the cross terms, which cannot be underestimated in such stacked systems, for which we usually only refer to the π–π stacking interactions. The cross term is always attractive in the gas-phase, and it is larger for GC-rich DNA than for AT-rich DNA. So, that adds up to an extra stabilization of the GC-rich DNA. This outcome shows that the GC rich double strands of DNA are stronger bonded not only because of their stronger hydrogen bonds, but also due to their larger cross-terms between G and C′ and between G′ and C (–5.2 and −3.2 kcal mol−1 respectively at a twist angle of 36°, see Table 3). Other stacked base pairs with large cross terms are GCx, GG3 and GT* (–9.0 kcal mol−1, −10.8 kcal mol−1 and −7.6 kcal mol−1 at a twist angle of 36°).
| System | Twist angle | ΔEPauli | ΔVelstat | ΔEoi | ΔEdisp | ΔEint |
|---|---|---|---|---|---|---|
| a Calculated at the BP86-D/TZ2P level of theory. b Summation of the pairwise interactions calculated for the geometries of two stacked ATWC and GCWC. | ||||||
| π–π stacking between WC pairs | ||||||
| (A–T)/(A′–T′) | 0° | 26.5 | −2.5 | −5.5 | −22.4 | −3.9 |
| 36° | 15.1 | −5.2 | −3.7 | −18.3 | −12.2 | |
| (A–T)/(A′–T′) with Me-groups optimized | 0° | 21.5 | −1.6 | −3.6 | −22.1 | −5.8 |
| 36° | 14.9 | −5.2 | −3.7 | −18.3 | −12.2 | |
| (G–C)/(G′–C′) | 0° | 20.4 | 1.1 | −3.4 | −21.2 | −3.0 |
| 36° | 14.2 | −2.5 | −3.5 | −18.0 | −9.8 | |
| π––π stacking between bases | ||||||
| A/A′ | 0° | 11.1 | −0.8 | −1.5 | −10.8 | −2.0 |
| 36° | 7.3 | −2.7 | −1.5 | −8.5 | −5.4 | |
| G/G′ | 0° | 11.3 | 4.1 | −2.3 | −11.4 | 1.7 |
| 36° | 7.9 | 1.2 | −2.2 | −9.4 | −2.5 | |
| T/T′ | 0° | 15.5 | 0.2 | −4.0 | −9.9 | 1.8 |
| 36° | 7.5 | −1.6 | −2.2 | −7.6 | −3.8 | |
| C/C′ | 0° | 9.4 | 3.6 | −1.7 | −7.9 | 3.4 |
| 36° | 5.8 | 1.5 | −1.7 | −6.0 | −0.3 | |
| Cross interactions | ||||||
| A/T′ | 0° | 0.5 | −0.8 | −0.2 | −0.9 | −1.3 |
| 36° | 0.8 | −0.2 | −0.3 | −1.2 | −0.9 | |
| G/C′ | 0° | 0.6 | −3.9 | −0.8 | −1.0 | −5.0 |
| 36° | 0.9 | −4.0 | −0.9 | −1.2 | −5.2 | |
| A′/T | 0° | 0.5 | −0.8 | −0.2 | −0.9 | −1.3 |
| 36° | 0.7 | −0.4 | −0.3 | −1.1 | −1.1 | |
| G′/C | 0° | 0.6 | −3.9 | −0.8 | −1.0 | −5.0 |
| 36° | 1.1 | −2.1 | −0.8 | −1.4 | −3.2 | |
| Sum of pairwise interactions | ||||||
| ATWC-0° | 0° | 27.6 | −2.2 | −5.9 | −22.5 | −2.8 |
| 36° | 16.3 | −4.9 | −4.3 | −18.4 | −11.2 | |
| GCWC-0° | 0° | 21.9 | −0.1 | −5.6 | −21.3 | −4.9 |
| 36° | 15.7 | −3.4 | −5.6 | −18.0 | −11.3 | |
After having established that the cross-terms make a large contribution to the hydrogen bonding, we want to determine if there is a cooperativity between the hydrogen bonding and the stacking interactions. Therefore, the ΔΔEcoop is calculated as the difference between the hydrogen bond energy of the stack ΔE(X/X′)–(Y/Y′)HB, and the individual terms (2ΔEX–YHB + ΔEX/Y′cross + ΔEX′/Ycross). A negative value of ΔΔEcoop corresponds to cooperativity and a positive value to non-cooperative effect (see Tables 1 and 2). The largest non-cooperativity is found at a twist angle of 0° for the base pairs with a surplus of hydrogen bonds pointing in one direction. In the case of GCWC, GCRWC, GG1, GG3 and GGx the non-cooperative effect amounts to respectively 1.8, 2.6, 2.8, 2.2 and 3.0 kcal mol−1. A surplus of hydrogen bonds in one direction leads to a charge accumulation on one side of the stack and a charge depletion on the other side of the stack due to the donor–acceptor interactions in the hydrogen bonds.4 The DNA bases on top of each other will therefore repel each other slightly. This non-cooperative effect will be explained in more detail below.
The energy decomposition analysis for the hydrogen bonds between the stacked X/X′ and Y/Y′ is given in Table 4. As already observed for the base pairs alone, for the stacked systems we reconfirm the importance of the covalent character of hydrogen bonds, a component (ΔEoi over ΔVelstat + ΔEoi + ΔEdisp) which contributes up to 46% of all hydrogen-bonding forces in our set of model complexes.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a
| Base pair | ΔEPauli | ΔVelstat | ΔEoi | ΔEdisp | ΔEbond | Base pair | ΔEPauli | ΔVelstat | ΔEoi | ΔEdisp | ΔEbond |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Calculated at the BP86-D/TZ2P level of theory. | |||||||||||
| Watson–Crick | GG4 | 74.4 | −55.2 | −42.8 | −11.6 | −35.0 | |||||
| ATWC | 94.4 | −73.0 | −54.8 | −12.0 | −45.4 | GGx | 40.6 | −39.8 | −24.6 | −8.2 | −32.2 |
| GCWC | 117.8 | −105.0 | −81.0 | −13.8 | −82.0 | GT2 | 82.0 | −66.4 | −53.2 | −10.4 | −48.0 |
| Mismatches | GT3 | 89.4 | −70.8 | −58.8 | −11.0 | −51.4 | |||||
| AA2 | 71.0 | −57.6 | −39.0 | −10.6 | −36.2 | TT3 | 60.4 | −48.6 | −35.6 | −8.2 | −32.0 |
| AA3 | 57.0 | −47.0 | −30.4 | −10.4 | −30.8 | TT4 | 73.0 | −55.0 | −44.8 | −9.0 | −35.8 |
| AA4 | 83.2 | −66.0 | −46.4 | −10.8 | −40.2 | TT5 | 66.8 | −51.8 | −40.2 | −8.6 | −33.8 |
| AAx | 42.4 | −32.8 | −21.2 | −8.6 | −20.2 | Lactim mismatches | |||||
| AC2 | 72.6 | −61.8 | −43.8 | −11.4 | −44.2 | AC* | 103.4 | −79.4 | −58.8 | −12.6 | −47.4 |
| AC4 | 85.4 | −70.4 | −51.6 | −11.4 | −48.0 | A*C | 115.4 | −94.4 | −75.2 | −13.0 | −67.2 |
| ACx | 43.6 | −32.6 | −23.8 | −8.8 | −21.6 | GT* | 172.0 | −133.0 | −127.2 | −14.0 | −102.2 |
| ATH | 83.4 | −68.8 | −48.0 | −11.4 | −44.6 | G*T | 132.6 | −99.8 | −78.8 | −14.4 | −60.4 |
| ATRH | 80.8 | −67.2 | −46.2 | −11.2 | −43.6 | Difluorotoluene mismatches | |||||
| ATRWC | 91.0 | −71.0 | −52.2 | −12.0 | −44.0 | AF | 22.8 | −18.0 | −10.4 | −7.4 | −13.0 |
| CC3 | 89.4 | −79.4 | −58.8 | −12.0 | −60.8 | CF | 19.2 | −14.8 | −10.8 | −7.2 | −13.6 |
| CCx | 32.8 | −29.4 | −18.0 | −8.4 | −23.0 | GF | 25.6 | −21.0 | −14.4 | −9.0 | −18.6 |
| CT5 | 73.2 | −54.6 | −46.6 | −10.6 | −38.6 | TF | 14.6 | −12.4 | −7.2 | −5.8 | −10.8 |
| CT6 | 67.2 | −51.0 | −42.0 | −10.2 | −36.0 | Chlorouracil and uracil mismatches | |||||
| GA | 84.0 | −68.8 | −53.8 | −13.4 | −51.8 | AUClH | 86.6 | −70.2 | −51.4 | −11.4 | −46.6 |
| GA2 | 68.4 | −53.6 | −38.0 | −11.2 | −34.4 | AUClRH | 85.4 | −69.6 | −50.2 | −11.4 | −45.8 |
| GA3 | 68.2 | −56.8 | −43.8 | −12.4 | −44.8 | AUClRWC | 95.6 | −73.2 | −56.4 | −12.0 | −46.2 |
| GC1 | 81.8 | −67.6 | −50.2 | −11.6 | −47.6 | AUClWC | 98.6 | −75.4 | −59.0 | −12.2 | −48.0 |
| GCx | 107.0 | −96.6 | −73.8 | −11.2 | −74.6 | AUH | 83.8 | −69.0 | −48.6 | −11.2 | −45.0 |
| GCRWC | 41.6 | −39.0 | −25.2 | −8.4 | −31.0 | AURH | 81.0 | −67.0 | −46.4 | −11.0 | −43.6 |
| GG1 | 65.6 | −64.0 | −40.4 | −11.6 | −50.2 | AURWC | 90.8 | −70.4 | −52.2 | −11.8 | −43.6 |
| GG3 | 107.0 | −100.6 | −75.6 | −13.0 | −82.0 | AUWC | 95.0 | −73.6 | −55.4 | −11.8 | −46.0 |
Stacking interactions
The π–π stacking interactions present in the stacked dimers of the base pairs can be influenced by the twist angle, the solvent and hydrogen bonds. The stacking energy, ΔE(X–Y)/(X′–Y′)π–π is calculated as the energy difference between the stacked base pairs and the individual base pairs (X–Y and X′–Y′), both in gas phase and in aqueous solution and by considering the fully parallel base pairs with a twist angle (tw) of 0°, and the natural occurring twist angle of 36° (see Tables 1 and 2). Table 1 shows the corresponding values for the series of 31 Watson–Crick and mismatched base pairs, and Table 2 encloses those for the RNA and modified base pairs.The stacking interaction is always more attractive at a twist angle of 36° in gas phase (see Tables 1 and 2) and in water (see also Table S1 of the ESI†). In vacuo, the average gain in stacking energy by twisting from 0° to 36° amounts to −7.9 kcal mol−1, and in water to −2.2 kcal mol−1 (see Tables 1 and 2). ΔΔgas values in Tables 1 and 2 denote the energy difference between the stacking energy at a twist angle of 36° and at 0° in the gas phase. These ΔΔgas values range from −5.8 kcal mol−1 to −11.6 kcal mol−1.
The natural occurring DNA base pairs ATWC and GCWC will be explained in more detail, because of their biological importance. At the B-DNA twist angle and under solvated conditions, the stacking interaction is quite similar in energy for the Watson–Crick base pairs: the stacking interaction amounts to −9.8 kcal mol−1 for (A–T)/(A′–T′) and for (G–C)/(G′–C′) to −9.7 kcal mol−1. Thus, under natural conditions (solvation and twist-angle of 36°) the stabilization to structure of B-DNA by the π–π stacking between two ATWC pairs or two GCWC pairs is equalized.
In the gas phase, the ΔE(X–Y)/(X′–Y′)π–π amounts for AT to −12.2 kcal mol−1 at 36° and for GC to −9.8 kcal mol−1. These values confirm our previous values obtained at the LDA/TZ2P and KT1/TZ2P levels of theory.1d The decomposition of this stacking interaction into the individual terms of base–base stacking interaction (ΔEX/X′π–π) and cross terms (ΔEX/Y′π–π) is given in Table 3. For the stacked ATWC base pair, the largest contribution to the total stacking interaction comes from the base–base stacking interaction, ΔEX/X′π–π (−5.4 kcal mol−1 for A/A′ and −3.8 kcal mol−1 for T/T′) and not from the cross terms (–0.9 kcal mol−1 and −1.1 kcal mol−1). The stacking interaction for GCWC is built up in a different way. Unexpectedly, the cross terms play a much more important role than the stacking terms: ΔEX/X′π–π is −2.5 kcal mol−1 for X = G and −0.3 for X = C and the cross-terms are −5.2 kcal mol−1 and −3.2 kcal mol−1 at the natural twist angle.
The Watson–Crick base pairs improve their stacking interactions in the gas phase by −8.3 kcal mol−1 for ATWC and −6.8 kcal mol−1 for GCWC by increasing the twist angle from 0° to the natural angle of 36°. To understand how this increase is established, we carried out an energy decomposition analysis for both ATWC and GCWC stacked systems at both twist-angles (see Table 3). The enhanced stacking interaction at the experimental twist angle is partly due to a decrease of Pauli repulsion: −11.4 kcal mol−1 for ATWC and −6.2 kcal mol−1 for GCWC (see Table 3). The electrostatic interaction and the dispersion interaction counteract each other for both systems: ΔVelstat improves by twisting from 0° to 36° (–2.7 kcal mol−1 for ATWC and −3.6 kcal mol−1 for GCWC) and the dispersion interaction diminishes by 4.1 kcal mol−1 for ATWC and 3.2 kcal mol−1 for GCWC.
The stacking interaction can be divided up in the individual terms of base–base stacking (X/X′ and Y/Y′) and cross terms (X/Y′ and Y/X′), see Table 3. The energy decomposition of these individual terms reveals that the reduction of the Pauli repulsion is twice as large for the stacked T/T′ pair (−8.0 kcal mol−1), than for the other three stacked systems (−3.8 kcal mol−1, −3.4 kcal mol−1 and −3.6 kcal mol−1 for respectively, A/A′, G/G′ and C/C′). This larger reduction of the Pauli repulsion can be attributed to the release of the repulsive interaction between the two methyl groups of thymine bases. Relaxation of the methyl groups of thymine, while keeping the rest of the base pairs fixed, reduces the Pauli repulsion from 26.5 to 21.5 kcal mol−1 for a twist angle of 0° and from 15.1 to 14.9 kcal mol−1 for 36°. The values of the stacking interaction for AT show that it is not necessary to relax the methyl groups at a twist angle of 36° as the interaction energy and the decomposition thereof give almost the same values.
A comparison of the decomposed interaction energy at the natural twist angle for the stacked GCWC and the ATWC (with relaxed methyl groups) reveals that the larger interaction energy of the stacked ATWC pairs of −12.2 kcal mol−1 than of the stacked GCWC pairs (−9.8 kcal mol−1) can be attributed to the more attractive electrostatic interaction of −5.2 kcal mol−1 for ATWC as the other terms are almost similar in size (see Table 3). This difference in electrostatic interaction can be ascribed to accumulation of electronic charge on the guanine base as it has two proton donors and one acceptor. This difference between ATWC and GCWC is only apparent in the gas phase because solvated in water these charge accumulations are stabilized leading to equal stacking interactions under natural conditions (vide infra).
The repulsive interactions between methyl groups at a twist angle of 0° are visible also in other stacked base pairs, particularly base pairs which contain four thymine bases such as stacked TT3, TT4 and TT5. In Table 5, the decomposition of the stacking energy for TT3 is presented (see also Table S2 of the ESI†). At the twist angle of 0°, the Pauli repulsion amounts to 30.9 kcal mol−1 and lowers to 12.2 kcal mol−1 when the base pair is twisted to 36°. Also, in this case relaxation of the methyl groups reduces the Pauli repulsion at a twist angle of 0° (21.0 kcal mol−1) and results in an attractive stacking interaction at 0°. However, relaxation of the methyl groups has almost no effect at a twist angle of 36°.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a
| XY | Twist angle | ΔEPauli | ΔVelstat | ΔEoi | ΔEdisp | ΔEint |
|---|---|---|---|---|---|---|
| a Calculated at the BP86-D/TZ2P level of theory. b Summation of the pairwise interactions calculated for the different base pairs. The pairwise interactions can be found in the ESI. | ||||||
| π–π stacking (X–Y)/(X′Y′) | ||||||
| CCx | 0° | 18.6 | 6.4 | −3.5 | −16.9 | 4.7 |
| 36° | 12.4 | 0.1 | −3.7 | −13.9 | −5.1 | |
| GCRWC | 0° | 20.6 | 8.7 | −4.3 | −20.6 | 4.4 |
| 36° | 13.0 | 4.6 | −4.3 | −15.9 | −2.7 | |
| GGx | 0° | 22.5 | 8.1 | −4.6 | −24.2 | 1.9 |
| 36° | 14.4 | 2.2 | −4.5 | −18.6 | −6.5 | |
| TT3 | 0° | 30.9 | −0.7 | −8.1 | −21.0 | 1.2 |
| 36° | 12.2 | −2.1 | −3.6 | −15.6 | −9.1 | |
| TT3 (Me-groups optimized) | 0° | 21.0 | 1.0 | −4.2 | −20.6 | −2.8 |
| 36° | 12.3 | −2.3 | −3.6 | −15.7 | −9.4 | |
| Sum of pairwise interactions | ||||||
| CCx | 0° | 19.6 | 3.9 | −3.8 | −17.0 | 2.7 |
| 36° | 13.3 | −1.8 | −4.3 | −13.8 | −6.5 | |
| GCRWC | 0° | 21.6 | 5.6 | −4.6 | −20.5 | 1.9 |
| 36° | 13.9 | 2.0 | −4.6 | −16.0 | −4.7 | |
| GGx | 0° | 23.4 | 4.7 | −5.1 | −24.2 | −1.2 |
| 36° | 15.4 | −0.7 | −5.0 | −18.6 | −8.9 | |
| TT3 | 0° | 31.7 | −0.3 | −8.2 | −21.0 | 2.2 |
| 36° | 13.1 | −1.9 | −3.8 | −15.6 | −8.2 | |
| TT3 (Me-groups optimized) | 0° | 21.8 | 1.4 | −4.4 | −20.6 | −1.8 |
| 36° | 13.2 | −2.1 | −3.8 | −15.7 | −8.5 | |
The next point that we want to address is whether the π–π stacking interactions are influenced by the hydrogen bonds. At the twist angle of 0° where the influence is more pronounced, we compare the ΔE(X–Y)/(X′–Y′)π–π with the sum of the pairwise terms. The latter does not contain the influence by hydrogen bonding (see Tables 3 and 5). For the natural occurring stacks of ATWC, the interaction energy amounts to −3.9 kcal mol−1 at a twist of 0° and the sum to −2.8 kcal mol−1. The influence of the hydrogen bonds on the stacking interaction is thus small. Somewhat larger is the influence in the stacking interaction of the GCWC pairs. Two stacked GCWC pairs at a twist angle of 0° have an interaction energy of −3.0 kcal mol−1 and the individual terms sum up to −4.9 kcal mol−1. The influence of the hydrogen bonds on the stacking interactions in stacked GCWC pairs is larger than in the stacked ATWC pairs. The ATWC pair has two hydrogen bonds in opposite directions, which do not lead to charge accumulations on one of the bases. The odd number of hydrogen bonds in the GCWC base pair results in an electronic charge accumulation on guanine, which disfavors the electrostatic interaction in the stacked GCWC base pairs. ΔVelstat amounts to 1.1 kcal mol−1 for the stacked GCWC and the individual terms of the electrostatic interaction sum up to −0.1 kcal mol−1 (see Table 3).
This disfavoring of the stacking interactions by the hydrogen bonds is also visible for other stacked base pairs, that is CCx, GCRWC and GGx (see Table 5, and Table S2 of the ESI†). These base pairs experience charge accumulation because they have only one hydrogen bond (CCx) or two hydrogen bonds in the same direction (GCRWC and GGx) between the bases. The numbers for the stacked GGx are the most illustrative. The stacking interaction energy is repulsive for the stacked GGx at a twist angle of 0° by 1.9 kcal mol−1, whereas the sum of the individual terms is attractive by 1.2 kcal mol−1: a difference of 3.1 kcal mol−1. Also in this case, solvation in water will stabilize the charge accumulations.
Conclusions
The cohesion between B-DNA's single strands is not only determined by Watson–Crick hydrogen bonding but also by the diagonal interactions (cross terms) between a base in one base pair and the opposite base in the next base pair in the stack. These cross terms are particularly stabilizing between stacks of GC pairs which further reinforces the stability of GC-rich sequences which already benefit from stronger Watson–Crick hydrogen bonding (cf. Barone et al.20). This follows from our quantum chemical analyses of a series of 47 stacked dimers of Watson–Crick, mismatched and modified DNA base pairs, based on using dispersion-corrected density functional theory (DFT-D).Furthermore, solvation not only weakens but also equalizes both Watson–Crick hydrogen bonding in AT and GC base pairs as well as the π–π stacking interaction between two AT pairs and that between two GC pairs. In the gas phase, stacked GC pairs are involved in a significantly stronger stacking interaction than stacked AT pairs. In the condensed-phase, solvation stabilizes individual GC pairs more strongly than AT pairs because Watson–Crick pairing leads to a net charge separation in the former that benefits more from interaction with the solvent medium.
Interestingly, the experimental twist angle of 36° is crucial for the stability of B-DNA: it leads to a stabilization of around 8 kcal mol−1 compared to a twist angle of 0°. The increase in stabilization is mainly attributed to a reduction of Pauli repulsion between the π electrons of the aromatic bases and, in the case of thymine, the C–H bonds of the methyl substituents. Note that these Pauli repulsion effects derive from the existence of a non-negligible π–π overlap. This is exactly the overlap that is also behind DNA's capability to conduct holes after ionization.21
Acknowledgements
We thank the following organizations for financial support: the HPC-Europa2 Transnational Access program of the European Union, the Netherlands Organization for Scientific Research (NWO), the Ministerio de Ciencia e Innovación (MICINN, project number CTQ2011-25086), the DIUE of the Generalitat de Catalunya (project number 2009SGR528), the Netherlands National Research School Combination – Catalysis (NRSC-C), and the European Fund for Regional Development (FEDER, grant UNGI08-4E-003). Excellent service by the Amsterdam (SURFsara) and Barcelona (BSC-CNS) supercomputing centers is gratefully acknowledged.References
- (a) J. Cerny, M. Kabelac and P. Hobza, J. Am. Chem. Soc., 2008, 130, 16055–16059 CrossRef CAS PubMed; (b) C. D. M. Churchill, L. Navarro-Whyte, L. R. Rutledge and S. D. Wetmore, Phys. Chem. Chem. Phys., 2009, 11, 10657–10670 RSC; (c) C. D. Sherrill, Acc. Chem. Res., 2013, 46, 1020–1028 CrossRef CAS PubMed; (d) M. Swart, T. van der Wijst, C. Fonseca Guerra and F. M. Bickelhaupt, J. Mol. Model, 2007, 13, 1245–1257 CrossRef CAS PubMed.
- J. Poater, M. Swart, C. Fonseca Guerra and F. M. Bickelhaupt, Chem. Commun., 2011, 47, 7326–7328 RSC.
- J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737–738 CrossRef CAS.
- (a) C. Fonseca Guerra, T. van der Wijst and F. M. Bickelhaupt, Chem. – Eur. J., 2006, 12, 3032–3042 CrossRef PubMed; (b) C. Fonseca Guerra, F. M. Bickelhaupt and E. J. Baerends, Cryst. Growth Des., 2002, 2, 239–245 CrossRef; (c) C. Fonseca Guerra, T. van der Wijst and F. M. Bickelhaupt, Struct. Chem., 2005, 16, 211–221 CrossRef; (d) C. Greve, N. K. Preketes, H. Fidder, R. Costard, B. Koeppe, I. A. Heisler, S. Mukamel, F. Temps, E. T. J. Nibbering and T. Elsaesser, J. Phys. Chem. A, 2013, 117, 594–606 CrossRef CAS PubMed; (e) B. Koeppe, E. T. J. Nibbering and P. M. Tolstoy, Z. Phys. Chem., 2013, 227, 723–749 CrossRef CAS; (f) H. Fidder, M. Yang, E. T. J. Nibbering, T. Elsaesser, K. Röttger and F. Temps, J. Phys. Chem. A, 2013, 117, 845–854 CrossRef CAS PubMed.
- J. Poater, M. Swart, C. Fonseca Guerra and F. M. Bickelhaupt, Comput. Theor. Chem., 2012, 998, 57–63 CrossRef CAS PubMed.
- C. Fonseca Guerra, H. Zijlstra, G. Paragi and F. M. Bickelhaupt, Chem. – Eur. J., 2011, 17, 12612–12622 CrossRef CAS PubMed.
- V. I. Danilov, V. M. Anisimov, N. Kurita and D. Hovorun, Chem. Phys. Lett., 2005, 412, 285–293 CrossRef CAS PubMed.
- (a) K. M. Guckian, T. R. Krugh and E. T. Kool, J. Am. Chem. Soc., 2000, 122, 6841–6847 CrossRef CAS PubMed; (b) E. T. Kool, J. C. Morales and K. M. Guckian, Angew. Chem., Int. Ed., 2000, 39, 990–1009 CrossRef CAS; (c) J. C. Morales and E. T. Kool, J. Am. Chem. Soc., 2000, 122, 1001–1007 CrossRef CAS PubMed.
- (a) C. Fonseca Guerra and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2002, 41, 2092–2095 CrossRef; (b) C. Fonseca Guerra, F. M. Bickelhaupt and E. J. Baerends, ChemPhysChem, 2004, 5, 481–487 CrossRef PubMed.
- (a) P. Marlière, J. Patrouix, V. Döring, P. Herdewijn, S. Tricot, S. Cruveiller, M. Bouzon and R. Mutzel, Angew. Chem., Int. Ed., 2011, 50, 7109–7114 CrossRef PubMed; (b) C. G. Acevedo Rocha and N. Budisa, Angew. Chem., Int. Ed., 2011, 50, 6960–6962 CrossRef CAS PubMed.
- (a) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS; (b) C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1986, 84, 4524–4529 CrossRef CAS PubMed; (b) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS; (c) J. P. Perdew, Phys. Rev. B: Condens. Matter, 1986, 33, 8822–8824 CrossRef; (d) S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS PubMed.
- (a) A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC; (b) C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396–408 CrossRef CAS; (c) M. Swart, E. Rösler and F. M. Bickelhaupt, Eur. J. Inorg. Chem., 2007, 3646–3654 CrossRef CAS.
- (a) C. Fonseca Guerra, T. van der Wijst, J. Poater, M. Swart and F. M. Bickelhaupt, Theor. Chem. Acc., 2010, 125, 245–252 CrossRef; (b) T. van der Wijst, C. Fonseca Guerra, M. Swart, F. M. Bickelhaupt and B. Lippert, Angew. Chem., Int. Ed., 2009, 48, 3285–3287 CrossRef CAS PubMed.
- J. Sponer, P. Jurecka and P. Hobza, J. Am. Chem. Soc., 2004, 126, 10142–10151 CrossRef CAS PubMed.
- (a) J. Sponer, J. Leszczynski and P. Hobza, J. Phys. Chem., 1996, 100, 1965–1974 CrossRef CAS; (b) C. Fonseca Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, J. Am. Chem. Soc., 2000, 122, 4117–4128 CrossRef.
- (a) F. M. Bickelhaupt and E. J. Baerends, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86; (b) K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340 CrossRef CAS; (c) K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS PubMed; (d) J. Poater, M. Solà and F. M. Bickelhaupt, Chem. – Eur. J., 2006, 12, 2889–2895 CrossRef CAS PubMed; (e) T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS; (f) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- G. Barone, C. Fonseca Guerra and F. M. Bickelhaupt, ChemistryOpen, 2013, 2, 186–193 CrossRef CAS PubMed.
- K. Senthilkumar, F. C. Grozema, C. Fonseca Guerra, F. M. Bickelhaupt, F. D. Lewis, Y. A. Berlin, M. A. Ratner and L. D. A. Siebbeles, J. Am. Chem. Soc., 2005, 127, 14894–14903 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Stacking interaction energies and energy decomposition analyses of some stacked base pairs enclosed. See DOI: 10.1039/c4ob00427b |
| This journal is © The Royal Society of Chemistry 2014 |