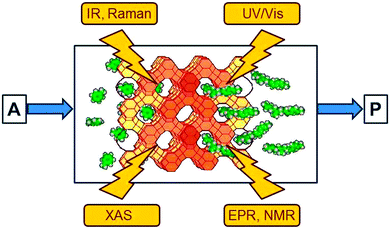
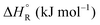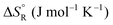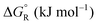Understanding catalysis†
Emil
Roduner
ab
aInstitute of Physical Chemistry, University of Stuttgart, D-70569 Stuttgart, Germany. E-mail: e.roduner@ipc.uni-stuttgart.de
bChemistry Department, University of Pretoria, Pretoria 0002, Republic of South Africa
First published on 14th October 2014
Abstract
The large majority of chemical compounds underwent at least one catalytic step during synthesis. While it is common knowledge that catalysts enhance reaction rates by lowering the activation energy it is often obscure how catalysts achieve this. This tutorial review explains some fundamental principles of catalysis and how the mechanisms are studied. The dissociation of formic acid into H2 and CO2 serves to demonstrate how a water molecule can open a new reaction path at lower energy, how immersion in liquid water can influence the charge distribution and energetics, and how catalysis at metal surfaces differs from that in the gas phase. The reversibility of catalytic reactions, the influence of an adsorption pre-equilibrium and the compensating effects of adsorption entropy and enthalpy on the Arrhenius parameters are discussed. It is shown that flexibility around the catalytic centre and residual substrate dynamics on the surface affect these parameters. Sabatier's principle of optimum substrate adsorption, shape selectivity in the pores of molecular sieves and the polarisation effect at the metal–support interface are explained. Finally, it is shown that the application of a bias voltage in electrochemistry offers an additional parameter to promote or inhibit a reaction.
Key learning points(1) It is essential to quantify spectroscopic work in order to judge the importance of observed transient features.(2) A catalyst can open a new reaction pathway with lower activation energy. It does it by providing a partial bond which stabilises the transition state and compensates for part of the energy required to break a bond in the reactant before stabilisation by the newly formed bond takes over. (3) Flexible adaptation of catalyst structure and electron distribution along the reaction path are essential for energy minimization thus lowering the activation energy, while mobility and dynamics of the adsorbed substrate reduce the activation entropy and keep the Arrhenius pre-exponential factor high. (4) There exists an optimum binding energy of substrates to a catalytic centre, strong enough to do catalysis but not too strong, in order to avoid blocking the centre by undesorbed product (Sabatier's principle). (5) Electrocatalysis allows promoting redox reactions at a molecular level by application of an electric potential. |
(1) Introduction
The term “catalysis” was coined in 1835 by the Swedish chemist Berzelius, but a suitable definition was introduced only many years later by Ostwald who wrote in 1894: “Catalysis is the acceleration of a slow chemical process by the presence of a foreign material”.1 Today, more than 100 years later, every student learns that a catalyst accelerates a reaction by lowering its activation energy, and he knows that the catalyst achieves this by attaching itself to the reactant molecule, thereby interacting with it. Although the catalyst participates in the reaction it is not used up and can transform many molecules. It therefore needs to be present only in catalytic amounts and can nevertheless transform large quantities. Beyond this, little is found about the action of a catalyst in elementary textbooks, although catalysis is one of the key principles in chemistry and a vast majority of chemical compounds have undergone one or more catalytic steps during their synthesis. During the past century, catalysis has revolutionised both, chemical industry and academia. Nevertheless, it has for a long time resembled more an art than a scientific discipline.This situation has changed with the advent of surface science when a large number of experimental techniques were developed which permitted studying in detail the interaction of adsorbate molecules on single crystal surfaces. This led to significant progress, but its significance for catalysis was limited by two facts: (1) most surface science techniques worked well only under high vacuum conditions and at temperatures where motion is frozen and chemical reaction is absent. Hence, significant efforts were undertaken to bridge the pressure gap to real conditions for practical applications.2 (2) With time it became clear that very often rough surfaces with defects in crystal facets, and corners and edges of crystals provide far better catalytic activity than perfect single crystal surfaces.3 Today, the gap between the ideal conditions of surface science and the conditions of practical relevance is no longer open, and advanced techniques have become available which can monitor the catalyst at work and on a nanoscale.4,5
Heterogeneous catalysis happens at the surface of a solid. It is therefore obvious that materials with a large surface area, i.e. fine powders or porous solids, make better use of the catalytic material and are more efficient than large single crystals. However, for porous materials there is often a debate whether the catalytic activity is restricted to the outer surface or whether and to which extent the surface inside the pores contributes. This is of course also a question of transport limitation in the pores. Furthermore, the preference for nanometer over micrometer size catalytic particles is not only a question of the economy of making better use of expensive materials like platinum metal. Small particles have a larger fraction of their atoms on the surface, but on top of this, an atom on the surface of a small metal particle has electronic properties which are significantly different from those on the surface of a large particle.6
In this tutorial we aim to contribute to closing a gap in spreading the understanding of some of the fundamental principles of the art of catalysis. Furthermore, we show how the mechanisms can be studied. In an attempt to make this often highly complex matter accessible we will focus on very few simple and therefore transparent systems.
(2) Elucidation of reaction mechanisms: shining light into a black box
(a) Variation of reactants and monitoring products
In homogeneous (single phase) systems the nature of a reaction mechanism can be clarified conveniently by means of kinetics, measuring the initial rate R0 of a reaction for different concentrations of reactants. If R0 is proportional to [A], the concentration of reactant A, then A is involved directly in the rate-determining step. If the [A] does not change in the course of the reaction (and A is not present in large excess so that the change in its concentration is just not observable) and R0 nevertheless depends on [A] then we conclude that A acts as a catalyst.In heterogeneous catalysis, products tend to be often very different from the reactants. A famous example is the methanol-to-gasoline (MTG) process that is successfully carried out using an acidic zeolite, originally H-ZSM-5 (Fig. 1). A catalyst that can form on the order of eight carbon–carbon bonds in a seemingly single step looks like a miraculous black box. What are the possibilities to light up this black box?
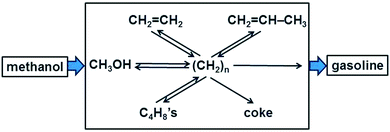 | ||
| Fig. 1 Schematic of the carbon pool mechanism in the formation of gasoline from methanol (adapted from ref. 7). | ||
The catalytic activity of a solid compound is easy to prove: in the absence of the catalyst the reaction does not occur, or it is much slower. But the mechanism is much more difficult to prove since concentrations have a different meaning and are also heterogeneous due to adsorption, and in porous systems due to transport limitations. A suitable contribution to clarify the mechanism rests on the variation of the nature of the reactants. If the mechanism consists of simple consecutive reactions, as in A → B → C → D → P, then the same product P must be found independently of whether the feed is A, B, C, or D. Also when the situation is more complex, as in the MTG process in Fig. 1, the mechanism was clarified in part by feeding one of the postulated intermediates, CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, in addition to 13C labelled methanol to the acidic zeolite type catalyst SAPO-34 which produces predominantly C2 to C4 alkenes.7 For a simple consecutive mechanism 13CH3OH → C2H4 → C3H6 → C4H8 → C5H10 →… one should expect to find only singly or triply 13C labelled propene, and in the singly labelled propene 13C could not occur in the central position. However, the experiment also yielded a doubly labelled product, revealing scrambling of the isotopic label.7 This supported the more complex mechanism shown in Fig. 1 in which there is a hydrocarbon pool consisting of fragments (CH2)n which react repeatedly to form various other intermediates or products.
CH2, in addition to 13C labelled methanol to the acidic zeolite type catalyst SAPO-34 which produces predominantly C2 to C4 alkenes.7 For a simple consecutive mechanism 13CH3OH → C2H4 → C3H6 → C4H8 → C5H10 →… one should expect to find only singly or triply 13C labelled propene, and in the singly labelled propene 13C could not occur in the central position. However, the experiment also yielded a doubly labelled product, revealing scrambling of the isotopic label.7 This supported the more complex mechanism shown in Fig. 1 in which there is a hydrocarbon pool consisting of fragments (CH2)n which react repeatedly to form various other intermediates or products.
(b) Quantitative and real time spectroscopic observation of reaction intermediates and catalytic centres
Spectroscopic methods provide an insight into the disappearance of the reactants and the formation of the intermediates and products in homogeneous and heterogeneous reaction systems. Spectra which display the difference relative to the initial state are particularly useful since the large, time-independent signals arising from solvent and catalyst are subtracted so that they do not mask the small signals of transient intermediates which are of interest. As indicated in Fig. 2, the following methods have become popular in heterogeneous catalysis:8• Electronic (UV/Vis) spectroscopy provides information about the oxidation state of the catalytic centre and of intermediates. It suffers somewhat from low resolution and needs a certain amount of transparency of the sample.
• Vibrational (IR and Raman) spectroscopy has proven to be extremely useful for the observation of reaction intermediates, with IR spectroscopy being particularly popular owing to its very high sensitivity.
• X-ray absorption spectroscopies (XAS) in several variants have undergone an enormous development over the past twenty years and have become unique tools. The element selective excitation provides direct information about the catalytic centres, often transition metals, and their immediate environment. Extended X-ray absorption fine structure (EXAFS) spectroscopy, for example, reveals coordination numbers and distances to the neighbouring atoms at distances up to about 0.5 nm. Details of the spectral response near the absorption edge provide additional information about the oxidation state of the excited atom and the symmetry of its immediate environment.
• Electron paramagnetic resonance (EPR) and nuclear magnetic resonance (NMR) methods are also element-specific (in the case of EPR to a certain extent) and complementary since NMR detects nuclei of diamagnetic compounds while EPR provides a sensitive access to paramagnetic intermediates and catalytic centres. NMR has also been used to observe the intermediates of the carbon pool mechanism (Fig. 1) in the methanol-to-olefin process.9
If one wants to judge the significance of an observed feature the absorption has to be compared with the loading by the adsorbed reactant and the number of catalytic centres. An example which relates to the oxidation reaction of benzene to phenol using molecular oxygen in Cu/HZSM-5 zeolite is given in Fig. 3. It shows the band of the ν13 in-plane vibration of benzene which is shifted slightly when the molecule is adsorbed on copper compared to adsorption on Brønsted acid sites (the latter is not distinguishable from adsorption on other places in the zeolite).10 Adsorption on the Brønsted acid sites can also be observed by a shift of the IR band of the corresponding OH group at 3610 cm−1, but adsorption of benzene changes the polarity of the OH group and the effective mass of the oscillator. This affects its band intensity so that quantification is nontrivial. However, for the ν13 vibration, charge distribution in benzene does not change significantly when the molecule is adsorbed on the catalyst. Hence, the extinction coefficient of the observed species is not affected much so that its literature value may be used, and the IR spectra can be quantified. The plateau for the Cu site on the right hand side of Fig. 3 reveals saturation, and calibration shows that this corresponds to one benzene molecule per Cu, which tells immediately that all Cu ions are accessible to benzene. Thus, quantitative spectroscopy contributes to the clarification of the question whether it is only the external surface of a porous solid that is catalytically active or whether the centres located inside pores are accessible and active.
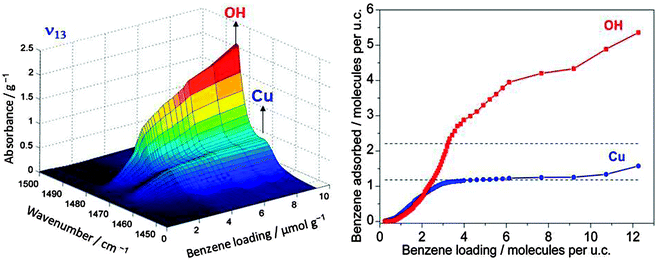 | ||
| Fig. 3 IR band of an in-plane vibrational band of benzene adsorbed on OH groups of Brønsted acid sites and on Cu ions (left). Calibration allows quantification of the absorption units (right). The plateau in the isotherm for adsorption of benzene on Cu is found to correspond to the full amount of Cu in the sample (adapted from ref. 10). | ||
In the same reaction system, Cu2+ is EPR active whereas Cu1+ does not give a signal, but it is important to know whether an observed signal represents e.g. 90% or 0.01% of the total copper content in a catalyst. This information requires calibration of the spin concentration.
Acid catalysis is one of the most common types of catalysis. Protonation by Brønsted acids polarises the system and leads to a new electron distribution in the protonated species, which activates the molecule and may induce the breaking of existing bonds and the formation of new bonds.
It is essential that the spectroscopic characterisation is carried out simultaneously with measurements of catalytic activity and selectivity and under working conditions. This methodology is known as operando spectroscopy.8,11
(c) Modelling reaction intermediates and transition states by quantum chemical calculations
Insight of a different kind comes from quantum chemical calculations. While experimental observations normally represent an ensemble average over many molecules or sites and often a superposition of different reactions, calculations have the advantage that they can be restricted to one specific site or process and therefore in principle provide a much cleaner picture. The disadvantage is that a representative fragment of the system has many atoms, which is difficult to handle in accurate calculations. The scheme for a way out of this dilemma is illustrated in Fig. 4, again for benzene oxidation, but here on zeolite CuHY.12 A hybrid method is used which calculates the immediate environment of the catalytic centre at a high quantum chemical (QC) level. This accurately treated cluster is embedded in the somewhat further remote environment which is treated at the less accurate molecular mechanics (MM) level that works with empirical force fields. This method is therefore called the QC-MM embedded method. The result shown in Fig. 4 demonstrates that one benzene molecule and molecular oxygen can bind simultaneously to the same Cu centre and form a conceivable intermediate of the Cu catalysed benzene oxidation with O2 to phenol.12 In contradiction to this, experimental work suggests that the reaction requires a bifunctional catalyst with benzene adsorbing on a Brønsted acid site and O2 being activated on Cu.13 The work illustrates that successful clarification of the catalytic mechanism is best achieved by a combination of product analysis with variation of reactants, in situ spectroscopy and quantum chemical simulations.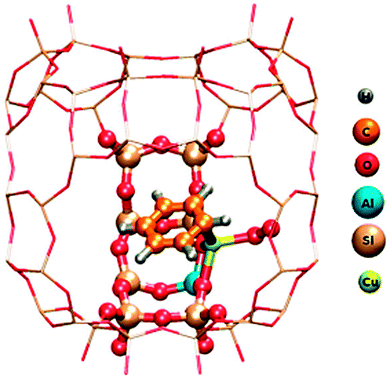 | ||
| Fig. 4 QM/MM model of C6H6 and O2 adsorbed both on Cu in Cu-exchanged Y zeolite. Atoms of the adsorbates, the catalytic Cu centre and a small nearby fraction of the zeolite computed at the Density Functional Theory quantum chemical level are marked by balls. The surrounding remaining part of the zeolite framework represented by the grid of sticks is treated at the empirical Molecular Mechanics level. The entire fragment is repeated periodically in 3 dimensions to ensure that it conforms to the structure of the extended crystal (reprinted from ref. 12). | ||
(3) Enhancing rate constants by lowering the activation energy: how does the catalyst do it?
When one speaks about activation energy one generally refers to the widely used Arrhenius equation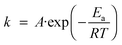 | (1) |
The high activation energies of chemical reactions are due to bond breaking. But breaking a bond is a reaction that often goes only uphill and ends on a high plateau. Such a reaction cannot be catalysed. Formation of new bonds brings the energy curve back down as the product is formed. A catalyst can provide transient weak bonds which lower the transition state energy by partly compensating for the energy required to break the old bond until formation of the new bond sets in and stabilises the system on the product side.
Formic acid (FA) decomposition will serve as an example for much of the following discussion. FA can dissociate spontaneously either by dehydrogenation or by dehydration. The corresponding thermodynamic parameters are given in Table 1 for gaseous (g) and liquid (l) FA. The dehydrogenation reaction of FA has been considered as a possible source for on-demand in situ hydrogen production for fuel cells in cars. FA is non-toxic, and a liquid fuel is far easier to store and transport over large distances. It would be essential that the dehydration reaction channel which leads to H2O and CO is suppressed since CO acts as a poison which blocks the surface of Pt-based fuel cell catalysts.
 , entropies
, entropies  , and free energies
, and free energies 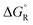 for the dehydrogenation and dehydration of formic acida,b
for the dehydrogenation and dehydration of formic acida,b
| Reaction | ||||||
|---|---|---|---|---|---|---|
a The values are based on the NIST library,14 given in the ESI, taken as the difference between values of products and reactants, and 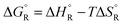 .
b The subscript R stands for reaction, the superscript ° for standard concentration in the chosen standard state (1 molar concentration for solutions, 1 bar pressure for gases, mol fraction x = 1 for near bulk systems; one has to be careful if one works with mixed standard states) and for standard temperature, T = 298.16 K. .
b The subscript R stands for reaction, the superscript ° for standard concentration in the chosen standard state (1 molar concentration for solutions, 1 bar pressure for gases, mol fraction x = 1 for near bulk systems; one has to be careful if one works with mixed standard states) and for standard temperature, T = 298.16 K.
|
||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
|
−14.5 | 95.8 | −43.0 | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
|
+26.7 | 137.8 | −14.4 | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
|
+31.5 | 212.5 | −31.8 | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
|
+28.7 | 135.6 | −11.7 | |||
These reactions have been studied extensively both in experiments and by theoretical calculations and are therefore suited as model reactions for this tutorial. We will focus on the dehydrogenation reaction (2) and (4) which is exothermic in the gas and spontaneous (exergonic) in both the gas and the liquid phase. In the following, various possibilities for catalytic acceleration of this reaction which is highly activated in the absence of a catalyst will be discussed. Activation energies obtained from experiment and from theoretical calculations are summarised in Table 2.
| Condition, catalyst | Case | E a (kJ mol−1) | log(A/s−1) | Method | Ref. |
|---|---|---|---|---|---|
| a PC: propylene carbonate, THF: tetrahydrofuran. b Values derived from the TOF data in ref. 19 and 21. | |||||
| Gas phase, no catalyst | Fig. 5 | 203 | Exp. | 15 | |
| 284 | Theory | 16 | |||
| Gas phase, 1H2O | Fig. 6 | 200 | Theory | 16 | |
| Gas phase, 2H2O | — | 190 | Theory | 16 | |
| Gas phase, water vapour | — | 101 | Exp. | 17 | |
| 136 ± 68 | Exp. | 18 | |||
| PC solution,a Fe complex | — | 77.0 ± 0.4 | 12.15(6)b | Exp. | 19 |
| THF solution,a Fe complex | — | 82.1 ± 1.3 | 12.5(2)b | Exp. | 19 |
| Gas phase, SiO2 supported Au nanoparticles | Fig. 9 | 58.5 | Exp. | 20 | |
| Ag42Pd58 2.2 nm C supported nanoparticles in aq. solution | — | 22 ± 1 | 9.7(4)b | Exp. | 21 |
(a) Uncatalysed gas-phase unimolecular dissociation
The formic acid conformer with the two H atoms in trans configuration is more stable than its cis form by 17 kJ mol−1, but the activation energy for isomerisation is low so that there is a fast pre-equilibrium. The cis form is the direct precursor of the reaction which is shown in Fig. 5. The activation energy for this uncatalysed reference reaction is predicted to amount to 284 kJ mol−1 (ref. 16) (measured from the energy of the trans conformer). This high value is partly due to the large strain in the four-atomic transition state. It is nevertheless much lower than the sum of the C–H and the O–H bond dissociation energies (in total ca. 846 kJ mol−1) which shows that the new H–H single and the new C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bonds are formed to a considerable extent before the other bonds are completely broken (for unknown reasons the calculated value of Ea is considerably higher than the value of 203 kJ mol−1 reported from experiment).15
O double bonds are formed to a considerable extent before the other bonds are completely broken (for unknown reasons the calculated value of Ea is considerably higher than the value of 203 kJ mol−1 reported from experiment).15
 | ||
| Fig. 5 Formic acid reactant in cis conformation and transition state for the dehydrogenation reaction in the absence of a catalyst. The breaking bonds and the newly forming bonds are indicated by broken lines in the transition state (drawn based on ref. 16). | ||
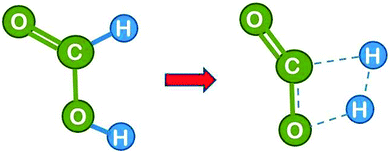
(b) Gas phase dissociation catalysed by one and two water molecules with the cyclic transition state
Next we consider the reaction in the presence of one water molecule which can assist via formation of a six-atom cyclic transition state. This reduces the strain in the transition state and leads to a dramatic reduction of the theoretical activation energy by 84 kJ mol−1 to 200 kJ mol−1,16 demonstrating that the water molecule can act as an efficient catalyst. Note that the H2 product is composed of one formic acid hydrogen and one atom from the water molecule. It is likely that the H3O+ transient passes in a Grotthuss type manner only the proton to the formate hydrogen, while the formate electron takes the route via the carbon atom, which effectively leads to a hydride transfer (the Grotthuss mechanism is a proton transport mechanism in which a proton is passed onto a water molecule, but a different proton is passed on further in the next step – it makes proton transport the fastest ion transport in water). This could be checked in the calculation by following the evolution of the charge distribution, but unfortunately the theoretical paper16 does not comment on this.We learn from this example that the water molecule opens up a new reaction path by forming transient bonds to the catalyst. This is a typical way by which a catalyst reduces the activation energy.
The reaction was also studied theoretically for the case of two assisting water molecules, which permits the formation of an 8-membered ring in the transition state (not shown here). This led to a reduction of the activation energy by another 10 kJ mol−1,16 again in a Grotthuss type reaction.
(c) Solvation of the reactant, transition state (and products) by immersion in a solvent
Solvation can have a pronounced effect on the activation energy of a reaction. It may be debated whether this should be called catalysis, since a solvent is present abundantly and not in catalytic amounts. The mechanism of its interaction is nevertheless not fundamentally different from that of a catalyst that is present in small amounts. The principle is explained in more detail for the slightly different reaction of H abstraction from the formate ion by H: HCOO− + H → OCO− + H2 (Fig. 7).22 This system differs from the model reaction in two ways. (i) There is a net negative charge on the system. (ii) Formally, the attacking hydrogen atom has been cleaved off from the formic acid anion, which means that an activation energy corresponding to the bond energy was spent in a previous reaction step.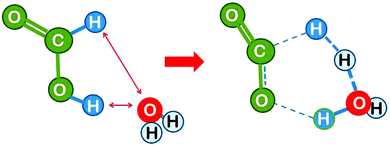 | ||
| Fig. 6 Formic acid reactant in cis conformation and transition state for dehydrogenation catalysed by a single water molecule (drawn based on ref. 16). | ||
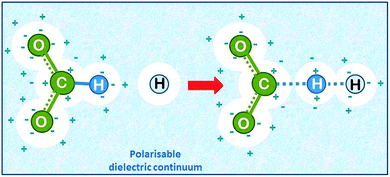 | ||
| Fig. 7 Hydrogen abstraction by atomic hydrogen from the formate ion in aqueous solution (drawn based on ref. 22). The solvent is added as a polarisable dielectric continuum (bluish) which has a cavity that matches the molecule (white spheres). The partial charges on the molecule induce opposite charges by polarising the solvent, which leads to energetic stabilisation. | ||
The kinetics of this reaction was studied for 6 combinations of the hydrogen isotopes D, H, and Mu (Muonium, Mu, is in a chemical sense an ultra-light isotope of hydrogen with a positive muon as a nucleus in place of a proton. Its mass is one-ninth of the mass of H23). The activation energies were found to be in the range 17.4–37.8 kJ mol−1. The differences are explained by the different zero-point vibrational energies of the isotopic variants.22
It came as a surprise that in marked contrast to the experimental finding even high level quantum chemical calculations predicted that the abstraction should occur with no barrier. The mystery was resolved when the solvent was added to the calculation as a continuum dielectric,24 and the calculation resulted in a transition state with 28.5 kJ mol−1 activation energy, in reasonable agreement with experiment. It should be noted that the ability of water to form hydrogen bonds is not taken into account in the polarised continuum model.
In this case, the solvent stabilises the reactant more than the transition state, which leads to an increase of the activation energy. This should perhaps be called “anti-catalysis”, but the mechanism is the same as for catalysis, and in other cases it could be the transition state which is more strongly solvated. Thus, for the last entry of Table 2 it was stated that water plays an indispensable role in the catalytic dehydrogenation of FA.21
A detailed inspection of the charge distribution along the reaction coordinate reveals further interesting insight (Fig. 8). When the approaching H atom is at a distance of >0.2 nm from the formate H the charge distribution is as expected: each of the oxygens carries nearly a full negative charge which is balanced to 50% by the positive charge at the carbon. The incoming H is neutral; the formate H is slightly negative, with a charge of −0.2 e. When the transition state is approached an amazing development sets in. The changes on the oxygens are not spectacular, but the incoming H acquires a large amount of negative charge. Up to 0.65 e is transferred at the cost of the formate H. Simultaneously, the positive charge on the carbon atom relaxes. Slightly beyond the transition state, at an H–H distance of 0.1 nm, the trend reverses in the expected direction of charge neutrality on the two hydrogens of the H2 product. The course of the reaction thus has to be described as a consecutive electron–proton transfer.
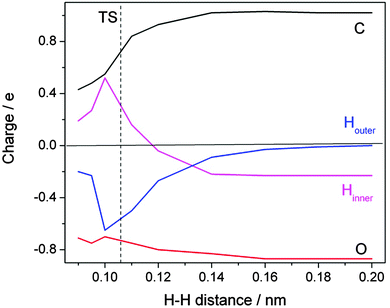 | ||
| Fig. 8 Evolution of calculated charge distribution along the reaction path for the hydrogen abstraction by atomic hydrogen from the formate ion in aqueous solution. The distance between the attacking (Houter, blue) and the abstracted (Hinner, magenta) hydrogen atoms is chosen to represent the reaction coordinate (redrawn based on ref. 22). | ||
This spectacular fluxionality of the electrons which leads to pronounced changes in charge polarisation is an important result of the calculation. Electrons find the optimum distribution to relax the system to the minimum energy at every point of the reaction coordinate and secure a low activation energy. Charge fluxionality is an essential feature of catalytic systems.
(d) Catalysis by a transition metal complex in a homogeneous solution
Our model reaction (2) in Table 1 was measured in homogeneous propylene carbonate and tetrahydrofuran solution using an iron(II) catalyst with a phosphorous coordinating tetradentate ligand.19 In such systems it is essential that the ligand coordination at the transition metal is incomplete in order to leave room for access of the substrate to the catalytic centre. A clear further reduction of the activation energy was observed compared with the previously discussed water catalysed systems. The reaction mechanism was investigated by high-pressure NMR spectroscopy and supported by quantum chemical calculations. Two competing reaction mechanisms were suggested to occur. The formate ion was thought to coordinate to the iron by one or both of its oxygens, and in both cases the rate-determining step consisted in a hydride elimination from the formate carbon. The reaction is discussed further at the end of Section 4.(e) Metal catalysis on a single crystal surface and on nanoparticles
The intact FA molecule chemisorbs weakly on Pd or Pt metal surfaces. However, there is a general agreement that HCOOH dissociates readily into surface-bound HCO2˙ and H˙. HCO2˙ adsorbs preferentially on large flat terrace sites in a bridge-bonded (bidentate) mode, as shown in Fig. 9a, where it is the precursor of CO2 formation.25 The CO2 product desorbs since it is only weakly chemisorbed. Alternatively, on unsaturated surface sites at small particles (adatoms, corner atoms, steps and kinks) which provide a higher binding energy it can bind in a linear fashion (monodentate, Fig. 9b). They lead preferentially to CO formation with strong bonding to most transition metals, and thus to catalyst poisoning.25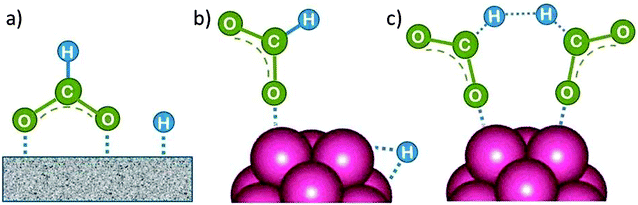 | ||
| Fig. 9 (a) First reaction intermediate of formic acid dehydrogenation on the surface of a single crystal (bidentate, bridged-bond), (b) on a nanocluster (monodentate, linear bond) metal catalyst. (c) While surface-bound H can recombine to form H2, hydrogen formation from the HCO2˙ fragment is suggested here to occur via a cyclic transition state, but other mechanisms have been considered as well.26 | ||
CO-free H2 production was found for a catalyst consisting of Au nanoparticles supported on SiO2.20 This is very attractive for applications to operate hydrogen fuel cells. The kinetics of HCOOH decay was of zero-order, i.e. the rate did not depend on the formic acid concentration. This means that under the conditions of investigation the catalyst operates at its full capacity because the substrate concentration is sufficiently high so that all available sites are active (compare production line work). The first step of FA decay, the dissociative adsorption to the state shown in Fig. 9b, is fast and does not influence the kinetics. The rate limiting step is thought to be the dissociation of the C–H bond, but the mechanism of this is not known in detail. While the surface-bound H atoms are mobile and can recombine to undergo activated desorption it is conceivable that a significant coverage of HCO2˙ fragments builds up on the metal surface. If two of these fragments come into close proximity as e.g. in the configuration suggested in Fig. 9c, the two H atoms may recombine to H2, leaving two CO2 molecules which will readily desorb. Aiming at a detailed understanding of the reaction mechanism, a large number of theoretical calculations have been carried out which model the reaction on various metal and metal oxide surfaces, and for various sites. A recent overview gives an impression of the complexity of this effort.26
With a TOF reaching 1.38 × 106 s−1 and an apparent activation energy of 22(1) kJ mol−1, monodisperse 2.2 nm AgPd nanoparticles with 42% Ag and 58% Pd show the best catalytic performance ever reported for the FA dehydrogenation reaction among all heterogeneous catalysts tested in aqueous solutions.20 Note the dramatic reduction of the activation energy which is partly compensated by a low pre-exponential factor (see Section 4).
It is instructive to look at more details about hydrogen adsorption. We will do it for the examples of a Pt(111) surface and a zeolite-supported Pt13 cluster. H2 chemisorbs dissociatively on a Pt surface. In order to do this spontaneously, the binding energy of the two H atoms to Pt must exceed the H–H binding energy of 436 kJ mol−1. The desorption energy of H2 from Pt(111) which amounts to 0.8 eV (77 kJ mol−1) represents this excess energy. Thus, the binding energy of each of the H atoms is ½(436 + 77) kJ mol−1, or 256 kJ mol−1, which is a respectable chemical bond. For the Pt13 clusters in KL zeolite this is even more impressive:27 from the 2.1 eV desorption energy we obtain a Pt–H bond energy of 319 kJ mol−1. The example demonstrates the necessary strength of interactions if bonds are to be dissociated, but we emphasise that full initial dissociation is not necessary for catalysis to occur when the new bonds can begin to form before the old bond is broken. On another point, strongly adsorbed species, even the seemingly innocent chemisorbed hydrogen in the above Pt13 cluster, can successfully block the surface so that catalysis is inhibited, as for example in the reaction with O2.27
It is commonly expected that the efficiency of a nanoparticle catalyst increases with decreasing particle size because the binding energy to the smaller particles is higher.6 In the case of the Au/SiO2 catalyst no such dependence was found.20 The effect will be discussed further below in context of Fig. 11. However, as expected, the turnover frequency (TOF, the number of molecules reacted per active centre and per unit time, a common measure of the efficiency) increases with temperature, and the activation energy determined for H2 production amounted to 58.5 kJ mol−1.20
(4) Reversibility of and compensation effect in catalytic reactions
The question is whether a catalyst that catalyses a reaction (e.g. the dehydrogenation of FA, reaction (2) of Table 1) will also catalyse the reverse reaction, the hydrogenation of CO2 to FA. Since the potential energy surface does not depend on the direction of the reaction the answer is a conditional yes. Provided that the catalyst can catalyse the forward and the backward reaction, both reactions follow the same minimum energy path and go through the same transition state. Thus the activation energy of the backward reaction will be reduced by the same amount as that of the forward reaction. The equilibrium constant equals the ratio of the rate constants of the forward and the backward reaction, and in this ratio all information about the transition state is lost. Thus, thermodynamics tells that the activation energy of the back reaction of (2) will exceed that of the forward reaction by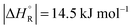 (Table 1).
(Table 1).
Certain catalysts can indeed catalyse both, the forward and the backward reaction. This is the case for example for electrochemical hydrogen oxidation to water and water reduction in electrolysis, but unfortunately, catalysts are often one-way workers. They can bind and activate a reactant, but they have to release the product which is the reactant for the reverse reaction. Thus, FA in our model reaction (2) is much easier to activate than the product CO2 which is difficult to activate since it binds to many catalysts only by van der Waals forces or weak chemical bonds. Therefore, a different catalyst has to be found for the back reaction. It should nevertheless be noted that the hydrogen-dependent carbon dioxide reductase is a reversible enzyme: it can reduce CO2 with H2 to FA, and it can also dehydrogenate FA.28
The above statement about reversibility does not mean that the rate constant of the backward reaction is (almost) the same as that of the forward reaction since also the pre-exponential factor plays a crucial role. On the basis of Eyring's absolute rate theory (transition state theory) for homogeneous kinetics the rate constant of the forward reaction, assuming that the rate determining step is unimolecular, is:29
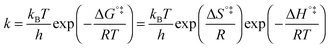 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k)/∂T, one obtains the activation energy, Ea = ΔH°‡ + RT, and the pre-exponential factor, ln(ekBT/h) + ΔS°‡/R, where e is Euler's number, 2.718.29ekBT/h is called the universal pre-exponential factor. It equals the Arrhenius pre-exponential factor for unimolecular reactions in the absence of any activation entropy and assumes a value of 1.70 × 1013 s−1 at 300 K.
k)/∂T, one obtains the activation energy, Ea = ΔH°‡ + RT, and the pre-exponential factor, ln(ekBT/h) + ΔS°‡/R, where e is Euler's number, 2.718.29ekBT/h is called the universal pre-exponential factor. It equals the Arrhenius pre-exponential factor for unimolecular reactions in the absence of any activation entropy and assumes a value of 1.70 × 1013 s−1 at 300 K.
If the rate-determining step is bimolecular, as in the backward reaction (indicated by a bar above the parameter symbol), the rate constant is:
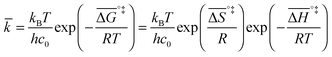 | (7) |
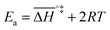 , and the pre-exponential factor,
, and the pre-exponential factor, 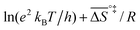 .29
.29
It is helpful to break catalytic reactions down into an adsorption step of the substrate (S) onto the empty catalyst sites (Cat) upon formation of the adsorbed state (SCat) followed by the catalytic elementary reaction to product (P):
| S + Cat ⇌ SCat → P + Cat | (8) |
The first part of eqn (8) corresponds to an adsorption pre-equilibrium characterised by an equilibrium constant KA (index ‘A’ for adsorption) with its thermodynamic parameters
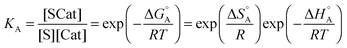 | (9) |
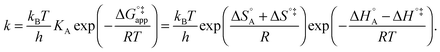 | (10) |
In eqn (6) and (7) we have tacitly assumed that the activation free energy, enthalpy and entropy represent their true values for the elementary catalytic reaction, although the experimental Arrhenius parameters represent at first apparent (or effective) values. When we include an adsorption equilibrium we understand from eqn (10) that the experimental apparent activation energy 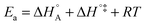 includes not only the true activation enthalpy but also the reaction enthalpy of the adsorption pre-equilibrium. In the same sense the pre-exponential factor,
includes not only the true activation enthalpy but also the reaction enthalpy of the adsorption pre-equilibrium. In the same sense the pre-exponential factor, 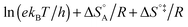 , contains the adsorption entropy. Since the adsorption enthalpy and entropy are both negative the adsorption pre-equilibrium decreases both, the apparent Arrhenius activation energy and the corresponding pre-exponential factor. Fig. 10 explains the influence of the adsorption enthalpy ΔHA on the apparent activation energy Eapp.
, contains the adsorption entropy. Since the adsorption enthalpy and entropy are both negative the adsorption pre-equilibrium decreases both, the apparent Arrhenius activation energy and the corresponding pre-exponential factor. Fig. 10 explains the influence of the adsorption enthalpy ΔHA on the apparent activation energy Eapp.
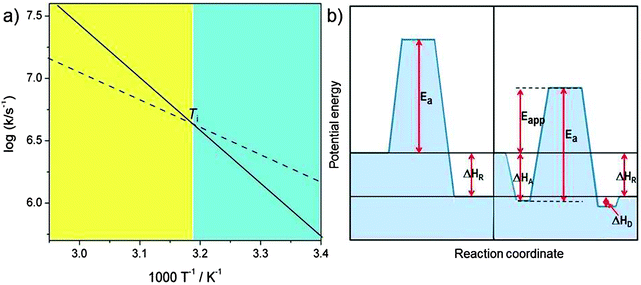 | ||
| Fig. 10 Schematic visualisation of the effect of an adsorption pre-equilibrium with adsorption enthalpy ΔHA. (a) The Arrhenius plot for the elementary catalytic reaction step with true activation energy Ea (solid line, corresponding to the left part of (b)) and the compensation effect with reduced Arrhenius pre-exponential factor and apparent activation energy Eapp = Ea − |ΔHA| (broken line, corresponding to the right side of (b)). The two curves in the Arrhenius plot cross at the isokinetic temperature Ti = ΔHA/ΔSA (ΔGA = 0). For T < Ti (blue shaded regime) the pre-equilibrium augments the rate constant because the adsorbed state is populated, for T > Ti (yellow shaded regime) entropy prevents significant adsorption (figure inspired from ref. 30). | ||
The extent of coverage of active sites, [SCat]/[Cat] = KA[S], plays an important role (this is to be distinguished from the often used fractional coverage, θ = [SCat]/([Cat] + [SCat]) which derives from the Langmuir equation for chemisorption). First of all, the sites should not be blocked (poisoned) by a molecule other than the substrate that should be converted. Under these premises, a value of KA[S] ≫ 1 means that all available active sites of the catalyst are busy doing catalysis on a bound substrate. This can be achieved by sufficiently high substrate concentration [S]. The reaction rate then saturates at its maximum value, i.e. it is independent of the concentration of substrate, the reaction is of zero-order with respect to [S] and its concentration decreases linearly with time (the catalyst works at its maximum capacity). In such a case, the Arrhenius parameters depend no longer on small changes in KA[S] and the activation energy approaches its true value. In contrast, for KA[S] ≪1, the rate becomes proportional to [S] and the kinetics is of first order and exhibits the maximum compensation effect. Real systems represent often intermediate cases, and it is not unusual to observe non-integer order of catalytic reactions. All aspects of this often intriguing compensation effect were reviewed competently by Bond et al.30
We are familiar with the fact that the molar entropy increases with the volume that is occupied by the molecules, i.e. it decreases with concentration. Eqn (9) links the concentrations (or partial pressures) with the adsorption entropy, 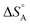 , which in turn has a large influence on the rate constant (eqn (10)) of the reaction via the apparent Arrhenius pre-exponential factor (reaction rates are of course always pressure- or concentration-dependent, but here the rate constant becomes dependent). A gas phase reactant has high entropy due to its free translational and rotational motion. Upon adsorption, this entropy is lost to a large extent, which can reduce the pre-exponential factor by many orders of magnitude. Gas phase reactions are therefore affected more than liquid phase reactions by the entropy loss on adsorption, and they show the largest compensation effect.
, which in turn has a large influence on the rate constant (eqn (10)) of the reaction via the apparent Arrhenius pre-exponential factor (reaction rates are of course always pressure- or concentration-dependent, but here the rate constant becomes dependent). A gas phase reactant has high entropy due to its free translational and rotational motion. Upon adsorption, this entropy is lost to a large extent, which can reduce the pre-exponential factor by many orders of magnitude. Gas phase reactions are therefore affected more than liquid phase reactions by the entropy loss on adsorption, and they show the largest compensation effect.
In this context it is instructive to comment on the specific effects on Arrhenius parameters of FA dehydrogenation on iron catalysts (see Table 2). Log(A/s−1) assumes values of 12.15 and 12.5 for the two solvents. This is barely one log unit below its theoretical entropy-neutral value of 13.2. The experiments were carried out in the presence of a large excess of substrate compared with catalyst concentration. It may therefore be assumed that one has KA[S] ≫1 and the catalyst is working at its maximum rate. This means that the Arrhenius parameters correspond to their true values. The pre-exponential factor is then compatible with a small value of the activation entropy, ΔS°‡ = 2.303 R (the factor 2.303 arises from the conversion between natural and decadic logarithm). This reflects mostly some steric strain in the transition state but should be free of adsorption entropy which is part of the (saturated) adsorption equilibrium but not of the rate-determining elementary catalytic step.
Note that the kinetic scheme as given in eqn (8) is formally identical to the one derived more than 100 years ago by Victor Henry for enzyme catalysis, today well-known as Michaelis–Menten kinetics.31 Enzymatic systems are characterised by the Michaelis constant KM, which is an enzyme–substrate complex decay constant (and it includes the decay to the catalytic product) in contrast to the above KA which is an adsorption complex formation constant. An extension of eqn (8) takes into account competitive inhibition of the kinetic activity when a non-reactive substrate blocks the active site. The same effect is known in heterogeneous catalysis under catalyst poisoning. It should provide useful to adapt the methods developed for the analysis of enzyme kinetics to other catalytic processes.
(5) Sabatier's principle of optimum adsorption
Heterogeneous catalytic processes consist of three steps: (i) adsorption of the substrate on the catalyst, (ii) the catalytic reaction (itself often a sequence of catalytic steps), and (iii) desorption of the products. After desorption, the catalyst is found in the same state as before adsorption and ready to assist the next catalytic transformation. Ideally, it can catalyse thousands of subsequent transformations, called catalytic cycles. Mechanisms in which the catalyst is not recycled are not catalytic.A very important relation dates back to the French chemist Paul Sabatier. It is demonstrated by the volcano plot in Fig. 11 and states that if the adsorption energy of the substrate (in Fig. 11 approximated by the heat of formation of the formate salt) is too low then the catalytic activity is low. If it is too large then the product will not desorb and block the surface, leading to catalyst poisoning.
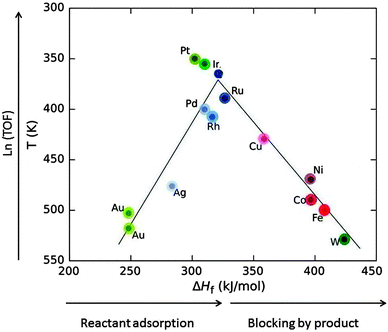 | ||
| Fig. 11 Volcano plot: the decomposition temperature at a specific rate (or the logarithm of turnover frequency, TOF) as a function of the heat of formation of transition metal formate salt show maximum activity at intermediate ΔHf values. Roughly, ΔHf increases in going from the right to the left in the periodic table (indicated by the saturation of the colour) for elements of the 4th (red), 5th (blue) and 6th group (green) (drawn based on data from ref. 34). | ||
Low coordinated (partly unsaturated) atoms like adatoms on surfaces or atoms at kinks, edges and corners generally provide a better bonding to substrates. Nanomaterials provide a larger fraction of such atoms. For this reason, and also because metal nanoparticles have an electronic structure with ionisation potential and electron affinity in between those of individual atoms and bulk metal, nanoparticles show catalytic activity different from that of the surfaces of bulk material, and it can be tuned by the particle size.32 For example, bulk gold is noble and therefore very suitable for jewellery because it does not tarnish. Being noble is equivalent to being unreactive. Bulk gold is therefore a bad catalyst. Gold nanoparticles have a quite different electronic structure with an ionisation potential and an electron affinity shifting by up to a few eV to values between those of gold atoms and bulk gold.6 These properties control bond formation. It was a considerable surprise at first when it was found that gold nanoparticles are excellent catalysts for a range of reactions.32,33 In Fig. 11, Au is listed as a bad catalyst, but for the work reported in Section 3, FA decomposition catalysed by Au nanoparticles of a size range of 1.9–6.5 nm had an onset temperature of 373 K, right near the top of the volcano. In this range it is understandable that no significant size-dependence was found since there is competition between the inclining and the declining slope of the volcano. For platinum which is an excellent catalyst for many reactions several cases are known where the activity decreases with decreasing particle size.32
(6) The importance of flexibility: continuous energy optimisation along the reaction path
A catalyst interacts with a reactant molecule by forming an adsorption complex with a transient bond. Thereby it polarises the molecule, i.e. it changes the electron distribution in a way that favours the formation of new bonds by holding molecules or molecular fragments in close proximity and perhaps in a special relative orientation until the reaction has succeeded. It also helps the breaking of existing bonds. Adsorption is one thing, but it is often not the complete story. Along the reaction path, the bond strengths and therefore the electron density distribution change. These changes are supported by flexible alterations of the local catalyst geometry, facilitated by low frequency vibrations. Edges, kinks and corners of crystals or clusters and catalyst surfaces with a rich variety of defects provide the necessary flexibility for energy lowering.3 Clusters of atoms with often variable shapes or the irregular surfaces of most nanoparticles which restructure continuously to adapt to the adsorbates are therefore often much more efficient catalysts than the rigid single crystal surfaces (Fig. 12). The highest flexibility will be found for clusters or small, amorphous nanoparticles near their stability limit, which may often lead to the highest catalytic activity. Also for enzymes which are soft structure protein catalysts, flexibility of the active site has been recognised as an essential requirement for their catalytic function.35The following description may further illuminate the catalytic process on a molecular level. The catalyst can lower the energy of a transition state in the same way as a quantum chemical calculation does: it performs a geometry optimisation at each point along the reaction coordinate. This means that the system moves the electrons and the atoms around to find the most stable geometry. Even the presence of a simple catalyst like an ion or a single crystal surface provides more options (more degrees of freedom) for geometry relaxation than in the isolated reactant. However, if the nearby environment of the catalytic binding site is also flexible this further increases the possible success of energy minimisation.
The high significance of the effect may be further illustrated by theoretical work which showed that the dissociation energy of CO adsorbed on a Ru(0001) single crystal surface changes as much as 30 kJ mol−1 when the Ru lattice constant is modulated by ±1.5%.36
The above discussion is related to the activation energy. However, the activation entropy, ΔS°‡ in eqn (2), is often of equal if not higher importance. It is dominated by the fact that the reactant loses a large fraction of its entropy which is due to the translational and rotational degrees of freedom when it gets immobilised by adsorption on the surface of a solid catalyst. A well-documented example is that of CO adsorption on 14 different surfaces for which it was shown that 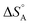 varies between −84 and −152 J mol−1 K−1 at 303 K,37 corresponding to 42–76% of the standard entropy of CO of 197.7 J mol−1 K−1 (of which 150 J mol−1 K−1 is of translational origin) and revealing considerable residual dynamics of the adsorbate. In the same set the chemisorption energy varies between 38 and 83 kJ mol−1, showing a somewhat scattered anti-correlation with
varies between −84 and −152 J mol−1 K−1 at 303 K,37 corresponding to 42–76% of the standard entropy of CO of 197.7 J mol−1 K−1 (of which 150 J mol−1 K−1 is of translational origin) and revealing considerable residual dynamics of the adsorbate. In the same set the chemisorption energy varies between 38 and 83 kJ mol−1, showing a somewhat scattered anti-correlation with 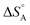 . This entropic aspect of adsorbate flexibility is often overlooked in catalysis, in particular in theoretical work, perhaps because it is non-trivial to calculate.
. This entropic aspect of adsorbate flexibility is often overlooked in catalysis, in particular in theoretical work, perhaps because it is non-trivial to calculate.
(7) The Schottky effect in supported metal catalysts
Metal particles prepared in the same way on different support materials do not always show the same catalytic performance. A pronounced dependence of the electronic properties and the catalytic behaviour of noble metal particles on the acid–base property of the support suggest that a support does more than just supporting a catalyst particle. Since it is not easy to separate support effects from those of all the other sources they have only relatively recently become a subject of systematic investigations.The supporting oxides are often not fully stoichiometric. Defects, in particular those related to hydrogen, for example HO− in place of O2−, turn an insulator into a superconductor. The interface between a metal and a superconductor is called a Schottky contact. Since the two materials have their highest energy electrons at different energy this leads to partial charge transfer across the junction. The polarisation of the catalyst that arises from this transfer promotes or impedes the ease of charge transfer to the adsorbed substrate and in this way affects the catalytic properties in an analogous way as a bias voltage does in electrochemical reactions (see Section 9). The effect is schematically shown in Fig. 13 for the example of TiO2. A more detailed explanation of the effect is given elsewhere.32
 | ||
| Fig. 13 (left) The most common and almost unavoidable impurity in TiO2 is HO−, which leads to additional charge-compensating electrons at neighbouring Ti atoms, energetically in levels located below the conduction band (CB). These donor state electrons can transfer to the partially filled valence band (VB) of the metallic catalyst particle, here Pt, leading to a charge polarised interface as is well-known for Schottky contacts in semiconductor physics. It is expected that this affects strongly the catalytic properties. (right) For the case of acceptor doping, or when surface-adsorbed O2 binds an electron upon formation of O2−˙, the charge polarization can be reversed. This is actually the experimentally observed case38 (figure reproduced from ref. 32). | ||
(8) Shape selectivity in zeolite pores and in enzymes
Zeolites are crystalline porous alumino-silicates. The pore diameter depends on the structure, but typically it is comparable with the cross section of molecules. Smaller molecules can enter whereas larger ones are sieved out. The zeolites are therefore also called molecular sieves. The pores can host catalytic centres such as Brønsted acid sites, transition metal ions, or metal clusters. Zeolites are widely used as adsorbents, ion exchange materials and as catalysts, in particular in the petrochemical industry. More than 200 unique framework structures have been identified, and about 40 of them occur naturally.Aluminium is incorporated in the zeolite framework, replacing silicon in tetrahedrally coordinated bond configuration. In order to make four bonds, Al needs an additional electron. The framework therefore bears negative charge that is balanced by cations which are not incorporated in the framework of bonds and therefore readily exchangeable. H+ exchange leads to Brønsted acid sites which are highly active in alkylation and isomerisation reactions. Interestingly, the reaction products do not occur in their thermodynamic equilibrium distribution even though the reactions are carried out at high temperature. This is ascribed to the shape selectivity which is imposed on the reactants, transition states and products as proposed first by Csicsery.39 The principle is shown schematically in Fig. 14.
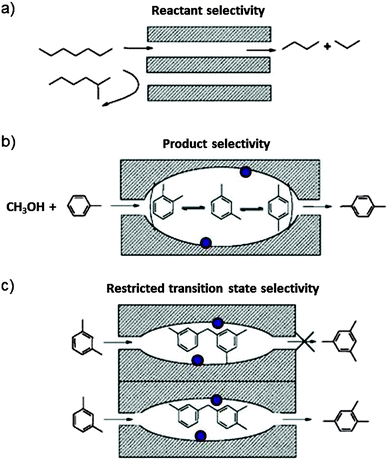 | ||
| Fig. 14 Schematic representation of shape-selectivity in the pores of zeolite molecular sieves. (a) Reactant selectivity: the pore opening transmits reactants which have a sufficiently narrow kinetic diameter and sieves out the bulkier ones. (b) Product selectivity: only products which are sufficiently slim can leave the zeolite cage reactor. The others are further catalytically rearranged until they can exit. (c) Transition state selectivity: the shape of the cage imposes constraints on the steric demand of possible products. The purple bullets indicate possible catalytic centres on the cage wall surface (reproduced from ref. 39 with permission from Elsevier). | ||
It is shown in Fig. 1 that reactions involving the carbon pool mechanism also lead to an undesired mixture of carbonaceous species with low H/C ratio, called coke. This soot-like deposit can block pores. A few such coke particles can completely block and deactivate a one-dimensional pore (compare Fig. 14a). Zeolites with three-dimensional pore architecture are much less susceptible to deactivation since one coke particle can block only one junction of the network of pores and access remains possible via other routes. Coked catalysts can be regenerated by heating in air, which burns the coke away and provides free access to all active centres again.
Enzymes are catalysts which are found in living organisms. The scientific community that deals with enzymes is quite different from the one that uses zeolites, and it uses a different language. In the sense of a unified approach it may nevertheless be fruitful to compare the two catalysts to perhaps learn from common principles. We have seen in Section 4 that the kinetics of solid catalysts is explained by essentially the same equations as enzyme kinetics. Enzymes exhibit very high shape selectivity. The binding pockets of enzymes which contain the catalytic centre permit highly restricted access to selected substrate molecules or even stereoisomers which are then activated at specific positions due to the fixed substrate orientation relative to the catalytic centre. In the concept of Fig. 14 the access of the substrate to the active site in the enzyme is reactant selectivity, and its transformation is transition state selectivity. In this sense, zeolites could be understood as rigid variants of enzymes for high temperature industrial use.
(9) What can electrocatalysts do more than a normal catalyst?
Spontaneous chemical reactions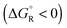 can be carried out in an electrochemical cell if they involve an oxidation (anode reaction) and a reduction (cathode reaction) by exchanging electrons across the surface of suitable electrodes. This has the advantage that the reaction free enthalpy (in real systems part of it) is obtained in the form of the preferred electrical energy instead of heat. Alternatively, a reaction that is non-spontaneous
can be carried out in an electrochemical cell if they involve an oxidation (anode reaction) and a reduction (cathode reaction) by exchanging electrons across the surface of suitable electrodes. This has the advantage that the reaction free enthalpy (in real systems part of it) is obtained in the form of the preferred electrical energy instead of heat. Alternatively, a reaction that is non-spontaneous 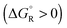 can be enforced by application of electrical energy.
can be enforced by application of electrical energy.
Many electrochemical reactions are carried out in conventional cells inspired from the original setup used by Galvani with the two electrodes separated by one or several centimetres. For investigations of equilibrium properties in the absence of a current this is fine. However, from fuel cells or electrolysis cells we learn that for energy applications with current densities of 1 A cm2 and more it is essential that the internal Ohmic resistance (which under current produces Joulean heat and leads to significant voltage loss) is minimised, requiring that the separation of the electrodes is small, realistically on the order of 50 μm. This is realised in a setup where the cathode and the anode catalysts are applied directly onto the opposite sides of a polymer electrolyte membrane, as shown in Fig. 15a.
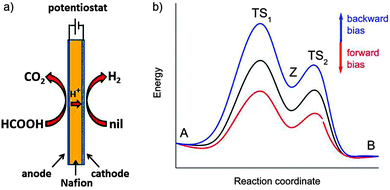
From Table 1 we see that the decomposition of formic acid is spontaneous. Nevertheless, we know that it is stable on the shelf because this reaction is highly activated (Table 2). Fig. 15 shows how the reaction can be conducted electrochemically to yield H2 and CO2. This reaction is called “electro-reforming”. It is analogous to water electrolysis in the sense that H2 is formed at the cathode under anaerobic conditions, while the anode is fuelled by a single compound, here HCOOH in place of H2O. Since the reaction is spontaneous an electrochemical setup is in principle not necessary. Suitable catalysts are currently being developed,19,40 but are not yet available with sufficiently high turnover frequencies. So is there an advantage of an electrochemical setup when there is no reactant necessary to fuel the cathode? Yes, there is: the applied voltage can polarise the formic acid molecule adsorbed at the anode and essentially pull off two electrons according to the reaction scheme:
| Anode: HCOOH(l) → CO2(g) + 2H+ + 2e− | (11) |
| Cathode: 2H+ + 2e− → H2(g) | (12) |
The total reaction is spontaneous, as reflected by 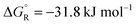 (eqn (4) in Table 1), which corresponds to a cell potential of +0.16 V for standard state conditions. Since two electrons are transferred the reaction occurs in two steps with an adsorbed radical intermediate, Z = HCOO˙. The applied voltage influences all electrode-adsorbed species. In particular, the energy of the intermediate and thus also of the transitions states, TS1 and TS2, can be lowered by application of a forward bias voltage, but if the anode catalyst is too active the bias voltage can be reversed so that the reaction is slowed down (Fig. 15b). Thus, the setup is suited to provide H2 on demand.
(eqn (4) in Table 1), which corresponds to a cell potential of +0.16 V for standard state conditions. Since two electrons are transferred the reaction occurs in two steps with an adsorbed radical intermediate, Z = HCOO˙. The applied voltage influences all electrode-adsorbed species. In particular, the energy of the intermediate and thus also of the transitions states, TS1 and TS2, can be lowered by application of a forward bias voltage, but if the anode catalyst is too active the bias voltage can be reversed so that the reaction is slowed down (Fig. 15b). Thus, the setup is suited to provide H2 on demand.
The computational hydrogen electrode model gives the free enthalpy change with the applied bias voltage U quantitatively as a linear function of n, the number of electron–proton pairs that have been transferred relative to the reactant:41
| ΔGn = ΔGn(U = 0) + n·e·U. | (13) |
e is the (positive) electron charge. Thus, for n = 1, an applied bias voltage of −100 mV corresponds to ΔG1 = −9.6 kJ mol−1. For transition states, half-integer numbers of n may be used in a first approximation. The method of applying a voltage finds its limitation in the free energy of intermediates and in particular of the adsorbed product which should not be shifted to values significantly below the free energy of the desorbed product, otherwise the reaction stops and the electrode gets blocked by undesorbed intermediates or products.
The electro-reforming reaction of aqueous solutions of formic acid was studied using a commercial electrochemical cell (a direct methanol demonstration cell).42 Upon increasing the applied voltage, an onset of current indicative of H2 formation was observed at 220 mV at room temperature, and a current density of 100 mA cm−2 was reached at 400 mV. This is not quite good enough for practical applications, but development of better catalysts will permit electro-reforming of both, methanol or formic acid, on-board of cars for use in hydrogen fuel cells.43
(10) Concluding remarks
Catalysis is in many aspects a more complex issue than presented here where only a number of fundamental principles are outlined. First of all, complexity comes with the reaction mechanism which sometimes offers competing pathways with multiple products and often consists of more steps than in the examples considered in this tutorial. Secondly, catalytic surfaces are often inhomogeneous, which leads to a blurred picture that makes it difficult to identify the main active sites. Moreover, we have concentrated on the decay of an individual reactant molecule. Catalysis of reactions with two reactants, as in the back reaction of the formic acid decay or in CO oxidation, 2CO + O2 → 2CO2, is more complex since one or both reactants may be bound to and activated by the catalyst to find together in the proper geometry. Although the compensation effect discussed in Section 4 is very common in heterogeneous catalysis, its characteristics may be somewhat different from that given in Fig. 10, and a number of alternative explanations have been reported.30 Finally, metal particles of different size behave quite differently,27,30,44 and there is a variety of catalyst–support effects which are in real systems often difficult to separate.References
- G. Ertl, Angew. Chem., Int. Ed., 2009, 48, 6600–6606 CrossRef CAS PubMed
.
- R. T. Vang, E. Lægsgaard and F. Besenbacher, Phys. Chem. Chem. Phys., 2007, 9, 3460–3469 RSC
.
- G. A. Somorjai, Langmuir, 1991, 7, 3176–3182 CrossRef CAS
.
- Themed issue: recent advances in the in-situ characterization of heterogeneous catalysts, ed. B. M. Weckhuysen, Chem. Soc. Rev. 2010, 9, 4557 ff.
- E. de Smit, I. Swart, J. F. Creemer, G. H. Hoveling, M. K. Gilles, T. Tyliszczak, P. J. Kooyman, H. W. Zandbergen, C. Morin, B. M. Weckhuysen and F. M. F. de Groot, Nature, 2008, 456, 222–225 CrossRef CAS PubMed
.
- E. Roduner, Chem. Soc. Rev., 2006, 35, 583–592 RSC
.
- I. M. Dahl and S. Kolboe, Catal. Lett., 1993, 20, 329–336 CrossRef CAS
.
-
In-situ Spectroscopy of Catalysts, ed. B. M. Weckhuysen, American Scientific Publishers, Stevenson Ranch, California, 2004, pp. 177–218 Search PubMed
.
- W. Wang, Y. Jiang and M. Hunger, Catal. Today, 2006, 113, 102–114 CrossRef CAS PubMed
.
- A. B. Ene, T. Archipov and E. Roduner, J. Phys. Chem. C, 2010, 115, 14571–14578 Search PubMed
.
- B. M. Weckhuysen, Phys. Chem. Chem. Phys., 2003, 5, 1–9 RSC
.
- S. Santra, H. Stoll and G. Rauhut, Phys. Chem. Chem. Phys., 2010, 12, 6345–6351 RSC
.
- A. Tabler, A. Häusser and E. Roduner, J. Mol. Catal. A: Chem., 2013, 379, 139–145 CrossRef CAS PubMed
.
- Data based on the NIST library: http://webbook.nist.gov/chemistry/.
- P. G. Blake, H. H. Davies and G. E. Jackson, J. Chem. Soc. B, 1971, 1923–1925 RSC
.
- N. Akyia and P. E. Savage, AIChE J., 1998, 44, 405–415 CrossRef
.
- T. B. Brill, J. W. Schoppelrei, P. G. Maiella and A. Belsky, Proc. 2nd Int. Conf. Solvotherm. Reactions, Committee of Solvothermal Technol. Res., Takamatsu, Kagawa, Japan, 1996, pp. 5–8.
- J. Yu and P. E. Savage, Ind. Eng. Chem. Res., 1998, 37, 2–10 CrossRef CAS
.
- A. Bodien, D. Mellmann, F. Gärtner, R. Jackstell, H. Junge, P. J. Dyson, G. Laurenczy, R. Ludwig and M. Beller, Science, 2011, 333, 1733–1736 CrossRef PubMed
.
- A. Gazsi, T. Básági and F. Solymosi, J. Phys. Chem. C, 2011, 115, 15459–15466 CAS
.
- S. Zhang, Ö. Metin, D. Su and S. Sun, Angew. Chem., Int. Ed., 2013, 52, 3681–3684 CrossRef CAS PubMed
.
- A. M. Lossack, E. Roduner and D. M. Bartels, Phys. Chem. Chem. Phys., 2001, 3, 2031–2037 RSC
.
-
E. Roduner, Muonium – an ultra-light isotope of hydrogen, in Isotope Effects in Chemistry and Biology, ed. A. Kohen and H.-H. Limbach, Taylor & Francis, Boca Raton, 2005 Search PubMed
.
- E. Cances, B. Mennuci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef CAS PubMed
.
- K. Tedsree, T. Li, S. Jones, C. W. A. Chan, K. M. K. Yu, P. A. J. Bagot, E. A. Marquis, G. D. W. Smith and S. C. E. Tsang, Nat. Nanotechnol., 2011, 6, 302–307 CrossRef CAS PubMed
.
- Q. Luo, M. Beller and H. Jiao, J. Theor. Comput. Chem., 2013, 12, 1330001 CrossRef
.
- C. Jensen, J. van Slageren, P. Jakes, R.-A. Eichel and E. Roduner, J. Phys. Chem. C, 2013, 117, 22732–22745 CAS
.
- K. Schuchmann and V. M. Iler, Science, 2013, 342, 1382–1385 CrossRef CAS PubMed
.
-
S. W. Benson, Thermochemical Kinetics: Methods for the Estimation of Thermochemical Data and Rate Parameters, John Wiley & Sons, New York, 2nd edn, 1973 Search PubMed
.
- G. C. Bond, M. A. Keane, H. Kral and J. A. Lercher, Catal. Rev.: Sci. Eng., 2000, 42, 323–383 CAS
.
- L. Michaelis, M. L. Menten, K. A. Johnson and R. S. Goody, Biochemistry, 2011, 50, 8264–8269 CrossRef PubMed
.
-
E. Roduner, Nanoscopic Materials: Size-Dependent Phenomena and Growth Principles, Royal Society of Chemistry, Cambridge, 2nd edn, 2014 Search PubMed
.
- M. Haruta, Gold Bull., 2004, 37, 27–36 CrossRef CAS
.
-
H. Knözinger and K. Kochloefl, Heterogeneous Catalysis and Solid Catalysts, Ullman's Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim, 2003 Search PubMed
.
- M. Kokkinidis, N. M. Glykos and V. E. Fadouloglou, Adv. Protein Chem. Struct. Biol., 2012, 87, 181–218 CAS
.
- B. Mavrikakis, B. Hammer and J. K. Nørskov, Phys. Rev. Lett., 1998, 81, 2819–2822 CrossRef
.
- X. Xia, R. Naumann d'Alnoncourt and M. Muhler, J. Therm. Anal. Calorim., 2008, 91, 167–172 CrossRef CAS PubMed
.
-
T. Kittel, PhD thesis, University of Stuttgart, 2014
.
- S. M. Csicsery, Zeolites, 1984, 4, 202–213 CrossRef CAS
.
- Y. Himeda, Green Chem., 2009, 11, 2018–2022 RSC
.
- A. A. Peterson, F. Abild-Peterson, F. Studt, J. Rossmeisl and J. K. Nørskov, Energy Environ. Sci., 2010, 3, 1311–1315 CAS
.
-
T. Bach, Diploma thesis, University of Stuttgart, 2012
.
- D. Poetzsch, T. Bach, J. E. Zerpa Unda and E. Roduner, Fuel Cells, 2014, 14, 508–516 CrossRef CAS
.
- N. V. Long, Y. Yong, C. M. Thi, Y. Cao, N. V. Minh and M. Nogami, Nano Energy, 2013, 2, 636–676 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cs00210e |
| This journal is © The Royal Society of Chemistry 2014 |