Machine learning enabled exploration of multicomponent metal oxides for catalyzing oxygen reduction in alkaline media

Abstract

Low-cost metal oxides have emerged as promising candidates used as electrocatalysts for the oxygen reduction reaction (ORR) due to their remarkable stability under oxidizing conditions, particularly in alkaline media. Recent studies suggest that multicomponent metal oxides, with their intricate compositions and synergistic effects, may outperform their single-metal oxide counterparts. However, exploring the considerable number of potential combinations of multicomponent metal oxides using experiments would be time- and cost-intensive. Herein, we analyzed 7798 distinct metal oxide ORR catalysts from previous high-throughput experiments, which included metal elements such as Ni, Fe, Mn, Mg, Ca, La, Y, and In. These catalysts were tested at different potentials, specifically 0.8 and 0.63 V vs. reversible hydrogen electrode (V_RHE). After feature engineering, we employed the XGBoost method to build the machine learning model and mapped the performance of unexplored compositions. Feature explanations suggested that for achieving high current density, attention should be paid to a high number of itinerant electrons (interant electron) and high configuration entropy. Finally, we identified promising regions within 15 different ternary metal oxides with higher catalytic activities for catalyzing the ORR at 0.8 and 0.63 V_RHE, respectively. We found that for the current density at 0.8 V_RHE, the ternary systems Mn–Ca–La, Mn–Ca–Y, and Mn–Mg–Ca show promising potential for further investigations, in particular for hydrogen fuel cells. Similarly, for the current density at 0.63 V_RHE, the Mn–Fe–X (X = Ni, La, Ca, and Y) and Mn–Ni–X (X = Ca, Mg, La, and Y) systems deserve close attention in the future, as they may contribute to the production of hydrogen peroxide (H₂O₂) as a commodity. This study highlights the significant potential of artificial intelligence in accelerating catalyst design and materials discovery, thereby paving the way for future advancements in sustainable energy technologies.

---

Xue Jia

Xue Jia is currently an Assistant Professor at the Advanced Institute for Materials Research, Tohoku University, Japan (2022–now). She received her PhD degree in materials science from Harbin Institute of Technology, Shenzhen, China (2018–2022), and her MS degree in materials engineering from Harbin Institute of Technology, China (2015–2017). She has a research background in materials informatics that spans more than five years. Her current research interests primarily focus on data science and machine learning for exploring energy materials, including electrocatalysts and thermoelectric materials.

1. Introduction

Fossil fuel overconsumption has led to increasing environmental issues, such as energy shortage, global warming, and air pollution.^1,2 Consequently, it is significant to develop sustainable technologies for storing, converting, and utilizing renewable energy sources to replace conventional energy sources.³ These technologies always rely on electrochemical reactions associated with facilitating the transformation of H₂O, CO₂, and N₂ into fuels and chemicals.^4,5 Therefore, to accelerate these reactions, it is essential to explore highly efficient electrocatalysts, i.e., with high stability and exceptional activity, which play a crucial role in advancing the transition towards a cleaner, more sustainable energy landscape.^6–8

The oxygen reduction reaction (ORR) is a critical electrochemical process occurring within the potential range of ∼0.6–1.23 V referenced to the reversible hydrogen electrode (RHE), essential for efficient energy storage and conversion.^9,10 This reaction involves two different pathways and can be applied in different fields:^11,12 the first one is a four-electron (4e) pathway occurring at high potentials (e.g., 0.8 V_RHE), which is significant in hydrogen fuel cells and metal–air batteries;^13,14 the other pathway is a two-electron (2e) pathway prevailing at lower potentials (e.g., 0.63 V_RHE), contributing to the production of hydrogen peroxide (H₂O₂) as a commodity.^15,16 Various materials may exhibit a preference for different pathways, and even the same material can adopt different pathways upon adjusting its structure.¹¹

Conventionally, the state-of-the-art electrocatalysts for the ORR are Pt-based materials. The ORR pathway for Pt can be tailored through modifications of its coordination, enabling versatility for various desired applications.^11,17 However, the widespread application of Pt-based electrocatalysts is hindered by their high cost and scarcity.¹⁸ Low-cost metal oxides are a class of potential alternatives with high stability under oxidizing conditions, particularly in alkaline media where they generally demonstrate greater stability compared to acidic conditions.¹⁹ Currently, some metal oxides, such as Mn-based oxides (e.g., MnO₂ (ref. 20) and Li₂MnO₃ (ref. 21)), perovskite-type oxides (e.g., LaCoO₃ (ref. 22) and ZnSnO₃ (ref. 23)), and recently discovered Sb-based oxides (e.g., Sb₂WO₆ (ref. 24)), have demonstrated good electrocatalytic performance for either 4e- or 2e-ORR under alkaline conditions.

Multicomponent metal oxides, owing to their complex chemical compositions and synergetic effects, may exhibit enhanced performance compared to single-metal oxide compositions.^25–28 Recently, Guevarra et al.²⁹ synthesized 7798 different complex multicomponent metal oxides by considering combinations of two, three, and four elements with 10 atom% intervals among Ni, Fe, Mn, Mg, Ca, La, Y, and In. This dataset is, to the best of our knowledge, the largest metal oxide dataset for the ORR reported to date. Subsequently, they characterized the ORR activities at different potentials, i.e., high potential (0.8 V_RHE) and low potential (0.63 V_RHE), under alkaline conditions. While these high throughput experimental results offer guidance for further research on multicomponent metal oxides, the activities may only reach local optimal values since there are numerous other potential combinations if we narrow down the intervals among these metal elements. However, conducting all these experiments to identify compositions with higher activities that reach the global optimal values would be time- and cost-intensive.³⁰ Meanwhile, though theoretical computations and microkinetic modeling are powerful tools that aid in catalyst design, the tremendous first principles computational costs associated with the complicated electronic and ionic structures of metal oxides significantly hamper the development of a precise microkinetic model.¹⁹ This is in part because one needs to employ electric field effect simulations to model the pH-dependent energetics under an RHE scale, and use explicit models with molecular dynamics to precisely acquire the potential of zero-charge (PZC) values.¹⁴

Materials informatics,³¹ which enables the extraction of trends and patterns from materials data through data mining methods (e.g., machine learning, ML), offers a promising approach to accelerate materials design and understanding.^32–34 Currently, it has contributed to many remarkable achievements in the field of catalyst materials, including the successful exploration of Cu–Al catalysts for the CO₂ reduction reaction,³⁵ a Ti–Na₂WO₄/TiO₂ catalyst for oxidative coupling of methane,^36,37 Cu-based nanoclusters for the hydrogen evolution reaction,³⁸ and boron-doped single atom catalysts for the nitrogen reduction reaction.³⁹ Furthermore, there are also endeavors related to the exploration of ORR catalysts utilizing the combination of large datasets and ML techniques, including single-atom catalysts,⁴⁰ PtFeCu,⁴¹ and Fe–N–C-based ORR catalysts.⁴² Therefore, machine learning is a proven effective method for accelerating the design of multicomponent catalysts.

Motivated by the current stages, herein, we focused on screening potential multicomponent metal oxides for the 4e- and 2e-ORR activities using ML based on a large experimental dataset generated by high-throughput experimentation. Initially, we collected two datasets, both of which have the same compositions but different target values, i.e., current density qualified at 0.8 and 0.63 V_RHE, respectively. Then, we conducted a data cleaning process to remove noisy data, resulting in 5353 entries at 0.8 V_RHE and 6902 entries at 0.63 V_RHE. Subsequently, a set of descriptors was generated and analyzed using feature analysis primarily based on Pearson correlation coefficients. Next, we employed the eXtreme Gradient Boosting (XGBoost) algorithm to predict the performance of unexplored multicomponent metal oxides and conducted features explanation analysis, given its superior predictive performance compared to other tested methods such as Light Gradient Boosting Machine (LightGBM), artificial neural network (ANN), symbolic regression, and deep representation learnings. Based on the obtained predictive models, we identified promising regions within 15 different ternary metal oxides with relatively high catalytic activities at 0.8 and 0.63 V_RHE for catalyzing the ORR. We found that for the current density at 0.8 V_RHE, the ternary systems Mn–Ca–La, Mn–Ca–Y, and Mn–Mg–Ca would be recommended for further investigations. For the current density at 0.63 V_RHE, Mn–Fe–X (X = Ni, La, Ca, and Y) and Mn–Ni–X (X = Ca, Mg, La, and Y) systems deserve close attention in the future. Most importantly, this study indicates the potential of ML in expediting catalyst design and materials discovery, paving the way for future advancements in sustainable energy technologies.

2. Method

2.1 Dataset and features

The multicomponent metal oxide catalyst data for the ORR were obtained from previous works.²⁹ The dataset includes 7798 distinct samples containing two, three, and four metals across eight elements, namely Ni, Fe, Mn, Mg, Ca, La, Y, and In. The general formulas of these samples are A_xB_1−x oxides, A_xB_yC_1−x−y oxides, and A_xB_yC_zD_{1−x−y−z} oxides (note: A, B, C, and D represent different metal elements). The target properties are the catalytic activities, quantified as the geometric current density at 0.8 and 0.63 V_RHE, respectively. The Matminer library⁴³ is a tool for generating input features (i.e., independent variables) in materials science. In our dataset, the compositions contain at most 4 different metal elements. Therefore, we used the module “WenAlloys” of the Matminer⁴⁴ designed for calculating features for alloys in the matminer featurizers composition alloy part, and finally obtained 25 input features for the oxide materials.

2.2 ML algorithms

We employed XGBoost,⁴⁵ LightGBM,⁴⁶ ANN,⁴⁷ symbolic regression,^48,49 deep representation learning from stoichiometry (ROOST)^50,51 and compositionally restricted attention-based networks (CrabNet)^52,53 to develop predictive models for current densities in the unit of μA cm⁻². Details can be found in the ESI.† Data scaling preprocessing, development of ANN models, and performance evaluations, including the calculation of the coefficient of determination (R²) and root mean squared error (RMSE), were conducted using the Scikit-learn Python library.⁵⁴ XGBoost and LightGBM models were developed using the XGBoost⁴⁵ and LightGBM⁴⁶ libraries, respectively. The symbolic regression model was built using the PySR library,⁴⁸ while the ROOST and CrabNet models were implemented using their respective open resources.^50–53 The Matplotlib⁵⁵ and Mpltern⁵⁶ tools were employed to plot the ternary plots.

3. Results and discussion

3.1 Workflow

Fig. 1 illustrates the workflow of the ML process employed to explore ORR multicomponent catalysts under alkaline conditions. Following this workflow, we respectively built the ML model for the prediction of activity properties under 0.8 and 0.63 V_RHE. The dataset utilized in this study was obtained from high-throughput experimentation,²⁹ including compositions and activity properties, i.e., current densities (J, μA cm⁻²) under 0.8 and 0.63 V_RHE. Subsequently, we generated input features and conducted feature analysis to represent various compositions, and then they were defined as the inputs to establish the relationship between features and current densities through ML modeling. We employed both neural network- and tree-based models with varying hyperparameters and selected the optimal model (i.e., the models with the hypermeters shown in the ESI†) by evaluating and comparing their performance. Based on the best model, we utilized it to predict the current densities under both 0.8 and 0.63 V_RHE for unexplored composition spaces. Finally, the outcomes of our predictions provided valuable guidance for further experimental investigations.

Fig. 1 Workflow of the ML-based analytical process employed to explore multicomponent ORR catalysts under alkaline conditions.

3.2 Data preprocessing and feature generation

We collected two datasets, both of which have the same compositions but different target values, i.e., current density qualified at 0.8 and 0.63 V_RHE, respectively. Upon inspecting the datasets, we identified some compositions with the original current density values ≤0. These data points were considered as noise and therefore removed, resulting in a total of 6416 remaining data entries under 0.8 V_RHE and 7577 remaining data entries under 0.63 V_RHE. The distribution of current densities under both potentials is depicted in Fig. S1a and b.† For the analysis of current density in the context of the ORR, a logarithmic function was always employed to assess the distribution, which enhanced visualizing the data of current density during processing. Therefore, we used the current density values after logarithmic transformation as the final target predicted values. Fig. 2a and b show the current density values with logarithmic transformation under 0.8 and 0.63 V_RHE, respectively. Fig. 2a shows that under 0.8 V_RHE, the predominant distribution lies within the range of −2 to 0.6 lg(μA cm⁻²), while a smaller portion falls within −6 to −2 lg(μA cm⁻²). Similarly, under 0.63 V_RHE, the majority is observed within the range of −1.0 to 0.6 lg(μA cm⁻²), with a minority falling between −2.5 and −1.0 lg(μA cm⁻²) (Fig. 2b).

Fig. 2 (a and b) Distribution of current densities under (a) 0.8 V_RHE and (b) 0.63 V_RHE with the values after logarithmic transformation. (c and d) Pearson correlations among 16 features in the (c) 0.8 V_RHE and (d) 0.63 V_RHE datasets.

Twenty-five features were generated for both datasets under 0.8 and 0.63 V_RHE using the Matminer.⁴³ However, some features were in the string but not the values, while others consistently had a value of zero across all the data. Consequently, we removed these features, resulting in 21 remaining features for each dataset, including the difference of atomic radii, difference of electronegativity, valence electron concentration, etc. Fig. S1c and d† show the heatmap of Pearson correlations among these features. Some features exhibited high Pearson correlations (red color in the figure, except the diagonal part), which should be excluded since the high correlation will have a negative impact on the ML model. Consequently, we retained 16 features with low correlation for both datasets, respectively, as illustrated in Fig. 2c and d. The remaining features for the datasets under 0.8 and 0.63 V_RHE are the same.

To further assess the data quality, we can construct a quick ML model and compare the disparity between the experimental and predicted values. Neural networks have been developed for half a century and have made significant progress due to their capability to handle non-linear relationships.⁵⁷ Therefore, the ANN was employed as the initial approach to build the models. The performance of two models, each built based on one of the two datasets and evaluated through 10-fold cross-validation, is illustrated in Fig. 3a and b. Fig. 3a shows that the R² and RMSE values of the model on the dataset at 0.8 V_RHE are ∼0.71 and ∼0.468 lg(μA cm⁻²), respectively. For the model of the dataset at 0.63 V_RHE (Fig. 3b), the R² and RMSE are ∼0.74 and ∼0.328 lg(μA cm⁻²), respectively. The related hyperparameters of these models can be found in the ESI.† We found a cluster of data points deviating significantly from the expected trend in Fig. 3a and b, indicating inconsistency within the dataset. This phenomenon can be attributed to two factors: experimental errors, as mentioned in the source paper of the dataset,²⁹ and the unbalanced distribution as discussed in Fig. 2a and b. Therefore, it is reasonable to categorize these data as the noises of the dataset. The most effective way to address these noises is to remove the relevant data points, given our substantial dataset size. Therefore, we firstly compared the bias between the experimental and predicted values for each sample, as illustrated in the insets of Fig. 3a and b. Then we excluded data with a bias greater than 0.5. Finally, we obtained 5353 data points for the 0.8 V_RHE dataset and 6902 data points for the 0.63 V_RHE dataset, with the distribution of current densities shown in Fig. 3c and d for our further ML modeling. Additionally, Fig. 3e illustrates that the 0.8 V_RHE dataset includes 8 materials with one metal element, 225 materials with two metal elements, 1429 materials with three metal elements, and 3691 materials with four metal elements. Similarly, Fig. 3f shows that the 0.63 V_RHE dataset includes 8 materials with one metal element, 228 materials with two metal elements, 1714 materials with three metal elements, and 4952 materials with four metal elements.

Fig. 3 (a and b) Performance of the initial ANN model based on the 10-fold cross validation in the (a) 0.8 V_RHE and (b) 0.63 V_RHE datasets. (c and d) Distribution of current densities after cleaning the noisy data in the (c) 0.8 V_RHE and (d) 0.63 V_RHE datasets. (e and f) Statistics of the materials with various number of elements in the (e) 0.8 V_RHE and (f) 0.63 V_RHE datasets.

3.3 Comparison among different ML models

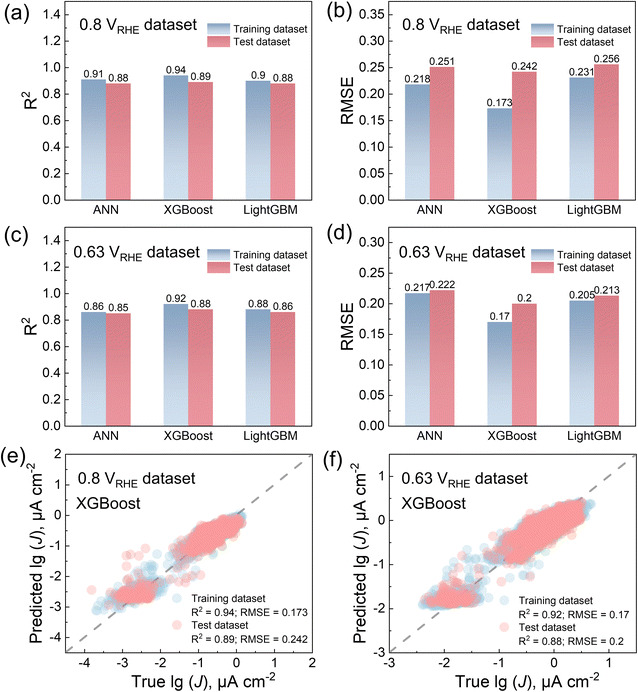
Based on the selected data above, both the two datasets were divided into an 80% training set and a 20% test set, respectively. ANN, XGBoost, and LightGBM were selected to build the ML models and compare their performance on the training dataset. The reason for selecting XGBoost⁴⁵ and LightGBM⁴⁶ was their high performance across various ML tasks.^58,59 Hyperparameters were optimized using 10-fold cross-validation to prevent overfitting, with the details shown in the ESI.† The 10-fold cross-validation results are shown in Fig. S2.†

For the 0.8 V_RHE dataset, the R² scores for the training and test sets are “0.91, 0.88”, “0.94, 0.89”, and “0.90, 0.88”, respectively for ANN, XGBoost, and LightGBM (Fig. 4a). The RMSE values for the training and test sets are “0.218, 0.251 lg(μA cm⁻²)”, “0.173, 0.242 lg(μA cm⁻²)”, and “0.231, 0.256 lg(μA cm⁻²)”, respectively for ANN, XGBoost, and LightGBM (Fig. 4b). For the 0.63 V_RHE dataset, the R² scores for the training and test sets are “0.86, 0.85”, “0.92, 0.88”, and “0.88, 0.86”, respectively for ANN, XGBoost, and LightGBM (Fig. 4c). The RMSE values of the training and test sets are “0.217, 0.222 lg(μA cm⁻²)”, “0.170, 0.200 lg(μA cm⁻²)”, and “0.205, 0.213 lg(μA cm⁻²)”, respectively for ANN, XGBoost, and LightGBM (Fig. 4d). Therefore, XGBoost demonstrates a superior performance on both our training and test sets. Fig. 4e and f illustrate the comparison between the experimental and the predicted values by XGBoost, highlighting its accuracy in the data training. The additional comparison results for the ANN and LightGBM can be found in Fig. S3.†

Fig. 4 (a and b) Comparison of (a) R² and (b) RMSE among the models built by ANN, XGBoost, and LightGBM on the training and test sets at 0.8 V_RHE. (c and d) Comparison of (c) R² and (d) RMSE among the models built by ANN, XGBoost, and LightGBM on the training and test sets at 0.63 V_RHE. (e and f) Comparison between the experimental and predicted values by XGBoost on the training and test sets at (e) 0.8 V_RHE and (f) 0.63 V_RHE. The unit of RMSE is lg(μA cm⁻²).

Furthermore, there may be other methods that can perform better compared to the above models built by elemental features and the XGBoost method. One such method is using symbolic regression,^48,49 which can offer better interpretability, as it provides searches for the optimal mathematical formula between a set of features shown in Fig. 2c and d and target values. The equation results for the 0.8 V_RHE and 0.63 V_RHE datasets are shown in Tables S3 and S4.† The best R² score, even lower than 0.2, indicates the presence of strong nonlinear relationships between features and target values, making it difficult to find equations based on our datasets. Additionally, there are methods to generate vector features based solely on the elements and stoichiometry of compositions, rather than relying on elemental property features generated by Matminer. These methods can be combined with deep learning approaches, which may offer better performance, such as ROOST^50,51 and CrabNet.^52,53 Fig. S4† illustrates the performance of models constructed using ROOST and CrabNet on both the training and test datasets. The R² value shows a slight improvement compared to Fig. 4e and f when Matminer features and XGBoost methods were combined. However, the features and models fail to capture the differences among compositions with low target values, as the true values are different, but predicted values almost always fall in the same narrow ranges (Fig. S4†). Therefore, for the utilization of XGBoost, considering its comparable performance with deep learning models and interpretability based on feature importance, this model is ultimately chosen for our prediction.

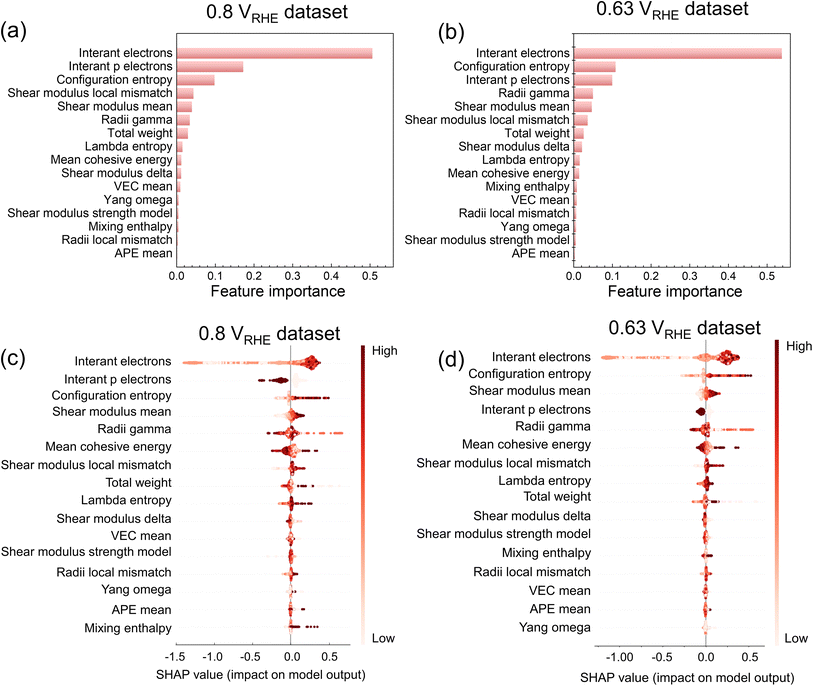
Fig. 5a and b illustrate the feature importance in predicting current densities at 0.8 and 0.63 V_RHE using XGBoost embedded in the XGBoost Library.⁴⁵ The top three important features for the 0.8 V_RHE dataset are the number of itinerant electrons (interant electrons), the number of itinerant electrons in the p electron orbitals (interant p electrons), and configuration entropy, sorted by the importance from high to low (Fig. 5a), while for the 0.63 V_RHE dataset, the top three features are the same but the order is sorted as interant electrons, configuration entropy, and interant p electrons. The SHapley Additive exPlanations (SHAP) method⁶⁰ offers an explanation for the output of ML models. Fig. 5c and d display the SHAP values derived from the XGBoost model. These values indicate the features' influence on the model output, ordered by their mean absolute SHAP value across the dataset. Although there are slight differences among the feature importance order compared to Fig. 5a and b due to different calculation methods, the top three important features remain almost consistent. In the 0.8 V_RHE dataset (Fig. 5c), the interant electron emerges as the most important feature with the highest SHAP value. A higher value of interant electron corresponds to a positive SHAP value, suggesting a positive influence on the current density. Conversely, a lower value indicates a negative influence. The interant p electron consistently exerts a negative influence on the current density. Configuration entropy, on the other hand, exhibits a positive influence on current density when its value is higher. Fig. 5d illustrates the distribution of SHAP values in the 0.63 V_RHE dataset. The influence trends of features on current densities are similar to those observed in the 0.8 V_RHE dataset. These plots suggest that for achieving a high current density, more attention should be paid to the high interant electron values and high configuration entropy.

Fig. 5 (a and b) Feature importance in predicting current densities at (a) 0.8 V_RHE and (b) 0.63 V_RHE using the XGBoost. (c and d) SHAP values derived from the XGBoost model in the (c) 0.8 V_RHE and (d) 0.63 V_RHE datasets.

3.4 Mapping the activity and providing predictions

Mn, Ni, and Fe are the commonly studied elements in metal oxides for alkaline ORR.^61,62 Besides, the experimental dataset also indicates that the addition of La can enhance activity, which is in agreement with a recent study which found that oxidized La can serve as an active site for the ORR in alkaline media.⁶³ Consequently, our investigation primarily focuses on systems containing at least on Mn, Ni, Fe, or La. Specifically, we explored materials containing three metal elements due to their ease of forming a single phase. This results in 52 possible ternary compositions. The interval between compositions was set at 1 atom%, resulting in 5591 compositions for each system, totaling 266 032 different compositions.

3.4.1 Prediction of current density at 0.8 V_RHE. The predicted current densities at 0.8 V_RHE for these compositions were generated using our developed XGBoost model. In Fig. 6, the top fifteen ternary systems with the highest maximum values are presented, sorted from highest to lowest. The prediction of the other 37 ternary systems can be found in Fig. S5–S7.† These fifteen systems include the Mn–Ca–X (X = La/Y/Mg/Ni/Fe/In) system (Fig. 6a–d, f and h) and the Mn–La–X (X = Mg/Ni/Fe/Y/In) system (Fig. 6e, g, i–k), as well as the Mn–Ni–X (X = Fe/Y) and Mn–Mg–X (X = Y/Fe) systems (Fig. 6l–o). It is notable that the inclusion of Mn significantly contributes to the current density, as each of these systems contains Mn.

Fig. 6 Predictive current density values at 0.8 V_RHE for the fifteen ternary systems based on the trained XGBoost model. (a–o) Ternary systems of (a) Mn–Ca–La, (b) Mn–Ca–Y, (c) Mn–Mg–Ca, (d) Mn–Ni–Ca, (e) Mn–Mg–La, (f) Mn–Ca–Fe, (g) Mn–Ni–La, (h) Mn–Ca–In, (i) Mn–Fe–La, (j) Mn–La–Y, (k) Mn–La–In, (l) Mn–Ni–Fe, (m) Mg–Mg–Y, (n) Mn–Ni–Y, and (o) Mn–Mg–Fe.

Table 1 shows the compositions with the highest current density values for each system, corresponding to Fig. 6. Readers can combine Table 1 with Fig. 6 to identify regions with high performance in these ternary systems. We found that the ternary Mn–Ca–X (X = La/Y/Mg) system (Fig. 6a–c) demonstrates the highest values. However, in most ternary systems, the compositions with the highest current densities are actually binary metal oxides. For example, in Mn–Ca–X (X = Ni/In) (#4 and #8 in Table 1), the composition with optimal values is Mn_0.62Ca_0.38, and in Mn–La–X (X = Mg/Ni/Fe/Y/In) (#5, #7, and #9–11 in Table 1), it is Mn_0.84La_0.16. This suggests that the inclusion of Ni and Mg in Mn–Ca, and Mg/Ni/Fe/Y/In in Mn–La, may not contribute to the improvement of current densities. Therefore, for the current density at 0.8 V_RHE, the ternary systems Mn–Ca–La, Mn–Ca–Y, and Mn–Mg–Ca would be recommended for further investigations.

Table 1 Compositions with the highest predicted current density values (denoted as: Com. with max. value) for each system

No.	Ternary system	Com. with max. value	No.	Ternary system	Com. with max. value
1	Mn–Ca–La	Mn0.59Ca0.21La0.2	9	Mn–Fe–La	Mn0.84La0.16
2	Mn–Ca–Y	Mn0.57Ca0.25Y0.18	10	Mn–La–Y	Mn0.84La0.16
3	Mn–Mg–Ca	Mn0.85Mg0.04Ca0.11	11	Mn–La–In	Mn0.84La0.16
4	Mn–Ni–Ca	Mn0.62Ca0.38	12	Mn–Ni–Fe	Mn0.95Ni0.01Fe0.04
5	Mn–Mg–La	Mn0.84La0.16	13	Mn–Mg–Y	Mn0.81Mg0.01Y0.18
6	Mn–Ca–Fe	Mn0.98Fe0.02	14	Mn–Ni–Y	Mn0.81Y0.19
7	Mn–Ni–La	Mn0.84La0.16	15	Mn–Mg–Fe	Mn0.98Fe0.02
8	Mn–Ca–In	Mn0.89Ca0.38

---

3.4.2 Prediction of ORR current density at 0.63 V_RHE. Similarly, the predicted values at 0.8 V_RHE for these unexplored compositions were also generated using our developed XGBoost model. Fifteen ternary systems exhibit maximum current density values greater than 0.25, as shown in Fig. 7. The prediction of the other 37 ternary systems can be found in Fig. S8–S10.† From this observation, it can also be inferred that the inclusion of Mn is crucial in contributing to the current density since each of these systems contains Mn. Among these systems, the Mn–Fe–X (X = La/Ca/Y/Ni/Mg/In) system (Fig. 7a–d, f–g) yields the highest values, followed by the Mn–Ni–X (X = Ca/Mg/La/Y/In) system (Fig. 7e, h–k). Additionally, Mn–Ca–X (X = La/Mg/Y) and Mn–Mg–X (X = La) systems (Fig. 7l–o) also show promising ORR performance. Table 2 shows the compositions with the highest current density values for each system, corresponding to Fig. 7. Readers can combine Table 2 with Fig. 7 to identify regions with high performance in these ternary systems.

Fig. 7 Predictive current density values at 0.63 V_RHE for the fifteen ternary systems based on the trained XGBoost model. (a–o) Ternary systems of (a) Mn–Fe–La, (b) Mn–Ca–Fe, (c) Mn–Fe–Y, (d) Mn–Ni–Fe, (e) Mn–Ni–Ca, (f) Mn–Mg–Fe, (g) Mn–Fe–In, (h) Mn–Ni–Mg, (i) Mn–Ni–La, (j) Mn–Ni–Y, (k) Mn–Ni–In, (l) Mn–Ca–La, (m) Mg–Mg–Ca, (n) Mn–Ca–Y, and (o) Mn–Mg–La.

Table 2 Compositions with the highest predicted current density values (denoted as: Com. with max. value) for each system

No.	Ternary system	Com. with max. value	No.	Ternary system	Com. with max. value
1	Mn–Fe–La	Mn0.78Fe0.14La0.08	9	Mn–Ni–La	Mn0.89Nin0.01La0.1
2	Mn–Ca–Fe	Mn0.69Ca0.1Fe0.21	10	Mn–Ni–Y	Mn0.87Nin0.01Y0.12
3	Mn–Fe–Y	Mn0.8Fe0.03Y0.17	11	Mn–Ni–In	Mn0.99Nin0.01
4	Mn–Ni–Fe	Mn0.97Ni0.01Fe0.02	12	Mn–Ca–La	Mn0.7Ca0.1La0.2
5	Mn–Ni–Ca	Mn0.89In0.01Ca0.1	13	Mn–Mg–Ca	Mn0.78Mg0.13Ca0.09
6	Mn–Mg–Fe	Mn0.98Fe0.02	14	Mn–Ca–Y	Mn0.78Ca0.14Y0.08
7	Mn–Fe–In	Mn0.98Fe0.02	15	Mn–Mg–La	Mn0.69Mg0.1La0.21
8	Mn–Ni–Mg	Mn0.89In0.01Mg0.1

---

Additionally, we observed that for the Mn–Mg–Fe and Mn–Fe–In systems, the compositions with optimal values are Mn_0.98Fe_0.02 (Table 2), suggesting that the inclusion of Mg or In into the Mn–Fe system may not provide advantages for the activity. However, the addition of La (#1 in Table 2), Ca (#2 in Table 2), Y (#3 in Table 1), and Ni (#4 in Table 2) into Mn–Fe systems may be beneficial to the ORR performance. Similarly, in the case of Mn–Ni–In, the optimal composition is Mn_0.99Ni_0.01, indicating that In is not advantageous for the Mn–Ni system. Conversely, adding Fe, Ca, Mg, La, or Y can show favorable effects on the Mn–Ni system.

Previous experimental results have indicated that Mn–Ni–Fe and Mn–Ni–Fe–La systems warrant attention for alkaline ORR at 0.63 V_RHE.³⁶ Our current findings further expand upon this by revealing that Mn–Fe–X (X = La/Ca/Y) and Mn–Ni–X (X = Ca/Mg/La/Y) systems also exhibit comparable ORR activities.

4. Conclusions

In summary, we have analyzed a large alkaline ORR dataset from high-throughput experiments and performed data cleaning by analyzing the target values. Sixteen features with low Pearson correlation coefficients were obtained and defined as effective inputs to develop the model. Comparing the performance of ANN, XGBoost, and LightGBM, XGBoost demonstrated superior performance. Feature explanations based on the model suggested that high interant electron values and high configuration entropy may contribute to a higher current density. Finally, XGBoost models were employed to further provide predictions for potential catalysts. We found that the ternary systems Mn–Ca–La, Mn–Ca–Y, and Mn–Mg–Ca show promising potential for further investigations, particularly in applications related to hydrogen fuel cells at ∼0.8 V_RHE. Mn–Fe–X (X = Ni/La/Ca/Y) and Mn–Ni–X (X = Ca/Mg/La/Y) systems also deserve close attention as they may contribute to the production of hydrogen peroxide (H₂O₂) at ∼0.63 V_RHE. It is important to note that although the data and the model may possess certain biases, the identification of trends between compositions and activities remains valuable. Researchers can conduct more target experiments to delve deeper into these investigations. Most importantly, this study underscores the potential of artificial intelligence in expediting catalyst design and materials discovery, paving the way for future advancements in sustainable energy technologies.

Data availability

The relevant data and codes for this study are available at https://github.com/XueJiaAIMR/ORR-Dataset.

Author contributions

Xue Jia: conceptualization, data curation, investigation, formal analysis, methodology, writing – original draft, funding acquisition. Hao Li: supervision, conceptualization, writing – review and editing, project administration, funding acquisition.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by JSPS KAKENHI (No. JP23K13599), the Hirose Foundation, and the Ensemble Grants for Early Career Researchers 2023 of Tohoku University.

References

1. Y. Wang, X. Zheng and D. Wang, Design concept for electrocatalysts, Nano Res., 2022, 15, 1730–1752,  DOI:10.1007/s12274-021-3794-0.
2. J. C. Meier, I. Katsounaros, C. Galeano, H. J. Bongard, A. A. Topalov, A. Kostka, A. Karschin, F. Schüth and K. J. J. Mayrhofer, Stability investigations of electrocatalysts on the nanoscale, Energy Environ. Sci., 2012, 5, 9319–9330,  10.1039/c2ee22550f.
3. H. Liu, X. Jia, A. Cao, L. Wei, C. D’agostino and H. Li, The surface states of transition metal X-ides under electrocatalytic conditions, J. Chem. Phys., 2023, 158, 124705,  DOI:10.1063/5.0147123.
4. J. Masa, C. Andronescu and W. Schuhmann, Electrocatalysis as the Nexus for Sustainable Renewable Energy: The Gordian Knot of Activity, Stability, and Selectivity, Angew. Chem., Int. Ed., 2020, 59, 15298–15312,  DOI:10.1002/anie.202007672.
5. T. Wang, Z. Guo, H. Oka, A. Kumatani, C. Liu and H. Li, Origin of electrocatalytic nitrogen reduction activity over transition metal disulfides: critical role of in situ generation of S vacancy, J. Mater. Chem. A, 2024, 12, 8438–8446,  10.1039/d4ta00307a.
6. M. B. Stevens, M. Anand, M. E. Kreider, E. K. Price, J. Z. Zeledón, L. Wang, J. Peng, H. Li, J. M. Gregoire and J. Hummelshøj, New challenges in oxygen reduction catalysis: a consortium retrospective to inform future research, Energy Environ. Sci., 2022, 15, 3775–3794.
7. S. Park, Y. Shao, J. Liu and Y. Wang, Oxygen electrocatalysts for water electrolyzers and reversible fuel cells: status and perspective, Energy Environ. Sci., 2012, 5, 9331–9344,  10.1039/c2ee22554a.
8. S. Zhao, Y. Yang and Z. Tang, Insight into Structural Evolution, Active Sites, and Stability of Heterogeneous Electrocatalysts, Angew. Chem., Int. Ed., 2022, 61, e202110186,  DOI:10.1002/anie.202110186.
9. Z. Wang, Y.-R. Zheng, I. Chorkendorff and J. K. Nørskov, Acid-Stable Oxides for Oxygen Electrocatalysis, ACS Energy Lett., 2020, 5, 2905–2908,  DOI:10.1021/acsenergylett.0c01625.
10. X. Ge, A. Sumboja, D. Wuu, T. An, B. Li, F. W. T. Goh, T. S. A. Hor, Y. Zong and Z. Liu, Oxygen Reduction in Alkaline Media: From Mechanisms to Recent Advances of Catalysts, ACS Catal., 2015, 5, 4643–4667,  DOI:10.1021/acscatal.5b00524.
11. J. Zhao, C. Fu, K. Ye, Z. Liang, F. Jiang, S. Shen, X. Zhao, L. Ma, Z. Shadike, X. Wang, J. Zhang and K. Jiang, Manipulating the oxygen reduction reaction pathway on Pt-coordinated motifs, Nat. Commun., 2022, 13, 685,  DOI:10.1038/s41467-022-28346-0.
12. M. K. Debe, Electrocatalyst approaches and challenges for automotive fuel cells, Nature, 2012, 486, 43–51,  DOI:10.1038/nature11115.
13. C. Santoro, P. Bollella, B. Erable, P. Atanassov and D. Pant, Oxygen reduction reaction electrocatalysis in neutral media for bioelectrochemical systems, Nat. Catal., 2022, 5, 473–484,  DOI:10.1038/s41929-022-00787-2.
14. D. Zhang, Z. Wang, F. Liu, P. Yi, L. Peng, Y. Chen, L. Wei and H. Li, Unraveling the pH-Dependent Oxygen Reduction Performance on Single-Atom Catalysts: From Single- to Dual-Sabatier Optima, J. Am. Chem. Soc., 2024, 146, 3210–3219,  DOI:10.1021/jacs.3c11246.
15. X. Mei, X. Zhao, Y. Chen, B. Deng, Q. Geng, Y. Cao, Y. Li and F. Dong, Highly Efficient H₂O₂ Production via Two-Electron Electrochemical Oxygen Reduction over Fe-Doped CeO₂, ACS Sustainable Chem. Eng., 2023, 11, 15609–15619,  DOI:10.1021/acssuschemeng.3c04194.
16. H. He, S. Liu, Y. Liu, L. Zhou, H. Wen, R. Shen, H. Zhang, X. Guo, J. Jiang and B. Li, Review and perspectives on carbon-based electrocatalysts for the production of H₂O₂via two-electron oxygen reduction, Green Chem., 2023, 25, 9501–9542,  10.1039/D3GC02856A.
17. J. Liu, M. Jiao, L. Lu, H. M. Barkholtz, Y. Li, Y. Wang, L. Jiang, Z. Wu, D. Liu, L. Zhuang, C. Ma, J. Zeng, B. Zhang, D. Su, P. Song, W. Xing, W. Xu, Y. Wang, Z. Jiang and G. Sun, High performance platinum single atom electrocatalyst for oxygen reduction reaction, Nat. Commun., 2017, 8, 15938,  DOI:10.1038/ncomms15938.
18. Y. Nie, L. Li and Z. Wei, Recent advancements in Pt and Pt-free catalysts for oxygen reduction reaction, Chem. Soc. Rev., 2015, 44, 2168–2201,  10.1039/c4cs00484a.
19. H. Li, S. Kelly, D. Guevarra, Z. Wang, Y. Wang, J. A. Haber, M. Anand, G. T. K. K. Gunasooriya, C. S. Abraham, S. Vijay, J. M. Gregoire and J. K. Nørskov, Analysis of the limitations in the oxygen reduction activity of transition metal oxide surfaces, Nat. Catal., 2021, 4, 463–468,  DOI:10.1038/s41929-021-00618-w.
20. M. S. El-Deab and T. Ohsaka, Manganese oxide nanoparticles electrodeposited on platinum are superior to platinum for oxygen reduction, Angew. Chem., Int. Ed., 2006, 45, 5963–5966.
21. X. Zhong, M. Oubla, X. Wang, Y. Huang, H. Zeng, S. Wang, K. Liu, J. Zhou, L. He, H. Zhong, N. Alonso-Vante, C.-W. Wang, W.-B. Wu, H.-J. Lin, C.-T. Chen, Z. Hu, Y. Huang and J. Ma, Boosting oxygen reduction activity and enhancing stability through structural transformation of layered lithium manganese oxide, Nat. Commun., 2021, 12, 3136,  DOI:10.1038/s41467-021-23430-3.
22. D. B. Meadowcroft, Low-cost Oxygen Electrode Material, Nature, 1970, 226, 847–848,  DOI:10.1038/226847a0.
23. J. Qian, W. Liu, Y. Jiang, Y. Mu, Y. Cai, L. Shi and L. Zeng, Enhanced Catalytic Performance in Two-Electron Oxygen Reduction Reaction via ZnSnO₃ Perovskite, ACS Sustainable Chem. Eng., 2022, 10, 14351–14360,  DOI:10.1021/acssuschemeng.2c04965.
24. X. Jia, Z. Yu, F. Liu, H. Liu, D. Zhang, E. Campos dos Santos, H. Zheng, Y. Hashimoto, Y. Chen, L. Wei and H. Li, Identifying Stable Electrocatalysts Initialized by Data Mining: Sb₂WO₆ for Oxygen Reduction, Adv. Sci., 2024, 11, 2305630,  DOI:10.1002/advs.202305630.
25. J. N. Al-Saeedi and V. V. Guliants, High-throughput experimentation in multicomponent bulk mixed metal oxides: Mo-V-Sb-Nb-O system for selective oxidation of propane to acrylic acid, Appl. Catal., A, 2002, 237, 111–120,  DOI:10.1016/S0926-860X(02)00324-1.
26. M. B. Gawande, R. K. Pandey and R. V. Jayaram, Role of mixed metal oxides in catalysis science—versatile applications in organic synthesis, Catal. Sci. Technol., 2012, 2, 1113–1125,  10.1039/c2cy00490a.
27. H. Lu, D. S. Wright and S. D. Pike, The use of mixed-metal single source precursors for the synthesis of complex metal oxides, Chem. Commun., 2020, 56, 854–871,  10.1039/c9cc06258k.
28. C. Yuan, H. B. Wu, Y. Xie and X. W. (David) Lou, Mixed Transition-Metal Oxides: Design, Synthesis, and Energy-Related Applications, Angew. Chem., Int. Ed., 2014, 53, 1488–1504,  DOI:10.1002/anie.201303971.
29. D. Guevarra, J. A. Haber, Y. Wang, L. Zhou, K. Kan, M. H. Richter and J. M. Gregoire, High Throughput Discovery of Complex Metal Oxide Electrocatalysts for the Oxygen Reduction Reaction, Electrocatalysis, 2022, 13, 1–10,  DOI:10.1007/s12678-021-00694-3.
30. S. N. Steinmann, Q. Wang and Z. W. Seh, How machine learning can accelerate electrocatalysis discovery and optimization, Mater. Horiz., 2023, 10, 393–406,  10.1039/d2mh01279k.
31. T.-Y. Zhang and X.-J. Liu, Informatics is fueling new materials discovery, J. Mater. Inf., 2021, 1, 6,  DOI:10.20517/jmi.2021.09.
32. X. Jia, H. Yao, Z. Yang, J. Shi, J. Yu, R. Shi, H. Zhang, F. Cao, X. Lin, J. Mao, C. Wang, Q. Zhang and X. Liu, Advancing thermoelectric materials discovery through semi-supervised learning and high-throughput calculations, Appl. Phys. Lett., 2023, 123, 203902,  DOI:10.1063/5.0175233.
33. X. Jia, A. Aziz, Y. Hashimoto and H. Li, Dealing with the big data challenges in AI for thermoelectric materials, Sci. China Mater., 2024, 67, 1173–1182,  DOI:10.1007/s40843-023-2777-2.
34. X. Jia, Y. Deng, X. Bao, H. Yao, S. Li, Z. Li, C. Chen, X. Wang, J. Mao, F. Cao, J. Sui, J. Wu, C. Wang, Q. Zhang and X. Liu, Unsupervised machine learning for discovery of promising half-Heusler thermoelectric materials, npj Comput. Mater., 2022, 8, 34,  DOI:10.1038/s41524-022-00723-9.
35. M. Zhong, K. Tran, Y. Min, C. Wang, Z. Wang, C.-T. Dinh, P. De Luna, Z. Yu, A. S. Rasouli, P. Brodersen, S. Sun, O. Voznyy, C.-S. Tan, M. Askerka, F. Che, M. Liu, A. Seifitokaldani, Y. Pang, S.-C. Lo, A. Ip, Z. Ulissi and E. H. Sargent, Accelerated discovery of CO₂ electrocatalysts using active machine learning, Nature, 2020, 581, 178–183,  DOI:10.1038/s41586-020-2242-8.
36. T. N. Nguyen, T. T. P. Nhat, K. Takimoto, A. Thakur, S. Nishimura, J. Ohyama, I. Miyazato, L. Takahashi, J. Fujima, K. Takahashi and T. Taniike, High-Throughput Experimentation and Catalyst Informatics for Oxidative Coupling of Methane, ACS Catal., 2020, 10, 921–932,  DOI:10.1021/acscatal.9b04293.
37. K. Sugiyama, T. N. Nguyen, S. Nakanowatari, I. Miyazato, T. Taniike and K. Takahashi, Direct Design of Catalysts in Oxidative Coupling of Methane via High-Throughput Experiment and Deep Learning, ChemCatChem, 2021, 13, 952–957,  DOI:10.1002/cctc.202001680.
38. X. Mao, L. Wang, Y. Xu, P. Wang, Y. Li and J. Zhao, Computational high-throughput screening of alloy nanoclusters for electrocatalytic hydrogen evolution, npj Comput. Mater., 2021, 7, 46,  DOI:10.1038/s41524-021-00514-8.
39. M. Zafari, D. Kumar, M. Umer and K. S. Kim, Machine learning-based high throughput screening for nitrogen fixation on boron-doped single atom catalysts, J. Mater. Chem. A, 2020, 8, 5209–5216,  10.1039/C9TA12608B.
40. H. Sun, Y. Li, L. Gao, M. Chang, X. Jin, B. Li, Q. Xu, W. Liu, M. Zhou and X. Sun, High throughput screening of single atomic catalysts with optimized local structures for the electrochemical oxygen reduction by machine learning, J. Energy Chem., 2023, 81, 349–357,  DOI:10.1016/j.jechem.2023.02.045.
41. H. Chun, E. Lee, K. Nam, J.-H. Jang, W. Kyoung, S. H. Noh and B. Han, First-principle-data-integrated machine-learning approach for high-throughput searching of ternary electrocatalyst toward oxygen reduction reaction, Chem Catal., 2021, 1, 855–869,  DOI:10.1016/j.checat.2021.06.001.
42. W. J. M. Kort-Kamp, M. Ferrandon, X. Wang, J. H. Park, R. K. Malla, T. Ahmed, E. F. Holby, D. J. Myers and P. Zelenay, Adaptive learning-driven high-throughput synthesis of oxygen reduction reaction Fe–N–C electrocatalysts, J. Power Sources, 2023, 559, 232583,  DOI:10.1016/j.jpowsour.2022.232583.
43. L. Ward, A. Dunn, A. Faghaninia, N. E. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom and M. Dylla, Matminer: an open source toolkit for materials data mining, Comput. Mater. Sci., 2018, 152, 60–69.
44. C. Wen, Y. Zhang, C. Wang, D. Xue, Y. Bai, S. Antonov, L. Dai, T. Lookman and Y. Su, Machine learning assisted design of high entropy alloys with desired property, Acta Mater., 2019, 170, 109–117,  DOI:10.1016/j.actamat.2019.03.010.
45. T. Chen and C. Guestrin, XGBoost: A Scalable Tree Boosting System, in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, New York, NY, USA, 2016, pp. 785–794,  DOI:10.1145/2939672.2939785.
46. G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye and T.-Y. Liu, LightGBM: a highly efficient gradient boosting decision tree, in Proceedings of the 31st International Conference on Neural Information Processing Systems, Curran Associates Inc., Red Hook, NY, USA, 2017, pp. 3149–3157.
47. P. D. Wasserman, Neural Computing: Theory and Practice, Van Nostrand Reinhold Co., USA, 1989.
48. M. Cranmer, Interpretable machine learning for science with PySR and SymbolicRegression. jl, arXiv, 2023, preprint, arXiv:2305.01582,  DOI:10.48550/arXiv.2305.01582.
49. B. Weng, Z. Song, R. Zhu, Q. Yan, Q. Sun, C. G. Grice, Y. Yan and W.-J. Yin, Simple descriptor derived from symbolic regression accelerating the discovery of new perovskite catalysts, Nat. Commun., 2020, 11, 3513,  DOI:10.1038/s41467-020-17263-9.
50. R. Goodall, ROOST – Representation Learning from Stoichiometry, 2020,  DOI:10.5281/zenodo.4133793.
51. R. E. A. Goodall and A. A. Lee, Predicting materials properties without crystal structure: deep representation learning from stoichiometry, Nat. Commun., 2020, 11, 6280,  DOI:10.1038/s41467-020-19964-7.
52. A. Y.-T. Wang, M. S. Mahmoud, M. Czasny and A. Gurlo, CrabNet for Explainable Deep Learning in Materials Science: Bridging the Gap Between Academia and Industry, Integr. Mater. Manuf. Innov., 2022, 11, 41–56,  DOI:10.1007/s40192-021-00247-y.
53. A. Y.-T. Wang, S. K. Kauwe, R. J. Murdock and T. D. Sparks, Compositionally restricted attention-based network for materials property predictions, npj Comput. Mater., 2021, 7, 77,  DOI:10.1038/s41524-021-00545-1.
54. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830.
55. J. D. Hunter, Matplotlib: A 2D Graphics Environment, Comput. Sci. Eng., 2007, 9, 90–95,  DOI:10.1109/MCSE.2007.55.
56. Y. Ikeda, B. Grabowski and F. Körmann, Mpltern 0.3.0: Ternary Plots as Projections of Matplotlib, 2019,  DOI:10.5281/zenodo.3528355.
57. L. Wang and K. Fu, Artificial Neural Networks, in Wiley Encyclopedia of Computer Science and Engineering, 2009, pp. 181–188,  DOI:10.1002/9780470050118.ecse021.
58. J. Zhang, K. Zhang, S. Xu, Y. Li, C. Zhong, M. Zhao, H.-J. Qiu, M. Qin, X.-D. Xiang, K. Hu and X. Lin, An integrated machine learning model for accurate and robust prediction of superconducting critical temperature, J. Energy Chem., 2023, 78, 232–239,  DOI:10.1016/j.jechem.2022.11.047.
59. J. Zhang, Z. Zhu, X.-D. Xiang, K. Zhang, S. Huang, C. Zhong, H.-J. Qiu, K. Hu and X. Lin, Machine Learning Prediction of Superconducting Critical Temperature through the Structural Descriptor, J. Phys. Chem. C, 2022, 126, 8922–8927,  DOI:10.1021/acs.jpcc.2c01904.
60. S. M. Lundberg and S.-I. Lee, A Unified Approach to Interpreting Model Predictions, Advances in Neural Information Processing Systems, ed. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Curran Associates, Inc., 2017, https://proceedings.neurips.cc/paper_files/paper/2017/file/8a20a8621978632d76c43dfd28b67767-Paper.pdf.
61. W. Xiong, H. Yin, T. Wu and H. Li, Challenges and Opportunities of Transition Metal Oxides as Electrocatalysts, Chem.–Eur. J., 2023, 29, e202202872,  DOI:10.1002/chem.202202872.
62. Y. Wang, J. Li and Z. Wei, Transition-metal-oxide-based catalysts for the oxygen reduction reaction, J. Mater. Chem. A, 2018, 6, 8194–8209,  10.1039/c8ta01321g.
63. R. Zhao, Z. Chen, Q. Li, X. Wang, Y. Tang, G. Fu, H. Li, J.-M. Lee and S. Huang, N-doped LaPO₄: an effective Pt-free catalyst for electrocatalytic oxygen reduction, Chem Catal., 2022, 2, 3590–3606,  DOI:10.1016/j.checat.2022.11.008.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta01884b

---