Open Access Article
Open Access ArticleEngineering anomalous elastic properties of coordination polymers and their amorphization by employing flexible linkers†
Aleksandra
Półrolniczak
 ,
Szymon
Sobczak
,
Szymon
Sobczak
 and
Andrzej
Katrusiak
and
Andrzej
Katrusiak
 *
*
Department of Materials Chemistry, Faculty of Chemistry, Adam Mickiewicz University, Uniwersytetu Poznańskiego 8, 61-614 Poznań, Poland. E-mail: katran@amu.edu.pl
First published on 29th November 2023
Abstract
The common property of all materials is their elasticity, directly related to the chemical components and interactions in their structure. However, the progress in constructing better devices is irreversibly tied to the understanding and designing of static or dynamic structural responses of strained materials. Such structural-property relationships have been explained for polymeric frameworks involving flexible 1,6-hexanediamine (HDA) linkers, with discrete HDA conformers. In the structure of ambient-pressure polymer Cd(HDA)2(NO3)2 the HDA linkers are conformationally disordered. This tetragonal phase α is stable down to 190 K, when the HDA linkers order in different conformations, which triggers a ferroelastic transition to the triclinic phase δ; the flash-cooling of phase α overcools it to 100 K. High pressure induces a ferroelastic transition to triclinic phase β at 1.10 GPa, followed by an isostructural transition to phase γ at 2.00 GPa. All four phases α–δ differ in the configurations of HDA conformers and Cd-coordination involving nitrate linkers. The unusual convex-shaped monotonic compression of Cd(HDA)2(NO3)2 phases α, β and γ has been explained by the mechanism of buckling-sticks: the increasing strain and mounting energy accumulated in the buckling HDA linkers is released by their conversions to shorter conformers. An analogous conformational transition takes place in Cd2(HDA)3(NO3)4 at 1.50 GPa. In another polymer Cu(HDA)2(MeCN)2·2BF4 the conformational changes induce its very high compressibility and partial amorphization above 1.20 GPa, caused by the non-coordinated conversions of the HDA conformers.
1. Introduction
The understanding of relations between the elastic properties of materials and their microscopic structure is essential for both scientific and technological purposes. It allows engineers to design materials with desired qualities, like hardness, stiffness or flexibility, ensuring that materials withstand specific mechanic requirements and thermodynamic conditions, making them safer and more reliable. More broadly, delving into the relationship between macroscopic and microscopic properties deepens our understanding of matter. This scientific knowledge not only advances materials science but also contributes to the overall progress in areas like nanotechnology and microelectronics, which rely on materials with specific properties at the smallest scale and is fundamental for advancing these fields. In recent decades, a vast number of coordination polymers (CP) were synthesized for various technological applications, such as selective sorption of gases, separation of fine reagents, templated reactions, chemical and physical sensing, storage of energetic or hazardous agents, etc.1,2 The design of such polymeric frameworks requires a thorough understanding of the aggregation of the metal centre and ligands; however, the physical properties of such materials are difficult to predict.3,4 The underlying structure and chemical interactions in polymers are pivotal factors collectively shaping their free energy surface and determining their physicochemical properties.5 The compression of the frameworks often depends on the hinge-like movement of rigid linkers about the metal centres, for example in the structures described by the wine-rack model.6 Presently, we have investigated the performance of the aliphatic diamine ligand 1,6-hexanediamine (HDA), capable of switching its conformation, which enhances the framework deformation. Owing to its flexibility, HDA is widely used in the syntheses of organic materials (e.g. Nylon-66), plastics and detergents. HDA is generally considered safe, and it is used for preserving food and for producing medical plastic materials.7–10 The free electron pairs of two amino groups in HDA easily coordinate various metal cations.11–13 To our knowledge, the first HDA-based 3-dimensional framework, Cd(HDA)Ni(CN4), was synthesized in 1983 by Davies and Maver.14 Later, other connections involving HDA linkers were studied.15–18 However, the elastic properties of HDA polymers remain unknown. High pressure is well suited for combined studies of the crystal strain and structural distortions of the framework, which can be precisely determined by single-crystal X-ray diffraction (SCXRD).19,20The compression of coordination polymers depends on various variables, such as the metal-centre coordination scheme, topology of connections, the size and shape of voids, the chemical character of linkers, their capability to form intermolecular interactions, the type of pressure-transmitting medium (PTM), or the speed of compression.21–24 The compression of this kind of crystalline sample can proceed as a one-component (CP) or multi-component (CP + PTM) system, through monotonic changes and phase transitions.25,26 In the one-component structure, high pressure decreases the void spaces and distances between molecules. The reduced volume can increase the thermally-induced collisions, which for specific components can trigger a chemical reaction.27,28 On the other hand, the compression of porous crystals in small-molecule liquids or gases can trigger a significantly different response compared to the compression in a large-molecule PTM.29–31 Apart from the molecular size, other properties of the PTM, such as its density, viscosity, and freezing pressure can also promote, hamper or prohibit the formation of the CP–PTM compounds. A considerable variety of possible structural responses of coordination polymers to external stimuli often leads to strongly anisotropic and anomalous effects, such as the negative linear or area compressibility,32–35 phase transitions,36–38 amorphization,39–42 topochemical reactions,43,44 and sorption.45,46 All these effects can be modelled and studied in confined space of high-pressure reactors, providing sustainable means for exploring new paths for materials synthesis and modifications,19,47 bringing insightful information about correlating their structure–property relationships.
In the broader context of materials science, the understanding of materials behaviour under highly strained conditions is of paramount importance. The study of the elastic properties of coordination polymers in such environments not only aids in predicting how materials will behave under stress, leading to new materials of enhanced properties, which at the same time resist damage or failure more effectively. In our present report, we focus on the role of flexible HDA linkers for the elastic properties under high-pressure conditions. The importance of molecular conformation on the bulk material properties, particularly in the regions of monotonic transformations, phase transitions and amorphization that are of industrial relevance. The conformational flexibility is common in nature, where the functions of biopolymers like cellulose, nucleic acids and proteins are connected to the structural transformations of biomolecules. The enhanced compressibility, volume changes at order–disorder phase transitions can find various practical applications, such as shock absorbing layers and barocaloric refrigeration and air conditioning.48–50
Presently, we have investigated the structural mechanism of compression in three coordination polymers involving HDA linkers: Cd(HDA)2(NO3)2, Cd2(HDA)3(NO3)4, and Cu(HDA)2(MeCN)2·2BF4 (Fig. 1). The ambient-pressure phase α of Cd(HDA)2(NO3)2 transforms into one low-temperature and two high-pressure phases, followed by the progressing sample amorphization at 4 GPa. The α phase of Cd2(HDA)3(NO3)4 transforms to phase β at 1.50 GPa, and its amorphization starts above 4.50 GPa. The crystal of Cu(HDA)2(MeCN)2·2BF4 can be monotonically compressed to 1.20 GPa, when it gradually becomes amorphous. In the structures of these new phases of Cd(HDA)2(NO3)2 and Cd2(HDA)3(NO3)4, the HDA linkers transform between disordered, extended and differently bent conformations. The switching between HDA conformers is accompanied by the coordination-scheme modifications around the metal centre, which further increases the capability of the frameworks for efficiently absorbing the external stress.
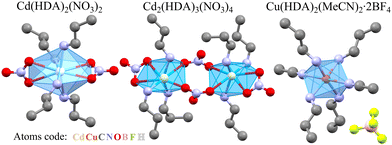 | ||
| Fig. 1 Three coordination polymers with HDA linkers; their halves coordinating one metal cation are shown, and the H-atoms are omitted for clarity. | ||
2. Experimental
All solvents and precursors for the synthesis of Cd(HDA)2(NO3)2, Cd2(HDA)3(NO3)4 and Cu(HDA)2(MeCN)2·2BF4, were purchased from Merck and used without further purification. Single crystals necessary for structural analysis were produced using the one-pot diffusion method.26,51,52 To initiate the diffusion process, the chosen inorganic salt was dissolved in 5 mL of xylene, which was then carefully placed on top of 5 mL of acetonitrile. To slow-down the diffusion process, 2 mL of an acetonitrile–xylene mixture in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) ratio was placed between the two substrate layers. After seven days, many transparent, colourless (Cd(HDA)2(NO3)2, Cd2(HDA)3(NO3)4) and blue (Cu(HDA)2(MeCN)2·2BF4) crystals precipitated.
1 (v/v) ratio was placed between the two substrate layers. After seven days, many transparent, colourless (Cd(HDA)2(NO3)2, Cd2(HDA)3(NO3)4) and blue (Cu(HDA)2(MeCN)2·2BF4) crystals precipitated.
2.1. Synthesis of Cd(HDA)2(NO3)2
A solution of 0.154 g (0.5 mmol) cadmium(II) nitrate tetrahydrate in 5 mL of acetonitrile was carefully covered by 2 mL of the acetonitrile–xylene layer. Separately, 0.058 g (0.5 mmol) HDA was dissolved in 5 mL xylene and carefully placed as the top layer.2.2. Synthesis of Cd2(HDA)3(NO3)4
Cadmium(II) nitrate tetrahydrate (0.154 g, 0.5 mmol) was dissolved in 5 ml of acetonitrile, followed by the addition of HDA (0.034 g, 0.3 mmol) in 5 ml of xylene. The solutions were separated with the acetonitrile–xylene layer.2.3. Synthesis of Cu(HDA)2(MeCN)2·2BF4
A solution of 0.118 g (0.5 mmol) copper(II) tetrafluoroborate hexahydrate in 5 mL acetonitrile was prepared. Separately, 0.058 g (0.5 mmol) HDA was dissolved in 5 mL xylene. The xylene solution was then carefully layered over the acetonitrile solution, with a 2 mL mixture of acetonitrile and xylene (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) placed between the two layers.
1, v/v) placed between the two layers.
2.4. Single-crystal experiments under extreme conditions
All high-pressure experiments were carried out in a modified Merrill-Bassett diamond-anvil cell (DAC), with diamond anvils mounted directly on steel supports with conical windows.53 The gaskets were made of stainless steel 0.3 mm thick, with a hole 0.4 mm in diameter. The Cd(HDA)2(NO3)2 single crystal was isothermally compressed up to 3.70 GPa, Cd2(HDA)3(NO3)4 up to 4.30 GPa, and Cu(HDA)2(MeCN)2·2BF4 up to 1.20 GPa. Daphne 7575 oil was used as the pressure-transmitting medium (PTM) to maintain hydrostatic conditions up to 4.00 GPa at room temperature.54 Before increasing the pressure above 4 GPa, the DAC was heated up to 330 K first to minimize the possibility of the PTM freezing.55 Increasing the temperature to 330 K required for preserving the hydrostaticity of the pressure-transmitting medium, an air-stream heating gun with a digital temperature control was used. The temperature inside the DAC was independently monitored using a laser thermometer. The pressure inside the DAC was measured using the ruby-fluorescence method with a Photon Control spectrometer, affording the accuracy of 0.02 GPa.56 High-pressure single-crystal X-ray diffraction data were collected using a KUMA4CCD diffractometer with a sealed X-ray tube and MoKα radiation 0.71073 Å. The DAC was centred using the gasket-shadow method.57 The DAC absorption, gasket shadowing, and sample absorption were calculated using the Redshabs program.58Low-temperature data were collected using an Xcalibur EOS-CCD diffractometer equipped with a gas-flow Oxford Cryostream attachment. Cd(HDA)2(NO3)2 was studied in the 298 to 100 K range in 50 K steps, when the crystal was gradually cooled at a rate of 40 K min−1, and in a separate experiment the crystal was flash-cooled to 100 K. The CrysAlisPro software was used for data collection and initial data reduction.59
The structure was solved by direct methods (SHELXS) and refined with SHELXL,60 and the Olex2 software was used.61 All non-H atoms were refined with anisotropic thermal parameters. H atoms were located in the difference Fourier map and from the molecular geometry. The structures of the investigated compounds contain no voids or pores capable of absorbing any guests, as illustrated in Fig. S13–S15 (ESI†). The crystallographic information is presented in Table 1. The detailed experimental and crystallographic data were deposited in the Cambridge Structural Database with the CCDC numbers 2262338–2262371.†
| Compound | Cd(HDA)2(NO3)2 | Cd2(HDA)3(NO3)4 | Cu(HDA)2(MeCN)2·2BF4 | |||||
|---|---|---|---|---|---|---|---|---|
| Phase | α | β | γ | δ | α | β | α | α |
| Pressure (GPa) | 0.0001 | 1.10 | 2.10 | 0.0001 | 0.0001 | 2.10 | 0.0001 | 0.0001 |
| Temperature (K) | 298 | 298 | 298 | 100 | 298 | 298 | 298 | 100 |
| Space group | I41/a |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/n | P21 | Fddd | Fddd |
| Unit-cell: a (Å) | 9.7855(7) | 9.350(2) | 9.264(3) | 9.973(8) | 14.3304(4) | 14.206(2) | 12.9608(7) | 13.084(2) |
| b (Å) | 9.7855(7) | 9.725(3) | 9.585(3) | 12.170(1) | 7.0034(2) | 6.6183(4) | 14.1880(8) | 13.9110(14) |
| c (Å) | 21.071(3) | 11.181(5) | 11.069(4) | 18.058(2) | 16.3600(7) | 14.935(2) | 27.6850(17) | 27.113(3) |
| α (°) | 90 | 110.90(3) | 110.41(3) | 74.687(7) | 90 | 90 | 90 | 90 |
| β (°) | 90 | 105.07(3) | 105.98(3) | 74.744(7) | 97.033(3) | 96.11(3) | 90 | 90 |
| γ (°) | 90 | 95.91(2) | 97.17(3) | 68.239(7) | 90 | 90 | 90 | 90 |
| Z/Z′ | 8/0.5 | 4/2 | 4/2 | 8/4 | 4/1 | 4/1 | 8/0.25 | 8/0.25 |
| V m | 252.21 | 223.82 | 214.65 | 241.21 | 407.39 | 349.05 | 636.37 | 616.86 |
3. Results and discussion
The macroscopic strain of any material is accommodated by atomic-scale distortions in the microscopic structure. In the bottom-up approach, the chemical components, their aggregation and structural distortions predefine the macroscopic elastic properties. These structure–property relationships are discussed below for a series of coordination polymers Cd(HDA)2(NO3)2, Cd2(HDA)3(NO3)4 and Cu(HDA)2(MeCN)2·2BF4, all involving the easily transformable HDA linkers in different coordination schemes.3.1. Monotonic compression of Cd(HDA)2(NO3)2
At 298 K, in the structure of Cd(HDA)2(NO3)2 phase α, the cadmium cation is coordinated by four HDA linkers and by two NO3− anions in symmetric bidentate-chelating mode (Fig. 1 and Table 1).62 This 3-dimensional framework is highly symmetric: all HDA ligands lie on the inversion centres located at the midpoint of the C3–C3i bond and bind the Cd2+ cations, located at the centres of![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) axes. The ethylene fragment C3H2–C3iH2 of the HDA ligand is disordered in two sites, labelled A and B. Surprisingly, the disorder magnitude increases as phase α is compressed: from the site occupation factors SOFA = 0.28(2) and SOFB = 0.72(2) at 298 K/0.1 MPa to SOFA = 0.44(3) and SOFB = 0.56(3) at 0.85 GPa (Fig. S4, ESI†). In most systems, the compression enhances the interactions between disordered sites and their crystal environments, increasing the internal energy. This effect can be diminished when the disorder is eliminated. Thus the counterintuitive increase of the disorder in α-Cd(HDA)2(NO3)2 indicates that the reduced length of HDA linkers favours the less-populated disordered site A. This is a clear indication that the conformation of HDA linkers and the crystal compression are strongly interdependent. This asymptotic change of the SOFA and SOFB values to 0.5 is terminated at the phase transition at 1.10 GPa.
axes. The ethylene fragment C3H2–C3iH2 of the HDA ligand is disordered in two sites, labelled A and B. Surprisingly, the disorder magnitude increases as phase α is compressed: from the site occupation factors SOFA = 0.28(2) and SOFB = 0.72(2) at 298 K/0.1 MPa to SOFA = 0.44(3) and SOFB = 0.56(3) at 0.85 GPa (Fig. S4, ESI†). In most systems, the compression enhances the interactions between disordered sites and their crystal environments, increasing the internal energy. This effect can be diminished when the disorder is eliminated. Thus the counterintuitive increase of the disorder in α-Cd(HDA)2(NO3)2 indicates that the reduced length of HDA linkers favours the less-populated disordered site A. This is a clear indication that the conformation of HDA linkers and the crystal compression are strongly interdependent. This asymptotic change of the SOFA and SOFB values to 0.5 is terminated at the phase transition at 1.10 GPa.
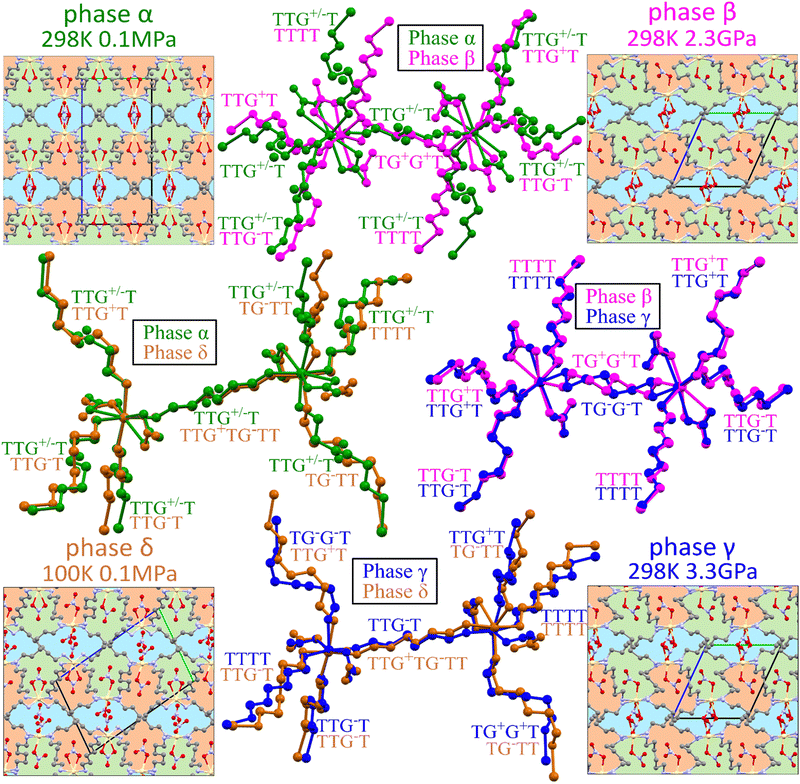
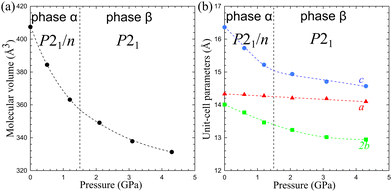
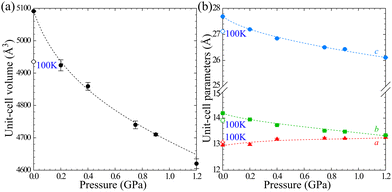
The volume compression of phase α up to 1.10 GPa is monotonic and the average compressibility calculated for this pressure range as βv = −1/V ∂V/∂p is 0.092(2) GPa−1. The linear compressibilities defined as βa = −1/a ∂a/∂p and βc = −1/c ∂c/∂p for direction [100] and [001], respectively, exhibit the clearly non-linear behaviour. In the pressure range between 0.1 MPa and 0.20 GPa the compressibility βa = 0.033(1) GPa−1 is significantly larger than βc = 0.027(1) GPa−1, but above this pressure, βa rapidly decreases, and between 0.50 GPa and 0.85 GPa βa = 0.012(1) GPa−1, while βc = 0.026(1) GPa−1. These changes, and particularly the convex shape of the compression function of parameter c (Fig. 2), herald a transition to phase β at 1.10 GPa, marked by an abrupt volume drop of circa 2.5%. The triclinic symmetry of phase β implies that the transition between phases α and β is ferroelastic. The unit-cell of phase β comprises one node, i.e. half of the unit-cell contents of phase α, as described by the transformation matrices specified in Fig. 2(b) (cf.Table 1).
 | ||
| Fig. 2 The unit-cell parameters of crystal Cd(HDA)2(NO3)2, all calculated for the tetragonal setting of phase α (cf. the matrices in Fig. 2(b)) as a function of pressure. The ESD's are smaller than the plotted symbols. The vertical dashed lines mark the critical pressures between the phases. The lines joining the points are for guiding the eye only. | ||
3.2. Anomalous compression of Cd(HDA)2(NO3)2
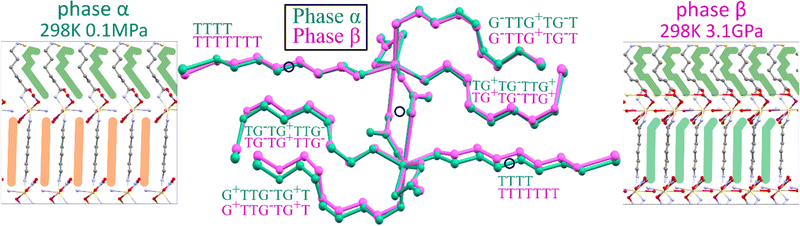
The 1st-order transition of Cd(HDA)2(NO3)2 from phase α to phase β is marked by the volume discontinuity. The unit-cell parameters a and c abruptly shrink by about 2%, while b increases its length by circa 2% (Fig. 2) and the crystal displays a strong shear strain and the unit-cell angle increases up to circa 7° for angle βα (Fig. S1, ESI†). All these changes sum up to the 2.5% volume drop.Our X-ray diffraction determination of the crystal structure of phase β shows that the HDA linkers become ordered, their conformation changes and the coordination scheme around the cadmium cation is modified. The main structural changes are: the metal-anion bonding is altered, as one of two NO3− groups rotates and moves away from the Cd cation (cf. Fig. S2 in the ESI†); the significant change in coordination angles at the metal centre breaks the site symmetry of the Cd cation, from S4 to C1, which reduces the symmetry of the crystal field, too; the changed Cd-coordination scheme interplays with the new conformations assumed by the HDA ligands. In phase β, the four HDA linkers remain located on the inversion centres, which are independent special positions of space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . The Ci-symmetric HDA conformers can be described by three torsion angles N1–C1–C2–C3 (τ1), C1–C2–C3–C3i (τ2) and C2–C3–C3i–C2i (τ3), where superscript i indicates the atoms related through one of the independent inversion centres (symmetry codes: 2 − x, −y, −z; 1 − x, 2 − y, −z; 3 − x, 2 − y, 1 − z; and 1 − x, 1 − y, 1 − z). An additional torsion angle Cd–N1–C1–C2 (τo) describes the position of the coordination bond Cd–N relative to the HDA linker. The torsion angles in HDA are close either to 180° or to ± 60°, which corresponds to anti (denoted T) or gauche+/gauche− (G+/G−) conformations, in analogy to the tetrahedral form assumed by all ethane-like molecules.63 Hence, the HDA conformers and their coordination directions can be conveniently represented by 7-letter descriptors, as shown in Fig. 3. These full 7-letter descriptors can be shortened to the 4-letter descriptors for the Ci symmetric HDA linkers. For phase α, descriptor TTG+T for site A can be extended to TTG+TG−TT and descriptor TTG−T for site B extends to TTG−TG+TT. Thus, in phase α only one HDA conformer is present, but in two symmetry-independent sites A and B, with different SOFs.
. The Ci-symmetric HDA conformers can be described by three torsion angles N1–C1–C2–C3 (τ1), C1–C2–C3–C3i (τ2) and C2–C3–C3i–C2i (τ3), where superscript i indicates the atoms related through one of the independent inversion centres (symmetry codes: 2 − x, −y, −z; 1 − x, 2 − y, −z; 3 − x, 2 − y, 1 − z; and 1 − x, 1 − y, 1 − z). An additional torsion angle Cd–N1–C1–C2 (τo) describes the position of the coordination bond Cd–N relative to the HDA linker. The torsion angles in HDA are close either to 180° or to ± 60°, which corresponds to anti (denoted T) or gauche+/gauche− (G+/G−) conformations, in analogy to the tetrahedral form assumed by all ethane-like molecules.63 Hence, the HDA conformers and their coordination directions can be conveniently represented by 7-letter descriptors, as shown in Fig. 3. These full 7-letter descriptors can be shortened to the 4-letter descriptors for the Ci symmetric HDA linkers. For phase α, descriptor TTG+T for site A can be extended to TTG+TG−TT and descriptor TTG−T for site B extends to TTG−TG+TT. Thus, in phase α only one HDA conformer is present, but in two symmetry-independent sites A and B, with different SOFs.
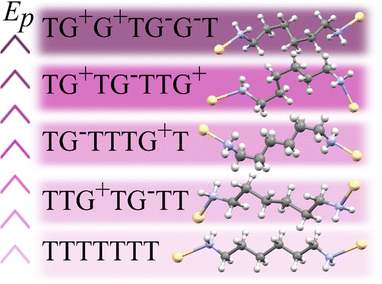 | ||
| Fig. 3 A sequence of selected HDA linkers coordinating Cd cations arranged according to the potential energies (Ep) of isolated conformers,59 from the lowest-Ep conformer TTTT, up. | ||
The volume compressibility of phase β, βvβ = 0.027(3) GPa−1 is significantly lower compared to phase α, βvα = 0.092(2) GPa−1, although the convex pressure dependence of parameter c is retained. This exceptional compression can be connected with the progressing structural changes in the Cd coordination and HDA conformation. The transition to phase β eliminates the disorder of the HDA linkers, and also differentiates their conformations: from one disordered between two conformers TTG+T/TTG−T in phase α; to four ordered conformers TTG+T, TTG−T, TTTT and TG+G+T in phase β (Fig. 4). It should be noted that in phase β the neighbouring coordination centres have the HDA conformers ‘reflected’ in the inversion centres, to TTG−T, TTG+T, TTTT and TG−G−T, respectively. Consequently, in the structure of phase β there are 3 conformer types TTG−TG+TT, TG−G−TG+G+ and TTTTTTT present in the ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. These HDA conformations and the Cd coordination characteristic of phase β, are preserved up to 2.00 GPa, when an isostructural transition to phase γ takes place, marked by discontinuities of the unit-cell parameters (Fig. 2).
1. These HDA conformations and the Cd coordination characteristic of phase β, are preserved up to 2.00 GPa, when an isostructural transition to phase γ takes place, marked by discontinuities of the unit-cell parameters (Fig. 2).
In the γ-phase, the set of 4 HDA conformers coordinating each Cd cation – either TTTT, TTG−T, TTG+T and TG−G−T, or TTTT, TTG+T, TG+G+T and the 3 conformers types – TTTTTTT, TTG−TG+TT and TG−G−TG+G+T – are retained, but the structure of phase γ is clearly differentiated by the reversal of conformer TG+G+TG−G−T to TG−G−TG+G+T. In other words, the frameworks of phases β and γ can be overlaid with all its components well matched, except for the reversed TG+G+T and TG−G−T linkers, as shown in Fig. 4. It can be observed that the positions of anions NO3− are hardly changed. Thus the main difference between the structures of phases β and γ is the reversal of HDA conformer TG+G+TG−G−T. It coincides with the large discontinuity of the unit-cell parameter b and subtle discontinuities of parameters a and c (Fig. 2). This structural feature of reversed conformation in one HDA linker leads to a significantly larger compressibility of phase γ (βvγ = 0.062(2) GPa−1) than that of phase β (βvβ = 0.027(3) GPa−1).
3.3. Temperature effect on Cd(HDA)2(NO3)2
Lowering temperature hardly affects the disorder in the HDA linkers in phase α. The TTG+T and TTG−T conformers disordered with SOFA = 0.28(2) and SOFB = 0.72(2) at 298 K, at 250 K refined to SOFA = 0.30(1) and SOFB = 0.70(1); and at 200 K to SOFA = 0.25(1) and SOFB = 0.75(1). This indicates that the disorder is either static or that its relaxation time is very long. Our next measurement at 150 K revealed a new triclinic phase δ, of space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) different from the high-pressure phases β and γ (Table 1). The unit-cell of phase δ is twice larger than those of phases β and γ (Fig. 4). In phase δ, the crystal symmetry is reduced to P
different from the high-pressure phases β and γ (Table 1). The unit-cell of phase δ is twice larger than those of phases β and γ (Fig. 4). In phase δ, the crystal symmetry is reduced to P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and the unit cell accommodates 4 symmetry-independent formula units. Consequently, the asymmetric unit in phase δ includes two Cd2+ cations, four HDA molecules, and four NO3− anions. The cations and anions are located at general (asymmetric) positions, and there are six independent halves of the HDA molecules lying on the inversion centres. Thus, the main structural changes in phase δ involve the coordination schemes of two independent Cd2+ cations, as well as the conformations of the HDA linkers, one asymmetric and six Ci-symmetric ones. Their conformation is approximated by one full 7-letter descriptor and six 4-letter descriptors. Both Cd2+ cations are similarly octahedrally coordinated by six ligands: two NO3 anions, and four HDA linkers (Fig. 4). The HDA conformers around cadmium cations are listed in Table 2. The uneven distribution of conformers correlates with twice more populated TTG−T of SOFB = 0.72(2) observed for phase α at 298 K. Interestingly, phase α can be flash-cooled to 100 K. This observation combined with measurements performed at 250 and 200 K, suggests that the disorder is either static at room temperature or that the kinetics of dynamic disorder is slow compared to rapid freezing of phase α into its metastable state. Noteworthy, in phase α supercooled to 100 K the disorder of the HDA linker in its two sites increases to SOFA = 0.40(2) and SOFB = 0.60(2). This is caused by the thermal contraction increasing the crystal-field energy (Fig. S3, ESI†): the crystal volume at 100 K is similar to that of the crystal compressed to 0.60 GPa, hence the similar disorder rate at these low-temperature/ambient pressure and room-temperature/high-pressure conditions (see Section 3.1).
and the unit cell accommodates 4 symmetry-independent formula units. Consequently, the asymmetric unit in phase δ includes two Cd2+ cations, four HDA molecules, and four NO3− anions. The cations and anions are located at general (asymmetric) positions, and there are six independent halves of the HDA molecules lying on the inversion centres. Thus, the main structural changes in phase δ involve the coordination schemes of two independent Cd2+ cations, as well as the conformations of the HDA linkers, one asymmetric and six Ci-symmetric ones. Their conformation is approximated by one full 7-letter descriptor and six 4-letter descriptors. Both Cd2+ cations are similarly octahedrally coordinated by six ligands: two NO3 anions, and four HDA linkers (Fig. 4). The HDA conformers around cadmium cations are listed in Table 2. The uneven distribution of conformers correlates with twice more populated TTG−T of SOFB = 0.72(2) observed for phase α at 298 K. Interestingly, phase α can be flash-cooled to 100 K. This observation combined with measurements performed at 250 and 200 K, suggests that the disorder is either static at room temperature or that the kinetics of dynamic disorder is slow compared to rapid freezing of phase α into its metastable state. Noteworthy, in phase α supercooled to 100 K the disorder of the HDA linker in its two sites increases to SOFA = 0.40(2) and SOFB = 0.60(2). This is caused by the thermal contraction increasing the crystal-field energy (Fig. S3, ESI†): the crystal volume at 100 K is similar to that of the crystal compressed to 0.60 GPa, hence the similar disorder rate at these low-temperature/ambient pressure and room-temperature/high-pressure conditions (see Section 3.1).
| Compound | Phase α | Phase β | Phase γ | Phase δ | |
|---|---|---|---|---|---|
| Cd(HDA)2(NO3)2 | (α: 298 K; <1.10 GPa) | (β: 298 K; 1.10–2.00 GPa) | (γ: 298 K; >2.00 GPa) | (δ: >150 K; 0.1 MPa) | |
| Site A TTG+T | HDA-1 TTG+T | HDA-1 TTG+T | HDA-1 TTG+TTG−TT | ||
| Site B TTG−T | HDA-2 TTTT | HDA-2 TTTT | HDA-2 TTG−T | HDA-5 TTTT | |
| HDA-3 TTG−T | HDA-3 TTG−T | HDA-3 TTG−T | HDA-6 TG−TT | ||
| HDA-4 TG+G+T | HDA-4 TG−G−T | HDA-4 TTG+T | HDA-7 TG−TT | ||
| Cd2(HDA)3(NO3)4 | (α: 298 K; <1.50 GPa) | (β: 298 K; >1.50 GPa) | |||
| HDA-1 TG+TG−TTG+ | HDA-1 TG+TG−TTG+ | ||||
| HDA-2 TTTT | HDA-2 TTTTTTT | ||||
| HDA-3 TG−TG+TTG− | |||||
| Cu(HDA)2(MeCN)2·2BF4 | HDA-1 TTTT | ||||
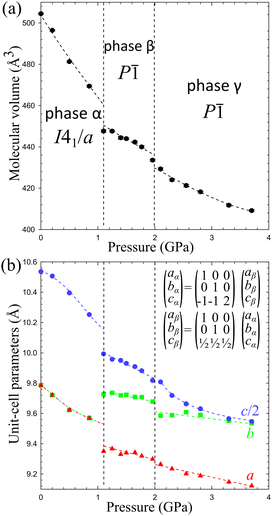
3.4. Compression of Cd2(HDA)3(NO3)4
Under ambient conditions, Cd2(HDA)3(NO3)4 crystallizes in monoclinic phase α (Table 1). The pseudo-octahedral coordination sphere of Cd2+ ions involves three HDA molecules and three NO3− anions. There are one-and-a-half independent HDA linkers, hence one 7-letter descriptor and one 4-letter descriptor are required for describing their conformation (Table 2). These descriptors are TG+TG−TTG+ and TTTT, respectively. The low-energy HDA conformer TTTT extends along the least-compressed crystal direction [x] (Fig. 5). Hence the high volume compressibility βv = 0.141(4) GPa−1 of phase α is associated with the conformational freedom of asymmetric HDA linkers TG+TG−TTG+. The deformation of the coordination geometry results from the bidentate coordination mode of one NO3− ion. Its two oxygen atoms can be considered as one coordination site due to their small bite angle. The remaining two anions link the adjacent metallic centres in an anti–anti mode, forming a Cd2(HDA)6(NO3)4 moiety related by an inversion centre located at the midpoint of this dinuclear centre (Fig. 6).The phase transition between phases α and β can be associated with the region between the initial stronger and weaker compression at about 1.50 GPa (Fig. 5). The transition is clearly corroborated by disappeared systematic absences of the glide plane n (Fig. S7, ESI†), marking the symmetry lowering to space group P21, a subgroup of space group P21/n of phase α. The absence of a discontinuous volume change and the group–subgroup symmetry relationship between phases α and β suggest the 2nd order character of this phase transition.
In phase β, the nitrate linkers become independent and freely change their alignment, which leads to tight packing affecting the elastic properties of Cd2(HDA)3(NO3)4. Above 1.50 GPa, direction c is no longer the softest, βc = 0.022(1) GPa−1 (compared to βc = 0.098(1) GPa−1 in phase α), and c decreases only by 2.5% up to 4.30 GPa. This is a drastic change, which also affects the volume compression. Due to the lower symmetry of phase β, three HDA conformers TG+TG−TTG+, TTTTTTT and TG−TG+TTG− become fully independent (Fig. 6). The three unconstrained linkers provide additional means to absorb mechanical stress, increasing the number of degrees of freedom to 21 (compared to 10 in phase α). It must be noted that although the HDA-conformer descriptors remain the same for phases α and β, the changes in the torsion angles along the Cd←N–C–C–C–C–C–C–N→Cd chains are very strong, of tens of degrees. These distortions in phase β significantly differentiate two independent HDA linkers TG+TG−TTG+ from its reflection TG−TG+TTG−, as well as the halves of the TTTTTTT linker. The further compression to 4.30 GPa triggers a gradual amorphization of phase β, and above 5.00 GPa no diffraction reflections can be collected. It is plausible that the relatively rigid linkers, consistent with the HDA molecules in the TTTTTTT conformation, at some point yield under pressure by changing their conformation in an uncorrelated manner, which eventually leads to the loss of long-range translational order and pressure-induced amorphization of the crystal.
In Cd2(HDA)3(NO3)4, the cation is connected with three HDA linkers and three NO3− anions. One of the nitrate, is linked to two cadmium cations forming a rare bimetallic centre (only in 3% from all 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760 nitrate complexes deposited in the CCDC database, ver. 2022.3.0 features a NO3 group in the bridging coordination mode). The other nitrate ligand occupying one coordination site, interacts with the neighbouring bimetallic centre through a π–hole interaction to the adjacent nitrate group additionally aggregating the framework. Recently it was proposed that interactions analogous to those between hydrogen and halogen bonds,64 where electron-rich entities interact with positive electrostatic potential, may occur in conjugated π-systems. Such a directional NO3⋯NO3 interactions can contribute the aggregation of the neighbouring Cd2(HDA)6(NO3)4 units. This attractive interaction appears similar to that observed in 4-amino-4′-nitrobiphenyl, where NO2⋯NO2 interactions were found to be equally or even less repulsive than NH2⋯NO2 interactions.64 The attractive character of the NO3⋯NO3 interaction well agrees with a significant reduction of the contact distance to 3.30 Å at 1.20 GPa (Fig. 7). The pressure-induced changes in the structure of unusual binuclear metallic centres increases the compression along the [z] direction, as testified by the decreasing distance between the metallic centres.
760 nitrate complexes deposited in the CCDC database, ver. 2022.3.0 features a NO3 group in the bridging coordination mode). The other nitrate ligand occupying one coordination site, interacts with the neighbouring bimetallic centre through a π–hole interaction to the adjacent nitrate group additionally aggregating the framework. Recently it was proposed that interactions analogous to those between hydrogen and halogen bonds,64 where electron-rich entities interact with positive electrostatic potential, may occur in conjugated π-systems. Such a directional NO3⋯NO3 interactions can contribute the aggregation of the neighbouring Cd2(HDA)6(NO3)4 units. This attractive interaction appears similar to that observed in 4-amino-4′-nitrobiphenyl, where NO2⋯NO2 interactions were found to be equally or even less repulsive than NH2⋯NO2 interactions.64 The attractive character of the NO3⋯NO3 interaction well agrees with a significant reduction of the contact distance to 3.30 Å at 1.20 GPa (Fig. 7). The pressure-induced changes in the structure of unusual binuclear metallic centres increases the compression along the [z] direction, as testified by the decreasing distance between the metallic centres.
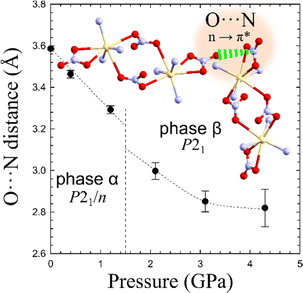 | ||
| Fig. 7 Distance O⋯N between adjacent bidentate NO3–ligands interacting by a π* ← n O⋯N interaction aggregating adjacent binuclear centers (cf. Fig. S11, ESI†). | ||
3.5. Amorphization of Cu(HDA)2(MeCN)2·2BF4
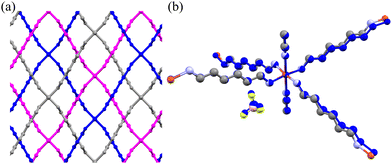
Under ambient conditions, Cu(HDA)2(MeCN)2·2BF4 crystallizes in the orthorhombic space group Fddd. The HDA linkers bind the [Cu(MeCN)2]2+ centres into three interwoven frameworks of diamond-like topology, with the cages accommodating the tetrafluoroborate anions (Fig. 1, 8 and Fig. S12, ESI†).65 The presence of the tetrahedral anions additionally support the interwoven diamond-like frameworks, and no phase transitions were detected in the low-temperature range down to 100 K and under high pressure up to 1.20 GPa. In the highly-symmetric Cu(HDA)2(MeCN)2·2BF4 structure all HDA linkers are symmetry-related, located on inversion centres. However, starting from about 1.20 GPa we observed a gradual decrease of reflection intensities marking the amorphization of the crystal. It is plausible that the mechanical stress leads to uncorrelated changes in the HDA conformers resulting in the destruction of the long-range order. The crystal volume at 1.20 GPa appears lower than expected from the curve fitted to the point in the 0–1 GPa range, which is consistent with the conformational shortening of the HDA linkers (Fig. 3).The crystal compression up to 1.20 GPa is monotonic with no significant conformational changes (Fig. 8(b)). The compression is strongly non-linear and anisotropic (Fig. 9). The latter is visible in the compression of the crystal along [z], by about −3% between 0.1 MPa and 1.00 GPa, and in the negative linear compressibility (NLC) of about 1% (βa = −0.044(1) GPa−1). The Cu(HDA)2(MeCN)2·2BF4 crystal displays a similar anisotropy in its thermal expansion, when cooled to 100 K. This behaviour is consistent with the rule of reverse effects of pressure and temperature, and the crystal exhibits negative thermal expansion along [x].66,67
The mechanism of the NLC can be explained by the wine-rack mechanism.21,68,69 The strongest compression occurs along the shortest diameter of the voids (i.e. along [z], Fig. 8(a)) and the NLC in such structures usually occurs along the longest diameter of the voids, which is consistent for the Cu(HDA)2(MeCN)2·2BF4 crystal.
3.6. Applications of pressure-induced effects in Cd(HDA)2(NO3)2, Cd2(HDA)3(NO3)4 and Cu(HDA)2(MeCN)2·2BF4
All three compounds Cd(HDA)2(NO3)2, Cd2(HDA)3(NO3)4, and Cu(HDA)2(MeCN)2·2BF4 begin to amorphize above 4.0, 4.5, and 1.2 GPa, respectively. This process correlates with the number of TTTT conformers of HDA. The structure of Cu(HDA)2(MeCN)2·2BF4 built exclusively from the HDA conformers TTTT displays the lowest amorphization pressure; the next lowest one is Cd(HDA)2(NO3)2, which can be connected to one TTTT conformer among 4 linkers; in Cd2(HDA)3(NO3)4 phase β there are no TTTT conformers (Ci-symmetric ones), while torsion angles in the only TTTTTTT conformer are significantly distorted, up to 55°, from the idealized conformation anti (180°).The anomalous compression and the symmetry change of Cd(HDA)2(NO3)2 involve (i) the Cd2+ coordination; (ii) disorder of HDA ligands and (iii) the conformational changes of the HDA ligands. The unusual convex pressure dependence of the linear compression indicates that more force is initially required for the unit compression than at higher pressure. In other words, the linear compressibility βx = −1/x ∂x/∂p at T = const. increases with pressure, which is opposite to the usual concave shape of the compression, i.e. a gradual decrease of βx (Table 3). The mechanism of the structural transformations leading to the convex compression can be connected with the gradual conformational changes, and in particular, in the framework of Cd(HDA)2(NO3)2, with the gradual bending of the HDA linkers (the buckling-stick mechanism).
| Compound | Phase | β v (GPa−1) | β a (GPa−1) | β b (GPa−1) | β c (GPa−1) |
|---|---|---|---|---|---|
| Cd(HDA)2(NO3)2 | α | 0.092(2) | 0.033(1) | 0.033(1) | 0.027(1) |
| (α: 298 K; <1.10 GPa) | β | 0.027(3) | 0.012(1) | 0.003(1) | 0.026(1) |
| (β: 298 K; 1.10–2.00 GPa) | γ | 0.062(2) | 0.016(1) | −0.002(1) | 0.045(1) |
| (γ: 298 K; >2.00 GPa) | |||||
| Cd2(HDA)3(NO3)4 | α | 0.141 (4) | 0.002(1) | 0.043(1) | 0.098(1) |
| (α: 298 K; <1.50 GPa) | β | 0.043(2) | 0.003(1) | 0.019(1) | 0.022(1) |
| (β: 298 K; >1.50 GPa) | |||||
| Cu(HDA)2(MeCN)2·2BF4 | α | 0.219(2) | −0.044(1) | 0.081(1) | 0.076(1) |
Interestingly, the volume compressibility βv for crystal Cu(HDA)2(MeCN)2·2BF4 is the highest, and that for Cd2(HDA)3(NO3)4 is the second highest (Table 3). These βv values belong to the largest ones reported in the literature (cf. Table S1 in the ESI†). The large volume compressibility at 0.1 MPa is advantageous for barocaloric applications,48,49 however the volume drop at the phase transition, due to their high critical pressure (Table 3), above 1 GPa, significantly hinders their immediate application.
It can be noted that the compressibility of all coordination polymers studied in this work is strongly anisotropic. For the crystals of Cu(HDA)2(MeCN)2·2BF4 the largest negative linear compressibility (NLC) is observed. The NLC is also observed for the high-pressure γ-phase of Cd(HDA)2(NO3)2, while the α-phase of Cd2(HDA)3(NO3)4 exhibits a nearly zero linear compressibility along [100]. Such materials are sought for their possible applications in sensors and compression resisting devices.
4. Conclusion
The compression of Cd(HDA)2(NO3)2, Cd2(HDA)3(NO3)4 and Cu(HDA)2(MeCN)2·2BF4 highlights the role of flexible HDA linkers for the elastic properties of coordination polymers. Their monotonic compression and phase transitions primarily involve the conformational disorder and transformations of HDA ligands. Several anomalous compression effects and phase transitions related to the HDA linkers have been revealed. For the structure of Cd(HDA)2(NO3)2 the unusual convex compression, meaning that more force is needed for unit compression under lower pressures than at higher pressures, has been explained by the buckling-stick mechanism. This increasing compression is terminated by a conformational conversion of HDA linkers, triggering a ferroelastic phase transition. In the new phase, the new HDA conformers lead to increased linear compression due to the buckling-stick mechanism resulting in another conformational phase transition. Interestingly, in the analogous structure of Cd2(HDA)3(NO3)4 only one single-crystal to single-crystal phase transition occurs. At still higher pressure both these coordination polymers undergo pressure-induced amorphization.The triple-interwoven diamond-like frameworks of Cu(HDA)2(MeCN)2·2BF4, formed from the lowest-energy HDA conformers TTTT, does not undergo phase transitions but begin to lose their long-range order already at 1.20 GPa.
The intricate interplay between the structural dynamics and elastic properties of coordination polymers revealed in these solid-state transformations highlights the pivotal role of conformational conversions of the HDA linkers. Owing to their conformational flexibility and stepwise transformations, the elastic properties of coordination frameworks involving the HDA linkers are more complex and the landscape of structural transformations becomes more rich compared to the coordination polymers with the rigid linkers only. Therefore the application of soft linkers offers new avenues for controlling and manipulating properties of coordination polymers. We hope that our work will stimulate further investigations on anomalous elastic properties in coordination polymers, their transitions and amorphization, and that it will be useful for the design and optimization of materials for a variety of new applications. For example, the linear compressibility increasing with pressure can be applied in smart shock-absorbing layers, for engineering stress-dependent clinging surfaces, or other elements (surfaces and objects) of counterintuitive elasticity.
Author contributions
A. P. performed the syntheses, crystallizations, and high-pressure X-ray diffraction characterization and wrote the draft of the article; contributed to the conception, design, and data acquisition. S. S. discussed the idea, methodology, results, commented on the manuscript; contributed to conception, design, and data acquisition. A. K. supervision, writing – review & editing. All the authors contributed to the last version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the Polish National Science Centre (grant no. UMO-2019/35/N/ST5/01838). AP also thanks grant POWR.03.02.00-00-I026/16 co-financed by the European Union through the European Social Fund under the Operational Program Knowledge Education Development for the financial support.Notes and references
- H. C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674 CrossRef CAS PubMed.
- H. C. J. Zhou and S. Kitagawa, Chem. Soc. Rev., 2014, 43, 5415–5418 RSC.
- Y. R. Lee, J. Kim and W. S. Ahn, Korean J. Chem. Eng., 2013, 30, 1667–1680 CrossRef CAS.
- M. Safaei, M. M. Foroughi, N. Ebrahimpoor, S. Jahani, A. Omidi and M. Khatami, Trends Anal. Chem., 2019, 118, 401–425 CrossRef CAS.
- C. L. Hobday and G. Kieslich, Dalton Trans., 2021, 50, 3759–3768 RSC.
- I. E. Collings and A. L. Goodwin, J. Appl. Phys., 2019, 126, 1–13 CrossRef.
- Y. Lv, H. Cui, P. Liu, F. Hao, W. Xiong and H. Luo, J. Catal., 2019, 372, 330–351 CrossRef CAS.
- C. W. Chen, Z. Y. Yang, H. C. Yang, Y. Z. Hsieh, C. Liu, Y. C. Chuang, J. J. Le, S. P. Rwei, I. J. Hsu and H. H. Chen, Polymer, 2021, 232, 124162 CrossRef CAS.
- V. Balladur, P. Fouilloux and C. de Bellefon, Appl. Catal., A, 1995, 133, 367–376 CrossRef CAS.
- R. A. Omar, A. I. Gheni and K. A. Omar, Indian J. Nat. Sci., 2016, 66, 976–997 Search PubMed.
- M. N. Uddin, M. S. Amin, M. S. Rahman, S. Khandaker, W. Shumi, M. A. Rahman and S. M. Rahman, Appl. Organomet. Chem., 2021, 35, 1–17 Search PubMed.
- Y. G. Li, Q. B. Jiang, K. Cheng, H. Yan and H. L. Zhu, Z. Anorg. Allg. Chem., 2009, 635, 2572–2578 CrossRef CAS.
- A. Pladzyk and K. Baranowska, J. Mol. Struct., 2014, 1058, 252–258 CrossRef CAS.
- J. E. D. Davies and A. M. Maver, J. Mol. Struct., 1983, 102, 203–204 CrossRef CAS.
- S. Jiang, R. Shi, H. Cheng, C. Zhang and F. Zhao, Green Energy Environ., 2017, 2, 370–376 CrossRef.
- K. Kim, S. Park, K. M. Park and S. S. Lee, Cryst. Growth Des., 2011, 11, 4059–4067 CrossRef CAS.
- X. Huang, M. Roushan, T. J. Emge, W. Bi, S. Thiagarajan, J. H. Cheng, R. Yang and J. Li, Angew. Chem., Int. Ed., 2009, 48, 7871–7874 CrossRef CAS PubMed.
- S. Akine, M. Miyashita and T. Nabeshima, J. Am. Chem. Soc., 2017, 139, 4631–4634 CrossRef CAS PubMed.
- F. X. Coudert, Chem. Mater., 2015, 27, 1905–1916 CrossRef CAS.
- I. E. Collings and A. L. Goodwin, J. Appl. Phys., 2019, 126, 181101 CrossRef.
- A. Półrolniczak, S. Sobczak, V. Nikolayenko, L. Barbour and A. Katrusiak, Dalton Trans., 2021, 50, 17478–17481 RSC.
- K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2008, 130, 10524–10526 CrossRef CAS PubMed.
- J. Im, N. Yim, J. Kim, T. Vogt and Y. Lee, J. Am. Chem. Soc., 2016, 138, 11477–11480 CrossRef CAS PubMed.
- S. Sobczak and A. Katrusiak, Cryst. Growth Des., 2018, 18, 1082–1089 CrossRef CAS.
- S. Sobczak and A. Katrusiak, Inorg. Chem., 2019, 58, 11773–11781 CrossRef CAS PubMed.
- A. Półrolniczak and A. Katrusiak, Mater. Adv., 2021, 2, 4677–4684 RSC.
- A. Półrolniczak, S. Sobczak and A. Katrusiak, Inorg. Chem., 2018, 57, 8942–8950 CrossRef PubMed.
- V. I. Nikolayenko, S. A. Herbert and L. J. Barbour, Chem. Commun., 2017, 53, 11142–11145 RSC.
- C. L. Hobday, C. H. Woodall, M. J. Lennox, M. Frost, K. Kamenev, T. Düren, C. A. Morrison and S. A. Moggach, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- S. C. McKellar, J. Sotelo, A. Greenaway, J. P. S. Mowat, O. Kvam, C. A. Morrison, P. A. Wright and S. A. Moggach, Chem. Mater., 2016, 28, 466–473 CrossRef CAS.
- P. D. Southon, L. Liu, E. A. Fellows, D. J. Price, G. J. Halder, K. W. Chapman, B. Moubaraki, K. S. Murray, J. F. Létard and C. J. Kepert, J. Am. Chem. Soc., 2009, 131, 10998–11009 CrossRef CAS PubMed.
- W. Li, M. R. Probert, M. Kosa, T. D. Bennett, A. Thirumurugan, R. P. Burwood, M. Parinello, J. A. K. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2012, 134, 11940–11943 CrossRef CAS PubMed.
- A. U. Ortiz, A. Boutin, K. J. Gagnon, A. Clearfield and F. X. Coudert, J. Am. Chem. Soc., 2014, 136, 11540–11545 CrossRef CAS PubMed.
- Z. Chen, B. Xu, Q. Li, Y. Meng, Z. Quan and B. Zou, Inorg. Chem., 2020, 59, 1715–1722 CrossRef CAS PubMed.
- W. Cai, A. Gładysiak, M. Anioła, V. J. Smith, L. J. Barbour and A. Katrusiak, J. Am. Chem. Soc., 2015, 137, 9296–9301 CrossRef CAS PubMed.
- M. Andrzejewski and A. Katrusiak, J. Phys. Chem. Lett., 2016, 279–284 Search PubMed.
- R. J. Angel, N. L. Ross, E. C. Spencer, J. A. K. Howard and B. E. Hanson, J. Am. Chem. Soc., 2009, 131, 4022–4026 CrossRef PubMed.
- E. C. Spencer, M. S. R. N. Kiran, W. Li, U. Ramamurty, N. L. Ross and A. K. Cheetham, Angew. Chem., Int. Ed., 2014, 53, 5583–5586 CrossRef CAS PubMed.
- M. Andrzejewski, N. Casati and A. Katrusiak, Dalton Trans., 2017, 46, 14795–14803 RSC.
- X. Zhang, G. Li, Y. Zhang, D. Luo, A. Yu, X. Wang and Z. Chen, Nano Energy, 2021, 86, 106094 CrossRef CAS.
- A. S. Babal, B. E. Souza, A. F. Möslein, M. Gutiérrez, M. D. Frogley and J. C. Tan, ACS Appl. Electron. Mater., 2021, 3, 1191–1198 CrossRef CAS.
- A. S. Poryvaev, D. M. Polyukhov and M. V. Fedin, ACS Appl. Mater. Interfaces, 2020, 12, 16655–16661 CrossRef CAS PubMed.
- A. Hazra and T. K. Maji, Inorg. Chem., 2020, 59, 12793–12801 CrossRef CAS PubMed.
- S. Kusaka, A. Kiyose, H. Sato, Y. Hijikata, A. Hori, Y. Ma and R. Matsuda, J. Am. Chem. Soc., 2019, 141, 15742–15746 CrossRef CAS PubMed.
- T. Iizuka, N. Hosono and T. Uemura, Dalton Trans., 2022, 51, 13204–13209 RSC.
- A. J. Graham, D. R. Allan, A. Muszkiewicz, C. A. Morrison and S. A. Moggach, Angew. Chem., Int. Ed., 2011, 50, 11138–11141 CrossRef CAS PubMed.
- E. Patyk-Kaźmierczak, M. R. Warren, D. R. Allan and A. Katrusiak, Phys. Chem. Chem. Phys., 2017, 19, 9086–9091 RSC.
- M. Szafrański, W. J. Wei, Z. M. Wang, W. Li and A. Katrusiak, APL Mater., 2018, 6(10), 100701 CrossRef.
- D. Boldrin, Appl. Phys. Lett., 2021, 118(17), 170502 CrossRef CAS.
- G. C. Pugh, J. R. Burns and S. Howorka, Nat. Rev. Chem., 2018, 2, 113–130 CrossRef CAS.
- M. Andrzejewski and A. Katrusiak, J. Phys. Chem. Lett., 2017, 8, 929–935 CrossRef CAS PubMed.
- W. Cai and A. Katrusiak, Nat. Commun., 2014, 5, 4337 CrossRef CAS PubMed.
- L. Merrill and W. A. Bassett, Rev. Sci. Instrum., 1974, 45, 290–294 CrossRef.
- Idemitsu Kosan Co Ltd; Daphne Oil 7575 Data sheet.
- D. Staško, J. Prchal, M. Klicpera, S. Aoki and K. Murata, High Press. Res., 2020, 40, 525–536 CrossRef.
- G. J. Piermarini, S. Block, J. D. Barnett and R. A. Forman, J. Appl. Phys., 1975, 46, 2774–2780 CrossRef CAS.
- A. Budzianowski and A. Katrusiak, High-Pressure Crystallographic Experiments with a CCD Detector, Kluwer Acad. Publ., Dordrecht, Netherlands, 2004, pp. 101–113 Search PubMed.
- A. Katrusiak, REDSHABS- Program for Correcting Reflections Intensities for DAC Absorption, Gasket Shadowing and Sample Crystal Absorption, Adam Mickiewicz Univ. Poznań, 2003 Search PubMed.
- Agilent, CrysAlis PRO, CrysAlis PRO, Agilent Technologies Ltd., Yarnton, England, 2014 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- C. C. Addison, N. Logan, S. C. Wallwork and C. D. Garner, Q. Rev. Chem. Soc., 1971, 25, 289–322 RSC.
- L. F. Esteves, H. F. Dos Santos and L. A. S. Costa, J. Mol. Graphics Modell., 2015, 61, 290–296 CrossRef CAS PubMed.
- F. Montisci, A. Lanza, N. Casati and P. Macchi, Cryst. Growth Des., 2018, 18, 7579–7589 CrossRef CAS.
- V. A. Blatov, M. O’Keeffe and D. M. Proserpio, CrystEngComm, 2010, 12, 44–48 RSC.
- R. M. Hazen and L. W. Finger, Comparative Crystal Chemistry: Temperature, Pressure, Composition and the Variation of Crystal Structure, Wiley, New York, 1982 Search PubMed.
- J. Marciniak and A. Katrusiak, J. Phys. Chem. C, 2017, 121, 22303–22309 CrossRef CAS.
- Q. Zeng, K. Wang and B. Zou, ACS Mater. Lett., 2020, 2, 291–295 CrossRef CAS.
- X. Zhou, L. Zhang, H. Zhang, Q. Liu and T. Ren, Phys. Status Solidi B, 2016, 253, 1977–1993 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: List of torsion angles; detailed crystallographic data; void size change. Cd(HDA)2(NO3)2: unit-cell angle change; Cd–O, Cd–N, Cd–Cd distances; site occupation factor of disordered carbon atoms in phase α; Cd2(HDA)3(NO3)4: Cd–O, Cd–N, Cd–Cd distances; beta angle; h0l layers; conformational changes figure; scheme of adjacent binuclear centres; Cu(HDA)2(MeCN)2·2BF4: Cu–B, Cu–F, Cu–Cu, Cu–N distances; unit cell figure. CCDC 2262338–2262371. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3tc01732j |
| This journal is © The Royal Society of Chemistry 2023 |