Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unraveling the effects of gas species and surface wettability on the morphology of interfacial nanobubbles†
Kadi
Hu
a,
Liang
Luo
 b,
Xiaoming
Sun
b,
Xiaoming
Sun
 ab and
Hui
Li
ab and
Hui
Li
 *a
*a
aBeijing Advanced Innovation Center for Soft Matter Science and Engineering, Beijing University of Chemistry Technology, Beijing 100029, PR China. E-mail: hli@mail.buct.edu.cn
bState Key Laboratory of Chemical Resource Engineering, Beijing University of Chemical Technology, Beijing 100029, PR China
First published on 24th May 2022
Abstract
The morphology of interfacial nanobubbles (INBs) is a crucial but controversial topic in nanobubble research. We carried out atomistic molecular dynamics (MD) simulations to comprehensively study the morphology of INBs controlled by several determinant factors, including gas species, surface wettability, and bubble size. The simulations show that H2, O2 and N2 can all form stable INBs, with the contact angles (CAs, on the liquid side) following the order CA(H2) < CA(N2) < CA(O2), while CO2 prefers to form a gas film (pancake) structure on the substrate. The CA of INBs demonstrates a linear relation with the strength of interfacial interaction; however, a limited bubble CA of ∼25° is found on superhydrophilic surfaces. The high gas density and high internal pressure of the INBs are further confirmed, accompanied by strong interfacial gas enrichment (IGE) behavior. The morphology study of differently sized INBs shows that the internal density of the gas is drastically decreased with the bubble size at the initial stage of bubble nucleation, while the CA remains almost constant. Based on the simulation results, a modified Young's equation is presented for describing the extraordinary morphology of INBs.
Introduction
Interfacial nanobubbles (INBs), widely existing at solid–liquid interfaces, are considered a main factor to produce the hydrophobic interaction, playing key roles in determining various interfacial properties and causing many interfacial problems that need to be reconsidered.1 Therefore, INBs hold great potential in a wide range of industrial applications,2 such as cleaning and decontamination,3 mineral flotation,4–6 slip drag reduction,7 nanomaterial engineering,8,9 nanofluidics,10,11 biosensors,12 as well as energy conversion.13 Among their numerous unusual physicochemical properties, the morphology of INBs is of particular interest, due to the large inconsistency between the observed contact angle (CA, θ) of nanobubbles and macrobubbles. In electrochemical gas evolution reactions (GERs), it was found that the extraordinary morphology of the produced INBs can block the contact between electrolytes and electrode surfaces, severely affecting the mass transfer and conductance during the reactions.14,15 Recent studies have further shown the CA of INBs is also relevant to the overpotential in GERs.16 Thus, understanding the morphology of INBs is not only of great fundamental interest but also crucial importance in material applications and electrolysis.17–25There have been great discrepancies in the observed behaviors of INBs under different experimental conditions. In most previous observations, INBs were found to have large and retarded CAs (on the liquid side).26–31 Atomic force microscopic (AFM) observations showed that the CA of INBs seems to have little relevance to the interfacial hydrophobicity but generally ranges from 150° to 170°, which is significantly larger than the corresponding CA of a macroscopic bubble on the same surface.32–34 It is believed that such oversized CA is a result of the joint actions of line tension, surface tension, and pinned contact line.35–44 The larger CA also gives the bubble a larger curvature radius, which can lower the internal Laplace pressure and help to stabilize the bubble.42 Theoretical models based on the surface pancakes and interfacial gas enrichment (IGE) were also proposed for understanding the anomalous CA of nanobubbles,45–49 which was further confirmed by the observed nanobubble-on-pancake object.50 On the other hand, some other experimental investigations have provided opposite views on the shape of INBs. For example, Wang et al. argued the nanobubbles should have a CA similar to a macrobubble, and the AFM characterization cannot reflect the real shape of the nanobubble due to the large curvature radius of the probe tip.51 Besides the tip effect of AFM, it was found that many other uncontrollable conditions, such as contamination, heterogeneity of surface, chemical composition of liquid, gas content in the bubble, and so on, may also lead to the contradictive experimental results,29,52–56 indicating there is a certain gap between the experimentally observed morphology of INBs and their real appearance.
In addition to the experimental investigations, atomistic molecular dynamics (MD) simulation is also a promising tool to investigate the dynamics of solid–liquid–gas interfaces at the molecular level, and it has been widely employed to study the behaviors of INBs in recent years.15,57–60 In the simulation of an argon vapor bubble on a solid surface, Maruyama et al. found the CA of INBs on solid surface could be modified by the potential parameters between gas and solid.57 Nagayama et al. revealed that the bubble nucleation also shows a remarkable dependence on the solid–liquid interfacial interaction.58 Zhang et al. explored the size dependence of the isothermal compressibility of the gas bubble, leading to a size-dependent bubble CA.59 Lohse et al. revealed that INBs are stabilized by a non-equilibrium mechanism, where the dense layer of gas at the solid–liquid interface effectively changes the substrate chemistry, leading to the universal CA.60 Although these simulations have already illustrated that the CA of nanobubbles is relevant to surface wettability and bubble size, systematic studies of the quantitative relationships between morphology of INBs and the possible determinant factors, including gas species, surface energy, and bubble size, are still lacking.
In the present work, we carry out a series of atomistic MD simulations to investigate the morphology of INBs formed from the most common types of gas molecules produced in GERs (e.g., H2, O2, CO2, and N2) on flat solid surfaces. The quantitative relationships between nanobubble CA and gas species, bubble size, and surface energy are systematically established. The key structural parameters, including density distribution and internal pressure of INBs, are also observed at various CAs. The present simulation work has given a complete illustration of the morphology of INBs, which sheds important new light on relevant interfacial physical phenomena and applications.
Methods
The large-scale atomic/molecular parallel simulator (LAMMPS) software was used for the MD simulations.61 There are two kinds of simulation systems in the present work: one is the interfacial nanobubble system, and the other is the water droplet system on the same substrate (Fig. S1, ESI†). The substrate (in the size of 14 × 14 nm2) is an atomic flat surface in a graphene-like honeycomb lattice. Periodic boundary conditions are employed in the x and y directions, and the mirror boundary condition is used in the z direction. In the nanobubble simulation, the space around the bubble is full of water molecules, and at the same time, a vacuum space is also added to the simulation box to create a liquid–vapor interface far from the bubble.The water molecules are treated using the SPC/E model.62 The Lennard–Jones potential 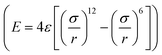 with a cutoff of 12.0 Å is employed for the van der Waals interaction. The interaction parameters are shown in Table S1,† and parameters between different types of atoms are calculated through the Lorentz–Berthelot combining rules
with a cutoff of 12.0 Å is employed for the van der Waals interaction. The interaction parameters are shown in Table S1,† and parameters between different types of atoms are calculated through the Lorentz–Berthelot combining rules 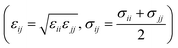 . The particle–particle particle-mesh (PPPM) solver is employed to compute the long-range coulombic interactions and the 1/r6 interactions.
. The particle–particle particle-mesh (PPPM) solver is employed to compute the long-range coulombic interactions and the 1/r6 interactions.
All the MD simulations are performed in constant-volume and constant-temperature (NVT) ensembles. The Nosé–Hoover thermostat is employed to control the temperature at 300 K.63 A cubic cluster consisting of water molecules or gas molecules is initially placed with the shortest distance of ∼2.5 Å above the graphene substrate to relax to a droplet or droplet-like bubble. The substrate is fixed during the MD simulation. The time step is set as 1.0 fs. After full relaxation, simulations with time >20 ns are performed to make sure all these systems can reach the equilibrium states.
Results and discussion
Morphology of INBs with different gas species
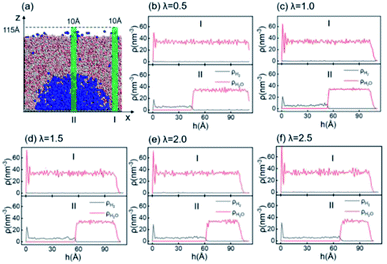
Since inhomogeneity always exists on real surfaces, the surface pinning often plays a key role in the formation of INBs. The pinning positions can fix the triple-line of bubbles, thereby apparently affecting their morphology and CA, leading to the uncertainty of characterization of the pristine morphology of INBs. To probe the intrinsic behaviours of INBs without any wetting hysteresis, we employ a homogeneous atomic-flat model surface in the graphene lattice, whose surface energy can be adjusted by modifying the van der Waals parameters. Firstly, we compare the evolution of INBs filled with different types of gas (H2, O2, CO2, and N2) on the graphene surface. As shown by the MD trajectory in Fig. 1a, the initial cubic H2 cluster turns into a hemisphere in a short time (<0.05 ns) and remains almost unchanged from 0.5 to 20 ns, indicating the H2-INB is very stable with a constant CA (from the water side) close to the macrobubble on the substrate. Similarly, the O2- and N2-clusters (Fig. 1b and d) also show similar stability. By contrast, the CO2 cluster demonstrates a complete wetting behaviour (Fig. 1c), where the CO2 bubble continuously spreads on the substrate until it becomes a thin film formed by one or two layers of gas molecules. The different morphology evolutions of H2/O2/N2-INBs and CO2-INB are also reflected by the evolution of their contact areas on the substrate. As shown in Fig. 1d and e, the contact area of H2-INB reaches a maximum value within the first 1 ns, while the contact area of CO2-INB is increased until it covers the whole area of the simulation box rapidly. It is noteworthy that after the initial extension, the contact area of INBs slightly decreases in the next 5 ns, due to dissolving of gas molecules (H2, O2, and N2) in the bulk water before the solution is completely saturated, and after that, the radius remains a constant during the rest of the simulation period (5–20 ns).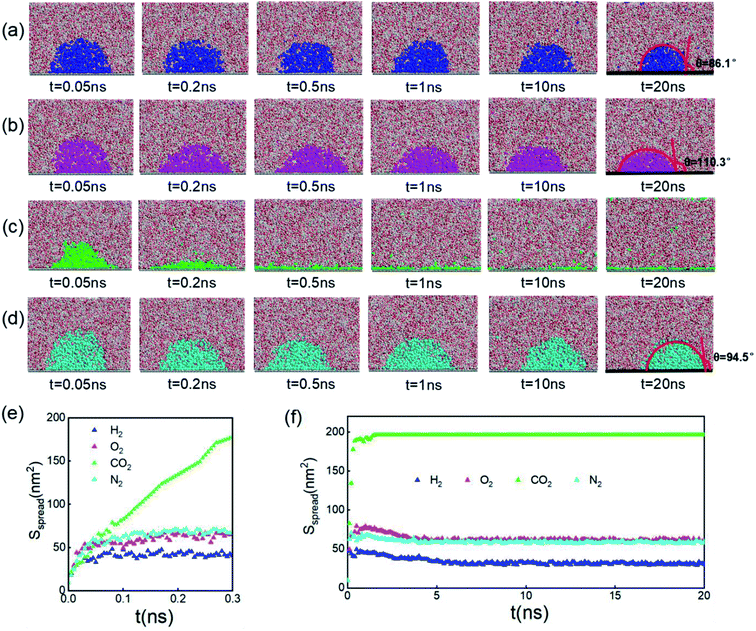 | ||
| Fig. 1 Time evolution of (a) H2-, (b) O2-, (c) CO2-, and (d) N2-INBs on the graphene surface starting from a cubic morphology. (e) The evolution of spreading areas of INBs with different gases during the first 0.3 ns and (f) the 0–20.0 ns simulation periods. (a)–(d) Denote the side view of the snapshots, while the plane view of the snapshots is shown in Fig. S2.† | ||
The stable shapes during the last periods of simulations are used to statistically evaluate the CAs of H2-, O2-, and N2-INBs. The whole simulation box is split into cubic meshes with a lattice size of 3.0 Å, and the local water density in each mesh is recorded based on the MD trajectories. The CA is derived by fitting the water–air interface with the grids, with the local density being half of the bulk water, as shown in Fig. 2a.64 The obtained CAs for the three bubble species are in the order of CA(O2-INB) (θ = 110.3°) > CA(N2-INB) (θ = 94.5°) > CA(H2-INB) (θ = 86.1°), as shown in Fig. 1a–d, while the gas film of CO2 can be considered to possess a super large CA (θ ≈ 180°). Consistent with previous reports,57 the bubble CA value is strongly dependent on the strength of interaction between the substrate and adsorbed molecules, which is determined by the energy parameters (ε) of the Lennard–Jones (LJ) potential. As listed in Table S1,† the gas–solid interaction is stronger than the liquid–solid interaction in the CO2–H2O system, indicating the CO2–solid interface is more energetically favourable than the water–solid interface. In fact, the INB filled with CO2 may form a film structure with the triple line pinned by some surface pinning sites, thereby yielding a super large CA. On the contrary, the gas–solid interaction is weaker than the liquid–solid interaction in the H2–H2O, O2–H2O, and N2–H2O systems, indicating all three gas species can form stable INBs on an atomic flat surface. It is also found that the LJ potentials of H2, N2, and O2 follow the same order as the CA values of INBs with different gas species.
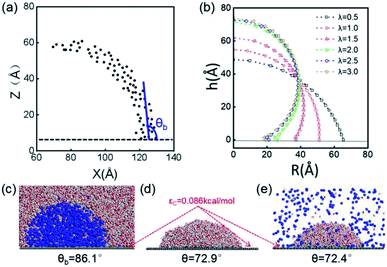 | ||
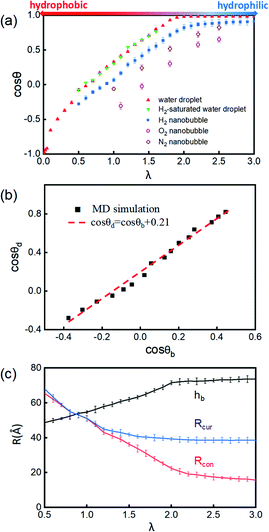
| Fig. 2 (a) Schematic presentation of contact angle calculation. Black points represent the half-water-density areas to characterize the surface of the nanobubble or water droplet; the red curve is a fit to black points; and the blue line denotes the tangent of the bubble/droplet surface. (b) Shapes of INBs on the surface with different wettabilities. λ is a coefficient of substrate wettability; we multiply the initial energy parameter of the substrate εC = 0.086 kcal mol−1 by λ (0.01–3.0) to change the surface wettability from hydrophobic to hydrophilic. The corresponding snapshots are shown in Fig. S3.† Snapshots of (c) H2 nanobubble, (d) water nanodroplet and (e) water nanodroplet with excessive H2 molecules. H2 molecules are represented by blue balls; H2O molecules consist of red (O) and white (H) balls, and graphene atoms are denoted by the gray balls. | ||
According to the present simulations, different species of gas molecules demonstrate significantly different behaviors in forming INBs: CO2 prefers to form a gas film rather than a stable nanobubble at the water–solid interface; O2 and N2 are willing to adopt INBs with larger CAs; and H2 forms an INB with a smaller CA. Such result is consistent with the previous model study of Molinero et al.,15 who found three stationary states of nanobubble nucleation: micropancakes (when gas–solid interaction is larger than liquid–solid interaction), interfacial nanobubbles, and solution nanobubbles (when gas–solid interaction is smaller than liquid–solid interaction).21 Furthermore, it is worth noting that more CO2 molecules, rather than O2 and N2, are found to be dispersed in the water solution, confirming the higher solubility of CO2 (Fig. 1b–d).
INB morphology vs. surface wettability
The surface wettability of the solid substrate is another key factor determining the morphology of INBs. We compare the morphology of INBs filled with various gas species on surfaces with different surface energies. It is found that the CO2-INBs always form gas films on both hydrophobic and hydrophilic surfaces. By contrast, the H2/O2/N2-INBs display a macrodroplet-like shape, whose intrinsic CA can be modified by the strength of interfacial van der Waals interaction. Consistent with the method in previous works,57,64,65 a coefficient λ is employed to multiply the energy parameter ε of the substrate to tune the hydrophobicity of the surface model. When the value of λ is sufficiently large, the substrate becomes superhydrophilic, while a superhydrophobic substrate is obtained when λ approaches 0. As demonstrated in Fig. 2b, the statistic CA of INBs can be greatly varied by the value of λ. Although the pancake shape is not formed, as compared in Fig. 2c and d (εC = 0.086 kcal mol−1), the CA of H2-INB (θ = 86.1°) is apparently larger than the corresponding CA of pure water droplet (θ = 72.9°). Furthermore, the H2-saturated water droplet (Fig. 2e) shows an identical CA (θ = 72.4°) to the pure water droplet, excluding the possibility of the drop in water surface tension being caused by dissolved H2.The cosine values of simulated CAs of H2/O2/N2-INBs, water droplets, and H2-saturated water droplets on substrates versus λ are demonstrated in Fig. 3a. All the CAs of the INBs (θb) and the water droplet (θd) have consistent trends with the surface energy parameter λ. However, when the surface gets more hydrophobic, O2-INB and N2-INB are more likely to form gas films like CO2-INB, so that the accurate value of bubble CA is difficult to obtain due to the limited size of the simulation box. Therefore, we take the H2-INBs (whose morphology is closer to the macrodroplet) as the example to comprehensively analyze the microscopic structure in detail. In the range of 0.5 < λ < 2.0, the values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θd and cos
θd and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θb have a linear relation (Fig. 3b), which can be expressed by cos
θb have a linear relation (Fig. 3b), which can be expressed by cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θd = cos
θd = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θb + 0.21. Since it has been experimentally confirmed that the CA of water microdroplet is consistent with that of the macroscopic droplet (the same as macrobubble),59Fig. 3b is also provided with the relation between H2-INB and the macrobubbles. Besides the CA, the morphology of H2-INB can also be characterized by the radius of contact area (Rcon), the curvature radius of the spherical INB (Rcur), and the bubble height (hb), which also show approximately linear relations with λ in the range of 0.5 < λ < 2.0 (Fig. 3c).
θb + 0.21. Since it has been experimentally confirmed that the CA of water microdroplet is consistent with that of the macroscopic droplet (the same as macrobubble),59Fig. 3b is also provided with the relation between H2-INB and the macrobubbles. Besides the CA, the morphology of H2-INB can also be characterized by the radius of contact area (Rcon), the curvature radius of the spherical INB (Rcur), and the bubble height (hb), which also show approximately linear relations with λ in the range of 0.5 < λ < 2.0 (Fig. 3c).
In the superhydrophobic region (λ < 0.5), the CA values of both nanobubble and nanodroplet approach to 180° (Fig. 3b). However, in the superhydrophilic region (λ ≥ 2.0), when the water droplet starts to completely wet the substrate (θd = 0), the H2-INB still has a relatively large CA (θb = 34.8°). More interestingly, with the further increase of interfacial hydrophilicity, the CA of the INB tends to maintain a limit value (θb ≈ 25°) rather than approaching to zero. Correspondingly, Rcon shows the same trend in this range (Fig. 3c). Combining with Fig. 2b and S3,† it is found that the nanobubble shape is no longer a regular spherical cap on a superhydrophilic surface; a neck-like structure with a height of ∼3 Å (one-molecule thick) appears at the triple line. In addition, such bubble necking structure is more obvious on the substrate with higher surface energy. It is known that the necking of a macrobubble usually appears during the pinch-off process, which can minimize the surface energy of the bubble.66 Here, the necking structure of H2-INB is due to the intrusion of water thin film with a minimum thickness (monolayer of water molecules) at the bubble/solid interface, implying the higher internal pressure of INB with a smaller curvature radius (due to the smaller CA on the liquid side) making it more difficult to deform on a superhydrophilic surface. Such phenomenon is also reflected from the context of INBs being extraordinarily stable and having extremely strong adhesion even on hydrophilic substrates. As shown in Fig. 3c, the unchanged curvature radius of bubbles in the region of the superhydrophilic surface also indicates that the necking structure can avoid the further increase of internal pressure of the nanobubble, thereby increasing the stability of the INB on a superhydrophilic surface. Therefore, unlike the traditional viewpoint that the superhydrophilic surface should be completely wet by water, the H2-INB can still stably sit on the superhydrophilic substrate, according to the present simulations. Finally, it is noteworthy that the CA of H2-saturated water droplet is identical to the CA of pure water droplet (Fig. 3a), indicating that for the H2-INB system, the surface tension change of water due to dissolved H2 is negligible in affecting the nanobubble behaviors. On the other hand, for the gases with higher solubility, such as CO2 and O2, their effects on surface tension may be more considerable, therefore affecting the morphology of the corresponding nanobubbles. Such point remains to be evidenced in future work.
Microstructure of INBs
According to the Young–Laplace equation, the extremely high curvature of nanobubbles leads to much higher gas density inside the bubble, which has been already confirmed in many previous studies, and such high gas density has been considered to be related to the high stability of nanobubbles.67–71Fig. 4 shows the density distributions of H2 and H2O outside and inside the H2-INB covered regions (region I and region II in Fig. 4a) along the z direction (from the water–solid interface to the water–air interface) with different λ values. In region I (bulk water outside the bubble region), the number density of H2 molecules is close to zero due to the low solubility of H2 in water, and the average density of water of ∼33.6 H2O molecules per nm3 (∼1.005 g cm−3) is identical to the bulk water. The density of the main body of the nanobubble (region II) is ∼5.6 H2 atoms per nm3 (about 26.5% of liquid hydrogen density). Such high density of nanobubbles is also reported in previous investigations.65 In addition, there are two peaks significantly higher than the average value in the density profile of water, revealing the stratification of water close to the liquid/solid interface. A similar stratification is also observed for the density of H2 molecules in the vicinity of the solid/liquid interface, where a peak value is found at ∼3 Å high on the density profile, confirming the interfacial gas enrichment (IGE) phenomenon of nanobubbles discovered in previous works.49 Moreover, the maximum density of the gas layer (Fig. S4†) is found to be proportional to the interaction parameter εsg/εll. Based on the IGE effect, Nikolai et al. proposed a bubble adsorption model, which indicates that the high-density pancake adsorption on the surface can reduce the surface energy, leading to the reduction of the gas–solid surface tension.72–74 It is noteworthy that the IGE behavior is not significant at the liquid–bubble interface, where the density of H2 is only slightly higher than in the bulk region of the bubble (Fig. 4b–f). Furthermore, the density distribution in region II also shows the fact that there are no H2O molecules inside the nanobubble. According to the density distribution (Fig. 4) and H2-INB snapshots on the hydrophilic surfaces (when λ > 2.0) (Fig. S3†), the INBs are composed of two parts: the bubble neck (which is about 2–3 gas molecule layers thick) and the main bubble, and the density of the bubble neck is much higher than that of the main bubble. Our simulations demonstrate that the internal structure of the INB is not homogenous, and with the increase of surface hydrophilicity, the bubble neck becomes more and more obvious. Therefore, we can consider that the density difference between the neck and the main body of the nanobubble leads to the higher stability and morphology change of the INB.Another important and controversial feature of nanobubbles is the internal pressure. According to the traditional theory, the Laplace pressure of INBs is extremely large due to their ultra-small radius, which should be harmful to the stability of the bubble. Here, the internal pressure is predicted within the cubic region with the lattice of 2.0 nm (yellow area in Fig. 5a) after the bubble is fully relaxed by a ∼20 ns MD simulation. The pressure is computed based on the following formula:
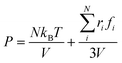 | (1) |
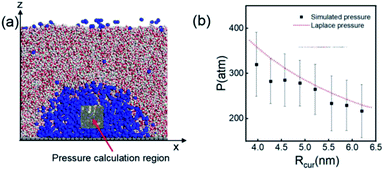 | ||
| Fig. 5 (a) A 20 × 20 × 20 Å3 volume is taken for pressure calculation, which is always inside the nanobubble. (b) Comparison of simulated internal pressure with the theoretical Laplace pressure. The time evolution of pressure when Rcur = 5.21 nm (λ = 1.0) is shown in Fig. S5.† | ||
Size-dependence of INB morphology
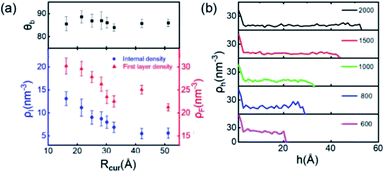
Finally, we simulate the morphologies and behaviors of INBs containing 200, 500, 600, 700, 800, 900, 1000, 1500, and 2000 H2 molecules, corresponding to the Rc values in the range of 1–5 nm, to mimic the initial nucleation and growth processes, and investigate the size dependence of the INBs' CA. The systems are set to make sure that all the initial numbers of H2 molecules placed inside the bubble meet the condition of system saturation due to the extremely low solubility of hydrogen in water. It is found that the cluster with 200 H2 molecules cannot appear as an INB, while all the other clusters can form stable INBs with unchanged CAs during MD simulations (simulation time > 10 ns). As shown in Fig. 6a, the CAs of H2-INBs with Rc values ranging from 1.5 to 5 nm show almost identical CAs (θ ≈ 86°). By contrast, the gas density inside the INB and the first H2 layer density have an apparently negative correlation with the bubble radius (red curve in Fig. 6a). Furthermore, the hydrogen gas is almost uniformly distributed inside the INBs with similar IGE peaks at liquid–air interfaces, as shown in Fig. 6b.Previous studies have already gained a physical picture of the formation process of INBs with pinning sites: gas molecules first blanket the pinning surface to form a pancake, and then transform into an increasingly full spherical coronal nanobubble without changing the three-phase contact area.15,16 Our simulations further reveal the mechanism of nucleation of INBs on the atomic flat surface without any pinning points, where the growth of INB follows a constant contact angle (CCA) mode. In addition, gas density is also an important indicator for nanobubble nucleation. The present simulations show that the critical gas nuclei may adopt a very high density (>60% of the density of liquid hydrogen) in the initial nucleation stage, then the density rapidly decreases to ∼25% of the liquid–H2 density during the growth process.
Modified Young's equation for INBs
It is well known that the CA of a droplet on a smooth surface can be described by Young's equation,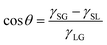 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and λ (λ = 0.5–2.0 in the present work), as displayed in Fig. 3a. Due to the higher gas density in the nanobubble, the CA of INB can be described by a modified Young's equation,
θ and λ (λ = 0.5–2.0 in the present work), as displayed in Fig. 3a. Due to the higher gas density in the nanobubble, the CA of INB can be described by a modified Young's equation,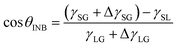 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θINB and λ in a certain range (0.5< λ < 2.0) as well, as shown in Fig. 3a. And eqn (3) is also helpful to understand the CAs of INBs with different gas species. Since the H2 molecule has the weakest interaction with the substrate, leading to smaller ΔγSG than other gas species, the CA of H2-INB is closest to that of a water droplet. In contrast, the large value of ΔγSG for CO2 makes the right side of eqn (3) lower than −1, leading to a super large CA of CO2-INB of ∼180°. Finally, in the size-dependent study, the IGE peak area of INBs almost remains constant at different bubble sizes (Fig. 6b), indicating the ΔγSG also remains constant at different sizes. Due to the much weaker H2–water and H2–H2 interactions (pure van der Waals interaction) than the water–water hydrogen bonding interaction, the denominator of eqn (3) is mainly contributed by γLG, which can also be considered as a constant. Thereby, the CA of INBs does not demonstrate obvious size dependence in the size range of the present simulations (1.5 nm < Rc < 5.0 nm).
θINB and λ in a certain range (0.5< λ < 2.0) as well, as shown in Fig. 3a. And eqn (3) is also helpful to understand the CAs of INBs with different gas species. Since the H2 molecule has the weakest interaction with the substrate, leading to smaller ΔγSG than other gas species, the CA of H2-INB is closest to that of a water droplet. In contrast, the large value of ΔγSG for CO2 makes the right side of eqn (3) lower than −1, leading to a super large CA of CO2-INB of ∼180°. Finally, in the size-dependent study, the IGE peak area of INBs almost remains constant at different bubble sizes (Fig. 6b), indicating the ΔγSG also remains constant at different sizes. Due to the much weaker H2–water and H2–H2 interactions (pure van der Waals interaction) than the water–water hydrogen bonding interaction, the denominator of eqn (3) is mainly contributed by γLG, which can also be considered as a constant. Thereby, the CA of INBs does not demonstrate obvious size dependence in the size range of the present simulations (1.5 nm < Rc < 5.0 nm).
Conclusions
In summary, MD simulations have been carried out to comprehensively investigate the main factors, including the gas species, surface energy of substrate, and bubble size, that affect the morphology and behavior of INBs. It is found that H2 can form an INB on an atomic flat surface with a shape of a macrodroplet; O2 and N2 can also form stable INBs but with significantly larger CAs than that of H2-INB, while CO2 is more likely to form a gas film (pancake) structure on the surface due to its strong gas–solid interaction. The CAs of INBs show a linear relation with the strength of van der Waals interaction of the substrate, demonstrating a consistent trend with the CA of water droplets. The high density and high pressure of the gas inside the INB are also confirmed, as well as the strong IGE effect at the solid–liquid interface. In addition, it is also found that the density of gas is sensitive to the bubble size at the initial stage of bubble nucleation, while the bubble CA remains almost constant. It is further revealed that all the above simulation results can be understood by a modified Young's equation. Our simulations give deep insights into the morphology and microstructure of nanobubbles, which are also of great importance to the relevant applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the National Science Foundation of China (21935001, 91934303) and Beijing Natural Science Foundation (Z210016).References
- M. Alheshibri, J. Qian, M. Jehannin and V. S. J. Craig, A History of Nanobubbles, Langmuir, 2016, 32, 11086–11100 CrossRef CAS.
- D. Lohse and X. Zhang, Surface Nanobubbles and Nano-droplets, Rev. Mod. Phys., 2015, 87, 981–1035 CrossRef CAS.
- S. Yang and A. Duisterwinkel, Removal of Nanoparticles from Plain and Patterned Surfaces Using Nanobubbles, Langmuir, 2011, 27, 11430–11435 CrossRef CAS PubMed.
- S. Calgaroto, K. Q. Wilberg and J. Rubio, On the Nanobubbles Interfacial Properties and Future Applications in Flotation, Miner. Eng., 2014, 60, 33–40 CrossRef CAS.
- A. Sobhy and D. Tao, High-Efficiency Nanobubble Coal Flotation, Coal Prep., 2013, 33, 242–256 CrossRef CAS.
- M. Fan, T. Daniel and H. Rick, Nanobubble Generation and Its Application in Froth Flotation (Part I): Nanobubble Generation and Its Effects on Properties of Microbubble and Millimeter Scale Bubble Solutions, Min. Sci. Technol., 2010, 20, 1–19 CAS.
- S. C. Hendy and N. J. Lund, Effective Slip Lengths for Flows over Surfaces with Nanobubbles: The Effects of Finite Slip, J. Phys.: Condens. Matter, 2009, 21, 114202 CrossRef.
- S. Darwich, K. Mougin, L. Vidal, E. Gnecco and H. Haidara, Nanobubble and Nanodroplet Template Growth of Particle Nanorings versus Nanoholes in Drying Nanofluids and Polymer Films, Nanoscale, 2011, 3, 1211–1217 RSC.
- L. Gao, G. Ni, Y. Liu, B. Liu, A. H. C. Neto and K. P. Loh, Face-to-Face Transfer of Wafer-Scale Graphene Films, Nature, 2014, 505, 190–194 CrossRef CAS.
- J. Lee, T. Laoui and R. Karnik, Nanofluidic Transport Governed by the Liquid/Vapour Interface, Nat. Nanotechnol., 2014, 9, 317–323 CrossRef CAS PubMed.
- L. Bocquet, Bubbles as Osmotic Membranes, Nat. Nanotechnol., 2014, 9, 249–251 CrossRef CAS.
- M. Holmberg, A. Kühle, J. Garnæs, K. A. Mørch and A. Boisen, Nanobubble Trouble on Gold Surfaces, Langmuir, 2003, 19, 10510–10513 CrossRef CAS.
- E. Lukianova-Hleb, Y. Hu, L. Latterini, L. Tarpani, S. Lee, R. A. Drezek, J. H. Hafner and D. O. Lapotko, Plasmonic Nano-bubbles as Transient Vapor Nanobubbles Generated around Plasmonic Nanoparticles, ACS Nano, 2010, 4, 2109–2123 CrossRef CAS PubMed.
- X. Zhao, H. Ren and L. Luo, Gas Bubbles in Electrochemical Gas Evolution Reactions, Langmuir, 2019, 35, 5392–5408 CrossRef CAS PubMed.
- Y. A. Perez Sirkin, E. D. Gadea, D. A. Scherlis and V. Molinero, Mechanisms of Nucleation and Stationary States of Electrochemically Generated Nanobubbles, J. Am. Chem. Soc., 2019, 141, 10801–10811 CrossRef CAS PubMed.
- E. D. Gadea, Y. A. Perez Sirkin, V. Molinero and D. A. Scherlis, Electrochemically Generated Nanobubbles: Invariance of the Current with Respect to Electrode Size and Potential, J. Phys. Chem. Lett., 2020, 11, 6573–6579 CrossRef CAS PubMed.
- V. Tsionsky, A. Kaverin, L. Daikhin, G. Katz and E. Gileadi, An Experimental Verification of the Possible Influence of Gas Nano-bubbles on the Response of an Electrochemical Quartz Crystal Microbalance, Phys. Chem. Chem. Phys., 2005, 7, 1830–1835 RSC.
- J. L. Parker and P. M. Claesson, Direct Measurements of the Attraction between Solvophobic Surfaces in Ethylene Glycol and Mixtures with Water, Langmuir, 1992, 8, 757–759 CrossRef CAS.
- L. Luo and H. S. White, Electrogeneration of Single Nano-bubbles at Sub-50-nm-Radius Platinum Nanodisk Electrodes, Langmiur, 2013, 29, 11169–11175 CrossRef CAS PubMed.
- Q. Chen, H. S. Wiedenroth, S. R. German and H. S. White, Electrochemical Nucleation of Stable N2 Nanobubbles at Pt Nanoelectrodes, J. Am. Chem. Soc., 2015, 137, 12064–12069 CrossRef CAS PubMed.
- Q. Chen, L. Luo and H. S. White, Electrochemical Generation of a Hydrogen Bubble at a Recessed Platinum Nanopore Electrode, Langmuir, 2015, 31, 4573–4581 CrossRef CAS PubMed.
- S. R. German, Q. Chen, M. A. Edwards and H. S. White, Electrochemical Measurement of Hydrogen and Nitrogen Nanobubble Lifetimes at Pt Nanoelectrodes, J. Electrochem. Soc., 2016, 163, H3160–H3166 CrossRef CAS.
- E. R. White, M. Mecklenburg, S. B. Singer, S. Aloni and B. C. Regan, Imaging Nanobubbles in Water with Scanning Transmission Electron Microscopy, Appl. Phys. Express, 2011, 4, 055201 CrossRef.
- D. Shin, J. B. Park, Y. J. Kim, S. J. Kim, J. H. Kang, B. Lee, S. P. Cho, B. H. Hong and K. S. Novoselov, Growth Dynamics and Gas Transport Mechanism of Nanobubbles in Graphene Liquid Cells, Nat. Commun., 2015, 6, 6068 CrossRef PubMed.
- S. Yasuda, K. Tamura, T. O. Terasawa, M. Yano and H. Asaoka, Confinement of Hydrogen Molecules at Graphene–Metal Interface by Electrochemical Hydrogen Evolution Reaction, J. Phys. Chem. C, 2020, 124, 5300–5307 CrossRef CAS.
- A. C. Simonsen, P. L. Hansen and B. Klösgen, Nanobubbles Give Evidence of Incomplete Wetting at a Hydrophobic Interface, J. Colloid Interface Sci., 2004, 273, 291–299 CrossRef CAS PubMed.
- N. Ishida, T. Inoue, M. Miyahara and K. Higashitani, Nano Bubbles on a Hydrophobic Surface in Water Observed by Tapping-Mode Atomic Force Microscopy, Langmuir, 2000, 16, 6377–6380 CrossRef CAS.
- S. Yang, S. M. Dammer, N. Bremond, H. J. W. Zandvliet, E. S. Kooij and D. Lohse, Characterization of Nanobubbles on Hydrophobic Surfaces in Water, Langmuir, 2007, 23, 7072–7077 CrossRef CAS PubMed.
- M. A. J. van Limbeek and J. R. T. Seddon, Surface Nanobubbles as a Function of Gas Type, Langmuir, 2011, 27, 8694–8699 CrossRef CAS PubMed.
- X. Zhang, G. Li, N. Maeda and J. Hu, Removal of Induced Nanobubbles from Water/Graphite Interfaces by Partial Degassing, Langmuir, 2006, 22, 9238–9243 CrossRef CAS.
- N. D. Petsev, L. G. Leal and M. S. Shell, Universal Gas Adsorption Mechanism for Flat Nanobubble Morphologies, Phys. Rev. Lett., 2020, 125, 146101 CrossRef CAS PubMed.
- W. Guo, H. Shan, M. Guan, L. Gao, M. Liu and Y. Dong, Investigation on Nanobubbles on Graphite Substrate Produced by the Water–NaCl Solution Replacement, Surf. Sci., 2012, 606, 1462–1466 CrossRef CAS.
- H. Peng, G. R. Birkett and A. V. Nguyen, Progress on the Surface Nanobubble Story: What Is in the Bubble? Why Does It Exist?, Adv. Colloid Interface Sci., 2015, 222, 573–580 CrossRef CAS PubMed.
- X. Zhang, N. Maeda and V. S. J. Craig, Physical Properties of Nanobubbles on Hydrophobic Surfaces in Water and Aqueous Solutions, Langmuir, 2006, 22, 5025–5035 CrossRef CAS PubMed.
- Y. Takata, H. Matsubara, T. Matsuda and Y. Kikuchi, Study on Line Tension of Air/Hexadecane/Aqueous Surfactant System, Colloid Polym. Sci., 2008, 286, 647–654 CrossRef CAS.
- J. Drelich, The Significance and Magnitude of the Line Tension in Three-phase (Solid-Liquid-Fluid) Systems, Colloids Surf., A, 1996, 116, 43–54 CrossRef CAS.
- B. M. Law, S. P. Mcbride, J. Y. Wang, H. S. Wi, G. Paneru, S. Betelu, B. Ushijima, Y. Takata, B. Flanders and F. Bresme, Line Tension and Its Influence on Droplets and Particles at Surfaces, Prog. Surf. Sci., 2017, 92, 1–39 CrossRef CAS.
- W. Ducker, Contact Angle and Stability of Interfacial Nano-bubbles, Langmuir, 2009, 25, 8907–8910 CrossRef CAS.
- X. Zhang, M. H. Uddin, H. Yang, G. Toikka and W. Ducker, Effects of Surfactants on the Formation and the Stability of Interfacial Nanobubbles, Langmuir, 2012, 28, 10471–10477 CrossRef CAS PubMed.
- D. Lohse and X. Zhang, Pinning and Gas Oversaturation Imply Stable Single Surface Nanobubbles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 031003 CrossRef PubMed.
- Y. Liu and X. Zhang, Nanobubble Stability Induced by Contact Line Pinning, J. Chem. Phys., 2013, 138, 014706 CrossRef PubMed.
- Y. Liu and X. Zhang, A Unified Mechanism for the Stability of Surface Nanobubbles: Contact Line Pinning and Super-saturation, J. Chem. Phys., 2014, 141, 134702 CrossRef PubMed.
- Y. Sun, G. Xie, Y. Peng, W. Xia and J. Sha, Stability Theories of Nanobubbles at Solid–Liquid Interface: A Review, Colloids Surf., A, 2016, 495, 176–186 CrossRef CAS.
- N. Kameda and S. Nakabayashi, Size-induced Sign Inversion of Line Tension in Nanobubbles at a Solid/Liquid Interface, Chem. Phys. Lett., 2008, 461, 122–126 CrossRef CAS.
- B. Zhao, X. Wang, S. Wang, R. Tai, L. Zhang and J. Hu, In Situ Measurement of Contact Angles and Surface Tensions of Interfacial Nanobubbles in Ethanol Aqueous Solutions, Soft Matter, 2016, 12, 3303–3309 RSC.
- Y. H. Lu, C. W. Yang and I. S. Hwang, Molecular Layer of Gaslike Domains at a Hydrophobic-Water Interface Observed by Frequency-Modulation Atomic Force Microscopy, Langmuir, 2012, 28, 12691–12695 CrossRef CAS PubMed.
- Y. H. Lu, C. W. Yang and I. S. Hwang, Atomic Force Microscopy Study of Nitrogen Molecule Self-assembly at the HOPG–Water Interface, Appl. Surf. Sci., 2014, 304, 56–64 CrossRef CAS.
- B. Zhao, X. Wang, Y. Song and J. Hu, Stiffness and Evolution of Interfacial Micropancakes Revealed by AFM Quantitative Nanomechanical Imaging, Phys. Chem. Chem. Phys., 2015, 17, 13598–13605 RSC.
- D. Li, Y. Pan, X. Zhao and B. Bhushan, Study on Nanobubble-on-Pancake Objects Forming at Polystyrene/Water Interface, Langmuir, 2016, 32, 11256–11264 CrossRef CAS PubMed.
- X. H. Zhang, X. Zhang, J. Sun, Z. Zhang, G. Li, H. Fang, X. Xiao, X. Zeng and J. Hu, Detection of Novel Gaseous States at the Highly Oriented Pyrolytic Graphite–Water Interface, Langmuir, 2007, 23, 1778–1783 CrossRef CAS PubMed.
- Y. Wang, X. Luo, W. Qin and F. Jiao, New Insights into the Contact Angle and Formation Process of Nanobubbles Based on Line Tension and Pinning, Appl. Surf. Sci., 2019, 481, 1585–1594 CrossRef CAS.
- Z. Zou, N. Quan, X. Wang, S. Wang, L. Zhou, J. Hu, L. Zhang and Y. Dong, The Properties of Surface Nanobubbles Formed on Different Substrates, Chin. Phys. B, 2018, 27, 086083 Search PubMed.
- B. M. Borkent, S. de Beer, F. Mugele and D. Lohse, On the Shape of Surface Nanobubble, Langmuir, 2010, 26, 260–268 CrossRef CAS PubMed.
- R. P. Berkelaar, J. R. T. Seddon, H. J. W. Zandvliet and D. Lohse, Temperature Dependence of Surface Nanobubbles, ChemPhysChem, 2012, 13, 2213–2217 CrossRef CAS PubMed.
- R. Zhao and Z. Liang, Mechanism of Contact Angle Saturation and an Energy-Based Model for Electrowetting, Chin. Phys. B, 2016, 25, 066801 CrossRef.
- Y. Wang, X. Shan, H. Wang, S. Wang and N. Tao, Plasmonic Imaging of Surface Electrochemical Reactions of Single Gold Nanowires, J. Am. Chem. Soc., 2017, 139, 1376–1379 CrossRef CAS PubMed.
- S. Maruyama and T. Kimura, A Molecular Dynamics Simulation of a Bubble Nucleation on Solid Surface, Trans. Jpn. Soc. Mech. Eng., 2000, 65, 3461–3467 CrossRef.
- G. Nagayama, T. Tsuruta and P. Cheng, Molecular Dynamics Simulation on Bubble Formation in a Nanochannel, Int. J. Heat Mass Transfer, 2006, 49, 4437–4443 CrossRef CAS.
- H. Zhang and X. Zhang, Size Dependence of Bubble Wetting on Surfaces: Breakdown of Contact Angle Match between Small Sized Bubbles and Droplets, Nanoscale, 2019, 11, 2823–2828 RSC.
- J. H. Weijs, J. H. Snoeijer and D. Lohse, Formation of Surface Nanobubbles and the Universality of Their Contact Angles: A Molecular Dynamics Approach, Phys. Rev. Lett., 2012, 108, 104501 CrossRef PubMed.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The Missing Term in Effective Pair Potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, Insitute of Physics, 1988, pp. 267–301 Search PubMed.
- T. Koishi, K. Yasuoka, S. Fujikawa, T. Ebisuzaki and X. Zeng, Coexistence and Transition between Cassie and Wenzel State on Pillared Hydrophobic Surface, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 8435–8440 CrossRef CAS PubMed.
- B. Shi and V. K. Dhir, Molecular Dynamics Simulation of the Contact Angle of Liquids on Solid Surfaces, J. Chem. Phys., 2009, 130, 204715 Search PubMed.
- J. C. Burton, R. Waldrp and P. Taborek, Scaling and Instabilities in Bubble Pinch-Off, Phys. Rev. Lett., 2005, 94, 184502 CrossRef CAS PubMed.
- L. Zhang, H. Chen, Z. Li, H. Fang and J. Hu, Long Lifetime of Nanobubbles Due to High Inner Density, Sci. China, Ser. G: Phys., Mech. Astron., 2008, 51, 219–224 CrossRef.
- C. Wang, Z. Li, J. Li and X. Peng, High Density Gas State at Water/Graphite Interface Studied by Molecular Dynamics Simulation, Chin. Phys. B, 2008, 17, 2646–2654 CrossRef CAS.
- L. Zhou, X. Wang, H. Shin, J. Wang, R. Tai, X. Zhang, H. Fang, W. Xiao, L. Wang, C. Wang, X. Gao, J. Hu and L. Zhang, Ultra-high Density of Gas Molecules Confined in Surface Nanobubbles in Ambient Water, J. Am. Chem. Soc., 2020, 142, 5583–5593 CrossRef CAS PubMed.
- S. Wang, L. Zhou, X. Wang, C. Wang, Y. Dong, Y. Zhang, Y. Gao, L. Zhang and J. Hu, Force Spectroscopy Revealed a High-Gas-Density State Near the Graphite Substrate Inside Surface Nanobubbles, Langmuir, 2019, 35, 2498–2505 CrossRef CAS PubMed.
- F. Y. Ushikubo, T. Furukawa, R. Nakagawa, M. Enari, Y. Makino, Y. Kawagoe, T. Shiina and S. Oshita, Evidence of the Existence and the Stability of Nano-bubbles in Water, Colloids Surf., A, 2010, 361, 31–37 CrossRef CAS.
- N. Siemons, H. Bruining, H. Castelijns and K. H. Wolf, Pressure Dependence of the Contact Angle in a CO2-H2O-Coal System, J. Colloid Interface Sci., 2006, 297, 755–761 CrossRef CAS PubMed.
- J. Wu, T. Farouk and C. A. Ward, Pressure Dependence of the Contact Angle, J. Phys. Chem. B, 2007, 111, 6189–6197 CrossRef CAS PubMed.
- M. Sarmadivaleh, A. Z. Al-Yaseri and S. Iglauer, Influence of Temperature and Pressure on Quartz-Water-CO2 Contact Angle and CO2-Water Interfacial Tension, J. Colloid Interface Sci., 2015, 441, 59–64 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Figures showing more details about simulations and table presenting the interaction parameters between atoms. See https://doi.org/10.1039/d2na00009a |
| This journal is © The Royal Society of Chemistry 2022 |