Open Access Article
Open Access ArticleUnraveling biogeochemical complexity through better integration of experiments and modeling
Adam J.
Siade
ab,
Benjamin C.
Bostick
 c,
Olaf A.
Cirpka
c,
Olaf A.
Cirpka
 d and
Henning
Prommer
d and
Henning
Prommer
 *ab
*ab
aSchool of Earth Sciences, University of Western Australia, Crawley WA 6009, Australia. E-mail: henning.prommer@csiro.au
bCSIRO Land and Water, Private Bag No. 5, Wembley WA 6913, Australia
cLamont-Doherty Earth Observatory, Columbia University, Palisades, NY 10964, USA
dCenter for Applied Geoscience, University of Tübingen, Tübingen, Germany
First published on 29th October 2021
Abstract
The evolution of groundwater quality in natural and contaminated aquifers is affected by complex interactions between physical transport and biogeochemical reactions. Identifying and quantifying the processes that control the overall system behavior is the key driver for experimentation and monitoring. However, we argue that, in contrast to other disciplines in earth sciences, process-based computer models are currently vastly underutilized in the quest for understanding subsurface biogeochemistry. Such models provide an essential avenue for quantitatively testing hypothetical combinations of interacting, complex physical and chemical processes. If a particular conceptual model, and its numerical counterpart, cannot adequately reproduce observed experimental data, its underlying hypothesis must be rejected. This quantitative process of hypothesis testing and falsification is central to scientific discovery. We provide a perspective on how closer interactions between experimentalists and numerical modelers would enhance this scientific process, and discuss the potential limitations that are currently holding us back. We also propose a data-model nexus involving a greater use of numerical process-based models for a more rigorous analysis of experimental observations while also generating the basis for a systematic improvement in the design of future experiments.
Environmental significanceProcess-based numerical modeling is an important tool that has a huge potential to aid in unravelling biogeochemical complexity. Here we make the argument that process-based models can assist in a more rigorous analysis of biogeochemical experiments while also being used to optimize the design of experiments to extract greater value from the collected data. In this Perspectives article we argue that modeling is currently widely underutilized. We explore possible reasons and endeavor to stimulate an intensified collaboration between experimentalists and modelers. This will ultimately lead to a better qualitative understanding and improved quantification capabilities for biogeochemical processes in subsurface and other environmental systems. |
Introduction
The environment is complex. A gram of saturated sediment typically contains a multitude of phases that undergo changes or react through a myriad of physical, biological and chemical processes, effectively controlling solution composition, and overall water quality. Addressing this complexity is a central challenge in environmental science, which is usually done through either reductionist or empirical approaches. A salient example of this complexity is groundwater arsenic (As) contamination, which affects an estimated 200 million people globally.1 Early on, this research was motivated by empirical observations that linked groundwater arsenic to high dissolved iron (Fe) levels,2 and laboratory studies soon followed that established that geogenic As in sediments was readily liberated through the microbial reductive dissolution of Fe(III) oxides.3,4 Although these and other studies have provided valuable insight into the origin and mitigation of groundwater As contamination, additional studies have shown that Fe reduction is highly influenced by Fe mineralogy,5,6 As is not consistently released by Fe(III) reduction alone,7,8 and other microbial metabolisms9 or variably reactive carbon substrates10,11 can be critical in As partitioning. Clays and other phases also affect As cycling by, e.g., controlling aqueous Fe(II) concentrations, and thereby, secondary mineral formation.12 Clearly, we need to consider the essential components of this complexity within our characterization of environmental systems to understand the source and fate of arsenic in groundwater. However, the fate of arsenic serves here only as an example; similar statements could be made for other examples of geochemical and biogeochemical cycling, including nutrient cycling and greenhouse-gas emissions.Taking a reductionist approach to quantifying biogeochemical behavior precludes the ability to comprehend the true complexity of such systems; and, it is often the case that accepting or rejecting a particular hypothesis can only be done if the complexity of the system is properly addressed. We therefore argue that less empirical, more process-based, modeling approaches are essential in achieving this aim. While the use of process-based modeling is routine for complex systems in other disciplines of the earth sciences, the application of such analyses in biogeochemistry are relatively rare, which is perhaps due to a difference in scope. That is, for example, in hydrology and climate science, process-based models are routinely and systematically utilized to interpret and enhance the value of experimental data with a focus on the processes that affect the model's ability to make predictions, e.g., predicting future climate evolution, or the generation and growth of storms. In contrast, process-based biogeochemical models serve to characterize the system itself, most often without the need to make predictions of future behavior. Many well-developed theories/methods underpinning the use of models for system characterization exist, including, for example, Bayesian inference methods.13,14 However, the implementation of such methods requires expertise in numerical and stochastic modeling. It is certainly possible for scientists to be experts across both experimentation and modeling, but in our experience, such scientists are rare, and thus multidisciplinary collaboration is likely to be the most realistic method for conducting system characterization through data-model interaction. In fact, we argue that it is the lack of this type of collaboration throughout the biogeochemistry community that has created skepticism about the benefits of process-based modeling, stifling its application, and in the worst case holding back scientific discovery.
Modeling for system characterization
Hypothesis testing in biogeochemistry often requires the quantification of a myriad of complex interacting processes, and under such circumstances, process-based modeling is the only avenue available. The primary source of uncertainty in biogeochemical studies is arguably centered on the conceptual system understanding. The critical challenge (or art) of conceptual-model design, and its implementation in numerical models, lies not in simply including all states and processes thinkable to the system description, but in analyzing and selecting which ones are relevant for the overall system behavior at the considered spatial and temporal scale. Therefore, the level of complexity considered in the model must be high enough that the primary mechanisms affecting the model-simulated output (corresponding to observations) encompass the majority of those occurring in nature. Models that are too simple may incur systematic bias, preventing them from matching observed data, or producing parameter estimates that are beyond reason. Conversely, models that are too complex for the given amount of data, cannot uniquely be calibrated, and their parameters suffer from excessive variance. The identification of the adequate level of complexity needed for a particular model is therefore an iterative process between modifying the conceptual model, transferring it to a numerical model, calibrating it, and analyzing the residuals.If a particular conceptual/numerical model cannot convincingly reproduce the observed data, regardless of the combination of parameter values that it employs, the model is falsified and must be rejected. Conversely, if a model adequately represents the observed data, it may still be conceptually flawed. Complex, highly-parameterized models have the potential to produce good agreement with observed data simply due to the high flexibility in parameter values, and not necessarily because they imitate the truth.15 Therefore, justifying that a conceptual model has a high likelihood involves at least three criteria: (i) it must adhere to expert knowledge about the system under investigation, (ii) it must be able to reproduce observed data to a reasonable degree with plausible parameter estimates, and (iii) the estimates of highly relevant parameters must have reasonably low variance, i.e., they must be identifiable. There are theories that attempt to combine all three of these factors into a single statistic that can be used to rank conceptual models according to their overall likelihood; such an analysis is often referred to as model discrimination.16
As example for the application to geochemical transport, a few recent studies have successfully adopted the approach of iteratively advancing the conceptual model and calibrating it to observation data to gain new insights into the biogeochemical processes controlling arsenic partitioning and transport.17–25 Rawson et al.19 performed a model-based analysis in which several conceptual models were tested for their ability to represent the release, transport and attenuation of arsenite in cm-scale column experiments. Each of the conceptual models was calibrated through an automatic parameter estimation process, before the most plausible model was selected. They concluded that in addition to arsenic sorption processes, the incorporation of arsenic within newly formed magnetite likely played a major role in explaining the observed attenuation of aqueous arsenic. At a similarly small scale, Rathi et al.,23 compiled and analyzed a range of literature data sets from batch- and stir-flow experiments that investigated the kinetic controls on the oxidation of arsenite by Mn-oxides to develop a process-based numerical model. They tested a range of increasingly complex models, where their most plausible conceptual model consisted of a three-phase oxidation mechanism driven by the accessibility of Mn(IV) and Mn(III) edge sites, and regulated by solution pH and surface passivation by Mn(II). At the km-scale, Wallis et al.25 used numerical modeling to analyze a shallow aquifer in Van Phuc, Vietnam, where arsenic was mobilized at the Red River/aquifer interface, before forming over several decades a large arsenic plume within the Holocene aquifer. They showed, through the testing of a suite of conceptual/numerical models that the hypothesis that a significant fraction of arsenic release was attributed to the reductive dissolution of Fe-oxides in the Holocene aquifer was invalid, while arsenic release within a spatially confined zone of river muds, a “biogeochemical reaction hotspot”, was able to adequately reproduce field observations and therefore the more plausible explanation.
Gaining more value from data through biogeochemical modeling
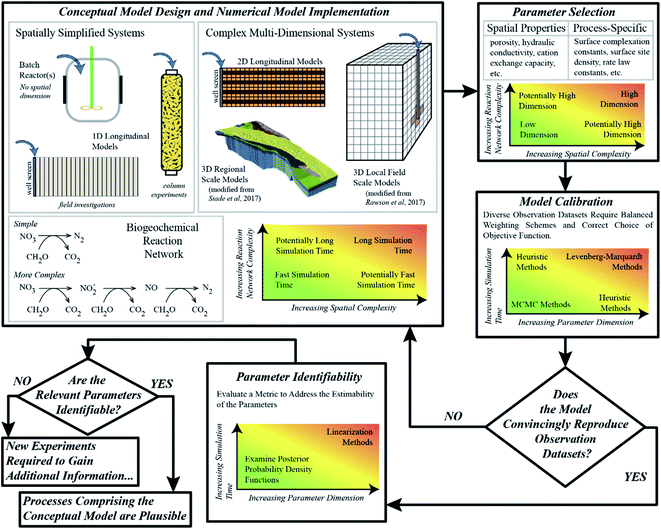
As briefly illustrated above, process-based numerical models provide biogeochemists with the ability to test the plausibility of hypotheses of system behavior on quantitative grounds; however, the procedure by which this can be accomplished can be tedious, as to date no “routine” or universally-applicable workflows have been established, and some challenges are yet to be overcome. Nevertheless, we propose a general series of steps, and the considerations needed for each step, with the overall aim to enhance the value of experimental data. This overall iterative procedure is outlined in Fig. 1, and the individual steps are discussed in some detail below. It is important to point out here, that models can never fully describe the system behavior in the real-world; but, through the iterative process outlined below, they may considerably enhance the knowledge collected from experiments.Conceptual model design and numerical implementation
A key component of any scientific inquiry is to design and carry out experiments that probe the effect of specific processes or variables. In most cases, these specific processes are a subset of the potential processes that are active in a given environment. For example, experiments that study arsenic mobility in groundwater systems will need to consider a wide range of geochemical processes that control the redox zonation and other factors that control the partitioning of arsenic between the aqueous and solid phases. Aside from a wide array of biogeochemical processes, the physical processes of groundwater flow and solute transport also play an important role in explaining observations. Experimental complexity is therefore derived from implicit decisions about which processes are critical to the experiment, and thus which measurements and data are essential, useful, or likely ancillary. These decisions and input data are subsequently passed on to form the basis of process-based conceptual models. Conceptual model complexity therefore comes in two basic forms, the complexity of the (i) comprehensive reaction networks, and (ii) multi-dimensional flow and transport system under consideration. Several conceptual models, each considering different reaction systems and hydrological frameworks, may seem qualitatively reasonable according to the experimental data.Each considered conceptual model needs to be translated into a numerical model by (i) choosing a combination of equilibrium expressions and rate laws for all reactions, (ii) selecting the most suitable software, (iii) selecting the dimensionality of the domain and discretizing the problem in space and time, and (iv) defining initial and boundary conditions. It is important to note that the combination of complex reaction networks and complex flow-and-transport processes may result in a computational burden that severely limits rigorous uncertainty analysis and model calibration. Therefore, finding a balance between computational limitations and an adequate complexity can be challenging.
Parameter selection
The implementation of model parameters is often confusing amongst modelers and experimentalists from different research disciplines. Each parameter has a characteristic variability or uncertainty, but the implicit significance of that uncertainty depends on the type of parameter, and the community describing it. Groundwater hydrologic modelers, for example, will often think of parameter uncertainty as a way to encapsulate spatial heterogeneity. Biogeochemical models on the other hand, while also sometimes considering the spatial variability of aquifer properties,25 often focus more on parameters attributed to biogeochemical processes, that are often uniform in space. This is in particular the case for the simulation of laboratory experiments which commonly employ well-mixed, homogenous sediment material to ensure that process-based parameters can be assumed to be uniform. Typical parameters may include equilibrium constants for surface complexation reactions, or reaction rate constants that are embedded in reaction rate laws. As a result, biogeochemical models, where most applications focus on the laboratory scale, have to date far fewer parameters than highly resolved groundwater flow models. For example, Siade et al.26 presented a regional groundwater model with over 400 parameters that consisted of only three fundamental parameter types. In contrast, only 30 parameters were employed by Rawson et al.20 for reactive transport modeling of the fate of arsenic during a sucrose injection experiment; however, they consisted of a number of parameter types ranging from hydraulic conductivity to porosity to kinetic reaction rate constants to surface complexation constants. While the latter numerical model may be viewed by many biogeochemists as overly complex, i.e., as “merely a fitting exercise”, compared to the former study, a parameter dimension of 30 may be seen by groundwater hydrologists as relatively small and consequently biased in its simplicity. This contradiction is precisely why parameter dimension alone cannot be used to determine how conclusive a modeling study may or may not be, and that instead, one must evaluate the balance between parameter variability and the amount of independent information available in the calibration data set.Model calibration
The aim of model calibration, also referred to as “inverse modeling” or “history matching”, is to systematically adjust model parameters in an effort to minimize the residuals, that is, the differences between observations and the corresponding simulation results. Unlike most groundwater hydrological studies, which in many cases primarily involve the spatially and temporally distributed observations of hydraulic head, biogeochemical models generally involve a wider range of independent observation data types, each of which is collected at different frequencies. For example, Sun et al.,21 who investigated a novel arsenic immobilization technique via column experiments, considered not only several solute concentrations (arsenic, iron, nitrate, calcium, among others) and pH in the effluent but also the observed iron mineral composition as well as the partitioning of arsenic among the various solid phases within the sediments. This resulted in a complex calibration problem in which the weighting of different observation data types had to be carefully considered for effective calibration. In idealized theory, the weights of the observations should only reflect the uncertainty of the measurements. In practice, however, it might be necessary to give rare but valuable measurements larger weights than other, more frequently taken measurements, whereas in other cases it might be useful to consider integrative metrics such as mean breakthrough times rather than the original concentration measurements as the data to be fitted. All of that is needed to ensure that the objective function is consistent with qualitative or visual assessments of the agreement between model results and observations.Biogeochemical models involve many parameters and many different types of observations, and the relationship between those parameters and data can be complex and, more often than not, highly nonlinear. Understanding the nature of this nonlinearity in an attempt to approach model calibration consistently turns out to be dreary and dreadfully complex topic but wildly significant for our ability to describe environmental systems.27 In modeling practice, two major categories of calibration schemes have shown reasonable success in this regard: linearization-based methods such as the Levenberg–Marquardt method,28,29 and ensemble-based methods such as Markov Chain Monte Carlo (MCMC) methods.30,31 Algorithms employing the former method usually converge within a few iterations towards a minimum of the objective function, but may not be able to obtain the global minimum in highly nonlinear problems32 and provide only a linearized estimate of the posterior parameter uncertainty, that is, the remaining parameter uncertainty after calibration. Consequently, for biogeochemical models, ensemble-based algorithms may be more suitable as they do not rely on model linearization. However, a debilitating drawback is their computational expense, as they require typically thousands of model executions, which is compounded by high parameter dimension and long simulation times. Nevertheless, for studies involving models that execute quickly and have reasonable parameter dimensions, ensemble-based methods are preferable.33,34 While there is no overall best choice, to date algorithms based on successive linearization are often the only practical option available. However, in recent years heuristic algorithms, such as particle swarm optimization (PSO),35 have shown great promise in being a good compromise between being able to obtain the global solution to highly nonlinear inverse problems but at a computational expense much less than MCMC methods.18,19,21–23,32,36–40 However, it is important to note that, like the Levenberg–Marquardt-type methods, such heuristic methods do not necessarily provide an immediate nonlinear estimation of parameter uncertainty.
Parameter identifiability
The most important consideration of properly-applied biogeochemical models is that the parameters are highly identifiable, that is, they can be estimated with a narrow range of uncertainty considering the given model and its complexity. Demonstrating that parameters are identifiable, even in models that contain many such parameters, ensures that the modeling is not “merely a fitting exercise”, a critique often leveled against modeling studies. Ensuring that parameters are highly identifiable, given the available experimental data, requires that the information content of this data is balanced with the degree of the employed parameter variability; that is, it requires that the model calibration is “well-posed” or “well-determined”.15 To gauge this, it is essential that scientists employ either parameter sensitivity analyses, which do not require the model to be calibrated,41–45 or methods for quantifying parameter uncertainty.46–53 Without the application of such analyses, models are poorly described and potentially meaningless – and they would indeed become merely a fitting exercise.Therefore, in order to judge the merits of a model calibration exercise, one must first ask how identifiable the parameters are – it is quite possible that the information available can be sufficient to support a relatively large number of parameters. If a model has poorly identifiable parameters some questions have to be answered before dismissing the model altogether: (1) are the uncertainties of the poorly identifiable parameters due to correlation? If so, compensatory effects exist and the model may be simplified by employing combinations of parameters. (2) How well can the parameter values be constrained by prior knowledge from previous studies or expert knowledge? In any case, a Bayesian framework should be employed to make uncertainty transparent, and all decisions on inclusion of prior knowledge must be made transparent as well.
Conceptual model evaluation
Ultimately, the output of a numerical model reflects the underlying conceptual model, and can be directly compared to experimental data. If a conceptual model and its subsequent numerical model cannot match observed data adequately, then it must be rejected, and a new conceptual model generated, as visualized in Fig. 1. If the observed data can be adequately reproduced by the model, its parameter estimates agree with prior knowledge, and the parameters central to the salient processes comprising the hypothesis under investigation are overall deemed identifiable, then the conceptual model can be considered plausible for the given observation data, and the hypothesis cannot be rejected. Despite the existence of a number of biogeochemical studies involving numerical modeling, very few of them19,20,23,25,32 employ such an iterative conceptual model identification procedure.The biogeochemical data-model nexus
One may find that by using the above described system characterization procedure, several plausible conceptual models may emerge, indicating that conceptual uncertainty remains even after the application of expert knowledge, experimental data, and model calibration. Or, one may find that numerous parameters have been deemed unidentifiable. It is easy at this point for investigators to feel that modeling is generally inconclusive and impossible. However, we argue that such modeling results are an objective indicator that more, or different, data are required to constrain the problem in order to derive a conclusive outcome, which is actually an important result. The numerical model(s), while uncertain, now provides the scientist with a tool for quantitatively ascertaining what type of data should be collected to maximize the gain of information – a powerful advantage that our experience suggests cannot be determined through expert knowledge alone. The general procedure by which a mathematical model is used to define/optimize the collection of new data is termed optimal design of experiments and is a broad field in stochastic modeling,54–56 which has penetrated into many fields of earth sciences,26,57–60 but remains relatively absent in biogeochemistry.Optimal design of experiments
Setting up biogeochemical monitoring strategies involves deciding what to measure where and when. In laboratory experiments even more decisions are to be taken, such as the hydrochemical composition of the feed solution, the length of a column, the flow rates, temperature control, etc. Because resources are limited, it is impossible to measure “everything everywhere at all times”, so researchers must be careful when designing their experiments. Many experimentalists trust only their experience, which can be misleading as it is not straightforward to determine which type of data contains the most information possible for addressing the scientific question at hand due to the complexity of the interacting processes of the system.Optimal-design methods employ mathematical optimization focused on minimizing (or maximizing) a metric of the model by changing experimental conditions or measurement types/locations/times. Classical applications in groundwater hydrology focus mainly on minimizing the parameter/predictive uncertainty of the model. In biogeochemical modeling, the primary source of uncertainty is on the conceptual level and hence, the data to be collected should be targeted to make different conceptual models better distinguishable from each other upon calibration.
A key problem in optimal design of experiments is that clearly before taking the measurements, the measured values cannot be known. If the target metric depended linearly on the measurement not yet taken, reduction of its uncertainty would not depend on the measurement value itself. This is the premise of linearized data-worth analysis.61 In most cases of biogeochemical modeling, where models are highly nonlinear and the focus is on conceptual uncertainty, this assumption is not valid, thus implying that uncertainty reduction by a measurement depends on the measurement value. In this case the prior distribution of the measurements must be sampled to evaluate the expected reduction of uncertainty.62
Even if optimal experimental design were conducted, it is still difficult at best, and impractical at worst to foresee which measurements will be most relevant to still unforeseen processes that could be important. Therefore, we argue that biogeochemical characterization studies should be thought of as an iterative or continuous task. That is, (i) once initial data sets have been acquired, (ii) model-based interpretation is performed to quantify parameter and conceptual uncertainty, then (iii) modeling is used to optimally design further experiments, (iv) resulting in more data, and (v) repeat. Thus, the interaction between data and models should be thought of as cyclical.
What is holding us back, and where do we go from here?
Despite the powerful advantages that calibration, discrimination, and experimental design can provide to biogeochemical studies, these technologies remain vastly underutilized. We argue that there are two overarching reasons why this may be the case, (i) the different perspective of biogeochemistry compared to other disciplines of earth sciences renders many existing algorithms inadequate, and (ii) from our perhaps biased experience, there is still a wide, systemic collaboration gap between experimentalists and numerical/stochastic modelers, perhaps due to the traditional focus of different educational backgrounds (e.g., geo/environmental science and microbiology versus engineering/physics).Technical difficulties
Biogeochemical studies almost always focus on conceptual uncertainty and the high degree of nonlinearity of such models compromises the use of linearization techniques, and leads to excessive computer runtimes. These issues often jeopardize the use of both linearization methods and ensemble-based Bayesian analyses due to the issues discussed previously. Therefore, scientists must make the best of the computing resources available to them, and be clear about the limitations of the methods they employ. This may mean, for example, that if linearization methods are used to quantify identifiability, a clear statement of the limitations therein should be provided.24These limitations indicate that progress is needed for the biogeochemistry community, through the development of new uncertainty quantification algorithms with these types of models in mind. Perhaps, one important characteristic of such models is that the parameter dimension is often not very high (usually in the lower tens). However, due to long computer runtimes, ensemble-based methods may still not be suitable. Therefore, perhaps a trade-off could be made between the purity of ensemble-based Bayesian methods and an increased efficiency, without introducing too much bias. Modifications of heuristic algorithms, for example, may prove to be a promising avenue, e.g., by observing how differential evolution has improved MCMC methods.49 Machine learning algorithms may also hold the promise of reducing computational costs.45,63 As the field of Bayesian inference is rapidly evolving, more efficient techniques can be expected to become available in the future.
Expertise and communication
Considering that experimentalists and numerical modelers often come from different educational backgrounds focused on different aspects of mathematics and science, it is easy for them to fall into “comfort zones” where research efforts subsequently become one-sided, hindering the rate of scientific progress. We therefore argue that scientists in both groups should step outside their comfort zones and work hard to become experts across both disciplines. Since this merger is likely to happen post-PhD, effective communication across disciplines therefore becomes critical in order to achieve this. For example, a scientist who excels at mathematics and statistics may not bring the level of biogeochemical intuition needed to make true scientific discovery, and conversely, experimentalists who rely on intuition alone to design and interpret their experiments may also miss out on opportunities for discovery due to the sheer complexity of the system they are trying to analyze. But, with both groups of scientists working closely together, not only will such a collaboration provide the potential for accelerated significant scientific progress, it will also allow both groups to broaden their scientific understanding so that, individually, they become far more effective scientists.Concluding comment
There is a long history of experimentation within the biogeochemical community, with numerous high-value datasets published throughout the literature. Many of these datasets have not been rigorously interpreted through modeling, and their underlying conceptual models are only speculative. Therefore, there are numerous opportunities to re-examine these datasets and conceptual models through numerical modeling in an effort to add additional value to them.18 To do so requires that the data, including metadata (information on the type of measurements, experimental conditions etc.), be presented and collated from experiments, and published for use. It has become standard practice among several scientific societies that papers are only published if the associated data are made available via public repositories,64 and likewise the software codes used in modeling and data analysis should be made public. The exploration of data, both legacy and new, through numerical/inverse modeling also aids the experimentalist with the ability to design additional experiments, a necessary step in moving science forward. Therefore, with well-developed theories and procedures specifically tailored to this field, and an increased level of collaboration across disciplines, biogeochemists not only have the opportunity to extract new value from data acquired years ago, but also the ability to maximize information gained from new future experiments down the road.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AJS was supported by the Department of Water and Environmental Regulation and Water Corporation through the project “Advanced Modelling Methodologies for Groundwater Resource Management and Asset Investment Planning”. BCB was supported by National Science Foundation (NSF) grant EAR 15-21356 and National Institute of Environmental Health Sciences grant ES010349. OAC was supported by funding provided by Deutsche Forschungsgemeinschaft (DFG) through the AdvectAs project (grant Ci 26/15-1).References
- J. Podgorski and M. Berg, Global Threat of Arsenic in Groundwater, Science, 2020, 368(6493), 845–850, DOI:10.1126/science.aba1510.
- R. T. Nickson, J. M. Mcarthur, P. Ravenscroft, W. G. Burgess and K. M. Ahmed, Mechanism of Arsenic Release to Groundwater, Bangladesh and West Bengal, Appl. Geochemistry, 2000, 15(4), 403–413, DOI:10.1016/S0883-2927(99)00086-4.
- J. Zobrist, P. R. Dowdle, J. A. Davis and R. S. Oremland, Mobilization of Arsenite by Dissimilatory Reduction of Adsorbed Arsenate, Environ. Sci. Technol., 2000, 34(22), 4747–4753, DOI:10.1021/es001068h.
- F. S. Islam, A. G. Gault, C. Boothman, D. A. Polya, J. M. Chamok, D. Chatterjee and J. R. Lloyd, Role of Metal-Reducing Bacteria in Arsenic Release from Bengal Delta Sediments, Nature, 2004, 430(6995), 68–71, DOI:10.1038/nature02638.
- J. M. Zachara, J. K. Fredrickson, S. M. Li, D. W. Kennedy, S. C. Smith and P. L. Gassman, Bacterial Reduction of Crystalline Fe3+ Oxides in Single Phase Suspensions and Subsurface Materials, Am. Mineral., 1998, 83(11–12 part 2), 1426–1443, DOI:10.2138/am-1998-11-1232.
- D. Zhang, H. Guo, W. Xiu, P. Ni, H. Zheng and C. Wei, In-Situ Mobilization and Transformation of Iron Oxides-Adsorbed Arsenate in Natural Groundwater, J. Hazard. Mater., 2017, 321, 228–237, DOI:10.1016/j.jhazmat.2016.09.021.
- I. Wallis, H. Prommer, T. Pichler, V. Post, S. B. Norton, M. D. Annable and C. T. Simmons, Process-Based Reactive Transport Model to Quantify Arsenic Mobility during Aquifer Storage and Recovery of Potable Water, Environ. Sci. Technol., 2011, 45(16), 6924–6931, DOI:10.1021/es201286c.
- S. Fakhreddine, H. Prommer, S. M. Gorelick, J. Dadakis and S. Fendorf, Controlling Arsenic Mobilization during Managed Aquifer Recharge: The Role of Sediment Heterogeneity, Environ. Sci. Technol., 2020, 54(14), 8728–8738, DOI:10.1021/acs.est.0c00794.
- S. C. Ying, B. D. Kocar, S. D. Griffis and S. Fendorf, Competitive Microbially and Mn Oxide Mediated Redox Processes Controlling Arsenic Speciation and Partitioning, Environ. Sci. Technol., 2011, 45(13), 5572–5579, DOI:10.1021/es200351m.
- N. Mladenov, Y. Zheng, M. P. Miller, D. R. Nemergut, T. Legg, B. Simone, C. Hageman, M. M. Rahman, K. M. Ahmed and D. M. Mcknight, Dissolved Organic Matter Sources and Consequences for Iron and Arsenic Mobilization in Bangladesh Aquifers, Environ. Sci. Technol., 2010, 44(1), 123–128, DOI:10.1021/es901472g.
- D. Postma, F. Larsen, N. T. Thai, P. T. K. Trang, R. Jakobsen, P. Q. Nhan, T. V. Long, P. H. Viet and A. S. Murray, Groundwater Arsenic Concentrations in Vietnam Controlled by Sediment Age, Nat. Geosci., 2012, 5(9), 656–661, DOI:10.1038/ngeo1540.
- R. Gubler and L. K. ThomasArrigo, Ferrous Iron Enhances Arsenic Sorption and Oxidation by Non-Stoichiometric Magnetite and Maghemite, J. Hazard. Mater., 2021, 402, 123425, DOI:10.1016/j.jhazmat.2020.123425.
- M. Höge, T. Wöhling and W. Nowak, A Primer for Model Selection: The Decisive Role of Model Complexity, Water Resour. Res., 2018, 54(3), 1688–1715, DOI:10.1002/2017wr021902.
- W. Nowak and A. Guthke, Entropy-Based Experimental Design for Optimal Model Discrimination in the Geosciences, Entropy, 2016, 18(11) DOI:10.3390/e18110409.
- W. W. Yeh, Review of Parameter Identification Procedures in Groundwater Hydrology: The Inverse Problem, Water Resour. Res., 1986, 22(2), 95–108, DOI:10.1029/wr022i002p00095.
- M. Ye, P. D. Meyer and S. P. Neuman, On Model Selection Criteria in Multimodel Analysis, Water Resour. Res., 2008, 44(3) DOI:10.1029/2008wr006803.
- L. Liu, P. J. Binning and B. F. Smets, Evaluating Alternate Biokinetic Models for Trace Pollutant Cometabolism, Environ. Sci. Technol., 2015, 49(4), 2230–2236, DOI:10.1021/es5035393.
- J. Jamieson, H. Prommer, A. H. Kaksonen, J. Sun, A. J. Siade, A. Yusov and B. Bostick, Identifying and Quantifying the Intermediate Processes during Nitrate-Dependent Iron(II) Oxidation, Environ. Sci. Technol., 2018, 52(10), 5771–5781, DOI:10.1021/acs.est.8b01122.
- J. Rawson, H. Prommer, A. Siade, J. Carr, M. Berg, J. A. Davis and S. Fendorf, Numerical Modeling of Arsenic Mobility during Reductive Iron-Mineral Transformations, Environ. Sci. Technol., 2016, 50(5), 2459–2467, DOI:10.1021/acs.est.5b05956.
- J. Rawson, A. Siade, J. Sun, H. Neidhardt, M. Berg and H. Prommer, Quantifying Reactive Transport Processes Governing Arsenic Mobility after Injection of Reactive Organic Carbon into a Bengal Delta Aquifer, Environ. Sci. Technol., 2017, 51(15), 8471–8480, DOI:10.1021/acs.est.7b02097.
- J. Sun, H. Prommer, A. J. Siade, S. N. Chillrud, B. J. Mailloux and B. C. Bostick, Model-Based Analysis of Arsenic Immobilization via Iron Mineral Transformation under Advective Flows, Environ. Sci. Technol., 2018, 52(16), 9243–9253, DOI:10.1021/acs.est.8b01762.
- L. Stolze, D. Zhang, H. Guo and M. Rolle, Model-Based Interpretation of Groundwater Arsenic Mobility during in Situ Reductive Transformation of Ferrihydrite, Environ. Sci. Technol., 2019, 53(12), 6845–6854, DOI:10.1021/acs.est.9b00527.
- B. Rathi, J. Jamieson, J. Sun, A. J. Siade, M. Zhu, O. A. Cirpka and H. Prommer, Process-Based Modeling of Arsenic(III) Oxidation by Manganese Oxides under Circumneutral PH Conditions, Water Res., 2020, 185 DOI:10.1016/j.watres.2020.116195.
- D. Schafer, J. Sun, J. Jamieson, A. J. Siade, O. Atteia and H. Prommer, Model-Based Analysis of Reactive Transport Processes Governing Fluoride and Phosphate Release and Attenuation during Managed Aquifer Recharge, Environ. Sci. Technol., 2020, 54(5), 2800–2811, DOI:10.1021/acs.est.9b06972.
- I. Wallis, H. Prommer, M. Berg, A. J. Siade, J. Sun and R. Kipfer, The River–Groundwater Interface as a Hotspot for Arsenic Release, Nat. Geosci., 2020, 13(4), 288–295, DOI:10.1038/s41561-020-0557-6.
- A. J. Siade, J. Hall and R. N. Karelse, A Practical, Robust Methodology for Acquiring New Observation Data Using Computationally Expensive Groundwater Models, Water Resour. Res., 2017, 53(11), 9860–9882, DOI:10.1002/2017wr020814.
- G. A. F. Seber and C. J. Wild, Nonlinear Regression, John Wiley & Sons, Ltd, Hoboken, New Jersey, 2003 Search PubMed.
- K. A. Levenberg, Method For The Solution Of Certain Non-Linear Problems In Least Squares, Q. Appl. Math., 1944, 2(2), 164–168 Search PubMed.
- D. W. Marquardt, An Algorithm for Least-Squares Estimation of Nonlinear Parameters, J. Soc. Ind. Appl. Math., 1963, 11(2), 431–441, DOI:10.1137/0111030.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, Equation of State Calculations by Fast Computing Machines, J. Chem. Phys., 1953, 21(6), 1087–1092, DOI:10.1063/1.1699114.
- W. K. Hastings, Monte Carlo Sampling Methods Using Markov Chains and Their Applications, Biometrika, 1970, 57(1), 97–109, DOI:10.1093/biomet/57.1.97.
- B. Rathi, H. Neidhardt, M. Berg, A. Siade and H. Prommer, Processes Governing Arsenic Retardation on Pleistocene Sediments: Adsorption Experiments and Model-Based Analysis, Water Resour. Res., 2017, 53(5), 4344–4360, DOI:10.1002/2017wr020551.
- P. Ramin, A. L. Brock, F. Polesel, A. Causanilles, E. Emke, P. De Voogt and B. G. Plosz, Transformation and Sorption of Illicit Drug Biomarkers in Sewer Systems: Understanding the Role of Suspended Solids in Raw Wastewater, Environ. Sci. Technol., 2016, 50(24), 13397–13408, DOI:10.1021/acs.est.6b03049.
- F. Malaguerra, J. C. Chambon, P. L. Bjerg, C. Scheutz and P. J. Binning, Development and Sensitivity Analysis of a Fully Kinetic Model of Sequential Reductive Dechlorination in Groundwater, Environ. Sci. Technol., 2011, 45(19), 8395–8402, DOI:10.1021/es201270z.
- R. Eberhart and J. Kennedy, New Optimizer Using Particle Swarm Theory, in Proceedings of the International Symposium on Micro Machine and Human Science, IEEE, 1995, pp. 39–43, DOI:10.1109/mhs.1995.494215.
- L. Stolze, D. Zhang, H. Guo and M. Rolle, Surface Complexation Modeling of Arsenic Mobilization from Goethite: Interpretation of an in-Situ Experiment, Geochim. Cosmochim. Acta, 2019, 248, 274–288, DOI:10.1016/j.gca.2019.01.008.
- B. Rathi, A. J. Siade, M. J. Donn, L. Helm, R. Morris, J. A. Davis, M. Berg and H. Prommer, Multiscale Characterization and Quantification of Arsenic Mobilization and Attenuation During Injection of Treated Coal Seam Gas Coproduced Water into Deep Aquifers, Water Resour. Res., 2017, 53(12), 10779–10801, DOI:10.1002/2017wr021240.
- H. Prommer, J. Sun, L. Helm, B. Rathi, A. J. Siade and R. Morris, Deoxygenation Prevents Arsenic Mobilization during Deepwell Injection into Sulfide-Bearing Aquifers, Environ. Sci. Technol., 2018, 52(23), 13801–13810, DOI:10.1021/acs.est.8b05015.
- A. J. Siade, B. Rathi, H. Prommer, D. Welter and J. Doherty, Using Heuristic Multi-Objective Optimization for Quantifying Predictive Uncertainty Associated with Groundwater Flow and Reactive Transport Models, J. Hydrol., 2019, 577 DOI:10.1016/j.jhydrol.2019.123999.
- L. Stolze, J. B. Wagner, C. D. Damsgaard and M. Rolle, Impact of Surface Complexation and Electrostatic Interactions on PH Front Propagation in Silica Porous Media, Geochim. Cosmochim. Acta, 2020, 277, 132–149, DOI:10.1016/j.gca.2020.03.016.
- I. T. Jolliffe, Principal Component Analysis, Springer, New York, NY, 2002 Search PubMed.
- J. Doherty and R. J. Hunt, Two Statistics for Evaluating Parameter Identifiability and Error Reduction, J. Hydrol., 2009, 366(1–4), 119–127, DOI:10.1016/j.jhydrol.2008.12.018.
- P. G. Constantine, E. Dow and Q. Wang, Active Subspace Methods in Theory and Practice: Applications to Kriging Surfaces, SIAM J. Sci. Comput., 2014, 36(4), A1500–A1524, DOI:10.1137/130916138.
- I. M. Sobol, Global Sensitivity Indices for Nonlinear Mathematical Models and Their Monte Carlo Estimates, Math. Comput. Simul., 2001, 55(1–3), 271–280, DOI:10.1016/S0378-4754(00)00270-6.
- D. Erdal, S. Xiao, W. Nowak and O. A. Cirpka, Sampling Behavioral Model Parameters for Ensemble-Based Sensitivity Analysis Using Gaussian Process Emulation and Active Subspaces, Stoch. Environ. Res. Risk Assess., 2020, 1–18, DOI:10.1007/s00477-020-01867-0.
- A. F. M. Smith and A. E. Gelfand, Bayesian Statistics without Tears: A Sampling-Resampling Perspective, Am. Stat., 1992, 46(2), 84–88, DOI:10.1080/00031305.1992.10475856.
- D. V. Lindley, Bayesian Statistics, Society for Industrial and Applied Mathematics, 1972, DOI:10.1137/1.9781611970654.
- J. S. Press Subjective and Objective Bayesian Statistics; Wiley Series in Probability and Statistics, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2002, DOI:10.1002/9780470317105.
- J. A. Vrugt, C. J. F. Ter Braak, C. G. H. Diks, B. A. Robinson, J. M. Hyman and D. Higdon, Accelerating Markov Chain Monte Carlo Simulation by Differential Evolution with Self-Adaptive Randomized Subspace Sampling, Int. J. Nonlinear Sci. Numer. Simul., 2009, 10(3), 273–290, DOI:10.1515/ijnsns.2009.10.3.273.
- E. H. Keating, J. Doherty, J. A. Vrugt and Q. Kang, Optimization and Uncertainty Assessment of Strongly Nonlinear Groundwater Models with High Parameter Dimensionality, Water Resour. Res., 2010, 46(10) DOI:10.1029/2009wr008584.
- E. Laloy and J. A. Vrugt, High-Dimensional Posterior Exploration of Hydrologic Models Using Multiple-Try DREAM (ZS) and High-Performance Computing, Water Resour. Res., 2012, 48(1) DOI:10.1029/2011wr010608.
- M. Sadegh and J. A. Vrugt, Approximate Bayesian Computation Using Markov Chain Monte Carlo Simulation: DREAM (ABC), Water Resour. Res., 2014, 50(8), 6767–6787, DOI:10.1002/2014wr015386.
- M. Tonkin and J. Doherty, Calibration-Constrained Monte Carlo Analysis of Highly Parameterized Models Using Subspace Techniques, Water Resour. Res., 2009, 45(1) DOI:10.1029/2007wr006678.
- K. Chaloner and I. Verdinelli, Bayesian Experimental Design: A Review, Stat. Sci., 1995, 10(3), 273–304, DOI:10.1214/ss/1177009939.
- P. Müller, Simulation Based Optimal Design, Handbook of Statistics, Elsevier, January 1, 2005, pp. 509–518, DOI:10.1016/s0169-7161(05)25017-4.
- M. P. F. Berger and W. K. Wong, An Introduction to Optimal Designs for Social and Biomedical Research, John Wiley & Sons, Ltd, Chichester, UK, 2009, DOI:10.1002/9780470746912.
- P. C. Leube, A. Geiges and W. Nowak, Bayesian Assessment of the Expected Data Impact on Prediction Confidence in Optimal Sampling Design, Water Resour. Res., 2012, 48(2) DOI:10.1029/2010wr010137.
- P. Brunner, J. Doherty and C. T. Simmons, Uncertainty Assessment and Implications for Data Acquisition in Support of Integrated Hydrologic Models, Water Resour. Res., 2012, 48(7) DOI:10.1029/2011wr011342.
- A. M. Dausman, J. Doherty, C. D. Langevin and M. C. Sukop, Quantifying Data Worth Toward Reducing Predictive Uncertainty, Ground Water, 2010, 48(5), 729–740, DOI:10.1111/j.1745-6584.2010.00679.x.
- N.-Z. Sun and W. W.-G. Yeh, Coupled Inverse Problems in Groundwater Modeling: 2. Identifiability and Experimental Design, Water Resour. Res., 1990, 26(10), 2527–2540, DOI:10.1029/wr026i010p02527.
- O. A. Cirpka, C. M. Bürger, W. Nowak and M. Finkel, Uncertainty and Data Worth Analysis for the Hydraulic Design of Funnel-and-Gate Systems in Heterogeneous Aquifers, Water Resour. Res., 2004, 40(11) DOI:10.1029/2004wr003352.
- H. V. Pham and F. T. C. Tsai, Bayesian Experimental Design for Identification of Model Propositions and Conceptual Model Uncertainty Reduction, Adv. Water Resour., 2015, 83, 148–159, DOI:10.1016/j.advwatres.2015.05.024.
- A. J. Siade, T. Cui, R. N. Karelse and C. Hampton, Reduced-Dimensional Gaussian Process Machine Learning for Groundwater Allocation Planning Using Swarm Theory, Water Resour. Res., 2020, 56(3) DOI:10.1029/2019wr026061.
- M. D. Wilkinson, M. Dumontier, Ij. J. Aalbersberg, G. Appleton, M. Axton, A. Baak, N. Blomberg, J. W. Boiten, L. B. da Silva Santos, P. E. Bourne, J. Bouwman, A. J. Brookes, T. Clark, M. Crosas, I. Dillo, O. Dumon, S. Edmunds, C. T. Evelo, R. Finkers, A. Gonzalez-Beltran, A. J. G. Gray, P. Groth, C. Goble, J. S. Grethe, J. Heringa, P. A. C. t Hoen, R. Hooft, T. Kuhn, R. Kok, J. Kok, S. J. Lusher, M. E. Martone, A. Mons, A. L. Packer, B. Persson, P. Rocca-Serra, M. Roos, R. van Schaik, S. A. Sansone, E. Schultes, T. Sengstag, T. Slater, G. Strawn, M. A. Swertz, M. Thompson, J. Van Der Lei, E. Van Mulligen, J. Velterop, A. Waagmeester, P. Wittenburg, K. Wolstencroft, J. Zhao and B. Mons, Comment: The FAIR Guiding Principles for Scientific Data Management and Stewardship, Sci. Data, 2016, 3(1), 1–9, DOI:10.1038/sdata.2016.18.
| This journal is © The Royal Society of Chemistry 2021 |