Open Access Article
Open Access ArticleSingle-molecule conductance oscillations in alkane rings†
Ali K.
Ismael
 *ab and
Colin J.
Lambert
*ab and
Colin J.
Lambert
 *a
*a
aDepartment of Physics, Lancaster University, Lancaster LA1 4YB, UK. E-mail: k.ismael@lancaster.ac.uk; c.lambert@lancaster.ac.uk
bDepartment of Physics, College of Education for Pure Science, Tikrit University, Tikrit, Iraq
First published on 11th March 2019
Abstract
We investigate the single-molecule electrical conductance of alkane rings connected to gold electrodes and demonstrate that their logarithmic conductances are ocillatory functions of length. This contrasts with the logarithmic conductances of alkane chains, which decay linearly with length. This non-classical behaviour is attributed to conformational effects in the alkane rings, which tend to be more (less) planar when their branches contain even (odd) numbers of CH2 groups. Surprisingly the conductances of alkane rings with two parallel conductance paths are predicted to be lower then those of the corresponding linear chains with only one conductance path.
1 Introduction
As any high-school science pupil will attest, the electrical conductance of two identical conductors connected in parallel is double the conductance of a single conductor. On the other hand, when two conductors are connected in parallel within a molecule, the resulting conductance rarely follows such a classical law. An early theoretical study1 suggested that the resulting conductance should be increased by a factor of four, rather than the classical conductance factor of two. To test this prediction experimentally, Vazquez et al.2 measured the conductance of four pairs of double-backbone and single-backbone molecular junctions and found their conductance ratios to lie between 2.8 and 1.6, i.e. the ratios were either higher or lower than the classical value of 2, but none reached the ratio of 4. More recent theoretical studies have demonstrated that conductances of inter-molecular parallel branches combine in a variety ways, depending on the precise chemistry of their connectivity within a molecule.3–10 This variability is a consequence of multi-path quantum interference within multi-branched molecules and is clear evidence that electron transport through single molecules is phase-coherent, even at room temperature.11–19 All of the above studies have focused on quantum interference within the pi system of multi-path molecules, whereas transport through their Sigma systems has been largely ignored. Sigma transport is not only of interest in non-conjugated molecules, where extended pi systems are absent, but also in conjugated molecules exhibiting destructive quantum interference, where transport in the pi channel is suppressed.20 The importance of Sigma-mediated transport was demonstrated in a recent realisation of a molecular-scale transistor, where the room-temperature on–off ratio was found to be 100 times higher in a self-assembled monolayer (SAM) formed from non-conjugated molecules, compared with a SAM formed from conjugated molecules.2The aim of the present paper is to examine how parallel electrical conductances combine in multi-branch, non-conjugated molecules, by examining Sigma-mediated transport in ring-like alkanes coupled to gold electrodes. Linear alkane chains are a well-studied paradigm of phase-coherent electron tunnelling through single-molecule Sigma systems. In common with other linear molecular chains, such as oligoynes4 and fluorenes,21 their conductance G is found to decay exponentially with length, as G ∼ exp − βn, where n is the number of methylene units (e.g. n = 8 for octane dithiol) in the alkane chain. The decay constant β is measured to be approximately 0.9 per methylene group, although there is approximately a 10% variation in the value reported by different experimental groups and results depend slightly on the nature of the binding to the gold electrodes.22–27 In what follows, we show that despite the absence of an extended pi system, when alkane chains are connected in parallel to form double-branched molecules, their conductances combine in a non-classical manner.
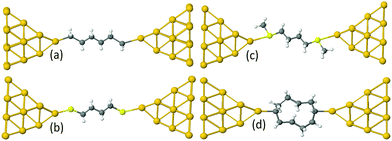
Examples of linear chains with three different anchor groups are shown in Fig. 1. The top left chain (Au–C) is coupled to the electrodes by a gold–carbon covalent bond. The bottom left chain (Au–S) is coupled to the gold by thiol anchor groups. The top right alkane chain (Au–SMe) is connected to gold electrodes via thiomethyl anchor groups. The bottom right alkane ring (Au–C) is coupled to the electrodes by a gold–carbon covalent bond. To aid the discussion of their conductances, we assign an integer n to each chain (see Fig. 1), such that chains of equal n have comparable lengths. For Au–SMe and Au–S terminated chains, n is defined to equal the number of methyl units along the length of the chain between the sulfurs. For the Au–C linked chains, where the terminal CH2 units are regarded as anchor groups, n is defined to be two less than the number of CH2 units. In the case of double-branch alkane rings, n is defined to be the number of CH2 units in each branch, excluding the terminal CH units, which covalently couple to the electrodes. In other words, for a ring with N methyl units, n = (N − 2)/2.
2 Methods
We started by modelling terminal groups-Au binding, and then relaxed each compound in the presence of fixed leads. Using the density functional (DFT) code SIESTA28 (for more detail see geometry of isolated alkane in the ESI†) the optimum geometries of isolated alkane linear chains and rings, were obtained by relaxing the molecules until all forces on the atoms were less than 0.05 eV Å−1 (Fig. S1 and Table S1, ESI†). We used a double-zeta plus polarization orbital basis set, norm-conserving pseudopotentials, the local density approximation (LDA) exchange correlation functional, and to define the real space grid, an energy cutoff of 200 Rydbergs. We also computed results using GGA and found that the resulting transmission functions were comparable29,30 with those obtained using LDA (see Fig. S9, ESI†). To simulate the likely contact configuration during a break-junction experiment,31,32 we employed leads constructed from 6 layers of Au(111), each containing 30 gold atoms and further terminated with a pyramid of gold atoms. After relaxing each molecular junction with lengths varying from n = 4 to n = 9, we calculated the electrical conductance using the Gollum quantum transport code (for more details see Section 9 of the ESI†).333 Results and discussion
For the terminal Au–C, the covalent bond distance is found to be 2.3 Å, with a Au–C–C angle (θ) of 123°. For thiol-terminal the Au–S distance is 2.5 Å, with a Au–S–C angle of 120° and for SMe-terminal the Au–S distance is slightly bigger at 3.0 Å, with a Au–S–C angle close to 180° as illustrated in Fig. 1, (for more detail see Fig. S3 and S5, ESI†). Fig. S6 (ESI†) shows the conductance G for linear alkane chains as a function of length with three different terminal groups: thiol, methyl sulphides and direct contact Au–C (corresponding to Fig. 1a–c). This study shows that G is sensitive to the terminal group and demonstrates that the conductance is highest for the covalent bond Au–C and lowest for the methyl sulphide (SMe) terminal group, in agreement with earlier experimental and theoretical studies.22–24,34–36 For comparison, the red line in Fig. 2 shows experimental results (n = 4, 6 and 8)37 for the conductances with covalent Au–C bonds to the electrodes, while the black line shows our theoretical calculations (n = 4,…9). The slope of the experimental line is in good agreement with our theoretical results, although the intercept differs, partly because experimentally a range of unknown tip configurations are sampled.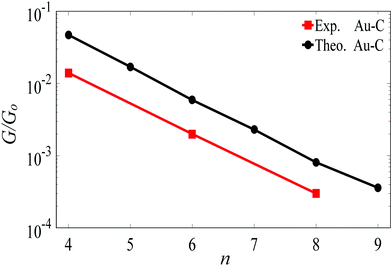 | ||
| Fig. 2 Length dependence of the conductance of a single-molecule Au|linear alkane|Au junction, with Au–C covalent bonds connecting the ends of the alkane to the gold electrodes. The black line shows our DFT results. The red lines shows experimental results from ref. 37. The lines are guides to the eye. | ||
For Au–C coupling to the electrodes, Fig. 3 shows a comparison between the conductances of the above linear chains with those of the corresponding alkane rings, for n = 4 to 9 CH2 units. The conductance of the n = 4 ring is almost the same of its corresponding linear chain, but for larger n, the conductances of rings are significantly smaller than those of the corresponding chains (specifically at n = 5 and 7).
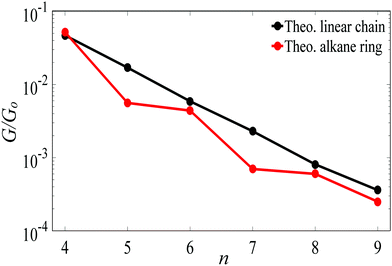 | ||
| Fig. 3 The theoretical length dependence of the single-junction Au|alkane chain/ring|Au conductance for Au–C terminal group. | ||
This result is entirely non-classical, since the conductance of two parallel classical conductors is twice that of a single conductor. We now demonstrate that this behaviour of alkane rings is largely determined by the conformations adopted by the two branches of the ring. To demonstrate this feature, we relax rings with n = 4,…9. Then the geometries are frozen and we cut each ring into two halves, to yield two frozen alkane chains formed from the upper or lower branches of the ring. These branches are then separately attached to gold electrodes, as shown in Fig. 4 for the case n = 4. If their conductances combine classically, then the conductance of the ring would be the sum of the conductances of the two branches.
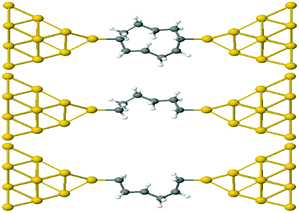 | ||
| Fig. 4 Schematic representation of Au–C covalently bonded full (n = 4) alkane ring and two (n = 4) half rings, formed from the upper and lower branches without further relaxation. | ||
Fig. 5 shows a comparison, between the conductance of alkane rings (red circles) and the conductances of their two branches (black and blue circles), obtained by connecting the upper and lower branches to Au electrodes without further relaxation and saturating the cut bonds with hydrogen atoms.2 In principle, the two branches could be identical, but in practice, they have slightly different conformations, which results in small differences in their conductances. For comparison, the black-dashed and red lines reproduce the theoretical conductances of linear chains and rings shown in Fig. 3. As shown in Fig. 5 the conductance of a given ring is significantly higher than the sum of the conductances of the associated branches (green circles).
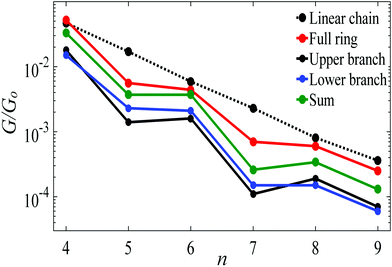 | ||
| Fig. 5 Length dependence of the Au|full/half ring/chain|Au conductances with Au–C bonds to the electrodes. The red circles show the conductances of alkane rings versus the number of CH2 units n. For each n, the blue and black circles show the conductances of the corresponding two branches, obtained by placing each branch of the ring between gold electrodes, without further relaxation. The green circles show the sum of the branch conductances. The black-dashed and red lines show the theoretical conductances of the corresponding linear chains and rings, reproduced from Fig. 3. | ||
The red curve in Fig. 5 shows that the conductance of alkane rings oscillates as the ring size (n) increases. To demonstrate that this oscillation is largely determined by the conformations adopted by the two branches of the ring, rather than quantum interference, Table S1 (ESI†) shows the relaxed geometries of each ring after relaxation (see Table S1 and Fig. S2, ESI†). This reveals that the even-numbered rings tend to be more planar than the odd-numbered rings and consequently, as shown in Fig. 5, their conductances (and those of their frozen branches) are below the trend line of the even numbered rings. This consequence of conformation is demonstrated in Fig. S8 (ESI†), where is shown that if the geometry of the odd-numbered branches is artificially forced into a more planar conformation, then their conductances increase towards the trend line of even numbered branches.
3 Conclusions
In conclusion, we have studied the single-molecule conductance of a series of alkane rings and compared them with the conductances of linear chains of comparable lengths. We find that a logarithmic plot of the conductances of the latter falls on a straight line, whereas the logarithmic conductances of the former exhibit conductance oscillations. We find that the conductances of the branches belonging to alkane rings combine non-classically, with the conductance of the rings exceeding the sum of the conductances of their branches. Furthermore, the conductances of alkane rings are found to be lower than those of the corresponding linear chains. These non-classical features are attributed to conformational effects, rather than quantum interference in the Sigma systems of the molecules. Our study establishes that non-classical effects in alkane rings play an important role in determining the conductance of their single-molecule junctions.Author contributions
A. K. I. and C. J. L. originally conceived the concept, calculations were carried out by A. K. I. Both authors have given approval to the final version of the manuscript. Both authors provided essential contributions to interpreting the data reported in this manuscript. A. K. I. coordinated the writing of the manuscript with input from C. J. L.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. K. I and C. J. L. acknowledge financial support from the UK EPSRC, through grant no. EP/M014452/1, EP/P027156/1 and EP/N03337X/1. This work was additionally supported by the European Commission is provided by the FET Open project 767187 – QuIET and the EU project Bac-to-Fuel. A. K. I. is grateful for financial assistance from Tikrit University (Iraq), and the Iraqi Ministry of Higher Education (SL-20).References
- M. Magoga and C. Joachim, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 16011 CrossRef CAS.
- H. Vazquez, R. Skouta, S. Schneebeli, M. Kamenetska, R. Breslow, L. Venkataraman and M. Hybertsen, Nat. Nanotechnol., 2012, 7, 663 CrossRef CAS PubMed.
- K. P. Dou and C.-C. Kaun, J. Phys. Chem. C, 2016, 120, 18939–18944 CrossRef CAS.
- C. Lambert, Chem. Soc. Rev., 2015, 44, 875–888 RSC.
- H. Sadeghi, J. A. Mol, C. S. Lau, G. A. D. Briggs, J. Warner and C. J. Lambert, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2658–2663 CrossRef CAS PubMed.
- X. Zhao, G. Kastlunger and R. Stadler, Phys. Rev. B, 2017, 96, 085421 CrossRef.
- T. Hansen and G. C. Solomon, J. Phys. Chem. C, 2016, 120, 6295–6301 CrossRef CAS.
- S. Sangtarash, H. Sadeghi and C. J. Lambert, Nanoscale, 2016, 8, 13199–13205 RSC.
- A. K. Ismael, I. Grace and C. J. Lambert, Phys. Chem. Chem. Phys., 2017, 19, 6416–6421 RSC.
- R. Sparks, V. M. Garcia-Suarez, D. Z. Manrique and C. J. Lambert, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075437 CrossRef.
- A. Borges, E.-D. Fung, F. Ng, L. Venkataraman and G. C. Solomon, J. Phys. Chem. Lett., 2016, 7, 4825–4829 CrossRef CAS PubMed.
- C. Jia, M. Famili, M. Carlotti, Y. Liu, P. Wang, I. M. Grace, Z. Feng, Y. Wang, Z. Zhao and M. Ding, Sci. Adv., 2018, 4, eaat8237 CrossRef PubMed.
- S. Ballmann, R. Härtle, P. B. Coto, M. Elbing, M. Mayor, M. R. Bryce, M. Thoss and H. B. Weber, Phys. Rev. Lett., 2012, 109, 056801 CrossRef PubMed.
- S. V. Aradhya, J. S. Meisner, M. Krikorian, S. Ahn, R. Parameswaran, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nano Lett., 2012, 12, 1643–1647 CrossRef CAS PubMed.
- V. Kaliginedi, P. Moreno-García, H. Valkenier, W. Hong, V. M. García-Suárez, P. Buiter, J. L. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 5262–5275 CrossRef CAS PubMed.
- S. V. Aradhya and L. Venkataraman, Nat. Nanotechnol., 2013, 8, 399 CrossRef CAS PubMed.
- C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. Woerde, R. Eelkema, F. C. Grozema and H. S. van der Zant, Angew. Chem., 2013, 125, 3234–3237 CrossRef.
- H. Valkenier, C. M. Guédon, T. Markussen, K. S. Thygesen, S. J. van der Molen and J. C. Hummelen, Phys. Chem. Chem. Phys., 2014, 16, 653–662 RSC.
- F. Prins, A. Barreiro, J. W. Ruitenberg, J. S. Seldenthuis, N. Aliaga-Alcalde, L. M. Vandersypen and H. S. van der Zant, Nano Lett., 2011, 11, 4607–4611 CrossRef CAS PubMed.
- W. Hong, H. Valkenier, G. Mészáros, D. Z. Manrique, A. Mishchenko, A. Putz, P. M. García, C. J. Lambert, J. C. Hummelen and T. Wandlowski, Beilstein J. Nanotechnol., 2011, 2, 699 CrossRef PubMed.
- G. J. Ashwell, B. Urasinska, C. Wang, M. R. Bryce, I. Grace and C. J. Lambert, Chem. Commun., 2006, 4706–4708 RSC.
- L. Venkataraman, J. E. Klare, I. W. Tam, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nano Lett., 2006, 6, 458–462 CrossRef CAS PubMed.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- T. Lee, W. Wang, J. F. Klemic, J. J. Zhang, J. Su and M. A. Reed, J. Phys. Chem. B, 2004, 108, 8742–8750 CrossRef CAS.
- D. J. Wold, R. Haag, M. A. Rampi and C. D. Frisbie, J. Phys. Chem. B, 2002, 106, 2813–2816 CrossRef CAS.
- C. Li, I. Pobelov, T. Wandlowski, A. Bagrets, A. Arnold and F. Evers, J. Am. Chem. Soc., 2008, 130, 318–326 CrossRef CAS PubMed.
- W. Haiss, R. J. Nichols, H. van Zalinge, S. J. Higgins, D. Bethell and D. J. Schiffrin, Phys. Chem. Chem. Phys., 2004, 6, 4330–4337 RSC.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- A. K. Ismael, K. Wang, A. Vezzoli, M. K. Al-Khaykanee, H. E. Gallagher, I. M. Grace, C. J. Lambert, B. Xu, R. J. Nichols and S. J. Higgins, Angew. Chem., Int. Ed., 2017, 56, 15378–15382 CrossRef CAS PubMed.
- I. L. Herrer, A. K. Ismael, D. C. Milán, A. Vezzoli, S. Martín, A. González-Orive, I. Grace, C. Lambert, J. L. Serrano and R. J. Nichols, J. Phys. Chem. Lett., 2018, 9, 5364–5372 CrossRef CAS PubMed.
- M. Fernández, C. Sabater, W. Dednam, J. Palacios, M. Calvo, C. Untiedt and M. J. Caturla, Phys. Rev. B, 2016, 93, 085437 CrossRef.
- C. Sabater, C. Untiedt, J. Palacios and M. J. Caturla, Phys. Rev. Lett., 2012, 108, 205502 CrossRef CAS PubMed.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. Bailey and K. Gillemot, New J. Phys., 2014, 16, 093029 CrossRef.
- Y. S. Park, A. C. Whalley, M. Kamenetska, M. L. Steigerwald, M. S. Hybertsen, C. Nuckolls and L. Venkataraman, J. Am. Chem. Soc., 2007, 129, 15768–15769 CrossRef CAS PubMed.
- F. Chen, X. Li, J. Hihath, Z. Huang and N. Tao, J. Am. Chem. Soc., 2006, 128, 15874–15881 CrossRef CAS PubMed.
- D. Boese and H. Schoeller, EPL, 2001, 54, 668 CrossRef CAS.
- J. R. Widawsky, W. Chen, H. Vazquez, T. Kim, R. Breslow, M. S. Hybertsen and L. Venkataraman, Nano Lett., 2013, 13, 2889–2894 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8tc05565c |
| This journal is © The Royal Society of Chemistry 2019 |