Guest-dependent spin transitions in Hofmann-like Fe^II SCO metal–organic frameworks: hints from quantum chemistry calculations

Abstract

The family of 3D Hofmann-like Fe^II coordination polymers with the formula [Fe(bpd)[M^II(CN)₄]]·2G, M = Pt, Pd, and Ni is known for having a large capacity to host guest molecules (G) such as nitrobenzene or naphthalene. The presence of the guest molecules modulates the spin-crossover properties. In fact, these clathrates present a large hysteresis loop, in one single step or two well separated steps depending on the guest. In this work, we analyse by means of state-of-the-art DFT-based calculations the main effects governing the occurrence of the multistep spin transition, and the differences due to the nature of the divalent M metal and the encapsulated guest molecules. The study determines the relative stability of the mixed-spin state, the amplitude and nature of the host–guest and guest–guest intermolecular interactions, and the key role played by the C≡N stretching modes of the M-cyanide units. Our results provide hints on the distinct roles of each of these factors and how they promote or prevent a direct transition from the high-spin state to the low-spin state.

---

1. Introduction

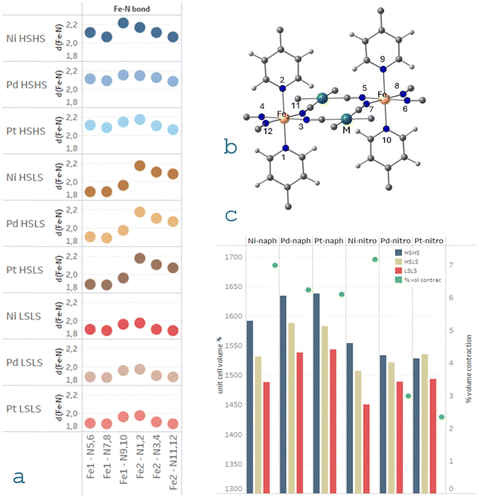
The first 3D Hofmann-like Fe^II coordination polymers with spin-crossover (SCO) properties were reported by Real et al.^1,2 two decades ago. Since this first study, the SCO Hofmann-type family has grown rapidly.^3–14 These systems combine the appealing properties of the metal–organic frameworks (MOFs),^15–17 such as chemical stability, porosity and tunability, with the spin crossover between the high-spin (S = 2, HS) and the low spin (S = 0, LS) states of the Fe^II centres. As in the molecular SCO complexes, the LS ↔ HS switching is reversible and is accompanied by detectable changes in the structural, magnetic and optical properties of the system. The spin state change can be promoted by external factors, such as temperature, pressure, light, pH, … and in the case of the Hofmann-like SCO MOFs, the transition can be additionally triggered by the presence of guest molecules hosted on the pores of the MOF framework.^8,18–24

The SCO Hofmann 3D Fe^II clathrates have the general formula [Fe(L)[M^II(CN)₄]]·G and [Fe(L)[M^I(CN)₂]₂]·G with L being a pillaring bis-monodentate pyridine-like ligand, M^II = Ni, Pd, and Pt and M^I = Cu, Ag, Au and G being the guest molecule.^11,25 Their structure is based on planar layers, where quasi-octahedral Fe^II ions alternate with M metal centres, bonded to four cyanide ligands in a square planar geometry. The layers are interconnected by the nitrogen-containing L ligands, where nitrogen atoms occupy the axial position of Fe centres. Different pillaring L ligands of increasing length have been employed, resulting in accessible voids of increasing volume: 18% of the unit cell for L = pz,²⁶ 40% for L = bpe,²⁷ azpy,²⁸ bpac,¹⁰ and 49% for L = bpeben,²⁹ and dpsme.³⁰

Recently, a new SCO–MOF series with formula [Fe(L)[M^II(CN)₄]]·2G has been reported,^22,31 where L = bis(4-pyridyl)butadiyne, bpb and M^II = Pt, Pd, and Ni (Fig. 1). They host two guest molecules G of nitrobenzene or naphthalene, hereafter referred to as M-nitro or M-naph, respectively. This family is characterized by the largest available volume within the isoreticular series [Fe(L)-[M^II(CN)₄]]·G. Indeed, they undergo cooperative spin transitions with large hysteresis loops, in two well defined steps in the case of naphthalene clathrates, M-naph. For M-nitro derivatives, the transition takes place in a single step, except for Ni-nitro which displays two sharp steps separated by a very narrow plateau (ca. 2 K wide). The average critical temperatures and the thermodynamic parameters resulting from differential scanning calorimetric measurements are reported in Table 1. Ni-naph exhibits the lowest transition temperature and the widest plateau (ca. 40 K wide). Transition temperatures are lower for M-naph than M-nitro, for the three M metals considered (Table 1). In fact, it is assumed that the high-spin state is more stabilized for large guests, and then the transition to LS occurs at lower temperatures.

Fig. 1 (a) General representation of the MOF–SCO, with nitrobenzene guest molecules. The two positions for the guest molecules are highlighted in blue (G1) and red (G2). Blue and green circles correspond to Fe and M atoms, respectively. Coordination for guest molecules G1 (b) and G2 (c) with the closest pyridyl groups.

Table 1 Thermodynamic parameters from calorimetric measurements for M-naph and M-nitro systems. Average critical temperature, T_c = (T_c↑ + T_c↓)/2, average transition enthalpy (kJ mol⁻¹) and entropy (J K⁻¹ mol⁻¹) per Fe center²²

Systems		ΔH1	ΔS1	T c1	ΔH2	ΔS2	T c2
Two steps	Ni-naph	8.85	49.3	180.0	—	—	131.3
	Pd-naph	12.00	56.5	212.5	10.42	52.4	198.8
	Pt-naph	9.45	44.9	210.5	8.62	44.1	195.5
	Ni-nitro	8.53	36.4	234.0	7.60	32.2	226.0
One step	Pd-nitro	20.22	87.1	232.4	—	—	—
	Pt-nitro	19.29	86.3	223.5	—	—	—

---

It is widely agreed that the way the guest molecules modulate the SCO properties of the MOF results from a subtle balance of electronic, structural, and steric effects. But until now, it has been difficult to establish universal relationships that allow predicting the magnetic properties of the MOF–SCO Fe^II clathrates. We have recently analysed by means of quantum chemistry calculations the different physical effects giving rise to two-step transitions in Pt-naph clathrates and a one-step transition in Pt-nitro derivatives.³² We mainly focused on three aspects: the effect of ligand field on metallic sites, the relative stability of the intermediate spin state, and the intermolecular host–guest and guest–guest interactions. The aim of this work is to extend this analysis to the whole family of M-naph and M-nitro clathrates to discern the effect, if any, of the metal M centre on the magnetic properties, the vibrational energy of the host, the relative stability of the intermediate states and the amplitude and nature of the intermolecular interactions. Briefly, the goal is to try to establish some general trends common to all the members of the family that explain the guest-dependent spin-transition behaviour of these MOF–SCO Fe^II clathrates.

2. Description of the systems and computational details

The computational models were built on the basis of the CCDC crystallographic data deposited by Piñeiro-López et al.²² (CCDC 1550075–1550084†) for low, middle and high temperature phases. All compounds crystallize in the triclinic P1̄ space group, apart from Ni-nitro that belongs to the monoclinic space group P2/m.

2.1. Computational models and thermodynamics

The whole system (MOF and guest molecules) was optimized employing periodic density theory functional (DFT) in the framework of the Vienna ab initio simulation package (VASP).^33–36 In all the considered systems, the unit cell contains four guest molecules and two Fe centres that can show a low-spin state (LSLS solution), a high-spin state (HSHS solution) or a mixed state (HSLS solution). For the HSLS mixed state of Ni-nitro and Pd-nitro systems, no X-ray data are available, and the computational models were obtained from two independent optimizations starting from the high and low temperature solutions. All the reported results correspond to the HSLS model from the low temperature geometry, more stable than those resulting from the high-temperature one. For Pd-nitro, the X-ray data at low temperature present two different orientations of the nitrobenzene molecule on position 2. We have built models with both sets of coordinates, and all the reported results correspond to their average.

The revised Perdew–Burke–Ernzerhof (rPBE)³⁷ functional was used and the van der Waals dispersion effects were included by the DFT-D3 method of Grimme et al.³⁸ with Becke–Johnson damping.³⁹ The projector-augmented wave (PAW)⁴⁰ potentials were employed for all the atoms. The optimization includes the lattice parameters of the unit cell and the atomic positions. All the calculations refer to the Γ-point of Brillouin's zone, with an energy cut-off of 800 eV for the plane-wave basis set representing the valence electrons. Electronic relaxation was performed until the change in the total energy between two consecutive steps is smaller than 10⁻⁶ eV and the ionic relaxation has been performed until the Hellmann–Feynman forces were lower than 0.01 eV Å⁻¹. Three different spin configurations were modelled: HSHS, LSLS and a mixed spin solution, HSLS. The spin-polarized calculations were constrained to a fixed difference between the number of electrons in the spin up (N_α) and spin down (N_β). Hence, the HSHS, HSLS, and LSLS configurations require an N_α − N_β = 8 (four unpaired electrons at each centre), N_α − N_β = 4, and N_α = N_β, respectively. The optimized geometries for each system and spin state are available in the ESI† file.

The transition enthalpy and entropy per Fe center were also evaluated to compare with the experimental data. As previously mentioned, the translational and rotational contributions to the transition enthalpy (ΔH_trans and ΔH_rot) and entropy (ΔS_trans and ΔS_rot) were neglected and only the dominant vibrational and electronic parts are finally considered.^41,42 Hence,

ΔH(T) = ΔH_elec + ΔZPE + ΔH_vib + ΔH_rot + ΔH_trans ≈ ΔH_elec + ΔZPE + ΔH_vib

ΔS(T) = ΔS_elec + ΔS_vib + ΔS_rot + ΔS_trans ≈ ΔS_elec + ΔS_vib

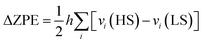where ΔE_elec corresponds to the difference in the computed energy for the HS and LS solutions, and ΔZPE is the difference between the zero-point vibrational energy of both states, evaluated in the framework of the harmonic approximation as one-half of the sum of the vibrational frequency shifts upon spin transition: . The vibrational contribution for each phase is computed at the average transition temperature (T_c↑ + T_c↓)/2, as follows:^41,43,44

The electronic contribution to the entropy can be considered as temperature independent and computed as S_elec = R ln(2S + 1), with S equals to the total spin of the system. To evaluate the frequencies, the finite difference approach has been employed to calculate the second-order derivatives of the total energy, with exigent criteria in the optimization runs to obtain the complete set of real frequencies. Hence, all calculations were performed with accurate precision mode in VASP calculations, with a convergence criterion for the forces of 0.01 eV Å⁻¹. The finite difference approach has been used without imposing the symmetry in the displacements (IBRION = 5), with a central difference mode (NFREE = 2), i.e each ion is displaced in each direction by a small positive and negative displacement (POTIM = 0.02).

2.2. Host–guest and guest–guest interactions

The unit cell of the MOF contains two Fe sites and four guest molecules (Fig. 2). We have evaluated different host–guest and guest–guest interactions by specific single-point calculations.

Fig. 2 Types of host–guest and guest–guest interactions in M-naph and M-nitro systems. G1 and G2 molecules in blue and red, respectively.

The average interaction energy of the guest molecules with the host is calculated as follows:

E_int(host–guest) = [E_sys − (E_H + 4E_G)]/4

where E_sys corresponds to the total energy of the MOF with four guest molecules occupying the voids of the unit cell, E_H is the energy of the MOF in the absence of guests, but with the same geometry as the whole system, and E_G is the energy of an isolated guest molecule.

The host–guest interaction energy for each position (G1 or G2) can be estimated as:

E_int(host–Gi) = [E_HGi − (E_H + 2E_G)]/2

where E_HGi is the total energy of the MOF containing just two guest molecules in position 1 (E_HG1) or position 2 (E_HG2), calculated with the optimized geometry of the whole system.

The interaction among guest molecules is evaluated as:

E_int(Gi–Gj) = [E_GiGj − (E_Gi + E_Gj)]/2

where E_GiGj is obtained from a single point calculation of the four guest molecules in the optimized geometry of the whole system. E_Gi refers instead to single-point calculations of two guest molecules on position i (1 or 2). Guest molecules occupying position 1 in the void are sandwiched between the pyridyl groups of the bpb ligand and cannot interact among themselves, but they can interact with the neighbouring guest molecules in position 2 (Fig. 2).

3. Results and discussion

We report the results obtained for Pd and Ni MOF–SCO derivatives hosting nitrobenzene and naphthalene molecules. We also include in the discussion our previous results for Pt derivatives³² to facilitate the comparison.

3.1. Optimized geometry

All systems were fully optimized for each electronic configuration and the frequencies of the normal vibrational modes were computed to ensure the minima on the potential energy surface. Fig. 3 shows the Fe–N distances for each spin state of the M-naph Fe(II)-SCO clathrates, for M = Ni, Pd, and Pt. Similar trends are obtained for the M-nitro family. The corresponding bond lengths around each Fe centre and the optimized cell parameters are reported in Tables S1 and S2 (ESI†), respectively, together with the available experimental data. A reasonable agreement is found among the optimized and the X-ray data structures for all the systems considered. For each centre, as expected, the longest Fe–N bond distances correspond to the axial positions (N1, N2, N9 and N10). The Fe–N distances are almost insensitive to the nature of the M metal centre, following similar behaviour when moving from the high-spin solution to the low-spin one. The same behaviour is observed in the experimental Fe–N distances (Table S1, ESI†). These Fe–N distances modulate the strength of the Fe ligand field. As far as the nature of the M metal centre does not modify the length of these bonds, we expect similar trends on the Fe ligand field parameters for Pd and Ni derivatives than those we have previously evaluated for Pt clathrates.³²Ab initio ligand field theory calculations indicated that the field is slightly stronger for the Fe centre close to the guest molecule in position 2, but very similar for nitrobenzene- and naphthalene-containing derivatives.³² Then, the strength of the ligand field around the Fe site is not responsible for the dissimilar SCO behaviour found for M-naph and M-nitro clathrates.

Fig. 3 Geometrical parameters obtained from DFT calculations. (a) Optimized Fe–N distances for M-naph compounds on different spin solutions HSHS, HSLS and LSLS. (b) Two Fe(II) centers connected through the M(CN)₄ units (M, Fe, N, C, H atoms represented by green, orange, blue, grey, and white balls, respectively). (c) Volume of the optimized unit cell for M-naph and M-nitro systems. The green circles correspond to the percentage of volume contraction when moving from high-temperature to low-temperature phases [100·(V_HSHS − V_LSLS)/V_LSLS].

However, the metal M impacts on the unit cell volume (Fig. 3) show the following trend: Pt > Pd > Ni, the same trend than the atomic radii of these elements. The only exception corresponds to the high-temperature structures of M-nitro where the order is reversed, the Ni-based system presenting higher unit cell volume than the other two M-nitro compounds. This could be correlated with the fact that Ni-nitro crystallizes in the monoclinic space group P2/m, while the rest belongs to the triclinic P1̄ space group. The unit cell volume is larger for naphthalene derivatives than nitrobenzene ones, in line with the volume of the guest molecule (Fig. 3). Moreover, the larger the guest volume, the lower the transition temperatures, as can be seen in Table 1. As usual the HS to LS spin transition is accompanied by a unit cell volume contraction. This contraction represents about 6% of the low-temperature cell volume for M-naph and Ni-nitro, while only 2–3% for Pt-nitro and Pd-nitro (Fig. 3c). Interestingly, the larger contraction correlates with those systems presenting two-step transitions.

The available X-ray data indicate that the mixed state is an ordered intermediate, where the Fe1 centre close to the G1 guest rests on the LS state, while the Fe2 centre, close to the G2 guest, switches to the HS state.²² This is correctly reproduced by our calculations for M-naph and Ni-nitro, all systems with two-step transitions, where the intermediate is stable. In the case of Pd-nitro and Pt-nitro, in the hypothesized HSLS mixed state, our calculations show that the Fe1 centre presents a HS state, while Fe2 centre is the LS one. This distribution is more stable than the reverse one and could be related to the occurrence of a one-step SCO phenomenon.

3.2. Transition energy, enthalpy, and entropy

Regarding the relative stability, the LSLS solution is the most stable, its geometry corresponds with the low-temperature phase of all systems considered, separated by about 70 kJ mol⁻¹ to the HSHS configuration. Fig. 4 reports on the electronic energy difference ΔE_trans among the low-spin, mixed state, and high-spin configurations (see details in Table S3, ESI†). Regarding thermal corrections, the reported values have been calculated at the experimental transition temperatures, following the suggestion by Robert et al.⁴⁵ who previously noted the non-negligible effect of temperature on ΔH_trans and ΔS_trans. To compare, we have also evaluated ΔH_trans and ΔS_trans at 298 K (Fig. S1, ESI†). No significant temperature dependence of ΔH_trans is observed (changes due to temperature are about 2–7%) while the entropy is more sensitive (with changes about 4–38%).

Fig. 4 (top panel) Electronic energy difference per Fe center between HSHS, HSLS and LSLS solutions, and (bottom panel) enthalpy difference per Fe center, ΔH_trans, evaluated at the experimental transition temperatures. The horizontal green line separates the systems that accomplish the condition for a two-step transition (above the line) to those undergoing a one-step transition (below the line).

It is worth noting that the electronic energy gap between the different spin solutions, and hence, the transition enthalpies are overestimated, as usual for DFT-based evaluations, reflecting the inherent difficulties of DFT approaches in treating at the same foot open and closed shell systems (the overall experimental ΔH values are 16–22 kJ mol⁻¹, Table 1).²² But what is more important is the ratio between the transition enthalpies of the two subsequent steps are correctly reproduced, and relevant conclusions can be obtained from these trends, even when the absolute values are overestimated. On the other hand, entropy changes are mainly in line with experimental estimates (the overall ΔS values are 70–109 J K⁻¹ mol⁻¹, Table 1), as far as they only depend on the vibration frequencies, and hence, on the optimized geometries, nicely reproduced by this approach.

As stated previously^46–49 the relative stabilization (δ) of the mixed state HSLS with respect to the barycentre of the HSHS–LSLS separation is a necessary condition for the occurrence of a two-step transition. The horizontal green line in Fig. 4 separates those systems that accomplish this condition (above the line) from those where a one-step transition is favoured (below the line). The calculated ΔE_trans between HSLS and LSLS solutions correctly predicts the occurrence of one- or two-step transitions for M-naph and M-nitro solutions, except for Ni-nitro, where the HSLS solution is just 0.3 kJ mol⁻¹ above the barycentre (Fig. 4). The situation is reverted once the zero-point energy correction (ZPE) and thermal contributions are included (Table 2 and Table S3, ESI†). In fact, for Ni-nitro, the ΔE_trans between HSLS and LSLS is 37.1 kJ mol⁻¹, the difference in the ZPE correction is ΔZPE(HSLS–LSLS) = −8.6 kJ mol⁻¹, while the vibrational contributions to the enthalpy transition is 3.4 kJ mol⁻¹ (Table S3, ESI†), which gives ΔH_trans = 31.9 kJ mol⁻¹ (Table 2). In general, the ΔZPE correction is in the range of [−6, −8] kJ mol⁻¹, and decreases the separation between the high-spin and low-spin solutions while the thermal corrections to the transition enthalpy is positive and around 2–3 kJ mol⁻¹. The calculated enthalpy transitions are in line with the occurrence of one-step spin transition for Pt-nitro and Pd-nitro and two-steps for M-naph and Ni-nitro (Fig. 4). Additionally, the stabilization of the mixed spin state with respect to the barycentre can be related with the plateau wide. Hence, the larger the stabilization of the intermediate state, the wider the plateau. Our calculations give a stabilization of about 11 kJ mol⁻¹ for the mixed state of Ni-naph and 7.7 and 6.4 kJ mol⁻¹ for Pd-naph and Pt-naph. This is in line with the decrease of the plateau when moving from Ni-naph (ca. 40k wide) to Pt-naph and Pt-naph (ca. 7–9k wide).

Table 2 Calculated transition enthalpies ΔH (kJ mol⁻¹) and entropies ΔS (J K⁻¹ mol⁻¹) per Fe center for M-naph and M-nitro systems, transition enthalpy barycentre, ΔH_av = ½[HSHS(T_c1) − LSLS(T_c2)], and relative stabilization of HSLS state with respect to the barycentre, δ. Enthalpies and entropies calculated at the experimental transition temperatures reported in Table 1

	HSHS–HSLS		HSLS–LSLS		Barycentre	Stabilization
	ΔH1 (Tc1)	ΔS1 (Tc1)	ΔH2 (Tc2)	ΔS2 (Tc2)	ΔHav	δ = ΔH2 − ΔHav
Ni-naph	30.2	32.4	25.1	25.2	36.9	−11.8	Two steps
Pd-naph	37.7	64.2	29.3	42.4	37.0	−7.7
Pt-naph	34.6	67.6	29.1	33.1	35.5	−6.4
Ni-nitro	32.5	24.1	31.9	48.8	34.4	−2.4
Pd-nitro	31.3	24.0	33.4	49.9	32.4	1.1	One step
Pt-nitro	28.6	65.7	33.5	27.9	31.0	2.5

---

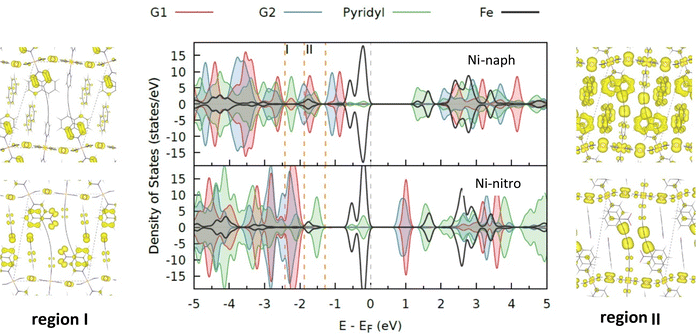
Additional insight can be obtained from the projected density of states (pDOS), as shown in Fig. 5 for the LSLS state of Ni derivatives. The pDOS shows the individual participation of Fe, bpb ligands and guest molecules on the occupied and empty states of the whole system. These plots provide information about the mixing of the bands of the host crystal, mainly the π orbitals of the bpb ligands, with the orbitals of the guest molecules. In these systems, the occupied bands close to the Fermi level are mainly localized on Fe centres (black lines in Fig. 5). In the case of Ni-naph, immediately below these bands we find the HOMO and HOMO−1 orbitals of the G1 and G2 naphthalene molecules (red and blue lines, respectively). While the HOMOs do not mix with the host states, the HOMO−1 orbitals mix with the highest occupied bands of the bpb ligands (region II in Fig. 5). The electronic density corresponding to this region is represented on the right-hand of this figure and shows a high degree of hybridization between the host and guest molecules. This will be reflected on the adsorption energies of naphthalene molecules, as shown in next section. In the case of Ni-nitro, no relevant mixing between host and guest states appears in this region. Indeed, nitrobenzene states appear at lower energy than the naphthalene ones and are instead slightly mixed with the HOMO−1 states of bpb, corresponding to region I in Fig. 5 (left hand, bottom panel). In this case, weaker interactions are expected between the host and the nitrobenzene molecules. Similar trends are observed for Pd and Pt derivatives,³² the main difference among them consists of contribution of the M centred bands to the plots of the electronic density (higher for Ni than Pd or Pt, in line with their increasing electronegativity).

Fig. 5 (middle) Projected density of states of Ni-naph and Ni-nitro derivatives on Fe, guest molecules and bpb ligand for the LSLS state. Partial electronic density for regions I (left) and II (right) corresponding to the energy windows [E_F −2.43, E_F −1.88] eV and [E_F −1.88, E_F −1.28] eV, respectively (isosurface value = 0.01 e bohr⁻³).

3.3. Host–guest and guest–guest intermolecular interactions

The intermolecular interactions established among host and guest molecules has been invoked as one of the determinant factors governing the occurrence of one-step or two-step transition.³²Table 3 and Fig. 6 collects the different host–guest and guest–guest intermolecular interactions for all considered systems. These interactions act as an extra energy contribution that stabilizes a specific spin state, in such a way that this extra stabilization can play against spin switching. The stronger the interactions, the higher the internal pressure disfavouring the spin conversion and favouring a two-step transition. In general, the host–guest interactions are stronger for naphthalene molecules than for nitrobenzene, in both positions, in line with the larger size of naphthalene that allows a larger number of contacts with the host.²² This confirms the trends suggested by our previous calculations on Pt-nitro and Pt-naph derivatives,³² and corroborates the information provided by the pDOS plots in Fig. 5. In fact, the amplitude of these interactions is quite similar for Pd and Pt derivatives, while Ni-based MOFs behave differently. The preferred adsorption site is position 1 for both guest molecules. In this position, the molecule is sandwiched between the pyridyl rings of two close bpd ligands and stabilized by face-to-face π interactions. In position 2, the interaction is driven by two types of contacts, edge-to-face σ–π between the C–H bonds of the molecule and π rings of the bpb ligand, and face-to-face π packing with the bpb ligand (Fig. 2). In this position, the guest molecules present weaker interactions with the host, particularly for nitrobenzene.

Table 3 Host–guest and guest–guest interaction energy (kJ mol⁻¹) for M-nitro and M-naph systems

	Ni-naph		Pd-naph		Pt-naph		Ni-nitro		Pd-nitro		Pt-nitro
	HSHS	LSLS	HSHS	LSLS	HSHS	LSLS	HSHS	LSLS	HSHS	LSLS	HSHS	LSLS
H–G	−112.2	−106.4	−104.7	−103.0	−107.7	−109.2	−95.3	−95.5	−100.4	−103.6	−101.5	−103.5
H–G1	−110.3	−93.0	−94.6	−88.9	−94.4	−95.8	−94.8	−96.4	−92.5	−98.0	−95.1	−99.4
H–G2	−85.5	−90.9	−85.4	−86.4	−89.6	−92.6	−69.6	−71.9	−82.8	−84.9	−82.9	−84.1
G1–G2	−36.2	−37.8	−38.7	−38.8	−37.9	−37.8	−27.6	−29.5	−30.6	−30.4	−29.7	−30.3
G2–G2	−26.2	−29.0	−24.4	−17.7	−26.7	−26.6	7.7	13.8	−26.0	−20.6	−23.6	−11.3

---

Fig. 6 Host–guest and guest–guest interactions (kJ mol⁻¹) in M-naph and M-nitro systems.

The intermolecular G1–G2 and G2–G2 guest–guest interactions are also stronger for naphthalene than nitrobenzene, due to the larger size of naphthalene. A singular case is Ni-nitro where G2–G2 interactions are repulsive due to the unique orientation of the G2 molecules in the system, with a face-to-face packing of the NO₂ groups of neighbouring molecules. The O⋯O distance between two NO₂ is 3.18 Å in the HS state, and 3.12 Å in the LS state, in line with a more repulsive interaction for the LSLS state, that favours a two-step conversion.

Regarding the dependence on the spin state, some general trends can be extracted from the data in Table 3 and Fig. 6. For all systems, G1–G2 interactions are almost spin independent, while the host–G2 interactions are stronger in the LS state, playing in favour of a one-step transition. The host–G1 interactions are stronger for the HS state in M-naph systems, while LS states are favoured by these interactions in the M-nitro systems. This extra energy contribution in the HS state could correlate with the presence of two-steps in M-naph systems. The most significant case is Ni-naph, where the host–G1 interaction stabilizes the HS state by an extra amount of 17 kJ mol⁻¹ with respect to the LS state, that can be correlated with the 40k wide plateau of this system. In general, G2–G2 interactions are more attractive for the HS state than the LS one, which contribute to a two-step conversion.

3.4. Vibrational analysis

Additional insight into how the guest molecules modulate the host properties can be obtained from the analysis of the vibrational contributions,^41,50 but the large number of vibration modes prevents an exhaustive analysis. We focus on the C≡N stretching modes of the M-cyanide units (Fig. 7). These N atoms occupy the equatorial position in the Fe coordination sphere, then this vibration mode is directly involved in the structural changes accompanying the spin transition. The nature of the metal atom in the M-cyanide units affects the strength of the C≡N bonds, the strongest found in Pt-derivatives, followed by Pd > Ni (Fig. 7a). This could be in line with the exceptionally low transition temperature reported for Ni-naph.

Fig. 7 (a) Frequencies of the C≡N stretching modes for M-naph and systems in LS (light colour) and HS (dark colour) states. (b) Difference (in cm⁻¹) of the same vibration mode in the M-naph and M-nitro systems for the HS state, ν_i,naph(HS) − ν_i,nitro(HS). Similar behaviour is found for the LS state. (c) Redshift of the C≡N frequencies (in cm⁻¹) when moving from the LS to HS state for M-naph (large light-coloured symbols) and M-nitro (small dark-coloured symbols).

Additionally, we observe that the guest molecules impact the vibrational energy of the host structure. Fig. 7b shows the wavenumber difference of the same vibration mode for M-naph and M-nitro systems in the HS state. The individual C≡N frequencies are higher for systems containing naphthalene as the guest molecule than for nitrobenzene. As in previously inspected parameters, Ni-containing MOFs do not follow this trend.

For all systems, the C≡N stretching modes present higher frequencies for the LS than the HS states (Fig. 7a). This C≡N stretching redshift that accompanies the LS to HS transition, weakens the C–N bonds and helps the volumetric expansion of the crystal. The LS to HS redshift is larger for M-nitro than M-naph, except for Ni where we observed the opposite behaviour (Fig. 7c). These C≡N stretching modes transmit an extra vibrational energy contribution to the lattice in the case of M-nitro and favours a single step transition.

4. Conclusions

The [Fe(bpb)[M^II(CN)₄]]·2G grids synthesized by Real et al. show the highest effective loading capacity so far described for the family of Hofmann-like SCO–MOFs. The six M-guest clathrates (M = Ni, Pd, and Pt, guest = nitrobenzene and naphthalene) show very similar structures but different SCO behaviours. M-naph and Ni-nitro derivatives show cooperative two-step SCO transition, although with different stability of the HSLS intermediate state, ranging from the 40k-wide HSLS plateau of Ni-naph, to the quite narrow plateau (ca. 2k) of Ni-nitro. In contrast, Pd-nitro and Pt-nitro display cooperative one-step spin transitions.

In this work, we have analysed and quantified the different electronic, structural and steric effects governing the occurrence of one-step or two-step spin transitions in [Fe(bpb)[M^II(CN)₄]] Hofmann clathrates. This study relies on DFT periodic calculations of the whole system to evaluate the relative stability of the low-, high- and mixed spin solutions, and to separately assess the host–guest and guest–guest intermolecular interactions, as well as the relevance of the nature of the metal in the [M^II(CN)₄] units.

Our results indicate that the Fe–N distances are almost insensitive to the nature of the M metal centre, following similar behaviour for all systems when moving from the high-spin solution to the low-spin one. We found very similar ligand field around Fe centres for Pt-nitro and Pt-naph, and we expect similar trends for Ni and Pd derivatives. Then the ligand field on the Fe centre is not responsible for different behaviours found for M-nitro and M-naph clathrates.

The optimized structures are in good agreement with the available experimental data, and the volume contraction when moving from the HS state to the LS state is correctly reproduced. Indeed, it is found that this contraction is higher for all the systems with a two-step transition. Then a high structural change accompanying the SCO plays in favour of the two-step transition.

The condition of the stabilization of the intermediate HSLS with respect to the halfway between the LS state and the HS state to observe two-steps is accomplished for M-naph and Ni-nitro, where the calculated HSLS enthalpy is below the barycentre. A linear relationship is found between the stabilization with respect to the barycentre and the width of the plateau.

In all systems, the host–guest and guest–guest interactions are stronger for naphthalene than nitrobenzene and almost independent of the M metal, except for Ni. These interactions are slightly spin-dependent. Hence, host–G1 interactions are stronger for the HS state in M-naph systems, and this extra energy contribution could correlate with the presence of two-steps in the M-naph family.

Finally, our calculations show the role of the vibronic effects on the guest-dependent SCO transition. In particular, the transition from the LS state to the HS state is accompanied by the redshift of the C≡N stretching frequencies of the [M^II(CN)₄] units. The redshift is larger for M-nitro than for M-naph, except for Ni derivatives. These modes contribute additional vibrational energy to the lattice in the cases of Pt-nitro and Pd-nitro, favouring a single step transition.

In summary, it is difficult to isolate a single factor governing the strong cooperativity found in the [Fe(bpb)[M^II(CN)₄]]·2G Hofmann-like MOF–SCO and the dependence on the encapsulated guest molecules. Electronic, structural, and non-covalent effects act simultaneously and contribute differently to the spin transition mechanism. This study provides hints on the distinct roles of each of these factors and how they promote or block a direct transition from the high-spin state to the low-spin state. Our results provide clues that help in interpreting the differential SCO behaviour of these compounds and could be useful to many other systems where the SCO phenomenon is modulated by guest molecules.

Author contributions

D. A.-O.: investigation and data analysis R. S.-A.: investigation, conceptualization, supervision, project administration, and funding acquisition. C. J. C: conceptualization, validation, data analysis, data curation, writing, review, editing, visualization, project administration, and funding acquisition.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support through grant PID2021-127674NB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF_A way of making Europe”, and project US1380922 funded by Consejería de Economía, Conocimiento, Empresas y Universidad (Junta de Andalucía) and European Regional Development Fund (ERDF) under “Programa Operativo FEDER 2014-2020”. The technical support of the Supercomputing Team of the Centro Informático Científico de Andalucía (CICA) and the access to the computational facilities of the “Centro de Servicios de Informática y Redes de Comunicaciones” (CSIRC, Universidad de Granada, Spain) are also acknowledged.

References

1. V. Niel, J. M. Martinez-Agudo, M. C. Muñoz, A. B. Gaspar and J. A. Real, Cooperative spin crossover behavior in cyanide-bridged Fe(II)-M(II) bimetallic 3D Hofmann-like networks (M = Ni, Pd, and Pt), Inorg. Chem., 2001, 40, 3838–3839.
2. V. Niel, M. C. Muñoz, A. B. Gaspar, A. Galet, G. Levchenko and J. A. Real, Thermal-, Pressure-, and Light-Induced Spin Transition in Novel Cyanide-Bridged FeII AgI Bimetallic Compounds with Three-Dimensional Interpenetrating Double Structures {FeIILx[Ag(CN)2]2} G, Chem. – Eur. J., 2002, 8, 2446–2453.
3. Z.-P. Ni, J.-L. Liu, M. N. Hoque, W. Liu, J.-Y. Li, Y.-C. Chen and M.-L. Tong, Recent advances in guest effects on spin-crossover behavior in Hofmann-type metal-organic frameworks, Coord. Chem. Rev., 2017, 335, 28–43.
4. M. C. Muñoz and J. A. Real, Thermo-, piezo-, photo- and chemo-switchable spin crossover iron(II)-metallocyanate based coordination polymers, Coord. Chem. Rev., 2011, 255, 2068–2093.
5. V. Martínez, I. Boldog, A. B. Gaspar, V. Ksenofontov, A. Bhattacharjee, P. Gütlich and J. A. Real, Spin Crossover Phenomenon in Nanocrystals and Nanoparticles of [Fe(3-Fpy)2M(CN)4] (MII = Ni, Pd, Pt) Two-Dimensional Coordination Polymers, Chem. Mater., 2010, 22, 4271–4281.
6. J. A. Real, A. B. Gaspar and M. C. Muñoz, Thermal, pressure and light switchable spin-crossover materials, Dalton Trans., 2005, 2062–2079.
7. G. Molnar, S. Cobo, J. A. Real, F. Carcenac, E. Daran, C. Vien and A. Bousseksou, A combined top-down/bottom-up approach for the nanoscale patterning of spin-crossover coordination polymers, Adv. Mater., 2007, 19, 2163.
8. P. D. Southon, L. Liu, E. A. Fellows, D. J. Price, G. J. Halder, K. W. Chapman, B. Moubaraki, K. S. Murray, J. F. Létard and C. J. Kepert, Dynamic interplay between spin-crossover and host-guest function in a nanoporous metal-organic framework material, J. Am. Chem. Soc., 2009, 131, 10998–11009.
9. A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Molecular spin crossover phenomenon: recent achievements and prospects, Chem. Soc. Rev., 2011, 40, 3313–3335.
10. C. Bartual-Murgui, N. A. Ortega-Villar, H. J. Shepherd, M. C. Muñoz, L. Salmon, G. Molnár, A. Bousseksou and J. A. Real, Enhanced porosity in a new 3D Hofmann-like network exhibiting humidity sensitive cooperative spin transitions at room temperature, J. Mater. Chem., 2011, 21, 7217–7222.
11. M. C. Muñoz and J. Antonio Real, in Polymeric Spin-Crossover Materials, Spin-Crossover Materials, 2013, pp. 121–146.
12. H. Peng, S. Tricard, G. Félix, G. Molnár, W. Nicolazzi, L. Salmon and A. Bousseksou, Re-Appearance of Cooperativity in Ultra-Small Spin-Crossover [Fe(pz){Ni(CN)4}] Nanoparticles, Angew. Chem., Int. Ed., 2014, 53, 10894–10898.
13. F.-L. Liu, D. Li, L.-J. Su and J. Tao, Reversible three equal-step spin crossover in an iron(ii) Hofmann-type metal–organic framework, Dalton Trans., 2018, 47, 1407–1411.
14. C.-J. Zhang, K.-T. Lian, G.-Z. Huang, S. Bala, Z.-P. Ni and M.-L. Tong, Hysteretic four-step spin-crossover in a 3D Hofmann-type metal–organic framework with aromatic guest, Chem. Commun., 2019, 55, 11033–11036.
15. S. E. Skrabalak and R. Vaidhyanathan, The Chemistry of Metal Organic Framework Materials, Chem. Mater., 2023, 35, 5713–5722.
16. L. Gagliardi and O. M. Yaghi, Three Future Directions for Metal–Organic Frameworks, Chem. Mater., 2023, 35, 5711–5712.
17. B. I. Z. Ahmad, K. T. Keasler, E. E. Stacy, S. Meng, T. J. Hicks and P. J. Milner, MOFganic Chemistry: Challenges and Opportunities for Metal–Organic Frameworks in Synthetic Organic Chemistry, Chem. Mater., 2023, 35, 4883–4896.
18. X. Bao, H. J. Shepherd, L. Salmon, G. Molnár, M.-L. Tong and A. Bousseksou, The Effect of an Active Guest on the Spin Crossover Phenomenon, Angew. Chem., Int. Ed., 2013, 52, 1198–1202.
19. J. E. Clements, J. R. Price, S. M. Neville and C. J. Kepert, Hysteretic Four-Step Spin Crossover within a Three-Dimensional Porous Hofmann-like Material, Angew. Chem., Int. Ed., 2016, 55, 15105–15109.
20. F. J. Valverde-Muñoz, C. Bartual-Murgui, L. Piñeiro-López, M. C. Muñoz and J. A. Real, Influence of Host–Guest and Host–Host Interactions on the Spin-Crossover 3D Hofmann-type Clathrates {FeII(pina)[MI(CN)2]2}·xMeOH (MI = Ag, Au), Inorg. Chem., 2019, 58, 10038–10046.
21. L. Piñeiro-López, M. Seredyuk, M. C. Muñoz and J. A. Real, Effect of Guest Molecules on Spin Transition Temperature in Loaded Hofmann-Like Clathrates with Improved Porosity, Eur. J. Inorg. Chem., 2020, 764–769.
22. L. a Piñeiro-López, F. J. Valverde-Muñoz, M. Seredyuk, M. C. Muñoz, M. Haukka and J. A. Real, Guest Induced Strong Cooperative One- and Two-Step Spin Transitions in Highly Porous Iron(II) Hofmann-Type Metal–Organic Frameworks, Inorg. Chem., 2017, 56, 7038–7047.
23. Y. Li, M. Liu, Z.-S. Yao and J. Tao, Temperature-dependent hysteretic two-step spin crossover in two-dimensional Hofmann-type compounds, Dalton Trans., 2020, 49, 7245–7251.
24. B. Brachňaková, J. Moncoľ, J. Pavlik, I. Šalitroš, S. Bonhommeau, F. J. Valverde-Muñoz, L. Salmon, G. Molnár, L. Routaboul and A. Bousseksou, Spin crossover metal–organic frameworks with inserted photoactive guests: on the quest to control the spin state by photoisomerization, Dalton Trans., 2021, 50, 8877–8888.
25. I. S. Kuzevanova, O. I. Kucheriv, V. M. Hiiuk, D. D. Naumova, S. Shova, S. I. Shylin, V. O. Kotsyubynsky, A. Rotaru, I. O. Fritsky and I. Y. A. Gural'skiy, Spin crossover in iron(ii) Hofmann clathrates analogues with 1,2,3-triazole, Dalton Trans., 2021, 50, 9250–9258.
26. M. Ohba, K. Yoneda, G. Agustí, M. C. Muñoz, A. B. Gaspar, J. A. Real, M. Yamasaki, H. Ando, Y. Nakao and S. Sakaki, et al., Bidirectional Chemo-Switching of Spin State in a Microporous Framework, Angew. Chem., Int. Ed., 2009, 48, 4767–4771.
27. F. J. Muñoz-Lara, A. B. Gaspar, M. C. Muñoz, M. Arai, S. Kitagawa, M. Ohba and J. A. Real, Sequestering Aromatic Molecules with a Spin-Crossover FeII Microporous Coordination Polymer, Chem. – Eur. J., 2012, 18, 8013–8018.
28. G. Agustí, S. Cobo, A. B. Gaspar, G. Molnár, N. O. Moussa, P. Á. Szilágyi, V. Pálfi, C. Vieu, M. Carmen Muñoz and J. A. Real, et al., Thermal and Light-Induced Spin Crossover Phenomena in New 3D Hofmann-Like Microporous Metalorganic Frameworks Produced As Bulk Materials and Nanopatterned Thin Films, Chem. Mater., 2008, 20, 6721–6732.
29. F. J. Muñoz-Lara, A. B. Gaspar, M. C. Muñoz, V. Ksenofontov and J. A. Real, Novel Iron(II) Microporous Spin-Crossover Coordination Polymers with Enhanced Pore Size, Inorg. Chem., 2013, 52, 3–5.
30. N. F. Sciortino, K. R. Scherl-Gruenwald, G. Chastanet, G. J. Halder, K. W. Chapman, J.-F. Létard and C. J. Kepert, Hysteretic Three-Step Spin Crossover in a Thermo- and Photochromic 3D Pillared Hofmann-type Metal–Organic Framework, Angew. Chem., Int. Ed., 2012, 51, 10154–10158.
31. L. Piñeiro-López, M. Seredyuk, M. C. Muñoz and J. A. Real, Two- and one-step cooperative spin transitions in Hofmann-like clathrates with enhanced loading capacity, Chem. Commun., 2014, 50, 1833–1835.
32. D. Arias-Olivares, R. Sánchez-de-Armas and C. J. Calzado, Theoretical approach to the one-step versus two-step spin transitions in Hofmann-like FeII SCO metal-organic frameworks, Mater. Today Chem., 2023, 30, 101489.
33. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
34. G. Kresse and J. Hafner, Ab initio molecular dynamics simulation of the liquid metal - amorphous semiconductor transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
35. G. Kresse and J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
36. G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
37. B. Hammer, L. B. Hansen and J. K. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
38. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
39. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
40. P. E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979.
41. G. Molnár, M. Mikolasek, K. Ridier, A. Fahs, W. Nicolazzi and A. Bousseksou, Molecular Spin Crossover Materials: Review of the Lattice Dynamical Properties, Ann. Phys., 2019, 531, 1900076.
42. M. Sorai and S. Seki, Phonon coupled cooperative low-spin 1A1high-spin 5T2 transition in [Fe(phen)2(NCS)2] and [Fe(phen)2(NCSe)2] crystals, J. Phys. Chem. Solids, 1974, 35, 555–570.
43. G. Molnar, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Spin Crossover Nanomaterials: From Fundamental Concepts to Devices, Adv. Mater., 2018, 30, 17003862.
44. B. Fultz, Vibrational thermodynamics of materials, Prog. Mater. Sci., 2010, 55, 247–352.
45. S. Vela, M. Fumanal, J. Ribas-Arino and V. Robert, Towards an accurate and computationally-efficient modelling of Fe(II)-based spin crossover materials, Phys. Chem. Chem. Phys., 2015, 17, 16306–16314.
46. J. A. Real, H. Bolvin, A. Bousseksou, A. Dworkin, O. Kahn, F. Varret and J. Zarembowitch, Two-step spin crossover in the new dinuclear compound [Fe(bt)(NCS)2]2bpym, with bt = 2,2'-bi-2-thiazoline and bpym = 2,2'-bipyrimidine: experimental investigation and theoretical approach, J. Am. Chem. Soc., 1992, 114, 4650–4658.
47. V. Ksenofontov, A. B. Gaspar, V. Niel, S. Reiman, J. A. Real and P. Gütlich, On the nature of the plateau in two-step dinuclear spin-crossover complexes, Chem. – Eur. J., 2004, 10, 1291–1298.
48. S. Zein and S. A. Borshch, Energetics of Binuclear Spin Transition Complexes, J. Am. Chem. Soc., 2005, 127, 16197–16201.
49. J. Cirera and E. Ruiz, Theoretical modeling of two-step spin-crossover transitions in FeII dinuclear systems, J. Mater. Chem. C, 2015, 3, 7954–7961.
50. J. A. Wolny, R. Diller and V. Schünemann, Vibrational Spectroscopy of Mono- and Polynuclear Spin-Crossover Systems, Eur. J. Inorg. Chem., 2012, 2635–2648.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc01041h

---