Open Access Article
Open Access ArticleRevolutionizing ORR catalyst design through computational methodologies and materials informatics†
Lanna E. B.
Lucchetti
 a,
James M.
de Almeida
a,
James M.
de Almeida
 b and
Samira
Siahrostami
b and
Samira
Siahrostami
 *a
*a
aDepartment of Chemistry, Simon Fraser University, 8888 University Drive, Burnaby, BC. V5A 1S6, Canada. E-mail: samira_siahrostami@sfu.ca
bIlum School of Science, Brazilian Center for Research in Energy and Materials (CNPEM), Zip Code 13083-970, Campinas, São Paulo, Brazil
First published on 23rd July 2024
Abstract
Computational approaches, such as density functional theory (DFT) in conjunction with descriptor-based analysis and computational hydrogen electrode, have enabled exploring the intricate interactions between catalyst surfaces and oxygen species allowing for the rational design of materials with optimized electronic structure and reactivity for oxygen reduction reaction (ORR). The identification of active sites and the tuning of catalyst compositions at the atomic scale have been facilitated by computational simulations, accelerating the discovery of promising ORR catalysts. In this contribution, the insights provided by the computational analysis to understand the fundamental reasons behind inherent ORR overpotentials in the experimental reported catalysts are discussed. Various strategies to overcome the limitations in ORR catalysis using computational design are discussed. Several alternative earth-abundant and cost-effective materials suggested by computational guidance to replace platinum-based catalysts are reviewed. The accuracy of DFT and the role of solvent and electrolyte pH are outlined based on the understanding provided by the computational insight. Finally, an overview of recent achievements in employing materials informatics to accelerate catalyst material discovery for ORR is provided. These computational advancements hold great promise for the development of efficient and cost-effective ORR catalysts, bringing us closer to realizing the full potential of fuel cells as efficient electrochemical energy conversion technologies.
Broader contextRecent advancements in computational methodologies, particularly density functional theory (DFT) and materials informatics, have revolutionized catalyst design for oxygen reduction reactions (ORR). DFT, in conjunction with descriptor-based analysis and computational hydrogen electrode (CHE), not only aids in the rational design of catalysts but also offers insights into the influence of external factors such as solvent, field and pH effects on ORR activity. By enabling rational design strategies and accelerating the discovery of alternative materials, these approaches hold promise for overcoming limitations associated with traditional catalysts like platinum. Moreover, the integration of machine learning techniques and high-throughput DFT screening has facilitated the efficient generation and analysis of vast datasets, paving the way for the development of cost-effective and scalable ORR catalysts. This transformative landscape underscores the success of computational analysis in elucidating complex catalytic phenomena, offering unprecedented opportunities for the development of efficient and sustainable ORR catalysts, thus advancing the frontier of fuel cell technologies. |
1. Introduction
There is a growing interest in creating renewable energy conversion technologies for automotive applications, such as fuel cells and metal–air batteries. Because of their remarkable prospects and ability to solve several complicated challenges that have long persisted, fuel cells stand out as the most promising future energy technology. In most fuel cells, the anode and cathode are separated by a membrane/electrolyte. At the cathode, oxygen is reduced to water, while a fuel, such as hydrogen, methanol, ethanol, or formic acid, is oxidized at the anode, releasing electrons and protons that pass through the external circuit and membrane to reach the cathode. Thus, fuel combines with oxygen without burning via a moderate electrochemical mechanism, with an optimal turnover frequency of H2–O2 of about 83% at 25 °C.1 In practice, however, low-temperature fuel cells do not achieve such efficiency, owing to the sluggish oxygen reduction process (ORR) at the cathode which results in a significant voltage loss. Platinum (Pt) has long been utilized as the most efficient ORR catalyst. However, there are several downsides to the extensive use of Pt-based catalysts in fuel cells. One of the most significant concerns is Pt scarcity and high cost, which causes scalability issues. Furthermore, even with the costly Pt catalyst, there is a significant overpotential associated with ORR (Fig. 1a).2,3 Additionally, Pt-based catalysts have a low tolerance to methanol, which produces CO and blocks the active sites. As a result, the rational design of catalysts with even higher ORR activity than pure Pt is central to fuel-cell research. Various types of Pt-based catalysts have been largely examined over the past two decades. To boost the inherent activity of Pt-based catalysts, both alloying and morphological designs have been used.4–6 The timeline in Fig. 1b illustrates how Pt-based catalysts ORR performance has improved. As can be seen, the intrinsic activity of the catalysts has not changed, and there is still a 0.3 V overpotential that exists across these various Pt-based catalysts.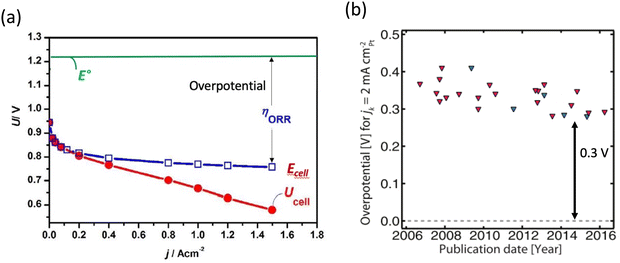 | ||
| Fig. 1 (a) Fuel cell electrochemical performance using Pt as catalyst. Copyright with permission from ref. 7 (b) timeline showing that the intrinsic activity of Pt-based catalysts has not been improved. Copyright with permission from ref. 8. | ||
Computational approaches, such as density functional theory (DFT), in conjunction with descriptor-based analysis and computational hydrogen electrode (CHE) model suggested by Nørskov et al.,9 have played a pivotal role in elucidating the underlying mechanisms of ORR, understanding experimental results, and predicting novel catalyst materials with enhanced activity and stability. Herein, we first overview how descriptor-based analysis in conjunction with the CHE model can be leveraged to understand the fundamentals behind the ORR catalysis. Then, we show how this understanding can help to explain the large ORR overpotential for the studied classes of materials and guide the design of novel materials. With several examples we show how these tools can be used to understand the ORR activity and stability of cost-effective and earth abundant materials such as transition metal nitrides and transition metal oxides. We also discuss the accuracy of DFT functionals in describing the ORR along with computational methods for modeling solvent, electrolyte and pH effects. Lastly, we review emerging artificial intelligence approaches for screening extensive materials spaces to accelerate ORR catalyst discovery with a focus on language processing techniques. We should highlight that the examples mentioned in this contribution only focus on computational advances in ORR catalysis, and that they are only a sample of the vast array of literature on this subject.10–12 Thus, this contribution is not intended to be exhaustive.
2. Fundamentals behind ORR catalysis
The past decade has witnessed significant progress in the computational understanding and design of catalysts for the ORR. Computational frameworks based on the surface science approach9 and DFT calculations have played a pivotal role in elucidating the underlying mechanisms of ORR and predicting novel catalyst materials with enhanced activity and stability. These approaches have enabled direct theoretical investigations of reaction mechanisms on various model systems. Two-electron or four-electron oxygen reduction pathways could occur, depending on the catalyst properties. The two-electron pathway is known as partial reduction resulting in hydrogen peroxide (eqn (1)) with OOH* as the only intermediate (eqn (2)). The full reduction of oxygen allows the four-electron reduction, resulting in water (eqn (3)). Herein, we only focus on the four-electron ORR which is of interest for emerging renewable energy technologies such as fuel cells, and rechargeable metal–air batteries. As mentioned above, currently, the sluggish oxygen reduction process hinders the efficiency of these technologies. Platinum (Pt) has long been utilized as the most efficient ORR catalyst, but it faces problems regarding scarcity and high-cost leading to scalability issues. Furthermore, even with the costly Pt catalyst, there is a significant overpotential associated with ORR (Fig. 1a). To establish computational understanding for ORR catalysis, we need to simulate the reaction mechanism. Associative and dissociative mechanisms have been proposed for the four-electron ORR. The associative mechanism (eqn (4)) involves three different intermediates, namely OOH*, O*, and OH* while dissociative one involves O*, and OH* (eqn (5)).Two-electron ORR:
| O2 + 2(H+ + e−) → H2O2 E° = 0.70 V | (1) |
| O2 + (H+ + e−) → OOH* + (H+ + e−) → H2O2 | (2) |
| O2 + 4(H+ + e−) → 2H2O2 E° = 1.23 V | (3) |
| O2 + (H+ + e−) → OOH* + (H+ + e−) → O* + (H+ + e−) → OH* + (H+ + e−) → 2H2O | (4) |
| 1/2O2 + (H+ + e−) → O* + (H+ + e−) → OH* + (H+ + e−) → H2O | (5) |
The associative mechanism is the commonly accepted mechanism for four-electron ORR. Taking this mechanism, the overall ORR catalytic activity is determined by the adsorption free energies of the reaction intermediates (OH*, O* and OOH*) to the catalyst surface. These adsorption free energies can be calculated using DFT calculations in conjunction with the CHE model, water stabilization,13 electric field effects,14 and entropic corrections.6 The CHE assumes the chemical potential of proton–electron pair is equal to the gas-phase H2. The electrode potential is considered by shifting the electron energy by –eU where e and U are the elementary charge and the electrode potential, respectively.9 These calculations can be used to build free energy diagrams along the reaction pathway (Fig. 2a and b). Fig. 2a displays the free energy diagrams for both the two- and the four-electron oxygen reduction reactions on ideal catalysts15 at U = 0 V. This demonstrates a hypothetical case where the reaction is running by short-circuiting the cell and all the steps are strongly exothermic. The maximum potential allowed by thermodynamics is obtained by shifting the chemical potential of the electrons at the equilibrium potential of U = 0.70 V and U = 1.23 V for the two- and the four-electron ORR mechanisms, respectively.9 In the ideal catalyst, all the steps in the free energy diagram are equivalent and take exactly as much as the equilibrium potential; hence they become thermoneutral at the equilibrium potential (green and magenta for four- and two-electron in Fig. 2a). In practice, as in the case of the Pt surface, however, these steps are not equivalent to the equilibrium potential, and the potential at which the electrochemical reaction occurs is less than the thermodynamic limit (Fig. 2b). This potential termed as thermodynamic limiting potential (UL) can be extracted from the free energy diagram and is defined as the highest potential at which all the reaction steps are downhill in free energy. The overpotential is determined by the difference between the UL and the equilibrium potential.15 The calculated UL for Pt(111) is 0.75 V, resulting in an overpotential of 0.48 V (Fig. 2b).
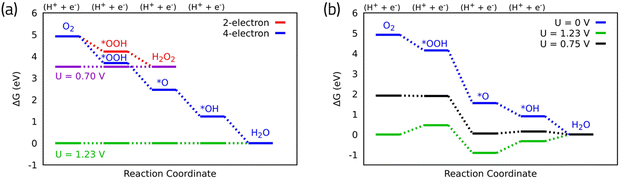 | ||
| Fig. 2 (a) Free energy diagram for oxygen reduction on ideal catalyst for two- and four-electron oxygen reduction. (b) Free energy diagram for oxygen reduction on Pt(111) associative mechanism. Data for Pt(111) are adapted from ref. 15. | ||
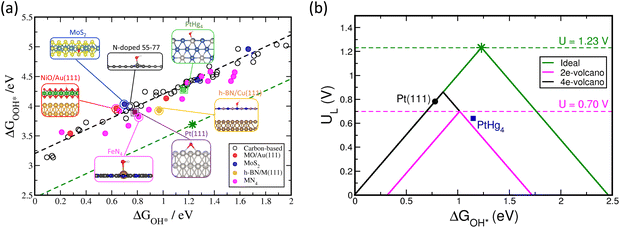
Fig. 3 displays the scaling relationship for the adsorption energies of the OH* and OOH* on a wide variety of catalysts structures. Based on this analysis, it has been demonstrated that the correlations between binding energies of different intermediates are observed on any catalyst surface (black dashed line in Fig. 3a).16–21 These correlations limit tuning the binding energy of one intermediate without affecting the binding energy of the other on any given catalyst surfaces. The green dashed line in Fig. 3a displays the ideal correlation between OH* and OOH*. The star point displays the sweet spot for ORR catalyst, with four equal steps in the free energy diagram from O2 to H2O (Fig. 3a). The fact that the variety of known and examined materials are far from the ideal line causes a large negative impact on the activity by fixing the energy difference between OH* and OOH* around 3.2 ± 0.2 eV.17–19 Because it takes two proton-coupled electron transfer steps to go from OOH* to OH* (reactions (2) and (3)), a potential of at least 3.2 eV/2e = 1.6 V is needed to complete these reaction steps. However, the thermodynamic limit is 1.23 V, which means that even the best catalyst surfaces will have an overpotential of about 1.6–1.2 V = 0.4 V.17–19
Using the Sabatier principle, the activity of the catalyst surface can be related to the binding energies of the adsorbates as descriptors. This leads to a volcano shape plot, with the optimal catalyst marked a balance between not too weak, nor too strong binding of the adsorbates (Fig. 3b).19,22 Although any of the three adsorbates in the ORR can be selected as a descriptor of the activity since all of them scale with each other, typically, O* or OH* are used as descriptors. Taking OH* as an example, Fig. 3b displays the ideal four-electron ORR activity volcano in green and the conventional four-electron volcano in black, which is different from the ideal volcano due to the scaling relations between OH* and OOH*. The negative impact of the scaling relation on the activity is clearly seen on the activity volcano, where the peak of the ideal four-electron volcano crosses the equilibrium potential as opposed to the conventional one. This indicates zero and ∼0.4 V overpotentials for the ideal and conventional volcano plots, respectively. Therefore, the scaling relation limitation imposed by thermodynamics sets an upper limit to the maximum activity that can be obtained using the known classes of two-dimensional materials. On the plus side, the scaling relations have proved quite useful in explaining trends in oxygen reduction activity across various classes of catalyst materials.9,22 It has also been successful in promoting the identification of new active catalysts for both two-19,23 and four-electron oxygen19 reduction reactions.
Fig. 3b also displays the two-electron ORR activity volcano for reduction of oxygen to hydrogen peroxide in magenta. Since this reaction has only one intermediate (OOH*) the peak of the volcano crosses the equilibrium potential at 0.70 V. This in principle indicates that it is possible to find a catalyst with maximum activity if it binds that single intermediate with optimal strength, not too weak, nor too strong.
Platinum has long been used as the most efficient catalyst for ORR. Based on the above-mentioned thermodynamic analysis, it has been demonstrated that the thermodynamic sink for the oxygen reduction reaction on Pt(111) is the last step in the free energy diagram, the reduction of OH* to water (Fig. 2b). In this thermodynamic picture, the ORR catalytic activity, relative to Pt(111), can be enhanced by weakening the binding energy of O* or OH*.9,19 However, due to the scaling relationship between the binding energies of OH* and OOH*, beyond a certain weakening, it becomes thermodynamically uphill to activate O2 and form OOH*. It has also been demonstrated that decreasing the binding energy of O* or OH* in the order of 0.1–0.2 eV weaker than Pt enhances the activity.9,19 This key understanding based on purely thermodynamic analysis paved the road for discovering new catalysts with enhanced ORR activity.19 Using DFT calculations, a wide range of Pt alloys have been studied for identifying the best composition with 0.1–0.2 eV weaker binding energy than Pt.19 Alloys of Pt and transition metals such as Co, Ni, Y and Sc were found to bind OH* weaker and showed enhanced ORR activity relative to pure Pt.19 Both electronic and geometric effects play roles in tailoring the surface binding energy towards the favored regime. During past years, enormous efforts have been made to experimentally synthesize different Pt alloys and benchmark their activities.6,12,21,24–29 Different design strategies have been investigated to control the structural composition and maximize the efficiency of the Pt alloy catalysts.24,30,31 In line with the computational efforts, Xin et al.30 proposed a model that relates the adsorption energies to the accessible physical properties of the metal element that forms alloy such as electronegativity, atomic radius, and spatial extent of valence orbitals.30 Based on this model, the chemical environment of the Pt atom sites can be related to the local chemical reactivity. The accuracy of this model was further verified by DFT calculations.30
In addition to Pt alloy catalysts, a wide range of the other bimetallic alloys have also been studied to identify catalysts with enhanced ORR activity.32–34 DFT calculations have also been used for mapping out the ORR activity of transition metal oxides,35–37 carbon-based materials36 and to less extent on transition metal nitrides38 and sulfides.39 We will delve into some of these findings in the forthcoming Section 4.
The DFT calculations have also been valuable in understanding the important role of the electrochemically most stable coverage of the ORR intermediates on the catalyst surface, as function of pH and potential.40 This is particularly important for the catalyst surfaces with strong oxygen binding energy such as Ni where it has been shown that the activity drastically changes by including oxygen covered surface.40 Using DFT calculations it has also been demonstrated that at low ORR potentials, the Pt surface is covered by the half-dissociated water layer and the O–O bond dissociation is clearly related to the local chemical environment.13 Based on DFT and atomistic model for the charged solid–electrolyte interface,41 the barriers for proton transfer to the adsorbates on the Pt surface and barriers for proton transport within the water layer have been estimated to be negligible.13 This, in turn, has enabled the modeling ORR through thermodynamic analysis alone, as a valid premise.
3. Guiding the design of next generation ORR catalysts
As mentioned previously, the activity of various examined catalyst surfaces is limited due to the scaling relation imposed by the OH* and OOH* correlations. Taking the associated ORR mechanism, the activity volcano is limited by two steps: OH* removal and OOH* formation on the surface. To deviate from the known scaling line and approach the ideal case, weaker OH* and stronger OOH* binding to the surface is desirable. Yet, achieving this goal has proven exceedingly challenging due to the scaling relation between OH* and OOH*, which renders it difficult to stabilize one oxygen intermediate while simultaneously destabilizing the other on a single catalyst surface.In the past years, several strategies have been devised to circumvent the scaling relation and hence increase the ORR activity.17,19,20,40–51 One strategy proposed by Siahrostami, S. et al.,38 is to divide the four-electron oxygen reduction reaction into two separate two-electron reduction reactions, i.e., (1) two-electron reduction of O2 to H2O2 and (2) two-electron reduction of H2O2 to H2O. They suggested that these reactions should be facilitated by separate catalyst materials: one highly active and selective for the partial reduction of O2 to H2O2, and the other effective at converting H2O2 to H2O with both high activity and selectivity. Including a proton donor/acceptor site and the right combination of binding sites has been computationally analyzed and proven to improve the scaling relation. This idea was explored for several functional groups such as –COOH, –OH, and –NH2 as proton-donor sites near proton-acceptor sites constructed of different transition metals coordinated with four nitrogen atoms (MN4). The combination of a nearby functional group such as –COOH and manganese metal coordinated with four nitrogen atoms (MnN4) was shown to make an ideal case for both ORR and OER.17 Alternatively, it has been shown that molecular configurations like diporphyrin, which feature two metal sites, can effectively stabilize the OOH* intermediate in a dissociated state across both active sites, resembling an O* + OH* intermediate. Through systematic DFT calculations, the ORR activity of such molecular catalysts has been extensively examined, revealing a notable reliance on factors such as the intermetallic distance and the type of metals involved.52
Single atom catalysts (SACs) have also proven to be interesting for circumventing the ORR scaling relation due to their distinct properties surpassing those of traditional metal catalysts.42 A comprehensive DFT investigation by considering more than 50 combinations of various metal single atoms embedded in various 2D substrates has unveiled distinctive electronic structure and geometric properties within SACs (Fig. 4a and b).42 These properties led to preferential stabilization of OOH* (inset in Fig. 4b), consequently disrupting the scaling relationship between OOH* and OH* (Fig. 4a), thereby enhancing ORR catalytic activity significantly via shifting the peak of activity volcano (Fig. 4b).
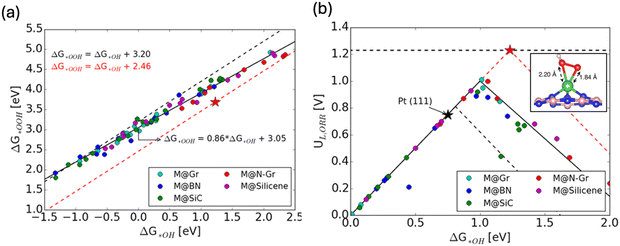 | ||
| Fig. 4 (a) Scaling relationship for the chemisorption energies of OH* and OOH* for various SACs. (b) Activity volcano plots for SACs (solid black), metal (111) (dashed black) and ideal catalyst (dashed red). Inset shows the bidentate adsorption stabilizes OOH* intermediate and results in overall improved activity. Copyright with permission from ref. 42. | ||
One of the interesting aspects of single-atom catalysts is their ability to interact with neighboring single-atom sites, which is crucial for fine-tuning their catalytic activity. It has been shown that adjacent single-atom catalysts, such as FeN3 embedded in a graphene structure, exhibit communicative behavior upon the adsorption of small molecules like CO and O2.50 This behavior is attributed to long-range spin coupling. The O–O bond in O2 is slightly more stretched when adsorbed on the second Fe site, and the adsorption energy changes by 0.18 eV. Interestingly, the Fe magnetic ordering shifts from ferromagnetic to antiferromagnetic in response to molecule adsorption.50
Dual-atom catalysts have also been recently investigated for the ORR. Xie, E. et al.53 studied 144 different dual-atom configurations with M1–N4 and M2–N4 moieties embedded in graphene structures (where M1 and M2 are Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Ir, Pt, or Au) using DFT calculations and machine learning techniques. They identified 13 dual-atom catalysts that lie at the peak of the ORR activity volcano, offering comparable performance to Pt but with the benefit of being composed of significantly cheaper and more abundant non-noble metals.
Another proposed strategy for overcoming the scaling relation in ORR is through confinement. Porous materials such as metal–organic frameworks (MOFs) have gained significant attention as potential ORR catalysts due to their unique properties in providing confined space.52,54–57 MOFs are composed of metal ions or clusters coordinated to organic ligands, forming a three-dimensional porous structure. The combination of metal nodes and organic linkers results in a highly ordered and tunable framework (Fig. 5). MOF structure provides numerous opportunities for confined spaces, potentially serving as an attractive platform for enhancing the ORR activity by altering the binding of OOH* and OH*. Fig. 5a and b show an example of Al2(OH)2TCPP-Co which is composed of cobalt porphyrin catalytic metal center, aluminum hydroxide inorganic backbone and carboxylate phenyl benzene linker. Controlling the linker length allows adjusting the spacing between porphyrin centers. MOF structure, in particular Al2(OH)2TCPP-Co, has a lot of similarities with the structure of cytochrome C oxidase enzyme (CcO) (Fig. 5c) which effectively oxidizes the catalytic cycle in respiration chain.58 The enzyme design consists of separated Fe and Cu metals coordinated with N atoms in a porphyrin type structure.58 This suggests that maximizing the efficiency of ORR could involve utilizing a metal–organic framework (MOF) structure featuring diverse metal catalytic centers within the cofacial porphyrin units. By employing a bimetallic model structure with an optimal distance between metal sites, illustrated schematically in Fig. 5d, a strategy can be devised to target specific metal combinations that bind oxygenated species differently, thus maximizing ORR activity. In such a model, if one metal site exhibits oxophilic properties, it can readily bind oxygen species during the initial ORR cycle. These oxygen species, while acting as spectators, block the oxophilic site from participating in the ORR reaction but interact favorably with ORR intermediates forming on the active site (the other metal site). The most favorable outcome of this model structure is the interaction of spectators with the OOH* intermediate, stabilizing it via hydrogen bonding. Due to the size disparity between OOH* and OH* adsorbates, there is no hydrogen bonding stabilization from the interaction of spectators with OH* absorbed on the active site.
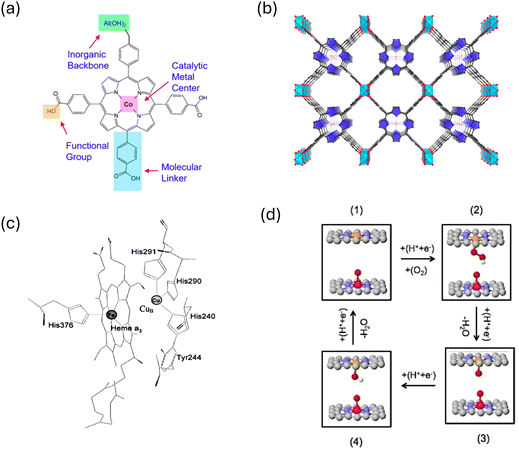 | ||
| Fig. 5 (a) and (b) Coordination entity for constructing Al2(OH)2TCPP-Co MOF. Adapted from ref. 55 with permission. (c) Cytochrome-C oxidase enzyme. Adapted from ref. 58 with permission. (d) Illustration of the bio-mimic prototype catalyst capable of circumventing the scaling relations. | ||
This hypothesis was examined in a recent computational study, affirming its effectiveness in controlling the scaling relations by varying the metal catalytic centers in Al2(OH)2TCPP-Co.59 A bimetallic model structure of Al2(OH)2TCPP-Co-M, where M represents an oxophilic element, was scrutinized in this study as a platform to explore the effect of a third dimension in circumventing the scaling between OH* and OOH* and enhancing ORR activity. The bimetallic Al2(OH)2TCPP-Co-M, featuring metal centers approximately 7 Å apart within the cofacial porphyrin units (Fig. 6a), was found to be optimal for the interaction of spectators with the OOH* intermediate. This study demonstrated that Al2(OH)2TCPP-Co-M, where M represents Fe, Cr, and Mn, effectively stabilizes the OOH* intermediate (Fig. 6b), consequently altering the scaling relation (Fig. 6c) and enhancing the ORR activity volcano relation (Fig. 6d). Particularly notable is the combination of Fe–OH as a spectator and Cr as an active site, which provided the most effective confined local chemical environment for ORR, exhibiting the lowest calculated overpotential of 0.3 V (Fig. 6e and f).59
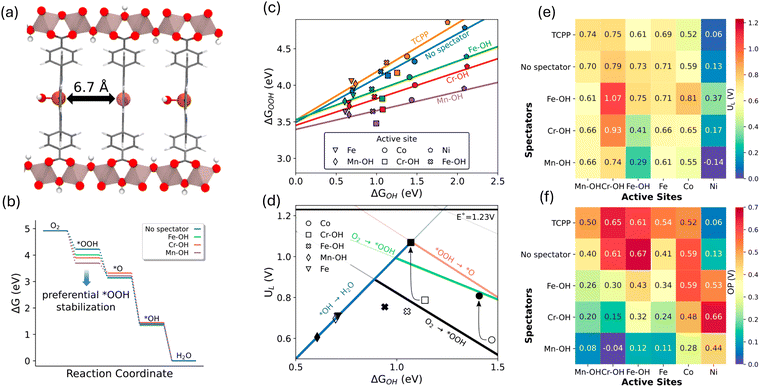 | ||
| Fig. 6 (a) Bimetallic model structure of Al2(OH)2TCPP-Co-M with an OH spectator siting on the oxophilic metal site. (b) Free energy diagram for ORR showing OOH* adsorbate free energy is most impacted by the spectator metal. (c) Scaling relations for the chemisorption energies of OOH* vs. OH* for various bimetallic MOFs. (d) ORR activity volcano plot showing a significant improvement using the confinement effect in bimetallic MOF (e) and (f) calculated limiting potentials and overpotentials for different combination of the bimetallic MOFs. Adapted from ref. 59 with permission. | ||
So far, we covered three strategies for circumventing the scaling relation between OOH* and OH*, including introducing oxophilic groups or proton-donor sites, using single atom catalysis, and fine-tuning the coordination environment through the third dimension. However, it is important to highlight additional strategies that have been suggested, which are well-covered in other review articles.44,46 These include introducing p-block elements via heteroatom doping,44,60 external field-assisted catalysis,46 using ligand-modified catalysts,44–46 strain effects induced by alloying including high entropy alloys,60 spectator or co-adsorbed species,45,55,59 geometry effects such as strain and surface curvature,47,48 and dual-sites catalysts.48,51,61 It is worth noting that geometry plays a major role in circumventing the scaling relationship among all the above strategies. One emerging approach is the concept of geometry-adaptive electrocatalysis, which holds significant potential in advancing catalytic performance. In a recent computational study by Cepitis et al.,45 the concept of geometry-adaptive electrocatalysis was examined to assess its ability to overcome the scaling relationship between OH* and OOH* Geometry-adaptive electrocatalysis represents a significant advancement in catalyst design. By allowing catalysts to dynamically adjust their geometry during reactions, this approach can potentially overcome limitations imposed by traditional scaling relations. This could lead to more efficient and effective ORR catalysts, where overpotential has been a persistent issue.45 If experimentally validated, this concept could pave the way for developing next generation electrocatalysts with unprecedented performance, accelerating progress in energy conversion and storage technologies. The authors demonstrated this concept using a model system of metal–nitrogen–carbon (M–N–C) catalysts, specifically the dual-atom site 2Co–N4 with variable curvature. Using DFT calculations, they demonstrated that altering the curvature of the catalyst can circumvent scaling through a dissociative mechanism, replacing the OOH* intermediate with O* on one site and OH* on another. This concept suggests the potential for discovering the ideal oxygen electrocatalyst.
Finally, we would like to emphasize that it is not merely about breaking scaling relationships; it is about breaking the right relationships in the right way to enhance the desired reactions without compromising catalytic efficiency.62,63 This nuanced understanding underscores the need for targeted strategies that carefully consider the geometric and coordination environment factors influencing catalysis.
4. Earth-abundant ORR catalysts
In addition to exploring novel chemistry and coordination environments to increase the intrinsic activity of the ORR catalyst, an interesting direction has emerged in the quest to identify catalysts that are both abundant on Earth and cost-effective. This endeavor aims to supersede Pt-based catalysts, paving the way for more scalable fuel cell technologies. Extensive research has been devoted to investigating various material classes.19,64–67 Here, we focus on two notable categories: transition metal nitrides and transition metal oxides. However, the exploration does not end here; readers are encouraged to delve into additional review articles for a comprehensive understanding of alternative materials.11,68–704.1. Transition metal nitrides (TMNs)
TMNs have lately received scholarly attention for their ability to selectively and efficiently catalyze the ORR.64,71,72 These materials are sometimes referred to as “interstitial alloys”, since the nitrogen atoms are incorporated into the interstitial sites of their parent metals.73 An interesting characteristic of TMNs is their dependence on the ratio of the metal atom radii to that of nitrogen. Lattice expansion due to a radii mismatch can cause a metal d-band contraction and a higher density of states around the Fermi level, resulting in different catalytic characteristics than those observed in the parent metal. Furthermore, multiple stoichiometries can be produced from the same metal, allowing for an even broader range of catalytic characteristics and potential applications.73 Herein we use DFT calculations in combination with descriptor-based analysis and CHE model to navigate through the vast chemical space of TMNs and identify promising ORR catalysts. We utilize the data published in ref. 74 that employs high-throughput screening of 800 different TMNs from 22 metals listed in the Materials Project database (Fig. 7a and b). This study shows that among the 800 TMNs, only 60 are thermodynamically stable with E above Hull (EHull) < 0.1 eV, indicating high stability with respect to decomposition at the same, fixed composition. Those 60 stable TMNs were considered for further investigation of CO2 reduction reaction and an extensive database of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 DFT calculations was reported. Among them, 6430 data belong to unique OH* (3220) and H* (3210) adsorption energy calculations. We leverage this data to search for bifunctional catalysts for ORR and hydrogen oxidation reaction (HOR) for the cathode and anode of the fuel cell, respectively. Fig. 7c illustrates the selection criteria employed to search for bifunctional ORR/HOR catalysts from the original dataset, taking Pt as the benchmark for both reactions. Using this screening scheme, 18 promising TMN candidates, composed of Fe, Co, Cr, Mn, Nb, and Ni, were obtained (Fig. 7d). These 18 shortlisted candidates are earth-abundant and low-cost elements making them highly suitable catalysts to replace rare-earth and expensive Pt-based catalysts. Interestingly, Co, Cr, Fe, and Mn nitrides have already been reported as active catalysts for the ORR in fuel cells.75,76 Co3N has been reported to show the best ORR performance, indicated by a mass activity of ∼170 A g−1 and an E1/2 of 0.862 V vs. RHE, which is within 30 mV from the commercial benchmark Pt/C.75 Computational modeling of CoN suggests a high activity with calculated limiting potential of 0.85 V.71 Nb4N5, is a new promising ORR catalysts we identified using the theoretical data analysis in Fig. 7d, which also finds applications as a superconductor material,77 and a high-performance electrode material for supercapacitors78 as well as for Li–S batteries.79
300 DFT calculations was reported. Among them, 6430 data belong to unique OH* (3220) and H* (3210) adsorption energy calculations. We leverage this data to search for bifunctional catalysts for ORR and hydrogen oxidation reaction (HOR) for the cathode and anode of the fuel cell, respectively. Fig. 7c illustrates the selection criteria employed to search for bifunctional ORR/HOR catalysts from the original dataset, taking Pt as the benchmark for both reactions. Using this screening scheme, 18 promising TMN candidates, composed of Fe, Co, Cr, Mn, Nb, and Ni, were obtained (Fig. 7d). These 18 shortlisted candidates are earth-abundant and low-cost elements making them highly suitable catalysts to replace rare-earth and expensive Pt-based catalysts. Interestingly, Co, Cr, Fe, and Mn nitrides have already been reported as active catalysts for the ORR in fuel cells.75,76 Co3N has been reported to show the best ORR performance, indicated by a mass activity of ∼170 A g−1 and an E1/2 of 0.862 V vs. RHE, which is within 30 mV from the commercial benchmark Pt/C.75 Computational modeling of CoN suggests a high activity with calculated limiting potential of 0.85 V.71 Nb4N5, is a new promising ORR catalysts we identified using the theoretical data analysis in Fig. 7d, which also finds applications as a superconductor material,77 and a high-performance electrode material for supercapacitors78 as well as for Li–S batteries.79
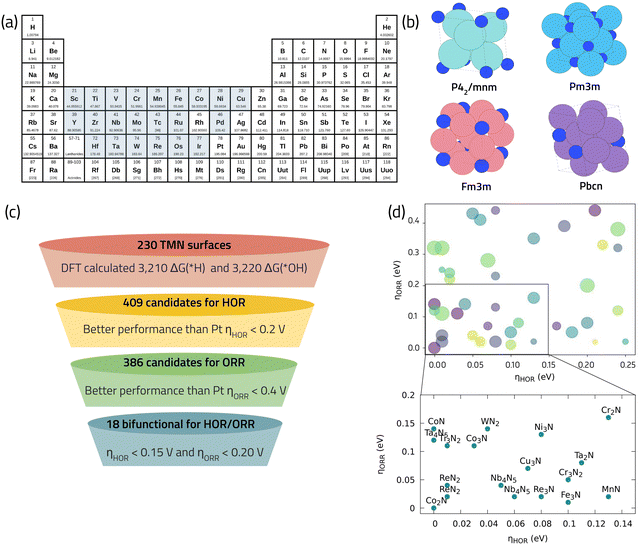 | ||
| Fig. 7 (a) Selected metals as base composition for TMNs from the materials project database. (b) Examples of different bulk crystalline structures of TMNs studied in ref. 74 with high thermodynamic stability. (c) Our selection criteria for identifying promising bifunctional TMNs for HOR/ORR. (d) Final promising list of bifunctional TMN candidates with low predicted overpotential for HOR/ORR. | ||
It is interesting to note that, among this dataset, there are many promising candidates to promote ORR or HOR individually, as it is shown in a histogram distribution of the original data presented in Fig. 8a and b. Namely, more than 600 TMN unique active sites can promote the HOR and more than 380 can promote the ORR taking *H and *OH as the HOR and ORR activity descriptors, respectively. Fig. 8c and d, shows the free energy diagrams on several shortlisted bifunctional TMNs in Fig. 7d that belong to first-row transition metals, and second/third row transition metals, respectively. We find that even though the obtained *OH adsorption energies for most surfaces agree with the data reported in ref. 74, the potential determining step does not come from the *OH formation in the examined catalysts. Instead, it arises from either the *O strong interaction with the surfaces, as in the case of CoN, MnN, and Nb4N5, with significantly negative Gibbs free energy values, or from the *OOH intermediate O–O bond scission, forming *O and *OH adsorbed in separate surface sites, as in the case of Cr3N2, Fe3N, Ni3N, ReN2, and Ta4N5. These observations highlight the importance of considering the complete reaction mechanism to assertively determine the catalytic activity.
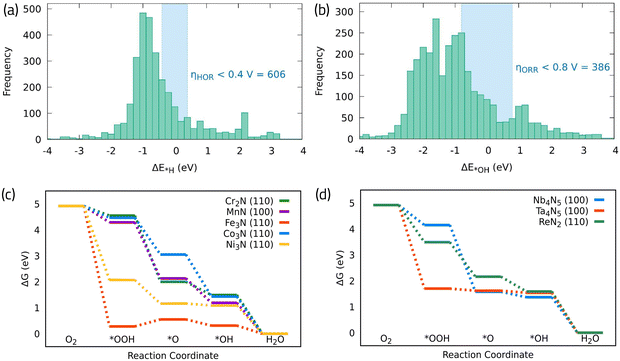 | ||
| Fig. 8 (a) and (b) Distribution of *H and *OH adsorption free energies across different TMNs studied in ref. 74, respectively. (c) Calculated free energy diagram for ORR on different first row (d) and second/third row TMN surfaces. The corresponding data and structures can be found in the ESI.† | ||
The fact that oxygen binds strongly to the TMNs is in line with the previous DFT calculations71 and experimental evidence,80,81 demonstrating the possibility of formation of an oxide layer under ORR conditions. Although this can be taken as a negative characteristic, potentially indicating that TMNs are not stable under operating potentials for fuel cell applications,82 Abroshan H. et al.71 demonstrated that the cobalt oxide layer formed on cobalt nitrides results in improving the ORR activity of TMN. Similarly, the formation of an oxide layer on nickel nitride80 and molybdenum nitride72 has been reported to improve not only its ORR activity, but also its stability.72 A DFT calculated and precisely tailored Pourbaix diagram for Ni3N, and Ni4N (as depicted in Fig. 9), has provided insights into the expansion of oxide phases, such as NiOOH during the relevant pH and potentials of ORR compared to bulk Ni.80 This analysis sheds further light on the intricate interplay between catalyst composition, electrochemical conditions, and oxide formation, crucial for understanding and optimizing catalyst performance in oxygen reduction reactions. This promoting effect of an oxide (or hydroxide) layer has also been experimentally observed in bimetallic nitrides, such as NiFeN and NiMoN,83 vanadium nitrides,84 and even for SACs/TMNs; where the hydroxyl coordination can improve the activity of the catalytic site by modulating the otherwise strong interaction with ORR intermediates.85
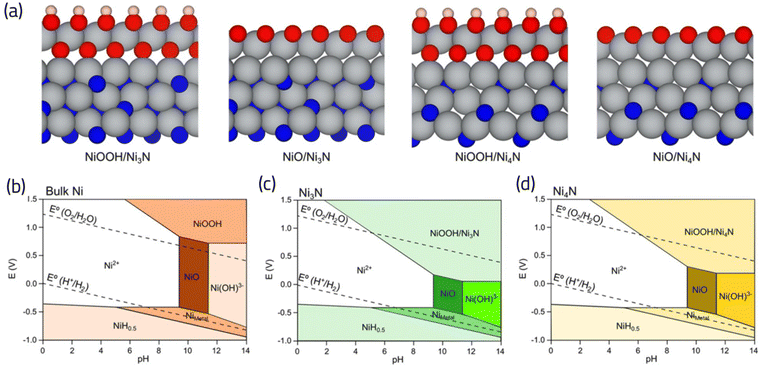 | ||
| Fig. 9 (a) Atomic structures showing formation of oxide (NiOOH and NiO) layers on Ni3N and Ni4N nitride surfaces. (b)–(d) Constructed Pourbiax diagrams for bulk Ni, Ni3N and Ni4N, respectively. The extension of NiOOH phase is evident in (b) and (c) compared to bulk Ni, highlighting the propensity of nitride surfaces to develop oxide films under the relevant pH and potentials of ORR. Adapted from ref. 80 with permission. | ||
Similar results have been observed when transition metal sulfides are considered as ORR catalysts. Zhao, W. et al.86 conducted comprehensive DFT calculations to investigate the oxygen reduction reaction (ORR) activity on CoS2 catalyst.86 Their findings suggest that sulfur is unlikely to serve as an active site for ORR as it binds oxygen intermediates too strongly. Additionally, they discovered that the undercoordinated Co metal site within CoS2 demonstrates lower activity compared to the highly active undercoordinated Co metal sites within Co oxide films. This indicates that the ORR active sites are likely the oxide films formed atop CoS2.
The sample studies mentioned above on ORR activity of transition metal nitrides and sulfides underscore the significance of accounting for the dynamic behaviors of readily available catalysts under ORR operating conditions and acknowledging the potential for oxide formation when constructing model structures. This relates to the importance of considering stability and the likelihood of catalyst surface restructuring during reaction conditions. To gain a deeper understanding of these effects, employing rigorous experimental techniques such as in situ and operando measurements offers valuable means for exploring such phenomena.68 Combined computational–experimental insights not only enhance the fundamental understanding of ORR mechanisms on earth-abundant catalysts but also hold promise for optimizing electronic structure of the catalysts to improve the efficiency of fuel cells and metal–air batteries.
4.2. Transition metal oxides
Transition metal oxides have garnered considerable interest recently owing to their abundance and low cost. These materials represent another class of compounds poised to revolutionize ORR catalysis, offering potential advantages in terms of both availability and durability compared to traditional Pt-based catalysts. One of the concerns, however, is their stability under ORR conditions in acidic media. A recent study by Wang, Z. et al.87 utilizes a large library of oxides reported in the Materials Project database to screen the oxides that are stable under acidic pH values and relevant ORR potentials. This study suggests that the oxides of Sb, Ti, Sn, W, Mo, and Ge are acid stable presenting an opportunity to explore new classes of materials for ORR. Beyond stability, it is important to determine the catalytic activity of these materials to achieve a high ORR performance.87A follow-up computational study,88 examined antimonate (SbO)-based oxides functionalized with first-row transition metals (MSb2O6, M = Mn, Fe, Co, and Ni), considering different crystalline surfaces, to tune their activity and selectivity towards the four-electron ORR. The results indicated that catalytic activity was dependent on surface orientation, with the lowest theoretical overpotentials observed for (110) planes in most cases, and (100) for MnSb2O6. MnSb2O6 demonstrated the highest theoretical activity, which was corroborated by electrochemical experiments. These antimonates outperformed their pure oxide equivalents, Mn2O3(110), Fe2O3(001), Co3O4(100), and NiO(100), demonstrating the possibility for mixing and integrating different metals to modify catalytic activity. Experimental results on MnSb2O6 showed high selectivity towards the two-electron ORR can be achieved with further functionalization with Cr, Fe, and Ni. This study highlights the importance of combining different elements to achieve optimal performance on oxides.
Another particularly interesting oxide listed among the shortlisted candidates in ref. 87, is oxides containing Sn. A common example is SnO2 which is known to have a low ORR catalytic activity on its own.89 Different strategies can be employed to improve its activity, such as different nanostructuring,89 introducing oxygen vacancies90 or heteroatom doping.91 Herein, we investigate the effect of 18 different metal single atoms as potential dopants to improve the SnO2(110) ORR activity, utilizing the DFT data reported in ref. 92. Fig. 10a shows the stability analysis for these structures, calculated in terms of formation energy vs. dissolution potential. The formation energy indicates how favorable it is for a given element to occupy a vacant Sn site, taking the pristine oxide and the crystalline metal as references, with negative values (below 0 eV) indicating energetically favorable formation energy. Furthermore, the dissolution potential determines if the SnO2-supported SACs will remain stable under ORR operating conditions.92 All of the investigated SACs have greater dissolution potentials than 1.23 V, i.e., the standard redox potential for four-electron ORR, indicating their stability against dissolution. On the other hand, they all have negative formation energies when doped into SnO2 substrate, meaning that they are thermodynamically stable single atoms. Fig. 10b depicts the theoretical overpotential on both the Sn site and the doped site, offering a means to track the influence of each metal dopant on the ORR overpotential adjacent to the Sn site. Fig. 10c shows the linear scaling5 relationship between *OH and *OOH binding energies. This analysis reveals that most SACs have an improved ORR performance compared to pristine SnO2, with the exceptions of Ca, Fe, and Ti. Sb, Nb, and Ta can significantly improve the ORR activity by lowering the overpotential even on the adjacent Sn site, which is highly desirable to reduce the required metal loading. The most promising SACs considering the doped metal as the active site are Ru and Pt, with low theoretical overpotentials around 0.35 and 0.45 V, respectively, placing them close to the top of the activity volcano plot (Fig. 10d).
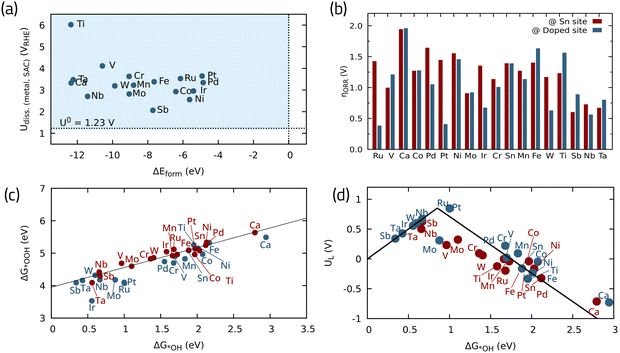 | ||
| Fig. 10 (a) Stability of single metal atoms in SnO2 in terms of dissolution potential vs. formation energies, (b) theoretical overpotentials for the ORR with different doped-metals in SnO2, (c) scaling relationship between ORR intermediates, and (d) activity volcano plot for the 4e-ORR. Data adapted from ref. 92 with permission. | ||
A similar approach has been reported by Mostaghimi, A. et al. to tune the ORR catalytic activity of tantalum pentoxide (Ta2O5).39 DFT calculations in conjunction with CHE and descriptor-based analysis was used to systematically investigate 22 transition metal atoms doped in Ta2O5(120). Their study revealed Pt, Rh, and Ir single atoms as the most promising catalytic active site, displaying improved ORR activity coupled with high stability.39
4.3. High entropy alloys (HEA) and high entropy oxides (HEO)
High entropy alloys (HEAs) and high entropy oxides (HEOs) are metallic and oxide compositions that include at least five primary elements in about equal quantities. Unlike standard alloys, which often include one or two dominating elements and a small number of secondary elements, HEAs and HEOs are designed to have numerous major elements with similar atomic sizes, resulting in a significant degree of disorder in the atomic structure, stabilizing the alloy as the entropic term dominates over the enthalpic one. Of note, not all HEAs and HEOs are stabilized by entropy alone, and understanding their stability is an active research area. This unusual composition opens millions of new materials to be explored in the phase-space93 with unique composition and electronic structure properties, and promising catalytic properties, making them increasingly interesting in ORR applications.94 Löffler, T. et al.94 synthesized highly ordered Pt4FeCoCuNi nanoparticles with outstanding performance for both HER and ORR. The authors highlight the role of the structure ordering as a key parameter to tune the catalytic activity, as it was the case for another high entropy metallic catalyst, PtFeCoNiCuZn.95 One of the other specific examples of high entropy alloys with high ORR activity is PdCuPtNiCo as reported experimentally by Chen, Y. et al.96 Their synthesized nanoparticles had an average size of (10.4 ± 0.4) nm and were selective for the 4e-ORR, as indicated by the electron transfer of 3.95–3.97 observed in their experiments, and a half-wave potential (E1/2) of 0.83 V, very close to commercial Pt/C. Their stability tests showed a very small increase in E1/2 after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles.
000 cycles.
Since the variety of binding sites of the different elements present in a HEA hinders computational modeling, it is crucial to have single-phase materials. Pittkowski, R. K. et al.97 investigated the PdCuPtNiCo using DFT calculations and demonstrated that the formation of HEA nanoparticles is governed by stochastic principles, meaning that their behavior and formation are influenced by random variables and probabilistic events rather than being entirely deterministic. They also showed that the inhibition of precursor mobility during the synthesis process favors the formation of a single phase in PdCuPtNiCo.97
The high entropy materials for ORR catalysis can go beyond metallic alloys and branch through other structures, such as perovskites, antiperovskites, oxides, and nitrides. Li, W. et al.98 investigated lanthanum-based transition metal oxides (LaTMO3) by substituting the B site with different transition metals (TM = Cr, Mn, Fe, Co, Ni) to form high-entropy oxides (HEOs) that tailor the e.g. occupancy by combining elements with different d-orbital electrons. La(Cr0.2Mn0.2Fe0.2Co0.2Ni0.2)O3 was reported as the HEO with the best ORR performance, exhibiting an overpotential of 493 mV and a 1.7% decline in half-wave potential after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. Despite these remarkable experimental results, the field still requires extensive exploration and development to utilize computational calculations as predictive models for such materials.
000 cycles. Despite these remarkable experimental results, the field still requires extensive exploration and development to utilize computational calculations as predictive models for such materials.
Currently, a lot of progress in the high entropy materials domain has been driven by experiments, and DFT calculations provide complementary analyses, often investigating limited combinations at a time. For instance, recent computational studies on the LaMO3 structure employed DFT calculations to address the role of changing only the M site, tuning oxygen vacancies, or exploring different phases.99–101 However, these efforts combined are still insufficient to predict the specific properties of an HEO such as the experimentally obtained La(Cr0.2Mn0.2Fe0.2Co0.2Ni0.2)O398 with acceptable accuracy. This concept was further elaborated in a recent work by Mints et al.102 where a machine learning model was first trained using Gaussian process (GP) regression using data from 350 synthesized nanoparticles via microwave solvothermal synthesis. After initial training and evaluation, the chemical space was reduced to IrOsPdPtRhRu. Each of these pure elements’ oxides in the rutile structure and (110) surface was taken as references for incorporating the remaining atoms. At this step, ML techniques were again employed to reduce the number of DFT calculations required. The authors highlight the trade-offs from each part of this analysis and how computation and experiment complement each other. They show how information from experimental data is crucial but insufficient to determine whether the best performances arise from intrinsic activity or structural modification induced by the different elements in HEOs. ML models yield apparent correlations that might stem from data artifacts, necessitating careful analysis and filtering to ensure the maximum catalytic activity is not wrongly inflated. These models serve as necessary tools since DFT calculations cannot be performed for the entire sample space with all possible combinations of compositions and non-equivalent adsorption sites. Finally, DFT calculations do not address structural change effects but can predict intrinsic activity, and discrepancies among all three methods might occur.
In another example, Svane and Rossmeisl103 combined DFT calculations with other computational methods to investigate HEOs with rutile structures composed of Ru, Ti, Ir, Os, and Rh. Initially, 450 adsorption calculations were performed with DFT, and this dataset was used to train a linear fit model that considered different adsorption sites, summing up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 possibilities. This framework enabled the computational prediction of the optimal composition of an HEO to achieve the lowest overpotentials. Apart from HEA and HEO, antiperovskite nitrides such as (InNCo2.7Mn0.3) have been studied in combination with Pt nanoparticles as a bifunctional catalyst for OER and ORR.104 This provide the opportunity to further explore high entropy TMNs where element modulation can be a very promising strategy to fine-tune different properties of these materials for ORR.105
000 possibilities. This framework enabled the computational prediction of the optimal composition of an HEO to achieve the lowest overpotentials. Apart from HEA and HEO, antiperovskite nitrides such as (InNCo2.7Mn0.3) have been studied in combination with Pt nanoparticles as a bifunctional catalyst for OER and ORR.104 This provide the opportunity to further explore high entropy TMNs where element modulation can be a very promising strategy to fine-tune different properties of these materials for ORR.105
In summary, modeling HEAs and HEOs with DFT poses a significant challenge, as obtaining any property in the HE materials requires numerous combinations of atomic distributions to accurately capture the random nature of these alloys. Trying to achieve that by brute force is unfeasible, as the number of simulations is too high, hence, methods to decrease the number of needed calculations, with some degree of approximation have been employed, such as virtual crystal approximation,106 coherent potential approximation,107 and alchemical potentials.108 Machine learning algorithms can be used to explore phase diagrams more efficiently, reducing the computational cost.109 Pedersen, et al.110 performed a Bayesian optimization of HEA compositions for ORR. Using DFT simulations, they estimated that approximately 50 experiments would be required to discover the optimal composition for quinary HEAs. Further details regarding this methodology will be provided in Section 7, where we delve into materials informatics for accelerating catalyst discovery for ORR.
5. Accuracy and limitations of the DFT analysis
5.1. Choice of the exchange–correlation functional
The accuracy of DFT calculations for predicting catalytic activities heavily depends on the choice of the exchange–correlation functional. The recent advancements in generalized gradient approximation (GGA)-based DFT functionals such as PBE, RPBE and BEEF-vdW allows accurate description of binding energy, with estimated errors ranging from 20 to 30 kJ mol−1.111 However, these functionals tend to overestimate the electronic and thermodynamic properties of bulk metal oxides. This overestimation primarily arises from a self-interaction error present in localized d- and f-electrons. To tackle this issue, the Hubbard U correction is commonly employed to address the strong onsite Coulomb interaction within oxides. However, determining suitable Hubbard U values is not straightforward and often requires benchmarking against experimental data. Cococcioni and Gironcoli112,113 proposed a method to calculate Hubbard U values using a linear-response approach, providing a potential solution to this challenge. Other approaches can also be adopted, such as hybrid functionals114 or Koopmans-compliant functionals.115 Hybrid functionals combine local density approximation (LDA) and GGA functionals with part of the exchange from Hartree–Fock, to improve the description of exchange–correlation contribution and improve the accuracy. There are many types of hybrid functionals (e.g. Heyd–Scuseria–Ernzerhof (HSE) and strongly constrained and appropriately normed (SCAN)). Some have been shown to have a good performance for calculating binding energies. For instance, PBE0 and HSE06,116 when compared to CCSD(T) benchmarks, show errors around 0.1 eV for calculating binding energies, where non-hybrid DFT methods such as PBE and RPBE have errors around 0.6 eV in some cases.114 Koopmans-compliant functionals have also shown improvement in describing binding energies by eliminating single and many-particle self-interactions, known to adversely affect adsorption energies.114,116 The main drawback of hybrid and Koopmans-compliant functionals is their computational cost, which are much higher than standard DFT or DFT+U approaches. Although, there are recent developments such as orbital-resolved DFT+U117 that could be an alternative to getting close to piecewise linearity without demanding much computational power.Among the hybrid functionals, HSE functionals are popular because they can increase the accuracy of traditional DFT functionals such as PBE, especially for calculating band gaps in semiconductors. HSE incorporates a fraction of the exact Hartree–Fock exchange energy, which improves the description of electronic properties compared to standard DFT functionals. Apart from band gaps, HSE functionals are known to provide more accurate predictions of electronic structures and other properties of molecules, solids, and surfaces. For instance, Patel, A. M. et al.93 reported that among 6 different functionals, the hybrid functional HSE06 with inclusion of dispersion corrections (D3)(BJ) provides the most accurate description of binding energies of ORR intermediates on a copper-modified covalent triazine framework.114 In another report, double atom catalysts (M2N6) have been investigated for the ORR with HSE06 and PBE functionals.118 The authors observed a similar trend with both, but employing HSE yielded a slightly better fit for the linear scaling relationships for reaction intermediates, and a shift in the spin magnetic moments of the adsorption site in respect to the peak of the volcano. Of note, HSE functionals are also computationally more expensive than standard DFT functionals, but slowly gaining more attention from the scientific community, because they can yield more reliable results for systems such as metal oxides with strong magnetic properties, where the standard functionals fail to accurately describe the electronic structure.
The SCAN semi local density functional is another hybrid functional that was invented by Sun, J. et al.119 It has been demonstrated to outperform GGA–PBE notably for a collection of 22 weak binding interaction energies, encompassing hydrogen bonds and van der Waals forces, with equilibrium values spanning from 0 to 20 kcal mol−1. Similarly, it exhibits superior performance for lattice constants across a range of 46 hydrocarbons.119 Additional enhancements to stability and performance have been achieved with rSCAN,120 which mitigates divergent behavior at low electron densities by regularizing SCAN's orbital indication function. Furthermore, the latest iteration, r2SCAN, combines both approaches, incorporating previous adjustments to the isoorbital functions while reinstating certain original constraints. Kothakonda, M. et al.121 showed that r2SCAN provide more accurate enthalpies of formation closely aligning with experimental values, particularly when compared to PBE, for weakly bound solids. However, the authors acknowledge that PBE and PBEsol still offer greater accuracy for compounds containing transition metal elements in terms of formation enthalpy values. Nonetheless, challenges persist for hybrid functionals. Notably, it has been recently observed that r2SCAN and r2SCAN+U (with Hubbard U corrections) do not correctly predict the ground state electronic configurations of narrow band gap transition metal oxides.122 Fundamental properties such as formation enthalpies, lattice parameters, band gaps and so on are still being tested to benchmark new hybrid functionals for different classes of materials. Of note, there is still considerable ground to cover in assessing whether these new functionals can offer improved descriptions of catalytic surfaces, along with their corresponding adsorption and reaction Gibbs free energy values, compared to those previously established in the literature.
5.2. Accuracy of activity volcano plots
Another crucial consideration when selecting functionals is to acknowledge that the accuracy of the volcano plot may be impacted by the choice of functional. Sargeant, E. et al. showed that the calculated energy of gas-phase molecules can deviate from their experimental values depending on the exchange–correlation functional.43 The authors note that the experimental value for the oxygen molecule is often taken as the reference to calculate the Gibbs free energy variations (ΔGexp (O2) = 4.92 eV), while the energy of this molecule calculated with a commonly used functional (GGA–PBE), would be, in fact, ΔGPBE (O2) = 4.46 eV. The difference between those values (4.46–4.92 = −0.46 eV, in this case) is significant enough to shift the peaks of the volcano plots and yield different theoretical overpotential values. More specifically, the overpotentials will be overestimated, while the *OH adsorption energies will be underestimated. The mismatch was also observed for other functionals, such as RPBE, BEEF-vdW, and PW91.43 This work shows the importance of semi-empirical corrections as a means of improving the accuracy of volcano plot predictions for ORR and OER catalysts. However, it is worth noting that when analyzing ORR trends, the potential concern about shifting the volcano plot may not be highly consequential. This is because, even if there's a systematic error affecting all the points, the trends in ORR activity can still be reliably captured.6. Solvent, field and pH effects
It is important to note that DFT calculations for calculating the adsorption energies of intermediates are performed in the gas phase. However, electrochemical reactions such as ORR deal with solvents and electrolytes. Thus, it is crucial to precisely consider the influence of water as well as the role of pH and cations in the electrolyte on the adsorption energies of reaction intermediates. Herein, we overview some of the computational efforts that have been conducted in the literature towards including such effects for ORR.6.1. Solvent effect
Describing solvent effects to accurately represent solid–water interfaces using computational methods poses significant challenges for computational modeling due to the differences in bonding characteristics between water molecules as opposed to their interaction with the surface. Various computational approaches have been taken. Classical molecular dynamics, based on force fields, have been shown to effectively capture the statistical nature of liquid water but cannot address bond cleavage and formation.123 While these simulations accurately reproduce the properties of water, they are unsuitable for investigating electrochemical processes, where new species form during reactions. Moreover, parameterizing force fields for each element and compound is a daunting task, especially when dealing with complex systems that include a catalyst surface (usually a metal, metal oxide, nitrides, or carbon-based solid), liquid water as the solvent, and various reaction intermediates (*O, *OH, *OOH). On the other hand, ab initio molecular dynamics (AIMD) can describe both the trajectory of liquid water molecules and the formation of reaction intermediates.123 However, AIMD is computationally demanding, making it impractical for significant surface models and high-throughput studies.123Describing water–solid interfaces using explicit water molecules and DFT calculations is limited by the number of atoms in a simulation cell and periodic boundary conditions, which hinder accurate liquid water descriptions. Consequently, periodic models with very few explicit water molecules are used. For close-packed metals, metal oxides, and carbon-based materials, hexagonal monolayers or bilayers are typically studied. These models study the impact of water structure on the adsorption energies of ORR reaction intermediates on several close-packed metal surfaces, using hexagonal water bilayer structures.13 These studies have revealed a sizable solvent stabilization (∼0.3 eV) on the energetics of the ORR intermediates such as OH* and OOH*, but little to no effect on O*. Modeling the solvent effects on transition metal oxides and nitrides has been less extensively studied and reported using explicit water molecules. Thus, the influence of water molecules on ORR intermediates adsorbed on oxides remains unclear, primarily due to the challenge of obtaining accurate models of explicit water structures on various crystal structures and composition of oxides owing to the dynamic behavior of water molecules near the catalyst surfaces. Siahrostami, S. et al.,124 investigated the explicit water structure on three rutile oxide structures including TiO2, RuO2 and IrO2. The goal was to describe the solvent effect on the oxygen evolution reaction (OER) intermediates. Their results show that the solvent has little impact on adsorption energies of the oxygen intermediates such as *O and *OH, except for the *OOH intermediate, where the solvent effect accounted for 0.4 eV of additional stabilization. Similarly, Gauthier, J. A. et al.125 investigated the water structure on IrO2(110) surfaces by combining DFT calculations with global optimization (minima hopping) and explicitly modeling 1–3 ice-like water bilayers. The most stable water structures were composed of octagonal rings in this metallic oxide, which can be regarded as analogous to the hexagonal water structure formed on metallic surfaces, given the larger interatomic distances on IrO2(110) surfaces. When multiple water layers were stacked, pentagonal and heptagonal rings appeared between them, coordinated by hydrogen bonds. These two studies examining the impact of water structure on OER on the 110 surface of rutile oxides, bear significant resemblance to the ORR owing to analogous oxygen intermediates and can be used to estimate the solvent effect on other oxide surfaces.
For other classes of catalysts, such as transition metal nitrides, it is a common practice to use implicit solvent models to describe the solvent effect on the energetics of reaction intermediates as reported in the ORR study on CoN by Abroshan et al.71 Implicit solvent models in which liquid water is modeled as a polarizable dielectric medium has been recently implemented in periodic DFT codes to describe solid–water interfaces.123,126 These models are less computationally demanding and do not require exhaustive sampling of water molecules. However, as reported by Heenen et al.,127 the accuracy of the implicit solvent models in describing solvation effects at the solid–liquid interface remains unclear. This is because implicit solvent models usually do not account for the directional and steric interactions present with explicit solvent molecules. Thus, further research needs to be established to benchmark the implicit solvation models on the new classes of solid surfaces beyond metals.127
6.2. Electrolyte and pH Effects
Gaining computational insights into the pH effect on ORR activity and selectivity has been challenging, largely due to the disparity between the bulk property nature of pH and the surface properties addressed in DFT calculations, resulting in limited success. In a study by Kelly, S. et al.,128 pH was related to the field effect, with the argument that cations in an alkaline environment can induce a local field effect on adsorbed intermediates on the catalyst surface. For example, an alkaline environment (0.1 M KOH) has a high concentration of cations (K+), in the electric double layer (EDL, region near the charged electrode surface where ions are present in solution). Hence, a local positive field is expected to be induced on the ORR intermediates adsorbed on the electrode surface in alkaline environment. They investigated the field effect on adsorbed oxygen species using sawtooth potential (Fig. 11a) and showed that it is stronger for weak binding surfaces such as metallic gold. Then, they conducted a microkinetic modeling (Fig. 11b) and concluded that for weak binding surfaces, kinetic barriers of the ORR depend on the electrolyte pH, with theoretically predicted overall barrier heights decreasing as pH values increase.128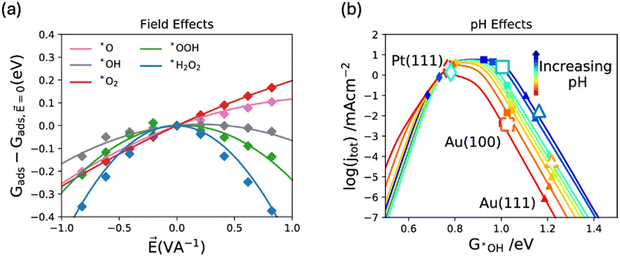 | ||
| Fig. 11 (a) Field effects on different oxygen reduction reaction intermediates and (b) activity volcano plot for the overall reaction at 0.9 V vs. RHE under different fields. Adapted from ref. 128 with permission. | ||
The CHE model falls short in describing the field effect and consequently the pH effect, largely because the ORR intermediates binding energies are obtained from a zero-charge system and depend solely on the reversible hydrogen electrode (RHE) scale. The field effects vary significantly with the pH, because of the equation below:
USHE = URHE + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10) × pH ln(10) × pH | (6) |
This relationship shows that for URHE fixed at 1.00 V, USHE varies within a range of 1.00 V to 0.17 V from pH = 0 to pH = 14, respectively, leading to different electric field strengths in the electric double layer.128 The double layer contribution can be pivotal in an electrochemical process as it has recently been shown in the literature,129 and it is not accounted for in standard DFT calculations. In addition to the electric double layer, variations in behavior under different pH levels and/or field strengths can also be affected by changes in the catalyst surface's potential of zero charge (PZC), resulting from its interaction with reaction intermediates.130 These alterations can only be identified through explicit consideration of field effects in geometry optimization calculations of the adsorbed species. Furthermore, by uncoupling the contribution of the proton–electron pair, an evident dependency of the catalytic surface work function potential arises. This accounts for the observed magnitude difference in the additional stabilization obtained when field effects are considered between pure metal,128 metallic oxides,131 and carbon-based67 surfaces, for example. A previous work from Duan and Henkelman130 also treated the Au(100) surface as a case study using the double-reference method.132 In this case, the solvent/metal interface is modeled by varying the number of electrons of the system. In order to compensate for the supercell charge difference, a uniform background counter charge is applied. Generally, by explicitly considering the field effects, the adsorption Gibbs free energy variation will fit a second order polynomial relationship, (Fig. 11a), where GADS is the adsorption Gibbs free energy at a given applied field (E), and the fitted coefficients α and μ are the intrinsic dipole moment and polarizability, respectively, as follows:
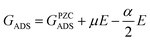 | (7) |
7. Materials informatics for expediting catalyst discovery for ORR
High throughput computational screening allows semi-automated simulations, where thousands of materials can be simulated and analyzed with little human intervention, allowing the creation of large databases.134–136 With the large number of simulated materials, organized in databases, machine learning algorithms can be employed for either classifications or prediction of materials properties.74,137 This synergy has led to the emergence of a new area, materials informatics,137–139 which is changing the paradigm on computational methodologies for materials science, with the catalysts design also being impacted by this new methodology. In addition, natural language processing techniques140–142 are also being incorporated into the materials informatics frameworks, initially for data extraction from the literature by using regular expressions, then language models started to be employed for new applications of existing materials.143High-throughput DFT calculations have become a widespread practice to screen catalyst materials and generate datasets to train machine learning (ML) models. This approach has shown great promise for discovering highly active catalysts for ORR. Wang, Y. et al.,65 conducted a high-throughput computational screening study on carbon-supported single metal atom catalysts. They carried out 180 simulations with various metals supported by different carbon structures and discovered that ΔGOH serves as a reliable descriptor for ORR catalytic activity. They narrowed down the candidate catalysts to just five, which showed potential to outperform platinum. Sun, H. et al.144 conducted a high-throughput screening for M–NC single-atom catalysts, encompassing various central metal atoms and environmental atoms. Their initial calculations produced 1344 structures, of which they subjected 448 structures to DFT calculations using uniform distribution sampling. Utilizing this dataset, they trained an ML model to predict the overpotential, employing ΔGOH as a descriptor for ORR catalytic activity. The authors employed 35 features independent of DFT results to train the ML model. They used feature importance methods to evaluate which factors contributed most to describing the target properties. For both the overpotential and the fourth step ΔG, the metal-related features accounted for approximately 88% of the contribution. These features included atomic radius, electronegativity, first ionization potential, electron affinity, the number of d electrons, the number of electrons in the outer shell, and the element's period in the periodic table. Other features related to atoms in layers 1 to 4 were also evaluated but contributed significantly less to the model. This led to the conclusion that if the central atom is not suitable for ORR, changing the surrounding atoms will have little effect on improving the catalytic process.
Of note, a model reliant on DFT calculations would not be suitable for predicting properties already obtained from DFT results. Their most effective model yielded an RMSE of 0.37 eV for ΔGOH and 0.25 V for the overpotential, enabling them to infer these properties for the remaining 896 systems within the observed accuracy. To validate the accuracy of the ML-predicted results, the optimal candidates underwent further optimization using simulated DFT calculations to confirm their viability. To optimize their prediction, the authors trained another model, including a geometric feature (the sum of the bond lengths in the first layer) and the Bader charge. Performing all the DFT calculations to obtain these properties would negate the need for a model, as the targets would already be available. Therefore, the authors trained a model using the previous 35 features to predict these two new features, then inferred their ΔG and overpotentials. This model improved the RMSE by 0.02 eV.144 They ended up reporting 30 highly active structures for ORR. Similarly, Chen, Y. et al.,145 applied ML algorithms trained with DFT results, for M–N4–Gr/MXene heterojunction nanosheets. To accelerate their screening process, they applied regression algorithms to predict the overpotential, and their best model reached an RMSE of 0.10 eV. The authors also reached four suggestions of catalysts with low overpotentials.
While the fusion of high-throughput DFT screening and ML algorithms presents significant opportunities for novel catalyst design, it is not devoid of limitations. High-throughput DFT calculations demand significant computational resources, which are not accessible to all researchers. On the other hand, the ML methods do not offer the same precision as DFT, and they are still not able to achieve the chemical accuracy of 1 kcal mol−1. A major concern when applying ML techniques to aid catalyst discovery is that these often result in “black box” models, making it impossible to understand the underlying chemical and physical properties that contribute to good catalytic activity purely from ML selection. To address this challenge, explainable AI146 has emerged as an alternative to combine the low cost and extensive data screening capability of ML models with the incorporation of theoretical and physical principles, particularly in material discovery. Coupling both high-throughput and machine learning (ML) in active learning process has proven to be a key.147 Active learning algorithms can be implemented in ORR catalyst design to enhance the efficiency and effectiveness of discovering new catalysts. This approach involves iteratively training machine learning models on an initial dataset of known ORR catalysts, using strategies like uncertainty sampling to select the most informative samples from a pool of unlabeled data. These selected samples are then experimentally tested, and the results are added to the training set to refine the model. This cycle continues until the model achieves a satisfactory performance or the available resources are exhausted. Active learning helps prioritize experiments that provide the most value in terms of information gain, thereby speeding up the discovery process. The implementation of active learning for ORR seems to be in its early phase, with limited literature currently available on the topic. Zhang X. et al.,148 studied platinum-based alloys, and identified five promising candidates for ORR with low overpotentials after just three iterations of the active learning process. Of note, none of the features used for the ML model involved DFT simulations. Another active learning study, by Omidvar N. et al.,146 investigated Pt monolayer core–shell catalysts. The authors employed active learning to investigate Pt monolayer core–shell catalysts using theory-infused neural network (TinNet) algorithms,149 and explored approximately 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 candidates generated from roughly 1500 thermodynamically stable bulk structures sourced from databases. They performed 8 iterations and successfully identified previously known ORR catalysts with high activity, thereby validating their methodology. A theory module based on the Newns–Anderson model Hamiltonians, which models chemisorption processes, was incorporated into the neural networks to provide model interpretability. By factoring in material costs within their selection process, they steered away from precious metals and identified 17 candidate materials that offer both cost-effectiveness and high ORR performance. These examples indicate the great potential of active learning methods in expediting catalyst discovery for ORR. However, the main challenge is to develop machine learning models that can provide reasonable performance with few calculations. These models do not need to be very precise since they are primarily used to suggest promising candidates, with precise results obtained through subsequent calculations. Nevertheless, the models must reliably estimate whether a catalyst will perform well or poorly. Additionally, there is a trade-off between exploring and exploiting the phase space. Focusing solely on simulation suggestions for the best-performing catalysts predicted by the model might lead to missing optimal regions in the phase space where better catalysts could be discovered. Therefore, when performing calculations for new suggestions, it is crucial to maintain a balance between evaluating both good and poor-performing catalysts to ensure comprehensive exploration of the phase space.
000 candidates generated from roughly 1500 thermodynamically stable bulk structures sourced from databases. They performed 8 iterations and successfully identified previously known ORR catalysts with high activity, thereby validating their methodology. A theory module based on the Newns–Anderson model Hamiltonians, which models chemisorption processes, was incorporated into the neural networks to provide model interpretability. By factoring in material costs within their selection process, they steered away from precious metals and identified 17 candidate materials that offer both cost-effectiveness and high ORR performance. These examples indicate the great potential of active learning methods in expediting catalyst discovery for ORR. However, the main challenge is to develop machine learning models that can provide reasonable performance with few calculations. These models do not need to be very precise since they are primarily used to suggest promising candidates, with precise results obtained through subsequent calculations. Nevertheless, the models must reliably estimate whether a catalyst will perform well or poorly. Additionally, there is a trade-off between exploring and exploiting the phase space. Focusing solely on simulation suggestions for the best-performing catalysts predicted by the model might lead to missing optimal regions in the phase space where better catalysts could be discovered. Therefore, when performing calculations for new suggestions, it is crucial to maintain a balance between evaluating both good and poor-performing catalysts to ensure comprehensive exploration of the phase space.
Current methodologies clearly result in a significant volume of data being generated in literature. Some of this data is organized into databases, however, most findings are dispersed across published papers, in PDF format, with XML format emerging more recently. To address this challenge, natural language processing (NLP) methods hold significant promise. They can leverage the wealth of existing data, derived from both experimental and theoretical studies. Surprisingly, NLP methodologies seem underutilized in the literature for the ORR studies, with most works focusing on CO2RR. In the study by Suvarna, M. et al.150 data collecting has been performed for ORR, OER, HER, and CO2RR. They reported the most used metals precursors, carrier materials, and solvents, with Fe being the most investigated metal for ORR. For example, ZIF-8 frameworks were commonly used as precursors in preparing ORR catalysts. Hence, NLP methods are a powerful tool for obtaining data from literature, although its main limitation is a method to extract data from published literature. Accessing papers collectively is challenging, as not all journals permit such access or may impose additional fees, on top of the standard access fees paid by research institutions. Furthermore, the usual brute-force techniques are poor and demanding to obtain context-based information, hence, the large language models (LLMs) are playing a transformative role, as they are particularly good at capturing the context with long term relations. Another limitation is the cost to perform API queries with the best performing LLMs, although running LLMs locally is becoming feasible, as the performance of open weight models is improving fast.
Currently, there are only a few works that broadly apply NLP to include ORR results. Here, we discuss two insightful examples from the literature that contribute to advancements in ORR catalyst design. Qin, et al.151 employed NLP for insights into the development of electrocatalysts. They gathered 604![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 933 abstracts from the literature and trained a named entity recognition (NER) model. The authors identified electrocatalysts and their performance, extracting 22
933 abstracts from the literature and trained a named entity recognition (NER) model. The authors identified electrocatalysts and their performance, extracting 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 records of catalysts from their corpus. Although the data obtained was limited for ORR, they found that platinum remains the preferred material for ORR, despite many alternative materials being studied. These results differ from our findings, where we show a trend toward metal nitrides for ORR, as discussed in the next paragraph. Another NLP study by Muthukkumaran et al.152 focused on discovering perovskite-based electrocatalysts. The authors retrained a SciBERT model with 1.74 million abstracts, using it to generate new perovskite compositions with synthetic embedding. To evaluate the proposed compositions, they applied various cosine similarity measures, including the similarity to “electrocatalyst” and comparisons between word embeddings obtained from the language model and those generated by the algorithms. The authors concluded that nickel-based perovskites are promising candidates for catalysts.
000 records of catalysts from their corpus. Although the data obtained was limited for ORR, they found that platinum remains the preferred material for ORR, despite many alternative materials being studied. These results differ from our findings, where we show a trend toward metal nitrides for ORR, as discussed in the next paragraph. Another NLP study by Muthukkumaran et al.152 focused on discovering perovskite-based electrocatalysts. The authors retrained a SciBERT model with 1.74 million abstracts, using it to generate new perovskite compositions with synthetic embedding. To evaluate the proposed compositions, they applied various cosine similarity measures, including the similarity to “electrocatalyst” and comparisons between word embeddings obtained from the language model and those generated by the algorithms. The authors concluded that nickel-based perovskites are promising candidates for catalysts.
To illustrate the potential of the NLP techniques for ORR, we mined 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 515 abstracts from the web of science query “oxygen reduction reaction”, encompassing all relevant studies on this topic (Fig. 12). We further filtered the results, by keeping the abstracts that did not have expressions related to other catalytic processes, leading to the final number of literatures down to 20
515 abstracts from the web of science query “oxygen reduction reaction”, encompassing all relevant studies on this topic (Fig. 12). We further filtered the results, by keeping the abstracts that did not have expressions related to other catalytic processes, leading to the final number of literatures down to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 237. This allowed us to narrow down to papers that are more focused on the ORR. Research on ORR began in the early 1990s, experiencing a growing trend since then. However, it was not until 2006 that there were more than 100 works, and the milestone of 1000 papers was surpassed in 2014. By 2022, the number of works had reached 2000. With the collected and filtered abstracts, we employed the large language model Llama 3 70b,153 to extract which materials were used as catalysts in each work. The analysis was performed since 2006, as the previous years did not have enough papers to provide good statistics. Fig. 12a plots all the materials mentioned in the abstracts as catalysts that had at least 0.6% of the total mentions for at least four years. Platinum prevails in publications as a state-of-the-art catalyst material. However, its mentions have been steadily decreasing over time, even when accounting for its potential inclusion as a catalyst benchmark, which could increase its occurrences. Examining the lower portion of Fig. 12a reveals the trends of other materials. For instance, there is a declining trend in the share of works utilizing Pd, Au, Ag, Pt–Co, Cu, Pt–Ni, Ru, and others. For Fe, Co, and particularly Fe–N, the share of works is on the rise. To highlight emerging trends in materials, we have plotted those with increasing trends over the last four years and at least 0.08% of mentions in 2023, as depicted in Fig. 12b. Many materials containing nitrogen are experiencing growth, notably Fe–N, as mentioned earlier, along with Co–N, Fe–NC, M–N (metal–nitrogen), g-C3N4 (graphitic carbon nitride), Mn–N, and Cu–N. Transition metals like Co and Fe are also experiencing an upward trajectory, albeit not as significantly compared to the initial years of analysis, given their already similar shares. Fe3C and Mn are also witnessing increases, albeit with lower total shares. There is a diversification in the materials under study, with platinum losing shares while others gain prominence. Thus, it is evident that NLP techniques can offer valuable insights from the analysis of entire literature sets, even when focusing solely on abstracts, which are readily accessible without paywalls. A more comprehensive study could delve into this dataset, offering a detailed examination of rising and declining trends in research for each material, given that many materials were excluded due to the applied filters. Furthermore, properties such as overpotentials, limiting potentials, or faradaic efficiencies could be extracted, associated with materials, facilitated by recent advancements in LLMs, representing a promising avenue for future research. Access to full texts via mass paper download tools from publishers could significantly expand the scope of NLP work, although such tools are not readily and affordably accessible.
237. This allowed us to narrow down to papers that are more focused on the ORR. Research on ORR began in the early 1990s, experiencing a growing trend since then. However, it was not until 2006 that there were more than 100 works, and the milestone of 1000 papers was surpassed in 2014. By 2022, the number of works had reached 2000. With the collected and filtered abstracts, we employed the large language model Llama 3 70b,153 to extract which materials were used as catalysts in each work. The analysis was performed since 2006, as the previous years did not have enough papers to provide good statistics. Fig. 12a plots all the materials mentioned in the abstracts as catalysts that had at least 0.6% of the total mentions for at least four years. Platinum prevails in publications as a state-of-the-art catalyst material. However, its mentions have been steadily decreasing over time, even when accounting for its potential inclusion as a catalyst benchmark, which could increase its occurrences. Examining the lower portion of Fig. 12a reveals the trends of other materials. For instance, there is a declining trend in the share of works utilizing Pd, Au, Ag, Pt–Co, Cu, Pt–Ni, Ru, and others. For Fe, Co, and particularly Fe–N, the share of works is on the rise. To highlight emerging trends in materials, we have plotted those with increasing trends over the last four years and at least 0.08% of mentions in 2023, as depicted in Fig. 12b. Many materials containing nitrogen are experiencing growth, notably Fe–N, as mentioned earlier, along with Co–N, Fe–NC, M–N (metal–nitrogen), g-C3N4 (graphitic carbon nitride), Mn–N, and Cu–N. Transition metals like Co and Fe are also experiencing an upward trajectory, albeit not as significantly compared to the initial years of analysis, given their already similar shares. Fe3C and Mn are also witnessing increases, albeit with lower total shares. There is a diversification in the materials under study, with platinum losing shares while others gain prominence. Thus, it is evident that NLP techniques can offer valuable insights from the analysis of entire literature sets, even when focusing solely on abstracts, which are readily accessible without paywalls. A more comprehensive study could delve into this dataset, offering a detailed examination of rising and declining trends in research for each material, given that many materials were excluded due to the applied filters. Furthermore, properties such as overpotentials, limiting potentials, or faradaic efficiencies could be extracted, associated with materials, facilitated by recent advancements in LLMs, representing a promising avenue for future research. Access to full texts via mass paper download tools from publishers could significantly expand the scope of NLP work, although such tools are not readily and affordably accessible.
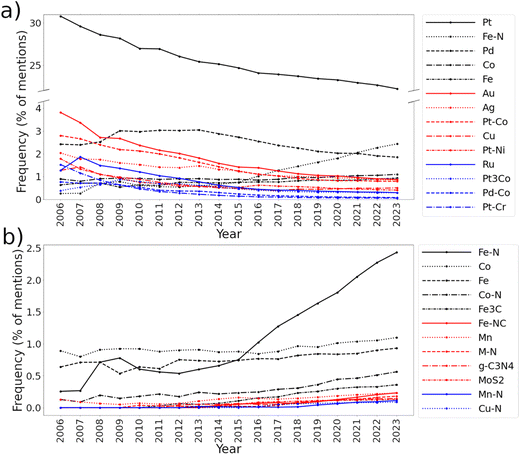 | ||
| Fig. 12 (a) Number of publications per year for all reported materials for ORR. (b) Number of publications per year for rising trends over the last four years. | ||
8. Summary and perspectives
Computational methodologies, including DFT in conjunction with descriptor-based analysis and CHE, have revolutionized the study of catalyst surfaces and their interactions with oxygen species. This approach enabled rational design of materials with optimized electronic structure and reactivity for ORR. By identifying active sites and fine-tuning catalyst compositions at the atomic level, computational simulations have expedited the discovery of promising ORR catalysts. The insights gained from computational analyses have shed light on the fundamental causes of ORR overpotentials observed in experimental catalysts. Various strategies have been explored to overcome limitations in ORR catalysis through computational design. Alternative earth-abundant and cost-effective materials such as transition metal nitrides and oxides have been recommended by computational guidance, providing opportunities for replacing costly platinum-based catalysts and solving the scalability issue of fuel cell technology. The accuracy of DFT calculations and the influence of solvent and electrolyte pH remain ongoing challenges to tackle using computational methodologies.In addition to unraveling atomistic-level information that contributes to understanding the origin of catalytic performance, computational methods also serve as predictive tools to guide experimental synthesis. Numerous examples in the literature demonstrate the effectiveness of computational screening in identifying novel ORR catalysts. These include the discovery of various Pt-alloys,4,6,7,19 oxides68 such as antimonates (MSb2O6, M = Mn, Fe, Co, and Ni),88 and high-entropy alloys like Pt4FeCoCuNi.94 Recently Ir alloys (Ir3M, where M represents 3d, 4d, and 5d transition metals) predicted as active ORR catalysts using DFT calculations, which were subsequently synthesized and verified through experimental testing.61
Recent advancements in employing materials informatics, including machine learning approaches like NLP, provide opportunities to accelerate catalyst material discovery for ORR. Furthermore, the application of high-throughput DFT screening techniques has enhanced this process. These methods enable the efficient production and analysis of vast datasets, facilitating the identification of trends and patterns that inform the design of novel ORR catalyst materials. Computational advancements in machine learning models, coupled with high-throughput DFT screening, hold immense promise for developing efficient and cost-effective ORR catalysts. Ultimately, these efforts aim to advance fuel cells as highly efficient electrochemical energy conversion technologies, bringing us closer to realizing their full potential.
As more data is generated with high-throughput screenings, the importance of databases to store these calculations cannot be overstated. These databases ensure that the results of calculations are accessible across different fields, particularly in experimental research and development. This is crucial not only to ensure the reproducibility of DFT calculations and to reduce unnecessary computational time and resources being employed for redundant analysis but, most importantly, to accelerate catalyst design. A recent milestone in this regard is the creation of catalysis-Hub,136 a comprehensive database of reaction energies obtained from electronic structure calculations, with a user-friendly web interface, to which more than 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 calculations have been uploaded since its announcement.
000 calculations have been uploaded since its announcement.
Author contributions
S. S. conceived the idea and structure of the review paper, wrote the first draft, and supervised L. E. B. L. in conducting the screening study on ORR activity of transition metal nitrides. J. M. A. performed the natural language processing. All authors collectively contributed content to enrich the paper and participated in revising and editing.Data availability
The data supporting this article have been included as part of the ESI.† This file contains all original data for the DFT calculations presented in the main manuscript Fig. 8.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. S. and L. E. B. L. gratefully acknowledge the support from Natural Sciences and Engineering Research Council (NSERC) of Canada (Discovery Grant No. RGPIN-2023-05298). L. E. B. L. and J. M. A. gratefully acknowledge the support from INCT Materials Informatics (CNPq 406447/2022-5). The calculations in this study were facilitated by the resources provided through Central Computacional Multiusuário (CCM-UFABC) computing infrastructure.References
- S. P. S. Badwal, S. S. Giddey, C. Munnings, A. I. Bhatt and A. F. Hollenkamp, Front. Chem., 2014, 2, 1–28 CrossRef CAS PubMed
.
- S. Siahrostami, M. E. Björketun, P. Strasser, J. Greeley and J. Rossmeisl, Phys. Chem. Chem. Phys., 2013, 15, 9326–9334 RSC
.
- M. T. M. Koper, Chem. Sci., 2013, 4, 2710–2723 RSC
.
- M. Escudero-Escribano, P. Malacrida, M. H. Hansen, U. G. Vej-Hansen, A. Velázquez-Palenzuela, V. Tripkovic, J. Schiøtz, J. Rossmeisl, I. E. L. Stephens and I. Chorkendorff, Science, 2016, 352, 73–76 CrossRef CAS PubMed
.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed
.
- C. Chen, Y. Kang, Z. Huo, W. Huang, H. L. Xin, J. D. Snyder, D. Li, J. A. Herron, M. Mavrikakis, M. Chi, K. L. More, Y. Li, N. M. Markovic, G. A. Somorjai, P. Yang, Z. Zhu and V. R. Stamenkovic, Science, 2014, 343, 1339–1343 CrossRef CAS PubMed
.
- I. E. L. Stephens, A. S. Bondarenko, U. Grønbjerg, J. Rossmeisl and I. Chorkendorff, Energy Environ. Sci., 2012, 5, 6744–6762 RSC
.
- Z. W. She, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, 1–12 Search PubMed
.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef
.
- Q. Chen, Z. Zhang, R. Zhang, M. Hu, L. Shi and Z. Yao, Processes, 2023, 11, 361 CrossRef CAS
.
- Y. Zhao, D. P. Adiyeri Saseendran, C. Huang, C. A. Triana, W. R. Marks, H. Chen, H. Zhao and G. R. Patzke, Chem. Rev., 2023, 123, 6257–6358 CrossRef CAS PubMed
.
- M. Shao, Q. Chang, J. P. Dodelet and R. Chenitz, Chem. Rev., 2016, 116, 3594–3657 CrossRef CAS PubMed
.
- V. Tripković, E. Skúlason, S. Siahrostami, J. K. Nørskov and J. Rossmeisl, Electrochim. Acta, 2010, 55, 7975–7981 CrossRef
.
- G. S. Karlberg, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 5158–5161 RSC
.
- H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2008, 10, 3722–3730 RSC
.
- S. Siahrostami, C. Tsai, M. Karamad, R. Koitz, M. García-Melchor, M. Bajdich, A. Vojvodic, F. Abild-Pedersen, J. K. Nørskov and F. Studt, Catal. Lett., 2016, 146, 1917–1921 CrossRef CAS
.
- M. Busch, N. B. Halck, U. I. Kramm, S. Siahrostami, P. Krtil and J. Rossmeisl, Nano Energy, 2016, 29, 126–135 CrossRef CAS
.
- A. Vojvodic and J. K. Nørskov, Natl. Sci. Rev., 2015, 2, 140–149 CrossRef CAS
.
- J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556 CrossRef CAS PubMed
.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, ACS Catal., 2012, 2, 1654–1660 CrossRef CAS
.
- S. Siahrostami, A. Verdaguer-Casadevall, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero-Escribano, E. A. Paoli, R. Frydendal, T. W. Hansen, I. Chorkendorff, I. E. L. Stephens and J. Rossmeisl, Nat. Mater., 2013, 12, 1137–1143 CrossRef CAS PubMed
.
- A. Verdaguer-Casadevall, D. Deiana, M. Karamad, S. Siahrostami, P. Malacrida, T. W. Hansen, J. Rossmeisl, I. Chorkendorff and I. E. L. Stephens, Nano Lett., 2014, 14, 1603–1608 CrossRef CAS PubMed
.
- I. E. L. Stephens, A. S. Bondarenko, F. J. Perez-Alonso, F. Calle-Vallejo, L. Bech, T. P. Johansson, A. K. Jepsen, R. Frydendal, B. P. Knudsen, J. Rossmeisl and I. Chorkendorff, J. Am. Chem. Soc., 2011, 133, 5485–5491 CrossRef CAS PubMed
.
- P. Strasser, S. Koh, T. Anniyev, J. Greeley, K. More, C. Yu, Z. Liu, S. Kaya, D. Nordlund, H. Ogasawara, M. F. Toney and A. Nilsson, Nat. Chem., 2010, 2, 454–460 CrossRef CAS PubMed
.
- A. L. Strickler, A. Jackson and T. F. Jaramillo, ACS Energy Lett., 2017, 2, 244–249 CrossRef CAS
.
- V. Stamenkovic, B. S. Mun, K. J. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Nørskov, Angew. Chem., Int. Ed., 2006, 45, 2897–2901 CrossRef CAS PubMed
.
- V. R. Stamenkovic, B. Fowler, B. S. Mun, G. Wang, P. N. Ross, C. A. Lucas and N. M. Markovic, Science, 2007, 315, 493–497 CrossRef CAS PubMed
.
- C. M. Pedersen, M. Escudero-Escribano, A. Velázquez-Palenzuela, L. H. Christensen, I. Chorkendorff and I. E. L. Stephens, Electrochim. Acta, 2015, 179, 647–657 CrossRef CAS
.
- Z. Peng and H. Yang, Nano Today, 2009, 4, 143–164 CrossRef CAS
.
- H. Xin, A. Holewinski and S. Linic, ACS Catal., 2012, 2, 12–16 CrossRef CAS
.
- M. D. Bhatt, G. Lee and J. S. Lee, Energy Fuels, 2017, 31, 1874–1881 CrossRef CAS
.
- H. Y. Su, Y. Gorlin, I. C. Man, F. Calle-Vallejo, J. K. Norskov, T. F. Jaramillo and J. Rossmeisl, Phys. Chem. Chem. Phys., 2012, 14, 14010–14022 RSC
.
- D. F. Abbott, S. Mukerjee, V. Petrykin, Z. Bastl, N. B. Halck, J. Rossmeisl and P. Krtil, RSC Adv., 2015, 5, 1235–1243 RSC
.
- D. Higgins, M. Wette, B. M. Gibbons, S. Siahrostami, Ch. Hahn, M. Escudero-Escribano, M. García-Melchor, Z. Ulissi, R. C. Davis, A. Mehta, B. C. Clemens, J. K. Nørskov and T. F. Jaramillo, ACS Appl. Energy Mater., 2018, 1(5), 1990–1999 CrossRef CAS
.
- M. Lehtimäki, H. Hoffmannová, O. Boytsova, Z. Bastl, M. Busch, N. B. Halck, J. Rossmeisl and P. Krtil, Electrochim. Acta, 2016, 191, 452–461 CrossRef
.
- J. W. F. To, J. W. D. Ng, S. Siahrostami, A. L. Koh, Y. Lee, Z. Chen, K. D. Fong, S. Chen, J. He, W. G. Bae, J. Wilcox, H. Y. Jeong, K. Kim, F. Studt, J. K. Nørskov, T. F. Jaramillo and Z. Bao, Nano Res., 2017, 10, 1163–1177 CrossRef CAS
.
- A. Seifitokaldani, O. Savadogo and M. Perrier, Electrochim. Acta, 2014, 141, 25–32 CrossRef CAS
.
- J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Chem. Phys. Lett., 2008, 466, 68–71 CrossRef CAS
.
- S. Back, A. H. Bagherzadeh Mostaghimi and S. Siahrostami, ChemCatChem, 2024, 14, e202101763 CrossRef
.
- N. B. Halck, V. Petrykin, P. Krtil and J. Rossmeisl, Phys. Chem. Chem. Phys., 2014, 16, 13682–13688 RSC
.
- H. Wan, T. M. Østergaard, L. Arnarson and J. Rossmeisl, ACS Sustainable Chem. Eng., 2019, 7, 611–617 CrossRef CAS
.
- S. Back, A. R. Kulkarni and S. Siahrostami, ChemCatChem, 2018, 10, 3034–3039 CrossRef CAS
.
- E. Sargeant, F. Illas, P. Rodríguez and F. Calle-Vallejo, Electrochim. Acta, 2022, 426, 140799 CrossRef CAS
.
- Z. F. Huang, J. Song, S. Dou, X. Li, J. Wang and X. Wang, Matter, 2019, 1, 1494–1518 CrossRef
.
- R. Cepitis, V. Ivaništšev, J. Rossmeisl and N. Kongi, Catal. Sci. Technol., 2024, 14, 2105–2113 RSC
.
- J. Pérez-Ramírez and N. López, Nat. Catal., 2019, 2, 971–976 CrossRef
.
- J. Su, C. B. Musgrave, Y. Song, L. Huang, Y. Liu, G. Li, Y. Xin, P. Xiong, M. M. J. Li, H. Wu, M. Zhu, H. M. Chen, J. Zhang, H. Shen, B. Z. Tang, M. Robert, W. A. Goddard and R. Ye, Nat. Catal., 2023, 6, 818–828 CrossRef CAS
.
- R. Cepitis, N. Kongi, J. Rossmeisl and V. Ivaništšev, ACS Energy Lett., 2023, 8, 1330–1335 CrossRef CAS PubMed
.
- H. Wan, A. W. Jensen, M. Escudero-Escribano and J. Rossmeisl, ACS Catal., 2020, 10, 5979–5989 CrossRef CAS
.
- Q. K. Li, X. F. Li, G. Zhang and J. Jiang, J. Am. Chem. Soc., 2018, 140, 15149–15152 CrossRef CAS PubMed
.
- P. Guo, B. Liu, F. Tu, Y. Dai, Z. Zhang, Y. Xia, M. Ma, Y. Zhang, L. Zhao and Z. Wang, Energy Environ. Sci., 2024, 17, 3077–3087 RSC
.
- A. Mahmood, W. Guo, H. Tabassum and R. Zou, Adv. Energy Mater., 2016, 6, 1600423 CrossRef
.
- E. Xie and X. Wang, J. Phys. Chem. Lett., 2023, 14, 9392–9402 CrossRef CAS PubMed
.
- C. H. Kjaergaard, J. Rossmeisl and J. K. Nørskov, Inorg. Chem., 2010, 49, 3567–3572 CrossRef CAS PubMed
.
- N. Kornienko, Y. Zhao, C. S. Kley, C. Zhu, D. Kim, S. Lin, C. J. Chang, O. M. Yaghi and P. Yang, J. Am. Chem. Soc., 2015, 137, 14129–14135 CrossRef CAS PubMed
.
- J. Albo, D. Vallejo, G. Beobide, O. Castillo, P. Castaño and A. Irabien, ChemSusChem, 2017, 10, 1100–1109 CrossRef CAS PubMed
.
- I. Hod, M. D. Sampson, P. Deria, C. P. Kubiak, O. K. Farha and J. T. Hupp, ACS Catal., 2015, 5, 6302–6309 CrossRef CAS
.
- C. H. Kjaergaard, J. Rossmeisl and J. K. Nørskov, Inorg. Chem., 2010, 49, 3567–3572 CrossRef CAS PubMed
.
- T. Sours, A. Patel, J. Nørskov, S. Siahrostami and A. Kulkarni, J. Phys. Chem. Lett., 2020, 11, 10029–10036 CrossRef CAS PubMed
.
- A. I. Hutu, E. Pervolarakis, I. N. Remediakis, H. H. Kristoffersen and J. Rossmeisl, J. Phys. Chem. C, 2024, 128, 10251–10258 CrossRef CAS
.
- J. Cho, I. Jang, H. S. Park, S. H. Choi, J. H. Jang, H. J. Kim, S. P. Yoon, S. J. Yoo and H. C. Ham, Appl. Catal., B, 2018, 235, 177–185 CrossRef CAS
.
- M. J. Kolb and F. Calle-Vallejo, J. Mater. Chem. A, 2022, 10, 5937–5941 RSC
.
- F. Calle-Vallejo, Appl. Phys. Lett., 2024, 11, 021305 CAS
.
- S. Dong, X. Chen, X. Zhang and G. Cui, Coord. Chem. Rev., 2013, 257, 1946–1956 CrossRef CAS
.
- Y. Wang, R. Hu, Y. Li, F. Wang, J. Shang and J. Shui, Nano Res., 2022, 15, 1054–1060 CrossRef CAS
.
- T. Li, Y. Yao, B. H. Ko, Z. Huang, Q. Dong, J. Gao, W. Chen, J. Li, S. Li, X. Wang, R. Shahbazian-Yassar, F. Jiao and L. Hu, Adv. Funct. Mater., 2021, 31, 2010561 CrossRef CAS
.
- Z. Duan and G. Henkelman, J. Phys. Chem. C, 2020, 124, 12016–12023 CrossRef CAS
.
- M. B. Stevens, M. Anand, M. E. Kreider, E. K. Price, J. Z. Zeledón, L. Wang, J. Peng, H. Li, J. M. Gregoire, J. Hummelshøj, T. F. Jaramillo, H. Jia, J. K. Nørskov, Y. Roman-Leshkov, Y. Shao-Horn, B. D. Storey, S. K. Suram, S. B. Torrisi and J. H. Montoya, Energy Environ. Sci., 2022, 15, 3775–3794 RSC
.
- K. Wan, T. Chu, B. Li, P. Ming and C. Zhang, Adv. Sci., 2023, 10, 2203391 CrossRef CAS PubMed
.
- Q. Deng, R. Huang, L. H. Shao, A. V. Mumyatov, P. A. Troshin, C. An, S. Wu, L. Gao, B. Yang and N. Hu, Phys. Chem. Chem. Phys., 2023, 25, 12565–12586 RSC
.
- H. Abroshan, P. Bothra, S. Back, A. Kulkarni, J. K. Nørskov and S. Siahrostami, J. Phys. Chem. C, 2018, 122, 4783–4791 CrossRef CAS
.
- M. B. Stevens, M. E. Kreider, A. M. Patel, Z. Wang, Y. Liu, B. M. Gibbons, M. J. Statt, A. V. Ievlev, R. Sinclair, A. Mehta, R. C. Davis, J. K. Nørskov, A. Gallo, L. A. King and T. F. Jaramillo, ACS Appl. Energy Mater., 2020, 3, 12433–12446 CrossRef CAS
.
- Y. Zhong, X. H. Xia, F. Shi, J. Y. Zhan, J. P. Tu and H. J. Fan, Adv. Sci., 2016, 3, 1500286 CrossRef PubMed
.
- A. G. Yohannes, C. Lee, P. Talebi, D. H. Mok, M. Karamad, S. Back and S. Siahrostami, ACS Catal., 2023, 13, 9007–9017 CrossRef CAS
.
- R. Zeng, Y. Yang, X. Feng, H. Li, L. M. Gibbs, F. J. Disalvo and H. D. Abruña, Sci. Adv., 2022, 8, 1584 CrossRef PubMed
.
- Z. G. Yang, H. M. Xu, T. Y. Shuai, Q. N. Zhan, Z. J. Zhang, K. Huang, C. Dai and G. R. Li, Nanoscale, 2023, 15, 11777–11800 RSC
.
- K. R. Babu and G. Y. Guo, Phys. Rev. B, 2023, 108, 064505 CrossRef CAS
.
- H. Cui, G. Zhu, X. Liu, F. Liu, Y. Xie, C. Yang, T. Lin, H. Gu and F. Huang, Adv. Sci., 2015, 2, 1500126 CrossRef PubMed
.
- H. Shi, J. Qin, P. Lu, C. Dong, J. He, X. Chou, P. Das, J. Wang, L. Zhang and Z. S. Wu, Adv. Funct. Mater., 2021, 31, 2102314 CrossRef CAS
.
- M. E. Kreider, A. Gallo, S. Back, Y. Liu, S. Siahrostami, D. Nordlund, R. Sinclair, J. K. Nørskov, L. A. King and T. F. Jaramillo, ACS Appl. Mater. Interfaces, 2019, 11, 26863–26871 CrossRef CAS PubMed
.
-
M. E. Kreider, M. B. Stevens, A. Gallo, H. Abroshan, S. Back, S. Siahrostami, J. K. Nørskov and T. F. Jaramillo, 2024, US11929512
.
- S. Zhang, J. Wang, R. Wu, L. Liu, B. Pan and C. Liu, J. Alloys Compd., 2022, 900, 163506 CrossRef CAS
.
- L. Yu, Q. Zhu, S. Song, B. McElhenny, D. Wang, C. Wu, Z. Qin, J. Bao, Y. Yu, S. Chen and Z. Ren, Nat. Commun., 2019, 10, 1–10 CrossRef
.
- P. J. Hanumantha, M. K. Datta, K. S. Kadakia, D. H. Hong, S. J. Chung, M. C. Tam, J. A. Poston, A. Manivannan and P. N. Kumta, J. Electrochem. Soc., 2013, 160, A2195–A2206 CrossRef CAS
.
- N. Wang, S. Gan, Y. Mao, J. Xiao, C. Xu and T. Zhou, Phys. Chem. Chem. Phys., 2023, 26, 2449–2456 RSC
.
- W. W. Zhao, P. Bothra, Z. Lu, Y. Li, L. P. Mei, K. Liu, Z. Zhao, G. Chen, S. Back, S. Siahrostami, A. Kulkarni, J. K. Nørskov, M. Bajdich and Y. Cui, ACS Appl. Energy Mater., 2019, 2, 8605–8614 CrossRef CAS
.
- Z. Wang, Y. R. Zheng, I. Chorkendorff and J. K. Nørskov, ACS Energy Lett., 2020, 5, 2905–2908 CrossRef CAS
.
- G. T. K. K. Gunasooriya, M. E. Kreider, Y. Liu, J. A. Zamora Zeledón, Z. Wang, E. Valle, A. C. Yang, A. Gallo, R. Sinclair, M. B. Stevens, T. F. Jaramillo and J. K. Nørskov, ACS Nano, 2022, 16, 6334–6348 CrossRef CAS PubMed
.
- Y. Zhang, M. Wang, W. Zhu, M. Fang, M. Ma, F. Liao, H. Yang, T. Cheng, C. W. Pao, Y. C. Chang, Z. Hu, Q. Shao, M. Shao and Z. Kang, Angew. Chem., Int. Ed., 2023, 62, e202218924 CrossRef CAS PubMed
.
- A. Yatheendran, R. Rajan and N. Sandhyarani, Langmuir, 2023, 39, 11708–11719 CrossRef CAS PubMed
.
- Y. He, C. Qu, N. Ren and D. Liang, Chin. Chem. Lett., 2023, 109262 Search PubMed
.
- S. Jimenez-Villegas, S. R. Kelly and S. Siahrostami, J. Mater. Chem. A, 2021, 10, 6115–6121 RSC
.
- E. P. George, D. Raabe and R. O. Ritchie, Nat. Rev. Mater., 2019, 4, 515–534 CrossRef CAS
.
- T. Löffler, A. Ludwig, J. Rossmeisl and W. Schuhmann, Angew. Chem., Int. Ed., 2021, 60, 26894–26903 CrossRef PubMed
.
- T. Chen, C. Qiu, X. Zhang, H. Wang, J. Song, K. Zhang, T. Yang, Y. Zuo, Y. Yang, C. Gao, W. Xiao, Z. Jiang, Y. Wang, Y. Xiang and D. Xia, J. Am. Chem. Soc., 2024, 146, 1174–1184 CrossRef CAS PubMed
.
- Y. Chen, X. Zhan, S. L. A. Bueno, I. H. Shafei, H. M. Ashberry, K. Chatterjee, L. Xu, Y. Tang and S. E. Skrabalak, Nanoscale Horiz., 2021, 6, 231–237 RSC
.
- R. K. Pittkowski, C. M. Clausen, Q. Chen, D. Stoian, W. van Beek, J. Bucher, R. L. Welten, N. Schlegel, J. K. Mathiesen, T. M. Nielsen, J. Du, A. W. Rosenkranz, E. D. Bøjesen, J. Rossmeisl, K. M. Ø. Jensen and M. Arenz, EES Catal., 2023, 1, 950–960 RSC
.
- W. Li, Z. Zhao, J. Zhao, Y. Wang and X. Wang, J. Mater. Sci. Technol., 2024, 194, 236–246 CrossRef
.
- Q. Li, Y. X. Deng, Y. A. Zhu, Y. Li, Z. J. Sui, D. Chen and W. K. Yuan, Catal. Today, 2020, 347, 142–149 CrossRef CAS
.
- C. Y. Liu, L. Celiberti, R. Decker, K. Ruotsalainen, K. Siewierska, M. Kusch, R. P. Wang, D. J. Kim, I. I. Olaniyan, D. Di Castro, K. Tomiyasu, E. van der Minne, Y. A. Birkhölzer, E. M. Kiens, I. C. G. van den Bosch, K. N. Patil, C. Baeumer, G. Koster, M. Lazemi, F. M. F. de Groot, C. Dubourdieu, C. Franchini and A. Föhlisch, Commun. Phys., 2024, 7, 1–7 CrossRef
.
- I. Koriba, B. Lagoun, A. Guibadj, S. Belhadj, A. Ameur and A. Cheriet, Comput. Condens. Matter, 2021, 29, e00592 CrossRef
.
- V. A. Mints, K. L. Svane, J. Rossmeisl and M. Arenz, ACS Catal., 2024, 14, 6936–6944 CrossRef CAS
.
- K. L. Svane and J. Rossmeisl, Angew. Chem., 2022, 134, e202201146 CrossRef
.
- L. Du, M. Lv, J. Zhang, H. Song, D. Dang, Q. Liu, Z. Cui and S. Liao, ACS Appl. Energy Mater., 2020, 3, 5293–5300 CrossRef CAS
.
- M. Yuan, X. Gao, X. Gu, C. Dong, S. Wang, M. Wen and K. Zhang, J. Am. Ceram. Soc., 2023, 106, 1356–1368 CrossRef CAS
.
- T. Li, J. W. Morris, N. Nagasako, S. Kuramoto and D. C. Chrzan, Phys. Rev. Lett., 2007, 98, 105503 CrossRef PubMed
.
-
V. Levente, Computational Quantum Mechanics for Materials Engineers, Springer-Verlag London Limited, London, 2007 Search PubMed
.
-
S. Q. Wang and H. Q. Ye, Product Design and Manufacturing, Trans Tech Publications Ltd, 2011, 338, pp. 380–383 Search PubMed
.
- M. Rittiruam, J. Noppakhun, S. Setasuban, N. Aumnongpho, A. Sriwattana, S. Boonchuay, T. Saelee, C. Wangphon, A. Ektarawong, P. Chammingkwan, T. Taniike, S. Praserthdam and P. Praserthdam, Sci. Rep., 2022, 12, 16653 CrossRef PubMed
.
- J. K. Pedersen, C. M. Clausen, O. A. Krysiak, B. Xiao, T. A. A. Batchelor, T. Löffler, V. A. Mints, L. Banko, M. Arenz, A. Savan, W. Schuhmann, A. Ludwig and J. Rossmeisl, Angew. Chem., Int. Ed., 2021, 60, 24144–24152 CrossRef CAS PubMed
.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44 CrossRef CAS
.
- M. Cococcioni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef
.
- B. Himmetoglu, A. Floris, S. De Gironcoli and M. Cococcioni, Int. J. Quantum Chem., 2014, 114, 14–49 CrossRef CAS
.
- A. M. Patel, S. Ringe, S. Siahrostami, M. Bajdich, J. K. Nørskov and A. R. Kulkarni, J. Phys. Chem. C, 2018, 122, 29307–29318 CrossRef CAS
.
- E. B. Linscott, N. Colonna, R. De Gennaro, N. L. Nguyen, G. Borghi, A. Ferretti, I. Dabo and N. Marzari, J. Chem. Theory Comput., 2023, 19, 7097–7111 CrossRef CAS PubMed
.
- G. Kresse, A. Gil and P. Sautet, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 073401 CrossRef
.
- E. Macke, I. Timrov, N. Marzari and L. C. Ciacchi, arXiv, 2023, preprint, arXiv:2312.13580, DOI:10.48550/arXiv.2312.13580.
- P. Lv, W. Lv, D. Wu, G. Tang, X. Yan, Z. Lu and D. Ma, Phys. Rev. Appl., 2023, 19, 054094 CrossRef CAS
.
- J. Sun, A. Ruzsinszky and J. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed
.
- A. P. Bartók and J. R. Yates, J. Chem. Phys., 2019, 150, 161101 CrossRef PubMed
.
- M. Kothakonda, A. D. Kaplan, E. B. Isaacs, C. J. Bartel, J. W. Furness, J. Ning, C. Wolverton, J. P. Perdew and J. Sun, ACS Mater. Au, 2023, 3, 102–111 CrossRef CAS PubMed
.
- S. Swathilakshmi, R. Devi and G. Sai Gautam, J. Chem. Theory Comput., 2023, 19, 4202–4215 CrossRef CAS PubMed
.
- A. Groß and S. Sakong, Chem. Rev., 2022, 122, 10746–10776 CrossRef PubMed
.
- S. Siahrostami and A. Vojvodic, J. Phys. Chem. C, 2015, 119, 1032–1037 CrossRef CAS
.
- J. A. Gauthier, C. F. Dickens, L. D. Chen, A. D. Doyle and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 11455–11463 CrossRef CAS
.
- S. Ringe, N. G. Hörmann, H. Oberhofer and K. Reuter, Chem. Rev., 2022, 122, 10777–10820 CrossRef CAS PubMed
.
- H. H. Heenen, J. A. Gauthier, H. H. Kristoffersen, T. Ludwig and K. Chan, J. Chem. Phys., 2020, 152, 144703 CrossRef CAS PubMed
.
- S. R. Kelly, C. Kirk, K. Chan and J. K. Nørskov, J. Phys. Chem. C, 2020, 124, 14581–14591 CrossRef CAS
.
- J. L. Hübner, L. E. B. Lucchetti, H. N. Nong, D. I. Sharapa, B. Paul, M. Kroschel, J. Kang, D. Teschner, S. Behrens, F. Studt, A. Knop-Gericke, S. Siahrostami and P. Strasser, ACS Energy Lett., 2024, 9, 1331–1338 CrossRef PubMed
.
- Z. Duan and G. Henkelman, ACS Catal., 2019, 9, 5567–5573 CrossRef CAS
.
- H. Li, S. Kelly, D. Guevarra, Z. Wang, Y. Wang, J. A. Haber, M. Anand, G. T. K. K. Gunasooriya, C. S. Abraham, S. Vijay, J. M. Gregoire and J. K. Nørskov, Nat. Catal., 2021, 4, 463–468 CrossRef CAS
.
- C. D. Taylor, S. A. Wasileski, J. S. Filhol and M. Neurock, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165402 CrossRef
.
- X. Mao, L. Wang and Y. Li, ACS Catal., 2024, 14, 5429–5435 CrossRef CAS
.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072 CrossRef CAS
.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed
.
- K. T. Winther, M. J. Hoffmann, J. R. Boes, O. Mamun, M. Bajdich and T. Bligaard, Sci. Data, 2019, 6, 1–10 CrossRef PubMed
.
- T. Toyao, Z. Maeno, S. Takakusagi, T. Kamachi, I. Takigawa and K. I. Shimizu, ACS Catal., 2020, 10, 2260–2297 CrossRef CAS
.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 1–13 CrossRef
.
- G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, JPhys Mater., 2019, 2, 032001 CrossRef CAS
.
- W. Wang, X. Jiang, S. Tian, P. Liu, D. Dang, Y. Su, T. Lookman and J. Xie, npj Comput. Mater., 2022, 8, 1–12 CrossRef
.
-
Y. Dong, N. Kourtellis, B. Hammer and J. A. Lozano, Machine Learning and Knowledge Discovery in Databases, Springer Nature, Switzerland, 2021 Search PubMed
.
- L. Bandeira, H. Ferreira, J. M. de Almeida, A. Jardim de Paula and G. M. Dalpian, ACS Sustainable Chem. Eng., 2024, 12, 4411–4422 CrossRef CAS
.
- T. Gupta, M. Zaki, N. M. A. Krishnan and Mausam, npj Comput. Mater., 2022, 8, 1–11 CrossRef
.
- H. Sun, Y. Li, L. Gao, M. Chang, X. Jin, B. Li, Q. Xu, W. Liu, M. Zhou and X. Sun, J. Energy Chem., 2023, 81, 349–357 CrossRef CAS
.
- Y. Chen, H. Cui, Q. Jiang, X. Bai, P. Shan, Z. Jia, S. Lu, P. Song, R. Feng, Q. Kang, Z. Liang and H. Yuan, ACS Appl. Nano Mater., 2023, 6, 7694–7703 CrossRef CAS
.
- N. Omidvar, S. H. Wang, Y. Huang, H. S. Pillai, A. Athawale, S. Wang, L. E. K. Achenie and H. Xin, Electrochem. Sci. Adv., 2024, 1–12 Search PubMed
.
- R. A. Flores, C. Paolucci, K. T. Winther, A. Jain, J. A. G. Torres, M. Aykol, J. Montoya, J. K. Nørskov, M. Bajdich and T. Bligaard, Chem. Mater., 2020, 32, 5854–5863 CrossRef CAS
.
- X. Zhang, Z. Wang, A. M. Lawan, J. Wang, C. Y. Hsieh, C. Duan, C. H. Pang, P. K. Chu, X. F. Yu and H. Zhao, InfoMat, 2023, 5, e12406 CrossRef CAS
.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed
.
- M. Suvarna, A. C. Vaucher, S. Mitchell, T. Laino and J. Pérez-Ramírez, Nat. Commun., 2023, 14, 7964 CrossRef CAS PubMed
.
-
N. Qin, L. Wei and H. Chen, Insights into the development of electrocatalysts based on information extracted from literatures using natural language processing, 2024 Search PubMed
.
- A. Muthukkumaran, S. Raghunathan, A. Ravichandran and R. Rengaswamy, AIChE J., 2023, 69, e18068 CrossRef CAS
.
- H. Touvron, T. Lavril, G. Izacard, X. Martinet, M.-A. Lachaux, T. Lacroix, B. Rozière, N. Goyal, E. Hambro, F. Azhar, A. Rodriguez, A. Joulin, E. Grave and G. Lample, arXiv, 2023, preprint, arXiv: 2302.13971 DOI:10.48550/arXiv.2302.13971.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ey00104d |
| This journal is © The Royal Society of Chemistry 2024 |