Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Transfer learning of hyperparameters for fast construction of anisotropic GPR models: design and application to the machine-learned force field FFLUX†
Bienfait K. Isamura and
Paul L. A. Popelier *
*
Department of Chemistry, The University of Manchester, Manchester, M13 9PL, UK. E-mail: paul.popelier@manchester.ac.uk
First published on 3rd September 2024
Abstract
The polarisable machine-learned force field FFLUX requires pre-trained anisotropic Gaussian process regression (GPR) models of atomic energies and multipole moments to propagate unbiased molecular dynamics simulations. The outcome of FFLUX simulations is highly dependent on the predictive accuracy of the underlying models whose training entails determining the optimal set of model hyperparameters. Unfortunately, traditional direct learning (DL) procedures do not scale well on this task, especially when the hyperparameter search is initiated from a (set of) random guess solution(s). Additionally, the complexity of the hyperparameter space (HS) increases with the number of geometrical input features, at least for anisotropic kernels, making the optimization of hyperparameters even more challenging. In this study, we propose a transfer learning (TL) protocol that accelerates the training process of anisotropic GPR models by facilitating access to promising regions of the HS. The protocol is based on a seeding–relaxation mechanism in which an excellent guess solution is identified by rapidly building one or several small source models over a subset of the target training set before readjusting the previous guess over the entire set. We demonstrate the performance of this protocol by building and assessing the performance of DL and TL models of atomic energies and charges in various conformations of benzene, ethanol, formic acid dimer and the drug fomepizole. Our experiments suggest that TL models can be built one order of magnitude faster while preserving the quality of their DL analogs. Most importantly, when deployed in FFLUX simulations, TL models compete with or even outperform their DL analogs when it comes to performing FFLUX geometry optimization and computing harmonic vibrational modes.
1. Introduction
The artificial intelligence revolution has recently caused major paradigm shifts in many research fields resulting in the promotion of various unconventional data-driven approaches. In computational chemistry, the integration of traditional simulation techniques with machine learning has given rise to a new class of unconventional force fields known as machine-learned potentials (MLPs).1–3 These next-generation force fields find their motivation in the necessity to circumvent the exorbitant cost of on-the-fly electronic structure calculations.In essence, MLPs aim to reach the accuracy of high-level quantum mechanics approaches at a cost comparable to that of classic force fields. They owe their current success to the predictive capability and efficiency of the underlying machine learning (ML) models, which are trained on high-quality electronic energies and/or forces. Once trained, these models can be deployed in simulations to rapidly evaluate the same properties on previously unseen compounds. The development of various interfaces with existing computational packages has facilitated the deployment of MLPs in simulations,4 enabling these packages to accomplish fast and accurate ML-aided geometry optimizations and MD simulations.5–7
FFLUX is a polarisable MLP that relies on pre-trained Gaussian process regression (GPR) models of atomic energies and multipole moments to action molecular dynamics (MD) simulations.8 This next-generation force field has been successfully utilized to investigate the bulk properties of liquid water9 and the polymorphism of formamide,10 to cite only these examples. The outcome of FFLUX simulations depends heavily on the predictive capability of the underlying models, which is in turn dictated by the choice of model hyperparameters. Regrettably, optimal hyperparameters are never known in advance. Instead, they must be determined by navigating the landscape of a given loss function. Because tiny changes in the hyperparameters’ values can cause disproportional fluctuations in the quality of a model, it is important that optimal hyperparameters be accurately determined. Unfortunately, the exercise of fine-tuning GPR model hyperparameters does not scale well with the size of the training set, namely ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N3) in terms of computational complexity and
(N3) in terms of computational complexity and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N2) for memory. Even more annoying is the complexity of the hyperparameter space, which usually blows up with the number of input features, at least for anisotropic kernels, making it even more challenging to locate optimal kernel parameters within a reasonable amount of time.
(N2) for memory. Even more annoying is the complexity of the hyperparameter space, which usually blows up with the number of input features, at least for anisotropic kernels, making it even more challenging to locate optimal kernel parameters within a reasonable amount of time.
The unfavorable scaling of GPs is the main bottleneck discouraging their application to large datasets. Several solutions have been proposed to address this problem. For brevity, we will only mention the two most conceptually appealing solutions. The first solution consists of applying so-called reduced-rank approximations.11 These sparse GPs have been proven to considerably speed up the training process of GPR models while reducing the memory requirement. These schemes attempt to avoid any explicit manipulation (especially inversion) of the full covariance matrix but work on projections in different subspaces. Popular sparse GP algorithms exhibit ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N2N) computational complexity and
(N2N) computational complexity and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (MN) storage demand, with M (M < N) being the number of active points.12 Despite this outstanding improvement, these schemes often fail to preserve the desired predictive accuracy of full GP inference. This is because the selection of the so-called “inducing points, support points, pseudo-points or even active points is more challenging than it may seem and when inappropriately done, might have unexpected and usually disagreeable repercussions on the sparsity, numerical stability, and predictive accuracy of sparse GPs. Furthermore, as long as the selection of active/pseudo-points is coupled with the optimization of hyperparameters, there are more variables to fit, which (unless carefully handled) increases the risk of overfitting as recognized in the case of sparse spectrum GPR.13
(MN) storage demand, with M (M < N) being the number of active points.12 Despite this outstanding improvement, these schemes often fail to preserve the desired predictive accuracy of full GP inference. This is because the selection of the so-called “inducing points, support points, pseudo-points or even active points is more challenging than it may seem and when inappropriately done, might have unexpected and usually disagreeable repercussions on the sparsity, numerical stability, and predictive accuracy of sparse GPs. Furthermore, as long as the selection of active/pseudo-points is coupled with the optimization of hyperparameters, there are more variables to fit, which (unless carefully handled) increases the risk of overfitting as recognized in the case of sparse spectrum GPR.13
The second solution exploits the nature of the solver used to invert the covariance matrix. Indeed, there is empirical proof that GPR models can be trained more effectively if an iterative solver, like a preconditioned conjugate gradient, were used in place of the usual Cholesky decomposition, which is a direct solver.14,15 It is true that iterative solvers not only eliminate the need for storing the entire covariance matrix but also reduce the complexity from ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N3) to
(N3) to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N2). However, since their convergence is never guaranteed, even when boosted by tailored preconditioners, it is not always clear how much the hyperparameters, the regression weights, and subsequently the quality of the final model have been compromised. Therefore, although elegant and recommended for extremely large datasets, both sparse GPs and iterative solvers only offer a tangible advantage when memory allocation is a concern. Otherwise, to preserve the outstanding and desired predictive capability of exact GP inference on (relatively) big yet manageable datasets, alternative strategies for fast training of full GPR models employing direct solvers must be promoted.16,17
(N2). However, since their convergence is never guaranteed, even when boosted by tailored preconditioners, it is not always clear how much the hyperparameters, the regression weights, and subsequently the quality of the final model have been compromised. Therefore, although elegant and recommended for extremely large datasets, both sparse GPs and iterative solvers only offer a tangible advantage when memory allocation is a concern. Otherwise, to preserve the outstanding and desired predictive capability of exact GP inference on (relatively) big yet manageable datasets, alternative strategies for fast training of full GPR models employing direct solvers must be promoted.16,17
Assuming the covariance matrix can fit in memory, it is right to think that GPR models can be built more efficiently by minimizing the number of times the full covariance matrix must be inverted when optimizing model GPR hyperparameters. One way to achieve this is to ensure that the tuning of a target model is started from an excellent, yet easily accessible, set of hyperparameters. Having an excellent guess solution, as opposed to random initialization, is expected to facilitate the location of promising areas of the hyperparameter space (HS) and, as a result, to naturally reduce the number of iterations required to locate a reasonable estimation of the optimal hyperparameters. However, since each HS is unique, finding a good starting set of hyperparameters is never trivial, and may become impossible if one has to set it up manually. Here we propose a protocol that systematically solves the problem, based on the concept of “transfer of knowledge (hyperparameters)” or transfer learning (TL).
The current proof-of-concept study aims (i) to demonstrate the transferability of hyperparameters in anisotropic GP regression, and (ii) to document the balance between the predictive accuracy and building cost of atomic GPR models trained via direct and transfer learning of hyperparameters. The protocol presented in Section 2.4.1 has been implemented in our in-house program FEREBUS.18–20 The latter program is a GPR engine written in free format modern Fortran, and accelerated via Open Multi-Processing. We claim the universality of this TL protocol as it does not impose any specific requirement in terms of datasets. The only design choices are that (i) the covariance matrix fits in memory, (ii) each GPR model is trained to reproduce a unique target property (single-objective GPR), and (iii) the chosen kernel is anisotropic and defined in terms of automatic relevance determination. The third design choice can be justified by evoking the well-known higher flexibility and superior predictive capability of anisotropic GPR models as compared to their isotropic analogs.21
The protocol proposed here follows a two-phase seeding–relaxation mechanism in which an excellent guess solution is located by training one (or possibly several) source model(s) over a subset of the (target) training set, before relaxing that guess for a few iterations on the entire training set. The protocol has been tested by building and deploying both direct and TL models in FFLUX simulations. These models were trained on the electronic energies and charges of topological quantum atoms in various conformations of benzene (BZ), formic acid dimer (FAD), ethanol (ETL), and fomepizole (FPL) (4-methylpyrazole). As in previous studies from our group, we rely on quantum chemical topology (QCT)22 tools to realize an exhaustive real-space partitioning of molecular properties into atomic/local contributions. However, unlike the usual assessment of our GPR models based on atom-wise predictions,23,24 we focus here on the ability of these atomic GPR models to reconstruct molecular energies and charges. This allows us to obtain an overall appreciation of the quality of all atomic models without having to explicitly look at each of them.
We show (i) that TL of hyperparameters accelerates the training process of anisotropic GPR models while preserving the predictive accuracy of direct models, (ii) that frozen-seed (FS) TL models, i.e. TL modes whose guess solution (seed) was not relaxed, can suffer from sub-optimality when the source dataset is small and non-representative of the target dataset and (iii) that TL models exhibit competitive performance to their DL analogs when deployed in FFLUX simulations.
The remainder of this paper is organized as follows: in Section 2, we cover the theory this work is built on. Computational details, including dataset generation, model construction, optimization settings, and FFLUX simulation details are presented in Section 3. Section 4 is devoted to presenting and discussing our results, focusing on the learning capability of DL models and the comparison between DL and TL models. Finally, we reiterate the main findings in the conclusion.
2. Theory
2.1. FFLUX: a polarisable QCT-based force field
The logical premise underlying the architecture of most MLPs is that the total energy E of a molecular system can be decomposed into a sum of local contributions Ei, i.e.,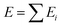 . This partitioning procedure is either automated within the ML architecture25,26 or carefully performed before training.8 In the first case, one obtains a collection of “sites” energies that might fluctuate in unexpected ways depending on the learning architecture. Unlike pre-calculated, physically justified atomic energies, these quantities may not reflect any well-defined physical quantity. The second option is the choice of the polarisable force field FFLUX. The latter relies on atomic GPR models of justifiable atomic energies and multipole moments.
. This partitioning procedure is either automated within the ML architecture25,26 or carefully performed before training.8 In the first case, one obtains a collection of “sites” energies that might fluctuate in unexpected ways depending on the learning architecture. Unlike pre-calculated, physically justified atomic energies, these quantities may not reflect any well-defined physical quantity. The second option is the choice of the polarisable force field FFLUX. The latter relies on atomic GPR models of justifiable atomic energies and multipole moments.
The reference (“exact”) atomic energies and multipole moments that our GPR models are trained on are determined using a combination of two QCT methods: the quantum theory of atoms in molecules (QTAIM)27 and the interacting quantum atoms (IQA)28 energy decomposition method.
On the one hand, QTAIM allows molecules and clusters to be compartmented into non-overlapping regions/basins known as topological quantum atoms. Each such quantum atom Ω is surrounded by an interatomic surface S(Ω) characterized by a zero flux of the gradient vector field of the electron density ∇ρ(r).
| ∇ρ(r)·n(r) = 0 for all points on S | (1) |
On the other hand, the IQA29 methodology exploits the first and second-order reduced density matrices to exhaustively decompose the total energy of a molecular system into atomic contributions EAIQA. Each atomic IQA energy encloses an intra-atomic (EAintra) and an interatomic (EABintra) component (eqn (2)). The latter components can be further partitioned into finer contributions as shown in eqn (3) and (4).
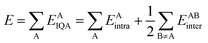 | (2) |
| EAintra = TA + VAne + VAee | (3) |
| VABinter = VABnn + VABne +VABen + VABee | (4) |
The fact that VABee can be split into a Coulombic (VABcout) and an exchange–correlation (VABxc) energy term makes it possible to rewrite VABinter in a more compact way as the sum of a purely classical (VABcl) and an exchange–correlation term (VABxc).
| VABinter = VABcl + VABxc | (5) |
Our in-house MD simulator DL-FFLUX8 utilizes flexible multipole moments (up to Q4m) to describe long-range electrostatic interactions, while short-range interactions are captured within EIQA. Only EIQA models are required to action FFLUX simulations of single molecules in the gas phase such as the ones reported in this study.
2.2. Gaussian process regression
Gaussian process (GP) regression is a non-parametric interpolation technique that provides both accurate predictions and reliable estimates of the uncertainty associated with each prediction. The approach can be derived from Bayesian statistics building on the concept of “Gaussian processes”. For the sake of brevity, we recommend to interested readers the seminal book by Rasmussen and Williams.11Training a GPR model over a dataset of D = {X, y} made of N observations is a challenging task that requires finding the optimal set of model hyperparameters (![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e12d.gif) θk) and the regularisation noise (σn2). Here we rely on the iterative hold-out cross-validation (IHOCV)20 approach to determine these hyperparameters. The IHOCV protocol proceeds by minimizing the predictive root-mean-square error of intermediary models over a sufficiently large internal validation set.
θk) and the regularisation noise (σn2). Here we rely on the iterative hold-out cross-validation (IHOCV)20 approach to determine these hyperparameters. The IHOCV protocol proceeds by minimizing the predictive root-mean-square error of intermediary models over a sufficiently large internal validation set.
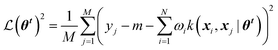 | (6) |
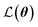 is the loss function, m is the prior mean function of the GP, θt is a candidate solution (set of temporary hyperparameters), and M and N are the number of validation and training geometries, respectively. Without any loss of generality, m is chosen here to be constant and equal to the arithmetic mean of the target property values
is the loss function, m is the prior mean function of the GP, θt is a candidate solution (set of temporary hyperparameters), and M and N are the number of validation and training geometries, respectively. Without any loss of generality, m is chosen here to be constant and equal to the arithmetic mean of the target property values 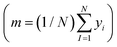 . Such a mean function guarantees the physicality of all predictions30 even in the extrapolation regime.
. Such a mean function guarantees the physicality of all predictions30 even in the extrapolation regime.
The coefficients ωi in eqn (6) are regression weights. These parameters are collected in the weights vector ω calculated as shown in eqn (7), where ym is a mean-shifted vector of target properties, i.e.y − 1m, and KXX is the covariance matrix defined in eqn (8),
| ω = KXX−1ym | (7) |
| Kij = k(xi, xj|θk) + δijσn2 | (8) |
Every data point (geometry) in the input space is encoded in a vector of fixed length x using the so-called ALF (atomic local frame) representation,31 while similarities between geometries in the ALF space are described using the composite kernel defined in eqn (9),
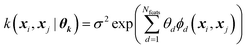 | (9) |
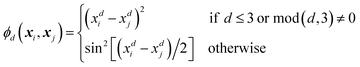 | (10) |
Assuming a GPR model has already been trained, predictions can be made for any new geometry x* using eqn (11),
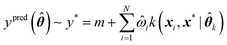 | (11) |
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e12d.gif) k is a set of optimal kernel parameters and
k is a set of optimal kernel parameters and ![[small omega, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b4.gif) i is the optimal regression weight associated with the ith training geometry.
i is the optimal regression weight associated with the ith training geometry.
2.3. Context and related work
The concept of transfer learning (TL) has a long history in the deep learning community.32,33 Despite the peculiarities of each proposed TL protocol, they are all characterized by the sharing of knowledge between domains and corresponding tasks. A typical scenario is one in which prior knowledge about one or several source tasks is leveraged to improve the learning process of a target learner. This setting deviates from the direct or traditional learning paradigm where models are built directly on the target domain.Transfer learning has shown tremendous success in numerous fields, including computational chemistry,34 computer vision,35 and natural language processing,36 to cite only a few. The TL idea is often resorted to when it comes to (i) improving the predictive capability of (target) regression models and/or (ii) accelerating their training process. The concept has allowed computational chemists to address the scarcity of high-quality data, such as CCSD(T) energies and atomic forces. In general, a big source model, most often a neural network, is trained on a myriad of lower-quality data, and the knowledge (weights and biases) accumulated into the previous source model is leveraged to reduce the risk of overfitting the small high-quality training data.37 The training (readjustment) of the target model thus benefits from the existing knowledge, such as physical trends and positions of stationary points, already captured by the large source model. Most importantly, only part of the ML architecture has to be updated, which can save a lot of CPU time.
Rather than focusing on explicitly improving the predictive capability of a given model, our TL protocol (presented in the next paragraph) aims at speeding up the training process of a large target anisotropic GPR model while maintaining the quality of an equivalent but bad scaling DL model. By equivalent we mean a model trained on the same (number of) geometries. Our protocol accelerates the construction of target GPR models by transferring guess hyperparameters from one (or possibly several) smaller source models.
Related to our work are two previous papers that need to be mentioned here. In the first paper,38 the authors state that anisotropic kernel parameters optimized on a small dataset could be used unchanged to build a final model over a bigger training set. This argument translates to what we have re-branded “frozen-seed” TL (see Section 2.4.1). Although it makes sense, this assumption ignores the discrepancies between the source and target domains. In some contexts, this can lead to a significant loss of accuracy as compared to an equivalent DL model. To prevent this, our approach allows the hyperparameters learned on the source domain to relax on the target training set, for a few iterations.
The second paper dates back to 2017.39 In this work, different authors apply the golden-section search algorithm40 to locate an isotropic approximate solution, which they then utilize as the starting point for a gradient-based optimization in the actual anisotropic space. Their gradient-enhanced kriging was shown to achieve better results as compared to random initialization. Like our protocol, their workflow involves two phases. However, unlike us, they choose to unjustifiably ignore the heterogeneity inherent to the input space during the first step, yet without prior feature scaling. Furthermore, their protocol does not incorporate any regularisation noise in the first phase, a choice that exposes it to high risks of numerical instability.40 In contrast, our protocol works entirely in the actual HS, with tuneable regularisation noise.
2.4. Transfer learning of hyperparameters
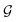 and the relaxation phase
and the relaxation phase 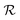 .
.where {θr} is a random set of candidate solutions, θ0 and
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e12d.gif) are the guess and the best achievable (optimal) solutions, respectively.
are the guess and the best achievable (optimal) solutions, respectively.
Two types of models are involved in the design of the protocol: a source model and a target model. The source model is trained on a subset S of the target dataset T. We propose the name knowledge compression coefficient η for the ratio between the sizes of the datasets S and T. A second control parameter called relaxation weight ζ is also defined as the ratio between the number of relaxation iterations χ and the total number of iterations τ.
| η = |S|/|T| | (12) |
| ζ = χ/τ | (13) |
The notation TLζη is introduced to denote a transfer learning task defined by the two control parameters η and ζ. Depending on the value of ζ , one can distinguish two special cases: (i) ζ = 1 and (ii) ζ = 0 . The first case leads to fully seeded TL, while the second case gives rise to a class of unrelaxed models that we have coined frozen-seed transfer learning (FS-TL) models. The notation FS-TLη will sometimes be used to denote FS-TL models.
Guessing phase
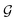 .
.
Step 1: subsampling. A source training set S is generated by random subsampling of the target training set T. Besides random selection, FEREBUS is equipped with two enhanced sampling techniques, namely passive and stratified sampling. Both techniques have been widely discussed elsewhere.41
Step 2: training of source model. Once the dataset S has been generated, a source model is trained over it using our grey wolf optimizer described in Section 2.5. For a single-source TL task, this process starts with an initial pool of random solutions {θr} and returns a unique guess solution (θ0). In the case of multisource TL, Ns. solutions are collected and the transfer of these solutions to the target model is briefly discussed in Section 1 of the ESI.†
Relaxation phase
 .
.
Step 3: guess perturbation. For single-source TL such as those examined in this work, only one guess solution is available at the end of phase
 . Since our metaheuristic optimizer requires W agents (candidate solutions) to scrutinize the HS, with W > 3, phase
. Since our metaheuristic optimizer requires W agents (candidate solutions) to scrutinize the HS, with W > 3, phase  starts by re-populating the matrix P of candidate solutions. For this purpose, we first transfer θ0 to P, then generate the remaining W − 1 candidate solutions (θ0pert) via restricted small random walks around θ0. The dth component of each perturbed solution is computed using eqn (14),
starts by re-populating the matrix P of candidate solutions. For this purpose, we first transfer θ0 to P, then generate the remaining W − 1 candidate solutions (θ0pert) via restricted small random walks around θ0. The dth component of each perturbed solution is computed using eqn (14),| θ0pert,d = θ0d (1 + rmaxε) | (14) |
By default, rmax is set to 0.25 (the same value is used in this work). However, the optimal value of this parameter is problem-dependent and should be adjusted such that the θ0pert solutions are of similar to better quality than θ0. Large rmax values may lead to solutions of poor quality (situated far from θ0), while very small values can restrict the accessible region of the HS. We recommend that FEREBUS users perform a grid search between 0.10 and 0.50 (step of 0.05) to find the most appropriate value for their system and choose the value delivering the best models.
Step 4: training of target model. Once P is available, the algorithm can proceed to the final step, i.e., training the target model.
 and
and 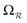 ).
).
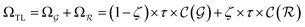 | (15) |
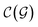 and
and 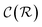 are respectively the complexity/cost of a single iteration within the guessing and relaxation
are respectively the complexity/cost of a single iteration within the guessing and relaxation 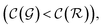 and τ the total number of iterations. By default, phase
and τ the total number of iterations. By default, phase 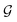 lasts (1 −ζ) × τ iterations, while phase
lasts (1 −ζ) × τ iterations, while phase 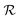 is propagated for ζ × τ iterations. This behavior can be changed by setting the full_seeding directive to 1, in which case the guessing phase runs over τ iterations.
is propagated for ζ × τ iterations. This behavior can be changed by setting the full_seeding directive to 1, in which case the guessing phase runs over τ iterations.In general, 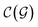 and
and 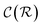 are dominated by the inversion of the associated covariance matrices, which scale as
are dominated by the inversion of the associated covariance matrices, which scale as 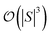 and
and 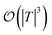 , respectively. Keeping in mind that
, respectively. Keeping in mind that 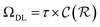 and neglecting input/output delays one obtains:
and neglecting input/output delays one obtains:
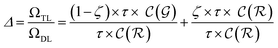 | (16) |
The previous equation can be written more concisely as:
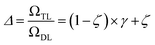 | (17) |
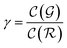 is the relative complexity of a single training iteration in the guess and relaxation phases of a TLζη task.
is the relative complexity of a single training iteration in the guess and relaxation phases of a TLζη task.
We distinguish two asymptotic cases depending on the choice of η: (i) |S| = |T| and (ii) |S| ≪ |T|. In the first case, γ = 1 such that Δ = 1. This implies that the TL protocol reduces to DL when S is set to be the same as T (η = 1). In the second case, γ ∼ 0 and Δ → ζ. In this scenario, the expected speed-up (Δ−1) is upper-bounded by ζ−1, the inverse of the relaxation weight. In between these two extreme cases, the TL protocol guarantees acceleration if and only if Δ < 1, i.e. from eqn (17),
| (1 − ζ) × γ + ζ < 1 ⇒ γ < 1 | (18) |
The previous condition is always true in the case of single-source TLζη tasks. This is because S⊂T implies that 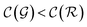 and γ < 1. However, in the case of multi-source TLζη tasks, the speed-up condition becomes:
and γ < 1. However, in the case of multi-source TLζη tasks, the speed-up condition becomes:
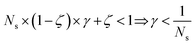 | (19) |
A final scenario to consider here is when the full_seeding flag is activated. This flag sets ζ to 0 in the guessing phase only, leading to a total of (1 + ζ) × τ iterations including τ steps in phase 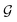 and ζ × τ steps in phase
and ζ × τ steps in phase 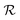 . By setting ζ to 0 in the first right-hand term of eqn (16), the speed-up conditions for single-source and multi-source TL models become γ < 1 − ζ and γ < (1 − ζ)/Ns, respectively.
. By setting ζ to 0 in the first right-hand term of eqn (16), the speed-up conditions for single-source and multi-source TL models become γ < 1 − ζ and γ < (1 − ζ)/Ns, respectively.
2.5. GWO-RUHL: an enhanced grey wolf optimizer
The choice of optimizer is a determinant factor of the performance of our TL protocol. FEREBUS relies on our recently reported enhanced grey wolf optimizer (GWO-RUHL)42 because of its excellent exploration and exploitation capabilities.Like vanilla GWO,43 the GWO-RUHL algorithm is a metaheuristic optimizer inspired by the predation mechanism and leadership hierarchy of grey wolves. This optimizer utilizes a team of W agents to scrutinize the HS. Every agent is encoded as a vector of the same dimension as the HS and constitutes a candidate solution. At the end of each iteration, all candidate solutions are ranked in ascending order of proximity to the optimal solution. The α, β, and δ agents are the best solutions or leaders. Their positions serve to orient the movement of non-leader solutions (called ω solutions) toward more promising regions of the search space. The position of an ω solution j is updated following eqn (20)–(22),
| Dl,d = |Cl,d·θl,d(t) − θj,d(t)| | (20) |
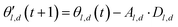 | (21) |
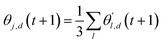 | (22) |
| Al,d(t) = 2a(t)r1 − a(t) | (23) |
| Cl,d(t) = 2a(t)r2 | (24) |
Improving over vanilla GWO, our GWO-RUHL(n,p) algorithm (n and p are explained below) accounts for the natural desire of ω wolves to occupy high-ranked positions in the leadership hierarchy. This is achieved by inserting in the previous search mechanism a new operator Û, which acts on the current population P and promotes a certain number n of ω solutions toward new positions situated in the vicinity of the centroid of the three leaders (positions believed to host better solutions). This operation, ÛP = P′, is repeated every p iteration and each promoted (lucky) solution is calculated using eqn (25),
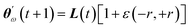 | (25) |
3. Computational details
3.1. Conformational sampling
The initial datasets were made of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 geometries of each of the four molecules of interest. Geometries of BZ and ETL were retrieved from the original MD17 database,44 while those of FAD and FPL were obtained through unbiased semi-empirical molecular dynamics (USEMD) simulations.
000 geometries of each of the four molecules of interest. Geometries of BZ and ETL were retrieved from the original MD17 database,44 while those of FAD and FPL were obtained through unbiased semi-empirical molecular dynamics (USEMD) simulations.
USEMD simulations were performed in the gas phase without periodic boundary conditions using the GFN2-xTB method45 as implemented in the atomic simulation environment (ASE) Python package.4 Each simulation was performed in the canonical NVT ensemble at 300 K using the Langevin thermostat with a friction coefficient of 0.01 fs−1. All simulations were propagated for 1 ns with a timestep of 1 fs. Snapshots were retrieved every 100 fs leading to a generous population of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 geometries. Fig. 2 shows the conformational space sampling of each molecule of interest.
000 geometries. Fig. 2 shows the conformational space sampling of each molecule of interest.
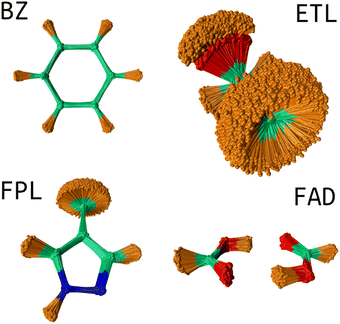 | ||
| Fig. 2 Conformational space sampling: the overlaid geometries were rotated about the first trajectory frame using the Kabsch algorithm.46 This image shows the pronounced flexibility of the ETL molecule allowing for full rotation of the CH3 and OH groups. The sampled conformation space of FAD involves stretching of the two hydrogen bonds and movements about the plane of the molecule. BZ is very rigid while FPL shows fairly considerable structural fluctuations around the CH3, CH and NH groups. | ||
3.2. QTAIM/IQA calculations, featurisation, and dataset filtering
Once collected, all the geometries were passed to our in-house ICHOR31 package. The latter is a Python package that automates the calculation of both input features and target properties. Wavefunctions were extracted via single-point calculations at B3LYP/6-31+G(d,p) (FAD and FPL) and B3LYP/aug-cc-pVTZ (BZ and ETL) levels of theory using GAUSSIAN16.47 Each wavefunction was then processed by AIMAll1948 to compute the atomic QTAIM/IQA properties using equations described in Section 2.1. Concomitantly, each geometry was encoded as a vector of fixed length using the so-called atomic local frame (ALF) molecular descriptor.31 The resulting features were combined with the target properties (IQA and Q00), leading to an initial database that was later filtered by removing all geometries for which the molecular energy and charge could not be reconstructed within margins of 1 kJ mol−1 and 1 me. The filtered database was randomly split into training, validation, and test sets. A summary of the filtering results is provided in Section 2 of the ESI.†3.3. Model construction and optimization settings
All atomic GPR models were trained following the IHOCV protocol using 8 cores on compute nodes equipped with Cascade Lake Xeon Gold 6230 CPUs of 2.10 GHz clock speed each. The smallest DL models (1000 training geometries) were also retrained using 1, 4, 12, 16 and 20 cores to assess the effect of computing resources on the building cost.Preliminary experiments were conducted to determine the validation set size and the number of candidate solutions that provide a reasonable trade-off before accuracy, cost, and consistency of predictive metrics upon successive runs. The results obtained for the smallest direct learning (DL) models suggested that a validation set of 500 geometries produced the best models. All the models were tested on 1000 geometries.
Optimization runs were carried out for a maximum of τ = 200 iterations using a set of 50 active agents identified among an initial random population of 500 candidate solutions thrown on the HS. The following control parameters were chosen for the GWO-RUHL(n,p) algorithm: amax = 2.0 (except in phase  of all TLζη tasks where amax was set to 1.0 to promote the exploitation/intensification of the HS43), r = 0.20, n = 5 and p = 5. As per n and p values, 5 non-leader solutions were promoted every 5 iterations toward promising regions of the HS, whose boundaries were defined as [0.0,3.0] and [10−14,10−4] for the kernel parameters and regularisation noise, respectively. To avoid unphysical solutions, FEREBUS makes sure all solutions crossing the walls of the previous HS are randomly reinitialized inside the boundaries of the HS during the optimization process.49 All FEREBUS control parameters referred to in this paper are described in Table S1 of the ESI.†
of all TLζη tasks where amax was set to 1.0 to promote the exploitation/intensification of the HS43), r = 0.20, n = 5 and p = 5. As per n and p values, 5 non-leader solutions were promoted every 5 iterations toward promising regions of the HS, whose boundaries were defined as [0.0,3.0] and [10−14,10−4] for the kernel parameters and regularisation noise, respectively. To avoid unphysical solutions, FEREBUS makes sure all solutions crossing the walls of the previous HS are randomly reinitialized inside the boundaries of the HS during the optimization process.49 All FEREBUS control parameters referred to in this paper are described in Table S1 of the ESI.†
Before we compare the performance and training costs of DL and TL models, we took care to first assess the training cost and learning capability of DL models. For this purpose, we monitored the training timings and predictive mean absolute errors (MAEs) of each DL model as we varied several factors, including the number of training points (from 1000 to 8000 geometries) and the validation set size (between 25 and 500 geometries). We made sure these datasets did not overlap with each other or with the test set.
After careful examination of DL models, we moved on to building and assessing the performance of TL models. Single-source TL models were built by targeting the largest DL models. For each atom and target property, we trained 9 = 3 × 3 different single-source TL models for all combinations of η (0.00, 0.10, 0.25) and ζ (0.00, 0.05, 0.10) parameters. Unless otherwise stated, (i) guess solutions were perturbed using a maximum deviation parameter rmax of 0.25, and (ii) no prior scaling of the features and target properties was applied.
By design, FEREBUS builds atomic GPR models. However, molecular predictions can be easily obtained through reconstruction using eqn (26),
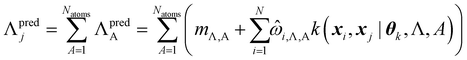 | (26) |
3.4. Normal mode calculations
Normal mode calculations were carried out for each molecule of interest. The GAUSSIAN optimized geometry (at the reference level of theory specified in Section 3.2) was slightly perturbed by moving each atom 0.01 Å back and forth in the XYZ directions. Then, atomic forces were computed using analytical formulae implemented in DL_FFLUX. Using the previous atomic forces and the perturbed geometries, normal modes, and vibrational frequencies were computed using the finite-difference method implemented in Phonopy.50 These calculations involved the diagonalization of a mass-weighted Hessian matrix whose eigenvectors and eigenvalues identify with the normal modes and vibrational frequencies, respectively.3.5. Geometry optimisation
The program DL_FFLUX is built on DL_POLY 451,52 and shares many of its routines. One of these is the “Zero Kelvin” optimizer thanks to which DL_FFLUX can perform geometry optimization calculations by maintaining the velocity of atoms below 10 K during a short simulation. In this way, the movement of atoms follows the direction of calculated forces and torques. DL_FFLUX geometry optimization calculations were propagated for 2 ps with a timestep of 1 fs in the NVT ensemble using the Nosé–Hoover thermostat and a relaxation time of 0.2 ps. The starting geometries q0 were carefully generated by perturbing the GAUSSIAN minimum (qmin) along its normal modes. For each normal mode q, q0 was defined as shown in eqn (27),| q0 = qmin + DF × q | (27) |
4. Results and discussion
4.1. Performance of DL models
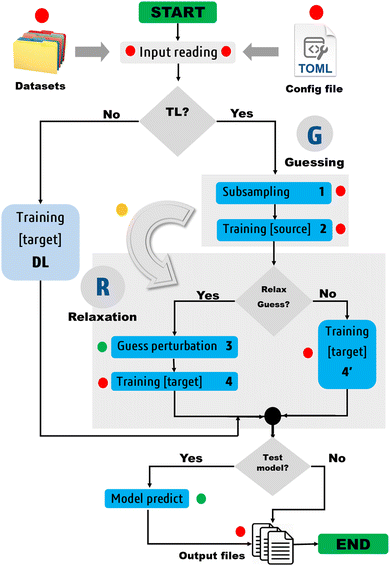
Fig. 3 depicts the molecular learning curves of DL models. The corresponding element-wise learning curves and molecular learning S-curves are collected in Section 5 of the ESI.† Notice that the curves in Fig. 3 are well-behaved53 in the sense that the models progressively and consistently improve their generalization aptitude as we increase the training set size. Such learning curves are characteristics of well-posed learning problems and are sometimes called monotonic54 curves. Theoretical studies on the link between GP assumptions and learning behavior suggest that ill-behaved learning curves (with bumps) could be indicative of a misspecified GP.55
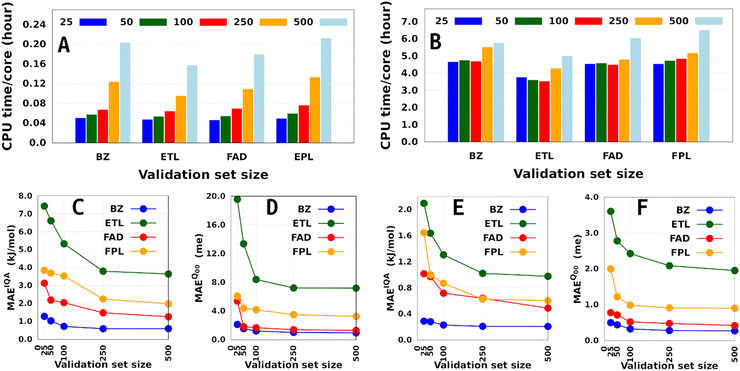
The performance of EIQA models improved by a factor of 2.9, 3.7, 2.6, and 3.3 as we augmented the training set from 1000 to 8000 geometries in the case of BZ, ETL, FAD, and FPL, respectively. Similar refinement factors of 3.5, 3.7, 3.1, and 3.6 were respectively observed for Q00 models. The fact that the predictive MAEs of the largest DL models lie within the limit of chemical accuracy (∼4 kJ mol−1) advocates for the adequateness of these models to be deployed in ML-aided simulations. Furthermore, except for ETL, all the largest DL models managed to reproduce molecular charges with predictive MAEs below 1 me.
The learning curves in Fig. 3 demonstrate the peculiarity of each system in terms of performance, learning slopes/rate and saturation point location. These overall and unique features reflect the different molecular flexibilities and levels of complexity of the conformational spaces under investigation. For instance, the fact that BZ is a very rigid molecule justifies the outstanding ability of the DL models to reproduce its atomic properties. In contrast, despite its smaller size, ETL is relatively more flexible than BZ and this attribute is mirrored by the higher predictive MAE values observed for DL models of ETL compared to those of BZ. From another perspective, the same reasoning explains why the local properties of atoms that move more tend to be more difficult to machine-learn.
Finally, it is worth emphasising that static performance metrics (such as the MAE values reported in this section) are not always conclusive. Since the training and test sets come from the same dataset, they inherit its caveats. For this reason, the computed MAEs cannot tell how robust a model is, that is, how it will behave in a real deployment scenario such as in a FFLUX simulation. One must then be careful when inferring conclusions from such metrics. In particular, this is true when it comes to guessing the relative stability of MLP-driven simulations, which is mostly a matter of the extent of the conformational space coverage.
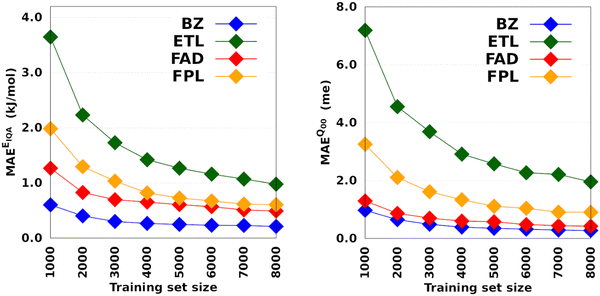
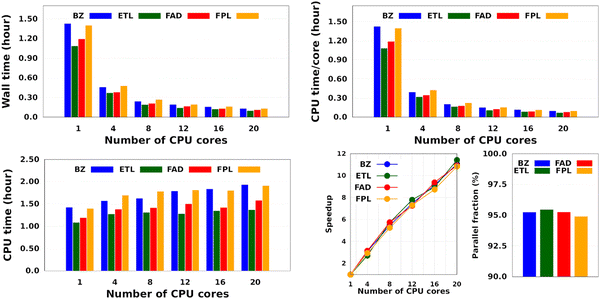
Fig. 4 shows the CPU/core and wall times of atomic GPR-DL models trained on 1000 to 8000 geometries. The raw data are collected in Table S3 in Section 6 of the ESI.† The timings reported in this study correspond to the shortest CPU/core and wall times recorded for a set of EIQA and Q00 models trained on the same geometries. Comparing the shortest timings is meant to alleviate the undesired and biasing effect of architecture-related noise.
According to Fig. 4, the training cost increases monotonically with the size of the training set. For a fixed model size (number of training geometries), it is the dimension of the HS (Nfeats + 2) that controls the training cost. This explains why training the largest DL model of FPL (Nfeats = 30) took 90 minutes longer than ETL (Nfeats = 21). In general, CPU/core and wall times increase in the order ETL < FAD < BZ < FPL. A slightly different pattern is observed for models trained on 6000 to 8000 geometries, where the training costs of BZ and FAD models are swapped. We attribute this effect to the datasets themselves, more specifically to how the relative positions of geometries in the input space affect the condition number of the covariance matrix. Indeed, adverse effects of ill-conditioning can be amplified by the dimension of the covariance matrix, which may have been the case between FAD and BZ models as we kept extending their knowledge content.
Intuitively, one should expect the training time of anisotropic GPR models to also depend on the number of computing resources available at runtime. Fig. 5 shows the training CPU/core and wall times of DL models trained on 1000 geometries using an increasing number of CPU cores, namely 1, 4, 8, 12, 16, and 20 cores. We reiterate that the results reported elsewhere in this work were obtained using 8 cores. It turns out that, unlike the total CPU time, which is less sensitive to the number of cores requested per training job (random variations due to system calls), the wall times (and the CPU time per core) decrease almost linearly with the number of CPU cores engaged in the training process. Notice also that for the smallest training set, the CPU/core and wall times differ by up to 17%, which suggests that in these cases, the program spent a non-negligible portion of the wall time dealing with non-CPU-related delays, such as waiting for resources to be available. Furthermore, the fact that the speedup increases monotonically (yet not linearly) with the number of CPU cores is a strong argument in favor of the reasonably good parallelization of our GPR engine (with ∼95% parallelization according to Amdahl's law57). We reiterate that FEREBUS relies on OpenMP to distribute the workload over several threads in the hottest parts of the code.18,19,42 These hot spots correspond to routines that compute the loss functions for each candidate solution.
Besides the training set size and the computing resources available, the size of the fixed validation set is another important factor that determines both the generalization aptitude and training cost of anisotropic GPR models within the IHOCV framework. Fig. 6 illustrates the training costs (CPU times per core) and predictive MAEs of various DL models trained on 1000 and on 8000 geometries using an increasing number of validation geometries (25 to 500). In general, it is right to think that the training time will always increase with the number of validation geometries. However, we find that the extent of this effect is both system-dependent and inversely proportional to the size of the training set. Notice that the smallest DL model is more affected than the largest DL model, with overhead factors of up to 4.3 and 1.4, respectively. The fact that the validation-induced overhead decreases with the training-validation split encourages, when affordable, the selection of larger validation sets dealing with large training sets. Additionally, because larger validation sets are more representative of the data being machine-learned, they tend to produce models that do not overfit them and generalize better on the test set.58 We note in passing that model overfitting is a general problem in machine learning diagnosed when a model overestimates its generalization capability, thus performing poorly on the test set. Although more pronounced in artificial neural networks due to a large number of parameters,38,59,60 it also affects GPs.61
Finally, although offering non-negligible speed-up (especially on small training sets), validation sets containing less than 100 geometries seem inappropriate as far as the generalization aptitude of the final model is concerned. However, we must emphasize that the optimal size of a fixed validation set is problem-dependent and is likely to change with the test set size, the complexity of the conformational space, and the chosen data sampling technique. Talking of the latter, it is to be anticipated that enhanced sampling techniques such as adaptive sampling62 could help reduce the size of an optimal validation set by selecting the most informative geometries from the initial sample pool. Unfortunately, applying such techniques often comes at the price of higher computational cost, which needs to be examined carefully to appreciate the significance of their improvement as compared to random selection.
4.2. Performance of TL models
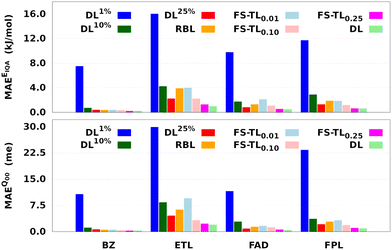
Fig. 7 and Table 1 respectively report the predictive MAEs and training costs of the baseline and FS-TL models. The raw predictive MAEs and acceleration factors are collected in Tables S3 and S4 (ESI†). It turns out that FS-TL models always outperform their local GP analogs when it comes to reconstructing both the molecular IQA energies and charges. Fig. 7 and Table S4 (ESI†) suggest that the predictive MAEs of TL0.000.01 models can be an order of magnitude lower than those of DL1% ones, with the highest deviation factors of ∼19 recorded for BZ. However, as one extends the size of the local GPs, their performance converges toward that of equivalent FS-TL models, whose enhanced performance is due to the explicit awareness of the target domain.
| Model | CPU time per core | Wall time | ||||||
|---|---|---|---|---|---|---|---|---|
| BZ | ETL | FAD | FPL | BZ | ETL | FAD | FPL | |
| DL | 5.751 | 4.990 | 6.033 | 6.498 | 6.675 | 5.508 | 6.488 | 7.101 |
| DL1% | 0.011 | 0.007 | 0.009 | 0.009 | 0.013 | 0.009 | 0.010 | 0.012 |
| DL10% | 0.155 | 0.117 | 0.144 | 0.168 | 0.187 | 0.141 | 0.170 | 0.202 |
| DL25% | 0.516 | 0.409 | 0.455 | 0.559 | 0.598 | 0.467 | 0.521 | 0.635 |
| TL0.000.01 | 0.041 | 0.032 | 0.039 | 0.042 | 0.061 | 0.047 | 0.056 | 0.065 |
| TL0.000.10 | 0.144 | 0.130 | 0.129 | 0.162 | 0.171 | 0.158 | 0.155 | 0.200 |
| TL0.000.25 | 0.433 | 0.369 | 0.428 | 0.468 | 0.489 | 0.433 | 0.486 | 0.533 |
| RBL | 0.295 | 0.288 | 0.332 | 0.336 | 0.328 | 0.318 | 0.365 | 0.369 |
As expected, the predictive capability of FS-TL models improves as the source domain becomes more and more similar to the target domain. For instance, FS-TL0.01, FS-TL0.10, and FS-TL0.25 EIQA models of BZ (FPL) recovered 53.7% (32.8%), 62.1% (51.9%) and 97.7% (98.2%) of the predictive accuracy of the largest DL model, while respectively achieving speedup factors of 109.4 (109.2), 39.0 (35.5), and 13.7 (13.3). However, we note that seeding FS-TL hyperparameters on a small and non-representative source dataset leads to suboptimal performance. In such cases, the guess hyperparameters are of poor quality and must be refined via relaxation on the target domain. More specifically, FS-TL models seeded on less than 10% of the target training set tend to perform significantly worse than the largest DL models, even though doing better than the local GP baselines. In terms of building cost, FS-TL0.10 and DL10% models exhibit comparable CPU and wall times, which corroborates the fact that the training of FS-TL models does not involve any expensive relaxation of the guess solution.
On the other hand, we find that the performance of RBL models is always lower than that of TL0.000.25 models, while their building cost lies in between those of TL0.000.10 and TL0.000.25 models. Most importantly, despite consuming two to three times fewer CPU hours than the RBL models, TL0.000.10 models perform much better. Additionally, unlike FS-TL models, the quality of RBL models might fluctuate considerably due to the unpredictable nature of random candidate solutions. It also stands to reason to think that the overall quality of such random solutions will generally deteriorate with the size of the molecule (∼dimension of the hyperparameter space) and the complexity of the conformational space. This intuitive, yet justifiable hypothesis disqualifies RBL models as a viable option for the fast construction of anisotropic GPR models.
The above findings suggest that a unique FS-TL model always performs better than any single local GP built on the same subspace of the target dataset as the source model of the FS-TL model. Similarly, FS-TL models, which are aware of the target domain, are expected to perform better than any approximative sparse GP model whose inducing points are the same as the source dataset (geometries) of the FS-TL model. However, we anticipate cohorts of local GPs16 trained on smartly clustered subsets of a target dataset to demonstrate enhanced performance, comparable to relaxed TL and full DL models.
Fig. 8 reports the performance of the largest DL and a series of shortly relaxed TL models trained on 8000 geometries using a validation set of 500 geometries. The relaxation weight was kept small (<0.10) to achieve a significant speed-up. Table 2 gives the training timings in terms of CPU time per core and wall time. Tables S5 and S6 (ESI†) respectively collect the raw predictive MAEs and speedup factors of the relaxed TL models.
| Model | CPU time per core | Wall time | ||||||
|---|---|---|---|---|---|---|---|---|
| BZ | ETL | FAD | FPL | BZ | ETL | FAD | FPL | |
| DL | 5.751 | 4.990 | 6.033 | 6.498 | 6.675 | 5.508 | 6.488 | 7.101 |
| TL0.050.01 | 0.340 | 0.217 | 0.295 | 0.358 | 0.398 | 0.248 | 0.330 | 0.414 |
| TL0.050.10 | 0.420 | 0.309 | 0.366 | 0.445 | 0.474 | 0.351 | 0.399 | 0.509 |
| TL0.050.25 | 0.728 | 0.597 | 0.715 | 0.773 | 0.839 | 0.676 | 0.785 | 0.895 |
| TL0.100.01 | 0.667 | 0.446 | 0.498 | 0.668 | 0.773 | 0.507 | 0.554 | 0.777 |
| TL0.100.10 | 0.679 | 0.587 | 0.629 | 0.674 | 0.767 | 0.649 | 0.687 | 0.747 |
| TL0.100.25 | 1.077 | 0.821 | 0.951 | 1.121 | 1.252 | 0.916 | 1.070 | 1.242 |
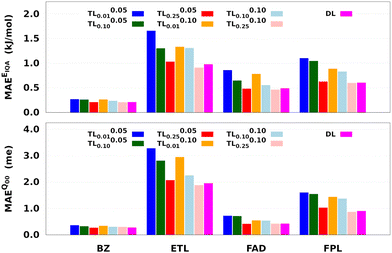
Two main observations come out of Fig. 8. First, it can be seen that, for a given relaxation weight, the performance of TL models increases with the size of the source model. Most importantly, TL models trained on 25% of the target dataset and a relaxation weight of 0.10 (20 relaxation iterations) outperform the equivalent DL models. For instance, TL0.100.25 models of ETL achieve MAEs of 0.91 kJ mol−1 and 1.8 me against 0.98 kJ mol−1 and 1.9 me for the largest DL model. Second, we observe that TLζ0.01 and TLζ0.10 (ζ ≠ 0) models achieve much better predictive accuracy when compared to FS-TL0.01 and FS-TL0.10 models. This observation confirms the relevance of guess relaxation on small source models.
Table 2 and Table S6 (ESI†) suggest that relaxed TL models can be built five to eight times faster than their DL analogs while preserving the quality of the latter or even outperforming them. It is important to mention that, as long as the size of the source model is large enough, FS-TL models already offer a reasonable cost/accuracy trade-off when it comes to reproducing molecular IQA energies. Indeed, FS-TL0.25 EIQA models are capable of recovering 98% of the largest DL model's performance. However, unlike IQA energies, FS-TL models struggle more when it comes to reconstructing the molecular charge. Even with a source dataset of 2000 geometries, FS-TL0.25 Q00 models of ETL, FAD, and FPL respectively recovered 86.7%, 71.6%, and 87.2% of the DL model's performance (less than 90%). Fig. 8 and Table S6 (ESI†) indicate that a short relaxation of the previous FS-TL0.25 Q00 guess solutions (for only 10 iterations; ζ = 0.05) leads to excellent accuracy recovery rates of 94.3%, 101.9%, and 92.3%.
4.3. Prediction of vibrational normal modes
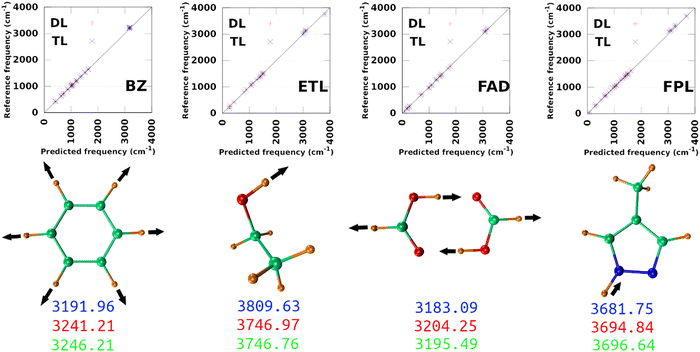
The largest DL and best-performing single-source TL models (TL0.100.25) were employed to compute the harmonic normal modes and frequencies of BZ, ETL, FAD, and FPL in their respective ground states. The predicted frequencies were compared with reference values calculated using GAUSSIAN1647 at the appropriate levels of theory (see Section 3.2). Fig. 9 shows scatter plots of the reference frequencies as functions of the predicted ones. The predictive MAEs are collected in Table 3 along with the ID (number) of the worst predicted normal mode and the maximum absolute frequency deviation. Individual vibrational frequencies are collected in Section 9 of the ESI† (Tables S7–S10).| Model | MAE(RMSE)DL | MAE(RMSE)TL | WPMDL | WPMTL | Δvmax,DL | Δvmax,TL | RDL2 | RTL2 |
|---|---|---|---|---|---|---|---|---|
| BZ | 15.21(20.01) | 16.18(20.81) | 30 | 30 | 49.26 | 54.25 | 1.00 | 1.00 |
| ETL | 23.25(30.14) | 19.02(21.52) | 1 | 1 | 76.67 | 63.21 | 0.99 | 0.99 |
| FAD | 15.05(20.13) | 11.92(16.17) | 23 | 23 | 54.91 | 42.65 | 1.00 | 1.00 |
| FPL | 23.99(31.15) | 20.57(28.27) | 25 | 29 | 92.49 | 75.24 | 0.99 | 0.99 |
As per Table 3, both the DL and TL models achieve decent frequency predictions as compared to the reference levels of theory. In all cases, TL models achieve similar to slightly better average predictions as compared to their DL analogs. The fact that the MAEs of FFLUX-predicted frequencies lie within 100 cm−1 (1.2 kJ mol−1) of the reference data advocates for the outstanding quality of both series of models. This conclusion corroborates the excellent Pearson's R2 correlation coefficients between the reference and FFLUX-predicted frequencies.
In general, DL and TL models struggle more with higher frequency modes occurring in the frequency region >3000 cm−1. For instance, the worst predicted normal modes of BZ are related to the ring-breathing mode that appears around 3191.96 cm−1 at the B3LYP/aug-cc-pVTZ level. The only exception to this pattern is ETL for which the worst predicted mode is the lowest frequency normal mode (263.3 cm−1 at the B3LYP/aug-cc-pVTZ level of theory). This unexpected observation can be attributed to a poor sampling along the directions of this normal mode. Interestingly, this observation offers an opportunity to improve the quality of the original DL and TL models via data augmentation with carefully sampled geometries along specific eigenvectors of the mass-weighted Hessian matrix.
4.4. Geometry optimisation
Both DL and TL models were employed in “Zero Kelvin” FFLUX simulations for geometrical optimization. Table 4 collects the average energy difference and root mean square deviation between the GAUSSIAN and FFLUX-optimised geometries. Fig. 10 shows overlayed geometries of the optimized molecules. We also compare in Table S12 (ESI†) the electronic energy range within the starting pool of geometries and the training geometries.| Model | ΔEDL | ΔETL | RMSDDL | RMSDTL |
|---|---|---|---|---|
| BZ | 0.328 | 0.275 | 0.001 | 0.001 |
| ETL | 0.145 | 0.042 | 0.091 | 0.062 |
| FAD | 0.070 | 0.049 | 0.074 | 0.044 |
| FPL | 0.529 | 0.371 | 0.035 | 0.037 |
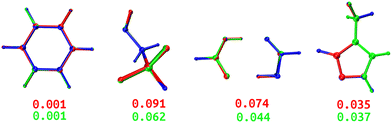 | ||
| Fig. 10 Overlayed optimized geometries of BZ, ETL, FAD, and FPL. The blue-colored structure is the GAUSSIAN reference, while the red and green ones are FFLUX-optimized structures using the DL and TL models, respectively. Both structures were rotated with respect to the reference using the Kabsch algorithm.46 The RMSD (Å) between each FFLUX predicted minimum and the reference structure are also shown. | ||
As expected, TL models outperform or at least compete with their DL analogs in terms of energetics and minimum structure prediction. Most importantly, we find that, despite being sometimes launched from geometries located outside the training space, all FFLUX optimization runs using both the DL and TL models outstandingly converged toward the nearest vicinity of the reference minimum structure (ΔE < 1 kJ mol−1 and RMSD < 0.1 Å). Table S12 (ESI†) indicates that, in all cases, the pool of starting geometries covered a large energy range an order of magnitude bigger than the training set. This finding demonstrates, at least partly, the extrapolation capability of our GPR models.
5. Conclusion
The exorbitant training cost of GPs is the main bottleneck that prevents or discourages their application on large datasets. Several solutions have been proposed to address this issue, including reduced-rank approximations and the usage of iterative solvers. However, most of these schemes do not always preserve the desired and outstanding predictive capability of exact (full) GP inference.In this study, we have proposed a transfer learning (TL) protocol that mitigates the training cost of anisotropic GPR models, while not sacrificing accuracy. The protocol works by transferring hyperparameters from one (or several) small source models to the target GPR model. Performance comparisons between direct learning (DL) and TL models prove that the latter can be trained several times faster while preserving the desired predictive capability of the former. More specifically, TL models trained on 25% of the target training set, and relaxed for 5% to 10% of the total number of iterations, can be built 5 to 8 times faster than their DL analogs, while always recovering more than 90% of the predictive capability of the latter or even outperforming them. We have also shown that, in the case of EIQA models, FS-TL0.25 models can already recover up to 98% of the DL's performance for an order of magnitude speed-up (∼13). However, failing to relax the guess solution (hyperparameters) can result in suboptimal models when the source training set is small and very dissimilar to the target one.
Most importantly, when deployed in FFLUX simulations, TL models of atomic IQA energies and charges exhibit similar to better performance than their DL analogs. TL models behave better than DL models when it comes to guiding geometry optimization and normal mode calculations. Although the TL protocol requires the covariance matrix to fit in memory, it can be praised for being simple and intuitive, let alone that the underlying ideas can be easily coupled with existing GP scaling techniques that mitigate the huge memory requirement of full GPR model training. Work is already underway in our group to accomplish this.
Data availability
Any data are readily available from the corresponding author upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. K. I. acknowledges UK Research and Innovation (UKRI) for the award of a MADSIM PhD studentship. He also expresses his gratitude to the BEBUC scholarship system for continued financial support. P. L. A. P. is grateful to the European Research Council (ERC) for the award of an Advanced Grant underwritten by the UKRI-funded Frontier Research grant EP/XO24393/1.References
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- C. M. Handley, G. I. Hawe, D. B. Kell and P. L. Popelier, Phys. Chem. Chem. Phys., 2009, 11, 6365–6376 RSC.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csányi, Adv. Neural Inf. Process. Syst., 2022, 35, 11423–11436 Search PubMed.
- S. Chmiela, V. Vassilev-Galindo, O. T. Unke, A. Kabylda, H. E. Sauceda, A. Tkatchenko and K.-R. Müller, Sci. Adv., 2023, 9, eadf0873 CrossRef PubMed.
- Z. Wang, H. Wu, L. Sun, X. He, Z. Liu, B. Shao, T. Wang and T.-Y. Liu, J. Chem. Phys., 2023, 159, 035101 CrossRef.
- B. C. B. Symons, M. K. Bane and P. L. A. Popelier, J. Chem. Theory Comput., 2021, 17, 7043–7055 CrossRef.
- B. C. Symons and P. L. Popelier, J. Chem. Theory Comput., 2022, 18, 5577–5588 CrossRef PubMed.
- M. Brown, J. Skelton and P. Popelier, J. Chem. Theory Comput., 2023, 19, 7946–7959 CrossRef PubMed.
- C. K. Williams and C. E. Rasmussen, Gaussian processes for machine learning, MIT Press, Cambridge, MA, USA, 2006 Search PubMed.
- E. Snelson and Z. Ghahramani, Adv. Neural Inf. Process. Syst., 2006, 18, 1259–1266 Search PubMed.
- M. Lázaro-Gredilla, J. Quinonero-Candela, C. E. Rasmussen and A. R. Figueiras-Vidal, J. Mach. Learn. Res., 2010, 11, 1865–1881 Search PubMed.
- J. Gardner, G. Pleiss, K. Q. Weinberger, D. Bindel and A. G. Wilson, Adv. Neural Inf. Process. Syst., 2018, 31, 7576–7586 Search PubMed.
- J. Sun, L. Cheng and T. Miller, Molecular Energy Learning Using Alternative Blackbox Matrix-Matrix Multiplication Algorithm for Exact Gaussian Process, 2021 Search PubMed.
- C. Hu, S. Zeng and C. Li, Appl. Soft Comput., 2023, 148, 110866 CrossRef.
- M. M. Noack, H. Krishnan, M. D. Risser and K. G. Reyes, Sci. Rep., 2023, 13, 3155 CrossRef PubMed.
- N. Di Pasquale, M. Bane, S. J. Davie and P. L. Popelier, Wiley Online Library, 2016, pp. 2606–2616 Search PubMed.
- M. J. Burn and P. L. A. Popelier, Digital Discovery, 2023, 2, 152–164 RSC.
- B. K. Isamura and P. L. Popelier, AIP Adv., 2023, 13, 095202 CrossRef CAS.
- M. M. Noack, G. S. Doerk, R. Li, J. K. Streit, R. A. Vaia, K. G. Yager and M. Fukuto, Sci. Rep., 2020, 10, 17663 CrossRef CAS PubMed.
- P. L. Popelier, The chemical bond II: 100 years old and getting stronger, 2016, pp. 71–117 Search PubMed.
- M. J. Burn and P. L. A. Popelier, J. Chem. Theory Comput., 2023, 19, 1370–1380 CrossRef CAS.
- M. L. Brown, J. M. Skelton and P. L. Popelier, J. Phys. Chem. A, 2023, 127, 1702–1714 CrossRef CAS.
- T. van der Heide, J. Kullgren, P. Broqvist, V. Bačić, T. Frauenheim and B. Aradi, Comput. Phys. Commun., 2023, 284, 108580 CrossRef CAS.
- S. Klawohn, J. P. Darby, J. R. Kermode, G. Csányi, M. A. Caro and A. P. Bartók, J. Chem. Phys., 2023, 159, 174108 CrossRef CAS PubMed.
- A. Becke, The quantum theory of atoms in molecules: from solid state to DNA and drug design, John Wiley & Sons, 2007 Search PubMed.
- M. Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
- J. M. Guevara-Vela, E. Francisco, T. Rocha-Rinza and Á. Martín Pendás, Molecules, 2020, 25, 4028 CrossRef CAS.
- S.-G. Hwang, B. L'Huillier, R. E. Keeley, M. J. Jee and A. Shafieloo, J. Cosmology Astroparticle Phys., 2023, 2023, 014 CrossRef.
- M. J. Burn and P. L. A. Popelier, Mater. Adv., 2022, 3, 8729–8739 RSC.
- S. J. Pan and Q. Yang, IEEE Trans. Knowledge Data Eng., 2009, 22, 1345–1359 Search PubMed.
- F. Zhuang, Z. Qi, K. Duan, D. Xi, Y. Zhu, H. Zhu, H. Xiong and Q. He, Proc. IEEE, 2020, 109, 43–76 Search PubMed.
- P. O. Dral, J. Phys. Chem. Lett., 2020, 11, 2336–2347 CrossRef CAS.
- X. Li, Y. Grandvalet, F. Davoine, J. Cheng, Y. Cui, H. Zhang, S. Belongie, Y.-H. Tsai and M.-H. Yang, Image Vision Comput., 2020, 93, 103853 CrossRef.
- J. Wang and Y. Chen, Introduction to Transfer Learning: Algorithms and Practice, Springer, 2022, pp. 275–279 Search PubMed.
- M. S. Chen, J. Lee, H.-Z. Ye, T. C. Berkelbach, D. R. Reichman and T. E. Markland, J. Chem. Theory Comput., 2023, 19, 4510–4519 CrossRef CAS PubMed.
- A. Kamath, R. A. Vargas-Hernández, R. V. Krems, T. Carrington and S. Manzhos, J. Chem. Phys., 2018, 148, 241702 CrossRef PubMed.
- J. Ollar, C. Mortished, R. Jones, J. Sienz and V. Toropov, Struct. Multidisciplinary Optimization, 2017, 55, 2029–2044 CrossRef.
- Y.-C. Chang, N-dimension golden section search: Its variants and limitations, 2009 Search PubMed.
- H. Yu and S. Kim, Passive sampling for regression, 2010 Search PubMed.
- B. K. Isamura and P. L. Popelier, Artif. Intell. Chem., 2023, 1, 100021 CrossRef.
- S. Mirjalili, S. M. Mirjalili and A. Lewis, Adv. Eng. Software, 2014, 69, 46–61 CrossRef.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Nat. Commun., 2018, 9, 3887 CrossRef.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef PubMed.
- W. Kabsch, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 922–923 CrossRef.
- M. e Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian, Inc., Wallingford, CT, 2016.
- T. A. Keith, TK Gristmill Software, Overland Park, KS, USA, 2019, 23 Search PubMed.
- S. M. Kandathil, T. L. Fletcher, Y. Yuan, J. Knowles and P. L. Popelier, J. Comput. Chem., 2013, 34, 1850–1861 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef.
- M. F. Guest, A. M. Elena and A. B. Chalk, Mol. Simul., 2021, 47, 194–227 CrossRef CAS.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- T. Viering and M. Loog, IEEE Trans. Pattern Anal. Mach. Intell., 2022, 45, 7799–7819 Search PubMed.
- T. Viering, A. Mey and M. Loog, Proc. Mach. Learn. Res. vol., 2019, 99, 1–4 Search PubMed.
- P. Sollich, Lect. Notes Comput. Sci., 2005, 199–210 Search PubMed.
- O. Roussel, J. Satisfiability, Boolean Modeling Comput., 2011, 7, 139–144 Search PubMed.
- G. Amdahl, Validity of the single processor approach to achieving large scale computing capabilities, 1967 Search PubMed.
- Y. Xu and R. Goodacre, J. Anal. Test., 2018, 2, 249–262 CrossRef PubMed.
- M. Gallegos, B. K. Isamura, P. L. Popelier and A. N. Martín Pendás, J. Chem. Inf. Model., 2024, 64, 3059–3079 CrossRef PubMed.
- C. F. G. D. Santos and J. P. Papa, ACM Computing Surveys (CSUR), 2022, 54, 1–25 CrossRef.
- R. O. Mohammed and G. C. Cawley, Over-fitting in model selection with Gaussian process regression, 2017 Search PubMed.
- M. J. Burn and P. L. A. Popelier, J. Chem. Phys., 2020, 153, 054111 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01862a |
| This journal is © the Owner Societies 2024 |