Computational insights into the interaction of water with the UiO-66 metal–organic framework and its functionalized derivatives†
Jierui
Zhang
a,
Francesco
Paesani
 *b and
Martina
Lessio
*b and
Martina
Lessio
 *a
*a
aSchool of Chemistry, The University of New South Wales, Sydney, NSW 2052, Australia. E-mail: martina.lessio@unsw.edu.au
bDepartment of Chemistry and Biochemistry, University of California San Diego, La Jolla, CA, USA. E-mail: fpaesani@ucsd.edu
First published on 6th July 2023
Abstract
The UiO-66 metal–organic framework (MOF) has been identified as a promising hydrophilic material for water harvesting. Recent studies show that its water uptake ability at low relative humidity (RH) can be improved by incorporating hydrophilic functional groups into the framework. In this work, we provide computational insights into the adsorption of water in UiO-66 and its functionalized derivatives to reveal the role played by different adsorption sites and functional groups in the adsorption mechanism. We started by developing molecular models for UiO-66, UiO-66-NH2, UiO-66-OH, and UiO-66-(OH)2 compatible with the MB-pol data-driven many-body potential of water. We then benchmarked these models against ab initio data. We used these models to perform molecular dynamics simulations and calculate radial distribution functions, IR spectra, and two-dimensional density distribution maps for water in the MOFs. These results consistently show that the μ3-OH sites are the preferential interaction sites for water in UiO-66 and all its variants, and the formation of localised water clusters inside the octahedral pores is responsible for the abrupt step in the experimental adsorption isotherms. Furthermore, the presence of functional groups in the framework allows water to cluster in the octahedral pores at lower RH, thus making the MOF a more efficient water harvester. Overall, this study provides molecular-level insights into the pore filling process of UiO-66 and its functionalized derivatives, which are needed for the design of efficient water harvesting materials based on MOFs.
Introduction
Freshwater is an essential resource for human lives and is needed for many critical aspects, such as drinking, energy production, irrigation, and industry. Currently, around two-thirds of the world's population suffer severe clean freshwater shortage for at least one month each year.1 The shortage of freshwater is thus a significant global concern exacerbated by the growing world population, expansion of agriculture irrigation, and increasing industrial pollution. Generally, wastewater purification and seawater desalination plants are located in coastal regions and long-distance transportation is required to deliver freshwater to inland and higher mountain regions.2 Thus, the exploitation of new readily accessible water resources is crucial for the expansion of freshwater availability to address the water scarcity issue worldwide. Water is present in the air in the form of vapor and droplets. This atmospheric water represents a potential source of freshwater that is not restricted by geographical conditions and could provide more freshwater than all the rivers on Earth.3 The development of efficient atmospheric water harvesting methods is thus a critical step towards addressing the growing demand for freshwater resources. The methods currently available such as conventional fog capture and dewing require either large energy inputs or high relative humidity (RH) which make their application in arid regions unfeasible.4–6 Therefore, an ideal atmospheric water harvesting system should be able to collect water from dry air (low RH) with a low energy supply.Recently, metal–organic frameworks (MOFs) have garnered significant interest in the scientific community as promising water harvesters.7 MOFs are crystalline porous materials constructed from inorganic secondary building units (SBUs) and organic linkers. The MOF properties are determined by the linkers and SBUs topologies, with thousands of combinations discovered to date.8 This offers a systematic way to design an ideal water harvester with high stability,7,9–11 high water capacity,7,12–14 low energy consumption,7,15–17 and high water affinity with hydrophilic functional groups (e.g. –OH) incorporated within the framework.18–21 In spite of these promising features, the application of MOFs in water harvesting technologies is still an emerging area of research and more fundamental insights into the adsorption mechanism are required in order to scale up this technology.
UiO-66 is a well characterized and established hydrophilic water-stable MOF. It is composed of zirconium oxide SBUs (Zr6O4(OH)4) that are 12-fold connected in a face-centered-cubic arrangement by 1,4-benzenedicarboxylic acid (H2BDC) organic linkers.10 The high connectivity and strong Zr–O coordination bonds within the SBU contribute to the outstanding water stability of UiO-66.10,22 Experimental studies have demonstrated that UiO-66 can undergo multiple water adsorption-desorption cycles with steady adsorption performance and minimum distortion of the structure.7,11,23 In addition, the water adsorption isotherms of UiO-66 can be tuned by introducing hydrophilic functionalized BDC linkers, which allow for significantly improving the adsorption ability at lower RH.18–20 Overall, the outstanding stability, reversible water uptake ability, and the possibility to tailor the physical and chemical properties of UiO-66 through functionalization make it an extremely promising material for water harvesting and an excellent system to study in order to develop improved MOFs for water harvesting.
Computational chemistry methods are widely applied and effective tools for the study of MOFs due to their predictive power and their ability to provide molecular-level insights inaccessible to experiments.24–26 Previous computational studies of UiO-66 have employed generic force fields13,21,27,28 to conduct classical molecular dynamics (MD) simulations aimed at understanding the key water-MOF interactions and the diffusion process of water across the MOF cavities. An exception to this, is the vibrational spectroscopy study of water within defective UiO-66 performed by Caratelli et al. using ab initio MD simulations.29 In this work, we introduce a family of force fields for UiO-66 and its functionalized derivatives that are derived from ab initio data and can model the frameworks as flexible objects. Recent simulation studies investigating the influence of guest molecule adsorption in the UiO-66 framework have highlighted the importance of considering framework flexibility to accurately reproduce experimental results.30 These newly developed force fields are specifically designed to be compatible with the MB-pol data-driven many-body potential for water.31–34 MB-pol has been shown to accurately predict the properties of water from the gas to the condensed phases.34–37 We employ the newly developed force fields in MD simulations to investigate structural and dynamical properties of water in UiO-66 and its functionalized derivatives. In particular, we compute radial distributional functions (RDF), two-dimensional density distribution maps, and infrared (IR) spectra for water as a function of RH. These computed properties provide general insights into the pore filling process and the driving force that initiates water adsorption and the formation of water clusters within the frameworks. Moreover, the dynamical properties help us unravel the influence of –NH2, –OH and –(OH)2 functionalization on the MOF's water adsorption ability. The understanding of these mechanisms at the molecular level is critical to establishing design principles of new porous materials for atmospheric water harvesting purposes with improved water adsorption abilities.
Computational details
Force field
We developed a family of force fields for UiO-66 and its functionalized derivatives by using a genetic algorithm (GA)38 to fit all the parameters describing the UiO-66 SBU and the framework-water interactions to reference energies obtained from density functional theory (DFT)39,40 calculations.38 The DFT reference energies were obtained for a cluster model of the UiO-66 framework representing the local environment around the inorganic metal node. The cluster model was prepared by truncating the periodic MOF structure and replacing the 12 BDC linkers with formate capping groups (Fig. S1, ESI†). This cluster structure includes all the relevant atoms for an accurate description of all the interaction sites for hydrogen-bonding with water. These include the linker carboxylate oxygen atoms (Olinker), the hydroxide group (μ3-OH) and the oxygen atoms (μ3-O) interconnecting the Zr atoms (Fig. S1, ESI†).The periodic MOF structure was optimized using the Vienna Ab initio Simulation Package (VASP)41–44 with the PBE functional and Grimme's D3 dispersion correction.45–47 The electronic wavefunction was described using a plane-wave basis with 700 eV kinetic energy cutoff and the projector-augmented-wave (PAW) potentials available in VASP. The Brillouin zone was sampled using a 2 × 2 × 2 k-point mesh generated based on the Monkhorst–Pack scheme. All the calculations involving the metal node cluster were performed with the ωB97X-D3BJ functional46–49 using the ORCA software package (version 5.0.1).50–52 Geometry optimizations were performed using the def2-SVP53,54 basis set for all the atoms except for Zr atoms. A larger def2-TZVPP53,54 basis set and the effective core potential def2-ECP55 were used to describe the valence and core electrons for Zr atoms, respectively. Single-point energy refinements were performed using the def2-TZVP53,54 basis set for all atoms and the def2-TZVPP53,54 basis set (with the def2-ECP) for the Zr atoms.
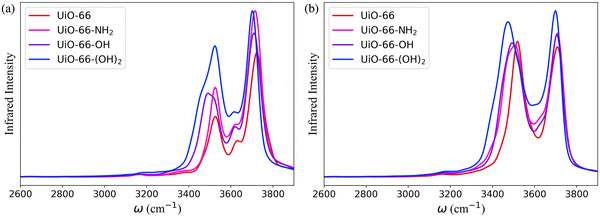
The bonded force field parameters for the UiO-66 inorganic units were fitted to single-point energies of 300 configurations of the cluster model with one of the Zr atoms distorted relative to its equilibrium position. The bonded force field parameters for the atoms of the organic linkers were extracted from the General Amber Force Field (GAFF).56 In addition, the bond force constants for the N–H and O–H groups of BDC-NH2, BDC-OH and BDC-(OH)2 were modified to align with the experimental infrared (IR) spectra for UiO-66-NH2,57–59 UiO-66-OH and UiO-66-(OH)2 (Fig. S3, ESI†).59–61 In the simulations, only the neutral state of these functional groups has been considered. The occurrence of proton exchange reactions between MOFs and water is influenced by the phase of water and the pH of the environment, and it is important to note that the adsorbed water cannot be definitively categorized as either liquid or gas.62 In gas phase, the ionic dissociation energy of water is observed to be prohibitively high.63–65 On the other hand, studies on –NH2, –OH and –(OH)2 functionalized MOFs exposed to liquid water at neutral pH show that the protonation or deprotonation of these groups does not occur.66–68 The many-body potential energy function (MB-pol)31–34 was used to model water within the system. MB-pol has been shown to accurately reproduce the properties of water for both gas and condensed phases,34–36 which is well suited for an accurate representation of the properties of water adsorbed in MOFs.62,69,70
All Lennard-Jones (LJ) force field parameters were taken from GAFF56 except for Zr for which the parameters were obtained from the Universal Force Field (UFF).27 The LJ parameters for the description of the interaction between different atom types were derived using Lorentz–Berthelot mixing rules.71 When applying Lorentz–Berthelot mixing rules71 to the interactions involving water, the LJ parameters of the TIP4P/2005 water model72 were used since TIP4P/2005 is the closest empirical water model to MB-pol.62,69,70 This strategy has proven successful in previous MD simulations incorporating MB-pol water model to study water–MOF interactions.62,70,73 In addition, Buckingham force field parameters describing the van der Waals (vdW) interactions between the oxygen atoms (OW) of the water molecules with μ3-OH, and the hydrogen atoms (HW) of the water molecules with μ3-O and Olinker interaction sites were specifically fitted to DFT reference energies using the GA to obtain a more accurate representation of these interactions. To this end, we first optimized cluster model structures with a water molecule hydrogen-bonded to the μ3-OH, μ3-O and Olinker sites (Fig. S4, ESI†). These geometry optimizations were performed with constrains applied to the entire cluster model in order to maintain the rigidity of the framework. We then generated 110 configurations with the water molecule located at varying distances from the μ3-OH, μ3-O and Olinker interaction sites for which the interaction energies were calculated at the DFT level of theory and corrected for the basis set superposition error (BSSE) using the counterpoise method.74,75 Finally, the partial charges of the atoms in the metal node and organic linkers were calculated using the Charge Model 5 (CM5)76 as implemented in Gaussian 1677 with the same DFT functional and basis set used for the single point energy refinements.
Molecular dynamics simulations
All MD simulations were performed with an in-house software based on the DL_POLY_2 simulation package78 using the force fields described in the previous sections for all MOF variants and the MB-pol31–34 model for water. The equations of motions were propagated using the velocity-Verlet algorithm79 with a time step of 0.2 fs33 and the non-bonded interactions were truncated at 9.0 Å with long-range electrostatics calculated by Ewald summation.80 The time step was established according to the study by Medder et al.33 The initial configurations of UiO-66 and its functionalized derivatives interacting with water molecules were generated using PACKMOL.81 The number of water molecules in the MOF structure at different RH values was derived from the experimental water adsorption isotherm for UiO-66 (see Section 3 in the ESI†).11 The water molecules were randomly distributed into the 1 × 1 × 1 cubic unit cell of the UiO-66 framework (20.7465 Å cell parameter). Each system went through a randomization at 1000 K and 1 atm for 10 ps, followed by a 40 ps gradual cooling process carried out in the isothermal-isobaric ensemble (constant number of atoms, pressure, and temperature, NPT) at 1 atm and 500 K for 20 ps, and at 1 atm and 298 K for 20 ps. The production runs were then carried for 1 ns in the NPT ensemble at 1 atm and 298 K. In all NPT simulations the temperature was controlled using a massive Nosé-Hoover chain thermostat where each degree of freedom was coupled to a Nosé–Hoover thermostat chain of length four, while the pressure was controlled by a Nosé–Hoover barostat based on the algorithm introduced by Tuckerman.79 The RDFs, two-dimensional density distribution maps, and infrared spectra were averaged from five independent trajectories of 50 ps carried out in the microcanonical ensemble (constant number of atoms, volume, and energy, NVE) with the volume fixed at the average value calculated from previous NPT simulations.Theoretical infrared spectra
The IR spectra of water adsorbed in the different UiO-66 variants were calculated according to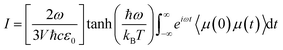 | (1) |
Results and discussion
UiO-66 has a type V isotherm (Fig. 1a), displaying a gradual increase in water adsorption at 10–30% RH, followed by a sudden rise at 30% RH. The first step towards a molecular-level understanding of the pore filling process behind these experimental observations is the identification of the possible interaction sites for water. There are two types of cavities within UiO-66, the octahedral and the tetrahedral pores. Each octahedral pore is interconnected to eight tetrahedral pores.10,22 The octahedral and tetrahedral pores in UiO-66 provide different interaction environments for water (Fig. 1b). In the octahedral cavity, the Olinker from the BDC ligands are the only accessible sites for the formation of hydrogen-bonding interactions with water. In contrast, water molecules in the tetrahedral pores can interact with the μ3-O and μ3-OH sites, in addition to the Olinker sites.10,22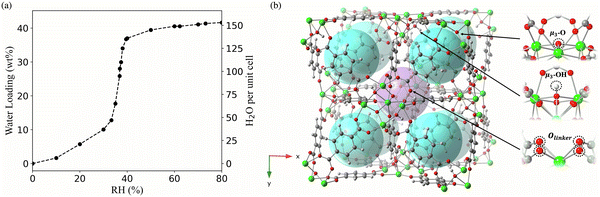 | ||
| Fig. 1 (a) The experimental adsorption isotherm of UiO-66 at 0–80% relative humidity (RH) and room temperature. The left y-axis represents the weight percentage (wt%) of water in the MOF measured experimentally, while the right y-axis represents the number of water molecules per UiO-66 unit cell included in the simulation. Data sourced from Furukawa et al.11 (b) Pores and bonding sites for water adsorption in UiO-66; each octahedral pore (purple sphere) is surrounded by eight tetrahedral pores (blue spheres); the three bonding sites (μ3-OH, μ3-O and Olinker) available for water in the pores are labeled with black arrows. | ||
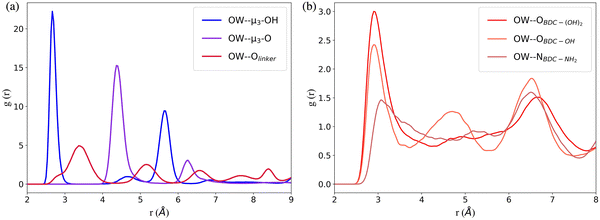
The RDFs between the oxygen atoms (OW) of water and the oxygen atoms of the interaction sites within UiO-66 at 10% RH were calculated to determine the initial binding sites (Fig. 2a). The RDF describing the spatial correlation between the OW atoms and the oxygen atoms of the μ3-OH groups peaks at a shorter distance (2.7 Å) compared to the corresponding peaks in the RDFs between OW and the oxygen atoms of μ3-O (4.4 Å) and Olinker (3.4 Å). This reveals that the affinity between water and the three interaction sites on the SBUs follows the trend: μ3-OH > Olinker > μ3-O. This finding is consistent with previous computational studies showing that water preferentially binds to the μ3-OH in UiO-66.13,21,28,29 Moreover, this aligns with the experimental observation that μ3-OH is the primary adsorption site for water in MOF-801, a MOF containing the same inorganic SBUs as UiO-66.11 The μ3-O sites are present in the tetrahedral cavities with the μ3-OH sites and the two peaks at 4.4 Å and 6.5 Å for the OW⋯μ3-O correspond to the distance between the μ3-O and the water molecules bonded to neighboring μ3-OH sites. Hence, at 10% RH water does not bind to the μ3-O sites in UiO-66.
In the functionalized UiO-66 MOFs the –NH2, –OH and –(OH)2 functional groups are the secondary preferential bonding sites, with the RDFs between OW and the nitrogen or oxygen atoms in the –NH2 (3.0 Å), –OH (2.9 Å) and –(OH)2 (2.9 Å) functional groups peaking at a larger distance compared to μ3-OH (2.7 Å) and at a lower distance compared to Olinker (3.4 Å), as shown in Fig. 2b. We note that the OW⋯μ3-OH and OW⋯Olinker RDFs for the functionalized MOFs (Fig. S7, ESI†) peak at the same distance as for UiO-66.
The simulated IR spectra of water in the framework as a function of RH monitor the change in the hydrogen-bonding topology of water confined in the MOF pores at the different stages of the adsorption process. In Fig. 3a, the far infrared region (<1000 cm−1) describes the collective librational modes (i.e., rocking, wagging, and twisting motion) of water that are difficult to isolate. The peak around 1650 cm−1 represents the H–O–H bending mode of water which aligns with the experimentally observed water bending signal.82,83 The relatively weak and wide band centered at 1979 cm−1 (highlighted in the inset of Fig. 3a) is the combination band that arises from the coupling of the bending vibration with one or more librational modes. Beyond 2600 cm−1 the IR spectrum is characterized by the broad band of hydrogen-bonded (3400–3500 cm−1) and non-hydrogen-bonded (∼3713 cm−1) O–H stretching vibrations of water adsorbed in the MOF pores (Fig. 3b). The latter arises at low RH due to the presence of water molecules bound to the μ3-OH groups of the framework which are not hydrogen-bonded to other water molecules. As RH increases, an extended hydrogen-bonding network forms, which weakens the intramolecular bonds of water. This leads to a red-shift of the free O–H stretch and a broadening of the band in the 3400–3500 cm−1 region.
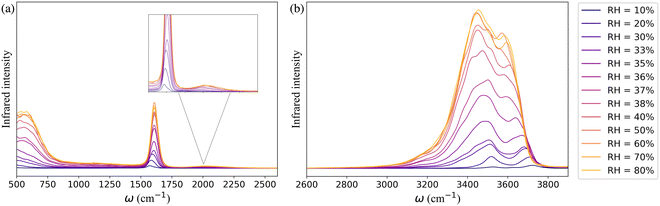 | ||
| Fig. 3 The theoretical IR spectra of water within the UiO-66 confinement at 10–80% RH in the range (a) 500–2600 cm−1 and (b) 2600–3900 cm−1. | ||
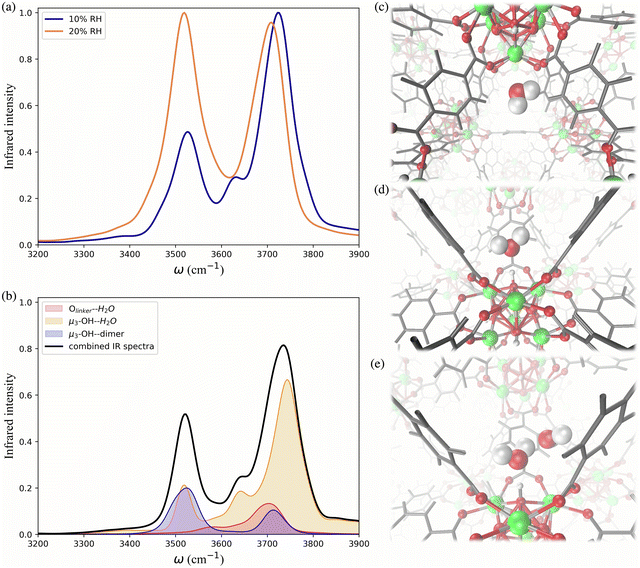
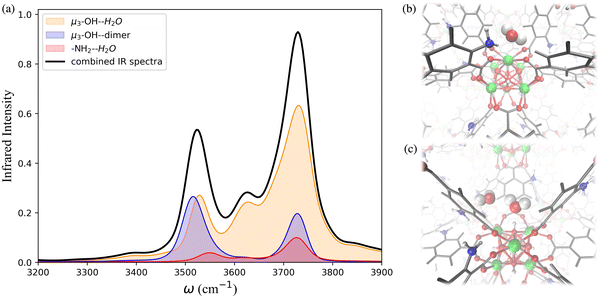
To further investigate the hydrogen-bonding connectivity in the pores of pristine UiO-66, we calculated the IR spectra of water molecules located at different interaction sites within the MOF pores (Fig. 4b) at 10% RH where the contribution of water-MOF and water–water interactions can be identified more easily. Based on the RDFs, μ3-OH and Olinker are the preferential binding sites at 10% RH, where approximately 67% and 13% of the water are located around the μ3-OH sites and Olinker, respectively. When interacting with the Olinker, water acts as a hydrogen-bond donor, which gives rise to the non-hydrogen-bonded O–H stretch and the hydrogen-bonded O–H stretch in the IR spectrum (Fig. 4a) at ∼3713 cm−1 and ∼3582 cm−1, respectively.10,59 The water hydrogen-bonded to the μ3-OH acts as a hydrogen-bond acceptor, resulting in symmetric (∼3632 cm−1) and asymmetric (∼3743 cm−1) O–H stretches. Interestingly, because of the electric coupling associated with the hydrogen bond between the μ3-OH group and water, the O–H stretching of water also reports on the vibration of μ3-OH at 3526 cm−1 (Fig. 4a), which is in agreement with the vibrational frequency of μ3-OH measured experimentally for UiO-66.10,59 We determined the IR signal of water induced by the vibration of the hydrogen-bond donating interaction sites on the framework (e.g., μ3-OH) by labeling the H atoms of the sites with deuterium (D) (refer to Section 4 in ESI†). The symmetric and asymmetric O–H stretch signals are only significant at low water loading (i.e., 10% RH) since under these conditions water is not donating hydrogen bonds to neighboring water molecules.84 The remaining water molecules (approximatively 20%) are part of water dimers interacting with μ3-OH sites. These involve a water molecule accepting a hydrogen-bond from a μ3-OH site while donating a hydrogen-bond to a neighboring water molecule. The signal at 3526 cm−1 is contributed by the hydrogen-bonded O–H stretch of the water dimer, while the non-hydrogen-bonded free O–H stretch can be observed at 3713 cm−1. All these observed vibrational modes of water are consistent with a recent study by Zhang et al., where they selectively measured the IR signals of the different O–H stretches in a water dimer.84
As the water loading increases at 20% RH, there are two main signals with similar intensity around 3500 and 3700 cm−1 (Fig. 4a). These peaks correspond to the vibrational signals of water dimers just discussed. In addition, the symmetric (∼3632 cm−1) and asymmetric vibrations (∼3743 cm−1) corresponding to water acting as a hydrogen-bond acceptor have been weakened. These results indicate that an extended formation of hydrogen-bonds between water molecules occurs at 20% RH. Overall, the IR spectra of water in UiO-66 show that at low water loading (10% RH), the μ3-OH is the primary binding site and the formation of water dimers bonded to this site outweighs the interaction of water with the Olinker sites. As the water loading increases additional water tends to form water clusters around the μ3-OH site.
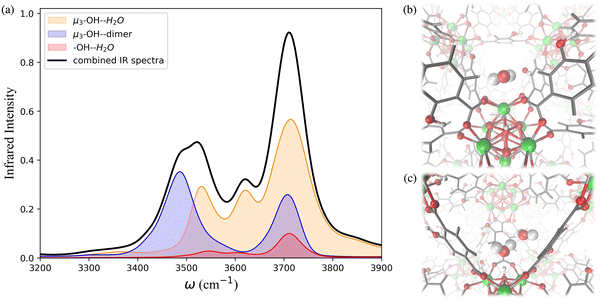
The IR spectra calculated for the functionalized MOFs (Fig. 5) show similar profiles to the IR spectra of UiO-66 with some variations caused by the dipole moment induced by the presence of functional groups within the MOFs. In order to understand which interactions are responsible for the different features of the IR spectra for the functionalized MOFs we analyzed the contributions from water interacting with the different sites of the UiO-66 variants at 10% RH (Fig. 6a and 7a). In these MOFs, ∼10% of water is located around the Olinker sites. Since the –NH2 and –OH functional groups are located close to the Olinker, the water molecules at these sites can simultaneously interact with the adjacent –OH and –NH2 functional groups. Thus, in addition to the non-hydrogen-bonded (∼3713 cm−1) and hydrogen-bonded O–H stretch (∼3582 cm−1) associated with a hydrogen-bond donor, the O–H stretch vibrations of the water molecules located near the Olinker in UiO-66 (Fig. 4b), also report on the vibrations of the –OH and –NH2 functional groups due to electric couplings (spectral features at ∼3550 cm−1 in Fig. 6a and 7a). In UiO-66-OH, the remaining water molecules are bonded to the μ3-OH sites (∼57%), or form dimers near the μ3-OH sites (33%). Similar results were obtained for UiO-66-NH2, with 63% of the water molecules involved in μ3-OH⋯H2O interactions and 27% in water dimers hydrogen-bonded to the μ3-OH sites. Overall, while the μ3-OH⋯H2O interaction remains the preferred interaction, there are more water dimers formed in the functionalized MOFs compared to UiO-66. The spectral feature corresponding to the hydrogen-bonded O–H stretch in the water dimers occurs at a lower frequency in UiO-66-OH (3492 cm−1) relative to UiO-66-NH2 (3515 cm−1) as shown in Fig. 5 at both 10% and 20% RH. This is due to water interacting with the –OH functional groups being more polarized and forming stronger hydrogen-bonds with the water hydrogen-bonded to the μ3-OH sites. This finding aligns with the calculated RDFs showing that –NH2 interacts less strongly with water relative to –OH. Overall, the formation of more water dimers and larger polarization effects associated with the –OH group are responsible for the broadening of the hydrogen-bonded O–H stretching signal observed in –OH functionalized MOFs compared to UiO-66.
Another change in the IR spectra of the functionalized MOFs is that the signal corresponding to non-hydrogen-bonded O–H stretching vibrations of water is slightly red-shifted to 3709 cm−1 (Fig. 5a) compared to UiO-66 (3723 cm−1). This redshift can be explained by the fact that water bonded to the μ3-OH sites in the functionalized MOFs has a higher tendency to donate hydrogen bonds to either water (thus forming dimers) or nearby functional groups. This leads to a greater contribution of non-hydrogen-bonded O–H stretching from hydrogen-bond-donating molecules in the spectra of the functionalized MOFs relative to UiO-66 (mostly asymmetric O–H stretch contribution from hydrogen-bond accepting waters above 3700 cm−1, Fig. 4b). This explanation is supported by the fact that the peak corresponding to the non-hydrogen-bonded O–H stretch of μ3-OH⋯H2O in the IR spectra of water in the functionalized MOFs (yellow curve in Fig. 6a and 7a) arises at a slightly lower frequency (3713 cm−1) than the same peak (3743 cm−1) in the UiO-66 spectrum (yellow curve in Fig. 4b). This observation is consistent with the study performed by Zhang et al. that reported the non-hydrogen-bonded signal of a hydrogen-bond donating water molecule at a lower frequency than the asymmetric stretch of a hydrogen-bond accepting water molecule.84 Thus, we find that the presence of the –OH and –NH2 functional groups can (1) provide an additional attractive force for water to locate near the Olinker atoms and (2) stabilize the formation of water dimers. The former aids the formation of water clusters within the octahedral pores, while the latter allows water to form hydrogen-bonded chains anchored in the tetrahedral pores (where the strongest μ3-OH adsorption sites are located) and reaching into the octahedral pores. Both features seed the formation of water clusters within the larger octahedral pores, thus explaining why the burst uptake of water is observed at lower RH for the functionalized MOFs in several experimental studies.20,85,86
The two-dimensional density distribution maps of water within UiO-66 when RH = 10–40% provide further insights into the pore filling process. At low water loading (RH = 10%, Fig. 8), the water is predominantly located at the μ3-OH sites in the tetrahedral pores. This aligns with our RDF results and predicted IR spectra, as well as previous findings in the literature, showing that at low water loading water occupies the tetrahedral pores first.13,28 Subsequent adsorbed water (RH = 20–30%) tends to form hydrogen-bonded networks with water molecules adsorbed at the μ3-OH sites within the tetrahedral pores. This results in water being preferentially located in the tetrahedral pores at these RH levels. Moreover, the water molecules tend to fill the tetrahedral pores that already contain water molecules rather than evenly distribute across all tetrahedral pores (Fig. S8, ESI†), suggesting that the formation of water clusters stabilizes the water molecules within the tetrahedral pores. This observation is consistent with the IR spectra showing that the extended formation of hydrogen-bonded water chains is mainly responsible for the IR signal at 20% RH (Fig. 4). Due to the symmetry of the UiO-66 framework, water clusters can form in any of the tetrahedral pores without a bias for specific ones (Fig. S8, ESI†). A similar phenomenon also occurs at 30% RH, where the formation of water clusters is preferred within the tetrahedral pores. However, the tetrahedral pores become unable to accommodate the water molecules as water loading increases beyond 30% RH (Fig. 8). The additional water molecules tend to diffuse across the octahedral cavities interconnecting the tetrahedral pores and achieve a relatively more even distribution compared to water within UiO-66 at 20% RH. As the RH increases beyond 30%, water clusters start to form within the octahedral pores as shown in Fig. 8. This RH level corresponds to the adsorption step (burst uptake of water) in the experimental adsorption isotherm (Fig. 1a).11 Thus, we conclude that the hydrogen-bonded chains of water anchoring on the μ3-OH sites in the tetrahedral pores and reaching into the octahedral pores provide the driving force for water clusters to form in the larger octahedral cavities, resulting in the burst uptake of water.
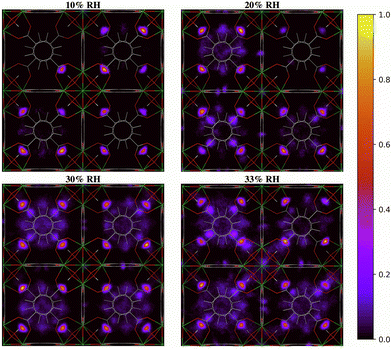 | ||
| Fig. 8 Two-dimensional density distribution maps for water within UiO-66 at 10–40% relative humidity (RH) along the xy-plane. Refer to Fig. 1b to identify the position of the different pores and relevant interaction sites in the density maps. The scale bar indicates the density of water relative to the highest density region in the unit cell. | ||
The two-dimensional density distribution maps for the functionalized MOFs show that, although water preferentially occupies the μ3-OH sites at low water loading, some water molecules are located near the functional groups of the linkers at 20% RH (Fig. 9). Moreover, water molecules are distributed more evenly across the framework compared to UiO-66 at the same water loading. In fact, significant numbers of water molecules are in the octahedral pores in the presence of functional groups (Fig. 9) compared to unfunctionalized UiO-66 at 30% RH (Fig. 8). This result aligns with the IR spectra, which indicate that the presence of functional groups favors the formation of H2O⋯H2O hydrogen-bonded chains that facilitate the diffusion of water molecules across the pores and help stabilize water near the Olinker interaction sites within the octahedral pores. Overall, these results provide a molecular-level understanding of why functionalized UiO-66 MOFs show an abrupt increase in water uptake at lower water loadings relative to UiO-66.
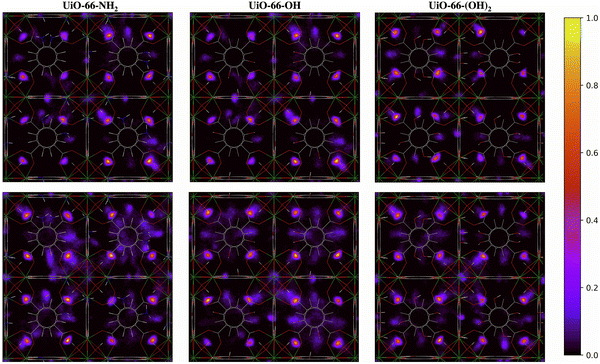 | ||
| Fig. 9 Two-dimensional density distribution maps for water within UiO-66-NH2, UiO-66-OH, UiO-66-(OH)2 with the same number of water molecules per unit cell as UiO-66 at 20% (top panel) and 30% (bottom panel) relative humidity (RH) along the xy-plane. Refer to Fig. 1b to identify the position of the different pores and relevant interaction sites in the density maps. The scale bar indicates the density of water relative to the highest density region in the unit cell. | ||
Conclusions
The UiO-66 MOF is a promising material for atmospheric water harvesting and experimental studies have demonstrated that its adsorption performance at low RH (10–30%) can be further improved via the introduction of hydrophilic functional groups.7,20,86 Molecular-level insights into the interaction between water and MOFs are required to maximise the performance of these materials in water harvesting and use this technology at the industrial scale. In this work, we developed MD force field models for UiO-66 and its –NH2, –OH and –(OH)2 functionalized derivatives based on results from DFT calculations and experimental IR spectra. We then used MD simulations to compute the RDFs, IR spectra, and two-dimensional density distribution maps of water in the MOFs to gain a molecular-level understanding of water adsorption in UiO-66 and the influence of functionalization on this process. The pore filling process initiates at the μ3-OH sites, which have the highest affinity for water in UiO-66 and its functionalized derivatives. When an adequate amount of water has been adsorbed and the tetrahedral pores have been filled as RH increases, hydrogen-bonded water chains anchoring on the μ3-OH sites in the tetrahedral pores and reaching into the octahedral pores start to form. This phenomenon can be linked to the burst uptake of water shown in the experimental adsorption isotherm in UiO-66.11 The presence of hydrophilic functional groups such as –OH provides an additional driving force for the formation of hydrogen-bonded water chains leading to the octahedral pores being filled with water at lower relative humidity. In addition to functional groups, recent studies have demonstrated that missing linker and missing cluster defects that are commonly present in UiO-66 can significantly increase its adsorptive performance.12,13,87 Work is currently underway in our group to develop an accurate force field for defective UiO-66 and study its interaction with water. Overall, the present work provides a molecular-level understanding of why the functionalized MOFs show the adsorption step to occur at lower RH compared to unfunctionalized UiO-66. This knowledge can be used for the design of improved MOFs for water harvesting.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The research by J.Z. is supported by an Australian Government Research Training Program (RTP) Scholarship. F.P. was supported by the Department of Energy, Basic Energy Science (BES) Office through award no. DE-SC0022332. We are grateful for computational resources and services from the National Computational Infrastructure (NCI), provided by the Australian Government under the National Computational Merit Allocation Scheme, and the computational cluster Katana supported by Research Technology Services at UNSW Sydney. Ching-Hwa Ho, Kelly M. Hunter, and Hilliary O. Frank are acknowledged for helpful suggestions and training during this project.References
- M. M. Mekonnen and A. Y. Hoekstra, Four Billion People Facing Severe Water Scarcity, Sci. Adv., 2016, 2(2), e1500323, DOI:10.1126/sciadv.1500323
.
- N. Voulvoulis, Water Reuse from a Circular Economy Perspective and Potential Risks from an Unregulated Approach, Curr. Opin. Environ. Sci. Health, 2018, 2, 32–45, DOI:10.1016/j.coesh.2018.01.005
.
-
P. Gleick, et al., in Water Resources, Encyclopaedia of Climate and Weather, ed. S. H. Schneider, Oxford University Press, New York, 1996, vol. 2, pp. 817–823 Search PubMed
.
- X. Zhou, H. Lu, F. Zhao and G. Yu, Atmospheric Water Harvesting: A Review of Material and Structural Designs, ACS Mater. Lett., 2020, 2(7), 671–684, DOI:10.1021/acsmaterialslett.0c00130
.
- O. Klemm, R. S. Schemenauer, A. Lummerich, P. Cereceda, V. Marzol, D. Corell, J. van Heerden, D. Reinhard, T. Gherezghiher, J. Olivier, P. Osses, J. Sarsour, E. Frost, M. J. Estrela, J. A. Valiente and G. M. Fessehaye, Fog as a Fresh-Water Resource: Overview and Perspectives, Ambio, 2012, 41(3), 221–234, DOI:10.1007/s13280-012-0247-8
.
- Y. Jin, L. Zhang and P. Wang, Atmospheric Water Harvesting: Role of Surface Wettability and Edge Effect, Global Challenges, 2017, 1(4), 1700019, DOI:10.1002/gch2.201700019
.
- N. Hanikel, M. S. Prévot and O. M. Yaghi, MOF Water Harvesters, Nat. Nanotechnol., 2020, 15(5), 348–355, DOI:10.1038/s41565-020-0673-x
.
- N. Stock and S. Biswas, Synthesis of Metal-Organic Frameworks (MOFs): Routes to Various MOF Topologies, Morphologies, and Composites, Chem. Rev., 2012, 933–969, DOI:10.1021/cr200304e
.
- H. Jasuja and K. S. Walton, Effect of Catenation and Basicity of Pillared Ligands on the Water Stability of MOFs, Dalton Trans., 2013, 42(43), 15421, 10.1039/c3dt51819a
.
- J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, A New Zirconium Inorganic Building Brick Forming Metal Organic Frameworks with Exceptional Stability, J. Am. Chem. Soc., 2008, 130(42), 13850–13851, DOI:10.1021/ja8057953
.
- H. Furukawa, F. Gándara, Y. B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, Water Adsorption in Porous Metal-Organic Frameworks and Related Materials, J. Am. Chem. Soc., 2014, 136(11), 4369–4381, DOI:10.1021/ja500330a
.
- Y. Feng, Q. Chen, M. Jiang and J. Yao, Tailoring the Properties of UiO-66 through Defect Engineering: A Review. Industrial and Engineering Chemistry Research, Am. Chem. Soc., 2019, 17646–17659, DOI:10.1021/acs.iecr.9b03188
.
- P. Ghosh, Y. J. Colón and R. Q. Snurr, Water Adsorption in UiO-66: The Importance of Defects, Chem. Commun., 2014, 50(77), 11329–11331, 10.1039/C4CC04945D
.
- B. Shan, S. M. McIntyre, M. R. Armstrong, Y. Shen and B. Mu, Investigation of Missing-Cluster Defects in UiO-66 and Ferrocene Deposition into Defect-Induced Cavities, Ind. Eng. Chem. Res., 2018, 57(42), 14233–14241, DOI:10.1021/acs.iecr.8b03516
.
- K. Hyunho, Y. Sungwoo, R. S. R, N. Shankar, K. E. A, F. Hiroyasu, U. A. S, Y. O. M and W. E. N, Water Harvesting from Air with Metal-Organic Frameworks Powered by Natural Sunlight, Science, 2017, 356(6336), 430–434, DOI:10.1126/science.aam8743
.
- H. Kim, S. Yang, S. R. Rao, S. Narayanan, E. A. Kapustin, H. Furukawa, A. S. Umans, O. M. Yaghi and E. N. Wang, Water Harvesting from Air with Metal-Organic Frameworks
Powered by Natural Sunlight, Renewable Resour., 2017, 356(6336), 430–432 CrossRef CAS
.
- F. Fathieh, M. J. Kalmutzki, E. A. Kapustin, P. J. Waller, J. Yang and O. M. Yaghi, Practical Water Production from Desert Air, Sci. Adv., 2018, 4(6), eaat3198, DOI:10.1126/sciadv.aat3198
.
- F. Jeremias, V. Lozan, S. K. Henninger and C. Janiak, Programming MOFs for Water Sorption: Amino-Functionalized MIL-125 and UiO-66 for Heat Transformation and Heat Storage Applications, Dalton Trans., 2013, 42(45), 15967, 10.1039/c3dt51471d
.
- J. Canivet, J. Bonnefoy, C. Daniel, A. Legrand, B. Coasne and D. Farrusseng, Structure–Property Relationships of Water Adsorption in Metal–Organic Frameworks, New J. Chem., 2014, 38(7), 3102–3111, 10.1039/C4NJ00076E
.
- X. Tang, Y. Luo, Z. Zhang, W. Ding, D. Liu, J. Wang, L. Guo and M. Wen, Effects of Functional Groups of –NH2 and –NO2 on Water Adsorption Ability of Zr-Based MOFs (UiO-66, Chem. Phys., 2021, 543, DOI:10.1016/j.chemphys.2021.111093
.
- F.-F. Lu, X.-W. Gu, E. Wu, B. Li and G. Qian, Systematic Evaluation of Water Adsorption in Isoreticular UiO-Type Metal–Organic Frameworks, J. Mater. Chem. A, 2023, 11(3), 1246–1255, 10.1039/D2TA07392G
.
- J. Winarta, B. Shan, S. M. Mcintyre, L. Ye, C. Wang, J. Liu and B. Mu, A Decade of UiO-66 Research: A Historic Review of Dynamic Structure, Synthesis Mechanisms, and Characterization Techniques of an Archetypal Metal–Organic Framework, Cryst. Growth Des., 2020, 20(2), 1347–1362, DOI:10.1021/acs.cgd.9b00955
.
- A. D. Wiersum, E. Soubeyrand-Lenoir, Q. Yang, B. Moulin, V. Guillerm, M. Yahia, S. ben; Bourrelly, A. Vimont, S. Miller, C. Vagner, M. Daturi, G. Clet, C. Serre, G. Maurin and P. L. Llewellyn, An Evaluation of UiO-66 for Gas-Based Applications, Chem. – Asian J., 2011, 6(12), 3270–3280, DOI:10.1002/asia.201100201
.
- J. L. Mancuso, A. M. Mroz, K. N. Le and C. H. Hendon, Electronic Structure Modeling of Metal–Organic Frameworks, Chem. Rev., 2020, 120(16), 8641–8715, DOI:10.1021/acs.chemrev.0c00148
.
- J. D. Evans, G. Fraux, R. Gaillac, D. Kohen, F. Trousselet, J.-M. Vanson and F.-X. Coudert, Computational Chemistry Methods for Nanoporous Materials, Chem. Mater., 2017, 29(1), 199–212, DOI:10.1021/acs.chemmater.6b02994
.
- F.-X. Coudert and A. H. Fuchs, Computational Characterization and Prediction of Metal–Organic Framework Properties, Coord. Chem. Rev., 2016, 307, 211–236, DOI:10.1016/j.ccr.2015.08.001
.
- A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations, J. Am. Chem. Soc., 1992, 114(25), 10024–10035, DOI:10.1021/ja00051a040
.
- S. Wang, G. Zhou, Y. Sun and L. Huang, A Computational Study of Water in UiO-66 Zr-MOFs: Diffusion, Hydrogen Bonding Network, and Confinement Effect, AIChE J., 2021, 67(3), e17035, DOI:10.1002/aic.17035
.
- C. Caratelli, J. Hajek, E. J. Meijer, M. Waroquier and V. Van Speybroeck, Dynamic Interplay between Defective UiO-66 and Protic Solvents in Activated Processes, Chem. – Eur. J., 2019, 25(67), 15315–15325, DOI:10.1002/chem.201903178
.
- P. B. Shukla and J. K. Johnson, Impact of Loading-Dependent Intrinsic Framework Flexibility on Adsorption in UiO-66, J. Phys. Chem. C, 2022, 126(41), 17699–17711, DOI:10.1021/acs.jpcc.2c04629
.
- V. Babin, C. Leforestier and F. Paesani, Development of a “First Principles” Water Potential with Flexible Monomers: Dimer Potential Energy Surface, VRT Spectrum, and Second Virial Coefficient, J. Chem. Theory Comput., 2013, 9(12), 5395–5403, DOI:10.1021/ct400863t
.
- V. Babin, G. R. Medders and F. Paesani, Development of a “First Principles” Water Potential with Flexible Monomers. II: Trimer Potential Energy Surface, Third Virial Coefficient, and Small Clusters, J. Chem. Theory Comput., 2014, 10(4), 1599–1607, DOI:10.1021/ct500079y
.
- G. R. Medders, V. Babin and F. Paesani, Development of a “First-Principles” Water Potential with Flexible Monomers. III. Liquid Phase Properties, J. Chem. Theory Comput., 2014, 10(8), 2906–2910, DOI:10.1021/ct5004115
.
- F. Paesani, Getting the Right Answers for the Right Reasons: Toward Predictive Molecular Simulations of Water with Many-Body Potential Energy Functions, Acc. Chem. Res., 2016, 49(9), 1844–1851, DOI:10.1021/acs.accounts.6b00285
.
- S. K. Reddy, S. C. Straight, P. Bajaj, C. Huy Pham, M. Riera, D. R. Moberg, M. A. Morales, C. Knight, A. W. Götz and F. Paesani, On the Accuracy of the MB-Pol Many-Body Potential for Water: Interaction Energies, Vibrational Frequencies, and Classical Thermodynamic and Dynamical Properties from Clusters to Liquid Water and Ice, J. Chem. Phys., 2016, 145(19), 194504, DOI:10.1063/1.4967719
.
- G. R. Medders and F. Paesani, Dissecting the Molecular Structure of the Air/Water Interface from Quantum Simulations of the Sum-Frequency Generation Spectrum, J. Am. Chem. Soc., 2016, 138(11), 3912–3919, DOI:10.1021/jacs.6b00893
.
- G. R. Medders and F. Paesani, Infrared and Raman Spectroscopy of Liquid Water through “First-Principles” Many-Body Molecular Dynamics, J. Chem. Theory Comput., 2015, 11(3), 1145–1154, DOI:10.1021/ct501131j
.
-
D. E. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning, Addison-Wesley Longman Publishing Co., Inc., USA, 1st edn, 1989 Search PubMed
.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138, DOI:10.1103/PhysRev.140.A1133
.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871, DOI:10.1103/PhysRev.136.B864
.
- G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561, DOI:10.1103/PhysRevB.47.558
.
- G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal-Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251–14269, DOI:10.1103/PhysRevB.49.14251
.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169
.
- G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0
.
- E. R. Johnson and A. D. Becke, A Post-Hartree-Fock Model of Intermolecular Interactions: Inclusion of Higher-Order Corrections, J. Chem. Phys., 2006, 124(17), 174104, DOI:10.1063/1.2190220
.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465, DOI:10.1002/jcc.21759
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104, DOI:10.1063/1.3382344
.
- N. Mardirossian and M. Head-Gordon, ΩB97X-V: A 10-Parameter, Range-Separated Hybrid, Generalized Gradient Approximation Density Functional with Nonlocal Correlation, Designed by a Survival-of-the-Fittest Strategy, Phys. Chem. Chem. Phys., 2014, 16(21), 9904, 10.1039/c3cp54374a
.
- A. Najibi and L. Goerigk, The Nonlocal Kernel in van der Waals Density Functionals as an Additive Correction: An Extensive Analysis with Special Emphasis on the B97M-V and ΩB97M-V Approaches, J. Chem. Theory Comput., 2018, 14(11), 5725–5738, DOI:10.1021/acs.jctc.8b00842
.
- F. Neese, The ORCA Program System, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78, DOI:10.1002/wcms.81
.
- F. Neese, Prediction of Molecular Properties and Molecular Spectroscopy with Density Functional Theory: From Fundamental Theory to Exchange-Coupling, Coord. Chem. Rev., 2009, 253(5–6), 526–563, DOI:10.1016/j.ccr.2008.05.014
.
- F. Neese, Software Update: The ORCA Program System—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1606, DOI:10.1002/wcms.1606
.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297, 10.1039/b508541a
.
- F. Weigend, Accurate Coulomb-Fitting Basis Sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8(9), 1057, 10.1039/b515623h
.
- D. Andrae, U. Huermann, M. Dolg, H. Stoll and H. Preu, Energy-Adjustedab Initio Pseudopotentials for the Second and Third Row Transition Elements, Theor. Chim. Acta, 1990, 77(2), 123–141, DOI:10.1007/BF01114537
.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and Testing of a General Amber Force Field, J. Comput. Chem., 2004, 25(9), 1157–1174, DOI:10.1002/jcc.20035
.
- Y. Fang, L. Zhang, Q. Zhao, X. Wang and X. Jia, Highly Selective Visible-Light Photocatalytic Benzene Hydroxylation to Phenol Using a New Heterogeneous Photocatalyst UiO-66-NH2-SA-V, Catal. Lett., 2019, 149(9), 2408–2414, DOI:10.1007/s10562-019-02842-3
.
- H. Veisi, M. Abrifam, S. A. Kamangar, M. Pirhayati, S. G. Saremi, M. Noroozi, T. Tamoradi and B. Karmakar, Pd Immobilization Biguanidine Modified Zr-UiO-66 MOF as a Reusable Heterogeneous Catalyst in Suzuki–Miyaura Coupling, Sci. Rep., 2021, 11(1), 21883, DOI:10.1038/s41598-021-00991-3
.
- K. I. Hadjiivanov, D. A. Panayotov, M. Y. Mihaylov, E. Z. Ivanova, K. K. Chakarova, S. M. Andonova and N. L. Drenchev, Power of Infrared and Raman Spectroscopies to Characterize Metal-Organic Frameworks and Investigate Their Interaction with Guest Molecules, Chem. Rev., 2021, 10, 1286–1424, DOI:10.1021/acs.chemrev.0c00487
.
- Z. H. Rada, H. R. Abid, J. Shang, H. Sun, Y. He, P. Webley, S. Liu and S. Wang, Functionalized UiO-66 by Single and Binary (OH)2 and NO2 Groups for Uptake of CO2 and CH4, Ind. Eng. Chem. Res., 2016, 55(29), 7924–7932, DOI:10.1021/acs.iecr.5b04061
.
- Z. S. Moghaddam, M. Kaykhaii, M. Khajeh and A. R. Oveisi, Synthesis of UiO-66-OH Zirconium Metal-Organic Framework and Its Application for Selective Extraction and Trace Determination of Thorium in Water Samples by Spectrophotometry, Spectrochim. Acta, Part A, 2018, 194, 76–82, DOI:10.1016/j.saa.2018.01.010
.
- A. J. Rieth, K. M. Hunter, M. Dincă and F. Paesani, Hydrogen Bonding Structure of Confined Water Templated by a Metal-Organic Framework with Open Metal Sites, Nat. Commun., 2019, 10(1), 4771, DOI:10.1038/s41467-019-12751-z
.
- A. Kumar and P. Kumar, Gas Phase Acidity of Water Clusters, Phys. Chem. Chem. Phys., 2022, 24(30), 18236–18244, 10.1039/D2CP01578A
.
- T. Yagasaki, K. Iwahashi, S. Saito and I. Ohmine, A Theoretical Study on Anomalous Temperature Dependence of PKw of Water, J. Chem. Phys., 2005, 122(14), 144504, DOI:10.1063/1.1878712
.
- NIST web page. https://webbook.nist.gov/ (accessed 2023-06-21).
- K. C. Kim, D. Yu and R. Q. Snurr, Computational Screening of Functional Groups for Ammonia Capture in Metal–Organic Frameworks, Langmuir, 2013, 29(5), 1446–1456, DOI:10.1021/la3045237
.
- J. Jiang and O. M. Yaghi, Brønsted Acidity in Metal–Organic Frameworks, Chem. Rev., 2015, 115(14), 6966–6997, DOI:10.1021/acs.chemrev.5b00221
.
- A. H. Ibrahim, W. A. El-Mehalmey, R. R. Haikal, M. E. A. Safy, M. Amin, H. R. Shatla, S. G. Karakalos and M. H. Alkordi, Tuning the Chemical Environment within the UiO-66-NH 2 Nanocages for Charge-Dependent Contaminant Uptake and Selectivity, Inorg. Chem., 2019, 58(22), 15078–15087, DOI:10.1021/acs.inorgchem.9b01611
.
- J. C. Wagner, K. M. Hunter, F. Paesani and W. Xiong, Water Capture Mechanisms at Zeolitic Imidazolate Framework Interfaces, J. Am. Chem. Soc., 2021, 143(50), 21189–21194, DOI:10.1021/jacs.1c09097
.
- K. M. Hunter, J. C. Wagner, M. Kalaj, S. M. Cohen, W. Xiong and F. Paesani, Simulation Meets Experiment: Unraveling the Properties of Water in Metal-Organic Frameworks through Vibrational Spectroscopy, J. Phys. Chem. C, 2021, 125(22), 12451–12460, DOI:10.1021/acs.jpcc.1c03145
.
- H. A. Lorentz, Ueber Die Anwendung Des Satzes Vom Virial in Der Kinetischen Theorie Der Gase, Ann. Phys., 1881, 248(1), 127–136, DOI:10.1002/andp.18812480110
.
- J. L. F. Abascal and C. Vega, A General Purpose Model for the Condensed Phases of Water: TIP4P/2005, J. Chem. Phys., 2005, 123(23), 234505, DOI:10.1063/1.2121687
.
- C.-H. Ho, M. L. Valentine, Z. Chen, H. Xie, O. Farha, W. Xiong and F. Paesani, Structure and Thermodynamics of Water Adsorption in NU-1500-Cr, Commun. Chem., 2023, 6(1), 70, DOI:10.1038/s42004-023-00870-0
.
- S. Simon, M. Duran and J. J. Dannenberg, Effect of Basis Set Superposition Error on the Water Dimer Surface Calculated at Hartree-Fock, Møller-Plesset, and Density Functional Theory Levels, J. Phys. Chem. A, 1999, 103, 1640–1643 CrossRef CAS
.
- S. Simon, M. Duran and J. J. Dannenberg, How Does Basis Set Superposition Error Change the Potential Surfaces for Hydrogen-bonded Dimers?, J. Chem. Phys., 1996, 105(24), 11024–11031, DOI:10.1063/1.472902
.
- A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, Charge Model 5: An Extension of Hirshfeld Population Analysis for the Accurate Description of Molecular Interactions in Gaseous and Condensed Phases, J. Chem. Theory Comput., 2012, 8(2), 527–541, DOI:10.1021/ct200866d
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. NakatsujiGaussian 16, Gaussian Inc, Wallingford CT, 2016 Search PubMed
.
- W. Smith and T. R. Forester DL_POLY_2.0: A General-Purpose Parallel Molecular Dynamics Simulation Package; 1996.
-
M. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation, Oxford university press, 2010 Search PubMed
.
-
R. L. Andrew, Molecular Modeling Principles and Applications, Prentice Hall, London, 2001 Search PubMed
.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations, J. Comput. Chem., 2009, 30(13), 2157–2164, DOI:10.1002/jcc.21224
.
- J. E. Bertie and Z. Lan, Infrared Intensities of Liquids XX: The Intensity of the OH Stretching Band of Liquid Water Revisited, and the Best Current Values of the Optical Constants of H2O(l) at 25 °C between 15
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 1 Cm−1, Appl. Spectrosc., 1996, 50(8), 1047–1057, DOI:10.1366/0003702963905385
000 and 1 Cm−1, Appl. Spectrosc., 1996, 50(8), 1047–1057, DOI:10.1366/0003702963905385 .
- K. Ramasesha, L. de Marco, A. Mandal and A. Tokmakoff, Water Vibrations Have Strongly Mixed Intra- and Intermolecular Character, Nat. Chem., 2013, 5(11), 935–940, DOI:10.1038/nchem.1757
.
- B. Zhang, Y. Yu, Z. Zhang, Y. Y. Zhang, S. Jiang, Q. Li, S. Yang, H. S. Hu, W. Zhang, D. Dai, G. Wu, J. Li, D. H. Zhang, X. Yang and L. Jiang, Infrared Spectroscopy of Neutral Water Dimer Based on a Tunable Vacuum Ultraviolet Free Electron Laser, J. Phys. Chem. Lett., 2020, 11(3), 851–855, DOI:10.1021/acs.jpclett.9b03683
.
- S. I. Kim, T. U. Yoon, M. B. Kim, S. J. Lee, Y. K. Hwang, J. S. Chang, H. J. Kim, H. N. Lee, U. H. Lee and Y. S. Bae, Metal–Organic Frameworks with High Working Capacities and Cyclic Hydrothermal Stabilities for Fresh Water Production, Chem. Eng. J., 2016, 286, 467–475, DOI:10.1016/j.cej.2015.10.098
.
- P. M. Schoenecker, C. G. Carson, H. Jasuja, C. J. J. Flemming and K. S. Walton, Effect of Water Adsorption on Retention of Structure and Surface Area of Metal-Organic Frameworks, Ind. Eng. Chem. Res., 2012, 51(18), 6513–6519, DOI:10.1021/ie202325p
.
- A. F. Hernandez, R. K. Impastato, M. I. Hossain, B. D. Rabideau and T. G. Glover, Water Bridges Substitute for Defects in Amine-Functionalized UiO-66, Boosting CO 2 Adsorption, Langmuir, 2021, 37(35), 10439–10449, DOI:10.1021/acs.Langmuir.1c01149
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational details for the DFT and MD calculations as well as force field development and benchmarking; additional RDF plots and two-dimensional density distribution maps for water within UiO-66 and its functionalized derivatives. See DOI: https://doi.org/10.1039/d3tc01313h |
| This journal is © The Royal Society of Chemistry 2023 |