Computational investigation of α-SiO₂ surfaces as a support for Pd

Abstract

The properties of a supported metal catalyst depend crucially on the interaction between the active metal and the support. A case in point is Pd supported on silica, Pd/SiO₂, which is widely used in oxidation catalysis. There is a need for a broad range of computational models that describe the interaction of Pd with silica surfaces so that active site models can be proposed and tested. In this work, we create well-defined, reproducible, periodic models of SiO₂ surfaces and investigate their interaction with Pd using dispersion-corrected DFT. We use crystalline α-SiO₂ as a useful starting point for creating and estimating the adsorption properties of metals on SiO₂ surfaces, which can represent the specific isolated functional groups present on more complex amorphous silica surfaces. We have modelled α-SiO₂ (001), (100) and (101) surfaces containing isolated siloxane and silanol functional groups and estimated their affinity towards the adsorption of Pd atoms regarding an isolated gaseous Pd atom and the fcc Pd solid. This provides additional information on the ease with which Pd can be dispersed on the surfaces in question. From our model, we characterise the surface energies of the α-SiO₂ (hkl) surfaces and calculate the geometries of the Pd₁/α-SiO₂ (hkl) adsorption site on each surface. We estimate that Pd₁(g) will prefer to adsorb close to strained four-membered siloxane rings or on a vicinal silanol group of α-SiO₂ (101).

---

1 Introduction

One of the best-known applications of catalysis is pollution control for the emissions from the fuel burnt in combustion engines.^1–9 Highly refined catalysts consisting of precious metals supported on oxides have dramatically reduced the amount of CO and NOx emitted.⁸ However, a remaining problem is mitigating methane emissions from incomplete fuel combustion.¹ As methane has a global warming potential of 84–87 times that of CO₂, it is essential to drive down its release from point sources such as combustion engines.^1,9 Unburnt fuel is generally controlled through oxidation catalysis.⁷ The catalytic conversion of unburnt fuels is well-known on silica (SiO₂)-supported palladium (Pd).^7,10–16 Silica is the predominant support surface for this application due to its low cost and structural integrity.^6,17 Although silica would not be expected to play as active a role in oxidation as reducible supports such as ceria,¹⁸ the interaction of the active metal with the support in heterogeneous catalysis will influence the activity of the catalytic system.^6,17

Silica is a non-reducible oxide with silicon in a formal oxidation state of Si⁴⁺ tetrahedrally coordinated by O²⁻ anions.^6,19 It is well known that the local structure reflects a high degree of covalent bonding.^6,17 The structure consists of chains of corner-sharing [SiO₄]⁴⁻ tetrahedra forming siloxane (Si–O) ring structures in various sizes.⁶ Under humid conditions below 973 K, the siloxane rings can hydroxylate, forming a variety of silanol (SiOH) functional groups.⁶

The silica support used in catalysis is generally synthesised in its amorphous form through sol–gel or flame pyrolysis techniques and is characterised by conventional analytical methods.^6,7,17 However, the characteristics of the Pd/SiO₂ systems result from interactions between metal and support at the molecular level. Thus, molecular modelling is useful for rapidly characterising surfaces and testing proposals for active site structures.⁶ This is because computer models can provide molecular structures that are precisely defined and characterised at the atomic level. These models can assist in the clarification of the data derived from experimental techniques such as X-ray spectroscopy and solid-state NMR.⁶ It is vital to construct well-defined surfaces if this system's characteristics and catalytic activity are to be investigated systematically.⁶ The methods by which surfaces and active sites are modelled have developed rapidly in recent decades. However, our understanding of systems like Pd/SiO₂ remains limited.^6,20

Computational models of amorphous silica surfaces have been constructed in previous studies.^17,21–25 The amorphous structure was created by annealing large unit cells of β-cristobalite at high temperatures.¹⁷ Cleaving slab models from the resulting structures exposes surfaces with a range of siloxane ring structures. Hydroxylation to take up Si–O dangling bonds¹⁷ and the placement of OH groups at under co-ordinated Si cations allows surface passivation. Mimicking the reaction with H₂O.¹⁷ From these computational models, various ring sizes of siloxane (O₃Si–O–SiO₃) bridges and distinct silanol (O₃Si–OH) functional groups were identified in conjunction and their calculated vibrational frequencies compared with experimental IR analyses. However, this approach is computationally expensive as the periodic unit cell model must contain more than 400 atoms to allow the surface to appear amorphous.

A study performed by Tosoni et al.,²⁶ describes a useful approach to model amorphous silica that drastically diminishes the required computational resources. Their method involves the crystalline edingtonite as the starting point for amorphous silica from which a variety of hydroxylated surfaces can be obtained. From their results, the theoretical infrared spectra were in good agreement with the experimental spectral data obtained from dry and wet amorphous silica. Tosoni et al. also conclude that theoretical water adsorption energies can be underestimated if dispersive forces are neglected.²⁶

An alternative method for modelling a silica support is to use the surfaces of crystalline α-SiO₂ for which the relatively small unit cell lowers the computational cost compared to other approaches. Specific siloxane and silanol functional groups found on the larger amorphous models can also be isolated by cutting surfaces of specific Miller indexes of the crystalline α-SiO₂. This method has been widely used to model the surface structure of α-SiO₂ in many atomistic forcefield and DFT computational studies.^17,27–40

In this study, we have created well-defined and reproducible models of silica support and used these to consider the interaction of Pd atoms with the clean stoichiometric surfaces and hydroxylated forms. We use the crystalline α-SiO₂ bulk as a starting point and use the advantage of the small bulk unit cell to investigate the effect of slab thickness on the results from our surface models. Through a combination of molecular dynamics (MD) and geometry optimisation, we reconstruct 4 to 8 layered slabs of the (001), (100) and (101) Miller planes that were cut from the α-SiO₂ bulk. The reconstruction produces two distinct isolated six-membered siloxane ring structures from the (001) and (100) Miller planes and an isolated four-membered siloxane ring from the (101) Miller plane.^41–43 For the silanol groups, we isolate two distinct geminal silanols (O₂Si(OH)₂) from the (001) and (100) planes as well as a vicinal silanol (O₃Si(OH)) from the (101) plane by hydroxylating the α-SiO₂ surfaces. The surface energies of each slab are initially calculated in each case as a function of slab thickness.^34,44–46 Furthermore, we report the adsorption energy of water on the α-SiO₂ surfaces that are required for complete hydroxylation.

Following optimisation of the stoichiometric and hydroxylated surfaces, a single Pd atom was adsorbed on all the possible adsorption sites available on each of the 4 layered α-SiO₂ surface surfaces. We identify the optimal adsorption sites for the Pd and closely examine the geometric properties of each adsorption site. We include van der Waals corrections and study their effect on surface and adsorption energy. This approach allows us to relate Pd's calculated adsorption energy to the silica surface's surface energy, showing that high surface energy implies a higher affinity for Pd adsorption. Similarly, the effect of hydroxyl groups on the adsorption energy of Pd to a surface will be discussed.

2 Computational details

All first-principles calculations of the periodic models were executed with the Cambridge Serial Total Energy Package (CASTEP) software⁴⁷ with initial model preparation using Biovia Materials Studio.

The Perdew–Burke–Ernzerhof⁴⁸ (PBE) was employed as the exchange correlated DFT functional.⁴⁹ Plane-wave basis sets were used to model the electronic wave functions in conjunction with on-the-fly generated (OTFG) ultrasoft pseudopotentials. Tests showed that calculated energies for bulk silica and Pd reference structures were fully converged with a plane wave basis cut-off energy of 700 eV. This value was used for all geometry optimisation calculations in this study. The effects of the attractive van der Waals forces were also considered for all periodic models by adding the Tkatchenko-Scheffler (TS) dispersion correction.⁴⁹ We will refer to the method used here as PBE-TS. A self-consistent dipole correction was applied in all cases where Pd was present on α-SiO₂ surfaces.

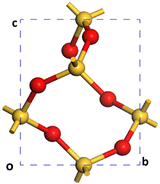
A Monkhorst–Pack grid was used to sample the Brillouin zone in all the models that lacked sufficient real space periodicity.^50,51 For the bulk reference cell of α-SiO₂ with a Si₃O₆ stoichiometry (Fig. 1), a 3 × 3 × 4 k-point mesh was employed in reciprocal space.⁵¹ For 1 × 1 × 1 α-SiO₂ slabs, k-points were set to 3 × 3 × 1. All slabs were created with a 15 Å vacuum gap.

Fig. 1 The periodic Si₃O₆ bulk of crystalline α-SiO₂ as calculated with PBE-TS (a = b = 4.98 Å, c = 5.40 Å, α = β = 90°, γ = 120°). Cell vector a is into the page, label “o” marks the origin of coordinates. Atoms are coloured Si: yellow and O: red.

For the Pd bulk, the fcc unit cell containing four atoms, a 6 × 6 × 6 k-point mesh was sufficient to converge the calculated lattice energy. For Pd adsorption to silica surfaces, the adsorption for Pd on the slab models produced for each surface was compared with a larger surface area (2 × 3 × 1) supercell to allow the interaction between periodic images to be assessed. For supercell calculations, only the Γ-point (k-points: 1 × 1 × 1) was used.⁵¹

The reference structures for H₂O representing the gaseous and liquid phases (see ESI,† Section S1) of the water adsorbate were calculated using the same plane wave cut-off as silica calculations and with only the reciprocal space Γ-point included.^52,53

The BFGS minimisation algorithm was used for all optimisation calculations. The geometry relaxation was accepted when the forces on all atoms were calculated to be <0.01 eV Å⁻¹.

Molecular dynamics (MD) calculations for finding the initial geometries of reconstructed silica surfaces were carried out with a PBE GGA and a plane-wave basis cut-off of 300 eV.⁴⁷ The NVT ensemble was employed with a Nose–Hoover thermostat set to a target temperature of 700 K.⁴⁷ All NVT-MD calculations were performed at the Γ-point.⁴⁷ Simulation times of 36 ps with a timestep of 1 fs were found to be sufficient for surface reconstructions to take place.

The surface energies, E_surf, of the cleaved and reconstructed α-SiO₂ slabs were calculated using:

where E_slab and E_bulk are the calculated total energies of the surface slab model and bulk reference, respectively. The factor, n, is the ratio of the number of formulae SiO₂ units in the slab and bulk models. All slab models were constructed to be stoichiometric with equivalent top and bottom faces so there is no dipole across the slab. 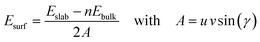No constraints were imposed on the atoms so both faces of the slab could relax, hence the factor of 2 in the denominator of eqn (1). The surface area of one face of the slab, A, was calculated from the cell vectors defining the 2D surface cell, u, and v, along with the angle between them, γ.

The surface energies for hydroxylated α-SiO₂ slabs were calculated assuming that the hydroxyl groups have been created by the reaction of the water on the surface. The surface energy then becomes:

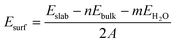Here, m, is the number of water molecules required to form the surface hydroxyl groups and E_H2O is the calculated energy per water molecule for water in the reference state calculation.

The adsorption energy, E_ads, for any adsorbate, M, (H₂O or Pd) at a particular position on an α-SiO₂ slab was calculated using:

E_ads = (E_slab-M − E_slab − n_ME_Mref)/n_M (3)

here E_slab-M, is the calculated energy for the simulation slab with n_M instances of the adsorbate in place, E_slab, is the calculated energy for the fully relaxed slab without M and E_Mref is the calculated energy per species M in the reference state. Accordingly, for the hydroxylated surface, we report the average dissociated adsorption energy per water molecule and for the Pd atom case, we report adsorption energies relative to a gas phase isolated Pd atom to assess the strength of interaction between the adsorbed Pd and the surface. We also report adsorption energies relative to a Pd atom in the bulk fcc structure of the metal. This gives some insight into the ease with which isolated Pd atoms on a silica surface would agglomerate into nanoparticles.

3 Building surface slab models

Initially, a 1 × 1 × 1 unit-cell of crystalline α-SiO₂ bulk³⁸ (see Fig. 1) was optimised with no added constraints on the lattice parameters to obtain a bulk structure with lattice parameters optimised at the PBE-TS level of theory. The values for cell constants a = b = 4.98 Å, c = 5.40 Å, α = β = 90°, γ = 120° agree well with the experimental reference of a = b = 4.91 Å, c = 5.40 Å, α = β = 90°, γ = 120°.^19,34

To study the surface structure and relaxation of α-SiO₂, symmetric slabs were cut from the relaxed bulk on the (001), (100) and (101) Miller planes and optimised.³⁸ Care was taken to ensure that all silica slabs used in this study are stoichiometric and non-polar, with equivalent faces at the top and bottom surfaces of the slab. To achieve this, a bulk layer was defined for each surface consisting of 9 atomic layers for the (001), (100) and (101), respectively. Only slabs consisting of an integer number of these bulk layers were used in these calculations.

The cleaved α-SiO₂ (hkl) surfaces with four bulk layers are shown in Fig. 2a–c. The lattice parameters for the slabs were kept fixed at the optimised bulk values during relaxation to ensure sufficient bulk properties within the slab.

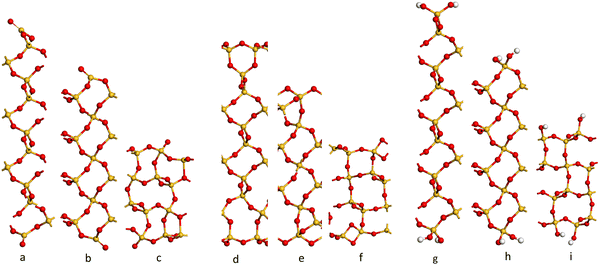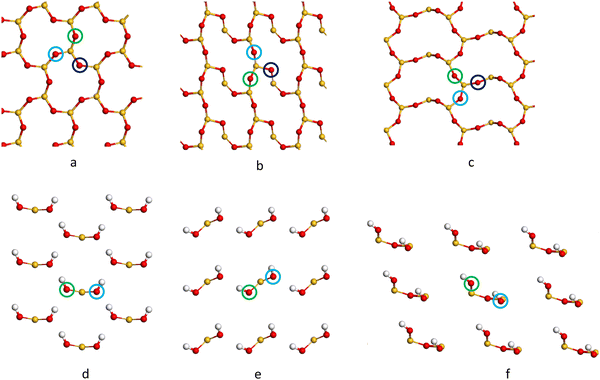
Fig. 2 Side view of the cleaved (C) (a–c) containing 39, 39 and 36 atomic layers respectively), reconstructed (R) (d–f) and hydroxylated (H) (g–i) α-SiO₂ surfaces. (a, d and g) (001), (b, e and h) (100) and (c, f and i) (101) α-SiO₂ surfaces, respectively. Atoms are coloured Si: yellow and O: red.^{27,29–31,33,34,54–56}

Fig. 2a–c shows that the cuts used to create these surfaces result in dangling bonds for oxygen anions and under co-ordinated Si cations. It has been previously noted that the surfaces may reconstruct to remove these high-energy features by forming new Si–O–Si bridges at the surface.³⁴ These reconstructions did not occur spontaneously when the slabs were optimised as part of this work, suggesting there is a barrier to the formation of these new surface features.

To explore the surface reconstruction further, the optimised cleaved slabs, α-SiO₂ C(hkl), were subjected to high temperature (700 K) NVT-MD for 36 ps. During the NVT-MD runs, all the oxygen anions with dangling bonds formed new siloxane bridges available under co-ordinated Si cations. The new surface structures did not break to reform dangling bonds within the run time of the NVT-MD. The newly reconstructed, α-SiO₂(hkl), slabs were then optimised with lattice constraints to obtain the optimised reconstructed surfaces, which will be denoted “R”.

This high temperature MD approach also demonstrated that surface reconstruction is not a unique structure. On some occasions, the upper and lower faces of the slabs became structurally inequivalent following the MD runs. In these cases, new slabs were constructed by taking half of the reconstructed slab (upper or lower section) and then symmetry operations valid for the cleaved slabs were used to generate slabs with symmetry-related surface structures consistent with the reconstructions found. In this way, the surface energies of the reconstructed slabs with equivalent surfaces on either side could be calculated and the lowest energy reconstruction identified. We also constructed slabs by swapping the top 4 atomic layers between slabs of differing thicknesses and reoptimized the new structures. With these additional approaches, we could ensure that a range of surface reconstructions had been considered and the lowest surface energy for each slab identified.

For α-SiO₂ R(001) and R(100), two distinct six-membered siloxane rings are present on the top layer of the surface, while a strained four-membered siloxane ring is present on the top layer of the α-SiO₂ R(101) surface. Four-membered rings are not seen in the bulk crystalline forms of silica and introduce an edge-sharing tetrahedra motif.^42,43,57 Such motifs have been reported as defects in silica surfaces for samples having undergone high temperature (1400 K) annealing treatments and used to assign characteristic IR bands at 888 cm⁻¹ and 908 cm⁻¹.⁴¹ The rings form following a condensation reaction of vicinal hydroxyl groups under these high temperature conditions. Below 900 K, these bands rapidly disappear on exposure of samples to water which is explained by the strained four-membered rings being opened as surface hydroxyl groups are reformed during the dissociative adsorption of water. Simulation has also been used to follow this process with a much lower calculated barrier seen for the formation of hydroxyl groups from water on reaction with four-membered rings than with higher order ring structures on model silica surfaces.⁴² Despite the high level of strain seen for four-membered rings in surface structures calculations have been used to suggest that edge-sharing tetrahedra may the preferred motif for constructing 1-D silica chains or isolated rings.⁴³

To examine the effect of hydroxylation on the interaction of the surface with Pd, separate models were constructed in which the dangling bonds of the α-SiO₂ C(hkl) slabs were hydroxylated by placing an H atom on the dangling O atom bonds and OH on the under co-ordinated Si on both surfaces of the slab. The hydroxylated α-SiO₂ H(hkl) slabs were optimised with cell constraints. For the α-SiO₂ H(001) and H(100) surfaces, two distinct sets of surface geminal silanol groups were found. While for the α-SiO₂ R(101), vicinal silanol groups were produced on the surfaces. In all cases, the resulting structure could be related to dissociating an integer number of water molecules.

The surface energies for the α-SiO₂ C/R/H(hkl) slabs were calculated using eqn (1) and (2). The dependence of surface energy on slab thickness and van der Waals interactions were focal points for our study.

4 Results

4.1 The geometry optimisation of the α-SiO₂ bulk and the cleaved α-SiO₂ (hkl) slabs

The geometry optimisations performed on the α-SiO₂ bulk (relaxed lattice parameters) and α-SiO₂ slabs (fixed lattice parameters) cleaved from the bulk structure on the relevant Miller planes are shown in Table 1.

Table 1 The lattice parameters of the cleaved 1 × 1 × 1 α-SiO₂ (hkl) slabs structures as calculated with the PBE functional using a 700 eV plane-wave cut-off

	α-SiO2 C(hkl)
	Bulk	(001)	(100)	(101)
a/Å	4.98	4.98	4.98	7.35
b/Å	4.98	4.98	5.40	4.98
c/Å	5.40
α/°	90	90	90	90
β/°	90	90	90	90
γ/°	120	120	90	110

---

The lattice parameters calculated for the α-SiO₂ bulk structure are very close to those derived by experimental methods.^19,34 These parameters also agree with previous modelling studies employing PBE on α-SiO₂. The cell vectors for the cleaved α-SiO₂ slabs (4–8 α-SiO₂ bulk layers) were fixed to retain these bulk properties.³⁴ Therefore, the α-SiO₂ slabs all have a fixed surface area regardless of layer thickness.

4.2 The surface energies of the α-SiO₂ slabs

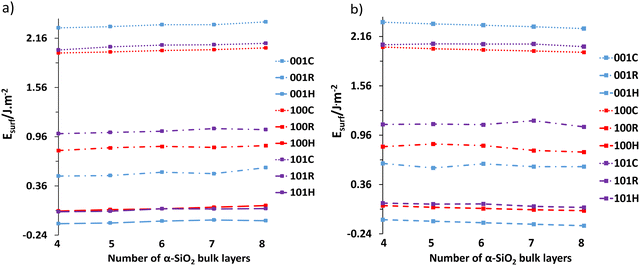
Following the reconstruction and hydroxylation of the cleaved slabs, the surface energies were calculated as a function of layer thickness using eqn (1) and (2). Fig. 3 shows the surface energy dependence on layer thickness with Fig. 3a showing data at the PBE level, and Fig. 3b data with van der Waals interactions included (PBE-TS).

Fig. 3 (a) The surface energies of the 4 to 8 layered cleaved (C), reconstructed (R) and hydroxylated (H) α-SiO₂ surfaces at the PBE level of theory, and (b) the cleaved (C) reconstructed (R) and hydroxylated (H) α-SiO₂ surfaces with TS dispersion corrections included (PBE-TS).

In both cases, the increase in layer thickness has a negligible effect on the surface energy of cleaved, reconstructed and hydroxylated α-SiO₂ slabs. However, in the case of reconstructed α-SiO₂ slabs obtained from MD calculations, the variance of surface energy as a function of layer thickness is more pronounced. As noted in the methodology section the optimised surface structures found from the high temperature MD simulations showed that there are multiple minima present, and we used the techniques described there to identify the lowest energy surface for each slab. Even so, there appears still to be small differences in the atomic arrangements on the slabs following this procedure that result in the variation in surface energy seen. The absolute differences between the calculated surface energies for slabs of different thicknesses are only between 0.01 J m⁻² and 0.04 J m⁻².

The surface energies of the cleaved α-SiO₂ slabs (∼2.0–2.2 J m⁻²) are higher than the reconstructed (∼0.5–1.0 J m⁻²) and hydroxylated (∼−0.25–0.1 J m⁻²) surfaces. This finding is in good agreement with previous calculations.³⁴ The reconstructed slabs have lower energies than the cleaved surfaces as the reconstruction removes dangling bonds on the surfaces. For the hydroxylated surfaces negative surface energies are possible because of the surface energy calculation using eqn (2) which includes the reaction with water to form hydroxyl groups. The stabilisation of the cleaved surfaces by reconstruction and the ability of the MD simulation to cause the reconstruction in quite short MD runs (36 ps) would indicate that the cleaved surface will reconstruct easily under ambient conditions.³⁴

It is also important to note the effect of the dispersion corrections (see Fig. 3b). PBE-TS calculations yield more positive surface energies than the corresponding PBE results at the same layer thickness. This is because dispersion is an attractive contribution to the inter-ion interaction energy and on surface creation, the surface ions lose higher-order neighbours. Increasing layer thickness also induces a slight stabilisation in the surface energy when dispersion interactions are included as the thicker slabs include more long-range interactions between surface ions and those in the centre of the slab.

We consider all slab thicknesses for water adsorption in the subsequent phase of the study. However, for palladium adsorption, only the four-layered reconstructed and hydroxylated slabs were considered.

4.3 The adsorption of H₂O on the cleaved 1 × 1 × 1 α-SiO₂ slabs

The adsorption energies of water from both the liquid and gaseous phases on the 1 × 1 × 1 α-SiO₂ (hkl) slabs were calculated with eqn (3). The reference state energies per water molecule were calculated by separately optimising a single water molecule in isolation for the gas phase reference and a 4 × 4 × 4 array containing 64 water molecules in a periodic simulation cell chosen to match the liquid density of water (1 g cm⁻¹). The energy reference for the liquid phase of water was taken from the average energy per water molecule across 14 optimisations of the 4 × 4 × 4 array. The starting geometries for these optimisations were taken from equally spaced snapshots from the trajectory of a 3.5 ps NVE MD calculation (T = 300 K, full details in ESI,† Section S1). The liquid water reference taken in this way was found to have an associated standard deviation of 7.4 meV (PBE) and 5.2 meV (PBE-TS) per water molecule.

The resulting adsorption energies of gaseous and liquid water using the reconstructed 1 × 1 × 1 α-SiO₂ R(hkl) slabs as the clean silica surface reference energies are shown in Table 2.

Table 2 The adsorption energies (eV) of water on 4–8 layered α-SiO₂ 1 × 1 × 1 R slabs with PBE and with PBE-TS approaches

		H2O/α-SiO2 R(hkl)
		PBE					PBE-TS
Surface	Layers:	4	5	6	7	8	4	5	6	7	8
(001)	H2O(l)	−0.78	−0.78	−0.80	−0.76	−0.87	−0.92	−0.87	−0.96	−0.94	−0.97
	H2O(g)	−1.17	−1.17	−1.19	−1.15	−1.26	−1.45	−1.40	−1.49	−1.47	−1.49
(100)	H2O(l)	−1.22	−1.27	−1.28	−1.23	−1.23	−1.21	−1.29	−1.29	−1.21	−1.20
	H2O(g)	−1.63	−1.66	−1.67	−1.62	−1.62	−1.74	−1.82	−1.82	−1.74	−1.73
(101)	H2O(l)	−2.05	−2.07	−2.03	−2.11	−2.07	−2.06	−2.10	−2.07	−2.24	−2.10
	H2O(g)	−2.43	−2.45	−2.42	−2.49	−2.46	−2.59	−2.62	−2.60	−2.77	−2.63

---

In all cases, it is found that water will dissociate and chemisorb to the surface of any α-SiO₂ R(hkl) slab. The stabilising hydrogen bonds in the liquid water model lower the reference energy compared to the gaseous phase calculation. Correspondingly, the adsorption energy values relative to the liquid state are consistently 0.39 eV (PBE) and 0.53 eV (PBE-TS) less favourable than those for the gas state reference. The thickness of the simulation slab has little influence on the calculated water adsorption energy. The small variations seen in the values with slab thickness follow the pattern seen for the calculation of surface energy for the hydroxylated surface discussed earlier.

The inclusion of attractive van der Waals forces on the calculated adsorption energies is significant. For the gas phase reference, the PBE-TS calculated adsorption energy is between 0.11 eV and 0.32 eV more negative than the corresponding PBE values. As the dispersion energy of the reference gas phase calculation is practically zero this gives an estimate of the van der Waals contribution to the interaction between water and the various surfaces. In contrast, the PBE-TS values are only 0.01–0.18 eV more negative than the related PBE data, suggesting that the van der Waals interaction with the surface is about the same as the van der Waals energy of a water molecule in liquid water.

From the data in Table 2, it is evident that favourable water adsorption follows the trend (101) ≫ (100) > (001), and that the adsorption energy of water on the (101) surface is approximately twice that of the (001) surface. The water adsorption energy for (101) is also very close to the value calculated by Bandura et al.³³ (−2.26 eV) for the same surface. Thus, the formation of vicinal silanols for the model surfaces studied here is favoured over the formation of geminal silanol groups. At first, this seems surprising as experimental dehydration studies show that vicinal silanol groups desorb at lower temperatures than do geminal.⁵⁷ However, it should be remembered that the vicinal groups seen on the (101) surface are formed from the strained four-membered ring seen on the reconstructed surface. This means that a large part of the dissociated adsorption energy of water will be from the energy gained by opening up the 4 membered rings.

4.4 The adsorption of Pd on reconstructed and hydroxylated α-SiO₂ slabs

4.4.1 The adsorption of Pd₁ on reconstructed and hydroxylated 1 × 1 × 1 α-SiO₂ slabs. Following optimisation of the reconstructed and hydroxylated slabs, the surfaces of 4 layered α-SiO₂ slabs were used to study the adsorption of a single Pd atom. An initial survey of adsorption positions for Pd showed that the Pd atom will have an affinity for surface oxygen anions. This allowed us to identify possible adsorption sites on each of the 1 × 1 × 1 slab models as those shown in Fig. 4.

Fig. 4 The top view of the extended representations of the 1 × 1 × 1 reconstructed α-SiO₂, (a) R(001), (b) R(100), (c) R(101) and hydroxylated (d) H(001), (e) H(100) and (f) H(101) slabs and the possible Pd₁ adsorption sites on each surface. Colours are used to identify sites with site “a”: green, site “b”: indigo and site “c” dark blue. Atoms are coloured Si: yellow, O: red and H: white. Only the topmost atoms in each case are shown for clarity.

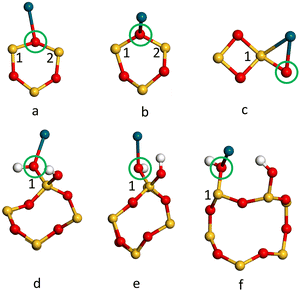
The adsorption energies (E_ads/eV) of Pd₁/α-SiO₂ were considered for both Pd(s) and Pd(g) reference states and are listed in Table 3, which also compares values from PBE and PBE-TS calculations. From the values listed in Table 3, energy would be required to remove a Pd atom from bulk Pd and place it on the silica surface as a Pd₁ adsorbate.⁵⁸ The high positive values (2.8–3.34 eV) indicate that Pd deposited on silica would be expected to form nanoparticles where Pd–Pd bonds can stabilise the structures. Even so, relative to the gas phase, Pd atoms will adsorb spontaneously on any adsorption sites shown in Fig. 4, except for site b on the α-SiO₂ H(101) surface (Fig. 4(f), indicated by the blue ring). This indicates that favourable interactions between metal atoms and the surface are present for all Miller indices.

Table 3 The E_ads (eV) of Pd₁ on reconstructed and hydroxylated 1 × 1 × 1 α-SiO₂ slabs

Pd1/α-SiO2 R/H(hkl)
		Reconstructed						Hydroxylated
		(001)		(100)		(101)		(001)		(100)		(101)
		PBE	-TS^a	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a
a -TS heading implies PBE-TS calculation results.
Pd(g)
Site a	−0.39	−0.58	−0.35	−0.50	−0.85	−0.95	−0.67	−0.81	−0.72	−0.98	−0.57	−0.76
Site b	−0.33	−0.54	−0.31	−0.56	−0.67	−0.82	−0.65	−0.80	−0.80	−0.77
Site c	−0.33	−0.52	−0.23	−0.44	−0.39	−0.54
Pd(s)
Site a	3.34	3.17	3.42	3.18	2.88	2.79	3.07	2.93	3.01	2.76	3.16	2.98
Site b	3.40	3.20	3.38	3.24	3.06	2.92	3.08	2.95	2.93	2.97
Site c	3.40	3.22	3.50	3.30	3.34	3.20

---

From Table 3, it is also evident that the attractive van der Waals forces play a significant role in the calculation of adsorption energies of Pd₁/α-SiO₂(hkl). PBE-TS calculations estimate adsorption energies of 0.03–0.25 eV more favourable towards Pd(g) adsorption than the estimates provided by PBE alone.

It is estimated that the adsorption of Pd(g) will, in all cases, prefer adsorption sites of type a on the α-SiO₂ surface (See Fig. 4). When the TS correction is considered, the trend of favourable Pd(g) adsorption on α-SiO₂ follows the order (101) > (001) > (100) for the reconstructed surfaces and (100) > (101) > (001) for hydroxylated surfaces.

4.4.2 The adsorption of Pd₁ on reconstructed and hydroxylated 2 × 3 × 1 α-SiO₂ slabs. The Pd/α-SiO₂ R/H(hkl) with Pd at the lowest energy adsorption sites from the 1 × 1 × 1 α-SiO₂ slabs in Table 2 were extended to 2 × 3 × 1 supercells and images of Pd within the supercell removed to model Pd₁ adsorption at lower coverage. The supercell structures were then reoptimized and the adsorption energies were recalculated with eqn (3). The geometries of these adsorption sites at the lower Pd coverage were then closely examined. The adsorption sites of Pd₁ on the 2 × 3 × 1 α-SiO₂ R/H(hkl) supercell are illustrated in Fig. 5, and the adsorption energies (accounting for the TS dispersion correction) along with the geometric information obtained by our calculations are shown in Table 4.

Fig. 5 The geometries of the optimal adsorption sites of Pd(g) on the 2 × 3 × 1 (a) R(001), (b) R(100), (c) R(101) and hydroxylated (d) H(001), (e) H(100) and (f) H(101) α-SiO₂ slabs. In each case, the local environment of the adsorbed Pd atom and the surface siloxane ring is shown looking side on to the slab with other atoms removed for clarity. Atoms are coloured Si: yellow, Pd: dark blue, O: red and H: white.

Table 4 The adsorption energies (eV) of Pd₁ on reconstructed and hydroxylated 2 × 3 × 1 α-SiO₂ slabs accounting for (TS) dispersion correction

Pd1/α-SiO2 R/H(hkl)
	Reconstructed						Hydroxylated
	(001)		(100)		(101)		(001)		(100)		(101)
	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a
a -TS heading implies PBE-TS calculation results.
E ads Pd(g)/eV	0.03	0.06	−0.20	−0.20	−1.01	−1.16	−0.67	−0.70	−0.73	−0.76	−0.71	−0.84
E ads Pd(s)/eV	3.76	3.80	3.53	3.54	2.73	2.58	3.06	3.05	3.01	2.98	3.02	2.90
Pd–O/Å	2.23		2.14		2.14		2.15		2.25		2.24
Pd–O–Si1/°	119.14		106.66		72.89		129.1		111.2		98.32
Pd–O–Si2/°	91.23		116.65		N/A		N/A		N/A		N/A

---

The adsorption energies calculated for the Pd₁ on reconstructed and hydroxylated 2 × 3 × 1 α-SiO₂ R/H(hkl) surfaces differ from those calculated for the 1 × 1 × 1 surface. This suggests that interaction between Pd atom periodic images in the smaller cell affects the results. For the adsorption energies in Table 4, the trend of favourable adsorption is (101) > (100) > (001) for the reconstructed and the hydroxylated α-SiO₂ R/H(hkl) surfaces. The α-SiO₂ R(101) surface has the lowest energy adsorption site for Pd₁(g) overall with a calculated Pd(g) adsorption energy more than 0.3 eV lower than the α-SiO₂ H(101) case. The Pd₁(g) adsorption energy on the α-SiO₂ R(001) supercell has been calculated to be positive (0.06 eV), suggesting a relatively low population of adsorbed metal atoms on this surface. From the adsorption energies observed for Pd₁ interacting with silanol groups, it is evident that Pd₁(g) adsorption to vicinal silanols on α-SiO₂ H(101) (−0.84 eV) would be preferred over adsorption to geminal silanols on the H(001) (−0.70 eV) and H(100) (−0.76 eV) surfaces.

In addition to the adsorption energies of a Pd onto silica surfaces, the lateral Pd interactions as well as Mulliken charge transfers from the Pd metal to the silica surface were calculated for the 1 × 1 × 1 and 2 × 3 × 1 periodic cells. The results of these calculations are presented in Tables 5 and 6 respectively. These results confirm that the 1 × 1 × 1 slabs show a notably greater interaction between periodic images of Pd atoms than do the 2 × 3 × 1 periodic cells. The variation on the calculated interaction also shows a notably lower variation between surface models for the 2 × 3 × 1 slabs than for the 1 × 1 × 1.

Table 5 Lateral Pd interaction (eV) on adsorption site a for 1 × 1 × 1 and 2 × 3 × 1 Pd₁/α-SiO₂ R/H(hkl)

	Reconstructed						Hydroxylated
	(001)		(100)		(101)		(001)		(100)		(101)
	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a	PBE	-TS^a
a -TS heading implies PBE-TS calculation results.
1 × 1 × 1	−0.26	−0.27	−0.19	−0.20	−0.17	−0.17	−0.26	−0.27	−0.07	−0.08	−0.07	−0.08
2 × 3 × 1	−0.15	−0.14	−0.14	−0.14	−0.16	−0.16	−0.14	−0.14	−0.14	−0.15	−0.16	−0.16

---

Table 6 Pd to surface Mulliken charge transfer (|e|) on adsorption site a for 1 × 1 × 1 and 2 × 3 × 1 Pd₁/α-SiO₂ R/H(hkl)

	Reconstructed			Hydroxylated
	(001)	(100)	(101)	(001)	(100)	(101)
1 × 1 × 1	0.11	0.15	0.24	0.07	0.02	0.20
2 × 3 × 1	0.13	0.07	0.35	0.06	0.07	0.20

---

To further understand the metal surface interaction the charge transfer between Pd₁ and each surface was calculated using the Mulliken charge assigned to the Pd atom. The results are summarised in Table 6. In all cases, the Pd atom becomes positively charged on interaction with the surface and so has donated electron density to the silica surface. For the reconstructed (dehydrated) surface the effect is greatest for the (101) surface and is particularly notable for the larger area 2 × 3 × 1 cell. In this case, the Pd adsorbs near the strained four-membered ring on the surface (Fig. 5c). For the hydroxylated surface the (101) surface again has a significantly higher charge transfer to Pd₁ and the most favourable adsorption energy (Table 5).

5 Conclusions

From 4, 5, 6, 7 and 8 layers of crystalline α-SiO₂ bulk, we cleave surfaces on the (001), (100) and (101) Miller planes in 1 × 1 × 1 unit cells. These cleaved surfaces were then reconstructed and separately hydroxylated to isolate specific siloxane and silanol functional groups on the top and bottom surfaces of the α-SiO₂ slab models. For α-SiO₂ (001) and (100), we isolate two distinct six-membered siloxane functional groups after reconstruction and two distinct geminal silanols following hydroxylation. We calculate the surface energy of the cleaved, reconstructed, and hydroxylated surfaces as a function of slab thickness.

Our results show that the geometries and lattice parameters obtained for the α-SiO₂ bulk are in good agreement with previous experimental and computational studies in the literature. The surface energies calculated for the α-SiO₂ (hkl) are also in good agreement with previous work. We found that cleaved α-SiO₂ (hkl) surfaces are stabilised after reconstruction to remove O dangling bonds and under co-ordinated Si cations. The calculated surface energy is lowered further by hydroxylation. The highest surface energy was found for the α-SiO₂ (101) surface for both reconstructed and hydroxylated surfaces. The number of bulk layers in the α-SiO₂ (hkl) slab has a minimal effect on the calculated surface energy. Even so, a small increase in surface stability was observed upon increasing slab thickness when van der Waals forces were included. This is likely due to the long-range nature of dispersion and the increased number of interactions as slabs become thicker.

Water adsorption occurs more easily on the α-SiO₂ (101) to form vicinal silanol groups as opposed to geminal silanol groups on the α-SiO₂ (100) and α-SiO₂ (001) slabs studied here. Water adsorption is not affected by slab thickness but is significantly stronger for the gas phase reference when attractive van der Waals forces are accounted for. Using the liquid phase reference for water the dispersion interaction with the surface is approximately balanced by that in bulk water and so only minor changes in the calculated dissociative adsorption energy are observed.

For the adsorption of Pd on the 1 × 1 × 1 unit cells of α-SiO₂ (hkl) surfaces, we determine the optimal adsorption sites for Pd. When we consider the Pd₁(g)/α-SiO₂ (hkl) adsorption energies in periodic systems that have greater surface areas (2 × 3 × 1 supercells), we find that the Pd₁ has a positive adsorption energy on the Pd₁(g)/α-SiO₂ (001) surface. In the case of reconstructed Pd₁(g)/α-SiO₂ (100), weak adsorption energies (E_ads ≥ −0.2 eV) are observed, which are indicative of a mixed physisorption/chemisorption interaction. Chemisorption (E_ads ≤ −0.4 eV) is observed for all other adsorption sites.

Furthermore, it was confirmed that Pd(g) would prefer chemisorption on the Pd₁(g)/α-SiO₂ (101) surface regardless of the functional group. Thus, it has been observed computationally that in the case of Pd₁(g) adsorption, strained four-membered siloxane adsorption sites are preferred over six-membered siloxanes. As completely dehydrated silica surfaces with edge-sharing tetrahedra can only be prepared by high temperature annealing and exclusion of water from subsequent processing this observation may have little relevance to experiment. For the more technologically relevant hydroxylated surfaces, Pd₁(g) will prefer adsorption to vicinal silanol groups on H(101) rather than geminal silanol groups. When we compare the adsorption energies of Pd₁(g) with Pd₁(s), we can conclude that isolated Pd atoms will experience a driving force to conglomerate on the surface of α-SiO₂ and so form nanoclusters.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Johnson Matthey plc. for providing support throughout this work including the provision of a PhD studentship for CL. Computing facilities for this work were provided by Supercomputing Wales (Hawk), the Supercomputing Facilities at the Centre for High-Performance Computing (CHPC) facility in South Africa and via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431), this work used the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk) and UK Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/P020194).

References

1. G. A. Olah, Angew. Chem., Int. Ed., 2005, 44, 2636–2639.
2. S. E. Bozbag, P. Sot, M. Nachtegaal, M. Ranocchiari, J. A. van Bokhoven and C. Mesters, ACS Catal., 2018, 8, 5721–5731.
3. P. J. Kulesza, I. S. Pieta, I. A. Rutkowska, A. Wadas, D. Marks, K. Klak, L. Stobinski and J. A. Cox, Electrochim. Acta, 2013, 110, 474–483.
4. R. Palkovits, M. Antonietti, P. Kuhn, A. Thomas and F. Schuth, Angew. Chem., Int. Ed., 2009, 48, 6909–6912.
5. P. Khirsariya and R. K. Mewada, Procedia Eng., 2013, 51, 409–415.
6. F. Rascón, R. Wischert and C. Copéret, Chem. Sci., 2011, 2, 1449–1456.
7. K. W. Kolasinski, Surface science: foundations of catalysis and nanoscience, John Wiley & Sons, 2012.
8. P. Jena, S. N. Khanna and B. K. Rao, Clusters and Nano-Assemblies: Physical and Biological Systems, World Scientific, 2005.
9. B. Han, Y. Yang, Y. Xu, U. J. Etim, K. Qiao, B. Xu and Z. Yan, Chin. J. Catal., 2016, 37, 1206–1215.
10. Y. Han, D. Kumar and D. Goodman, J. Catal., 2005, 230, 353–358.
11. S. Sitthisa, T. Pham, T. Prasomsri, T. Sooknoi, R. G. Mallinson and D. E. Resasco, J. Catal., 2011, 280, 17–27.
12. D. Gerçeker and I. Önal, Appl. Surf. Sci., 2013, 285, 927–936.
13. B. K. Min, A. K. Santra and D. W. Goodman, Catal. Today, 2003, 85, 113–124.
14. K. Okumura, E. Shinohara and M. Niwa, Catal. Today, 2006, 117, 577–583.
15. C. Copéret, M. Chabanas, R. Petroff Saint-Arroman and J. M. Basset, Angew. Chem., Int. Ed., 2003, 42, 156–181.
16. K.-I. Muto, N. Katada and M. Niwa, Appl. Catal., A, 1996, 134, 203–215.
17. A. Comas-Vives, Phys. Chem. Chem. Phys., 2016, 18, 7475–7482.
18. H. J. Kim, M. G. Jang, D. Shin and J. W. Han, ChemCatChem, 2020, 12, 11–26.
19. L. Levien, C. T. Prewitt and D. J. Weidner, Am. Mineral., 1980, 65, 920–930.
20. T. Das, S. Tosoni and G. Pacchioni, J. Chem. Phys., 2021, 154, 134706–134721.
21. C. Coperet, A. Comas-Vives, M. P. Conley, D. P. Estes, A. Fedorov, V. Mougel, H. Nagae, F. Nunez-Zarur and P. A. Zhizhko, Chem. Rev., 2016, 116, 323–421.
22. N. T. Huff, E. Demiralp, T. Cagin and W. A. Goddard III, J. Non-Cryst. Solids, 1999, 253, 133–142.
23. F. Tielens, C. Gervais, J. F. Lambert, F. Mauri and D. Costa, Chem. Mater., 2008, 20, 3336–3344.
24. A. Pedone, G. Malavasi, M. C. Menziani, U. Segre and A. N. Cormack, Chem. Mater., 2008, 20, 4356–4366.
25. A. Pedone, G. Malavasi, M. C. Menziani, U. Segre, F. Musso, M. Corno, B. Civalleri and P. Ugliengo, Chem. Mater., 2008, 20, 2522–2531.
26. S. Tosoni, B. Civalleri, F. Pascale and P. Ugliengo, J. Phys.: Conf. Ser., 2008, 117, 012026.
27. Y.-W. Chen, C. Cao and H.-P. Cheng, Appl. Phys. Lett., 2008, 93, 181911–181915.
28. J. M. Rimsza, R. E. Jones and L. J. Criscenti, Langmuir, 2017, 33, 3882–3891.
29. S. S. Rath, H. Sahoo, B. Das and B. K. Mishra, Miner. Eng., 2014, 69, 57–64.
30. G. M. Rignanese, J. C. Charlier and X. Gonze, Phys. Chem. Chem. Phys., 2004, 6, 1920–1925.
31. O. I. Malyi, V. V. Kulish and C. Persson, RSC Adv., 2014, 4, 55599–55603.
32. P. N. Plessow, R. S. Sánchez-Carrera, L. Li, M. Rieger, S. Sauer, A. Schaefer and F. Abild-Pedersen, J. Phys. Chem. C, 2016, 120, 10340–10350.
33. A. V. Bandura, J. D. Kubicki and J. O. Sofo, J. Phys. Chem. C, 2011, 115, 5756–5766.
34. T. P. Goumans, A. Wander, W. A. Brown and C. R. Catlow, Phys. Chem. Chem. Phys., 2007, 9, 2146–2152.
35. A. Ruiz Puigdollers, P. Schlexer, S. Tosoni and G. Pacchioni, ACS Catal., 2017, 7, 6493–6513.
36. M. Pfeiffer-Laplaud and M.-P. Gaigeot, J. Phys. Chem. C, 2016, 120, 4866–4880.
37. J. W. Han and D. S. Sholl, Phys. Chem. Chem. Phys., 2010, 12, 8024–8032.
38. X. Wang, Q. Zhang, X. Li, J. Ye and L. Li, Minerals, 2018, 8, 58–74.
39. W. Ji, Q. Tang, Z. Shen, M. Fan and F. Li, Appl. Surf. Sci., 2020, 501, 144233–144242.
40. A. Abramov, A. Keshavarz and S. Iglauer, J. Phys. Chem. C, 2019, 123, 9027–9040.
41. C. M. Chiang, B. R. Zegarski and L. H. Dubois, J. Phys. Chem. B, 1993, 97, 6948–6950.
42. S. Bromley, M. Zwijnenburg and T. Maschmeyer, Phys. Rev. Lett., 2003, 90, 035502.
43. A. Rimola, P. Ugliengo and M. Sodupe, Comput. Theor. Chem., 2015, 1074, 168–177.
44. Y. Zhu, B. Luo, C. Sun, J. Liu, H. Sun, Y. Li and Y. Han, Miner. Eng., 2016, 92, 72–77.
45. W. Sun and G. Ceder, Surf. Sci., 2013, 617, 53–59.
46. X. Wang, W. Liu, H. Duan, B. Wang, C. Han and D. Wei, Powder Technol., 2018, 329, 158–166.
47. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567–570.
48. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
49. R. G. Parr, Annu. Rev. Phys. Chem., 1983, 34, 631–656.
50. D. J. Chadi and M. L. Cohen, Phys. Rev. B: Solid State, 1973, 8, 5747.
51. J. Singleton, Band theory and electronic properties of solids, Oxford University Press, 2001.
52. J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505–234518.
53. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
54. V. V. Murashov, J. Phys. Chem. B, 2005, 109, 4144–4151.
55. M. Koudriachova, J. Beckers and S. De Leeuw, Comput. Mater. Sci., 2001, 20, 381–386.
56. N. H. de Leeuw, F. M. Higgins and S. C. Parker, J. Phys. Chem. B, 1999, 103, 1270–1277.
57. L. Zhuravlev, Colloids Surf., A, 2000, 173, 1–38.
58. A. Kokalj, Corros. Sci., 2022, 196, 109939–109954.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04722e

---