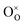Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The application of QM/MM simulations in heterogeneous catalysis
Gabriel Adrian
Bramley
,
Owain Tomos
Beynon
 ,
Pavel Viktorovich
Stishenko
and
Andrew James
Logsdail
,
Pavel Viktorovich
Stishenko
and
Andrew James
Logsdail
 *
*
Cardiff Catalysis Institute, School of Chemistry, Cardiff University, Park Place, CF10 3AT, UK. E-mail: LogsdailA@cardiff.ac.uk
First published on 8th February 2023
Abstract
The QM/MM simulation method is provenly efficient for the simulation of biological systems, where an interplay of extensive environment and delicate local interactions drives a process of interest through a funnel on a complex energy landscape. Recent advances in quantum chemistry and force-field methods present opportunities for the adoption of QM/MM to simulate heterogeneous catalytic processes, and their related systems, where similar intricacies exist on the energy landscape. Herein, the fundamental theoretical considerations for performing QM/MM simulations, and the practical considerations for setting up QM/MM simulations of catalytic systems, are introduced; then, areas of heterogeneous catalysis are explored where QM/MM methods have been most fruitfully applied. The discussion includes simulations performed for adsorption processes in solvent at metallic interfaces, reaction mechanisms within zeolitic systems, nanoparticles, and defect chemistry within ionic solids. We conclude with a perspective on the current state of the field and areas where future opportunities for development and application exist.
1 Introduction
QM/MM (Quantum mechanics/molecular mechanics) techniques are a key methodology for computational simulations of extended systems.1 The core of this technique lies in the partition of the system into separate regions, with quantum mechanics applied to a central region of interest, and classical mechanics applied to the environment. The partitioning allows for favourable scaling when performing simulations of large systems, where high accuracy methods such as density functional theory (DFT) or post-Hartree Fock can calculate the energetics of salient features for the system under study; meanwhile, the electrostatics of the extended system are included through classical empirical force-fields, thereby significantly reducing the computational workload compared to optimising the electronic structure of the entire extended system.2Both cluster and periodic QM/MM models have been extensively used for problems in structural biology;3,4 however, multiscale approaches are also gaining popularity in heterogeneous catalysis, which is motivated by the ability of QM/MM to calculate system observables with greater speed and accuracy compared to fully ab initio simulations. For example, in systems with strong concentration effects (i.e., in the simulation of charge defects, or the adsorption of molecules with strong lateral interactions5), an aperiodic embedded-cluster QM/MM model can be used to calculate the energetics at the dilute limit, while the influence of the wider system is abstracted using a larger classical embedding representation. In contrast, a periodic QM simulation would require an infeasibly large simulation cell to correctly model defects in the dilute limit, or compromise accuracy by allowing interactions between charge defects in uncharacteristically close proximity to one another.6
The QM/MM method is also ideal for calculating salient system information with high accuracy methods, while representing less chemically relevant regions with computationally cheap classical simulations. This benefit has been widely employed for simulations of periodic and embedded-cluster QM/MM models of zeolites, for example detailing fundamental reactions in the MTH process at the H-ZSM-5 zeolite.7 For such systems, modelling of the entire unit cell of the zeolite was avoided by limiting the QM simulation to the adsorbate and a small segment of the zeolite, which emulates chemistry sought in the full periodic simulation. The reduction of the size of the QM calculation in turn enables application of post-Hartree Fock methods or higher-level density functional theory (DFT), e.g. including contributions of exact exchange, allowing for greater accuracy when describing the energetics of adsorption and reactivity.
In addition to reducing the cost of conventional geometry and single point energy evaluations, QM/MM enables the evaluation of free energy changes in dynamic solvent environments. This has been achieved by representing the solvent with a classical force-field, paired with techniques such as Thermodynamic Integration (TI)8,9 and Free Energy Perturbation (FEP).10,11 The schemes use QM/MM to calculate the free energy of adsorption in the aqueous environment, which provides a realistic comparison to experimental studies in aqueous solvent. Multiscale solvation schemes drastically reduce the cost of evaluating the dynamic solvent environment, which would otherwise be infeasible with a full ab initio simulation. These approaches have a promising future in describing liquid-phase catalytic processes at surfaces and nanoparticles.
In this review, the application of QM/MM methods to a range of challenges in heterogeneous catalysis are presented, demonstrating the potential of the approach. To aid our discussion, the fundamental theory of QM/MM and important considerations for configuring simulations are first introduced. Then, applications of QM/MM are presented in domains of solvent simulations, zeolite studies, metallic surfaces and nanoparticles, and the simulation of defects in ionic solids. To finalise our discussion, emergent and potentially impactful methodologies are discussed, as well as developments necessary to improve the uptake and ease of use of the QM/MM methodology in heterogeneous catalysis.
 | ||
| Fig. 1 A simple diagrammatic representation of the subtractive and additive QM/MM schemes. The former is carried out using three separate calculations, corresponding to a QM calculation of region 1, a MM calculation for the combined region 1 & 2, and another MM calculation for the inner region (eqn (1)). The additive scheme is carried out using two calculations, of the inner and outer regions using QM and MM, respectively, with the coupling interactions between the QM and MM regions introduced by a separate coupling term (eqn (2)). | ||
2 Basics of QM/MM
2.1 Subtractive and additive coupling schemes
As outlined, QM/MM calculations require partitioning of a model such that different methods can be applied to each sub-partition (Fig. 1). The expression for the QM/MM total energy term is typically presented via two dominant schemes; additive and subtractive.Subtractive schemes are a conceptually simple method wherein three separate calculations are performed for the central region of interest (1) embedded in an extended representation of the environment (2),
| EsubQM/MM = E1QM + (E12MM − E1MM), | (1) |
In contrast, additive schemes calculate the inner and outer regions on the level of QM and MM, respectively, and the interaction between the two regions is treated though an additional coupling term
| EaddQM/MM = E1QM + E2MM + E12couple, | (2) |
Although the two approaches are in principle mathematically equivalent under conditions when the QM and MM potential energy landscape are commensurate,14 in reality challenges occur due to the difficulty in reaching equivalence in the landscapes. The challenges primarily concern the treatment of the QM/MM boundary, which we will discuss in depth in Section 2.3.
2.2 Embedding schemes
Embedding methods can be further categorised in their treatment of coupling between the QM and MM regions (i.e., mechanical, electrostatic and polarisable). Mechanical coupling simply considers interactions between the internal and external region through MM structural parameters. Although conceptually simple, mechanical coupling introduces significant inaccuracies unless a specific force-field is generated that commensurately describes the interactions between the QM and MM regions. These inaccuracies are exacerbated when significant changes in electron density or geometry occur, which requires updated force-field terms to correctly describe the altered structure.4In contrast, electrostatic embedding includes the MM charges within the one-electron Hamiltonian, introducing the influence of the embedding charges into the self-consistency cycle; polarisable schemes then introduce coupling of the MM region with the charge density of the QM region, thereby dynamically altering the dipoles of atomic centers in the MM region depending on the quantum mechanical charge. Within the additive QUASI scheme, this is implemented through the polarisable shell model for the MM atoms.2,15,16 Polarisable embedding has also been implemented to the subtractive ONIOM scheme under the ONIOM(QM:MM)-PE framework, which is employed to calculate the interaction between the classical charges and the dielectric continuum of an implicit solvent environment.17
QM/MM calculations are feasible with both open and periodic boundary conditions.18–22 Embedded-cluster QM/MM models commonly have open boundary conditions, which allows for the facile calculation of charge without periodic interactions; charged models under periodic boundary conditions interact with their periodic replicas, which at high concentrations can distort the desired energetics energy from the dilute limit.23 The open boundary conditions also provide direct access to an absolute energy reference (i.e., the vacuum level), allowing alignment of the band edges of any materials;24 in contrast, the reference energy level of simulations of 3D periodic systems is ill-defined due to the arbitrary choice of the average background potential (i.e., where G → 0).25,26 It is noted that 2D periodic systems have access to a reference energy level, where methods such as the Coulomb cut-off may yield a definite vacuum energy level;27 however, periodic 2D models do not accurately represent charged systems by default.28,29 Discussion of modern approaches for correcting the periodic representation of charged systems are summarised by Walsh.30 It should also be noted that QM/MM has also been formulated for periodic boundary conditions, such as the formulation of QM-Pot.20 Alternative implementations of periodic QM/MM via the Particle Mesh Ewald (PME) method are demonstrably useful for representing the long range electrostatics of the dynamic solvent environment without introducing artificial cut-offs.18,19
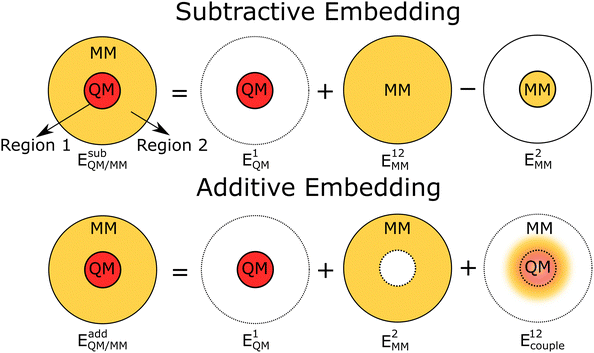
Beyond the atomistic QM and MM representations, long range polarisation of an extended aperiodic bulk system may be treated through a simple additive term known as the Jost correction:31,32
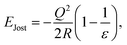 | (3) |
A notable drawback in the QM/MM methodology is the confinement of electronic states within the QM region. Although the localised states of the valence electrons are well-represented, the diffuse conduction states are shifted significantly upwards in energy.33 As a consequence, studies that require the conduction band as an energy reference (such as those in Section 3.4) often elect to use experimental values of the conduction band minimum (CBM) for the bulk.34,35
2.3 QM/MM boundary and link atoms
At the boundary of the QM/MM interface, the electron density of the QM atoms can spill over into the positively charged MM region. This is especially problematic for covalent compounds, where atoms with incomplete valences must be terminated to prevent nonphysical radicals forming at the boundary.A common scheme for completing the valence shell of boundary atoms is the link atom approach,36 which involves placing a capping QM atom along the bond length between the boundary QM and MM atoms, usually in the form of a hydrogen atom; however, double-counting of the energetic terms associated with the link atom must be accounted.
The subtractive scheme of eqn (1) naturally cancels the discrepancies introduced by the link atom; both the QM and MM calculations for the inner region 1 contain energy contributions for the H atom, which are subtracted from one another. Provided the force-field correctly emulates the potential energy surface for the QM/MM region boundaries, the difference in energies calculated for the classical link atom in E1MM and the original boundary atom in E12MM may be treated as an extrapolative correction to the quantum mechanical energy from the artificial link to the correct boundary atom.12,14 However, an improperly parameterised force-field – which incorrectly describes the interaction across the boundary – may lead to discontinuities across the potential energy surface.4
The additive scheme in its strict form (eqn (2)) provides no such correction for link atoms; however, eqn (2) may be adapted to include elements of the subtractive expression,2
| Eadd,linkQM/MM = E1QM + E2MM + E12couple − ElinkMM, | (4) |
Ionic species at the boundary may be represented using Gaussian-based effective core potentials (ECPs) or numerical pseudopotentials (PSPs), which emulate the presence of a boundary QM atom without introducing further QM species. ECPs are widely available from the literature, though typically optimised for molecular systems, due to the prevalence of Gaussian basis sets for such calculations;37 PSPs, in contrast, can be generated and tested for solid state systems using widely available frameworks.38 For PSPs, the local potential represents the long-range electrostatic features of the atom, whilst the nonlocal expressions, such as those in the Kleinman–Bylander formalism, effectively project the orbitals of the QM region away from the pseudopotentials, thereby preventing charge spillover. Boundary ECPs and PSPs have been most commonly applied for ionic solids, but extensions to covalent systems have been implemented; known as the pseudobond approach, frozen, specially parameterised hybridised basis functions may be placed on the ECPs to represent the bonding interaction with the missing atom.39 This has been readily used for proteins and organic systems, where a single parameterised C(sp3) hybridised basis function is placed on the boundary carbon atoms.40
2.4 Force-field parameterisation
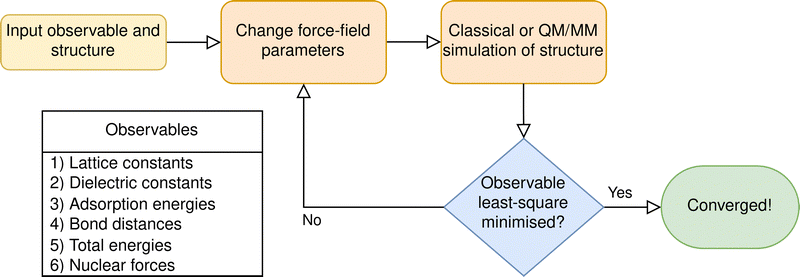
The QM/MM approach can potentially utilise the same diversity of force-fields applied in solely classical simulations, provided an appropriate interface exists between the classical potential and QM Hamiltonian; however, the selected parameters should ideally reproduce both the structure and potential energy surface of the associated quantum calculation. The consistency of the QM and MM structural landscapes is necessary to avoid lattice parameters or bond lengths in the MM region that deviate significantly from those of the underlying QM method, as these would introduce an artificial strain on the QM region and may distort the region of interest from its analogous full QM ground state.In bulk and condensed systems, the energetic discontinuity between the two regions can lead to significant displacement of QM atoms from their equilibrium positions.41 These errors occur even if the selected force-field matches the structural properties of the corresponding QM method, resulting in significant errors in QM/MM dynamical simulations.42,43 The discrepancy can be alleviated by introducing a buffer region,41 where the forces on the boundary QM atoms are calculated using terms from an equivalent MM atom (see also: Section 2.5). Alternatively, MM atoms at the QM/MM boundary can be replaced by pseudopotentials.31 However, parameterising force-fields to match the energetics of the QM and MM regions more reliably reduces the energetic discontinuity without introducing additional corrective potentials.42–44
There are numerous strategies for selecting force-fields to satisfy the above conditions. Many studies transfer an optimised force-field designed to minimise the error of observables relative to experiment; however, this approach may lead to energetic and structural discontinuity between the classical and quantum regions, especially if the QM method deviates from the empirical structure. Therefore, it is often desirable to generate bespoke force-fields for the structure under study, which match the structural properties or bonding energies of the QM method (Fig. 2). To achieve such a parameterisation, software such as GULP45 and Paramfit46 for AMBER force-fields represent two approaches: the former minimising the errors of the least squares fit with respect to calculated observables; the latter using a genetic algorithm to match the energetics and forces of a classical force-field with corresponding QM simulations for a set of molecules. An alternative technique is demonstrated by Zimmerman, Li et al.,47,48 where successive QM/MM simulations are used to optimise an adsorption energy by iteratively improving the Lennard-Jones parameters. The iterative approach was applied to calculate the adsorption energy of a set of small organic molecules to a range of zeolites, reducing the mean absolute error (MAE) with respect to experiment from 6.7 kcal mol−1, calculated with the default CHARMM force-field, to 1.4 kcal mol−1. The reduced error demonstrates optimisation of the force-fields is a key component for ensuring accuracy in QM/MM simulations.
In the case of polarisable embedding, the dielectric response of the force-field must also align with calculated QM properties. However, in some scenarios (particularly for two-body shell potentials of TiO2), optimising the static dielectric constants may be incompatible with the objective of acquiring compatible equilibrium lattice constants.49 Although some studies have generated accurate force-fields for both the high frequency dielectric constants and lattice parameters, post-processing corrections must be applied to acquire accurate energetics associated with long-range polarization.15
Many-body fully polarisable force-fields, parameterised to match the energies of the QM functional, have been posed as a method for ensuring energetic continuity between the QM and MM regions for condensed systems.50,51 However, their applicability to most heterogeneous catalytic systems with small band-gaps are limited; whilst the contribution from successive n-body energetic terms is expected to decrease monotonically, significant oscillations remain in conductors up to the 7-body term.52 As a result, the force-field potential cannot be truncated to lower-order terms, introducing large computational expense for extended metallic systems.
As an alternative, the recent popularisation of machine-learning methods has opened a new avenue for force-field construction to support QM/MM simulations.53,54 Zhang et al. highlight that machine-learned potentials (MLPs) may, in principle, naturally eliminate the energetic and force discontinuities describing the ML–MM and QM regions on a matched potential energy surface. Furthermore, hybrid-DFT QM/MM has been used to as a reference to optimise standalone MLPs for free-energy simulations of enzymes in the solution phase; accuracies of ∼1 kcal mol−1 were obtained with respect to the hybrid QM/MM simulations.54 Another approach, known as Δ-ML,55 looks to generate either correction potentials or energetic/force terms56,57 that correct lower accuracy but inexpensive semi-empirical QM/MM methods to a reference, higher order functional. The Δ-ML approach can significantly reduce the cost of the QM calculation, making it more feasible to perform dynamic simulations and obtain free energies at QM accuracy. We note the above implementations have largely been applied to biochemical systems, but the underlying principles should in future be applied to challenges in heterogeneous catalysis.
2.5 Strategies for QM region selection
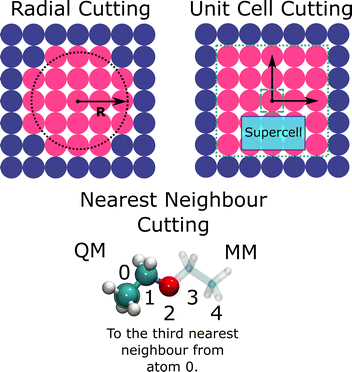
When selecting the core QM region (1), the primary aim is to minimise the number of atoms within the expensive energy evaluation while retaining the structure, charge, and energetic landscape of a fully QM simulation (Fig. 3). For any system, it is necessary to perform a convergence study that systematically expands the QM region, and achieves convergence of a target property with respect to periodic simulations, an extremely large QM region, or experiment. The simplest and most common scheme is expansion of the QM region as a sphere from a central point. Although conceptually simple, as we discuss later, this technique can include chemically unimportant features within the QM energy evaluation.Alternatively, one can expand the QM region via the number of nearest neighbours from a central atom. This approach is popular within zeolite studies, where target properties, such as adsorption energy of reactants, are observed to converge at five nearest neighbours.7,58 Furthermore, as zeolites have a well understood topology defined in terms of rings and cages, graph theory approaches can be used to select atoms associated with a substructure of interest.59
For catalytic surfaces constructed from ionic solids (e.g., MgO and TiO2), special care must be taken in the definition of the QM region. Although adsorption energetics are relatively insensitive to the shape and size of the cluster, the simple radius model produces relatively large errors for charged defect formations.60 In this work with an embedded-cluster model, analysis of the frontier molecular orbitals showed that QM regions utilising a cubic shape align far better with the frontier orbitals of the periodic structure, whereas the spherical models erroneously accumulate charge at the QM/MM boundary. More research is required to construct a formal heuristic for the optimal shape and size of the QM region. Recently, the SKZCAM scheme61 has demonstrated the validity of a radial scheme based on the radial distribution function of symmetrically related sites from a central vacancy; the approach systematically increases the size of the QM region to establish a smallest converged cluster, where the value of a desired observable plateaus with respect to larger cluster sizes.
In protein studies, it has been remarked the QM region size converges asymptotically with respect to an extremely large QM cluster, especially for mechanical embedding.62 Even with electrostatic embedding, however, QM regions of several hundreds, or even thousands of atoms, may be necessary to replicate the correct partial charges for negatively charged systems63 and NMR chemical shifts64 compared to the full QM simulation. Recent schemes such as the charge shift analysis (CSA) and Fukui shift analysis (FSA) have been employed to analyse which fragments significantly influence the partial charges of the active site.65 Using an embedded system with a very large QM region as a comparison, fragments are systematically placed within the MM region and the effect on the charge of the QM region is calculated; fragments producing a charge shift of less than ‖0.04–0.05‖ e are placed within the MM region. Compared to the simple radius convergence strategy, this technique can significantly improve the efficiency of QM/MM simulations by eliminating hundreds of atoms from the QM region; however, studies for ionic solids demonstrate that even small clusters are relatively well converged in terms of NMR shieldings,66 though studies including larger QM regions are needed to determine whether the slow convergence found in proteins precludes accuracy below 0.5 ppm.
Partitioning of the QM and MM regions in dynamics simulations requires more consideration. This is especially relevant for bi-phasic simulations with significant chemical interactions between the solute and solvent, meaning the first solvent shell must be included in the QM region.67,68 However, with a static definition of QM and MM atoms, exchange of QM with MM solvent molecules over time exposes the QM region of interest to short-range classic forces, decreasing the accuracy of the simulation. To account for this discrepancy, adaptive QM/MM schemes have been implemented to dynamically switch atoms between quantum and classical definitions based on their proximity to the quantum region.69 The sudden change in the physics of individual atoms as they cross the boundary can cause a significant discontinuity in the potential energy surface, motivating the development of schemes such as Permuted Adaptive Partition (PAP),70 ONIOM-XS,71 and Size-Consistent Multipartitioning (SCMP).72 These schemes introduce a buffer region between the QM and MM regions, which smoothly interpolate energetics and forces of molecules as they switch definition between the two regions. Recently, adaptive partitioning schemes have been extended to covalent solids, potentially expanding their applicability for heterogeneous catalytic applications.73 Machine-learned methods such as BurNN have also been implemented to provide corrective potentials for QM/MM buffer region.74 The corrective approach introduces a Δ-learning correction, yielding a potential that describes mutual polarisation between the buffer and inner QM region quantum mechanically.
Although the adaptive partitioning schemes above are widely adopted, Watanabe et al. discovered artefacts remain in both the energetics and statistical ensembles of dynamical QM/MM simulations with SCMP adaptive partitioning;43 this was attributed a physical mismatch in structure and physics between the QM calculation and the selected force-fields.42 Force-field solutions are explored in Section 2.4.
2.6 QM/MM codes
QM/MM has been implemented internally in a variety of quantum chemistry and classical molecular mechanics packages, as well as in specialised wrapper software that interfaces these packages. The software implementations vary in their use of subtractive and additive schemes, as well as their implementation of mechanical/electrostatic/polarisable embedding approaches. The implementations may be further distinguished in their use of quantum caps; most employ ECPs and hydrogen atoms, which allows for simulations of molecular systems.When implemented directly in existing QM or MM packages, direct interfaces to external software are typically realised to evaluate the quantum or classical energetic terms, though the calculation of the MM energy has also been implemented within QM software (with limitations to the range of MM formalisms available75). Alternative, more flexible implementations of QM/MM have been realised in wrapper packages that have multiple external interfaces to QM and MM energy calculators (commonly referred to as drivers), with examples including ASE,76 ChemShell,77 and LICHEM78 (Fig. 4). These codes connect a range of QM and MM packages, which is advantageous for broadening functionality; external drivers remain under separate management, but can then provide energetics, forces and densities when required. Management of geometry optimisations, transition state searches or molecular dynamics are performed at the wrapper level. Furthermore, wrappers may be developed to target specific systems or observables; for example, fromage79 is centered around calculation of excited states within molecular crystals, whereas PIMD80 focuses on simulating the dynamics of condensed systems and enhanced sampling techniques. In principle, the wrapper platforms are designed to be extensible, meaning they may be expanded to a greater variety of driver codes; however, not all software packages support all QM/MM formalisms, with some QM and/or MM package modification necessary to access more advanced features, such as polarisable embedding or capping ECPs.
 | ||
Fig. 4 A network showcasing some of the QM/MM external interfaces and connections to their respective QM and MM drivers. Cross-hatched codes have additional internal interfaces that perform the operations associated with embedding internally, and interface with a specific set of codes. Ordering of entries is chosen to reduce intersection between connections. a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AMBER,81 CHARMM,82 GROMACS,83 DL_POLY,84 GULP,45 ForceField,85 BOSS,86 LAAMPS,87 TINKER.88 AMBER,81 CHARMM,82 GROMACS,83 DL_POLY,84 GULP,45 ForceField,85 BOSS,86 LAAMPS,87 TINKER.88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bASE,76 fromage,79 ChemShell,77 Hybrid NAMD,89 AMS,90 PIMD,91 LICHEM.78 bASE,76 fromage,79 ChemShell,77 Hybrid NAMD,89 AMS,90 PIMD,91 LICHEM.78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cCRYSTAL,92 GPAW,93 ABINIT,94 CP2K,75,95 GAMESS,96 Gaussian,97 MOLPRO,98 ORCA,99 Quantum Espresso,100,101 TURBOMOL,102 VASP,103 NWCHEM,104 FHI-AIMS,105 Dalton,106 DMol3,107 QChem,108 MOLCAS,109 DFTB,110 DFTB+,110 TeraChem,111,112 ADF.90 cCRYSTAL,92 GPAW,93 ABINIT,94 CP2K,75,95 GAMESS,96 Gaussian,97 MOLPRO,98 ORCA,99 Quantum Espresso,100,101 TURBOMOL,102 VASP,103 NWCHEM,104 FHI-AIMS,105 Dalton,106 DMol3,107 QChem,108 MOLCAS,109 DFTB,110 DFTB+,110 TeraChem,111,112 ADF.90 | ||
3 Use cases
3.1 QM/MM solvent at the interface
Single configuration adsorption and transition state searches in vacuum are the mainstay of most DFT studies in heterogeneous catalysis; however, solvent has a significant influence on the energetics of adsorption and reaction kinetics in heterogeneous reactive systems.113–117 These effects arise from a variety of phenomena including the stabilisation of charged transition states with polar molecules, the introduction of an energy penalty (and entropic gain) for displacing solvent from the catalytic surface,114 and the active participation of the solvent in the reaction mechanism as a co-catalyst or reagent.116Simulating the dynamic solvent environment necessary for liquid-phase catalysis is a challenging problem with a solely quantum mechanical approach. Firstly, many solvent molecules must be simulated, which drastically increases the computational expense of the simulation. More importantly, the dynamic nature of the solvent environment requires configurational sampling through Monte Carlo or molecular dynamic (MD) approaches. The large number of energy and force evaluations required to obtain equilibrated observables further increases the computational work load. Although ab initio MD simulations of surface/water interfaces have become feasible with advances in parallel computing,118 kinetic studies require the evaluation of a large quantity of snapshots to represent the evolution of reaction coordinates over time. Implicit solvent techniques are also posed as a feasible alternative for calculating solvent properties of biphasic systems quantum mechanically; however, QM/MM maintains the atomistic representation of the dynamic solvation shell, while accelerating the MD simulation through a classical representation of the solvent. As such, QM/MM approaches provide an attractive alternative for representing the solvent environment.
Faheem et al. formulated such a model using the eSMS (explicit surface-metal-solvent) approach,11 primarily for modelling organic reactions at periodic metallic surfaces. The eSMS-FEP technique includes two forms of embedding to calculate the total energy of the surface/adsorbate complex: A subtractive QM-in-QM scheme is utilised to represent the energetics of the fully periodic metallic surface; and an additive coupling based on the polarisable embedding electrostatic cluster method (PEECM)119 to calculate the contributions from solvent. The system is calculated using a metallic cluster (with size converged with respected to energetics) and adsorbate, which is in turn embedded in an extended system of classical point charges representing both the metallic surface and the solvent environment. The total energy expression is thus:
| AeSMSQM/MM = Evac,periodicQM − Evac,clusterQM + Asolv,clusterQM/MM, | (5) |
Calculations of the free energy changes of activation and reaction were performed with a free energy perturbation (FEP) approach.10 The coupling between the degrees of freedom of the adsorbate and the solvent requires sampling over a huge configurational space; therefore, a potential of mean force (PMF)120 approach can be used to decouple the degrees of freedom of the solvent system by treating the force of the water on the fixed QM system as a mean-field. In effect, the PMF approach integrates out the degrees of freedom associated with the water shell for a given snapshot, meaning integration of the free energy over the reaction pathway can be performed solely using the evolution of the adsorbate reaction coordinates. Although the PMF technique drastically reduces the dimensionality of the FEP calculation, it effectively excludes the impact of solvent on the entropy of adsorbate itself, which introduces a small error. This topic will be discussed further at the end of this section.
The eSMS and FEP techniques have been used primarily to investigate the cleavage of O–H and C–H bonds for various polyols on transition metal surfaces. Initial studies focused on comparing eSMS to its implicit solvent counterpart, iSMS (implicit solvent-metal-surface).121 Overall, the eSMS schemes predict that the presence of solvent stabilises the free energy of activation (ΔG‡react) for the cleavage of the O–H and C–H bond by 21.2 kJ mol−1 and 3.9 kJ mol−1, respectively; in contrast, the iSMS model predicts a quantitatively lower stabilisation of 3.9 kJ mol−1 and 1.0 kJ mol−1, respectively. The findings emphasise the benefits from an explicit atomistic representation of the solvent environment to capture the energetic changes of reaction; however, the authors also demonstrate that care must be taken when selecting the force-field for the metal and solvent. In particular, the Spohr–Heinzinger and metallic Lennard-Jones potential displayed differences in the structure of water molecules at surface, with the solvation shell with the latter being denser than the former. Although the overall qualitative findings were unchanged, a variation of up to 19.2 kJ mol−1 was observed for the free energy changes of solvation.121
Subsequent studies with the eSMS-FEP approach investigated the impact of the solvent environment on the catalytic activity of different metallic species.122 Using the model C–H and O–H cleavage reaction, the overall free energy change and the kinetic barriers are drastically altered by the elemental composition of the metallic surface. In the most extreme case, the activation energy of the O–H bond cleavage is predicted to be ∼53.0 kJ mol−1 lower for Cu (111), and only ∼11.6 kJ mol−1 lower for Au (111), when compared to vacuum.
The differences in activation energy are primarily rationalised by the degree of charge transfer between the metallic surface and the transition state moieties, which varies with electronic structure for the metallic surface; the interfacial water molecules both reduce the surface dipole of the periodic slab model,123 and they are involved in transfer of charge density back into the metallic surface.118 Overall, the degree of transition state stabilisation correlates strongly with the change in charge transfer for both C–H and O–H cleavage. A secondary factor was the change in the number of hydrogen bonds around the transition state, especially for O–H cleavage, due to the disruption of existing hydrogen bonds caused by the loss of hydrogen. These contributing factors were compiled into a linear descriptor, where the authors further introduced ΔGgas as a variable, which corrects for the greater solvent-induced changes in activation energies for cleavage reactions with large barriers in the gas phase. Fig. 5 shows the resulting strong linear correlation for a descriptor consisting of ΔGgas and the charge transfer between the cleaved fragments, providing strong evidence that these factors strongly influence the change in reaction kinetics for the solvated system. Overall, these studies demonstrate that multiscale atomistic representations of the solvent environment can support the identification of specific solvent effects on reaction energy for different catalytic surfaces.
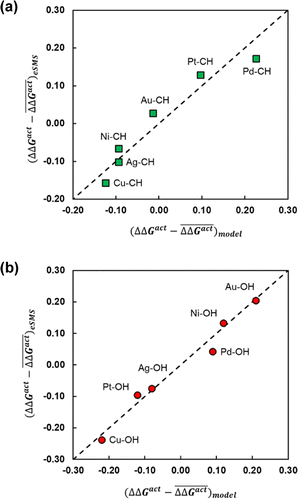 | ||
Fig. 5 The effect of solvent on the free energy of activation with respect to vacuum (ΔΔGact = ΔGactsolv − ΔGactvac) for the bond cleavage of (a) O–H and (b) C–H in ethylene glycol over noble metal surfaces. The figures compare the errors with respect to the mean ΔΔGact for a parameterised descriptor 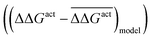 and values calculated with the eSMS method and values calculated with the eSMS method 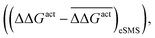 where bars indicate the mean. The descriptor includes the degree of charge transfer and the gas phase activation barrier of reaction. (a) is performed with a linear fit, while (b) uses a quadratic fit. All energies in eV. Reprinted from ref. 122 under a Creative Commons license (CC BY 4.0). where bars indicate the mean. The descriptor includes the degree of charge transfer and the gas phase activation barrier of reaction. (a) is performed with a linear fit, while (b) uses a quadratic fit. All energies in eV. Reprinted from ref. 122 under a Creative Commons license (CC BY 4.0). | ||
Addressing the structural dependence of water on the selected classical potentials, Steinmann et al. and Clabaut et al.124,125 developed a set of bespoke force-fields (GAL17 and GAL19) that introduce specific parameters for interaction with periodic noble metal surfaces. After parameterisation against an ensemble of 826 water configurations obtained through DFT, the overall force-field predicts an average error for water adsorption energies of 0.4 kcal mol−1. The force-fields were then utilised within a QM/MM study to model the adsorption of phenol and benzene to the Pt (111) surface,9 introducing the solvHybrid method (Fig. 6).
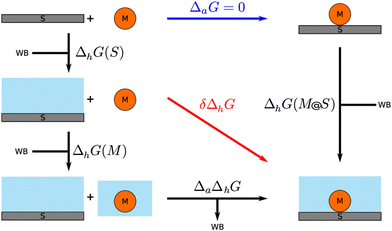 | ||
| Fig. 6 The thermodynamic cycle for the MM-FEP scheme implemented in the SolvHybrid framework. Reprinted with permission from ref. 9. Copyright 2020 American Chemical Society. | ||
The SolvHybrid technique differs from the eSMS-FEP approach of Saleheen and Faheem in several key ways. Similar to the MM-FEP scheme of Steinmann et al.,22 the energy of the QM region is computed with a fully periodic simulation, as opposed to the subtractive cluster eSMS scheme. This gives greater flexibility to vary the adsorbate coverage, as the simulation inherits the periodicity of the unit cell, whereas the cluster model implicitly assumes adsorption is taken to the dilute limit. However, the water environment must have the same periodicity as the metallic surface, meaning the classical charges of water are represented with the Particle-Mesh-Ewald (PME) method of CHARMM82,126 as opposed to the PEECM approach. A further important contrast between the two approaches is the use of mechanical as opposed to an electrostatic embedding. Finally, SolvHybrid calculates free energy changes through thermodynamic integration (TI) as opposed to the FEP method.
Adopting the nomenclature of their publication, the overall free energy of adsorption in solvent is then represented as
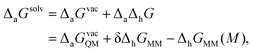 | (6) |
Considering the adsorption of benzene and phenol, a decrease in the adsorption energy with respect to vacuum was correctly identified (Fig. 7). Compared to experimental results obtained through cyclic voltammetry (−9 kJ mol−1/−14 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 114,128), the QM/MM approach obtained a free energy change of solvation of −40 kJ mol−1 at saturation coverage. This represents the correct qualitative decrease in the adsorption free energy in solvent relative to vacuum, which is calculated to be −118 kJ mol−1 using experimentally derived values for the enthalpy of adsorption,129 and the computationally derived entropy of adsorption via TI127 at 300 K at a coverage of 1/16. The discrepancy of ∼30 kJ mol−1 may be rationalised through the accumulated errors in the choice of density functional, the free energy change of desolvating the metallic surface, and utilising the gas phase adsorption entropy in place of the aqueous entropy. Furthermore, as with gas phase studies of coverage dependent adsorption energies, the use of a single periodic configuration of phenol as opposed to an ensemble of different orientations can introduce a further error of up to approximately 10 kJ mol−1.5
114,128), the QM/MM approach obtained a free energy change of solvation of −40 kJ mol−1 at saturation coverage. This represents the correct qualitative decrease in the adsorption free energy in solvent relative to vacuum, which is calculated to be −118 kJ mol−1 using experimentally derived values for the enthalpy of adsorption,129 and the computationally derived entropy of adsorption via TI127 at 300 K at a coverage of 1/16. The discrepancy of ∼30 kJ mol−1 may be rationalised through the accumulated errors in the choice of density functional, the free energy change of desolvating the metallic surface, and utilising the gas phase adsorption entropy in place of the aqueous entropy. Furthermore, as with gas phase studies of coverage dependent adsorption energies, the use of a single periodic configuration of phenol as opposed to an ensemble of different orientations can introduce a further error of up to approximately 10 kJ mol−1.5
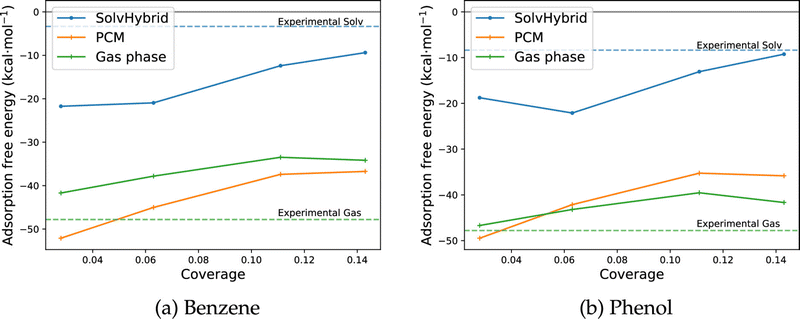 | ||
| Fig. 7 ΔGsolvads calculated for benzene and phenol on the Pt (111) surface across a range of coverages in the aqueous environment, performed using the MM-FEP scheme. Reprinted with permission from ref. 9. Copyright 2020 American Chemical Society. | ||
Lim et al. demonstrate an alternative implementation to the TI and FEP approaches in the DFT-CES/2PT method (DFT in Classical Explicit Solvents – Two Phase Thermodynamic mode).130 The calculation of free energies of solvation in DFT-CES/2PT differs significantly from the previously discussed approaches in two ways: (1) the electrostatic embedding of the solvent environment is included in the one-electron Hamiltonian of the QM environment through a mean-field potential of the water environment, which determines the reorganisation energy of the QM region in the MM environment (Ereorg); and (2) ΔGsolv is determined through vibrational density of state functions, which is decomposed into gas-like diffusive modes and solid-like vibrational modes.131,132 Overall, the total free energy of solvation is expressed as a sum of the previous terms,
| ΔGtotsolv = Ereorg + ΔGsolv, | (7) |
When applied to a small test set of molecules, ΔGtotsolv yielded a MAE of 5.51 kJ mol−1 with respect to experiment, which compared favourably to the MAE of the highly parameterised SM8 implicit solvent model (3.68 kJ mol−1).130 DFT-CES/2PT was then used to calculate the free energy of adhesion of water to a range of graphite and metallic facets.133,134 Comparisons with experimentally derived values for the work of adhesion show the DFT-CES/2PT accurately determines the energetics of the interface (Gim et al.135 74.27 mJ m−2vs. experiment 72.8 mJ m−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136). Through analysis of the surface concentration of water and the degree of hydrogen bond formation, the authors also conclude the wettability of graphite is brought about by solid–liquid interactions and the increased concentration of water at the surface, which increases the population of stabilising hydrogen bonds.
136). Through analysis of the surface concentration of water and the degree of hydrogen bond formation, the authors also conclude the wettability of graphite is brought about by solid–liquid interactions and the increased concentration of water at the surface, which increases the population of stabilising hydrogen bonds.
Further studies suggest that Ag, Au, Pd and Pt surfaces are superhydrophillic, tending towards parallel arrangements of water at the interface.133 Additionally, the rotational and transnational diffusivity (derived from the mean-square displacement of the molecules from their initial position) across each studied facet was significantly lower than the bulk. However, the water adlayer still maintained a degree of diffusivity at 300 K, demonstrating that water remains in a liquid-like phase at the interface. This contrasts with the commonly utilised hexaganol ice-like bi-layer structure found at low temperatures.137
Overall, the QM/MM approach allowed the simulation of complex, dynamic systems at reduced cost compared to full QM methods, providing atomistic insight into the interfaces relevant for catalysis. Such simulations are valuable due to the challenges in gathering experimental observations for aqueous/metallic interfaces; for example, microscopy or calorimetry techniques, which require ultra-high vacuum conditions with cryogenic temperatures to maintain the stability of the aqueous layer.133,138,139
Furthermore, the eSMS-FEP and SolvHybrid techniques demonstrate novel QM/MM approaches for calculating the free energies of solvation for catalytic systems and interfaces. An obvious limitation is the use of a single configuration of the adsorbate for each reaction co-ordinate frame. The configurational limitations are necessary for computationally tractable simulations, though the lack of dynamics for the adsorbate introduces an error by excluding the influence of solvent on the entropy of the adsorbate/surface complex. The approach of Clabaut9 addresses this challenge somewhat by calculating the overall free energy of solvation for the unadsorbed molecule, and the gas phase entropy of adsorption to approximate the entropy in solvent. Although the QM/MM approaches capture the majority of the entropy changes – which originate from the energetically favourable displacement of solvent from the catalyst surface113,128 – the effect of solvent on the entropy of the adsorbed compound warrants further investigation.
3.2 Reactions and heteroatom substitution in zeolites
Zeolites are a class of aluminosilicate materials that have gained much interest due to a range of applications in industry, such as molecular sieves and fluid catalytic cracking of petrochemicals, and are potential catalysts for reactions important for green and sustainable chemistry. Zeolites are crystalline frameworks composed of interlinking SiO4 and AlO4− tetrahedra (T-sites), which form a porous 3D network of cavities and channels with dimensions of 3–20 Å.140,141 The existence of AlO4− tetrahedra within zeolite frameworks creates a need for a cation to compensate the negative charge on the alumina, and when this compensating cation is a proton, Brønsted acidity is induced within the framework.142,143 Furthermore, doping the zeolite framework with heteroatoms induces Lewis acidity,144i.e., the ability of a species to donate electron density.145 In combination, zeolites can behave independently as Brønsted- or Lewis-acid catalysts, or as a bifunctional mixture.146–149 The strong Brønsted- and Lewis-acid properties place zeolite catalysts at the forefront of materials for green and sustainable energy; therefore, advancing simulation techniques for the study of zeolite catalysts is of the utmost importance.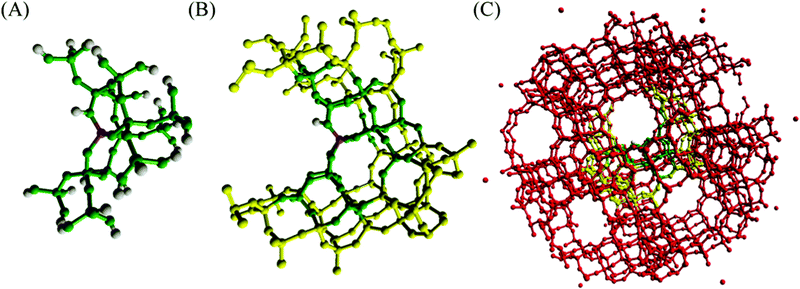 | ||
| Fig. 8 Embedded cluster model of H-ZSM-5 (A) QM region (green) (B) QM region and inner MM region (yellow) (C) QM region, inner MM region, outer MM region (red). Reproduced from ref. 7 with permission from the Royal Society of Chemistry. | ||
QM/MM methods have become a popular approach to model catalytic zeolitic systems due to the local nature of the active site (Fig. 8).150–155 QM calculations on small cluster models of the active site have long been used to model zeolite active sites; however, discrepancies from experiment in structures and energies can arise due to the small size of the cluster models relative to the extended frameworks. Phenomena such as steric constraints, which are characteristic of adsorption in zeolites, are not well described due to insufficient incorporation of the zeolite pore in the models. Periodic calculations (typically with DFT for reactive processes) are a reliable alternative method for modelling zeolites, but these calculations are generally restricted to small unit cells and/or low-level DFT functionals, such as the generalised gradient approximation (GGA), as the expensive nature of running higher-level exchange–correlation (XC) functionals or larger unit cells creates a computational bottleneck. In this regard, QM/MM methods allow calculations on large models, facilitating the capture of long-range interactions and steric constraints of the zeolite pore whilst using a small QM region around the active site, subsequently allowing for the use of higher-order XC functionals (such as hybrids) or application of correlated methods. As a consequence, QM/MM methods, through embedded-cluster or periodic models (ONIOM, QM-pot) can be applied to investigate a range of zeolite catalysts with applications in heterogeneous catalysis.
Brønsted-acid zeolite catalysts have been successfully employed for the conversion of methanol to hydrocarbons (MTH).156,157 As methanol production may be conducted through the reduction of CO2, or derived from biomass, recent interest has been elevated by the potential as a green route to hydrocarbon synthesis. Embedded-cluster QM/MM investigations by O'Malley et al. considered the deprotonation, methanol adsorption, and methoxylation energies in H-ZSM-5 and H-Y zeolites, investigating the influence of framework topology and active site location on sorbate behaviour.158 The study used a mixture of GGA (PW91) and hybrid (B3LYP and B97-2) DFT, and found that the latter predicted higher deprotonation energies for acid sites in H-ZSM-5 and H-Y. The result was attributed to the superior localisation of electrons when using the hybrid-DFT approach; however, each functional preserved the hierarchy of deprotonation energy, as H-Y < H-ZSM-5 (sinusoidal) < H-ZSM-5 (intersection) < H-ZSM-5 (straight), with the site type given in parenthesis for H-ZSM-5, showing consistency in the trends irrespective of modelling approach. Furthermore, the results for H-ZSM-5 (intersection) using the GGA functional PW91 was 122 kJ mol−1 lower (1093.4 kJ mol−1) than those calculated via ab initio molecular dynamics simulations on MFI structures using the same functional.159 The authors attribute this discrepancy to the sorbate–sorbate interactions or charge compensation, which occurs in periodic systems in contrast to the more complete representation of polarisation afforded in embedded-cluster QM/MM methods. The final result highlights that, even at the GGA level of theory, aperiodic embedded-cluster QM/MM approaches can offer advantages over periodic modelling approaches.
The MTH process was investigated further with the embedded-cluster QM/MM method by Nastase et al.7,58,160 Initially,7 the adsorption of multiple methanol molecules in H-ZSM-5 and H-Y zeolites was investigated, concluding that the arrangement of hydrogen bonds between methanol and the framework significantly influence the adsorption strength. By investigating the different orientations of methanol on the Brønsted-acid sites (Fig. 9), the importance of dispersion in the calculations was identified. Values calculated using the dispersion-corrected hybrid B97-D and second order Møller–Plesset perturbation theory (MP2), which accurately accounts for dispersion effects, are in good agreement (Table 1); quantitatively the results also allign to previous dispersion-corrected studies with PBE-D (−115 kJ mol−1), and to experiment (−110 kJ mol−1).161,162 The dispersion corrected adsorption energies qualitatively correlate with other hybrid-DFT methods, such as B97-3, but quantitatively disagree by ∼50 kJ mol−1, which highlights the need to account for dispersion and the localised nature of electrons. The validation achieved with hybrid-DFT and MP2 are made accessible by QM/MM, owing to the size of the QM region in their models (74 atoms), which is much lower than the number in a periodic DFT calculations (288 atoms).
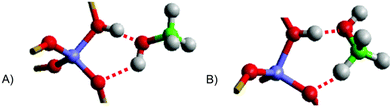 | ||
| Fig. 9 Representations of methanol adsorption configurations in H-ZSM-5. (A) “end-on” coordination (B) “side-on” coordination. Reproduced from ref. 7 under a Creative Commons license (CC BY 3.0). | ||
| Site | B97-3 | B97-D | MP2 | |||
|---|---|---|---|---|---|---|
| EO | SO | EO | SO | EO | SO | |
| H-Y | −70 | −65 | −106 | −100 | −102 | −96 |
| H-ZSM-5 [T12] | −81 | −78 | −124 | −120 | −117 | −113 |
| H-ZSM-5 [T4] | −82 | −80 | −126 | −115 | −121 | −112 |
| H-ZSM-5 [T1] | −81 | −85 | −115 | −114 | −107 | −113 |
Nastase et al. applied QM/MM methods to study subsequent intermediates formed during the initial stages of the MTH process, namely on dimethyl ether (DME) and carbene species.58,163 DME adsorption on Brønsted-acid sites of H-Y and H-ZMS-5 resulted in pronounced proton transfer over the intersectional site in H-ZSM-5, which correlates with greater Brønstead-acidity, and potential superior catalytic performance compared to H-Y. Here, QM/MM was used to perform transition state calculations with hybrid XC functionals, which again is challenging with periodic DFT, and the active site was observed as remaining deprotonated during the reaction for DME production, which contrasts with previous reports. The discrepancy was attributed to the difficulty with GGA-type modelling to localise the electron density, reinforcing the importance of employing higher-level approaches.
As an alternative embedded-cluster QM/MM models, periodic QM/MM approaches have also been developed and applied extensively towards the modelling of Brønsted-acidity. The group of Sauer have developed such approaches in the QM-pot method,20,164 where any error that arises from replacing large periodic systems with small cluster models can be reconciled through QM treatment of the active site in the periodic model, and classical potentials to treat the rest of the framework. The approach addressed drawbacks of earlier QM/MM techniques that used mechanical embedding, as the QM-pot method incorporates long-range electrostatic embedding. The QM-pot method has been used to investigate deprotonation energies for zeolite Y, CHA, MOR, and ZSM-5, which were found to be, 1171, 1190, 1195, and 1200 kJ mol−1, respectively, in good agreement with experiment.165 The energies were calculated using the Hartree–Fock (HF) approximation and treated a posteriori with MP2 for consideration of correlation, where the authors noted that their method allows for total relaxation of the framework and negated the large computational overhead associated with using the HF level of theory.
The adsorption of hydrocarbons is the initial step for acid-catalysed hydrocarbon conversions and is a widely investigated process in zeolite catalysis. Continuing the investigation on Brønsted-acid sites in zeolites, the group of Sauer investigated the interaction of propene, butene, and pentene, within H-FER framework.166 The calculated adsorption energies, using B3LYP, were in good agreement with experiment, and predictions of the stability of adsorbed species were achievable; for example, adsorbed secondary alkaloids were significantly more stable than alkenes. Furthermore, the study found that adsorption energies predicted with QM-pot were more accurate than periodic-DFT, owing to the better description of van der Waals interactions by force-fields over periodic-DFT. Therefore, through application of QM/MM methods, Sauer et al. were able to utilise an improved representation of dispersion interactions as afforded by force-field methods for zeolitic systems.
The incorporation of heteroatoms, such as main group or transition metal elements, can enhance the catalytic ability of a zeolite framework. The insertion of Lewis-acid heteroatoms into the BEA framework, such as Ti and Sn, creates catalysts that have demonstrable activity for Bayer–Villiger oxidation (BVO), Meerween–Pondorf–Verley (MPV) reduction, and glucose to fructose isomerisation, which are used in the up-cycling of chemicals.167 Considering the example of BVO, cyclic ketones are converted into lactones that are subsequently used for biomass-related reactions and as fuels.147 The Ti- and Sn-containing zeolites allow the use of hydrogen peroxide as an oxidant rather than more harmful oxidising agents, such as the traditionally meta-chloroperoxybenzoic acid (mCPBA); furthermore, the reaction is more environmentally benign, producing only water. However, the catalytic processes are complex, and QM/MM again provides access to high-level theory for modelling of the reaction process.
Through QM/MM methods applied via the ONIOM approach, Montejo-Valencia et al. examined the Lewis-acidity and hydrothermal stability of Ti, Sn, and Ge doped beta frameworks (Fig. 10).168 A hybrid ω-B97XD XC functional was made feasible via QM/MM, and allowed comparison of relative energetics in polymorph A (BEA) and polymorph C (BEC) of the beta framework. The comparison of polymorphs is necessary as superior catalytic activity and selectivity were suggested for BEC in some reactions.169 Considering 3 T-sites in each framework (T1–T3), T1 was the most stable site for Ti, Sn, and Ge substitution in the BEC framework (Fig. 11); in contrast, for BEA, both T1 and T2 were the most stable sites for Ti, with energies of 14.84 and 14.89 kcal mol−1, respectively. Calculations on hydrolysed Ti, Ge, and Sn (with one water molecule coordinated), combined with correlation of the Lewis-acidity and the energy of the lowest unoccupied molecular orbital (LUMO), showed Ti-BEC as having the lowest LUMO energies, and thus greatest potential Lewis-acidity, of all heteroatoms for that framework.
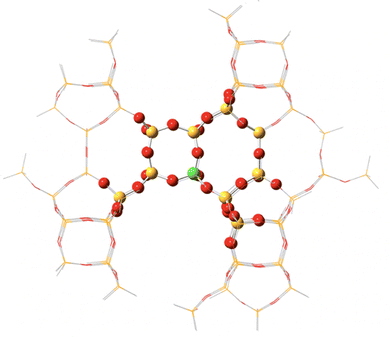 | ||
| Fig. 10 Representation of an ONIOM model of M-BEC (394 atoms, M/Si ratio of 1/114), M = Ti, Sn, or Ge. QM atoms in region 1 are represented as spheres, whilst a stick framework is used to represent region 2 atoms (MM). Reprinted from ref. 168. Copyright 2015 American Chemical Society. | ||
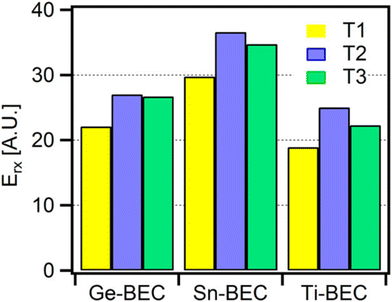 | ||
| Fig. 11 Energetics of heteroatom substitution into different T-sites of the BEC framework. Reprinted from ref. 168. Copyright 2015 American Chemical Society. | ||
The study of hydrolysis energies concludes that Ti-substituted BEA and BEC have the highest hydrothermal stability for substituted beta frameworks, and that the electronic properties of both frameworks are similar; thus, as the crystalline structure of BEC contains fewer native defects, Ti-BEC could be a superior catalyst. The advantages of the QM/MM methods are noted by the authors in their investigation, especially for capturing the long-range interactions within the framework in contrast to small cluster models. Furthermore, the use of the hybrid ω-B97XD XC functional provided more accurate electronic properties, which could be correlated to Lewis-acidity through analysis of frontier orbital energies.
Zeolites containing late transition metals have also been demonstrated as good catalysts for several reactions in recent years;170 of these, Cu-containing zeolites are able to produce phenol via the oxidation of benzene, which offers higher selectivity than the traditional cumene synthesis for phenol, and removes acetone formation as a by-product. Archipov et al. studied the adsorption of benzene on Cu containing zeolite-Y, which is an important step in the reaction for phenol production.171 With application of QM/MM via the QM-pot approach, the authors were able to study the catalytic formation of phenol through hydroxylation of benzene by molecular oxygen. Key mechanistic aspects were made feasible, such as the preferential binding of Cu to the SIII cationic site of the supercage in the zeolite, with the results agreeing with prior studies. Furthermore, hybrid-DFT (B3LYP) was applied via QM/MM to simulate vibrational frequencies on the SIII site, giving values in excellent agreement with FTIR, again highlighting the benefit of high-level XC functionals in producing accurate reaction observations.
The choice of XC functional for modelling Cu-containing zeolites was explored further by Morpurgo et al., through application of QM/MM with ONIOM.172 The computed structure of Cu-ZSM-5, as well as the energies and frequencies of adsorbed NO, were benchmarked for several XC functionals and basis sets (Table 2). Overall, hybrid-DFT consistently outperformed GGAs when compared with experiment. NO adsorption energies calculated by B3LYP, PBE1PBE, and M06 were very close to experiment (25–26 vs. 24 kcal mol−1), in contrast with PBE and BLYP, which overestimated adsorptions energies (35–38 kcal mol−1). Considering the context of heterogeneous catalysis, the importance of functional choice for describing chemical phenomena is clearly re-iterated, as density functionals at the GGA-level are inferior to hybrid functionals for prediction of accurate NO adsorption energies. The outcome emphasises how QM/MM provides an approach that facilitates use of these otherwise expensive approaches.
| Site-orient. | E ads | E def | Scaled νN–O |
|---|---|---|---|
| B3LYP/T(Q)ZVP:HF/3-12G | |||
| T1-in | −25.73 | 0.37 | 1850.2 |
| T1-out | −25.75 | 0.45 | 1848.1 |
| T7-in | −25.76 | 0.35 | 1857.5 |
| T7-out | −25.69 | 0.27 | 1860.4 |
| BLYP/T(Q)ZVP:HF/3-12G | |||
| T1-in | −34.50 | 0.55 | 1821.7 |
| T1-out | −34.54 | 0.62 | 1816.3 |
| T7-in | −34.56 | 0.49 | 1821.6 |
| T7-out | −34.49 | 0.42 | 1819.2 |
| PBE1PBE/T(Q)ZVP:HF/3-12G | |||
| T1-in | −26.14 | 0.39 | 1860.5 |
| T1-out | −26.24 | 0.42 | 1857.9 |
| T7-in | −26.29 | 0.40 | 1865.1 |
| T7-out | −26.07 | 0.28 | 1869.7 |
| PBE/T(Q)ZVP:HF/3-12G | |||
| T1-in | −36.93 | 2.07 | 1838.0 |
| T1-out | −37.47 | 2.06 | 1834.3 |
| T7-in | −37.09 | 1.76 | 1841.0 |
| T7-out | −37.17 | 1.67 | 1843.6 |
| B3LYP/T(Q)ZVP:B3LYP/LANL2D7 | |||
| T1-in | −25.14 | 0.30 | 1842.9 |
| T1-out | −25.14 | 0.35 | 1842.7 |
| T7-in | −25.62 | 0.31 | 1844.8 |
| T7-out | −25.71 | 0.26 | 1843.7 |
| M06/T(Q)ZVP:M06/LANL2D7 | |||
| T1-in | −25.64 | 3.91 | 1859.5 |
| T1-out | −26.61 | 3.58 | 1854.0 |
| T7-in | −25.22 | 3.10 | 1862.2 |
| T7-out | −26.00 | 3.15 | 1869.8 |
Taking further advantage of the reduced computational workloads enabled by QM/MM, studies may be centered around accurate, high throughput workflows that can validate the lowest energy state for a large ensemble of systems. Such studies are of particular importance in zeolites, where the silicate framework contains a large number of silicon (T) sites which may be occupied by Al. Furthermore, the Brønsted acid protons may occupy any of the neighbouring oxygens. Considering the further combinations introduced by the inclusion of multiple Al sites within the active region, the configurational space expands to an assay of thousands of structures; for standard DFT approaches, especially with hybrid functionals, such a study could not be conducted without drastic time and resource commitments. To address this challenge, Aljama et al.173 implemented a workflow to explore the most stable site for Pd+ and Pd2+ exchange in Al-doped BEA and CHA frameworks, which was then utilised to measure the adsorption energies of NO.
In order to determine the most stable structures, the workflow of Aljama et al. permuted over all possible combinations of Al substitution, Pd cation placements, and Brønsted acid positions. The approach filters the less stable candidates with cheaper GGA methods, and then applies more accurate hybrid simulations to the most stable structures, in a six step workflow: (1) generating all possible combinations of Al substituted T-sites, including double-substitutions within three and four nearest neighbours of one another, and including iterations over the possible positions of the Brønsted protons; (2) selecting the optimum QM region by including the rings containing the relevant substituted T-sites; (3) exchanging one/two Brønsted acid proton(s) for Pd+/Pd2+ to gauge stable configurations through single-point energy evaluations; (4) taking the more stable positions and performing geometry optimisations with QM/MM on the GGA level (B97-D3); (5) taking the five most stable candidates for each Al configuration and performing optimisations at the hybrid-DFT level (ω-B97XD); (6) using the same most stable structures, introduce the NO adsorbate and calculate the binding energy. Overall, the approach required >7000 calculations, which is a significant reduction on the full configurational search space, whilst still representing a systematic and complete search for the global minima of NO adsorption for a combinatorially complex energy landscape.
The position of the Brønsted acid protons had a sizeable effect on energy of formation for Pd cation exchange. Overall, Pd2+ and Pd+ generally favoured the occupation of Brønsted acid sites centered on the zeolitic 6-membered ring (6MR) for the CHA and BEA frameworks. Furthermore, the adsorption energies of NO onto the Pd cations correlated negatively with the energy of formation for the metal Pd cation exchange site, which is attributed to the reduced electron density for backbonding/donation. Additionally, NO adsorption to the Pd+ cation complex was generally more stable than adsorption to Pd2+ when the corresponding metal 1+/2+ cations had similar energies of exchange. Aljama et al. posit this results stems from the presence of unpaired electrons at the Pd2+/NO site, whereas the Pd+H+/NO adsorption complex often resulted in spin-free electron configurations.
The importance of QM/MM methods in studying zeolitic heterogeneous catalysts is clear: it provides an ability to incorporate long-range interactions with an affordable computing overhead, whilst sorbate–sorbate interactions and unrealistic metal loadings can be avoided using aperiodic embedded-cluster approaches. Furthermore, high-accuracy treatments of electronic structure can be applied to the core active site of the catalytic reactions, which are otherwise infeasible with e.g. periodic DFT. Hybrid-DFT and correlated methods are beneficial in accurately describing chemical phenomena that are crucial in catalysis, such as adsorption and transition states. In addition, the reduced computational cost of QM/MM enables the development of high throughput workflow, where large assays of structures are required. Sweeping over the large configurational spaces intrinsic to zeolites would be incredibly expensive with standard periodic DFT approaches. However, the QM/MM approach provides unique opportunities to perform large studies that sample over a large chemical space, and provide insights that may otherwise be lost in smaller studies.
3.3 Nanoparticles
Nanoparticle-based materials are one of the more widely used types of heterogeneous catalyst across chemical industry. Tremendous efforts continue to be applied to the study and improvement of chemical processes with nanoparticles. A set of degrees of freedom enables fine tuning of nanoparticle activity and selectivity: size, shape, composition, surface decoration, support, and more. The issues of catalyst stability, and adjusting to reaction condition, is particularly acute for nanoparticle-based catalysis, due to the inherent instability of a material surface.For accurate simulations of nanoparticle-based catalysts, one takes into account a nanoparticle, reacting species, support, and solvent. The size of such systems, along with large timescales and an interest in high-throughput screening, makes it necessary to focus efforts into development and employment of multiscale models and methods. Similar approaches are being used for simulation of nanoparticles for biomedical applications, in particular for drug delivery, so here we will also consider such studies.
Depending on the locality of the electronic states, the typical schemes for partitioning a nanoparticle system with QM/MM approaches are:
1. QM representation of the entire nanoparticle and adsorbed species; MM for environment; or
2. QM representation of the adsorption complex (adsorbate and active site); MM for remainder of nanoparticle and environment.
A MM treatment of a solvent environment around a nanoparticle is equivalent to that considered in Section 3.1, though with reduced dimensionality of the catalyst model. An example of explicit solvent representation within a QM/MM simulation is shown for dopamine molecules bound to the TiO2 nanoparticle in the water solvent environment (Siani et al.174), where a generalized Amber force-field (GAFF)175 was used for water, and SCC-DFTB theory for dopamine molecules and nanoparticle. Similar explicit solvation was considered in electrochemical CO2 reduction to ethylene on Au nanoparticles in a water environment, which was simulated with the recently developed ReQM method by Naserifar et al.176 The ReQM method implements a subtractive QM/MM approach and is based on a special polarisable force-field, RexPoN.176 RexPoN is a reactive force-field that has terms for non-bonded (van der Waals) interactions, for valence bonds, and supports dynamic polarization and charge distribution via the PQEq model.177
The ReQM method was used to simulate 2443 different adsorption complexes of CO and HOCO on the disordered Au surface with explicit water solvent, where the PBE-D3 flavour of DFT was used for a cluster of Au with an adsorption site and adsorbed species, and RexPoN was used for then whole system, which additionally included up to 306 water molecules as a solvent. The adsorption site clusters were generated by cutting out an 8 Å cluster from the surface of the 10 nm Au nanoparticle (168![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419 atoms), following the approach of Chen et al.178 Then ReQM simulation results were used to train a neural-network model that was used to test over 10
419 atoms), following the approach of Chen et al.178 Then ReQM simulation results were used to train a neural-network model that was used to test over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 more different adsorption sites. Overall, QM/MM has facilitated an exhaustive screening of the adsorption sites on the Au nanoparticle, without simulating of the full-size nanoparticles itself.
000 more different adsorption sites. Overall, QM/MM has facilitated an exhaustive screening of the adsorption sites on the Au nanoparticle, without simulating of the full-size nanoparticles itself.
A QM/MM scheme tailored to bulk metals and surfaces has been developed by Zhang, Lu, and Curtin,179 and subsequently applied to nanoparticle systems. That scheme separates the simulated system in 3 nested regions denoted I, II, and III. The total energy is estimated as follows:
| Etotal[I + II + III] = EQM[I + II] + EMM[II + III] − EMM[II], | (8) |
| Etotal[I + II + III] = EQM[I + II] + EMM[III] + E12couple. | (9) |
Here the E12couple term can be derived from eqn (8) and (9) as follows:
| E12couple = EMM[II + III] − EMM[II] − EMM[III]. | (10) |
Therefore, the Zhang, Lu, and Curtin scheme is essentially an additive QM/MM method with a purely classical coupling term. Region I would contain the catalytic active site or an adsorption complex of interest, whilst regions II and III contain solid metal. The solid metal regions can be described with e.g. a classical EAM-like potential,180 and no special treatment of their borders is necessary for evaluation of EMM[II + III] and EMM[II].
For calculation of EQM[I + II], the constrained DFT (cDFT) method is employed. A constraining potential is imposed in region II, near the border with region III, which penalizes deviation of the density in region II from the so-called “target electronic density” during subsequent DFT calculations. The target density is defined as a function of metal nuclei coordinates fitted to the bulk density. Compared against the widely used frozen-density embedding181 method, the penalizing potential approach is favoured as it does not require an orbital-free approximation of the kinetic energy functional, which itself is not always available.
Application of the Zhang, Lu, and Curtin approach revealed how surface strain in core–shell metal nanoparticles can alter their catalytic activity towards oxygen reduction reactions, including studies of Pt–Cu,182 Ni–Pd, Ag–Pd,183 and Fe–Pt184 nanoparticles. In these papers, EAM potentials were used for the whole nanoparticles, and the DFT with constraining potential was used for the adsorption complexes of interest. The QM/MM approach allowed simulation of nanoparticles with curvature that is inaccessible in standard periodic approaches, whilst also accommodating large nanoparticle sizes of up to 270![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms.183
000 atoms.183
For metal nanoparticles, the ONIOM13,36 method has been efficiently applied to simulate interactions of large organic molecules with nanoclusters.185 The novelty of the ONIOM formulation is its focus on the possibility of using more than two layers of theory, for example QM1/QM2/MM 3-layer ONIOM. Due to absence of the coupling Hamiltonian term HMM–QM in the subtractive scheme, it is simple to use different levels of theory and stack as many of them as necessary; however, the important shortcoming of the subtractive scheme is the need of a classical force-field for the QM region. For organic molecules, the requirement of a force-field is not typically problematic, and the development of the Universal Force Field (UFF) paved the way to simulation of metal-organic systems. Previously, Ananikov et al.185 reviewed numerous ONIOM studies of influence of ligand structure and molecular environment on activity and selectivity of metal-organic catalysts and surface-deposited nanoclusters, and the reader is directed to this work for further detail. Some recent applications of the ONIOM technique include simulation of DOPA molecules adsorption on gold nanoparticles186 and amino acid adsorption on bimetallic surfaces in water solvent.187 In both cases, QM was used for the adsorbed molecules and the first 2 or 3 layers of the metal support, with the UFF used for the rest of the support metal. Geometry of the adsorption complexes, adsorption energies, electron density distribution were computed.187 Some of simulated systems were compared with pure periodic DFT calculations186 and experiments, and overall good agreement was observed.186 These results again show the potential for multiscale QM/MM methods for study of nanoparticulate catalytic systems.
3.4 Defects in metal oxides
The engineering of metal oxide materials is an important field within heterogeneous catalysis, particularly for the development of economical and sustainable processes.188 Materials such as TiO2 have been highlighted as powerful photocatalysts, with reactions such as water splitting for hydrogen generation at room temperature labelled as the “holy grail” of catalytic chemistry;189 however, there are many gaps in our understanding of these processes, including the identity of charge carriers and acceptors and the characterisation of excess charge mediated reaction steps.189 Similarly, the transformation of CO2 to longer chain hydrocarbons in carbon capture utilisation (CCU) processes190,191 can be catalysed by rock salt oxides such as MgO and MnO; however, the low sorbant capacity of the unmodified MgO surface motivates studies into the rational design of catalysts with higher thermal stabilities and CO2 adsorption energies.191 All these catalysts are desirable due to their wide availability and low manufacturing costs.192Accurate modelling of these materials requires high-level electronic structure methods, due to the impact of the frontier orbital energy levels on the reaction chemistry. As we have explored elsewhere in this review, the reduction of the QM system allows the use of higher-level DFT, such as hybrid functionals, which can correctly localise defects and represent the energetics of defect formation.35 In this context, QM/MM provides a tool for explaining experimental observations193,194 and guiding the design of future catalysts.195
The embedded-cluster approach provides further advantages regarding the accuracy of the defect formation energies, as they can be calculated at the dilute limit, due to the use of open boundary conditions and an extended structure of MM charges;196 furthermore, the atomistic representation of the extended system incorporates long-range electrostatics, accounting for polarisation in both the QM and MM via polarisable embedding schemes. Berger et al. note, however, that challenges persist for highly polarisable systems with high dielectric constants (e.g., TiO2). In such systems, the MM potential can introduce significant overpolarization of species at the QM/MM boundary.15 As a result, the calculation of ionization energies requires self-consistent polarization of the MM region to accurately calculate defect formation energies.15,197,198
The advantages of the QM/MM embedding approach have motivated simulations of ionic solids with relevance for heterogeneous catalysis. Many studies of metal oxides are concerned with the calculation of defect formation energies, particularly oxygen vacancies at the material surface. These charge-donating defects are critical in mediating many catalytic processes, either through enhanced adsorption energies or quantities of charge transfer at critical reaction steps.199Ab initio calculations of the stability and formation energies of oxygen defects can guide design for more efficient heterogeneous catalysts; however, experimental determination for the concentration and formation enthalpies of defects remains a challenge, with disagreements of up to 2 eV (for MgO bulk) existing between experimental and computed values of neutral defects.200,201 The high-level and aperiodic approaches facilitated by QM/MM allow for accurate computational results, and improved understanding of defect engineering.
Using the Kröger–Vink nomenclature, the formation of the oxygen defect, VO, from a generic ionic oxide surface, MO, is expressed as,
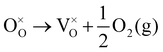 | (11) |
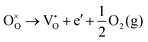 | (12) |
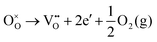 | (13) |
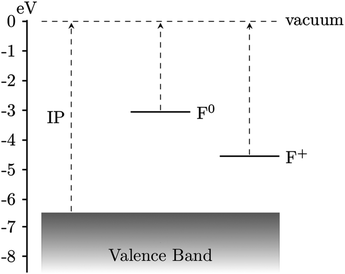 | ||
| Fig. 12 A schematic of the relative energy levels of MgO for the pristine material, and with oxygen vacancies with neutral (F0), and a single charge (F+), with respect to the vacuum level and valence band maximum (VBM). Reprinted from ref. 194 under a Creative Commons license (CC BY 3.0). | ||
Table 3 summarises results from the literature for oxygen vacancy formation in MgO, MnO, and TiO2. As discussed above, QM/MM enables the facile calculation of charged defects at the dilute limit. Here, the defect formation energy (ΔEF) is defined by,
| ΔEF(VqO) = E(VqO) − E(MO) − μO + qεf, | (14) |
| Catalyst | Defect charge state | Bulk QM/MM | Bulk ab initio | Surface QM/MM | Surface ab initio |
|---|---|---|---|---|---|
| a Ref. 200,202 HSE06. Extrapolated to dilute limit. Virtual crystal approximation. VBM corrected with additional term, which references a low lying core 1s state of a bulk-like Mg atom within a slab relative to vacuum to the same 1s state in bulk. b Ref. 200,203 B3LYP/PBE0 (references respectively). c Ref. 200,202 HSE06/PBE0. Extrapolated to dilute limit. Virtual crystal approximation. d Ref. 35 B3LYP. e Ref. 204 PBEsol + U. f Ref. 205 HSE06. Extrapolated to dilute limit. VBM energy band aligned to electrostatic potential of supercell slab referenced to vacuum.6 g Ref. 15 HSE06. Rutile (110). h Ref. 206 sX-LDA Rutile (110); Lany and Zunger correction scheme.6 | |||||
| MgO | F0 | — | 7.04a | 6.46/6.26b | 6.34/6.33c |
| F+ | — | 3.40a | 2.26/2.54b | 2.76/2.56c | |
| F2+ | — | 0.56a | −0.04/−0.30b | 0.55/0.12c | |
| MnO | F0 | 5.88d | 4.92e | 5.88d | — |
| F+ | 3.03d | — | 2.81d | — | |
| F2+ | 0.60d | — | 0.63d | — | |
| TiO2 | F0 | — | 4.4f | 4.8g | 4.53h |
| F+ | — | 2.2f | 1.6g | 2.28h | |
| F2+ | — | −1.4f | −1.6g | −2.05h | |
Comparing the results for oxygen vacancies in MgO, where the periodic approach used an extrapolative scheme to the dilute limit and a virtual-crystal crystal approximation,202 both ab initio and QM/MM approaches produce the same overall trend: ΔEF of the neutral surface defect are highest, and within very close agreement (0.12 eV),203 which is expected due to the charge neutrality of the system. Differences between the QM/MM and ab initio results increase as a function of defect charge, with greater magnitude than the neutral defect (F+: 0.50 eV, F2+: 0.59 eV) and the periodic ab initio results consistently more positive. Some of these discrepancies can be justified by differences between density functionals (B3LYP vs. HSE06), as shown by the variation between HSE06 and PBE0 in periodic DFT (F0: 0.01 eV, F+: 0.20 eV, F2+: 0.43 eV). Fundamentally, however, energies of charged defects in periodic models of surfaces are ill-defined, and require non-trivial corrections, which may be the major cause of the differences; an embedded-cluster QM/MM simulation carried out using the PBE0 density functional, matching the periodic work, shows that cluster models give lower defect formation energy for the same functional (F0: 6.26 eV, F+: 2.54 eV, F2+: −0.30 eV), again with increasing magnitude of difference between aperiodic and periodic models as the charge increases.
Differences in ΔEF are of similar magnitude for the more polarisable TiO2 rutile (110) surface,15,206 ranging from 0.27 to 0.68 eV, though here the relative defect stability with each method changes as a function of charge. Again the caveats with respect to charge-corrections for 2D periodic ab initio simulations apply; furthermore, Berger et al. report errors in their embedded-cluster QM/MM calculations of ±0.3 eV, due to the use of an analytical correction that accounts for the poor representation of the static dielectric constant within the force-field.15 Irrespective, both periodic and QM/MM simulations again show defects with higher charge are more stable, and the formation of the F2+ vacancy is most favourable. These observations open opportunities with dopant engineering, as p-type doping would lower the Fermi level and thus may increase the occurrence of vacancies at the surface,207 which allows for the tuning of catalytic properties for the ionic solid surface. However, it is important to note that charged defects are mutually repulsive and more sensitive to concentration effect compared to the neutral defects.202 As such, in spite of the high thermodynamic stability of F2+ defects in the dilute limit, it is expected that their formation would be disfavoured at higher concentrations.
Overall, embedded-cluster and periodic studies show agreement for neutral defects when taken to the dilute limit, and with appropriate schemes used to correct the spurious interactions; however, the agreement weakens for charged defects, which is likely due to the ill-defined nature of the total energy for charged periodic slab models. The QM/MM embedding approach is advantageous due to the ability to perform the calculations with a single structure, whereas periodic work may use extrapolative schemes, requiring multiple simulations of increasing size. Of course, the accuracy of an embedding approach is dependent on the polarisation response of the MM region, for which a force-field must be parameterised to the ab initio parameters in order to emulate the dielectric properties.15 The requirement of an accurate force-field is undoubtedly a hurdle for adoption, requiring specialist knowledge, and also presents challenges when target observables are incommensurate during fitting (e.g. static dielectric and lattice constants49).
In addition to calculating the oxygen vacancy formation energies, QM/MM embedded-cluster methods have been applied to the surface adsorption of molecules involved with heterogeneous catalysis. For example, the adsorption of CO2 on MgO (100) with QM/MM, using the B3LYP density functional, reveals both charged and uncharged oxygen vacancies radically alter the energetics of adsorption.194 Considering the parallel and perpendicular orientation of CO2 with respect to the surface (Fig. 13 and Table 4), Downing et al. demonstrated that both the neutral and singly-charged vacancy stabilise both bonding modes compared to the pristine surface. The vertical binding mode becomes more favourable compared to the perpendicular, with increased binding strength when there is greater charge transfer between the MgO and the bonding O of CO2. Relaxation of the perpendicular CO2 eliminates the oxygen vacancy, restoring the pristine Mg (100) surface and a CO molecule; thus, design considerations for catalytic transformation directly to hydrocarbons, rather than via Fischer Tropsch, should look to weaken this binding mode, or investigate alternative oxide materials with weaker CO2 binding. In this regard, comparable studies on the MnO (100) surface demonstrate a weaker adsorption of CO2 for the F0 vacancy compared to MgO (−2.61 eV vs. −3.23 eV).35,194 As a result, instead of dissociating to CO and healing the oxygen vacancy, the oxygen of CO2 is incorporated into the vacancy while the molecule adopts a weakened bent configuration.
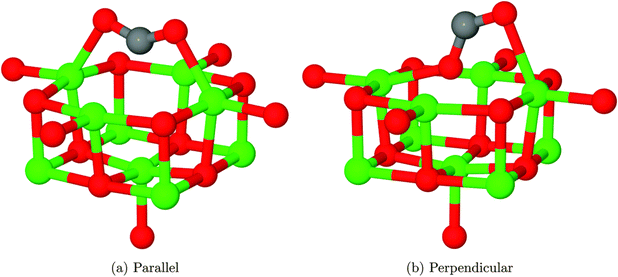 | ||
| Fig. 13 Parallel and perpendicular adsorption modes of CO2 adsorption on an MgO surface with an F0 defect containing two localised electrons. Figure reprinted from ref. 194 under a Creative Commons license (CC BY 3.0). | ||
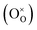 , and those with a neutral-, single-, and double-charged oxygen vacancy. Calculations performed with the B3LYP functional. High-spin and low-spin are denoted as HS and LS, respectively. Reprinted from ref. 35 under a Creative Commons license (CC-BY). All values in eV
, and those with a neutral-, single-, and double-charged oxygen vacancy. Calculations performed with the B3LYP functional. High-spin and low-spin are denoted as HS and LS, respectively. Reprinted from ref. 35 under a Creative Commons license (CC-BY). All values in eV
Complementary QM/MM studies for Mn-doped MgO, again with the B3LYP density functional, demonstrate that extrinsic defects can drastically alter the catalytic properties of the surface. In addition to modifying the adsorption energies (Table 4), the introduction of the Mn-dopant leads to the formation of various spin configurations for the Mn 3d states neighbouring the F+-centre.208 The most significant change in chemical behaviour is the dissociation of CO2 for the perpendicular binding mode, previously only observed for the vertical orientation, with a notable strengthening in binding energy for the low-spin vs. the high-spin state (−0.62 eV vs. −2.00 eV). Mulliken charge analysis reveals that, in the low spin configuration, the previously trapped electron instead transfers to the Mn-centre, causing a reduction from the 2+ to the 1+ state. Further study using other redox-active dopants, differing charge states, and a wider range of adsorbates may reveal further surface reactions activated by the charged vacancies. Furthermore, considering the relative energetics of each defect, we note that the neutral defect is significantly less stable than both the singly and double-charged defect centres across the presented metal oxides. As such, accessing the desired reactivity of a specific defect may require materials engineering which improves the stability of certain defect charges relative to others.
In summary, the QM/MM method has been demonstrated as a powerful technique for representing charged ionic solids and surfaces relevant for heterogeneous catalysis, facilitating the application of high-level theory, and facile investigation of charged defects. However, limitations that prevent widespread uptake are noted, including difficulties in defining a force-field that captures the dielectric and structural properties of highly polarisable materials. Furthermore, due to the difficulty in counting and identifying charged defect sites experimentally, there is a lack of empirical data to validate calculated quantities. While the development of such spectroscopic techniques remains an active area of development,207,209 QM/MM simulations may act as a powerful predictive tool to support and validate these technical advances.
4 Conclusions
In this review, the QM/MM methodology has been demonstrated as a powerful tool for modelling challenging phenomena, structures and reactions in heterogeneous catalysis. The most consistent advantage observed is the reduction in the size of the quantum mechanical calculation, which allows for the use of more computationally expensive (and accurate) density functionals and quantum chemistry methods. Alternatively, by reducing the cost of individual energy evaluations, transition state searches and geometry optimisations, QM/MM can complete a greater number of simulations within the same time-frame as a standard QM simulation. Therefore, studies may be designed to cover a greater range of reactions or structures without compromising accuracy or introducing infeasible computational cost. As a result, calculations of binding energies relevant to catalysis better confer with experiment, and provide a more accurate representation of catalytic processes.A growing body of literature is using QM/MM for configurational sampling, particularly focusing on the solvation environment within the explicit solvent model.9,11,210 As many heterogeneous catalytic processes occur in the aqueous environment, the application to solvation is a promising direction of study that will enable a more realistic computational representation of the reaction environment. Furthermore, the move towards free energy calculations for adsorption and reaction energetics is a positive step towards better predictive studies of reaction mechanisms. We hope these efforts will facilitate the calculation of equilibrium constants and kinetic parameters with far better accuracy, delivering quantitative agreement with experiment that can drive forward computational catalytic design.
In addition, the embedded-cluster QM/MM framework presents certain advantages over periodic calculations when modelling charged systems. As shown for charged defects in ionic solids, embedding calculations allow for a natural method of representing the charged defect, while including the long range polarisation response of the extended system. As a result, quantities such as the defect formation energy can be calculated at the dilute limit without the need for extrapolative/correction techniques necessary in periodic models. However, for both pristine and defective materials, the QM/MM approach suffers from the artificial confinement of charge, especially in the case of more diffuse states.211 Although a posteriori corrections exist for reducing the errors introduced,34,211 the ability to accurately model diffuse charge states warrants further investigation and development.
A point of concern is the more complex calculation set-up for QM/MM simulations, especially compared to QM simulations; currently, the prospective user needs to be knowledgeable in QM, MM, and the coupling approach used. In addition to the standardisation of interfaces, which are objectives of some specific QM/MM software projects,77 the existing infrastructures require the user to specify the QM region and converge force-field parameters on a structure-by-structure basis. Furthermore, these force-fields require the structural, energetic, and possibly dielectric properties of the classical region to match that of the bulk material, in order to prevent calculation artefacts occurring. These additional input parameters add a barrier to uptake of the embedding methodology, when compared to the more black box nature of pure DFT. To ensure the widespread adoption of QM/MM methods, development should focus on automatically generating these inputs. In particular, any prospective automated QM/MM workflow should optimise both the partitioning of the QM/MM regions and force-field parameters, either through 'on-the-fly' generation or the composition of sensible defaults for a range of systems. The outcome would be an overall lower barrier to entry for new users.
There are also undoubtedly opportunities for the introduction of data-driven protocols with regards model configuration, and particularly representation of the embedding environment, which should be empowered by recent developments in the application of machine-learning across other computational chemistry fields. In particular, the implementation of Δ-machine learning into QM/MM has shown low-cost, semi-empirical methods such as Tight Binding DFT (TB-DFT) coupled with data-driven corrections may yield energetics comparable to ab initio DFT.56,57,212–214 Application of these ML approaches to representation of the surrogate energy landscapes could drastically improve the computational tractability of QM/MM methods in heterogeneous catalysis, allowing for dynamic simulations in the condensed phase with DFT accuracy. Adoption of these approaches undoubtedly presents exciting future opportunities for multiscale modelling.
Author contributions
The article was conceptualised, drafted and critical revised by all authors, and all have provided approval of publication.Conflicts of interest
There are no conflicts to declare.Acknowledgements
OTB gratefully appreciates financial support from the Coleg Cymraeg Cenedlaethol scholarship programme. GAB, PVS, and AJL gratefully appreciate funding by the UKRI Future Leaders Fellowship program (MR/T018372/1). The authors gratefully acknowledge Oscar Van Vuren for support with proofreading and provision of feedback.Notes and references
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS
.
- P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schäfer and C. Lennartz, THEOCHEM, 2003, 632, 1–28 CrossRef CAS
.
- C. E. Tzeliou, M. A. Mermigki and D. Tzeli, Molecules, 2022, 27, 2660 CrossRef CAS
.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS
.
- N. Chaudhary, A. Hensley, G. Collinge, Y. Wang and J.-S. McEwen, J. Phys. Chem. C, 2020, 124, 356–362 CrossRef CAS
.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef
.
- S. A. F. Nastase, A. J. OMalley, C. R. A. Catlow and A. J. Logsdail, Phys. Chem. Chem. Phys., 2019, 21, 2639–2650 RSC
.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS
.
- P. Clabaut, B. Schweitzer, A. W. Götz, C. Michel and S. N. Steinmann, J. Chem. Theory Comput., 2020, 16, 6539–6549 CrossRef CAS
.
- T. P. Straatsma, H. J. C. Berendsen and J. P. M. Postma, J. Chem. Phys., 1986, 85, 6720–6727 CrossRef CAS
.
- M. Faheem and A. Heyden, J. Chem. Theory Comput., 2014, 10, 3354–3368 CrossRef CAS
.
- T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery, K. Morokuma and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 815–826 CrossRef CAS
.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS
.
- L. Cao and U. Ryde, Front. Chem., 2018, 6, 89 CrossRef
.
- D. Berger, H. Oberhofer and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075308 CrossRef
.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90–103 CrossRef
.
- S. Caprasecca, C. Curutchet and B. Mennucci, J. Comput. Chem., 2012, 8, 4462–4473 CAS
.
- K. Nam, J. Gao and D. M. York, J. Chem. Theory Comput., 2005, 1, 2–13 CrossRef CAS
.
- J. P. Pederson and J. G. McDaniel, J. Chem. Phys., 2022, 156, 174105 CrossRef CAS
.
- J. Sauer and M. Sierka, J. Comput. Chem., 2000, 21, 1470–1493 CrossRef CAS
.
- C. J. Bodenschatz, S. Sarupria and R. B. Getman, J. Phys. Chem. C, 2015, 119, 13642–13651 CrossRef CAS
.
- S. N. Steinmann, P. Sautet and C. Michel, Phys. Chem. Chem. Phys., 2016, 18, 31850–31861 RSC
.
- M. Leslie and N. J. Gillan, J. Phys. C: Solid State Phys., 1985, 18, 973–982 CrossRef CAS
.
- A. Walsh, C. R. A. Catlow, M. Miskufova and A. A. Sokol, J. Phys.: Condens. Matter, 2011, 23, 334217 CrossRef
.
- J. Ihm, A. Zunger and M. L. Cohen, J. Phys. C: Solid State Phys., 1979, 12, 4409–4422 CrossRef CAS
.
- L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 7412–7414 CrossRef CAS
.
- C. A. Rozzi, D. Varsano, A. Marini, E. K. U. Gross and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205119 CrossRef
.
- M. Chagas da Silva, M. Lorke, B. Aradi, M. Farzalipour Tabriz, T. Frauenheim, A. Rubio, D. Rocca and P. Deák, Phys. Rev. Lett., 2021, 126, 076401 CrossRef CAS
.
- H.-P. Komsa, N. Berseneva, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. X, 2014, 4, 031044 CAS
.
- A. Walsh, npj Comput. Mater., 2021, 7, 1–3 CrossRef
.
- A. A. Sokol, S. T. Bromley, S. A. French, C. R. A. Catlow and P. Sherwood, Int. J. Quantum Chem., 2004, 99, 695–712 CrossRef CAS
.
- W. Jost, J. Chem. Phys., 1933, 1, 466–475 CrossRef CAS
.
- M. Casanova-Páez and E. Menéndez-Proupin, J. Phys.: Conf. Ser., 2018, 1043, 012043 CrossRef
.
- Z. Xie, Y. Sui, J. Buckeridge, C. R. A. Catlow, T. W. Keal, P. Sherwood, A. Walsh, M. R. Farrow, D. O. Scanlon, S. M. Woodley and A. A. Sokol, J. Phys. D: Appl. Phys., 2019, 52, 335104 CrossRef CAS
.
- A. J. Logsdail, C. A. Downing, T. W. Keal, P. Sherwood, A. A. Sokol and C. R. A. Catlow, J. Phys. Chem. C, 2019, 123, 8133–8144 CrossRef CAS
.
- L. W. Chung, H. Hirao, X. Li and K. Morokuma, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 327–350 CAS
.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS
.
- D. Berger, A. J. Logsdail, H. Oberhofer, M. R. Farrow, C. R. A. Catlow, P. Sherwood, A. A. Sokol, V. Blum and K. Reuter, J. Chem. Phys., 2014, 141, 024105 CrossRef
.
- Y. Zhang, T.-S. Lee and W. Yang, J. Chem. Phys., 1999, 110, 46–54 CrossRef CAS
.
- Y. Zhang, J. Chem. Phys., 2005, 122, 024114 CrossRef
.
- Y. Zhao, C. Wang, Q. Peng and G. Lu, Comput. Mater. Sci., 2010, 50, 714–719 CrossRef CAS
.
- T. Jiang, S. Simko and R. E. Bulo, J. Chem. Theory Comput., 2018, 14, 3943–3954 CrossRef CAS
.
- H. C. Watanabe and Q. Cui, J. Chem. Theory Comput., 2019, 15, 3917–3928 CrossRef CAS
.
- J. Rey, S. Blanck, P. Clabaut, S. Loehlé, S. N. Steinmann and C. Michel, J. Phys. Chem. B, 2021, 125, 10843–10853 CrossRef CAS
.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS
.
- R. M. Betz and R. C. Walker, J. Comput. Chem., 2015, 36, 79–87 CrossRef CAS
.
- P. M. Zimmerman, M. Head-Gordon and A. T. Bell, J. Chem. Theory Comput., 2011, 7, 1695–1703 CrossRef CAS
.
- Y.-P. Li, J. Gomes, S. Mallikarjun Sharada, A. T. Bell and M. Head-Gordon, J. Phys. Chem. C, 2015, 119, 1840–1850 CrossRef CAS
.
- C. R. A. Catlow, C. M. Freeman, M. S. Islam, R. A. Jackson, M. Leslie and S. M. Tomlinson, Philos. Mag. A, 1988, 58, 123–141 CrossRef CAS
.
- E. Lambros, F. Lipparini, G. A. Cisneros and F. Paesani, J. Chem. Theory Comput., 2020, 16, 7462–7472 CrossRef CAS
.
- J. Nochebuena, S. Naseem-Khan and G. A. Cisneros, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1515 CAS
.
- A. Hermann, R. P. Krawczyk, M. Lein, P. Schwerdtfeger, I. P. Hamilton and J. J. P. Stewart, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 013202 CrossRef
.
- Y.-J. Zhang, A. Khorshidi, G. Kastlunger and A. A. Peterson, J. Chem. Phys., 2018, 148, 241740 CrossRef
.
- Y. Yang, O. A. Jiménez-Negrón and J. R. Kitchin, J. Chem. Phys., 2021, 154, 234704 CrossRef CAS
.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS
.
- L. Shen, J. Wu and W. Yang, J. Chem. Theory Comput., 2016, 12, 4934–4946 CrossRef CAS
.
- L. Shen and W. Yang, J. Chem. Theory Comput., 2018, 14, 1442–1455 CrossRef CAS
.
- S. A. F. Nastase, A. J. Logsdail and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2021, 23, 17634–17644 RSC
.
- J. Sauer, Acc. Chem. Res., 2019, 52, 3502–3510 CrossRef CAS
.
- M. Kick and H. Oberhofer, J. Chem. Phys., 2019, 151, 184114 CrossRef CAS
.
- B. X. Shi, V. Kapil, A. Zen, J. Chen, A. Alavi and A. Michaelides, J. Chem. Phys., 2022, 156, 124704 CrossRef CAS
.
- S. Roßbach and C. Ochsenfeld, J. Chem. Theory Comput., 2017, 13, 1102–1107 CrossRef
.
- D. E. P. Vanpoucke, J. Oláh, F. De Proft, V. Van Speybroeck and G. Roos, J. Chem. Inf. Model., 2015, 55, 564–571 CrossRef CAS
.
- D. Flaig, M. Beer and C. Ochsenfeld, J. Chem. Theory Comput., 2012, 8, 2260–2271 CrossRef CAS PubMed
.
- M. Karelina and H. J. Kulik, J. Chem. Theory Comput., 2017, 13, 563–576 CrossRef CAS
.
- A. Dittmer, R. Izsák, F. Neese and D. Maganas, Inorg. Chem., 2019, 58, 9303–9315 CrossRef CAS
.
- M. Zheng and M. P. Waller, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 369–385 CAS
.
- A. W. Duster, C.-H. Wang, C. M. Garza, D. E. Miller and H. Lin, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1310 Search PubMed
.
- T. Kerdcharoen, K. R. Liedl and B. M. Rode, Chem. Phys., 1996, 211, 313–323 CrossRef CAS
.
- A. Heyden, H. Lin and D. G. Truhlar, J. Phys. Chem. B, 2007, 111, 2231–2241 CrossRef CAS
.
- T. Kerdcharoen and K. Morokuma, Chem. Phys. Lett., 2002, 355, 257–262 CrossRef CAS
.
- H. C. Watanabe, T. Kubař and M. Elstner, J. Chem. Theory Comput., 2014, 10, 4242–4252 CrossRef CAS
.
- Z.-h Yang, Phys. Chem. Chem. Phys., 2020, 22, 17987–17998 RSC
.
- B. Lier, P. Poliak, P. Marquetand, J. Westermayr and C. Oostenbrink, J. Phys. Chem. Lett., 2022, 13, 3812–3818 CrossRef CAS
.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef
.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef
.
- Y. Lu, M. R. Farrow, P. Fayon, A. J. Logsdail, A. A. Sokol, C. R. A. Catlow, P. Sherwood and T. W. Keal, J. Chem. Theory Comput., 2019, 15, 1317–1328 CrossRef CAS
.
- H. Gökcan, E. A. Vázquez-Montelongo and G. A. Cisneros, J. Chem. Theory Comput., 2019, 15, 3056–3065 CrossRef
.
- M. Rivera, M. Dommett, A. Sidat, W. Rahim and R. Crespo-Otero, J. Comput. Chem., 2020, 41, 1045–1058 CrossRef CAS
.
- M. Shiga, M. Tachikawa and S. Miura, J. Chem. Phys., 2001, 115, 9149–9159 CrossRef CAS
.
-
D. Case, H. M. Aktulga, K. Belfon, I. Ben-Shalom, J. Berryman, S. Brozell, D. Cerutti, T. Cheatham, G. A. Cisneros, V. Cruzeiro, T. Darden, R. Duke, G. Giambasu, M. Gilson, H. Gohlke, A. Götz, R. Harris, S. Izadi, S. Izmailov and P. Kollman, Amber2022, University of California, San Francisco, 2022, https://www.ambermd.org Search PubMed
.
- B. Brooks, C. Brooks, A. MacKerell, L. Nilsson, R. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. Pastor, C. Post, J. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef
.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918 RSC
.
- ForceField 2022.1, SCM, Theoretical Chemistry, Vrike Universiteit, Amsterdam, Netherlands, https://www.scm.com/.
-
W. L. Jorgensen, BOSS (4.9), Yale University, New Haven CT, U.S.A., https://www.zarbi.chem.yale.edu/software.html Search PubMed
.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS
.
- J. A. Rackers, Z. Wang, C. Lu, M. L. Laury, L. Lagardère, M. J. Schnieders, J.-P. Piquemal, P. Ren and J. W. Ponder, J. Chem. Theory Comput., 2018, 14, 5273–5289 CrossRef CAS
.
- M. C. R. Melo, R. C. Bernardi, T. Rudack, M. Scheurer, C. Riplinger, J. C. Phillips, J. D. C. Maia, G. B. Rocha, J. V. Ribeiro, J. E. Stone, F. Neese, K. Schulten and Z. Luthey-Schulten, Nat. Methods, 2018, 15, 351–354 CrossRef CAS
.
- ADF 2022.1, SCM, Theoretical Chemistry, Vrike Universiteit, Amsterdam, Netherlands, https://www.scm.com/.
-
M. Shiga, PIMD (2.5.0), Japan Atomic Energy Agency, Tokyo, Japan, 2022, https://www.ccse.jaea.go.jp/software/PIMD/index.en.html Search PubMed
.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed
.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef
.
- X. Gonze, B. Amadon, G. Antonius, F. Arnardi, L. Baguet, J.-M. Beuken, J. Bieder, F. Bottin, J. Bouchet, E. Bousquet, N. Brouwer, F. Bruneval, G. Brunin, T. Cavignac, J.-B. Charraud, W. Chen, M. Côté, S. Cottenier, J. Denier, G. Geneste, P. Ghosez, M. Giantomassi, Y. Gillet, O. Gingras, D. R. Hamann, G. Hautier, X. He, N. Helbig, N. Holzwarth, Y. Jia, F. Jollet, W. Lafargue-Dit-Hauret, K. Lejaeghere, M. A. L. Marques, A. Martin, C. Martins, H. P. C. Miranda, F. Naccarato, K. Persson, G. Petretto, V. Planes, Y. Pouillon, S. Prokhorenko, F. Ricci, G.-M. Rignanese, A. H. Romero, M. M. Schmitt, M. Torrent, M. J. van Setten, B. Van Troeye, M. J. Verstraete, G. Zérah and J. W. Zwanziger, Comput. Phys. Commun., 2020, 248, 107042 CrossRef CAS
.
- T. Laino, F. Mohamed, A. Laio and M. Parrinello, J. Chem. Theory Comput., 2005, 1, 1176–1184 CrossRef CAS
.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, Gaussian 16, Revision C.01, 2019 Search PubMed
.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS
.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS
.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS
.
- C. Ma, L. Martin-Samos, S. Fabris, A. Laio and S. Piccinin, Comput. Phys. Commun., 2015, 195, 191–198 CrossRef CAS
.
- TURBOMOLE (7.2), University of Karlsruhe and Forschingzentrum, Kalsruhe GmbH, Germany, 2017, https://www.turbomole.com.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102 CrossRef
.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS
.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 CAS
.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS
.
- H. L. Woodcock III, M. Hodošček, A. T. B. Gilbert, P. M. W. Gill, H. F. Schaefer III and B. R. Brooks, J. Comput. Chem., 2007, 28, 1485–1502 CrossRef
.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. K. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS
.
- B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrica, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-Z. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101 CrossRef CAS
.
- V. W. D. Cruzeiro, M. Manathunga, K. M. J. Merz and A. W. Götz, J. Chem. Inf. Model., 2021, 61, 2109–2115 CrossRef CAS
.
- S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, C. M. Isborn, S. I. L. Kokkila-Schumacher, X. Li, F. Liu, N. Luehr, J. W. Snyder Jr., C. Song, A. V. Titov, I. S. Ufimtsev, L.-P. Wang and T. J. Martínez, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1494 CAS
.
- N. S. Gould, S. Li, H. J. Cho, H. Landfield, S. Caratzoulas, D. Vlachos, P. Bai and B. Xu, Nat. Commun., 2020, 11, 1060 CrossRef CAS PubMed
.
- N. Singh, U. Sanyal, J. L. Fulton, O. Y. Gutiérrez, J. A. Lercher and C. T. Campbell, ACS Catal., 2019, 9, 6869–6881 CrossRef CAS
.
- T. J. Schwartz and J. Q. Bond, Chem. Commun., 2017, 53, 8148–8151 RSC
.
- J. J. Varghese and S. H. Mushrif, React. Chem. Eng., 2019, 4, 165–206 RSC
.
- C. Michel, J. Zaffran, A. M. Ruppert, J. Matras-Michalska, M. Jędrzejczyk, J. Grams and P. Sautet, Chem. Commun., 2014, 50, 12450–12453 RSC
.
- A. Groß and S. Sakong, Chem. Rev., 2022, 122, 10746–10776 CrossRef
.
- A. M. Burow, M. Sierka, J. Döbler and J. Sauer, J. Chem. Phys., 2009, 130, 174710 CrossRef
.
- H. Hu, Z. Lu and W. Yang, J. Chem. Theory Comput., 2007, 3, 390–406 CrossRef CAS
.
- M. Saleheen, M. Zare, M. Faheem and A. Heyden, J. Phys. Chem. C, 2019, 123, 19052–19065 CrossRef CAS
.
- M. Zare, M. Saleheen, S. K. Kundu and A. Heyden, Commun. Chem., 2020, 3, 1–10 CrossRef
.
- R. Rousseau, V. De Renzi, R. Mazzarello, D. Marchetto, R. Biagi, S. Scandolo and U. del Pennino, J. Phys. Chem. B, 2006, 110, 10862–10872 CrossRef CAS
.
- S. N. Steinmann, R. Ferreira De Morais, A. W. Götz, P. Fleurat-Lessard, M. Iannuzzi, P. Sautet and C. Michel, J. Chem. Theory Comput., 2018, 14, 3238–3251 CrossRef CAS
.
- P. Clabaut, P. Fleurat-Lessard, C. Michel and S. N. Steinmann, J. Chem. Theory Comput., 2020, 16, 4565–4578 CrossRef CAS
.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS
.
- R. Réocreux, C. Michel, P. Fleurat-Lessard, P. Sautet and S. N. Steinmann, J. Phys. Chem. C, 2019, 123, 28828–28835 CrossRef
.
- J. Akinola and N. Singh, J. Appl. Electrochem., 2021, 51, 37–50 CrossRef CAS
.
- S. J. Carey, W. Zhao, Z. Mao and C. T. Campbell, J. Phys. Chem. C, 2019, 123, 7627–7632 CrossRef CAS
.
- H.-K. Lim, H. Lee and H. Kim, J. Chem. Theory Comput., 2016, 12, 5088–5099 CrossRef CAS
.
- S.-T. Lin, M. Blanco and W. A. Goddard, J. Chem. Phys., 2003, 119, 11792–11805 CrossRef CAS
.
- S.-T. Lin, P. K. Maiti and W. A. I. Goddard, J. Phys. Chem. B, 2010, 114, 8191–8198 CrossRef CAS
.
- S. Gim, K. J. Cho, H.-K. Lim and H. Kim, Sci. Rep., 2019, 9, 14805 CrossRef
.
- K. J. Cho, S. Gim, H.-K. Lim, C. Kim and H. Kim, J. Phys. Chem. C, 2020, 124, 11392–11400 CrossRef CAS
.
- S. Gim, H.-K. Lim and H. Kim, J. Phys. Chem. Lett., 2018, 9, 1750–1758 CrossRef CAS
.
- I. Morcos, J. Chem. Phys., 1972, 57, 1801–1802 CrossRef CAS
.
- H. Ogasawara, J. Yoshinobu and M. Kawai, Chem. Phys. Lett., 1994, 231, 188–192 CrossRef CAS
.
- J. R. Rumptz and C. T. Campbell, ACS Catal., 2019, 9, 11819–11825 CrossRef CAS
.
- J. L. Daschbach, B. M. Peden, R. S. Smith and B. D. Kay, J. Chem. Phys., 2004, 120, 1516–1523 CrossRef CAS
.
- A. Corma, J. Catal., 2003, 216, 298–312 CrossRef CAS
.
- A. Corma, Chem. Rev., 1995, 95, 559–614 CrossRef CAS
.
- K. Wilson, Appl. Organomet. Chem., 2007, 21, 1002 CrossRef CAS
.
- M. Boronat and A. Corma, ACS Catal., 2019, 9, 1539–1548 CrossRef CAS
.
- A. A. Sokol, C. R. A. Catlow, J. M. Garcés and A. Kuperman, Adv. Mater., 2000, 12, 1801–1805 CrossRef CAS
.
- E. Derouane, J. Védrine, R. R. Pinto, P. Borges, L. Costa, M. Lemos, F. Lemos and F. R. Ribeiro, Catal. Rev., 2013, 55, 454–515 CrossRef CAS
.
- D. Padovan, A. Al-Nayili and C. Hammond, Green Chem., 2017, 19, 2846–2854 RSC
.
- B. Hernández, J. Iglesias, G. Morales, M. Paniagua, C. López-Aguado, J. L. García Fierro, P. Wolf, I. Hermans and J. A. Melero, Green Chem., 2016, 18, 5777–5781 RSC
.
- R. Otomo, T. Yokoi, J. N. Kondo and T. Tatsumi, Appl. Catal., A, 2014, 470, 318–326 CrossRef CAS
.
- G. Li, L. Gao, Z. Sheng, Y. Zhan, C. Zhang, J. Ju, Y. Zhang and Y. Tang, Catal. Sci. Technol., 2019, 9, 4055–4065 RSC
.
- J. T. Fermann, T. Moniz, O. Kiowski, T. J. McIntire, S. M. Auerbach, T. Vreven and M. J. Frisch, J. Chem. Theory Comput., 2005, 1, 1232–1239 CrossRef CAS
.
- A. Buin, J. Ma, Y. Huang, S. Consta and Z. Hui, J. Phys. Chem. C, 2012, 116, 8608–8618 CrossRef CAS
.
- K. Bobuatong, J. Sirijaraensre, P. Khongprachaab, P. Pan and J. Limtrakul, Technical Proceedings of the 2009 NSTI Nanotechnology Conference and Expo, NSTI-Nanotech 2009, 2009, vol. 3, pp. 292-295.
- S. A. French, A. A. Sokol, S. T. Bromley, C. R. A. Catlow, S. C. Rogers, F. King and P. Sherwood, Angew. Chem., Int. Ed, 2001, 40, 4437–4440 CrossRef CAS
.
- R. C. Deka and K. Hirao, J. Mol. Catal. A: Chem., 2002, 181, 275–282 CrossRef CAS
.
-
L. A. Clark, M. Sierka and J. Sauer, in Studies in Surface Science and Catalysis, ed. R. Aiello, G. Giordano and F. Testa, Elsevier, 2002, vol. 142 of Impact of Zeolites and other Porous Materials on the new Technologies at the Beginning of the New Millennium, pp. 643–649 Search PubMed
.
- C. Chang, J. Catal., 1977, 47, 249–259 CrossRef CAS
.
-
C. Maiden, Studies in Surface Science and Catalysis, Elsevier, 1988, vol. 36, pp. 1–16 Search PubMed
.
- A. J. O'Malley, A. J. Logsdail, A. A. Sokol and C. R. A. Catlow, Faraday Discuss., 2016, 188, 235–255 RSC
.
- F. Haase and J. Sauer, Microporous Mesoporous Mater., 2000, 35–36, 379–385 CrossRef CAS
.
- S. A. F. Nastase, C. R. A. Catlow and A. J. Logsdail, Phys. Chem. Chem. Phys., 2021, 23, 2088–2096 RSC
.
- S. Svelle, C. Tuma, X. Rozanska, T. Kerber and J. Sauer, J. Am. Chem. Soc., 2009, 131, 816–825 CrossRef CAS
.
- T. Omojola, A. J. Logsdail, A. C. van Veen and S. A. F. Nastase, Phys. Chem. Chem. Phys., 2021, 23, 21437–21469 RSC
.
- S. A. F. Nastase, A. J. Logsdail and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2021, 23, 17634–17644 RSC
.
- U. Eichler, C. M. Kölmel and J. Sauer, J. Comput. Chem., 1997, 18, 463–477 CrossRef CAS
.
- M. Brändle and J. Sauer, J. Am. Chem. Soc., 1998, 120, 1556–1570 CrossRef
.
- V. Nieminen, M. Sierka, D. Murzin and J. Sauer, J. Catal., 2005, 231, 393–404 CrossRef CAS
.
- R. Bermejo-Deval, R. S. Assary, E. Nikolla, M. Moliner, Y. Román-Leshkov, S.-J. Hwang, A. Palsdottir, D. Silverman, R. F. Lobo, L. A. Curtiss and M. E. Davis, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9727–9732 CrossRef CAS
.
- B. D. Montejo-Valencia and M. C. Curet-Arana, J. Phys. Chem. C, 2015, 119, 4148–4157 CrossRef CAS
.
- M. Moliner and A. Corma, Microporous Mesoporous Mater., 2014, 189, 31–40 CrossRef CAS
.
- Y. Shiota, K. Suzuki and K. Yoshizawa, Organometallics, 2006, 25, 3118–3123 CrossRef CAS
.
- T. Archipov, S. Santra, A. B. Ene, H. Stoll, G. Rauhut and E. Roduner, J. Phys. Chem. C, 2009, 113, 4107–4116 CrossRef CAS
.
- S. Morpurgo, J. Comput. Chem., 2015, 36, 660–669 CrossRef CAS
.
- H. A. Aljama, M. Head-Gordon and A. T. Bell, Nat. Commun., 2022, 13, 2910 CrossRef CAS
.
- P. Siani, S. Motta, L. Ferraro, A. O. Dohn and C. Di Valentin, J. Chem. Theory Comput., 2020, 16, 6560–6574 CrossRef CAS
.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS
.
- S. Naserifar, Y. Chen, S. Kwon, H. Xiao and W. A. Goddard, Matter, 2021, 4, 195–216 CrossRef CAS
.
- S. Naserifar, D. J. Brooks, W. A. Goddard and V. Cvicek, J. Chem. Phys., 2017, 146, 124117 CrossRef
.
- Y. Chen, Y. Huang, T. Cheng and W. A. Goddard, J. Am. Chem. Soc., 2019, 141, 11651–11657 CrossRef CAS
.
- X. Zhang, G. Lu and W. A. Curtin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 054113 CrossRef
.
- M. S. Daw and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443–6453 CrossRef CAS
.
- T. A. Wesolowski, S. Shedge and X. Zhou, Chem. Rev., 2015, 115, 5891–5928 CrossRef CAS
.
- X. Zhang and G. Lu, J. Phys. Chem. Lett., 2014, 5, 292–297 CrossRef CAS
.
- Z. Chen, X. Zhang and G. Lu, J. Phys. Chem. C, 2017, 121, 1964–1973 CrossRef CAS
.
- S. Zhang, X. Zhang, G. Jiang, H. Zhu, S. Guo, D. Su, G. Lu and S. Sun, J. Am. Chem. Soc., 2014, 136, 7734–7739 CrossRef CAS
.
- V. P. Ananikov, D. G. Musaev and K. Morokuma, J. Mol. Catal. A: Chem., 2010, 324, 104–119 CrossRef CAS
.
- F. Hajareh Haghighi, H. Hadadzadeh, H. Farrokhpour, Z. Amirghofran and S. Z. Mirahmadi-Zare, J. Phys. Chem. C, 2018, 122, 8680–8692 CrossRef CAS
.
- H. Farrokhpour, M. Ghandehari and K. Eskandari, Appl. Surf. Sci., 2018, 457, 712–725 CrossRef CAS
.
- J. C. Védrine, ChemSusChem, 2019, 12, 577–588 CrossRef
.
- Q. Guo, C. Zhou, Z. Ma and X. Yang, Adv. Mater., 2019, 31, 1901997 CrossRef CAS
.
- A. H. Chowdhury, P. Bhanja, N. Salam, A. Bhaumik and S. M. Islam, Mol. Catal., 2018, 450, 46–54 CrossRef CAS
.
- Q. Wang, J. Luo, Z. Zhong and A. Borgna, Energy Environ. Sci., 2010, 4, 42–55 RSC
.
- S. Wang, S. Yan, X. Ma and J. Gong, Energy Environ. Sci., 2011, 4, 3805–3819 RSC
.
- H. Pang, A. Sun, H. Xu and G. Xiao, Chem. Eng. J., 2021, 425, 130675 CrossRef CAS
.
- C. A. Downing, A. A. Sokol and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2013, 16, 184–195 RSC
.
- X. Du, X. Gao, W. Hu, J. Yu, Z. Luo and K. Cen, J. Phys. Chem. C, 2014, 118, 13617–13622 CrossRef CAS
.
- Q. Hou, J. Buckeridge, A. Walsh, Z. Xie, Y. Lu, T. W. Keal, J. Guan, S. M. Woodley, C. R. A. Catlow and A. A. Sokol, Front. Chem., 2021, 9, 780935 CrossRef CAS PubMed
.
- V. A. Nasluzov, E. A. Ivanova, A. M. Shor, G. N. Vayssilov, U. Birkenheuer and N. Rösch, J. Phys. Chem. B, 2003, 107, 2228–2241 CrossRef CAS
.
- P. Reinhardt, M. Causà, C. M. Marian and B. A. He\S, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 14812–14821 CrossRef CAS
.
- G. Zhuang, Y. Chen, Z. Zhuang, Y. Yu and J. Yu, Sci. China: Mater., 2020, 63, 2089–2118 CrossRef CAS
.
- N. A. Richter, PhD thesis, Technische Universität Berlin, 2013.
- L. A. Kappers, R. L. Kroes and E. B. Hensley, Phys. Rev. B: Condens. Matter Mater. Phys., 1970, 1, 4151–4157 CrossRef
.
- N. A. Richter, S. Sicolo, S. V. Levchenko, J. Sauer and M. Scheffler, Phys. Rev. Lett., 2013, 111, 045502 CrossRef
.
- P. V. Sushko, A. L. Shluger and C. R. A. Catlow, Surf. Sci., 2000, 450, 153–170 CrossRef CAS
.
- U. Aschauer, N. Vonrüti and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 054103 CrossRef
.
- A. Janotti, J. B. Varley, P. Rinke, N. Umezawa, G. Kresse and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085212 CrossRef
.
- H. Li, Y. Guo and J. Robertson, J. Phys. C: Solid State Phys., 2015, 119, 18160–18166 CAS
.
- G. Pacchioni and H. Freund, Chem. Rev., 2013, 113, 4035–4072 CrossRef CAS
.
- A. J. Logsdail, C. A. Downing, T. W. Keal, P. Sherwood, A. A. Sokol and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2016, 18, 28648–28660 RSC
.
- Y. Lu, F. Zheng, Q. Lan, M. Schnedler, P. Ebert and R. E. Dunin-Borkowski, Nano Lett., 2022, 22, 6936–6941 CrossRef CAS
.
- D. Liang, J. Hong, D. Fang, J. W. Bennett, S. E. Mason, R. J. Hamers and Q. Cui, Phys. Chem. Chem. Phys., 2018, 20, 3349–3362 RSC
.
- Z. Xie, Y. Sui, J. Buckeridge, C. R. A. Catlow, T. W. Keal, P. Sherwood, A. Walsh, D. O. Scanlon, S. M. Woodley and A. A. Sokol, Phys. Status Solidi A, 2017, 214, 1600445 CrossRef
.
- P. O. Dral, O. A. von Lilienfeld and W. Thiel, J. Chem. Theory Comput., 2015, 11, 2120–2125 CrossRef CAS
.
- L. Böselt, M. Thürlemann and S. Riniker, J. Chem. Theory Comput., 2021, 17, 2641–2658 CrossRef
.
- X. Pan, J. Yang, R. Van, E. Epifanovsky, J. Ho, J. Huang, J. Pu, Y. Mei, K. Nam and Y. Shao, J. Chem. Theory Comput., 2021, 17, 5745–5758 CrossRef CAS
.
| This journal is © the Owner Societies 2023 |